EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 648 (April 2021) A&A, 648 (2021) A76 Full HTML
Free Access
Issue
A&A
Volume 648, April 2021
Article Number A76
Number of page(s) 6
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202140428
Published online 15 April 2021

© ESO 2021

1 Introduction

Hydroxyl (OH) is a key radical in interstellar oxygen chemistry. The OH radical is expected to be particularly abundant in high-temperature environments driven by the presence of stellar ultraviolet (UV) photons, called the photon-dominated regions (PDRs; e.g., Sternberg & Dalgarno 1995; Hollenbach et al. 2009), and in shocked gas (i.e., Elitzur & de Jong 1978; Hollenbach & McKee 1979; Draine et al. 1983; Kaufman & Neufeld 1996). In these environments the gas attains the high temperatures (>300 K) needed to make the endothermic neutral-neutral reaction 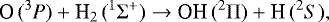O (3P)+H2 (1Σ+)→OH (2Π)+H (2S),\begin{equation*}\textrm{O}\,(^3{{P}}) + \textrm{H}_2\,(^1\Sigma^+) \rightarrow {\textrm{OH}}\,(^2\Pi) + \textrm{H}\,(^2{{S}}) ,\end{equation*}(1)

an important source of OH. Reaction (1) is thought to drive the formation of the OH observed in diffuse clouds (e.g., Neufeld et al. 2002; Godard et al. 2014), protostellar outflows (e.g., Melnick et al. 1990; Wampfler et al. 2013; Goicoechea et al. 2015), massive winds from extragalactic nuclei (e.g., Sturm et al. 2011; González-Alfonso et al. 2012), the UV-illuminated rims of molecular clouds (Goicoechea et al. 2011; Parikka et al. 2017), and the upper layers of protoplanetary disks (Mandell et al. 2008; Fedele et al. 2013). In addition, H2O photodissociation contributes to the production of OH (see Tabone et al. 2021) in environments that host high water vapor abundances and intense far-UV (FUV; photon energy <13.6 eV) radiation fluxes (e.g., Bergin et al. 2003; Tappe et al. 2008; Karska et al. 2013).

Many hydrogen abstraction reactions X + H2 → XH + X (e.g., with X = O, C+, C, S+, and S) are very endothermic and/or have sizable energy barriers (see, e.g., Gerin et al. 2016). Hence, the formation of the radical XH through thisgas-phase route is expected to be very slow in cold gas interstellar conditions. However, strongly illuminated PDRs such as the Orion Bar (an edge-on rim of the Orion molecular cloud; e.g., Tielens et al. 1993; Goicoechea et al. 2016) are characterized by both warm gas temperatures and enhanced abundances of FUV-pumped vibrationally excited molecular hydrogen (up to v = 10; see, e.g., Kaplan et al. 2017). It has long been suspected that the presence of large column densities of FUV-pumped H2 (v ≥1) could increase the reactivity of some of the above hydrogen abstraction reactions (Stecher & Williams 1972; Freeman & Williams 1982; Tielens & Hollenbach 1985; Sternberg & Dalgarno 1995).

To make realistic abundance predictions of the product XH, PDR models need to determine the H2 (v, j) level populations (typically very far from thermal) and include state-specific reaction rates in their chemical networks (Agúndez et al. 2010). These state-dependent reaction rates can either be measured in the laboratory (e.g., Hierl et al. 1997)or determined through ab initio calculations of potential energy surfaces (PESs), followed by a study of the scattering process. Recent calculations of state-specific rates for hydrogen abstraction reactions with X = C+ (Zanchet et al. 2013b), X = S+ (Zanchet et al. 2013a, 2019a), and X = S and SH+ (Goicoechea et al. 2021) can explain the abundances of CH+, SH+, and SH inferred from observations of the Orion Bar PDR (e.g., Nagy et al. 2013; Joblin et al. 2018; Goicoechea et al. 2021).

However, the reactivity of H2 (v, j) + X → XH + X collisions is a very selective process, often hard to estimate by simple educated guesses (Jambrina et al. 2012). In this study we carried out ab initio quantum calculations of reaction (1), which is endothermic by E∕k ~ 770 K (Huber & Herzberg 1979; Baulch et al. 2005; Ruscic et al. 2001; Joens 2001) and has an even higher vibrationally adiabatic barrier from H2 (v = 0, j = 0) of 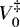V0‡$V_0^{\ddagger}$ = 5700 K (Eb ∕k = 6900 K without the respective zero point energies; Zanchet et al. 2019b). After determining the H2 state-dependent reaction rate coefficients, we investigated whether the reaction of O (3 P) with FUV-pumped vibrationally excited H2 enhances the formation of OH in strongly irradiated PDRs compared to models that simply use the thermal reaction rate coefficient. We did this by implementing PDR models adapted to the physical and illumination conditions of the Orion Bar, where the Herschel space telescope detected several far-infrared OH rotational lines (Goicoechea et al. 2011).

In Sect. 2 we give details of the PES and scattering calculations and how we obtained the state-specific rate coefficients of reaction (1), while in Sect. 3 we investigate the impact of the calculated rate coefficients on PDR models adapted to the Orion Bar.

2 Quantum calculations

Three PESs, two of symmetries 3A″ and one of symmetry 3A′ correlate adiabatically with the ground state of the reactants. Two of them, 13 A′ and 13 A″, also correlate with the ground electronic state of the products, and are necessary to describe the O (3 P) + H2 reaction. The two PESs are degenerate for collinear geometries, where the saddle point is found, at Eb ∕k = 6900 K with respectto the reactants asymptote (Zanchet et al. 2019b), while for non-collinear approaches the barrier is consistently lower on the 3 A″ PES. We performed adiabatic scattering calculations on both PESs for O (3 P) + H2 (v ≤ 7, j ≤ 10) to determine state-selected reaction rates between 100 and 3500 K using the procedure described below. Time-independent quantum mechanical (QM) scattering calculations were carried out applying the coupled-channel hyperspherical method implemented in the ABC code (Skouteris et al. 2000) to the set of PESs calculated by Zanchet et al. (2019b). Each PES consists of 5000 ab initio energies calculated using the internally contracted multireference configuration interaction (icMRCI) method including simple and double excitation, Davidson correction, and an aug-c-pV5Z basis set. The fits to the PESs obtained account for the degeneracy of the collinear saddle point very accurately (Zanchet et al. 2019b). They have been used by Jambrina et al. (2016) to simulate the experimental Λ-doublet populations of nascent OD with excellent agreement with the experimental results of Lahankar et al. (2013, 2014). It is also possible to explain the propensity towards Π(A′) Λ-doublet states as a consequence of the presence of a mechanism on the A″ PES that entails a change in the direction of the doubly occupied orbital of atomic oxygen (Jambrina et al. 2016, 2019).

Quantum mechanical scattering calculations on the 13A′ and 13A″ PESs were carried out at 60 total energies between 0.3 eV and 2.5 eV including all partial waves (J) to convergence (Jmax = 62 at the highest energies) and all helicity projections up to 26. Propagation was carried out in 300 log-derivative steps up to a hyperradius of 20 a0 including in the basis all the diatomic energy levels up to 3.25 eV. For v = 4, 5 j = 0 states, additional QM calculations were run at total energies slightly above the opening of vibrational states v = 4, 5 of H2. The excitation functions σR(Ecoll) for the O (3 P) + H2 (v, j) calculated on both PESs exhibit significant thresholds up to v = 4. As can be expected, the higher the internal energy of H2, the smaller the energy threshold becomes. However, only a fraction of the internal energy of H2 is used to surmount the barrier, and even though the energy of the (v = 1, j = 0) state of H2 is already above the electronic barrier, the reaction only becomes barrierless for H2 (v ≥ 4). Since the reaction is barrierless for v ≥ 4, state-specific reaction rates for H2 (v ≥ 4) are expected to be significantly large even at low temperatures.

To calculate the state-specific reaction rate coefficients up to temperatures of 3500 K, it was necessary to calculate integral cross sections for collision energies up to 2.5–3.0 eV. Since converged QM calculations are computationally very expensive for hot rovibrational states of H2 at these very high energies, we complemented the QM scattering calculations with batches of 2 × 106 quasiclassical trajectories (QCTs) per rovibrational state that were calculated using the procedure of Aoiz et al. (1992, 1998). In these batches of trajectories, the initial atom–diatom distance was set at 20 Å, and an integration step of 0.02 fs was used, guaranteeing a total energy conservation better than one part in 105. QCT calculations systematically predicted a higher energy threshold, but at the energies where the QCT and QM calculations were merged the agreement between the two sets of calculations was good, so any effect in the rate coefficients consequence of this merge should be negligible. The very high internal energy of H2 (v = 6, 7) prevented us from carrying out QM scattering calculations for these states, and thus we relied on QCT calculations. Since for H2 (v = 4, 5) the reactionis already barrierless, rate coefficients predicted by the QCT method for H2 (v = 6, 7) should be very similar to those obtained through QM calculations.

Once the state-specific rate coefficients were determined on the 3 A′ and 3 A″ PESs, the overall state-specific rate coefficients were calculated as k(T) = 3kA″ (T)+[2+exp(−ΔE1T)]kA′ (T)5+3⋅exp(−ΔE1T)+exp(−ΔE0T),\begin{equation*}k(T)\,{=}\,\frac{3 k_{A&#x0027;&#x0027;}(T) &#x002B; \left[ 2 &#x002B; \exp\left(-\frac{\Delta E_1}{T}\right) \right] k_{A&#x0027;}(T)}{5 &#x002B; 3\cdot \exp\left({-}\frac{\Delta E_1}{T}\right) &#x002B; \exp\left({-}\frac{\Delta E_0}{T}\right)}, \end{equation*}(2)

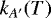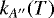where T is the temperature, k(T) is the overall state-specific rate coefficient, and kA′ (T)$k_{A&#x0027;}(T)$ and kA″ (T)$k_{A&#x0027;&#x0027;}(T)$ are the state-specific rate coefficients on the A′ and A″ PESs, respectively. Equation (2) accounts for the O (3P) spin-orbit splitting, where ΔE1 = 227.708 K and ΔE0 = 326.569 K are the energies of the spin-orbit states 3P1 and 3P0, respectively, over the ground state 3P2. Equation (2) also considers the correlation between the three levels of O (3 P) and the A′ and A″ PESs. As established by ab initio calculations including spin-orbit correction along the reaction path, the 13 A″ state correlates with three of the five components of O (3P2), and the 13A′ PES correlates with the other two components of O (3P2) and one component of O (3P1). The remaining three components of O (3P1,0) correlate with the non-reactive 23A″ state.

In Fig. 1 we show the state-specific rate coefficients for the reaction O (3 P) + H2 (v = 0–5, j = 0). It is clear from the figure that the vibrational excitation of H2 leads to a significant increase in k(T), especially at low temperatures. For example, at 500 K the ratio of the rate coefficients for v = 4 to v = 0 is 7.5 × 104, while at 1000 K this ratio is just 640. Interestingly, even for v = 5 the rate coefficient is not independent of temperature, as could be expected for a barrierless reaction. For v = 0–1, our results are in good agreement with those calculated by Balakrishnan (2004) on the PES of Rogers et al. (2000), which predicted a somewhat smaller collinear barrier. Also in agreement with previous results (Weck et al. 2006), we predict the existence of an energy barrier for v = 2–3. However, tothe best of our knowledge there are no previous calculations for v > 3 for which the reaction proceeds without a barrier.

thumbnail Fig. 1

Calculated rate coefficients of the reaction O (3P) + H2 (v, j = 0) for selected vibrational states v of H2.

3 Impact on the abundance of OH

Previous studies of the impact of reactions of vibrationally excited H2 on the chemistry of molecular clouds have shown that the most dramatic effect of including state-dependent rate coefficients is attained in dense and strongly UV-illuminated PDRs like the Orion Bar (Agúndez et al. 2010; Zanchet et al. 2013a,b, 2019a; Goicoechea et al. 2021). To evaluate the role of FUV-pumped vibrationally excited H2 reacting with atomic oxygen on the abundance of OH we therefore focus on the Orion Bar PDR.

We used the Meudon PDR code1 (Le Petit et al. 2006) in which we implemented the H2 (v, j) state-specific rate coefficient expressions for reaction (1) given in Table 1. We assume a cloud having an isobaric structure with a thermal pressure (Pth = nH T) of 2 × 108 cm−3 K, a total visual extinction of 10 mag, a FUV radiation field 104 times stronger than the interstellar radiation field of Draine (1978) illuminating one side of the cloud, and a cosmic-ray ionization rate of H2 of 10−16 s−1. The models include only gas-phase chemistry and formation of H2 on grain surfaces (Le Bourlot et al. 2012). To rigorously evaluate how the OH abundance is affected by the FUV-pumped non-thermal H2 population distribution in the reaction with O we ran a reference model in which we use a thermal rate coefficient for reaction (1), given by 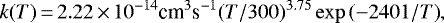k(T) = 2.22 × 10−14cm3s−1(T/300)3.75exp(−2401/T),\begin{equation*}k(T)\,{=}\,2.22\,{\times}\,10^{-14} \textrm{cm}^3 \textrm{s}^{-1} (T/300)^{3.75} \exp{(-2401/T)}, \end{equation*}(3)

where the temperature T is in degrees Kelvin. Equation (3) is obtained from a fit to the thermal rate coefficient calculated from the individual rate coefficient expressions for each (v, j) state of H2 given in Table 1. Therefore, any difference in the OH abundance between the model including state-specific rates and the reference model can be confidently ascribed to the effect of the non-thermal population distribution of H2 on the reactivity with O. In Fig. 2 we compare the thermal rate coefficient expression given by Eq. (3) with the experimental expression given in the compilation of Baulch et al. (2005) and, as can be seen in the figure, they are in very good agreement. In Fig. 2 we also compare the thermal rate coefficient with the state-specific rate coefficients calculated for the (v = 0, j = 0) and (v = 1, j = 0) states of H2. Even at low temperatures, excited rotational levels of H2 have non-negligible thermal populations and the increase in the rate coefficient with the quantum number j of H2 is enough to make the thermal rate coefficient higher than its (v = 0, j = 0) counterpart. In any case, at low temperatures the thermal rate coefficient is still well below the rate coefficient of the (v = 1, j = 0) state of H2.

In the top left panel of Fig. 3 we show the calculated abundance of OH in the edge (AV = 0–4) of the Orion Bar. It shows that OH reaches a maximum fractional abundance relative to H nuclei of ~ 10−6 in the AV = 0.5–1.0 range, decreasing at lower AV due to the high FUV flux, which dissociates molecules, and also at high AV, due to the lower temperatures encountered. The main effect of including state-specific rate coefficients for O + H2 occurs in the range AV = 1.3–2.3, where the OH abundance increases by up to one order of magnitude with respect to the reference model. However, this is not the region of maximum abundance of OH, and the impact on the column density of OH at AV = 4 is modest, just ~ 60%. The small change in the OH abundance at AV < 1.3 is related to the fact that in this region temperatures are high (see middle left panel in Fig. 3) and the reaction O + H2 occurs fast whether we consider the thermal rate coefficient or we use state-specific rates. In the reference model at AV > 1.3 temperatures decrease and the thermal rate coefficient of reaction O + H2 takes small values. In these more internal regions the reaction between O and H2 is no longer the main route to OH. Our pure gas-phase models point to the ion H3O+ as the main precursor of OH (through dissociative recombination with electrons) in these internal regions (see bottom right panel in Fig. 3), although this pathway has a limited efficiency resulting in a relatively low abundance of OH. However, when O + H2 state-specific rates are considered and the non-thermal population distribution of H2 is taken into account, reaction (1) becomes the main route to OH even in deeper regions, up to AV = 2.6, enhancing the abundance of OH. Far-UV pumping makes H2 to maintain a certain population of v ≥ 1 levels even at relatively deep regions of the cloud. As shown in the middle panel of Fig. 3, the fractional populations of v ≥ 1 levels are around 10−7 at AV = 1.3 and they decrease smoothly with increasing AV. The highest contribution to the formation of OH is provided by H2 v > 3 levels (see second panel from bottom in Fig. 3), for which the O + H2 reaction starts to attain high rate coefficients, close to the collision limit (see Fig. 1). The increase in the abundance of OH at AV > 1.3 when implementing state-specific rates is clearly a consequence of an enhancement in the O + H2 reaction rate. As shown in the bottom panel of Fig. 3, the O + H2 thermal rate coefficient goes down to very small values at increasing AV following the decrease in temperature, while non-thermal population of vibrational levels of H2 increases the reaction rate by orders of magnitude.

We expect that when implemented in more refined gas-grain models of PDRs and illuminated protoplanetary disks (i.e., including OH- and H2O-ice mantle formation and desorption; see, e.g., Hollenbach et al. 2009), these state-specific rate coefficients will provide more accurate OH abundances and line intensity estimations. Moreover, from our QM and QCT calculations it is possible to extract state-to-state rate coefficients that will allow us to include formation pumping in OH excitation models (e.g., Tabone et al. 2021) and to accurately model near future observations of OH in these environments with the James Webb Space Telescope (JWST).

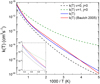thumbnail Fig. 2

Thermal rate coefficient calculated in this work, given by Eq. (3), is compared with the experimental value (Baulch et al. 2005). Rate coefficients for H2 in the (v = 0, j = 0) and (v = 1, j = 0) states are also shown for the sake of comparison. The inset highlights the behavior at high temperatures (>1000 K).
Table 1

Rate coefficient parameters for O(3P) + H2 (v, j).

thumbnail Fig. 3

Assorted quantities calculated in the PDR model of the Orion Bar plotted as a function of AV. The solid lines refer to the model including H2 state-specific rate coefficients for reaction (1), and the dashed lines to the reference model in which a thermal rate coefficient is used for reaction (1). Top right panel: contribution of each vibrational state of H2 to the total rate coefficient of the O + H2 reaction, expressed as f(H2(v)) × k(O + H2 (v)), where f(H2(v)) is the fractional population of H2 in the vibrational state v. Bottom right panel: contribution of the three main gas-phase reactions of formation of OH, expressed as a percentage of the total OH formation rate.

Acknowledgements

We acknowledge the anonymous referee for a constructive report that allowed to improve this article. We acknowledge the Spanish Ministerio de Ciencia e Innovación for funding support through the projects AYA2016-75066-C2-1-P, FIS2017-83473-C2, PGC2018-096444-B-I00, PID2019-106110GB-I00, and PID2019-107115GB-C21, and the European Research Council for support through project ERC Grant 610256 (NANOCOSMOS). A.V. and P.G.J. acknowledge funding by Fundación Salamanca City of Culture and Knowledge (programme for attracting scientific talent to Salamanca). M.A. also acknowledges funding support from the Ramón y Cajal programme of Spanish Ministerio de Ciencia e Innovación (grant RyC-2014-16277).

References

  1. Agúndez, M., Goicoechea, J. R., Cernicharo, J., Faure, A., & Roueff, E. 2010, ApJ, 713, 662 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aoiz, F. J., Bañares, L., & Herrero, V. J. 1998, J. Chem. Soc. Faraday Trans., 94, 2483 [Google Scholar]
  3. Aoiz, F. J., Herrero, V. J., & Sáez-Rábanos, V. 1992, J. Chem. Phys., 97, 7423 [Google Scholar]
  4. Balakrishnan, N. 2004, Geophys. Res. Lett., 31, L04106 [Google Scholar]
  5. Baulch, D. L., Bowman, C. T., Cobos, C. J., et al. 2005, J. Phys. Chem. Ref. Data, 34, 757 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bergin, E., Calvet, N., D’Alessio, P., & Herczeg, G. J. 2003, ApJ, 591, L159 [Google Scholar]
  7. Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
  8. Draine, B. T., Roberge, W. G., & Dalgarno, A. 1983, ApJ, 264, 485 [Google Scholar]
  9. Elitzur, M., & de Jong, T. 1978, A&A, 67, 323 [NASA ADS] [Google Scholar]
  10. Fedele, D., Bruderer, S., van Dishoeck, E. F., et al. 2013, A&A, 559, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Freeman, A., & Williams, D. A. 1982, Ap&SS, 83, 417 [CrossRef] [Google Scholar]
  12. Gerin, M., Neufeld, D. A., & Goicoechea, J. R. 2016, ARA&A, 54, 181 [NASA ADS] [CrossRef] [Google Scholar]
  13. Godard, B., Falgarone, E., & Pineau des Forêts, G. 2014, A&A, 570, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Goicoechea, J. R., Joblin, C., Contursi, A., et al. 2011, A&A, 530, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Goicoechea, J. R., Chavarría, L., Cernicharo, J., et al. 2015, ApJ, 799, 102 [Google Scholar]
  16. Goicoechea, J. R., Pety, J., Cuadrado, S., et al. 2016, Nature, 537, 207 [NASA ADS] [CrossRef] [Google Scholar]
  17. Goicoechea, J. R., Aguado, A., Cuadrado, S., et al. 2021, A&A, 647, A10 [EDP Sciences] [Google Scholar]
  18. González-Alfonso, E., Fischer, J., Graciá-Carpio, J., et al. 2012, A&A, 541, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Hierl, P. M., Morris, R. A., & Viggiano, A. A. 1997, J. Chem. Phys., 106, 10145 [Google Scholar]
  20. Hollenbach, D., & McKee, C. F. 1979, ApJS, 41, 555 [Google Scholar]
  21. Hollenbach, D., Kaufman, M. J., Bergin, E. A., & Melnick, G. J. 2009, ApJ, 690, 1497 [CrossRef] [Google Scholar]
  22. Huber, K. P., & Herzberg, G. 1979, Molecular Spectra and Molecular Structure, IV. Constants Of Diatomic Molecules (Berlin: Springer Science + Business Media, LLC) [Google Scholar]
  23. Jambrina, P. G., Garcia, E., Herrero, V. J., Sáez-Rábanos, V., & Aoiz, F. J. 2012, Phys. Chem. Chem. Phys., 14, 14596 [Google Scholar]
  24. Jambrina, P. G., Zanchet, A., Aldegunde, J., Brouard, M., & Aoiz, F. J. 2016, Nat. Comm., 7, 13439 [Google Scholar]
  25. Jambrina, P. G., Zanchet, A. Menendez, M., Herrero, V. J., & Aoiz, F. J. 2019, Phys. Chem. Chem. Phys., 21, 25389 [Google Scholar]
  26. Joblin, C., Bron, E., Pinto, C., et al. 2018, A&A, 615, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Joens, J. A. 2001, J. Phys. Chem. A., 105, 11041 [Google Scholar]
  28. Kaplan, K. F., Dinerstein, H. L., Oh, H., et al. 2017, ApJ, 838, 152 [NASA ADS] [CrossRef] [Google Scholar]
  29. Karska, A., Herczeg, G. J., van Dishoeck, E. F., et al. 2013, A&A, 552, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Kaufman, M. J., & Neufeld, D. A. 1996, ApJ, 456, 611 [Google Scholar]
  31. Lahankar, S. A., Zhang, J., McKendrick, K. G., & Minton, T. K. 2013, Nat. Chem., 5, 315 [Google Scholar]
  32. Lahankar, S. A., Zhang, J., Minton, T. K., & McKendrick, K. G. 2014, J. Am. Chem. Soc., 136, 12371 [Google Scholar]
  33. Le Bourlot, J., Le Petit, F., Pinto, C., Roueff, E., & Roy, F. 2012, A&A, 541, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Mandell, A. M., Mumma, M. J., Blake, G. A., et al. 2008, ApJ, 681, L25 [Google Scholar]
  36. Melnick, G. J., Stacey, G. J., Genzel, R., Lugten, J. B., & Poglitsch, A. 1990, ApJ, 348, 161 [Google Scholar]
  37. Nagy, Z., Van der Tak, F. F. S., Ossenkopf, V., et al. 2013, A&A, 550, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Neufeld, D. A., Kaufman, M. J., Goldsmith, P. F., Hollenbach, D. J., & Plume, R. 2002, ApJ, 580, 278 [Google Scholar]
  39. Parikka, A., Habart, E., Bernard-Salas, J., et al. 2017, A&A, 599, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Rogers, S., Wang, D., Kuppermann, A., & Walch, S. 2000, J. Phys. Chem. A, 104, 2308 [Google Scholar]
  41. Ruscic, B., Feller, D., Dixon, D. A., et al. 2001, J. Phys. Chem. A., 105, 1 [Google Scholar]
  42. Skouteris, D., Castillo, J. F., & Manolopoulos, D. E. 2000, Comp. Phys. Comm., 133, 128 [Google Scholar]
  43. Stecher, T. P., & Williams, D. A. 1972, ApJ, 177, L141 [NASA ADS] [CrossRef] [Google Scholar]
  44. Sternberg, A., & Dalgarno, A. 1995, ApJS, 99, 565 [NASA ADS] [CrossRef] [Google Scholar]
  45. Sturm, E., González-Alfonso, E., Veilleux, S., et al. 2011, ApJ, 733, L16 [Google Scholar]
  46. Tabone, B., van Hemert, M. C., van Dishoeck, E. F., & Black, J. H. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202039549 [Google Scholar]
  47. Tappe, A., Lada, C. J., Black, J. H., & Muench, A. A. 2008, ApJ, 680, L117 [Google Scholar]
  48. Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [Google Scholar]
  49. Tielens, A. G. G. M., Meixner, M. M., van der Werf, P. P., et al. 1993, Science, 262, 86 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  50. Wampfler, S. F., Bruderer, S., Karska, A., et al. 2013, A&A, 552, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Weck, P. F., Balakrishnan, N., Brandão, J., Rosa, C., & Wang, W. 2006, J. Chem. Phys., 124, 074308 [Google Scholar]
  52. Zanchet, A., Agúndez, M., Herrero, V. J., Aguado, A., & Roncero, O. 2013a, AJ, 146, 125 [NASA ADS] [CrossRef] [Google Scholar]
  53. Zanchet, A., Godard, B., Bulut, N., et al. 2013b, ApJ, 766, 80 [NASA ADS] [CrossRef] [Google Scholar]
  54. Zanchet, A., Lique, F., Roncero, O., Goicoechea, J. R., & Bulut, N. 2019a, A&A, 626, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Zanchet, A., Menendez, M., Jambrina, P. G., & Aoiz, F. J. 2019b, J. Chem. Phys., 151, 094307 [Google Scholar]

All Tables

Table 1

Rate coefficient parameters for O(3P) + H2 (v, j).

In the text

All Figures

thumbnail Fig. 1

Calculated rate coefficients of the reaction O (3P) + H2 (v, j = 0) for selected vibrational states v of H2.
In the text
thumbnail Fig. 2

Thermal rate coefficient calculated in this work, given by Eq. (3), is compared with the experimental value (Baulch et al. 2005). Rate coefficients for H2 in the (v = 0, j = 0) and (v = 1, j = 0) states are also shown for the sake of comparison. The inset highlights the behavior at high temperatures (>1000 K).
In the text
thumbnail Fig. 3

Assorted quantities calculated in the PDR model of the Orion Bar plotted as a function of AV. The solid lines refer to the model including H2 state-specific rate coefficients for reaction (1), and the dashed lines to the reference model in which a thermal rate coefficient is used for reaction (1). Top right panel: contribution of each vibrational state of H2 to the total rate coefficient of the O + H2 reaction, expressed as f(H2(v)) × k(O + H2 (v)), where f(H2(v)) is the fractional population of H2 in the vibrational state v. Bottom right panel: contribution of the three main gas-phase reactions of formation of OH, expressed as a percentage of the total OH formation rate.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.