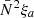| Issue |
A&A
Volume 648, April 2021
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202039464 | |
| Published online | 20 April 2021 | |
The effect of the centrifugal acceleration on period spacings of gravito-inertial modes in intermediate-mass stars
1
Institute of Astronomy, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
e-mail: jan.henneco@protonmail.com
2
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris Diderot, Sorbonne Paris Cité, 91191 Gif-sur-Yvette, France
3
Department of Astrophysics, IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
4
Max Planck Institute for Astronomy, Koenigstuhl 17, 69117 Heidelberg, Germany
Received:
17
September
2020
Accepted:
20
January
2021
Context. The Kepler and Transiting Exoplanet Survey Satellite (TESS) space telescopes delivered high-precision, long-duration photometric time series for hundreds of main-sequence stars, revealing their numerous gravito-inertial (g) pulsation modes. This high precision allows us to evaluate increasingly detailed theoretical stellar models. Recent theoretical work extended the traditional approximation of rotation, a framework to evaluate the effect of the Coriolis acceleration on g modes, to include the effects of the centrifugal acceleration in the approximation of slightly deformed stars, which so far have mostly been neglected in asteroseismology. This extension of the traditional approximation was conceived by re-deriving the traditional approximation in a centrifugally-deformed, spheroidal coordinate system.
Aims. We explore the effect of the centrifugal acceleration on g modes and assess its detectability in space-based photometric observations.
Methods. We implemented the new theoretical framework to calculate the centrifugal deformation of pre-computed 1D spherical stellar structure models and computed the corresponding g-mode frequencies, assuming uniform rotation. The framework was evaluated for a grid of stellar structure models covering a relevant parameter space for observed g-mode pulsators.
Results. The centrifugal acceleration modifies the effect of the Coriolis acceleration on g modes, narrowing the equatorial band in which they are trapped. Furthermore, the centrifugal acceleration causes the pulsation periods and period spacings of the most common g modes (prograde dipole modes and r modes) to increase with values similar to the observational uncertainties of the measured period spacing values in Kepler and TESS data.
Conclusions. The effect of the centrifugal acceleration on g modes is formally detectable in modern space photometry. The implementation of the used theoretical framework in stellar structure and pulsation codes will allow for more precise asteroseismic modelling of centrifugally deformed stars in order to assess its effect on mode excitation, trapping, and damping.
Key words: asteroseismology / waves / stars: oscillations / stars: rotation / stars: interiors / hydrodynamics
© ESO 2021
1. Introduction
Over the last decade, there have been major advancements in observational asteroseismology. Thanks to space missions such as Convection Rotation and planetary Transits (CoRoT; Auvergne et al. 2009), Kepler (Borucki et al. 2009), BRIght Target Explorer (BRITE) Constellation (Weiss et al. 2014), and TESS (Ricker et al. 2014), long-time-base, high-cadence, high-precision photometric light curves are now available for hundreds of thousands of stars. This has resulted in the detection and identification of g-mode oscillations, which have buoyancy as the main restoring force, in hundreds of γ Doradus (γ Dor) and slowly-pulsating B-type (SPB) stars (e.g., Tkachenko et al. 2013; Van Reeth et al. 2015; Pápics et al. 2017; Christophe et al. 2018; Li et al. 2019b,c, 2020; Pedersen et al. 2021).
γ Dor (Kaye et al. 1999) and SPB stars (Waelkens 1991) are main-sequence stars, with masses of 1.4 M⊙ ≲ M ≲ 1.9 M⊙ and 3 M⊙ ≲ M ≲ 9 M⊙, respectively. Their g-mode pulsations have periods between 0.3 and 5 days, and they are mostly sensitive to the near-core regions of the stars. Asteroseismic modelling of observed and identified g-mode pulsations allows us to constrain the physical processes taking place in the deep stellar interior (see e.g., Aerts et al. 2018). While similar on some fronts, major differences occur in the modelling of g modes compared to the case of stochastically-excited pressure modes (see Aerts 2021, for an extensive review on the overall methodology). For g modes in γ Dor and SPB stars, key processes to infer are convective core overshooting or convective penetration in the core boundary layers (e.g., Pedersen et al. 2018; Michielsen et al. 2019), interior magnetic fields (Prat et al. 2019, 2020; Van Beeck et al. 2020; Mathis et al. 2021; Bugnet et al. 2021), and microscopic or macroscopic mixing in the radiative envelope (e.g., Deal et al. 2016; Rogers & McElwaine 2017; Pedersen et al. 2018, 2021; Mombarg et al. 2020).
One of the most crucial aspects that has to be taken into account in stellar structure and evolution theory is rotation (Zahn 1992; Maeder & Zahn 1998; Mathis & Zahn 2004; Maeder 2009, and references therein). Aside from causing numerous physical processes such as rotational mixing, stellar rotation severely influences the behaviour of g-mode pulsations via the Coriolis acceleration (e.g., Lee & Saio 1997; Dintrans & Rieutord 2000; Aerts et al. 2019, for a review). For high-frequency oscillations (ω ≫ Ω, where ω is the angular pulsation frequency in the co-rotating frame and Ω is the angular rotation rate), the Coriolis acceleration can be treated as a perturbation (Hansen et al. 1977; Gough 1981). However, high-order g modes (with radial order n ≫ spherical degree ℓ) typically lie in the low-frequency range (ω ≲ Ω), where the Coriolis force also contributes to restoring the oscillations. Such g-mode pulsations, therefore, occur in the gravito-inertial regime and correspond to gravito-inertial waves (GIW). Hence, the Coriolis force can no longer be treated as a perturbation, and the hydrodynamical equations that govern the oscillations become an infinite set of coupled differential equations (Mathis 2009). However, approximate numerical solutions and general properties of GIW can still be obtained by truncating the infinite set of coupled differential equations (e.g., Berthomieu et al. 1978; Lee & Saio 1986, 1987; Dziembowski & Kosovichev 1987b,a; Dziembowski et al. 1987; Dintrans et al. 1999; Dintrans & Rieutord 2000; Mathis 2009).
The influence of the Coriolis force on GIW is commonly described using the traditional approximation of rotation (TAR). It was first developed by Eckart (1960) in his study of the dynamics of shallow atmospheres and oceans on Earth, and later introduced in stellar pulsation theory by Berthomieu et al. (1978) and Lee & Saio (1987). The main assumption of the TAR is that the stratification in which the waves propagate is sufficiently strong so as to limit vertical wave motions. As a consequence, the horizontal component of the rotation vector and, therefore, also the vertical component of the Coriolis acceleration can be neglected within the description of the GIW. This condition for stable stratification (both in chemical composition and in entropy) is typically met in the radiative near-core region of γ Dor and SPB stars. By applying the TAR, the hydrodynamical oscillation equations can be decoupled and rewritten in the form of the Laplace tidal equation (Laplace 1799).
Two additional assumptions made within the TAR are those of uniform rotation and spherical symmetry. Mathis (2009) abandoned the first assumption and included the effect of differential rotation within the framework of the TAR. Subsequently, the sensitivity of GIW to the effect of differential rotation was assessed by Van Reeth et al. (2018). The assumption of spherical symmetry is valid when the star is rotating sufficiently slowly to ignore the centrifugal acceleration, that is Ω ≪ Ωc, where 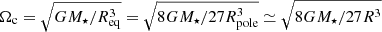 is the Roche critical rotation rate, G is the universal gravitational constant, and where Req and Rpole stand for the equatorial and polar radius of the star, respectively (see Maeder 2009, Chapter 2). However, a significant fraction of the γ Dor and SPB stars are moderate to fast rotators (Pápics et al. 2017; Li et al. 2020; Pedersen et al. 2021). Hence, the effect of the centrifugal deformation should be taken into account in the theoretical description of their g-mode pulsations.
is the Roche critical rotation rate, G is the universal gravitational constant, and where Req and Rpole stand for the equatorial and polar radius of the star, respectively (see Maeder 2009, Chapter 2). However, a significant fraction of the γ Dor and SPB stars are moderate to fast rotators (Pápics et al. 2017; Li et al. 2020; Pedersen et al. 2021). Hence, the effect of the centrifugal deformation should be taken into account in the theoretical description of their g-mode pulsations.
Mathis & Prat (2019) generalised the TAR for moderately-to-rapidly rotating stars by considering the effects of the centrifugal acceleration. First, they provided a prescription to deform a stellar structure model into a centrifugally deformed oblate spheroid. From the resulting perturbed physical quantities, a dimensionless deformation factor proportional to the square of the rotation rate could then be calculated. Secondly, this deformation factor was used to transition from a spherically symmetric to a spheroidal coordinate system, keeping only first-order terms in the deformation. Next, they re-derived the Laplace tidal equation within this new coordinate system, arriving at the so-called generalised Laplace tidal equation. Finally, the authors derived an asymptotic expression for the frequencies of GIW, including the effect of the centrifugal acceleration.
In this work, we have set up a parameter study with the goal of assessing the effect of the centrifugal acceleration on g-mode pulsations in rotationally deformed stars and their detectability in space-based photometric observations. By doing so, we expand upon the proof-of-concept study conducted in the theoretical work of Mathis & Prat (2019) and aim to answer the question of whether the effect of the centrifugal acceleration should be accounted for in asteroseimic modelling of observed g-mode pulsators. A brief summary of the theoretical results and numerical implementation by Mathis & Prat (2019), as well as our improvements to the theoretical framework, are provided in Sect. 2. The results of our upgraded implementation and parameter study follows in Sect. 3. We discuss the results and conclude in Sect. 4.
2. Methodology
2.1. Theoretical background
2.1.1. Deformation of stellar structure
Following Mathis & Prat (2019, Appendix A), the pressure P, density ρ, and gravitational potential ϕ in a centrifugally deformed star are written as the sum of a spherically symmetric, non-perturbed part (subscript ‘0’) and a perturbation (subscript ‘1’). This perturbation term itself is then expanded on an orthogonal basis of Legendre polynomials Pleg, l(cos θ) of degree l = 0, 2, where θ is the co-latitude and θ = 0 is on the rotation axis. Such an expansion corresponds to the projection of the perturbed quantities on a spheroidal surface in the moderately rapid rotation regime considered here. For fast rotators, additional terms of (even) degree l should be included, but that is beyond the current scope of our paper.
For the gravitational potential, with ϕ0 = −GM(r)/r and M(r) being the mass contained within a sphere of radius r, we have:
With the inclusion of the centrifugal acceleration, the hydrostatic equilibrium in the star is written as:
This last term corresponds to the gradient of the centrifugal potential (per unit mass) 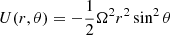 . The centrifugal potential itself is then also expanded on the same basis of Legendre polynomials as:
. The centrifugal potential itself is then also expanded on the same basis of Legendre polynomials as:
This implies that the modal amplitudes of the centrifugal potential are given by Ul = 0 = −(1/3)Ω2r2 and Ul = 2 = (1/3)Ω2r2.
The modal amplitudes of the pressure and density, Pl(r) and ρl(r), are recovered from the property that in the centrifugally deformed star, the equipotential surface (ϕ + U), the isobar surface, and the isodensity surface coincide and are given by (Mathis & Prat 2019, Appendix A):
For the modal amplitude of the gravitational potential, ϕl(r), it is required to solve the ‘perturbed’ Poisson equation
which is simply recovered by substituting the modal expansions of ϕ(r, θ) and ρ(r, θ) in the Poisson equation. Written in full, the perturbed Poisson equation reads:
with boundary conditions
and l ∈ {0, 2} (Sweet 1950; Zahn 1966; Mathis & Prat 2019, Appendix A).
Based on Lee & Baraffe (1995) and Mathis & Prat (2019), we now define the pseudo-radial coordinate a as follows:
At this point, we perform a transformation from a spherical coordinate system (r, θ, φ) to a spheroidal coordinate system (a, θ, φ). We note that ε represents a dimensionless deformation factor, defined in the spheroidal coordinate system. Again following Mathis & Prat (2019, Appendix A), an expression for the modal amplitudes of ε can be derived:
where AS is the surface pseudo-radius of the deformed star. The coordinate mapping described by these expressions for ε and a is more accurate than the linear approximation used by Mathis & Prat (2019) and closely agrees with the physical mapping described by, for example Zahn (1966) and Mathis & Zahn (2004), so that r is equal to the deformed surface radius RS(θ) at a = AS. However, while this physical mapping has a singularity at the stellar centre, our cubic expression ensures that a ≃ r when a → 0.
From the expressions for the modal amplitudes of the pressure, density, and deformation factor (Eqs. (4), (5), and (10)), it can be seen that the centrifugal acceleration enters the expressions of the perturbed quantities in the form of a second order perturbation in the stellar rotation rate Ω. In the expression for εl(a) given in Eq. (10), we have a dominant contribution from Ul (compared to ϕl). Hence, εl = 0 (εl = 2) is positive (negative), and the deformation factor ε is positive in the direction of the equator.
To facilitate the calculation of εl, we can map the radial coordinate r0 and the surface radius R of the spherically symmetric (non-deformed) stellar model onto a and AS, respectively. Within their respective stellar models, both the r0 and a coordinates coincide with the radial isobaric coordinate. Thus, we get
2.1.2. Generalised Laplace tidal equation
The Laplace tidal equation is an eigenvalue equation that can be derived from the oscillation equations by using the TAR. Its simple form immediately demonstrates the simplifying power of the latter approximation. Following Lee & Saio (1997), it can be written as:
with the operator 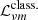 defined as:
defined as:
In order to avoid confusion later on, we refer to this equation as the ‘classical’ Laplace tidal equation (CLTE). Here, ∂x = ∂/∂x, x = cos θ, and ν = 2Ω/ω the spin parameter. The latter is a measure of the effect of rotation; pulsation modes for which ν > 1 (respectively ν < 1) are known as sub- (respectively super-) inertial modes. The eigenfunctions Θνkm are the radial Hough functions, after S. S. Hough, who pioneered in solving the Laplace tidal equation (Hough 1898), and 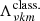 represent the eigenvalues of the equation. These radial Hough functions give the co-latitudinal distribution of the radial displacement of the star caused by the pulsations and in the limit ν → 0 reduce to
represent the eigenvalues of the equation. These radial Hough functions give the co-latitudinal distribution of the radial displacement of the star caused by the pulsations and in the limit ν → 0 reduce to 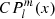 , where C is a constant and
, where C is a constant and 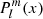 is the associated Legendre polynomial of degree l and order m. The eigenvalues reduce to ℓ(ℓ + 1) without rotation.
is the associated Legendre polynomial of degree l and order m. The eigenvalues reduce to ℓ(ℓ + 1) without rotation.
The convention is adopted in which, considering ν > 0, positive azimuthal orders (m > 0) denote ‘prograde’ modes and m < 0 stand for ‘retrograde’ modes. Since, in general, for each pair (m, ν) the CLTE yields an infinite set of solutions, the ordering number k is introduced. Inertial waves, such as r modes (which are normal modes of global Rossby waves influenced by buoyancy) (Saio et al. 2018), are not present in non-rotating stars and have k < 0. For k ≥ 0, the ordering number is related to the spherical degree l and azimuthal order through ℓ = |m|+k (Mathis & Prat 2019).
To include the effect of the centrifugal acceleration in the Laplace tidal equation, it was re-derived in the spheroidal coordinate system by Mathis & Prat (2019). The transition from a spherical to spheroidal coordinate system involves the following basis transformation:
with ε ≡ ε(a, θ) = ∑l = 0, 2εl(a)Pleg, l(x) the deformation factor introduced above. The resulting generalised Laplace tidal equation (GLTE) then is:
where
Utilising the same nomenclature as Mathis & Prat (2019), the eigenfunction wνkm = wνkm(a, θ) is called the modified radial Hough function. We note that the eigenvalue Λνkm(a) and modified radial Hough function have a parametric dependence on the pseudo-radial coordinate a, whereas in the spherically symmetric case there was no radial dependence of the solutions.
2.1.3. Asymptotic frequencies
Within the asymptotic regime, where the radial order n of the modes is much larger than the spherical degree ℓ (n ≫ ℓ), and where we consider modes with ω ≪ |N| and ω ≪ |Sℓ|, N and Sℓ being the Brunt-Väisälä and Lamb frequency, respectively, asymptotic expressions for the pulsation frequencies can be derived (Shibahashi 1979; Tassoul 1980; Unno et al. 1989). Following Mathis (2009) and Bouabid et al. (2013), these asymptotic expressions for the pulsation frequencies can be re-derived to include the effect of the centrifugal force. Mathis & Prat (2019) find the angular pulsation frequencies to be
and the pulsation periods to be
Here, 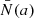 is the perturbed Brunt-Väisälä frequency profile (quantities denoted with a bar are defined within the spheroidal coordinate system). To account for the large diversity of pulsation mode cavities of g modes with different identification (k, m) or spin ν,
is the perturbed Brunt-Väisälä frequency profile (quantities denoted with a bar are defined within the spheroidal coordinate system). To account for the large diversity of pulsation mode cavities of g modes with different identification (k, m) or spin ν, 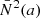 is calculated as a weighted average over the co-latitude θ:
is calculated as a weighted average over the co-latitude θ:
where Hr(a, θ) is the radial eigenfunction that corresponds to the eigenvalue Λνkm(a) in Eqs. (16) and (17), and
where 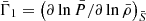 is the perturbed adiabatic exponent defined at constant (perturbed) entropy
is the perturbed adiabatic exponent defined at constant (perturbed) entropy 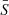 . The different quantities on the right-hand side of Eq. (19) all depend on both a and θ. In the integral in Eq. (17), a1 and a2 are the inner- and outer-boundaries of the mode cavity, determined as the region(s) within the star where
. The different quantities on the right-hand side of Eq. (19) all depend on both a and θ. In the integral in Eq. (17), a1 and a2 are the inner- and outer-boundaries of the mode cavity, determined as the region(s) within the star where 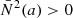 .
.
Another result from asymptotic theory is that, for a non-rotating, non-magnetic g-mode pulsator without chemical gradients, the pulsation periods of modes with consecutive radial orders are equidistant. The differences in mode periods, ΔPnkm = Pn + 1, km − Pnkm thus remain constant when plotted as a function of the period Pnkm or radial order n (Miglio et al. 2008). When constructing these so-called period spacing patterns for more realistic stellar models (including rotation and chemical gradients), they deviate from a constant, as first observed for a main-sequence massive early-type star by the CoRoT satellite (Degroote et al. 2010). Comparing theoretical and observed period spacing patterns then allows us to deduce information about rotation and chemical mixing in the deep interior of stars (Aerts 2021).
2.2. Computational implementation
The computational method to derive the asymptotic GIW frequencies from the solutions to Eq. (16) is provided in Appendix B. The implementation of the analytical framework of Mathis & Prat (2019) described above consists of three parts. First, a non-rotating 1D stellar structure model is calculated and perturbed for a selected uniform rotation rate, following Sect. 2.1.1. These 1D, non-rotating stellar structure models are calculated using the Modules for Experiments in Stellar Astrophysics1 (MESA; Paxton et al. 2019 and references therein) code. The resulting 2D (radial and latitudinal) profiles for r(a, θ) and ε are subsequently used as input for solving the GLTE given in Sect. 2.1.2. The solutions of the GLTE then allow us to compute the asymptotic pulsation frequencies based on Eq. (16).
The computational implementation of the first step involves solving the perturbed Poisson equation (e.g., through an iterative shooting scheme) for l = 0 and l = 2, yielding the modal amplitudes ϕl(r). These, in turn, are used to calculate the modal amplitudes of the pressure and density (Eqs. 4 and 5). Two challenges occur in the computation of the perturbed Brunt-Väisälä frequency profile. Firstly, the calculation of  (at constant entropy
(at constant entropy  ) requires detailed knowledge on how the equation of state changes under the influence of centrifugal deformation. This would require the framework of Mathis & Prat (2019) to be directly implemented in MESA. Secondly, high levels of numerical noise are introduced by the numerical derivatives of the physical quantities (such as the pressure and density) with respect to r and a, which is a well-known problem in stellar structure and evolution codes (Paxton et al. 2013). The details of how we treated these aspects are described in Appendix A.
) requires detailed knowledge on how the equation of state changes under the influence of centrifugal deformation. This would require the framework of Mathis & Prat (2019) to be directly implemented in MESA. Secondly, high levels of numerical noise are introduced by the numerical derivatives of the physical quantities (such as the pressure and density) with respect to r and a, which is a well-known problem in stellar structure and evolution codes (Paxton et al. 2013). The details of how we treated these aspects are described in Appendix A.
2.3. Solver for the GLTE
Several numerical methods are available for solving an eigenvalue problem such as the Laplace tidal equation, a number of which are discussed in Wang et al. (2016). As in Mathis & Prat (2019), the Chebyshev collocation method (Boyd 1976) is chosen. In such a method, the eigenfunctions of the problem, in this case the modified radial Hough functions, are expanded on a basis of N Chebyshev polynomials, where N is the number of collocation points. For the current work, we improved an existing solver for the CLTE of Prat et al. (2019) and Van Beeck et al. (2020), which was developed by one of us (VP), with two modifications.
Contrary to the CLTE, the GLTE has a parametric dependence on the radial coordinate (in this case a). In other words, at each cell of the MESA model, the solutions of the GLTE are different since ε(a, θ) depends on a. Furthermore, in order to select the solution corresponding to the desired mode identification (k, m) among the set of N solutions, the solver requires an estimate for the eigenvalue Λνkm(a). At the centre of the model, where ε = 0, the eigenvalue can be estimated by the solutions of the CLTE tabulated in the TAR module of the stellar pulsation code GYRE (Townsend & Teitler 2013; Townsend et al. 2018). Going from the centre to the surface, at each subsequent cell, the estimate is then provided by the eigenvalue from the previous cell. Since the effect of the centrifugal force increases from the centre to the surface (see Eqs. (2) and (10)), these eigenvalues increasingly diverge from the value at the centre. To keep the computation time manageable, an appropriate number of sample points in which the GLTE is solved must be selected. Thanks to the smooth behaviour of Λνkm(a) (see Sect. 3), it suffices to calculate solutions for ∼10 cells. These points are chosen equidistant in the cell index in the MESA model rather than in the physical distance. In that way, regions with higher cell density get a higher sampling. We note that Λνkm(a) profiles, which are required for asymptotic frequency calculations (see Eq. (16)) are retrieved through quadratic interpolation.
The calculation of the coefficients 𝒜, ℬ, 𝒞, 𝒟, ℰ, and their derivatives, which make up the coefficients of the GLTE, is subject to discontinuities when done from numerical differentiation. We therefore relied on analytical differentiation where possible. Only for ℰ and its derivative with respect to the co-latitudinal coordinate x did we approximate the term a∂aε by 3ε in order to avoid numerical issues. This approximation is justified by the cubic polynomial behaviour of the deformation factor. The coefficients, as implemented in the solver for the GLTE, are:
where εl = 2 = εl = 2(a) is the modal amplitude in the expression for ε = ε(a, θ) = ∑l = 0, 2εl(a)Pleg, l(x). The respective derivatives with respect to x = cos θ are:
3. Numerical results
3.1. Covered parameter space of equilibrium models
With the goal of exploring the effect of the centrifugal acceleration on the stellar structure and on high-order g-mode pulsations in more depth than was done in the proof-of-concept by Mathis & Prat (2019), the methodology described in the previous section has been applied to a range of MESA equilibrium models with varying input parameters. The ranges and values for these parameters are shown in Fig. 1.
-
Mass: the masses of the MESA models were chosen within the joint mass range of γ Dor [1.4, 1.9 M⊙] (Mombarg et al. 2019) and SPB [3, 9 M⊙] (Pápics et al. 2017; Pedersen et al. 2021) stars. The physical conditions inside these types of pulsating stars allowed the TAR to be applied and these are the two types of main-sequence stars for which g-mode period spacing patterns are observed.
-
Age: the age of the stellar models was quantified in terms of their core hydrogen-mass fraction Xc. Each model was computed with an initial hydrogen mass fraction Xini = 0.715 and evolved to its specified Xc.
-
Metallicity: the range in initial metal mass fraction, Z, covers values typical for stars in our Milky Way in the considered mass range. By considering a range, we assessed how the change in opacity caused by Z affects the Brunt-Väisälä profile and the g-mode pulsation frequencies.
-
Envelope mixing: the amount of mixing that occurs in the radiative envelope of the star is quantified by the diffusion coefficient Dmix and affects the profiles of the mass fractions, Xi, of all the isotopes considered in the chemical mixture adopted as input physics. As such, Dmix has an influence on the Brunt-Väisälä frequency. In each of the calculated MESA models, we considered Dmix to be constant throughout the radiative envelope, adopting values typical for g-mode pulsators (Van Reeth et al. 2016; Moravveji et al. 2016).
-
Convective core overshooting: this process is of major importance for stellar evolution in the considered mass range, yet it is least known among the various ingredients to be chosen as input physics (Claret & Torres 2019; Johnston et al. 2019; Li et al. 2019a; Tkachenko et al. 2020). Different formalisms exist which can describe this overshoot region. We adopted a diffusive exponentially-decaying overshooting (Freytag et al. 1996; Herwig 2000) quantified by the overshooting parameter fov.
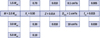 |
Fig. 1. Selected ranges and values for the input parameters of the 1D stellar structure models used in this work. |
Furthermore, each model was computed using the AGSS09 chemical abundances derived by Asplund et al. (2009) and a mixing length αMLT = 2 within the mixing length theory developed by Henyey et al. (1965). For convergence purposes, a hot wind with a Vink scaling factor of 1 was turned on in Vink et al. (2001). In order to avoid numerical issues, rotation was not taken into account during the MESA model calculations. The effects of rotation later entered into our models by applying the perturbation method which is described in Sect. 2.1.1.
3.2. Solutions of the GLTE
Here, we investigate the difference in solutions of the GLTE and CLTE. To illustrate these, we picked one baseline equilibrium model from our grid setup, as indicated in the highlighted row in Fig. 1. The behaviour was found to be equivalent for the other models so we do not discuss these results for brevity.
Figure 2 shows the solution spectrum for the GLTE for m = 2 with even and odd eigenfunctions. Four classes of solutions can be distinguished (Lee & Saio 1997): (i) the prograde g modes with ν > 0 and positive eigenvalues Λνkm(a), (ii) retrograde g modes with ν < 0 and positive eigenvalues, (iii) Rossby modes which are retrograde and have negative eigenvalues, and (iv) prograde convective modes with negative eigenvalues. Just as Rossby modes, the latter modes only appear in rotating stars and only exist for |ν|> 1. Specifically, these modes are able to propagate in convective regions under the joint force of the Coriolis acceleration and buoyancy.
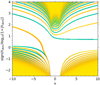 |
Fig. 2. Solution spectrum of the generalised Laplace tidal equation for modes with m = 2. Modes with even eigenfunctions are shown in blue, and those with odd eigenfunctions are in orange. Light (dark) colours correspond to solutions near the surface (core). The equilibrium model used as input for the computations has the same parameters as in the highlighted row in Fig. 1. |
Keeping in mind that the solutions plotted in the darkest colours correspond to those for the core and are therefore equivalent to the solutions of the CLTE (see Sect. 2.2), Fig. 2 reveals that the centrifugal deformation of the star causes a gradual shift in the eigenvalues. Whether this is an upward or downward shift depends on the mode identification (k, m) (we recall that solutions for negative spin parameters ν and m > 0 are equivalent to a solution with ν > 0 and m < 0). The numerical noise visible at higher values of |ν| is an artefact due to the limited number of Chebyshev collocation points (N = 200), but it can be seen that this does not affect the selected solutions. We determined that an increase in the number of collocation points causes a decrease in this noise.
The (normalised) eigenfunctions wνkm of the GLTE for a (k, m) = (0, 2) mode with ν = 2 are shown in Fig. 3. Equivalent figures for ν = 0.5 (super-inertial) and ν = 9 (sub-inertial) are displayed in Fig. 4. The eigenfunctions of the GLTE increasingly differ from those of the CLTE as the distance from the centre of the model to the surface increases. More specifically, the eigenfunctions migrate inwards, towards the equator (x = 0), causing a narrowing of the overall shape of the eigenfunctions. A similar behaviour is observed for other modes, such as prograde dipole (k, m) = (0, 1) modes shown in Fig. 5, retrograde quadrupole (k, m) = (0, −2), retrograde Rossby (k, m) = (−2, −1), quadrupole zonal (k, m) = (2, 0), and (k, m) = (1, 1) oscillation modes. Off-equator extrema, such as for the eigenfunctions of (k, m) = (0, −2) and (k, m) = (−2, −1) modes shown in Fig. 5, experience net inward shifts towards the equator.
 |
Fig. 3. Modified radial Hough functions wνkm(a, θ) (normalised) for ν = 2 and Ω/Ωc = 0.50. Solutions are plotted in a colour range from indigo to yellow from the stellar core to the surface. The green dashed line shows the solution of the CLTE. The number of collocation points for this computation was N = 200. |
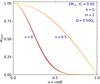 |
Fig. 4. Modified radial Hough functions wνkm(a, θ) (normalised) for Ω/Ωc = 0.50 and two different spin parameters. The 2.0 M⊙, Xc = 0.50 equilibrium model was used as input. The colour scheme and number of collocation points are identical to that of Fig. 3 (CLTE solutions have been left out for clarity). |
 |
Fig. 5. (a) Modified radial Hough functions wνkm(a, θ) (normalised) for three different modes (with specified spin parameter ν). Colour conventions are the same as those in Fig. 3. (b) Eigenvalue Λνkm(a) profiles corresponding to the eigenfunctions in (a). Points indicated with a ⋆ correspond to eigenvalues obtained by solving the GLTE. Red points were found via quadratic interpolation. The considered number of collocation points was N = 200. |
Figure 6 shows the eigenfunctions at the surface (a = AS) and the Λνkm(a) profiles for a M = 1.5 M⊙, Xc = 0.50 (Xc/Xini = 0.70) model for seven different rotation rates ranging from Ω = 0.1 Ωc to Ω = 0.7 Ωc. The figure is again for a quadrupole sectoral (k, m) = (0, 2) mode. We find that the narrowing of the shape of the eigenfunctions and the divergence of the eigenvalues from the value at the centre increase with an increasing rotation rate, as expected.
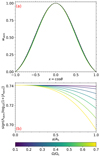 |
Fig. 6. (a) Modified radial Hough functions wνkm(a = AS, θ) for seven different rotation rates and ν = 2. (b) Eigenvalue Λνkm(a) profiles corresponding to the eigenfunctions in (a). |
3.3. Asymptotic period spacing patterns
We solved the GLTE for each model in our grid, covering a range of spin parameters for each of the models (see Appendix B). We restricted our study to the following three specific mode identifications: prograde dipole sectoral (k, m) = (0, 1) modes, prograde quadrupole sectoral (k, m) = (0, 2) modes, and retrograde Rossby modes with (k, m) = (−2, −1). The reason for this choice is that these GIW are most often observed in rotating g-mode pulsators (Pápics et al. 2017; Li et al. 2020). The computed period spacing pattern for prograde dipole modes of the baseline model for Xc = 0.50 (Xc/Xini = 0.70) is shown in Fig. 7. By comparing the centrifugally deformed period spacing pattern with their spherically symmetric counterpart, we find that the spacing values increase under the influence of the centrifugal acceleration. This increase is largest at lowest radial orders (short pulsation periods). Similar behaviour is found for (k, m) = (0, 2) modes.
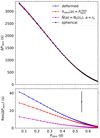 |
Fig. 7. Period spacing pattern in an inertial frame computed for (k, m) = (0, 1) modes in a centrifugally deformed 2.0 M⊙, Xc = 0.50 (Xc/Xini = 0.70), Z = 0.014, Dmix = 1 cm2 s−1, fov = 0.015 equilibrium model at Ω/Ωc = 0.50 (blue line). The black-dashed line shows the equivalent period spacing pattern for the same model, but without the effect of the centrifugal acceleration. The red and purple lines show the results for |
Essentially two effects are at play here: On the one hand, the centrifugal acceleration directly affects the g-mode pulsations, via a Λνkm(a)−profile that changes throughout the star from a = 0 to a = AS instead of just one  value for r0 = 0 → r0 = R. On the other hand, the stellar shape, including the Brunt-Väisälä frequency profile and the volume, are perturbed, which has an indirect effect on the g-mode pulsations. In order to isolate the effect of this deformation, we re-calculated the period spacing pattern for the centrifugally deformed star for
value for r0 = 0 → r0 = R. On the other hand, the stellar shape, including the Brunt-Väisälä frequency profile and the volume, are perturbed, which has an indirect effect on the g-mode pulsations. In order to isolate the effect of this deformation, we re-calculated the period spacing pattern for the centrifugally deformed star for 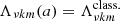 , with
, with 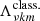 being the eigenvalue of the CLTE. This period spacing pattern is plotted in red in Fig. 7. Similarly, the purple period spacing pattern was calculated by setting
being the eigenvalue of the CLTE. This period spacing pattern is plotted in red in Fig. 7. Similarly, the purple period spacing pattern was calculated by setting 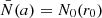 and a = r0, isolating the effect of the a−dependence of the solutions of the GLTE. Both effects lead to a net increase in the period spacings. Also for the (k, m) = (−2, −1) Rossby modes shown in Fig. 8, a net upward shift of the period spacing pattern occurs. The effect is larger at longer pulsation periods, which is equivalent to low radial orders for Rossby modes (Saio et al. 2018). In some cases, such as for retrograde g modes with (k, m) = (0,-1), we do find a net decrease in the period spacings ΔPnkm. In such cases, the Λνkm(a)−value increases under the influence of the centrifugal acceleration, and this counteracts the effect of the centrifugally modulated Brunt-Väisälä frequency profile
and a = r0, isolating the effect of the a−dependence of the solutions of the GLTE. Both effects lead to a net increase in the period spacings. Also for the (k, m) = (−2, −1) Rossby modes shown in Fig. 8, a net upward shift of the period spacing pattern occurs. The effect is larger at longer pulsation periods, which is equivalent to low radial orders for Rossby modes (Saio et al. 2018). In some cases, such as for retrograde g modes with (k, m) = (0,-1), we do find a net decrease in the period spacings ΔPnkm. In such cases, the Λνkm(a)−value increases under the influence of the centrifugal acceleration, and this counteracts the effect of the centrifugally modulated Brunt-Väisälä frequency profile 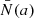 .
.
 |
Fig. 8. Theoretical period spacing pattern in the inertial frame for (k, m) = (−2, −1) modes in the same equilibrium model as in Fig. 7 at Ω/Ωc = 0.50 (blue line). The black-dashed line shows the equivalent period spacing pattern for the same model, but without the effect of the centrifugal acceleration. The red and purple show the isolated effect of |
3.4. Detectability in space-based photometric observations
To quantify the effect the centrifugal deformation of the star on the pulsation frequencies, we computed the frequency differences between asymptotic frequencies calculated in the classical formulation of the TAR and those calculated in the generalised formulation (through Eq. (16)). We consider these frequency differences as a function of the radial order n, as this is similar to the common diagnostic observables used in g-mode asteroseismic modelling (Aerts et al. 2018). We compare the obtained frequency differences with the frequency resolutions (1/Tobs) of Kepler and TESS light curves covering quasi-continuously observation times of Tobs = 4 years and Tobs = 351 days, respectively. In this way, we were able to deduce the radial orders nmax for which the frequency differences are expected to be detectable in the absence of instrumental effects and assuming excellent knowledge of the equilibrium models representing an observed star. In reality, asteroseismic modelling never represents the stellar oscillations perfectly, meaning that the optimal reported nmax leading to the largest frequency differences due to the centrifugal deformation are in fact lower limits of detectability in real applications of asteroseismology. The results for prograde dipole (k, m) = (0, 1) modes in the central (2.0 M⊙, Xc = 0.50) model rotating at 0.15 Ωc are displayed in Fig. 9. These computations were done for all the models in our grid and the considered modes. The results are listed in Table 1.
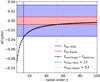 |
Fig. 9. Asymptotic frequency differences (black) for dipole (k, m) = (0, 1) modes at Ω = 0.15 Ωc for the central 2.0 M⊙, Xc = 0.50 MESA model. Red and blue bands represent the frequency resolution of Kepler and TESS, respectively. The respective values of nmax are indicated by vertical dashed lines. |
Potential detectability of the effect of the centrifugal acceleration in space-based photometric observations.
To assess whether the centrifugal acceleration is a necessary ingredient in asteroseismic modelling, we computed the fractional differences between asymptotic frequencies in centrifugally deformed and spherically symmetric stars for a range of rotation rates Ω/Ωc ∈ [0.10−0.70]. For these calculations, the central 2 M⊙, Xc = 0.5 equilibrium model was used. We restricted these tests to prograde dipole sectoral (k, m) = (0, 1) modes, as these are most frequently observed. The results are displayed in Fig. 10. The middle and bottom panel of this figure show that the deformation of the stellar structure and the divergence of the eigenvalues of the GLTE each cause an increase in δfnkm/fnkm (in absolute value) for increasing Ω = 0.1 Ωc to 0.7 Ωc. The fractional frequency differences caused by both effects are of the order of 1%. And while the indirect effect of the deformed stellar structure has a slightly larger impact, this again shows that both the deformation of the stellar structure itself and the generalisation of the TAR are required to accurately describe the effect of the centrifugal acceleration on GIW.
 |
Fig. 10. (a) Fractional frequency difference δfnkm/fnkm, with δfnkm = fcentrifugal − fspherical and fnkm = fcentrifugal as a function of the fractional rotation rate for n = 1 to n = 100. Calculations based on central 2 M⊙, Xc = 0.50 MESA model with Ω/Ωc ∈ [0.10−0.70], exhibiting prograde dipole sectoral (k, m) = (0, 1) modes. (b) Same as (a), but now with the isolated effect of the deformation of the Brunt-Väisälä frequency profile and radial coordinate (achieved by setting |
The frequency differences provide an assessment for the applicability of the analytical framework in Mathis & Prat (2019) in terms of the fraction of the critical rotation rate Ωc. For rotation rates near the critical value, that is Ω/Ωc = 0.80−0.99 (not shown in Fig. 10), the behaviour of δfnkm/fnkm deviates from the smooth curves in the figure for the lower values. This indicates that the assumptions in the analytical framework (e.g., only taking l = 0 and l = 2 projections into account) no longer hold for higher rotation rates than those shown in Fig. 10. The case where the centrifugal acceleration is treated in a non-perturbative manner will be part of a forthcoming work (Dhouib et al., in prep.).
4. Discussion and conclusions
The results in the previous section reveal that the centrifugal deformation of the star implies a shift in the extrema of the eigenfunctions towards the equator of the star. This effect becomes more outspoken towards the surface, since the centrifugal acceleration (and hence the dimensionless deformation factor ε) becomes more important as one moves from the centre to the outer layers. The eigenfunctions centred around the equator reveal narrower maxima, while the extrema of the off-equator eigenfunctions move inwards, towards the equator. We thus find that the effect of the centrifugal acceleration modifies that of the Coriolis acceleration included in the CLTE. More precisely, the Coriolis acceleration is responsible for a concentration of GIW towards the equator, while the centrifugal acceleration causes these equatorial bands to become narrower and the off-equator extrema of eigenfunctions shift inwards.
We found differences between the proof-of-concept study by Mathis & Prat (2019) and the quantitative numerical results in this work. The current new implementation uses a different approach for the computational aspects to solve the GLTE. In order to avoid numerical issues, Mathis & Prat (2019) made use of linearised expressions for the coefficients of the GLTE. However, such an approach has revealed the solutions to be rather dependent on the used number of collocation points. For this reason, we circumvented the use of numerical derivatives to solve the GLTE analytically where possible, as described in Sect. 2.2. In this way, the avoided crossings in the solution spectrum for the GLTE (Fig. 2; their Figs. 5 and 6) are circumvented here. Moreover, the current numerical approach leads to a relatively modest shift in the eigenfunctions towards the equator, as shown graphically in our Figs. 3, 5 and 6 as an improvement compared to the more pronounced behaviour found in Figs. 7 and 8 in Mathis & Prat (2019).
In essence, the centrifugal acceleration affects two aspects within the theoretical description of g-mode pulsators. On the one hand, the stellar structure as a whole becomes deformed, which naturally leads to changes in the Brunt-Väisälä frequency profile and therefore in the cavities of the gravity modes. This is an indirect effect. On the other hand, the g-mode oscillation equations, in the form of the Laplace tidal equations, are altered and get a radial dependence, propagating into deformed solutions compared to those of the CLTE. This is a direct effect. In the case of prograde sectoral modes, these aspects have similar effects on the mode frequencies, as demonstrated in Sect. 3.3.
The detectability of the effect of the centrifugal acceleration in space-based photometry decreases with increasing stellar age (decreasing Xc), increasing metallicity Z, and increasing core overshooting fov. Furthermore, as seen in in Table 1, the value of nmax increases with an increasing stellar mass and increasing rotation rate, since the deformation factor and rotation rate scale as ε ∼ Ω2.
Comparing the nmax values with radial-order distributions of observed GIW (Li et al. 2020; Pedersen et al. 2021), we conclude that the values we obtained here correspond well with the observations. This implies that it should be possible to detect differences between theoretically computed pulsation frequencies, assuming spherically symmetric versus deformed stellar models as computed in this work for real stars, provided that the comparison is done for models with the same input physics and rotation rate. The frequency differences as shown in Fig. 9 are of a similar order as typical uncertainties of the observed frequencies used in forward asteroseismic modelling (Aerts et al. 2018).
Frequency differences caused by other approximations that are commonly made in the TAR, such as the Cowling approximation and the neglect of the horizontal component of the rotation vector, are smaller than or comparable to those caused by the centrifugal acceleration. This is shown in Appendix C, where we obtain relative differences of ≲1% that are dependent on the stellar rotation rate, comparable to the differences between the TAR and the Mathis & Prat (2019) framework. A comparison between the TAR and full 2D computations carried out with the Adiabatic Code of Oscillation including Rotation (ACOR) by Ouazzani et al. (2017, Fig. 1) gave similar results. This indicates that, similar to the neglect of the centrifugal acceleration, other assumptions made within the TAR also have negligible or minor effects on the pulsation calculations. A limitation of the asymptotic expressions that is still present in the Mathis & Prat (2019) framework is that the effect of the centrifugal acceleration increases with a decreasing radial order of the g modes. At a low radial order, both the TAR and the asymptotic expressions cease to be valid.
In practice, Fig. 10 reveals that the fractional frequency differences due to the centrifugal acceleration remain well below 1% for high-order g modes in the asymptotic regime. Comparing this with typical fractional frequency differences in Aerts et al. (2018, Table 2) points out that the effect of the centrifugal acceleration is negligible compared to that introduced by some aspects of missing input physics, such as atomic diffusion in slow rotators among the g-mode pulsators (Mombarg et al. 2020) or near-core boundary mixing in fast rotating single SPB stars (Moravveji et al. 2016; Szewczuk & Daszyńska-Daszkiewicz 2018; Pedersen et al. 2021) and SPB binaries (Johnston et al. 2019). Hence, although the frequency differences induced by the centrifugal acceleration are expected to be detectable, one can ignore them for initial attempts of asteroseismic modelling. Once appropriate equilibrium models are found that explain the overall structure in the measured period spacing pattern of a star well, it is meaningful to test the effect of the centrifugal acceleration for those models to see if it brings an improved fit, particularly for stars with a relatively fast rotation.
Following the conclusions of Mathis & Prat (2019) and ours, a next logical step would be to include the effect of the centrifugal acceleration in stellar pulsation codes such as GYRE. Although our work has shown that the centrifugal acceleration can be treated as a lower-priority ingredient for forward asteroseismic modelling compared to other missing ingredients in the input physics, its effect is, in principle, detectable at the level of the mode computations. Hence, including it would lead to overall more realistic stellar pulsation predictions.
MESA version r11701. For more information about the different versions, see http://mesa.sourceforge.net/.
Acknowledgments
We thank the referee for their encouragement. We thank the MESA and GYRE developers for their efforts and for making their codes publicly available. The research leading to these results has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreements N°670519: MAMSIE with PI Aerts and N°647383: SPIRE with PI Mathis) and from the KU Leuven Research Council (grant C16/18/005: PARADISE). TVR is funded by the Research Foundation Flanders (FWO) by means of a Junior Postdoctoral Fellowship under grant agreement N°12ZB620N. VP and SM acknowledge support from the CNES PLATO grant at CEA/DAP.
References
- Aerts, C. 2021, Rev. Mod. Phys., 93, 15001 [Google Scholar]
- Aerts, C., Molenberghs, G., Michielsen, M., et al. 2018, ApJS, 237, 15 [Google Scholar]
- Aerts, C., Mathis, S., & Rogers, T. M. 2019, ARA&A, 57, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berthomieu, G., Gonczi, G., Graff, P., Provost, J., & Rocca, A. 1978, A&A, 70, 597 [Google Scholar]
- Borucki, W., Koch, D., Batalha, N., et al. 2009, in Transiting Planets, eds. F. Pont, D. Sasselov, M. J. Holman, et al., IAU Symp., 253, 289 [Google Scholar]
- Bouabid, M. P., Dupret, M. A., Salmon, S., et al. 2013, MNRAS, 429, 2500 [NASA ADS] [CrossRef] [Google Scholar]
- Boyd, J. P. 1976, PhD Thesis, Harvard University, USA [Google Scholar]
- Bugnet, L., Prat, V., Mathis, S., et al. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202039159 [Google Scholar]
- Christophe, S., Ballot, J., Ouazzani, R. M., Antoci, V., & Salmon, S. J. A. J. 2018, A&A, 618, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Torres, G. 2019, ApJ, 876, 134 [Google Scholar]
- Deal, M., Richard, O., & Vauclair, S. 2016, A&A, 589, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Degroote, P., Aerts, C., Baglin, A., et al. 2010, Nature, 464, 259 [Google Scholar]
- Dintrans, B., & Rieutord, M. 2000, A&A, 354, 86 [NASA ADS] [Google Scholar]
- Dintrans, B., Rieutord, M., & Valdettaro, L. 1999, J. Fluid Mech., 398, 271 [Google Scholar]
- Dziembowski, W., & Kosovichev, A. 1987a, Acta Astron., 37, 313 [Google Scholar]
- Dziembowski, W., & Kosovichev, A. 1987b, Acta Astron., 37, 341 [Google Scholar]
- Dziembowski, W., Kosovichev, A., & Kozlowski, M. 1987, Acta Astron., 37, 331 [Google Scholar]
- Eckart, C. 1960, Hydrodynamics of Oceans and Atmospheres (Oxford: Pergamon Press) [Google Scholar]
- Freytag, B., Ludwig, H. G., & Steffen, M. 1996, A&A, 313, 497 [NASA ADS] [Google Scholar]
- Gough, D. O. 1981, MNRAS, 196, 731 [Google Scholar]
- Hansen, C. J., Cox, J. P., & van Horn, H. M. 1977, ApJ, 217, 151 [Google Scholar]
- Henyey, L., Vardya, M. S., & Bodenheimer, P. 1965, ApJ, 142, 841 [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Hough, S. S. 1898, Philos. Trans. R. Soc. London Ser. A, 191, 139 [Google Scholar]
- Johnston, C., Aerts, C., Pedersen, M. G., & Bastian, N. 2019, A&A, 632, A74 [EDP Sciences] [Google Scholar]
- Kaye, A. B., Handler, G., Krisciunas, K., Poretti, E., & Zerbi, F. M. 1999, PASP, 111, 840 [Google Scholar]
- Laplace, P. S. 1799, Traité de Mécanique Cëleste (Paris: Imprimerie de Crapelet) [Google Scholar]
- Lee, U., & Baraffe, I. 1995, A&A, 301, 419 [NASA ADS] [Google Scholar]
- Lee, U., & Saio, H. 1986, MNRAS, 221, 365 [Google Scholar]
- Lee, U., & Saio, H. 1987, MNRAS, 224, 513 [Google Scholar]
- Lee, U., & Saio, H. 1997, ApJ, 491, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G., Bedding, T. R., Murphy, S. J., et al. 2019a, MNRAS, 482, 1757 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., & Antoci, V. 2019b, MNRAS, 487, 782 [Google Scholar]
- Li, C., Sun, W., de Grijs, R., et al. 2019c, ApJ, 876, 65 [Google Scholar]
- Li, G., Van Reeth, T., Bedding, T. R., et al. 2020, MNRAS, 491, 3586 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Springer A&A Library) [Google Scholar]
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- Mathis, S. 2009, A&A, 506, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Prat, V. 2019, A&A, 631, A26 [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Zahn, J. P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Bugnet, L., Prat, V., et al. 2021, A&A, 647, A122 [EDP Sciences] [Google Scholar]
- Michielsen, M., Pedersen, M. G., Augustson, K. C., Mathis, S., & Aerts, C. 2019, A&A, 628, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miglio, A., Montalbán, J., Noels, A., & Eggenberger, P. 2008, MNRAS, 386, 1487 [Google Scholar]
- Mombarg, J. S. G., Van Reeth, T., Pedersen, M. G., et al. 2019, MNRAS, 485, 3248 [Google Scholar]
- Mombarg, J. S. G., Dotter, A., Van Reeth, T., et al. 2020, ApJ, 895, 51 [Google Scholar]
- Moravveji, E., Townsend, R. H. D., Aerts, C., & Mathis, S. 2016, ApJ, 823, 130 [Google Scholar]
- Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., et al. 2017, MNRAS, 465, 2294 [Google Scholar]
- Pápics, P. I., Tkachenko, A., Van Reeth, T., et al. 2017, A&A, 598, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Pedersen, M. G., Aerts, C., Pápics, P. I., & Rogers, T. M. 2018, A&A, 614, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pedersen, M. G., Aerts, C., Pápics, P. I., et al. 2021, Nat. Astron., in press [Google Scholar]
- Prat, V., Mathis, S., Buysschaert, B., et al. 2019, A&A, 627, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prat, V., Mathis, S., Neiner, C., et al. 2020, A&A, 636, A100 [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, in Space Telescopes and Instrumentation 2014: Optical, Infrared, and Millimeter Wave, eds. J. Oschmann, M. Jacobus, M. Clampin, G. G. Fazio, H. A. MacEwen, et al., SPIE Conf. Ser., 9143, 914320 [Google Scholar]
- Rogers, T. M., & McElwaine, J. N. 2017, ApJ, 848, L1 [Google Scholar]
- Saio, H., Kurtz, D. W., Murphy, S. J., Antoci, V. L., & Lee, U. 2018, MNRAS, 474, 2774 [Google Scholar]
- Shibahashi, H. 1979, PASJ, 31, 87 [NASA ADS] [Google Scholar]
- Sweet, P. A. 1950, MNRAS, 110, 548 [Google Scholar]
- Szewczuk, W., & Daszyńska-Daszkiewicz, J. 2018, MNRAS, 478, 2243 [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [Google Scholar]
- Tkachenko, A., Aerts, C., Yakushechkin, A., et al. 2013, A&A, 556, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tkachenko, A., Pavlovski, K., Johnston, C., et al. 2020, A&A, 637, A60 [CrossRef] [EDP Sciences] [Google Scholar]
- Townsend, R. H. D., & Teitler, S. A. 2013, MNRAS, 435, 3406 [NASA ADS] [CrossRef] [Google Scholar]
- Townsend, R. H. D., Goldstein, J., & Zweibel, E. G. 2018, MNRAS, 475, 879 [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (University of Tokyo Press) [Google Scholar]
- Van Beeck, J., Prat, V., Van Reeth, T., et al. 2020, A&A, 638, A149 [EDP Sciences] [Google Scholar]
- Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015, ApJS, 218, 27 [Google Scholar]
- Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Reeth, T., Mombarg, J. S. G., Mathis, S., et al. 2018, A&A, 618, A24 [NASA ADS] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Waelkens, C. 1991, A&A, 246, 453 [NASA ADS] [Google Scholar]
- Wang, H., Boyd, J. P., & Akmaev, R. A. 2016, Geosci. Model Dev., 9, 1477 [Google Scholar]
- Weiss, W. W., Rucinski, S. M., Moffat, A. F. J., et al. 2014, PASP, 126, 573 [Google Scholar]
- Zahn, J. P. 1966, C. R. Acad. Sci. Paris Ser. B, 263, 1077 [Google Scholar]
- Zahn, J. P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
Appendix A: Centrifugal deformation of Brunt-Väisälä frequency profiles
After calculating the deformed stellar radius r(a, θ) using Eqs. (9) and (10), we computed the two-dimensional centrifugally deformed Brunt-Väisälä frequency profile
to ensure numerical stability and to account for the non-linear dependence of N2(a, θ) on the density 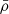 and the pressure
and the pressure 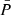 . These calculations were performed at discrete values of the co-latitude θ, and we used the calculation methods for
. These calculations were performed at discrete values of the co-latitude θ, and we used the calculation methods for 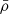 and
and 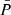 described in Sect. 2.1.1.
described in Sect. 2.1.1.
The perturbed adiabatic exponent 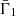 can then be estimated as follows:
can then be estimated as follows:
where quantities X from the spherical non-rotating input model are indicated as X0.
The perturbed gravitational acceleration is the gradient of the ‘effective’ gravitational potential 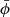 ;
;
The spheroidal gradient 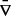 , defined as (Mathis & Prat 2019)
, defined as (Mathis & Prat 2019)
reduces to the total derivative d/da since the calculations of the perturbed quantities are discretised in the co-latitude θ, in other words, they are calculated for a specific, constant value of θ.
To avoid direct numerical differentiation of the perturbed pressure 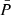 , it is rewritten as:
, it is rewritten as:
where we map the radius r0 of the non-deformed stellar model onto the pseudo-radius a, as in the evaluation of Eq. (11). Within their respective coordinate systems, both r0 and a coincide with the isobaric radial coordinate. Consequently, only the last derivative with respect to r0 in Eq. (A.9) has yet to be evaluated through numerical differentiation. This is numerically more stable than performing the derivation of 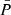 with respect to r. Similarly, for the derivative of the perturbed density
with respect to r. Similarly, for the derivative of the perturbed density 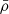 , we have the following:
, we have the following:
The last three derivatives with respect to a were again evaluated through numerical differentiation without numerical issues.
Finally, dP0/dr0 and dρ0/dr0 can be expressed in terms of physical quantities included in the (non-deformed) MESA stellar structure profiles. The former can be calculated by using hydrostatic equilibrium (in a spherically symmetric star):
and the latter can be retrieved from the non-perturbed squared Brunt-Väisälä frequency:
Appendix B: Computation of asymptotic frequencies
Here, we provide our strategy for computing the asymptotic frequencies and period spacing patterns presented in Sects. 3.3 and 3.4. This is summarised in a flow chart in Fig. B.1 and concerns the computation of the asymptotic frequencies for a given ‘pulsation mode’ with a mode identification (k, m) for a chosen ‘stellar structure model’ with a particular rotation rate (in terms of Ωc).
 |
Fig. B.1. Flow chart describing the strategy used in this work to compute asymptotic pulsation frequencies in a centrifugally deformed star. |
The period spacing pattern for a spherically symmetric, uniformly rotating star was computed within a radial order range of n = 1 to n = 100. This particular range was motivated by the radial order distributions of typically observed GIW (Li et al. 2020). Based on the resulting period spacing pattern, a suitable ν−range was chosen. To anticipate the (relatively small) effect of the centrifugal force on the asymptotic pulsation periods, small margins were taken above and below this range (typically ±0.5). In the next step, the GLTE was solved for a number of spin parameters within the predetermined range. A step size of 0.01 in ν was found suitable to avoid numerical inaccuracies, while maintaining reasonable computation times (typical values for νmax − νmin are of the order of 10). In the subsequent step, the expression for the asymptotic pulsation frequencies Eq. (16) is rewritten as follows:
and multiplied by 2 Ω to arrive at
The LHS of this equation was then evaluated at every ν in the spin parameter range, while the RHS was evaluated for every n ∈ [1; 100]. In the fourth step, the spin parameters νnkm corresponding to the radial orders n ∈ [1; 100] were computed through linear interpolation of the RHS of Eq. (B.2) to the (I(ν),ν) points from the previous step. Finally, the asymptotic angular frequencies ωnkm were retrieved by taking the inverse of the νnkm from the previous step and multiplying them by 2Ω. The corresponding asymptotic pulsation periods are Pnkm = 2π/ωnkm. The corresponding pulsation periods in the inertial (observer’s) frame 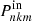 were then found through (Bouabid et al. 2013):
were then found through (Bouabid et al. 2013):
with Prot being the rotation period.
Appendix C: Comparison with other theoretical assumptions
Other assumptions that are included within the TAR are still made in the generalised framework developed by Mathis & Prat (2019), such as the neglect of the horizontal rotation vector component 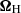 and the Cowling approximation. Here we assess the impact of these approximations on our results.
and the Cowling approximation. Here we assess the impact of these approximations on our results.
C.1. Neglect of the horizontal rotation vector
The spheroidal radial component of the momentum equation is given by Mathis & Prat (2019, Eq. 13) as
where 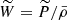 with
with 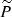 is the wave fluctuation of the pressure and
is the wave fluctuation of the pressure and 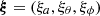 is the Lagrangian displacement vector. Within the generalised TAR framework, the two terms on the left-hand side (LHS) of Eq. (C.1) are neglected in favour of the
is the Lagrangian displacement vector. Within the generalised TAR framework, the two terms on the left-hand side (LHS) of Eq. (C.1) are neglected in favour of the 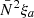 term on the right-hand side (RHS), and the second LHS-term contains the horizontal component of the rotation vector ΩH = Ω sin θ. Mathis & Prat (2019) combined the simplified Eq. (C.1) with the horizontal components of the momentum equation, and they solved the resulting system for a selected pulsation mode identification (k, m) and spin parameter value ν as a function of the normalised pressure
term on the right-hand side (RHS), and the second LHS-term contains the horizontal component of the rotation vector ΩH = Ω sin θ. Mathis & Prat (2019) combined the simplified Eq. (C.1) with the horizontal components of the momentum equation, and they solved the resulting system for a selected pulsation mode identification (k, m) and spin parameter value ν as a function of the normalised pressure 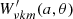 :
:
Expressions for the coefficients C(a,θ) and D(a,θ) are given in Eqs. (20)–(25).
We assessed the validity of neglecting the LHS terms in Eq. (C.1) by taking their ratios with the 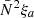 term and filling in the solution for
term and filling in the solution for 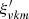 . For the first LHS term, we obtain
. For the first LHS term, we obtain
and for the second LHS term, we find
Hence, the errors introduced by neglecting the terms in Eq. (C.1) scale with 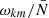 and
and 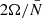 , respectively. We can ignore the contribution from the horizontal component of the rotation vector when the GIW propagate in a strongly stratified radiative region, that is for
, respectively. We can ignore the contribution from the horizontal component of the rotation vector when the GIW propagate in a strongly stratified radiative region, that is for 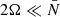 . This is further illustrated in Fig. C.1, where we compare the terms in the momentum equation Eq. (C.1) for a (n, k, m) = (50, 0, 1) pulsation mode in the central model of our MESA grid, with a rotation rate of Ω = 0.15 Ωc. The relative contribution of the neglected LHS terms, which include the Ω sin θ-component of the rotation vector, is ∼1%. The (normalised) components of the Lagrangian displacement (ξa, ξθ, ξϕ), calculated in this simulation using Eqs. (C.2)–(C.4), are shown in Fig. C.2. As can be seen, ξa ≪ ξθ, ξφ.
. This is further illustrated in Fig. C.1, where we compare the terms in the momentum equation Eq. (C.1) for a (n, k, m) = (50, 0, 1) pulsation mode in the central model of our MESA grid, with a rotation rate of Ω = 0.15 Ωc. The relative contribution of the neglected LHS terms, which include the Ω sin θ-component of the rotation vector, is ∼1%. The (normalised) components of the Lagrangian displacement (ξa, ξθ, ξϕ), calculated in this simulation using Eqs. (C.2)–(C.4), are shown in Fig. C.2. As can be seen, ξa ≪ ξθ, ξφ.
 |
Fig. C.1. Comparison of the terms in the momentum equation Eq. (C.1). The |
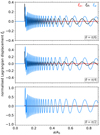 |
Fig. C.2. (Normalised) components of the Lagrangian displacement ξa (red), ξθ (black), and ξϕ (blue), calculated in the numerical simulations shown in Fig. C.1. The functions are shown at co-latitudes θ = π/6 (top), π/4 (middle), and π/2 (bottom). |
C.2. The Cowling approximation
We evaluated the Cowling approximation for the central MESA model in our grid (2 M⊙, Xc = 0.50) using GYRE for rotation rates Ω/Ωc ∈ [0.10−0.70], without the centrifugal acceleration. As shown in Fig. C.3, the relative differences between the pulsation frequencies, caused by the Cowling approximation, are ∝0.1%. These are smaller than the relative differences introduced by the centrifugal acceleration, but they increase with an increasing radial order of the g modes.
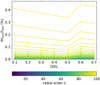 |
Fig. C.3. Relative pulsation frequency shifts δfnkm/fnkm caused by the Cowling approximation, with δfnkm = fCowling − fwithout Cowling and fnkm = fwithout Cowling, as a function of the fractional rotation rate for n = 1 to n = 100. Calculations were performed using the central 2 M⊙, Xc = 0.50 MESA model with Ω/Ωc ∈ [0.10−0.70], for prograde dipole sectoral (k, m) = (0, 1) modes. |
All Tables
Potential detectability of the effect of the centrifugal acceleration in space-based photometric observations.
All Figures
 |
Fig. 1. Selected ranges and values for the input parameters of the 1D stellar structure models used in this work. |
| In the text | |
 |
Fig. 2. Solution spectrum of the generalised Laplace tidal equation for modes with m = 2. Modes with even eigenfunctions are shown in blue, and those with odd eigenfunctions are in orange. Light (dark) colours correspond to solutions near the surface (core). The equilibrium model used as input for the computations has the same parameters as in the highlighted row in Fig. 1. |
| In the text | |
 |
Fig. 3. Modified radial Hough functions wνkm(a, θ) (normalised) for ν = 2 and Ω/Ωc = 0.50. Solutions are plotted in a colour range from indigo to yellow from the stellar core to the surface. The green dashed line shows the solution of the CLTE. The number of collocation points for this computation was N = 200. |
| In the text | |
 |
Fig. 4. Modified radial Hough functions wνkm(a, θ) (normalised) for Ω/Ωc = 0.50 and two different spin parameters. The 2.0 M⊙, Xc = 0.50 equilibrium model was used as input. The colour scheme and number of collocation points are identical to that of Fig. 3 (CLTE solutions have been left out for clarity). |
| In the text | |
 |
Fig. 5. (a) Modified radial Hough functions wνkm(a, θ) (normalised) for three different modes (with specified spin parameter ν). Colour conventions are the same as those in Fig. 3. (b) Eigenvalue Λνkm(a) profiles corresponding to the eigenfunctions in (a). Points indicated with a ⋆ correspond to eigenvalues obtained by solving the GLTE. Red points were found via quadratic interpolation. The considered number of collocation points was N = 200. |
| In the text | |
 |
Fig. 6. (a) Modified radial Hough functions wνkm(a = AS, θ) for seven different rotation rates and ν = 2. (b) Eigenvalue Λνkm(a) profiles corresponding to the eigenfunctions in (a). |
| In the text | |
 |
Fig. 7. Period spacing pattern in an inertial frame computed for (k, m) = (0, 1) modes in a centrifugally deformed 2.0 M⊙, Xc = 0.50 (Xc/Xini = 0.70), Z = 0.014, Dmix = 1 cm2 s−1, fov = 0.015 equilibrium model at Ω/Ωc = 0.50 (blue line). The black-dashed line shows the equivalent period spacing pattern for the same model, but without the effect of the centrifugal acceleration. The red and purple lines show the results for |
| In the text | |
 |
Fig. 8. Theoretical period spacing pattern in the inertial frame for (k, m) = (−2, −1) modes in the same equilibrium model as in Fig. 7 at Ω/Ωc = 0.50 (blue line). The black-dashed line shows the equivalent period spacing pattern for the same model, but without the effect of the centrifugal acceleration. The red and purple show the isolated effect of |
| In the text | |
 |
Fig. 9. Asymptotic frequency differences (black) for dipole (k, m) = (0, 1) modes at Ω = 0.15 Ωc for the central 2.0 M⊙, Xc = 0.50 MESA model. Red and blue bands represent the frequency resolution of Kepler and TESS, respectively. The respective values of nmax are indicated by vertical dashed lines. |
| In the text | |
 |
Fig. 10. (a) Fractional frequency difference δfnkm/fnkm, with δfnkm = fcentrifugal − fspherical and fnkm = fcentrifugal as a function of the fractional rotation rate for n = 1 to n = 100. Calculations based on central 2 M⊙, Xc = 0.50 MESA model with Ω/Ωc ∈ [0.10−0.70], exhibiting prograde dipole sectoral (k, m) = (0, 1) modes. (b) Same as (a), but now with the isolated effect of the deformation of the Brunt-Väisälä frequency profile and radial coordinate (achieved by setting |
| In the text | |
 |
Fig. B.1. Flow chart describing the strategy used in this work to compute asymptotic pulsation frequencies in a centrifugally deformed star. |
| In the text | |
 |
Fig. C.1. Comparison of the terms in the momentum equation Eq. (C.1). The |
| In the text | |
 |
Fig. C.2. (Normalised) components of the Lagrangian displacement ξa (red), ξθ (black), and ξϕ (blue), calculated in the numerical simulations shown in Fig. C.1. The functions are shown at co-latitudes θ = π/6 (top), π/4 (middle), and π/2 (bottom). |
| In the text | |
 |
Fig. C.3. Relative pulsation frequency shifts δfnkm/fnkm caused by the Cowling approximation, with δfnkm = fCowling − fwithout Cowling and fnkm = fwithout Cowling, as a function of the fractional rotation rate for n = 1 to n = 100. Calculations were performed using the central 2 M⊙, Xc = 0.50 MESA model with Ω/Ωc ∈ [0.10−0.70], for prograde dipole sectoral (k, m) = (0, 1) modes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



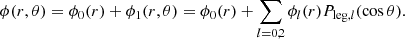
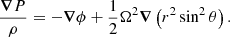
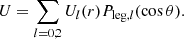
![$$ \begin{aligned}&P_{l}(r) = -\rho _{0}(r)\left[\phi _{l}(r) + U_{l}(r)\right] , \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq6.gif)
![$$ \begin{aligned}&\rho _{l}(r) = \frac{1}{{ g}_{0}(r)}\frac{\mathrm{{d}}\rho _{0}(r)}{\mathrm{{d}}r}\left[\phi _{l}(r) + U_{l}(r)\right] . \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq7.gif)
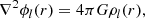
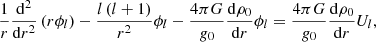
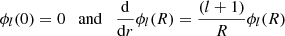
![$$ \begin{aligned} r = a\left[1+\varepsilon (a,\theta )\right]. \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq11.gif)
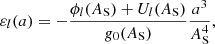
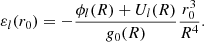
![$$ \begin{aligned} \mathcal{L} ^\mathrm{{class.}}_{\nu m}\left[\Theta _{\nu km}\right] = -\Lambda _{\nu km}^{\mathrm{class.} }\Theta _{\nu km}, \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq14.gif)
![$$ \begin{aligned}&\mathcal{L} ^\mathrm{{class.}}_{\nu m} = \frac{1-x^2}{1-\nu ^2 x^2}\partial ^2_{x} - \frac{2x\left(1-\nu ^2\right)}{\left(1-\nu ^2 x^2\right)^2}\partial _{x} \nonumber \\&\qquad \qquad + \left[\frac{m\nu \left(1+\nu ^2 x^2\right)}{\left(1-\nu ^2 x^2\right)^2} - \frac{m^2}{\left(1-x^2\right)\left(1-\nu ^2 x^2\right)}\right] . \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq16.gif)
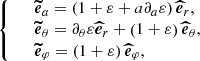
![$$ \begin{aligned}&\mathcal{L} _{\nu m}\left[{ w}_{\nu k m}\right] = \left(\frac{1-x^2}{{\mathcal{D} }}\right)\partial _x^2 { w}_{\nu km} \nonumber \\&\qquad \qquad \quad + \left[\frac{\left(1-x^2\right)\partial _x\mathcal{E} }{{\mathcal{D} }} + \partial _{x}\left(\frac{1-x^2}{{\mathcal{D} }}\right)\right]\partial _x { w}_{\nu km}\nonumber \\&\qquad \qquad \quad - \left[\frac{m^2}{\left(1-x^2\right)\mathcal{D} } - m\nu \frac{{\mathrm{d} }}{{\mathrm{d} }x}\left(\frac{x{\mathcal{C} }}{{\mathcal{D} }}\right) - m\nu \frac{x\mathcal{C} }{{\mathcal{D} }}\partial _{x}\mathcal{E} \right]{ w}_{\nu km} \nonumber \\&\qquad \qquad \ = -\Lambda _{\nu km}(a){ w}_{\nu km} , \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq21.gif)
![$$ \begin{aligned}&\mathcal{A} (a,\theta ) = 1+2\varepsilon ,\quad \mathcal{B} (a,\theta ) = \mathcal{A} + \tan \theta \partial _{\theta }\varepsilon \\&\mathcal{C} (a,\theta ) = \mathcal{B} /\mathcal{A} , \quad \mathcal{D} (a,\theta ) = \mathcal{A} \left[1-\nu ^2\cos ^2\theta \,\mathcal{C} ^2\right] \\&\mathcal{E} (a,\theta ) = 3\varepsilon + a\partial _{a}\varepsilon . \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq22.gif)
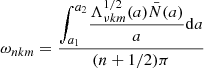
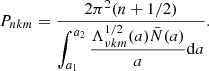
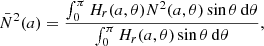
![$$ \begin{aligned} N^2(a,\theta ) = -\frac{\bar{g}}{r}\left[\frac{{\mathrm{d} }\ln \bar{\rho }}{{\mathrm{d} }\ln r} - \frac{1}{\bar{\Gamma }_{1}}\frac{{\mathrm{d} }\ln \bar{P}}{{\mathrm{d} }\ln r}\right] , \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq28.gif)
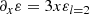
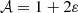
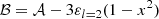
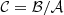
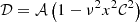
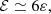
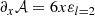
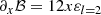
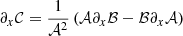
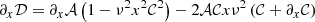
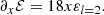
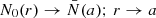
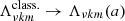
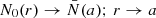
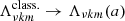
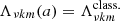
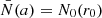
![$$ \begin{aligned} N^2(a,\theta ) = -\frac{\bar{g}}{r}\left[\frac{{\mathrm{d} }\ln \bar{\rho }}{{\mathrm{d} }\ln r} - \frac{1}{\bar{\Gamma }_{1}}\frac{{\mathrm{d} }\ln \bar{P}}{{\mathrm{d} }\ln r}\right]\, \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq56.gif)
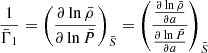
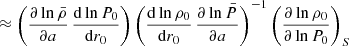
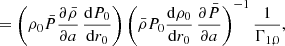
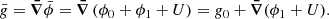
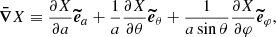
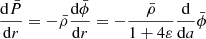
![$$ \begin{aligned}&\quad \ = -\frac{\bar{\rho }}{1+4\varepsilon }\left[{g}_{0} + \frac{{\mathrm{d} }}{{\mathrm{d} }a}(\phi _{1} + U)\right] \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq71.gif)
![$$ \begin{aligned}&\quad \ = -\frac{\bar{\rho }}{1+4\varepsilon }\left[{g}_{0} + \frac{{\mathrm{d} }}{{\mathrm{d} }r_0}(\phi _{1} + U)\right], \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq72.gif)
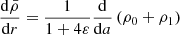
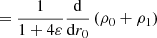
![$$ \begin{aligned}&\quad \ = \frac{1}{1 + 4\varepsilon }\left[\frac{{\mathrm{d} } \rho _{0}}{{\mathrm{d} } r_0} + \frac{{\mathrm{d} }}{{\mathrm{d} } r_0}\left(\frac{1}{{g}_{0}}\frac{{\mathrm{d} } \rho _{0}}{{\mathrm{d} } r_0}\left(\phi _{1} + U\right)\right)\right] \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq77.gif)
![$$ \begin{aligned}&\quad \ = \frac{1}{1+4\varepsilon }\frac{{\mathrm{d} } \rho _{0}}{{\mathrm{d} } r_0}\left[1 - \left(\frac{\phi _{1} + U}{{ g}_{0}^2}\right)\frac{{\mathrm{d} } {g}_{0}}{{\mathrm{d} } r_0} + \frac{1}{{g}_{0}}\frac{{\mathrm{d} } }{{\mathrm{d} } r_0}(\phi _{1} + U)\right]\nonumber \\&\qquad + \frac{\phi _{1} + U}{{ g}_{0}(1+4\varepsilon )}\frac{{\mathrm{d} }}{{\mathrm{d} } r_0}\left(\frac{{\mathrm{d} } \rho _{0}}{{\mathrm{d} } r_0}\right). \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq78.gif)
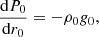
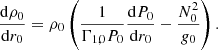
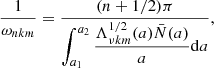
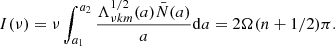
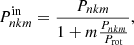
![$$ \begin{aligned}&-\bar{N}^2\left(\frac{\omega }{\bar{N}}\right)^2\left[\left(1 + 2\left(\varepsilon + a\partial _a\varepsilon \right)\right)\xi _a + \xi _\theta \partial _\theta \varepsilon \right] \nonumber \\&\qquad - i \bar{N}^2\left(\frac{\omega }{\bar{N}}\right)\left(\frac{2\Omega }{\bar{N}}\right)\left(1 + 2\varepsilon + a\partial _a\varepsilon \right)\sin \theta \,\xi _\varphi \nonumber \\&\qquad = -\partial _a\widetilde{W} - \bar{N}^2\xi _a - \frac{1}{\bar{\rho }^2}\partial _a\bar{\rho }\widetilde{P} , \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq86.gif)
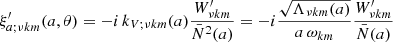
![$$ \begin{aligned}&\xi ^\prime _{\theta ;\nu km}(a,\theta ) = \frac{1}{a}\frac{1}{\omega _{km}^2}\frac{1}{\mathcal{D} }\left[\partial _\theta W^\prime _{\nu km} - m\nu \frac{\cos \theta }{\sin \theta }C W^\prime _{\nu km}\right] \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq93.gif)
![$$ \begin{aligned}&\xi ^\prime _{\varphi ;\nu km}(a,\theta ) = i\frac{1}{a}\frac{1}{\omega _{km}^2}\frac{1}{\mathcal{D} }\left[\nu C \cos \theta \partial _\theta W^\prime _{\nu km} - \frac{m}{\sin \theta }W^\prime _{\nu km}\right]. \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq94.gif)
![$$ \begin{aligned}&\bar{N}^2\left(\frac{\omega _{km}}{\bar{N}}\right)^2\left[\left(1 + 2\left(\varepsilon + a\partial _a\varepsilon \right)\right)\xi _{a;\nu km} + \xi _{\theta ;\nu km}\partial _\theta \varepsilon \right] \left[\bar{N}^2\xi _{a;\nu km}\right]^{-1}\nonumber \\&\qquad \simeq \left(\frac{\omega _{km}}{\bar{N}}\right)^2\left(1 + 8\varepsilon \right) + \left(\frac{\omega _{km}}{\bar{N}}\right)\frac{3\varepsilon _{l=2}}{\mathcal{D} \sqrt{\Lambda _{\nu km}}}\nonumber \\&\qquad \qquad \times \left[\frac{\sin 2\theta \,\partial _\theta W^\prime _{\nu km}}{2iW^\prime _{\nu km}} - \frac{m\nu C \cos ^2\theta W^\prime _{\nu km}}{iW^\prime _{\nu km}}\right] , \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq97.gif)
![$$ \begin{aligned}&i \bar{N}^2\left(\frac{\omega _{km}}{\bar{N}}\right)\left(\frac{2\Omega }{\bar{N}}\right)\left(1 + 2\varepsilon + a\partial _a\varepsilon \right)\sin \theta \,\xi _\varphi \left[ \bar{N}^2\xi _{a;\nu km}\right]^{-1}\nonumber \\&\quad \simeq \left(\frac{2\Omega }{\bar{N}}\right)\frac{\left(1 + 5\varepsilon \right)}{2\mathcal{D} \sqrt{\Lambda _{\nu km}}}\left[\sin \left(2\theta \right)\nu \mathcal{C} \frac{\partial _\theta W^\prime _{\nu km}}{iW^\prime _{\nu km}} - \frac{2m W^\prime _{\nu km}}{iW^\prime _{\nu km}}\right]. \end{aligned} $$](/articles/aa/full_html/2021/04/aa39464-20/aa39464-20-eq98.gif)