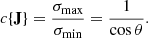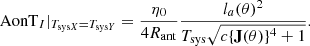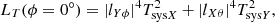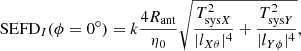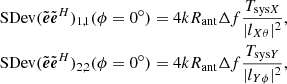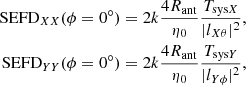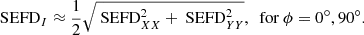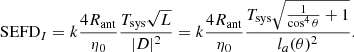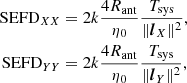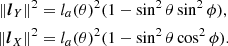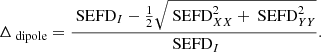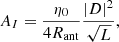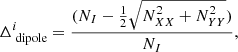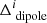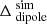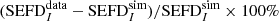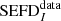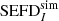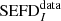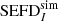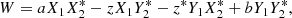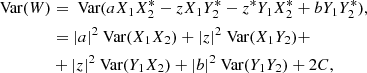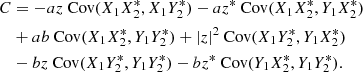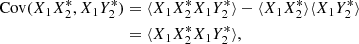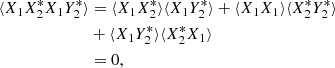| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 11 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202039445 | |
| Published online | 19 February 2021 | |
Sensitivity of a low-frequency polarimetric radio interferometer
International Centre for Radio Astronomy Research (ICRAR), Curtin University, Curtin 6102, Australia
e-mail: adrian.sutinjo@curtin.edu.au
Received:
16
September
2020
Accepted:
14
December
2020
Context. The sensitivity of a radio interferometer is a key figure of merit (FoM) for a radio telescope. The sensitivity of a single polarized interferometer is typically given as an antenna effective area over a system temperature, Ae/Tsys, assuming an unpolarized source. For a dual-polarized polarimetric interferometer intended to observe sources of unknown polarization, the state of polarization must not be assumed a priori. Furthermore, in contrast to the narrow field of view (FoV) of dish-based interferometers, the sensitivity of a polarimetric low-frequency radio interferometer warrants a careful review because of the very wide FoV of the dual-polarized antennas. A revision of this key FoM is particularly needed in the context of the Low-Frequency Square Kilometre Array (SKA-Low) where the sensitivity requirements are currently stated using Ae/Tsys for a single-polarized antenna system, which produces ambiguity for off-zenith angles.
Aims. This paper aims to derive an expression for the sensitivity of a polarimetric radio interferometer that is valid for all-sky observations of arbitrarily polarized sources, with neither a restriction on FoV nor with any a priori assumption regarding the polarization state of the source. We verify the resulting formula with an all-sky observation using the Murchison Widefield Array telescope.
Methods. The sensitivity expression was developed from first principles by applying the concept of system equivalent flux density (SEFD) to a polarimetric radio interferometer (not by computing Ae/Tsys). The SEFD was calculated from the standard deviation of the noisy flux density estimate for a target source due to system noise.
Results. The SEFD for a polarimetric radio interferometer is generally not 1/√2 of a single-polarized interferometer as is often assumed for narrow FoV. This assumption can lead to significant errors for a dual-polarized dipole based system, which is common in low-frequency radio astronomy: up to ∼15% for a zenith angle with a coverage of 45° and up to ∼45% for 60° coverage. The worst case errors occur in the diagonal planes of the dipole for very wide FoV. This is demonstrated through theory, simulation, and observations. Furthermore, using the resulting formulation, the calculation of the off-zenith sensitivity is straightforward and unambiguous.
Conclusions. For wide FoV observations pertinent to a low-frequency radio interferometer such as SKA-Low, the narrow FoV and the single-polarized sensitivity expressions are not correct and should be replaced by the formula derived in this paper.
Key words: instrumentation: interferometers / instrumentation: polarimeters / techniques: interferometric / telescopes / techniques: polarimetric
© ESO 2021
1. Introduction
A polarimetric radio interferometer consists of at least two dual-polarized antennas separated by a distance, as shown in Fig. 1. The treatment of radio interferometry in the context of dish antenna-based systems is quite vast as summarized in Thompson et al. (2017a). However, a low-frequency (≲350 MHz) radio interferometer (Tingay et al. 2013; van Haarlem et al. 2013; Ellingson et al. 2009; Labate et al. 2017a) notably differs from the dish antennas in that the low-frequency antennas are fixed with respect to the ground (as they do not mechanically point to the target) and the telescope field of view (FoV) is wide. This difference is particularly evident in the treatment of a polarimetric observation (Sutinjo et al. 2015a; Sokolowski et al. 2017).
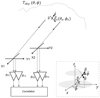 |
Fig. 1. Two dual-polarized low-frequency antennas forming an interferometer. The signal of interest is the partially polarized field |
Sensitivity is a metric for the faintest signal that can be measured by the telescope. In the context of radio astronomy, a conceptually meaningful measure is the system equivalent flux density (SEFD). We may think of the SEFD as the flux of the target source that equals the standard deviation of the noisy flux density estimate generated by the system. The conventional references for the sensitivity of a radio interferometer are Crane & Napier (1989) and Wrobel et al. (1999). The derivations in these references are based on a single polarized dish antennas, in particular the Very Large Array (VLA) and Very-Long-Baseline Interferometry (VLBA). The results were extrapolated to the dual-polarized system via a statistical argument, that is the sensitivity is 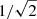 times that of a single polarized system (Crane & Napier 1989). We shall demonstrate that this is correct for the low-frequency interferometer only under certain conditions.
times that of a single polarized system (Crane & Napier 1989). We shall demonstrate that this is correct for the low-frequency interferometer only under certain conditions.
The need to derive the correct sensitivity metric for a radio polarimeter is being recognized (Piepmeier et al. 2008; Carozzi 2019; Warnick et al. 2012). Proper treatment of this is particularly important in next-generation low-frequency radio telescopes such as the low-frequency component of the Square Kilometre Array (Labate et al. 2017b) with very wide FoV and dual-polarized antennas with generally unequal responses at angles away from zenith. However, current requirements are still being stated using the antenna effective area over the system temperature (Ae/Tsys) which refers to a single-polarized antenna system (Dewdney 2016; Caiazzo 2017) assuming an unpolarized source. This leads to ambiguity in the interpretation of the off-zenith sensitivity requirement. The work in Piepmeier et al. (2008) generalized the concept of antenna temperature to Stokes parameters, which is a partial advance to Ae/Tsys for Stokes parameters. However, as we shall discuss, the SEFD approach is more straightforward; the result can be extended with caution to a comparable metric to Ae/Tsys. Discussions of SEFD for Stokes parameters was initiated in Carozzi (2019) and Warnick et al. (2012), but yet to be developed for the interferometer. Furthermore, in the context of the global collaboration towards SKA-Low, we seek an expression that has clear links to radio astronomy, and for which design implications may be readily inferred by engineers.
A polarimetric radio interferometer can estimate the flux density of a target source because of the dual-polarized antennas. Therefore, we expect to derive the SEFD directly for an arbitrary polarization without starting with Ae/Tsys, for which one has to assume something about the polarization of the incoming wave (Ko 1962). Strictly speaking, SEFD cannot be defined for a single-polarized radio telescope as it is unable to measure the flux density of a target source due to insufficient information. The best an observer can do in this case is assume that the target source is unpolarized and apply a correction factor based on that assumption. This obviously does not apply to a target source of unknown polarization and hence warrants a close review in Sect. 2.
2. Background and aim
The interferometer under consideration is depicted in Fig. 1. Two dual-polarized antennas separated by a certain distance on a co-planar surface are illuminated by a background sky which we assume to be unpolarized with noise temperature distribution Tsky(θ, ϕ) in the spherical coordinate system. A partially polarized source 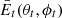 whose polarization property is unknown but is of interest is the target of observation. The study of polarization (polarimetry) is facilitated by the Stokes parameters (Wilson et al. 2009), which are formed by linear combinations of the correlator output.
whose polarization property is unknown but is of interest is the target of observation. The study of polarization (polarimetry) is facilitated by the Stokes parameters (Wilson et al. 2009), which are formed by linear combinations of the correlator output.
The observation of 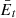 must contend with the undesired noise produced by Tsky and the amplifiers in Fig. 1. We call the combination of these undesired noise sources, the system noise. The system noise is the dominant source of random error in the observation (Wrobel et al. 1999). The higher the system noise relative to the antenna response in the direction of the target source, the higher the uncertainty in the resulting polarization estimates, which means the sensitivity of the instrument to
must contend with the undesired noise produced by Tsky and the amplifiers in Fig. 1. We call the combination of these undesired noise sources, the system noise. The system noise is the dominant source of random error in the observation (Wrobel et al. 1999). The higher the system noise relative to the antenna response in the direction of the target source, the higher the uncertainty in the resulting polarization estimates, which means the sensitivity of the instrument to 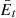 is low and vice versa.
is low and vice versa.
The aim of this work is to quantify the sensitivity of a radio interferometer for polarimetry of an arbitrarily located target signal of any polarization state. The SEFD (Wrobel et al. 1999) is the natural choice for the sensitivity metric because any source, be it fully polarized, partially polarized, or unpolarized, has an unambiguous flux density (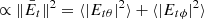 ) that is independent of its polarization state and the instrumentation used to observe it. Due to the dual-polarized antennas, the radio interferometer is suitable to detect the target source flux density. For comparison to the SEFD, we consider Ae/Tsys, which is often used as the figure of merit (FoM) of a radio telescope. The antenna effective area, Ae, is defined for matched polarization (IEEE 2014). The practice of using Ae/Tsys in radio astronomy implicitly assumes an unpolarized source, and thereby the polarization mismatch factor of 1/2 (Ko 1962) is attached to Ae (Thompson et al. 2017a),
) that is independent of its polarization state and the instrumentation used to observe it. Due to the dual-polarized antennas, the radio interferometer is suitable to detect the target source flux density. For comparison to the SEFD, we consider Ae/Tsys, which is often used as the figure of merit (FoM) of a radio telescope. The antenna effective area, Ae, is defined for matched polarization (IEEE 2014). The practice of using Ae/Tsys in radio astronomy implicitly assumes an unpolarized source, and thereby the polarization mismatch factor of 1/2 (Ko 1962) is attached to Ae (Thompson et al. 2017a),
Clearly, this does not apply to polarimetry which concerns an unknown polarization state.
The system equivalent noise contribution to sensitivity is conceptually simple. We consider the following thought experiment that is consistent with the approach outlined for the sensitivity calculation of a radio interferometer in Wrobel et al. (1999). Suppose we are able to turn the target source and the system noise ON or OFF at will. If we turn OFF the target source but keep the system noise ON and observe the response of the system in the target direction, we see random noise that can be quantified by its standard deviation; this is the system equivalent component. If we now reverse the situation by turning OFF the system noise and turning ON the target source, the SEFD is that flux density for which the expected value of the measurement due to the target source is equal to the standard deviation due to the system noise. We do not make an assumption regarding the polarization state of the target source. Also because the target is turned OFF during the system noise measurement, it stands to reason that the resulting SEFD is independent of the target electric field. Hence, we expect a sensitivity figure of merit that characterizes only the system, which is a desirable outcome. The conceptual approach outlined above, coupled with the statistical independence of the noise sources (as will be explained later), results in an efficient calculation of sensitivity in terms of SEFD. This result allows us to derive a measure with units of m2K−1 which is comparable to Ae/Tsys but applicable to the polarimeter.
3. Theory and SEFD calculation
3.1. The response to the target field
The open-circuit voltages seen at the inputs of the amplifiers connected to the antenna system 1 due to the target electric field (|t) is (Smirnov 2011; Sutinjo et al. 2015a; Sokolowski et al. 2017)1
The entries of the Jones matrix J has a unit of antenna length in m which transforms the electric field in V m−1 to voltage. The Jones matrix entries are direction dependent and deterministic quantities. The electric field components Etθ, Etϕ as well as the port voltages are complex random variables which we treat as complex envelope quantities. Similarly, the response of antenna system 2 to the same target is
We assume that the antenna system 2 consists of dual-polarized antennas of an identical design and response as the antenna system 1. The exponential term in Eq. (3) is a known phase shift due to the direction of the target and the position of the antenna system 2 relative to the antenna system 1. The exponent term can be removed from the measurement and will no longer be carried henceforth.
The correlator forms the outer product
The expected value of Eq. (4) is
where the quantity of interest is
from which the polarization property of the target is inferred using the Stokes parameters I, Q, U, V (Wilson et al. 2009; Smirnov 2011)2.
3.2. SEFD
In practice we obtain Eq. (6) from 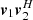 which is dominated by system noise, such that the result is an estimate of Eq. (6)
which is dominated by system noise, such that the result is an estimate of Eq. (6)
The Jones matrix must be invertible for polarimetry. As seen in Sect. 4.2 later, the Jones matrix of a dual-polarized dipole antenna system is invertible for angles above the horizon. The flux density of the target is defined as
in W m−2 and 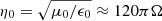 is the free space impedance; the subscript ⟨.⟩_, _ indicates the matrix entry; the magnitude of the complex envelope is taken as the root mean square (rms) value. The SEFDI (strictly speaking, the underscore .I is redundant but we choose to keep it to distinguish this true SEFD from the SEFDunpol. based on the assumption of an unpolarized target because the latter is so pervasive) therefore is the flux density of a target source which is equal to the standard deviation of the sum of the diagonal of the noisy estimate
is the free space impedance; the subscript ⟨.⟩_, _ indicates the matrix entry; the magnitude of the complex envelope is taken as the root mean square (rms) value. The SEFDI (strictly speaking, the underscore .I is redundant but we choose to keep it to distinguish this true SEFD from the SEFDunpol. based on the assumption of an unpolarized target because the latter is so pervasive) therefore is the flux density of a target source which is equal to the standard deviation of the sum of the diagonal of the noisy estimate 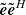 ,
,
The standard deviations of each diagonal entry of 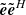 are also quantities of interest because these entries are produced in a typical radio astronomy correlation process. These quantities are conventionally called XX and YY after the diagonals of Eq. (4). However, in the spherical coordinate system, they are θθ and ϕϕ because they are estimates of |Eθ|2 and |Eϕ|2. Although, strictly speaking, we should not attempt to define SEFD for θθ or ϕϕ quantities separately because each one has insufficient information for reconstructing the flux density of an arbitrarily polarized target.
are also quantities of interest because these entries are produced in a typical radio astronomy correlation process. These quantities are conventionally called XX and YY after the diagonals of Eq. (4). However, in the spherical coordinate system, they are θθ and ϕϕ because they are estimates of |Eθ|2 and |Eϕ|2. Although, strictly speaking, we should not attempt to define SEFD for θθ or ϕϕ quantities separately because each one has insufficient information for reconstructing the flux density of an arbitrarily polarized target.
3.3. Calculation of standard deviation due to system noise
In this section, the target field is turned OFF. The system noise consists of sky noise and amplifier noise represented by voltage sources with subscripts .s and .n, respectively in Fig. 2. For example, VnX1 is the voltage noise due to the amplifier (more generally the receiver chain) connected to antenna X1; VnY2 is the voltage noise due to the amplifier connected to antenna Y1; VsX1 and VsY2 represent the sky noise seen at antennas X1 and Y2, respectively; VX1 and VY2 represent the total voltages seen at antennas X1 and Y2, respectively, which are the quantities that are processed by the correlator. The interaction between the voltage and current at the antenna ports is captured by the impedance matrix Z (Sutinjo et al. 2015a; Warnick et al. 2018). The noise sources due to the sky and the amplifiers are mutually independent. Every antenna is connected to its own receiver chain such that the receiver noise is independent from one another. The representation in Fig. 2 is a standard treatment for noise in a multiport system with a well-established history (Twiss 1955; Rothe & Dahlke 1956; Russer & Müller 1990) and application in receiving phased array systems (Warnick et al. 2009, 2018).
 |
Fig. 2. Circuit representation of the four-port network. The impedance matrix Z is a noiseless network describing relationship between the antenna voltages and currents. The sky noise and the amplifier noise sources are denoted by subscripts .s and .n, respectively. |
In the absence of the target field, the interferometer is illuminated by a diffuse sky noise such that the mutual coherence between antenna systems 1 and 2 is insignificant for separations greater than tens of wavelengths (Sutinjo et al. 2015b). In addition, for orthogonally polarized antenna elements, the isolation between the two polarizations (for example, X1 and Y1) is high such that the mutual coherence between them due to the diffuse sky is negligible. In antenna engineering terms, the antenna mutual coupling is considered insignificant for statistical calculation. This permits all voltage noise sources in Fig. 2 to be treated as independent noise which greatly simplifies the computation. Furthermore, if we assume all antennas are of an identical design, the impedance seen into each antenna port (Z11 = Zant) is identical at all four ports as shown in Fig. 3.
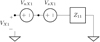 |
Fig. 3. Simplified impedance (noiseless) and noise sources seen at the antenna port. Z11 is the impedance seen at the antenna port 1. The same circuit is seen at Y1, X2, Y2 with subscript substitutions. |
We base our standard deviation calculation on the simplified circuit in Fig. 3. For that we need the statistics of Vn and Vs described as follows. Vs is a thermal noise source due to the antenna resistance Rant (the real part of Zant) at antenna temperature Tant which is the result of the integral of the product of the antenna pattern and Tsky (see Kraus 1988, chap. 17). Vn is also thermal noise source due to the amplifier noise which is represented by the same antenna resistance Rant at receiver noise temperature Trx. All voltage noise sources are mutually independent. We can combine Tsys = Tant + Trx as the system noise temperature of Rant.
The correlator output due to the sky and amplifier noise sources is
where VX1 = VsX1 + VnX1 and similarly for all other ports. The noisy estimates of the electric field outer product are formed by flanking Eq. (10) with the Jones matrix inverse as shown in Eq. (7). For brevity, we drop the leading V and introduce shorthand notation, for example, 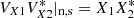 etc. This results in
etc. This results in
where
is the determinant of the Jones matrix.
3.3.1. Standard deviations of θθ and ϕϕ
It can be shown (see Appendix)
Because the antennas are of an identical design, the mean-square noise voltages are ⟨|X1|2⟩=⟨|X2|2⟩ = 4kTsysXRantΔf and ⟨|Y1|2⟩=⟨|Y2|2⟩ = 4kTsysYRantΔf with units V2, which are expected for a resistance Rant at temperature Tsys with noise bandwidth Δf. As a result, we get
and taking the square root
Similarly,
3.3.2. Calculation of SEFDI
Summing the two equations in Eq. (11), we obtain
where 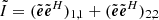 . Following the same reasoning in Sect. 3.3.1
. Following the same reasoning in Sect. 3.3.1
where the vector norms are
Taking  from Eq. (18) and dividing by η0 produces the desired result
from Eq. (18) and dividing by η0 produces the desired result
with units W m−2. If SEFDI is stated in W m−2 Hz−1, which is the case for noise-like sources in radio astronomy, then we remove Δf from the right hand side. The Δf provides the flexibility to account for deterministic sources (for example, a continuous wave with signal bandwidth less than Δf) of unknown polarization if required. D is the Jones matrix determinant in Eq. (12) and
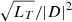 has units of K m−1.
has units of K m−1.
4. SEFD interpretation, special cases, examples, and application
Equation (20) is the desired result, but it bears no resemblance to commonly used quantities in radio astronomy which warrants further explanation. The purpose of this section is to interpret Eq. (20) by linking it to more familiar quantities, which is possible under certain assumptions and approximation.
4.1. Comparable measure to A/T
It is generally not possible to factor out Ae and Tsys as separate entities from Eq. (20). This is because TsysX and TsysY are inextricably linked with the components of the Jones matrix as shown in Eq. (21). Still, because of the long tradition of using of Ae/Tsys, it is useful to produce a comparable metric that has units of m2K−1. This can be done by simply inverting Eq. (20) and removing the Boltzmann constant, k,
4.1.1. Special case A/T for TsysX = TsysY = Tsys
In this condition, Tsys factors out of 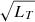 and we can write
and we can write
where
4.2. Short dipoles
We let the antenna elements be orthogonal crossed short dipoles with X dipole located on the X − Z plane (ϕ = 0°) and Y dipole located on the Y − Z plane (ϕ = 90°) (Sutinjo et al. 2015a)
la(θ) is a scalar multiplier that represents the electrical length of the antenna and the array factor due to a conductive ground screen. In this case
and
which are independent of ϕ. For TsysX = TsysY = Tsys,
The ϕ independence of Eq. (28) and its dependence on cos4θ merits further discussion because they are connected to the singular values of the Jones matrix of a short dipole. It has been shown in Carozzi (2019) that the ratio of the maximum singular value to the minimum singular value (that is the condition number, c{J}) of the Jones matrix determines the intrinsic cross-polarization ratio, IXR=(c{J}+1)2/(c{J}−1)2, of the dual-polarized antenna system. The Jones matrix of the orthogonal short dipole system in Eq. (25) is expressed as singular value decomposition
where U is an orthogonal rotation matrix and Σ is a diagonal matrix of singular values σmax = l(θ) and σmin = l(θ) cos θ. The condition number is
Hence Eq. (28) may be written as
4.3. Cardinal planes of orthogonal dual-polarized linear antennas
For ideal dual-polarized linear antennas, the Jones matrix becomes diagonal or antidiagonal in the cardinal planes. For example at ϕ = 0°, Eq. (25) becomes diagonal. In practice, this is approximately true. In this special case |D|2 = |lXθ|2|lYϕ|2 and
which leads to
where the SEFD is given in W m−2Hz−1 and is valid for arbitrary polarization. We see in Eq. (33) the sum of the squares of X-only and Y-only quantities under the square root. This is because the θθ and ϕϕ become fully independent measurements on the cardinal plane. Equations (15) and (16) become
and the standard deviation of the sum becomes the square root of the sum of the squares as expected. For this special case, we can make a connection to the SEFDunpol. assumption as described in Eq. (1). Following Eq. (15) and Eq. (16) we can write
such that
The ≈ sign serves as a reminder that the diagonal or anti-diagonal Jones matrix may be approached in practice but rarely fulfilled perfectly. It should be noted that Eq. (36) is valid for the cardinal plane only but is independent of the polarization state of the target field even though SEFDXX and SEFDYY assume the polarization mismatch factor 1/2 which is associated with an unpolarized target source. Also, because of the squares, the higher of the SEFDXX or SEFDYY will dominate the system SEFDI.
4.4. Limitation of the narrow FoV SEFD approximation
Equation (36) has a clear link to Wrobel et al. (1999) in that this is exactly expected for a narrow FoV in the vicinity of the beam centre since the FoV is always close to the cardinal planes. What is not expected is that Eq. (36) is generally incorrect, which becomes evident only when the FoV is very wide. For example, take the short dipole system assuming TsysX = TsysY = Tsys,
Assuming an unpolarized source,
where
Figure 4 shows the relative error of Eq. (36) if we apply it over the entire sky for the dual-polarized short dipole system
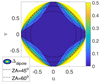 |
Fig. 4. Relative error of the narrow FoV SEFD approximation for the dual-polarized short dipole system. u = sin θ cos ϕ and v = sin θ sin ϕ. The ZA circles indicate the zenith angles of observation. |
It is evident that the maximum relative errors occur at the diagonal planes. For zenith angle (ZA) = 45° ,60° the maximum relative errors are approximately 15% and 45%, respectively. The error is positive in this example because SEFDI is higher than 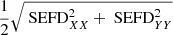 .
.
4.5. Relevance to next-generation low-frequency radio telescopes including SKA-Low
Equations (20) and (22) have an immediate relevance to SKA-Low sensitivity requirements and interpretation thereof, in particular SKA1-SYS_REQ2135 ‘SKA1_Low array sensitivity’ and SKA1-SYS_REQ2622 ‘Sensitivity for off zenith angles’ in Caiazzo (2017), which is the most recent at the time of writing. REQ2135 calls for A/T value at zenith per polarization which implies the assumption of an unpolarized source. At zenith, the A/T values of the orthogonal linearly polarized antennas are approximately the same, hence there is no ambiguity.
REQ2622 calls for maximum allowable degradation (30% at 60° elevation angle; 50% at 45° elevation angle) relative to the peak sensitivity (reasonably assumed to occur at zenith value). However at off-zenith angles, the A/T values of the orthogonally polarized antennas are different, and hence it is ambiguous how the degradation should be computed. Equation (20) or (22) removes this ambiguity by providing one sensitivity number over the entire visible sky. Furthermore, the SEFD or AonT given here makes no assumption regarding the polarization state of the source, which removes another limitation.
For example, we consider a dual-polarized bow-tie antenna used by the Murchison Widefield Array (MWA; Tingay et al. 2013; Sutinjo et al. 2015a; Sokolowski et al. 2017) depicted in Fig. 5. Suppose we seek to determine its off-zenith performance as suggested in REQ2622. For simplicity we let the Tsys be equal; hence it is adequate to compare the off-zenith effective area relative to the peak value. Figure 6 shows the simulated effective area assuming an unpolarized source (AeX|un. with factor 1/2 included) for the X-directed bow-tie element at 160 MHz. The result for the Y-directed element is identical, except for a 90° rotation (not shown). It is clearly evident that the effective area defined in this way produces two very different off-zenith values for the X and Y elements, in particular on the cardinal planes. The peak at zenith is 0.9 m2 for both X and Y elements, whereas at θ = 30° ,ϕ = 0° AeX|un. = 0.543 m2 and AeY|un. = 0.76 m2. This results in ambiguity as to which value (or combination of values) should be used to compute the degradation relative to peak.
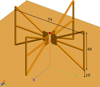 |
Fig. 5. Dual-polarized MWA bow-tie antenna simulated in FEKO (full-wave method-of-moments electromagnetic solver, https://altairhyperworks.com/product/FEKO). The dimensions shown are in cm. |
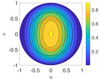 |
Fig. 6. Calculated AeX|un. in m2 at 160 MHz for the MWA bow-tie antenna where u = sin θ cos ϕ and v = sin θ sin ϕ. The red dashed line corresponds to 60° elevation angle and the black dash-dot line indicates 45° elevation angle. |
Now we contrast this with the approach given in this paper. Figure 7 shows the calculated quantity that we can think of as the effective area of the dual-polarized antenna as per Eq. (23) (assuming equal Tsys)
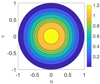 |
Fig. 7. Calculated AI in m2 at 160 MHz for the MWA bow-tie antenna where u = sin θ cos ϕ and v = sin θ sin ϕ. The red dashed line corresponds to 60° elevation angle and the black dash-dot line indicates 45° elevation angle. |
at 160 MHz. The peak value at zenith is 1.28 m2, whereas at θ = 30° ,ϕ = 0° the value is 0.885 m2. The degradation relative to the peak value is simply 1 − 0.885/1.28 = 0.309 ≈ 0.3; there is no ambiguity.
5. Validation: All-sky observation and simulation with the MWA
5.1. Overview and strategy
We use the MWA to validate the proposed SEFDI calculation using observational data. The MWA is the SKA-Low precursor operating in the frequency range 70 MHz to 300 MHz where an element is a bow-tie, as shown in Fig. 5. An MWA tile consists of a 4 × 4 array of these antennas. Validation of the equations in this paper is best done using an all-sky observation, as it permits evaluation of SEFD in the regions (off-zenith) where the difference is the most prominent. The array is shown in Fig. 8, where the element used for all-sky observation (#6) is highlighted in red.
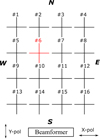 |
Fig. 8. MWA tile of 4 × 4 dual-polarized dipoles. The elements are aligned along N-S and W-E. The spacing between elements is 1.1 m. |
5.2. Simulation predictions for the MWA
The all-sky SEFD was calculated using Eqs. (20) and (36) for the MWA tile, with element number 6 being an active element, and the other 15 elements being passive. The excitation amplitude for the active element was 1, while for the passive element, it was 0. Although the passive elements were terminated with the low-noise amplifier (LNA) impedance, they still contributed to the array mutual coupling. The tile beam and scattering parameters were simulated using the full-wave software package FEKO. The frequency of interest was 154.88 MHz, which corresponded to the channel number 121. To calculate the system temperature, we also used measured S-parameters and noise parameters of the LNA (Sutinjo et al. 2018), as well as the Haslam 408 MHz all-sky map (Haslam et al. 1982) scaled to 154.88 MHz using a spectral index of −2.55 (Mozdzen et al. 2019). The Galactic contribution corresponded to the day and time of the observation. Defined in Eq. (21), LT is a matrix that requires the system temperatures for both polarizations (TsysX, TsysY), as well as the effective antenna lengths, which are the values of the Jones matrix in Eq. (2) computed using the simulated electric fields (Eθ, Eϕ) and port currents IX, IY (Sutinjo et al. 2015a). For the calculations of SEFDXX and SEFDYY, the system temperature and antenna effective area were determined according to Ung et al. (2020). The calculated values were Rant = 68.4 Ω, TsysX = 371.04 K, TsysY = 348.21 K.
The relative error as per Eq. (40) based on simulated data is shown in Fig. 9. The trends of high delta in the diagonal planes due to the approximation using Eq. (36) is similar to that of Fig. 4. The SEFDI calculated using Eq. (20) and the approximation using Eq. (36) agree to within 2.2% at zenith. However, the approximation is only valid in the cardinal planes. In the diagonal planes, the error reaches 40% between ZA = 60° and the horizon. The asymmetry in Fig. 9 is due to the mutual coupling from MWA bow-tie antennas surrounding element 6. Next, we describe the process of obtaining the SEFD using observational data, which is an independent method of validation.
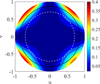 |
Fig. 9. Relative difference Δdipole as defined in Eq. (40) using simulated MWA data. The black solid line is at ZA = 60°, while the white dashed line is at ZA = 45°. |
5.3. Verification with the MWA data
The relative difference defined by Eq. (40) was verified using 108 s of MWA data collected in the all-sky observing mode. The data were collected on 2015 February 14 between 14:10:16 and 14:12:04 UTC in a configuration with only dipole 6 of the sixteen dipoles in every MWA tile enabled and the remaining dipoles terminated. The resulting primary beam is sensitive to nearly the entire hemisphere, which was modeled using the 2016 MWA beam model (Sokolowski et al. 2017) with only dipole 6 enabled. In order to verify the predicted Δdipole (Eq. (40)) for the short dipole system (Fig. 4), and more specifically for the simulation of the MWA dipole 6 (Fig. 9), the SEFDI over the entire hemisphere was derived from all-sky images.
5.3.1. All-sky images
The MWA data were converted into CASA measurement sets (McMullin et al. 2007) and downloaded using the MWA All-Sky Virtual Observatory interface (Sokolowski et al. 2020). In order to perform phase and flux density calibration, an all-sky model was generated using the Positional Update and Matching Algorithm3 (PUMA; Line 2018) and GaLactic and Extragalactic All-sky MWA catalog (GLEAM; Hurley-Walker et al. 2017). The CALIBRATE software (Offringa et al. 2016), upgraded with the newest 2016 MWA beam model (Sokolowski et al. 2017) was used to calibrate the all-sky visibilities and generate calibration solutions. The phases of the resulting calibration solutions were fitted with a linear function, while the amplitudes were fitted with a 5th order polynomial; both fits were then applied to the un-calibrated visibilities. The all-sky images, with 4 s time resolution, were formed from all correlations products (XX, YY, XY and YX) using the WSCLEAN4 program (Offringa et al. 2014). The Briggs robust weighting parameter (Briggs 1995) was set to −1, which is optimal for the MWA Phase 1 data with maximum baselines ≈3 km (Tingay et al. 2013) because weighting schemes closer to natural increase the classical confusion noise. The dirty maps were CLEANed with 100 000 iterations and a 0.1 Jy threshold.
The resulting XX and YY images were divided by corresponding images of the beam in X and Y polarizations generated with the 2016 beam model (Sokolowski et al. 2017), with only dipole 6 enabled. All the resulting images (XX, YY, XY and YX) were converted to Stokes images (I, Q, U and V) also using the 2016 beam model. The standard deviation of the noise in the central circular region of 30-pixel radius in Stokes I images was ≈0.46 Jy beam−1. The final products resulting from the above procedure were three sets (XX, YY and Stokes I) of 28 primary beam corrected all-sky images corresponding to the nt = 28 timesteps (108 s in total) of the analyzed MWA data.
5.3.2. Measuring the SEFD from noise in the all-sky images
The SEFDI in all directions in the sky was calculated from the standard deviation of difference all-sky images (later referred to as N) as SEFDI = αN, where 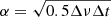 , Δt = 4 s is the integration time, and Δν = 30.72 MHz is the observing bandwidth. The factor 0.5 accounts for the fact that the standard deviation calculated from the difference images is higher than in the original images by
, Δt = 4 s is the integration time, and Δν = 30.72 MHz is the observing bandwidth. The factor 0.5 accounts for the fact that the standard deviation calculated from the difference images is higher than in the original images by 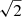 . The standard deviation of the noise can be calculated in a small region around each pixel in an all-sky image to form an all-sky noise image (it will also be referred to as the noise map). For this procedure to yield the noise originating from Tsys only (that is due to instrumental and sky noise), we require the contribution from the flux density variations across the region due to the astronomical sources (both point sources and diffuse emission) to be removed.
. The standard deviation of the noise can be calculated in a small region around each pixel in an all-sky image to form an all-sky noise image (it will also be referred to as the noise map). For this procedure to yield the noise originating from Tsys only (that is due to instrumental and sky noise), we require the contribution from the flux density variations across the region due to the astronomical sources (both point sources and diffuse emission) to be removed.
Following this approach, the three series (corresponding to XX, YY and Stokes I) of differences images (between the subsequent i-th and i − 1 image) were generated, resulting in nd = 27 difference images in each of XX, YY and Stokes I polarizations. The noise calculated in circular regions around pixels in the resulting difference images is distributed around a mean of zero and is not contaminated by the variations of the flux density within the circular regions due to astronomical sources contained inside these regions. The difference images were also visually inspected and verified to have mean value approximately zero and noise-like structure, without any subtraction artefacts, across the entire images. The XX and YY difference images had the characteristic oval-like shape of the primary beam of the MWA dipole in the corresponding polarization in-printed in the standard deviation, which could be best seen in the noise map images with the standard deviation lowest at the centre of the images and highest near the horizon. Therefore, the resulting standard deviation is purely due to instrumental and sky noise (Tsys).
In an alternative approach, standard deviation of the noise could be calculated from the series of flux density values along the time axis. This way has also been tested by calculating standard deviation (from the interquartile range) for each pixel in the difference images using nd values along the time axis. The resulting images of standard deviation (in XX, YY and Stokes I polarizations) were analyzed in the same way as the adopted approach using the circular regions and led to the same results.
The 2D noise maps over the entire hemisphere were calculated as follows. For each of the resulting difference images, the noise at each position on the sky (that is around each image pixel) was calculated as the standard deviation of all pixels within a radius of 30 pixels (≈91 synthesized beams) from the pixel being analyzed. The interquartile range divided by 1.35 was used in order to be more robust against any outlier data points due to radio-frequency interference (RFI), or residuals of astronomical sources in difference images. This procedure was applied to nd all-sky difference images resulting in nd noise maps (NI, NXX and NYY) for each of the polarizations (Stokes I, XX and YY respectively). These noise maps were used to calculate Δdipole defined in Eq. (40), by substituting SEFDI = αN and with the constant α cancelling out, resulting in the following equation:
where i is the image index. For each of the difference images (nd in total), the corresponding noise maps (NI, NXX and NYY) were used to calculate nd number of 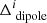 images according to Eq. (42). Visual inspection of these images revealed that although they were very similar to Figs. 4 and 9, the centres were quite noisy due to near zero values. Therefore, in order to reduce the noise, a median image
images according to Eq. (42). Visual inspection of these images revealed that although they were very similar to Figs. 4 and 9, the centres were quite noisy due to near zero values. Therefore, in order to reduce the noise, a median image  was calculated out of nd
was calculated out of nd
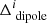 images and is shown in Fig. 10.
images and is shown in Fig. 10.
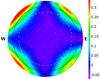 |
Fig. 10. Relative difference Δdipole calculated as the median of individual |
5.4. Comparison between data and simulations
Figure 10 is very similar to Fig. 4, and nearly identical to Fig. 9 showing the 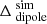 expected from the MWA simulations of the same observing setup.
expected from the MWA simulations of the same observing setup. 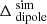 is defined as Δdipole (Eq. (40)) predicted by the MWA simulation (Sect. 5.2) in order to unequivocally distinguish it from the corresponding difference obtained from the MWA data, which is denoted as
is defined as Δdipole (Eq. (40)) predicted by the MWA simulation (Sect. 5.2) in order to unequivocally distinguish it from the corresponding difference obtained from the MWA data, which is denoted as  . Similarly,
. Similarly, 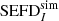 and
and 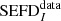 are defined as the SEFD calculated from the MWA simulation and data respectively. Figure 11 shows the percentage difference between the
are defined as the SEFD calculated from the MWA simulation and data respectively. Figure 11 shows the percentage difference between the  derived from the MWA data (Fig. 10) and
derived from the MWA data (Fig. 10) and 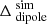 predicted by the simulations (Fig. 9). The absolute values of the differences are within a few percent in the centre (and to elevations as low as approximately 30°), reaching the largest values (exceeding |10%|) only near the horizon, where the MWA beam model becomes less reliable.
predicted by the simulations (Fig. 9). The absolute values of the differences are within a few percent in the centre (and to elevations as low as approximately 30°), reaching the largest values (exceeding |10%|) only near the horizon, where the MWA beam model becomes less reliable.
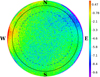 |
Fig. 11. Percentage difference of the MWA data |
In a similar way, the median 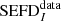 image was obtained from the data as the median of nd individual
image was obtained from the data as the median of nd individual 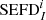 images calculated from the noise maps as
images calculated from the noise maps as 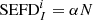 , and it was compared with the
, and it was compared with the 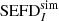 derived from the MWA simulations. Figure 12 shows the relative difference between the data and simulations, calculated as
derived from the MWA simulations. Figure 12 shows the relative difference between the data and simulations, calculated as 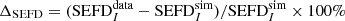 . The agreement between the data and simulations at zenith is remarkable with measured sensitivity
. The agreement between the data and simulations at zenith is remarkable with measured sensitivity 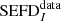 (ZA = 0°) = 463700 ± 200 Jy and simulated
(ZA = 0°) = 463700 ± 200 Jy and simulated 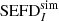 (ZA = 0°) = 463250 ± 20 Jy, which means the difference is ≈0.1%. Both values (
(ZA = 0°) = 463250 ± 20 Jy, which means the difference is ≈0.1%. Both values (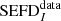 and
and 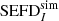 ) were calculated as the median and interquartile range based standard deviation in 10 pixels radius around the centre. These differences between the data and simulations remain mostly within ±5% above an elevation 45° and increase to ±20% only below an elevation of 30°. The increasing discrepancy between simulations and observational measurements at lower elevations reflects the fact that the FEKO model is an approximation, which generally becomes less accurate the further the beam is from zenith. This is consistent with prior findings in Sokolowski et al. (2017) regarding the beam model accuracy. These images provide the evidence that the data and simulations are in a very good agreement and demonstrate correctness of the findings presented in this paper.
) were calculated as the median and interquartile range based standard deviation in 10 pixels radius around the centre. These differences between the data and simulations remain mostly within ±5% above an elevation 45° and increase to ±20% only below an elevation of 30°. The increasing discrepancy between simulations and observational measurements at lower elevations reflects the fact that the FEKO model is an approximation, which generally becomes less accurate the further the beam is from zenith. This is consistent with prior findings in Sokolowski et al. (2017) regarding the beam model accuracy. These images provide the evidence that the data and simulations are in a very good agreement and demonstrate correctness of the findings presented in this paper.
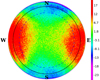 |
Fig. 12. Relative difference between the data and simulations, ΔSEFD (in percent), calculated as |
6. Conclusion
There are a few important conclusions. First, the SEFD is the proper figure of merit for a polarimetric interferometer, but not as commonly defined using Ae/Tsys one antenna polarization at a time. Rather, the SEFD for the dual-polarized antenna system is directly computable through the standard deviation of the flux density estimate over the entire sky with no assumption regarding the polarization state of the source. This is given by the formula in Eq. (20). Second, the SEFD defined in this way produces one number for the dual-polarized antenna system such that the sensitivity at off-zenith angles can be calculated with no ambiguity (see Sect. 4.5). Finally, the SEFD formula calculated based on full-wave simulation was validated with the MWA to a very good agreement using all-sky astronomical observations and electromagnetic simulations. The difference between the two are within the noise level of the observation in one case, and in another, within known accuracy levels of electromagnetic simulation for far off-zenith angles.
In this paper and as shown in Fig. 1, we use the standard spherical coordinate system (see Kraus 1988, chap. 2) and IEEE (2014). In this convention, the X antenna is aligned with the x-axis and the Y antenna with the y-axis at each dual-polarized antenna location. The angle ϕ is the angle with respect to the x-axis and θ to the z-axis. The polarization unit vectors 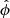 and
and 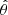 are tangential to the circles of constant θ and constant ϕ, respectively. The vector directions are determined by the directions of increasing ϕ and θ, respectively. Therefore at zenith (θ = 0° ,ϕ = 0° ), the co-polarized component of the X antenna is
are tangential to the circles of constant θ and constant ϕ, respectively. The vector directions are determined by the directions of increasing ϕ and θ, respectively. Therefore at zenith (θ = 0° ,ϕ = 0° ), the co-polarized component of the X antenna is 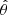 and the co-polarized component of the Y antenna is
and the co-polarized component of the Y antenna is 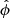 . Hence, lXθ and lYϕ are the diagonal entries in the Jones matrix in Eq. (2).
. Hence, lXθ and lYϕ are the diagonal entries in the Jones matrix in Eq. (2).
Equation (6) produces V = 1 (positive) for incident right-hand circularly polarized wave (RCHP). Positive V for RHCP is consistent with IAU (1973), Hamaker & Bregman (1996), Smirnov (2011), and IEEE (2019). Equation (7) in Smirnov (2011) has U + iV and U − iV in the top right and bottom left, respectively. Most likely, this is because Hamaker & Bregman (1996) and Smirnov (2011) use the International Astronomical Union (IAU) coordinate system (see: https://healpix.jpl.nasa.gov/html/intronode12.htm) whereas we use the spherical coordinate system. It is important to note that the unit vector 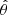 in the spherical coordinate system points south (
in the spherical coordinate system points south (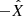 ) in the IAU coordinate system.
) in the IAU coordinate system.
Acknowledgments
The authors thank A/Prof C. Trott for feedback and discussions on the statistical calculations.
References
- Baudin, P. 2015, Wireless Transceiver Architecture: Bridging RF and Digital Communications, 1st edn. (Hoboken, NJ: Wiley) [Google Scholar]
- Briggs, D. S. 1995, Ph.D. Thesis, The New Mexico Institute of Mining and Technology, USA [Google Scholar]
- Caiazzo, M. 2017, SKA Phase 1 System Requirements Specification V11, Tech. Rep. SKA-TEL-SKO-0000008 (SKA Organisation) [Google Scholar]
- Carozzi, T. D. 2019, 2019 International Conference on Electromagnetics in Advanced Applications (ICEAA), 0979 [Google Scholar]
- Crane, P. C., & Napier, P. J. 1989, in Synthesis Imaging in Radio Astronomy, eds. R. A. Perley, F. R. Schwab, & A. H. Bridle, ASP Conf. Ser., 6, 139 [Google Scholar]
- Dewdney, P. 2016, SKA1 System Baseline Design V2, Tech. Rep. SKA-TEL-SKO-0000002, SKA Organisation [Google Scholar]
- Ellingson, S., Clarke, T., Cohen, A., et al. 2009, Proc. IEEE, 97, 1421 [NASA ADS] [CrossRef] [Google Scholar]
- Hamaker, J. P., & Bregman, J. D. 1996, A&A, 117, 161 [Google Scholar]
- Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&A, 47, 1 [Google Scholar]
- Hurley-Walker, N., Callingham, J. R., Hancock, P. J., et al. 2017, MNRAS, 464, 1146 [NASA ADS] [CrossRef] [Google Scholar]
- IAU 1973, IAU General Assembly [Google Scholar]
- IEEE 2014, IEEE Std 145–2013 (Revision of IEEE Std 145-1993), 1 [Google Scholar]
- IEEE 2019, IEEE Std 211–2018 (Revision of IEEE Std 211–1997), 1 [Google Scholar]
- Ko, H. C. 1962, Proc. IRE, 50, 1950 [Google Scholar]
- Kraus, J. D. 1988, Antennas, 2nd edn. (Singapore: McGraw-Hill) [Google Scholar]
- Labate, M. G., Braun, R., Dewdney, P., Waterson, M., & Wagg, J. 2017a, in 2017 XXXIInd General Assem. and Scientific Symp. of the Int. Union of Radio Sci. (URSI GASS), 1 [Google Scholar]
- Labate, M. G., Dewdney, P., Braun, R., Waterson, M., & Wagg, J. 2017b, 2017 11th European Conference on Antennas and Propagation (EUCAP), 2259 [Google Scholar]
- Line, J. L. B. 2018, PUMA: Low-frequency Radio Catalog Cross-matching [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Mozdzen, T., Mahesh, N., Monsalve, R., Rogers, A., & Bowman, J. 2019, MNRAS, 483, 4416 [Google Scholar]
- Offringa, A. R., McKinley, B., Hurley-Walker, N., et al. 2014, MNRAS, 444, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Offringa, A. R., Trott, C. M., Hurley-Walker, N., et al. 2016, MNRAS, 458, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Piepmeier, J. R., Long, D. G., & Njoku, E. G. 2008, IEEE Trans. Geosci. Remote Sens., 46, 516 [Google Scholar]
- Rothe, H., & Dahlke, W. 1956, Proc. IRE, 44, 811 [Google Scholar]
- Russer, P., & Müller, S. 1990, Int. J. Numer. Model. Electron. Networks Devices Fields, 3, 287 [Google Scholar]
- Smirnov, O. M. 2011, A&A, 527, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sokolowski, M., Colegate, T., Sutinjo, A. T., et al. 2017, PASA, 34, e062 [Google Scholar]
- Sokolowski, M., Jordan, C. H., Sleap, G., et al. 2020, PASA, 37, e021 [Google Scholar]
- Sutinjo, A., O’Sullivan, J., Lenc, E., et al. 2015a, Radio Sci., 50, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Sutinjo, A. T., Colegate, T. M., Wayth, R. B., et al. 2015b, IEEE Trans. Antennas Propag., 63, 5433 [Google Scholar]
- Sutinjo, A. T., Ung, D. C. X., & Juswardy, B. 2018, IEEE Trans. Antennas Propag., 66, 5511 [Google Scholar]
- Thompson, A. R., Moran, J. M., & Swenson, G. W. 2017a, Introduction and Historical Review (Cham: Springer International Publishing), 1 [Google Scholar]
- Thompson, A. R., Moran, J. M., & Swenson, G. W. 2017b, Response of the Receiving System (Cham: Springer International Publishing), 207 [Google Scholar]
- Tingay, S. J., Goeke, R., Bowman, J. D., et al. 2013, PASA, 30, 7 [Google Scholar]
- Twiss, R. Q. 1955, J. Appl. Phys., 26, 599 [Google Scholar]
- Ung, D. C. X., Sokolowski, M., Sutinjo, A. T., & Davidson, D. B. 2020, IEEE Trans. Antennas Propag., 68, 5395 [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warnick, K. F., Woestenburg, B., Belostotski, L., & Russer, P. 2009, IEEE Trans. Antennas Propag., 57, 1634 [Google Scholar]
- Warnick, K. F., Ivashina, M. V., Wijnholds, S. J., & Maaskant, R. 2012, IEEE Trans. Antennas Propag., 60, 184 [Google Scholar]
- Warnick, K. F., Maaskant, R., Ivashina, M. V., Davidson, D. B., & Jeffs, B. D. 2018, in Phased Arrays for Radio Astronomy, Remote Sensing, and Satellite Communications, EuMA High Frequency Technol. Ser., (Cambridge University Press) [Google Scholar]
- Wilson, T. L., Rohlfs, K., & Hüttemeister, S. 2009, Wave Polarization (Berlin, Heidelberg: Springer), 39 [Google Scholar]
- Wrobel, J. M., & Walker, R. C. 1999, in Sensitivity, eds. G. B. Taylor, C. L. Carilli, & R. A. Perley, ASP Conf. Ser., 180, 171 [Google Scholar]
Appendix A: Appendix: Treatment of statistics
The noise voltages in Fig. 2 are thermal noise sources which are zero-mean and Gaussian distributed. Our treatment uses complex envelope quantities; the real and imaginary components of the thermal noise voltages are independent and identically distributed (iid). The reasoning in Sect. 3.3 leads to Fig. 3 in which every noise source is independent. Therefore in our treatment, it is adequate to address only the statistics of independent and zero-mean Gaussian noise sources. In Eqs. (11) and 13, we see a sum of random variables as follows
where X1, X2, Y1, Y2 are complex random variables; a, b are real constants and z is a complex constant.
where C is the covariance of cross terms.
Because of independent noise, 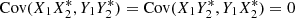 , which leaves
, which leaves 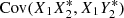 and similar terms in which there is a common X1 term separated by the comma (X1_,X1_), similarly
and similar terms in which there is a common X1 term separated by the comma (X1_,X1_), similarly 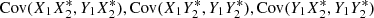 .
.
where the last line is due to independent zero-mean noise sources such that 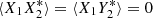 . To find
. To find 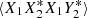 , we use a key formula for Z1, 2, 3, 4 that are zero-mean joint Gaussian random variables (Thompson et al. 2017b; Baudin 2015)
, we use a key formula for Z1, 2, 3, 4 that are zero-mean joint Gaussian random variables (Thompson et al. 2017b; Baudin 2015)
which is valid for real and complex zero-mean joint Gaussian random variables. Applying this to Eq. (A.4), we get
which is zero because of zero-mean independent noise. This is similarly the case for 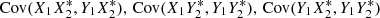 . In conclusion, 2C = 0 in Eq. (A.2).
. In conclusion, 2C = 0 in Eq. (A.2).
All Figures
 |
Fig. 1. Two dual-polarized low-frequency antennas forming an interferometer. The signal of interest is the partially polarized field |
| In the text | |
 |
Fig. 2. Circuit representation of the four-port network. The impedance matrix Z is a noiseless network describing relationship between the antenna voltages and currents. The sky noise and the amplifier noise sources are denoted by subscripts .s and .n, respectively. |
| In the text | |
 |
Fig. 3. Simplified impedance (noiseless) and noise sources seen at the antenna port. Z11 is the impedance seen at the antenna port 1. The same circuit is seen at Y1, X2, Y2 with subscript substitutions. |
| In the text | |
 |
Fig. 4. Relative error of the narrow FoV SEFD approximation for the dual-polarized short dipole system. u = sin θ cos ϕ and v = sin θ sin ϕ. The ZA circles indicate the zenith angles of observation. |
| In the text | |
 |
Fig. 5. Dual-polarized MWA bow-tie antenna simulated in FEKO (full-wave method-of-moments electromagnetic solver, https://altairhyperworks.com/product/FEKO). The dimensions shown are in cm. |
| In the text | |
 |
Fig. 6. Calculated AeX|un. in m2 at 160 MHz for the MWA bow-tie antenna where u = sin θ cos ϕ and v = sin θ sin ϕ. The red dashed line corresponds to 60° elevation angle and the black dash-dot line indicates 45° elevation angle. |
| In the text | |
 |
Fig. 7. Calculated AI in m2 at 160 MHz for the MWA bow-tie antenna where u = sin θ cos ϕ and v = sin θ sin ϕ. The red dashed line corresponds to 60° elevation angle and the black dash-dot line indicates 45° elevation angle. |
| In the text | |
 |
Fig. 8. MWA tile of 4 × 4 dual-polarized dipoles. The elements are aligned along N-S and W-E. The spacing between elements is 1.1 m. |
| In the text | |
 |
Fig. 9. Relative difference Δdipole as defined in Eq. (40) using simulated MWA data. The black solid line is at ZA = 60°, while the white dashed line is at ZA = 45°. |
| In the text | |
 |
Fig. 10. Relative difference Δdipole calculated as the median of individual |
| In the text | |
 |
Fig. 11. Percentage difference of the MWA data |
| In the text | |
 |
Fig. 12. Relative difference between the data and simulations, ΔSEFD (in percent), calculated as |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



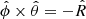
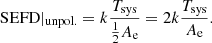
![$$ \begin{aligned} \boldsymbol{v}_1|_t&=\mathbf J \boldsymbol{e}_t, \nonumber \\ \left[ \begin{array}{c} V_{X1}|_t \\ V_{Y1}|_t \end{array} \right]&= \left[ \begin{array}{cc} l_{X\theta }&l_{X\phi } \\ l_{Y\theta }&l_{Y\phi } \end{array} \right] \left[ \begin{array}{c} E_{t\theta } \\ E_{t\phi } \end{array} \right]. \end{aligned} $$](/articles/aa/full_html/2021/02/aa39445-20/aa39445-20-eq11.gif)
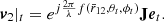
![$$ \begin{aligned} \boldsymbol{v}_1\boldsymbol{v}_2^H|_t=\mathbf J \boldsymbol{e}_t\boldsymbol{e}_t^H\mathbf J ^H= \left[ \begin{array}{cc} V_{X1}V_{X2}^*|_t&V_{X1}V_{Y2}^*|_t \\ V_{Y1}V_{X2}^*|_t&V_{Y1}V_{Y2}^*|_t \end{array} \right]. \end{aligned} $$](/articles/aa/full_html/2021/02/aa39445-20/aa39445-20-eq13.gif)
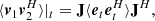
![$$ \begin{aligned} \langle \boldsymbol{e}_t\boldsymbol{e}_t^H\rangle&= \left[ \begin{array}{cc} \langle |E_{t\theta }|^2\rangle&\langle E_{t\theta }E_{t\phi }^*\rangle \\ \langle E_{t\theta }^*E_{t\phi } \rangle&\langle |E_{t\phi }|^2\rangle \end{array} \right]\nonumber \\&=\frac{1}{2}\left[ \begin{array}{cc} I+Q&U-jV \\ U+jV&I-Q \end{array}\right] \end{aligned} $$](/articles/aa/full_html/2021/02/aa39445-20/aa39445-20-eq15.gif)
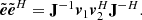
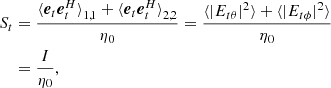
![$$ \begin{aligned} \text{ SEFD}_I=\frac{{\mathrm{SDev}}\left[(\tilde{\boldsymbol{e}}\tilde{\boldsymbol{e}}^H)_{1,1}+(\tilde{\boldsymbol{e}}\tilde{\boldsymbol{e}}^H)_{2,2}\right]}{\eta _0}. \end{aligned} $$](/articles/aa/full_html/2021/02/aa39445-20/aa39445-20-eq21.gif)
![$$ \begin{aligned} \boldsymbol{v}_1\boldsymbol{v}_2^H|_{\rm n,s}= \left[ \begin{array}{cc} V_{X1}V_{X2}^*|_{\rm n,s}&V_{X1}V_{Y2}^*|_{\rm n,s} \\ V_{Y1}V_{X2}^*|_{\rm n,s}&V_{Y1}V_{Y2}^*|_{\rm n,s} \end{array} \right], \end{aligned} $$](/articles/aa/full_html/2021/02/aa39445-20/aa39445-20-eq23.gif)

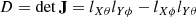
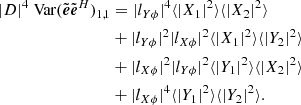
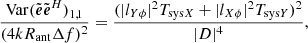
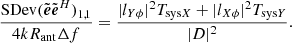
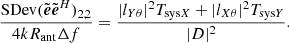
![$$ \begin{aligned} |D|^2\tilde{I}&=X_1X_2^*[|l_{Y\phi }|^2+|l_{Y\theta }|^2] \nonumber \\&+Y_1Y_2^*[|l_{X\phi }|^2+|l_{X\theta }|^2] \nonumber \\&-X_1Y_2^*[l_{X\phi }^*l_{Y\phi }+l_{X\theta }^*l_{Y\theta }] \nonumber \\&-Y_1X_2^*[l_{X\phi }l_{Y\phi }^*+l_{X\theta }l_{Y\theta }^*], \end{aligned} $$](/articles/aa/full_html/2021/02/aa39445-20/aa39445-20-eq31.gif)
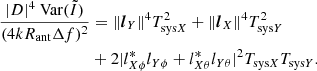
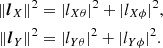
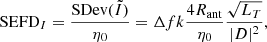
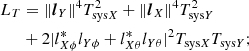
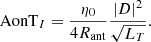
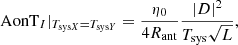
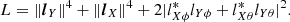
![$$ \begin{aligned} \mathbf J =l_a(\theta )\left[ \begin{array}{cc} \cos \theta \cos \phi&-\sin \phi \\ \cos \theta \sin \phi&\cos \phi \end{array} \right]; \end{aligned} $$](/articles/aa/full_html/2021/02/aa39445-20/aa39445-20-eq43.gif)
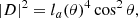
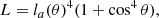
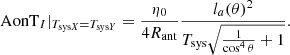
![$$ \begin{aligned} \mathbf J&=\left[ \begin{array}{cc} \cos \phi&-\sin \phi \\ \sin \phi&\cos \phi \end{array} \right]\left[ \begin{array}{cc} l(\theta ) \cos \theta&0 \\ 0&l(\theta ) \end{array} \right] \mathbf I \nonumber \\&=\mathbf U \mathbf \Sigma \mathbf V ^H. \end{aligned} $$](/articles/aa/full_html/2021/02/aa39445-20/aa39445-20-eq47.gif)