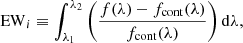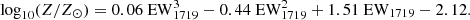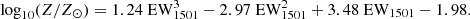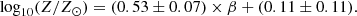| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202039244 | |
| Published online | 04 February 2021 | |
The VANDELS survey: The relation between the UV continuum slope and stellar metallicity in star-forming galaxies at z ∼ 3
1
INAF – Osservatorio Astronomico di Roma, Via di Frascati 33, 00078 Monte Porzio Catone, Italy
e-mail: antonello.calabro@inaf.it
2
INAF – Astronomical Observatory of Trieste, Via G.B. Tiepolo 11, 34143 Trieste, Italy
3
IFPU – Institute for Fundamental Physics of the Universe, Via Beirut 2, 34151 Trieste, Italy
4
SUPA, Institute for Astronomy, University of Edinburgh, Royal Observatory, Edinburgh EH9 3HJ, UK
5
INAF – Osservatorio Astronomico di Bologna, Via P. Gobetti 93/3, 40129 Bologna, Italy
6
University of Bologna, Department of Physics and Astronomy (DIFA), Via Gobetti 93/2, 40129 Bologna, Italy
7
Instituto de Investigación Multidisciplinar en Ciencia y Tecnología, Universidad de La Serena, Raúl Bitrán 1305, La Serena, Chile
8
Departamento de Física y Astronomía, Universidad de La Serena, Av. Juan Cisternas 1200 Norte, La Serena, Chile
9
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
10
Cosmic DAWN Center, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
11
Centre for Astrophysics Research, University of Hertfordshire, Hatfield AL10 9AB, UK
12
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
13
European Southern Observatory (ESO), Vitacura, Chile
14
DARK, Niels Bohr Institute, University of Copenhagen, Lyngbyvej 2, 2100 Copenhagen, Denmark
15
Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK
16
Observatoire de Genève, Université de Genève, 51 Ch. des Maillettes, 1290 Versoix, Switzerland
17
CNRS, IRAP, 14 avenue E. Belin, 31400 Toulouse, France
18
Tianjin Astrophysics Center, Tianjin Normal University, Binshuixidao 393, 300384 Tianjin, PR China
Received:
24
August
2020
Accepted:
12
November
2020
The estimate of stellar metallicities (Z*) of high-z galaxies are of paramount importance in order to understand the complexity of dust effects and the reciprocal interrelations among stellar mass, dust attenuation, stellar age, and metallicity. Benefiting from uniquely deep far-UV spectra of > 500 star-forming galaxies at redshifts 2 < z < 5 extracted from the VANDELS survey and stacked in bins of stellar mass (M*) and UV continuum slope (β), we estimate their stellar metallicities Z* from stellar photospheric absorption features at 1501 and 1719 Å, which are calibrated with Starburst99 models and are largely unaffected by stellar age, dust, IMF, nebular continuum, or interstellar absorption. Comparing them to photometric-based spectral slopes in the 1250–1750 Å range, we find that the stellar metallicity increases by ∼0.5 dex from β ∼ −2 to β ∼ −1 (1 ≲ A1600 ≲ 3.2), and a dependence with β holds at fixed UV absolute luminosity MUV and stellar mass up to ∼109.65 M⊙. As a result, metallicity is a fundamental ingredient for properly rescaling dust corrections based on MUV and M*. Using the same absorption features, we analyzed the mass-metallicity relation (MZR), and find it to be consistent with the previous VANDELS estimation based on a global fit of the FUV spectra. Similarly, we do not find a significant evolution between z ∼ 2 and z ∼ 3.5. Finally, the slopes of our MZR and Z* − β relation are in agreement with the predictions of well-studied semi-analytic models (SAM) of galaxy formation, while some tensions remain concerning the absolute metallicity normalization. The relation between the UV slope and stellar metallicity is fundamental to the exploitation of large volume surveys with next-generation telescopes and for the physical characterization of galaxies in the first billion years of our Universe.
Key words: galaxies: high-redshift / galaxies: abundances / galaxies: evolution / galaxies: stellar content
© ESO 2021
1. Introduction
Metals and dust are the main final products of stellar evolution, and hence they are key to understanding the history of star formation (SF) during the first 1–3 billion years following the birth of our Universe, during which the gas composition, the dust production mechanisms, and stellar properties were radically different from today (Maiolino et al. 2004; Dayal & Ferrara 2012). Indeed, feedback mechanisms from stars and active galactic nuclei (AGNs) not only can stop SF, but significantly affect the metal content of galaxies and new generations of stars. At the same time, this picture is complicated by the presence of dust, which may play a relevant role in obscuring even the most active star-forming galaxies, and thus providing a biased view of the intrinsic properties of high-z sources. Investigating how these quantities are related to each other and with additional properties, including the stellar mass (M*) and the star formation rate (SFR), is thus of paramount importance when it comes to constraining models of galaxy formation and evolution.
In previous years, thanks to the relative ease of performing observations and data reduction at optical wavelengths, impressive imaging campaigns have discovered large samples of (rest-frame) UV bright, star-forming galaxies in the redshift range between 2 and 4 (Steidel et al. 1995; Giavalisco et al. 1996; Giavalisco 2002; Hathi et al. 2010; Parsa et al. 2016). These efforts have begun to push the study of the UV luminosity function and SFR density up to the first 3 Gyr of the Universe (e.g., Bouwens et al. 2015; Finkelstein et al. 2015; Oesch et al. 2018). It was also possible to correct these quantities for the influence of dust when it became clear that dust attenuation is primarily responsible for the slope β of the UV continuum (Meurer et al. 1999; Steidel et al. 1999; Shapley et al. 2003; Pannella et al. 2009), which can be measured from narrow and broad photometric bands (e.g., Bouwens et al. 2009; Rogers et al. 2013; Castellano et al. 2012, 2014; Hathi et al. 2013; Pilo et al. 2019). Currently, UV-based, dust-corrected SFRs reach far higher sensitivity levels and statistics than any other alternative tracer at other wavelengths. More recently, some works (e.g., Pannella et al. 2015; McLure et al. 2018a) have shown that β values correlate with the stellar masses of the galaxies, which can then be used as indirect probes of attenuation, even though the mass derivation usually requires more information on the SED distribution of the objects at longer wavelengths.
Spectroscopy provides an alternative, powerful method to constrain galaxy evolution through measurements of accurate spectroscopic redshifts, kinematics, and gaseous and stellar metallicities. For example, Fanelli et al. (1988, 1992) proposed a series of UV absorption lines as useful tracers of the physical properties of young stellar populations, including, but not limited to, metal content, stellar wind strength, and IMF. Rix et al. (2004) and Leitherer et al. (2011) first introduced three absorption indexes around 1370, 1425, and 1978 Å to study a sample of star-forming galaxies at redshift ∼1. These features, which are mostly blends of multiple elements, were found to depend only on metallicity, according to Starburst99 stellar models (Leitherer et al. 1999). It became immediately clear that using these rest-frame UV features for high-redshift observations, where they fall in the optical or near-infrared (NIR) range, could provide a lot of insight about the nature of pristine, young galaxies.
To this aim, a series of spectroscopic campaigns started in 2014–2015 (e.g., VUDS, Le Fèvre et al. 2015), targeting thousands of star-forming galaxies at redshifts 2–4 to study their properties. Chisholm et al. (2019) measured the stellar metallicity of 19 galaxies at z ∼ 2, observed through the Magellan Spectrograph. Ultraviolet and optical rest-frame spectra of SF galaxies at z ∼ 2.4 were also obtained from Keck/LRIS and Keck/MOSFIRE by Steidel et al. (2016) and Topping et al. (2020), who investigated the relation between stellar and gas-phase metallicity. In the same direction, the ESO-VANDELS spectroscopic survey (Pentericci et al. 2018; McLure et al. 2018b) has continued to dig deep into this cosmic epoch, and currently represents the state-of-the-art investigation with respect to the number of targeted galaxies and depth reached. In fact, VANDELS observed, from 2015 to 2018, more than two thousand galaxies in the rest-frame UV down to a limiting magnitude of iAB ≃ 27.5 (at 5σ), with integration times ranging from 20 to 80 hours per source, ensuring enough S/N of the continuum for the derivation of reliable constraints on stellar mass, attenuation, SFR, and stellar metallicity. Most importantly, these performances enabled the determination, for the first time at redshift > 2.5, of the stellar metallicity from stacked spectra of galaxies in bins of stellar masses or Lyα equivalent width, by fitting stellar population synthesis templates to their entire FUV emission (Cullen et al. 2019, 2020). This has shed light on the chemical evolution of intermediate- and high-mass (8.5 < log10 M* < 10.2) systems before the peak of cosmic SF activity at z ∼ 2 (Madau & Dickinson 2014).
Despite this rapid progress, the growth of galaxies and the increase of SFR density in the early Universe are far from being completely understood. The main limitation in the analysis is not connected with data availablity, but with the systematic uncertainties involved in the determination of key physical quantities, and related to the known degeneracies involved in the estimation of several parameters. Most notably, the SED fitting technique is subject to the attenuation, age, metallicity, and IMF degeneracy. The stellar mass and β slope are usually taken as proxies for predicting the level of dust attenuation, but these correlations have a large scatter, which leaves dust corrections largely inaccurate, especially when applied to individual objects. Moreover, UV slopes can also be affected by other quantities than dust, namely the IMF, the stellar age, the nebular continuum, and the metallicity (Bouwens et al. 2009; Castellano et al. 2014; Raiter et al. 2010). In particular, the latter could have a crucial role in solving part of the degeneracies still affecting these scaling relations.
To derive stellar metallicities, a whole spectral fitting could still be influenced by complex dependencies on the age and IMF, which is typical for the majority of absorption complexes in the FUV. In addition, it needs a good quality spectrum over a large wavelength range. In order to reduce potential biases, single absorption lines provide an alternative method to measure the metallicity. Needing only specific indexes 10–20 Å wide, this method can work on a limited portion of the FUV spectral range, typically ∼100 Å, required for a good estimate of the underlying UV continuum. In addition, this estimate is also independent of dust extinction, and in most cases it is insensitive to stellar age and IMF, at least for slopes α close to Salpeter (within 0.2) and ages higher than ∼50 Myr. The reason for this behavior is that the depth of photospheric absorption features in the far-UV depends on the relative abundance of O and B stars. After an initial period of the same order of the average lifetime of these stars, if the SFR is constant, the same number of young stars forms, and their contribution to the UV spectrum does not change on average over time.
However, several studies conducted over the past 20 years have generated some uncertainties on the best absorption lines for measuring the metallicity (i.e., those least affected by age or IMF variations) and on the correct calibration functions to adopt. Moreover, many lines were found to be strongly contaminated by the interstellar medium (ISM) absorption, thus are not reliable tracers of the metallicity in stars. In addition, most of them were tested on a limited number of objects, with various FWHM resolution data (from 0.25 to 3.8 Å rest-frame) and redshift (from 0 to ∼3). For example, Sommariva et al. (2012) found that the 1978 Å index is quite sensitive to the IMF assumptions, but they defined three additional indexes near 1460, 1501, and 1533 Å, independent of age and IMF, from which they measured the stellar metallicity of five star-forming galaxies at redshift ∼3. While the 1460 Å feature is produced by NiII and the 1533 Å line by SiII, the absorption region at 1501 Å arises in the photosphere of young, hot stars and is due to the ionized SV species (Pettini et al. 1999; Quider et al. 2009). Leitherer et al. (2011) and Faisst et al. (2016) adopted other metal-sensitive indexes near 1400 and 1550 Å to study the metal content of a sample of local starbursts and star-forming galaxies at z ∼ 5. In particular, the CIV absorption feature around 1550 Å has a strong wind component, indicated by its P Cygni profile, whose strength is known to be correlated with the metallicities of the parent stars (Castor et al. 1975; Walborn et al. 1995). On the other hand, winds from hot stars also contribute to the absorptions at 1300 and 1400 Å, which are due to SiIII and SiIV, respectively. However, their metallicity is more representative of the ISM component of the galaxies: even though these lines are influenced by stellar photospheric absorption, they are mainly affected by interstellar absorption, and, in part for the second index, by nebular emission. More recently, thanks to ISM and radiative transfer models, Vidal-García et al. (2017) studied the influence of ISM absorption and emission for most of the commonly adopted stellar photospheric indexes in the literature, finding that the 1425 Å line and the ∼1719 Å complexes (already studied in Fanelli et al. 1992) are among the cleanest and least contaminated stellar metallicity tracers up to at least solar metallicity values. In particular, the latter index is a blend of medium and highly ionized species, including NIV (1718.6 Å), SiIV (1722.5, 1727.4 Å), and multiple transitions of AlII and FeIV ranging from 1705 to 1729 Å.
In this paper, we revisit most of the absorption indexes that have previously been adopted in the literature. Comparing the predictions of multiple stellar models, we infer new calibrations for spectra with various resolutions and measure the stellar metallicity of high-redshift galaxies at 2 < z < 5 from a combination of two robust UV absorption lines located at 1501 and 1719 Å. With these in hand, we explore how the metallicity is related to other properties, including UV slope, UV magnitude and stellar mass, and whether it can remove the degeneracies still affecting the scaling relations involving such quantities.
The paper is organized as follows. In Sect. 2, we describe the VANDELS spectral observations and the procedures adopted to measure the UV slope, the stellar mass, and the stellar metallicity. We conclude this part by illustrating the final sample selection for this work. In Sect. 3, we present our results. First, we explore the mass-metallicity relation from two UV absorption line metallicity tracers, and its evolution with redshift. Then, we investigate the role of stellar metallicity in the UV magnitude-β and stellar mass-β relations, and assess the dependence between β slope and metallicity. Finally, in Sect. 4 we discuss our results and compare them to SAMs of galaxy evolution. A summary with conclusions is featured in Sect. 5, while an appendix with additional material is included in the last part of the paper. In our analysis, we adopt AB magnitudes and a Chabrier (2003) initial mass function (IMF) to derive stellar masses, star-formation rates, and UV absolute magnitudes. Throughout this work, unless otherwise stated, we assume a cosmology with H0 = 70 kms−1 Mpc−1, Ωm = 0.3, ΩΛ = 0.7, and the most recent estimation of the solar metallicity Z⊙ = 0.0142 (Asplund et al. 2009). We also assume, by convention, a positive equivalent width (EW) for absorption lines and a negative EW for lines in emission.
2. Methodology
In this section, we describe VANDELS observations, the spectral reduction, and calibration. Then we illustrate, in detail, the derivation of the two key physical parameters of this work: the UV continuum slope from photometric data and the stellar metallicity from rest-frame UV spectra. Finally, we specify the sample selection adopted in our analysis.
2.1. Spectral observations and reduction
The galaxies analyzed in this study are selected from the ESO-VANDELS project (ESO Large Program ID 194.A- 2003(EK); P.I. L. Pentericci and R. McLure)1. VANDELS is, to date, the deepest optical spectroscopic survey of high redshift galaxies. We refer to the two introductory papers by McLure et al. (2018b) and Pentericci et al. (2018) for all the details concerning the observations and data reduction, and highlight here only the main characteristics. The survey targeted ∼2100 galaxies at redshift z ≥ 1 in an area of the sky of 0.2 deg2 in total, in the Ultra Deep Survey (UDS) and Chandra Deep Field South (CDFS) fields around the CANDELS region (Grogin et al. 2011; Koekemoer et al. 2011). The interesting targets for our goals are: (1) bright star-forming galaxies (SFG) with a photometric redshift ranging 2.5 < zphot < 5.5 and magnitude limit iAB < 25; and (2) lyman-break galaxies (LBG) in the range 3 < zphot < 5.5, which have fainter magnitudes and lower S/N compared to SFGs. The initial magnitude limits were H < 27 and iAB < 27.5 in this case. All targeted galaxies have specific SFRs (SSFRs) higher than 0.1 Gyr−1, even though the majority of them have SSFRs > 0.4 Gyr−1 and SFRs higher than 2.5 M⊙ yr−1.
The observations were performed with the VIMOS multi-object spectrograph mounted at the ESO-VLT, which delivers high-quality spectra in the 4900 Å < λ < 9800 Å wavelength range with an average resolving power R = 580, corresponding to an average spectral resolution in rest-frame of ≃2.8 Å. The VIMOS spectra were reduced in a fully automatic way with the EASYLIFE pipeline (Garilli et al. 2012). This procedure yields fully wavelength- and flux-calibrated 2D and 1D spectra, corrected for atmospheric and galactic extinction, and normalized to the i-band photometry available for all targets. As described in Pentericci et al. (2018), since an artificial flux loss was observed in the extreme blue end of the spectra (λ < 5600 Å) when compared to broad-band photometry, a statistically estimated empirical correction was applied in post-processing to ensure the correct flux density shape at lower wavelengths. This correction is in all cases no larger than 10–20% of the original flux density.
After the reduction process, the VANDELS team was in charge of measuring spectroscopic redshifts zspec for all the observed targets. The derivation of zspec was made with the help of the EZ software package (Garilli et al. 2010), which cross-correlates each spectrum with a subset of reference templates derived from previous VIMOS observations, representative of a large variety of stellar and galaxy types. The measurements were supervised by two independent team members and then further checked by the two co-PI before reaching a final agreement. A quality flag (from 0 to 9) was also assigned to each measurement, representing the probability of the redshift to be correct. Spectra with flags 3 or 4 are the most reliable, with > 95% and 100% probabilities of being correct, respectively. In these cases, multiple emission or absorption lines could be typically recognized in a moderate S/N continuum. The median accuracy of spectroscopic redshift determinations is 0.0005 (∼150 km s−1).
The first step of this work involved preselecting 872 galaxies from the parent catalog in VANDELS by requiring a secure spectroscopic redshift (flags 3 or 4) between 2 and 5. The former is slightly below the lower limit in the original selection, and includes some objects for which the photometric estimate (zphot) was slightly overestimated. The latter condition was set to have good quality spectra: above z = 5, galaxies’ spectra are too noisy to give a statistically significant contribution to our analysis, and none of them pass further constraints that will be introduced in the following sections to ensure good quality measurements of the parameters we considered in this work. We also specify that bright sources in the infrared, which could be starburst (off-MS) systems, are excluded from our selection. Our sample thus contains systems, either preselected as star-forming galaxies (based on specific SFR > 0.1 Gyr s−1) or Lyman-break galaxies, which are fairly representative of the main sequence of star formation (see McLure et al. 2018b).
2.2. Stacking procedure
In this paper, we derive the stellar metallicities from two photospheric absorption features of young O-B stars, located in the far-UV spectral range at 1501 and 1719 Å, as described in the introduction. These indicators are typically very faint, with EWs lower than 8 Å over a wavelength range of ∼10 Å, depending on the index, thus they require a high S/N continuum to be properly constrained, as we quantify below. For this reason, prior to the metallicity measurements, we stacked our spectra in multiple bins of different physical quantities (i.e., stellar mass, UV slope, UV absolute magnitude MUV, and redshift). In a representative example in Fig. A.1 in the Appendix, we show that the 1σ error on the equivalent width (hence on metallicity) is tightly correlated and strongly decreases with the S/N of the underlying continuum. Ideally, an S/N of at least ∼25–30 is required to measure Z with an uncertainty of the order of 0.3–0.4 dex in a single index, which improves to 0.1–0.2 dex by combining multiple indicators. Throughout the rest of this work, our bins will be constructed to ensure high enough S/N in each stacked spectrum, > 30 if possible, and > 20 in all cases. This was found to be the best compromise between minimization of the uncertainty on the final metallicity estimate and the number of bins needed to test our relations.
We illustrate here the general stacking procedure adopted in this paper. First, we converted all the spectra to a rest frame according to their spectroscopic redshifts estimated by the VANDELS collaboration. We normalized them using the median flux estimated in the range 1250 < λ < 2000 Å, and then resampled the spectra to a common wavelength grid of 0.4 Å per pixel, similarly to the sampling of Starburst99 stellar models, and which corresponds to nearly half of the wavelength sampling of individual galaxies in VANDELS. This way, we are less prone to introduce systematic biases in the calibration functions compared to resampling simultaneously both the original Starburst99 models to a coarser grid and the observed spectra. Then, we built composite spectra of all the objects falling in the same bin by taking the median flux at each dispersion point, while we calculated the noise from 500 simulations by each time taking a random 80% of the spectra in the bin, computing the median of individual flux values, and finally deriving the standard deviation of all the 500 realizations. We did not perform the bootstrap resampling with a replacement (requiring, for the subsets, the same size of the original sample) as this would be more affected by peculiar spectra, which could enter into the calculation many times. In addition, we did not derive the composite flux with an error-weigthed method, as this would bias the result toward lower redshift or more star-forming objects, which typically have higher S/Ns. We also remark that a coarser spectral resampling in the stacking procedure (e.g., 1 Å pixel−1) does not alter the results presented in the following sections and the uncertainties associated with the measured equivalent widths. Finally, as mentioned in Sect. 2.1, the redshift determinations in VANDELS are mainly based on the presence of UV rest-frame emission or absorption lines, which are produced by different components of the galaxies (e.g., stars, ISM, gas inflows/outflows), possibly in relative motion among them. It is thus useful to check our stacking procedure by using a common reference redshift for the galaxies, such as the systemic redshift (defined as the redshift of the bulk of the stars) as traced by the CIII]λλ1907–1909 Å emission line doublet (Shapley et al. 2003). Thanks to the relative brightness of this line, we identified a subset of 150 CIII] emitters by visual inspection of both the 2D and 1D spectra (S/N > 7). For this sample, we found that adopting either the value in the VANDELS release or the systemic redshift in the stacking procedure yields fully consistent metallicity measurements, and thus would not modify the results of this work.
2.3. Photometry in VANDELS fields and stellar masses from SED fitting
All targets in VANDELS have either space-based or ground-based photometric data available. The pointings in the UDS and CDFS fields are centered on the area covered by the CANDELS survey (Grogin et al. 2011; Koekemoer et al. 2011). For these regions, we have deep optical+near-IR (ACS + WFC3/IR) HST images, Spitzer images, and H-band selected, PSF-homogenized photometric catalogs assembled by Galametz et al. (2013) and Guo et al. (2013), including total magnitudes in six and ten space-based broad-band filters, in the UDS and CDFS fields, respectively. In the same area, photometric data from ground are also available, so we are able to cover the full range between band B (λcen ≃ 4450 Å) and IRAC channel 2 (λcen ≃ 4.5 μm). The limiting magnitude of this dataset is HAB < 27.05 (5σ).
On the other hand, ∼50% of the total VANDELS area (both CDFS and UDS) falls outside of CANDELS. In these regions, while some HST filters are still present, most of the optical+near-IR imaging is performed with ground-based facilities, including Subaru, CFHT, UKIRT, VISTA, and VLT. Photometric catalogs of H-band detected sources (HAB < 27.05) were produced by the VANDELS team using the SExtractor tool v2.8.6 (Bertin & Arnouts 1996), providing PSF-homogeneized photometry and total magnitudes in 13 and 11 broadband filters in UDS and CDFS, ranging, respectively, from 0.3 to 8.0 μm. In Table 1, we show the photometric bands that were used in all the fields covered by the VANDELS survey. More information on the observing campaigns, instruments adopted, and depth of the survey can be found in Table 1 of McLure et al. (2018b).
Photometric bands available in the four fields covered by the VANDELS survey and used for the estimation of stellar masses, SFR, and UV slope.
Using all the available photometry ranging from band U to the IRAC channel 2, the stellar masses are derived through the SED fitting technique as described in McLure et al. (2018b). This fit adopts the stellar population templates with solar metallicity of Bruzual & Charlot (2003), a Chabrier IMF, declining τ-model star formation histories (SFH) with τ ranging 0.3 < τ < 10.0 Gyr and ages ≥50 Myr. The dust is modeled with a Calzetti et al. (2000) attenuation law, with AV values in the 0 < AV < 3.0 range, while the effect of the intergalactic medium (IGM) transmission is taken into account following Inoue et al. (2014). Similarly, the UV-based SFRs are derived from the best-fit UV rest-frame absolute luminosity following Madau & Dickinson (2014) and then dust corrected using AV estimated from the same fit.
2.4. Beta slope and UV absolute-magnitude estimations
In this work, we assume that the UV continuum emission of each galaxy can be approximated with a power-law of the form f(λ)∝λβ (Meurer et al. 1999; Calzetti et al. 1994). To estimate the exponent β, we first converted all the observed (total) AB magnitudes into flux densities fλ, and removed all photometric bands whose bandwidths are outside the 1230–2750 Å rest-frame wavelength range, to exclude any contamination from the Lyα line, while the redward limit is the same as that adopted in Pilo et al. (2019). We note that the redward limit is slightly higher than in the original Calzetti et al. (1994) definition. This ensures more statistics for our analysis, while it does not introduce systematic biases to the results: we note that the central wavelength of the reddest bandpass does not typically lie outside of 2600 Å. When multiple photometric bands with similar pivot wavelengths were available, we determined the weighted average of their fluxes in order to provide a more uniform, evenly sampled coverage of the wavelength space. Then we fit a linear relation between log(λ) and log(fλ) using an orthogonal distance regression (ODR) technique (Boggs et al. 1992). From the best-fit relation and the spectroscopic redshift of each galaxy, we also estimated the UV absolute magnitude MUV at 1600 Å, M1600.
In the measurements of β, for each galaxy we could use a minimum of two to a maximum of six bands (four on average) from the list of Table 1. We proved the stability of our values by removing, for each galaxy, one or two random photometric bands from the initial dataset (keeping at least three bands), and computing again the slope with the same ODR fitting procedure. This yields determinations that are in qualitative agreement with the original values based on the full available dataset, and do not have systematic discrepancies, indicating that our results are not driven by some specific bands adopted in the fit, and are stable against the exact number of photometric points that are used in the fit. We note that the wavelength range for fitting the UV slope does not contain strong emission lines that can significantly affect the photometry, as those bands possibly contaminated by the Lyα line have always been excluded at the beginning.
On the other hand, since our galaxies are located in different fields for which a heterogeneous set of photometric filters is available, we checked for the presence of systematic differences among β determinations in the four different VANDELS fields. We found that our results are generally in agreement, except for galaxies in the CDFS-GROUND field, which show a higher UV slope at fixed stellar mass or selection magnitude. We also note that CDFS-GROUND data are of lower quality than those in UDS-GROUND, and most of the discrepant objects have a low S/N, with beta measurements just based on two bands. We found that applying a cut to the β uncertainty (σβ < 1), and requiring at least three data points to perform the fit, removes these outliers and restores the consistency of β distribution among all VANDELS fields. We also remark that these offsets do not affect the derivation of stellar masses in CDFS-GROUND, as these are based on fitting the entire SED up to IRAC channel 2, and they are most sensitive to the optical rest-frame range rather than the UV.
We compared our β estimations to those obtained from the best-fit photometric SED (see Sect. 2.3), while we provide a discussion about the UV slope inferred from VANDELS spectra in Appendix A.1. As far as the first are concerned, we found a systematic difference with the SED-based estimates of ∼ − 0.2 (i.e., 10% of β measurements), which is likely related to the different method adopted and to the different treatment of photometric bands at the left- and rightmost extremes of the 1230–2750 Å wavelength range. In particular, if we require only the central pivot wavelength not to exceed those limits (instead of the whole bandwidths), we obtain UV slopes ∼0.15 flatter, more in agreement with SED-fitting-based values. However, we remark that this difference is below the typical uncertainty of the β estimations for our galaxies ( (1σβ)median = 0.23). Overall, compared to β and MUV estimations based on the best-fit photometric SED, an advantage of our procedure is that it is not model dependent.
2.5. The UV absolute-magnitude – β relation
In Fig. 1, we show the distribution of beta slopes as a function of MUV, which is often taken as a reference to dust-correct the luminosity function. Our entire sample has a median β slope of −1.76 (1σ dispersion of 0.54) and MUV of −20.62 (σ = 0.57). A best-fit linear relation can be written explicitly as β = ( − 0.07 ± 0.03) × MUV − (3.18 ± 0.7), indicating a slight increase of β for bright objects at a 2σ significance level. A similar slope to our analysis was also found by Bouwens et al. (2009, 2014) for U- and B-dropouts at redshifts ∼2.5 and 4, and by Castellano et al. (2012) for LBGs at redshift ∼4.
 |
Fig. 1. UV slope vs. M1600 for VANDELS galaxies selected in this work with σβ ≤ 1 and at least three photometric bands available in the range 1230–2750 Å. Our data are color-coded according to three different redshift bins (2 < zbin1 < 3 < zbin2 < 4 < zbin3 < 5 in blue, dark red, and orange, respectively), with z estimated from VANDELS spectra. The median z in each bin is reported in the legend. For comparison, we show the M1600–β relations found by Hathi et al. (2016) at 2 < z < 2.5 (empty gray circles), Bouwens et al. (2009) at ∼2.5 (cyan circles), Bouwens et al. (2014) at ∼4 (empty black circles), and Castellano et al. (2014) for LBGs at z ∼ 4 (empty black diamonds and light gray dashed best-fit line). The relation found by Pilo et al. (2019) for LBGs at z ∼ 3 is displayed as a light green dashed line. |
Dividing the sample into three redshift bins, we also find a β evolution in our redshift range, increasing on average from −1.98 at z ∼ 4.1 to −1.59 at z ∼ 2.6, in agreement with the strong evolution in β expected in this cosmic epoch (e.g., Pannella et al. 2015), and with results found by other works at similar or slightly different redshifts. First, photometric-based UV slopes derived by Hathi et al. (2016) for star-forming galaxies in VUDS at redshifts 2 < z < 2.5 are slightly redder (by ∼0.15) than our estimates at zmedian = 2.58, across the same UV magnitude range −22 < MUV < −20. Then, our objects follow approximately the same distribution expected for star-forming galaxies at redshift ∼3: the median values of β calculated in our first two subsets around z ∼ 3 (zmedian = 2.58 and 3.46) are indeed largely consistent, over all the range of UV magnitudes, with z ∼ 3 LBGs in the COSMOS field presented by Pilo et al. (2019). The last bin at the highest redshift (4 < z < 5) was created to compare with the work of Castellano et al. (2012), which adopts a similar derivation of the UV slopes, and whose results are in agreement within the errors with our findings.
2.6. Metallicity calibrations from UV absorption indexes in Starburst99 models
Absorption lines in the UV rest-frame spectra carry important physical information about the properties of the host galaxies (Fanelli et al. 1988, 1992). While some of them are produced in the ISM of the galaxy itself, others are instead produced by chemical elements in the photospheres of hot, young, O and B stars, or in stellar winds generated by their radiation pressure. The latter two cases are extremely interesting as they can be used as stellar metallicity diagnostics. These include the indexes at 1501 and 1719 Å that are adopted in this paper.
In order to derive a proper conversion between absorption strength and Z*, we used Starburst99 WM basic models (Leitherer et al. 2010, 2011) to remain consistent with the previous VANDELS work on the stellar metallicity by Cullen et al. (2019). Moreover, among all currently available stellar templates, they offer the highest native spectral resolution across a wide range of wavelengths (0.4 Å in the range 900 < λ < 3000 Å), also offering the possibility to test the metallicity calibration functions for significantly higher resolutions than VANDELS. These models have also been widely tested in many studies on faint photospheric absorption lines (e.g., Rix et al. 2004; Sommariva et al. 2012; Leitherer et al. 2011). However, for completeness, a comparison with BPASS models (Eldridge et al. 2017) is also included in Appendix A.3.
We produced far-UV Starburst99 spectra assuming a continuous SFH and a grid with different stellar ages (50, 100, 150, 200, and 500 Myr; and 1, 1.5, and 2 Gyr), metallicities (0.05, 0.2, 0.4, 1, and 2.5 times solar), and the two IMFs available in the simulation (i.e., Salpeter and Kroupa)2. The lower limit of 50 Myr is also the lowest stellar age adopted in the SED fitting, while the upper bound of 2 Gyr corresponds approximately to the age of Universe at the median redshift of our sample.
The models, which have the same wavelength sampling of VANDELS stacked spectra (see Sect. 2.2), were smoothed with a gaussian kernel with σ = 1.3 Å to match the VANDELS average resolution. Afterwards, for each model, we measured the EWs of absorption features according to the following definition:
where f(λ) is the flux density spectrum across the absorption or emission feature, fcont(λ) is the continuum (both in erg/s/cm2/A), while λ1 and λ2 are the starting and ending wavelengths of the features. The list of features analyzed in this work, including the corresponding λ1 and λ2, are shown in Table 2.
Absorption complexes analyzed in this work.
The EW quantifies the relative absorption strength of the line with respect to the underlying UV continuum, hence it is critical to specify the calculation of fcont(λ) in Eq. (1). Given the relatively low resolution of VANDELS spectra, we cannot identify the “real” continuum level, as there are basically no spectral regions free of absorption. To overcome this problem, we adopted the so-called pseudo-continuum, which is defined by ranges relatively free of strong absorption or emission lines, as introduced by Rix et al. (2004). Therefore, for each index, we calculated fcont(λ) in Eq. (1) as the linear interpolation of the error-weighted average flux density in the closest blueward and redward pseudo-continuum windows defined in Table 3 of Rix et al. (2004). Since the original pseudo-continuum widths of ∼3–4 Å barely correspond to one resolution element in VANDELS spectra, we also increased them by ±3 Å, yielding a total width of ∼10 Å. This choice also produces more stable measurements that are less affected by noise. However, we remark that it does not affect the final results, provided that we use the same definition for both the calibrations and the observations.
In order to mitigate even more noise effects in observations, we estimated the EW of absorption lines in VANDELS stacks using Eq. (1) and taking the median value from 1000 Monte Carlo realizations, generated by perturbing the flux at each wavelength according to the noise spectrum. This procedure allows a robust estimate of the 1σ uncertainty of the associated EW as the standard deviation of those different realizations. Moreover, we find that our results are not significantly affected if we just perform a single estimate of the pseudo-continuum level and of the EW of absorption indexes, even though we do not have an associated error for the observation in this case.
We remind the reader that another approach to calculate the pseudo-continuum spectrum is based on fitting a spline to all the Rix et al. (2004) windows simultaneously, as done by Sommariva et al. (2012). However, we found that the two approaches yield very similar calibration functions and thus fully consistent results. In the rest of this paper, we use only the local fit explained above, because it has the clear advantage of being applicable even when the full far-UV spectrum is not available or if any of the pseudo-continuum windows have to be discarded because of contamination from sky-line residuals in individual observed spectra.
In Fig. 2, we show the main results of this analysis for the two absorption indexes adopted in this study. First, the EW1719 spans a large dynamic range of ∼2.5 Å (from 0.2 to 2.7) from 1% Z⊙ to solar metallicity, making it relatively easy to constrain Z within a ±0.1–0.15 dex uncertainty with the S/N imposed on our VANDELS stacks (see Fig. A.1). A third-order polynomial fit yields the following calibration:
 |
Fig. 2. Diagrams showing dependence between EW and metallicity for the 1501 and 1719 Å absorption line indexes that we adopt in this paper according to Starburst99 models. All the data points are derived assuming a constant SFH for 100 Myr and Kroupa IMF. The shaded gray region around the main relations represents the variation of EW with the IMF (Kroupa-Salpeter) and with the ages of the stellar population chosen (50 Myr–2 Gyr), as described in the text. The final metallicity calibrations are based on a third-order polynomial fit to the data points, and are shown with a continuous blue line in each panel. Their explicit forms are given in the text in Eqs. (2) and (3). |
Overall, we confirm that the EW of the 1719 Å metallicity tracer is largely independent of the IMF chosen and stellar age (Fig. 2, left). Since it is basically uncontaminated by ISM absorption even at higher (solar) metallicities, according to Vidal-García et al. (2017), we take this index as a reference as it should be the most reliable. We also notice that our definition for this index is slightly different from the original version, as this also allows us to fully include the leftmost blend generated by FeIV absorptions between 1709 and 1712 Å (visible later in Fig. 9).
Applying the same procedure as above to the index located at 1501 Å yields the following metallicity calibration inferred from a third-order polynomial fit (Fig. 2, right):
The 1501 Å index was first proposed by Sommariva et al. (2012) as a very promising metallicity tracer. However, because it is narrower, it also has the lowest spread in general, showing EWs ≤1 Å for all metallicities below solar.
In Fig. 3, we display the EWs of the 1719 and 1501 indexes obtained from five stacks in M* bins constructed to analyze the mass-metallicity relation (see later in Sect. 3.1), as they have the highest S/N among all the stacked spectra derived in this work. This figure indicates that the 1501 tracer not only shows EWs that are correlated to those of the 1719 index, but that the two EWs are qualitatively in agreement with the predictions of Starburst99 models. In other words, it means that calibrations built from the same Starburst99 templates yield very consistent metallicities from both the 1501 and 1719 Å indexes. We also caution that the two calibrations derived in this section could be safely applied in the metallicity regime spanned by the VANDELS data (Cullen et al. 2019), but we cannot verify whether significant ISM absorption would affect the lines at higher Z, or whether the models (at the VANDELS resolution) still simultaneously reproduce the two EWs outside of our range.
 |
Fig. 3. Comparison between equivalent widths of 1719 and 1501 Å absorption indexes predicted by Starburst99 models (big squares color-coded by metallicity). We show in each diagram the EWs measured in five VANDELS stacks (big stars), obtained via the same procedure adopted for synthetic templates. The stacks used here were produced at different stellar mass bins (see Sect. 3.1 and Table 3), whose median stellar masses (in log10 (M*/M⊙)) are highlighted in black above each point. The shaded gray area has the same meaning as in Fig. 2. |
As far as the remaining UV absorption lines are concerned, we find two different situations. Firstly, the EWs of absorption indexes located at 1370, 1425, 1460, 1533, and 1978 Å are weakly (or not at all) correlated with the EW of the 1719 index, and hence with the metallicity. The majority of these features measured in the stacked spectra are also very faint and would yield unrealistically low metallicities with very large uncertainties at our S/N and spectral resolution. As a result, they are unusable to constrain the chemical abundances from VANDELS spectra. Secondly, the absorption lines at 1400, 1550, and 1853 Å, even though they are correlated with the EW of the 1719 index, are systematically deeper than predicted by Starburst99 models, indicating they are also contaminated by ISM absorption at various degrees at subsolar metallicities. Since our work is based on the stellar metallicity and a modeling of the ISM is beyond our goals, we exclude them from the subsequent analysis.
We refer the reader to Appendix A.3 for a more detailed discussion of the EWs and calibrations obtained with all the indexes listed in Table 2. Hereafter, we focus exclusively on the two aforementioned metallicity indicators at 1719 and 1501 Å, displayed in Figs. 2 and 3. In order to define a unique, representative metallicity for the stacks derived in this paper, we considered the average metal abundance obtained from the EWs of those two indexes separately, and we used the error propagation to determine the final uncertainty on each estimation.
Finally, in Appendix A.4 we also explore for all the lines the effect of different IMFs. While modifying the IMF upper mass cut-off (up to 300 M⊙ yr−1) and the slope α of the high-mass end (within ∼0.2 of the Salpeter value α = −2.35) does not produce significant variations of the metallicity calibrations for the 1719 and 1501 absorption indexes, choosing even flatter slopes (e.g., α ≲ −2) would yield systematically higher metallicity values. However, typical main-sequence star-forming galaxies at z ∼ 3 with intermediate stellar masses (median M* = 109.7 M⊙) are not expected to have IMFs extremely different from Salpeter (e.g., Elmegreen 2006; Bouwens et al. 2012). According to Fontanot et al. (2018), flatter and top-heavy IMFs can be found for galaxies that are more massive and star-forming compared to those of our VANDELS selection. Finally, we remark that a more detailed analysis of a variable IMF on the mass-metallicity relation (MZR) and mass-UV slope relation is clearly beyond the aim of this paper.
2.7. Final sample selection
We include additional constraints to our sample selection criteria in order to exclude objects where UV slopes and/or metallicity indicators are not reliable. From the sample selected at the end of Sect. 2.1, we thus selected spectra free from bad sky-subtraction residuals, noise spikes, or reduction problems in the spectral windows used to estimate the pseudo-continuum level and the EW of the 1501 and 1719 metallicity tracers. This yields 732 galaxies (called subset #1), of which 372 are in the CDFS field. We use this subset to study the MZR and its evolution with redshift in the following section. The histogram distribution of spectroscopic redshifts for this selected sample is shown in Fig. 4.
 |
Fig. 4. Diagram showing distribution of spectroscopic redshifts of VANDELS galaxies selected for this work. The vertical dashed line indicates the median redshift of the sample (zmed = 3.38). |
Afterwards, we built a second, smaller subset requiring in addition a reliable estimate of the UV slope, with σβ < 1 and at least three photometric bands used in the fit, as already discussed in Sect. 2.4. We conclude in this case with 576 galaxies, which we refer to as subset #2 (all of them are included in the first subset) and that we consider for all the remaining diagrams. In this sample, 254 objects are located in the CDFS field. We remark that adopting this second galaxy subset for the mass-metallicity relation, the results would not be significantly altered; however, we preferred to maintain the larger sample in order to have better statistics to study the evolution in redshift of that relation. We also note that these criteria do not introduce biases in the stellar mass and beta distributions of the original sample, hence the selected galaxies are still representative of the star-forming main sequence.
3. Results
In this section, we explore how the stellar metallicity and UV continuum slope are related to each other and to other galaxy properties. We then assess the role of stellar metallicity in the estimation of dust attenuations for galaxies with different stellar masses and UV luminosities. As a first step, we take advantage of our new metallicity measurements to investigate the mass-metallicity relation from UV absorption lines, and compare the result with the relation presented in Cullen et al. (2019), derived from fitting Starburst99 models to the entire VANDELS FUV spectral range.
3.1. Mass-metallicity relation from UV absorption indexes
The MZR is a powerful diagnostic of the chemical evolution history of galaxies, with its shape and normalization providing important constraints on the star-formation history, feedback processes, and gas inflows and outflows (Maiolino & Mannucci 2019). On the left of Fig. 5, we show the stellar-mass MZR derived for our VANDELS subset #1 in the 2 < z < 5 redshift range from UV absorption tracers, as explained in Sect. 2.6. The data points represent the median stellar masses of galaxies residing in the same bin, and the chemical abundances from the corresponding stacks. We chose a stellar mass bin width of 0.25 dex (larger at the borders), as a compromise between the highest possible number of bins and a minimum S/N (= 30) required for each stacked spectrum to derive accurate metallicities. The final values of Z and errors (represented as black squares and vertical bars) were derived by averaging the estimates obtained from the two absorption indexes at 1501 and 1719 Å. In the top section of Fig. 5, we also report the corresponding metallicity estimates for each individual index with shaded dark cyan and red squares, respectively. For comparison purposes, we also include the MZR of Cullen et al. (2019), represented by gray circles, which is derived from the DR23 release of VANDELS with a similar selection to our (2 < z < 5.0 and zaverage = 3.5).
 |
Fig. 5. Left: mass-metallicity relation of star-forming galaxies in VANDELS, with median stacks in bins of stellar mass (black squares). The metallicities derived from single indexes (i.e., in order, 1550, 1719, and 1501 Å) are drawn with pale colored squares in blue, red, and dark cyan, respectively. The linear fit to the median metallicities in the 108.5 < M* < 1010.5 M⊙ range is highlighted with a dashed dark cyan line. Right: mass-metallicity relation followed by VANDELS star-forming galaxies at redshift < 3 (dark cyan squares) and > 3 (dark red squares). The median redshifts of the two subsets are 2.58 and 3.54, respectively. The relation for all the sample is overplotted in black. In both diagrams, the relation by Cullen et al. (2019), calculated at the same median redshift of our work (and of the VANDELS survey), is displayed with gray filled circles, while in the bottom panel we also include the MZR found by Zahid et al. (2017) at z ∼ 0.08 from the SDSS survey (olive squares) and by Gallazzi et al. (2014) for massive star-forming galaxies (M* > 1010.2 M⊙) at z ∼ 0.7. The linear fit to the MZR in the lower and higher redshift bin is drawn with a shaded dashed line in the corresponding color. The representative M* and metallicity estimated from the spectral stack of 75 star-forming galaxies at redshift ∼2 from Halliday et al. (2008) is shown with a cyan square and error bars. Finally, the stellar-mass gas-phase metallicity relation for star-forming galaxies at z ∼ 3.5 (Troncoso et al. 2014) is drawn with a green dashed line. |
As a first analysis, we note that the MZR built from our two absorption indicators, either taking the averages or the single values separately, is consistent within 1σ to that derived by Cullen et al. (2019). The metallicity rises by ∼0.5 dex, from log10(Z*/Z⊙)≃ − 1.1 to ≃ − 0.6, in the range of stellar masses between log10 (M*/M⊙) ≃ 9 and ≃10.2. The increasing trend of metallicity in this mass range can be approximated by a linear function (dashed dark cyan line), whose best-fit coefficients are displayed in Table 4. We notice that our relation is sampled by a lower number of points in the low-mass range compared to Cullen et al. (2019), as galaxies in this regime are generally fainter, and larger bins are necessary to reach the required S/N. Nevertheless, the upper limit at M* ≃ 108.5 M⊙ established by Cullen et al. (2019) and the metallicity of our lowest mass bin suggest that the same decreasing trend may also continue to stellar masses substantially lower than 109 M⊙. In Table 3, we present the definition of the bins used to build the MZR and the other relations studied in this work. It also includes, for each bin, the number of galaxies considered, the S/N reached in the stacked spectra, and the median properties of the corresponding subsets.
Summary of the best-fit relation parameters.
3.2. Redshift dependence of the MZR
In this section, we analyze the mass-metallicity relation as a function of redshift. To this aim, we divided our sample (subset #1) in two redshift bins with z lower and higher than 3. Then, we measured the metal content from our two indexes, as already done for the global relation, in four (three) bins of stellar masses, as can be seen in the right panel of Fig. 5. In the range of M* that is in common between the two subsets (log10 (M*/M⊙) from ∼9.5 to ∼10), the metallicities of the stacks in the upper redshift bin are systematically lower than at lower redshift, by ∼0.1 on average, even though all the estimates are still consistent within 1σ. Secondly, we fit a linear relation to all the data points belonging to the same redshift bin, finding a normalization difference between the two MZR (at 1010 M⊙) of 0.125 ± 0.134, hence they are consistent within the errors. The coefficient results for the two redshift bins are listed in Table 4. Furthermore, a series of Monte Carlo simulations, where we perturbed the median Z* and M* of the bins according to the estimated (Gaussian-like) uncertainties, yield a 28% probability of obtaining our results if there is no redshift evolution of the MZR normalization, hence the difference is again not statistically significant. We note that this result, even though obtained with a different approach, is in agreement with the conclusions of Cullen et al. (2019), who also find no clear monothonic decrease of stellar metallicity at fixed mass in the redshift range 2 < z < 5.
In the right section of Fig. 5, we also compare the shape of our relation with other studies at similar or different redshifts. First, Halliday et al. (2008) derived a stellar metallicity from the stacked spectrum of 75 star-forming galaxies at z ∼ 2 observed with the Galaxy Mass Assembly ultra-deep Spectroscopic Survey (GMASS). For their estimation, they used the absorption index at 1978 Å, which has been shown by subsequent studies to be significantly affected by stellar age and by the choice of the IMF (e.g., Sommariva et al. 2012), and also according to our work it is not a good indicator (see Appendix A.3). However, they also fit stellar population models to the far-UV spectra including the 1501 and 1719 absorption lines, and they found that observations are better reproduced by models with a metallicity of 0.2 × Z⊙, even though the correct value resides between 0.2 and 0.4 Z⊙. This suggests that no significant evolution of the MZR can be claimed down to z ∼ 2, or that the metallicity variation is very mild in the range 2 < z < 3.5.
Furthermore, other works were published at significantly lower redshifs than in our study. Zahid et al. (2017) investigated the MZR at redshifts z ∼ 0.08 (0.027 < z < 0.25) for star-forming galaxies extracted from the Sloan Digital Sky Survey (SDSS). Secondly, Gallazzi et al. (2014) analyzed a mass-selected sample of ∼70 galaxies at redshift ∼0.7, deriving an MZR representative of the whole galaxy population, both star-forming and quiescent. While a direct comparison to the latter cannot be performed, as we probe systematically lower stellar masses, the dataset of Zahid et al. (2017) shows that there is a decrease of stellar metallicity by ∼0.4 dex between z ∼ 0 and z ∼ 3 in all the mass range explored: from 109 to 1010.3 M⊙. Remarkably, the slopes of the mass-metallicity relations found at such different cosmic epochs are very similar. Fitting a linear relation between log10(M*/M⊙) = 8.5 and 10.5 indeed yields slopes that are all in agreement within 1σ. The results of the linear fit in this mass range for our two subsets at lower and higher redshifts are summarized in Table 3. This likewise suggests that if the linear fit holds up to M* ≃ 1010.5 M⊙, the same metallicity offsets might exist down to substantially lower stellar masses than those probed here.
Even though it is interesting to compare to results obtained at other cosmic epochs, we warn the reader that these studies adopt, in general, a different procedure for the derivation of the stellar metallicity, which might affect the measured level of normalization. Gallazzi et al. (2014) inferred Z* from the metal-sensitive absorption indexes [Mg2Fe] and [MgFe] in the optical spectrum, hence their metallicity might be representative of slightly older stellar populations compared to those probed with far-UV rest-frame absorption lines. A similar conclusion holds for the MZR of Zahid et al. (2017), who fit stellar population synthesis models to stacked spectra (in the optical range) of star-forming galaxies in bins of stellar mass. However, their relation is also consistent with the gas-phase metallicity obtained from emission lines. For comparison purposes, in the right section of Fig. 5 we also show the stellar-mass gas-phase metallicity relation at similar redshifts from Troncoso et al. (2014), which is approximately 0.2 dex above our MZR estimated from VANDELS. We refer the reader to Cullen et al. (2019) for a more detailed discussion of this comparison.
3.3. UV slope and stellar mass
Another way to study the evolution of galaxies in the early Universe is by tracing their dust attenuation as a function of stellar mass, metallicity, and redshift. After the formation of the first stars and galaxies, the dust content in the ISM is expected to increase during the first billion years, while generations of stars die and pollute their surrounding environment. The amount of dust absorption also limits our understanding of how star formation evolves in this cosmic epoch. While the easiest approach to inferring the dust attenuation for large samples of high-z, UV-detected galaxies relies on their UV continuum slopes, an alternative approach directly adopting the stellar masses has also become common in recent years. Indeed, a correlation between β (or AV) and M* has been found up to z ∼ 3.5 (e.g., Buat et al. 2012; Heinis et al. 2014; Pannella et al. 2015; Hathi et al. 2016; McLure et al. 2018a), with a 1σ scatter in β of the order of 0.5. It is thus interesting to investigate, with our large VANDELS sample, how these quantities are related.
In Fig. 6, we display, for our VANDELS selected subset #2, the UV slope as a function of stellar mass. We remark that here we only took those galaxies for which β is well constrained from the power-law fit to the available photometric data (see Sect. 2.4). Given the rapid evolution of β expected with cosmic time, we divided the main sample in two redshift bins, above and below the median redshift of the sample. Then we constructed additional subsamples of different stellar masses by requiring an equal number of objects for each subset, and we calculated the median β and the median absolute deviation (MAD) in all of these bins.
 |
Fig. 6. UV slope as a function of stellar mass in two redshift bins: 2 < z < 3.5 and 3.5 < z < 5 (red and blue, respectively), where 3.5 is the median redshift of VANDELS. A linear fit to the relations in each redshift bin is also shown via dashed lines with their corresponding colors. The M*–β relation from McLure et al. (2018a) at z < 3 is shown with a green line for comparison, while gray and cyan diamonds come from Pannella et al. (2015). On the left y-axis, A1600 is shown using the β–A1600 conversion of Meurer et al. (1999). |
We find that the median UV slopes in our stellar mass bins range from −2.2 to −1.4, which corresponds to an attenuation at 1600 Å (A1600) from ∼1 to ∼2.5 mag, assuming the Meurer et al. (1999) relation. We can see that, calculating the median β in 5 equal sized bins of stellar mass, more distant galaxies at 3 < z < 5 (blue squares) are bluer than the low-z subset (red squares) by ∼0.3 on average, even though the dispersion of the points around the median relations (larger for the high-z subset because of the higher uncertainties of individual measurements) is typically greater than the average difference between the two subsets (0.2 to 0.5). However, we also notice that such difference is more evident in the third and fourth bins of the lower-z sample, whose β values are significantly (> 1σ) redder compared to the second subset at z > 3. This result also indicates that dust attenuation is less relevant as redshift increases, as suggested by Bouwens et al. (2007).
The horizontal dashed line in Fig. 6 highlights the dust-free level of β. Despite some galaxies lying below this limit, we notice that the majority of them are still consistent within 1 or 2σ uncertainty, with very little or zero attenuation. We warn the reader that the intrinsic value of β in the absence of dust attenuation also has a second-order dependence on the stellar metallicity, stellar population age, and the IMF, hence the above line should be considered as an approximation.
We determined the dust-free value of β from the same Starburst99 models we used to calibrate the metallicity with absorption lines. Varying the stellar age and the stellar metallicity of the models, respectively, in the 50–500 Myr and 0.05–2.5 times Z⊙ ranges has a minor effect on the intrinsic β, in all cases no larger than 0.1. Given our small metallicity range, the contribution of Z* would be even smaller, of the order of ∼1%, thus largely negligible. As a result, the dust attenuation has by far the biggest effect on shaping the UV slope, as already claimed by Bouwens et al. (2012). In the following, we consider an intrinsic β of −2.67, found for an age of 100 Myr (assumed for the index calibrations) and metallicity −1.2 < log10 (Z/Z⊙) < − 0.5. This value is also consistent with the extrapolation from the β–A1600 relation of LBGs at z ∼ 4 by Castellano et al. (2014) (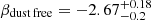 ) and from a similar analysis performed by de Barros et al. (2014).
) and from a similar analysis performed by de Barros et al. (2014).
Moreover, we also remark that assuming different dust attenuation laws and different dust geometries than the foreground screen may lead to a different conversion between A1600 and β (for more details, see, e.g., Reddy et al. 2018; Salim et al. 2018; McLure et al. 2018a). However, this would only produce a constant rescaling of the absolute attenuation axis (A1600), if all the galaxies obey the same law. In order to better constrain the A1600–β relation, we would need an independent estimate of dust attenuation for these galaxies, which could come from analyzing their far-IR emission.
In Fig. 6, for comparison we also show the results found by Pannella et al. (2015), Hathi et al. (2016), and McLure et al. (2018a) for star-forming galaxies in the redshift range between 2 and 3.3, with colored diamonds, empty gray circles, and a green line, respectively. In particular, we notice that the study of Pannella et al. (2015) at z ∼ 3.3 (compatible with our median redshift) comprises only galaxies more massive than 1010.5 M⊙, thus they lie outside the mass range where we have robust statistics in VANDELS. Secondly, the median photometric-based UV slopes of Hathi et al. (2016) are slightly above our estimates, which is likely due to the lower redshift range they probe in their study. Nevertheless, their results are in agreement within 1σ of our median β at zmedian = 2.58. Finally, despite the large dispersion of our points, the slope of our M*–β relations is in reasonable agreement in all redshift bins with that found by McLure et al. (2018a), even though our β measurements are systematically lower by ∼0.3, depending on the stellar mass range. We remark that the two analyses are performed with different methods: galaxies from McLure et al. (2018a) were indeed derived by fitting pure power-law SEDs to the photometry and requiring only central bandpasses not to lie outside the Calzetti ranges when estimating β. This effect was already discussed in Sect. 2.4 and accounts for an offset of ∼0.15–0.2 dex. An additional offset of 0.05–0.1 in β (lower than the typical β uncertainty) may come from the sample selection, because we are considering here only high-quality spectroscopic determinations (flags 3 and 4). In any case, this slight offset does not imply a significant physical difference compared to lower quality flags or to the full parent sample, as both of them are representative of the star-forming main sequence (McLure et al. 2018b).
3.4. Metallicity dependence of the M*–β and MUV–β relations
We have seen that the UV magnitude and the stellar mass can be used as proxies to infer the UV slope or the dust attenuation level in the UV, providing useful corrections to derive dust-unbiased luminosity functions and total SFRs of high-redshift galaxies. We analyze in the following whether the stellar metallicity plays any role in these conversions, and whether it can improve our estimate of dust attenuation.
In the top section of Fig. 7, we study the metallicity dependence of the MUV–β relation shown in Fig. 1. Given the evolution of β with cosmic time, to test variations of metallicity we have to focus on a limited range of redshifts throughout the analysis. Because of the higher S/N available, we considered the lowest redshift bin between z = 2 and z = 3. This allows us to explore a larger portion of the MUV–β plane and define four bins of galaxies with similar median z, using for separation both the M1600–β relation from the whole sample at z < 3 and the median UV magnitude of this subset. The stacked spectra in all four bins have an S/N above 25, ideal for our metallicity estimation method based on the absorption indexes described in Sect. 2.6.
 |
Fig. 7. Top: metallicity dependence of M1600–β relation for VANDELS star-forming galaxies at redshifts 2 < z < 3. The position of the stars (color-coded in metallicity) is representative of the median MUV and β of the galaxies in each bin. The metallicities (±1σ uncertainty) from the stacked spectra of galaxies in the same bin are written in black on the right side of each star. Single galaxies are drawn with squares. The best-fit relation (red dashed line) is used to divide the bins in β, while mass bins are shown with gray dashed lines. The resulting four bins are marked by 1, 2, 3, and 4. Bottom: Metallicity dependence of M*–β relation for the same subset of galaxies analyzed in the upper panel. The metallicity is calculated in four bins of stellar mass and UV slope, defined by the dashed lines. |
The result shown in the top section of Fig. 7 indicates a metallicity dependence of the MUV–β relation: galaxies with redder UV slopes (i.e., higher attenuation) have an enhanced metallicity at fixed UV absolute magnitude compared to less attenuated objects by ∼ + 0.2 dex, on average. The difference is larger than the typical 1σ uncertainties of the metallicity estimates, hence it is significant both for UV-bright and -faint sources. This also indicates a probability of less than ∼2% of obtaining this configuration if there is no dependence of the β–MUV relation on the stellar metallicity.
We also applied the same approach explained above, for the same galaxies, to the M*–β relation (Fig. 7, bottom). As in the previous case, for the separation, we used the median stellar mass of the subset (109.7 M⊙) and its best-fit M*–β relation, constructed by fitting a linear relation to the median β values in five bins of M*. This way, we were able to study the stellar metallicity in each stellar mass regime.
We can see in the bottom section of Fig. 7 that the largest increase in metallicity occurs in the direction of increasing stellar mass, which is further evidence of the tight relation between these two quantities already seen in Sect. 3.1. At fixed M*, a statistically significant difference (at > 2σ) of 0.3 dex in metallicity is found in the lower stellar mass range (M* < Mmedian) between galaxies with UV slopes lower and higher than the best-fit M*–β relation. In contrast, in the highest mass bin (M* > 109.65 M⊙), while the metallicity of redder galaxies is still higher than less attenuated objects, the difference is smaller (∼0.1 dex), and the two measurements are consistent within their 1σ errors.
Overall, Fig. 7 indicates that the stellar metallicity can explain part of the scatter of the MUV–β and M*–β relations. In particular, galaxies show a spread of metallicity with dust attenuation at fixed MUV and M*, even though more massive and evolved systems ((M* > 109.65 M⊙) tend to have more homogeneous metallicity values compared to lower mass systems.
3.5. The attenuation-metallicity relation
As we have shown in previous sections, both the metallicity and the UV slope increase with the stellar mass. Therefore, Z* and β should also be tightly related to each other. Given that β is mostly influenced by the level of dust attenuation in the galaxy (as discussed in Sect. 3.3), this also means that the light emitted by less or more chemically enriched stellar populations is subject to different levels of dimming. Analyzing VANDELS galaxies in bins of Lyα EW, Cullen et al. (2020) suggest an increase of Z* with UV slope. It is thus interesting to directly compare these two quantities, as done with the stellar metallicity and the stellar mass. From the physical point of view, the exact dependence between Z* and β is influenced by several, often simultaneous phenomena, including dust formation mechanisms in metal-rich or metal-poor environments, grain growth from the capture of heavy metal particles produced inside stars, destruction by supernovae (SNe) explosions, and ejection through AGN- or stellar-driven winds.
To investigate this relation, we consider the subset #2 selected in Sect. 2.7. Because of the larger uncertainties of β estimations compared to the stellar masses, and given the lower number of objects than those used for the MZR, we defined here three bins of galaxies, representative of a bluer, an intermediate, and a redder slope population, with median β values of ∼ − 2, ∼ − 1.5, and −1, respectively (see Table 3). In each bin, we stacked all the spectra according to the same procedure illustrated in Sect. 2.2, and we measured the metallicity from the 1501 and 1719 Å absorption features. The resulting trend is shown with black squares and error bars in Fig. 8. As for the MZR in Fig. 5, these represent the median β in each bin as a function of the stellar metallicity estimated for each stacked spectrum (from the average of the two indexes), with the β range and Z* uncertainty highlighted with horizontal and vertical error bars, respectively. We observe an increasing trend of metallicity toward redder spectra: Z rises by ∼0.5 dex between β = −2 and β = −1.1. Even though the metallicities from single indexes (drawn with pale red and dark-cyan smaller squares) show a larger uncertainty, they are remarkably in agreement with each other within 1σ and with the global relation, displaying a similar increase in metallicity from bluer to redder galaxy spectra.
 |
Fig. 8. Relation between UV slope and stellar metallicity for VANDELS galaxies. The average relation from the two indexes (1501 and 1719 Å) is drawn with black squares, while the pale colored squares represent the underlying metallicities from single absorption features. Horizontal bars associated with each of the three data points indicate the range of β slopes of galaxies in the same bin. The relation obtained from combining the best-fit MZR and the M*–β relation is highlighted with a cyan dashed line and cyan 1σ uncertainty area. On the top x-axis, A1600 is shown for comparison purposes, as determined from the β–A1600 conversion of Meurer et al. (1999). We warn the reader that this conversion may also depend, at a second order, on the metallicity itself. |
Since it was possible to model, with a first order polynomial, both the MZR (see Fig. 5, top) and the M*–β relation without redshift binning (derived from the same VANDELS data, although with a slightly larger sample in the first case), it is interesting to combine these two best-fit lines, removing the dependency on stellar mass. This could provide a consistency check of the results obtained with different approaches. The outcome of this exercise is shown in Fig. 8 with a dashed cyan line and shaded cyan region (representing 1σ confidence limits). We can see that it reproduces qualitatively the general trend established by our direct measurements of stellar metallicity in stacks of β (black squares).
Despite the relatively large uncertainties of our average data points, we also fit them with a linear relation, in order to quantitatively compare these results to the above-mentioned analytical calculation, and with the predictions of SAMs in the following section. This exercise yields the following equation:
We remark again that this is the simplest approximation, and we do not attempt to extrapolate or constrain more complex dependences between Z* and β, especially in the bluer and redder tails. However, it is important and reassuring to find a consistency between our best-fit Z*–β relation in Eq. (4) and that derived independently from two underlying trends of the stellar mass with the UV slope and the metallicity.
Finally, to highlight the variation of absorption line depth with increasing β for each of our two metallicity indexes, we plot the spectral portions of the stacks close to the 1501 and 1719 Å absorption complexes together. In Fig. 9, we draw the spectra obtained for the three stacks in bins of increasing UV slope, which also correspond to increasing levels of stellar metallicity. We find that the stacked spectrum derived in the first bin at lower β has a lower absorption EW in both of the above indexes. As we move to bins of higher UV slope, the depths of the absorption features increase in a visible manner. This visual inspection thus confirms the tight relation between β and Z already shown in Fig. 8. In the next section, we compare this observational trend with predictions of theoretical galaxy evolution models.
 |
Fig. 9. Stacked spectra between 1000 and 2500 Å in three bins of increasing βmedian: −1.98 (blue line), −1.51 (gray line), and −1.10 (red line; see also Table 3). The absorption complexes used in this work to estimate the metallicity, located at 1501 and 1719 Å, are highlighted with yellow vertical bands. Top two panels: three stacks are plotted together, and we zoom-in around the two metallicity indexes. A thicker line specifies both the width of each absorption complex, while shaded gray areas indicate the spectral ranges for the estimation of the pseudo-continuum. Spectral stacks of galaxies with redder UV slopes have deeper absorption features, hence higher metallicity. |
4. Discussion
Our findings show that the stellar metallicity is tightly related not only to the stellar mass of the galaxies, but also to the UV continuum slope, which is a proxy of the dust attenuation. In the following, we compare our results to theoretical predictions from SAMs of galaxy formation and evolution.
4.1. Comparison with semi-analytic models
The first model that we considered was developed by Menci and collaborators4 and it was first presented in Menci et al. (2002, 2004). Here, we use the most updated version of the SAM, which is described in Menci et al. (2014). To summarize its important features, it creates a subset of dark matter (DM) merging trees following the extended Press & Schechter (1974) statistics. The code then generates the merging history of DM galactic subhalos and describes the evolution of the baryonic component following the main physical mechanisms such as gas condensation and cooling, star formation, black-hole growth, and feedback processes, both of AGN or stellar origin. This allows the computation of the properties of the galaxies associated with each DM subhalo (which could eventually merge together) including, among others, their stellar mass, gas mass, and metallicities of both the gas and stellar components. The effects of dust extinction are not included. As far as the chemical abundance is concerned, it is calculated considering the whole star formation history of each model galaxy, adopting a yield (i.e., the fraction of metals in stars that returns to the ISM during their lifetime) of 0.02 and a recycled gas fraction of 0.45, appropriate for the Chabrier IMF. The model also adopts the instantaneous recycling approximation, and it does not distinguish between SNII and SNIa chemical enrichment. This SAM has been shown to accurately predict the observed luminosity function of galaxies from the local Universe to high-redshift (Menci et al. 2002), the quasar luminosity function up to z ∼ 4 (Menci et al. 2006), and the color bimodality of galaxies (Menci et al. 2005).
In order to have a more manageable dataset, especially for the visualization, we studied the distribution of galaxies in the M*–Z* plane, using a grid with 20 bins in mass (from log10 (M*/M⊙) = 8.3 in steps of 0.2) and 20 bins in metallicity (from log10(Z*) = − 3.35 in increasing steps of 0.3). Then, at a given mass, the fraction of galaxies residing in each bin of metallicity was calculated.
As an alternative approach, we also consider the GAlaxy Evolution and Assembly model (GAEA) for the formation and evolution of galaxies across cosmic time. This model represents an evolution with respect to the earlier De Lucia & Blaizot (2007) code. GAEA traces the evolution of the multiphase baryonic gas (i.e., hot gas, cold gas, stars) in the different galaxy components (i.e., disk, bulge and halo). The mass and energy exchanges between the different reservoirs are followed by solving a system of approximated differential equations, which account for the physical mechanism acting on the baryonic component, such as gas cooling, star formation, and stellar and AGN feedback. In detail, the main improvements in GAEA include an improved treatment of chemical enrichment and stellar feedback. De Lucia et al. (2014) relaxed the instantaneous recycling approximation (IRA) of stellar ejected metals assumed in the original version. They instead considered the different lifetimes of stars with varying initial masses (Padovani & Matteucci 1993) and track the enrichment of single chemical elements at various stages of stellar lives. Moreover, Hirschmann et al. (2016) proposed an improved feedback scheme aimed at reproducing the evolution of the galaxy stellar mass function up to z ∼ 3. This stellar feedback scheme is inspired by the results of hydrodynamical simulations and includes both stellar-driven winds able to efficiently eject the hot gas, and a mass-dependent reincorporation mechanism for the ejected material. These new prescriptions provide an explanation for the “anti-hierarchical” galaxy-evolution scenario, with low-mass galaxies increasing in number density toward lower redshifts at a faster pace than more massive counterparts. In detail, GAEA is able to reproduce the evolution of the galaxy stellar-mass function (GSMF) up to z ∼ 7, the cosmic SFR up to z ∼ 10 (Fontanot et al. 2017), the z ∼ 0 gas-phase MZR (De Lucia et al. 2020), and its redshift evolution (Fontanot et al., in prep.). In the following, we consider GAEA prediction corresponding to a realization based on the merger trees extracted from the millennium simulation carried out by Springel et al. (2005) and corresponding to a WMAP1 cosmology (i.e., ΩΛ = 0.75, Ωm = 0.25, Ωb = 0.045, n = 1, σ8 = 0.9, H0 = 73 km s−1 Mpc−1).
For a fair comparison with our results, we used a GAEA light cone produced inside the collaboration to mimick the VANDELS survey. This cone covers the same area of VANDELS and was generated following the procedure of Zoldan et al. (2017), with a stellar mass limit of 108.5 M* to match the lower limit of our galaxies. For each object identified in the cone, luminosities are calculated assuming a Chabrier IMF and Bruzual & Charlot (2003) stellar population models (see De Lucia et al. (2014) for more details), while SFRUV were derived from the unobscured UV luminosity Lν, 1600, ensuring they have similar timescales to those estimated from SED fitting. The models also predict the magnitudes observed in common broad photometric bands ranging from U to H. Effects of dust attenuation are included in the observed magnitudes, assuming the double screen model of Charlot & Fall (2000), with the light of younger stellar populations experiencing an additional effective absorption inside the birth clouds compared to older stars affected only by the ambient ISM attenuation. In the cone, we considered a filter set corresponding to those available in the framework of the VANDELS survey, therefore we could derive an estimate of the β slopes in the 1250–1750 Å range using similar techniques to the real data, as explained in Sect. 2.4. Finally, for each galaxy, the stellar metallicity was computed as the mass fraction of metal elements in the stellar component, normalized to Z⊙ = 0.0142. Before comparing to the models, we also matched the 3D distribution in redshift, stellar mass, and SFR of galaxies in the GAEA light-cone to that of VANDELS objects selected in this work.
The resulting M*–Z* diagrams from the two models are presented in the top section of Fig. 10. We can see that individual galaxies in GAEA span stellar metallicites log10(Z/Z⊙) between −1.2 and −0.2. A linear fit to individual galaxies yields a best-fit slope of 0.41 ± 0.02 and a normalization +0.27 dex higher compared to VANDELS observations. Considering the five stellar mass bins in the 109–1010.2 M⊙ range, the median metallicities in the bins increase mothonically from −0.7 to −0.4. For the galaxies modeled according to the approach of Menci et al. (2014), we draw a contour plot of their distribution in the M*–Z* diagram. We notice that for stellar masses ranging 109 < M* < 1010.2 M⊙, the stellar metallicities of the average star-forming galaxy population are also 0.2 dex higher than GAEA predictions, with log10(Z/Z⊙) varying from −0.8 to above solar. Overall, despite the different metallicity normalizations, the two relations have slopes that are remarkably in agreement with the observed MZR from VANDELS data. This suggests that models connect the natural evolution from low-mass, more metal-poor galaxies to high-mass, more chemically enriched systems in a way that is consistent with our observations.
 |
Fig. 10. Top: comparison between MZR derived from VANDELS (black squares and error bars) and from predictions of two SAMs: orange diamonds represent the median masses and metallicities of GAEA galaxies in five bins of stellar mass defined as for the observations. Blue contour regions indicate the fraction of galaxies in the SAM of Menci et al. (2014) with different Z* at a given mass, according to the 2D bins defined in the text. Bottom: comparison of VANDELS results with the UV-slope-metallicity relation predicted by the GAEA models. The large orange diamonds were derived with the same method of the upper panel. We highlight the best-fit relation for the VANDELS sample with a dashed black line, while the shaded gray area encloses its 1σ uncertainty region. |
In the bottom part of Fig. 10, we show the comparison between VANDELS data and GAEA models for the β–Z* relation. First, we notice that the range of UV slopes predicted by GAEA is consistent with the values found in our VANDELS selected sample. Nonetheless, over this range we confirm that the typical metallicities of GAEA galaxies are systematically higher than our estimates, although the tension is reduced to a 1-σ level (even less toward redder slopes, corresponding to β > −1.5). In order to understand if the model is able to reproduce the dependence of Z* from β, we performed a linear fit of individual mock galaxies, which provides the following best-fit relation: Z* = (0.36 ± 0.03) × β + (0.06 ± 0.05) (dashed red line in Fig. 10). While this relation is slightly flatter than VANDELS data, the two slopes are consistent at a 2σ level, and they agree even more if we consider bluer galaxies with β < −1.5. Overall, we remark that the existence of a well defined relation between the UV slope and the stellar metallicity is a success for this model.
Finally, it is interesting to ask where these constant metallicity offsets in the top part of Fig. 10 come from. It is worth stressing that our derivation of metallicity in GAEA represents, by construction, a mass-weighted metallicity. Cullen et al. (2019), using cosmological simulations at z ∼ 5, showed that mass-weighted metallicities are generally higher than FUV-weighted observed values estimated from the UV rest-frame spectra, by an amount of 0.1–0.2 dex, depending on the simulations adopted. This difference is due to the fact that younger and more metal-rich stellar populations are typically affected by a higher level of dust attenuation inside their birth clouds, while older (hence more metal-poor) stars are less attenuated and thus contribute more to the observed FUV emission. Unfortunately, the correct assessment of FUV-weighted metallicities in GAEA is beyond the current capabilities of the model, partly because of the simplified assumptions for dust obscuration (a screen model), and in part for the lack of spatial resolution in the treatment of star-forming disks, which do not allow a detailed treatment of individual star-forming regions. However, we notice that the results obtained in the framework of hydro-simulations (see e.g., Fig. 8 in Cullen et al. 2019) are on the right track toward reducing the tension between GAEA and VANDELS data. On the other hand, the discrepancy with the Menci et al. (2014) SAM is larger than what we can recover with FUV-weighting. In this case, we remind the reader that additional metallicity offsets can come from the treatment of the metal yield: if we decrease the effective total yield, we would obtain lower metallicities, more consistent with the observations. However, this approach cannot be used in GAEA, as this model does not treat yields as free parameters.
Finally, we also warn the reader that if we use BPASS models the calibration function for the 1719 Å index gives metallicities that are +0.25 dex higher, but no offsets with the Starburst99 results are found when using the 1501 Å index alone. While it is beyond the goals of this paper to discuss the origin of this discrepancy (which might be related to the different chemical composition and/or physics adopted by the two stellar models), it is true that applying the BPASS calibration on the 1719 Å index would make the observed relations more consistent at least with the GAEA predictions. However, we think this is unlikely, because the positive offset that we see for the 1719 Å absorption complex is not found for the other lines, as we see in more detail in Appendix A.3. Moreover, our result remains unaltered for the 1501 index and is consistent with the previous work of Cullen et al. (2019), based on fitting the entire FUV spectrum. To conclude, we stress again that, most importantly, the shape of the theoretical relations analyzed in this section appears to be consistent with our data.
4.2. Future developments
The UV slope remains a fundamental quantity to constrain the properties of galaxies at all redshifts, and search for more extreme candidates resembling even higher redshift systems. For example, in our sample we find a significant population of galaxies (∼33%) with a UV slope bluer than ∼ − 2. From Fig. 6, we see that these systems also have preferentially lower stellar masses (≲109.5 M⊙) and small dust attenuations (A1600 ≲ 1.5), according to the standard assumptions of the Meurer et al. (1999) calibration. As claimed in other works (e.g., Steidel et al. 1999; Ouchi et al. 2004; Bouwens et al. 2006, 2009, 2016; Hathi et al. 2008; Erb et al. 2010; Shivaei et al. 2018), a very blue UV slope indicates the presence of very young, metal-poor stellar populations, and it is suggestive of a higher ionizing photon production efficiency and escape of ionizing radiation from such galaxies, which are the typical conditions in the reionization epoch.
We have also seen how the measurement of stellar metallicity remains difficult, simultaneously requiring a high sensitivity (or many hours of integration) to enhance the S/N, and possibly a high spectral resolution. In Appendix A.5, we discuss the effect of the resolution on the metallicity calibration functions and on the reliability with which Z* can be constrained. On the other hand, Fig. 8 suggests that the UV slope can be used to derive a first approximate estimation of the metal abundance in stars and pre-select extremely metal-poor galaxy candidates with Z* around 1/10 Z⊙ or below, allowing us to save observational time and to better focus on specific targets. In the near future, new spectrographs like NIRSpec on board JWST or HIRES mounted at the ELT, thanks to their higher spectral resolution compared to VANDELS (R > 1000), will allow focused follow-ups of hundreds of galaxies to constrain their stellar metallicity from faint photospheric absorption lines, also at much higher redshifts and sensitivities (in the case of ELT) than those reached in this study. Thanks also to the improved imaging sensitivity in the infrared compared to current instruments, we can aim to measure the UV slope of the faintest systems at redshifts > 6. An important goal that remains is then to observe and characterize statistical samples of pristine (supposedly PopIII-star-dominated) galaxies, in order to constrain our Z*–β relation at even lower metallicities than our study and shed light on galaxy evolution in the earliest phases of our Universe.
5. Summary and conclusions
We selected a representative sample of star-forming main-sequence galaxies in the redshift range 2 < z < 5 and stellar mass 8.3 < M*/M⊙ < 10.6 with FUV rest-frame spectra obtained by the VANDELS survey. Measuring stellar metallicities from two UV rest-frame absorption lines, and estimating stellar masses and UV spectral slopes from photometric data, we studied the stellar-mass stellar-metallicity diagram, and the metallicity dependence of the stellar mass – β and UV magnitude – β relations. This sheds light on the role of metallicity on scaling relations that are typically adopted to infer dust corrections for optical and near-IR galaxies detected at high-z. We summarize our main findings in the following.
-
Using Starburst99 synthetic spectra adapted to VANDELS resolution, we calibrated the stellar metallicity with two absorption complexes located at 1501 and 1719 Å rest frames, which are largely independent of the IMF, age, dust content, and nebular continuum emission (Sect. 2.6). The EWs of these two indexes, measured in VANDELS stacked spectra, are well in agreement with Starburst99 model predictions, yielding fully consistent metallicity values in all the range explored with our data.
-
The MZR estimated from the above far-UV absorption indexes is consistent with the previous determination based on VANDELS data (Cullen et al. 2019), obtained through a global fitting to the full FUV spectrum with similar stellar models (Fig. 5).
-
The MZR does not significantly evolve from z ∼ 2 to z ∼ 3.5, in agreement with Cullen et al. (2019): even though a slightly lower metallicity (by 0.05 dex) is measured for typical star-forming galaxies at redshift z ∼ 3.5 compared to samples at lower zmedian ∼ 2.5 (from our VANDELS sample) and ∼2 (from Halliday et al. 2008), the difference is lower than the typical uncertainties currently associated with stellar metallicity estimates.
-
The stellar metallicity partly explains the scatter of the MUV–β and M*–β relations, hence Z* could discriminate between different dust attenuation correction levels (Fig. 7). Using a subset at 2 < z < 3 with higher S/N, we find a difference in metallicity of 0.2 dex, on average, between galaxies redder and bluer than the best-fit MUV–β and M*–β relations, even though more massive and evolved systems tend to have more uniform metallicity values.
-
The remarkable correlation between Z* and β seen in Fig. 8 suggests that the UV slope can be used as a proxy for the stellar metallicity. This would be of particular importance to constrain properties of galaxies at redshifts 2 < z < 5, and search for candidates with more extreme stellar populations in terms of their metal content, more closely resembling those typical of the reionization epoch.
-
We contrasted our findings with the predictions of two different SAMs, namely GAEA (Hirschmann et al. 2016) and Menci et al. (2014). We first constructed two mock galaxy catalogs with a redshift, stellar mass, and SFR distributions matched to our VANDELS data. We show that these models predict a slope of the mass-metallicity relation that is in agreement with that found from VANDELS star-forming galaxies, even though their metallicity normalizations are higher by ∼0.2 and ∼0.4 dex, respectively. In addition, the slope of the Z*–β relation predicted by GAEA is consistent with our result at a 2σ level. An offset of ∼0.1–0.2 dex between mass-weighted and FUV-weighted stellar metallicities, or a lower yield in Menci et al. (2014) SAM, could account for the different normalization between our data and model predictions.
Several instruments coming with next-generation telescopes like the JWST and ELT, thanks to the improved sensitivity, spectral coverage and spectral resolution, will make it possible to push the investigation of metal and dust enrichment down to the earliest epochs of stellar and galaxy formation for a large number of objects, and to assess the physical properties of the first systems born in the Universe. Similarly, Euclid will also allow us to measure the UV slope and the dust properties of young galaxies in large-volume surveys, with significantly higher statistics than today. In this context, the UV slope remains a powerful diagnostic tool to distinguish between galaxies of different metal contents, and, possibly, evolutionary stages.
Link to VANDELS project: http://vandels.inaf.it.
More details are found on the following web page: https://lbc.oa-roma.inaf.it/menci/.
Acknowledgments
We thank the anonymous referee for the useful and constructive comments. AC and MT acknowledge the support from grant PRIN MIUR 2017 20173ML3WW_s. RA acknowledges support from ANID FONDECYT Regular 1202007.
References
- Asplund, M., Grevesse, N., Sauval, A. J., et al. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., & Glazebrook, K. 2003, ApJ, 593, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boggs, P. T., Byrd, R. H., Rogers, J. E., & Schnabel, R. B. 1992, Software for Weighted Orthogonal Distance Regression [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Blakeslee, J. P., et al. 2006, ApJ, 653, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., et al. 2007, ApJ, 670, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., et al. 2009, ApJ, 705, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2012, ApJ, 754, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2014, ApJ, 793, 115 [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 803, 34 [Google Scholar]
- Bouwens, R. J., Smit, R., Labbé, I., et al. 2016, ApJ, 831, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Noll, S., Burgarella, D., et al. 2012, A&A, 545, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P. L., Carilli, C., Jones, G., et al. 2015, Nature, 522, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Castellano, M., Fontana, A., Grazian, A., et al. 2012, A&A, 540, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castellano, M., Sommariva, V., Fontana, A., et al. 2014, A&A, 566, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [Google Scholar]
- Chisholm, J., Rigby, J. R., Bayliss, M., et al. 2019, ApJ, 882, 182 [CrossRef] [Google Scholar]
- Cullen, F., McLure, R. J., Dunlop, J. S., et al. 2019, MNRAS, 487, 2038 [NASA ADS] [CrossRef] [Google Scholar]
- Cullen, F., McLure, R. J., Dunlop, J. S., et al. 2020, MNRAS, 495, 1501 [CrossRef] [Google Scholar]
- Dayal, P., & Ferrara, A. 2012, MNRAS, 421, 2568 [NASA ADS] [CrossRef] [Google Scholar]
- de Barros, S., Schaerer, D., & Stark, D. P. 2014, A&A, 563, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Kauffmann, G., & White, S. D. M. 2004, MNRAS, 349, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Tornatore, L., Frenk, C. S., et al. 2014, MNRAS, 445, 970 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Xie, L., Fontanot, F., et al. 2020, MNRAS, 498, 3215 [Google Scholar]
- Eldridge, J. J., Stanway, E. R., Xiao, L., et al. 2017, PASA, 34, e058 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 2006, ApJ, 648, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Pettini, M., Shapley, A. E., et al. 2010, ApJ, 719, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Faisst, A. L., Capak, P. L., Davidzon, I., et al. 2016, ApJ, 822, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Fanelli, M. N., O’Connell, R. W., & Thuan, T. X. 1988, ApJ, 334, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Fanelli, M. N., O’Connell, R. W., Burstein, D., et al. 1992, ApJS, 82, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Ryan, R. E., Papovich, C., et al. 2015, ApJ, 810, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., Hirschmann, M., & De Lucia, G. 2017, ApJ, 842, L14 [Google Scholar]
- Fontanot, F., La Barbera, F., De Lucia, G., et al. 2018, MNRAS, 479, 5678 [NASA ADS] [CrossRef] [Google Scholar]
- Galametz, A., Grazian, A., Fontana, A., et al. 2013, ApJS, 206, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Bell, E. F., Zibetti, S., et al. 2014, ApJ, 788, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Fumana, M., Franzetti, P., et al. 2010, PASP, 122, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Paioro, L., Scodeggio, M., et al. 2012, PASP, 124, 1232 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M. 2002, ARA&A, 40, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M., Steidel, C. C., & Macchetto, F. D. 1996, ApJ, 470, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Ferguson, H. C., Giavalisco, M., et al. 2013, ApJS, 207, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Halliday, C., Daddi, E., Cimatti, A., et al. 2008, A&A, 479, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hathi, N. P., Malhotra, S., & Rhoads, J. E. 2008, ApJ, 673, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Hathi, N. P., Ryan, R. E., Cohen, S. H., et al. 2010, ApJ, 720, 1708 [NASA ADS] [CrossRef] [Google Scholar]
- Hathi, N. P., Cohen, S. H., Ryan, R. E., et al. 2013, ApJ, 765, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Hathi, N. P., Le Fèvre, O., Ilbert, O., et al. 2016, A&A, 588, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinis, S., Buat, V., Béthermin, M., et al. 2014, MNRAS, 437, 1268 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann, M., De Lucia, G., & Fontanot, F. 2016, MNRAS, 461, 1760 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K., Shimizu, I., Iwata, I., et al. 2014, MNRAS, 442, 1805 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Tasca, L. A. M., Cassata, P., et al. 2015, A&A, 576, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [Google Scholar]
- Leitherer, C., Ortiz Otálvaro, P. A., Bresolin, F., et al. 2010, ApJS, 189, 309 [Google Scholar]
- Leitherer, C., Tremonti, C. A., Heckman, T. M., et al. 2011, AJ, 141, 37 [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., & Mannucci, F. 2019, A&ARv, 27, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Oliva, E., Ghinassi, F., et al. 2004, A&A, 420, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLure, R. J., Dunlop, J. S., Cullen, F., et al. 2018a, MNRAS, 476, 3991 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., Pentericci, L., Cimatti, A., et al. 2018b, MNRAS, 479, 25 [NASA ADS] [Google Scholar]
- Menci, N., Cavaliere, A., Fontana, A., et al. 2002, ApJ, 575, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Menci, N., Cavaliere, A., Fontana, A., et al. 2004, ApJ, 604, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Menci, N., Fontana, A., Giallongo, E., et al. 2005, ApJ, 632, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Menci, N., Fontana, A., Giallongo, E., et al. 2006, ApJ, 647, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Menci, N., Gatti, M., Fiore, F., et al. 2014, A&A, 569, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Oesch, P. A., Bouwens, R. J., Illingworth, G. D., et al. 2018, ApJ, 855, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Shimasaku, K., Okamura, S., et al. 2004, ApJ, 611, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., & Matteucci, F. 1993, ApJ, 416, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Pannella, M., Carilli, C. L., Daddi, E., et al. 2009, ApJ, 698, L116 [Google Scholar]
- Pannella, M., Elbaz, D., Daddi, E., et al. 2015, ApJ, 807, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Parsa, S., Dunlop, J. S., McLure, R. J., et al. 2016, MNRAS, 456, 3194 [Google Scholar]
- Pentericci, L., McLure, R. J., Garilli, B., et al. 2018, A&A, 616, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pettini, M., Ellison, S. L., Steidel, C. C., et al. 1999, ApJ, 510, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Pilo, S., Castellano, M., Fontana, A., et al. 2019, A&A, 626, A45 [EDP Sciences] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Quider, A. M., Pettini, M., Shapley, A. E., et al. 2009, MNRAS, 398, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Raiter, A., Schaerer, D., & Fosbury, R. A. E. 2010, A&A, 523, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reddy, N. A., Oesch, P. A., Bouwens, R. J., et al. 2018, ApJ, 853, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, S. A., Pettini, M., Leitherer, C., et al. 2004, ApJ, 615, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, A. B., McLure, R. J., & Dunlop, J. S. 2013, MNRAS, 429, 2456 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Boquien, M., & Lee, J. C. 2018, ApJ, 859, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Pettini, M., et al. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Shivaei, I., Reddy, N. A., Siana, B., et al. 2018, ApJ, 855, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Sommariva, V., Mannucci, F., Cresci, G., et al. 2012, A&A, 539, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Steidel, C. C., Pettini, M., & Hamilton, D. 1995, AJ, 110, 2519 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Giavalisco, M., et al. 1999, ApJ, 519, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Rudie, G. C., Strom, A. L., et al. 2014, ApJ, 795, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Strom, A. L., Pettini, M., et al. 2016, ApJ, 826, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Topping, M. W., Shapley, A. E., Reddy, N. A., et al. 2020, MNRAS, 495, 4430 [Google Scholar]
- Troncoso, P., Maiolino, R., Sommariva, V., et al. 2014, A&A, 563, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dokkum, P. G. 2008, ApJ, 674, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal-García, A., Charlot, S., Bruzual, G., et al. 2017, MNRAS, 470, 3532 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Lennon, D. J., Haser, S. M., et al. 1995, PASP, 107, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Zahid, H. J., Kudritzki, R.-P., Conroy, C., et al. 2017, ApJ, 847, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Zoldan, A., De Lucia, G., Xie, L., et al. 2017, MNRAS, 465, 2236 [Google Scholar]
Appendix A: Metallicity calibrations
A.1. Derivation of the UV slope from VANDELS spectra
The VANDELS spectra used in this paper offer an opportunity to compare our photometric-based UV slopes to those derived from the entire spectrum fitting. Following the original definition of β, we calculated the median flux in the 20 rest-frame spectral windows introduced by Calzetti et al. (1994) as free of absorption or emission lines in the 1250–2750 Å range. We then fit these points with a power slope function, as was done with the photometric data. We found that the spectroscopic measurements tend to give redder slopes compared to photometry-based determinations, and this is due primarily to the small range of rest-frame wavelengths spanned by our spectra, which in most cases do not probe λ > 2000 Å. Limiting the comparison to galaxies with most reliable β (σβ < 0.5) at redshifts ≤2.6, thus probing at least up to λrest ∼ 2600 Å, we recover a better agreement. However, we note that the shape correction in the bluest part of VANDELS spectra, explained in Sect. 2.1, was determined statistically. Since object-by-object variations are still possible, it is not desirable to completely rely on the spectra for the derivation of UV slopes. In addition, in some spectral windows in VANDELS spectra the continuum is not always detected, especially in the redder part, reducing the available range for proper measurements of colors. Because of these limitations, we preferred to adopt the UV slopes obtained from photometric data. This also enables a comparison with many other works at similar redshifts that are based, because of their simplicity, on photometric datasets.
A.2. Dependence of the metallicity uncertainty on the spectrum S/N
The S/N of the spectra strongly affects the uncertainty that we get on the equivalent width of the absorption lines, and hence on the accuracy of the metallicity estimation. The diagram in Fig. A.1 was derived from 500 simulations, adding an increasing random Gaussian noise to the theoretical Starburst99 templates, and then measuring the EW uncertainty as the standard deviation of all these different realizations. As a result, for both metallicity indexes adopted in this work, σEW follows an exponential decline as we increase the S/N of the stack from 5 to 40. In the same range, the uncertainty on the metallicity also decreases. Remarkably, these trends do not depend significantly on the metallicity of the model, while we can have different normalizations according to the index considered. The results of this paper are derived from spectral stacks with a minimum S/N of ∼21, therefore ensuring an uncertainty on log10(Z/Z⊙) lower than ∼0.4 from single indicators taken separately. For the mass-metallicity relation presented in Sect. 3.1, the minimum S/N is ∼32, which yields σlog10(Z/Z⊙) ≲ 0.2 in both cases.
 |
Fig. A.1. Relation between EW uncertainty (or stellar metallicity on the left y-axis) and input spectrum S/N. This is obtained through Monte Carlo simulations where Gaussian noise is added to Starburst99 templates with different metallicities. In this figure, different markers and colors refer to different metallicity indexes used in this work. For this example, we used the template with a metallicity of Z* = 0.2 × Z⊙, close to the value of our selected VANDELS galaxies. The vertical green line highlights the S/N range of the stacks that we analyze in this paper, while the smaller vertical gray bars indicate the S/N reached by the stacks in stellar mass from which the mass-metallicity relation is derived in Sect. 3.1. |
A.3. Metallicity calibrations for other indexes and with the BPASS model
In addition to Starburst99, we also tested other models among those most used in the literature. The Binary Population and Spectral Synthesis code (BPASS, Eldridge et al. 2017) is established as one of the most powerful for predicting the emission of simple stellar populations and galaxies from UV to mid-IR wavelengths. The main advantage of these models is that they also include binary stars’ evolutions, while the important limitation is related to the lower native spectral resolution (1 Å) compared to Starburst99.
In order to test the metallicity calibrations, we ran a series of BPASS models with both single stars and binary stars, an upper stellar mass limit of 100 and 300 M⊙, Chabrier IMF, and a constant SFH from 50 Myr to 2 Gyr, as was done for Starburst99 templates. The stellar metallicity was varied among all possible values allowed by the models: 0.001, 0.002, 0.003, 0.004, 0.006, 0.008, 0.01, 0.02, 0.03, and 0.04, which we rescaled to a solar metallicity of 0.0142 to be consistent with the assumption throughout this paper. We restricted the output spectra to the FUV rest-frame range between 1000 and 2500 Å and smoothed them to reach the same spectral resolution of VANDELS. Then, we measured the equivalent widths of the same absorption indexes introduced in Table 2, which are commonly used as metallicity tracers in the literature. In Fig. A.2, we show the relation between the model metallicity (both Starburst99 and BPASS) and the equivalent width of the following absorption complexes located at 1370, 1400, 1425, 1460, 1501, 1533, 1550, 1719, 1853, and 1978 Å. In Fig. A.3, we instead compare the EWs estimated for different indexes to the 1719 metallicity tracer, and we overplot the predictions of the two models we analyze in this appendix.
 |
Fig. A.2. Comparison between input stellar metallicity and the EW predicted by Starburst99 and BPASS synthetic spectra (violet diamonds and filled white circles, respectively), for nine absorption line indexes typically adopted in the literature to calibrate the metallicity. We considered a continuous SFH for an age varying between 50 Myr and 2 Gyr (shaded region). The markers in each panel refer instead to an age of 100 Myr, which is taken for the final calibration of the 1501 and 1719 indexes (see Fig. ). |
 |
Fig. A.3. Six panels compare the EW of the 1719 metallicity indicator to the EW of other absorption indexes in the FUV rest frame that were not considered in this work, either because no correlation was found with Z, or because the observational data are not in agreement with the predictions of any models (as in the case of significant ISM contamination). In each panel, we show the EW measurements from the five VANDELS stacks in stellar mass bins with colored stars (the median stellar mass of each stack is annotated in black). In addition, we superimpose EW–EW relations predicted by Starburst99 models (square symbols, with shaded gray area indicating different stellar ages from 50 Myr to 2 Gyr), and BPASS models (large circles). |
First we focus on the indexes adopted in this paper to estimate the stellar metallicity. It is important to recognize that the metallicity calibrations for the index at 1501 Å are tightly in agreement regarding the Starburst99 and BPASS models (Fig. A.2). On the other hand, for the 1719 index, they give slightly different predictions, with metallicities differing by ∼0.25 dex at fixed EWs.
The index at 1425 Å, already adopted in Sommariva et al. (2012), spans a small dynamic range according to Starburst99 models, varying from 0 to 1 Å in absorption in the entire possible metallicity range. In contrast with the 1501 index, the stellar models (converted to the VANDELS resolution) predict here a flattening of the EW at Z/Z⊙ > 0.5, so it is nearly impossible to constrain the metallicity above this value. Observationally, the EWs measured in the five bins are systematically below the model predictions by more than 1σ, unless the last bin at higher stellar masses, for which the EWs from 1719 and 1425 are in agreement with Starburst99.
The 1370 index, as the previous indicator, is very faint and does not allow an accurate derivation of log10 (Z/Z⊙). The observations show an EW systematically lower compared to model predictions at the same EW1719, even though three of them are marginally consistent within 1σ of the theoretical expectation.
For the 1460 absorption feature, the slope in the EW1460-Z diagram is very shallow, with the EW ranging from 0.3 to 0.8 Å, so that even a small error on the EW would leave the metallicity basically unconstrained. The values measured from the stacks, even though they are consistent with models within 2σ, tend to place systematically below, and we do not observe any increase of absorption depth at higher stellar masses. A similar behavior is seen for the 1533 index introduced by Sommariva et al. (2012).
The similar behavior of these three indexes could be due to the relatively low spectral resolution of our spectra, suggesting that much higher resolving power (and sensitivity) are needed to increase the contrast between absorption feature and pseudo-continuum, eventually identifying the real, unabsorbed continuum level. We thus excluded them from our analysis, and postpone any further test of such indexes to the availability of higher S/N and resolution spectra.
On the other hand, the 1400, 1550, and 1853 Å absorption features have EWs that are well above the value expected from a pure stellar component (based on Starburst99 templates). In the first and third cases, the observed EWs are between two- and three-times higher than pure stellar absorption expectations, which is likely due to ISM absorption contamination. Similarly, for the 1550 feature we measure EWs 1–1.5 Å higher than Starburst99 model predictions (but lower by the same amount if compared to BPASS). A more detailed discussion of the 1400 and 1550 Å absorption lines can be found in Talia et al. (in prep.). As a result of this analysis, these three lines were also excluded from our work.
Overall, for the vast majority of the indexes considered, the metallicity calibrations might vary with the model considered, just because of the slightly different spectral shapes of the templates. The different EW-metallicity relations predicted by BPASS and Starburst99 could be mostly related to a combination effect of different stellar atmosphere composition, stellar evolutionary tracks, stellar wind modeling, and composition, while the different native resolution of the models could also play a role. However, despite such differences, the 1501 Å tracer seems the most stable of the two models analyzed here, thus supporting the conclusions of this paper. Deeper and higher resolution spectra, available with the next-generation telescopes, will make it possible to enhance the accuracy of the metallicity measurements from the faintest absorption features and better analyze the comparison with different models.
A.4. IMF variations of the absorption lines
We explored the effect of different IMFs on all the indexes studied in this paper. In particular, we varied both the upper-mass cut-off Mmax,IMF and the slope in the high-mass end (αupper) compared to the standard assumptions adopted so far, that is, Salpeter or Kroupa functions, and Mmax,IMF = 100 M⊙.
Firstly, we increased the upper-mass cut-off to 300 M⊙, which results in only a slight variation of the equivalent width (at fixed metallicity) for the majority of the indexes (see Fig. A.4). The largest variation happens with the 1853 Å index, while for the others it is always smaller than 1%.
 |
Fig. A.4. Stellar metallicity vs. equivalent width predicted by Starburst99 models for the ten absorption lines studied in this paper. The gray squares are derived assuming a standard upper-mass cut-off of 100 M⊙, while the blue triangles are calculated assuming a cut-off mass of 300 M⊙. All the symbols are representative of a constant SFH and a stellar age of 100 Myr. The shaded regions allow the stellar age to vary between 50 and 100 Myr. The other details of the models are the same as in Fig. A.2. |
More interesting is the analysis of different slopes. Bouwens et al. (2012) assumed a Salpeter stellar IMF, and claimed there is no clear evolution from low to high redshift (z > 4). However, several papers have investigated possible deviations from standard IMFs in high-redshift galaxies. Elmegreen (2006) found that galaxy-averaged IMFs are in general not steeper than a Salpeter slope in the high-mass end. Exploring different cosmic SFHs, Baldry & Glazebrook (2003) found a best slope αupper = −2.15 (±0.2), slightly lower but still consistent with the Kroupa or Salpeter slope (∼ − 2.3). Fontanot et al. (2018) showed that αupper of the galaxy-wide IMF can vary with the SFR and the cosmic-ray (CR) density in the system. They found that it can be, in general, top heavy and shallower than the Kroupa IMF for SFR > 1 M⊙/yr at all CR densitites, which in any case occurs for the highest, “starburst-like” SFRs ≥100 M⊙ yr−1, which are not present in our VANDELS selection. Additionally, van Dokkum (2008) investigated the stellar IMF at the epoch of reionization as a function of the ISM clumping factor and the escape fraction of ionizing radiation. For different reionization histories, they found that galaxy-averaged IMFs could be flatter than a Salpeter slope, with αupper = −2.1 if it extends to 200 M⊙, or αupper = −1.65 if it extends to 50 M⊙.
Given these previous studies, we tested the effect of a Kroupa IMF with two different slopes in the high-mass end regime: a moderately shallower IMF αupper = −2.1, as in Baldry & Glazebrook (2003), and an extreme value of −1.65 (Fig. A.5). In the first case, we observe only a slight change of the metallicity calibration function for most of the indexes, with variations of the equivalent width of less than ∼5% in the metallicity range of our work. Typically, the largest variations (up to 8%) occur at solar and super-solar Z*. The only exceptions are the indexes at 1853 and 1978 Å, which can show a decrease of EW up to 0.25 Å. However, these indexes were not considered for our metallicity calculation.
 |
Fig. A.5. Stellar metallicity vs. equivalent width predicted by Starburst99 models for the ten absorption lines studied in this paper. The gray squares are derived assuming a Kroupa IMF, the blue triangles are built by changing the high-mass end slope to αupper = −2.15 (as in Baldry & Glazebrook 2003), while the red circles assume an extremely flat slope αupper = −1.65. All the symbols are representative of a constant SFH and a stellar age of 100 Myr. The shaded regions allow the stellar age to vary between 50 and 100 Myr. The other details of the models are the same as in Fig. A.2. |
Finally, for an extremely flat IMF slope (αupper = −1.65), the effects on the EW are not negligible for the majority of the absorption lines. In particular, for those adopted in this paper to derive the stellar metallicity, we observed an EW variation (at fixed Z*) of 0.15 and 0.3 Å for the 1501 and 1719 Å indexes, respectively, in the Z* range of our dataset. In other words, this IMF would produce a constant upward shift of stellar metallicity of 0.1–0.13 dex. However, we remark that this is a very unlikely IMF for typical star-forming galaxies at z ∼ 3 in the stellar mass range explored by VANDELS.
A.5. The effect of spectral resolution on the metallicity calibrations
The spectral resolution of the observations is important when it comes to determining the stellar metallicity from absorption lines. Indeed, it affects the calibration functions that are applied to the various indexes. This behavior can be understood if we consider that degrading the resolution tends to smooth the few narrow spectral regions that are intrinsically free of absorption and to decrease the overall pseudo-continuum level, lowering the contrast with the absorption features. As a result, the resolution affects the dynamic range of the EWs of the lines, setting a lower limit on the metallicities that can be reliably constrained. For each specific index, the minimum measurable metallicity can be defined as the value for which the corresponding equivalent width in absorption would be equal to the typical uncertainty of such measurement (i.e., the relative error is ∼100%). In this case, the EW estimation would be consistent with Z* = 0 within 1σ, and only an upper limit can eventually be determined.
We analyzed the effect of the resolution for all ten indexes presented in this work. In particular, we tested FWHM resolution elements two, three, and four times larger than those of VANDELS, where the latter value was set to ensure that it is still lower than the majority of absorption line widths. We also tested higher spectral resolutions, with σresolution equal to 1/2 and 1/3 of VANDELS. The results, displayed in Fig. A.6, show that degrading the resolution systematically decreases the EW of most of the absorption lines. It is also interesting to notice that the calibrations obtained for VANDELS and for the two improved resolutions are essentially the same for the majority of the lines, including those at 1501, 1533, 1550, and 1583 Å. For the 1719 Å absorption complex, the highest resolution spectra of our analysis would give higher equivalent widths than in the VANDELS case by ∼0.1–0.15 Å in the range 0.2 < Z⊙ < 1 (thus always below the typical uncertainties), while they are consistent at Z* < 0.2.
 |
Fig. A.6. Stellar metallicity vs. EW predicted by Starburst99 models for the ten absorption lines studied in this paper and for different spectral resolutions. The resolution elements σres tested are 1/2, 1/3, 1, 2, 3, and 4 times the VANDELS value. All the symbols are derived with a constant SFH and a stellar age of 100 Myr. The shaded regions allow the stellar age to vary between 50 and 100 Myr. |
In general, lower metallicities are more difficult to properly constrain as we increase σresolution. For example, with the worst resolution tested and the 1501 Å index, given its typical uncertainties of σEW ∼ 0.15–0.2 Å (see also Appendix A.2 for the dependence on the S/N), it is basically impossible to constrain the metallicity within 1σ better than the entire range of our study (−1.1 < log10(Z/Z⊙) < − 0.6). Overall, this analysis can provide a useful reference to evaluate the calibration functions for the ten indexes when observing at different spectral resolutions.
All Tables
Photometric bands available in the four fields covered by the VANDELS survey and used for the estimation of stellar masses, SFR, and UV slope.
All Figures
 |
Fig. 1. UV slope vs. M1600 for VANDELS galaxies selected in this work with σβ ≤ 1 and at least three photometric bands available in the range 1230–2750 Å. Our data are color-coded according to three different redshift bins (2 < zbin1 < 3 < zbin2 < 4 < zbin3 < 5 in blue, dark red, and orange, respectively), with z estimated from VANDELS spectra. The median z in each bin is reported in the legend. For comparison, we show the M1600–β relations found by Hathi et al. (2016) at 2 < z < 2.5 (empty gray circles), Bouwens et al. (2009) at ∼2.5 (cyan circles), Bouwens et al. (2014) at ∼4 (empty black circles), and Castellano et al. (2014) for LBGs at z ∼ 4 (empty black diamonds and light gray dashed best-fit line). The relation found by Pilo et al. (2019) for LBGs at z ∼ 3 is displayed as a light green dashed line. |
| In the text | |
 |
Fig. 2. Diagrams showing dependence between EW and metallicity for the 1501 and 1719 Å absorption line indexes that we adopt in this paper according to Starburst99 models. All the data points are derived assuming a constant SFH for 100 Myr and Kroupa IMF. The shaded gray region around the main relations represents the variation of EW with the IMF (Kroupa-Salpeter) and with the ages of the stellar population chosen (50 Myr–2 Gyr), as described in the text. The final metallicity calibrations are based on a third-order polynomial fit to the data points, and are shown with a continuous blue line in each panel. Their explicit forms are given in the text in Eqs. (2) and (3). |
| In the text | |
 |
Fig. 3. Comparison between equivalent widths of 1719 and 1501 Å absorption indexes predicted by Starburst99 models (big squares color-coded by metallicity). We show in each diagram the EWs measured in five VANDELS stacks (big stars), obtained via the same procedure adopted for synthetic templates. The stacks used here were produced at different stellar mass bins (see Sect. 3.1 and Table 3), whose median stellar masses (in log10 (M*/M⊙)) are highlighted in black above each point. The shaded gray area has the same meaning as in Fig. 2. |
| In the text | |
 |
Fig. 4. Diagram showing distribution of spectroscopic redshifts of VANDELS galaxies selected for this work. The vertical dashed line indicates the median redshift of the sample (zmed = 3.38). |
| In the text | |
 |
Fig. 5. Left: mass-metallicity relation of star-forming galaxies in VANDELS, with median stacks in bins of stellar mass (black squares). The metallicities derived from single indexes (i.e., in order, 1550, 1719, and 1501 Å) are drawn with pale colored squares in blue, red, and dark cyan, respectively. The linear fit to the median metallicities in the 108.5 < M* < 1010.5 M⊙ range is highlighted with a dashed dark cyan line. Right: mass-metallicity relation followed by VANDELS star-forming galaxies at redshift < 3 (dark cyan squares) and > 3 (dark red squares). The median redshifts of the two subsets are 2.58 and 3.54, respectively. The relation for all the sample is overplotted in black. In both diagrams, the relation by Cullen et al. (2019), calculated at the same median redshift of our work (and of the VANDELS survey), is displayed with gray filled circles, while in the bottom panel we also include the MZR found by Zahid et al. (2017) at z ∼ 0.08 from the SDSS survey (olive squares) and by Gallazzi et al. (2014) for massive star-forming galaxies (M* > 1010.2 M⊙) at z ∼ 0.7. The linear fit to the MZR in the lower and higher redshift bin is drawn with a shaded dashed line in the corresponding color. The representative M* and metallicity estimated from the spectral stack of 75 star-forming galaxies at redshift ∼2 from Halliday et al. (2008) is shown with a cyan square and error bars. Finally, the stellar-mass gas-phase metallicity relation for star-forming galaxies at z ∼ 3.5 (Troncoso et al. 2014) is drawn with a green dashed line. |
| In the text | |
 |
Fig. 6. UV slope as a function of stellar mass in two redshift bins: 2 < z < 3.5 and 3.5 < z < 5 (red and blue, respectively), where 3.5 is the median redshift of VANDELS. A linear fit to the relations in each redshift bin is also shown via dashed lines with their corresponding colors. The M*–β relation from McLure et al. (2018a) at z < 3 is shown with a green line for comparison, while gray and cyan diamonds come from Pannella et al. (2015). On the left y-axis, A1600 is shown using the β–A1600 conversion of Meurer et al. (1999). |
| In the text | |
 |
Fig. 7. Top: metallicity dependence of M1600–β relation for VANDELS star-forming galaxies at redshifts 2 < z < 3. The position of the stars (color-coded in metallicity) is representative of the median MUV and β of the galaxies in each bin. The metallicities (±1σ uncertainty) from the stacked spectra of galaxies in the same bin are written in black on the right side of each star. Single galaxies are drawn with squares. The best-fit relation (red dashed line) is used to divide the bins in β, while mass bins are shown with gray dashed lines. The resulting four bins are marked by 1, 2, 3, and 4. Bottom: Metallicity dependence of M*–β relation for the same subset of galaxies analyzed in the upper panel. The metallicity is calculated in four bins of stellar mass and UV slope, defined by the dashed lines. |
| In the text | |
 |
Fig. 8. Relation between UV slope and stellar metallicity for VANDELS galaxies. The average relation from the two indexes (1501 and 1719 Å) is drawn with black squares, while the pale colored squares represent the underlying metallicities from single absorption features. Horizontal bars associated with each of the three data points indicate the range of β slopes of galaxies in the same bin. The relation obtained from combining the best-fit MZR and the M*–β relation is highlighted with a cyan dashed line and cyan 1σ uncertainty area. On the top x-axis, A1600 is shown for comparison purposes, as determined from the β–A1600 conversion of Meurer et al. (1999). We warn the reader that this conversion may also depend, at a second order, on the metallicity itself. |
| In the text | |
 |
Fig. 9. Stacked spectra between 1000 and 2500 Å in three bins of increasing βmedian: −1.98 (blue line), −1.51 (gray line), and −1.10 (red line; see also Table 3). The absorption complexes used in this work to estimate the metallicity, located at 1501 and 1719 Å, are highlighted with yellow vertical bands. Top two panels: three stacks are plotted together, and we zoom-in around the two metallicity indexes. A thicker line specifies both the width of each absorption complex, while shaded gray areas indicate the spectral ranges for the estimation of the pseudo-continuum. Spectral stacks of galaxies with redder UV slopes have deeper absorption features, hence higher metallicity. |
| In the text | |
 |
Fig. 10. Top: comparison between MZR derived from VANDELS (black squares and error bars) and from predictions of two SAMs: orange diamonds represent the median masses and metallicities of GAEA galaxies in five bins of stellar mass defined as for the observations. Blue contour regions indicate the fraction of galaxies in the SAM of Menci et al. (2014) with different Z* at a given mass, according to the 2D bins defined in the text. Bottom: comparison of VANDELS results with the UV-slope-metallicity relation predicted by the GAEA models. The large orange diamonds were derived with the same method of the upper panel. We highlight the best-fit relation for the VANDELS sample with a dashed black line, while the shaded gray area encloses its 1σ uncertainty region. |
| In the text | |
 |
Fig. A.1. Relation between EW uncertainty (or stellar metallicity on the left y-axis) and input spectrum S/N. This is obtained through Monte Carlo simulations where Gaussian noise is added to Starburst99 templates with different metallicities. In this figure, different markers and colors refer to different metallicity indexes used in this work. For this example, we used the template with a metallicity of Z* = 0.2 × Z⊙, close to the value of our selected VANDELS galaxies. The vertical green line highlights the S/N range of the stacks that we analyze in this paper, while the smaller vertical gray bars indicate the S/N reached by the stacks in stellar mass from which the mass-metallicity relation is derived in Sect. 3.1. |
| In the text | |
 |
Fig. A.2. Comparison between input stellar metallicity and the EW predicted by Starburst99 and BPASS synthetic spectra (violet diamonds and filled white circles, respectively), for nine absorption line indexes typically adopted in the literature to calibrate the metallicity. We considered a continuous SFH for an age varying between 50 Myr and 2 Gyr (shaded region). The markers in each panel refer instead to an age of 100 Myr, which is taken for the final calibration of the 1501 and 1719 indexes (see Fig. ). |
| In the text | |
 |
Fig. A.3. Six panels compare the EW of the 1719 metallicity indicator to the EW of other absorption indexes in the FUV rest frame that were not considered in this work, either because no correlation was found with Z, or because the observational data are not in agreement with the predictions of any models (as in the case of significant ISM contamination). In each panel, we show the EW measurements from the five VANDELS stacks in stellar mass bins with colored stars (the median stellar mass of each stack is annotated in black). In addition, we superimpose EW–EW relations predicted by Starburst99 models (square symbols, with shaded gray area indicating different stellar ages from 50 Myr to 2 Gyr), and BPASS models (large circles). |
| In the text | |
 |
Fig. A.4. Stellar metallicity vs. equivalent width predicted by Starburst99 models for the ten absorption lines studied in this paper. The gray squares are derived assuming a standard upper-mass cut-off of 100 M⊙, while the blue triangles are calculated assuming a cut-off mass of 300 M⊙. All the symbols are representative of a constant SFH and a stellar age of 100 Myr. The shaded regions allow the stellar age to vary between 50 and 100 Myr. The other details of the models are the same as in Fig. A.2. |
| In the text | |
 |
Fig. A.5. Stellar metallicity vs. equivalent width predicted by Starburst99 models for the ten absorption lines studied in this paper. The gray squares are derived assuming a Kroupa IMF, the blue triangles are built by changing the high-mass end slope to αupper = −2.15 (as in Baldry & Glazebrook 2003), while the red circles assume an extremely flat slope αupper = −1.65. All the symbols are representative of a constant SFH and a stellar age of 100 Myr. The shaded regions allow the stellar age to vary between 50 and 100 Myr. The other details of the models are the same as in Fig. A.2. |
| In the text | |
 |
Fig. A.6. Stellar metallicity vs. EW predicted by Starburst99 models for the ten absorption lines studied in this paper and for different spectral resolutions. The resolution elements σres tested are 1/2, 1/3, 1, 2, 3, and 4 times the VANDELS value. All the symbols are derived with a constant SFH and a stellar age of 100 Myr. The shaded regions allow the stellar age to vary between 50 and 100 Myr. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.