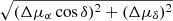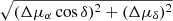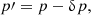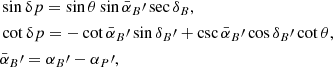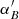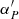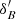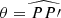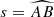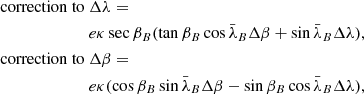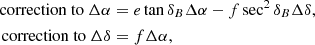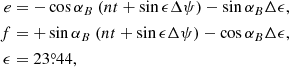| Issue |
A&A
Volume 645, January 2021
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 18 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202038776 | |
| Published online | 08 January 2021 | |
New precise positions in 2013–2019 and a catalog of ground-based astrometric observations of 11 Neptunian satellites (1847–2019) based on Gaia-DR2
1
Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210033, PR China
e-mail: yuanye@pmo.ac.cn
2
School of Astronomy and Space Science, University of Science and Technology of China, Hefei, Anhui 230026, PR China
3
University of Chinese Academy of Sciences, Beijing 100049, PR China
Received:
29
June
2020
Accepted:
1
October
2020
Context. Developing high-precision ephemerides for Neptunian satellites requires not only the continuation of observing campaigns but also the collection and improvement of existing observations. So far, no complete catalogs of observations of Neptunian satellites are available.
Aims. We aim to provide new, precise positions, and to compile a catalog including all available ground-based astrometric observations of Neptunian satellites. The observations are tabulated in a single and consistent format and given in the same timescale, the Terrestrial Time (TT), and reference system, the International Celestial Reference System (ICRS), including necessary changes and corrections.
Methods. New CCD observations of Triton and Nereid were made at Lijiang 2.4-m and Yaoan 0.8-m telescopes in 2013–2019, and then reduced based on Gaia-DR2. Furthermore, a catalog called OCNS2019 (Observational Catalog of Neptunian Satellites (2019 version)) was compiled, after recognizing and correcting errors and omissions. Furthermore, in addition to what was considered for the COSS08 catalog for eight main Saturnian satellites, all observed absolute and relative coordinates were converted to the ICRS with corrections for star catalog biases with respect to Gaia-DR2. New debiasing tables for both the modern and old star catalogs, which were previously not provided based on Gaia-DR2, are developed and applied. Treatment of missing positions of comparison bodies in conversions of observed relative coordinates are proposed.
Results. OCNS2019 and the new debiasing tables are publicly available online. OCNS2019 includes 24996 observed coordinates of 11 Neptunian satellites obtained over 3741 nights from 1847 to 2019. All observations are given in TT and ICRS. The star catalog biases are removed, which are significant for Nereid and outer satellites. We obtained 880 (5% of total now available) new coordinates for Triton over 41 nights (1% of total observation nights so far), and 790 (14%) for Nereid over 47 nights (10%). The dispersions of these new positions are about 0.″03 for Triton and 0.″06 for Nereid.
Conclusions. OCNS2019 should be useful in improving ephemerides for the above-mentioned objects.
Key words: catalogs / astrometry / ephemerides / planets and satellites: individual: Neptune / methods: observational / methods: data analysis
© ESO 2021
1. Introduction
To support current and future scientific investigations of the Neptune system and relevant space exploration missions (e.g., NASA’s Trident, Mitchell et al. 2019; Prockter et al. 2013), high-precision ephemerides for Neptunian satellites are needed (Jacobson 2009; Brozović et al. 2011, 2020; Emelyanov & Arlot 2011; Jacobson et al. 2012; Emelyanov & Samorodov 2015). The precision of ephemerides and determined dynamical parameters depends both on the precision of observations and on the length of the time interval covered by observations (Desmars et al. 2009a; Emelyanov 2010; Jacobson et al. 2012; Arlot et al. 2012; Emelyanov & Samorodov 2015; Lainey 2016). Therefore, not only the continuation of observing campaigns but also the collection and improvement of existing observations are required. In the present work, we provide new precise positions, and compile an observational catalog including all available ground-based astrometric observations of Neptunian satellites. So far, no complete catalog tabulating all observations of Neptunian satellites in a consistent format and in the same timescale and reference system is available. In fact, most of the available observations are presented in formats which are specific to their respective publications, and are consequently in various formats of data type, timescale, coordinates, and so on.
New CCD observations of Triton and Nereid were made at Lijiang 2.4-m and Yaoan 0.8-m telescopes in 2013–2019, and then reduced based on Gaia-DR2 (Gaia Collaboration 2018). Among all the available observed coordinates of Triton, we obtained 880 (5% of total now available) new coordinates for Triton over 41 nights (1% of total observation nights so far), and 790 (14%) for Nereid over 47 nights (10%). Our analysis shows that the standard deviations of the residuals with respect to the ephemeris positions given with DE430/NEP081xl1 are about 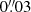 for Triton and
for Triton and 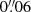 for Nereid.
for Nereid.
For the compilation of the observational catalog, we extract most data from three databases: the Natural Satellite Data Center (NSDC2; Arlot & Emelyanov 2009), the Minor Planet Center (MPC3), and the JPL Solar System Dynamics Website (JPL-SSD4). Although these databases are frequently updated, a few errors and omissions can be recognized by using the SAO/NASA Astrophysics Data System (ADS).
Since the discovery of the first Neptunian satellite, Triton (more than 170 years ago), many observations of Neptunian satellites have been made and published in different formats. However, for convenience of use, it is preferable that all observations are tabulated in a single and consistent format, as done by Desmars et al. (2009b) for their COSS08, an observational catalog of eight main Saturnian satellites. Furthermore, we convert all the observed coordinates to the International Celestial Reference System (ICRS).
Each star catalog has its unique systematic relations with the ICRS (Schwan 2001). For absolute coordinates actually referenced to a star catalog, the biases induced by star position errors should be corrected. Considering the Gaia-DR2 catalog as an extremely accurate realization of the ICRS, Eggl et al. (2020) determined the biases with respect to the Gaia-DR2 for the 26 modern star catalogs commonly used as a reference for the ICRS. Here, we apply their provided debiasing tables 5 to the Neptunian satellites for the first time. In addition, we also develop and apply debiasing tables to the currently used modern star catalog, Tycho-1 (ESA 1997), and the old ones, the Yale Zone Catalogs (Yale University 1997), which were not studied by Eggl et al. (2020).
Conversions of observed relative coordinates, except for the separations independent of coordinate systems, require complementary positions of comparison bodies. However, these positions are usually unavailable in observational data. Here, a treatment is proposed for this based on the ephemeris positions given with DE438/NEP081xl. Analytical estimations and test calculations show that the introduced error of < ∼ 5 μas is negligible.
The new precise positions are described in Sect. 2. The compilation procedure is described in Sect. 3. The final observational catalog is presented and analyzed in Sect. 4. We call this catalog OCNS2019, which stands for the Observational Catalog of Neptunian Satellites (2019 version). Conclusions are given in Sect. 5.
2. New precise positions of Triton and Nereid (2013–2019)
2.1. CCD observations
All CCD observations are made with the 0.8-m reflector at the Yaoan station (IAU observatory code, O49, assigned by MPC6) of Purple Mountain Observatory and the 2.4-m reflector at the Lijiang station (O44) of Yunnan Astronomical Observatory. For more instrumental details, for example of the used reflectors and CCD detectors, see Table 1. A total of 440 frames of CCD images (41 nights) were obtained for Triton and 395 frames (47 nights) for Nereid. The exposure time is about 0.2–2 min for Triton and 1–5 min for Nereid, depending on the settings of telescopes, the weather conditions, and the topocentric zenith distances. However, some frames can be used to provide both observed positions of Triton and Nereid. According to the standard procedure of astrometric observations, the flat-field, bias, and dark frames were also taken.
Instrumental details for the used reflectors and CCD detectors.
2.2. Astrometric reduction based on Gaia-DR2
A robust and stable astrometric reduction procedure was carried out according to Ofek (2019). The observed positions of Triton and Nereid were obtained with respect to the reference stars in the same fields of view. Here, following the advice of Arlot et al. (2012) and Ofek (2019), Gaia-DR2 is used as a reference catalog. After matching the reference stars with the positions in Gaia-DR2, a plate model was applied between the pixel and standard coordinates for each reference star as suggested by Ofek (2019). Specifically, the plate model is selected based on the number of matched stars (Nm*) by applying the following rules:
5 ≤ Nm* < 10: an affine transformation;
10 ≤ Nm* < 75: an affine transformation + tip/tilt terms;
75 ≤ Nm* < 120: an affine transformation + tip/tilt terms + 3rd order Chebyshev polynomials of the second kind;
Nm* ≥ 120: an affine transformation + tip/tilt terms + 3rd and 4th order Chebyshev polynomials of the second kind.
Finally, the observed astrometric positions of Triton and Nereid are easily obtained by the calibration of parameters involved in the plate models. For more details on the reduction procedure, see Table 2.
Details of the astrometric reduction.
2.3. Analysis of the observational data
To check and analyze our new observed coordinates (O), we make a comparison with a theory (C). In the present paper, the ephemerides used in calculating C are DE438/NEP081xl. Finally, in Table 3, the statistics of the (O − C) residuals are given for each satellite at each observatory and each opposition.
Statistics of (O − C) residuals for our new observational data using the ephemerides DE438/NEP081xl.
Comparisons with previously published data were also made. In Sects. 4.2 and 4.3 we present statistics for all available ground-based astrometric observations. According to Table 7, our new observed coordinates account for 5% (=880/18626) of the total for Triton and 14% (=790/5508) for Nereid. Correspondingly, the observation nights account for 1% (=41/3446) of the total nights spent observing Triton and 10% (=47/480) of the total nights spent observing Nereid. As seen in Fig. 9 and Table A.1, our new observed coordinates have a small dispersion on the whole. In particular, the dispersion is significantly smaller than those not reduced with Gaia data.
Furthermore, the residuals of our new observed coordinates for Triton were checked for the significant trend due to the Triton ephemeris around Neptune. As the period of Triton orbiting around Neptune is about six days, a six-day periodic variation was checked. For this, we considered the Triton observations in obsTime = 58438.5–58450.6, which covers the 12 days with the highest observation frequency. For Right Ascension and Declination, respectively, the mean residuals per day were analyzed by applying a nonequispaced fast Fourier transform (NFFT; Keiner et al. 2009). Results show that there are no significant six-day (or other) periodic terms; that is, the amplitudes of these terms are much smaller than the standard deviations of residuals. This is probably because the Triton ephemeris around Neptune is sufficiently accurate. Indeed, it is generally believed that, on the basis of the accurate Triton ephemeris, the Neptune ephemeris around the Sun can be improved by observations of Triton (Poroshina 2013; Folkner et al. 2014; Pitjeva & Pitjev 2014).
3. Compilation of ground-based astrometric observations of Neptunian satellites (1847–2019)
3.1. Items of data and useful information on observations
In order to use the observational data correctly and effectively, we require information about the instruments, the timescales and reference systems, and so on used by observers when they made reductions and published their results. The following list shows all the items useful for defining an observation consisting of at least one coordinate of an astronomical object. For each item, its label and type are on the left and right sides of an equal sign, respectively, followed by its description.
(1) Items for data source:
-
db = < String> The database from which the observation is extracted. The values can be NSDC = NSDC, MPC = MPC, SSD = JPL-SSD, ADS = ADS, and so on. Our new observational data derived in Sect. 2 are labeled with db = OCNS.
-
df = < String> The name of the file containing the observation in the database. The value ref signifies that the data are directly extracted from the original publication.
-
pubRef = < String> The reference to the publication that refers to the observations. For example, the Astrophysics Data System (ADS) reference, the Digital Object Identifier (DOI), the URL for the address of a resource on the internet, and so on.
-
pubSrc = < String> This specifies the origin of the reference. The values can be ADS, DOI, URL, and so on.
(2) Items for instrument and technique:
-
site = < Enumeration (string)> The IAU observatory code.
-
inst = < String> Description of the instruments used, such as the observatory, detector, telescope, design, aperture, and/or focal length.
-
type = < Enumeration (character)> Observation type. In the present study, the only one involved is O = optical.
-
tech = < Enumeration (character)> Observation technology and the mode of instrumentation. C = CCD; P = photographic; M = micrometer; T = automatic meridian transit circle measures; A = the observation is extracted and only available from MPC and has been converted to the FK5/J2000 system by rotating FK4/B1950 coordinates.
(3) Items for timescale and reference system:
-
ts = ⟨Enumeration (string)⟩ The timescale associated with the observation.
TT = Terrestrial Time (TT);
TDT = Terrestrial Dynamical Time (TDT);
ET = Ephemeris Time (ET);
UTC = Coordinated Universal Time (UTC);
UT = Universal Time (UT);
GMT = Greenwich Mean Time (GMT) =UT − 12h;
PMT = Paris Mean Time (PMT);
LMT = local mean time;
CST = Central Standard Time (CST);
PST = Pacific Standard Time (PST).
-
rfs = ⟨String⟩ The reference system in which the observed coordinates are measured. If a star catalog is used in the astrometric reduction, it should be the fundamental reference system to which the star catalog is commonly used as a reference. In the present study, those involved are as follows. ICRS = ICRS; B⟨year⟩ = the mean equator and equinox of the FK4 system at the Besselian epoch specified by ⟨year⟩; TOD = the true equator and equinox of date.
-
rfsCnt = ⟨Enumeration (string)⟩ The center of rfs, which can be the observatory (for topocentric coordinates) or the center of the Earth (for geocentric coordinates). The corresponding IAU observatory code is used.
(4) Items for observational coordinates:
-
obs = ⟨Enumeration (string)⟩ The observables associated with the observation. In the present study, only angular observables used for an optical observation are involved. Such observables are absolute coordinates and four kinds of relative coordinates, namely: ABS = absolute coordinates, (α, δ), where α is the Right Ascension in hours and δ is the Declination in degrees; PAS = position angle and separation (p, s) for a relative position. Here, p is given in degrees and s in arc-seconds; TAN = tangential coordinates, (ΔX, ΔY), for a relative position measured in a plane tangent to the celestial sphere and referenced to the point of tangency, with ΔX towards east and ΔY towards north. Both coordinate components are given in arc-seconds; DIF = differential coordinates (Δα cos δ0, Δδ) for a relative position measured from a given point (α0, δ0) on the celestial sphere, where Δα = α − α0 and Δδ = δ − δ0. Both coordinate components are given in arc-seconds; DRD = observed differences between two absolute coordinates (Δα, Δδ) for a relative position. Δα and Δδ are defined as DIF. Both coordinate components are given in arc-seconds.
-
obsTime = ⟨Decimal⟩ Mid-time of the observation expressed in MJD (Modified Julian Day);
-
obsCnt = ⟨Integer⟩ The origin of the measure of observed coordinates. For an absolute position, this is equal to zero; for a relative position, it is equal to the NAIF ID code7 for a Solar-System body.
-
obsTrg = ⟨Integer⟩ The NAIF ID code of the measured target.
-
obsCoord = ⟨Array of decimals (length = 2)⟩ Observed coordinates. For a missing coordinate component (p or s), nan is used.
(5) Items for decimal precision
-
dpTime = ⟨Decimal⟩ The decimal precision used in the timing of the observation, given in seconds;
-
dpCoord = ⟨Array of decimals (length = 2)⟩ The decimal precision used for measuring obsCoord. Both coordinate components are given in arc-seconds. For a missing component (p or s), nan is used.
(6) Items for reduction
-
astCat = ⟨Enumeration (string)⟩ The star catalog of reference used in the astrometric reduction. The values are the corresponding catalog code assigned by the MPC8. In addition, + = known ephemerides are used to provide reference Solar-System bodies; ? = unknown star catalogs, unspecified or unavailable, are used. / = neither a star catalog nor ephemerides are used (e.g., for tech = P, rfs = TOD is easily found by the trail of a star obtained by stopping the telescope);
-
aberr = ⟨Enumeration (character)⟩ Indicate whether the stellar aberration is excluded or included in obsCoord, and, if included, whether the aberration time is already corrected. Used indicators are
E = excluded;
I = included;
T = aberration time is corrected;
? = unknown.
-
refrac = ⟨Enumeration (character)⟩ Indicate whether the atmospheric refraction is excluded or included in obsCoord. Used indicators are E, I, and ? as aberr.
-
phase = ⟨Enumeration (character)⟩ Indicate whether the phase effect is excluded or included in obsCoord. Used indicators are E, I, and ? as aberr.
In the following, we give the additional items defining the converted data in TT and ICRS (Sects. 3.3 and 3.5), additional corrections for star catalog biases (Sect. 3.4), and residuals with respect to theory (Sect. 3.6):
(7) Items for converted data and corrections.
-
obsTt = ⟨Decimal⟩ Mid-time of the observation in TT, applying the conversions mentioned in Sect. 3.3.1, expressed in MJD;
-
obsCoordIcrsB = ⟨Array of decimals (length = 2)⟩ Observed coordinates resulting from the conversion of obsCoord from rfs to the ICRS mentioned in Sects. 3.3.2 and 3.5;
-
catBias = ⟨Array of decimals (length = 2)⟩ The star catalog bias corrections to be removed from obsCoordIcrsB as mentioned in Sect. 3.5. Each component corresponds to that of obsCoordIcrsB in the same position. If no corrections are needed, both components are zero.
(8) Items for residuals with respect to theory:
-
aberrRsd = ⟨Enumeration (character)⟩ If aberr ≠ ?, the indicators, E, I, and T, are directly used as aberr. Otherwise, lowercase indicators are used, applying the rules mentioned in Sect. 3.6;
-
refracRsd = ⟨Enumeration (character)⟩ If refrac ≠ ?, the indicators E and I are directly used as refrac. Otherwise, lowercase are used, applying the rules mentioned in Sect. 3.6;
-
phaseRsd = ⟨Enumeration (character)⟩ If phase ≠ ?, the indicators E and I are directly used as phase. Otherwise, lowercase are used, applying the rules mentioned in Sect. 3.6;
-
theoryRsd = ⟨String⟩ Theory used for computation of residuals;
-
rsdIcrsB = ⟨Array of decimals (length = 2)⟩ The (O − C) residuals before removing catBias, namely the differences between obsCoordIcrsB and theoretical coordinates referenced to the ICRS. Both coordinate components are given in arc-seconds;
-
rsdIcrsA = ⟨Array of decimals (length = 2)⟩ The (O − C) residuals after removing catBias, namely rsdIcrsB − catBias. Both coordinate components are given in arc-seconds.
3.2. Observational data collection
Nowadays, most ground-based astrometric observational data can be extracted from the following three databases:
-
db = NSDC: NSDC provides large numbers of published raw observational data of natural satellites, together with information about the reference frame used by the observer, the reduction made, and the timescale needed to link all the data (Arlot & Emelyanov 2009).
-
db = MPC: MPC provides observational data of natural outer irregular satellites of giant planets.
-
db = SSD: JPL-SSD provides observational data that are currently being used in creation and improvement of modern planetary and lunar ephemerides as well as the planetary satellite ephemerides.
As a general selecting rule for collection, we favor and retain the data in their original format (similar to the publications), as in Arlot & Emelyanov (2009). For observations reduced twice or more times in several references, the most recently reduced ones are retained.
Although these databases are frequently updated, a few errors and omissions in them are recognized by using the ADS.
On one hand, the following additional published observational data missing in the above databases are found by searching in the ADS:
-
Soulié et al. (1975): Three relative positions of Triton in 1970 were obtained, using the simultaneously observed Neptune as the comparison body.
-
van Biesbroeck et al. (1976): 11 absolute positions of Nereid in 1967–1969;
-
Veiga et al. (1996): 8 relative positions of Nereid with respect to Neptune in 1982–1985 and 53 of Triton in 1985–1988;
-
Dourneau et al. (2015): 189 absolute positions of Triton in 2007–2013;
-
Maris et al. (2018): 50 absolute positions of the outer satellite, Neso (obsTrg = 813).
On the other hand, verification of all the data and information in the above databases is carried out using the source information and references accessed via ADS:
-
Data errors in original publications. For example, as mentioned in van Biesbroeck et al. (1976), the time given by Rose (1974) is incorrect (NSDC/nm1006); several data entries are repeated in NSDC/nm1024 (Gomes-Júnior et al. 2015).
-
Incorrect information input. For example, the aberration times are already corrected (aberr = T≠I) for data in NSDC/nm0042 (Hall 1900), NSDC/nm0043 (Hall 1911), and NSDC/nm0044 (Hall & Burton 1913); the used star catalog is Tycho-1 (astCat = f≠g) for data in NSDC/nm0017 (Kiseleva et al. 2012).
-
Data loss. Six observed position angles are lost in NSDC/nm0035 (Hussey 1899).
-
Incorrect data lines. One position angle and one separation observed at two adjacent points in time are combined as one point in NSDC/nm0055 (Davis 1874); one observed separation of NSDC/nm0040 (Royal Observatory Greenwich 1908) and two observed position angles of NSDC/nm0070 (Neuĭmin & Pokrovskiĭ 1926) are incorrect; calendar time formats of NSDC/nm0059 (Royal Observatory Greenwich 1900) and NSDC/nm0074 (Wirtz 1905) and values of calendar times of NSDC/nm0006 are incorrect.
Table A.1 shows the main items of information for each set of the collected observational data. Our new data derived in Sect. 2 are also included in the collection and labeled with db = OCNS. In addition, broken links are updated.
3.3. Converting to the Terrestrial Time and the International Celestial Reference System
Tables 4 and 5 show the various timescales and reference systems, respectively, originally used by the collected observational data. As these data are not referenced to the same space-time coordinate system, they are timed in TT and expressed in the ICRS.
Statistics of timescales of observational data extracted from the sources.
Statistics of the reference systems of observational data extracted from the sources.
3.3.1. Timescales
Table 4 shows the three kinds of timescales (ts) appearing in the data collection: the dynamical time (TDT/ET), UTC, and the time standards based on Earth’s rotation (UT, local mean times, or standard times).
As TT continues TDT, which in turn succeeded ET, we apply TT = TDT = ET. At present, most observers use UTC in timing observations. The relationship between UTC and TT is conventionally provided by the International Earth Rotation Service (IERS)9. For many old observations, standard times or local mean times were used. Their differences from GMT = UT − 12h are simply the longitudes of locally chosen meridians.
The relationship between UT (strictly speaking, UT1) and TT is conventionally provided by the IERS and on the Long-term Delta T page10 provided by the United States Naval Observatory (USNO).
3.3.2. Reference systems
Table 5 shows the three kinds of reference systems (rfs) appearing in the data collection: the mean equator and equinox of the FK4 system at a particular epoch, the ICRS, and the true equator and equinox of date. There are conventional procedures for converting the observed absolute coordinates from these reference systems to the ICRS:
-
For the mean equator and equinox of FK4 system at a particular epoch, the classical procedure of transferring individual observations (Seidelmann 1992 pp. 179–180) is applied. Specifically, absolute coordinates are transformed back to the epoch of the observation on the FK4 system converted to the FK5 system of J2000 (FK5/J2000), and corrections for E-terms (the elliptic terms of aberration) and the FK4 − FK5 equinox offset are applied. Finally, the FK5/J2000 coordinates are converted to the ICRS (Mignard & Frœschlé 2000).
-
For the true equator and equinox of date, absolute coordinates are converted by applying sequential rotations for nutation, precession, and frame bias based on the IAU2006 model (Wallace & Capitaine 2006).
Among these observed absolute coordinates, as seen in Table 5, many are deduced using reference star catalogs. Although each of the star catalogs are commonly used as the reference to the ICRS or the FK4 system, the deduced coordinates, strictly speaking, are referenced to the star catalog itself. It is reasonable to break the systematic relation between a star catalog and the ICRS into the two parts (e.g., Schwan 2001):
-
(a)
The transformation between the reference system and the ICRS. This part models and eliminates the global transformation known a priori. Any residual corrections of zero point and equator are absorbed by the following bias correction.
-
(b)
The bias correction for the removal of remaining global rotations and regional biases between the catalog and the ICRS.
The treatment of the first part has been described in the previous paragraph. As for the second part, the procedure is developed and provided in Sect. 3.4.
Conversions of observed relative coordinates, except for the separations independent of coordinate systems, require the complementary positions of comparison bodies. However, these positions are usually unavailable in the observational data. A treatment is proposed and analyzed in Sect. 3.5.
3.4. Star-catalog bias corrections based on Gaia-DR2
3.4.1. Available debiasing tables based on Gaia-DR2
For the 26 modern star catalogs commonly used as a reference to the ICRS, Eggl et al. (2020) propose a treatment of the biases between them and the ICRS in absolute coordinates of minor planets. Considering the Gaia-DR2 catalog as an extremely accurate realization of the ICRS, Eggl et al. (2020) determine the biases by computing the median differences catalog−Gaia-DR2 in positions and proper motions at the comparison epoch T0= J2000.0 for the common stars in each of the divided tiles. The determined biases are contained in their provided debiasing tables.
The debiasing tables are applied for the first time to the absolute coordinates of Neptunian satellites. Table 6 provides the star catalogs used in the reduction of all the 15596 absolute coordinates. The catalogs can be identified for 15192 absolute coordinates (97.41%), in which 15070 (96.63%) use one of the catalogs studied in Eggl et al. (2020). In the present study, we use the finest debiasing table (NSIDE = 256)11 containing 786432 HEALPix (Górski et al. 2005) tiles.
Statistics on astrometric catalogs used for the reduction of absolute coordinates (obs = ABS) in OCNS2019.
As seen in Table 6, the Tycho-1 catalog and Yale Zone Catalogs are not studied by Eggl et al. (2020). For these catalogs, we first need to determine the biases and make new debiasing tables.
3.4.2. Debiasing table extensions for the modern catalog: Tycho-1
The Tycho-1 catalog is similar to the star catalogs studied in Eggl et al. (2020), however we make the comparison with Gaia-DR2 at the mean epoch of the catalog, that is, T0= J1991.25, as the positions depend less on the proper motions at this epoch (Schwan 2001). After transforming the positions and proper motions of Tycho-1 and Gaia-DR2 to T0, the biases are determined as in Eggl et al. (2020). Figure 1 shows the bias values for the Tycho-1 catalog at J1991.25 in the new debiasing table containing 786432 HEALPix tiles. The biases of Tycho-1 with respect to Gaia-DR2 are significant in proper motions and obviously different from those biases of Tycho-2.
 |
Fig. 1. Biases of the Tycho-1 catalog with respect to Gaia-DR2 at J1991.25. Top panels: local biases for positions along the directions of Right Ascension (left) and Declination (right), and bottom panels: biases for proper motions. The absolute value of color-bar limits for the top panels is the 99th percentile of |
3.4.3. Debiasing table extensions for the old catalogs: Yale Zone Catalogs
Yale Zone Catalogs are old catalogs published preceding the FK5 catalog (Fricke et al. 1988). They are a collection of catalogs of independent zones, but, as mentioned in Pierce (1978), adjacent and homogeneous zones can be combined and treated as one subsystem. In the present paper, we focus on the subsystem covering the observations reduced with the catalogs, that is, the combination of Volumes 16 and 17 of Yale Zone Catalogs (approximately, the region of Declination between −10° and −2°).
The comparison is made at the mean epoch of the combined catalog, that is, T0 = J1933.50. First, we applied the conversion for catalog positions and proper motions from the FK4 system to the ICRS (Seidelmann 1992, pp. 167–187), which is compatible with that applied to the observed coordinates referenced to this catalog (see Sect. 3.3.2). We then determined the biases between the converted catalog and Gaia-DR2 at T0 as for Tycho-1. Figure 2 shows the HEALPix map of the bias values for the selected Yale zones at J1933.50 in the new debiasing table containing 786432 HEALPix tiles. There are significant biases in both positions and proper motions with respect to Gaia-DR2.
 |
Fig. 2. Biases of Volumes 16 and 17 of Yale Zone Catalogs with respect to Gaia-DR2 at J1933.50, after having applied the conversion from the FK4 system to the ICRS. Top panels: local biases for positions along the directions of Right Ascension (left) and Declination (right), and bottom panels: biases for proper motions. The absolute value of the color-bar limits for the top panels is the 99th percentile of |
3.5. Converting observed relative coordinates to the International Celestial Reference System
https://naif.jpl.nasa.gov/pub/naif/generic_kernels/spk/planets/a_old_versions/de721_full.bsp
Observationally, there are two different methods for measuring the position of body A with respect to body B. One uses a micrometer (tech = M) to directly measure either a separation, s, or a position angle, p, referenced to the true equator of date (rfs = TOD), while the other uses the measurements obtained with a CCD or photographic plate (tech = C/P) to derive a pair of coordinate differences. Geometrically speaking, s is independent of coordinate systems.
3.5.1. Converting p
The conversion formula of p from the original reference system (ORS) to the ICRS writes
where
where B is the comparison body, P and P′ are the north poles of the ORS and ICRS, respectively, 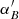 and
and 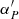 are the Right Ascensions of B and P referenced to the ICRS, respectively, δB and
are the Right Ascensions of B and P referenced to the ICRS, respectively, δB and 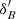 the Declination of B referenced to the ORS and ICRS, respectively, and
the Declination of B referenced to the ORS and ICRS, respectively, and 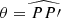 is the general precession and nutation in declination. The geometry of the conversion is also seen in Fig. 3.
is the general precession and nutation in declination. The geometry of the conversion is also seen in Fig. 3.
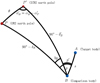 |
Fig. 3. Geometry of the conversion of the given observed coordinates of a body, A, relative to a comparison body, B. The north poles of the original and target reference systems (ORS and ICRS) are P and P′, respectively. |
Equation (1) shows that the conversion for p needs absolute positions of B, which are nevertheless usually unavailable in observational data. Fortunately, high-precision ephemerides can always provide sufficiently reliable theoretical estimates for absolute positions of B. In the present work, B can only be Neptune or Triton, and we use the DE438/NEP081xl ephemerides for them.
As DE438 is created based on DE430 (Folkner et al. 2014) with improved orbital data for Mercury, Mars, Jupiter, and Cassini (Folkner & Park 2018), the accuracy of DE438 for the Neptune system barycenter should be at the same level as DE430. Furthermore, Folkner et al. (2014) show that DE430 can provide positions of the Neptune system barycenter accurate to several thousand kilometers, or to several hundred milliarcseconds as observed from Earth. Indeed, as seen in Fig. 4, the maximum difference between the Neptune system barycenter positions as given by DE438 and another four high-precision planetary ephemerides developed by JPL (Folkner et al. 2014, 2009), IMCCE (Fienga et al. 2019), and IAA RAS (Pitjeva & Pitjev 2018) is about 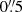 at the level of accuracy quantified by Folkner et al. (2014). In addition, Jacobson (2009) estimates that the error of relative positions between Triton and Neptune given with DE438/NEP081xl is within
at the level of accuracy quantified by Folkner et al. (2014). In addition, Jacobson (2009) estimates that the error of relative positions between Triton and Neptune given with DE438/NEP081xl is within 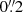 . Therefore, it is reasonable to say that DE438/NEP081xl can provide positions of B (Neptune or Triton) accurate to several hundred milliarcseconds. In the following discussions, the ephemeris error of B, εB, is taken as
. Therefore, it is reasonable to say that DE438/NEP081xl can provide positions of B (Neptune or Triton) accurate to several hundred milliarcseconds. In the following discussions, the ephemeris error of B, εB, is taken as 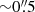 .
.
 |
Fig. 4. Differences in geocentric positions of the Neptune system barycenter between DE438 (Folkner & Park 2018) and other high-precision ephemerides: (1) DE430 (Folkner et al. 2014), the base of DE438; (2) DE721, which is very similar to DE421 (Folkner et al. 2009) but covers a longer time span; (3) INPOP19a (Fienga et al. 2019), the latest INPOP ephemerides developed by IMCCE; and (4) EPM2017 (Pitjeva & Pitjev 2018), the latest EPM ephemerides developed by IAA RAS. The vertical span in gray shows the time span covering the observed relative coordinates referenced to non-ICRS reference systems in OCNS2019. |
Neglecting nutation terms in θ, the following equation, to first order, gives the introduced error:
where 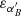 and
and 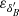 are the position error of B in
are the position error of B in 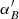 and
and 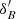 , respectively, t is the time from the standard epoch, J2000.0, to the observation epoch, and n is the rate of general precession in declination. For all observed p,
, respectively, t is the time from the standard epoch, J2000.0, to the observation epoch, and n is the rate of general precession in declination. For all observed p, 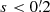 , |t| < 153 yr, and |δB| < 30°. Therefore, given
, |t| < 153 yr, and |δB| < 30°. Therefore, given 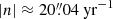 (Urban & Seidelmann 2014, p. 216), εp ∼ < 10−6 ⋅ εB ∼ 0.5 μas, which is much smaller than the observation error. That is to say, the influence of ephemeris use in the conversion is negligible.
(Urban & Seidelmann 2014, p. 216), εp ∼ < 10−6 ⋅ εB ∼ 0.5 μas, which is much smaller than the observation error. That is to say, the influence of ephemeris use in the conversion is negligible.
3.5.2. Converting a pair of coordinate differences
As seen in Fig. 3, given B and the pair of coordinate differences (Δ) between A and B, the absolute position of A can be obtained. Therefore, to convert Δ to the ICRS, we turn Δ into the absolute coordinates of A and B and then, after converting these two absolute coordinates to the ICRS (see Sect. 3.3.2), turn them back to a new pair of coordinate differences. Here also, as in Sect. 3.5.1, we use the high-precision ephemerides DE438/NEP081xl to provide B accurate to several hundred milliarcseconds (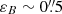 ). In this conversion, although the absolute coordinates of A and B are both affected by εB, the error of their differences, as is discussed below, is much smaller than s ⋅ ϵB.
). In this conversion, although the absolute coordinates of A and B are both affected by εB, the error of their differences, as is discussed below, is much smaller than s ⋅ ϵB.
Specifically, the effect of εB on the conversion of Δ, εΔ, can be roughly broken into the following three parts: ε1 for the differential corrections for E-terms, ε2 for the differential precession (and nutation) from the observation epoch to J2000.0, and ε3 for the differential equinox and bias corrections from the FK4 system to the ICRS. Test calculations show that, among these three parts, ε2 is dominant. Also, analytical estimations are given as follows:
To analytically estimate ε1 from the expressions for aberrational displacements due to E-terms (Smart & Green 1977, p. 186), we derive the conversion formula for differential corrections for E-terms, that is,
where Δλ = λA − λB, Δβ = βA − βB, 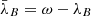 , λA and λB are the ecliptic longitudes of A and B, respectively, βA and βB are the ecliptic latitudes of A and B, respectively, κ is the constant of aberration, and e and ω are the eccentricity and the longitude of the perihelion of the Earth’s orbit, respectively. Differentiating Eq. (4) with respect to λB and βB, we find that ε1 ∼ < |(eκ sec2βB)⋅s ⋅ εB|. The values of κ and e may be taken as
, λA and λB are the ecliptic longitudes of A and B, respectively, βA and βB are the ecliptic latitudes of A and B, respectively, κ is the constant of aberration, and e and ω are the eccentricity and the longitude of the perihelion of the Earth’s orbit, respectively. Differentiating Eq. (4) with respect to λB and βB, we find that ε1 ∼ < |(eκ sec2βB)⋅s ⋅ εB|. The values of κ and e may be taken as 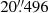 and 0.01673 (Seidelmann 1992, pp. 169–171), respectively. For all the observed coordinate differences, |βB| < 2′ and s < 6′. Therefore, ε1 ∼ < 3 × 10−9 ⋅ εB.
and 0.01673 (Seidelmann 1992, pp. 169–171), respectively. For all the observed coordinate differences, |βB| < 2′ and s < 6′. Therefore, ε1 ∼ < 3 × 10−9 ⋅ εB.
To analytically estimate ε2, we apply the approximate conversion formula for differential precession and nutation given in Seidelmann (1992, pp. 108–109), that is,
where Δα = αA − αB, Δδ = δA − δB,
where t is the time from the standard epoch, J2000.0, to the observation epoch, n is the rate of general precession in declination, and Δψ and Δϵ are the nutations in longitude and obliquity at t. Differentiating Eq. (5) with respect to αB and δB, we find that ε2 ∼ < |(nt sec2δB)⋅s ⋅ εB|. For all the observed coordinate differences, |δB| < 30o. If A is Triton, 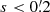 and |t| < 93 yr; if A is Nereid, s < 6′ and |t| < 51 yr. Therefore, ε2 ∼ < 10−5 ⋅ εB. Here ε3 contributes in a similar manner to the nutation terms in ε2 but is much smaller. Therefore, generally speaking, the total error, εΔ = ε1 + ε2 + ε3 ∼ < 10−5 ⋅ εB ∼ 5 μas, is much smaller than the observation error and so is negligible.
and |t| < 93 yr; if A is Nereid, s < 6′ and |t| < 51 yr. Therefore, ε2 ∼ < 10−5 ⋅ εB. Here ε3 contributes in a similar manner to the nutation terms in ε2 but is much smaller. Therefore, generally speaking, the total error, εΔ = ε1 + ε2 + ε3 ∼ < 10−5 ⋅ εB ∼ 5 μas, is much smaller than the observation error and so is negligible.
3.6. Computation of residuals between observed coordinates and theoretical ones
As presented in Sect. 2.3, residuals are purely indicative, and can be used to measure the accuracy of observed coordinates (O) in relation to theories (C). In the present paper, the ephemerides used in calculating C are DE438/NEP081xl for Triton and Nereid, DE438/NEP090 (Brozović et al. 2020) for inner satellites, and DE438/NEP086 (Brozović et al. 2011; Jacobson et al. 2012) for outer satellites.
When computing (O − C) residuals, some corrections like aberration, refraction, and phase effects have to be applied. Details on these corrections can be found in Desmars et al. (2009b). To deal with the observations missing information for corrections in the data publication, we apply the same rules as Desmars et al. (2009b).
4. The observational catalog: OCNS2019
4.1. Outputs
The OCNS2019 observations are tabulated in a consistent format. We generate an output for OCNS2019 with all observations sorted in ascending order by obsTt. The PSV (pipe -separated-values) format is chosen as the output layout. The catalog is available in electronic form at NADC (see address in acknowledgements).
In addition, the complementary debiasing tables extended for Tycho-1 and Yale Zone Catalogs are publicly available together. The debiasing table containing 786432 HEALPix tiles is used for catalog bias corrections in OCNS2019.
4.2. Temporal histograms of observed coordinates
Figure 5 gives the temporal distributions of numbers of observed coordinates for Triton, Nereid, the set of inner satellites, and the set of outer satellites, respectively, at each opposition. The distributions are relatively inhomogeneous. As seen in Fig. 5, there are not only significant gaps but also years with many observations. Because of this heterogeneity, distributions of observation nights are also given in Fig. 5.
 |
Fig. 5. Distribution of ground-based observations in OCNS2019 for Triton, Nereid, the set of inner satellites of Neptune (obsTrg = 805-808, i.e., Despina, Galatea, Larissa, and Proteus), and the set of outer satellites of Neptune (obsTrg = 809-813, i.e., Halimede, Psamathe, Sao, Laomedeia, and Neso). For each satellite or set of satellites, both the histogram of the number of observations, N, and the observation nights at each opposition, Ng, are presented. |
Table 7 gives the numbers of observed coordinates, the observation nights, and the covered years for each satellite. There are a total of 24996 observed coordinates obtained over 3741 nights.
Number of observed coordinates (N) and observation nights (Ng) of observational data in OCNS2019 for each satellite.
4.3. Statistics of star catalog bias corrections and computed residuals
Figure 6 shows the star catalog bias corrections with respect to Gaia-DR2. The corrections can reach about 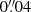 for inner satellites,
for inner satellites, 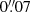 for Triton, and
for Triton, and 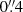 for Nereid and outer satellites. Because of the long distances from Neptune to Nereid and outer satellites, usually only absolute positions can be obtained due to the small fields of view. Furthermore, due to their faintness, the used reference stars are generally fainter and therefore have greater position biases than those used by Triton.
for Nereid and outer satellites. Because of the long distances from Neptune to Nereid and outer satellites, usually only absolute positions can be obtained due to the small fields of view. Furthermore, due to their faintness, the used reference stars are generally fainter and therefore have greater position biases than those used by Triton.
 |
Fig. 6. Star catalog bias corrections (catBias) of observed absolute coordinates (obs = ABS) in OCNS2019 with respect to Gaia-DR2. The four panels display the biases, respectively, for Triton, Nereid, the set of inner satellites (obsTrg = 805–808, i.e., Despina, Galatea, Larissa, and Proteus), and the set of outer satellites (obsTrg = 809–813, i.e., Halimede, Psamathe, Sao, Laomedeia, and Neso). Δα cos δ is the bias along the direction of Right Ascension and Δδ in Declination. The vertical dashed line in red denotes Δα cos δ = 0 and the horizontal dashed line shows Δδ = 0. |
Moreover, as shown in Fig. 7, for Triton, Nereid, and outer satellites, the star catalog bias corrections can reach the standard deviations of residuals (σ). More specifically, 143 (4%) nights of observational data for Triton, 151 (31%) for Nereid, and 8 (24%) for the outer satellites are corrected by more than 0.5σ. For these data, the comparisons of residuals with and without the catalog bias corrections are shown in Fig. 8. Systematic changes of residuals are noticeable, and in particular for outer satellites, after the catalog bias corrections, the data before 2012, which are used in the development of NEP086, have significant offsets from these ephemerides. Furthermore, when developing the ephemerides currently used in calculating C, the effect of star catalog biases is not systematically quantified and corrected. These catalog bias corrections can be used to improve the ephemerides.
 |
Fig. 7. Ratios of the star catalog bias corrections (catBias) to the standard deviations of the (O − C) residuals before removing catBias (rsdIcrsB). The four panels display the ratios, respectively, for Triton, Nereid, the set of inner satellites (obsTrg = 805–808, i.e., Despina, Galatea, Larissa, and Proteus), and the set of outer satellites (obsTrg = 809–813, i.e., Halimede, Psamathe, Sao, Laomedeia, and Neso). For each satellite/set, MEAN and SD indicate the mean and standard deviation, respectively, computed for each site and each opposition. The ephemerides used in calculating C are DE438/NEP081xl for Triton and Nereid, DE438/NEP090 for inner satellites, and DE438/NEP086 for outer satellites. Δα cos δ is along the direction of Right Ascension and Δδ Declination. |
 |
Fig. 8. Comparisons between rsdIcrsB and rsdIcrsA, the (O − C) residuals, respectively, before and after removing the known catalog biases (catBias). Only the observational data which are corrected by more than half of the standard deviations of residuals are shown in this figure. The ephemerides used in calculating C are DE438/NEP081xl for Triton and Nereid, and DE438/NEP086 for outer satellites (obsTrg = 809–813, i.e., Halimede, Psamathe, Sao, Laomedeia, and Neso). The three columns from left to right are the comparisons for Triton, Nereid, and outer satellites, respectively. The first and last rows are the comparisons along the directions of Right Ascension (Δα cos δ) and Declination (Δδ), respectively. |
Figure 9 shows the residuals of all the collected data after removing the known catalog biases. The last four columns of Table A.1 show the mean and standard derivation of these residuals for each reference. In general, the dispersion of the data reduced with Gaia data is significantly smaller than others.
 |
Fig. 9. (O − C) residuals (rsdIcrsA) between observed coordinates in OCNS2019 and theoretical ones after removing the known catalog biases with respect to Gaia-DR2. The ephemerides used in calculating C are DE438/NEP081xl for Triton and Nereid, DE438/NEP090 for inner satellites (obsTrg = 805–808, i.e., Despina, Galatea, Larissa, and Proteus), and DE438/NEP086 for outer satellites (obsTrg = 809–813, i.e., Halimede, Psamathe, Sao, Laomedeia, and Neso). Our new observed coordinates derived in Sect. 2 are marked by red dots (db = OCNS). |
5. Conclusions
The OCNS2019 catalog includes 24996 ground-based observed coordinates of 11 Neptunian satellites obtained over 3741 nights. All observations are tabulated in the same consistent format and given in the same timescale (TT) and reference system (ICRS). Biases induced by star position errors with respect to Gaia-DR2 are removed, which are significant for Nereid and outer satellites. Debiasing tables for the used catalogs, Tycho-1 and Yale Zone Catalogs, which are not studied in Eggl et al. (2020) are also developed and applied. We obtained 880 (5% of total now available) new coordinates for Triton over 41 nights (1% of total observation nights so far), and 790 (14%) for Nereid over 47 nights (10%). The dispersion of these new coordinates is small on the whole, and is significantly smaller than those not reduced with Gaia data. Therefore, this catalog should be useful in improving ephemerides for the above-mentioned objects. For the time being, the development of relevant ephemerides is ongoing.
The planetary ephemerides DE438 (Folkner & Park 2018) and satellite ephemerides NEP081xl (Jacobson 2009). They can be retrieved from the JPL Solar System Dynamics website https://ssd.jpl.nasa.gov/.
The MPC’s hosted list of IAU Observatory Codes is available at https://www.minorplanetcenter.net/iau/lists/ObsCodesF.html
The ID code used in the JPL Solar System Dynamics Group catalog, which is available at https://naif.jpl.nasa.gov/pub/naif/toolkit_docs/FORTRAN/req/naif_ids.html
The MPC’s hosted list of Catalog Codes is available at https://minorplanetcenter.net/iau/info/CatalogueCodes.html
Acknowledgments
The authors would like to thank J. Desmars for his constructive comments and useful suggestions, which are helpful for improving the present paper. This research is funded by the National Natural Science Foundation of China (NSFC) under grant Nos. 11178006, 11273066, 11533004, and 11673071. This research is also supported by the B-type Strategic Priority Program of the Chinese Academy of Sciences, Grant No. XDB41000000. This research has made use of data provided by the Lijiang 2.4-m Telescope at Yunnan Observatory and by the Yaoan High Precision Telescope at Purple Mountain Observatory, and the observational data extracted from the IAU Minor Planet Center (MPC), the Natural Satellite Data Center (NSDC), and the JPL Solar System Dynamics Website. This research has also made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Following tools have been essential to this research project: VizieR catalog access tools, CDS, Strasbourg, France; SAO/NASA Astrophysics Date System (ADS); JPL Horizons On-Line Ephemeris System; NASA/JPL-generated SPICE data and the allied software; Astropy, a community-developed core Python package for Astronomy. The OCNS2019 catalog and the new debiasing tables are available in electronic form at NADC via http://paperdata.china-vo.org/yuanye/ocns2019.zip.
References
- Aitken, R. G. 1899, Astron. Nachr., 149, 373 [CrossRef] [Google Scholar]
- Aitken, R. G. 1904, Lick Obs. Bull., 51, 157 [Google Scholar]
- Albrecht, S., & Smitil, E. 1909, Lick Obs. Bull., 5, 109 [Google Scholar]
- Alden, H. L. 1940, AJ, 49, 70 [CrossRef] [Google Scholar]
- Alden, H. L. 1943, AJ, 50, 110 [CrossRef] [Google Scholar]
- Arlot, J. E., & Emelyanov, N. V. 2009, A&A, 503, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arlot, J.-E., Desmars, J., Lainey, V., & Robert, V. 2012, Planet. Space Sci., 73, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Balanovskiĭ, I. A. 1923, Mitteilungen der Nikolai-Hauptsternwarte zu Pulkowo, 9, 85 [Google Scholar]
- Barnard, E. E. 1893, AJ, 13, 10 [CrossRef] [Google Scholar]
- Barnard, E. E. 1894, AJ, 14, 9 [CrossRef] [Google Scholar]
- Barnard, E. E. 1895, AJ, 15, 41 [CrossRef] [Google Scholar]
- Barnard, E. E. 1898, AJ, 19, 25 [CrossRef] [Google Scholar]
- Barnard, E. E. 1899, AJ, 20, 41 [CrossRef] [Google Scholar]
- Barnard, E. E. 1901, AJ, 22, 27 [CrossRef] [Google Scholar]
- Barnard, E. E. 1903, AJ, 23, 105 [CrossRef] [Google Scholar]
- Barnard, E. E. 1906a, AJ, 25, 41 [CrossRef] [Google Scholar]
- Barnard, E. E. 1906b, AJ, 25, 100 [CrossRef] [Google Scholar]
- Barnard, E. E. 1907, AJ, 25, 164 [CrossRef] [Google Scholar]
- Barnard, E. E. 1909, Astron. Nachr., 181, 321 [CrossRef] [Google Scholar]
- Barnard, E. E. 1910, AJ, 26, 144 [Google Scholar]
- Barnard, E. E. 1912, AJ, 27, 111 [Google Scholar]
- Barnard, E. E. 1913, AJ, 28, 10 [Google Scholar]
- Barnard, E. E. 1915, AJ, 29, 39 [Google Scholar]
- Barnard, E. E. 1916, AJ, 30, 2 [Google Scholar]
- Barnard, E. E. 1917, AJ, 30, 214 [Google Scholar]
- Barnard, E. E. 1919, AJ, 32, 103 [Google Scholar]
- Barnard, E. E. 1927, AJ, 37, 127 [CrossRef] [Google Scholar]
- Bastian, U., Röser, S., Nesterov, V. V., et al. 1991, A&AS, 87, 159 [Google Scholar]
- Bower, E. C., & Hall, A. 1923, AJ, 35, 108 [Google Scholar]
- Brozović, M., Jacobson, R. A., & Sheppard, S. S. 2011, AJ, 141, 135 [CrossRef] [Google Scholar]
- Brozović, M., Showalter, M. R., Jacobson, R. A., et al. 2020, Icarus, 338, 113462 [CrossRef] [Google Scholar]
- Burton, H. E. 1913, AJ, 28, 44 [Google Scholar]
- Burton, H. E., & Hall, Jr., A. 1919, AJ, 32, 113 [CrossRef] [Google Scholar]
- Christie, W. H. M. 1901, Greenwich Observations in Astronomy, Magnetism and Meteorology made at the Royal Observatory, Series 2, 61, D240 [Google Scholar]
- Christie, W. H. M. 1904, Greenwich Observations in Astronomy, Magnetism and Meteorology made at the Royal Observatory, Series 2, 64, G59 [Google Scholar]
- Christie, W. H. M. 1909, Greenwich Observations in Astronomy, Magnetism and Meteorology made at the Royal Observatory, Series 2, 69, G207 [Google Scholar]
- Colas, F., & Buil, C. 1992, A&A, 262, L13 [NASA ADS] [Google Scholar]
- Crawford, R. T. 1928, Lick Obs. Bull., 404, 8 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Davis, C. H. 1874, MNRAS, 35, 49 [Google Scholar]
- Desmars, J., Arlot, S., Arlot, J. E., Lainey, V., & Vienne, A. 2009a, A&A, 499, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desmars, J., Vienne, A., & Arlot, J.-E. 2009b, A&A, 493, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dourneau, G., Le Campion, J. F., Rapaport, M., et al. 2007, Notes Scientifiques et Techniques de l’Institut de Mecanique Celeste, 89 [Google Scholar]
- Dourneau, G., Le Campion, J. F., Bontemps, S., et al. 2015, Notes Scientifiques et Techniques de l’Institut de Mecanique Celeste, 97 [Google Scholar]
- Drew, D. A. 1897, AJ, 17, 131 [Google Scholar]
- Drew, D. A. 1899, AJ, 20, 30 [Google Scholar]
- Eggl, S., Farnocchia, D., Chamberlin, A. B., & Chesley, S. R. 2020, Icarus, 339, 113596 [CrossRef] [Google Scholar]
- Emelyanov, N. 2010, Planet. Space Sci., 58, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Emelyanov, N. V., & Arlot, J. E. 2011, MNRAS, 417, 458 [CrossRef] [Google Scholar]
- Emelyanov, N. V., & Samorodov, M. Y. 2015, MNRAS, 454, 2205 [Google Scholar]
- ESA 1997, VizieR Online Data Catalog: I/239 [Google Scholar]
- Fienga, A., Deram, P., Viswanathan, V., et al. 2019, Notes Scientifiques et Techniques de l’Institut de Mecanique Celeste, 109 [Google Scholar]
- Folkner, W. M., & Park, R. S. 2018, Planetary ephemeris DE438 for Juno, Tech. Rep. IOM392R-18-004 (Pasadena, CA: Jet Propulsion Laboratory) [Google Scholar]
- Folkner, W. M., Williams, J. G., & Boggs, D. H. 2009, Interplanetary Network Prog. Rep., 178, 1 [Google Scholar]
- Folkner, W. M., Williams, J. G., Boggs, D. H., Park, R. S., & Kuchynka, P. 2014, Interplanetary Network Prog. Rep., 196, 1 [Google Scholar]
- Fricke, W., Schwan, H., Lederle, T., et al. 1988, Veroeffentlichungen des Astronomischen Rechen-Instituts Heidelberg, 32, 1 [NASA ADS] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes-Júnior, A. R., Assafin, M., Vieira-Martins, R., et al. 2015, A&A, 580, A76 [CrossRef] [EDP Sciences] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, APJ, 622, 759 [CrossRef] [Google Scholar]
- Hall, A. 1876, Astron. Nachr., 88, 131 [Google Scholar]
- Hall, A. 1877, Astron. Nachr., 90, 161 [Google Scholar]
- Hall, A. 1900, AJ, 20, 191 [Google Scholar]
- Hall, A., Jr 1911, AJ, 26, 179 [CrossRef] [Google Scholar]
- Hall, A., Jr 1920, AJ, 33, 62 [CrossRef] [Google Scholar]
- Hall, A., Jr 1922, AJ, 34, 18 [CrossRef] [Google Scholar]
- Hall, A., Jr, & Burton, H. E. 1913, AJ, 28, 42 [CrossRef] [Google Scholar]
- Hammond, J. C. 1906, AJ, 25, 93 [Google Scholar]
- Hammond, J. C., & Rice, H. L. 1905, AJ, 24, 188 [Google Scholar]
- Harrington, R. S., & Walker, R. L. 1984, AJ, 89, 889 [Google Scholar]
- Harris, D., & van Biesbroeck, G. 1949, AJ, 54, 197 [CrossRef] [Google Scholar]
- Henry, P. 1884a, Bull. Astron. Ser. I, 1, 89 [Google Scholar]
- Henry, P. 1884b, Bull. Astron. Ser. I, 1, 178 [Google Scholar]
- Henry, P., Boinot, A., & Sy, F. 1886, Bull. Astron. Ser. I, 3, 488 [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
- Hussey, W. J. 1899, AJ, 20, 71 [Google Scholar]
- Hussey, W. J. 1902, Lick Obs. Bull., 17, 139 [Google Scholar]
- Jacobson, R. A. 2009, AJ, 137, 4322 [Google Scholar]
- Jacobson, R., Brozović, M., Gladman, B., et al. 2012, AJ, 144, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Keiner, J., Kunis, S., & Potts, D. 2009, ACM Trans. Math. Softw., 36 [Google Scholar]
- Kiseleva, T. P., Chanturiya, S. M., Vasil’eva, T. A., & Kalinichenko, O. A. 2012, Sol. Syst. Res., 46, 436 [CrossRef] [Google Scholar]
- Kostinsky, S. 1900, Astron. Nachr., 152, 277 [Google Scholar]
- Kostinsky, S. 1902, Astron. Nachr., 157, 287 [Google Scholar]
- Kulyk, I., Izakevich, E. M., & Shatokhina, S. 2009, Private Communication to NSDC, http://nsdb.imcce.fr/obspos/OBS_COLL/N/nm0016.html [Google Scholar]
- Lainey, V. 2016, Celestial Mech. Dyn. Astron., 126, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Landgraf, W. 1988, IAU Circ., 4542, 1 [Google Scholar]
- Lasker, B. M., Russel, J. N., & Jenkner, H. 1999, VizieR Online Data Catalog: I/255 [Google Scholar]
- Lassell, W. 1849a, MNRAS, 9, 103 [Google Scholar]
- Lassell, W. 1849b, MNRAS, 10, 8 [Google Scholar]
- Lassell, W. 1850, MNRAS, 10, 132 [Google Scholar]
- Lassell, W. 1851, MNRAS, 11, 61 [Google Scholar]
- Lassell, W. 1852a, MNRAS, 12, 155 [Google Scholar]
- Lassell, W. 1852b, MNRAS, 13, 37 [Google Scholar]
- Lassell, W. 1857, MNRAS, 17, 70 [Google Scholar]
- Lassell, W. 1864, MNRAS, 24, 209 [Google Scholar]
- Lindegren, L., Lammers, U., Bastian, U., et al. 2016, A&A, 595, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lohse, J. G. 1887, MNRAS, 47, 497 [Google Scholar]
- Maris, M., Carraro, G., Melita, M., & Parisi, G. 2018, Res. Notes Am. Astron. Soc., 2, 42 [CrossRef] [Google Scholar]
- Mignard, F., & Frœschlé, M. 2000, A&A, 354, 732 [NASA ADS] [Google Scholar]
- Mitchell, K. L., Prockter, L. M., Frazier, W. E., et al. 2019, Lunar Planet. Sci. Conf., 3200 [Google Scholar]
- Monet, D. G. 1998, Am. Astron. Soc. Meeting Abstracts, 193, 120.03 [Google Scholar]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Neuĭmin, G. N., & Pokrovskiĭ, K. D. 1926, Mitteilungen der Nikolai-Hauptsternwarte zu Pulkowo, 10, 418 [Google Scholar]
- Ofek, E. O. 2019, PASP, 131, 054504 [CrossRef] [Google Scholar]
- Owen, W. M. 1999a, Private Communication to NSDC, http://nsdb.imcce.fr/obspos/OBS_COLL/N/nm0005.html [Google Scholar]
- Owen, W. M. 1999b, Private Communication to NSDC, http://nsdb.imcce.fr/obspos/OBS_COLL/N/nm0006.html [Google Scholar]
- Parrish, N. M., & Stone, O. 1892, AJ, 12, 90 [Google Scholar]
- Pascu, D., Rohde, J. R., Seidelmann, P. K., et al. 2004, AJ, 127, 2988 [NASA ADS] [CrossRef] [Google Scholar]
- Perrine, C. D. 1903, Lick Obs. Bull., 39, 70 [Google Scholar]
- Perrotin, H. J. 1887, Bull. Astron. Ser. I, 4, 339 [Google Scholar]
- Pierce, D. A. 1978, Astronomical Papers Prepared for the Use of the American Ephemeris and Nautical Almanac, 22, 213 [Google Scholar]
- Pitjeva, E. V., & Pitjev, N. P. 2014, Celestial Mech. Dyn. Astron., 119, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Pitjeva, E. V., & Pitjev, N. P. 2018, Celestial Mech. Dyn. Astron., 130, 57 [Google Scholar]
- Poroshina, A. L. 2013, Astron. Lett., 39, 876 [Google Scholar]
- Prockter, L. M., Mitchell, K. L., Howett, C. J. A., et al. 2013, Lunar Planet. Sci. Conf., 3188 [Google Scholar]
- PUSNO6A-1911 1911, Publ. U.S. Naval Obs. Second Ser. 6, A1 [Google Scholar]
- Qiao, R. C., Yan, Y. R., Shen, K. X., et al. 2007, MNRAS, 376, 1707 [Google Scholar]
- Qiao, R. C., Zhang, H. Y., Dourneau, G., et al. 2014, MNRAS, 440, 3749 [Google Scholar]
- Roeser, S., & Bastian, U. 1988, A&AS, 74, 449 [NASA ADS] [Google Scholar]
- Rose, L. E. 1974, AJ, 79, 489 [CrossRef] [Google Scholar]
- Royal Observatory Greenwich 1800, MNRAS, 61, 9 [Google Scholar]
- Royal Observatory Greenwich 1899, MNRAS, 59, 501 [Google Scholar]
- Royal Observatory Greenwich 1903, MNRAS, 63, 503 [Google Scholar]
- Royal Observatory Greenwich 1904, MNRAS, 64, 835 [Google Scholar]
- Royal Observatory Greenwich 1905, MNRAS, 66, 10 [Google Scholar]
- Royal Observatory Greenwich 1906, MNRAS, 67, 91 [Google Scholar]
- Royal Observatory Greenwich 1907, MNRAS, 68, 33 [Google Scholar]
- Royal Observatory Greenwich 1908, MNRAS, 68, 586 [Google Scholar]
- Royal Observatory Greenwich 1913, MNRAS, 73, 155 [Google Scholar]
- Rümker, C. 1849, MNRAS, 9, 221 [Google Scholar]
- Schaeberle, J. M. 1895, AJ, 15, 25 [Google Scholar]
- Schaeberle, J. M. 1897, AJ, 17, 62 [Google Scholar]
- Schaeberle, J. M. 1898, AJ, 18, 168 [Google Scholar]
- Schaefer, M. W., & Schaefer, B. E. 1988, Nature, 333, 436 [CrossRef] [Google Scholar]
- Schwan, H. 2001, A&A, 373, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seidelmann, P. K. 1992, Explanatory Supplement to the Astronomical Almanac (University Science Books) [Google Scholar]
- Smart, W. M., & Green, R. M. 1977, Textbook on Spherical Astronomy (Cambridge University Press) [CrossRef] [Google Scholar]
- Soulié, G., Dupouy, Teulet, Broqua, & Dulou 1975, A&AS, 22, 49 [Google Scholar]
- TMO 2014, CCD Astrometric Measurements from Table Mountain Observatory, https://ssd.jpl.nasa.gov/dat/planets/ccd1.tmo.html [Google Scholar]
- Urban, S. E., & Seidelmann, P. K. 2014, Am. Astron. Soc. Meeting Abstracts, 223, 247.20 [Google Scholar]
- Urban, S. E., Corbin, T. E., & Wycoff, G. L. 1998, AJ, 115, 2161 [NASA ADS] [CrossRef] [Google Scholar]
- USNO 2013, CCD Astrometric Measurements from US Naval Observatory Flagstaff Using the Flagstaff Astrometric Scanning Transit Telescope, https://ssd.jpl.nasa.gov/dat/planets/ccd1.nofs.html [Google Scholar]
- USNO 2014, Flagstaff Astrometric Scanning Transit Telescope Planet and Planetary Satellite Observations, https://www.usno.navy.mil/USNO/astrometry/optical-IR-prod/solsys/fastt-plansat [Google Scholar]
- USNOM17Q-1881 1881, Astronomical and Meteorological Observations made at the U.S. Naval Observatory [Google Scholar]
- van Biesbroeck, G., Vesely, C. D., Aksnes, K., & Marsden, B. G. 1976, AJ, 81, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Veiga, C. H., & Martins, R. V. 1998, A&AS, 131, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veiga, C. H., & Vieira Martins, R. 1996, A&AS, 120, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veiga, C. H., Vieira Martins, R., Le Guyader, C., & Assafin, M. 1996, A&AS, 115, 319 [Google Scholar]
- Veiga, C. H., Martins, R. V., & Le Guyader, C. 1999, A&AS, 136, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veillet, C. 1982, A&A, 112, 277 [Google Scholar]
- Veillet, C., & Bois, E. 1988, A&A, 189, 303 [Google Scholar]
- Vieira Martins, R., Veiga, C. H., Bourget, P., Andrei, A. H., & Descamps, P. 2004, A&A, 425, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, R. L., & Harrington, R. S. 1988, AJ, 95, 1562 [Google Scholar]
- Walker, R. L., Christy, J. W., & Harrington, R. S. 1978, AJ, 83, 838 [Google Scholar]
- Wallace, P. T., & Capitaine, N. 2006, A&A, 459, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, N., Peng, Q. Y., Peng, H. W., et al. 2017, MNRAS, 468, 1415 [Google Scholar]
- Winlock, J., & Pickering, E. C. 1888, Ann. Harvard College Obs., 13, 86 [Google Scholar]
- Wirtz, C. W. 1905, Astron. Nachr., 169, 33 [Google Scholar]
- Yale University 1997, VizieR Online Data Catalog: I/141 [Google Scholar]
- Yizhakevych, O. M., Andruk, V. M., & Pakuliak, L. K. 2016, Odessa Astron. Publ., 29, 155 [CrossRef] [Google Scholar]
- Young, C. A. 1888, AJ, 8, 14 [Google Scholar]
- Yu, Y., Qiao, R. C., Yan, D., et al. 2018, Planet. Space Sci., 152, 82 [CrossRef] [Google Scholar]
- Yu, Y., Cheng, X., Qiao, R. C., et al. 2019, Planet. Space Sci., 165, 205 [CrossRef] [Google Scholar]
- Zacharias, N., Urban, S. E., Zacharias, M. I., et al. 2004, AJ, 127, 3043 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Monet, D. G., Levine, S. E., et al. 2005, VizieR Online Data Catalog: I/297 [Google Scholar]
- Zacharias, N., Finch, C., Girard, T., et al. 2010, AJ, 139, 2184 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Ground-based astrometric observational data of Neptunian satellites collected in OCNS2019
Sets of ground-based astrometric observational data for Neptunian satellites collected in OCNS2019.
All Tables
Statistics of (O − C) residuals for our new observational data using the ephemerides DE438/NEP081xl.
Statistics of the reference systems of observational data extracted from the sources.
Statistics on astrometric catalogs used for the reduction of absolute coordinates (obs = ABS) in OCNS2019.
Number of observed coordinates (N) and observation nights (Ng) of observational data in OCNS2019 for each satellite.
Sets of ground-based astrometric observational data for Neptunian satellites collected in OCNS2019.
All Figures
 |
Fig. 1. Biases of the Tycho-1 catalog with respect to Gaia-DR2 at J1991.25. Top panels: local biases for positions along the directions of Right Ascension (left) and Declination (right), and bottom panels: biases for proper motions. The absolute value of color-bar limits for the top panels is the 99th percentile of |
| In the text | |
 |
Fig. 2. Biases of Volumes 16 and 17 of Yale Zone Catalogs with respect to Gaia-DR2 at J1933.50, after having applied the conversion from the FK4 system to the ICRS. Top panels: local biases for positions along the directions of Right Ascension (left) and Declination (right), and bottom panels: biases for proper motions. The absolute value of the color-bar limits for the top panels is the 99th percentile of |
| In the text | |
 |
Fig. 3. Geometry of the conversion of the given observed coordinates of a body, A, relative to a comparison body, B. The north poles of the original and target reference systems (ORS and ICRS) are P and P′, respectively. |
| In the text | |
 |
Fig. 4. Differences in geocentric positions of the Neptune system barycenter between DE438 (Folkner & Park 2018) and other high-precision ephemerides: (1) DE430 (Folkner et al. 2014), the base of DE438; (2) DE721, which is very similar to DE421 (Folkner et al. 2009) but covers a longer time span; (3) INPOP19a (Fienga et al. 2019), the latest INPOP ephemerides developed by IMCCE; and (4) EPM2017 (Pitjeva & Pitjev 2018), the latest EPM ephemerides developed by IAA RAS. The vertical span in gray shows the time span covering the observed relative coordinates referenced to non-ICRS reference systems in OCNS2019. |
| In the text | |
 |
Fig. 5. Distribution of ground-based observations in OCNS2019 for Triton, Nereid, the set of inner satellites of Neptune (obsTrg = 805-808, i.e., Despina, Galatea, Larissa, and Proteus), and the set of outer satellites of Neptune (obsTrg = 809-813, i.e., Halimede, Psamathe, Sao, Laomedeia, and Neso). For each satellite or set of satellites, both the histogram of the number of observations, N, and the observation nights at each opposition, Ng, are presented. |
| In the text | |
 |
Fig. 6. Star catalog bias corrections (catBias) of observed absolute coordinates (obs = ABS) in OCNS2019 with respect to Gaia-DR2. The four panels display the biases, respectively, for Triton, Nereid, the set of inner satellites (obsTrg = 805–808, i.e., Despina, Galatea, Larissa, and Proteus), and the set of outer satellites (obsTrg = 809–813, i.e., Halimede, Psamathe, Sao, Laomedeia, and Neso). Δα cos δ is the bias along the direction of Right Ascension and Δδ in Declination. The vertical dashed line in red denotes Δα cos δ = 0 and the horizontal dashed line shows Δδ = 0. |
| In the text | |
 |
Fig. 7. Ratios of the star catalog bias corrections (catBias) to the standard deviations of the (O − C) residuals before removing catBias (rsdIcrsB). The four panels display the ratios, respectively, for Triton, Nereid, the set of inner satellites (obsTrg = 805–808, i.e., Despina, Galatea, Larissa, and Proteus), and the set of outer satellites (obsTrg = 809–813, i.e., Halimede, Psamathe, Sao, Laomedeia, and Neso). For each satellite/set, MEAN and SD indicate the mean and standard deviation, respectively, computed for each site and each opposition. The ephemerides used in calculating C are DE438/NEP081xl for Triton and Nereid, DE438/NEP090 for inner satellites, and DE438/NEP086 for outer satellites. Δα cos δ is along the direction of Right Ascension and Δδ Declination. |
| In the text | |
 |
Fig. 8. Comparisons between rsdIcrsB and rsdIcrsA, the (O − C) residuals, respectively, before and after removing the known catalog biases (catBias). Only the observational data which are corrected by more than half of the standard deviations of residuals are shown in this figure. The ephemerides used in calculating C are DE438/NEP081xl for Triton and Nereid, and DE438/NEP086 for outer satellites (obsTrg = 809–813, i.e., Halimede, Psamathe, Sao, Laomedeia, and Neso). The three columns from left to right are the comparisons for Triton, Nereid, and outer satellites, respectively. The first and last rows are the comparisons along the directions of Right Ascension (Δα cos δ) and Declination (Δδ), respectively. |
| In the text | |
 |
Fig. 9. (O − C) residuals (rsdIcrsA) between observed coordinates in OCNS2019 and theoretical ones after removing the known catalog biases with respect to Gaia-DR2. The ephemerides used in calculating C are DE438/NEP081xl for Triton and Nereid, DE438/NEP090 for inner satellites (obsTrg = 805–808, i.e., Despina, Galatea, Larissa, and Proteus), and DE438/NEP086 for outer satellites (obsTrg = 809–813, i.e., Halimede, Psamathe, Sao, Laomedeia, and Neso). Our new observed coordinates derived in Sect. 2 are marked by red dots (db = OCNS). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.