| Issue |
A&A
Volume 643, November 2020
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 10 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202039243 | |
| Published online | 13 November 2020 | |
Light-time effect detected in fourteen eclipsing binaries⋆
1
Astronomical Institute, Charles University, Faculty of Mathematics and Physics, V Holešovičkách 2, 180 00 Praha 8, Czech Republic
e-mail: zasche@sirrah.troja.mff.cuni.cz
2
Private Observatory, Pohoří 71, 254 01 Jílové u Prahy, Czech Republic
3
Private Observatory, Výpustky 5, 614 00 Brno, Czech Republic
4
BSObservatory, Modrá 587, 760 01 Zlín, Czech Republic
5
Institute of Physics, Czech Academy of Sciences, Na Slovance 1999/2, 182 21 Praha 8, Czech Republic
Received:
24
August
2020
Accepted:
14
September
2020
The available minima timings of 14 selected eclipsing binaries (V1297 Cas, HD 24105, KU Aur, GU CMa, GH Mon, AZ Vel, DI Lyn, DK Her, GQ Dra, V624 Her, V1134 Her, KIC 6187893, V1928 Aql, V2486 Cyg) were collected and analyzed. Using the automatic telescopes, surveys, and satellite data, we derived more than 2500 times of eclipses, accompanied with our own ground-based observations. These data were used to detect the period variations in these multiple systems. The eclipse timing variations were described using the third-body hypothesis and the light-time effect. Their respective periods were derived as 2.5, 16.2, 27, 20, 64, 5.6, 22, 115, 27, 42, 6.9, 11.2, 4.1, and 8.4 years for these systems, respectively. The predicted minimal mass of the third body was calculated for each of the systems, and we discuss here their prospective detectability. The light curves of HD 24105, GH Mon, DK Her, V1134 Her, KIC 6187893, V1928 Aql, and V2486 Cyg were analyzed using the PHOEBE program, resulting in physical parameters of the components. Significant fractions of the third light were detected during the light-curve analysis, supporting our hypothesis of the triple-star nature of all these systems. The majority of these systems (nine out of 14) were already known as visual doubles. Our study shifts them to possible quadruples, what makes them even more interesting.
Key words: binaries: eclipsing / stars: fundamental parameters
Photometric data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/643/A130
© ESO 2020
1. Introduction
The role of classical eclipsing binaries (EBs) in modern astrophysics is undisputable. Surprisingly, after a century of their intensive research, they still represent the most general method used to derive the basic stellar properties with the highest accuracy (see e.g., Southworth 2012). Quantities such as masses, radii, or luminosities can be derived with unprecedented precision at the level of about 1% only, also yielding the distance at about the same precision: nowadays even outside of our own Galaxy (Pietrzyński et al. 2019).
Besides this role of EBs as independent distance indicators, their physical parameters should obviously be used for calibrating the existing stellar evolution models (Torres et al. 2010). Moreover, the EBs with their precise eclipses can also serve a different purpose: as ideal tics measuring precise time intervals. Hence, studying the deviations from the predicted ephemerides via studying the delays with eclipse timing variations (ETVs) is nowadays a classical method, which can be used for revealing some of the hidden properties of the binaries themselves (Sterken 2005).
This method of ETV analysis usually employs a standard light-time effect hypothesis of additional body orbiting around a barycenter (hereafter LITE, see e.g., Irwin 1959, and Mayer 1990). Such an approach is substantiated by the fact that if the third bodies move on sufficiently long orbits, we can assume that the whole system is almost like a two-body problem. However, when the orbits are closer to each other (and the ratio of periods 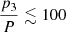 ), then the dynamical interaction of the third body on the inner double cannot be neglected. These tight triples show many different ETV signals, depending on their masses, orientations of the orbits, eccentricities, and so on. See, for example, Borkovits et al. (2003, 2011). However, such tight multiples can usually only be detected with dense data obtained with high cadency over a certain time interval, like in Borkovits et al. (2015). Moreover, these close third bodies are also able to cause other effects like orbital precession or even inclination changes of the inner eclipsing double.
), then the dynamical interaction of the third body on the inner double cannot be neglected. These tight triples show many different ETV signals, depending on their masses, orientations of the orbits, eccentricities, and so on. See, for example, Borkovits et al. (2003, 2011). However, such tight multiples can usually only be detected with dense data obtained with high cadency over a certain time interval, like in Borkovits et al. (2015). Moreover, these close third bodies are also able to cause other effects like orbital precession or even inclination changes of the inner eclipsing double.
On the other hand, many studies on potential triples discovered via ETV applying the LITE hypothesis were later found to be unrealistic, when new data were available. Therefore, we have to be cautious of our interpretation, and our result is still rather a hypothesis waiting to be proven by other methods, such as spectroscopy. Besides the LITE, there are also some alternative mechanisms present that cause the ETVs, especially in contact systems, like the modulation through spots and magnetic activity cycles: for example, the so-called Applegate mechanism (Applegate 1992).
The importance of the third bodies on the origin and subsequent evolution of the binaries (also including the role of the Kozai cycles) has been discussed elsewhere: for example, Eggleton & Kiseleva-Eggleton (2001) or Tokovinin (2008). However, the origin of these hierarchical multiples is still being discussed and remains an open question (Czekala et al. 2019).
2. Methods
Our method of detection and characterization of the sample binaries uses a classical approach assuming only one body on a quite distant orbit, meaning there is no dynamical interaction, and only the LITE term was used for ETV analysis. With this method, we would be able to find preferably the bodies with periods of a few years to decades, and with LITE semiamplitudes of the order of 0.01 day (quite similarly to our former analysis, Zasche et al. 2014a). This limitation mainly comes from the fact that the data cadence is typically limited, and the precision of the individual times of eclipses critically depends on the quality of the light curve (LC) and depth of a particular eclipse.
The times of eclipses for the ETV analysis were collected from published papers. Additionally to the published eclipses, we also computed the new ones from the available data. These were our new dedicated observations of these targets (from ground-based observatories, using typically small amateur telescopes), as well as the rich databases of photometric observations of these binaries from existing archives. The PDR code (Zejda et al. 2019) was used to obtain some of these data. These datasets were the following:
– HIP: the HIPPARCOS satellite, observing in special Hp filter, between 1989 and 1993 (Perryman et al. 1997).
– NSVS: the ROTSE-I experiment, unfiltered photometry, with a time span from 1999 to 2000 (Woźniak et al. 2004).
– OMC: five-cm camera onboard the INTEGRAL satellite, observing in V filter since 2002 (Mas-Hesse et al. 2003).
– ASAS: All Sky Automated Survey, observing since 1997 in V and I filters (Pojmanski 2002).
– ASAS-SN: ASAS for supernovae, 24 telescopes, V and g filters (Shappee et al. 2014; Kochanek et al. 2017).
– SuperWASP: 20-cm telescopes, using special filters, observing since 2004 (Pollacco et al. 2006).
– Pi of the sky: small robotic cameras, observing since 2004, unfiltered (Burd et al. 2005).
– CRTS: Catalina Survey, 70-cm telescope, observing since 2007, unfiltered (Drake et al. 2009).
– Kepler: Kepler satellite, 95-cm telescope, observed from 2009 to 2018 in special filter (Borucki et al. 2010).
– TESS: TESS satellite, 10-cm diameter, observing since 2018 in special filter (Ricker et al. 2015).
– KWS: Kamogata/Kiso/Kyoto wide-field survey, observing in BVIc filters (Maehara 2014).
– MASCARA: small 17-mm wide-field cameras, observing since 2017, unfiltered (Burggraaff et al. 2018).
– ZTF: the Zwicky Transient Facility, 120-cm telescope, g, and r filters (Masci et al. 2019).
For the derivation of times of mid-eclipse, our automatic fitting procedure (AFP, Zasche et al. 2014b) was used. It uses an LC template and phased LCs at particular time intervals when the phase coverage of both minima is sufficient. Therefore, the cadency of these derived minima highly depends on the particular survey, its cadency, and the precision of individual photometric data points.
For the systems where no previous LC solution exists, we also performed an LC analysis. This was typically based on the best available LC for that particular system, meaning from the source (from the aforementioned list) that provides the best phase coverage as well as the lowest scatter of the individual observations. The individual cases are discussed in more detail below.
For the LC solution, we used PHOEBE, ver 0.32svn (Prša & Zwitter 2005) software. It uses a well-known Wilson & Devinney (1971) algorithm, with its later modifications. We usually assumed fixed coefficients of albedo and gravity brightening, according to the assumed temperature. The mass ratio was kept fixed during the whole analysis due to missing radial velocities. Hence, only the primary temperature was a necessary input for PHOEBE in the beginning. This was taken as a typical effective temperature for a particular spectral type (as given in Table 1), or was assumed according to its photometric index following the tables by Pecaut & Mamajek (2013), with recent updates available online1. The main-sequence assumption was naturally used as a simplest approach due to our having only very limited information about these binaries.
Relevant information for the analyzed systems.
3. The individual systems under analysis
The selected eclipsing binaries in our sample were required to have the following: a range of magnitudes between six and 13 and an orbital period of up to four days; a times-of-minima dataset sufficiently large for a period analysis; an obvious variation in the O − C diagram; and a third-body hypothesis never published before.
Using these criteria, 14 systems were found to be suitable for the present analysis. We focus on individual systems one-by-one in the following subsections. Basic information about these stars is summarized in Table 1, which presents the position on the sky as well as photometric indices and published spectral types, if available.
3.1. V1297 Cas
The first system in our sample is V1297 Cas (=HD 232102 = NSVS 1557555), which is also the one with the latest spectral type classification (K0 according to Cannon 1927). It was quite recently studied photometrically, when Barani et al. (2017) published their BVIc light curves. Their detailed analysis revealed that this W UMa-type contact binary with an orbital period of about 0.27 days has an inclination of about 85° and mass ratio q = 0.55. What was quite surprising is the fact that they also detected quite a large fraction of the third light in their LC solution. There was about 58% in B, while about 49% in Ic, together with a hot spot and asymmetric LC.
According to these findings, the indication of the third component in the system would not be so surprising. Therefore, we collected all available times of minima: from Barani et al. (2017), as well as from other publications. Moreover, we also derived more than 170 additional eclipse timings based on other photometric sources. These were: ASAS-SN, KWS, TESS, NSVS, and SuperWASP. These new minima times greatly accompanied the existing data, clearly revealing the periodic variation. The ETV signal together with the fit is plotted in Fig. 1. The LITE hypothesis was used, resulting in the parameters given in Table 2. The variation with about 2.5-yr periodicity is clearly visible here.
 |
Fig. 1. Period analysis of V1297 Cas. The open circles stand for the secondary, while the filled dots for the primary minima. The larger the symbol, the higher the precision. The solid line represents the predicted third-body variation using the light-time effect hypothesis. |
Final parameters of the LITE orbits, corresponding to the LITE fits plotted in the figures.
From the LITE parameters, we also tried to estimate the properties of the distant body. Mass function of the third body resulted in about 0.3 M⊙. This indicates that the third body should have at least M3, min = 1.32 M⊙ (assuming the coplanar orbits). On the other hand, Barani et al. (2017) estimated the spectral type of the third body as G7. To conclude, we can certainly state that the third component is the dominant body in the system. From the Gaia (Gaia Collaboration 2018) parallax, we can also compute the predicted angular separation of the third component on the sky for a prospective interferometric detection. Here, it resulted in about 36 mas, which is within the capabilities of modern instruments, hence it is realistic to assume that it will be detected soon.
3.2. HD 24105
Another target in our sample was HD 24105, which is in fact one component of a visual double named HEI 9AB (or EPIC 211160717). Its photometric variability with period of about 1.26 days was discovered by the STEREO satellite (Wraight et al. 2011), however no detailed analysis of the binary has been carried out so far.
The two visual components are about 4.4″ distant, hence the photometry should be contaminated with the other component. According to the Washington Double Star catalog (WDS2; Mason et al. 2001), there has been no obvious movement on the visual orbit of the two components over the last 80 years. According to similar parallaxes and proper motions from Gaia DR2 (Gaia Collaboration 2018), the pair is really physical, but with an estimated period of the order of ∼kyr.
By far the best quality of the LC is the one by the Kepler satellite. Therefore, we used this photometry for the LC solution. This fit is presented in Fig. 2. The parameters of the fit are given in Table 3. As one can see, the fit is of very high quality, both components are rather detached, moving in circular orbit around each other. Both minima are about the same depth. The level of the third light resulted in about 20% of the total light, which set some constraints on the third-body parameters.
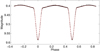 |
Fig. 2. Light curve of HD 24105 based on Kepler data, together with our final fit. |
Parameters of the LC fits.
Our analysis of ETV is plotted in Fig. 3. Parameters of the LITE are also given in Table 2. The apparent variation of its orbital period shows a modulation with period of about 16 yr, which is slightly more than the time interval covered with data nowadays. Therefore, we believe our result is reliable, but should be slightly updated when new observations emerge. The level of the third light is also in accordance with the predicted third-body hypothesis. Our predicted third body should be detected interferometrically on order-of-magnitude closer separations than the component already observed at 4.4″, and this would be a challenging task.
 |
Fig. 3. Period analysis of HD 24105. |
3.3. KU Aur
The next eclipsing binary in our sample is KU Aur (=TYC 2422-20-1). Its photometric variability together with its eclipsing nature and correct orbital period of about 1.3 days were discovered by Popowa (1961). Later, the object was observed and its LC analyzed by Lacy (2004), revealing its semidetached configuration with a rather deep primary, but only shallow secondary, eclipse. Its spectral type was most recently given as F8 by the LAMOST survey (Luo et al. 2015). According to the Gaia catalog, a close (< 1″) visual component also exists.
However, the ETV analysis has not been published so far, despite its extensive collection of eclipse timings ranging over 80 years. Therefore, we collected all available published minima (> 90 datapoints), and also added the new ones from the SuperWASP, ASAS-SN, and KWS surveys (25 eclipse timings). With this dataset, we were able to identify the periodic variation in the O − C diagram, which is plotted in Fig. 4. The LITE variation is clearly evident, having a period of about 27 yr and an amplitude of about 14 min. The putative third body should have its minimal mass of about the same as the secondary component, but it should be undetectable interferometrically. However, the LC analysis published by Lacy (2004) also revealed a small contribution of the third light, which can be identified with our detected component.
 |
Fig. 4. Period analysis of KU Aur. |
3.4. GU CMa
Another eclipsing system included in our analysis is GU CMa (=HD 52721), which has an orbital period of 1.61 days. This is probably the most interesting system, astrophysically speaking, in our sample. Due to its nature as an emission line star of spectral type Be (B2Vne, B3e, from Skiff 2014), its relatively high brightness of about 6.6 mag in V filter, and its location near the equator, this star became a quite frequent target for different investigators using various means. Moreover, it also probably belongs to a star association named CMa R1. All of these yielded more than 200 publications on this target, from which surprisingly only very few were on its eclipsing nature, and none of them were on the ETV analysis. The last and probably the most detailed analysis of its LC was that one by Shokry et al. (2018). They concluded that the system is a semidetached one, with a secondary evolved from the main sequence.
We collected all available published times of eclipses from the literature (12 records), to which we also added nine from our new observations, and, finally, 108 were derived from various photometric surveys (HIPPARCOS, ASAS, ASAS-SN, KWS, TESS, and MASCARA). With this huge dataset, we carried out an analysis, which is plotted in Fig. 5. The ETV modulation has a period of about 19.7 years. As one can see, the last period of the outer orbit is well covered, but the older observations are missing. Our resulting parameters (see Table 2) should hence be taken as preliminary. However, what can clearly be seen even with our data is a rapid period change near its periastron passage caused by very high eccentricity. Such a result is noteworthy, because such a high eccentricity is only known for several systems as it stands.
 |
Fig. 5. Period analysis of GU CMa. |
From the LITE parameters, we can roughly estimate the angular distance of the predicted third component. This resulted in about 40 mas, which should be detectable with modern techniques. GU CMa is also known as a visual double, but its detected companion at a separation of about 0.6″ is definitely another member of this multiple system.
3.5. GH Mon
The system GH Mon (=GSC 04818-02919) was discovered as a variable by Wachmann (1968). Its orbital period is of about 0.7 days and it is one of the only seldom-investigated stars. No detailed analysis of this system has been published so far: only several eclipse times. Its spectral type was classified as F6 from LAMOST by Luo et al. (2015). Again, from the Gaia catalog, it has a close (≈2″) visual component.
Therefore, we performed an LC analysis using the PHOEBE code and the ASAS-SN data, which seemed to be of the best quality among the other photometric surveys for this star. This solution is presented in Fig. 6, while its parameters are given in Table 3. The orbit of eclipsing components is circular, with the secondary component being slightly evolved from the main sequence, but still in a detached configuration.
 |
Fig. 6. Light curve of GH Mon based on ASAS-SN data. |
For the ETV analysis, we used all archival data together with our new derived ones. The final O − C diagram with its periodicity of about 64 yr is plotted in Fig. 7, and the parameters of the fit are given in Table 2. Obviously, the outer period is too long, and the coverage is still rather poor. However, the last minima times since 2005 show clear evidence of the period change. What is interesting is the fact that even after subtraction of this LITE fit, there also remains a small additional variation with smaller amplitude and shorter pseudo-period on the residuals. However, any statement about a possible fourth body in the system would still be rather premature.
 |
Fig. 7. Period analysis of GH Mon. |
3.6. AZ Vel
The star named AZ Vel has also been rather neglected in binary star research. The discovery was made by Guthnick & Schneller (1939), who also gave its proper orbital period of about 0.776 days and an Algol-type LC classification. However, since then no detailed analysis had been carried out until our recent paper on AZ Vel, which was based on the photometric data from the INTEGRAL/OMC (Zasche 2010). The result was that the system is a detached one, but its spectral type and primary temperature is still rather uncertain (the system’s spectrum has not yet been obtained in any publication).
We collected all available times of eclipses and enlarged the dataset with the new ones from the OMC, ASAS, and ASAS-SN surveys. On this collection of more than 60 minima covering 20 years, we performed an ETV analysis. The results can be seen in Fig. 8 and clearly show the ETV variation with a periodicity of 5.65 yr. AZ Vel seems to be the only system where quadratic ephemerides were also used besides the LITE hypothesis. Its interpretation is still an open question due to the fact that we are dealing with a detached configuration of the eclipsing double.
 |
Fig. 8. Period analysis of AZ Vel, showing slow period increase. |
3.7. DI Lyn
The system named DI Lyn (or also A Hya = HD 82780) is an Algol-type eclipsing binary discovered originally on the HIPPARCOS data (Perryman et al. 1997). Later, Wolf & Caffey (1998) analyzed the BVRI LCs together with the radial velocities resulting in a set of physical parameters of both components of F2V spectral type. Moreover, additional more distant components also exist in the system, making the whole system at least a quintuple one. Besides the eclipsing 1.7-day component A, component B also exists, with a 28-day period detected spectroscopically. Quite recently, Tokovinin et al. (2019) published the solution of the visual orbit of the Aa-Ab subsystem, resulting in an orbital period of 50.34 yr. The last additional component at about a 25″ distance is also a physical one according to its parallax and proper motion. We invite the reader to consult the paper by Tokovinin et al. (2006) summarizing the whole architecture of the system.
Due to the fact that the LC had already been analyzed, we only collected all available times of eclipses for the proper ETV analysis. Apart from our observations of eclipses, we also used the TESS data to derive new eclipse times. Therefore, we analyzed the data spanning over 12 years. With these data, we carried out an ETV analysis on DI Lyn. Our analysis showed that the period of an ETV modulation is of about 22 yr, and the rest of the parameters are given in Table 2, while the plot with the LITE fit is given in Fig. 9.
 |
Fig. 9. Period analysis of DI Lyn, compared with orbit from Tokovinin et al. (2019). |
Due to the fact that the orbit of the Aa-Ab pair had already been analyzed, we also tried to identify the ETV detected in our data with this 50.34-yr orbit. Such a comparison is also plotted in Fig. 9 as a blue dashed curve, where we fixed the orbital parameters given by Tokovinin et al. (2019) and computed only the ephemerides of the 1.7-day eclipsing binary and the LITE amplitude. The periastron passage of both these solutions seem to be close to each other, indicating that this ETV variation really belongs to the Aa-Ab orbit. However, fixing the orbital parameters from Tokovinin et al. (2019) to our dataset, we get about a 46% worse sum of square residuals than with all of our parameters that were released freely and converged into the solution presented in Table 2. Such a discrepancy should be studied in upcoming years: observing the target year-by-year and following the ETV curve.
3.8. DK Her
The eclipsing system DK Her (or HD 155700), with an orbital period of about 1.9 days, shows very different depths of both eclipses. Despite the fact that its eclipsing nature has been known for many decades, an analysis of the star is still missing. Neither LC analysis nor period analysis can be found in published papers concerning the star. The only piece of information is a spectrum from LAMOST (Luo et al. 2015), where the authors gave the type of A1IV. DK Her was also found to be a visual binary. The two components separated by about 10″ on the sky, are physical according to Gaia (similar parallax and proper motion).
Therefore, we performed an LC as well as an eclipse timing analysis. To study the LC, we used the data from the ASAS-SN survey, and particularly the g-band filter. The result of our analysis is plotted in Fig. 10. As one can see, the luminosity ratio is very extreme here, which is also seen at the shape of the LC, with an almost invisible secondary minimum.
 |
Fig. 10. Light curve of DK Her based on ASAS-SN data. |
The analysis of eclipse times collected over the last century is plotted in Fig. 11. Due to very deep primary eclipses, we also believe that the old visual and photographic minima times are reliable enough to be used in the ETV analysis. The parameters of our fit are given in Table 2, showing that this is the system with the longest orbital period in our sample of stars (115 yr). However, despite the period of a putative third body being long, it is almost covered with data nowadays.
 |
Fig. 11. Period analysis of DK Her. |
3.9. GQ Dra
The system named GQ Dra (=HD 158260 = HIP 85277) is a variable of the β Lyrae type with an orbital period of 0.766 days, and it was discovered from the HIPPARCOS data. The first study on this star was the one of Atay et al. (2000), but this gave no detailed analysis of its LC. A very detailed analysis was published later by Qian et al. (2015), revealing that the star is a classical semidetached system with secondary filling its respective Roche lobe. The authors speculated about a possible mass transfer between the components due to their period analysis of eclipse times. Its spectral type was derived as A3 (Heckmann 1975), which is quite typical for this type of semidetached stars. The LAMOST survey published its type as A6IV (Luo et al. 2015). Moreover, the system GQ Dra is also known as a visual binary, with both components 4″ away from each other, and no mutual orbital motion can be seen during the last century (Mason et al. 2001). Also, no astrometric acceleration can be seen in the proper motion data (Brandt 2018). However, such an effect caused by our LITE orbit depends on the masses and orientation of the orbit toward the observer.
Because of the fact that the LC was analyzed in detail by Qian et al. (2015), we decided only to perform the ETV analysis of the minima timings. Most of these data were taken from the already published minima compilations. We also added new eclipse times derived from the HIPPARCOS, NSVS, and SWASP photometry. Besides that, several were added from our dedicated ground-based observations. This dataset covers a time span of 30 years, and the result of our analysis is plotted in Fig. 12. The parameters are given in Table 2, with the amplitude of LITE only being about 9.5 min, and the period about 27.4 yr. The rapid period change close to the year 2020 is evident now, indicating rather high eccentricity of the orbit. All of these findings should be confirmed later in the upcoming period of the outer orbit.
 |
Fig. 12. Period analysis of GQ Dra. |
3.10. V624 Her
The 3.89-d eclipsing system V624 Her (=HD 161321 = HIP 86809) is the brightest star in our sample. Due to its magnitude, it has been studied quite often in the past. Besides that, it was also classified as a metallic star (Popper 1984), with the primary component even having the largest radius among the known Am stars with known properties. Popper (1984) derived the basic physical parameters of the system, as well as both components based on adequately good photometry and spectroscopy. Moreover, the star is also known as a visual double, but with both components rather distant on the sky (≈40″). According to the Gaia values it is probably optical.
Owing to the already published solution of LC and RV curves by Popper (1984), we decided only to carry out a detailed ETV analysis of V624 Her. We collected all available times of eclipses from the literature, and we added several more from the ASAS and MASCARA surveys, and the satellite HIPPARCOS. This dataset covers more than 50 years of eclipse time monitoring. The result of our fitting is plotted in Fig. 13, with a periodicity of about 42 years, while the parameters are given in Table 2. The distant visual component is definitely different to the one detected with LITE. Such a closer component (with predicted angular separation of about 140 mas; see Table 2) could possibly be detected via interferometry due to the high level of brightness of the star (eclipsing the binary itself), however the problematic issue would be the luminosity ratio (low brightness of the third component).
 |
Fig. 13. Period analysis of V624 Her. |
3.11. V1134 Her
The star V1134 Her (=GSC 01031-01766) is probably the least studied system in our compilation. It is a contact-eclipsing binary with an orbital period of about 0.6 days, however no detailed analysis about the star has been published so far. Concerning its spectral type, it is rather uncertain. No spectral observation exists, hence we can only estimate its type from the photometric indices. Some (B − V) indices from APAS Henden et al. (2015), or UCAC4 Zacharias et al. (2013) range from 0.59 to 0.61 mag, yielding spectral types of about G0-1V. On the other hand, the (J − H) values from 2MASS (Skrutskie et al. 2006) would better fit spectral types of about F7V. Therefore, we decided to use the temperature estimation based on the Gaia DR2 by Bai et al. (2019), which gives Teff = 6651 K for the LC analysis. The photometric analysis was carried out on the data provided by ASAS-SN (Shappee et al. 2014) and its V filter. For the results of the LC fitting, see Table 3 and the final fit presented in Fig. 14. As one can see, the third component significantly contributes to the total luminosity of the whole system.
 |
Fig. 14. Light curve of V1134 Her based on ASAS-SN data. |
The ETV analysis of eclipse times is presented in Fig. 15. Most of these data were derived from the surveys ASAS and ASAS-SN, and several new ones also from our dedicated observations. The period variation caused by LITE is rather fast, having a period of only about 6.9 years. Its coverage with current data is sufficient for such an analysis, but new observations in the coming years would be of great benefit to confirm our hypothesis with higher conclusiveness.
 |
Fig. 15. Period analysis of V1134 Her. |
3.12. KIC 6187893
Only one system from our sample was discovered with Kepler satellite: KIC 6187893 (=TYC 3128-1653-1). The star shows a rather detached LC with an orbital period of about 0.8 days. Its spectral type was derived as F7 from the LAMOST survey data (Luo et al. 2015), but its effective temperature was estimated as 5854 K (Zhang et al. 2019).
Therefore, we fixed this temperature as the effective temperature of the primary component and carried out the LC analysis. We decided to show (Fig. 16) our fit on the best-quality data from Kepler compared with the other data from different photometric surveys like SWASP, ASAS-sn, or TESS. Not only are there different scatters, but also different eclipse depth is clearly seen in these plots. This effect is caused by the varying angular resolution (pixel size) of the particular survey telescope. The results of our LC fitting are given in Table 3 (results given for the most precise LC fit on the Kepler data).
 |
Fig. 16. Light curves of KIC 6187893 showing the comparison of quality of different data sources. |
The analysis of minima times is plotted in Fig. 17. The periodic signal is clearly visible there, with a periodicity of about 11 yr. The data from the Kepler satellite were the richest among those available, as well as being of the highest quality. However, the other photometric observations nicely completed the whole third-body period, which is now fully covered with data. From the very large fraction of the third light from the LC solution, it appears that the third-body orbit must be very inclined to produce such a large light contribution with such a low LITE amplitude.
 |
Fig. 17. Period analysis of KIC 6187893. |
3.13. V1928 Aql
The next system under our analysis is V1928 Aql (=HD 180848 = TYC 1042-1657-1), which had never been studied before as an eclipsing binary, but which has already been known as a visual double star for a long time. Its two components are about 7″ distant from each other. Its photometric variability with a period of about 0.52 days was discovered by our team (Zasche et al. 2017), and since then has been quite frequently observed. Nassau & Blanco (1957) included the star on their list of carbon stars in the Milky Way, however no other more recent information about this concern has since been published. The classification of the system is currently given as A3 (Heckmann 1975).
For the LC analysis, we used the ASAS photometry in V filter, which seems to be of the best quality due to the relatively high brightness of the star. The result of our fitting is plotted in Fig. 18. The system is a contact one with very similar components, and the third light value is very small (see Table 3 with the parameters). Such a finding should be confronted with the results from our ETV analysis. These results are given in Table 2, while the plot is given in Fig. 19. V1928 Aql shows the lowest amplitude of LITE among the stars in our sample, and it has an ETV period of about 4.14 years. This is the reason why the plot given in Fig. 19 seems to be rather scattered. However, the scatter of the older ASAS data from between 2002 and 2010 is caused by our method of minima derivation, by which the whole season of observations is used to construct the seasonal LC subsequently analyzed. Even during one season, there is an apparent period change blurring the shape of the LC.
 |
Fig. 18. Light curves of V1928 Aql based on ASAS data. |
 |
Fig. 19. Period analysis of V1928 Aql. |
3.14. V2486 Cyg
The last system in our list of analyzed binaries is V2486 Cyg (=GSC 03173-01826 = BD+39 4506). It was discovered as a variable by Strohmeier (1962), but since then no analysis of the system has been published except for the times of eclipses. It is an Algol-type binary with an orbital period of about 1.27 days. It is also known as a visual double pair, but with no obvious mutual motion of the two components, which are about 20″ from each other. However, due to quite different parallaxes and proper motions of both components (Gaia Collaboration 2018), their physical relationship is rather questionable.
Due to missing LC analysis, we decided to include our solution in this study. Its spectral type had been classified as either A2 (Heckmann 1975) or A0 (Götz & Wenzel 1964). Therefore, we fixed its primary temperature as 8840 K. The final fit of our own data obtained in standard Johnson-Cousins BVRI filters is plotted in Fig. 20, while the parameters are given in Table 3. In the table, the fractional luminosities are given for the V filter. These values significantly differ between different filters: in the blue region, the primary component is almost as luminous as the tertiary (45%:52%), while in the red band the third component significantly dominates (35%:56%). From these numbers, it can clearly be seen that the putative third component is much more red than the primary, and it probably also dominates the luminosity of the whole system.
 |
Fig. 20. Differential BVRI light curves of V2486 Cyg. |
Such a finding is well supported by our ETV analysis. From the available eclipse times, it can clearly be seen (Fig. 21) that the period variation with a periodicity of about 8.4 yr is undoubtable. From this solution, we derive a minimal third-body mass of at least 2.3 M⊙, which is more than that of the primary component. Such a result is in good agreement with the high third light value from the LC solution.
 |
Fig. 21. Period analysis of V2486 Cyg. |
Moreover, during our photometric monitoring of the system V2486 Cyg, we discovered that the close-by target TYC 3173-01309-1 is also a variable. Its type is W UMa, and its period is of about 0.3952 days.
4. Conclusion
We carried out a thorough analysis of period variations for 14 new eclipsing systems showing apparent period changes. These changes can be attributed to hidden distant components in these systems, making them even more interesting multiples. For cases like DI Lyn (which was up to now classified as a quintuple) such a finding is of high importance when studying its long-term stability.
The powerful method of ETV analysis still brings some benefits to modern stellar astrophysics. It is so simple that even non-professional astronomers (like the co-authors of the present study) can significantly contribute with their small or moderate-sized telescopes. The method can also detect the third-body periods that are otherwise barely detectable. The mutliple-system statistics of outer periods still have two observational peaks: in shorter periods, due to spectroscopic triples, and the longer-period ones are detected via interferometry or direct imaging (see e.g., Tokovinin 2008). The ETV analysis of eclipsing binaries can serve as an effective method for bridging the gap between these two peaks. However, for a final confirmation of these suspected triples, one needs precise spectroscopy in order to detect them directly in the spectra, or at least to reveal a change in the systemic velocity of the binary itself.
Acknowledgments
This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. We would also like to thank the Pierre Auger Collaboration for the use of its facilities. The operation of the robotic telescope FRAM is supported by the grant of the Ministry of Education of the Czech Republic LM2018102. The data calibration and analysis related to the FRAM telescope is supported by the Ministry of Education of the Czech Republic MSMT-CR LTT18004 and MSMT/EU funds CZ.02.1.01/0.0/0.0/16_013/0001402. We also thank the ASAS, SWASP, CRTS, TESS, MASCARA, ZTF, and Kepler teams for making all of the observations easily available. This paper makes use of data from the DR1 of the WASP data (Butters et al. 2010) provided by the WASP consortium, and the computing and storage facilities at the CERIT Scientific Cloud, reg. no. CZ.1.05/3.2.00/08.0144, which is operated by Masaryk University, Czech Republic. The CSS survey is funded by the National Aeronautics and Space Administration under Grant No. NNG05GF22G issued through the Science Mission Directorate Near-Earth Objects Observations Program. The CRTS survey is supported by the U.S. National Science Foundation under Grants AST-0909182 and AST-1313422. Work is based on the data from the OMC Archive at CAB (INTA-CSIC), pre-processed by ISDC. We would also like to thank Mr. Peter Nosáľ for using his photometric data of V1134 Her. This research has made use of the SIMBAD and VIZIER databases, operated at CDS, Strasbourg, France and of NASA Astrophysics Data System Bibliographic Services.
References
- Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Atay, E., Alis, S., Keskin, M. M., et al. 2000, IBVS, 4988, 1 [Google Scholar]
- Bai, Y., Liu, J., Bai, Z., et al. 2019, AJ, 158, 93 [CrossRef] [Google Scholar]
- Barani, C., Acerbi, F., & Martignoni, M. 2017, New A, 57, 37 [CrossRef] [Google Scholar]
- Borkovits, T., Érdi, B., Forgács-Dajka, E., et al. 2003, A&A, 398, 1091 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkovits, T., Csizmadia, S., Forgács-Dajka, E., et al. 2011, A&A, 528, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkovits, T., Rappaport, S., Hajdu, T., et al. 2015, MNRAS, 448, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brandt, T. D. 2018, ApJS, 239, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Burd, A., Cwiok, M., Czyrkowski, H., et al. 2005, New A, 10, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Burggraaff, O., Talens, G. J. J., Spronck, J., et al. 2018, A&A, 617, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butters, O. W., West, R. G., Anderson, D. R., et al. 2010, A&A, 520, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cannon, A. J. 1927, Ann. Harvard College Observ., 100, 33 [Google Scholar]
- Czekala, I., Chiang, E., Andrews, S. M., et al. 2019, ApJ, 883, 22 [CrossRef] [Google Scholar]
- Drake, A. J., Djorgovski, S. G., Mahabal, A., et al. 2009, ApJ, 696, 870 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Eggleton, P. P., & Kiseleva-Eggleton, L. 2001, ApJ, 562, 1012 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Götz, Von W., & Wenzel, W. 1964, MitVS, 2, 85 [Google Scholar]
- Guetter, H. H. 1968, PASP, 80, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Guthnick, P., & Schneller, H. 1939, AN, 268, 165 [Google Scholar]
- Heckmann, O. 1975, AGK 3. Star catalogue of positions and proper motions north of–2.5 deg. declination, ed. W. Dieckvoss (Hamburg-Bergedorf: Hamburger Sternwarte) [Google Scholar]
- Henden, A. A., Levine, S., Terrell, D., et al. 2015, American Astronomical Society Meeting Abstracts #225 [Google Scholar]
- Irwin, J. B. 1959, AJ, 64, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S., Shappee, B. J., Stanek, K. Z., et al. 2017, PASP, 129, 104502 [Google Scholar]
- Lacy, C. H. S. 2004, IBVS, 5499, 1 [Google Scholar]
- Luo, A.-L., Zhao, Y.-H., Zhao, G., et al. 2015, Res. Astron. Astrophys., 15, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Maehara, H. 2014, J. Space Sci. Inf. Jpn., 3, 119 [Google Scholar]
- Mas-Hesse, J. M., Giménez, A., Culhane, J. L., et al. 2003, A&A, 411, L261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masci, F. J., Laher, R. R., Rusholme, B., et al. 2019, PASP, 131, 018003 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., et al. 2001, AJ, 122, 3466 [Google Scholar]
- Mayer, P. 1990, BAICz, 41, 231 [Google Scholar]
- Nassau, J. J., & Blanco, V. M. 1957, ApJ, 125, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gallenne, A., et al. 2019, Nature, 567, 200 [Google Scholar]
- Pickles, A., & Depagne, É. 2010, PASP, 122, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Pojmanski, G. 2002, AcA, 52, 397 [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Popowa, M. 1961, AN, 286, 81 [Google Scholar]
- Popper, D. M. 1984, AJ, 89, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S.-B., Zhou, X., Zhu, L.-Y., et al. 2015, AJ, 150, 193 [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Roeser, S., & Bastian, U. 1988, A&AS, 74, 449 [NASA ADS] [Google Scholar]
- Shappee, B. J., Prieto, J. L., Grupe, D., et al. 2014, ApJ, 788, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Shokry, A., Saad, S. M., Hamdy, M. A., et al. 2018, New A, 59, 8 [CrossRef] [Google Scholar]
- Skiff, B. A. 2014, VizieR Online Data Catalog, B/mk [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2012, Orbital Couples: Pas de Deux in the Solar System and the Milky Way, 51 [Google Scholar]
- Sterken, C. 2005, The Light-time Effect in Astrophysics: Causes and Cures of the O-C Diagram, ASPC, 335, 3 [Google Scholar]
- Strohmeier, W. 1962, IBVS, 17, 1 [Google Scholar]
- Tokovinin, A. 2008, MNRAS, 389, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A., Thomas, S., Sterzik, M., et al. 2006, A&A, 450, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tokovinin, A., Everett, M. E., Horch, E. P., et al. 2019, AJ, 158, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&A Rev., 18, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wachmann, A. A. 1968, Astron. Abh. Hamburger Sternwarte, 7, 381 [Google Scholar]
- Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, G. W., & Caffey, J. F. 1998, IBVS, 4649, 1 [Google Scholar]
- Woźniak, P. R., Vestrand, W. T., Akerlof, C. W., et al. 2004, AJ, 127, 2436 [Google Scholar]
- Wraight, K. T., White, G. J., Bewsher, D., et al. 2011, MNRAS, 416, 2477 [NASA ADS] [CrossRef] [Google Scholar]
- Young, R. K. 1945, Pub. David Dunlap Observ., 1, 311 [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zasche, P. 2010, New A, 15, 150 [CrossRef] [Google Scholar]
- Zasche, P., Wolf, M., Uhlař, R., et al. 2014a, AJ, 147, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Zasche, P., Wolf, M., Vraštil, J., et al. 2014b, A&A, 572, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zasche, P., Uhlař, R., Svoboda, P., et al. 2017, IBVS, 6204, 1 [Google Scholar]
- Zejda, M., Skýba, O., Krajčovič, M., Gajdoš, P., & Fedurco, M. 2019, CoSka, 49, 132 [Google Scholar]
- Zhang, J., Qian, S.-B., Wu, Y., et al. 2019, ApJS, 244, 43 [CrossRef] [Google Scholar]
All Tables
Final parameters of the LITE orbits, corresponding to the LITE fits plotted in the figures.
All Figures
 |
Fig. 1. Period analysis of V1297 Cas. The open circles stand for the secondary, while the filled dots for the primary minima. The larger the symbol, the higher the precision. The solid line represents the predicted third-body variation using the light-time effect hypothesis. |
| In the text | |
 |
Fig. 2. Light curve of HD 24105 based on Kepler data, together with our final fit. |
| In the text | |
 |
Fig. 3. Period analysis of HD 24105. |
| In the text | |
 |
Fig. 4. Period analysis of KU Aur. |
| In the text | |
 |
Fig. 5. Period analysis of GU CMa. |
| In the text | |
 |
Fig. 6. Light curve of GH Mon based on ASAS-SN data. |
| In the text | |
 |
Fig. 7. Period analysis of GH Mon. |
| In the text | |
 |
Fig. 8. Period analysis of AZ Vel, showing slow period increase. |
| In the text | |
 |
Fig. 9. Period analysis of DI Lyn, compared with orbit from Tokovinin et al. (2019). |
| In the text | |
 |
Fig. 10. Light curve of DK Her based on ASAS-SN data. |
| In the text | |
 |
Fig. 11. Period analysis of DK Her. |
| In the text | |
 |
Fig. 12. Period analysis of GQ Dra. |
| In the text | |
 |
Fig. 13. Period analysis of V624 Her. |
| In the text | |
 |
Fig. 14. Light curve of V1134 Her based on ASAS-SN data. |
| In the text | |
 |
Fig. 15. Period analysis of V1134 Her. |
| In the text | |
 |
Fig. 16. Light curves of KIC 6187893 showing the comparison of quality of different data sources. |
| In the text | |
 |
Fig. 17. Period analysis of KIC 6187893. |
| In the text | |
 |
Fig. 18. Light curves of V1928 Aql based on ASAS data. |
| In the text | |
 |
Fig. 19. Period analysis of V1928 Aql. |
| In the text | |
 |
Fig. 20. Differential BVRI light curves of V2486 Cyg. |
| In the text | |
 |
Fig. 21. Period analysis of V2486 Cyg. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


