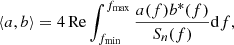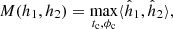| Issue |
A&A
Volume 643, November 2020
|
|
|---|---|---|
| Article Number | A167 | |
| Number of page(s) | 11 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202038730 | |
| Published online | 20 November 2020 | |
LENSINGGW: a PYTHON package for lensing of gravitational waves
1
Dipartimento di Fisica “Enrico Fermi”, Università di Pisa, Pisa 56127, Italy
2
INFN Sezione di Pisa, Pisa 56127, Italy
e-mail: giulia.pagano@pi.infn.it
3
Nikhef – National Institute for Subatomic Physics, Science Park, 1098 XG Amsterdam, The Netherlands
e-mail: o.hannuksela@nikhef.nl
4
Department of Physics, Utrecht University, Princetonplein 1, 3584 CC Utrecht, The Netherlands
5
Department of Physics, The Chinese University of Hong Kong, Shatin, NT, Hong Kong
e-mail: tgfli@cuhk.edu.hk
Received:
24
June
2020
Accepted:
22
September
2020
Advanced LIGO and Advanced Virgo might be able to observe the first lensed gravitational waves in the coming years. With the addition of the KAGRA and LIGO India detectors to the detector network and with the future construction of the Einstein Telescope we might be able to observe hundreds of lensed events. Ground-based gravitational-wave detectors can resolve arrival-time differences on the order of the inverse of the observed frequencies. The LIGO and Virgo frequency band spans from a few Hz to a few kHz, therefore the typical time resolution of current interferometers is on the order of milliseconds. When microlenses are embedded in galaxies or galaxy clusters, lensing can become more prominent and result in observable time delays at LIGO and Virgo frequencies. Therefore, gravitational waves might offer an exciting alternative probe of microlensing. However, only a few lensing configurations have currently been worked out in the context of gravitational-wave lensing. In this paper, we present LENSINGGW, a PYTHON package designed to handle both strong lensing and microlensing of compact binaries and the related gravitational-wave signals in the geometrical optics limit. This synergy paves the way for systematic parameter space investigations and for the detection of arbitrary lens configurations and compact sources. Here we focus on the LIGO and Virgo frequencies. We demonstrate the working mechanism of LENSINGGW and its use in studying microlenses that are embedded in galaxies.
Key words: gravitational lensing: strong / gravitational lensing: micro / gravitational waves / methods: numerical
© ESO 2020
1. Introduction
The Advanced LIGO (Aasi et al. 2015; Abbott et al. 2016a) and Advanced Virgo (Acernese et al. 2015) gravitational-wave detectors observed ten binary black hole mergers during observation runs O1 and O2 (Abbott et al. 2019a) and dozens of such mergers during observation campaign O3 (LIGO Scientific Collaboration and Virgo Collaboration 2019). With the prospect that the additional detectors KAGRA and LIGO India will join the global gravitational-wave (GW) network (Somiya 2012; Aso et al. 2013; Akutsu et al. 2018; Iyer et al. 2011), with the recently approved A+ detector upgrade (Abbott et al. 2018a) and with the future construction of the Einstein Telescope (Maggiore et al. 2020), this number is expected to eventually reach several hundred detections (Abbott et al. 2016b, 2019a).
As the number of detections grows, several novel avenues will open in the field of GWs (Abbott et al. 2018b). One example of such an avenue is gravitationally lensed GWs, the first of which may be possible to observe in the next few years (Ng et al. 2018; Li et al. 2018; Oguri 2018). It has been suggested that lensed GWs might offer interesting applications in fundamental physics, astrophysics, and cosmology (Sereno et al. 2011; Liao et al. 2017; Collett & Bacon 2017; Fan et al. 2017; Baker & Trodden 2017; Lai et al. 2018; Dai et al. 2018; Mukherjee et al. 2020; Oguri 2019; Pang et al. 2020; Jung & Shin 2019; Cao et al. 2019; Hou et al. 2020; Sun & Fan 2019; Hannuksela et al. 2020). The first searches for GW lensing signatures in the LIGO and Virgo data were carried out recently (Hannuksela et al. 2020; Li et al. 2019; McIsaac et al. 2020; Singer et al. 2019; Pang et al. 2020), but failed to find clear evidence of lensing, although early detections were discussed (Broadhurst et al. 2018, 2019).
When gravitational waves propagate near massive astrophysical objects, their trajectories will curve, resulting in gravitational lensing and multiple images. As we observe the waves from each multiple image, their amplitudes will have changed because of the focusing by lensing. They will arrive at different times because they have traveled along different trajectories at the same speed (Ohanian 1974; Bliokh & Minakov 1975; Bontz & Haugan 1981; Thorne 1983; Deguchi & Watson 1986; Nakamura 1998; Takahashi & Nakamura 2003; Oguri 2018; Broadhurst et al. 2018, 2019; Contigiani 2020).
However, unlike in the lensing of electromagnetic waves, where incoming photons are classified as lensed by their angular direction, LIGO and Virgo require entirely different and novel methods to classify GWs as lensed: by statistically distinguishing them as identical events using GW templates and Bayesian analysis (Haris et al. 2018; Hannuksela et al. 2019; Li et al. 2019; McIsaac et al. 2020). In contrast to being limited by the angular resolution of optical detectors, the precision at which we will observe these waves in the interferometers is limited by the millisecond time resolution of LIGO and Virgo.
In contrast to the images produced by galaxies and galaxy clusters (strong lensing), the lensing effects that are induced by masses of roughly 10−6 ≲ M/M⊙ ≲ 106 are referred to as microlensing (Schneider et al. 2006). We assume that microlenses lie in the path of strongly lensed waves. In this case, the strong lens can enhance the microlensing effect (Diego et al. 2018, 2019), which results in beating patterns that might allow us to infer the lensing object properties, such as its mass (see references Lai et al. 2018; Christian et al. 2018 for applications to intermediate-mass and stellar-mass black hole and star lenses). Diego et al. (2019) have recently demonstrated that strongly lensed GWs from extragalactic sources are more likely to be microlensed because the effective Einstein radius of the microlenses grows in size because of the strongly lensing galaxy.
The inference of such signals relies on our ability to correctly identify the lensed GW. To model these lensed GWs, we need to be able to predict the properties of lensed images formed by generic matter distributions.
When microlenses are embedded in a macromodel (a galaxy or a galaxy cluster), microimages separated by scales as small as microarcseconds can form (Diego et al. 2019). In order to model this interaction, we must consider strong lensing and microlensing together (Diego et al. 2019). To model the lensed GW accurately, we have to identify both the strongly lensed images that are formed by the galaxy or galaxy cluster (whose typical separations are ≲arcsec Schneider et al. 2006; Collett 2015) and the microimages that are formed by the microlenses.
Software packages that address the lensing of GWs must then be able to predict images with diverse separations even when no a priori knowledge on their range is available. However, existing software programs for gravitational lensing focus on light lensing rather than on GW lensing (Birrer & Amara 2018; Keeton 2011). As a consequence, they do not model lensed gravitational waveforms and target strongly lensed images as opposed to microimages.
Specifically, this implies that software programs for the lensing of light are not optimized to simultaneously resolve the scales of the strongly lensed image separations and of the microimage separations. However, the identification of both types of images is required to accurately model the lensed signal in the context of GWs. A dedicated approach that targets both the strong and microlensing scales is therefore required in case of gravitational-wave gravitational lensing.
In this paper, we present LENSINGGW, a software package for modeling lensed GW signals of compact binaries from arbitrary lens models. LENSINGGW has been designed to simultaneously handle the scales of strong lensing and of microlensing. Thus, it can determine the strongly lensed images produced by galaxies or galaxy clusters and microimages induced by microlenses, without prior assumptions on the image structure, while retaining fast performance. The code is designed to provide GW astronomers and data analysts with a user-friendly tool for the analysis of lensed GW signals. In addition to supplying the ordinary output of lensing codes, such as image positions, magnifications, and time delays, LENSINGGW also simulates lensed and unlensed GWs and their associated detector strain for generic lensing configurations, including multicomponent strong lenses with an arbitrary number of microlenses.
These simulations are required to assess the detectability of lensed events through mismatch and signal-to-noise ratio (S/N) calculations (Allen et al. 2012) and to investigate the parameter space in which microlensing becomes relevant. Thus, this work is a step toward establishing a complete lensing framework for GWs, an effort which has seen a recent push from both astronomy and GW modeling sides (Smith et al. 2019, 2018; Robertson et al. 2020; Diego et al. 2019; Cao et al. 2014; Dai & Venumadhav 2017; Dai et al. 2017, 2018; Lai et al. 2018; Christian et al. 2018; Haris et al. 2018; Hannuksela et al. 2019; Mehta et al., in prep.).
We review the theoretical framework for lensing in Sect. 2 and present our software in Sect. 3. Results validating our code for simple test cases are illustrated in Sect. 4. The application of LENSINGGW to scenarios of astrophysical interest is demonstrated in Sect. 5, where we present an example mismatch computation and a more realistic lensing system with microlenses embedded within a galaxy. We conclude in Sect. 6.
2. Lensing of gravitational waves
Lensing modifications to the GW waveform can be solved in the wave optics limit from the Einstein field equations, when the gravitational potential U is too weak to change the polarization of the wave (U ≪ 1) and when the gravitational wave can be separated from the background space-time (Nakamura 1998; Takahashi & Nakamura 2003). However, when the wavelength of the gravitational wave is much larger than the object size and the wave travels near the object, the wave may no longer be separated from the background and wave scattering occurs (see, e.g., Takahashi et al. 2005).
When the distances between the observer, lens, and source are large, the thin-lens approximation holds, and two quantities describe the gravitational lens: its relative position to the source η, and its two-dimensional projected mass distribution Σ(ξ) ≡ ∫ρ(ξ, z)dz, where ρ(ξ, z) is the density of the lens at a given position (ξ, z) on the image plane. The source displacement η and image position ξ can be related to the angular coordinates by
where DS, DL, and DLS are the angular diameter distances from the observer to the source, to the lens, and from the lens to the source, respectively. An illustration of the lens configuration is given in Fig. 1.
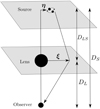 |
Fig. 1. Gravitational lens configuration in the thin-lens approximation. The lensing configuration is described by the source displacement from the line of sight η, the angular diameter distance from the observer to the source DS, to the lens DL, from lens to the source DLS, and by the relative position of the image in the image plane ξ. |
Here we consider the geometrical optics approximation, which is valid when the GW wavelength is smaller than the characteristic size of the space-time curvature (Takahashi & Nakamura 2003). Therefore, we limit ourselves to microlenses that are larger than about 100 M⊙. Small wave-optics corrections may occur for these scenarios in the low-mass limit (see Sect. 3.2 for discussion on the applicability of this approximation), however.
In the geometrical optics limit, the lens focuses the original GW from several paths towards an observer, forming multiple images. The image positions and time-delays can be solved from the lens equation
where ∇θ is the two-dimensional nabla operator with respect to θ, and ψ(θ) is the two-dimensional deflection potential. The latter can generally be solved from the two-dimensional Poisson equation,
where κ = Σ(DLθ)/Σcr, Σ is the surface mass density of the lens and Σcr = (c2/(4πG))DS/(DLDLS). Solving Eq. (2) yields N different solutions, which give the image positions {θj}.
Given the image positions {θj}, it is possible to retrieve the individual magnifications {μj} and time delays {td, j} for each image by direct substitution (Diego et al. 2019):
The lensing effect induced on the waveform is expressed by the magnification function,
and the lensed waveform is then
that is, a combination of N different signals with magnifications μj, relative time delays td, j, and overall phase shifts πnj. Here, λ and λlens indicate the sets of parameters that describe the unlensed GW and the lens, whereas the Morse indices nj are nj = 0, 1/2, 1 when θj is a minimum, saddle, and maximum of the time delay td(θ, β), respectively.
3. LENSINGGW
In order to determine the lensed images of a source, we have to solve the lens equation (Eq. (2)). That is, a system of two nonlinear, algebraic, coupled equations of two variables. In addition, the gravitational potential ψ may not be analytic. No procedure is guaranteed to find a complete set of solutions unless the initial values given to the algorithm are close enough to the actual images (Press et al. 2007). For these reasons, gravitational-lensing software packages that provide solutions of the lens equation (Birrer & Amara 2018; Keeton 2011) usually rely on a backward procedure: the image plane is tiled into pixels, whose centers (or edges, depending on the package) serve as a dummy input for θ in the lens equation.
For a given potential, putative source positions are predicted for each pixel (ray-shooting), and tiles hosting candidate solutions are identified by comparing the source position that they predict to the true one. For example, LENSTRONOMY1 (Birrer & Amara 2018) considers those that when ray-shooted, minimize the distance from the source locally. To achieve better precision, programs such as LENSTRONOMY also provide them as seeds to a numerical root finder.
When stellar-mass lenses are embedded into galaxies or galaxy clusters, microimages are likely to form on top of strongly lensed images and can be separated by as little as a microarcsec (Diego et al. 2019). Despite circumventing the initial value problem, ray-shooting algorithms that rely on predetermined pixel size and possibly standard root finders may prove inadequate in such scenarios. Two or more images may not be identified as separate solutions if they lie in the same pixel.
In order to resolve the microlensed images, the fixed tile must be smaller than the image separations, which are not known a priori. The sky area spanned by strongly lensed images, however, is ≲arcsec2 (Schneider et al. 2006; Collett 2015), and investigating it at such fine resolution is highly time-consuming. Nevertheless, when both galaxies or galaxy clusters and microlenses are involved, a complete solution of the system requires identification of strongly lensed and microlensed images. In addition, the overall potential may vary profoundly on short length scales. This is particularly true when many microlenses are involved: standard integrators may stall and oscillate between points corresponding to nearby solutions without converging.
Finally, gravitational-wave analysis is performed using signal templates predicted by general relativity (GR). The inference of compact source parameters relies on matching gravitational-wave detector strains to a bank of known gravitational waveforms (Allen et al. 2012). This method allowed LIGO and Virgo to unveil a stellar-mass population of binary black holes and produce a catalog of their properties (Abbott et al. 2019a), to perform tests of GR (Abbott et al. 2016c, 2019b,c), and to detect a binary neutron star coalescence (Abbott et al. 2017). However, lensed signals resulting from the superposition of multiple images can differ significantly from unlensed GWs. As a consequence, matched filtering of lensed GWs with unlensed templates could result in missed detections or possibly biased measurements of the binary parameters.
Lensed gravitational waves might also constitute a probe of microlensing. Even when microimages are as close as microarcseconds, observable beating patterns may originate in the GW signal if the time delays between the images are higher than the millisecond time resolution of the interferometers (Lai et al. 2018; Abbott et al. 2019a). Thus, lensed templates might unveil microlenses and dark matter substructures on the path traveled by the wave (Liao et al. 2018). Therefore we must be able to predict GW signals from arbitrary lens configurations.
LENSINGGW has been designed to address these necessities: on the one hand, it implements a new solver tailored to handle very different scales in the lens potentials; on the other hand, it supplies unlensed and lensed GW signals from arbitrary lensed systems through dedicated modules. Such lensed waveforms can serve as injections in parameter estimation (PE) studies to demonstrate the inference of astrophysical parameters of lensed compact sources through Bayesian analysis. We will demonstrate Bayesian PE of lensed systems solved with LENSINGGW in a follow-up study (Pagano et al., in prep.).
The source code of LENSINGGW and examples are hosted on GitLab2.
3.1. Lens equation solver
The numerical solver implemented in LENSINGGW introduces two novelties: a two-step procedure designed to simultaneously resolve strongly lensed images and microimages, and a dedicated procedure to handle sources (images) close to the caustics (critical curves), or lines of infinite magnification in the source (image) plane. Moreover, additional features allow us to assess the effect of the components of multicomponent lens models and to increase the resolution of the algorithm near the source position.
3.1.1. Two-step procedure
It has been proposed in the literature that a lens model ought to be studied by splitting it into a macromodel (galaxy or galaxy cluster) and a micromodel (the remaining lenses): see, for instance, Dobler & Keeton (2006). The two-step procedure of LENSINGGW implements two main innovations with respect to previous algorithms:
-
It exploits the distinction into macromodel and micromodel to guide the search for solutions of the lens equation.
-
It selectively zooms into the image plane by iteratively subtiling pixels that are classified as candidate solutions until the desired precision is reached; the number of iterations of this refinement, hence the finest grid resolution, is dynamically adjusted by the algorithm and does not need to be specified in advance.
Images are found in two steps: first, the macromodel is considered, and the images formed by it (macroimages) are found. The sky region in which the search is performed is centered on the source position, and its size is specified by the user: images that form outside of it will not be found. The macroimages serve as initial guesses for the image positions of the complete model (macromodel + micromodel). A further inspection is carried out around them, now considering the full lensing system. This significantly reduces the sky area in which to search for the images of the complete system and also decouples different scales in the lensing potentials.
The rationale is that in realistic lensing scenarios where microlenses are embedded in galaxies or galaxy clusters, it is possible to identify a dominant deflector (the galaxy or galaxy cluster), and the remaining lenses (the microlenses) represent a small perturbation to its potential. Thus, their effect is that of splitting or shifting the macroimages by a small amount with respect to the macroimage separations. Their locations can then guide the inspection of the complete model. Image separations may still be large if that is not the case, but a larger window can nevertheless be set for the complete model and cover all the relevant areas. Therefore the distinction between macromodel and micromodel is arbitrary: it only establishes which deflector is considered first. For instance, the macromodel can be composed of several lensing components, such as a bulge, a disk, and a halo.
At both steps, the search windows are tiled, and pixels classified as candidate solutions are found through ray-rooting, according to what is implemented in LENSTRONOMY. This routine is justified because true solutions must exactly reproduce the source position when ray-shooted. Thus, approximate solutions should minimize their ray-shooted distance from the actual source locally. Pixels that already reach the desired precision are stored as images, while all the other tiles hosting a candidate solution are iterated over: they constitute the centers of the next grids, whose sides are twice the size of the original pixel, to avoid missing solutions at the boundaries. The tiling and the iteration are repeated on the new grids until no more candidate regions are found or the safety threshold pixel size of 10−25 rad (∼10−20 arcsec) is reached. This is a conservative choice motivated by the fact that typical microimages separations are orders of magnitude above such a threshold. We recall here that recent studies have found them to form as close as microarcsec (Diego et al. 2019). Thus, if microimages have not been identified in the zoomed region at this resolution, the iteration is likely to be driven by numerical artifacts and can be interrupted without loss of solutions. This process prevents the algorithm from becoming stuck between nearby images and guarantees that each interesting area is studied at a finer resolution. The procedure is exemplified in Fig. 2.
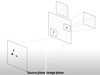 |
Fig. 2. Iterative procedure of LENSINGGW. The image plane is ray-shooted to the source plane via the lens equation. Pixels whose projected distances from the source (the star) are local minima are iterated over through adaptive grids. The process stops when no more minima are found or a minimum pixel size is reached. |
The advantage of our approach compared to methods based on fixed tiles or a predetermined number of subtiles is that it allows the identification of both strongly lensed and microlensed images on a broad sky region while retaining fast performance and assuming no a priori knowledge on the image separations. The zoom is performed on each area on a case-by-case basis: regions in which no images are present will not be zoomed at all. Strongly lensed images will require a moderate number of iterations to reach the desired precision. At the same time, more layers of grid refinement will be employed where microimages are present, allowing us to resolve all the images. The tile and grid extensions are adjusted dynamically in each area and at each iteration; therefore, the refinement is focused only where needed.
On the other hand, as previously mentioned, methods that rely on fixed tiles or subtiles can identify arbitrary image separations only when the whole sky region is tiled at the finest needed resolution, which requires the scale of these separations to be known in advance. LENSINGGW can overcome these limitations.
We demonstrate the performance of LENSINGGW with respect to the fixed-tile approach on a system that produces both strongly lensed images and microimages. We considered an elliptical galaxy at the origin of the image plane with mass MG = 1012 M⊙, ellipticity ϵ = 0.1, and core radius Rc = 500 pc at redshift zL = 0.5. The galaxy potential is
where θc = Rc/DL, 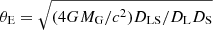 is the Einstein radius and θ = (θx, θy) is the two-dimensional coordinate in the image plane. A point source placed inside the diamond-shaped caustic at redshift zS = 2 and sky position (RA, Dec) = (0.05, 0)⋅θE rad produces five strongly lensed images, whose time delays span from some days to several months and with total magnification μ = ∑i ∈ macroimages|μi| = 21.3. To produce microlensing in one region of the macromodel, we injected ∼600 point mass microlenses with masses mi ∈ [100, 200] M⊙ in an area of ∼14 milliarcsec × 14 milliarcsec around the position of the most magnified macroimage. The microlenses are uniformly distributed in mass and position until the target density of 12 M⊙ pc2 is reached: this is the same surface mass density as was adopted in Diego et al. (2019) for lensed extragalactic gravitational waves at high macromodel magnifications.
is the Einstein radius and θ = (θx, θy) is the two-dimensional coordinate in the image plane. A point source placed inside the diamond-shaped caustic at redshift zS = 2 and sky position (RA, Dec) = (0.05, 0)⋅θE rad produces five strongly lensed images, whose time delays span from some days to several months and with total magnification μ = ∑i ∈ macroimages|μi| = 21.3. To produce microlensing in one region of the macromodel, we injected ∼600 point mass microlenses with masses mi ∈ [100, 200] M⊙ in an area of ∼14 milliarcsec × 14 milliarcsec around the position of the most magnified macroimage. The microlenses are uniformly distributed in mass and position until the target density of 12 M⊙ pc2 is reached: this is the same surface mass density as was adopted in Diego et al. (2019) for lensed extragalactic gravitational waves at high macromodel magnifications.
We present the images found by LENSINGGW and by the fixed-tile ray-shooting in Fig. 3. Both programs inspected a sky region of ∼4.7 arcsec × 4.7 arcsec centered on the source position. LENSINGGW required ∼0.044% of the runtime employed by the fixed-tile algorithm, inspected ∼1/4 of the pixels, and recovered both the macro- and microimages. The pixel size of the fixed-tile approach was set to the lowest resolution below the minimum microimage separation. However, it was still too large to resolve the shape of the potential between the microimages and identify the individual solutions: the fixed-tile method identified only the macroimages. Thus, increasingly smaller pixels would have needed to be tried out until the microimages are recovered by this method, resulting in a much longer runtime.
 |
Fig. 3. Comparison between the LENSINGGW lens equation solver and a fixed-tile algorithm. Right ascension (RA) and declination (Dec) of the images recovered by LENSINGGW (red crosses) and by a fixed-tile routine (gray x) for an elliptical galaxy plus ∼600 microlenses injected around the most magnified macroimage. The strongly lensed images (top panel) are correctly recovered by both algorithms. However, the zoom into the microlensed image (bottom right) shows that LENSINGGW is able to recover eight microimages, while the fixed-tile approach identifies them as a single image. The solution of the system with LENSINGGW required ∼19 s on a standard machine and ∼12 h with the fixed-tile method at the lowest tile resolution below the microimage separations. The zoom into a strongly lensed image without microlenses (bottom left) is also shown for completeness. Coordinates are relative to the galaxy center. |
The solver can be applied to arbitrary lensing potentials and mass distributions. It accepts lens profiles with the same structure as those defined in LENSTRONOMY (Birrer & Amara 2018) and is compatible with every lensing potential already implemented therein. The lensing framework (the combination of the lenses into a lens model, the ray-shooting, the selection of pixels classified as candidate solutions, and the computation of caustics and critical curves) derive from LENSTRONOMY.
3.1.2. Near-caustic sources
When the source approaches the caustics, or curves of infinite magnification in the source plane, the grid refinement may identify an increasingly large number of pixels that might be candidate solutions. In these cases, spurious approximate minima are present at a given iteration. However, the solver iterates on each of them by default.
The user can then aid the solver to convergence by introducing a cut on the candidate solutions. This feature relies on the fact that regions hosting solutions of the lens equation are expected to improve their ray-shooted distance to the actual source at every iteration. Thus, the user can indicate an improvement criterion to select pixels that are classified as candidate solutions. In particular, they can set
-
a minimum ray-shooted distance threshold
 to select solutions in the first grid among the pixels that are classified as candidates. This allows for further screening of the interesting regions before the iteration. It should be used when the number of good pixels identified by the algorithm is extremely high already in the first grids;
to select solutions in the first grid among the pixels that are classified as candidates. This allows for further screening of the interesting regions before the iteration. It should be used when the number of good pixels identified by the algorithm is extremely high already in the first grids; -
how much this distance should improve between subsequent iterations for the candidate solution to be still iterated over. This means a multiplicative factor δ, 0 < δ ≤ 1 that corrects
 as
as 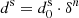 at the nth iteration. It allows us to select from unreasonable numbers of pixels during the procedure.
at the nth iteration. It allows us to select from unreasonable numbers of pixels during the procedure.
Combining these functionalities has proven to overcome nonconverging cases, allowing LENSINGGW to retrieve the correct solutions. We illustrate this through the elliptical galaxy of the previous example: we removed the microlenses and considered a lower galaxy mass of MG = 1010 M⊙ to reduce the area that is affected by the galaxy and investigated a smaller window. We moved the source toward the caustics until the solver without cut no longer converged. We then applied the cut with 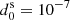 rad and improvement factor δ = 0.1, which led to the correct identification of all the five macroimages. We recorded the number of pixels selected by the algorithm as the iteration proceeds and compared it to the tiles that were selected when no cut was applied. The comparison is shown in Fig. 4: the improvement criterion controls the number of candidate solutions and leads the solver to convergence in a reasonable number of iterations. In contrast, the standard setup leads to an increasingly large number of selected tiles, with more than 105 pixels that might host candidate solutions at the eighth iteration.
rad and improvement factor δ = 0.1, which led to the correct identification of all the five macroimages. We recorded the number of pixels selected by the algorithm as the iteration proceeds and compared it to the tiles that were selected when no cut was applied. The comparison is shown in Fig. 4: the improvement criterion controls the number of candidate solutions and leads the solver to convergence in a reasonable number of iterations. In contrast, the standard setup leads to an increasingly large number of selected tiles, with more than 105 pixels that might host candidate solutions at the eighth iteration.
 |
Fig. 4. Performance of the improvement criterion for pixel selection over the default selection method for near-caustic sources. The number of candidate solutions selected for the zoom at each iteration by the default-solving algorithm (gray diamonds) and by the improvement criterion (red triangles) for the elliptical galaxy of Fig. 3 when the source approaches the caustics. The improvement criterion controls the number of tiles to iterate over and recovers the five macroimages in seven iterations, whereas the standard selection routine identifies an ever-increasing number of pixels, which selects more than 105 tiles for the zoom at the eighth iteration. |
By default, LENSINGGW does not apply the cut because it discards potential solutions: when no spurious minima are identified, its use could result in missed images. Therefore the cut is recommended only when the number of candidate pixels increases dramatically and prevents the solver from converging.
3.1.3. Additional features
The user can inspect the macromodel separately from the microlenses by enabling the OnlyMacro flag in the solver settings. This is important, for instance, when the effect of the microlenses on a galaxy or galaxy cluster is assessed. Within LENSINGGW, the study of the macromodel without (with) micromodel can be performed by enabling (disabling) this functionality. For example, if the elliptical galaxy of Fig. 3 is marked as macromodel and OnlyMacro is active, LENSINGGW identifies the five strongly lensed images displayed in the top panel of the figure. When the flag is disabled, the elliptical galaxy and the microlenses are instead considered together, and the microimages in the bottom right panel are recovered in addition to the strongly lensed ones.
In the same manner, the user can flag certain components of a lens model (e.g., a bulge and a disk) as the macromodel, and the remainder as the micromodel (such as a halo). The user can then use the OnlyMacro option to study the model with and without the micromodel. We recall here that this is possible because the distinction between macro- and micromodel is arbitrary and only indicates which lens models are considered for the first step of the solving algorithm.
Depending on the lens position, the images can also form close to the position where the image in the absence of lenses would form (the unlensed image position). The user can require a further zoom close to the unlensed image position through the NearSource flag. Should they wish to span a wider area around the lens while retaining details close to the unlensed image, this functionality allows specifying two windows with a different number of pixels for the first step. Thus, one window can be used to investigate the larger region and cover the whole lens, while the other one can be used to span a much smaller area around the unlensed image position, increasing the resolution where it may be needed.
3.2. GW signals
When the number of images and the relative time delays of a lensing configuration are found, we typically wish to conduct a further parameter estimation on the signal. Parameter estimation studies of compact binary coalescences (CBCs) are performed through templates of gravitational signals predicted by GR and their projection onto the detectors, or strain. Templates are needed to assess the detectability of the signals and the characteristics of the source. If unlensed gravitational-wave strains are used in filtering microlensed gravitational-wave data, the search method that allows us to identify a signal in the detector data (matched filtering Allen et al. 2012) becomes suboptimal.
As an illustrative example, we show the filtering process for a microlensed gravitational waveform within a LIGO detector at design sensitivity. We simulated a gravitational wave from a binary black hole of masses m1 = m2 = 150 M⊙, microlensed into two images of comparable magnifications and relative time delay of 10 ms. We filtered the data using a lensed and an unlensed strain, finding that the unlensed waveform returns a lower matched-filter S/N (Fig. 5). It is therefore fundamental that software packages for lensing of CBCs come with an infrastructure for gravitational waves that predicts GWs from arbitrary lensed systems. LENSINGGW provides this infrastructure through specific modules that compute unlensed templates and strains through LALSIMULATION (LIGO Scientific Collaboration 2018) and their lensed counterparts in ground-based detectors. Thus, any waveform development in the LIGO Scientific Collaboration Algorithm Library Suite LALSUITE (LIGO Scientific Collaboration 2018) will benefit LENSINGGW.
 |
Fig. 5. Matched filtering with lensed and unlensed waveforms. Top panel: example microlensed gravitational-wave strain (black line) and corresponding detector data with noise (blue data). The unlensed strain is also shown for comparison (orange line). Bottom panel: matched filter S/N of the detector data using the microlensed waveform (black line) and the unlensed waveform (orange line). The microlensed gravitational-wave strain matches the data better and thus returns a higher matched S/N. Here, a high S/N example is considered for illustration, and both signals are normalized so that their optimal S/Ns are the same. |
Magnifications are currently computed within the geometrical optics approximation of Eq. (6). The approximation is valid for galaxies and galaxy clusters at LIGO and Virgo frequencies, but may not be valid in general for small isolated lenses when wave optics effects become important. In Fig. 6 we show the geometrical optics and wave optics magnifications for an isolated point lens of mass ML = 100 M⊙. The difference between the two approaches rapidly reduces in the most sensitive frequency band of the interferometers (f ≳ 100 Hz) and for higher source displacements. However, we caution that smaller isolated microlenses and source-point lens separations may react differently. Therefore we focused on lenses with ML ≳ 100 M⊙ and source-point lens displacements ≳0.45 ⋅ θE. Future extensions will cover wave optics, but we do not cover it here.
 |
Fig. 6. Comparison between the geometrical optics amplification and the wave optics amplification for an isolated point mass. We compare the geometrical optics approximation (full lines) with the wave optics magnification (dashed lines) for an isolated point lens of mass ML = 100 M⊙ at the origin of the image plane and source position β = (0, β1) rad. The error on the geometrical optics approximation rapidly reduces for frequencies f ≳ 100 Hz and systems with higher source displacements. |
4. Validation
We tested the solver on two scenarios proposed in the literature: a microlens embedded in a host galaxy at high magnifications, and two equal-mass point lenses. The two models aim to show that LENSINGGW can correctly recover the lensed images for potentials that involve different scales and comparable masses. This demonstrates that it is a valid tool for generic lensing configurations.
4.1. Diego et al. (2019)
Diego et al. (2019) proposed among many other models the case of a point-mass microlens of ML = 100 M⊙ embedded in a galaxy or galaxy cluster at redshift z = 0.5. The galaxy is described by a potential with both convergence and external shear and with total magnification μ = 30. We considered the configuration in which a source is placed at redshift z = 2 and angular position β/θE = 0.05, where 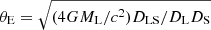 is the Einstein radius of the microlens. In the positive parity side of the galaxy (i.e., where the images are minima or maxima of the time delay), this case leads to four microimages, two of which lie within the critical curves and two outside them (see Fig. 5 of Diego et al. 2019).
is the Einstein radius of the microlens. In the positive parity side of the galaxy (i.e., where the images are minima or maxima of the time delay), this case leads to four microimages, two of which lie within the critical curves and two outside them (see Fig. 5 of Diego et al. 2019).
We set the galaxy to be the macromodel and defined the point lens as the micromodel, which we placed at the macroimage position. The images recovered by LENSINGGW for this scenario are illustrated in Fig. 7.
 |
Fig. 7. Microimages recovered by LENSINGGW for the galaxy plus point lens system of Diego et al. (2019): RA and Dec relative to the galaxy center. The off-axis source (red dot) is lensed by the galaxy, and a shifted image forms (blue dot). When a 100 M⊙ point lens is added at the position of the macroimage, it splits it into four microimages (black crosses). Two of them form inside the critical curve (black line) and two outside of it with magnifications μ and normalized time delays td. The caustic (red line) and a color map of the magnification in the RA−Dec plane are shown for completeness. The system demonstrates the applicability of LENSINGGW to microlenses embedded in galaxies or galaxy clusters. |
The image geometry is correctly recovered with respect to the critical curves. Magnifications, time delays, and image separations are comparable to what was found in reference (Diego et al. 2019). The exact source and point-lens positions are not specified in Diego et al. (2019). The numerical values of the recovered quantities are not identical for this reason.
4.2. Schneider & Weiss (1986)
We now consider the case of two point lenses of equal masses. Schneider & Weiss (1986) have extensively studied this scenario: the authors calculated the number of images and their approximate positions for a variety of source positions and lens displacements. Images were identified by specifying the quadrant of the image plane they form in and whether they are inside the critical curves.
Seven configurations from reference Schneider & Weiss (1986) have been tested: in Fig. 8 we show the off-axis case corresponding to 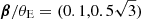 and lens positions x/θE = ( ± 0.5, 0), where θE is the Einstein radius given by the total mass ML1 + ML2 = 200 M⊙. Source and lenses were placed at redshift z = 2 and z = 0.5, respectively. Here, we considered the point lens closest to the source as macromodel and the farthest as micromodel. The same result is obtained when both lenses are indicated as macromodel simultaneously, and the OnlyMacro option is enabled (see Sect. 3.1.3). We recall that the macromodel can be formed by multiple lenses and that its definition is arbitrary.
and lens positions x/θE = ( ± 0.5, 0), where θE is the Einstein radius given by the total mass ML1 + ML2 = 200 M⊙. Source and lenses were placed at redshift z = 2 and z = 0.5, respectively. Here, we considered the point lens closest to the source as macromodel and the farthest as micromodel. The same result is obtained when both lenses are indicated as macromodel simultaneously, and the OnlyMacro option is enabled (see Sect. 3.1.3). We recall that the macromodel can be formed by multiple lenses and that its definition is arbitrary.
 |
Fig. 8. Images recovered by LENSINGGW for a binary point lens: RA and Dec relative to the binary center of mass. The source (red dot) is lensed by two point masses (black dots) of M1 = M2 = 100 M⊙. When only one deflector is considered, two macroimages (blue dots) form. When the second lens is added, three total images (black crosses) form: their positions with respect to the critical curve (black line) and to the origin are consistent with the predictions of Schneider and Weiß. Magnifications (μ), normalized time delays (td), the caustic (red line), and a color map of the magnification in the RA−Dec plane are shown for completeness. The system confirms the applicability of the LENSINGGW algorithm to comparable-mass potentials. |
For this scenario, the authors predicted three images: one outside the critical curve in the first quadrant, and two inside the critical curve, in the third and fourth quadrant. The geometry illustrated in Fig. 8 shows that LENSINGGW is able to recover the correct solutions.
5. Applications
In this section, we demonstrate possible applications of LENSINGGW to scenarios of astrophysical interest. First, we use it to investigate the parameter space of the source parameters and perform a systematic detectability study of the resulting lensed GWs. We then apply it to investigate the effects of strongly lensed image properties on microlensing in a lensing system with hundreds of microlenses embedded within a galaxy. In what follows, we consider ground-based gravitational-wave detectors at design sensitivity.
We recall here that the inner product between two signals a and b is defined as (Cutler & Flanagan 1994)
where a(f) and b(f) are the Fourier transforms of a(t) and b(t), the asterisk denotes complex conjugation, Sn(f) is the one-sided power spectral density (PSD) of the instrument, and fmin and fmax define the relevant frequency band.
The agreement between two GW signals h1 and h2 is commonly quantified as the noise-weighted inner product of the normalized waveforms, maximized over the time and phase of coalescence,
where 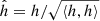 is the normalized waveform. When two signals have identical phasing, this statistics, or match, equals one: their distinguishability is then quantified through the mismatch: ℳ(h1, h2) = 1 − M(h1, h2).
is the normalized waveform. When two signals have identical phasing, this statistics, or match, equals one: their distinguishability is then quantified through the mismatch: ℳ(h1, h2) = 1 − M(h1, h2).
5.1. Parameter space investigation and detectability study
We show the effect of the component masses of the compact source on the distinguishability of lensed signals for the lens model of Sect. 4.1. We simulated a compact source in the Hanford detector: the unlensed signal is produced by a nonspinning binary with sky position (RA, Dec) = (0, 0.05 ⋅ θE) rad, redshift z = 2 and inclination ι = 2.6 rad. We varied the black hole masses in the ℳc − q plane, where ℳc = (m1 − m2)3/5/(m1 + m2)1/5 is the chirp mass and q = m2/m1 ≤ 1 is the mass ratio of the binary. For each configuration, we predicted the source images and modeled the lensed and unlensed signals in the LIGO detector through LENSINGGW. We then computed their mismatch: a large mismatch is necessary to distinguish a lensed signal as such. However, we note that degeneracies in the parameter space may lead to a low mismatch if the lensed wave resembles an unlensed signal with different parameters.
As shown in Fig. 9, higher mass ratios and lower chirp masses exhibit larger mismatches. This is expected because these signals span a broader frequency band and the dephasing due to the superposition of the images can accumulate over a longer interval. However, the computation of the microimages and the study of the lensed and unlensed strains is essential to assess how the mismatch varies with the source parameters or the lens model. It is therefore crucial to develop software like LENSINGGW, which incorporates the physics of lensing and GW signals while retaining fast performance.
 |
Fig. 9. Source parameter space investigation with LENSINGGW: Mismatch study of a nonspinning compact binary. Each dot represents a pair of component masses in the ℳc − q plane, lensed by the galaxy plus the point-lens model presented by Diego et al. (2019). All other source parameters are fixed. The point-lens mass is ML = 100 M⊙, and is placed at the position of the macroimage formed by the galaxy. For each configuration, the mismatch between the lensed and unlensed GWs is displayed in a color map; darker colors denote larger mismatches (see the color bar at the right). A large mismatch is necessary to distinguish a lensed signal as such. |
5.2. Effect of strongly lensed images on microlensing
We demonstrate how LENSINGGW can be used to study the effect of a macromodel on microlens substructures. We investigated the strain produced by the microimages induced on top of a strongly lensed image by a fixed micromodel for different magnifications and parities of the strongly lensed image.
We considered the elliptical galaxy plus microlenses of Sect. 3.1 with galaxy mass MG = 1012 M⊙ and investigated three source positions: (0.05, 0)⋅θE rad, (0.15, 0)⋅θE rad and (0.18, 0)⋅θE rad. In this scenario, the larger the source position, the closer the source to the caustic. In this way, we can inspect the change in the results when the magnification of each macroimage is enhanced while retaining the total number and geometry of the strongly lensed images.
For each scenario, we considered both the most magnified image at the positive-parity side of the galaxy (i.e., where the image is a minimum or a maximum of the time delay) and the one in the negative-parity side (where the image is a saddle point). The two sides are expected to behave differently as the region of low magnification is larger than the region of high magnification in the negative-parity side, resulting in a higher probability of a GW being demagnified by the microlenses than magnified by them. See references Diego et al. (2018, 2019), Diego (2019) for a more in-depth discussion.
To quantify the effect on gravitational waves, we first solved for the macromodel (the galaxy) only by means of the LENSINGGW OnlyMacro option and find the images’ magnifications and Morse indices through the dedicated routines. Through those, we identify the macroimage of interest and inject the fixed microlens distribution around it for each source position. We then solve for the complete model and compare the lensed and unlensed strains found by LENSINGGW. We consider a nonspinning binary of masses m1 = 45 M⊙, m2 = 36 M⊙ and inclination ι = 2.6 at redshift zS = 2 as source. We use a fixed window of 1.4 milliarcsec × 1.4 milliarcsec (∼50 times the Einstein radius of the more massive microlens) for the second step of the iterative procedure. We show the strains in the Hanford detector for the positive- and negative-parity sides in Fig. 10.
 |
Fig. 10. Effects of strongly lensed image properties on microlensing. Normalized strains obtained by LENSINGGW in the Hanford detector for a compact binary lensed by an elliptical galaxy and ∼600 microlenses (as documented in Sec. 3.1). Microlensing is enhanced by strong lensing on the positive parity side (top panel) and the negative parity side (bottom panel) of the galaxy. As the magnification of the macroimage |μ| is increased (dark yellow curves, from bottom to top in each panel), the microimages lead to more prominent oscillations at the positive-parity side. In contrast, the negative-parity side exhibits the opposite behavior. Inspection of the image properties through LENSINGGW attributes this to the difference in relative magnifications and time delays among the microimages produced by the different scenarios. In both cases, microlensing boosts the S/N of the unlensed signal (light yellow curve) and turns it from a subthreshold event to a detectable one, as demonstrated by the superposed noise curves of LIGO and Virgo (gray lines). |
The unlensed signal is subthreshold in the Virgo detector and just above threshold in LIGO. However, the amplification of the microimages enhances its amplitude, turning it into a detectable signal on both sides of the galaxy (compare, in particular, the strains to the superposed noise curves of the instruments). The amplitude of the signal increases with the macroimage magnification, and the longest time delays between the microimages are on the order of hundreds of milliseconds. This value is higher than the time differences produced by isolated point lenses. The result confirms that increasing the macromodel magnification enhances the effects of microlensing, both in amplitudes and time delays, as found in Diego et al. (2019).
However, in addition to this, we find that in the positive parity side (top panel), the oscillations induced by microlensing become more prominent as the magnification of the strongly lensed image increases. In contrast, the negative parity side (bottom panel) exhibits the opposite behavior. This behavior depends on the relative magnifications and time delays of the microimages on the different sides of the galaxy and on the set of microimages that contribute the most to the gravitational-wave signal. As the effect on the strain is a combination of the various microimage contributions, the lensed waves would be difficult to model analytically. This offers another confirmation of the importance of developing software packages that target arbitrary lensing configurations and related gravitational-wave signals, such as LENSINGGW.
The execution required ∼19 s on an Intel Core i7-7700HQ CPU with 2.80 GHz for each source position. This makes LENSINGGW an ideal candidate for systematic studies of this type.
6. Conclusions
It has been proposed that intermediate-mass black holes, dense stellar clusters, and primordial black holes might be probed by gravitational-wave lensing in the future (Jung & Shin 2019; Lai et al. 2018; Christian et al. 2018; Diego 2020). Detections of microlensed GWs might also unveil dark matter substructures (Liao et al. 2018). Moreover, if unaccounted for, microlensed signals can introduce biases in the inferred source properties of compact binaries due to the lensed waveform distortions.
We have presented LENSINGGW, a PYTHON package for predicting lensed GWs in ground-based detectors from arbitrary lens models and compact sources. We have validated LENSINGGW in two scenarios that produce microlensing: a microlens embedded in a galaxy (Diego et al. 2019), where microimages form on top of a strongly lensed image, and a binary point-mass system (Schneider & Weiss 1986), showing that the software package can recover the correct results. Moreover, we have demonstrated that the new solving algorithm implemented in LENSINGGW outperforms standard fixed-tile algorithms when it is applied to hundreds of microlenses embedded in galaxies. The evaluation only takes some seconds on a standard machine as opposed to the several hours that are required by the fixed-tile approach. This makes LENSINGGW a valid candidate for investigations of realistic scenarios.
We have shown how LENSINGGW can be applied to investigations of astrophysical interest, such as the effect of the source properties on the detectability of lensed GWs and the effects of strongly lensed images on microlensed strains. LENSINGGW is able to predict lensed GW signals resulting from arbitrary lensing systems such as isolated galaxies or galaxies with hundreds of microlenses by its ability to generate lensed and unlensed gravitational waves.
https://gitlab.com/gpagano/lensinggw. Documentation is hosted on GitLab pages, at https://gpagano.gitlab.io/lensinggw/
Acknowledgments
We thank Walter Del Pozzo, Gregorio Carullo, and Simon Birrer for useful discussions. OAH is supported by the research program of the Netherlands Organization for Scientific Research (NWO). TGFL is partially supported by grants from the Research Grants Council of Hong Kong (Project No. 14306218), Research Committee of the Chinese University of Hong Kong, and the Croucher Foundation of Hong Kong.
References
- Aasi, J., Abbott, B. P., Abbott, R., et al. 2015, Classical Quantum Gravity, 32, 074001 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, B. P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2016a, Phys. Rev. Lett., 116, 131103 [CrossRef] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016b, ApJ, 833, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, B. P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2016c, Phys. Rev. Lett., 116, 221101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2017, Phys. Rev. Lett., 119, 161101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2018a, https://dcc.ligo.org/LIGO-T1800133 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T., et al. 2018b, Liv. Rev. Relativ., 21, 3 [Google Scholar]
- Abbott, B. P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2019a, Phys. Rev. X, 9, 031040 [Google Scholar]
- Abbott, B. P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2019b, Phys. Rev. Lett., 123, 011102 [CrossRef] [Google Scholar]
- Abbott, B. P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2019c, Phys. Rev. D, 100, 104036 [CrossRef] [Google Scholar]
- Acernese, F., Agathos, M., Agatsuma, K., et al. 2015, Classical Quantum Gravity, 32, 024001 [NASA ADS] [CrossRef] [Google Scholar]
- Akutsu, T., Ando, M., Araki, S., et al. 2018, Prog. Theor. Exp. Phys., 2018, 013F01 [CrossRef] [Google Scholar]
- Allen, B., Anderson, W. G., Brady, P. R., Brown, D. A., & Creighton, J. D. E. 2012, Phys. Rev. D, 85, 122006 [CrossRef] [Google Scholar]
- Aso, Y., Michimura, Y., Somiya, K., et al. 2013, Phys. Rev. D, 88, 043007 [NASA ADS] [CrossRef] [Google Scholar]
- Baker, T., & Trodden, M. 2017, Phys. Rev. D, 95, 063512 [NASA ADS] [CrossRef] [Google Scholar]
- Birrer, S., & Amara, A. 2018, Astrophysics Source Code Library [record ascl:1804.012] [Google Scholar]
- Bliokh, P., & Minakov, A. 1975, Astrophys. Space Sci., 34, L7 [CrossRef] [Google Scholar]
- Bontz, R. J., & Haugan, M. P. 1981, Astrophys. Space Sci., 78, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Broadhurst, T., Diego, J. M., & Smoot, G., III 2018, ArXiv e-prints [arXiv:1802.05273] [Google Scholar]
- Broadhurst, T., Diego, J. M., & Smoot, G. F., III 2019, ArXiv e-prints [arXiv:1901.03190] [Google Scholar]
- Cao, Z., Li, L.-F., & Wang, Y. 2014, Phys. Rev. D, 90, 062003 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., Qi, J., Cao, Z., et al. 2019, Sci. Rep., 9, 11608 [CrossRef] [Google Scholar]
- Christian, P., Vitale, S., & Loeb, A. 2018, Phys. Rev. D, 98, 103022 [NASA ADS] [CrossRef] [Google Scholar]
- Collett, T. E. 2015, ApJ, 811, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Collett, T. E., & Bacon, D. 2017, Phys. Rev. Lett., 118, 091101 [CrossRef] [Google Scholar]
- Contigiani, O. 2020, MNRAS, 492, 3359 [CrossRef] [Google Scholar]
- Cutler, C., & Flanagan, E. E. 1994, Phys. Rev. D, 49, 2658 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, L., & Venumadhav, T. 2017, ArXiv e-prints [arXiv:1702.04724] [Google Scholar]
- Dai, L., Venumadhav, T., & Sigurdson, K. 2017, Phys. Rev. D, 95, 044011 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, L., Li, S.-S., Zackay, B., Mao, S., & Lu, Y. 2018, Phys. Rev. D, 98, 104029 [NASA ADS] [CrossRef] [Google Scholar]
- Deguchi, S., & Watson, W. 1986, ApJ, 307, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Diego, J. M. 2019, A&A, 625, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diego, J. M. 2020, Phys. Rev. D, 101, 123512 [CrossRef] [Google Scholar]
- Diego, J. M., Kaiser, N., Broadhurst, T., et al. 2018, ApJ, 857, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Diego, J. M., Hannuksela, O. A., Kelly, P. L., et al. 2019, A&A, 627, A130 [CrossRef] [EDP Sciences] [Google Scholar]
- Dobler, G., & Keeton, C. R. 2006, MNRAS, 365, 1243 [CrossRef] [Google Scholar]
- Fan, X.-L., Liao, K., Biesiada, M., Piórkowska-Kurpas, A., & Zhu, Z.-H. 2017, Phys. Rev. Lett., 118, 091102 [CrossRef] [Google Scholar]
- Hannuksela, O., Haris, K., Ng, K., et al. 2019, ApJ, 874, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Hannuksela, O. A., Collett, T. E., Çalışkan, M., & Li, T. G. 2020, MNRAS, 498, 3395 [CrossRef] [Google Scholar]
- Haris, K., Mehta, A. K., Kumar, S., Venumadhav, T., & Ajith, P. 2018, ArXiv e-prints [arXiv:1807.07062] [Google Scholar]
- Hou, S., Fan, X.-L., Liao, K., & Zhu, Z.-H. 2020, Phys. Rev. D, 101, 064011 [CrossRef] [Google Scholar]
- Iyer, B., et al. 2011, LIGO India, Tech. Rep. LIGO-M1100296, https://dcc.ligo.org/LIGO-M1100296/public [Google Scholar]
- Jung, S., & Shin, C. S. 2019, Phys. Rev. Lett., 122, 041103 [NASA ADS] [CrossRef] [Google Scholar]
- Keeton, C. R. 2011, Astrophysics Source Code Library [record ascl:1102.003] [Google Scholar]
- Lai, K.-H., Hannuksela, O. A., Herrera-Martín, A., et al. 2018, Phys. Rev. D, 98, 083005 [NASA ADS] [CrossRef] [Google Scholar]
- Li, S.-S., Mao, S., Zhao, Y., & Lu, Y. 2018, MNRAS, 476, 2220 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A. K. Y., Lo, R. K. L., Sachdev, S., et al. 2019, ArXiv e-prints [arXiv:1904.06020] [Google Scholar]
- Liao, K., Fan, X. L., Ding, X. H., Biesiada, M., & Zhu, Z. H. 2017, Nat. Commun., 8, 1148 [Erratum: Nat. Commun., 8, 2136 (2017)] [NASA ADS] [CrossRef] [Google Scholar]
- Liao, K., Ding, X., Biesiada, M., Fan, X.-L., & Zhu, Z.-H. 2018, ApJ, 867, 69 [NASA ADS] [CrossRef] [Google Scholar]
- LIGO Scientific Collaboration 2018, LIGO Algorithm Library – LALSuite, Free Software (GPL) [Google Scholar]
- LIGO Scientific Collaboration and Virgo Collaboration 2019, https://gcn.gsfc.nasa.gov/gcn3/24045.gcn3 [Google Scholar]
- Maggiore, M., Van Den Broeck, C., Bartolo, N., et al. 2020, JCAP, 2020, 050 [CrossRef] [Google Scholar]
- McIsaac, C., Keitel, D., Collett, T., et al. 2020, Phys. Rev. D, 102, 084031 [CrossRef] [Google Scholar]
- Mukherjee, S., Wandelt, B. D., & Silk, J. 2020, Phys. Rev. D, 101, 103509 [CrossRef] [Google Scholar]
- Nakamura, T. T. 1998, Phys. Rev. Lett., 80, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, K. K., Wong, K. W., Broadhurst, T., & Li, T. G. 2018, Phys. Rev. D, 97, 023012 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M. 2018, MNRAS, 480, 3842 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M. 2019, Rep. Prog. Phys., 82, 126901 [CrossRef] [Google Scholar]
- Ohanian, H. C. 1974, Int. J. Theor. Phys., 9, 425 [CrossRef] [Google Scholar]
- Pang, P. T. H., Hannuksela, O. A., Dietrich, T., Pagano, G., & Harry, I. W. 2020, MNRAS, 495, 3740 [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery Frontmatt, B. P. 2007, Numerical Recipes, 3rd edn. (Cambridge: Cambridge University Press) [Google Scholar]
- Robertson, A., Smith, G. P., Massey, R., et al. 2020, MNRAS, 495, 3727 [CrossRef] [Google Scholar]
- Schneider, P., & Weiss, A. 1986, A&A, 164, 237 [NASA ADS] [Google Scholar]
- Schneider, P., Kochanek, C., & Wambsganss, J. 2006, in Gravitational Lensing: Strong, Weak and Micro, eds. G. Meylan, P. Jetzer, & P. North (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Sereno, M., Jetzer, P., Sesana, A., & Volonteri, M. 2011, MNRAS, 415, 2773 [CrossRef] [Google Scholar]
- Singer, L. P., Goldstein, D. A., & Bloom, J. S. 2019, ArXiv e-prints [arXiv:1910.03601] [Google Scholar]
- Smith, G. P., Berry, C., Bianconi, M., et al. 2018, in IAU Symposium, eds. G. González, & R. Hynes, 338, 98 [Google Scholar]
- Smith, G. P., Bianconi, M., Jauzac, M., et al. 2019, MNRAS, 485, 5180 [NASA ADS] [CrossRef] [Google Scholar]
- Somiya, K. 2012, Classical Quantum Gravity, 29, 124007 [Google Scholar]
- Sun, D., & Fan, X. 2019, ArXiv e-prints [arXiv:1911.08268] [Google Scholar]
- Takahashi, R., & Nakamura, T. 2003, ApJ, 595, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, R., Suyama, T., & Michikoshi, S. 2005, A&A, 438, L5 [CrossRef] [EDP Sciences] [Google Scholar]
- Thorne, K. S. 1983, Gravitational Radiation, 1 [Google Scholar]
All Figures
 |
Fig. 1. Gravitational lens configuration in the thin-lens approximation. The lensing configuration is described by the source displacement from the line of sight η, the angular diameter distance from the observer to the source DS, to the lens DL, from lens to the source DLS, and by the relative position of the image in the image plane ξ. |
| In the text | |
 |
Fig. 2. Iterative procedure of LENSINGGW. The image plane is ray-shooted to the source plane via the lens equation. Pixels whose projected distances from the source (the star) are local minima are iterated over through adaptive grids. The process stops when no more minima are found or a minimum pixel size is reached. |
| In the text | |
 |
Fig. 3. Comparison between the LENSINGGW lens equation solver and a fixed-tile algorithm. Right ascension (RA) and declination (Dec) of the images recovered by LENSINGGW (red crosses) and by a fixed-tile routine (gray x) for an elliptical galaxy plus ∼600 microlenses injected around the most magnified macroimage. The strongly lensed images (top panel) are correctly recovered by both algorithms. However, the zoom into the microlensed image (bottom right) shows that LENSINGGW is able to recover eight microimages, while the fixed-tile approach identifies them as a single image. The solution of the system with LENSINGGW required ∼19 s on a standard machine and ∼12 h with the fixed-tile method at the lowest tile resolution below the microimage separations. The zoom into a strongly lensed image without microlenses (bottom left) is also shown for completeness. Coordinates are relative to the galaxy center. |
| In the text | |
 |
Fig. 4. Performance of the improvement criterion for pixel selection over the default selection method for near-caustic sources. The number of candidate solutions selected for the zoom at each iteration by the default-solving algorithm (gray diamonds) and by the improvement criterion (red triangles) for the elliptical galaxy of Fig. 3 when the source approaches the caustics. The improvement criterion controls the number of tiles to iterate over and recovers the five macroimages in seven iterations, whereas the standard selection routine identifies an ever-increasing number of pixels, which selects more than 105 tiles for the zoom at the eighth iteration. |
| In the text | |
 |
Fig. 5. Matched filtering with lensed and unlensed waveforms. Top panel: example microlensed gravitational-wave strain (black line) and corresponding detector data with noise (blue data). The unlensed strain is also shown for comparison (orange line). Bottom panel: matched filter S/N of the detector data using the microlensed waveform (black line) and the unlensed waveform (orange line). The microlensed gravitational-wave strain matches the data better and thus returns a higher matched S/N. Here, a high S/N example is considered for illustration, and both signals are normalized so that their optimal S/Ns are the same. |
| In the text | |
 |
Fig. 6. Comparison between the geometrical optics amplification and the wave optics amplification for an isolated point mass. We compare the geometrical optics approximation (full lines) with the wave optics magnification (dashed lines) for an isolated point lens of mass ML = 100 M⊙ at the origin of the image plane and source position β = (0, β1) rad. The error on the geometrical optics approximation rapidly reduces for frequencies f ≳ 100 Hz and systems with higher source displacements. |
| In the text | |
 |
Fig. 7. Microimages recovered by LENSINGGW for the galaxy plus point lens system of Diego et al. (2019): RA and Dec relative to the galaxy center. The off-axis source (red dot) is lensed by the galaxy, and a shifted image forms (blue dot). When a 100 M⊙ point lens is added at the position of the macroimage, it splits it into four microimages (black crosses). Two of them form inside the critical curve (black line) and two outside of it with magnifications μ and normalized time delays td. The caustic (red line) and a color map of the magnification in the RA−Dec plane are shown for completeness. The system demonstrates the applicability of LENSINGGW to microlenses embedded in galaxies or galaxy clusters. |
| In the text | |
 |
Fig. 8. Images recovered by LENSINGGW for a binary point lens: RA and Dec relative to the binary center of mass. The source (red dot) is lensed by two point masses (black dots) of M1 = M2 = 100 M⊙. When only one deflector is considered, two macroimages (blue dots) form. When the second lens is added, three total images (black crosses) form: their positions with respect to the critical curve (black line) and to the origin are consistent with the predictions of Schneider and Weiß. Magnifications (μ), normalized time delays (td), the caustic (red line), and a color map of the magnification in the RA−Dec plane are shown for completeness. The system confirms the applicability of the LENSINGGW algorithm to comparable-mass potentials. |
| In the text | |
 |
Fig. 9. Source parameter space investigation with LENSINGGW: Mismatch study of a nonspinning compact binary. Each dot represents a pair of component masses in the ℳc − q plane, lensed by the galaxy plus the point-lens model presented by Diego et al. (2019). All other source parameters are fixed. The point-lens mass is ML = 100 M⊙, and is placed at the position of the macroimage formed by the galaxy. For each configuration, the mismatch between the lensed and unlensed GWs is displayed in a color map; darker colors denote larger mismatches (see the color bar at the right). A large mismatch is necessary to distinguish a lensed signal as such. |
| In the text | |
 |
Fig. 10. Effects of strongly lensed image properties on microlensing. Normalized strains obtained by LENSINGGW in the Hanford detector for a compact binary lensed by an elliptical galaxy and ∼600 microlenses (as documented in Sec. 3.1). Microlensing is enhanced by strong lensing on the positive parity side (top panel) and the negative parity side (bottom panel) of the galaxy. As the magnification of the macroimage |μ| is increased (dark yellow curves, from bottom to top in each panel), the microimages lead to more prominent oscillations at the positive-parity side. In contrast, the negative-parity side exhibits the opposite behavior. Inspection of the image properties through LENSINGGW attributes this to the difference in relative magnifications and time delays among the microimages produced by the different scenarios. In both cases, microlensing boosts the S/N of the unlensed signal (light yellow curve) and turns it from a subthreshold event to a detectable one, as demonstrated by the superposed noise curves of LIGO and Virgo (gray lines). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



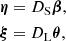
![$$ \begin{aligned} \nabla _{\boldsymbol{\theta }} \left[ \frac{1}{2} (\boldsymbol{\theta }-\boldsymbol{\beta })^2 - \psi (\boldsymbol{\theta }) \right] = 0, \end{aligned} $$](/articles/aa/full_html/2020/11/aa38730-20/aa38730-20-eq2.gif)
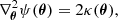
![$$ \begin{aligned}&t_{\mathrm{d},j}=t_{\rm d}(\boldsymbol{\theta }_j, \boldsymbol{\beta }) = \frac{D_{\rm L} D_{\rm S}}{D_{\rm LS}} \frac{1+z_{\rm L}}{c} \left[ \frac{1}{2} (\boldsymbol{\theta }_j-\boldsymbol{\beta })^2 - \psi (\boldsymbol{\theta }_j) \right], \end{aligned} $$](/articles/aa/full_html/2020/11/aa38730-20/aa38730-20-eq4.gif)
![$$ \begin{aligned}&\mu _j = \left[ 1/\det \left( \frac{\partial \boldsymbol{\beta }}{\partial \boldsymbol{\theta }} \right) \right]_{\boldsymbol{\theta } = \boldsymbol{\theta }_j}. \end{aligned} $$](/articles/aa/full_html/2020/11/aa38730-20/aa38730-20-eq5.gif)
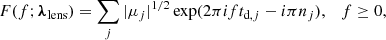
![$$ \begin{aligned} h_{\rm lensed}(f; {\boldsymbol{\lambda }}, \boldsymbol{\lambda }_{\rm lens}) =&\sum _{j=1}^N \left[ |\mu _j|^{1/2} \exp (2 \pi i f t_{\mathrm{d},j} -i \pi n_j) \right]\nonumber \\&\times h(f; {\boldsymbol{\lambda }}), \end{aligned} $$](/articles/aa/full_html/2020/11/aa38730-20/aa38730-20-eq7.gif)