| Issue |
A&A
Volume 643, November 2020
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201937114 | |
| Published online | 02 November 2020 | |
The VLA-COSMOS 3 GHz Large Project: Average radio spectral energy distribution of active galactic nuclei
1
Department of Physics, Faculty of Science, University of Zagreb, Bijenička cesta 32, 10000 Zagreb, Croatia
e-mail: ktisanic@phy.hr
2
INAF – Osservatorio di Astrofisica e Scienza dello Spazio, Via Gobetti 93/3, 40129 Bologna, Italy
3
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
4
Department of Astronomy, University of Cape Town, Private Bag X3, Rondebosch 7701, South Africa
Received:
15
November
2019
Accepted:
19
August
2020
Context. As the Square Kilometer Array (SKA) is expected to be operational in the next decade, investigations of the radio sky in the range of 100 MHz–10 GHz have become important for simulating SKA observations. In determining physical properties of galaxies from radio data, the radio spectral energy distribution (SED) is often assumed to be described by a simple power law, usually with a spectral index of 0.7 for all sources. Even though radio SEDs have been shown to exhibit deviations from this assumption, both in differing spectral indices and complex spectral shapes, it is often presumed that their individual differences can be canceled out in large samples.
Aims. Since the average spectral index around 1 GHz (observed-frame) is important for determining physical properties of large samples of galaxies, we aim to test whether individual differences in the spectra of radio-identified active galactic nuclei align with the simple assumption of α = 0.7 and test the evolution of the parameters of the synchrotron aging model with redshift and radio luminosity.
Methods. We use a sample of 744 radio-excess active galactic nuclei (RxAGN), defined as those that exhibit more than a 3σ radio luminosity excess with respect to the value expected only from the contribution from star formation, out to z ∼ 4. We constructed their average radio SED by combining Very Large Array (VLA) observations of the COSMOS field at 1.4 GHz and 3 GHz with Giant Meterwave Radio Telescope (GMRT) observations at 325 MHz and 610 MHz. To account for nondetections in the GMRT maps, we employed the survival analysis technique. We binned the RxAGN sample into luminosity- and redshift-complete subsamples. In each bin, we constrained the shape of the average radio SED by fitting a broken power-law model.
Results. We find that the RxAGN sample can be described by a spectral index of α1 = 0.28 ± 0.03 below the break frequency νb = (4.1 ± 0.2) GHz and α2 = 1.16 ± 0.04 above it, while a simple power-law model, capturing fewer spectral features, yields a single spectral index of 0.64 ± 0.07. By binning in 1.4 GHz of radio luminosity and redshift, we find that the power-law spectral index is positively correlated with redshift and that the broken power-law spectral index above 4 GHz is positively correlated with both the redshift and source size. By selecting sources with sizes less than 1 kpc, we find a subsample of flat-spectrum sources, which can be described by a spectral index of α = 0.41 ± 0.07 and a broken power-law spectral index of α1 = 0.1 ± 0.1 (α2 = 0.55 ± 0.09) below (above) a break frequency of νb = (2.7 ± 0.5) GHz.
Conclusions. We have constrained the radio SED for a sample of RxAGN in the COSMOS field using available VLA and GMRT data, corresponding to the rest-frame frequency range from ∼0.3 GHz to ∼10 GHz. We describe our derived average radio SED of RxAGN using power-law and broken power-law models, yielding a radio SED that steepens above ∼4 GHz.
Key words: galaxies: evolution / galaxies: statistics / radio continuum: galaxies / galaxies: active
© ESO 2020
1. Introduction
In recent years, the investigation of the radio sky at sub-GHz frequencies has received more attention (see e.g., Padovani 2016) since the advent of the Low-Frequency Array (LOFAR), which can operate in the 15−200 MHz frequency range (van Haarlem et al. 2013). Moreover, the Square Kilometer Array (SKA, Braun 1996; Dewdney et al. 2009) is expected to operate at frequencies from 50 MHz to 20 GHz1 with nanojansky sensitivities (Norris et al. 2013), while precursors, such as the Murchison Widefield Array Commissioning Survey (Hurley-Walker et al. 2014), have already started producing catalogs of sources detected at ∼100 MHz. Our ability to make predictions for these new instruments is tied to the knowledge of the spectral energy distribution (SED) of sources upon which semi-empirical simulations are devised (Wilman et al. 2008).
The radio SED of sources in the frequency range of 1−10 GHz are often assumed to be described by a simple power law, with a spectral index of α = 0.7 (using the convention S ∼ ν−α, Condon 1992). The simple power-law shape of the radio SED is expected to be mainly due to synchrotron radiation, arising either from supernova remnants, tracing star formation, or from the vicinity of supermassive black holes, tracing active galactic nuclei (AGN) activity. However, the radio SEDs have been shown to exhibit deviations from these simple relationships by having different spectral indices and complex spectral shapes (see, e.g., Condon et al. 1991; Kukula et al. 1998; Kimball & Ivezić 2008; Clemens et al. 2008, 2010; Leroy et al. 2011; Murphy 2013; Calistro Rivera et al. 2017; Galvin et al. 2018; Tisanić et al. 2019). For example, quasars have been shown to have spectral indices in the 1−10 GHz range which may be either steep (> 0.5) or flat (< 0.5) (Kukula et al. 1998). At 150 MHz, Toba et al. (2019) find an even greater variety in radio spectral indices, ranging from 0.5 to 2.5.
In the simple picture, the shape of the radio SED of individual sources at higher frequencies is related to the synchrotron aging process and additionally to free-free emission in star-forming galaxies, while the lower-frequency part of the spectrum may be influenced by the different absorption processes (see, e.g., Condon 1992). In bright samples (∼1 Jy), alongside flat-spectrum sources (α < 0.5), a significant fraction (40−50%) shows either a steeper SED (α > 0.5), or a peaked or inverted spectrum, (Kapahi 1981; Peacock & Wall 1982; De Zotti et al. 2010). Kimball & Ivezić (2008) found that individual SEDs of complex and resolved sources (at a 5″ resolution) are best described by a spectral index of ∼0.8, while unresolved sources have a flat spectral shape (α ∼ 0). They point out that emission from extended radio lobes tends to be steeper, while flatter emission might arise from compact quasar cores and jets due to self-absorbed synchrotron emission. Synchrotron aging is usually described either assuming a single injection of electrons with a constant or isotropic pitch angle, or assuming continuous injection of electrons (Kardashev 1962; Jaffe & Perola 1973; Pacholczyk 1977). Absorption processes affecting the SED shape are synchrotron self-absorption and free-free absorption, which have been used to explain radio spectra of gigahertz peaked-spectrum and compact steep-spectrum sources (O’Dea 1998; Collier et al. 2018). O’Dea & Baum (1997) found that the source size for these types of sources is negatively correlated with turnover frequency in their spectra (Fanti et al. 1990; O’Dea & Baum 1997), while sources have been found with turnover frequencies above 10 GHz (Edge et al. 1998). By using LOFAR observations, Calistro Rivera et al. (2017) find statistically significant steepening in their AGN SED in the 150 MHz − 600 MHz range compared to AGN SEDs around 1 GHz.
Previous studies of radio SEDs of individual sources find that the average value of the spectral index is consistent with the expected value of α = 0.7 (e.g., Kukula et al. 1998; Toba et al. 2019). Radio luminosity functions of AGN have been shown to differ for flat and steep spectrum sources (Dunlop & Peacock 1990). Novak et al. (2018) quantify the impact of different SED shapes on radio luminosity functions by pointing out that while the differences in individual galaxies’ SEDs can be canceled out for large samples, even a slight change of 0.1 in the mean value of the spectral index could result in a 0.1 dex change in rest-frame luminosities.
In this paper we present a survival analysis study of the average radio SED of a sample of radio-excess AGN in the Cosmological Evolution Survey (COSMOS) field, identified by an excess in radio luminosity compared to that expected solely from star-forming processes. A combination of radio data available in the COSMOS field offers a way to construct approximately luminosity-complete samples out to z ∼ 4, farther than would be possible when considering sources individually. We construct average radio SEDs following the method detailed in Tisanić et al. (2019).
In Sect. 2 we describe the available observations and data used in the constriction of the radio SEDs and the selection of the radio-excess AGN sample. In Sect. 3 we briefly summarize the method used to construct the radio SEDs and describe models used to analyze its shape. We use the convention that a steeper SED means a larger spectral index (S ∼ ν−α) throughout this paper and adopt the following cosmological parameters: ΩM = 0.3, ΩΛ = 0.7, and H0 = 70 km s−1 Mpc−1.
2. Data and sample
To assess the radio SED, we combined catalogs of the radio data in the COSMOS field at four observer-frame frequencies: 325 MHz and 610 MHz, obtained with the Giant Meterwave Radio Telescope (GMRT) (Tisanić et al. 2019), and at 1.4 GHz (Schinnerer et al. 2010) and 3 GHz (Smolčić et al. 2017a), obtained with the Karl G. Jansky Very Large Array (VLA). Here we briefly describe the VLA (Sect. 2.1) and GMRT (Sect. 2.2) data and the selection of the sample used in this paper (Sect. 2.3).
2.1. VLA data
We have combined catalogs of the VLA-COSMOS 3 GHz Large Project (hereafter VLA3LP, Smolčić et al. 2017a) and the VLA-COSMOS 1.4 GHz Joint Project (hereafter VLA1.4JP, Schinnerer et al. 2010).
The VLA3LP map was constructed from 384 h of observations of the 2deg2 COSMOS field. Observations were carried out over 192 pointings in the S-band with VLA in A and C antenna configurations. These were wide-band observations with a total bandwidth of 2084 MHz derived from 16 spectral windows, each 128 MHz wide. The final mosaic reached a median root-mean-square (RMS) of 2.3 μJy beam−1 at a resolution of 0.75″. Considering the large bandwidth and the volume of the data, each pointing was imaged separately using the multi-scale multi-frequency synthesis algorithm (hereafter MSMF, Rau & Cornwell 2011) and then combined into a single mosaic. The MSMF algorithm had been found to be optimal for both resolution and image quality in terms of the RMS noise and sidelobe contamination (Novak et al. 2015). The VLA3LP catalog has been derived using BLOBCAT (Hales et al. 2012) with a 5σ threshold. In total, 10 830 sources were recovered (67 of which were multi-component sources). For more details, see Smolčić et al. (2017a).
The VLA1.4JP catalog is a joint catalog comprised of the VLA-COSMOS 1.4 GHz Large Project (Schinnerer et al. 2007) and VLA-COSMOS 1.4 GHz Deep Project (Schinnerer et al. 2010) surveys, as described in Schinnerer et al. (2010). The VLA1.4JP catalog was constructed by combining the observations of the entire 2deg2 COSMOS field at a resolution of 1.5″ × 1.4″ (Schinnerer et al. 2007), and observations of the central 50′×50′ subregion of the COSMOS field at a resolution of 2.5″ × 2.5″ (Schinnerer et al. 2010). The average RMS in the resulting map was found to be 12 μJy. The VLA1.4LP observations consisted of 240 h of observations over 23 pointings spread out over the entire COSMOS field in the L band centered at 1.4 GHz and with a total bandwidth of 37.5 MHz in VLA A configuration and 24 h in the C configuration. The VLA1.4DP observations supplemented the 7 central pointings with an additional 8.25 h of observations per pointing using the A configuration and the same L-band configuration. These new measurements were then combined in the uv-plane with the VLA1.4LP observations. The VLA1.4JP catalog was constructed by using the SExtractor package (Bertin & Arnouts 1996) and the AIPS task SAD, yielding 2865 sources (Schinnerer et al. 2010).
2.2. GMRT data
The 325 MHz observations of a single pointing were carried out with the GMRT using a bandwidth of 32 MHz (Tisanić et al. 2019). The observations lasted for 45 h in total, comprising four observations with a total on-source time of ∼40 h. They were reduced using the Source Peeling and Atmospheric Modeling pipeline (SPAM; Intema et al. 2017) pipeline and imaged at a resolution of 10.8″ × 9.5″. A primary beam correction was applied to the pointing. We measured a median RMS of 97 μJy beam−1 over the ∼2deg2 COSMOS field. In total, 633 sources were identified using BLOBCAT down to 5σ. By employing a total-over-peak flux density criterion, we consider 177 of these sources to be resolved (derived by mirroring the fifth percentile of the total-over-peak flux density derived in bins of the signal-to-noise ratio, see Tisanić et al. 2019, for details).
The 610 MHz observations are described in detail in Tisanić et al. (2019). They were carried out at a central frequency of 608 MHz using a bandwidth of 32 MHz. Observations lasting 86 h were conducted (spread over eight observations with an average time on source per pointing of ∼4 h) during which a total of 19 pointings were observed. The data were reduced using the SPAM pipeline and imaged at a resolution of 5.6″ × 3.9″. A primary beam correction and average pointing error corrections were applied to each pointing prior to mosaicing. We measured a median RMS of 39 μJy beam−1 in the final mosaic over the ∼2deg2 COSMOS field. BLOBCAT was used to extract 999 sources down to 5σ, 196 of which we consider to be resolved by a total-over-peak flux density criterion (see Tisanić et al. 2019, and preceding paragraph for details).
2.3. The 1.4 GHz selected sample
In order to obtain at least two data points per source for the SED analysis, following Tisanić et al. (2019) we have defined and analyzed a 1.4 GHz-selected sample of sources from the VLA1.4JP catalog that were detected in the VLA3LP counterpart catalog. The 3 GHz data have lower RMS (∼2 μJy beam−1) than the ∼12 μJy beam−1 RMS of the 1.4 GHz data. This procedure introduced only minimal potential biases stemming from the 1.4 to 3 GHz spectral index distribution, as almost all 1.4 GHz sources (∼90%, Smolčić et al. 2017a) have counterparts at 3 GHz.
Smolčić et al. (2017b) obtained photometric redshifts by cross-correlating the 3 GHz Source Catalog with multi-wavelength counterparts, drawn from three catalogs. This resulted in 7729 COSMOS2015 (Laigle et al. 2016), 97 i-band (Capak et al. 2007), and 209 IRAC (Sanders et al. 2007) counterparts to the 8696 3 GHz sources found within the 1.77 deg2 subarea of the COSMOS field. Spectroscopic redshifts were taken from the COSMOS spectroscopic catalog containing 97102 sources with a counterpart (M. Salvato, priv. comm.). In total, 7911 out of the 8035 sources had determined redshifts, of which 2734 had spectroscopic, and 5177 photometric redshifts. To determine the physical properties of the AGN host galaxies, a three-component SED-fitting procedure (Delvecchio et al. 2017) was applied using all of the available photometry.
As described by Smolčić et al. (2017b), AGN were divided into moderate-to-high radiative luminosity AGN (HLAGN) and low-to-moderate radiative luminosity AGN (MLAGN), which are analogs of high- and low-excitation emission line AGN, respectively. As summarized in Fig. 10 in Smolčić et al. (2017b), HLAGN were identified as either X-ray AGN (i.e., having X-ray luminosity LX > 1042 ergs s−1, Szokoly et al. 2004), mid-infrared AGN (using the criteria from Donley et al. 2012), or using optical-to-millimeter SED fitting (Delvecchio et al. 2017). MLAGN were identified by requiring red optical colors MNUV − Mr+ > 3.5 and no Herschel-band detections. The MLAGN class contains both AGN exhibiting an excess in radio luminosity (described below) and quiescent AGN.
Within this dataset, we use a sample of radio-excess active galactic nuclei (RxAGN). The class of RxAGN is identified by their 3σ radio excess with respect to the value of radio luminosity expected only from the contribution from star formation calculated using the infrared luminosity (see Smolčić et al. 2017b; Delhaize et al. 2017; Delvecchio et al. 2017). We separate RxAGN into low-to-moderate luminosity quiescent RxAGN (RxQMLAGN), low-to-moderate luminosity star-forming RxAGN (RxSMLAGN), and moderate-to-high luminosity RxAGN (RxHLAGN), depending on whether they satisfy the MLAGN or HLAGN criteria. We have combined flux densities at 1.4 GHz from the 1.4 GHz-selected sample of RxAGN sources with their corresponding flux densities at 3 GHz. To this dataset, we have added flux densities of corresponding sources in the GMRT catalogs, matched using TOPCAT.
In summary, we have selected a sample of RxAGN in the COSMOS with high completeness for redshifts within z ∈ [0, 4], and 1.4 GHz radio luminosities within log L1.4 [W Hz−1] ∈ [24, 26], as shown in Fig. 1. In Fig. 2 we show the mean completeness correction for the sample of RxAGN as a function of redshift. Mean completeness corrections for different redshift bins were computed using the 3 GHz flux densities of sources in the RxAGN sample. The completeness corrections used were interpolated from the completeness correction table of the VLA3LP catalog (see Table 2 in Smolčić et al. 2017a). The mean completeness is ∼100% up to z ∼ 1 and decreases at higher redshift, but is higher than ∼75% out to redshift z = 4. In total, our sample comprises 744 RxAGN, of which 230 are RxHLAGN, 134 RxQMLAGN and 380 are RxSMLAGN.
 |
Fig. 1. Radio luminosity density L1.4 [W Hz−1] and redshift for RxAGN (black points). Red points correspond to the selected redshift and radio luminosity sample of RxAGN used in this work and are contained within log L1.4 [W Hz−1] ∈ [24, 26] and z ∈ [0, 4]. The histograms show the distribution of radio luminosity and redshift for all RxAGN and the RxAGN sample used in this work with black and red bars, respectively. The radio luminosity-redshift distribution is used to choose a complete sample of RxAGN. |
 |
Fig. 2. Mean completeness correction for the sample of RxAGN as a function of redshift. The mean completeness (solid line), with its corresponding standard deviation (shaded interval), were estimated for different redshift bins using the 3 GHz flux densities and interpolated completeness corrections for the VLA-COSMOS 3 GHz Large Project catalog (Table 2 in Smolčić et al. 2017a). The mean completeness correction is used to quantify the completeness in the RxAGN sample, which is higher than 75% up to z ∼ 4. |
3. Methods
We have used the method developed and described in detail by Tisanić et al. (2019) to derive survival-analysis based estimates of the average radio SED. In Sect. 3.1 we give a brief overview of the procedure used to construct the average radio SEDs. In Sect. 3.2 we give an overview of models used to describe the radio SED.
3.1. Construction of average radio SEDs
We present the radio SED as flux density vs. frequency in logarithmic space. To achieve uniform frequency binning, we used equally separated bins in log space of the rest-frame frequencies. For each bin, we computed the mean of the log rest-frame frequency and its standard deviation. We then combined the normalized flux densities and normalized upper limits, defined as 5 times the local RMS value at the position of the source, of individual galaxies into a single dataset. We normalized flux densities of both detections and upper limits to a value based on a linear fit to the 1.4 GHz and 3 GHz spectra of individual sources, evaluated at the median rest-frame log-frequency of sources in our sample. If there were no upper limits within the bin, we computed the mean normalized log-flux density and its standard deviation for each bin. If there were upper limits within a particular bin, we estimated the mean normalized log-flux density and its standard deviation from the constructed best-fitting Weibull model of the survival function to the Kaplan-Meier survival function.
Finally, we fit a broken power-law (BPL) to the normalized log-flux density, 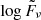 ,
,
which is described by the rest-frame frequency, νr, normalizing frequency νn, the break frequency νb, normalization constant C, and the spectral indices α1 (below νb) and α2 (above νb). The fitting was performed by employing the orthogonal distance regression method bounded within the 2σ confidence interval of parameters, as derived by using the Markov chain Monte Carlo (MCMC) method. The normalization constant C is included in the models to ensure statistical validity of our fits and is hereafter implied by the use of “∼” in the following equations. We also discuss the SED shape by employing models of synchrotron self-absorption and synchrotron aging, as outlined below.
3.2. Description of synchrotron spectrum
The spectrum of a synchrotron radio source is influenced by synchrotron self-absorption (SSA) and synchrotron aging (SA) processes. Here we briefly describe the influence of both processes on the radio SED.
If the synchrotron emission is described as a power law with spectral index α, the resulting SSA SED for a homogeneous source has the following shape (constructed using the transfer equation and a power-law SED absorption coefficient from Pacholczyk 1977):
This model produces a peak around ν = ν1 and a simple power-law SED with a spectral index α for ν ≫ ν1.
If a source is initially described with a spectral index α, the spectrum will deviate from a power law at later times due to electrons losing energy over time. This produces a spectrum that is steepened by Δα, a parameter that varies between single injection and continuous injection models, at frequencies higher than the break frequency νb (see, e.g., Condon 1992):
We investigate the combined influence of both effects on the shape of our radio SED by introducing a fraction of synchrotron-aged flux density, f,
This equation reproduces Eq. (2) for ν ∼ ν1 ≪ νb, and f → 0, and Eq. (3) for ν1 ≪ ν ∼ νb, and f → 1. The model presented in Eq. (4) is chosen so that it can describe a population of sources that have either a synchrotron aged SED or a synchrotron self-absorbed SED. In this case, the fraction f would represent the fraction of the sample having a synchrotron-aged spectral shape. A further complication to this simple picture would be that a source in the sample has both contributions present, but this would greatly increase the number of free parameters.
In contrast to simple models discussed in Tisanić et al. (2019), for which the fitting procedure was developed, model of Eq. (4) has multiple break frequencies. It is, therefore, a priori unclear which parameters can be fixed to a particular value. Therefore, to further discuss models of synchrotron self-absorption and aging, we have employed the MBAM in Sect. 5.1. The method is summarized in Sect. 3.3 and is explained in detail in Transtrum et al. (2010), Transtrum & Qiu (2014).
3.3. Manifold boundary approximation method
The radio SED parameters have been estimated using the orthogonal distance regression constrained to the 2σ MCMC-derived confidence intervals. However, this procedure yielded large estimated parameter errors due to the complex shape of the fitting function. Moreover, as in Tisanić et al. (2019), the MCMC estimates are not simple ellipses, which we had solved by fixing the obvious choice of the greatest uncertainty, the break frequency. Upon applying the same procedure to, for example, Eq. (4), we have found that it is not easy to determine the parameters that have the greatest impact on the derived uncertainties. We have therefore employed the Manifold Boundary approximation method (MBAM) to determine which of the model parameters contributes to the estimated errors the most (for details, see for example, Transtrum et al. 2010; Transtrum & Qiu 2014).
The MBAM method solves the geodesic equation in parameter space to determine the least-precise parameter (or combination of parameters). The method consists of computing the Fisher information metric (FIM) from the model parameters (labeled θμ) following the Transtrum & Qiu (2014) algorithm, described below.
The method first recognizes that in the space of model residuals of Nd measurements there is an Nd dimensional manifold, ℛ, with FIM equaling the Euclidean metric,
Each measurement’s residual, ri, is defined as the difference between the data point yi, with uncertainty σi, and the particular model’s evaluation fi as ri = (yi − fi)/σi. The particular model’s parameters, which we label θ1, ⋯, θNp, constitute an Np-dimensional manifold, ℳ. Residuals are therefore an embedding of the model manifold in the residuals’ manifold. The metric on ℳ, g, is therefore computed using the pullback, r*, as
The geodesic equation in ℳ
is then solved as an initial value problem, where 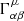 are the Christoffel symbols of the second kind. The initial position is chosen to be the best-fitting parameters
are the Christoffel symbols of the second kind. The initial position is chosen to be the best-fitting parameters 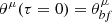 . The “velocity”, dθμ/dτ(τ = 0), is chosen to be the eigenvector of the FIM corresponding to the smallest eigenvalue. The components of the eigenvector corresponding to the smallest eigenvalue at a sufficiently large τ are compared to the values at τ = 0.
. The “velocity”, dθμ/dτ(τ = 0), is chosen to be the eigenvector of the FIM corresponding to the smallest eigenvalue. The components of the eigenvector corresponding to the smallest eigenvalue at a sufficiently large τ are compared to the values at τ = 0.
4. Results
In this section we constrain the shape of the average radio SED of RxAGN and subsets of the RxAGN sample. In Sect. 4.1, we derive the SED for the RxAGN sample, in Sect. 4.2 we describe the SEDs of subsamples of the RxAGN sample and analyze correlations with redshift different RxAGN subsamples, source size and further classifications in Sect. 4.3.
4.1. RxAGN SED
In Fig. 3, we show the mean normalized log-flux density and the corresponding standard deviation of the distribution of normalized log-flux densities for each rest-frame frequency bin. Using a simple power-law (PL) model, the RxAGN SED, shown in the left panel of Fig. 3, can be described by a spectral index of 0.64 ± 0.07. However, as can be seen from Fig. 3, this model does not describe the dataset well. Therefore, we fit the BPL model to account for spectral curvature, as shown in the right panel of Fig. 3. The spectral indices of this model are α1 = 0.28 ± 0.03, and α2 = 1.16 ± 0.04, while the break frequency, which in the full model was poorly constrained by νb = (4.1 ± 0.2) GHz, was fixed to 4 GHz to reduce parameter uncertainties, as described in Tisanić et al. (2019).
 |
Fig. 3. Radio SED of RxAGN as normalized log-flux density vs. rest-frame frequency for z ∈ [0, 4] and log L1.4 [W Hz−1] ∈ [24, 26]. A single power-law (left panel) and a broken power-law (right panel) model of the radio SED are shown as red lines with red confidence intervals. Detections are shown as gray points, upper limits as yellow arrows, bins without upper limits as green points and bins with upper limits as magenta points. The plots show the best fitting power-law (0.64 ± 0.07) and broken power-law (α1 = 0.28 ± 0.03, α2 = 1.16 ± 0.04 and νb = (4.1 ± 0.2) GHz) models. |
To investigate how SA and SSA processes could produce the observed SED, we have fit Eq. (4) to the RxAGN dataset. By blindly applying this model, the RxAGN SED is described with the following set of parameters, exhibiting varying degrees of uncertainties, f = 0.7 ± 0.3, αSA = 0.4 ± 0.5, αSSA = 0.8 ± 0.6, ν1 = (1 ± 2) GHz, νb = (6 ± 2) GHz, Δα = 2 ± 1. As can be seen in the upper panel of Fig. 4, this model describes the data well, but is not very informative regarding the constraints of the spectral index and the fraction f. We have therefore used the MBAM method to reduce the uncertainties of these parameters, with the resulting SED shown in the lower panel of Fig. 4. We have found that the model is best constrained by setting νb → ∞, which corresponds to a reduced model described using a synchrotron self-absorbed SED with a spectral index labeled αSSA, and a power-law SED with a spectral index labeled αSA and without any aging break. The thus derived model parameters are αSA = 0.7 ± 0.2, αSSA = 1.1 ± 0.5, ν1 = (3.0 ± 0.3) GHz and f = 0.8 ± 0.3. In Fig. 4, we show that this reduced model describes the same data points with a similar SED shape as the full model.
 |
Fig. 4. Average radio SED of the RxAGN sample with the model from Eq. (4) fit. Upper panel: resulting model before applying the MBAM model reduction method (described in Sect. 3.3), while the lower panel shows the best-fitting model after reducing the number of parameters with the MBAM method, used to better constrain this complex model. |
Figure 5 shows the behavior of the components of the eigenvector corresponding to the smallest FIM eigenvalue for the radio SED of RxAGN. In the best fitting point (middle panel of Fig. 5), the eigenvector’s components are pointing in a direction that does not purely indicate the most uncertain parameter. However, along a geodesic, for sufficiently large τ, the movement along a geodesic halts in each direction other than Δα, as indicated by diminishing values of the logarithmic parameter derivatives in the left panel of Fig. 5. The eigenvector corresponding to the smallest FIM eigenvalue, now computed at the end of the geodesic curve, clearly shows that the least determined parameter is Δα. Moreover, as indicated by the blue line in the left panel of Fig. 5, the geodesic curve significantly varies only in the Δα direction, pointing toward Δα → ∞. This reduced model also reduces the need for νb.
 |
Fig. 5. Behavior of logarithmic derivative of parameters along the geodesic curve (left panel) and the components of the FIM eigenvector corresponding to the smallest eigenvalue at the beginning (end) of the geodesic curve are shown in the middle (right) panel the model from Eq. (4). The figure shows the details of the MBAM method used in constraining the parameters of this complex model. |
4.2. Subsamples
In order to test if the shape of the radio SED of RxAGN depends on parameters such as redshift and radio luminosity, we split the RxAGN dataset in bins of redshift and 1.4 GHz radio luminosity and fit both the PL and the BPL models to each bin separately. The resulting SEDs are shown in Fig. 6 and the best-fitting PL spectral indices are shown for each selected bin in Fig. 7 for the whole RxAGN dataset. The bins, whose boundaries are outlined by black dashed lines in Fig. 7, split the RxAGN sample into four bins and additionally include two bins, for lower and higher 1.4 GHz radio luminosities. All bins have a mean completeness correction higher than 75%.
 |
Fig. 6. SEDs derived for subsets of the RxAGN sample divided by redshift, z, and radio luminosity, log L1.4 [W Hz−1]. Shown is the best-fitting power-law model for each bin. The panels show the radio SEDs for different subsets of RxAGN and correspond to numbered bins presented in Table 1 and Fig. 8. |
 |
Fig. 7. Spectral indices derived for subsets of the RxAGN sample divided by redshift, z, and radio luminosity, log L1.4 [W Hz−1], described in Sect. 5.2. The color-scale in the left panel shows the spectral index of the PL model, while the color-scales in the middle and right panels show the spectral indices α1 and α2 of the broken power-law model. Bins are outlined by black dashed lines. The panels show the spectral indices radio SEDs shown in Fig. 6 for different subsets of RxAGN and correspond to numbered bins presented in Table 1 and Fig. 8. |
We have further used source sizes of RxAGN (Bondi et al. 2018) to investigate whether there is a correlation of spectral indices with the source size, D, or the type of the source (RxHLAGN, RxSMLAGN, RxQMLAGN) in different bins. To this end, we further split the dataset in mutually independent subsets of RxHLAGN, RxQMLAGN and RxSMLAGN (see Sect. 2.3 for details). In Fig. 8 we show the dependence of the BPL spectral indices on source size for subsets of the RxAGN dataset binned in redshift and 1.4 GHz radio luminosity. We show the determined spectral indices for various bins in Table 1.
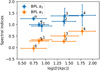 |
Fig. 8. Dependence of the broken power-law spectral indices below and above a break frequency of 4 GHz (α1 and α2, respectively) on the source size, log D [kpc], for the subsets of the RxAGN dataset for different values of in log D [kpc], with corresponding errors in spectral indices. The error bars for log D [kpc] show the standard deviations of log D [kpc] within each bin. The numbers indicate the bin number in Table 1. The table lists the spectral indices radio SEDs shown in Fig. 6 for different subsets of RxAGN and correspond to numbered bins presented in Fig. 8. |
Parameters of the power-law and broken power-law models, and source size, log D [kpc], derived for subsets of the RxAGN sample divided by redshift, z, and radio luminosity, log L1.4 [W Hz−1], described by the mean and standard deviation of redshifts and radio luminosity for each bin.
In order to investigate the possibility that there might be sources in our sample that are severely influenced by SSA, we split our sample by selecting all sources having source sizes less than 1 kpc. This size is expected for gigahertz-peaked sources (O’Dea 1998; Collier et al. 2018). From the turnover frequency-linear size relation (Orienti & Dallacasa 2014) we expect that this requirement should select sources with turnover frequencies above 1 GHz. The constraint on source size less than 1 kpc produces a sample of 25 sources, for which we construct a PL and BPL SED.
The PL model yields an SED with a spectral index of α = 0.41 ± 0.07, while the BPL model describes the spectrum with a spectral index of α1 = 0.1 ± 0.1 below νb = (2.7 ± 0.5) GHz and α2 = 0.55 ± 0.09 above νb. The resulting SED is shown in Fig. 9.
 |
Fig. 9. Radio SED of a sample of flat-spectrum sources, produced by selecting all sources having sizes less than 1 kpc. Red line shows the broken power-law model. We find that selecting sources with sizes less than 1 kpc produces a sample of flat-spectrum sources, described by a spectral index of α = 0.41 ± 0.07 and a broken power-law spectral index of α1 = 0.1 ± 0.1 (α2 = 0.55 ± 0.09) below (above) a break frequency of νb = (2.7 ± 0.5) GHz. |
4.3. Significance of correlations
In Fig. 10, we show the components of the correlation matrix with given p-values of correlation coefficients. If we adopt a p-value cut, P < 0.1, this correlation matrix shows the following. Firstly, there is a positive correlation of the PL spectral index α with both the redshift and radio luminosity. Secondly, there is a positive correlation of the PL spectral index α with both the redshift and radio luminosity. And thirdly, there is a positive correlation of the BPL spectral index α2 with source size, radio luminosity and the PL spectral index α.
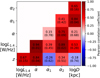 |
Fig. 10. Correlation matrix for properties of subsets of the RxAGN sample. Colors indicate positive or negative Pearson correlation coefficient, written on the plot for each parameter pair with its corresponding p-value in parentheses. The considered variables in the correlation matrix are the 1.4 GHz radio luminosity, log L1.4 [W Hz−1], power-law spectral index α, broken power-law spectral indices α1 and α2, and source size, log D [kpc]. The correlation matrix presented in this figure indicates the presence and significance of correlations between different properties of the subsets of the RxAGN sample. |
We have further tested the level of significance of the various correlations presented in the correlation matrix. To this end, we have computed the p-values of parameters in linear models for all subsets of parameters using the Analysis of variance (ANOVA) method, as implemented in the STATSMODELS package (Seabold et al. 2010). The goal of this method was to minimize overfitting the spectral indices, while retaining the ability to discern models by how well they explain the variability between the subsets of RxHLAGN, RxQMLAGN and RxSMLAGN. The ANOVA results are shown in Table 2 and are based on spectral indices presented in Table 1 and visualized in Fig. 11. We find that the PL spectral index and the BPL spectral index α2 can both be described by a model containing only redshift and source size with a significance value of P < 0.01. The parameters of the corresponding linear models are
 |
Fig. 11. Distribution of the broken power-law spectral indices for the subsets of the RxAGN sample. Black crosses are spectral indices derived for individual bins, listed in Table 1. Blue intervals denote α1 while orange intervals denote α2. The distributions of the broken power-law spectral indices are used to determine the parameters that explain the differences between the RxAGN subsets using the ANOVA method summarized in Table 2. |
Summary of ANOVA results for the power-law and broken power-law spectral indices for RxAGN subsamples for models selected by requiring P < 0.1.
which is in line with correlations from the correlation matrix.
We investigate weaker variations that might be present between the spectral index subsets by employing a p-value cut of P < 0.1, the least stringent of the commonly used p-value cuts. We find that only the BPL spectral index α1 can be described using source type and source size. The parameters of the corresponding linear models are
5. Discussion
In this section we explore the properties of the derived radio SED of RxAGN. In Sect. 5.1, we investigate the cause for the derived SED shape. In Sect. 5.2 we analyze possible correlations with redshift of different RxAGN subsamples, source size and further classifications, while in Sect. 5.3 we discuss the SED for the subsample of flat-spectrum sources.
5.1. Possible cause of the SED shape
It is clear from Fig. 3 that a simple PL model does not describe the SED well. Using the BPL model yields an SED shape with a spectral index difference Δα = α2 − α1 = 0.88 ± 0.05. This spectral index difference is higher than expected from the simple Kardashev-Perola model of synchrotron aging (Δα = 0.5, Kardashev 1962; Kardashev et al. 1962). This may indicate that the SEDs of individual sources may be better described by either more complex models of synchrotron aging (Jaffe & Perola 1973; Tribble 2014) or the SED shapes are affected by processes of synchrotron self-absorption or free-free absorption (Menon 1983; Tingay & de Kool 2003; Kameno et al. 2005).
The SED shape derived by the MBAM method shows a “bump” at ∼3 GHz and a low frequency steepening around 0.6−1 GHz. For sources detected at both GMRT and VLA frequencies, there seems to be a deficit in flux computed at 610 MHz based on the VLA fluxes. This correction is appropriate for some of the sources, while blindly applying a 20% correction of the total flux density introduced overcorrections in others. The flux density offset is different when computed based on the 1.4 GHz catalog and when computed using the 3 GHz catalog, indicating complications due to complex spectral shapes. Since this frequency range is dominated by the 610 MHz GMRT catalog fluxes, to account for possible biases in the fluxes at this frequency, we have performed again the SED fitting procedure without the 610 MHz catalog. We find a similar steepening in the SED when using only the 325 MHz, 1.4 GHz and 3 GHz data, indicating that the effect may be due to the intrinsic shape of the SED and not due to systematic effects of a particular catalog. Alternatively, this result could explain the findings of Calistro Rivera et al. (2017), since the observed feature in our SED effectively produces a steeper spectrum below 1 GHz with a flattening around 1 GHz. Moreover, the fraction of SSA emission (1 − f = 0.2 ± 0.03, obtained using Eq. (4) and the MBAM procedure) described by a steep SSA spectral index is in line with Kapahi (1981) and Peacock & Wall (1982), suggesting the presence of gigahertz-peaked or inverted spectrum sources in our sample.
As an alternative, we have fit the free-free absorption models both in the form of a foreground-screen and as a mixed model, as described in Tisanić et al. (2019). The foreground-screen model has a spectral index of α = 0.8 ± 0.1 with an optical depth at 1 GHz of τ1 = 0.2 ± 0.1, while the mixed model has a spectral index of α = 0.9 ± 0.1 and an optical depth at 1 GHz of τ1 = 1.3 ± 0.5.
5.2. SED shape dependence on various observables
The BPL spectral indices are rising with source size, which would imply that the radio SEDs of larger sources are more influenced by larger-scale features (jets). Blundell et al. (1999) argue that sources at higher redshift are on average younger than sources at lower redshift and thus have interactions of their jets occurring closer to the host galaxy. This could explain the trend of the rising BPL spectral index α2 with both the redshift and source size. Ker et al. (2012) find that the strongest correlation is between spectral index and source size, with redshift correlation becoming more important around ∼1 GHz. This might explain the ANOVA giving higher importance to redshift dependence for the higher frequency BPL spectral index (α2) than for α1. Furthermore, only the spectral index below 4 GHz shows (weak) correlation with the type of source. The ANOVA test suggests a 2σ lower spectral index α1 for RxSMLAGN than for other subsets, as shown in Fig. 11.
For a 10 kpc sized source which is close to the values of log D [kpc] for bins listed in Table 1 these correlations would imply a broken power-law radio SED described by a spectral index of 0.9 ± 0.2 above 4 GHz and a spectral index (0−0.3)±0.1 below 4 GHz, with the higher value estimated for RxHLAGN and the lower value estimated for RxSMLAGN. As a consistency check, if we approximate our RxAGN sample as having z ∼ 2, we are in agreement with our parameters of α1 and α2 for the average radio SED of RxAGN, reported in Sect. 4.
The positive correlation of spectral indices with source size may be explained by the size-turnover frequency relation for gigahertz-peaked sources (Orienti & Dallacasa 2014). Smaller source size (< 1 kpc) implies a high turnover frequency, thereby producing smaller α1 values in an averaged sample. The higher-frequency spectral index could also be affected by this relation, since the spectral peak could be broadened, producing a flatter radio SED (O’Dea et al. 1991). The redshift dependence could be related to the difference in luminosity functions of flat and steep spectrum sources (Jarvis & Rawlings 2002).
5.3. Flat spectrum sources
Both the PL and the BPL spectral indices classify our sample below 1 kpc as having a flat spectrum by the usually accepted α < 0.5 criterion (see, e.g., De Zotti et al. 2010). Since the break frequency is larger than 1 GHz, the < 1 kpc sample does not show a significant contribution of compact steep-spectrum sources (a spectral index of ∼0.75 above a turnover frequency of 0.5 GHz, Kapahi 1981; Peacock & Wall 1982; O’Dea 1998; De Zotti et al. 2010).
We find a spectral index difference of Δα = α2 − α1 = 0.45 ± 0.1, which is less than the theoretical limit imposed by pure synchrotron self-absorption (Mhaskey et al. 2019). This indicates that other absorption processes may also influence the flat spectrum radio SED, such as free-free absorption (Kameno et al. 2005; Tingay & de Kool 2003). We have performed a fit of the SSA model on the < 1 kpc sample, yielding a flat spectral index of αSSA = 0.53 ± 0.06 above a break frequency of ν1 = (0.9 ± 0.1) GHz. A broader rest-frame frequency range is needed to determine if this is due to a single SSA component, or a result of multiple break frequencies (Kellermann & Pauliny-Toth 1969; Cotton et al. 1980). As an alternative, we have fit the free-free absorption models both in the form of a foreground-screen, wherein absorption occurs in front of the source, and as a mixed model, wherein absorption occurs within the source, as described in Tisanić et al. (2019). The foreground-screen model has a spectral index of α = 0.6 ± 0.1 with an optical depth at 1 GHz of τ1 = 0.4 ± 0.1, while the mixed model has a spectral index of α = 0.6 ± 0.1 and an optical depth at 1 GHz of τ1 = 1.2 ± 0.4. Both models point to a similar spectral index and differ in optical depth at 1 GHz.
6. Summary
We have constrained the average radio SED for a sample of AGN in the COSMOS field using available VLA and GMRT data in the rest-frame frequency range from ∼0.3 GHz to ∼10 GHz. The radio-excess AGN (RxAGN) sample contained sources which exhibit a 3σ excess of 1.4 GHz radio luminosity, compared to that expected solely from star-forming processes occurring within the AGN host galaxies. The RxAGN sample is relatively complete (75%) in redshift out to z ∼ 4 and in radio luminosity range from 1024 W Hz−1 to 1026 W Hz−1.
We find that if we fit the radio SED for this sample with a single power-law model, the resulting spectral index is 0.64 ± 0.07. However, such a model does not capture all the features of the RxAGN radio SED which can be better described by a broken power law with a spectral index of α1 = 0.28 ± 0.03, below 4 GHz, and α2 = 1.16 ± 0.04, above 4 GHz. The derived radio SED can be even better described by models involving both synchrotron self-absorption and synchrotron aging processes.
By binning in both the 1.4 GHz radio luminosity and redshift, we have found (at P < 0.01 significance) that the single power-law spectral index is positively correlated with redshift and that the broken power-law spectral index above 4 GHz is positively correlated with both the redshift and source size. With a somewhat lesser significance (P < 0.05), we find that also the BPL spectral index below 4 GHz is positively correlated with source size. For a subsample of sources having sizes less than 1 kpc, we find a flat spectrum radio SED described by a single power-law spectral index of α = 0.41 ± 0.07. Using the broken power-law model we find a flat spectrum radio SED with a spectral index of α1 = 0.1 ± 0.1 (α2 = 0.55 ± 0.09) below (above) νb = (2.7 ± 0.5) GHz.
Our derived average radio SEDs of RxAGN span a frequency range from 300 MHz to 10 GHz and thus cover a significant portion of the expected SKA frequency window. The spectral indices we find in the frequency range from 300 MHz to 4 GHz are significantly lower than the often assumed values in large surveys around 1 GHz, indicating a greater impact of complex radio SED shapes on the derived properties of galaxies. Our radio SEDs offer a way to better understand future observations in the 300 MHz − 10 GHz regime by going beyond the often assumed simple power-law radio SED shape.
Acknowledgments
This research was funded by the European Union’s Seventh Framework program under grant agreement 337595 (ERC Starting Grant, “CoSMass”). JD acknowledges financial assistance from the South African Radio Astronomical Observatory (SARAO; www.ska.ac.za).
References
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blundell, K. M., Rawlings, S., & Willott, C. J. 1999, ApJ, 117, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, M., Zamorani, G., Ciliegi, P., et al. 2018, A&A, 618, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braun, R. 1996, The Westerbork Observatory Continuing Adventure in Radio Astronomy (Springer: Dordrecht), 167 [CrossRef] [Google Scholar]
- Calistro Rivera, G., Williams, W. L., Hardcastle, M. J., et al. 2017, MNRAS, 469, 3468 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Clemens, M. S., Vega, O., Bressan, A., et al. 2008, A&A, 477, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clemens, M. S., Scaife, A., Vega, O., & Bressan, A. 2010, MNRAS, 405, 887 [NASA ADS] [Google Scholar]
- Collier, J. D., Tingay, S. J., Callingham, J. R., et al. 2018, High-resolution Observations of Low-luminosity Gigahertz-Peaked Spectrum and Compact Steep Spectrum Sources, Tech. Rep. [Google Scholar]
- Condon, J. J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Condon, J. J., Huang, Z.-P., Yin, Q. F., & Thuan, T. X. 1991, ApJ, 378, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Cotton, W. D., Wittels, J. J., Shapiro, I. I., et al. 1980, ApJ, 238, L123 [NASA ADS] [CrossRef] [Google Scholar]
- De Zotti, G., Massardi, M., Negrello, M., & Wall, J. 2010, A&ARv, 18, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Delhaize, J., Smolčić, V., Delvecchio, I., et al. 2017, A&A, 602, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delvecchio, I., Smolčić, V., Zamorani, G., et al. 2017, A&A, 602, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dewdney, P. E., Hall, P. J., Schilizzi, R. T., & Lazio, T. J. L. W. 2009, IEEE Proc., 97, 1482 [Google Scholar]
- Donley, J. L., Koekemoer, A. M., Brusa, M., et al. 2012, ApJ, 748 [Google Scholar]
- Dunlop, J. S., & Peacock, J. A. 1990, MNRAS, 247, 19 [NASA ADS] [Google Scholar]
- Edge, A. C., Pooley, G., Jones, M., Grainge, K., & Saunders, R. 1998, IAU Colloq. 164: Radio Emission from Galactic and Extragalactic Compact Sources, 144, 187 [Google Scholar]
- Fanti, R., Fanti, C., Schilizzi, R. T., et al. 1990, A&A, 231, 333 [NASA ADS] [Google Scholar]
- Galvin, T. J., Seymour, N., Marvil, J., et al. 2018, MNRAS, 474, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Hales, C. A., Murphy, T., Curran, J. R., et al. 2012, MNRAS, 425, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley-Walker, N., Morgan, J., Wayth, R. B., et al. 2014, PASA, 31, e045 [NASA ADS] [CrossRef] [Google Scholar]
- Intema, H. T., Jagannathan, P., Mooley, K. P., & Frail, D. A. 2017, A&A, 598, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaffe, W. J. J., & Perola, G. C. C. 1973, A&A, 26, 423 [Google Scholar]
- Jarvis, M. J., & Rawlings, S. 2002, MNRAS, 319, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Kameno, S., Inoue, M., Wajima, K., Shen, Z. Q., & Sawada-Satoh, S. 2005, in Future Directions in High Resolution Astronomy, eds. J. Romney, & M. Reid, ASP Conf. Ser., 340, 145 [Google Scholar]
- Kapahi, V. K. 1981, A&AS, 43, 381 [NASA ADS] [Google Scholar]
- Kardashev, N. S. 1962, Sov. Astron., 5, 317 [Google Scholar]
- Kardashev, N. S., Kuz’min, A. D., & Syrovatskii, S. I. 1962, Sov. Astron., 6, 167 [Google Scholar]
- Kellermann, K. I., & Pauliny-Toth, I. I. K. 1969, ApJ, 155, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Ker, L. M., Best, P. N., Rigby, E. E., Röttgering, H. J., & Gendre, M. A. 2012, MNRAS, 420, 2644 [NASA ADS] [CrossRef] [Google Scholar]
- Kimball, A. E., & Ivezić, V. 2008, AJ, 136, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Kukula, M. J., Dunlop, J. S., Hughes, D. H., & Rawlings, S. 1998, MNRAS, 297, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Evans, A. S., Momjian, E., et al. 2011, ApJ, 739, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Menon, T. K. 1983, AJ, 88, 598 [CrossRef] [Google Scholar]
- Mhaskey, M., Gopal-Krishna, Dabhade, P., et al. 2019, MNRAS, 485, 2447 [Google Scholar]
- Murphy, E. J. 2013, ApJ, 777, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Afonso, J., Bacon, D., et al. 2013, PASA, 30, e020 [NASA ADS] [CrossRef] [Google Scholar]
- Novak, M., Smolčić, V., Civano, F., et al. 2015, MNRAS, 447, 1282 [NASA ADS] [CrossRef] [Google Scholar]
- Novak, M., Smolčić, V., Schinnerer, E., et al. 2018, A&A, 614, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Dea, C. P. 1998, PASP, 110, 493 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P., & Baum, S. A. 1997, AJ, 113, 148 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P., Baum, S. A., & Stanghellini, C. 1991, ApJ, 380, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Orienti, M., & Dallacasa, D. 2014, MNRAS, 438, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Pacholczyk, A. G. 1977, Radio galaxies: Radiation transfer, Dynamics, Stability and Evolution of a Synchrotron Plasmon, 89 [Google Scholar]
- Padovani, P. 2016, A&ARv, 24, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A., & Wall, J. V. 1982, MNRAS, 198, 843 [NASA ADS] [Google Scholar]
- Rau, U., & Cornwell, T. J. 2011, A&A, 532, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, D. B., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [Google Scholar]
- Schinnerer, E., Smolčić, V., Carilli, C. L., et al. 2007, ApJS, 172, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Sargent, M. T., Bondi, M., et al. 2010, ApJS, 188, 384 [Google Scholar]
- Seabold, S., & Perktold, J. 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 57 [Google Scholar]
- Smolčić, V., Novak, M., Bondi, M., et al. 2017a, A&A, 602, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smolčić, V., Delvecchio, I., Zamorani, G., et al. 2017b, A&A, 602, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szokoly, G. P., Bergeron, J., Hasinger, G., et al. 2004, ApJS, 155, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Tingay, S. J., & de Kool, M. 2003, AJ, 126, 723 [Google Scholar]
- Tisanić, K., Smolčić, V., Delhaize, J., et al. 2019, A&A, 621, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toba, Y., Yamashita, T., Nagao, T., et al. 2019, ApJS, 243, 15 [CrossRef] [Google Scholar]
- Transtrum, M. K., & Qiu, P. 2014, Phys. Rev. Lett., 113, 098701 [CrossRef] [Google Scholar]
- Transtrum, M. K., MacHta, B. B., & Sethna, J. P. 2010, Phys. Rev. Lett., 104, 060201 [NASA ADS] [CrossRef] [Google Scholar]
- Tribble, P. C. 2014, MNRAS, 261, 57 [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilman, R. J., Miller, L., Jarvis, M. J., et al. 2008, MNRAS, 388, 1335 [NASA ADS] [Google Scholar]
All Tables
Parameters of the power-law and broken power-law models, and source size, log D [kpc], derived for subsets of the RxAGN sample divided by redshift, z, and radio luminosity, log L1.4 [W Hz−1], described by the mean and standard deviation of redshifts and radio luminosity for each bin.
Summary of ANOVA results for the power-law and broken power-law spectral indices for RxAGN subsamples for models selected by requiring P < 0.1.
All Figures
 |
Fig. 1. Radio luminosity density L1.4 [W Hz−1] and redshift for RxAGN (black points). Red points correspond to the selected redshift and radio luminosity sample of RxAGN used in this work and are contained within log L1.4 [W Hz−1] ∈ [24, 26] and z ∈ [0, 4]. The histograms show the distribution of radio luminosity and redshift for all RxAGN and the RxAGN sample used in this work with black and red bars, respectively. The radio luminosity-redshift distribution is used to choose a complete sample of RxAGN. |
| In the text | |
 |
Fig. 2. Mean completeness correction for the sample of RxAGN as a function of redshift. The mean completeness (solid line), with its corresponding standard deviation (shaded interval), were estimated for different redshift bins using the 3 GHz flux densities and interpolated completeness corrections for the VLA-COSMOS 3 GHz Large Project catalog (Table 2 in Smolčić et al. 2017a). The mean completeness correction is used to quantify the completeness in the RxAGN sample, which is higher than 75% up to z ∼ 4. |
| In the text | |
 |
Fig. 3. Radio SED of RxAGN as normalized log-flux density vs. rest-frame frequency for z ∈ [0, 4] and log L1.4 [W Hz−1] ∈ [24, 26]. A single power-law (left panel) and a broken power-law (right panel) model of the radio SED are shown as red lines with red confidence intervals. Detections are shown as gray points, upper limits as yellow arrows, bins without upper limits as green points and bins with upper limits as magenta points. The plots show the best fitting power-law (0.64 ± 0.07) and broken power-law (α1 = 0.28 ± 0.03, α2 = 1.16 ± 0.04 and νb = (4.1 ± 0.2) GHz) models. |
| In the text | |
 |
Fig. 4. Average radio SED of the RxAGN sample with the model from Eq. (4) fit. Upper panel: resulting model before applying the MBAM model reduction method (described in Sect. 3.3), while the lower panel shows the best-fitting model after reducing the number of parameters with the MBAM method, used to better constrain this complex model. |
| In the text | |
 |
Fig. 5. Behavior of logarithmic derivative of parameters along the geodesic curve (left panel) and the components of the FIM eigenvector corresponding to the smallest eigenvalue at the beginning (end) of the geodesic curve are shown in the middle (right) panel the model from Eq. (4). The figure shows the details of the MBAM method used in constraining the parameters of this complex model. |
| In the text | |
 |
Fig. 6. SEDs derived for subsets of the RxAGN sample divided by redshift, z, and radio luminosity, log L1.4 [W Hz−1]. Shown is the best-fitting power-law model for each bin. The panels show the radio SEDs for different subsets of RxAGN and correspond to numbered bins presented in Table 1 and Fig. 8. |
| In the text | |
 |
Fig. 7. Spectral indices derived for subsets of the RxAGN sample divided by redshift, z, and radio luminosity, log L1.4 [W Hz−1], described in Sect. 5.2. The color-scale in the left panel shows the spectral index of the PL model, while the color-scales in the middle and right panels show the spectral indices α1 and α2 of the broken power-law model. Bins are outlined by black dashed lines. The panels show the spectral indices radio SEDs shown in Fig. 6 for different subsets of RxAGN and correspond to numbered bins presented in Table 1 and Fig. 8. |
| In the text | |
 |
Fig. 8. Dependence of the broken power-law spectral indices below and above a break frequency of 4 GHz (α1 and α2, respectively) on the source size, log D [kpc], for the subsets of the RxAGN dataset for different values of in log D [kpc], with corresponding errors in spectral indices. The error bars for log D [kpc] show the standard deviations of log D [kpc] within each bin. The numbers indicate the bin number in Table 1. The table lists the spectral indices radio SEDs shown in Fig. 6 for different subsets of RxAGN and correspond to numbered bins presented in Fig. 8. |
| In the text | |
 |
Fig. 9. Radio SED of a sample of flat-spectrum sources, produced by selecting all sources having sizes less than 1 kpc. Red line shows the broken power-law model. We find that selecting sources with sizes less than 1 kpc produces a sample of flat-spectrum sources, described by a spectral index of α = 0.41 ± 0.07 and a broken power-law spectral index of α1 = 0.1 ± 0.1 (α2 = 0.55 ± 0.09) below (above) a break frequency of νb = (2.7 ± 0.5) GHz. |
| In the text | |
 |
Fig. 10. Correlation matrix for properties of subsets of the RxAGN sample. Colors indicate positive or negative Pearson correlation coefficient, written on the plot for each parameter pair with its corresponding p-value in parentheses. The considered variables in the correlation matrix are the 1.4 GHz radio luminosity, log L1.4 [W Hz−1], power-law spectral index α, broken power-law spectral indices α1 and α2, and source size, log D [kpc]. The correlation matrix presented in this figure indicates the presence and significance of correlations between different properties of the subsets of the RxAGN sample. |
| In the text | |
 |
Fig. 11. Distribution of the broken power-law spectral indices for the subsets of the RxAGN sample. Black crosses are spectral indices derived for individual bins, listed in Table 1. Blue intervals denote α1 while orange intervals denote α2. The distributions of the broken power-law spectral indices are used to determine the parameters that explain the differences between the RxAGN subsets using the ANOVA method summarized in Table 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



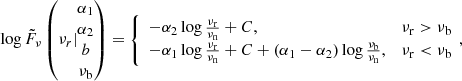
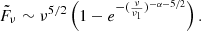
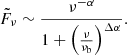
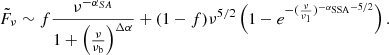
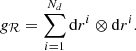
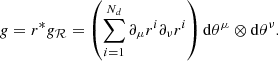
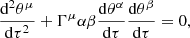
![$$ \begin{aligned} \alpha&= 0.39\pm 0.07+ (0.17\pm 0.03)z\\ \alpha _2&= 0.6\pm 0.2+ (0.27\pm 0.09)\log D\mathrm {[kpc]} + (0.15\pm 0.05)z, \end{aligned} $$](/articles/aa/full_html/2020/11/aa37114-19/aa37114-19-eq11.gif)
![$$ \begin{aligned} \alpha _1&= (0.0\pm 0.2)+ (0.3\pm 0.2)\log D\,\mathrm {[kpc]} \\ \alpha _1&={\left\{ \begin{array}{ll}0.0\pm 0.1+(0.3\pm 0.1)\log D\,\mathrm {[kpc]} -0.2\pm 0.1,\, \mathrm{RxSMLAGN} \\ 0.0\pm 0.1+(0.3\pm 0.1)\log D\,\mathrm {[kpc]} ,\,\text {for others} \end{array}\right.} . \end{aligned} $$](/articles/aa/full_html/2020/11/aa37114-19/aa37114-19-eq12.gif)