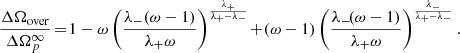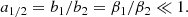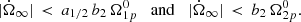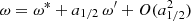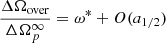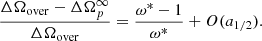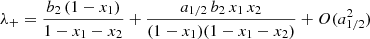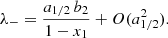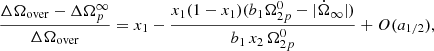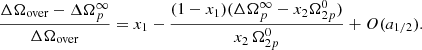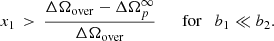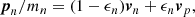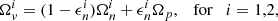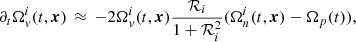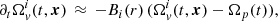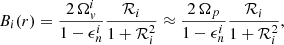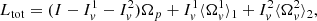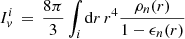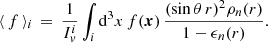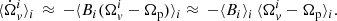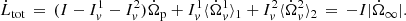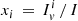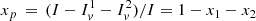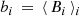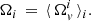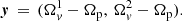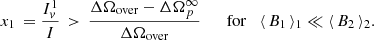| Issue |
A&A
Volume 642, October 2020
|
|
|---|---|---|
| Article Number | A223 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202038340 | |
| Published online | 23 October 2020 | |
Bayesian estimate of the superfluid moments of inertia from the 2016 glitch in the Vela pulsar
1
Dipartimento di Fisica, Università degli Studi di Milano, Via Celoria 16, 20133 Milano, Italy
e-mail: alessandro.montoli@unimi.it
2
Istituto Nazionale di Fisica Nucleare, sezione di Milano, Via Celoria 16, 20133 Milano, Italy
3
Nicolaus Copernicus Astronomical Center of the Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warszawa, Poland
e-mail: mantonelli@camk.edu.pl
Received:
4
May
2020
Accepted:
31
August
2020
Context. The observation of the first pulse-to-pulse glitch in the Vela pulsar opens a new window among theoretical speculations on the internal dynamics of neutron stars as it allows us for testing models to factor in the circumstances of the first moments of a glitch. Several works in the literature have already considered the observational and physical parameters of the star by employing a minimal model with three rigidly rotating components.
Aims. We improve the analytical study of the minimal three-component model for pulsar glitches by solving it with generic initial conditions for the two initial lags of their superfluid components. The purpose is to use this solution to fit the data of the 2016 Vela glitch by employing a Bayesian approach and to obtain a probability distribution for the physical parameters of the model and for observational parameters, such as the glitch rise time and the relaxation timescale.
Methods. The fit is achieved through Bayesian inference. Due to the presence of an increase in the timing residuals near the glitch time, an extra magnetospheric component was added to the three-component model to deal with this phenomenon. A physically reasonable, non-informative prior was set on the different parameters of the model, so that the posterior distribution could be compared with state-of-the-art information obtained from microphysical calculations. By considering a model with a tightened prior on the moment of inertia fractions and by comparing it with the original model by means of Bayesian model selection, we studied the possibility of a crust-limited superfluid reservoir.
Results. We obtained the posterior distribution for the moment of inertia fractions of the superfluid components, the coupling parameters, and the initial velocity lags between the components. An analysis of the inferred posterior also confirmed the presence of an overshoot in that glitch and set an upper limit of ∼6 s on the glitch rise timescale. The comparison between the two models with different priors on the moment of inertia fractions appears to indicate a need for a core participation in the glitch phenomenon, regardless of the uncertain strength of the entrainment coupling.
Key words: dense matter / stars: neutron / pulsars: general / pulsars: individual: PSR J0835-4510 / stars: rotation
© ESO 2020
1. Introduction
One of the timing anomalies observed in the regular emission from radio pulsars are glitches, which are sudden accelerations of the rotation of a pulsar followed by a slow relaxation towards a post-glitch phase of slow and smooth spin down (see e.g. Lyne et al. 2000; Espinoza et al. 2011). These events are quite rare and capturing an observation of a glitch in the act requires continuous monitoring.
The modelling of pulsar glitches requires at least two different components in the star (Baym et al. 1969): a normal component, which is coupled on short timescales to the magnetosphere, and a superfluid component, which stores angular momentum by pinning it to impurities in the crust (Anderson & Itoh 1975) or to fluxtubes in the core of the star (Alpar 2017). This reservoir occasionally releases angular momentum to the observable normal component of the star, giving rise to the glitch, even though the matter of exactly what triggers the glitch itself is still under debate (Haskell & Melatos 2015). On the other hand, the location of the superfluid reservoir is also unknown. For years, it has been assumed to be located in the crust of the star due to the fact that about the 1.7% of the Vela spin-down is reversed, on average, during a glitch – a proportion that is close to what it is theoretically expected for the moment of inertia fraction carried by the unbound neutrons in the crust (Datta & Alpar 1993; Link et al. 1999). However, recent works have shown that it is not possible to account for the large glitches of the Vela pulsar if we limit the superfluid reservoir to just the dripped neutrons in the inner crust (Andersson et al. 2012; Chamel 2013; Carreau et al. 2019) and that at least a small shell of the outer core of the star has to be taken into account (Ho et al. 2015; Montoli et al. 2020). These results are based on a statistical parameter of a glitching pulsar, also known as activity, which quantifies the mean spin-up rate of the star due to glitches (e.g. Fuentes et al. 2017), as well as on a microphysical parameter, the entrainment coupling, which is responsible for a non-dissipative interaction between the two components of the star (see Haskell & Sedrakian 2018; Chamel 2017b for recent reviews). The values of the entrainment parameter in the crust and the scale of its effects are, however, still open to discussion (Martin & Urban 2016; Watanabe & Pethick 2017; Chamel 2017a; Sauls et al. 2020).
Up until now, most of the information about pulsar glitches was obtained through the analysis of the frequency and sizes of glitches, which, together with theoretical modelling, have been used to constrain the structure of neutron stars (Ho et al. 2015; Delsate et al. 2016; Pizzochero et al. 2017). More recently, a glitch of the Vela pulsar in December 2016 has been observed with unprecedented precision, making it possible to detect every single pulsation during the glitch (Palfreyman et al. 2018). This kind of measurement has opened new possibilities for contrasting our theoretical understanding of the glitch phenomenon with timing data (Graber et al. 2018; Ashton et al. 2019b; Pizzochero et al. 2020; Gügercinoğlu & Alpar 2020).
To extract useful information from the data reported by Palfreyman et al. (2018), Ashton et al. (2019b) performed a Bayesian fit to the time of arrival (TOA) of the single pulses with an “agnostic” timing solution containing few parameters that set the glitch amplitude and the typical timescales of the process. In this way, it has been possible to put an upper limit to the spin-up rise time of ∼12 s, lowering the early ∼40 s boundary (Dodson et al. 2002, 2007), and to confirm the presence of an overshoot – in other words, the acceleration of the rotation of the star up to velocities larger than that of steady state equilibrium – in the data.
In Pizzochero et al. (2020), the agnostic timing solution used by Ashton et al. (2019b) has been written in terms of the parameters of a minimal three-component model – two superfluid and one normal – for the pulsar rotation. These parameters are linked to structural and rotational properties of the glitching star, such as the fractions of the moment of inertia of the superfluid components, the initial lag between the two superfluid components and the normal one, and the coupling parameters between them.
The aim of this paper is to extend the formalism of the theoretical discussion of three-component models presented in Pizzochero et al. (2020) – hereafter Paper I – and to refine the statistical procedure behind the least mean squares fit made there by employing a fully Bayesian approach. The difference with respect to the analysis of Ashton et al. (2019b) is that here, the underlying fit model is not agnostic but it has a clear interpretation in terms of the minimal three-component model used to describe the underlying pulsar dynamics: this allows us to fit not only the glitch timescales and the glitch amplitude, but to also infer some structural properties of the neutron star.
In contrast to what was done in Paper I, here we employ the whole dataset of Palfreyman et al. (2018). As noted in previous works (Palfreyman et al. 2018; Ashton et al. 2019b), an increase of the timing residuals has been detected in the vicinity of the glitch time. This can be interpreted as the signature of a magnetospheric change accompanying the glitch (Palfreyman et al. 2018). Since a three-component model is equipped to take this kind of phenomena into account, additional modelling is needed. In Ashton et al. (2019b), an extra phenomenological term was introduced to deal with this decrease in the rotational frequency. In this work, we extend the three-component model, speculating on an instantaneous decoupling and recoupling of the magnetosphere to the crust.
This paper is outlined as follows: in Sect. 2, we present the three-component model, extended with respect to the one used in Paper I, along with theoretical considerations on the glitch overshoot occurrence. In Sect. 3, we first present some considerations about the data set of Palfreyman et al. (2018) and then describe the statistical modelling behind the fit we performed. The results of the Bayesian fit are described in Sects. 4 and 5. The appendices are devoted to technical aspects of glitch models with three rigid components: in Appendix A, we derive the general solution of the three component model (i.e. we extend the solution in Paper I by allowing for general initial conditions). In Appendix B, the constraint on the moment of inertia of the superfluid component found by Sourie & Chamel (2020) is derived in the present, more general, setting. In Appendix C, we show how it is possible to take into account the entrainment coupling in glitch models with several rigid components.
2. Model
Following the seminal idea of Baym et al. (1969), we model a glitch by formally dividing a spinning neutron star into several rigidly rotating components that can exchange angular momentum. The minimal model we adopt here consists of two superfluid components – corresponding to different, non-overlapping regions of the star where neutron superfluidity is expected – and a normal component that extends over the whole stellar interior. The normal component, labelled with the p subscript, is usually believed to be coupled with the magnetic field of the star and, thus, observable from Earth, while the two superfluid components (labelled 1 and 2) act as reservoirs for angular momentum and their rotation cannot be tracked from Earth.
Following Paper I, we assume that the two superfluid components do not interact directly between themselves, but they interact only with the normal component. The strength of this interaction is set by two phenomenological coupling parameters, b1 and b2. Finally, all these three components lose angular momentum with a constant rate given by the electromagnetic braking torque. Therefore, the system of equations for the evolution of these three components is the natural three-component extension of the dynamical system introduced by Baym et al. (1969), namely,
where xj with j = {1, 2, p} is the fraction of moment of inertia of the jth component with respect to the total moment of inertia, and 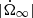 is the steady state spin down. The partial moments of inertia must sum up to the total one, so that we impose
is the steady state spin down. The partial moments of inertia must sum up to the total one, so that we impose
The system in (1) is valid for t ≥ 0, where we have set t = 0 as the time at which the glitch is triggered. Prior to the glitch moment, the values of b1, 2 could have a different value, for example, they may be assumed to be equal to zero if the two superfluid components are perfectly pinned at t < 0, but their actual pre-glitch value is not important for our scope. Since b1, 2 set the post-trigger creep rate of vortex lines (Alpar et al. 1984b), what is important in the present analysis is that their values remain almost constant during the glitch spin-up phase and the first moments of the relaxation (see e.g. Celora et al. 2020, for models where these mutual friction coefficients are functions of the velocity lag between the components). Hence, a limitation of the model would be to drop the still poorly understood problem of the post-glitch repinning process, during which the creep rate is expected to decrease as the velocity lag between the superfluid and the normal component becomes smaller and smaller (Sedrakian 1995; Haskell & Melatos 2016).
The system in (1) is solved in Appendix A by making a change of variables: instead of Ωi, it is more convenient to use the angular velocity lags Ωip = Ωi − Ωp between the ith superfluid component and the normal one. The first part of Eq. (1) can be integrated to obtain the angular velocity residue:
where 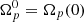 is the angular velocity of the normal component just before the glitch starts. The dynamics of the two lags, Ωip, must satisfy the other two equations of the system, that can be solved for arbitrary initial conditions
is the angular velocity of the normal component just before the glitch starts. The dynamics of the two lags, Ωip, must satisfy the other two equations of the system, that can be solved for arbitrary initial conditions 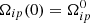 ; see Appendix A (on the contrary, the solution presented in Paper I is a particular one since it is valid only for a particular subset of initial conditions for the lags). The general form of the solution has the form (cf. with Paper I and Ashton et al. 2019b):
; see Appendix A (on the contrary, the solution presented in Paper I is a particular one since it is valid only for a particular subset of initial conditions for the lags). The general form of the solution has the form (cf. with Paper I and Ashton et al. 2019b):
where ω, λ± > 0 and 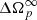 are time-independent functions of the parameters in the system (1), defined in (A.16)–(A.19).
are time-independent functions of the parameters in the system (1), defined in (A.16)–(A.19).
Since 0 < λ− < λ+, we have that 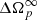 is the asymptotic value of the glitch amplitude (depending on the initial conditions it could be either positive or negative). Moreover,
is the asymptotic value of the glitch amplitude (depending on the initial conditions it could be either positive or negative). Moreover, 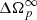 can be thought to represent the glitch jump that could be extracted from the analysis of post-glitch timing data when the glitch is not observed in the act (see e.g. Fig. 11 in Antonelli & Pizzochero 2017).
can be thought to represent the glitch jump that could be extracted from the analysis of post-glitch timing data when the glitch is not observed in the act (see e.g. Fig. 11 in Antonelli & Pizzochero 2017).
As already noted in previous works, the angular velocity of the observable component shows an evolution with two different timescales, one given by 1/λ+ and a longer one given by 1/λ−. In fact, Eq. (4) has the same functional form of the agnostic model used to fit the Vela 2016 glitch by Ashton et al. (2019b); the difference here is that we make an exact connection between the “solution” parameters in Eq. (4) and the “structural” parameters in Eq. (1), which have a physical interpretation.
Next we study the conditions under which an overshoot of the normal component can be produced, a situation that can never occur in a model with only two rigid components and a constant coupling parameter. We note, however, that it is possible to obtain an overshoot with a two-component model of the kind pionereed by Alpar et al. (1981), where the superfluid component can develop non-uniform rotation (see e.g. Alpar et al. 1984b; Larson & Link 2002; Haskell et al. 2012; Antonelli & Pizzochero 2017; Graber et al. 2018) due to the fact that the coupling with the normal component – which depends on the non-uniform lag itself and on stratification – may not be constant in both space and time. This is not surprising as a fluid model has infinite degrees of freedom that can react on different timescales – and not just two (i.e. Ω1 and Ω2), as in the present minimal model.
The overshoot is realised if there exists a certain time, tmax > 0, such that 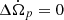 and
and 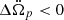 . The first derivative of Eq. (4) gives:
. The first derivative of Eq. (4) gives:
which needs to be positive. Since λ+ > λ− > 0 (see Eq. (A.7)), we have that tmax is a real number when ω < 0 or ω > 1. The additional condition, 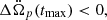 requires that ω > 0. Therefore, the overshoot occurs for ω > 1, which also guarantees that tmax > 0. In particular, we have a very delayed overshoot if ω → 1+, while for ω → +∞ we find a lower bound to the duration of the spin-up phase, namely,
requires that ω > 0. Therefore, the overshoot occurs for ω > 1, which also guarantees that tmax > 0. In particular, we have a very delayed overshoot if ω → 1+, while for ω → +∞ we find a lower bound to the duration of the spin-up phase, namely,
The condition for an overshoot can be translated in terms of time residuals with respect to the steady spin-down evolution, which are given by (cf. Graber et al. 2018)
For an overshooting glitch, tmax corresponds to a flex point, after which 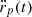 is positive. On the other hand, in a non-overshooting glitch there is no flex point and rp(t) is always concave down.
is positive. On the other hand, in a non-overshooting glitch there is no flex point and rp(t) is always concave down.
We note that all the equations above are symmetric under the exchange of the label 1 with 2. Therefore, to break this degeneracy and physically distinguish one superfluid component from the other, we impose that the superfluid component 2 is the one with the biggest initial lag. This may be due to a stronger pinning in the region of component 2 or simply because it happened that the glitch initiated in this condition (the initial conditions are unknown and depend on the past history of the system). Hence, the superfluid component 1 is, by definition, the one with a smaller initial lag,
3. Analysis of the 2016 Vela glitch
Following a Bayesian approach, we find the posterior probability distribution for the phenomenological parameters of the model in Eq. (1).
3.1. Magnetospheric change and data set
The data made available by Palfreyman et al. (2018) span a 4200s time window, with the glitch time positioned roughly at the centre of the dataset. The authors calculate a first estimate of the glitch date, set at 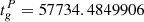 MJD. Moreover, they identify some peculiarities during the glitch: at a time,
MJD. Moreover, they identify some peculiarities during the glitch: at a time, 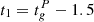 s, an increase of the residuals is detected. This kind of behaviour can be linked to an effective slow-down of the star before the actual glitch (Ashton et al. 2019b) or to a magnetospheric change (Palfreyman et al. 2018) that could cause a delay on the emission of the pulsations of the star, perhaps even due to a starquake (Bransgrove et al. 2020). Of course, this phenomenon cannot be described using the model presented in Sect. 2, thus, further modelling is necessary to fit the timing data. To do so, we assume that the magnetosphere instantaneously decouples and recouples from the rotation of the crust of the star, lagging behind the actual angular velocity of the charged component. This amounts to introducing a fourth component with negligible inertia (the magnetosphere) that is always locked to the p-component apart for an instantaneous jump at t = ΔtM, namely,
s, an increase of the residuals is detected. This kind of behaviour can be linked to an effective slow-down of the star before the actual glitch (Ashton et al. 2019b) or to a magnetospheric change (Palfreyman et al. 2018) that could cause a delay on the emission of the pulsations of the star, perhaps even due to a starquake (Bransgrove et al. 2020). Of course, this phenomenon cannot be described using the model presented in Sect. 2, thus, further modelling is necessary to fit the timing data. To do so, we assume that the magnetosphere instantaneously decouples and recouples from the rotation of the crust of the star, lagging behind the actual angular velocity of the charged component. This amounts to introducing a fourth component with negligible inertia (the magnetosphere) that is always locked to the p-component apart for an instantaneous jump at t = ΔtM, namely,
where Δr0 and ΔtM are additional phenomenological parameters that have to be fitted together with xi, bi, and the initial lags, Ωip. Due to its instantaneous behaviour, Eq. (9) is non-physical, but it provides a simple mathematical form for this magnetospheric slip, which is suggested by the data; its impulsive character is a crude simplification of a complex dynamical problem. Hence, the modelling in (9) represents the minimal choice to extend the system (1) to take into account this additional piece of physics that is present in the data of Palfreyman et al. (2018).
The residual function of the “observable component” (that is now the magnetosphere) takes the form:
where we extended the function, rp(t), to pre-glitch times, t < 0, by means of the Heaviside step function ϑ. The sign of ΔtM is unknown and can be either negative (the magnetospheric change happened before the glitch) or positive (the magnetospheric change follows the glitch trigger). Finally, the data provided by Palfreyman et al. (2018) are lacking with regard to the uncertainty on the single measure of the residual. We estimate it from the standard deviation of all the data before t1, as it is quite certain that before that time, the star had not yet undergone the glitch. In this way, we find σ = 0.25 ms and we assume this value to be valid also for the post-glitch measurements.
3.2. Bayesian modelling
We now describe the statistical modelling used to obtain a probability distribution for the parameters involved in the model. From Eq. (7) we have up to a maximum of six parameters: the two coupling parameters, b1, 2; the two moment of inertia fractions, x1, 2; and the two initial lags 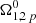 . The number of these parameters can be reduced by assuming the initial lag for the component 1 to be that of the steady state, so that the model can be simplified to the one discussed in Paper I. Here, we keep the discussion as general as possible, thus, keeping
. The number of these parameters can be reduced by assuming the initial lag for the component 1 to be that of the steady state, so that the model can be simplified to the one discussed in Paper I. Here, we keep the discussion as general as possible, thus, keeping 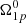 as a free parameter to be fitted.
as a free parameter to be fitted.
The residuals of Eq. (7) have to be considered with respect to the glitch date, tg, which is itself a parameter of the model. Moreover, the magnetospheric slip defined in Eq. (10) has to be included in the model as well. In other words, the residual function, r(t), which describes all the pre-glitch and post-glitch data is:
where tM = tg + ΔtM is the date of the magnetospheric slip. In the following, the estimate of these two date parameters, tg and tM, is given with respect to the glitch date 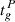 calculated in the analysis of Palfreyman et al. (2018).
calculated in the analysis of Palfreyman et al. (2018).
We collectively note all the nine parameters of the model as:
The probability distribution for these parameters can be obtained as the posterior distribution of a Bayesian inference (MacKay 2003),
where the functions P(𝒟 | 𝒫), P(𝒫) and P(𝒟) are the likelihood, the prior and the evidence, respectively and
represents the data used for the fit, that is, the time of arrival of the pulses, ti, and the measured residual, ri, with respect to the model of a uniform spin-down.
Assuming that the measurement for a single pulsation is independent of the measurements of the others, we write the likelihood as (see also Ashton et al. 2019b):
where σ is the uncertainty on the single measure as calculated in Sect. 3.1. By writing the likelihood in this way, however, we made a further simplification: here, the uncertainty σ is referred only to the time residual, ri, while the same uncertainty must affect the time of arrival ti as well, as the two quantities are interdependent. In fact, an hypothetical variation of the time of arrival would generate the same variation in ri and vice versa. Thus, the correct likelihood should be a normal distribution with variance σ2 and set diagonally on the (ti, ri) space. Since the uncertainty on the measure of the TOAs is of the order of a fraction of ms, while the pulsations arrive on timescales of a tenth of a second, we neglect this correction and use the distribution in Eq. (15).
We assume most of the variables to be independent from the others, so to factorise the prior for the parameters P(𝒫) into smaller parts. We set the probability distribution of the moment of inertia fractions xi as a uniform distribution between 0 and 1, with the constraint that the sum is less than unity,
For each of the two coupling parameters bi we chose a log-uniform distribution as we do not know the order of magnitude of the coupling parameters and we would like to explore a wide range of orders of magnitude,
In this way, we took a first step in breaking the symmetry between the two superfluid components by setting two different (but overlapping) priors on the two coupling parameters. Similarly, we chose a log-uniform distribution for the prior of the initial lags 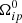 . Since the two priors in (17) and (18) are largely overlapping, we definitively break this symmetry by setting a prior on the initial lags that automatically implements the condition (8)
. Since the two priors in (17) and (18) are largely overlapping, we definitively break this symmetry by setting a prior on the initial lags that automatically implements the condition (8)
We determine the prior on the shift on the timing residuals given by the magnetospheric change to be as broad as possible: since the pulsation of the Vela has a frequency of ≈10 Hz, we set the prior on Δr0 to be a uniform distribution between −100 ms and 100 ms. In this way, we cover a whole pulsation, which can be up to 0.1 seconds early or 0.1 seconds late,
Finally, we set the two priors on the two dates, tg and tM, respectively to be uniform between −100 s and 100 s and between −1000 s and 100 s with respect to the glitch date 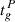 obtained by Palfreyman et al. (2018). We do not set further conditions on the relation between them. In this way, it is, in principle, possible to understand whether the magnetospheric change preceeded the glitch, or vice versa (see also Ashton et al. 2019b):
obtained by Palfreyman et al. (2018). We do not set further conditions on the relation between them. In this way, it is, in principle, possible to understand whether the magnetospheric change preceeded the glitch, or vice versa (see also Ashton et al. 2019b):
The whole prior distribution P(𝒫) is the product of all these independent probability distributions, defined in Eqs. (16)–(22):
4. Results of the Bayesian fit
We set the angular velocity at the time of the glitch to a value of 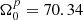 rad s−1, while for the angular velocity derivative, we use the value
rad s−1, while for the angular velocity derivative, we use the value 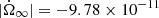 rad s−2 (see e.g. Dodson et al. 2002). The posterior distribution for the nine parameters in (12) has been inferred by employing the dynesty nested sampler (Speagle 2020), as implemented in the Bilby Python package (Ashton et al. 2019a). The results for these nine parameters are shown in Fig. 1, with the 16th, 50th, and 84th percentiles for each variable reported in Table 1.
rad s−2 (see e.g. Dodson et al. 2002). The posterior distribution for the nine parameters in (12) has been inferred by employing the dynesty nested sampler (Speagle 2020), as implemented in the Bilby Python package (Ashton et al. 2019a). The results for these nine parameters are shown in Fig. 1, with the 16th, 50th, and 84th percentiles for each variable reported in Table 1.
 |
Fig. 1. Cornerplot of the posterior distribution. On the diagonal, the marginalised posterior distribution for each parameter of the model is plotted. The vertical lines represent the 16th and 84th percentiles of these distributions. The numerical values are reported in Table 1. The prior distribution is plotted in orange as a comparison: for the jump in the residuals Δr0 and the magnetospheric time tM this is almost invisible, due to the width of the distribution. The covariance plots are located off-diagonal. |
16th, 50th, and 84th percentiles for the marginalised posterior for the different variables of the model.
4.1. Magnetospheric event
In Fig. 2, we show the two distributions for the glitch time, tg, and the magnetospheric change time, tM, along with some characteristic times defined in Palfreyman et al. (2018): the authors detected a missing pulse at time t0 and a persistent increase of the residuals which took place between t1 and t2. The glitch time tg is not well-constrained by the fit and it is broadly distributed, with 68% of the probability lying between the glitch time calculated in Palfreyman et al. (2018) and 53.1 seconds before it. A strong correlation is also present between the glitch time, tg, and the initial residual due to the magnetospheric slip. In Fig. 3, we present the result of the fit, expressed as the median and the 16th and 84th percentiles, superimposed on the data. As we can remark based on this figure, the correlation is probably due to the fact that an anticipated glitch with a higher initial residual and a postponed glitch with a lower initial residual can fit the data equally well (see also Ashton et al. 2019b about this).
 |
Fig. 2. Probability distribution for the inferred glitch time tg and the time of the magnetospheric slip tM. For comparison, some characteristic times obtained in Palfreyman et al. (2018) are superimposed: the time of a null pulse t0, the start and the end of the rise of the residuals t1 and t2, and the glitch time |
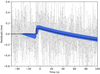 |
Fig. 3. Result of the fit. We plot the data obtained by Palfreyman et al. (2018) in grey, joined by a line, and the fitted curve: for each time t every 0.1 s between −50 s and 100 s, we calculate the probability distribution for r(t) starting from the samples of the posterior distribution. The median of the probability distribution for the residual function r(t) defined in (11) is plotted in black, while the blue region indicates the 16th–84th percentile zone. The reference time t = 0 is set to be the glitch time |
A tighter prior on the glitch time would allow for a better resolution on the probability distribution for the other parameters, for example x1, which present a correlation of one of its peaks with the glitch time (see Fig. 1). The magnetospheric time tM presents two clear peaks, one at 6.4 s and one 2.6 s before the Palfreyman et al. (2018) glitch time. Unfortunately, the large uncertainty on tg does not allow us to conclude whether the magnetospheric change is before or after the triggering of the glitch.
4.2. Timescales, overshoot parameter, and glitch size
The probability distributions for the rise timescale, 1/λ+, the relaxation timescale, 1/λ−, the overshoot parameter, ω, and the asymptotic glitch size, 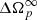 , are given in Fig. 4. The rise time, 1/λ+, peaks close to 0s (the limit at which the rise is practically instantaneous) and 90% of the distribution lies within 6.02 s (cf. with Fig. 2 of Ashton et al. 2019b). This is a more stringent constraint with respect to the ∼12 s obtained in Ashton et al. (2019b), which is probably due to the different type of theoretical modelling underlying the fit (they used a single-timescale model to fit this parameter). The value obtained for the relaxation timescale is
, are given in Fig. 4. The rise time, 1/λ+, peaks close to 0s (the limit at which the rise is practically instantaneous) and 90% of the distribution lies within 6.02 s (cf. with Fig. 2 of Ashton et al. 2019b). This is a more stringent constraint with respect to the ∼12 s obtained in Ashton et al. (2019b), which is probably due to the different type of theoretical modelling underlying the fit (they used a single-timescale model to fit this parameter). The value obtained for the relaxation timescale is 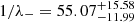 s: this value is also similar to that of previous glitches of the Vela; for example, the 2000 and the 2004 glitches (Dodson et al. 2002, 2007).
s: this value is also similar to that of previous glitches of the Vela; for example, the 2000 and the 2004 glitches (Dodson et al. 2002, 2007).
 |
Fig. 4. Probability distributions for the glitch rise timescale, 1/λ+, the relaxation timescale, 1/λ−, the overshoot parameter, ω, and the glitch size, |
Finally, the parameter ω obtained here has a value of 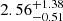 , which is a clear indication of the presence of an overshoot (Ashton et al. 2019b), and the glitch size is 1.014 ± 0.002 ⋅ 10−4 rad s−1, in good accordance with the previous estimate in Paper I.
, which is a clear indication of the presence of an overshoot (Ashton et al. 2019b), and the glitch size is 1.014 ± 0.002 ⋅ 10−4 rad s−1, in good accordance with the previous estimate in Paper I.
4.3. Comparison with a model with “active” and “passive” superfluid components
For a better comparison with the results in Paper I, we also performed a fit by fixing 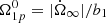 , the value corresponding to the steady-state lag. In this way, we determine component 1 to be a “passive” one (in fact, a superfluid component that rotates with the steady state lag does not contribute to the angular momentum reservoir, which is the scenario considered in Paper I). In this case, we have to fit eight parameters instead of nine. We do not report the results here, as it yields fully compatible values for all the parameters shown in Fig. 1. This establishes that the differences with respect to Paper I are mostly due to the difference in the fitting procedure and not to the assumption that component 1 is at a steady state at t = 0 (i.e. it is “passive”). Moreover, the steady-state lag for the superfluid component 1, which is on the order of 10−8 − 10−9 rad s−1, as calculated with the inferred values, is compatible to the results obtained here for the model with a free initial condition for
, the value corresponding to the steady-state lag. In this way, we determine component 1 to be a “passive” one (in fact, a superfluid component that rotates with the steady state lag does not contribute to the angular momentum reservoir, which is the scenario considered in Paper I). In this case, we have to fit eight parameters instead of nine. We do not report the results here, as it yields fully compatible values for all the parameters shown in Fig. 1. This establishes that the differences with respect to Paper I are mostly due to the difference in the fitting procedure and not to the assumption that component 1 is at a steady state at t = 0 (i.e. it is “passive”). Moreover, the steady-state lag for the superfluid component 1, which is on the order of 10−8 − 10−9 rad s−1, as calculated with the inferred values, is compatible to the results obtained here for the model with a free initial condition for 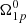 , again indicating a single reservoir.
, again indicating a single reservoir.
Regarding the Bayes factors, the eight-parameter model with 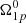 fixed is only marginally preferable to that with a free initial condition, having a Bayes factor, Z, of lnZ ≈ 1.4, which is too low to claim a strong preference between the two models (Kass & Raftery 1995).
fixed is only marginally preferable to that with a free initial condition, having a Bayes factor, Z, of lnZ ≈ 1.4, which is too low to claim a strong preference between the two models (Kass & Raftery 1995).
Some considerations can be made for the other initial lag, 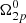 , which is distributed with a probability of the 68% in the range 3 × 10−4 ÷ 1.1 × 10−3 rad s−1. In the years just before the glitch considered here, the Vela had undergone two glitches, as reported by the Jodrell Bank Glitch Catalogue1 (Espinoza et al. 2011): one in 2014, which is at least three orders of magnitude smaller than the one considered here, and one in 2013, which is the largest ever achieved in the Vela and of a comparable size with respect to that of 2016. Starting from the equation for the conservation of angular momentum in system (1), we can notice that if we assume perfect pinning, (
, which is distributed with a probability of the 68% in the range 3 × 10−4 ÷ 1.1 × 10−3 rad s−1. In the years just before the glitch considered here, the Vela had undergone two glitches, as reported by the Jodrell Bank Glitch Catalogue1 (Espinoza et al. 2011): one in 2014, which is at least three orders of magnitude smaller than the one considered here, and one in 2013, which is the largest ever achieved in the Vela and of a comparable size with respect to that of 2016. Starting from the equation for the conservation of angular momentum in system (1), we can notice that if we assume perfect pinning, (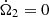 ) and
) and 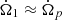 , the angular velocity lag Ω2p builds up at a constant rate,
, the angular velocity lag Ω2p builds up at a constant rate,
Following Montoli et al. (2020), we estimate the lag accumulated before the 2016 glitch by assuming that the largest glitch (the one in 2013) has completely emptied the angular momentum reservoir (i.e. the lag between the components is null after the glitch). Furthermore, the 2014 glitch is so small that it is not expected to empty the accumulated reservoir substantially. In this case, the expected angular velocity lag Ω2p just before the 2016 glitch is
which is one order of magnitude larger than what obtained from the fit. This discrepancy can be interpreted in terms of vortex-creep: since a lag of ∼0.01 rad s−1 is expected by assuming perfect pinning of the superfluid 2 in the period between the 2013 and 2016 glitches, one possibility is that vortex creep is realised in place of perfect pinning, so that only the 10% of the maximum achievable lag is actually stored.
Finally, Fig. 1 reveals the presence of a strong correlation between the moment of inertia fraction x2 and the lag 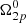 : a different prior on the superfluid fraction, x2, peaked or constrained to smaller values due, for example, to microphysical constraints, would give a smaller posterior value for it, thus yielding larger values of the initial lag.
: a different prior on the superfluid fraction, x2, peaked or constrained to smaller values due, for example, to microphysical constraints, would give a smaller posterior value for it, thus yielding larger values of the initial lag.
5. Physical interpretation of the fit
We now discuss what information can be extracted from the fitted values of the phenomenological parameters, xi and bi. The physical interpretation of xi and bi is a slightly subtle matter due to the possible presence of entrainment between each superfluid component and the normal component (see Appendix C).
5.1. Moments of inertia and mutual friction parameters
To take into account the entrainment coupling, we interpret the lags between the two superfluid components and the normal one according to Eqs. (C.2) and (C.15), so that a system like that of Eq. (1) still holds without the need to encode additional “entrainment torques”. The downside is that the fractions of the moments of inertia, xi, contain a dependence on the entrainment parameter (Antonelli & Pizzochero 2017),
where I is the total moment of inertia, R is the radius of the star, 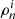 and
and 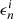 are the mass density, and the entrainment parameter of the i = 1, 2 component. The parameter
are the mass density, and the entrainment parameter of the i = 1, 2 component. The parameter 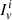 is the moment of inertia for the relative superfluid component corrected by entrainment, whereas the actual region that contributes to the integral is where
is the moment of inertia for the relative superfluid component corrected by entrainment, whereas the actual region that contributes to the integral is where 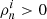 , see Eq. (C.7). For zero entrainment,
, see Eq. (C.7). For zero entrainment, 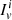 reduces to
reduces to 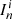 . We note that it is still possible to enforce relation (2), even in the presence of entrainment. As discussed in Appendix C, this is because xp also changes due to entrainment (see Eq. (C.12)), in a way that keeps the value of total angular momentum (C.6) constant (see also Antonelli et al. 2018).
. We note that it is still possible to enforce relation (2), even in the presence of entrainment. As discussed in Appendix C, this is because xp also changes due to entrainment (see Eq. (C.12)), in a way that keeps the value of total angular momentum (C.6) constant (see also Antonelli et al. 2018).
Similarly, also the coupling parameters bi, when expressed as spatial averages over some internal region of the star, contain some entrainment correction (see Eqs. (C.5) and (C.13)),
Here, ℬi is the dimensionless mutual friction coefficient, usually expressed in terms of the drag-to-lift ratio ℛi (see e.g. Andersson et al. 2006; Sourie & Chamel 2020) as
Both ℬi and ℛi are expected to have a spherical radial dependence as their value depends on the physical quantities in the stellar interior and on the particular mechanism that acts to dissipate energy at the microscopic scale of a vortex core.
The coupling parameters, b1 and b2, yield some information about the phenomena which cause the interaction between the superfluid component and the normal component. For the core superfluid, it is thought that electron scattering off magnetised vortices causes the drag between the superfluid and the normal component and then the subsequent exchange of angular momentum (Alpar et al. 1984a). For the crustal superfluid, two different phenomena may occur, whether the relative velocity between the two components is small (phonon excitation, Jones 1990) or large (Kelvin waves excitation, Jones 1992; Epstein & Baym 1992). These two phenomena are believed to yield coupling parameters with rather different orders of magnitude.
If we interpret the results obtained here for b1 and b2 as the coupling parameters for the core and the crustal superfluid (which seems unlikely given the posterior distribution of x2, as discussed in the following subsection), respectively, then we can compare these results with the theoretical calculations done in the literature. From Eq. (27) it is immediate to obtain
where the average values ⟨ 1 − ϵn ⟩crust ≈ 4 and ⟨ 1 − ϵn ⟩core ≈ 1 have been taken from Chamel (2012) and Chamel & Haensel (2006) respectively, while 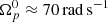 has been employed. Using the percentile values in Table 1, we obtain:
has been employed. Using the percentile values in Table 1, we obtain:
However, if the crustal lattice is amorphous or contains a large number of defects, only weak entrainment is expected (Sauls et al. 2020), so we may use ⟨ 1 − ϵn ⟩crust ≈ 1 and obtain
The orders of magnitude of the coupling parameters calculated here are in good agreement with the most recent theoretical calculations for both the crust (Graber et al. 2018) and the core superfluid (Andersson et al. 2006). While this is a Newtonian model, a fully relativistic model would yield values for ⟨ ℬ ⟩crust corrected by a factor of the order of ≈2 (Sourie et al. 2017; Gavassino et al. 2020).
5.2. Extension of the superfluid regions
The fitted values for x1, 2 allow us some room for speculating on the spatial extension of the angular momentum reservoir. Similarly to Paper I, the results show that nearly the x1 ≈ 60% of the total moment of inertia refers to the component with a smaller initial lag (i.e. the component that before the glitch was likely to be only weakly pinned, so it did not develop a substantial lag). On the other hand, we find x2 ≈ 15% for the “strongly pinned” superfluid. This value is too large to be accommodated in the crust of the star alone, whatever the value of the entrainment in the crust, thus requiring that some of the reservoir superfluid should be located in the core of the star (Ho et al. 2015; Montoli et al. 2020).
This can be seen in Fig. 5: here, we plot the moment of inertia fraction Iv(nB)/I of a spherical shell extending from a radius R(nB) to the radius R(nd),
 |
Fig. 5. Comparison between the possible values of the superfluid moment of inertia fraction Iv(nB)/I and the possible values of x2 according to its posterior distribution P(x2). We plot the points (Iv(nB)/I, nB), where the baryon density nB is expressed in units of the nuclear saturation density n0 = 0.17 fm−3. The inner-crust, i.e. nd < nB ≲ 0.5n0, corresponds to the orange-shaded region. The upper panel refers to the BSk21 EoS (Goriely et al. 2010), the lower one to the SLy4 EoS (Douchin & Haensel 2001). The curves represent the points (Iv(nB)/I, nB) when entrainment corrections are included (red-dashed) by using the values calculated by Chamel & Haensel (2006) and Chamel (2012) and when entrainment coupling is set to zero (gray-solid). The posterior P(x2) is superimposed as a background histogram, with the 16th, 50th and 84th percentiles shown with black dotted lines. The two green dash-dotted lines indicate an upper limit (corresponding to the 84th percentile) to the extension of the superfluid 2 region if the mass of the Vela is M = 2M⊙. |
where nB is a generic baryon density such that nB > nd, while nd is the drip-point density that defines the boundary between the inner and outer-crust.
We can try to match the theoretical value Iv(nB)/I with the fitted value of x2. This would tells us that the superfluid 2 region extends between the densities nd and nB. However, differently from what was done in Paper I, the Bayesian fit does not provide a single value for x2, but a posterior distribution (see Fig. 1). For this reason, in Fig. 5, along with Iv(r)/I, we also superimpose the posterior P(x2).
The fraction Iv(nB)/I is calculated for different masses and two different unified equations of state (EoS), SLy4 (Douchin & Haensel 2001) and BSk21 (Goriely et al. 2010). We plot the cases with (red dashed lines) and without (grey solid lines) entrainment, where the coefficients ϵn for the core and the crust of the star are taken from Chamel & Haensel (2006) and Chamel (2012), respectively. Although P(x2) is doubly peaked, even the narrower peak on the left lies outside the crustal region for both the EoSs and for all the cases considered (with or without entrainment and for different masses). Moreover, this peak falls rapidly to zero for x2 ≲ 0.05: it is for this reason that in all the cases considered, the value of Iv(nB)/I calculated at the crust-core interface lies in a region with very small or null values of P(x2), and well outside the 16–84 percentile region.
To check this result, we replicate the fit, but imposing the condition that x1 + x2 < 0.05 and keeping all the priors on the other parameters untouched. In this way, we limit the moment of inertia fraction to a portion that should coincide mostly with the crust of the star: this value is an upper limit to the moment of inertia of the unbound neutrons in the crust when realistic equations of state are taken into account (see e.g. Fig. 3 in Antonelli et al. 2018).
With the restriction x1 + x2 < 5%, we obtain non-physical posteriors for some of the parameters, in particular for the glitch rise time tg, the initial residual Δr0 and the magnetospheric time tM. More importantly, since the nested sampling algorithm allows to estimate the evidence of the two models (the one with x1 + x2 < 1 and the one with x1 + x2 < 5%), the natural logarithm of the Bayes factor between the two models is ≈5.6, favouring the model with x1 + x2 < 1. A Bayes factor, Z, such that log Z > 5 can be considered a strong evidence for a model with respect to another one (Kass & Raftery 1995). This test thus confirms the necessity of the inclusion of the superfluid in the core for the glitch process. We note that differently from the earlier results of Andersson et al. (2012) and Chamel (2013), the present result is independent of the presence of strong entrainment in the crust: this is because the imposed constraint, x1 + x2 < 5%, can easily accommodate the fraction of the moment of inertia of the superfluid component in the whole crust either with or without entrainment corrections.
Finally, considering the value of x2 ≈ 0.3 at the 84th percentile as an upper limit to Iv(r)/I, from Fig. 5, we can also conclude that the region relative to this superfluid component is the one extending from the drip point to nB ≈ 1.5n0 at most (for the BSk21 EoS and a star of 2 M⊙, as indicated by the horizontal dash-dotted line in the upper panel). Similarly, we find that the region corresponding to component 2 extends, at most, up to nB ≈ 2n0 if the Sly4 EoS is used.
6. Conclusions
Motivated by previous analyses of the 2016 Vela glitch (Ashton et al. 2019b), we studied the minimal analytical model that is able to describe a pulsar glitch with overshoot, which requires three rigidly rotating components, where one is normal and two are superfluid.
First, we improved the solution of the model presented in Paper I (Pizzochero et al. 2020): we derived an analytic form for the time evolution of the observable component angular velocity (the calculations are in Appendix A) and found the overshoot condition, dropping the assumption that the initial condition for one of the two superfluids is that of being at the steady state (we called such a component “passive” in Paper I). Moreover, we obtained the constraint on the fraction of the moment of inertia for the “slow” superfluid component from Sourie & Chamel (2020) in the present general formulation that includes superfluid entrainment; see (C.16).
We performed a Bayesian fit of the phenomenological parameters of the model using the data obtained by Palfreyman et al. (2018) for the 2016 Vela glitch: the basic form of the fitted function is identical to the one used by Ashton et al. (2019b), however, here, we write it in terms of the physical parameters of the system. The presence of a rise of the mean of the residuals close to the expected glitch time requires us to model this phenomenon. We decided to use a minimal “magnetospheric slip” model, in which at a time, tM – which is a priori different from the glitch time, tg – the magnetosphere instantly decouples from and then recouples to the crust of the star, with a resulting apparent deceleration of its rotation. This model, while it is likely to be oversimplified, allows us to fit the data and also account for this additional phenomenon that cannot be modeled with just a three-component model.
Based on the fit, we estimated the coupling parameters between the superfluid components and the normal component, which have orders of magnitude compatible to those obtained in theoretical calculations for the drag given by Kelvin wave excitation (Graber et al. 2018) and electron scattering off magnetised vortices (Alpar et al. 1984a; Andersson et al. 2006). It has also been possible to obtain the fraction of the moment of inertia of the two superfluid components of the model. The marginalised posterior for the moment of inertia ratio of the superfluid, which acts as a main angular momentum reservoir is rather broad. Nevertheless, it gives a clear indication that it is unlikely that the superfluid reservoir is limited to the crust of the star.
This claim has been double-checked by tightening the prior for the superfluid moment of inertia fractions to values that are similar to the crustal superfluid moment of inertia in a light star without entrainment. The evidence for this model is much smaller than that with the larger prior, confirming the unlikelihood of a superfluid reservoir limited to the crust of the star. In contrast to what discussed in Andersson et al. (2012) and Chamel (2013), the strength of this result is its independence from the entrainment parameter.
It has been possible to obtain the angular velocity lag between the pinned component and the normal component at the moment of the glitch, and it turned out to be an order of magnitude smaller with respect to the maximum lag achievable by Vela between the 2013 and the 2016 glitches. This can be interpreted in terms of the presence of vortex creep inside the star in the three years before the 2016 glitch, which turns out to be very efficient in dissipating the lag that could be built up in between glitches.
The fit on the angular velocity of the star following the glitch allows us to calculate some other interesting quantities, such as an upper bound on the glitch rise timescale of ∼6 s and the following relaxation timescale (similar to that measured in other Vela glitches, such as Dodson et al. 2002, 2007). The theoretical formalisation and the subsequent fit of the “overshoot parameter” of ω allow us to confirm the presence of an overshoot in the 2016 Vela pulsar glitch (Ashton et al. 2019b; Pizzochero et al. 2020).
Finally, we would like to stress the importance of a Bayesian approach in tackling this kind of problem: our previous knowledge of the Vela pulsar can be used in choosing the prior for the Bayesian inference. As this was the first pulse-to-pulse observation of a glitch, not much information can be inserted into the model. As more glitches of the Vela are recorded, however, more information on the particular parameters that we do not expect to change from glitch to glitch (such as the coupling parameters) can be gathered and used as priors for future observations. On the other hand, it may also be the case that the analysis of a new glitch will give very different results for the moment of inertia fractions or the coupling parameters, indicating that the location of the superfluid regions that undergo unpinning depend on the past history of the star.
Since the integration is over the i-region, and the two superfluid regions do not overlap, we can drop the unnecessary i labels on the density and on the entrainment parameter. We do the same in (C.8).
Acknowledgments
Partial support comes from PHAROS, COST Action CA16214, and from INFN, the Italian Institute for Nuclear Physics. The authors would like to thank Gregory Ashton for fruitful discussions. Marco Antonelli acknowledges support from the Polish National Science Centre Grant SONATA BIS 2015/18/E/ST9/00577, P.I.: B. Haskell.
References
- Alpar, M. A. 2017, J. Astrophys. Astron., 38, 44 [CrossRef] [Google Scholar]
- Alpar, M. A., Anderson, P. W., Pines, D., & Shaham, J. 1981, ApJ, 249, L29 [CrossRef] [Google Scholar]
- Alpar, M. A., Pines, D., Anderson, P. W., & Shaham, J. 1984a, ApJ, 276, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Alpar, M. A., Langer, S. A., & Sauls, J. A. 1984b, ApJ, 282, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, P. W., & Itoh, N. 1975, Nature, 256, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, N., Glampedakis, K., Ho, W. C. G., & Espinoza, C. M. 2012, Phys. Rev. Lett., 109, 241103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Andersson, N., Sidery, T., & Comer, G. L. 2006, MNRAS, 368, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Antonelli, M., & Pizzochero, P. M. 2017, MNRAS, 464, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Antonelli, M., Montoli, A., & Pizzochero, P. M. 2018, MNRAS, 475, 5403 [NASA ADS] [CrossRef] [Google Scholar]
- Ashton, G., Lasky, P. D., Graber, V., & Palfreyman, J. 2019a, Nat. Astron., 417, [Google Scholar]
- Ashton, G., Hübner, M., Lasky, P. D., et al. 2019b, ApJS, 241, 27 [CrossRef] [Google Scholar]
- Baym, G., Pethick, C., Pines, D., & Ruderman, M. 1969, Nature, 224, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Bransgrove, A., Beloborodov, A. M., & Levin, Y. 2020, ApJ, 897, 173 [CrossRef] [Google Scholar]
- Carreau, T., Gulminelli, F., & Margueron, J. 2019, Phys. Rev. C, 100, 055803 [CrossRef] [Google Scholar]
- Celora, T., Khomenko, V., Antonelli, M., & Haskell, B. 2020, MNRAS, 496, 5564 [CrossRef] [Google Scholar]
- Chamel, N. 2012, Phys. Rev. C, 85, 035801 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N. 2013, Phys. Rev. Lett., 110, 011101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chamel, N. 2017a, J. Astrophys. Astron., 38, 43 [CrossRef] [Google Scholar]
- Chamel, N. 2017b, J. Low Temp. Phys., 189, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Haensel, P. 2006, Phys. Rev. C, 73, 045802 [NASA ADS] [CrossRef] [Google Scholar]
- Datta, B., & Alpar, M. A. 1993, A&A, 275, 210 [NASA ADS] [Google Scholar]
- Delsate, T., Chamel, N., Gürlebeck, N., et al. 2016, Phys. Rev. D, 94, 023008 [CrossRef] [Google Scholar]
- Dodson, R. G., McCulloch, P. M., & Lewis, D. R. 2002, ApJ, 564, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Dodson, R., Lewis, D., & McCulloch, P. 2007, Ap&SS, 308, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Epstein, R. I., & Baym, G. 1992, ApJ, 387, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, C. M., Lyne, A. G., Stappers, B. W., & Kramer, M. 2011, MNRAS, 414, 1679 [NASA ADS] [CrossRef] [Google Scholar]
- Fuentes, J. R., Espinoza, C. M., Reisenegger, A., et al. 2017, A&A, 608, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavassino, L., Antonelli, M., Pizzochero, P. M., & Haskell, B. 2020, MNRAS, 494, 3562 [CrossRef] [Google Scholar]
- Goriely, S., Chamel, N., & Pearson, J. M. 2010, Phys. Rev. C, 82, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Graber, V., Cumming, A., & Andersson, N. 2018, ApJ, 865, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Gügercinoğlu, E., & Alpar, M. A. 2020, MNRAS, 496, 2506 [CrossRef] [Google Scholar]
- Haskell, B., & Melatos, A. 2015, Int. J. Mod. Phys. D, 24, 1530008 [NASA ADS] [CrossRef] [Google Scholar]
- Haskell, B., & Melatos, A. 2016, MNRAS, 461, 2200 [CrossRef] [Google Scholar]
- Haskell, B., & Sedrakian, A. 2018, in Superfluidity and Superconductivity in Neutron Stars, eds. L. Rezzolla, P. Pizzochero, D. I. Jones, N. Rea, & I. Vidaña (Cham: Springer International Publishing), 401 [Google Scholar]
- Haskell, B., Pizzochero, P. M., & Sidery, T. 2012, MNRAS, 420, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, W. C. G., Espinoza, C. M., Antonopoulou, D., & Andersson, N. 2015, Sci. Adv., 1, e1500578 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, P. B. 1990, MNRAS, 243, 257 [Google Scholar]
- Jones, P. B. 1992, MNRAS, 257, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Kass, R. E., & Raftery, A. E. 1995, J. Am. Stat. Assoc., 90, 773 [CrossRef] [Google Scholar]
- Larson, M. B., & Link, B. 2002, MNRAS, 333, 613 [CrossRef] [Google Scholar]
- Link, B., Epstein, R. I., & Lattimer, J. M. 1999, Phys. Rev. Lett., 83, 3362 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Shemar, S. L., & Smith, F. G. 2000, MNRAS, 315, 534 [NASA ADS] [CrossRef] [Google Scholar]
- MacKay, D. J. C. 2003, Information Theory, Inference & Learning Algorithms (Cambridge University Press) [Google Scholar]
- Martin, N., & Urban, M. 2016, Phys. Rev. C, 94, 065801 [NASA ADS] [CrossRef] [Google Scholar]
- Montoli, A., Antonelli, M., & Pizzochero, P. M. 2020, MNRAS, 492, 4837 [NASA ADS] [CrossRef] [Google Scholar]
- Palfreyman, J., Dickey, J. M., Hotan, A., Ellingsen, S., & van Straten, W. 2018, Nature, 556, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzochero, P. M., Antonelli, M., Haskell, B., & Seveso, S. 2017, Nat. Astron., 1, 0134 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzochero, P. M., Montoli, A., & Antonelli, M. 2020, A&A, 636, A101 [CrossRef] [EDP Sciences] [Google Scholar]
- Sauls, J. A., Chamel, N., & Alpar, M. A. 2020, ArXiv e-prints [arXiv:2001.09959] [Google Scholar]
- Sedrakian, A. D. 1995, MNRAS, 277, 225 [Google Scholar]
- Sidery, T., Passamonti, A., & Andersson, N. 2010, MNRAS, 405, 1061 [NASA ADS] [Google Scholar]
- Sourie, A., & Chamel, N. 2020, MNRAS, 493, L98 [NASA ADS] [CrossRef] [Google Scholar]
- Sourie, A., Chamel, N., Novak, J., & Oertel, M. 2017, MNRAS, 464, 4641 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S. 2020, MNRAS, 493, 3132 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, G., & Pethick, C. J. 2017, Phys. Rev. Lett., 119, 062701 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Solution to the system
Here, we describe the procedure for solving the system in Eq. (1). As a first step, we rewrite the component 3 system by performing a change of variables: it is convenient to use the superfluid angular velocities as measured in the frame of the normal component, Ω1p and Ω2p. Furthermore, it is convenient to directly integrate the equation for Ωp to find that the angular velocity for the normal component with respect to the steady-state spin down solution is given by
where we have defined the vectors
In this way, we only have to worry about the dynamics of the lag vector, y, that must satisfy the matrix equation,
where
and
The matrix B has two eigenvalues λ+ and λ−, given by
where the positive parameters T and D represent the trace and the determinant of B, respectively. We call the respective eigenvectors, e+ and e−, defined up to a normalisation constant; their explicit form is not needed here.
Using the fact that the parameters bi are positive and that the sum of the moment of inertia fractions xi cannot exceed unity, it is a straightforward exercise to prove that both the eigenvalues are always positive and in particular that λ+ > λ− > 0. Because of this positivity property, Eq. (A.3) allows for a stable steady-state solution y(t) = y∞ that is constant in time:
This particular solution is an attractor for the dynamics of the lag vector y: the internal forces induced by dissipation (set by the parameters bi) and the driving force (set by the parameter 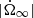 ) tend to balance out, killing off initial transients and settling the system into its typical behavior described by y∞. Since we have two natural timescales (one short, 1/λ+, and one long, 1/λ−), we can conclude that the steady state is reached in the limit t ≫ 1/λ−.
) tend to balance out, killing off initial transients and settling the system into its typical behavior described by y∞. Since we have two natural timescales (one short, 1/λ+, and one long, 1/λ−), we can conclude that the steady state is reached in the limit t ≫ 1/λ−.
The above property of the system allows to define the asymptotic amplitude of the glitch 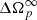 : we just have to take the limit t ≫ 1/λ− in Eq. (A.1) to obtain
: we just have to take the limit t ≫ 1/λ− in Eq. (A.1) to obtain
Instead of the lag vector y, it is more convenient to consider the dynamics of the residual with respect to the steady-state
that satisfies the linear equation,
Decomposing y0 − y∞ in the basis of the eigenvectors,
the general solution of Eq. (A.11) can be expressed as
Employing the decomposition (A.12) and (A.13) into (A.1), it is easy to find
where we have defined
Instead of using the eigenvectors, it is easier to find the value of ω in terms of the parameters of the system (1) by considering the value of the derivative of Eq. (A.14) at t = 0:
To write the general solution (A.14) in terms of the basic parameters of the model, we need to know that
while the eigenvalues are given by
Finally, we observe that to obtain a positive glitch amplitude both 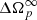 in Eq. (A.17) and
in Eq. (A.17) and 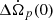 in Eq. (A.18) should be positive. This constrains the initial lags and it is possible to show that this requirement is fulfilled for any possible value of x1 and x2 if
in Eq. (A.18) should be positive. This constrains the initial lags and it is possible to show that this requirement is fulfilled for any possible value of x1 and x2 if
which will be used in Appendix B.
Appendix B: Constraint on the moment of inertia of the slow component
In Appendix A, we presented the general solution to the three-component system, which extends the particular solution discussed in Pizzochero et al. (2020). Building on this particular solution, Sourie & Chamel (2020) recently proposed a simple formula to constrain the moment of inertia fraction of one of the superfluid component. It is worth to extend their treatment in view of the more general approach used here.
First, following Sourie & Chamel (2020) we define the overshoot size ΔΩover as the maximum value touched during the spin-up phase. Using ΔΩover = ΔΩp(tmax) and Eq. (5), we immediately obtain
This quantity depends on the phenomenological input parameters of the model (i.e. the xi, bi and 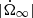 ) as well as on the initial condition
) as well as on the initial condition 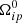 , for i = 1, 2. Up to this point, the role of the superfluid components 1 and 2 is symmetric (we do not assume Eq. (8) here) and all the formulas are invariant under the exchange of the two. However, let us assume that one of the two components, for example, that component 2 has a higher drag parameter with respect to the other, that is, b1 ≪ b2 and
, for i = 1, 2. Up to this point, the role of the superfluid components 1 and 2 is symmetric (we do not assume Eq. (8) here) and all the formulas are invariant under the exchange of the two. However, let us assume that one of the two components, for example, that component 2 has a higher drag parameter with respect to the other, that is, b1 ≪ b2 and
No further assumptions are needed on x1 and x2 (i.e. we do not need to specify which of the two components has higher inertia). This case is of physical interest (since we expect the nature and the strength of the friction mechanism to vary in different layers of the star) and allows to perform an expansion in the parameter a1/2.
Under the assumption (B.2), the constraint (A.20) tells us that
Taking into account the above inequalities and inserting the expansions
into (B.1), it is possible to safely take the limit a1/2 ≪ 1 to show that
and
Thanks to (A.19), we find that (B.5) and (B.6) state that:
The lowest-order term ω* in (B.4) can now be obtained by inserting the above equations into (A.15). Finally, the ratio in (B.8) turns out to be
or, equivalently,
Equation (B.3) tells us that the second term in the right hand side is always negative, such that to the lowest order in a1/2, the detection of an overshoot allows to constrain the fractional moment of inertia of the “slow” component (in this case x1) as
This is in complete accordance with Eq. (12) of Sourie & Chamel (2020). In Appendix C, we describe how to interpret x1 when there is superfluid entrainment between the components, see Eq. (C.16).
Appendix C: Including entrainment
It is straightforward to include the entrainment effect into our system of equations, provided that a convenient choice of the dynamical variables is made. In fact, using the “superfluid momentum” of pn instead of the “neutron velocity” of vn naturally leads to a redefinition of the phenomenological parameters of the hydrodynamic model (here, xi and bi for i = 1, 2), but the form of the dynamical equations remains unchanged (Antonelli & Pizzochero 2017). Originally, the argument was presented in the very special case of straight and rigid vortex lines in a Newtonian context, but it can be generalised to the case of “slack” vortices and of different superfluid domains, as well as to take into account for general relativistic corrections in the slow-rotation approximation (Antonelli et al. 2018; Gavassino et al. 2020).
Differently from Paper I, here we derive Eq. (1) starting from a local and fluid model. Hence, the present discussion is analogous to the one made by Sidery et al. (2010) and differs from it only with regard to the choice of variables, nonetheless, it is quite convenient in the present framework where we have to deal with three different components. The results of this section can be immediately extended to a generic number of non-overlapping superfluid components.
Locally, the momentum per particle pn of the superfluid neutrons is a linear combination of the neutron velocity vn and of the velocity of the normal component vp (which is a mixture of all the charged species and we assume it to be rigid),
where mn is the neutron mass and ϵn is the entrainment parameter (Haskell & Sedrakian 2018; Chamel 2017b).
If we have two different (non-overlapping) superfluid regions and the motion is circular, the above equation suggests to define two additional angular velocities 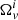 as
as
where Ωp is the observable angular velocity of the normal p-component while 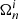 is the angular velocity of the neutrons in the region i = 1, 2. Working with the
is the angular velocity of the neutrons in the region i = 1, 2. Working with the 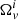 is convenient because, due to the Feynman-Onsager relation, they are a direct measure of the number of vortices in a certain superfluid region. Hence, the
is convenient because, due to the Feynman-Onsager relation, they are a direct measure of the number of vortices in a certain superfluid region. Hence, the 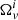 cannot change as long as the number of vortices is conserved. This defines the form of the equations of motion at a certain location x inside the star (Antonelli & Pizzochero 2017),
cannot change as long as the number of vortices is conserved. This defines the form of the equations of motion at a certain location x inside the star (Antonelli & Pizzochero 2017),
where ℛi is the drag-to-lift ratio that appears in the vortex-mediated mutual friction force between the superfluid and normal components (Andersson et al. 2006). In Eq. (C.3), we dropped a term 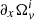 , absent for rigid rotation, hence the ≈ symbol. With the aid of (C.2), the above equation states:
, absent for rigid rotation, hence the ≈ symbol. With the aid of (C.2), the above equation states:
where the coefficient Bi(r) depends on the local values ℛi(r) and 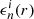 at a certain radius r inside the star (we assume spherical stratification), namely,
at a certain radius r inside the star (we assume spherical stratification), namely,
where 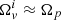 because the lags are small. When the variables
because the lags are small. When the variables 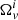 are used, the total angular momentum of the star Ltot is given by
are used, the total angular momentum of the star Ltot is given by
where I is the total moment of inertia and2
is a rescaled moment of inertia for the superfluid component (the integration extends over the region i and ρn(r) is the density of unbounded neutrons). Using standard spherical coordinates where θ is the colatitude, the parameters 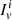 play the role of normalisation factors for the averages of functions over the i-region,
play the role of normalisation factors for the averages of functions over the i-region,
We now take the spatial average of Eq. (C.4),
Clearly, the last step is not rigorous but neglecting possible correlations between the local value of Bi and the spatial fluctuations of the lag 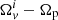 is the price we have to pay to obtain a rigid model from a fluid one. Finally, the only effect of the spin-down torque is to transport the angular momentum to infinity, so it can be introduced as
is the price we have to pay to obtain a rigid model from a fluid one. Finally, the only effect of the spin-down torque is to transport the angular momentum to infinity, so it can be introduced as
Equations (C.9) and (C.10) are formally equivalent to the system in (1), provided that we make the following identifications:
Similarly, the lag vector y in (A.2) should be interpreted as
We note that including all the entrainment corrections into the definition of the phenomenological parameters of the model has the advantage that the final system of equations does not change because of the additional entrainment couplings. Hence, no new calculations are needed to find the general solution of the system, which is formally identical to the case with no entrainment. In particular, the generalisation of the formula of Sourie & Chamel (2020) to the case in which there is entrainment is still represented by our Eq. (B.12), where
All Tables
16th, 50th, and 84th percentiles for the marginalised posterior for the different variables of the model.
All Figures
 |
Fig. 1. Cornerplot of the posterior distribution. On the diagonal, the marginalised posterior distribution for each parameter of the model is plotted. The vertical lines represent the 16th and 84th percentiles of these distributions. The numerical values are reported in Table 1. The prior distribution is plotted in orange as a comparison: for the jump in the residuals Δr0 and the magnetospheric time tM this is almost invisible, due to the width of the distribution. The covariance plots are located off-diagonal. |
| In the text | |
 |
Fig. 2. Probability distribution for the inferred glitch time tg and the time of the magnetospheric slip tM. For comparison, some characteristic times obtained in Palfreyman et al. (2018) are superimposed: the time of a null pulse t0, the start and the end of the rise of the residuals t1 and t2, and the glitch time |
| In the text | |
 |
Fig. 3. Result of the fit. We plot the data obtained by Palfreyman et al. (2018) in grey, joined by a line, and the fitted curve: for each time t every 0.1 s between −50 s and 100 s, we calculate the probability distribution for r(t) starting from the samples of the posterior distribution. The median of the probability distribution for the residual function r(t) defined in (11) is plotted in black, while the blue region indicates the 16th–84th percentile zone. The reference time t = 0 is set to be the glitch time |
| In the text | |
 |
Fig. 4. Probability distributions for the glitch rise timescale, 1/λ+, the relaxation timescale, 1/λ−, the overshoot parameter, ω, and the glitch size, |
| In the text | |
 |
Fig. 5. Comparison between the possible values of the superfluid moment of inertia fraction Iv(nB)/I and the possible values of x2 according to its posterior distribution P(x2). We plot the points (Iv(nB)/I, nB), where the baryon density nB is expressed in units of the nuclear saturation density n0 = 0.17 fm−3. The inner-crust, i.e. nd < nB ≲ 0.5n0, corresponds to the orange-shaded region. The upper panel refers to the BSk21 EoS (Goriely et al. 2010), the lower one to the SLy4 EoS (Douchin & Haensel 2001). The curves represent the points (Iv(nB)/I, nB) when entrainment corrections are included (red-dashed) by using the values calculated by Chamel & Haensel (2006) and Chamel (2012) and when entrainment coupling is set to zero (gray-solid). The posterior P(x2) is superimposed as a background histogram, with the 16th, 50th and 84th percentiles shown with black dotted lines. The two green dash-dotted lines indicate an upper limit (corresponding to the 84th percentile) to the extension of the superfluid 2 region if the mass of the Vela is M = 2M⊙. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



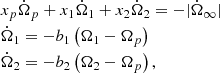
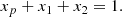
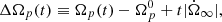
![$$ \begin{aligned} \Delta \Omega _p(t) \, = \, \Delta \Omega _p^\infty \left[ 1- \omega \, e^{-t \lambda _+} - (1-\omega )\, e^{-t \lambda _-} \right] , \end{aligned} $$](/articles/aa/full_html/2020/10/aa38340-20/aa38340-20-eq7.gif)
![$$ \begin{aligned} t_{\rm max} \, = \, \frac{1}{\lambda _+ - \lambda _-} \, \left[ \log \left( \frac{\lambda _+}{\lambda _-} \right) + \log \left( \frac{ \omega }{\omega -1} \right) \right] , \end{aligned} $$](/articles/aa/full_html/2020/10/aa38340-20/aa38340-20-eq13.gif)
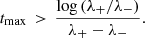
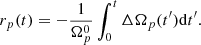
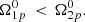
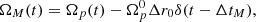
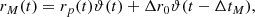
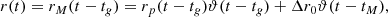
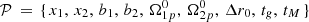
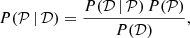
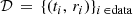
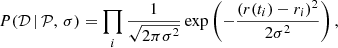
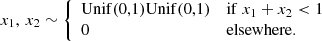
![$$ \begin{aligned}&b_1\, [\mathrm{s}^{-1}] \sim \mathrm{LogUnif(}10^{-6},\ 10^{0}) \end{aligned} $$](/articles/aa/full_html/2020/10/aa38340-20/aa38340-20-eq32.gif)
![$$ \begin{aligned}&b_2\, [\mathrm{s}^{-1}] \sim \mathrm{LogUnif(}10^{-4},\ 10^{2}) . \end{aligned} $$](/articles/aa/full_html/2020/10/aa38340-20/aa38340-20-eq33.gif)
![$$ \begin{aligned} \Omega _{1p}^0,\, \Omega _{2p}^0\, [\mathrm{rad\,s}^{-1}] \sim \left\{ \begin{array}{ll} \mathrm{LogUnif(}10^{-10},\ 10^{-1})\, \times&\\ \times \mathrm{LogUnif(}10^{-5},\ 10^{-1})&\mathrm{if}\ \Omega _{1p}^0 < \Omega _{2p}^0\\ 0&\mathrm{elsewhere}. \end{array}\right. \end{aligned} $$](/articles/aa/full_html/2020/10/aa38340-20/aa38340-20-eq35.gif)
![$$ \begin{aligned} \Delta r_0\, [ \mathrm{ms} ] \sim \mathrm{Unif}(-100,\, 100). \end{aligned} $$](/articles/aa/full_html/2020/10/aa38340-20/aa38340-20-eq36.gif)
![$$ \begin{aligned}&t_g\, [\mathrm{s}] \sim \mathrm{Unif(-100, 100),} \end{aligned} $$](/articles/aa/full_html/2020/10/aa38340-20/aa38340-20-eq38.gif)
![$$ \begin{aligned}&t_M\, [\mathrm{s}] \sim \mathrm{Unif(-1000, 100).} \end{aligned} $$](/articles/aa/full_html/2020/10/aa38340-20/aa38340-20-eq39.gif)
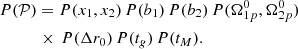
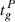
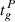
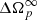
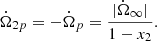
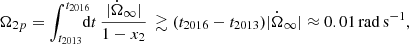
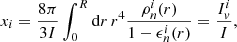
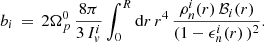
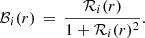
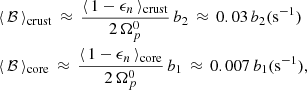
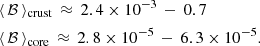
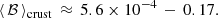
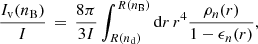
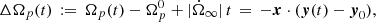
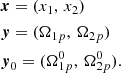
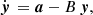
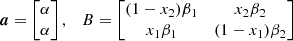
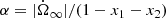
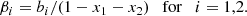
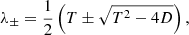
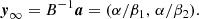
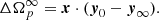
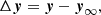
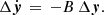
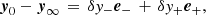
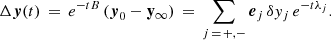
![$$ \begin{aligned} \Delta \Omega _p(t) \, = \, \Delta \Omega _p^\infty \left[ 1- \omega \, e^{-t \lambda _+} - (1-\omega )\, e^{-t \lambda _-} \right] , \end{aligned} $$](/articles/aa/full_html/2020/10/aa38340-20/aa38340-20-eq92.gif)
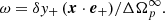
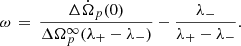
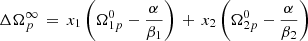
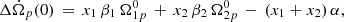
![$$ \begin{aligned} \begin{aligned}&\lambda _\pm \, = \, \frac{1}{2} \bigg [ \beta _1 (1-x_2) + \beta _2 (1-x_1) \\&~~\quad \quad \pm \sqrt{ [ \beta _1 (1 - x_2) + \beta _2 (1 - x_1) ]^2 - 4 \beta _1 \beta _2 x_p } \bigg ] . \end{aligned} \end{aligned} $$](/articles/aa/full_html/2020/10/aa38340-20/aa38340-20-eq97.gif)
![$$ \begin{aligned} |\dot{\Omega }_\infty | \, < \, \min _{i=1,2}[ \, b_i \, \Omega _{ip}^0 \, ] , \end{aligned} $$](/articles/aa/full_html/2020/10/aa38340-20/aa38340-20-eq100.gif)