| Issue |
A&A
Volume 642, October 2020
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202038056 | |
| Published online | 15 October 2020 | |
Reconstructing the gravitational lensing potential from the Lyman-α forest
1
Dipartimento di Fisica & Astronomia, Università di Bologna, via Gobetti 93/2, 40129 Bologna, Italy
e-mail: robertbenton.metcalf@unibo.it
2
INAF-Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
3
Jodrell Bank Centre for Astrophysics, University of Manchester, Alan Turing Building, Oxford Road, Manchester M13 9PL, UK
4
McWilliams Center for Cosmology, Department of Physics, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Received:
30
March
2020
Accepted:
17
May
2020
We demonstrate a method for reconstructing the weak lensing potential from the Lyman-α forest data. We derive an optimal estimator for the lensing potential on the sky based on the correlation between pixels in real space. This method effectively deals with irregularly spaced data, holes in the survey, missing data, and inhomogeneous noise. We demonstrate an implementation of the method with simulated spectra and weak lensing. It is shown that with a source density of ≳0.5 per square arcmin and ∼200 pixels in each spectrum (λ/Δλ = 1300) the lensing potential can be reconstructed with high fidelity if the relative absorption in the spectral pixels is signal dominated. When noise dominates the measurement of the absorption in each pixel the noise in the lensing potential is higher, but for reasonable numbers of sources and noise levels and a high fidelity map the lensing potential is obtainable. The lensing estimator could also be applied to lensing of the cosmic microwave background, 21 cm intensity mapping, or any case in which the correlation function of the source can be accurately estimated.
Key words: cosmology: miscellaneous / gravitational lensing: weak / methods: observational
© ESO 2020
1. Introduction
Weak gravitational lensing (Bartelmann & Schneider 2001; Bartelmann & Maturi 2017) describes the distortion of background sources of light by foreground matter in the regime where statistical averaging is needed to detect the effect. As any object at cosmological distances can be lensed, a variety of background sources apart from galaxies (Valdes et al. 1983; Kaiser 1992; Troxel et al. 2018), such as radio sources (Chang et al. 2004; Harrison et al. 2016) or even already-lensed images themselves (Birrer et al. 2018), can be studied with weak lensing techniques. These examples are discrete objects, and the statistical measures of weak lensing (e.g., Miralda-Escude 1991) that are applied to those observations treat them as such. This includes estimators of the foreground lensing matter distribution (e.g., Kaiser & Squires 1993; Jeffrey et al. 2020). In addition, a continuous background source field at cosmological distances can also be lensed, and a whole class of estimators has been developed to deal with this case, starting with the cosmic microwave background (CMB) as the source field (e.g., Bernardeau 1997; Metcalf & Silk 1997, 1998; Zaldarriaga & Seljak 1999; Hu & Okamoto 2002; Schaan & Ferraro 2019). In the continuous case, it is the statistical properties of the field that change as it is lensed, with both the scale and isotropy of correlations imparting information on the foreground matter (see reviews by Lewis & Challinor 2006; Hanson et al. 2010). In the present paper we develop and test the first estimator appropriate to a particular cosmological field for which lensing has not yet been observed, the Lyman-α (Lyα) forest.
In addition to the CMB, another continuous field that has been studied in this context is the emission from neutral hydrogen in the Universe close to the epoch of reionization, investigated using the 21 cm radio line (Madau et al. 1997; Furlanetto et al. 2006). In this case the field is in three dimensions as the use of a discrete line yields redshift information, and datacubes of line intensity are known as intensity maps (Wyithe & Morales 2007). Even at lower redshifts where galaxies act as increasingly discrete sources of 21cm emission, intensity maps can be made without identifying individual sources, and can trace large-scale structure more efficiently (Chang et al. 2010; Anderson et al. 2018). Estimators of weak lensing have been developed that are appropriate to 21cm intensity maps (Zahn & Zaldarriaga 2006; Metcalf & White 2007; Pourtsidou & Metcalf 2015; Foreman et al. 2018, see also Pourtsidou & Metcalf 2014 for the low redshift case). These are generalizations of the estimators applied to the CMB, and, similarly, they act on a continuous lensed source field, usually employing Fourier techniques.
The neutral hydrogen density field also absorbs radiation, and the Lyα line can be used to observe it in the spectra of background galaxies and quasars (which we refer to as sources here). The absorption signatures are the Lyman-α forest (Rauch 1998; Prochaska 2019), and are good tracers of the overall cosmological density field on scales larger than the gas pressure smoothing scale (of order 0.1 Mpc, Peeples et al. 2010). Clustering of the Lyα forest (see e.g., Croft et al. 1998; Hui et al. 1999; McDonald & Miralda-Escudé 1999, for some early work) is now a mainstream cosmological probe, and for example has been used to measure the Baryon Acoustic Oscillations (BAO) scale at z = 2–3 (Busca et al. 2013; Slosar et al. 2013; de Sainte Agathe et al. 2019), the power spectrum of mass fluctuations (e.g., Chabanier et al. 2019), and to constrain the properties of dark matter (e.g., Iršič et al. 2017). By including high-redshift galaxies as well as quasars, a higher source density can be reached at the expense of more telescope time. Lee et al. (2018) and Newman et al. (2020) have used this higher density to construct 3D maps of the neutral atomic hydrogen (HI).
The Lyα forest is well understood, and can be simulated in the context of CDM models (e.g., Bolton et al. 2017; Rogers et al. 2018; Chabanier et al. 2020). McQuinn & White (2011, 2015) studied the problem of measuring the power spectrum from the Lyα forest. Many significant observational datasets either exist (Ahumada et al. 2019; Lee et al. 2018; Newman et al. 2020), are planned, or are in progress (DESI Collaboration 2016; Dalton et al. 2018; Flagey et al. 2018) The forest is also the first weak lensing probe for which data exists that has full spectroscopic information, thus bypassing the difficulties of galaxy lensing associated with photometric redshifts (Bordoloi et al. 2010; Cunha et al. 2014). As such, the Lyα forest represents a useful source field for weak lensing, and Croft et al. (2018) and Metcalf et al. (2018) explored what will be possible, but without developing an estimator appropriate for the specific geometry of the forest.
The Lyα forest requires the development of a new lensing estimator because although it samples a continuous 3D field, the sampling is not uniform or space-filling. The absorption is imprinted in the spectra of sources (galaxies or quasars), which have an angular extent that is much smaller than the separation between them. The angular coverage is therefore effectively a set of delta functions, although the spectra are continuous along the line of sight (excepting masked contaminated regions). There is also noise in the pixel values in these spectra, including CCD readout noise, Poisson photon noise, flux calibration errors, and sky subtraction errors (see e.g., Bautista et al. 2015), and also potentially large-scale correlated noise from uncertainty in the zero level (continuum fitting, Blomqvist et al. 2015). However, the angular positions of the sources are usually determined to a much smaller uncertainty (< 0.05 arcsec, Ahn et al. 2012) than the mean lensing deflection angle of a few arcmins (Lewis & Challinor 2006), and are not a source of noise in themselves.
We are therefore not able to apply the usual quadratic estimators (e.g., Hu & Okamoto 2002; Metcalf & White 2009) to forest lensing, as these rely on uniform coverage with a regular grid. In our previous studies, reconstructing the lensing potential from simulated Lyα forest sightlines (Croft et al. 2018), we worked with a toy model mock survey, with all sources on an evenly spaced grid, a situation not applicable to observational data. In practice, the angular distribution of quasar and galaxy sources is not only irregular, but can be extremely sparse, with the data sets with the largest current total numbers having a mean separation between sources of order 10 arcmin (Blomqvist et al. 2019). In general, it would be extremely useful to have an estimator which can deal with a variety of different survey geometries and sampling, and that is our aim in this paper.
The method we develop is general, and although we focus here on the Lyα forest, it has applications to the weak lensing of other sources that can be treated as continuous and isotropic such as the CMB (Lewis & Challinor 2006) or spectral line intensity mapping (SLIM; e.g., Kovetz et al. 2017). The same method can be applied to any linear distortion in the 3D correlation function relative to expectations, including redshift distortions, or the scale of the BAOs.
The outline of the present paper is as follows. In the following section we review the necessary basics of Lyα observations. In Sect. 3 we calculate the effect lensing has on the second-order correlations between the Lyα absorption in the pixels in the spectra of quasars and galaxies. We derive our quadratic estimator for the lensing potential and discuss some of its properties in Sect. 4. The methods used to simulate data are described in Sect. 5 and in the Appendices. In Sect. 6 the estimator is tested on various simulated data sets. A final discussion is provided in Sect. 9. The Appendices contain details about simulating data and on using different expansions of the lensing potential in the estimator.
2. The Lyα forest
Neutral hydrogen will absorb photons through the Lyα transition (λα = 1215.67 Å) along the sight line to high-redshift sources. Because of cosmological redshifting, this absorption will appear at an observed wavelength, (1 + z)λα, where z is below the redshift of the source. In general, the redshift range of the Lyα forest is limited to ≳2 because of atmospheric opacity at lower wavelengths. In individual cases, the redshift range is limited on the high side by the redshift of the source and on the low side by confusion with absorption by the Lyβ line if not by the atmosphere. Damped Lyα systems cannot be used, and so they need to be masked out (see e.g., Font-Ribera et al. 2012). As a result of these considerations the volume probed by the Lyα forest is very irregularly sampled.
The flux at observed wavelength or pixel λ in the spectra of the qth source can be written (Busca et al. 2013; Slosar et al. 2011, 2013)
where Cq(λ) is the unabsorbed spectrum of the qth source, F̄(λ) is the mean transmission in the forest at λ, and nq, λ is uncorrelated pixel noise. Other factors such as the sky background, spectrograph transmissivity, and PSF are either negligible or can be absorbed into these quantities. The quantities δqλ are the fluctuations in the absorption which to first order are proportional to fluctuations in the column density of HI. However, for the purposes of this paper, the details of the relationship between δqλ and the HI density or the dark matter density are not important. Here, we assume that the statistical distribution of δqλ is isotropic and that its correlation function can be measured or modeled.
A two parameter model for the unabsorbed spectra, Cq(λ), the δqλs, and their covariance matrix can be found using different methods, for example those of Busca et al. (2013) and Slosar et al. (2011, 2013), or by fitting template spectra in the case of sources that are galaxies (Newman et al. 2020; Lee et al. 2018). One method is to find the maximum likelihood solution for δqλ by brute force minimization and then to approximate the covariance matrix as the Fisher matrix found numerically at the maximum likelihood solution. Here, F̄(λ) is found by averaging across all sources in the data or perhaps from another survey with a higher signal-to-noise ratio and higher resolution spectra (e.g., Faucher-Giguère et al. 2008). The fitting of these quantities will induce covariance between pixels that would not otherwise be there solely due to observational noise.
In this paper we assume that the modeling of Cq(λ) and F̄(λ) has already been done to find δqλ and the covariance matrix N. It may also be advantageous to transform the data using a function that makes the distribution of δqλ values strictly Gaussian (e.g., Croft et al. 1998), but we do not investigate that here.
3. The effect of lensing on the Lyα forest
As light passes through structures in the Universe it is deflected from a geodesic of the unperturbed, homogeneous metric. One way of representing this is to imagine many planes that are perpendicular to the unperturbed light ray. At each plane the ray is deflected. In the Born approximation, the perpendicular position at redshift z can be written as
where  is the deflection at the mth plane and the sum is over all planes at lower redshift (Petkova et al. 2014; Schneider et al. 1992). The angular position of the image is θ, the angular diameter distance between redshifts z1 and z2 is D(z1, z2), and D(z) = D(0, z). The usual scaled deflection angle αm(θ) is obtained by rescaling all deflection angles to redshift z. The total deflection for a light ray originating at redshift z is therefore the sum over all lensing planes below z,
is the deflection at the mth plane and the sum is over all planes at lower redshift (Petkova et al. 2014; Schneider et al. 1992). The angular position of the image is θ, the angular diameter distance between redshifts z1 and z2 is D(z1, z2), and D(z) = D(0, z). The usual scaled deflection angle αm(θ) is obtained by rescaling all deflection angles to redshift z. The total deflection for a light ray originating at redshift z is therefore the sum over all lensing planes below z,
In addition, for this paper we make the approximation that all the deflections of significance take place at a redshift smaller than the redshift of the Lyα absorption that we consider. This is a good first approximation which can be relaxed when the data warrants it.
In the weak lensing limit, the deflection field is curl free, and so a lensing potential can be defined, the gradient of which is the deflection
The gradient ∇ here is taken with respect to the angular coordinates θ. The potential is related to the convergence, κ(θ), by a Poisson equation
The convergence is the trace of the magnification matrix and in the weak lensing context can be interpreted as a weighted surface density on the sky,
where δ(θ,χ) is the density contrast at the radial coordinate, comoving distance χ, dA(χ) is the comoving angular size distance, Ωm is the matter density parameter, and Ho is the Hubble parameter.
Gravitational lensing moves the apparent position of a source on the sky. In the plane sky approximation (this approximation is relaxed in Appendix A.4), the observed absorption δo at the radial position r∥ and perpendicular position r⊥ is, to first order,
where δ(θ) is the intrinsic absorption, as it would have appeared without lensing. To first order in the deflection, the observed absorption correlation function will be changed by
where r = (|x‖ − x‖|,|x⊥ − x⊥′|), r = |r|, r⊥ = |x⊥ − x⊥′|, D̅ is the average angular distance to the two redshifts, and d(z) = D(z)/D̅(z,z′). Here, ξ(r⊥, r∥) is the intrinsic, pre-lensing correlation function, and γ is the angular separation of the two points x and x′. In deriving line (13) we have assumed that any two pixels that are strongly enough correlated to contribute to the lensing signal are at approximately the same angular size distance,  . This approximation can be relaxed if necessary, but is probably a good one. Line (14) serves to define the function 𝒢(D, r). We have written the intrinsic correlation function as a function of both r∥ and r⊥ to allow for redshift distortions caused by the radial velocities of the HI.
. This approximation can be relaxed if necessary, but is probably a good one. Line (14) serves to define the function 𝒢(D, r). We have written the intrinsic correlation function as a function of both r∥ and r⊥ to allow for redshift distortions caused by the radial velocities of the HI.
Our proposed method is based on modeling the deflection field ϕ(θ) in a form that is linear in the coefficients  for a set of basis functions fℓ(θ):
for a set of basis functions fℓ(θ):
The deflection field α = ∇ϕ at angular position θi is then related to the model parameters 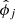 as
as
where ν = 1, 2 is the component of the deflection field, and  is the gradient of the basis function of the model, fℓ, in the point θi. Below we show specific instances of these models for a number of well-known expansions of the potential.
is the gradient of the basis function of the model, fℓ, in the point θi. Below we show specific instances of these models for a number of well-known expansions of the potential.
Including the noise correlation matrix Nij, the correlation (14) between pixels δi and δj can be written
where
and C is the correlation matrix between pixels including intrinsic correlations, noise, and correlations that come from the modeling procedure outlined in Sect. 2. The 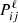 matrix will differ depending on the model for the potential and on how its derivatives are estimated.
matrix will differ depending on the model for the potential and on how its derivatives are estimated.
For example, if the potential is modeled by a discrete Fourier transform (DFT) with coefficients  and ℓ = (ℓ1,ℓ2), we can compute the deflection field,
and ℓ = (ℓ1,ℓ2), we can compute the deflection field,
and the  matrices (19),
matrices (19),
where θij = θi −θj and  .
.
More details for the implementation of this and other expansions are given in Appendix A. We use the Legendre expansion presented in Appendix A.1 for our numerical demonstrations for reasons that are explained below. We have also implemented and tested a bilinear, finite difference expansion on a grid and a Chebyshev expansion (Appendix A.2). The advantage of the Legendre and Chebyshev expansions is that they do not impose any boundary conditions and, unlike the bilinear case, they have continuous derivatives, meaning that the deflection field is continuous.
We note that two pixels (i, j) in the spectrum of a single source will have the same angular position and so  will be zero. Two pixels from different spectra will have uncorrelated noise, and so Nij will be zero, except perhaps through the estimate (1) of F̄(λ). The intrinsic correlation between the absorption must be isotropic in angle, and therefore ξ(rij) will be a function of only the absolute angular separation between the pixels and their radial separation.
will be zero. Two pixels from different spectra will have uncorrelated noise, and so Nij will be zero, except perhaps through the estimate (1) of F̄(λ). The intrinsic correlation between the absorption must be isotropic in angle, and therefore ξ(rij) will be a function of only the absolute angular separation between the pixels and their radial separation.
4. Quadratic estimator
We can express Eq. (18) in matrix form:
with the definition
Assuming that the δ-field is Gaussian, the Fisher matrix for the parameters  evaluated at
evaluated at  is
is
This is the standard result for a multivariant Gaussian and is easily derived.
We now consider the quantity
where (24) and the invariance of the trace under cyclic permutations was used. We can therefore construct the unbiased estimator that can be written in several different forms
where z = C−1δ.
The covariance of this estimator is
We now assume that the distribution of the pixel values prior to lensing is Gaussian. This allows us to calculate the fourth-order moment
Plugging this into (33) gives
This is the Cramér-Rao lower limit on the covariance of an unbiased estimator, and so estimator (29) is an efficient estimator, that is, the best that can be obtained given the assumptions.
In the above, we make the approximation that there is just one ϕ(θ) (or α(θ)) field for all pixels. The deflection field should be a function of the redshift of the pixels because of the distance factors and because some lensing of the high-redshift pixels will be caused by structures that are at the redshift of the lower redshift pixels (we call this self-lensing). The above formalism can be easily expanded so that there are a series of potential fields, ϕ(θ,zs), meaning that the range of angular size distances for the pixels is explicitly taken into account. When the data can support more free parameters, a slightly more complicated treatment can be done. For now, we consider the ϕ(θ field to be averaged over the redshifts of the Lyα forest.
To calculate the estimator (29), the inverse of the covariance matrix C must be found. The data vector z = C−1δ could be calculated by solving Cz = δ without finding C−1, but it is still needed to calculate the Fisher matrix and bias term. This can be very numerically burdensome in realistic cases.
4.1. Unconstrained modes and degeneracies
Only differences in the deflection between points appear in the estimator, and so the potential can only be constrained up to an additive constant and a constant gradient. Physically, the gradient is a uniform shift in the sky which does not change the relative positions of the sources.
In addition to these degeneracies, the data may not constrain some other properties of our reconstruction depending on the expansion and the distribution of sources on the sky. For example, if the parameters of the expansion each have a limited range of influence on the deflection field, as in a gridded representation of the potential, then regions that have no data in them, namely holes in the map or regions off the edge of the survey, will be unconstrained. In the extreme case where the number of model parameters exceeds the number of pairs, meaning that the problem is under-determined, there will clearly be combinations of parameters that are unconstrained, but it is not necessary for the number of parameters to be very high to have some unconstrained combinations. These unconstrained combinations correspond to eigenvectors of F that have zero eigenvalues and can therefore be identified.
The physical degeneracies (the offset and gradient) do not necessarily correspond perfectly to some combination of the expansion parameters. For example, the gradient over a small field cannot be expressed as a finite sum of discrete Fourier modes or spherical harmonics. In these expansions, the above procedure will not remove the gradient, and in such cases large artificial gradients can appear if they are not removed in a separate step. In other expansions, such as the Legendre expansion used later, the three degenerate modes are easily identified and removed.
Treating the deflection as a potential field necessarily removes the curl or B-mode component of the deflection field. This component is expected to be quite small in the weak lensing regime and so we ignore it here. If the B-modes ever become of interest, they could be reconstructed by solving for the scalar potential and the pseudo-scalar B-mode potential (Stebbins 1996) in a very similar way to what is done here.
4.2. Choice of basis
As the individual correlations between spectra provide limited information on the deflection field, it makes sense to try to reconstruct a smoothed version of the deflection field. Using a grid with a resolution higher than the density of sources would clearly make the problem under-determined. As shown above, one possible basis is that of discrete Fourier modes. The appearance of an artificial gradient as discussed in Sect. 4.1 is a significant drawback to this basis.
It is also possible to use the spherical harmonic coefficients as free parameters (Appendix A.4). This is probably not advantageous unless the data cover almost all of the sky. Otherwise there will be many unconstrained combinations of spherical harmonic modes, making it difficult to obtain a solution for the potential field. This approach might be advantageous for recovering the power spectrum of the potential, but this is not considered in this paper.
In what follows, we use the Legendre expansion in a square patch on the sky (Appendix A.1). This confers the following advantages: the degenerate modes can be easily removed, the deflection is continuous, there is no implicit periodicity, and the expansion can be cut off at a particular angular scale as with a DFT. The Legendre polynomial of order n has n zeros and so the effective angular scale for a mode is the field size divided by n.
4.3. Sparse case approximation
If the sources are clumped into groups that have relatively little cross-correlation in the absorption and noise between them, the computational cost of the quadratic estimator can be significantly reduced. In this case the covariance matrix is block-diagonal
where C(k) is the covariance matrix for the sources in the kth of n groups. Likewise,
The Fisher matrix (24) becomes
and the estimator (29) becomes
Calculating this estimator is faster by a factor of ∼1/n2, uses less memory by a factor of ∼1/n2 if each term is calculated in series, and has less numerical error than in the general case if the sources are evenly distributed among the groups; however if there is significant cross-correlation between the groups the estimator will be less than optimal.
The groupings could be in positions on the sky and/or in redshift bins. To reduce computational cost, the data could be broken up into redshift bins, the quantities  and
and  calculated, and then combined with Eq. (41) to get an overall estimate of the potential. This ignores correlations between bins, both intrinsic and in the noise, but might not entail a significant reduction in the signal-to-noise ratio.
calculated, and then combined with Eq. (41) to get an overall estimate of the potential. This ignores correlations between bins, both intrinsic and in the noise, but might not entail a significant reduction in the signal-to-noise ratio.
5. Simulation method
To simulate the observations and test our implementation of the estimator we need to simulate the absorption and the lensing potential. Here we describe how we carry this out.
5.1. Simulating the Lyα forest
We used two methods for simulating the absorption field. The first is to go directly from the covariance matrix C for the pixels to a simulated realization without simulating any pixels that are not sampled within the observed spectra. This is done as follows. The correlation matrix is calculated using the methods discussed in Appendix C. The Cholesky decomposition of the covariance matrix is
where L is a lower triangular matrix. This decomposition is done using the linear algebra package Eigen1.
We generate n normally distributed numbers:
where the xi are uncorrelated normally distributed numbers with variance 1, that is, white noise. This data set, δi, will have the desired covariance and be statistically equivalent to a sample taken from a Gaussian random field.
Another method is to directly simulate a Gaussian random field in 3D and then sample the field at the locations of the pixels. This would require a much larger array of simulated pixels than data voxels since it must resolve the pixels and contain enough modes to fully represent the fluctuations on the scale of the voxels. This is very computationally expensive and will give the same results to the extent that the absorption field is Gaussian random.
5.2. Simulating the lensing potential
We simulate the lensing potential by generating a two-dimensional Gaussian random field that is several times as large as the intended field size using the standard method in Fourier space. The field is then cropped to the desired size. This avoids imposing periodic boundary conditions and includes Fourier modes that are larger than the field size. The resolution of the cropped map is 512 × 512. The deflection is found by a finite difference method in configuration space. The power spectrum for the lensing potential is calculated with the CAMB (Lewis et al. 2000)2 and CosmoSIS (Zuntz et al. 2015)3 software. As discussed above, the constant and linear modes are not measurable, and so these are subtracted from the simulated fields before comparing them with the reconstructed field.
The parameters that are measured are the Legendre coefficients, and so the expected signal can be characterized by finding the standard deviation of these coefficients. This is done by simulating fields and calculating their coefficients by numerical integration. Figure 1 shows the standard deviation of the first 13 Legendre coefficients of 1000 simulations as a function of field size excluding the degenerate modes (0, 0), (1, 0), and (0, 1).
 |
Fig. 1. Standard deviation of the Legendre lensing potential modes (Appendix A.1) as a function of field size. Each standard deviation is estimated using 1000 simulated potential fields. |
6. Demonstrations
We carried out a series of simulations to test the ability of the algorithm to reconstruct the lensing potential. The source image positions are chosen randomly within the field. The lensing potential is simulated as described in Sect. 5.2 and the deflection at each of the source positions is calculated. The spectroscopic pixels are displaced according to the deflection and a realization of the absorption in each pixel is created as described in Sect. 5.1 and Appendix C. The estimator is then applied to these pixels to recover the Legendre coefficients of the lensing potential. These coefficients are used to create an image of the reconstructed potential that can be compared to the original. This is done many times with new realizations of the Lyα forest to calculate the variance in the recovered coefficients.
The parameters that characterize each simulation run are: (1) the angular size of the field over which the potential is reconstructed; (2) the pixel length, which is the length of the spectroscopic bin that is used to measure δ, expressed in comoving megaparsecs using the conversion appropriate to the background cosmology (this could be the pixel size of the spectrograph or an average over multiple pixels, but we still call it a “pixel” for simplicity); (3) the number of sources within the field; (4) the number of pixels in each spectrum (in real data this will vary among sources, but for the simulations it is the same for all sources); (5) the redshift of the lowest redshift pixel in each spectrum, which is taken to be the same for all sources; (6) the noise in each pixel, σδ, which for these tests we take to be uncorrelated between pixels; and (7) the number of coefficients in the expansion of the potential.
Spectra used for studying the Lyα forest typically consist of hundreds of pixels and the number of sources we expect to be in the hundreds to tens of thousands. This results in ∼104 to ∼108 pixel pairs, which makes the storage and manipulation of the matrices involved difficult. Fortunately, as we show in Sect. 7, the correlation between pixels at different redshifts (given the adopted pixel lengths) are small and so, for the purposes of these simulations, they can be considered independent. Using this property, we reconstruct the lensing potential using only two consecutive pixels in each spectrum. These pixels are at the same redshift for all the sources. The Lyα simulation within this redshift slice contains all the correct correlations between pixels. The optimal way to combine statistically independent redshift slices is to simply average them (see Sect. 4.3). Using this property, we find the final potential reconstruction by averaging the reconstructed lens maps from 100 redshift slices, each with different realizations of the forest. The result should have the same noise properties as the case with 200 pixels in each of the spectra. We do not simulate gaps in the spectra caused by masking, but this poses no fundamental problem. This procedure greatly reduces the computational cost.
Table 1 gives the parameter values for each of the simulations discussed below and some measures of the fidelity of the reconstruction are given in the last four columns. The signal-to-noise ratio, S/N, is calculated by dividing the expected variance in each coefficient due to signal (from Monte Carlo as in Fig. 1) by the variance expected for the estimator. This is done for each mode and the range is given in columns 9 and 10.
Simulation runs.
The χ2/n column in Table 1 is calculated for all of the coefficients (22 of them) that are measured for the particular random realization simulated, with the null hypothesis being that the data are only the expected noise without any lensing signal. The last column of the table is the p-value for the χ2 in the previous column, which represents the probability of getting a χ2 larger than what would be measured if there were no lensing signal. Small values signify stronger detections.
Figure 2a shows the input and reconstructed potential fields for case AA, 5000 sources in one square degree. The initial potential field has structure in it on a smaller scale than is represented by the finite Legendre series that is used in the reconstruction. In the central panel of Fig. 2a (and the others like it) we show the potential, which is constructed by calculating only the Legendre coefficients of the input field that we are trying to estimate and filtering the others out; as can be seen, it lacks some of the detail of the original input fields. The right hand panel of Fig. 2a (and the others like it) is the reconstructed field using the estimated Legendre coefficients. By chance, this field has relatively mild structure in the potential (no attempt was made to select better looking cases). Nevertheless, in the “AA” case, the reconstructed image broadly reproduces many of the features seen in the input field.
 |
Fig. 2. Lensing potential from the simulations of Table 1. The left panels of each case show the random realization of the input lensing potential with the mean and gradient subtracted. The central panels show only the reconstructed modes of the input field. The right panels show the reconstructed field using 100 (or, for KK, 200) stacked redshift layers. (a) Simulation AA, (b) Simulation DD, (c) Simulation EE, (d) Simulation FF, (e) Simulation CC, (f) Simulation BB, (g) Simulation GG, (h) Simulation II, (i) Simulation JJ, (j) Simulation KK. |
Figure 3a shows the results for the AA case more quantitatively. The upper panel shows predictions for the average signal and noise in each Legendre coefficient. The analytic predictions given in Sect. 4 for the variance of the estimator can be seen to agree well with the variances estimated from the simulations. Also, the noise in this case is well below the expected signal. In the lower panel of Fig. 3a are the actual input and output values for the particular potential field used in the simulation. The p-value in Table 1 is very small, indicating that a strong detection would be expected in this case.
 |
Fig. 3. Standard deviations of the Legendre modes of the lensing potential and the expected errors in the estimator (top panel of each case). The blue bars are the variance of the coefficients calculated from a thousand realizations of the lensing potential. The orange dots in the top panels are the expected standard deviation of the estimate of the coefficients according to the analytic formula (36). The smaller red dots are the variance among the 100 simulations. They are in good agreement in all cases. The green dots are the errors expected if 100 (200 for case KK) sets of the simulation are stacked as if they are at different redshifts. By comparing the green dots to the blue bars some idea of the signal-to-noise ratio can be gained. In this case, the noise levels for 200-pixel spectra are below the typical signal values expected. In the lower panels are the coefficients for the particular realization used in the simulation (blue bars) and the estimated values of those coefficients after stacking 100 (200 for case KK) realizations of the Lyα forest (orange dots). The modes are listed without the ones that are not measured (mn = 00, 10 and 01). (a) Simulation AA, (b) Simulation DD, (c) Simulation EE, (d) Simulation FF, (e) Simulation CC, (f) Simulation BB, (g) Simulation GG, (h) Simulation II, (i) Simulation JJ, (j) Simulation KK. |
Simulation run DD is shown in Figs. 2b and 3b. This case is for a smaller area (0.5 × 0.5 deg) with a higher source density as compared to run AA. The potential seems better recovered than in the AA run, but this appears to be only because the structure in the potential happens to be more robust. The upper panel of 3b shows that the signal-to-noise ratio would typically be smaller in this case than for AA, but still above a value of 1. We note that the scale in Fig. 3b is different from that in Fig. 3a. The expected fluctuations on a smaller field are smaller. In this case, χ2/n = 5.9, which gives a p-value that is too small to accurately calculate, meaning that the detection would be very strong.
Simulation run EE is for the same-sized field as DD, but with fewer sources, namely 500 compared to 2000. Figure 3c shows that the signal-to-noise ratio is smaller, but still apparently good enough to recover the major features in the field shown in Fig. 2c and yields a very small p-value. Run FF is the same, but with even fewer sources, that is, 200. Here it seems that the potential cannot be accurately recovered (Figs. 2d and 3d): χ2/n = 1.0, consistent with noise.
Run CC is the same as AA, but with one fifth the number of sources. From Fig. 2e it appears that a local peak in the potential is being detected, but not much more detail is present. Figure 3e confirms the impression, drawn from the comparing the reconstruction to the input potential, that the signal-to-noise is around one or slightly lower for the individual coefficients. The p-value is very small, indicating that a signal is strongly detected.
Run BB is with a larger field than AA and the same number of sources. Figures 2f, 3f, and the χ2 show that we should not expect to be able to reconstruct the potential with such low source densities despite the variance of the Legendre coefficients being larger on this scale than it is for smaller fields.
In the first six simulation runs listed in Table 1 the pixel noise was taken to be zero. This represents the optimistic case where the intrinsic variation in the absorption in each pixel is greater than the noise, that is, the signal dominates. This is not the case for the majority of sources in current surveys that reach the kind of source densities we are considering. For example, CLAMATO (Lee et al. 2018) and LATIS (Newman et al. 2020) both have median pixel noise σδ ∼ 0.58 which makes them noise-dominated for individual pixels (σIGM ∼ 0.28 in our case), although the bright quasar sources are signal dominated. For comparison, LATIS expects to have a source density of 2000 deg−2 over 1.7 deg2 and CLAMATO about half the density over 1 deg2.
In the final simulations, we added pixel noise that is taken to be constant and uncorrelated. In this case  . Run GG has 2000 deg−2 and σδ = 0.6. The results are shown in Figs. 2g and 3g. The signal is significantly reduced and although some structure does seem to be recovered, the p-value is 0.1 which signifies a marginal detection. The noise was reduced somewhat in run II to σδ = 0.5 (Figs. 2h and 3h). The image of the potential is better recovered, but the signal-to-noise ratio for the individual coefficients is always below one. The χ2 is larger than for GG probably due to chance.
. Run GG has 2000 deg−2 and σδ = 0.6. The results are shown in Figs. 2g and 3g. The signal is significantly reduced and although some structure does seem to be recovered, the p-value is 0.1 which signifies a marginal detection. The noise was reduced somewhat in run II to σδ = 0.5 (Figs. 2h and 3h). The image of the potential is better recovered, but the signal-to-noise ratio for the individual coefficients is always below one. The χ2 is larger than for GG probably due to chance.
Run JJ (Figs. 2i and 3i) has σδ = 0.6 but also shows a 2.5 times higher source density than GG; the fidelity is much improved and the p-value quite low. Finally, run KK (Figs. 2j and 3j) has smaller spectral pixels (Lpix = 1 Mpc), but the same total range in wavelength as the other runs. The other parameters are the same as in case GG. The fidelity is similarly to GG indicating that the signal-to-noise ratio is not sensitive to Lpix, at least in this regime.
Figure 4 shows the normalized covariance between estimated Legendre coefficients in case AA. These are estimated from the repeated simulations with random Lyα forests. It can be seen here that the estimates of the different coefficients are not strongly correlated and thus can be considered independent measurements. This plot looks very similar for all the other cases.
 |
Fig. 3. continued. |
 |
Fig. 4. Normalized covariance between the coefficient estimates in simulation run AA (Table 1). The estimates are consistent with being uncorrelated. |
7. Noise scaling
Figures 5–7 show the standard deviation of the estimator as a function of the number of spectral pixels per source, the size of the field on the sky, and the number of sources, respectively. These are calculated directly from the expected error given in Sect. 4. It can be seen in Fig. 5 that the variance scales as  indicating that each map of the Lyα forest at a constant redshift constitutes essentially an independent measurement of the lensing potential, at least for a pixel length of 2 Mpc. This means that a calculation of the noise with one or two pixels per source can be easily scaled to find the noise for more pixels and that the potential estimates can be “stacked” as was done in the previous section (we note that Sect. 4.3 shows that the optimal weighting is not the simple average of the estimates except in the cases where the noise, pixel positions, and intrinsic correlations are identical in each redshift bin).
indicating that each map of the Lyα forest at a constant redshift constitutes essentially an independent measurement of the lensing potential, at least for a pixel length of 2 Mpc. This means that a calculation of the noise with one or two pixels per source can be easily scaled to find the noise for more pixels and that the potential estimates can be “stacked” as was done in the previous section (we note that Sect. 4.3 shows that the optimal weighting is not the simple average of the estimates except in the cases where the noise, pixel positions, and intrinsic correlations are identical in each redshift bin).
 |
Fig. 5. Standard deviation of the Legendre lensing potential modes (Appendix A.1) computed using the estimator as a function of the number of pixels in each of the spectra for a 0.5 deg × 0.5 deg field with 500 sources. |
 |
Fig. 6. Standard deviation of the Legendre lensing potential modes (Appendix A.1) computed using the estimator as a function of the width of a square field with 1000 sources and a depth of 200 pixels. |
 |
Fig. 7. Standard deviation of the Legendre lensing potential modes (Appendix A.1) computed using the estimator as a function of the number of sources in a 1 deg × 1 deg field. This is for 200 pixels per source. |
Figure 6 shows that the scaling with the size of the field is not quite a power law. Nevertheless the error in each coefficient scales approximately as
where γ ≃ −0.5, β ≃ 2.6, and α ∼ 0.8 for the modes and ranges of parameters that we have investigated.
8. Sensitivity to the assumptions regarding the correlation function
It should be noted that the quadratic estimator contains the correlation function of the Lyα forest which must be estimated in some way and therefore might be erroneous. If the assumed covariance C is incorrect, the estimator will be biased. In the simplest case where the assumed correlation function is inaccurate by a normalization, C = a〈Δ〉 where a is a constant, the average of the estimator will be
meaning that there will be an erroneous scaling and bias. Given that the correlation function can be assumed to be isotropic and a smooth function of distance, it seems reasonable that it can be constrained well enough to allow for accurate measurement of the lensing. However, this is a problem that has not yet been investigated thoroughly.
9. Discussion
We derived a minimum variance estimator for the gravitational lensing potential using the Lyα forest and found that it can recover an image of the potential on ∼1 degree scales if the source density is high and the pixel noise is low. We carried out simulations that showed that our implementation functions as expected. At the source densities and noise levels currently available (Lee et al. 2018; Newman et al. 2020) the signal-to-noise ratio in the recovered map is expected to be marginal, but with improvements in either of these a high-fidelity map could be recovered.
The Extremely Large Telescope (ELT) should be able to reach a magnitude fainter than CLAMATO or LATIS which will mean source densities that are an order of magnitude greater (η ∼ 104 deg−3) and a reduction in the pixel noise to the point where it is subdominant for a much larger fraction of the pixels (Ellis & Dawson 2019; Schlegel et al. 2019). This should be a better case than even our most optimistic simulations and therefore high-fidelity lensing maps should be possible.
The estimator proposed here is computationally expensive. The storage is  and the computational time
and the computational time  . This could pose a limitation, but we believe this can be significantly reduced using certain methods that we are currently developing. A remaining question is whether the correlation function of the Lyα forest, which is needed for the estimator, is or can be determined to sufficient accuracy to not bias the lensing potential estimate. We do not believe that this poses a significant problem in the long run, but how well this can be done remains to be seen.
. This could pose a limitation, but we believe this can be significantly reduced using certain methods that we are currently developing. A remaining question is whether the correlation function of the Lyα forest, which is needed for the estimator, is or can be determined to sufficient accuracy to not bias the lensing potential estimate. We do not believe that this poses a significant problem in the long run, but how well this can be done remains to be seen.
No attempt has been made here to recover the lensing power spectrum from the Lyα forest. For the small field surveys studied here, any such estimate would be dominated by sample variance, but it might be possible for larger, sparser surveys (see Metcalf et al. 2018). Estimating the power spectrum will require a different approach and will be the subject of a future paper.
The method used by the Planck collaboration to map the lensing using the CMB is essentially to Wiener filter the temperature and polarization maps to fill in masked regions of the sky and then use an estimator based in spherical harmonic space (Planck Collaboration XVII 2014; Planck Collaboration XV 2016). This is not an optimal method and is not applicable to the Lyα forest because any map of the sky that takes full advantage of the accuracy of the source positions will have such high resolution and so few pixels containing sources that it would not be practical. Some effort has been made to develop a real-space lensing estimator for the CMB (Bucher et al. 2012). Our method could be applied to the CMB by treating each unmasked pixel as a source and would take into account window functions and inhomogeneous noise in an optimal way. For the whole Planck map, this might be computationally onerous, but it is certainly possible for smaller CMB surveys in its present form.
Acknowledgments
RACC was supported by NASA NNX17AK56G, NASA ATP 80NSSC18K101, NSF AST-1615940, NSF AST-1614853 and NSF AST-1909193.
References
- Ahn, C. P., Alexandroff, R., Allende Prieto, C., et al. 2012, ApJS, 203, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Ahumada, R., Allende Prieto, C., Almeida, A., et al. 2019, ApJ, 249, 3 [NASA ADS] [Google Scholar]
- Anderson, C. J., Luciw, N. J., Li, Y. C., et al. 2018, MNRAS, 476, 3382 [CrossRef] [Google Scholar]
- Bartelmann, M., & Maturi, M. 2017, Scholarpedia, 12, 32440 [NASA ADS] [CrossRef] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, J. E., Bailey, S., Font-Ribera, A., et al. 2015, JCAP, 2015, 060 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardeau, F. 1997, A&A, 324, 15 [NASA ADS] [Google Scholar]
- Birrer, S., Refregier, A., & Amara, A. 2018, ApJ, 852, L14 [CrossRef] [Google Scholar]
- Blomqvist, M., Kirkby, D., Bautista, J. E., et al. 2015, JCAP, 2015, 034 [NASA ADS] [CrossRef] [Google Scholar]
- Blomqvist, M., du Mas des Bourboux, H., Busca, N. G., et al. 2019, A&A, 629, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolton, J. S., Puchwein, E., Sijacki, D., et al. 2017, MNRAS, 464, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Bordoloi, R., Lilly, S. J., & Amara, A. 2010, MNRAS, 406, 881 [NASA ADS] [Google Scholar]
- Bucher, M., Carvalho, C. S., Moodley, K., & Remazeilles, M. 2012, Phys. Rev. D, 85, 043016 [NASA ADS] [CrossRef] [Google Scholar]
- Busca, N. G., Delubac, T., Rich, J., et al. 2013, A&A, 552, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabanier, S., Millea, M., & Palanque-Delabrouille, N. 2019, MNRAS, 489, 2247 [CrossRef] [Google Scholar]
- Chabanier, S., Bournaud, F., Dubois, Y., et al. 2020, MNRAS, 495, 1825 [CrossRef] [Google Scholar]
- Chang, T.-C., Refregier, A., & Helfand, D. J. 2004, ApJ, 617, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, T.-C., Pen, U.-L., Bandura, K., & Peterson, J. B. 2010, Nature, 466, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Cregg, P. J., & Svedlindh, P. 2007, J. Phys. A Math. Gen., 40, 14029 [CrossRef] [Google Scholar]
- Croft, R. A. C., Weinberg, D. H., Katz, N., & Hernquist, L. 1998, ApJ, 495, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Croft, R. A. C., Romeo, A., & Metcalf, R. B. 2018, MNRAS, 477, 1814 [CrossRef] [Google Scholar]
- Cunha, C. E., Huterer, D., Lin, H., Busha, M. T., & Wechsler, R. H. 2014, MNRAS, 444, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Dalton, G., Trager, S., Abrams, D. C., et al. 2018, SPIE Conf. Ser., 10702, 107021B [Google Scholar]
- de Sainte Agathe, V., Balland, C., du Mas des Bourboux, H., et al. 2019, A&A, 629, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DESI Collaboration (Aghamousa, A., et al.) 2016, ArXiv e-prints [arXiv:1611.00036] [Google Scholar]
- Ellis, R., & Dawson, K. 2019, BAAS, 51, 45 [Google Scholar]
- Faucher-Giguère, C.-A., Prochaska, J. X., Lidz, A., Hernquist, L., & Zaldarriaga, M. 2008, ApJ, 681, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Flagey, N., McConnachie, A., Szeto, K., et al. 2018, SPIE Conf. Ser., 10704, 107040V [Google Scholar]
- Font-Ribera, A., Miralda-Escudé, J., Arnau, E., et al. 2012, JCAP, 2012, 059 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman, S., Meerburg, P. D., van Engelen, A., & Meyers, J. 2018, JCAP, 7, 046 [CrossRef] [Google Scholar]
- Furlanetto, S. R., Oh, S. P., & Briggs, F. 2006, Phys. Rep., 433, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Gradshteyn, I. S., & Ryzhik, I. M. 2007, Table of Integrals, Series, and Products, seventh edn. (Amsterdam: Elsevier/Academic Press) xlviii+117100, translated from the Russian, Translation edited and with a preface by Alan Jeffrey and Daniel Zwillinger, With one CD-ROM (Windows, Macintosh and UNIX) [Google Scholar]
- Hamilton, A. J. S. 1993, ApJ, 417, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hanson, D., Challinor, A., & Lewis, A. 2010, Gen. Relativ. Gravit., 42, 2197 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, I., Camera, S., Zuntz, J., & Brown, M. L. 2016, MNRAS, 463, 3674 [NASA ADS] [CrossRef] [Google Scholar]
- Hilbert, S., Metcalf, R. B., & White, S. D. M. 2007, MNRAS, 382, 1494 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Okamoto, T. 2002, ApJ, 574, 566 [Google Scholar]
- Hui, L., Stebbins, A., & Burles, S. 1999, ApJ, 511, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Iršič, V., Viel, M., Haehnelt, M. G., Bolton, J. S., & Becker, G. D. 2017, Phys. Rev. Lett., 119, 031302 [CrossRef] [PubMed] [Google Scholar]
- Jalilvand, M., Majerotto, E., Durrer, R., & Kunz, M. 2018, J. Cosmol. Astropart. Phys., 2019, 020 [CrossRef] [Google Scholar]
- Jeffrey, N., Lanusse, F., Lahav, O., & Starck, J.-L. 2020, MNRAS, 492, 5023 [CrossRef] [Google Scholar]
- Kaiser, N. 1992, ApJ, 388, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., & Squires, G. 1993, ApJ, 404, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Kovetz, E. D., Viero, M. P., Lidz, A., et al. 2017, ArXiv e-prints [arXiv:1709.09066] [Google Scholar]
- Lai, K., Lidz, A., Hernquist, L., & Zaldarriaga, M. 2006, ApJ, 644, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, K.-G., Krolewski, A., White, M., et al. 2018, ApJS, 237, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Challinor, A. 2006, Phys. Rep., 429, 1 [Google Scholar]
- Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [Google Scholar]
- Madau, P., Meiksin, A., & Rees, M. J. 1997, ApJ, 475, 429 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P. 2003, ApJ, 585, 34 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P., & Miralda-Escudé, J. 1999, ApJ, 518, 24 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, M., & White, M. 2011, MNRAS, 415, 2257 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, M., & White, M. 2015, MNRAS, 448, 1403 [CrossRef] [Google Scholar]
- Metcalf, R. B., & Silk, J. 1997, ApJ, 489, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalf, R. B., & Silk, J. 1998, ApJ, 492, L1 [CrossRef] [Google Scholar]
- Metcalf, R. B., & White, S. D. M. 2007, MNRAS, 381, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalf, R. B., & White, S. D. M. 2009, MNRAS, 394, 704 [CrossRef] [Google Scholar]
- Metcalf, R. B., Croft, R. A. C., & Romeo, A. 2018, MNRAS, 477, 2841 [CrossRef] [Google Scholar]
- Miralda-Escude, J. 1991, ApJ, 380, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Neves, A. A. R., Padilha, L. A., Fontes, A., et al. 2006, J. Phys. A: Math. Gen., 39, L293 [CrossRef] [Google Scholar]
- Newman, A. B., Rudie, G. C., Blanc, G. A., et al. 2020, ApJ, 891, 147 [CrossRef] [Google Scholar]
- Peeples, M. S., Weinberg, D. H., Davé, R., Fardal, M. A., & Katz, N. 2010, MNRAS, 404, 1281 [NASA ADS] [Google Scholar]
- Petkova, M., Metcalf, R. B., & Giocoli, C. 2014, MNRAS, 445, 1954 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVII. 2014, A&A, 571, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XV. 2016, A&A, 594, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pourtsidou, A., & Metcalf, R. B. 2014, MNRAS, 439, L36 [CrossRef] [Google Scholar]
- Pourtsidou, A., & Metcalf, R. B. 2015, MNRAS, 448, 2368 [CrossRef] [Google Scholar]
- Prochaska, J. X. 2019, Saas-Fee Adv. Course, 46, 111 [CrossRef] [Google Scholar]
- Rauch, M. 1998, ARA&A, 36, 267 [Google Scholar]
- Rogers, K. K., Bird, S., Peiris, H. V., et al. 2018, MNRAS, 474, 3032 [CrossRef] [Google Scholar]
- Salvador, A. I., Sánchez, F. J., Pagul, A., et al. 2019, MNRAS, 482, 1435 [CrossRef] [Google Scholar]
- Schaan, E., & Ferraro, S. 2019, Phys. Rev. Lett., 122, 181301 [CrossRef] [Google Scholar]
- Schlegel, D., Kollmeier, J. A., & Ferraro, S. 2019, BAAS, 51, 229 [Google Scholar]
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses (Springer-Verlag) [Google Scholar]
- Slosar, A., et al. 2011, JCAP, 9, 001 [Google Scholar]
- Slosar, A., Iršič, V., Kirkby, D., et al. 2013, JCAP, 2013, 026 [NASA ADS] [CrossRef] [Google Scholar]
- Stebbins, A. 1996, ArXiv e-prints [arXiv:astro-ph/9609149] [Google Scholar]
- Troxel, M. A., MacCrann, N., Zuntz, J., et al. 2018, Phys. Rev. D, 98, 043528 [NASA ADS] [CrossRef] [Google Scholar]
- Uhlemann, C., Pichon, C., Codis, S., et al. 2018, MNRAS, 477, 2772 [CrossRef] [Google Scholar]
- Valdes, F., Tyson, J. A., & Jarvis, J. F. 1983, ApJ, 271, 431 [CrossRef] [Google Scholar]
- Wyithe, J. S. B., & Morales, M. F. 2007, MNRAS, 379, 1647 [CrossRef] [Google Scholar]
- Zahn, O., & Zaldarriaga, M. 2006, ApJ, 653, 922 [CrossRef] [Google Scholar]
- Zaldarriaga, M., & Seljak, U. 1999, Phys. Rev. D, 59, 123507 [NASA ADS] [CrossRef] [Google Scholar]
- Zuntz, J., Paterno, M., Jennings, E., et al. 2015, Astron. Comput., 12, 45 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Expansions
Here, we provide details for several possible expansions or parameterizations of the lensing potential.
A.1. Legendre expansion
The two dimensional Legendre expansion of the potential will be
where
where Pm(x) are the Legendre polynomials and
where  are the coordinates of the lower left-hand corner of the reconstructed field. Δθx and Δθy are the width and height of the field. All the sources are within this field.
are the coordinates of the lower left-hand corner of the reconstructed field. Δθx and Δθy are the width and height of the field. All the sources are within this field.
The orthogonality relation for these polynomials results in
The recursion relation
is used to calculate the value of the Pn(x) and the relation
is used to calculate its derivative.
Using (A.13), the deflection is
Some of the advantages of using the Legendre expansion are: (1) Periodic boundary conditions are not implicitly imposed; (2) unlike bilinear interpolation from a gridded potential, the deflection field is always continuous; and (3) unlike all the previous expansions, the degenerate constant and linear components of the potential field are completely contained in three coefficients, a00, a01 and a10, that can easily be removed.
A.2. Chebyshev expansion
The Chebyshev polynomials confer the same advantages as the Legendre polynomials as an expansion for the potential. They generally have more structure near the boundaries for a limited number of modes.
The Chebyshev polynomials of the first kind are given by the recursion relation
for the range −1 ≤ x ≤ 1. The derivative of them is given by
where Un(x) are the Chebyshev polynomials of the second kind and are given by
The two-dimensional Chebyshev expansion is defined as in the Legendre case:
where
Using (A.13), the deflection is
Using the orthogonality and normalization of these polynomials, we can find the coefficients given a potential field,
As in the Legendre case, modes a00, a01, and a10 are not measurable because they represent a constant potential and two linear or constant deflection components.
A.3. Discrete Fourier transform
The potential field in the flat-sky approximation can be expanded as a N1 × N2 pixel map ϕ[n1, n2], 0 ≤ ni ≤ Ni −1 using the discrete Fourier transform (DFT),
where 0 ≤ n < N, 0 ≤ k < N are multi-indices, and  are the N1 × N2 complex-valued modes of the expansion. The discrete field values correspond to the continuous field at the grid points θn ≡ nΔ, where Δ is the pixel size of the discrete map. We can interpolate the DFT (A.22) to obtain a continuous potential field over the field of view,
are the N1 × N2 complex-valued modes of the expansion. The discrete field values correspond to the continuous field at the grid points θn ≡ nΔ, where Δ is the pixel size of the discrete map. We can interpolate the DFT (A.22) to obtain a continuous potential field over the field of view,
where the frequencies lk = (lk1, lk2) are chosen to produce a real-valued interpolation,
The gradient of the potential field expansion (A.23) is the DFT deflection angle,
Inserting this into Eq. (19) yields the elements of matrix P for the DFT,
where Δθij ≡ θi − θj and  are the difference and average of positions θi, θj, respectively.
are the difference and average of positions θi, θj, respectively.
As stated above, the DFT (A.23) contains N1 × N2 modes  . However, not all are independent, since a real-valued field has a symmetry in its Fourier transform,
. However, not all are independent, since a real-valued field has a symmetry in its Fourier transform,
where the asterisk denotes complex conjugation. We can therefore only constrain roughly half of the modes in our reconstruction, which implicitly determines the other half. Making the cut in k2, we exclude all modes with 2k2 > N2. The remaining modes still contain the symmetry
meaning that we must further exclude 2k1 > N1 for k2 = 0 or 2k2 = N2.
Other modes cannot be constrained because their frequency lk vanishes, meaning that they do not contribute to the deflection field (A.25). This is the case for the constant mode (0, 0), which is intuitively clear, since the offset of a potential has no physical meaning. However, we must also exclude (N1/2, 0), (0, N2/2), (N1/2, N2/2) from the reconstruction if N1, N2, or both are even, which follows directly from the definition (A.24) of the frequencies.
Figure A.1 shows an example of the mode selection for even and odd image sizes. The modes that can be constrained in the reconstruction form the truncated vector  . We note that all constrained modes have a symmetric partner, so our reconstruction contains exactly half of all possible values for k that do not have vanishing frequencies.
. We note that all constrained modes have a symmetric partner, so our reconstruction contains exactly half of all possible values for k that do not have vanishing frequencies.
 |
Fig. A.1. Modes in a 8 × 8 (left) and 9 × 9 (right) DFT expansion. Light shaded modes are excluded due to symmetry, dark shaded modes are excluded due to vanishing frequency. |
The fact that we have truncated the vector of modes  implies further changes to the reconstruction. We cannot simply perform the estimation with a similarly truncated matrix P → P′, since the reconstruction requires the full
implies further changes to the reconstruction. We cannot simply perform the estimation with a similarly truncated matrix P → P′, since the reconstruction requires the full  . However, the product
. However, the product  can be rewritten in terms of
can be rewritten in terms of  and P′ using the symmetry
and P′ using the symmetry  ,
,
where the last equality now expresses everything in terms of the truncated quantities. Expanding P′ and  into real and imaginary parts P′=R + i Q and
into real and imaginary parts P′=R + i Q and  , the relation is evidently still linear in u and v:
, the relation is evidently still linear in u and v:
A.4. In spherical coordinates
When the survey covers a significant proportion of the sky it is necessary to reconstruct the lensing potential on the sphere. This requires only a change in the P matrix first introduced in Eq. (18). One approach to this problem is to expand the lensing potential in spherical harmonics instead of discrete Fourier modes as was done in Appendix A.3.
To derive the expression for P we go back to the expression for the lensed flux:
where ∇ is the gradient with respect to angle. To first order in the lensing potential the product of pixel values is
Averaging over the ensemble of δ(θi) fields gives
The potential will be expanded in spherical harmonics
so that the gradient of potential is
where  are the vector spherical harmonics.
are the vector spherical harmonics.
Isotropy requires that the correlation function be a function of only the angular separation between pixels, γij, and their radial positions. The angular separation is given by
The gradient of the correlation function with respect to the position of point i is
Using this the P matrix can be calculated as
We make the approximation that pairs of points that are correlated enough to contribute significantly to the potential estimate will be separated by a small angle (γ ≪ π). To a good approximation we can take
where D̅ij is the average comoving size distance to the pixels i and j.
Appendix B: Lyα forest power spectrum
For the power spectrum of the Lyα flux we use the model of McDonald (2003)
where Plin(k, z) is the linear power spectrum of matter and
is a transfer function with
The f(μ) factor is a result of redshift distortion and E(k, μ) comes from a combination of nonlinear structure formation, thermal broadening, and gas pressure effects.
In our simulations we use the following parameter values:
as suggested by McDonald (2003).
McDonald (2003) does not consider any evolution in the transfer function with redshift. We evolve the power spectrum only through the evolution in the linear power spectrum Plin(k, z) according to the usual linear theory. A more sophisticated model can be used in the future, but this seems adequate for the purposes of this paper.
Appendix C: Calculating the Lyα correlation function
We need to find the correlation function for pixels (or voxels) that are very narrow in the directions perpendicular to the line of sight but finite in length along the line of sight. The variation in the relative flux within a pixel of comoving length Lpix, or a frequency interval translated into a comoving length, will be
where jℓ(x) are the spherical Bessel functions and δ(x) is the relative density fluctuation, not the delta function. The correlation function is
where J0(x) is the Bessel function of the first kind.
For calculating the correlation function it is useful to expand it in Legendre polynomials (Hamilton 1993)
where μ = s∥/|s|=cos(α) and
Symmetry requires that ξℓ(s) = 0 for odd ℓ. Inserting (C.4) and using the integral
(Neves et al. 2006; Cregg & Svedlindh 2007) gives
Substituting the Lyα power spectrum (B.1) gives
with
For small k the prefactor, T2(k, μ), becomes independent of k (E(k, μ)→1) and so Iℓ(k) will be constant for large scales. The first few Iℓ(k) are shown in Fig. C.1 for the power spectrum discussed in Appendix B. The first five nonzero ξℓ(s) are plotted in Fig. C.2.
 |
Fig. C.1. Factor Iℓ(k) given in (C.11) for the power spectrum discussed in Appendix B with Lpix = 1 Mpc. |
 |
Fig. C.2. First five multipoles of the correlation function (C.10) as a function of separation for the power spectrum discussed in Appendix B with Lpix = 1 Mpc. The dotted curves are where the functions are negative. |
All Tables
All Figures
 |
Fig. 1. Standard deviation of the Legendre lensing potential modes (Appendix A.1) as a function of field size. Each standard deviation is estimated using 1000 simulated potential fields. |
| In the text | |
 |
Fig. 2. Lensing potential from the simulations of Table 1. The left panels of each case show the random realization of the input lensing potential with the mean and gradient subtracted. The central panels show only the reconstructed modes of the input field. The right panels show the reconstructed field using 100 (or, for KK, 200) stacked redshift layers. (a) Simulation AA, (b) Simulation DD, (c) Simulation EE, (d) Simulation FF, (e) Simulation CC, (f) Simulation BB, (g) Simulation GG, (h) Simulation II, (i) Simulation JJ, (j) Simulation KK. |
| In the text | |
 |
Fig. 3. Standard deviations of the Legendre modes of the lensing potential and the expected errors in the estimator (top panel of each case). The blue bars are the variance of the coefficients calculated from a thousand realizations of the lensing potential. The orange dots in the top panels are the expected standard deviation of the estimate of the coefficients according to the analytic formula (36). The smaller red dots are the variance among the 100 simulations. They are in good agreement in all cases. The green dots are the errors expected if 100 (200 for case KK) sets of the simulation are stacked as if they are at different redshifts. By comparing the green dots to the blue bars some idea of the signal-to-noise ratio can be gained. In this case, the noise levels for 200-pixel spectra are below the typical signal values expected. In the lower panels are the coefficients for the particular realization used in the simulation (blue bars) and the estimated values of those coefficients after stacking 100 (200 for case KK) realizations of the Lyα forest (orange dots). The modes are listed without the ones that are not measured (mn = 00, 10 and 01). (a) Simulation AA, (b) Simulation DD, (c) Simulation EE, (d) Simulation FF, (e) Simulation CC, (f) Simulation BB, (g) Simulation GG, (h) Simulation II, (i) Simulation JJ, (j) Simulation KK. |
| In the text | |
 |
Fig. 3. continued. |
| In the text | |
 |
Fig. 4. Normalized covariance between the coefficient estimates in simulation run AA (Table 1). The estimates are consistent with being uncorrelated. |
| In the text | |
 |
Fig. 5. Standard deviation of the Legendre lensing potential modes (Appendix A.1) computed using the estimator as a function of the number of pixels in each of the spectra for a 0.5 deg × 0.5 deg field with 500 sources. |
| In the text | |
 |
Fig. 6. Standard deviation of the Legendre lensing potential modes (Appendix A.1) computed using the estimator as a function of the width of a square field with 1000 sources and a depth of 200 pixels. |
| In the text | |
 |
Fig. 7. Standard deviation of the Legendre lensing potential modes (Appendix A.1) computed using the estimator as a function of the number of sources in a 1 deg × 1 deg field. This is for 200 pixels per source. |
| In the text | |
 |
Fig. A.1. Modes in a 8 × 8 (left) and 9 × 9 (right) DFT expansion. Light shaded modes are excluded due to symmetry, dark shaded modes are excluded due to vanishing frequency. |
| In the text | |
 |
Fig. C.1. Factor Iℓ(k) given in (C.11) for the power spectrum discussed in Appendix B with Lpix = 1 Mpc. |
| In the text | |
 |
Fig. C.2. First five multipoles of the correlation function (C.10) as a function of separation for the power spectrum discussed in Appendix B with Lpix = 1 Mpc. The dotted curves are where the functions are negative. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



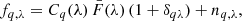
![$$ \begin{aligned}&\boldsymbol{x}_\perp (z) = \left[ \boldsymbol{\theta } D(z) - \sum _{m < z} D(z_m,z) ~ \hat{{\boldsymbol{\alpha }}}_m(\boldsymbol{\theta }) \right] \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq2.gif)
![$$ \begin{aligned}&\quad \quad = \left[ \boldsymbol{\theta } - \sum _{m < z} {\boldsymbol{\alpha }}_m(\boldsymbol{\theta }) \right] D(z), \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq3.gif)



![$$ \begin{aligned} \kappa ({\boldsymbol{\theta }}) = \frac{3}{2} \frac{\Omega _m H_o}{c^2} \int _o^{\chi _s} d\chi ~ \left[ \frac{d_A(\chi )d_A(\chi ,\chi _s) }{d_A(\chi _s)} \right] ~ \delta ({\boldsymbol{\theta }},\chi ), \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq8.gif)
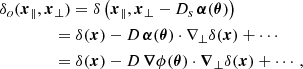

![$$ \begin{aligned}&\qquad \qquad \quad = \! \xi ({\boldsymbol{r}}) + \left[ D\, {\boldsymbol{\alpha }}({\boldsymbol{\theta }}) - D^{\prime }\,{\boldsymbol{\alpha }}({\boldsymbol{\theta }}^{\prime }) \right] \cdot \boldsymbol{\nabla }_\perp \xi (r_\parallel ,r_\perp ) \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq11.gif)
![$$ \begin{aligned}&\qquad \qquad \quad = \! \xi ({\boldsymbol{r}}) + \left[ D\, \alpha ^\sigma ({\boldsymbol{\theta }}) - D^{\prime }\, \alpha ^\sigma ({\boldsymbol{\theta }}^{\prime }) \right] \left[ \frac{\partial r_\perp }{\partial \boldsymbol{x}_\perp ^\sigma } \frac{\partial \xi }{\partial r_\perp } \right] \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq12.gif)
![$$ \begin{aligned}&\qquad \qquad \quad \simeq \! \xi ({\boldsymbol{r}}) + \left[ d(z)\, {\boldsymbol{\alpha }}({\boldsymbol{\theta }}) - d(z^{\prime })\, {\boldsymbol{\alpha }}({\boldsymbol{\theta }}^{\prime }) \right] \cdot \boldsymbol{\gamma } \,\left[ \frac{\overline{D}^2}{r_\perp } \frac{\partial \xi }{\partial r_\perp } \right] \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq13.gif)
![$$ \begin{aligned}&\qquad \qquad \quad \simeq \! \xi ({\boldsymbol{r}}) \! + \! \left[ d(z)\, {\boldsymbol{\alpha }}({\boldsymbol{\theta }}) \! - \! d(z^{\prime }) {\boldsymbol{\alpha }}({\boldsymbol{\theta }}^{\prime }) \right] \cdot \boldsymbol{\gamma } \!\left[ \frac{1}{|\boldsymbol{\gamma }|^2} \frac{\partial \xi }{\partial \ln r_\perp } \right] \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq14.gif)
![$$ \begin{aligned}&\qquad \qquad \quad = \! \xi ({\boldsymbol{r}}) + \left[ d(z) \, {\boldsymbol{\alpha }}({\boldsymbol{\theta }}) - d(z^{\prime })\, {\boldsymbol{\alpha }}({\boldsymbol{\theta }}^{\prime }) \right] \cdot {\boldsymbol{\gamma }} \,{\mathcal{G} }({\boldsymbol{r}}), \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq15.gif)








![$$ \begin{aligned} \left[ \boldsymbol{\Delta } \right]_{i,j} \equiv \delta _i \delta _j . \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq33.gif)
![$$ \begin{aligned} F^{\alpha \beta } = -\left\langle \frac{\partial ^2\ln {\mathcal{L} } }{\partial \tilde{\boldsymbol{\phi }}_\alpha \partial \tilde{\boldsymbol{\phi }}_\beta } \right\rangle = \frac{1}{2} \mathrm{tr}\left[ \mathbf{P}^\alpha \mathbf{C}^{-1} \mathbf{P^*}^{\beta } \mathbf{C}^{-1} \right]. \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq36.gif)
![$$ \begin{aligned}&\left\langle { \boldsymbol{\delta }^\intercal \mathbf{C}^{-1} \mathbf{P^*}^\mu \mathbf{C}^{-1} \boldsymbol{\delta } } \right\rangle = \left\langle { \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\mu \mathbf{C}^{-1} \boldsymbol{\Delta } \right] }\right\rangle \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq37.gif)
![$$ \begin{aligned}&\qquad \qquad \qquad \quad = \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\mu \mathbf{C}^{-1} \left( \mathbf{C} + \mathbf{P}^\nu \tilde{\phi }_\nu \right) \right] \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq38.gif)
![$$ \begin{aligned}&\qquad \quad \qquad \qquad = \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\mu \right] + \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\mu \mathbf{C}^{-1} \mathbf{P}^\nu \right] \tilde{\phi }_\nu \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq39.gif)
![$$ \begin{aligned}&\qquad \quad \qquad \qquad = \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\mu \right] + 2 F^{\mu \nu } \tilde{\phi }_\nu , \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq40.gif)
![$$ \begin{aligned}&\hat{\phi }_\mu = \frac{1}{2} F^{-1}_{\mu \nu } \left( \boldsymbol{\delta }^\intercal \mathbf{C}^{-1} \mathbf{P^*}^\nu \mathbf{C}^{-1} \boldsymbol{\delta } - \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\nu \right] \right)\end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq41.gif)
![$$ \begin{aligned}&\quad = \frac{1}{2} F^{-1}_{\mu \nu } \left( \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\nu \mathbf{C}^{-1} \boldsymbol{\Delta } \right] - \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\nu \right] \right) \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq42.gif)
![$$ \begin{aligned}&\quad = \frac{1}{2} F^{-1}_{\mu \nu } \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\nu \left( \mathbf{C}^{-1} \boldsymbol{\Delta } - \mathbf {I} \right) \right] \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq43.gif)
![$$ \begin{aligned}&\quad = \frac{1}{2} F^{-1}_{\mu \nu } \left( \boldsymbol{z}^\intercal \mathbf{P^*}^\nu \boldsymbol{z} - \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\nu \right] \right), \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq44.gif)

![$$ \begin{aligned}&\left. \qquad \qquad - \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P}^\mu \right] \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\nu \right] \right). \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq46.gif)




![$$ \begin{aligned} F^{\alpha \beta } = \frac{1}{2} \sum _{k=1}^n \mathrm{tr}\left[ \mathbf{P}_{(k)}^\alpha \mathbf{C}_{(k)}^{-1} \left( \mathbf{P}_{(k)}^{\beta }\right)^* \mathbf{C}_{(k)}^{-1} \right] = \sum _{k=1}^n F^{\alpha \beta }_{(k)} , \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq51.gif)
![$$ \begin{aligned}&\hat{\phi }_\mu = \frac{1}{2} F^{-1}_{\mu \nu } \sum _{k=1}^n \mathrm{tr}\left[ \mathbf{C}_{(k)}^{-1} \mathbf{P}_{(k)}^\nu \left( \mathbf{C}_{(k)}^{-1} \boldsymbol{\Delta }_{(k)} - \mathbf {I} \right) \right] \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq52.gif)

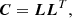


![$$ \begin{aligned} \left\langle {\hat{\phi }_\mu }\right\rangle = a ~\phi _\mu + \frac{(a-1)}{2} ~ F^{-1}_{\mu \nu } \mathrm{tr}\left[ \mathbf{C}^{-1} \mathbf{P^*}^\nu \right] , \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq61.gif)






![$$ \begin{aligned}&P_{n+1}(x) = \left[ ( 2 n + 1) x P_n(x) - n P_{n-1}(x) \right] / (n+1) \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq71.gif)
![$$ \begin{aligned} \frac{d}{dx} P_n(x) = P^{\prime }_n(x)= \frac{n}{(x^2 -1)} \left[ x P_n(x) - P_{n-1}(x) \right] \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq72.gif)



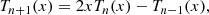





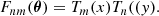



![$$ \begin{aligned} \phi [\boldsymbol{n}] = \sum _{k_1 = 0}^{N_1 - 1} \sum _{k_2 = 0}^{N_2 - 1} \hat{\phi }_{\boldsymbol{k}} \, e^{2\pi i \, k_1 n_1/N_1 + 2\pi i \, k_2 n_2/N_2} , \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq86.gif)












![$$ \begin{aligned} \delta ({\boldsymbol{\theta }}_i) \delta ({\boldsymbol{\theta }}_j) = \delta _i \delta _j + \delta _j \left[ \boldsymbol{\nabla }_i \phi _i \cdot \boldsymbol{\nabla }_i \delta _i \right] + \delta _i \left[ \boldsymbol{\nabla }_j \phi _j \cdot \boldsymbol{\nabla }_j \delta _j \right.]. \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq110.gif)
![$$ \begin{aligned}&\langle \delta ({\boldsymbol{\theta }}_i) \delta ({\boldsymbol{\theta }}_j) \rangle \!=\! \langle \delta _i \delta _j \rangle \!+\! \left[ \boldsymbol{\nabla }_i \phi _i \cdot \boldsymbol{\nabla }_i \langle \delta _j \delta _i \rangle \right] + \left[ \boldsymbol{\nabla }_j \phi _j \cdot \boldsymbol{\nabla }_j \langle \delta _i\delta _j \rangle \right] \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq111.gif)
![$$ \begin{aligned}&\qquad \qquad \ = \xi _{ij} + \left[ \boldsymbol{\nabla }_i \phi _i \cdot \boldsymbol{\nabla }_i \xi _{ij} \right] + \left[ \boldsymbol{\nabla }_j \phi _j \cdot \boldsymbol{\nabla }_j \xi _{ij} \right]. \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq112.gif)




![$$ \begin{aligned}&\qquad = \left[ \frac{\partial \gamma _{ij} }{\partial \theta _i} \hat{{\boldsymbol{\theta }}} + \frac{1}{\sin \theta _i} \frac{\partial \gamma _{ij}}{\partial \phi _i} \hat{\boldsymbol{\phi }} \right] \frac{\partial \xi (\gamma ,r_i,r_j)}{\partial \gamma } \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq118.gif)

![$$ \begin{aligned} P_{ij}^{\ell m} \!= \!\left[ \boldsymbol{\nabla }_i \gamma _{ij} \cdot \boldsymbol{\Psi }_\ell ^m(\theta _i,\phi _i) + \boldsymbol{\nabla }_j \gamma _{ij} \cdot \boldsymbol{\Psi }_\ell ^m(\theta _j,\phi _j) \right]\! \frac{\partial \xi (\gamma ,r_i,r_j)}{\partial \gamma }. \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq120.gif)




![$$ \begin{aligned}&E(k,\mu ) = \exp \left[ \left(\frac{k}{k_{nl}} \right)^{a_{nl}} - \left( \frac{k}{k_p} \right)^{a_p} - \left( \frac{k}{k_{\nu }} \mu \right)^{a_v} \right] \end{aligned} $$](/articles/aa/full_html/2020/10/aa38056-20/aa38056-20-eq125.gif)














