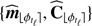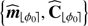| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 27 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201832745 | |
| Published online | 01 November 2018 | |
Exoplanet detection in angular differential imaging by statistical learning of the nonstationary patch covariances
The PACO algorithm
1
Université de Lyon, UJM-Saint-Etienne, CNRS, Institut d’Optique Graduate School, Laboratoire Hubert Curien UMR 5516, , 42023 Saint-Etienne, France
e-mail: olivier.flasseur@univ-st-etienne.fr, loic.denis@univ-st-etienne.fr
2
Université de Lyon, Université Lyon1, ENS de Lyon, CNRS, Centre de Recherche Astrophysique de Lyon UMR 5574, 69230 Saint-Genis-Laval, France
e-mail: maud.langlois@univ-lyon1.fr
Received:
31
January
2018
Accepted:
22
March
2018
Context. The detection of exoplanets by direct imaging is an active research topic in astronomy. Even with the coupling of an extreme adaptive-optics system with a coronagraph, it remains challenging due to the very high contrast between the host star and the exoplanets.
Aims. The purpose of this paper is to describe a method, named PACO, dedicated to source detection from angular differential imaging data. Given the complexity of the fluctuations of the background in the datasets, involving spatially variant correlations, we aim to show the potential of a processing method that learns the statistical model of the background from the data.
Methods. In contrast to existing approaches, the proposed method accounts for spatial correlations in the data. Those correlations and the average stellar speckles are learned locally and jointly to estimate the flux of the (potential) exoplanets. By preventing from subtracting images including the stellar speckles residuals, the photometry is intrinsically preserved. A nonstationary multi-variate Gaussian model of the background is learned. The decision in favor of the presence or the absence of an exoplanet is performed by a binary hypothesis test.
Results. The statistical accuracy of the model is assessed using VLT/SPHERE-IRDIS datasets. It is shown to capture the nonstationarity in the data so that a unique threshold can be applied to the detection maps to obtain consistent detection performance at all angular separations. This statistical model makes it possible to directly assess the false alarm rate, probability of detection, photometric and astrometric accuracies without resorting to Monte-Carlo methods.
Conclusions. PACO offers appealing characteristics: it is parameter-free and photometrically unbiased. The statistical performance in terms of detection capability, photometric and astrometric accuracies can be straightforwardly assessed. A fast approximate version of the method is also described that can be used to process large amounts of data from exoplanets search surveys.
Key words: techniques: image processing / techniques: high angular resolution / methods: statistical / methods: data analysis
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Direct imaging of exoplanets is a recent observational technique (Traub & Oppenheimer 2010) particularly adapted to the observation of young and massive exoplanets. It is complementary to conventional indirect imaging methods (Santos 2008) such as Doppler spectroscopy or the radial velocity technique that have led to the detection and characterization of several hundred subJovian mass exoplanets (Schneider et al. 2011). Direct imaging is also a privileged observation method to reconstruct the spectrum of low mass substellar objects (Vigan et al. 2010). This information is crucial for estimating physical parameters critical for the characterization of these objects. In particular, it is mandatory to estimate the objects age, surface gravity, composition, or effective temperature (Allard et al. 2003, 2007) and to predict their evolution (Burrows et al. 1997; Chabrier et al. 2000) by refining the numerical models of low mass objects and the exoplanet formation theories. Despite the promising future of direct imaging, only a few dozen exoplanets have been successfully detected to this day using this technique (Lagrange et al. 2009; Bonavita et al. 2014; Macintosh et al. 2015; Chauvin et al. 2017). This is mainly due to the difficulty in detecting a faint exoplanet signal given the very large contrast (greater than 10−5 in the near infrared) between the companions and their host star. In addition to the use of extreme adaptive optics, optical attenuation of the host star by using a coronagraph is mandatory to reach this level of contrast (Soummer 2004; Mawet et al. 2006). Currently, two exoplanet-searchers are optimized using these instrumental techniques for direct imaging observations: the Spectro-Polarimetry High-contrast Exoplanet REsearch (SPHERE; Beuzit et al. 2008) at the Very Large Telescope (VLT) of the European Southern Observatory (ESO) and the Gemini Planet Imager (GPI; Macintosh et al. 2014) at the GEMINI observatory. These two instruments offer spectroscopic observations capability in the near infrared via integral fields spectrographs (IFS) or long slit spectroscopy (Vigan et al. 2010). The VLT/SPHERE is also equipped with a differential imager, the InfraRed Dual Imaging Spectrograph (IRDIS; Dohlen et al. 2008a,b) optimized for imaging exoplanets using angular and spectral differential imaging. In order to enhance the achievable contrast, several observation strategies have been developed to exploit temporal or spectral diversity. Spectral differential imaging (SDI; Racine et al. 1999) is based on the assumption that stellar speckles from diffraction are strongly correlated from one wavelength to another (when the differential aberrations are small) after compensating for the wavelength scaling. Multiple images at different wavelengths can thus be combined to numerically suppress a large fraction of the stellar speckles. In addition, the SDI technique assumes that the exoplanet flux is detectable at one wavelength while it is too weak at the other wavelength. Angular differential imaging (ADI; Marois et al. 2006) consists of tracking the observation target over time (the telescope derotator is tuned to maintain the telescope pupil stable while the field of view rotates). Consequently, candidate companions describe an apparent motion along a predictive circular trajectory around the host star while the telescope pupil (including spiders) and coronagraph remain static. Speckles resulting from instrumental aberrations are thus strongly correlated from one exposure to the other. The images can be combined to cancel most of the speckles while preserving part of the signal from the off-axis sources. Their apparent motion helps to separate them from the speckle background. Detectability of the exoplanets therefore relies on the combined ability of the instrument and the numerical processing to suppress the light from the host star and extract the signal from the exoplanets from the remaining stellar speckles. Elaborate processing methods combining multi-temporal and/or multi-spectral data play a central role to reach the ultimate detection limit achievable by such instruments.
This paper is organized as follows. In Sect. 2 we review the current methods for exoplanet detection in ADI or SDI. In Sect. 3 we then introduce the principle of our method based on a modeling of patch covariances. The detailed implementation of the algorithm is described in Sect. 4. We assess the performance of our method on VLT/SPHERE-IRDIS datasets in Sect. 5. Finally, Sect. 6 draws the conclusions of the paper.
2. Current methods for exoplanet direct detection using angular and/or spectral differential imaging
Several methods have been developed to combine different images taken at several consecutive times and/or wavelengths. Stellar speckles can be attenuated by subtracting a reference stellar point spread function (PSF). This is the principle of the LOCI algorithm (Lafreniere et al. 2007). The reference stellar PSF to be subtracted to the data is created by a linear combination of images selected in a library of data acquired under experimental conditions similar to those of the observation of interest. The optimization of this combination is performed by minimizing, in the least squares sense, the residual noise inside multiple subsections of the image. To ensure a more efficient suppression of stellar leakages, the reference stellar PSF is generally extracted from data in which the exoplanets are to be detected. While attenuating at best the stellar speckles, cancellation of part of the signal from the exoplanets also occurs when the rotation of the field of view is small. This problem is more acute at the vicinity of the host star since displacements due to the rotation of the field of view are the smallest there. Many variants have been developed to partially alleviate this problem. A more elaborate version of LOCI called TLOCI (Marois et al. 2013, 2014) is currently considered as one of the most advanced standards for the detection and characterization of exoplanets by direct imaging. The main variation compared to the standard LOCI algorithm is related to the construction of the reference stellar PSF. Instead of only minimizing the noise (i.e., the norm of the residuals), TLOCI also maximizes the exoplanet signal-to-noise ratio (S/N) in the residuals. In other words, the influence of a specific choice of linear combination on the reduction of the flux of the candidate companion is also considered. The TLOCI algorithm is often calibrated for exoplanet signal self-subtraction by injecting “fake” exoplanets (faint point sources) into the data to determine the algorithm throughput at each position in the field of view after the speckle removal. For each fake exoplanet injected, the ratio of the exoplanet flux in the resulting image to its initial flux is estimated to produce the 1D-throughput as a function of the angular separation. The MLOCI algorithm (Wahhaj et al. 2015) injects fake point sources and maximizes their S/N, which also improves the S/N of the sources present in the data. In the ALOCI algorithm (Currie et al. 2012a,b), the data are divided into annuli and processed independently, thereby allowing different linear combinations at different angular separations in the definition of the stellar PSF. Another method, called ANDROMEDA (Mugnier et al. 2009; Cantalloube et al. 2015), forms differences of temporal images to suppress stellar speckles and performs the detection of differential off-axis PSFs (i.e., the signature of an exoplanet in the difference images). A generalized likelihood ratio test is then evaluated. Since the techniques discussed so-far are based on image differences that always reduce the amplitude of the signal due to the exoplanets, adapted post-processing calibrations must be applied to recover the photometry of the detected exoplanets. MOODS algorithm (Smith et al. 2009), based on the joint estimation of the exoplanet amplitude and of the stellar PSF (considered constant for all observations of a temporal dataset), circumvents this problem.
Another family of methods considers that the fluctuations of the stellar speckles (i.e., the stellar PSF) span a small-dimensional subspace. Exoplanets are thus detected on the subspace orthogonal to the subspace that captures fluctuations of the stellar speckles. The data are projected in an orthogonal basis created by principal components analysis (PCA). This is the principle of the KLIP algorithm (Soummer et al. 2012) which builds a basis of the subspace capturing the stellar PSF by performing a Karhunen-Loève transform of the images from the reference library. To obtain a model of the stellar PSF to subtract in order to attenuate the speckles, the science data is projected onto a predetermined number of modes. Even if the general principle is close to the LOCI type algorithms, KLIP is much faster thanks to the truncation. The sKLIP (Absil et al. 2013) algorithm partially prevents the subtraction of signal from the companions by building the reference library only from images where the candidate exoplanets underwent a sufficient rotation. The LLSG (Gonzalez et al. 2016) algorithm is also related to subspace methods. It locally decomposes a temporal serie of images into low-rank, sparse and Gaussian components. It is experimentally shown that the exoplanet signals mostly remain in the sparse term allowing for an improved detection. However, it is expected that this method is sensitive to outliers in the data (such as bad or hot pixels), which are also recovered in the sparse component together with the candidate exoplanets.
Finally, the last family of detection methods are based on a modeling of the stellar PSF based on diffraction modeling. PeX algorithm (Thiébaut et al. 2016; Devaney & Thiébaut 2017) models the chromatic dependence of speckles. MEDUSAE method (Ygouf 2012; Cantalloube 2016) performs an inversion to identify the phase aberrations in a physical model of the coronagraph and deconvolve the images to recover the circumstellar objects by exploiting spectral diversity and regularization terms.
All of these techniques have several tuning parameters that often require tuning by trial and error and the intervention of an expert, making the optimality difficult to reach. It is also often observed that the detection maps (or residual images) have nonstationary behaviors (typically with a variance that increases at smaller angular separations). As a result, it is necessary to carry out a pre-calibration step to control the probability of false alarm when using these techniques. This pre-calibration is tricky to perform in the presence of numerous background sources. The pre-calibration is also dependent on the injected fake exoplanet flux, resulting in a large processing time.
3. PACO: Exoplanet detection based on PAtch COvariances
The prereduction of the SPHERE datasets uses the Data Reduction Handling (DRH) pipeline (Pavlov et al. 2008) that was delivered by the SPHERE consortium with the instrument to ESO. Additional optimized prereduction tools allow accurate astrometric calibrations (Maire et al. 2016). These prereductions made use of the SPHERE data center (Delorme et al. 2017) which assembles raw images into calibrated datasets by performing several corrections: bad pixels identification and interpolation1, thermal background subtraction, flat-field correction, anamorphism correction, true north alignment, frame centering, compensation for spectral transmission, frame selection, and flux normalization. The outputs of these first steps are temporal sequences of coronagraphic images (organized in datasets with three dimensions hereafter), and of the associated off-axis PSF. Figure 1 shows an example of a science frame derived from VLT/SPHERE-IRDIS data and a view of two spatio-temporal slices extracted at two different locations (along the solid line: far from the host star, along the dashed line: near the host star). Within the central region (angular separations below 1 arcsec at the wavelength λ1 = 2.110 μm), the signal is dominated by stellar speckles due to the diffraction in presence of aberrations. At farther angular separations, the noise comes mainly from a combination of photon noise from thermal background flux and detector readout. Observation of the temporal fluctuations in the spatio-temporal cuts reveals spatial variations of the variance of the fluctuations but also an evolution of their spatial correlations. Beyond accounting for the average intensity of stellar speckles, we base our exoplanet detection method on a nonstationary modeling of short-range spatial covariances. To ease the statistical learning of these covariances directly from the data and to obtain a detection method based on local processing, we consider a decomposition of the field of view into small patches whose size covers the core of the off-axis PSF. Our detection method accounts for the (spatial) covariance of these patches, hence the name PACO for PAtch COvariance. In the following paragraphs, we describe into more details the proposed model, derive a detection criterion and characterize the photometric and astrometric accuracies.
 |
Fig. 1. Sample from a VLT/SPHERE-IRDIS dataset (HIP 72192 dataset at λ1 = 2.110 μm). Two spatio-temporal slices cut along the solid and dashed line are displayed at the bottom of the figure, emphasizing the spatial variations of the structure of the signal. |
3.1. Statistical model for source detection and characterization
To simplify the notations and the discussion, we have considered datasets at a single wavelength. If observations at several wavelengths are available, they can be split and processed independently from each other. Joint processing of multi-spectral data can be beneficial but requires some refinements that are beyond the scope of this paper and that will be covered by a following paper.
Science images obtained by high-contrast imaging within ADI have two components: (i) the signal of interest, due to the presence of exoplanets or background sources in the field of view, and (ii) a very strong background, produced by the stellar speckles and other sources of noise, that displays temporal fluctuations. The motion of the background sources/exoplanets due to the rotation of the field of view is precisely known. An exoplanet at some bidimensional angular location ϕ0 at a chosen initial time t0 is seen at location ϕt = ℱt(ϕ0) at time t, where ℱt is the geometrical transform (e.g., a rotation) modeling the apparent motion of the field of view between the observation configurations at time t0 and time t. We note that a reminder of the main notations used throughout the paper is given in Table 1.
Reminder of the main notations.
Since very few sources are within the field of view and these sources are faint, we have modeled locally the observed data as the super-imposition of a background (stellar speckles and noise) and at most one other source, unresolved and located in the immediate vincinity (no overlapping of several faint sources).
The observed intensity rθk, tℓ at the 2D pixel location θk and time tℓ, corresponding to the spatio-temporal index (k, ℓ) in the dataset, can then be decomposed into the two components: (1)
(1)
with α ≥ 0 the flux of the unresolved source (α = 0 in the absence of such source), hθk(ϕtℓ) = h(θk − ϕtℓ) the off-axis PSF, centered on the location ϕtℓ of the source at time tℓ and sampled at pixel location θk, and fθk, tℓ the background at spatio-temporal index (k, ℓ) which accounts for stellar speckles and noise.
The major difficulty in the detection of exoplanets lies in the fact that the amplitude of the background fθk, tℓ is much larger than the exoplanet contribution αhθk(ϕtℓ) and that it fluctuates from one time t to another. It is necessary to follow a statistical approach to account for these fluctuations. The collection of all observations {rθk, tℓ}k = 1 : N, ℓ=1 : T in the presence of an exoplanet initially located at ϕ0 with a flux α is then described as a random realization with a distribution given by the probability density function pf of the background: (2)
(2)
Based on this model and under the hypothesis that there are few sources within the field of view (so that each source can be considered separately), an unbiased estimation of the flux α knowing the initial angular location ϕ0 is provided by the maximum likelihood estimator: (3)
(3)
We note that  implicitly depends on the assumed position ϕ0 of the source. The detection of a point source at a given location ϕ0 can be formalized as a hypothesis test:
implicitly depends on the assumed position ϕ0 of the source. The detection of a point source at a given location ϕ0 can be formalized as a hypothesis test: (4)
(4)
Literally, this means that under hypothesis ℋ0 the collection of all observations corresponds to pure background (stellar speckles and noise) while under hypothesis ℋ1 it is the superimposition of the off-axis PSF with a flux α and some background.
By replacing α in ℋ1 with the maximum likelihood estimate  obtained from (3) for an assumed initial position ϕ0, the (generalized) likelihood of each hypothesis can be compared to form the generalized likelihood ratio test (GLRT, see for example Kay 1998a):
obtained from (3) for an assumed initial position ϕ0, the (generalized) likelihood of each hypothesis can be compared to form the generalized likelihood ratio test (GLRT, see for example Kay 1998a): (5)
(5)
In order to apply Eqs. (3) and (5) to the detection and photometric or astrometric estimations, it is necessary to specify the statistical model of the background. In most of the existing methods for exoplanet detection by ADI, some data preprocessing is applied in order to reduce the amplitude of the background term and whiten it (i.e., lessen its spatial correlations). Such preprocessing takes the form of (weighted) temporal differences in ADI, TLOCI and ANDROMEDA, a high-pass filtering, or the projection onto the subspace orthogonal to the dominant modes identified by a PCA in KLIP and its variations. ANDROMEDA distinguishes itself in that both its detection and estimation procedures are derived from a statistical framework (Eqs. (3) and (5) applied under the assumption of uncorrelated Gaussian noise). Rather than transforming the data so that a simple statistical model can be assumed (uncorrelated observations), we performed no preprocessing but account for the spatial correlations in our model. Given that more than a few tens of photons are collected at each detector pixel, the Poisson detection statistics can be approximated by a Gaussian distribution. The other contributions for the temporal fluctuations (thermal background noise, evolution of the speckle patterns due to evolving phase aberrations or the decentering of the star on the coronagraph) will be considered, in the absence of a more precise model, to be Gaussian distributed. This Gaussian approximation gives closed-form expressions that have a practical interest for the implementation. The spatial structure of the background is mainly due to that of the speckles (related to the angular resolution) and the interpolation steps in the data reduction pipeline. Most of these correlations are at small scale. Moreover, the off-axis PSF h(ϕ) has a core (also defined by the angular resolution) that is only a few pixels wide. Hence, in Eqs. (3) and (5), only pixels (k, ℓ) of the dataset such that hθk(ϕtℓ) is non negligible have an impact on the estimation or detection. These pixels are represented in green in Fig. 2.
 |
Fig. 2. Apparent motion of an exoplanet in an ADI stack of frames. Green patches contain, in each frame, the exoplanet (i.e., the off-axis PSF) superimposed with the background. The statistical model of a background patch is built locally based on observed patches at the same location but at different times (set of red patches). |
We denote the set of the K spatial pixels that form an extended spatial neighborhood centered at pixel θ k, at time tℓ, as the patch2 rθk, tℓ ∈ ℝK
. In the following, patches are sets of pixels with the shape of a discrete disk. If the radius of this disk is chosen large enough to encompass the core of the off-axis PSF, the collection of all pixel values {rθk, tℓ}k = 1 : N, ℓ=1 : T used in Eqs. (5) and (3) to detect or estimate the flux of an exoplanet located at ϕ0 can be reduced to the collection of patches {r⌊ϕt⌉, tℓ}ℓ = 1 : T (with ⌊ϕt⌉ the closest pixel to the subpixel location ϕt) that contains the exoplanet. Only the joint distribution of these observations need be modeled. Since the background is different in each patch (and possibly varies differently according to time), we used a different model for each patch (local adaptivity of the model), see Fig. 2. The reduced number T of available background patches at a given spatial location (typically, from a few tens to a hundred temporal frames) limits the correlations that can be accounted for. We chose to account only for spatial correlations3 and to use a multivariate Gaussian model to describe the distribution of each background patch. Patches at different times are considered to be statistically independent. Rather than defining the distribution pf of all background pixels, we then modeled only the distribution of background pixels in the patches of interest. This distribution pf({f⌊ϕt⌉, tℓ}ℓ = 1 : T) is modeled as a product of Gaussian distributions defined over each patch that would contain an exoplanet if that exoplanet was initially located at ϕ0
 (6)
(6)
with 𝒩(⋅ | m⌊ϕt⌉, C⌊ϕt⌉) the probability density function of the multivariate Gaussian (mean m and covariance C) that describes background patches centered at pixel ⌊ϕt⌉.
3.2. Statistical learning of the background
In our model, we have considered a common mean mθk and covariance Cθk for all T background patches {fθk, tℓ}ℓ = 1 : T centered at a given pixel location θk. Background patches are not directly available, only observed patches {rθk, tℓ}ℓ = 1 : T can be used to estimate the mean mθk and covariance Cθk. Moreover, the limited number T of temporal frames makes a direct estimation of Cθk by the sample covariance either rank deficient (if T < K) or too noisy. Some form of regularization must thus be enforced. Several strategies can be considered (see Appendix A and Fig. A.1). We found that a shrinkage approach (Kay & Eldar 2008) with a data-driven shrinkage factor was the best adapted to our problem due to its capability to balance locally the regularization and thanks to the absence of any tuning parameter. In a nutshell, a shrinkage covariance estimator  is defined by the convex combination of two estimators
is defined by the convex combination of two estimators  and
and 
 (7)
(7)
where  is the shrinkage weight. The two estimators
is the shrinkage weight. The two estimators  and
and  are chosen such that one estimator has very little bias (but a large variance) and the other one has fewer degrees of freedom, hence a much smaller variance, at the cost of an increased bias. The parameter
are chosen such that one estimator has very little bias (but a large variance) and the other one has fewer degrees of freedom, hence a much smaller variance, at the cost of an increased bias. The parameter  is set in order to achieve a bias–variance trade-off. As detailed in Appendix A, we defined
is set in order to achieve a bias–variance trade-off. As detailed in Appendix A, we defined  as the sample covariance matrix computed at location θk:
as the sample covariance matrix computed at location θk: (8)
(8)
the sample mean. The chosen estimator  is the diagonal matrix formed from the sample covariance:
is the diagonal matrix formed from the sample covariance:![$$ \begin{aligned} \bigl [\widehat{\mathbf{F }}_{\theta _k}\bigr ]_{ii}&=\frac{1}{T} \sum _{\ell =1}^T \bigl [\boldsymbol{r}_{\theta _k,t_\ell }-\widehat{\boldsymbol{m}}_{\theta _k}\bigr ]_{ii}^2=\bigl [\widehat{\mathbf{S }}_{\theta _k}\bigr ]_{ii}\end{aligned} $$](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq21.gif) (10)
(10)
![$$ \begin{aligned} \text{ and} \bigl [\widehat{\mathbf{F }}_{\theta _k}\bigr ]_{ij}&=0\; \text{ if} \;i\ne j. \end{aligned} $$](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq22.gif) (11)
(11)
Diagonal elements of the shrinkage estimator  then correspond to the empirical variance while off-diagonal elements (i.e., covariance terms) are shrunk toward 0 by a factor
then correspond to the empirical variance while off-diagonal elements (i.e., covariance terms) are shrunk toward 0 by a factor  , hence the name.
, hence the name.
The shrinkage factor  is locally adapted in an unsupervised data-driven way. In Appendix A we derive its expression4:
is locally adapted in an unsupervised data-driven way. In Appendix A we derive its expression4:![$$ \begin{aligned} \widehat{\rho }\,\Big (\,\widehat{\mathbf{S }}_{\theta _k}\Big )= \frac{ \mathrm{tr}\Big (\,{\widehat{\mathbf{S }}_{\theta _k}^2}\Big ) \,{+}\, \mathrm{tr}^2\Big (\,{\widehat{\mathbf{S }}_{\theta _k}}\Big ) - 2\sum _{i=1}^K\Big [\,{\widehat{\mathbf{S }}{_{\theta _k}}}\Big ]_{ii}^2 }{ \Big (T\,{+}\,1\Big )\Big ({ \mathrm{tr}\Big (\,{\widehat{\mathbf{S }}_{\theta _k}^2}\Big ) - \sum _{i=1}^K\Big [\,{\widehat{\mathbf{S }}{_{\theta _k}}}\Big ]_{ii}^2\Big ) } } \,\cdot \end{aligned} $$](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq26.gif) (12)
(12)
Remaining bad pixels after the prereduction (see introductory discussion in Sect. 3) take very large values at some dates. These aberrant values often impact exoplanet detection algorithms. By learning the local covariance of the patches, these large fluctuations are accounted for within our model (large pixel variance). We show in Sect. 5 that these bad pixels do not lead to false alarms.
3.3. Unbiased estimation of the background statistics
To account for the fact that observed patches {rθk, tℓ}ℓ = 1 : T do not contain pure background but also, in the presence of an exoplanet, the signal due to the exoplanet, estimation of the background statistics and of the exoplanet flux can be alternated, starting from an initial guess of pure background. At the n-th iteration, after a flux  has been estimated for the exoplanet assuming background statistics
has been estimated for the exoplanet assuming background statistics  (as explained in Sect. 3.4), the background statistics can be improved by computing
(as explained in Sect. 3.4), the background statistics can be improved by computing![$$ \begin{aligned} \left\{ \begin{array}{ll} \widehat{\boldsymbol{m}}_{\theta _k}^{(n\,{+}\,1)}&= \frac{1}{T}\sum _{\ell =1}^T\bigl (\boldsymbol{r}_{\theta _k,t_\ell }-\widehat{\alpha }^{(n)}\boldsymbol{h}_{\theta _k}(\phi _{t_\ell })\bigr )\\ \widehat{\mathbf{S }}_{\theta _k}^{(n\,{+}\,1)}&=\frac{1}{T} \sum _{\ell =1}^T \bigl (\boldsymbol{r}_{\theta _k,t_\ell }-\widehat{\alpha }^{(n)}\boldsymbol{h}_{\theta _k}(\phi _{t_\ell })-\widehat{\boldsymbol{m}}_{\theta _k}^{(n\,{+}\,1)}\bigr ) \\&\cdot \,\bigl (\boldsymbol{r}_{\theta _k,t_\ell }-\widehat{\alpha }^{(n)}\boldsymbol{h}_{\theta _k}(\phi _{t_\ell })-\widehat{\boldsymbol{m}}_{\theta _k}^{(n\,{+}\,1)}\bigr )^{\mathrm{t} }\\ \bigl [\widehat{\mathbf{F }}_{\theta _k}^{(n\,{+}\,1)}\bigr ]_{ii}&=\bigl [\widehat{\mathbf{S }}_{\theta _k}^{(n\,{+}\,1)}\bigr ]_{ii}\\ \widehat{\rho }^{(n\,{+}\,1)}&=\widehat{\rho }\bigl (\widehat{\mathbf{S }}_{\theta _k}^{(n\,{+}\,1)}\bigr )\\ \widehat{\mathbf{C }}^{(n\,{+}\,1)}&=(1-\widehat{\rho }^{(n\,{+}\,1)}) \,\widehat{\mathbf{S }}^{(n\,{+}\,1)}\,{+}\,\widehat{\rho }^{(n\,{+}\,1)}\,\widehat{\mathbf{F }}^{(n\,{+}\,1)}. \end{array}\right. \end{aligned} $$](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq29.gif) (13)
(13)
This iterative procedure is applied to provide unbiased estimates of the flux of an exoplanet, after detection. Indeed, should the contribution of the exoplanet not be subtracted prior to computing the statistics of the background, the mean would contain a fraction of the PSF of the exoplanet (1/Tth of the flux of the exoplanet if the exoplanet is visible only in one of the patches centered on pixel θk). The covariance would then encode that there are significant variations in the background in the form of an appearing and disappearing PSF. The subsequent estimation of the source flux would be penalized by these errors on the mean and covariance of the background. A few iterations of Eq. (13) and exoplanet flux re-estimations corrects the statistics of the background and prevents from biasing the estimation of the photometry by an erroneous statistical model of the background.
Experiments have shown that the unbiased estimation of the flux of the exoplanet is not beneficial in the exoplanet detection phase. While it improves the signal of the exoplanets, it changes the distribution of the test in the absence of exoplanet, which makes the setting of a detection threshold (see Appendix A for details) more difficult. Therefore, we computed the background statistics  and
and  based on Eqs. (7)–(12) to compute a detection map (see Sect. 3.5), and alternate Eq. (13) with a re-estimation of the flux for the photometric and astrometric estimations of a detected source (see Sects. 3.4 and 3.6).
based on Eqs. (7)–(12) to compute a detection map (see Sect. 3.5), and alternate Eq. (13) with a re-estimation of the flux for the photometric and astrometric estimations of a detected source (see Sects. 3.4 and 3.6).
3.4. Estimation of the flux of an exoplanet
Under our multivariate Gaussian model of the background, the maximum likelihood estimator given in Eq. (3) for an assumed initial location ϕ0 has a simple expression (see for example Kay 1998b): (14)
(14)
where we recall that h⌊ϕtℓ⌉(ϕtℓ) denotes the off-axis PSF for a source at (subpixel) location ϕtℓ sampled over a patch of K pixels and whose center is ⌊ϕtℓ⌉, the nearest pixel to ϕtℓ.
The maximum likelihood estimator  given in Eq. (14) depends linearly on the data, hence its variance can be easily derived. Noting that
given in Eq. (14) depends linearly on the data, hence its variance can be easily derived. Noting that  with
with  and
and  , we obtain:
, we obtain: (17)
(17)
since a is deterministic. The variance of b is the sum of the variances of the bℓ terms since they are mutually independent (corresponding to different temporal frames). From its expression in Eq. (16), the variance of bℓ is given by: (18)
(18)
Our assumptions amount to approximating the distribution of the term  by a centered Gaussian of covariance
by a centered Gaussian of covariance  . The variance of bℓ therefore simplifies to:
. The variance of bℓ therefore simplifies to: (19)
(19)
Thus an estimator of the variance of  is
is  and the standard deviation of
and the standard deviation of  can be estimated by:
can be estimated by: (20)
(20)
Obviously, the flux of the source is necessarily positive, we denote by  the flux obtained under a positivity constraint5 (see Thiébaut & Mugnier 2005; Mugnier et al. 2009):
the flux obtained under a positivity constraint5 (see Thiébaut & Mugnier 2005; Mugnier et al. 2009): (21)
(21)
We assume that, if positivity is imposed, the covariance of  can be approximated by
can be approximated by  , in Eq. (20).
, in Eq. (20).
3.5. Detection of exoplanets
Under our multivariate Gaussian model of the background, the generalized likelihood ratio test (Eq. (5)) takes the simplified form (22)
(22)
with aℓ and bℓ defined according to Eqs. (15) and (16).
As discussed in Thiébaut & Mugnier (2005), Smith et al. (2009) and Mugnier et al. (2009), it is beneficial to enforce a positivity constraint on the flux α in the detection test, in other words, to use the estimate  to derive the GLRT expression, leading to
to derive the GLRT expression, leading to (23)
(23)
As noted in Mugnier et al. (2009), the test (Eq. (23)) is equivalent to the test (24)
(24)
when η ≥ 0 and with  . This test can be interpreted as the S/N
. This test can be interpreted as the S/N  of the estimation of the (unconstrained) flux of the source α. We note that with our definition, the S/N is a signed quantity that is negative whenever
of the estimation of the (unconstrained) flux of the source α. We note that with our definition, the S/N is a signed quantity that is negative whenever  .
.
The test (S/N test) in Eq. (24) is attractive because the test value  linearly depends on the data. Under our Gaussian model for the data, the S/N
linearly depends on the data. Under our Gaussian model for the data, the S/N  is thus also Gaussian distributed (with unit variance) which simplifies the statistical analysis of the test in terms of false alarm rate or detection probability. This analysis is carried out in the following.
is thus also Gaussian distributed (with unit variance) which simplifies the statistical analysis of the test in terms of false alarm rate or detection probability. This analysis is carried out in the following.
In the hypothesis test (Eq. (4)), we considered an hypothetical initial location of the source ϕ0. To detect all sources within the field of view and locate their positions, the test (S/N test) should be evaluated at locations ϕ0 sampled over the field of view. By refining the sampling of the field of view, the off-axis PSFs h⌊ϕtℓ⌉(ϕtℓ) better matches the data and the estimate  is more accurate, at the cost of a larger computational effort. Sampling of the field of view is discussed in Sect. 4.3.
is more accurate, at the cost of a larger computational effort. Sampling of the field of view is discussed in Sect. 4.3.
3.6. Statistical guarantees
3.6.1. Distribution of the detection criterion
Figure 3 illustrates a S/N map  computed using the PACO method on a VLT/SPHERE-IRDIS dataset (obtained on the HIP 72192 star as described in more detail in Sect. 5) consisting of 96 temporal frames in which the two real known faint point sources are masked. Visual inspection of the S/N map (top of Fig. 3) indicates that the detection criterion is stationary over the field of view, even close to the coronagraphic mask. The empirical distribution of the S/N values (bottom of Fig. 3) shows that the S/N distribution can be considered as centered (since the empirical mean is 0.01) and approximately reduced (since the empirical standard deviation is 0.93) Gaussian. This distribution passes successfully the Lilliefors normality test (Lilliefors 1967) at the 5% significance level. The small discrepancy with theoretical model may be due to the correlations in the data. However, the hypothesis that the variance of the S/N under ℋ0 is equal to one is conservative in the sense that the probability of false alarm is slightly overestimated. Owing to the homogeneous distribution of the S/N criterion across the field of view, this small bias could be easily fixed by rescaling the S/N by a single factor that is empirically estimated6.
computed using the PACO method on a VLT/SPHERE-IRDIS dataset (obtained on the HIP 72192 star as described in more detail in Sect. 5) consisting of 96 temporal frames in which the two real known faint point sources are masked. Visual inspection of the S/N map (top of Fig. 3) indicates that the detection criterion is stationary over the field of view, even close to the coronagraphic mask. The empirical distribution of the S/N values (bottom of Fig. 3) shows that the S/N distribution can be considered as centered (since the empirical mean is 0.01) and approximately reduced (since the empirical standard deviation is 0.93) Gaussian. This distribution passes successfully the Lilliefors normality test (Lilliefors 1967) at the 5% significance level. The small discrepancy with theoretical model may be due to the correlations in the data. However, the hypothesis that the variance of the S/N under ℋ0 is equal to one is conservative in the sense that the probability of false alarm is slightly overestimated. Owing to the homogeneous distribution of the S/N criterion across the field of view, this small bias could be easily fixed by rescaling the S/N by a single factor that is empirically estimated6.
 |
Fig. 3. S/N map in absence of object (the two real known faint point sources denoted FPS1 and FPS2 are masked) and its corresponding empirical distribution using the HIP 72192 dataset described in Sect. 5 at λ2 = 2.251 μm. |
Under the hypothesis ℋ0, the S/N follows a centered and reduced Gaussian law whatever the angular separation. It is thus possible to apply a unique threshold τ to the S/N maps and obtain a consistent detection performance at all angular separations (i.e., a constant false alarm rate). The accordance between the S/N and a Gaussian distribution makes it possible to directly assess the false alarm rate, probability of detection, photometric and astrometric accuracies without post-processing and/or resorting to Monte Carlo methods (injection of fake exoplanets in the data) in contrast to several state-of-the-art methods (Lafreniere et al. 2007; Cantalloube et al. 2015; Ruffio et al. 2017).
3.6.2. Probabilities of false alarm and of true detection
The probability of false alarm (PFA) is the probability that the test (Eq. (24)) yields ℋ1 while ℋ0 is actually true: (25)
(25)
where Φ is the cumulative distribution function of the standard normal distribution. The conventional contrast at 5 σ ensures a probability of false alarm equal to PFA(5) = 2.87 × 10−7.
The probability of detection (PD) is the probability that the test (Eq. (24)) decides correctly for a detection![$$ \begin{aligned} \text{ PD}(\tau ,\alpha )&= \Pr (\widehat{\alpha }/\widehat{\sigma }_{\alpha } > \tau \,\vert \,\mathcal{H} _{1}) \nonumber \\&= \int _{\tau }^{+\infty } \frac{1}{\sqrt{2\,\pi }} \, \exp \left({\frac{-\left[ x - \alpha /\widehat{\sigma }_{\alpha } \right]^2}{2}}\right) \,\mathrm{d} x \nonumber \\&= 1 - \Phi (\tau -\alpha /\widehat{\sigma }_{\alpha }) . \end{aligned} $$](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq64.gif) (26)
(26)
The minimum amplitude α such that the probability of detection be at least equal to some prescribed value PD when the detection threshold τ is set according to a given PFA level can be computed by inverting and combining Eqs. (25) and (26): (27)
(27)
For example, at τ = 5, a probability of detection of 50% is achieved for  and a probability of detection of 80% for
and a probability of detection of 80% for  . Figure 4 illustrates the S/N distribution under the two hypothesis as well as the probabilities of false alarm and of detection.
. Figure 4 illustrates the S/N distribution under the two hypothesis as well as the probabilities of false alarm and of detection.
 |
Fig. 4. S/N distribution under ℋ0 (in blue) and ℋ1 (in red). The hatched area is equal to the probability of false alarm (PFA) while the filled area is equal to the probability of detection (PD). |
3.6.3. Astrometric accuracy
An (asymptotically) unbiased estimator of the position of the source is provided by the maximum likelihood position which is the solution of a non-convex optimization problem. In practice, this problem can be solved by exhaustive search at a finite resolution refined by a local optimization as for example proposed by Soulez et al. (2007) in digital lensless microscopy for the detection of parametric objects spread in a volume. The astrometric accuracy, that is, the accuracy on the spatial location of the detected objects can be statistically predicted using the Cramér-Rao lower bounds (CRLBs) which represents the minimal variance of any unbiased estimator. The CRLBs are obtained from the diagonal of the inverse of Fisher information matrix (Kendall et al. 1948). Using a parametric model of the off-axis PSF h and noting again that the collection of patches {rθk, tl}l = 1 : T located at the angular position θk is described by a multi-variate Gaussian process 𝒩(⋅ | mθk, Cθk), it is possible to derive the CRLBs from the observed intensity model given in Eq. (1). In the following, Ω = {α, x0, y0} (with ϕ0 = {x0, y0} the angular position of an exoplanet at time t0) denotes the vector of parameters from which the CRLBs are computed. For a given angular position θk, the Fisher information matrix  can be expressed as
can be expressed as![$$ \begin{aligned} {[\mathbf{I}_{\theta _{k}}^\mathrm{F} (\boldsymbol{\Omega })}]_{i,j}\,{=}\,{\frac{\partial {\alpha }{\boldsymbol{h}}_{\theta _{k}}(\boldsymbol{\Omega })}{\partial \boldsymbol{\Omega }_{i}}} ^{\mathrm{t} }\cdot \mathbf{C }_{\theta _{k}}^{-1} \cdot \frac{\partial {\alpha }{\boldsymbol{h}}_{\theta _{k}}(\boldsymbol{\Omega })}{\partial \boldsymbol{\Omega }_{j}}, \end{aligned} $$](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq69.gif) (28)
(28)
in which the term α
hθk represents the off-axis PSF (an isotropic Gaussian can typically be used as a continuous model to compute the derivatives). It follows that the standard deviation δ
θk on the estimation of the parameter vector Ω is given by![$$ \begin{aligned} {[\mathbf{\delta }_{\theta _{k}}]_i \,{=}\,\sqrt{[{\mathbf{I }_{\theta _{k}}^\mathrm{F} (\boldsymbol{\Omega })^{-1}}]_{i,i}}} \end{aligned} $$](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq70.gif) (29)
(29)
For simplicity, we denote by δ = {δα, δx0, δy0} the spatial maps (obtained for all angular positions θk of the field of view) representing the accuracy on the parameters Ω = {α, x0, y0}. Appendix B gives the analytical expression of δ as a function of the Fisher information matrix terms. We note that δα is not dependent on α while δx0 and δy0 are proportional to α −1. Figure 5 gives a view of δα, δx0 and δy0 as well as the correlation coefficients ραx0, ραy0 and ρx0y0 between estimated parameters obtained on the HIP 72192 dataset at λ1 = 2.110 μm. As expected, the estimation error of Ω = {α, x0, y0} increases near the host star. The figure also emphasizes that the Cramér-Rao bounds {δα, δx0, δy0} decrease quickly with the angular separation. Moreover, a small estimation error on one of the three parameters has little impact on the estimation of the other two parameters (low absolute correlation coefficients) except for certain localized areas of the field of view. The resulting Cramér-Rao bounds can be usefully considered to evaluate the error on the estimated parameters. For example, for the two real faint point sources located around the HIP 72192 star (their positions are symbolized by a circle in Fig. 5, the products α ⋅ δx0 and α ⋅ δy0 are closed to 0.7 × 10−5 pixel. It means that at a contrast α = 10−5, the sources can be located with an accuracy of about 0.7 pixel.
 |
Fig. 5. Upper line: minimal standard deviation (Cramér-Rao lower bounds) δ = {δα, δx0, δy0} on the estimated parameters Ω = {α, x0, y0} (δx0 and δy0 are normalized by the inverse of the flux α of the exoplanet and expressed in pixels unit). Middle line: magnification of the area near the host star. Lower line: coefficients of correlation ρ = {ραx0, ραy0, ρx0y0} between the estimated parameters Ω = {α, x0, y0}. The computation is performed on the HIP 72192 dataset at λ1 = 2.110 μm. The positions of the two real faint point sources in the dataset (which are not visible on these maps because it does not act of detection maps) are represented by a circle. |
4. Implementation details of PACO
This section is devoted to the description of the implementation of the PACO algorithm presented in Sect. 3. A simplified and faster version for the detection step is also described. This fast version can be useful to conduct pre-analyses in large surveys.
4.1. Optimal patches size
The patches considered in the PACO algorithm define the characteristic size of the areas in which the statistics of the background fluctuations are modeled. Since the core of the off-axis PSF is close to circular symmetry, circular patches are used. Their size obeys a trade-off: on the one hand, the larger the patches, the more energy from the source is contained in the patches which improves the S/N; on the other hand, learning the covariance of larger patches requires more samples (i.e., more temporal frames).
In practice, since the sources to be detected are faint compared to the level of stellar speckles and their temporal fluctuations, only the core of the off-axis PSF is necessary to perform the detection and a patch size corresponding to twice the off-axis PSF full width at half maximum (FWHM) appears to be a good compromise. A more precise (and automatic) determination of the optimal size of the patches with respect to number of time frames and the structure of the background correlations can be carried out by Monte Carlo simulations. False planets are randomly injected into the data and receiver operating characteristic (ROC) curves representing the detection probabilities as a function of the false alarm rate are constructed for different patch sizes. The patch size maximizing the area under the ROC curve is then adopted. Figure 6 gives ROC curves for three patch sizes and shows that the choice K = 49 pixels per patch maximizes the area under the curve and is therefore the best compromise for performing the detection on the HIP 7192 dataset (with 4.5 pixels FWHM) for fake injected exoplanets of flux α ∈ [10−6;10−5]. The number of pixels per patch K needs to be determined only once for a given instrument since the FWHM of the off-axis PSF varies only marginally from one observation to another.
 |
Fig. 6. Influence of patch size: ROC curves for K = {13, 49, 113} pixels in each patch. The ROC curves are obtained by inserting fake exoplanets of flux α ∈ [10−6;10−5] on the HIP 72192 dataset at λ1 = 2.110 μm. |
4.2. The PACO algorithm: detailed implementation
As explained in Sect. 3, within the PACO pipeline, the detection and estimation steps are performed by two very similar schemes. First, the detection is performed on the whole field of view using the PACO detection procedure. This step produces a map of S/N which is statistically grounded and which can be directly thresholded at a controlled false alarm rate. The estimated flux is however biased by the presence of the exoplanet in the collection of patches used to model the background fluctuations. Thus, a different procedure named PACO estimation is launched in a second step on each detected source in order to refine the flux estimation. This latter procedure provides unbiased flux estimates (i.e., no a posteriori Monte Carlo-based bias correction is necessary).
Algorithm 1 summarizes the PACO detection procedure as described more formally in Sect. 3. Step 1 consists of forming the collection of patches 𝒫ℓ on which the statistics of the background must be learned. These patches are all centered at the same position ϕtℓ where the source would be at time tℓ, assuming it was initially at position ϕ0. In Step 2, the background statistics, i.e. the empirical mean  and the regularized covariance
and the regularized covariance  , are computed based on Eqs. (7)–(12). Step 3 then forms the numerator and denominator of the test statistics by accumulating values aℓ and bℓ defined by Eqs. (15) and (16). In Algorithm 1, the background statistics are computed assuming no exoplanet is present (i.e., hypothesis ℋ0) and are thus biased. This is especially notable when the apparent motion of the exoplanet over time is limited and the source flux is large.
, are computed based on Eqs. (7)–(12). Step 3 then forms the numerator and denominator of the test statistics by accumulating values aℓ and bℓ defined by Eqs. (15) and (16). In Algorithm 1, the background statistics are computed assuming no exoplanet is present (i.e., hypothesis ℋ0) and are thus biased. This is especially notable when the apparent motion of the exoplanet over time is limited and the source flux is large.
Since the data analysis of large surveys is a crucial issue in astronomy, we also propose a simplified and faster version of the PACO detection procedure which is summarized by Algorithm 2. Compared to applying Algorithm 1 to a given set of assumed initial source positions to compute a map of the detection criterion, the fast version has a computational burden reduced by a factor at least equal to the number T of temporal frames. The acceleration relies on the precomputation of terms that appear multiple times in the sums of Eqs. (15) and (16) when considering all possible source locations. Computations of the background statistics are thus recycled. The S/N map is obtained in a second step by interpolating the precomputed terms denoted by c and d in Algorithm 2 in order to align the field of view at all times according to the transform ℱtℓ which is, in general, a rotation. Such interpolations result in a low-pass filtering of the criterion map which slightly degrades the detection performance of PACO (see Sect. 5). The complexity of the fast version given in Algorithm 2 is dominated by the pre-calculation step (Step 1). Denoting by N the number of angular positions ϕ0 to process, this step requires N × T products of vectors with K elements as well as the resolution of N linear systems of size K × K. For example, the application of this fast algorithm requires approximately two minutes to process a dataset made of 96 temporal frames of size 1024 × 1024 pixels versus approximately three hours for the complete algorithm using a basic parallelization done in  on 24 cores (processor Intel Xeon E5–46170 at 2.90 GHz and K = 49 pixels per patch).
on 24 cores (processor Intel Xeon E5–46170 at 2.90 GHz and K = 49 pixels per patch).
PACO detection – Computation of the S/N values at initial 2D angular positions 𝒢 of an unresolved source.
Input: Set G of initial 2D angular positions.
Input: Spatio-temporal dataset {rθkℓ,tℓ} k = 1:N,ℓ = 1:T.
Output: S/N map at all initial positions in 𝒢.
forall ϕ0 ∈ 𝒢 do
a ← 0
b ← 0
for ℓ = 1 : T do
▹ Step 1. Extract the relevant patches:
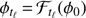
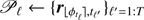
▹ Step 2. Learn the background statistics from the patches in 𝒫ℓ:
▹ Step 3. Update a and b:
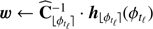
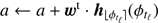 (Eq. (15))
(Eq. (15))
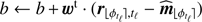 (Eq. (16))
(Eq. (16))
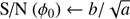 (Eq. (24))
(Eq. (24))
Once the detection step is performed by Algorithm 1 or Algorithm 2, the potential detections obtained by thresholding the S/N map at level τ should be photometrically characterized using the statistically unbiased PACO estimation procedure summarized in Algorithm 3. As discussed in Sect. 3.2, this can be done by alternating between an estimation of the flux of the exoplanet and of the statistics of the background7. The resulting estimate  for a source located at ϕtℓ = ℱtℓ(ϕ0) on the frame tℓ (ℓ = 1 : T) corresponds to the minimum of the following cost function:
for a source located at ϕtℓ = ℱtℓ(ϕ0) on the frame tℓ (ℓ = 1 : T) corresponds to the minimum of the following cost function:
fast PACO detection – Fast computation of the S/N values at initial 2D angular positions 𝒢 of an unresolved source.
Input: Uniform grid 𝒢 of 2D angular positions.
Input: Spatio-temporal dataset {rθkℓ,tℓ} k = 1:N,ℓ = 1:T.
Output: S/N map at all initial positions in 𝒢.
▹ Step 1. Precompute terms:
forall ϕ0 𝒢 do
▹Step 1a. Build the collection of patches centered at ϕ0:
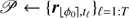
▹ Step 1b. Learn the corresponding background statistics and pre-compute terms:
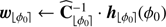
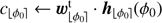
for 𝓁 = 1: T do
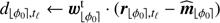
▹ Step 2. Compute the S/N values:
forall ϕ0 ∈ 𝒢 do
a ← 0
b ← 0
for 𝓁 = 1 : T do

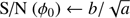 (Eq. (24))
(Eq. (24))
in which Wi, j = 1 if i = j,  elsewhere, {i, j}∈⟦1; K⟧2, ⊙ stands for entrywise multiplication (i.e., Hadamard product), and
elsewhere, {i, j}∈⟦1; K⟧2, ⊙ stands for entrywise multiplication (i.e., Hadamard product), and  . The expression of 𝒞(α) in Eq. (30) comes from the co-log-likelihood under a Gaussian assumption, where matrix W is introduced in order to bias the covariance estimate toward a diagonal covariance (i.e., in order to replace the maximum likelihood covariance estimate given by the sample covariance with the shrinkage estimator described in Sect. 3.2).
. The expression of 𝒞(α) in Eq. (30) comes from the co-log-likelihood under a Gaussian assumption, where matrix W is introduced in order to bias the covariance estimate toward a diagonal covariance (i.e., in order to replace the maximum likelihood covariance estimate given by the sample covariance with the shrinkage estimator described in Sect. 3.2).
Figure 7 illustrates the cost function 𝒞(α) that is minimized by our alternating estimation scheme. This cost function is unimodal in the tested range of contrasts (from 5 × 10−6 to 10−1) indicating that PACO estimation procedure would also correctly characterize exoplanets having a rather high flux. The minimum of the cost function is located near the correct value ( ) with a discrepancy in agreement with the standard deviation
) with a discrepancy in agreement with the standard deviation  . Minimizing 𝒞(α) therefore yields an unbiased estimator of the flux. In practice, to minimize 𝒞(α), we followed the alternating scheme in Eqs. (13) which is easily implementable and converges within a few iterations (see Sect. 5.3). Our method for an unbiased estimation of the flux is summarized in Algorithm 3.
. Minimizing 𝒞(α) therefore yields an unbiased estimator of the flux. In practice, to minimize 𝒞(α), we followed the alternating scheme in Eqs. (13) which is easily implementable and converges within a few iterations (see Sect. 5.3). Our method for an unbiased estimation of the flux is summarized in Algorithm 3.
PACO estimation – Unbiased estimation of the flux 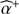 of an unresolved source at initial 2D angular position ϕ0.
of an unresolved source at initial 2D angular position ϕ0.
Input: 2D angular position ϕ0 of source at t0.
Input: Spatio-temporal dataset {rθkℓ,tℓ} k = 1:N,ℓ = 1:T.
Input: Optional initial estimate  by default.
by default.
Input: Relative precision ϵ ϵ (0, 1).
Output: Estimated flux  of the source.
of the source.
⊳ Alternated estimation 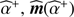 and
and 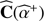 :
: 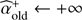
While 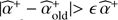 do
do
a ← 0
b ← 0
For ℓ 1 : T do
⊳ step 1 Build the collection of patches:
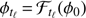
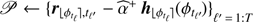
⊳ Step 2 Learn the background statistics:
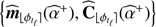 (Eq. (13))
(Eq. (13))
⊳ Step 3 Update the flux terms â+
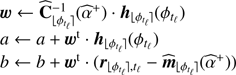
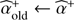
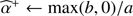 (Eq. (14))
(Eq. (14))
Jointly to the refining of the flux estimation, the source location is also improved by testing subpixel locations on a refined grid around the location provided by PACO detection. The step size of this refined grid can be set according to the Cramér-Rao lower bound established in Sect. 3.6.3 so that the grid bias is negligible compared to the theoretical localization standard deviation.
4.3. Sampling of possible exoplanet locations
The physical position ϕ of an unresolved source may not exactly correspond to a sample of the data, i.e., a pixel θk. To deal with this, in PACO, we consider patches centered at the nearest pixel ⌊ϕtℓ⌉ of the source position ϕtℓ = ℱtℓ(ϕ0) in frame tℓ when it is assumed to be initially at ϕ0. This means that patches are not exactly centered at the source position ϕtℓ with a potential loss of optimality. However, we expect that this loss be small because the pixel size is usually chosen to be much smaller than the diffraction limit (Beuzit et al. 2008). There is another issue related to the sampling because the detection is carried out on maps with necessarily a finite resolution for the assumed initial position ϕ0. One can expect a negative bias for the S/N: the further the detected position in the criterion map to the actual source position, the worse the value of the criterion. The faintest sources may be undetected because of this bias. Fortunately, the direct model in Eq. (1) assumed by PACO does not impose any finite precision for the source position ϕtℓ in each frame, so detection maps can be computed at a resolution small enough to avoid the problem. To limit the computational burden, one would however like to use a somewhat coarse sampling for the detection map. There is a trade-off to find and, in this section, we attempted to evaluate the S/N bias caused by a given sampling of the detection map. We assumed that the detection map is computed for initial positions on an uniformly sampled grid 𝒢s defined by: (31)
(31)
where (i1, i2) stand for the two components of 2D angular positions, Δ is the pixel size in the data, s is a chosen sub-sampling factor and Θ is the angular area where to perform the detection.
The ratio 𝔼(S/N(𝒢s(ϕ0) | ϕ0))/𝔼(S/N(ϕ0 | ϕ0)) informs about the fraction of S/N lost due to the sampling grid 𝒢s under consideration, with 𝒢s(ϕ0) = arg minϕ ∈ 𝒢s∥ϕ − ϕ0∥2. The expected value of the S/N under the ℋ1 hypothesis at any angular position θ = 𝒢s(ϕ0) knowing that the exoplanet is initially located at ϕ0
 (32)
(32)
In practice, this expectation ratio is evaluated in the most unfavorable case for the considered grid, that is to say when the exoplanet is exactly located between two adjacent grid nodes. Figure 8 gives a map of the ratio 𝔼(S/N(𝒢s(ϕ0) | ϕ0))/𝔼(S/N(ϕ0 | ϕ0)) for a uniform grid with sampling size Δ/s for s ∈ {1/4, 1/2, 1, 2, 4} and Δ the pixel size of the data. We note that values of s smaller than one correspond to a downsampling of the data pixels, while values greater than one correspond to an upsampling of the pixels. Figure 8 em-phasizes that the choice s = 1 (corresponding to a calculation of the detection criteria in each pixel of the data) generates values of the ratio 𝔼(S/N(𝒢s(ϕ0) | ϕ0))/𝔼(S/N(ϕ0 | ϕ0)) between 0.91 and 0.97. The maximum loss is less than 10% on the S/N values when the exoplanet is exactly located between two pixels. The choice s = 4 ensures a maximum loss on the value of the S/N lower than 0.7% at any point of the field of view at the price of a computational cost of the algorithm multiplied by a factor 16. On the opposite, the choice s = 1/2, reduces the computational cost of the algorithm by a factor of four at the price of a maximum potential loss between 10 and 30% (depending on the position in the field of view) on the S/N values if the exoplanet is located exactly between two pixels defined by the sampling grid under consideration. Table 2 summarizes the impact of the choice of the sampling factor s on the maximum expected S/N reduction and the computation time.
 |
Fig. 8. Effect of the sampling grid on S/N: ratio 𝔼(S/N(𝒢s(ϕ0) | ϕ0)/𝔼(S/N(ϕ0 | ϕ0)) for s ∈ {1/4, 1/2, 1, 2, 4} computed on the HIP 72192 dataset at λ1 = 2.110 μm. It informs about the maximum expected reduction in S/N if the exoplanet is not exactly centered on a pixel of the sampling grid. |
Influence of the sampling factor s on the S/N and on the computation time.
5. Performance on VLT/SPHERE-IRDIS data
The performance of PACO is evaluated on three datasets acquired at the VLT by the SPHERE-IRDIS instrument8 using the dual band filters K1 and K2. Two of these datasets are derived from observations of the HD 131399 system located in the Upper Centaurus Lupus association (De Zeeuw et al. 1999; Rizzuto et al. 2011; Pecaut & Mamajek 2013). The center young star of A1V-type forms a triple system with two other K- and G-type stars located at a projected distance of about 3 arcsec (Dommanget & Nys 2002; Houk & Smith-Moore 1988) from the central star. An exoplanet candidate has been recently detected at a projected distance of about 0.83 arcsec from the central star (Wagner et al. 2016). However, more recent observations made it possible to refine the reconstruction of the spectrum of the candidate companion and its astrometry. This new information proved to be incompatible with the bound exoplanet hypothesis. It has been shown that it is more likely to be a background brown dwarf (Nielsen et al. 2017). Both datasets provide observations up to about 5.5 arcsec. To illustrate the performance of the PACO algorithm, we display a region approximately 1.7 arcsec of radius, centered around the star A of the triple system, in order to limit the impact of the other two stars of the system. The dataset from the first epoch (2015 – ESO program 095.C-0389) was acquired under average observational conditions and we selected 92 temporal frames taken with a detector integration time of 16 s (total exposure of 24 min) associated with a total apparent rotation of the field of view of 36.71°. The dataset from the second period (2016 – DDT program 296.C-5036) was acquired under good observational conditions, but it only consists in 56 selected temporal frames taken with a detector integration time of 32 s (total exposure of 30 min) associated with a total apparent rotation of the field of view of 39.51°. In order to also illustrate the performance of the PACO algorithm on the whole field of view offered by the VLT/SHPERE-IRDIS instrument, we also consider a dataset from the observation of the A0-type star HIP 72192 (HD 129791) hosting two confirmed faint point sources. The considered epoch was acquired under average observational conditions under the 2015 – ESO program 095.C-0389 and consists in 96 temporal frames taken with a detector integration time of 16 s (total exposure of 24 min) associated with a total apparent rotation of the field of view of 17.28°.
The performances of the PACO algorithm are compared in terms of detection maps and contrast curves obtained with the two current cutting-edge algorithms TLOCI (Marois et al. 2013) and KLIP (PCA; Soummer et al. 2012) implemented in the SpeCal pipeline reduction tool (Galicher et al. 2018) whose principles were briefly described in Sect. 2. The SpeCal pipeline also offers the possibility to apply an unsharp filter after the speckle removal algorithm to improve the visual quality of the reduction map, reduce the pollution of the stellar leakages and artificially increase the S/N of the detected point source objects. We note that it is expected that this post-processing partially deteriorates the statistical properties of the resulting detection maps. The performances of PACO are compared to the processing standard algorithms TLOCI and KLIP both with and without unsharp filtering. As explained in Sect. 4.2, with PACO no post-processing is applied on the data nor on the reduction maps other than the conventional data reduction pipeline described in Sect. 3. We also compared PACO in terms of detection capabilities with the recent and emerging algorithm LLSG (Gonzalez et al. 2016) using the VIP reduction pipeline (Gonzalez et al. 2017). The parameters of the different algorithms used are manually tuned to provide the best results.
5.1. Detection maps
Figure 9 shows S/N maps computed with PACO, TLOCI and KLIP algorithms on the HD 131399 (2015) dataset at λ1 = 2.110 μm. When setting a threshold of S/N ≥ 5 on PACO detection map, only one detection is obtained and this detection corresponds to the faint point source already detected by the other authors. Setting the same threshold on the S/N detection maps produced by TLOCI and KLIP algorithms lead to several false detections. In the case of TLOCI, there are seven S/N values larger than that of the real source, leading to seven false detections. An eighth false detection is obtained due to a local maximum above the threshold S/N = 5. With the KLIP algorithm, there are two detections corresponding to local maxima above the threshold S/N = 5 but these are all false detections located close to the coronographic mask. The faint point source is not detected with an S/N larger than five and would be detected only by lowering the threshold below S/N = 4.3. By limiting the amount of signal subtraction, PACO achieves the largest S/N value for the real faint point source (S/N = 8.6, to compare with TLOCI: S/N = 6.5 and KLIP: S/N = 4.3). The second local maxima derived from the PACO S/N is at S/N = 3.6, which illustrates the ability of PACO to distinguish without ambiguity the faint point source. Moreover, in the absence of sources, the S/N map is stationary and false alarms are well controlled: the PFA when the S/N threshold τ is fixed at five is close to the theoretical value of 2.87 × 10−7: no false alarm are obtained at this threshold in the region of interest. It can be observed that both TLOCI and KLIP have nonstationary detection maps in the absence of source and the probability of false alarms at the S/N threshold of five is much larger than the theoretical value of 2.87 × 10−7. Hence, the detection threshold must be set manually on these detection maps to prevent false detections, or the numerous false detections must be discarded by analyzing follow-up observations.
 |
Fig. 9. S/N maps computed with the PACO, TLOCI and KLIP algorithms on the HD 131399 (2015) dataset at λ1 = 2.110 μm. A common threshold at S/N = 5 is applied to defined the detections. A known faint source is present in the field of view. It is identified by a pink circle. |
In order to better evaluate the performance of PACO, we also turned to the injection of fake exoplanets on the HIP 72192 dataset at different angular separations. We have injected 30 fake companions spread on five angular separations at competitive levels of contrast as summarized in Table 3. The considered level of injection approximately corresponds to a detection at mean S/N = 5 using PACO detection Algorithm 1. As discussed previously, the dataset also contains two real faint point sources. Figure 10 shows S/N maps computed with the PACO, TLOCI, KLIP and LLSG algorithms. For TLOCI and KLIP, post-processing by unsharp filtering is also considered. For LLSG, since the resulting S/N depends on the threshold used during the decomposition, the S/N is not statistically grounded. As a result, we have multiplied the signed S/N by a factor 25 to be in a range comparable to the other methods. For this algorithm, we have also performed the detection by discarding a centered circular area of 1 arcsec of radius since the detection seems to be very difficult near the host star. For each reduction map, the S/N of the 60 largest local maxima is given in decreasing order on the same figure. As expected, the S/N maps from PACO are stationary, robust to defective pixels (which have led to aberrant data on a wider scale than one pixel in the science images) and to strong stellar leakages on some frames due to a small decentering of the coronagraph.
Angular separation and contrast of the injected fake sources on the HIP 72192 dataset at λ1 = 2.110 μm.
 |
Fig. 10. S/N maps computed with the PACO, TLOCI, KLIP and LLSG algorithms. For TLOCI and KLIP, an unsharp filtering applied to S/N maps as post-processing is also considered. For LLSG, the resulting signed S/N is multiplied by a factor of 25 to fall within a comparable range than the other methods. For this latest algorithm, detection is in addition performed by discarding a centered circular area of 1 arcsec in radius. The first 32 detections are marked on each S/N map using square patterns. The 60 first detections are plotted as bar charts below each S/N map, ordered by decreasing S/N values, with true detections in pink (true background sources) or blue (injected fake sources), and false detections in red. Circles indicate the location of the real and injected faint point sources. PACO is the only algorithm capable of detecting correctly all sources without any false detection. |
The S/N maps derived from PACO are statistically grounded, allowing to be directly interpreted in terms of PFA without resorting to injections of fake companions via Monte Carlo simulations. It is clearly not the case for TLOCI which seems very sensitive to defective pixels and to large stellar leakages. KLIP performs better than TLOCI but it also produces nonstationary detection maps, particularly on the northeastern area. This area has been identified with PACO as an area where the detection of exoplanets is more difficult (see the contrast map on the last row, first column, in Fig. 14). Since PACO locally learns the background fluctuations, the aberrant data or the larger stellar leakages can also be learned locally as typical background fluctuations and are not interpreted in the detection stage as the signature of an exoplanet. The unsharp filtering applied on the detection maps from TLOCI and KLIP improves their visual quality since areas with large S/N values due to the stellar leakages are largely attenuated, but the detection performance of these algorithms are not significantly improved by this post-processing. LLSG outperforms KLIP far from the host star but the detection maps from LLSG are clearly not statistically grounded since the LLSG decomposition is also coupled with an entry-wise thresholding. As a result, the S/N derived from LLSG depends on the choice of the threshold used during the decomposition. A high threshold eliminates a large part of the noise (with the risk of also eliminating faint signals from exoplanets) and artificially increases the S/N of the detected objects. Moreover, the detection of exoplanets near the host star seems to be very difficult based on the LLSG results since the signatures from fake exoplanets are visible but are at the level of false alarms and cannot be easily retrieved by a visual inspection. Finally, only PACO detects with S/N ≥ 5 the faintest real point source in the field of view.
Additional detection results are presented in Appendix C where fake exoplanets with a higher flux α are injected in the data at the same locations. These complementary results illustrate that, with larger fluxes, all algorithms detect more sources. At these larger fluxes, PACO detects the fake planets with significantly larger S/N values than the other algorithms and the gap between the last true detection and the first false alarm is improved.
Figure 11 summarizes the performance of the tested algorithms on the HIP 72192 dataset via receiver operating characteristics (ROC). ROC curves represent the true positive rate (TPR) as a function of the false detection rate. Since the false detection rate cannot be easily assessed, the TPR is represented as a function of the number of false detections (represented in log scale). As discussed in Gonzalez et al. (2017), this type of representation is very useful to evaluate and compare the performance of exoplanet hunter algorithms. This figure highlights that PACO is the only tested algorithm able to detect both the injected fake exoplanets and the real faint sources without false alarms, thereby outperforming TLOCI, KLIP and LLSG algorithms.
 |
Fig. 11. ROC curves showing the true positive rate (fraction of sources correctly detected) as a function of the number of false alarms (i.e., false detections) for each detection map. Values displayed on each curve correspond to the detection threshold used. |
Figure 12 gives the S/N maps computed with the fast version of PACO on the HD 131399 (2015) and HIP 72192 datasets at λ1 = 2.110 μm without injected fake exoplanet. It can be noted that the PACO Algorithm 1 and its fast version (Algorithm 2) lead to very similar detection maps. A low-pass effect is observed on maps derived from fast PACO due to the approximations made (see Sect. 4.2). Although the real faint point sources present in the data are detected with slightly lower values of S/N (reduction in S/N less than 5%) with the fast PACO algorithm, they remain detectable without ambiguity for a conventional detection threshold of τ = 5.
 |
Fig. 12. S/N maps computed with the fast version of PACO on the HD 131399 (2015) and HIP 72196 dataset at λ1 = 2.110 μm. Detections over the S/N threshold of five are shown, they correspond to known background faint point sources. |
5.2. Contrast curves and detection statistics
This section is devoted to the quantitative evaluation of the performance of PACO via contrast curves and contrast maps. For a given probability of false alarm PFA (hence, a given detection threshold τ), the contrast represents the minimum flux (normalized to the host star flux) that a source must have to be detected by the algorithm with a probability of detection PD. Throughout this section, we consider a target probability of false alarm of 2.87 × 10−7 reached when thresholding the S/N detection maps at τ = 5. The resulting contrast is conventionally referred as “contrast at 5 σ” in the literature. Since the statistical distribution of the S/N is well controlled with PACO (see discussion in Sect. 3.6.1), the probability of false alarm and probability of detection can be predicted at each location ϕ0 based on the local statistics  and
and  using Eq. (27). The resulting contrast is however a lower bound since it would only be achievable with exact knowledge of the local statistics
using Eq. (27). The resulting contrast is however a lower bound since it would only be achievable with exact knowledge of the local statistics  and
and  . Given that these local mean and covariance must be estimated in the presence of a source, the actual achievable contrast is higher (i.e., worse). Hence, theoretical curves/maps are referred to as “PACO oracle” (achievable should an oracle provide the background statistics
. Given that these local mean and covariance must be estimated in the presence of a source, the actual achievable contrast is higher (i.e., worse). Hence, theoretical curves/maps are referred to as “PACO oracle” (achievable should an oracle provide the background statistics  and
and  , even in Monte Carlo sithe presence of a source). To assess the actual detection performance of the algorithm, we computed, based on Monte Carlo simulations, the contrast required to detect sources with a probability of detection of 50% when applying a threshold at τ = 5. These contrasts are referred to simply as “PACO” in the curves displayed in the following figures.
, even in Monte Carlo sithe presence of a source). To assess the actual detection performance of the algorithm, we computed, based on Monte Carlo simulations, the contrast required to detect sources with a probability of detection of 50% when applying a threshold at τ = 5. These contrasts are referred to simply as “PACO” in the curves displayed in the following figures.
We first illustrate that the lower bound on the achievable contrast (as reached by “PACO oracle”) obtained using Eq. (27) are correct. Figure 13 displays the contrast curve as a function of the angular separation on the HIP 131399 (2015) dataset at λ2 = 2.251 μm. The theoretical contrast map for PACO oracle as obtained from Eq. (27) is radially averaged to obtain a curve of contrast as a function of the angular separation between the source and the host star. Two curves are drawn corresponding to probabilities of detection equal to 50% and 80%. Superimposed to these curves, Monte Carlo simulation results show the contrast necessary to achieve the targeted probabilities of detection in “oracle mode”, that is, when the statistics of the background are computed on data with no injected source. These contrasts are in good match with the theoretical curves which validates the use of (Eq. (27)) to compute this contrast lower-bound. Figure 14 gives the maps of contrast for a probability of detection PD = 50% obtained with PACO oracle on the HD 131399 (2015), HD 131399 (2016) and HIP 72192 datasets, at λ1 = 2.110 μm and λ2 = 2.251 μm. As expected, this contrast improves when the angular separation increases since the stellar leakages decrease farther from the star. Figure 14 emphasizes that some local areas are less favorable than others for the detection of low-flux exoplanets, because the spatial structures of the background fluctuations may be mis-interpreted as low-flux sources. For example, the contrast is locally higher in the northeastern area of the HIP 72192 dataset at λ1 = 2.110 μm. This explains the difficulties of current algorithms in this area as emphasized in Sect. 5.1. While other algorithms suffer from an increased false detection rate in these areas (due to a lack of local adaptivity of the methods), PACO has a constant false alarm rate. Only the probability of detection is decreased is these more difficult regions, as expected.
 |
Fig. 13. Contrast curves obtained with PACO: comparison between predictive contrast map from PACO derived from Eq. (27) (denoted as “PACO (oracle)”) radially averaged and Monte Carlo simulations (denoted as “PACO (oracle Monte Carlo)”) by injection of fake exoplanets on the HD 131399 (2015) dataset at λ2 = 2.251 μm. The two cases are considered with absence of exoplanet during the learning of the statistics of the background (oracle mode). |
 |
Fig. 14. Contrast maps for a probability of detection PD = 50% obtained with PACO for HD 131399 (2015), HD 131399 (2016) and HIP 72192 datasets at λ1 = 2.110 μm and λ2 = 2.251 μm. |
We now investigate the actual performance of PACO (i.e., without oracle knowledge of the background statistics). The statistics of the background are impacted by the presence of the exoplanet which decreases the S/N (and hence increases the required contrast to achieve the same probability of detection than in oracle mode). Figure 15 shows contrast curves derived from PACO oracle (i.e., using Eq. (27)) and PACO (as obtained by Monte Carlo, i.e., actual contrasts). It emphasizes that PACO oracle gives a reliable approximation of the achievable contrast far from the host star (at angular separations larger than 2 arcsec). At smaller angular separations, PACO oracle over-estimates the achievable contrast because it neglects the impact of the source signal when computing background statistics. At these small angular separations, the motion of the source is limited which makes background contamination by the source non-negligible. In these cases, resorting to Monte Carlo simulations is thus necessary to obtain an accurate estimation of the achievable contrast. Superimposed to these curves, we give the contrast curves provided by TLOCI and KLIP algorithms. These latter curves must however be analyzed with care. S/N maps computed on the dataset in which we injected fake sources (Fig. 10) indeed illustrated that thresholding at S/N = 5 the detection maps of TLOCI and KLIP leads to numerous false alarms (many more than expected if the detection map were distributed according to a standard Gaussian distribution in the absence of source). The contrast curves provided therefore correspond to a different probability of false alarm rate that is not constant in the field of view and that is very favorable to these algorithms. These curves therefore cannot be directly compared to those drawn for PACO. The actual difference between the minimal contrast for source detection with PACO and TLOCI or KLIP would be much larger should the same false alarm rate be considered.
 |
Fig. 15. Contrast curves derived from PACO, TLOCI and KLIP for a probability of detection PD ∈ {50%;80%} at λ1 = 2.110 μm and λ2 = 2.251 μm for the HD 131399 (2015), HD 131399 (2016) and HIP 72192 datasets respectively. Contrast curves as provided by KLIP and TLOCI do not correspond to a 5σ false alarm rate contrarily to the contrast curves of PACO. The achievable contrasts are thus significantly over-optimistic for KLIP and TLOCI, see discussion in the text (Sect. 5.2). |
5.3. Photometric accuracy
This section is devoted to the analysis of the capability of PACO to correctly estimate the flux α of a detected source. As explained in Sects. 3.2 and 4.2, the estimation pipeline of PACO is very similar to the PACO algorithm used for detection. The main difference lies in the joint estimation of the flux of the source and the background statistics to prevent from under-estimating the flux of the source. To evaluate the photometric performance of PACO at different angular separations, we performed the following numerical experiment: we injected fake exoplanets with contrast decreasing with the angular separation (see Table 3). For each angular separation, 50 different injections (at different known locations in the field of view) were performed and each time the flux was estimated at those known locations using PACO estimation Algorithm 3. Table 4 reports the mean estimated flux  , the bias and the photometric standard deviation relative to the source flux. It shows that the bias is negligible compared to the standard deviation, at all angular separations. Additional results are given in Appendix C, illustrating that the standard deviation depends on the source location (some areas are more favorable than others) but not on the source amplitude, as expected from the theoretical study, see Eq. (20).
, the bias and the photometric standard deviation relative to the source flux. It shows that the bias is negligible compared to the standard deviation, at all angular separations. Additional results are given in Appendix C, illustrating that the standard deviation depends on the source location (some areas are more favorable than others) but not on the source amplitude, as expected from the theoretical study, see Eq. (20).
Photometric accuracy evaluated by Monte Carlo simulation with 50 injections of fake sources for each angular separation, on the HIP 72192 dataset at λ1 = 2.110 μm.
Figure 16 gives the estimated flux  as the function of the number of iteration with the PACO estimation Algorithm 3 for the three known faint point sources. They show that the iterative estimation scheme converges within a few iterations. Figure 17 gives the local maps of the estimated flux at λ1 = 2.110 μm for the two real faint sources around the HIP 72192 star as well as for the known point source of the HD 131399 (2015) dataset. The estimated flux is compared to the estimated flux obtained without performing an alternate estimation between the flux and the statistics of the background. For the two considered cases, the estimation is performed with a sampling corresponding to the data pixel grid (i.e., sampling factor s = 1) and with a subpixel sampling (sampling factor s = 4). The flux of the objects (and the S/N values) are also significantly under-estimated if the estimation of the flux is not alternated with the estimation of the background statistics. This shows that both (i) the location refinement and (ii) the joint estimation of the source flux and of the background statistics are required to obtain an accurate estimate of fluxes.
as the function of the number of iteration with the PACO estimation Algorithm 3 for the three known faint point sources. They show that the iterative estimation scheme converges within a few iterations. Figure 17 gives the local maps of the estimated flux at λ1 = 2.110 μm for the two real faint sources around the HIP 72192 star as well as for the known point source of the HD 131399 (2015) dataset. The estimated flux is compared to the estimated flux obtained without performing an alternate estimation between the flux and the statistics of the background. For the two considered cases, the estimation is performed with a sampling corresponding to the data pixel grid (i.e., sampling factor s = 1) and with a subpixel sampling (sampling factor s = 4). The flux of the objects (and the S/N values) are also significantly under-estimated if the estimation of the flux is not alternated with the estimation of the background statistics. This shows that both (i) the location refinement and (ii) the joint estimation of the source flux and of the background statistics are required to obtain an accurate estimate of fluxes.
 |
Fig. 16. Estimated flux as the function of the number of iterations of PACO estimation Algorithm 3 for the three known faint point sources (FPS) of the HIP 72192 and HD 131399 (2015) datasets. |
 |
Fig. 17. Local S/N maps and estimated flux at λ1 = 2.110 μm around the known real faint point sources (FPS1 and FPS2) located around the HIP 72192 star and the known real faint point source (FPS3) located around the HD 131399 system. Panel a: S/N of detection derived from PACO detection Algorithm 1. Panel b: estimated flux derived from PACO detection Algorithm 1. Panel c: estimated flux derived from PACO estimation algorithm alternating between the estimation of the flux and the computation of the background statistics. Panels e, d, f: Respectively correspond to panels a, b, c computed on a subpixel grid with a sampling factor s = 4. The superimposed white grid represents the original sampling grid (sampling factor s = 1). |
6. Conclusion
This paper presents a new method (PACO) dedicated to exoplanet detection in angular differential imaging. PACO differs from the existing methods in its local modeling of the background statistics that captures together the average speckles and the spatial correlations. The decision in favor of the presence or absence of an exoplanet is made by a binary hypotheses test. Since no image subtraction is performed, photometry is well preserved by the method. PACO is completely parameter-free, from the computation of a detection map to its thresholding to extract meaningful detections and the estimation of fluxes of the detected sources. We believe that this is a significant advantage to obtain consistent performances and deploy the method in large exoplanet surveys.
PACO is statistically grounded so that the false alarm rate, the probability of detection and the contrast can be assessed without necessarily resorting to Monte Carlo methods. Since the performance of the detection and estimation method is theoretically well understood, it paves the way to the co-design of the next generation of instruments for exoplanet detection, the instrumental design and/or observation planning being easily related to detection performances through the predicted contrast and photometric or astrometric accuracies.
We showed using three datasets from the VLT/SPHERE-IRDIS instrument that the proposed method achieves significantly better detection performance than current cutting-edge algorithms such as TLOCI and KLIP-PCA as well as the recent and emerging algorithm LLSG. The detection maps are robust to defective pixels and other aberrant data points arising during the SPHERE observations or data pre-processing pipeline. The detection maps obtained using PACO also have a stationary behavior even in the vicinity of the host star. A joint processing of data from different wavelengths can further improve the detection maps and push down the detection limit but requires some refinements that will be developed in a future paper.
Acknowledgments
This work has been supported by the CNRS through Défi Imag’In project RESSOURCES. This work has made use of the SPHERE Data Center, jointly operated by Osug/Ipag (Grenoble, France), Pytheas/Lam/Cesam (Marseille, France), OCA/Lagrange (Nice, France) and Observatoire de Paris/Lesia (Paris, France).
References
- Absil, O., Milli, J., Mawet, D., et al. 2013, A&A, 559, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allard, F., Guillot, T., Ludwig, H.-G., et al. 2003, IAU Symp., 211, 325 [Google Scholar]
- Allard, F., Allard, N. F., Homeier, D., et al. 2007, A&A, 474, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2008, Proc. SPIE, 7014, 701418 [Google Scholar]
- Bonavita, M., Daemgen, S., Desidera, S., et al. 2014, ApJ, 791, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Marley, M., Hubbard, W., et al. 1997, ApJ, 491, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Cantalloube, F. 2016, PhD Thesis, Université Grenoble Alpes, France [Google Scholar]
- Cantalloube, F., Mouillet, D., Mugnier, L., et al. 2015, A&A, 582, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Chauvin, G., Desidera, S., Lagrange, A.-M., et al. 2017, A&A, 605, L9 [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y., Wiesel, A., Eldar, Y. C., & Hero, A. O. 2010, IEEE Trans. Signal Process., 58, 5016 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Debes, J., & Rodigas, T. J. 2012a, ApJ, 760, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Fukagawa, M., Thalmann, C., Matsumura, S., & Plavchan, P. 2012b, ApJ, 755, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Delorme, P., Meunier, N., Albert, D., et al, 2017, in SF2A Proceedings, eds. C. Reyléet al., 347 [Google Scholar]
- Devaney, N., & Thiébaut, É. 2017, MNRAS, 472, 3734 [NASA ADS] [CrossRef] [Google Scholar]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Dohlen, K., Langlois, M., Saisse, M., et al. 2008a, Proc. SPIE, 7014, 70143L [Google Scholar]
- Dohlen, K., Saissea, M., Orignea, A., et al. 2008b, Proc. SPIE, 7018, 701859 [CrossRef] [Google Scholar]
- Dommanget, J., & Nys, O. 2002, VizieR Online Data Catalog: I/274 [Google Scholar]
- Galicher, R., Boccaletti, A., Mesa, D., et al. 2018, A&A, 615, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, C. G., Absil, O., Absil, P.-A., et al. 2016, A&A, 589, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, C. A. G., Wertz, O., Absil, O., et al. 2017, AJ, 154, 12 [CrossRef] [Google Scholar]
- Houk, N., & Smith-Moore, M. 1988, Michigan Catalogue of Two-dimensional Spectral Types for the HD Stars. Vol. 4 [Google Scholar]
- Kay, S. M. 1998a, Fundamentals of Statistical Signal Processing. Vol. 2: Detection Theory (Upper Saddle River, NJ: Prentice Hall) [Google Scholar]
- Kay, S. M. 1998b, Fundamentals of Statistical Signal Processing. Vol. 1: Estimation Theory (Upper Saddle River, NJ: Prentice Hall) [Google Scholar]
- Kay, S., & Eldar, Y. C. 2008, IEEE Signal Process. Mag., 25, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Kendall, M. G., Stuart, A., & Ord, J. K. 1948, The Advanced Theory of Statistics, Vol. 1 (JSTOR) [Google Scholar]
- Lafreniere, D., Marois, C., Doyon, R., Nadeau, D., & Artigau, E. 2007, ApJ, 660, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A.-M., Gratadour, D., Chauvin, G., et al. 2009, A&A, 493, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ledoit, O., & Wolf, M. 2004, J. Multivariate Anal., 88, 365 [CrossRef] [Google Scholar]
- Lilliefors, H. W. 1967, J. Am. Stat. Assoc., 62, 399 [CrossRef] [Google Scholar]
- Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, Proc. Natl. Acad. Sci., 111, 12661 [Google Scholar]
- Macintosh, B., Graham, J., Barman, T., et al. 2015, Science, 350, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Maire, A., Langlois, M., Dohlen, K., et al. 2016, Proc. SPIE, 9908, 990834 [CrossRef] [Google Scholar]
- Marois, C., Lafreniere, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Marois, C., Correia, C., Véran, J.-P., & Currie, T. 2013, Proc. IAU, 8, 48 [CrossRef] [Google Scholar]
- Marois, C., Correia, C., Galicher, R., et al. 2014, Proc. SPIE, 9148, 91480U [CrossRef] [Google Scholar]
- Mawet, D., Riaud, P., Baudrand, J., et al. 2006, A&A, 448, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mugnier, L. M., Cornia, A., Sauvage, J.-F., et al. 2009, J. Opt. Soc. Am. A, 26, 1326 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, E. L., De Rosa, R. J., Rameau, J., et al. 2017, AJ, 154, 218 [Google Scholar]
- Pavlov, A., Möller-Nilsson, O., Feldt, M., et al. 2008, Proc. SPIE, 7019, 701939 [CrossRef] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, A&AS, 208, 9 [Google Scholar]
- Racine, R., Walker, G. A., Nadeau, D., Doyon, R., & Marois, C. 1999, PASP, 111, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Rizzuto, A., Ireland, M., & Robertson, J. G. 2011, MNRAS, 416, 3108 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffio, J.-B., Macintosh, B., Wang, J. J., et al. 2017, ApJ, 842, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C. 2008, New Astron. Rev., 52, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, I., Ferrari, A., & Carbillet, M. 2009, IEEE Trans. Signal Process., 57, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Soulez, F., Denis, L., Fournier, C., Thiébaut, É., & Goepfert, C. 2007, J. Opt. Soc. Am. A, 24, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R. 2004, ApJ, 618, L161 [Google Scholar]
- Soummer, R., Pueyo, L., & Larkin, J. 2012, ApJ, 755, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Thiébaut, E., & Mugnier, L. 2005, Proc. IAU, 1, 547 [CrossRef] [Google Scholar]
- Thiébaut, É., Devaney, N., Langlois, M., & Hanley, K. 2016, Proc. SPIE, 9909, 99091R [CrossRef] [Google Scholar]
- Traub, W. A., & Oppenheimer, B. R. 2010, Exoplanets, 111 [Google Scholar]
- Vigan, A., Moutou, C., Langlois, M., et al. 2010, MNRAS, 407, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, K., Apai, D., Kasper, M., et al. 2016, Science, 353, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Cieza, L. A., Mawet, D., et al. 2015, A&A, 581, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ygouf, M. 2012, PhD Thesis, Université Grenoble Alpes, France [Google Scholar]
Appendix A:
Estimation of the local patch covariance
Several estimators of the covariance have been considered to characterize the multivariate Gaussian model of a background patch, at a given location θk. There are two aspects that must be considered when selecting an appropriate estimator: (i) observed patches not only contain the background, but possibly also signal from an exoplanet, and (ii) there are few observations (the number of time frames T is typically between a few tens and a hundred) compared to the number of parameters to estimate in the covariance matrix (K(K + 1)/2 ∼ 103 parameters, with K ∼ 50 the number of pixels in a patch). In this appendix, we discuss and compare several alternatives to address these two issues.
The problem of the superimposition of background and exoplanet signals can be handled by several ways, given that, because of the apparent motion of the field of view, an exoplanet is not visible at the same location throughout the temporal stack. A first strategy consists in discarding patches where an hypothetical exoplanet located at ϕ0 would be visible. A second strategy is to discard patches that are the most correlated with the off-axis PSF (i.e., patches that most likely contain an exoplanet). Another solution is to use robust estimators in which the exoplanet signal being considered as an outlier (as in LLSG, see Gonzalez et al. 2016). A finer solution consists in jointly estimating the flux of the exoplanet and the statistics of the background.
All these methods have been compared and we found the last approach to be the most successful. Approach 1 has a significant drawback: by excluding (during the learning of background statistics) all patches that are later considered in the exoplanet detection test (Eq. (24)), the test becomes much noisier. Approach 2 is more satisfactory in this respect, but does not completely solve the problem: estimation of the flux of an exoplanet is biased due to the errors in the estimation of parameters cmk and bCk. Approach 3 based on robust estimators can be implemented in several ways. We considered replacing the sample mean by the median and a two-step estimation of the covariance, where, in the second step, patches rθk leading to large Mahalanobis distances  were discarded in the computation of the covariance matrix. Only the last approach based on a joint estimation of the exoplanet flux and the background statistics led to truly unbiased estimates of the photometry in our numerical experiments.
were discarded in the computation of the covariance matrix. Only the last approach based on a joint estimation of the exoplanet flux and the background statistics led to truly unbiased estimates of the photometry in our numerical experiments.
The second aspect, namely, the lack of observations on which to base the estimation of the covariance, requires the use of estimators with controlled variance. Indeed, the sample covariance estimator  defined in Eq. (8) has a variance that is too large. When the number of time frames T is smaller than the number K of pixels in a patch,
defined in Eq. (8) has a variance that is too large. When the number of time frames T is smaller than the number K of pixels in a patch,  is moreover rank-deficient and cannot be inverted to compute the detection criterion or to estimate the flux of an exoplanet. This problem can be overcome by introducing a regularization or by combining two estimators. A classical regularization consists of adding a fraction of identity matrix I to ensure that the covariance matrix is invertible:
is moreover rank-deficient and cannot be inverted to compute the detection criterion or to estimate the flux of an exoplanet. This problem can be overcome by introducing a regularization or by combining two estimators. A classical regularization consists of adding a fraction of identity matrix I to ensure that the covariance matrix is invertible: (A.1)
(A.1)
where ϵ should be set small enough to introduce a negligible bias. This regularized estimator can be shown to correspond to the minimizer: (A.2)
(A.2)
which is a maximum a posteriori estimator with a (conjugate) prior defined as an inverse matrix gamma distribution:  .
.
Another family of estimator is formed by shrinkage estimators that combine two (or more) estimators to balance their properties. A typical choice consists of a first estimator that is unbiased but that suffers from a large variance, and a second estimator with much smaller variance but larger bias (reduced degrees of freedom). Following the work of Ledoit & Wolf (2004) and Chen et al. (2010), we considered the combination of the sample covariance matrix  and the diagonal matrix
and the diagonal matrix  whose diagonal entries are the empirical variances (see Eqs. (10) and (11)). The shrinkage estimator is then defined by the convex combination of Eq. (7) that we recall here:
whose diagonal entries are the empirical variances (see Eqs. (10) and (11)). The shrinkage estimator is then defined by the convex combination of Eq. (7) that we recall here: (A.3)
(A.3)
If the samples based on which the estimators  and
and  are computed are distributed according to a multivariate distribution with covariance Σ
, then the optimal value ρ
⋆ that minimizes the expected risk
are computed are distributed according to a multivariate distribution with covariance Σ
, then the optimal value ρ
⋆ that minimizes the expected risk ![$ {\mathbb{E}}[{\lVert}{{\widehat{\mathbf{C}}}}-{\boldsymbol{\Sigma}}{\rVert}_{\text{ F}}^{2}] $](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq131.gif) is given by
is given by (A.4)
(A.4)
![$$ \begin{aligned}&= \frac{ \sum _{i,j}\mathrm{Var}\big ({\big [{\widehat{\mathbf{S }}}\big ]_{ij}}\big ) - \sum _{i,j}\mathrm{Cov}\big ({\big [{\widehat{\mathbf{S }}}\big ]_{ij}, \big [{\widehat{\mathbf{F }}}\big ]_{ij}}\big ) }{ \mathbb{E} \big ({||{\widehat{\mathbf{S }}- \widehat{\mathbf{F }}}||_{\text{ F}}^2}\big ) }\,\cdot \end{aligned} $$](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq133.gif) (A.5)
(A.5)
where the subscript O in ρO is used to emphasize that this value of ρ can be computed only provided that an oracle provides the underlying covariance Σ. The specific form of estimators  and
and  and the Gaussian assumption lead to the simplified form for ρO:
and the Gaussian assumption lead to the simplified form for ρO:![$$ \begin{aligned} \rho _\mathrm{O} = \frac{\mathrm{tr}(\boldsymbol{\Sigma }^2)+\mathrm{tr}^2(\boldsymbol{\Sigma })-2\sum _{i=1}^K [\boldsymbol{\Sigma }]_{ii}^2}{(T+1)\mathrm{tr}(\boldsymbol{\Sigma }^2)+\mathrm{tr}^2(\boldsymbol{\Sigma })-(T+2)\sum _{i=1}^K [\boldsymbol{\Sigma }]_{ii}^2}\,, \end{aligned} $$](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq136.gif) (A.6)
(A.6)
which is an extension of the result given in Chen et al. (2010) to our estimator  . This expression cannot be applied in practice, however. An approximate value
. This expression cannot be applied in practice, however. An approximate value  is obtained by replacing the unknown covariance matrix Σ
by a previous estimate. This is the principle of the oracle-approximating shrinkage estimator of Chen et al. (2010). The following recursion can be applied
is obtained by replacing the unknown covariance matrix Σ
by a previous estimate. This is the principle of the oracle-approximating shrinkage estimator of Chen et al. (2010). The following recursion can be applied![$$ \begin{aligned} \left\{ \begin{array}{l} \widehat{\rho }_{j+1}\,{=}\,\displaystyle \frac{ \mathrm{tr}(\widehat{\mathbf{\Sigma }}_j\widehat{\mathbf{S }}) + \mathrm{tr}^2(\widehat{\mathbf{\Sigma }}_j) - 2\sum _{i=1}^K[\widehat{\mathbf{\Sigma }}_j]_{ii}\,[\widehat{\mathbf{S }}]_{ii} }{ (T+1)\,\mathrm{tr}(\widehat{\mathbf{\Sigma }}_j\widehat{\mathbf{S }}) + \mathrm{tr}^2(\widehat{\mathbf{\Sigma }}_j) - (T+2)\sum _{i=1}^K [\widehat{\mathbf{\Sigma }}_j]_{ii}\,[\widehat{\mathbf{S }}]_{ii} }\\ \widehat{\mathbf{\Sigma }}_{j+1}\,{=}\,(1 - \widehat{\rho }_{j+1})\,\widehat{\mathbf{S }}+ \widehat{\rho }_{j+1}\,\widehat{\mathbf{F }}\end{array} \right. . \end{aligned} $$](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq139.gif) (A.7)
(A.7)
This sequence converges to a fixed point that is either  or the more useful value
or the more useful value![$$ \begin{aligned} \widehat{\rho }= \frac{\mathrm{tr}(\widehat{\mathbf{S }}^2)+\mathrm{tr}^2(\widehat{\mathbf{S }})-2\sum _{i=1}^K[\widehat{\mathbf{S }}]_{ii}^2}{(T+1)(\mathrm{tr}(\widehat{\mathbf{S }}^2)-\sum _{i=1}^K[\widehat{\mathbf{S }}]_{ii}^2),} \end{aligned} $$](/articles/aa/full_html/2018/10/aa32745-18/aa32745-18-eq141.gif) (A.8)
(A.8)
which is also given in Eq. (12).
Figure A.1 compares the S/N maps computed with PACO considering different regularization schemes. It shows that the shrinkage estimation of the covariance matrices achieves better performance than a simple regularization by adding a fraction of identity matrix. This may be due to the local and automatic adaptation of the strength of the regularization to the data. The shrinkage estimation of the covariance matrices is also applied considering the two algorithms derived from the general PACO principle: Algorithm 1 preferentially used during the detection step and Algorithm 3 preferentially used during the estimation step. It shows that the unbiased estimation of the flux of the exoplanet using Algorithm 3 is not beneficial in the exoplanet detection phase. Indeed, it improves the signal of the exoplanets, but it also changes the distribution of the test in the absence of exoplanet, which makes more difficult the setting of a detection threshold since the S/N does not follow a standard normal distribution.
 |
Fig. A.1. S/N maps computed with the PACO algorithm. Left: S/N map obtained with the PACO detection Algorithm 1. Covariance matrices are regularized by adding the fraction ϵ = 10−6 of identity matrix (see Eq. (A.1)). Middle: S/N map obtained with the PACO detection Algorithm 1. Covariance matrices are estimated using the shrinkage principle (see Eqs. (A.3) and (A.8)). Right: S/N map obtained with the PACO estimation Algorithm 3. Covariance matrices are estimated using the shrinkage principle (see Eqs. (A.3) and (A.8)). The first 32 detections are marked on the maps using square patterns. The 60 first detections are plotted as bar charts below each S/N map, ordered by decreasing S/N values, with true detections in pink (true background sources) or blue (injected fake sources), and false detections in red. Circles indicate the location of all faint point sources. |
Even a hand-tuned threshold does not improve the limit detection contrast, the increase of the probability of false alarm exceeding the improvement of the detection probability.
Appendix B:
Fast computation of the CRLBs
In this appendix, we briefly detail how to compute efficiently a map of the CRLBs for the parameters Ω = {α, x0, y0} (see Eq. (29)). The fast computation is based on the closed-form expression of the inverse of Fisher information matrix (B.1)
(B.1)
leads, for the estimated vector Ω = {α, x0, y0}, to the respective CRLBs (B.2)
(B.2)
 (B.3)
(B.3)
 (B.4)
(B.4)
is the determinant of I F .
The minimal standard deviations are given by  . The correlation coefficients between parameters are obtained by
. The correlation coefficients between parameters are obtained by (B.6)
(B.6)
 (B.7)
(B.7)
 (B.8)
(B.8)
Appendix C:
Additional results on fake exoplanet injections on the HIP 72192 dataset
This appendix presents additional detection results obtained on the HIP 72192 dataset at λ1 = 2.110 μm. The injections are performed at higher fluxes than those considering in Sect. 5.1.
We have considered two higher levels of brightness for the 30 injected fake exoplanets as summarized in Table C.1. We note that even at the highest level of brightness (level 3), the considered fluxes remain realistic and challenging since the contrast between fake companions and the host star is less than 5 × 10−6 far from the host star.
Angular separation and contrast of the injected fake sources on the HIP 72192 dataset for the two additional levels of injection at λ1 = 2.110 μm.
Figures C.1 and C.2 show S/N maps computed with the PACO, TLOCI, KLIP and LLSG algorithms for the two new levels of injection reported in Table C.1. Figure C.3 presents the corresponding ROC curves. As expected, the performance of the state-of-the-art algorithms increase when the flux of the injected fake exoplanets increases. TLOCI and LLSG lead to very similar detection capabilities. KLIP (PCA) outperforms TLOCI since it is significantly less sensitive to false detections. However the detection remains difficult near the host star with these methods. As a result, the detection of 75% of the faint point sources at the highest level of brightness (level 3) forced to reduce the detection threshold to 3.8 leading to approximately 100 false detections with TLOCI and KLIP. PACO is the only method able to detect the 30 fake and two true sources without any false alarm.
 |
Fig. C.1. S/N maps computed with the PACO, TLOCI, KLIP and LLSG algorithms considering the injection level 2. For TLOCI and KLIP, an unsharp filtering applied to S/N maps as post-processing is also considered. For LLSG, the resulting signed S/N is multiplied by a factor of 25 to fall within a comparable range than the other methods. For this latest algorithm, detection is in addition performed by discarding a centered circular area of 1 arcsec in radius. The first 32 detections are marked on each S/N map using square patterns. The 60 first detections are plotted as bar charts below each S/N map, ordered by decreasing S/N values, with true detections in pink (true background sources) or blue (injected fake sources), and false detections in red. Circles indicate the location of the real and injected faint point sources. PACO is the only algorithm capable of detecting correctly all sources without any false detection. |
 |
Fig. C.2. S/N maps computed with the PACO, TLOCI, KLIP and LLSG algorithms considering the injection level 3. For TLOCI and KLIP, an unsharp filtering applied to S/N maps as post-processing is also considered. For LLSG, the resulting signed S/N is multiplied by a factor of 25 to fall within a comparable range than the other methods. For this latest algorithm, detection is in addition performed by discarding a centered circular area of 1 arcsec in radius. The first 32 detections are marked on each S/N map using square patterns. The 60 first detections are plotted as bar charts below each S/N map, ordered by decreasing S/N values, with true detections in pink (true background sources) or blue (injected fake sources), and false detections in red. Circles indicate the location of the real and injected faint point sources. PACO is the only algorithm capable of detecting correctly all sources without any false detection. |
 |
Fig. C.3. ROC curves showing the true positive rate (fraction of sources correctly detected) as a function of the number of false alarms (i.e., false detections) for each detection maps on the HIP 72192 dataset at λ1 = 2.110 μm considering the levels 2 and 3 of injection. Values displayed on each curve correspond to the detection threshold used. |
As in Sect. 5.3 we have performed Monte Carlo photometric estimation of 50 injections at the considered angular distances using the mean flux given in Table C.1 for the two additional levels of contrast using the PACO algorithm. Table C.2 gives the mean estimated flux, the estimation bias and the ratio between the empirical standard deviation and the mean estimated flux. PACO also provides a statistical unbiased photometric estimation even for high levels of flux, which results into a high contamination of the collection of patches by the point source itself during the computation of the background statistics. As the standard deviation of the estimated flux does not depends on the flux of the point source, the confidence in the estimation improves when the flux of the point source increases.
Photometric accuracy evaluated by Monte Carlo simulation with 50 injections of fake sources for each angular separation, on the HIP 72192 dataset at λ1 = 2.110 μm for the two additional levels of injection.
All Tables
Angular separation and contrast of the injected fake sources on the HIP 72192 dataset at λ1 = 2.110 μm.
Photometric accuracy evaluated by Monte Carlo simulation with 50 injections of fake sources for each angular separation, on the HIP 72192 dataset at λ1 = 2.110 μm.
Angular separation and contrast of the injected fake sources on the HIP 72192 dataset for the two additional levels of injection at λ1 = 2.110 μm.
Photometric accuracy evaluated by Monte Carlo simulation with 50 injections of fake sources for each angular separation, on the HIP 72192 dataset at λ1 = 2.110 μm for the two additional levels of injection.
All Figures
 |
Fig. 1. Sample from a VLT/SPHERE-IRDIS dataset (HIP 72192 dataset at λ1 = 2.110 μm). Two spatio-temporal slices cut along the solid and dashed line are displayed at the bottom of the figure, emphasizing the spatial variations of the structure of the signal. |
| In the text | |
 |
Fig. 2. Apparent motion of an exoplanet in an ADI stack of frames. Green patches contain, in each frame, the exoplanet (i.e., the off-axis PSF) superimposed with the background. The statistical model of a background patch is built locally based on observed patches at the same location but at different times (set of red patches). |
| In the text | |
 |
Fig. 3. S/N map in absence of object (the two real known faint point sources denoted FPS1 and FPS2 are masked) and its corresponding empirical distribution using the HIP 72192 dataset described in Sect. 5 at λ2 = 2.251 μm. |
| In the text | |
 |
Fig. 4. S/N distribution under ℋ0 (in blue) and ℋ1 (in red). The hatched area is equal to the probability of false alarm (PFA) while the filled area is equal to the probability of detection (PD). |
| In the text | |
 |
Fig. 5. Upper line: minimal standard deviation (Cramér-Rao lower bounds) δ = {δα, δx0, δy0} on the estimated parameters Ω = {α, x0, y0} (δx0 and δy0 are normalized by the inverse of the flux α of the exoplanet and expressed in pixels unit). Middle line: magnification of the area near the host star. Lower line: coefficients of correlation ρ = {ραx0, ραy0, ρx0y0} between the estimated parameters Ω = {α, x0, y0}. The computation is performed on the HIP 72192 dataset at λ1 = 2.110 μm. The positions of the two real faint point sources in the dataset (which are not visible on these maps because it does not act of detection maps) are represented by a circle. |
| In the text | |
 |
Fig. 6. Influence of patch size: ROC curves for K = {13, 49, 113} pixels in each patch. The ROC curves are obtained by inserting fake exoplanets of flux α ∈ [10−6;10−5] on the HIP 72192 dataset at λ1 = 2.110 μm. |
| In the text | |
 |
Fig. 7. Normalized cost function 𝒞 obtained with Eq. (30) for injected fake exoplanet with different fluxes αGT. The dashed lines indicate the values found by the proposed alternate scheme in Eqs. (13). |
| In the text | |
 |
Fig. 8. Effect of the sampling grid on S/N: ratio 𝔼(S/N(𝒢s(ϕ0) | ϕ0)/𝔼(S/N(ϕ0 | ϕ0)) for s ∈ {1/4, 1/2, 1, 2, 4} computed on the HIP 72192 dataset at λ1 = 2.110 μm. It informs about the maximum expected reduction in S/N if the exoplanet is not exactly centered on a pixel of the sampling grid. |
| In the text | |
 |
Fig. 9. S/N maps computed with the PACO, TLOCI and KLIP algorithms on the HD 131399 (2015) dataset at λ1 = 2.110 μm. A common threshold at S/N = 5 is applied to defined the detections. A known faint source is present in the field of view. It is identified by a pink circle. |
| In the text | |
 |
Fig. 10. S/N maps computed with the PACO, TLOCI, KLIP and LLSG algorithms. For TLOCI and KLIP, an unsharp filtering applied to S/N maps as post-processing is also considered. For LLSG, the resulting signed S/N is multiplied by a factor of 25 to fall within a comparable range than the other methods. For this latest algorithm, detection is in addition performed by discarding a centered circular area of 1 arcsec in radius. The first 32 detections are marked on each S/N map using square patterns. The 60 first detections are plotted as bar charts below each S/N map, ordered by decreasing S/N values, with true detections in pink (true background sources) or blue (injected fake sources), and false detections in red. Circles indicate the location of the real and injected faint point sources. PACO is the only algorithm capable of detecting correctly all sources without any false detection. |
| In the text | |
 |
Fig. 11. ROC curves showing the true positive rate (fraction of sources correctly detected) as a function of the number of false alarms (i.e., false detections) for each detection map. Values displayed on each curve correspond to the detection threshold used. |
| In the text | |
 |
Fig. 12. S/N maps computed with the fast version of PACO on the HD 131399 (2015) and HIP 72196 dataset at λ1 = 2.110 μm. Detections over the S/N threshold of five are shown, they correspond to known background faint point sources. |
| In the text | |
 |
Fig. 13. Contrast curves obtained with PACO: comparison between predictive contrast map from PACO derived from Eq. (27) (denoted as “PACO (oracle)”) radially averaged and Monte Carlo simulations (denoted as “PACO (oracle Monte Carlo)”) by injection of fake exoplanets on the HD 131399 (2015) dataset at λ2 = 2.251 μm. The two cases are considered with absence of exoplanet during the learning of the statistics of the background (oracle mode). |
| In the text | |
 |
Fig. 14. Contrast maps for a probability of detection PD = 50% obtained with PACO for HD 131399 (2015), HD 131399 (2016) and HIP 72192 datasets at λ1 = 2.110 μm and λ2 = 2.251 μm. |
| In the text | |
 |
Fig. 15. Contrast curves derived from PACO, TLOCI and KLIP for a probability of detection PD ∈ {50%;80%} at λ1 = 2.110 μm and λ2 = 2.251 μm for the HD 131399 (2015), HD 131399 (2016) and HIP 72192 datasets respectively. Contrast curves as provided by KLIP and TLOCI do not correspond to a 5σ false alarm rate contrarily to the contrast curves of PACO. The achievable contrasts are thus significantly over-optimistic for KLIP and TLOCI, see discussion in the text (Sect. 5.2). |
| In the text | |
 |
Fig. 16. Estimated flux as the function of the number of iterations of PACO estimation Algorithm 3 for the three known faint point sources (FPS) of the HIP 72192 and HD 131399 (2015) datasets. |
| In the text | |
 |
Fig. 17. Local S/N maps and estimated flux at λ1 = 2.110 μm around the known real faint point sources (FPS1 and FPS2) located around the HIP 72192 star and the known real faint point source (FPS3) located around the HD 131399 system. Panel a: S/N of detection derived from PACO detection Algorithm 1. Panel b: estimated flux derived from PACO detection Algorithm 1. Panel c: estimated flux derived from PACO estimation algorithm alternating between the estimation of the flux and the computation of the background statistics. Panels e, d, f: Respectively correspond to panels a, b, c computed on a subpixel grid with a sampling factor s = 4. The superimposed white grid represents the original sampling grid (sampling factor s = 1). |
| In the text | |
 |
Fig. A.1. S/N maps computed with the PACO algorithm. Left: S/N map obtained with the PACO detection Algorithm 1. Covariance matrices are regularized by adding the fraction ϵ = 10−6 of identity matrix (see Eq. (A.1)). Middle: S/N map obtained with the PACO detection Algorithm 1. Covariance matrices are estimated using the shrinkage principle (see Eqs. (A.3) and (A.8)). Right: S/N map obtained with the PACO estimation Algorithm 3. Covariance matrices are estimated using the shrinkage principle (see Eqs. (A.3) and (A.8)). The first 32 detections are marked on the maps using square patterns. The 60 first detections are plotted as bar charts below each S/N map, ordered by decreasing S/N values, with true detections in pink (true background sources) or blue (injected fake sources), and false detections in red. Circles indicate the location of all faint point sources. |
| In the text | |
 |
Fig. C.1. S/N maps computed with the PACO, TLOCI, KLIP and LLSG algorithms considering the injection level 2. For TLOCI and KLIP, an unsharp filtering applied to S/N maps as post-processing is also considered. For LLSG, the resulting signed S/N is multiplied by a factor of 25 to fall within a comparable range than the other methods. For this latest algorithm, detection is in addition performed by discarding a centered circular area of 1 arcsec in radius. The first 32 detections are marked on each S/N map using square patterns. The 60 first detections are plotted as bar charts below each S/N map, ordered by decreasing S/N values, with true detections in pink (true background sources) or blue (injected fake sources), and false detections in red. Circles indicate the location of the real and injected faint point sources. PACO is the only algorithm capable of detecting correctly all sources without any false detection. |
| In the text | |
 |
Fig. C.2. S/N maps computed with the PACO, TLOCI, KLIP and LLSG algorithms considering the injection level 3. For TLOCI and KLIP, an unsharp filtering applied to S/N maps as post-processing is also considered. For LLSG, the resulting signed S/N is multiplied by a factor of 25 to fall within a comparable range than the other methods. For this latest algorithm, detection is in addition performed by discarding a centered circular area of 1 arcsec in radius. The first 32 detections are marked on each S/N map using square patterns. The 60 first detections are plotted as bar charts below each S/N map, ordered by decreasing S/N values, with true detections in pink (true background sources) or blue (injected fake sources), and false detections in red. Circles indicate the location of the real and injected faint point sources. PACO is the only algorithm capable of detecting correctly all sources without any false detection. |
| In the text | |
 |
Fig. C.3. ROC curves showing the true positive rate (fraction of sources correctly detected) as a function of the number of false alarms (i.e., false detections) for each detection maps on the HIP 72192 dataset at λ1 = 2.110 μm considering the levels 2 and 3 of injection. Values displayed on each curve correspond to the detection threshold used. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.