| Issue |
A&A
Volume 641, September 2020
|
|
|---|---|---|
| Article Number | A175 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202038414 | |
| Published online | 28 September 2020 | |
Determining mass-accretion and jet mass-loss rates in post-asymptotic giant branch binary systems⋆
1
Department of Physics and Astronomy, Macquarie University, Sydney, NSW 2109, Australia
e-mail: dylan.bollen@kuleuven.be
2
Astronomy, Astrophysics and Astrophotonics Research Centre, Macquarie University, Sydney, NSW 2109, Australia
3
Instituut voor Sterrenkunde (IvS), Celestijnenlaan 200D, KU Leuven 3001, Belgium
Received:
13
May
2020
Accepted:
27
July
2020
Aims. In this study we determine the morphology and mass-loss rate of jets emanating from the companion in post-asymptotic giant branch (post-AGB) binary stars with a circumbinary disc. In doing so we also determine the mass-accretion rates onto the companion, and investigate the source feeding the circum-companion accretion disc.
Methods. We perform a spatio-kinematic modelling of the jet of two well-sampled post-AGB binaries, BD+46°442 and IRAS 19135+3937, by fitting the orbital phased time series of Hα spectra. Once the jet geometry, velocity, and scaled density structure are computed, we carry out radiative transfer modelling of the jet for the first four Balmer lines to determine the jet densities, thus allowing us to compute the jet mass-loss rates and mass-accretion rates. We distinguish the origin of the accretion by comparing the computed mass-accretion rates with theoretically estimated mass-loss rates, both from the post-AGB star and from the circumbinary disc.
Results. The spatio-kinematic model of the jet reproduces the observed absorption feature in the Hα lines. The jets have an inner region with extremely low density in both objects. The jet model for BD+46°442 is tilted by 15° with respect to the orbital axis of the binary system. IRAS 19135+3937 has a smaller tilt of 6°. Using our radiative transfer model, we find the full 3D density structure of both jets. By combining these results, we can compute the mass-loss rates of the jets, which are of the order of 10−7 − 10−5 M⊙ yr−1. From this we estimate mass-accretion rates onto the companion of 10−6 − 10−4 M⊙ yr−1.
Conclusions. Based on the mass-accretion rates found for these two objects, we conclude that the circumbinary disc is most likely the source feeding the circum-companion accretion disc. This is in agreement with the observed depletion patterns in post-AGB binaries, which is caused by re-accretion of gas from the circumbinary disc that is under-abundant in refractory elements. The high accretion rates from the circumbinary disc imply that the lifetime of the disc will be short. Mass transfer from the post-AGB star cannot be excluded in these systems, but it is unlikely to provide a sufficient mass-transfer rate to sustain the observed jet mass-loss rates.
Key words: stars: AGB and post-AGB / binaries: spectroscopic / circumstellar matter / stars: mass-loss / ISM: jets and outflows / accretion, accretion disks
© ESO 2020
1. Introduction
Binarity can have a significant impact on the evolution of stars from low to intermediate mass. The binary interactions in these systems can alter their mass-loss history, orbital parameters, and lifetimes and can lead to other phenomena such as excretion and accretion discs, jets, and bipolar nebulae (Hilditch 2001). Post-AGB stars in binary systems are no exception. They are stars of low to intermediate mass in a final transition phase after the AGB (Van Winckel 2003). The luminous post-AGB star in these binary systems is in orbit with a main-sequence (MS) companion of low mass (0.1−2.5 M⊙, Oomen et al. 2018). Due to their binary interaction history, post-AGB binary systems end up with periods and eccentricities that are currently unexplained by theory (Van Winckel 2018).
During the previous AGB phase, the star endures a period of mass loss as high as 10−4 − 10−3 M⊙ yr−1 (Ramstedt et al. 2008). When in a binary system, the mass loss of the AGB star can be concentrated on the orbital plane of the system, with the bulk of the mass being ejected via the L2 Lagrangian point (Hubová & Pejcha 2019; Bermúdez-Bustamante et al. 2020). The focused mass loss of the star can then become a circumbinary disc (Shu et al. 1979; Pejcha et al. 2016; MacLeod et al. 2018). Observational studies have confirmed the presence of such discs in post-AGB binary systems. Many post-AGB stars have a near-IR dust excess in their spectral energy distribution (SED) that can be explained by dust in the proximity of the central binary system. The observed dust excess is a clear signature of dust residing in a circumbinary disc, close to the system (De Ruyter et al. 2006; Deroo et al. 2006, 2007; Kamath et al. 2014, 2015). The compact nature of the infrared dust excess has also been confirmed through interferometric studies (Bujarrabal et al. 2013; Hillen et al. 2013, 2016; Kluska et al. 2018). Additionally, Hillen et al. (2016) and Kluska et al. (2018) identified a flux excess at the location of the companion in the reconstructed interferometric image of post-AGB binary IRAS 08544−4431. This flux excess is too large to originate from the companion, and most likely stems from an accretion disc around the companion.
Another commonly observed phenomenon in post-AGB binaries is a high-velocity outflow or jet (Gorlova et al. 2012). Optical spectra of these objects show a blue-shifted absorption feature in the Balmer lines during superior conjunction when the companion star is located between the post-AGB star and the observer (Gorlova et al. 2012, 2015), as can be seen in Fig. A.1. The absorption feature in the Balmer lines is interpreted in terms of a jet launched from the vicinity of the companion that scatters the continuum light from the post-AGB star travelling towards the observer during this phase in the binary orbit (Gorlova et al. 2012). Due to the orbital motion of the binary, the photospheric light of the post-AGB star shines through various parts of the jet, providing a tomography of the jet. Hence, the orbital-phase dependent variations in the Balmer lines of these jet-creating post-AGB binaries contain an abundance of information about the jet and the binary system (Bollen et al. 2017, 2019).
The jets are likely launched by an accretion disc around the companion. An unknown component in these jet-creating post-AGB binaries is the source feeding the circum-companion accretion disc that launches the jet. Direct observations of the mass-transfer to the circum-companion disc do not exist. The two plausible sources are the post-AGB star, which could transfer mass via the first Lagrangian point (L1) to the companion, and the re-accretion from the circumbinary disc around the system. While this mass transfer has not yet been observed directly, we observe refractory element depletion in the atmosphere of post-AGB stars in binary systems (Waters et al. 1992; Van Winckel et al. 1995; Gezer et al. 2015; Kamath & Van Winckel 2019). It has been suggested that this depletion pattern is caused by re-accretion of circumbinary gas, which is depleted of refractory elements by the formation of dust in the disc. Oomen et al. (2019) modelled this depletion pattern by implementing the re-accretion of metal-poor gas in their evolutionary models obtained using the Modules for Experiments in Stellar Astrophysics (MESA) code. They compared these models with 58 observed post-AGB stars and found that initial mass-accretion rates must be greater than 3 × 10−7 M⊙ yr−1 in order to obtain the observed depletion patterns.
In our previous study (Bollen et al. 2017) we used the time series of Hα line profiles to show that jets in post-AGB binaries are wide and can reach velocities of ∼700 km s−1. These velocities are of the order of the escape velocity of a MS star, pointing to the nature of the companion. In our recent study (Bollen et al. 2019) we created a more sophisticated spatio-kinematic model for the jets, from which we determined their geometry, velocity, and scaled density structure.
In this paper, we fully exploit the potential of the tomography of the jet from the first four Balmer lines: Hα, Hβ, Hγ, and Hδ. We compute a radiative transfer model of the jet, with the aim of estimating the mass-loss rate of the jet. We do this in two main parts: (1) the spatio-kinematic modelling, as described by Bollen et al. (2019), and (2) the radiative transfer modelling of the jet. Here, we focus on part 2 and the mass-ejection and -accretion rates. We use two well-sampled, jet-launching post-AGB binaries for our analysis: BD+46°442 (Gorlova et al. 2012; Bollen et al. 2017) and IRAS 19135+3937 (Gorlova et al. 2015; Bollen et al. 2019). Both objects have been observed for the past ten years with the HERMES spectrograph mounted on the Mercator telescope, La Palma, Spain (Raskin et al. 2011), providing a good amount of data covering the orbital phase of the binary.
The paper is organised as follows. We describe the methods of our spatio-kinematic modelling and radiative transfer modelling in Sect. 2. We present the results for BD+46°442 and IRAS 19135+3937 in Sects. 3 an 4, respectively. We discuss these results in Sect. 5 and give a conclusion and summary in Sect. 6.
2. Methods
In this study, we expand on the spatio-kinematic model carried out in our previous work (Bollen et al. 2019) by adding new components in the jet structure and we include a new radiative transfer model. Splitting the calculations into two parts, the spatio-kinematic modelling and the radiative transfer modelling, allows us to fit the jet structure and obtain the jet mass-loss rates. In the following subsections, we give a short description of the spatio-kinematic modelling part of the fitting, including improvements of the technique pioneered by Bollen et al. (2019), followed by a description of the new radiative transfer modelling.
2.1. Spatio-kinematic modelling of the jet
To obtain the geometry and kinematics of the jet, we follow the model-fitting routine used by Bollen et al. (2019). In brief, we create a spatio-kinematic model of the jet, from which we reproduce the absorption features in the Hα line. The modelled lines are then fitted to the observations. To fit our model to the data, we use the emcee-package, which applies an MCMC algorithm (Foreman-Mackey et al. 2013). This gives us the best-fitting parameters for the jet.
The model consists of three main components: the post-AGB star, the MS companion, and the jet. The location of the post-AGB star and the companion are determined for each orbital phase by the orbital parameters listed in Table B.1. The jet in the model is a double cone, centred on the companion. The post-AGB star is approximated as a uniform flat disc facing the observer. We trace the light travelling from the post-AGB star, along the line of sight towards the observer. When a ray from the post-AGB star goes through the jet, the amount of absorption by the jet is calculated. The absorption is determined by the optical depth
with cτ the scaling parameter and Δs the length of the line element at position s(θ, z). The scaled density ρsc in this model is dimensionless and is a function of the polar angle θ and height z in the jet:
Here p is the exponent, which is a free parameter in the model; θout is the outer jet angle; and z is the height of the jet above the centre of the jet cone. Hence, we calculate the relative density structure, which can then be scaled by the scaling parameter cτ, in order to fit the synthetic spectra to the observations. By doing so the computations of optical depth are fast. The absolute density of the jet is estimated in Sect. 2.2.
In this model we implement the same three jet configurations as in Bollen et al. (2019): a stellar jet, an X-wind, and a disc wind. The velocity profile used for the stellar jet and X-wind models is defined as
where vout and vin are the outer and inner velocities, and with
Here pv is a free parameter, and f2 is defined as
where θout is the outer jet angle and θcav the cavity angle of the jet.
The velocity profile of the disc wind is dependent on the Keplerian velocity at the location in the disc from where the material is ejected. For the inner jet region between the jet cavity and the inner jet angle (θcav < θ < θin), we have
with vin, cav the jet velocity at the cavity angle (θcav) and vin, sc the jet velocity at the inner boundary angle (vin). For the outer jet region (θin < θ < θout) the velocity is defined as
with
We define the scaled inner velocity as vin, sc = vM ⋅ (tanθin)−1/2 and the scaled outer velocity as vout, sc = cv ⋅ vout. The parameter vout is the outer jet velocity, which is equal to the Keplerian velocity at the launching point in the disc. The scaling factor cv can have values between 0 and 1. Hence, the disc wind velocity is lower than or equal to the Keplerian velocity from its launching point in the disc.
In the three jet configurations, we included two important updates. The first update is the ability to model a jet whose axis is tilted with respect to the direction perpendicular to the orbital plane. As can be seen in Fig. 1, the absorption feature is not completely centred on the phase of superior conjunction, i.e. when the MS companion is between the post-AGB primary and the observer. This can be explained by a tilt in the jet, causing the absorption feature to be observed later in the orbital phase. A tilted jet in the binary system would lead to a precessing motion of the jet. This is not uncommon and has been previously observed in pre-planetary nebulae (Sahai et al. 2017; Yung et al. 2011). We implemented this jet tilt as an extra free parameter in our fitting routine.
 |
Fig. 1. Dynamic spectra for the Balmer lines of BD+46°442. Upper left: Hα, upper right: Hβ, lower left: Hγ, lower right: Hδ. The black dashed line indicates the phase of superior conjunction. The white line indicates the radial velocity of the post-AGB star. The colour gradient represents the strength of the line at each phase. |
The second update to our model presented in Bollen et al. (2019) is the introduction of a jet cavity for the X-wind and the disc wind configurations. In Bollen et al. (2019) we showed that the density in the innermost region of the outflow is extremely low, thus barely contributing to the absorption. This is in agreement with the disc wind theory of Blandford & Payne (1982) and the X-wind theory of Shu et al. (1994). According to these theories the disc material is launched at angles of 30° with respect to the jet axis, although farther from the launch point the angle can decrease substantially due to magnetic collimation. In our model, we allow some flexibility for the cavity angle parameter by giving it a lower limit of 20°. We compare the new version of the spatio-kinematic model with the older version, which does not include the cavity and tilt, during our analysis in Sects. 3.1 and 4.1.
2.2. Radiative transfer model of the jet
The spatio-kinematic model is used as input for the radiative transfer model. Hence, the geometry, velocity, and scaled density structure are fixed with the values estimated from the spatio-kinematic model. By calculating the radiative transfer through the jet, the absolute jet densities can be determined, from which we can then calculate the jets’ mass-ejection rate. Here, we use the equivalent width (EW) of the Balmer lines to fit the model to the observations. The fitting parameters are the absolute jet densities and temperatures instead of relative density differences throughout the jet. Hence, the optical depth calculations become more CPU intensive.
2.2.1. Radiative transfer
In our radiative transfer code we assume thermodynamic equilibrium, and that the jet medium is isothermal. Hence, each line of sight through the jet to the disc of the star will have the same temperature. Here we use the formal solution of the 1D radiative transfer equation, where the source function Sν is described by the Planck function Bν (see chapter 1 Rybicki & Lightman 1979). For the incident intensity of the post-AGB star in the model we use a synthetic stellar spectrum from Coelho (2014), which is chosen based on the parameters of the post-AGB star.
Using the Boltzmann equation, and by expressing the Einstein coefficients in terms of the oscillator strength f12, the absorption coefficient αν can be written as
with nl and nu the densities in the lower and upper energy level, flu the oscillator strength, and ΔE the energy difference between the upper and lower energy levels. Hence, the computation of the intensity is dependent on the number density nl, the temperature T, and the normalised line profile ϕν. This normalised line profile ϕν is described as a Doppler profile for Hβ, Hγ, and Hδ. For Hα, we follow the description in Muzerolle et al. (2001), Kurosawa et al. (2006), and Kurosawa et al. (2011) instead. As Muzerolle et al. (2001) showed, the Stark broadening effect can become significant in the optically thick Hα line. Hence, we describe the line profile of Hα with the Voigt profile:
Here ΔνD is the Doppler width of the line, a = Γ/4πΔνD, and y = (ν − ν0)/ΔνD with ν0 the line centre. The Doppler line width ΔνD is a function of the thermal velocity vD:
We use the damping constant Γ described by Vernazza et al. (1973), which is given by the sum of the natural broadening, Van der Waals broadening, and the linear Stark broadening effects:
Here CRad, CVdW, and CStark are the broadening constants of the natural broadening, Van der Waals, and Stark broadening effects, respectively; nHI is the neutral hydrogen number density; and ne is the electron number density. For the broadening constants, we use the values from Luttermoser & Johnson (1992): Crad = 8.2 × 10−3 Å, CVdW = 5.5 × 10−3 Å, and CStark = 1.47 × 10−2 Å.
2.2.2. Numerical integration of the radiative transfer equation
In our model we divide the light from the post-AGB star into Nr rays. To compute the radiative transfer through the jet, we solve the 1D radiative transfer equation numerically. Hence, we iterate over each grid point along each ray, as shown in Fig. 2. This ray is split into Nj grid points between the point of entry and exit in the jet. The intensity at a grid point i along the ray is computed as follows:
 |
Fig. 2. Schematic representation of the radiative transfer calculations in the jet. The ray travelling from the star to the observer is split into Nj grid points where it passes through the jet. Each grid point has a density ρ and a velocity v. We iterate over each grid point in order to determine the resulting intensity along this line for each wavelength. |
Hence, if we want to calculate the intensity through the whole line of sight through the jet, the observed intensity Iν(τn) will be
Since the ray has been divided into discrete intervals, the optical depth τi will be calculated as
with κν, i the opacity. This procedure is iterated for each ray from the post-AGB star and each frequency ν. Hence, in general, the model consists of Nr rays leaving the post-AGB surface, which are divided in Nj grid points and for which the intensity is computed for a total of Nν frequencies. As we are assuming that the jet is isothermal and the jet velocities significantly smaller than the speed of light (v/c ≪ 1), we do not need to compute the Planck function Bν for each grid point. However, this more general formulation will allow non-isothermal jet models to be computed in the future.
2.2.3. Equivalent width as tracer of absorption
The photospheric light from the post-AGB star that travels through the jet will be scattered by the hydrogen atoms in the jet, causing the absorption features in the Balmer lines. To quantify this scattering in our model and the observations we use the EW of the Balmer lines as fitting parameter. We do this for two main reasons. The first is that the EW of a line will be higher for stronger extinction. Hence, the EW quantifies the amount of scattering by the jet. The EW is highly dependent on the level populations of hydrogen at the location where the line of sight passes through the jet. In our model these level populations are determined by the local density and by the temperature of the jet at those locations.
Second, the ratio of EW between the four Balmer lines (Hα, Hβ, Hγ, and Hδ) is also dependent on the chosen jet temperature and density. This ratio can change dramatically when these two parameters are changed. This makes the EW an ideal quantity in our fitting to find the absolute jet densities and temperatures.
3. Jet model for BD+46°442.
BD+46°442 is a jet-launching post-AGB binary system for which we obtained 36 spectra during one-and-a-half orbital cycles of the binary orbit of 140.82 days (Van Winckel et al. 2009; Oomen et al. 2018). In this study we adopt the orbital parameters listed in Oomen et al. (2018, see Appendix B). The scattering by the jet is observable in the first four Balmer lines (Hα, Hβ, Hγ, and Hδ), hence we focus on these line for our analysis. The Balmer lines are shown in Appendix C. The signal-to-noise ratio of the spectra lies between S/N = 22 and S/N = 60 in the Hα line, and drops to values between S/N = 12 and S/N = 37 in the Hδ line. In Fig. 1 we present the dynamic Balmer line spectra for BD+46°442. In the dynamic spectra we plot the continuum-normalised spectra as a function of orbital phase and interpolate between each of the spectra. In this way the orbital phase-dependent variations in the line become apparent.
3.1. Spatio-kinematic model of BD+46°442
We compare the quality of the fit for the three jet configurations through their reduced chi-square and Bayesian Information Criteria (BIC) values1. The best-fitting model is the X-wind with a reduced chi-square of 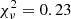 . A chi-square lower than unity indicates that the model is over-fitting the data. In our case, this is caused by overestimating the uncertainty on the data, which is determined from the signal-to-noise ratio of the spectra (σ = (S/N)−1) and the uncertainty in the emission feature of the synthetic spectra that is provided as input for the modelling. We impose a χ2 of unity for the best-fitting model and scale the χ2 of the other models appropriately, in order to compare their relative difference. The scaled chi-square values are
. A chi-square lower than unity indicates that the model is over-fitting the data. In our case, this is caused by overestimating the uncertainty on the data, which is determined from the signal-to-noise ratio of the spectra (σ = (S/N)−1) and the uncertainty in the emission feature of the synthetic spectra that is provided as input for the modelling. We impose a χ2 of unity for the best-fitting model and scale the χ2 of the other models appropriately, in order to compare their relative difference. The scaled chi-square values are 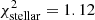 ,
, 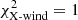 , and
, and 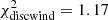 . Hence, the X-wind configuration gives a slightly better fitting result compared to the other two configurations. This is also confirmed by the BIC values of the three models. The X-wind has the lowest BIC and therefore fits the data best: BICstellar − BICX-wind = 1007 and BICdiscwind − BICX-wind = 1452. For this reason we use the best-fitting parameters from the spatio-kinematic modelling of the X-wind for further calculations. We note, however, that the relative difference in χ2 between the three model configurations is not significant, and thus we conclude that the three model configurations fit the data equally well.
. Hence, the X-wind configuration gives a slightly better fitting result compared to the other two configurations. This is also confirmed by the BIC values of the three models. The X-wind has the lowest BIC and therefore fits the data best: BICstellar − BICX-wind = 1007 and BICdiscwind − BICX-wind = 1452. For this reason we use the best-fitting parameters from the spatio-kinematic modelling of the X-wind for further calculations. We note, however, that the relative difference in χ2 between the three model configurations is not significant, and thus we conclude that the three model configurations fit the data equally well.
The best-fitting parameters of the model are tabulated in Table 1, and its model spectra are shown in the upper right panel of Fig. 3. The binary inclination for this model is about 50°. The jet has a half-opening angle of 35°. The inner boundary angle θin = 29° is the polar angle in the jet along which the bulk of the mass will be ejected. The geometry of the binary system and the jet are represented in Fig. 4. The material that is ejected in the inner regions of the jet reaches velocities up to 490 km s−1. These velocities are of the order of the escape velocity from the surface of a MS star, confirming the nature of the companion. The velocities at the outer edges are lower at 41 km s−1. The radius of the post-AGB star in the best-fitting model is 27.2 R⊙ (0.127 AU).
 |
Fig. 3. Interpolated observed and modelled dynamic spectra of the Hα line. The upper spectra are the observations (left) and model spectra (right) of BD+46°442. The lower spectra are the observations and model spectra of IRAS 19135+3937. The colours represent the normalised flux. |
 |
Fig. 4. Geometry of the binary system and the jet of BD+46°442 at superior conjunction, when the post-AGB star is directly behind the jet, as viewed by the observer. In all three plots the full orange circle denotes the post-AGB star. The orange star indicates the location of the companion. The red cross is the location of the centre of mass of the binary system. The radius of the post-AGB star is to scale. The jet is represented in blue, and the colour indicates the relative density of the jet (see colour scale). The dashed black line is the jet axis and the dotted white lines are the inner jet edges. The jet cavity is the inner region of the jet. Upper left panel: system viewed along the orbital plane from a direction perpendicular to the line of sight to the observer. Right panel: jet viewed from an angle perpendicular to the X-axis. The post-AGB star is located behind the companion and its jet in this image. The jet tilt is noticeable from this angle. Lower left panel: binary system viewed from above, perpendicular to the orbital plane. The grey dashed lines represent the Roche radii of the two binary components and the full black line shows the Roche lobes. |
Best-fitting jet configuration and parameters for the spatio-kinematic model of BD+46°442 and IRAS 19135+3937.
Additionally, we implemented a jet tilt and jet cavity in this model (see Sect. 2.1). The resulting model has a cavity angle of 20°. The jet tilt for BD+46°442 is relatively large with ϕtilt = 15°. The effect of this tilt is noticeable in the resulting model spectra. The jet absorption feature is not centred at orbital phase 0.5, but at a later phase between 0.55 and 0.6. To evaluate the performance of the new modified spatio-kinematic model that includes a jet cavity and tilt, we do an additional model fitting with the old version that does not include these features and compare the two model fitting results. The χ2 of the new model (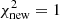 ) is lower than the old version (
) is lower than the old version (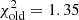 ). If we account for the two extra parameters in the new model by comparing the BIC instead, we get a difference in BIC between the two results of Δ BIC = 2980, with the lower BIC for the new model, implying a better fit for this model. This demonstrates that the implemented jet cavity and jet tilt improve the spatio-kinematic model for this object.
). If we account for the two extra parameters in the new model by comparing the BIC instead, we get a difference in BIC between the two results of Δ BIC = 2980, with the lower BIC for the new model, implying a better fit for this model. This demonstrates that the implemented jet cavity and jet tilt improve the spatio-kinematic model for this object.
3.2. Radiative transfer model of BD+46°442
We apply the radiative transfer model for BD+46°442 to compute the amount of absorption caused by the jet that blocks the light from the post-AGB star. The setup for the radiative transfer model is similar to that described in Sect. 2.1. For each ray of light the background intensity Iν, 0 is the background spectrum given in Sect. 3.1. For each orbital phase we calculate the amount of absorption by the jet for each ray. Additionally, the output from the MCMC fitting routine in Sect. 3.1 (i.e. the spatio-kinematic model of BD+46°442) is used as input in our the radiative transfer model. Hence, there are only two fitting parameters: jet number density nj and jet temperature Tj. We assume the jet temperature to be uniform for the segment of the jet through which the rays travel. The jet number density nj is defined as the number density at the inner edge of the jet θin at a height of 1 AU. In the case of BD+46°442 the best-fitting jet configuration is an X-wind. Hence, the density in the jet at each grid point can be determined from the density profile of the jet that was used for the X-wind in the spatio-kinematic model. This density profile is defined as
with p either the exponent for the inner-jet region pin or the outer-jet region pout, which was determined in Sect. 3.1.
We use a grid of jet temperatures between 4400 K and 6000 K in steps of 100 K and the logarithm of the jet densities 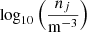 between 14 and 18 in logarithmic steps of 0.1. This makes a total of 697 grid calculations.
between 14 and 18 in logarithmic steps of 0.1. This makes a total of 697 grid calculations.
As described in Sect. 2.2.3, the EW of the Balmer lines represents the amount of absorption by the jet. In order to find the best-fitting model for our grid of temperatures and densities, we fit the EW of the Balmer lines in the model to those of the observed Balmer lines for each spectra.
We fit the model to the data with a χ2–goodness-of-fit test. Hence, the reduced 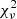 value for a model will be
value for a model will be
with ν the degrees of freedom, No the number of spectra (36 for BD+46°442, and 22 for IRAS 19135+3937), EWo and EWm the equivalent width of the observed and modelled line, and σ the standard deviation determined by the signal-to-noise ratio of the spectra.
The resulting 2D 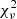 distribution for jet densities and temperatures is shown in Fig. 5 and the corresponding EW of the model in Fig. 7. The best-fitting model has a jet density of nj = 2.5 × 1016 m−3 and jet temperature of Tj = 5600 K. In order to determine the uncertainties on the fitting parameters, we convert the 2D chi-squared distribution into a probability distribution:
distribution for jet densities and temperatures is shown in Fig. 5 and the corresponding EW of the model in Fig. 7. The best-fitting model has a jet density of nj = 2.5 × 1016 m−3 and jet temperature of Tj = 5600 K. In order to determine the uncertainties on the fitting parameters, we convert the 2D chi-squared distribution into a probability distribution:
 |
Fig. 5. Two-dimensional reduced chi-squared distribution for the grid of jet densities nj and temperatures Tj for the fitting of BD+46°442. The white dot gives the location of the minimum reduced chi-square value |
 |
Fig. 7. Equivalent width of the absorption by the jet for BD+46°442 as a function of orbital phase. The four panels show the EW in Hα (top left), Hβ (top right), Hγ (bottom left), and Hδ (bottom right). The circles are the measured EWs of the absorption feature by the jet in the observations with their respective errors. The full line is the EW of the absorption feature for the best-fitting model. |
The marginalised probability distribution can be found for each parameter via
From these distributions we can determine a mean and standard deviation. This gives us a jet density and temperature of 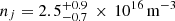 and Tj = 5600 ± 80 K.2
and Tj = 5600 ± 80 K.2
4. Jet model for IRAS 19135+3937
The second post-AGB binary system that we model is IRAS 19135+3937. For this object, we obtained 22 spectra during a full cycle with an orbital period of 126.97 days (Van Winckel et al. 2009; Oomen et al. 2018). As for BD+46°442, we adopt the orbital parameters of this system found by Oomen et al. (2018). The individual and dynamic spectra are shown in Appendix C and Fig. 6, respectively. The signal-to-noise ratio for these spectra lie between S/N = 26 and S/N = 49 in Hα. In Hδ the signal-to-noise ratio ranges between S/N = 5 and S/N = 20.
 |
Fig. 6. Dynamic spectra for the Balmer lines of IRAS 19135+3937. Upper left: Hα, upper right: Hβ, lower left: Hγ, lower right: Hδ. The black dashed line indicated the phase of superior conjunction. The white line indicates the radial velocity of the post-AGB star. The colour gradient represents the strength of the line at each phase. |
4.1. Spatio-kinematic model of IRAS 19135+3937
The spatio-kinematic structure of IRAS 19135+3937 was modelled by Bollen et al. (2019). Here, we update it with the addition of the jet tilt and the jet cavity. The best-fitting jet configuration is a disc wind, but all three models produce similar fits, as was the case in the fitting of Bollen et al. (2019) (BICstellar − BICdisc wind = 87 and BICX-wind − BICdisc wind = 116). The best-fitting model parameters are tabulated in Table 1. This model has an inclination angle of i = 72° for the binary system and a jet angle of θout = 67°. These angles are about 7° lower than those found in the model fitting of Bollen et al. (2019). The jet reaches velocities up to 640 km s−1. At its edges the jet velocity is vout ⋅ cv = 3 km s−1. The post-AGB star in our model has a radius of 22.5 R⊙ (0.105 AU), which is about 30% smaller than that found by Bollen et al. (2019). The geometry of the binary system and the jet are shown in Fig. 8. We compare the quality of the fit for the best-fitting model of Bollen et al. (2019) with the best-fitting model in this work. The BIC for the model fitting in our work is significantly lower than the BIC found by Bollen et al. (2019) (ΔBICold − BICnew = 4190). This shows that the jet tilt and jet cavity significantly improve the model fitting. The jet tilt for this object is relatively small (ϕtilt = 5.7°). This is expected since there is no noticeable lag in the absorption feature in the spectra. The jet for this object has a significant jet cavity of θcav = 24°.
4.2. Radiative transfer model of IRAS 19135+3937
We apply the radiative transfer model for IRAS 19135+3937. The best-fitting spatio-kinematic model found in Sect. 4.1 for IRAS 19135+3937 is a disc wind. We use this spatio-kinematic model and its model parameters as input to calculate the radiative transfer in the jet for a grid of jet densities and temperatures. The density profile for the disc wind is similar to the X-wind (see Eq. (16)). The grid of temperatures and densities is the same as for BD+46°442.
The 2D χ2 distribution for the fitting is shown in Fig. 9 and the associated EW of the model is shown in Fig. 10. We calculate the marginalised probability distributions for nj and Tj, given by Eqs. (19) and (20), from which we can determine the mean and standard deviations. This gives a jet density of 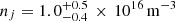 and jet temperature of Tj = 5330 ± 180 K.
and jet temperature of Tj = 5330 ± 180 K.
 |
Fig. 9. Two-dimensional reduced chi-square distribution for the grid of jet densities nj and temperatures Tj for the fitting of IRAS 19135+3937. The white dot gives the location of the minimum reduced chi-square value |
5. Discussion
By fitting the spatio-kinematic structure of the jet and estimating its density structure, we obtained crucial information about the jet. We can now estimate how much mass is being ejected by the jet, which is essential for understanding the mass accretion onto the companion and determining the source feeding this accretion.
5.1. Jet mass-loss rate
The velocity and density structure of the jets, calculated by fitting the models, is used to estimate the mass-ejection rate. The mass-ejection rate of the jet for both systems is estimated by calculating how much mass passes through the jet at a height of 1 AU from the launch point.
In the case of BD+46°442, the velocity and density profiles are determined by the X-wind configuration (see Sect. 4.1). We calculate the density at a height of z = 1 AU using Eq. (3). The mass-ejection rate can be found by the integral
with r = 1 AU ⋅ tanθ. The velocity at each location in the jet is defined by Eq. (3). In this way we find a mass-ejection rate of 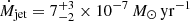 for BD+46°442.
for BD+46°442.
For IRAS 19135+3937, the data is best fit by a disc wind model (see Sect. 3.1), whose velocity profile is described by Eqs. (6) and (7) for the inner and outer jet regions, respectively. From Eq. (21), we find a mass-ejection rate of 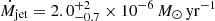 . We list these values as lower and upper limits in Table 2.
. We list these values as lower and upper limits in Table 2.
Derived mass-accretion and mass-loss rates in the two binary systems.
5.2. Ejection efficiency
By assuming an ejection efficiency Ṁjet/Ṁacc, we can link the jet mass-loss rate (Ṁjet) to the mass-accretion rate (Ṁacc), and hence obtain a range of possible accretion rates onto the circum-companion disc. By doing so, we can assess if the mass transfer from either the post-AGB or the circumbinary disc, or both can contribute enough mass to the circum-companion disc in order to sustain the observed jet mass-loss rates.
Ejection efficiency has not been determined for post-AGB binary systems, but the same theory (i.e., magneto centrifugal driving) applies to YSOs, which have been studied extensively (Ferreira et al. 2007, and references therein). Moreover, discs in YSOs are comparable in size to those in our post-AGB binary systems (Hillen et al. 2017) and their mass-ejection rates are similar to the rates estimated for jets in post-AGB systems (10−8 − 10−4 M⊙ yr−1; Calvet et al. 1998; Ferreira et al. 2007). Current estimates of ejectioEWn efficiencies for T Tauri stars are in the range Ṁjet/Ṁacc ∼ 0.01 − 0.1 (Cabrit et al. 2007; Cabrit 2009; Nisini et al. 2018). This said, the spread in these values is large and some studies have even found ratios higher than 0.3 (Calvet et al. 1998; Ferreira et al. 2006; Nisini et al. 2018).
In this work we adopt a wide range of ejection efficiencies for both of our post-AGB binary objects, according to the typical ranges found through observations of YSOs: 0.01 < Ṁjet/Ṁaccr < 0.3. Under these assumptions, and by using the jet mass-loss rates from Sect. 5.1, the accretion rates onto the two companions are (see Table 2)
Next, we use these results to look at possible sources feeding the accretion.
5.3. Sources of accretion onto the companion
There are two possible sources of mass transfer onto the companion. The first is the post-AGB primary itself, moving mass via the first Lagrange point L1 and creating a circum-companion accretion disc. The second possibility is re-accretion of gas from the circumbinary discs (Van Winckel 2003; De Ruyter et al. 2006; Dermine et al. 2013).
5.3.1. Scenario 1: Mass transfer from the post-AGB star to the companion
We first assume that the accretion onto the companion is due to mass transfer from the primary via L1. To estimate the mass-transfer rate by the post-AGB star, we follow the prescription in Ritter (1988):
Here e is Euler’s number; kB is the Boltzmann constant; G is the gravitational constant; mH is the hydrogen mass; and μ1, ph, T1, R1, M1, and ρ1, ph are the mean molecular weight, the temperature, the radius, and the mass of the primary star, respectively. The parameter F(q) is defined as
with q = M2/M1 the mass ratio, R1, RL the Roche lobe radius of the post-AGB star, and a the binary separation. In Eq. (24) g(q) is defined as
with x the distance between the mass centre of the post-AGB star and L1 in terms of the binary separation (a).
We assume a neutral cosmic mixture which implies a mean molecular weight of μ1, ph = 0.8. We note that this prescription is based on Roche lobe overflow for a star filling its Roche lobe, transferring mass to the companion. In this case the radius of the star R1 is equal to the Roche radius R1, RL. However, from our results in in the spatio-kinematic modelling, the post-AGB stars in these two systems do not fill their Roche lobes, as is shown in the geometrical representation of the systems in Figs. 4 and 8. The observations also support this result since a star that could fill at least 80% of its Roche lobe would show ellipsoidal variations in its light curve (Wilson & Sofia 1976). The light curves of BD+46°442 and IRAS 19135+3937 do not show these variations (Bollen et al. 2019). Hence, we extrapolate Eq. (23) by using the radius of the primary R1 instead of the Roche radius R1, RL.
Additionally, since we find that the post-AGB star does not fill its Roche lobe, the mass transfer would occur via a mechanism that is less efficient and weaker than RLOF. A few other possibilities being wind-RLOF and Bondi-Hoyle-Lyttleton (BHL) accretion. In the case of wind-RLOF, the stellar wind will be focused to the orbital plane and most of the mass will be lost through the L1 point, towards the secondary (Mohamed et al. 2007). The mass-transfer efficiency of wind-RLOF would vary between a few percent and 50% (de Val-Borro et al. 2009; Abate et al. 2013). In the case of BHL accretion, the accretion efficiency would be significantly lower at about 1−10% (Abate et al. 2013; Mohamed & Podsiadlowski 2012). Hence, the upper limit for mass transfer through wind-RLOF would be lower than that of RLOF. The upper limit for BHL accretion would be several orders of magnitude lower. Hence, by equating the mass-transfer from the post-AGB star using Eq. (23), we can get a good estimation for an upper limit of mass-transfer from the post-AGB star to the companion.
To determine the photospheric density, we use the MESA stellar evolution code (MESA Paxton et al. 2011, 2013, 2015, 2018, 2019) to calculate the evolution of a post-AGB star with the correct mass. We subsequently use the photospheric density from the MESA output at the time-step when the post-AGB star is the same size as our star. This gives us a value of 10−10 g cm−2 for the photospheric density of the star (ρ1, ph). The mass of the post-AGB star M1 is set to 0.6 M⊙, which is a typical value for these objects. The mass of the companion M2 is determined from the mass function f(M1) and the inclination of the binary system found in the spatio-kinematic model fitting:
This gives a mass of 1.07 M⊙ for the companion star of BD+46°442, resulting in a mass ratio of q = 1.79. We find the Roche radius of the post-AGB star using the formula by Eggleton (1983):
Using these values for Eq. (23), we find the mass-transfer rate from the post-AGB star to the companion in BD+46°442 to be Ṁ1 = 3.5 × 10−7 M⊙ yr−1. This value is less than the lower limit of the jet mass-loss rate in BD+46°442 (see Table 2). Moreover, in Sect. 5.1, we found the mass-accretion rate to be in the range of 1.7 × 10−6 M⊙ yr−1 < Ṁaccr < 1 × 10−4 M⊙ yr−1, which is about five times the theoretical value for the upper-limit of mass-transfer from the post-AGB star to the companion. Hence, it is unlikely that the post-AGB star can contribute enough mass to the circum-companion disc to sustain the observed jet outflow.
We conduct a similar analysis for IRAS 19135+3937 and we come to a similar conclusion. The mass of the companion is M2 = 0.46 M⊙ and the mass ratio would be q = 0.77. We use the same values for μ1, ph and ρ1, ph, giving us a mass-transfer rate of ṀRLOF = 1.7 × 10−7 M⊙ yr−1. Hence, this upper limit for mass-transfer from the post-AGB star for IRAS 19135+3937 is also lower than the lower limit for the jet mass-loss rate of IRAS 19135+3937 and thus too low to match a measured mass-accretion rate in the range 4 × 10−6 M⊙ yr−1 < Ṁaccr < 4 × 10−4 M⊙ yr−1.
We conclude that it is unlikely that the mass transfer from the post-AGB star alone is responsible for feeding the accretion disc around the companion.
5.3.2. Scenario 2: Re-accretion from the circumbinary disc
Here, we consider the possibility of mass accretion from the circumbinary disc onto the central binary system. In order to give an estimate of re-accretion by the circumbinary disc of BD+46°442 and IRAS 19135+3937, we use the mass-loss equation by Rafikov (2016), that defines the mass loss from the disc to the central binary as a function of time,
where M0, disc is the initial disc mass. These circumbinary discs have average disc masses of M0, disc = 10−2 M⊙ (Gielen et al. 2007; Bujarrabal et al. 2013, 2018; Hillen et al. 2017; Kluska et al. 2018). Bujarrabal et al. (2013, 2018) derived disc masses of circumbinary discs of post-AGB binary systems ranging from 6 × 10−4 to 5 × 10−2 M⊙. We use this range to estimate the mass-loss rate from the disc.
The initial viscous time of the disc t0 is defined by Rafikov (2016) as
where μ is the mean molecular weight, ab is the binary separation, α is the viscosity parameter, σ is Stefan-Boltzmann constant, L1 is the luminosity of the post-AGB star, ζ is a constant factor that accounts for the starlight that is intercepted by the disc surface at a grazing incidence angle, η is the ratio of angular momentum of the disc compared to that of the central binary, and IL characterises the spatial distribution of the angular momentum in the disc. We fix several values at the same values as Rafikov (2016) and Oomen et al. (2019): μ = 2mp, α = 0.01, ζ = 0.1, and IL = 1, with mp the mass of a proton. The luminosity L1 of BD+46°442 and IRAS 19135+3937 are 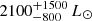 and
and 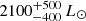 , respectively (Oomen et al. 2019). The angular momentum of the circumbinary disc is typically of the order of the angular momentum of the central binary system (Bujarrabal et al. 2018; Izzard & Jermyn 2018). We set a range of η between 1.4 and 2, where a value of 1.4 is appropriate for a disc with the bulk of its mass located at the inner disc rim.
, respectively (Oomen et al. 2019). The angular momentum of the circumbinary disc is typically of the order of the angular momentum of the central binary system (Bujarrabal et al. 2018; Izzard & Jermyn 2018). We set a range of η between 1.4 and 2, where a value of 1.4 is appropriate for a disc with the bulk of its mass located at the inner disc rim.
Using Eq. (28) and assuming t = 0, we can calculate a range of possible mass-loss rates by the disc. We find a range of 3 × 10−8 M⊙ yr−1 < Ṁdisc < 6 × 10−6 M⊙ yr−1 for BD+46°442, while in the case of IRAS 19135+3937, we find that the re-accretion rate from the circumbinary disc is in the range of 5 × 10−8 M⊙ yr−1 < Ṁdisc < 9 × 10−6 M⊙ yr−1 (Table 2). When the disc matter falls onto the central binary, it will be accreted by both the post-AGB star and the companion. Hence, the mass lost by the circumbinary disc should be twice the mass accreted by the circum-companion accretion disc. If we compare the mass-accretion rate for BD+46°442 and IRAS 19135+3937 with the estimated mass-loss rate by the circumbinary disc, it shows that re-accretion from the circumbinary disc is a plausible mechanism for the formation of the jet.
We note that only the higher estimates for mass-accretion rates from the circumbinary disc can explain our observationally derived rates. Hence, this would imply that for these two systems the disc masses are at the high end of the range (M0, disc > 10−2 M⊙) and that we are observing the early stages of the re-accretion by the circumbinary disc. Nevertheless, our findings are in good agreement with Oomen et al. (2019), who estimated that accretion rates should be higher than 3 × 10−7 M⊙ yr−1 and that disc masses should be higher than ∼10−2 M⊙.
6. Summary and conclusion
In this paper our aim was to determine mass-transfer rates of jet-creating post-AGB binaries. We fully exploited the time series of high-resolution optical spectra from these binary systems. We presented a new radiative transfer model for these jets and applied this model to reproduce the Balmer lines of two well-sampled post-AGB binary systems: BD+46°442 and IRAS 19135+3937. With this model we were able to study the mass-loss rate of the jet and mass-accretion rate onto the companion, and to constrain the source of the accretion in these systems: the post-AGB star or the circumbinary disc. Additionally, we expanded the spatio-kinematic model from Bollen et al. (2019). Our main conclusions can be summarised as follows:
-
We successfully reproduced the observed absorption feature in the Hα line profiles of our test sources with our improved spatio-kinematic model of the jet. By doing so, we obtained the kinematics and 3D morphology of the jet. The implementation of the jet tilt in the model reproduced the observed lag of the absorption feature in the Balmer lines. This tilt is significant for both objects, with values of 15° and 6° for BD+46°442 and IRAS 19135+3937, respectively. Likewise, the new jet cavity in the model improves the jet representation, as was suggested by Bollen et al. (2019).
-
We showed that we can acquire a 3D jet morphology by modelling the amount of absorption in the Hα lines from our spatio-kinematic model of the jet. By combining the results of the spatio-kinematic and radiative transfer modelling, we found the crucial parameters to calculate jet mass-loss rates: jet velocity and geometry from the spatio-kinematic model and jet density structure from the radiative transfer model.
-
We computed the mass-loss rate of the jet by combining the results of our spatio-kinematic model and radiative transfer model. The computed mass-loss rates for the jets in BD+46°442 and IRAS 19135+3937 are in the ranges (5−10) × 10−7 M⊙ yr−1 and (1.3−4) × 10−6 M⊙ yr−1, respectively, as shown in Table 2. These mass-ejection rates are comparable to the mass-ejection rates for the jets in planetary nebulae and pre-planetary nebulae (Tocknell et al. 2014; Tafoya et al. 2019). Tocknell et al. (2014) found the mass-ejection rates to be 1−3 × 10−7 M⊙ yr−1 and 8.8 × 10−7 M⊙ yr−1 for the Necklace and NGC 6778, respectively. These mass-ejection rates imply correspondingly high mass-accretion rates onto the companion that range between 1.7 × 10−6 M⊙ yr−1 and 1 × 10−4 M⊙ yr−1 for BD+46°442 and 4 × 10−6 M⊙ yr−1 and 4 × 10−4 M⊙ yr−1 for IRAS 19135+3937.
-
By determining the jet mass-loss rate we added an additional constraint on the nature of the accretion onto these systems. While the uncertainties are high, the circumbinary disc is the preferred source of accretion feeding the jet rather than the post-AGB star: the accretion rates from the post-AGB stars are too low to justify the observed jet mass-loss rates. We note, however, that the simultaneous accretion from the circumbinary disc and from the post-AGB star cannot be ruled out. Re-accretion from the circumbinary disc also naturally explains the abundance pattern of the post-AGB star and is in agreement with the study by Oomen et al. (2019), who showed that high re-accretion rates (> 3 × 10−7 M⊙ yr−1) are needed in order to reproduce the observed depletion patterns of post-AGB stars. These high re-accretion rates from the circumbinary disc can prolong the lifetime of the post-AGB star, and can thus have an important impact on the evolution of these objects, provided that the disc can sustain the mass loss.
In our future studies, we will perform a comprehensive analysis of the whole diverse sample of jet-creating post-AGB binary systems by using both the spatio-kinematic and radiative transfer models. The observational properties of these binaries and their jets are non-homogeneous. Hence, by analysing the whole sample, we aim to obtain strong constraints on the source of the accretion and identify correlations between mass accretion, depletion patterns, and the orbital properties of post-AGB binaries.
Acknowledgments
This work was performed on the OzSTAR national facility at Swinburne University of Technology. OzSTAR is funded by Swinburne University of Technology and the National Collaborative Research Infrastructure Strategy (NCRIS). DK acknowledges the support of the Australian Research Council (ARC) Discovery Early Career Research Award (DECRA) grant (95213534). HVW acknowledges support from the Research Council of the KU Leuven under grant number C14/17/082. The observations presented in this study are obtained with the HERMES spectrograph on the Mercator Telescope, which is supported by the Research Foundation - Flanders (FWO), Belgium, the Research Council of KU Leuven, Belgium, the Fonds National de la Recherche Scientifique (F.R.S.-FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland and the Thüringer Landessternwarte Tautenburg, Germany.
References
- Abate, C., Pols, O. R., Izzard, R. G., Mohamed, S. S., & de Mink, S. E. 2013, A&A, 552, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bermúdez-Bustamante, L. C., García-Segura, G., Steffen, W., & Sabin, L. 2020, MNRAS, 493, 2606 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Bollen, D., Van Winckel, H., & Kamath, D. 2017, A&A, 607, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bollen, D., Kamath, D., Van Winckel, H., & De Marco, O. 2019, A&A, 631, A53 [CrossRef] [EDP Sciences] [Google Scholar]
- Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., et al. 2013, A&A, 557, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bujarrabal, V., Castro-Carrizo, A., Van Winckel, H., et al. 2018, A&A, 614, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabrit, S. 2007, in Star-Disk Interaction in Young Stars, eds. J. Bouvier, & I. Appenzeller, IAU Symp., 243, 203 [Google Scholar]
- Cabrit, S. 2009, Astrophys. Space Sci. Proc., 13, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N. 1998, in AIP Conf. Ser., eds. S. S. Holt, & T. R. Kallman, 431, 495 [CrossRef] [Google Scholar]
- Coelho, P. R. T. 2014, MNRAS, 440, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- De Ruyter, S., Van Winckel, H., Maas, T., et al. 2006, A&A, 448, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Val-Borro, M., Karovska, M., & Sasselov, D. 2009, ApJ, 700, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Dermine, T., Izzard, R. G., Jorissen, A., & Van Winckel, H. 2013, A&A, 551, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deroo, P., van Winckel, H., Min, M., et al. 2006, A&A, 450, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deroo, P., Acke, B., Verhoelst, T., et al. 2007, A&A, 474, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J., Dougados, C., & Cabrit, S. 2006, A&A, 453, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferreira, J., Dougados, C., & Whelan, E. 2007, Jets from Young Stars I: Models and Constraints, 723 [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Gezer, I., Van Winckel, H., Bozkurt, Z., et al. 2015, MNRAS, 453, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Gielen, C., Van Winckel, H., Waters, L. B. F. M., Min, M., & Dominik, C. 2007, A&A, 475, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gorlova, N., Van Winckel, H., Gielen, C., et al. 2012, A&A, 542, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gorlova, N., Van Winckel, H., Ikonnikova, N. P., et al. 2015, MNRAS, 451, 2462 [NASA ADS] [CrossRef] [Google Scholar]
- Hilditch, R. W. 2001, An Introduction to Close Binary Stars (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Hillen, M., Verhoelst, T., Van Winckel, H., et al. 2013, A&A, 559, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillen, M., Kluska, J., Le Bouquin, J.-B., et al. 2016, A&A, 588, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillen, M., Van Winckel, H., Menu, J., et al. 2017, A&A, 599, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubová, D., & Pejcha, O. 2019, MNRAS, 489, 891 [CrossRef] [Google Scholar]
- Izzard, R., & Jermyn, A. 2018, Galaxies, 6, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Kamath, D., & Van Winckel, H. 2019, MNRAS, 486, 3524 [NASA ADS] [CrossRef] [Google Scholar]
- Kamath, D., Wood, P. R., & Van Winckel, H. 2014, MNRAS, 439, 2211 [NASA ADS] [CrossRef] [Google Scholar]
- Kamath, D., Wood, P. R., & Van Winckel, H. 2015, MNRAS, [Google Scholar]
- Kluska, J., Hillen, M., Van Winckel, H., et al. 2018, A&A, 616, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurosawa, R., Harries, T. J., & Symington, N. H. 2006, MNRAS, 370, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Kurosawa, R., Romanova, M. M., & Harries, T. J. 2011, MNRAS, 416, 2623 [NASA ADS] [CrossRef] [Google Scholar]
- Luttermoser, D. G., & Johnson, H. R. 1992, ApJ, 388, 579 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, M., Ostriker, E. C., & Stone, J. M. 2018, ApJ, 868, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Mohamed, S., & Podsiadlowski, P. 2007, in 15th European Workshop on White Dwarfs, eds. R. Napiwotzki, & M. R. Burleigh, ASP Conf. Ser., 372, 397 [Google Scholar]
- Mohamed, S., & Podsiadlowski, P. 2012, Balt. Astron., 21, 88 [Google Scholar]
- Muzerolle, J., Calvet, N., & Hartmann, L. 2001, ApJ, 550, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Nisini, B., Antoniucci, S., Alcalá, J. M., et al. 2018, A&A, 609, A87 [EDP Sciences] [Google Scholar]
- Oomen, G.-M., Van Winckel, H., Pols, O., et al. 2018, A&A, 620, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oomen, G.-M., Van Winckel, H., Pols, O., & Nelemans, G. 2019, A&A, 629, A49 [CrossRef] [EDP Sciences] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pejcha, O., Metzger, B. D., & Tomida, K. 2016, MNRAS, 461, 2527 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2016, ApJ, 830, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Ramstedt, S., Schöier, F. L., Olofsson, H., & Lundgren, A. A. 2008, A&A, 487, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ritter, H. 1988, A&A, 202, 93 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley) [Google Scholar]
- Sahai, R., Vlemmings, W. H. T., Gledhill, T., et al. 2017, ApJ, 835, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Lubow, S. H., & Anderson, L. 1979, ApJ, 229, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F., Najita, J., Ostriker, E., et al. 1994, ApJ, 429, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Tafoya, D., Orosz, G., Vlemmings, W. H. T., Sahai, R., & Pérez-Sánchez, A. F. 2019, A&A, 629, A8 [CrossRef] [EDP Sciences] [Google Scholar]
- Tocknell, J., De Marco, O., & Wardle, M. 2014, MNRAS, 439, 2014 [NASA ADS] [CrossRef] [Google Scholar]
- Van Winckel, H. 2003, ARA&A, 41, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Van Winckel, H. 2018, ArXiv e-prints [arXiv:1809.00871] [Google Scholar]
- Van Winckel, H., Waelkens, C., & Waters, L. B. F. M. 1995, A&A, 293, L25 [NASA ADS] [Google Scholar]
- Van Winckel, H., Lloyd Evans, T., Briquet, M., et al. 2009, A&A, 505, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1973, ApJ, 184, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Waters, L. B. F. M., Trams, N. R., & Waelkens, C. 1992, A&A, 262, L37 [NASA ADS] [Google Scholar]
- Wilson, R. E., & Sofia, S. 1976, ApJ, 203, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Yung, B. H. K., Nakashima, J.-I., Imai, H., et al. 2011, ApJ, 741, 94 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The absorption feature in the Hα line
 |
Fig. A.1. Hα line of BD+46°442 at two different phases in the orbital period. The Hα line displays a double-peaked emission feature with a central absorption feature during inferior conjunction (black solid line), when the post-AGB star is between the jet and the observer. During superior conjunction, when the jet is between the post-AGB star and the observer, we observe a blue-shifted absorption feature in the Hα line (blue dotted line). |
Appendix B: Orbital parameters of BD+46°442 and IRAS 19135+3937
Spectroscopic orbital solutions of the primary component of BD+46°442 and IRAS 19135+3937 (Oomen et al. 2018).
Appendix C: Balmer lines of BD+46°442 and IRAS 19135+3937
 |
Fig. C.1. Balmer lines of BD+46°442 as a function of wavelength. The spectra are given in arbitrary units and offset according to their orbital phase. Numbers on the right vertical axis indicate the orbital phase of the spectra (from 0 to 100). The dashed vertical lines represent the centre of each Balmer line. |
All Tables
Best-fitting jet configuration and parameters for the spatio-kinematic model of BD+46°442 and IRAS 19135+3937.
Spectroscopic orbital solutions of the primary component of BD+46°442 and IRAS 19135+3937 (Oomen et al. 2018).
All Figures
 |
Fig. 1. Dynamic spectra for the Balmer lines of BD+46°442. Upper left: Hα, upper right: Hβ, lower left: Hγ, lower right: Hδ. The black dashed line indicates the phase of superior conjunction. The white line indicates the radial velocity of the post-AGB star. The colour gradient represents the strength of the line at each phase. |
| In the text | |
 |
Fig. 2. Schematic representation of the radiative transfer calculations in the jet. The ray travelling from the star to the observer is split into Nj grid points where it passes through the jet. Each grid point has a density ρ and a velocity v. We iterate over each grid point in order to determine the resulting intensity along this line for each wavelength. |
| In the text | |
 |
Fig. 3. Interpolated observed and modelled dynamic spectra of the Hα line. The upper spectra are the observations (left) and model spectra (right) of BD+46°442. The lower spectra are the observations and model spectra of IRAS 19135+3937. The colours represent the normalised flux. |
| In the text | |
 |
Fig. 4. Geometry of the binary system and the jet of BD+46°442 at superior conjunction, when the post-AGB star is directly behind the jet, as viewed by the observer. In all three plots the full orange circle denotes the post-AGB star. The orange star indicates the location of the companion. The red cross is the location of the centre of mass of the binary system. The radius of the post-AGB star is to scale. The jet is represented in blue, and the colour indicates the relative density of the jet (see colour scale). The dashed black line is the jet axis and the dotted white lines are the inner jet edges. The jet cavity is the inner region of the jet. Upper left panel: system viewed along the orbital plane from a direction perpendicular to the line of sight to the observer. Right panel: jet viewed from an angle perpendicular to the X-axis. The post-AGB star is located behind the companion and its jet in this image. The jet tilt is noticeable from this angle. Lower left panel: binary system viewed from above, perpendicular to the orbital plane. The grey dashed lines represent the Roche radii of the two binary components and the full black line shows the Roche lobes. |
| In the text | |
 |
Fig. 5. Two-dimensional reduced chi-squared distribution for the grid of jet densities nj and temperatures Tj for the fitting of BD+46°442. The white dot gives the location of the minimum reduced chi-square value |
| In the text | |
 |
Fig. 7. Equivalent width of the absorption by the jet for BD+46°442 as a function of orbital phase. The four panels show the EW in Hα (top left), Hβ (top right), Hγ (bottom left), and Hδ (bottom right). The circles are the measured EWs of the absorption feature by the jet in the observations with their respective errors. The full line is the EW of the absorption feature for the best-fitting model. |
| In the text | |
 |
Fig. 6. Dynamic spectra for the Balmer lines of IRAS 19135+3937. Upper left: Hα, upper right: Hβ, lower left: Hγ, lower right: Hδ. The black dashed line indicated the phase of superior conjunction. The white line indicates the radial velocity of the post-AGB star. The colour gradient represents the strength of the line at each phase. |
| In the text | |
 |
Fig. 8. Similar to Fig. 4, but for IRAS 19135+3937. |
| In the text | |
 |
Fig. 9. Two-dimensional reduced chi-square distribution for the grid of jet densities nj and temperatures Tj for the fitting of IRAS 19135+3937. The white dot gives the location of the minimum reduced chi-square value |
| In the text | |
 |
Fig. 10. As for Fig. 7, but for IRAS 19135+3937. |
| In the text | |
 |
Fig. A.1. Hα line of BD+46°442 at two different phases in the orbital period. The Hα line displays a double-peaked emission feature with a central absorption feature during inferior conjunction (black solid line), when the post-AGB star is between the jet and the observer. During superior conjunction, when the jet is between the post-AGB star and the observer, we observe a blue-shifted absorption feature in the Hα line (blue dotted line). |
| In the text | |
 |
Fig. C.1. Balmer lines of BD+46°442 as a function of wavelength. The spectra are given in arbitrary units and offset according to their orbital phase. Numbers on the right vertical axis indicate the orbital phase of the spectra (from 0 to 100). The dashed vertical lines represent the centre of each Balmer line. |
| In the text | |
 |
Fig. C.2. Similar to Fig. C.1, but for IRAS 19135+3937. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



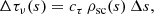
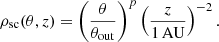
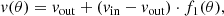
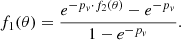
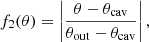
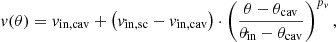
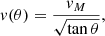
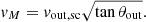
![$$ \begin{aligned} \alpha _\nu (s) = \frac{\pi e^2}{m_e c}\phi _\nu n_l(s) f_{lu}\Big [1 - {e}^{-\Delta E/kT}\Big ], \end{aligned} $$](/articles/aa/full_html/2020/09/aa38414-20/aa38414-20-eq9.gif)
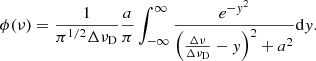
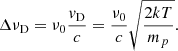
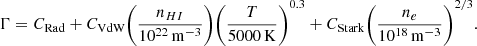
![$$ \begin{aligned} I_\nu (\tau _i) = I_\nu (\tau _{i-1}) \,{e}^{-(\tau _{i-1}-\tau _{i})} + B_\nu (\tau _{i})\,\Big [1-{e}^{-(\tau _{i-1} - \tau _{i})}\Big ]. \end{aligned} $$](/articles/aa/full_html/2020/09/aa38414-20/aa38414-20-eq13.gif)
![$$ \begin{aligned}&I_\nu (\tau _n) = \,I_\nu (\tau _{0})\,{e}^{-(\tau _{0}-\tau _{n})} + B_\nu (\tau _{n})\,\Big [1-{e}^{-(\tau _{n-1} - \tau _{n})}\Big ] \nonumber \\&\qquad \quad + \sum \limits _{i=1}^{n-1} B_\nu (\tau _{i})\,\Big [1-{e}^{-(\tau _{i-1} - \tau _{i})}\Big ]\,{e}^{-(\tau _{i}-\tau _{n})}. \end{aligned} $$](/articles/aa/full_html/2020/09/aa38414-20/aa38414-20-eq14.gif)
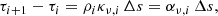
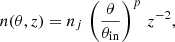
![$$ \begin{aligned}&\chi ^2_\nu = \frac{1}{\nu }\Bigg ( \sum _i^{N_o}\left[\frac{\big (\mathrm{EW}^{\,o,\,\mathrm{H}\alpha }_i - \mathrm{EW}^{\,m,\mathrm{H}\alpha }_i\big )^2}{\big (\sigma ^{\mathrm{H}\alpha }_{i}\big )^2}\right] + \sum _i^{N_o}\left[\frac{\big (\mathrm{EW}^{\,o,\,\mathrm{H}\beta }_i - \mathrm{EW}^{\,m,\mathrm{H}\beta }_i\big )^2}{\big (\sigma ^{\mathrm{H}\beta }_{i}\big )^2}\right]\nonumber \\&\qquad + \sum _i^{N_o}\left[\frac{\big (\mathrm{EW}^{\,o,\,\mathrm{H}\gamma }_i - \mathrm{EW}^{\,m,\mathrm{H}\gamma }_i\big )^2}{\big (\sigma ^{\mathrm{H}\gamma }_{i}\big )^2}\right] + \sum _i^{N_o}\left[\frac{\big (\mathrm{EW}^{\,o,\,\mathrm{H}\delta }_i - \mathrm{EW}^{\,m,\mathrm{H}\delta }_i\big )^2}{\big (\sigma ^{\mathrm{H}\delta }_{i}\big )^2}\right]\Bigg ), \end{aligned} $$](/articles/aa/full_html/2020/09/aa38414-20/aa38414-20-eq25.gif)
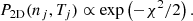
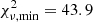
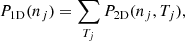
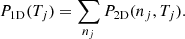
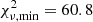
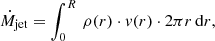
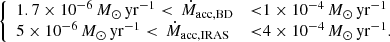
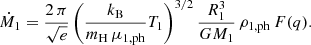
![$$ \begin{aligned} F(q) = \Bigg [ \Big (g(q)-(1+q)\Big )\,g(q) \Bigg ]^{-1/2} \left(\frac{R_{\rm 1, RL}}{a}\right)^{-3}, \end{aligned} $$](/articles/aa/full_html/2020/09/aa38414-20/aa38414-20-eq39.gif)
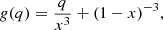
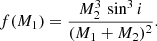
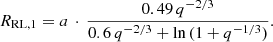
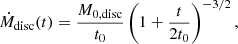
![$$ \begin{aligned} t_0 = \frac{4}{3}\frac{\mu }{k_{\rm B}}\frac{a_b}{\alpha } \left[ \frac{4\pi \sigma (GM_b)^2}{\zeta L_1} \right]^{1/4} \left( \frac{\eta }{I_L}, \right)^2 , \end{aligned} $$](/articles/aa/full_html/2020/09/aa38414-20/aa38414-20-eq44.gif)