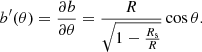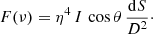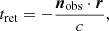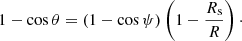| Issue |
A&A
Volume 639, July 2020
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 20 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202037979 | |
| Published online | 09 July 2020 | |
Radio and high-energy emission of pulsars revealed by general relativity
Université de Strasbourg, CNRS, Observatoire Astronomique de Strasbourg, UMR 7550, 67000 Strasbourg, France
e-mail: quentin.giraud@astro.unistra.fr
Received:
18
March
2020
Accepted:
14
May
2020
Context. According to current pulsar emission models, photons are produced within their magnetosphere and current sheet, along their separatrix, which is located inside and outside the light cylinder. Radio emission is favoured in the vicinity of the polar caps, whereas the high-energy counterpart is presumably enhanced in regions around the light cylinder, whether this is the magnetosphere and/or the wind. However, the gravitational effect on their light curves and spectral properties has only been sparsely researched.
Aims. We present a method for simulating the influence that the gravitational field of the neutron star has on its emission properties according to the solution of a rotating dipole evolving in a slowly rotating neutron star metric described by general relativity.
Methods. We numerically computed photon trajectories assuming a background Schwarzschild metric, applying our method to neutron star radiation mechanisms such as thermal emission from hot spots and non-thermal magnetospheric emission by curvature radiation. We detail the general-relativistic effects onto observations made by a distant observer.
Results. Sky maps are computed using the vacuum electromagnetic field of a general-relativistic rotating dipole, extending previous works obtained for the Deutsch solution. We compare Newtonian results to their general-relativistic counterpart. For magnetospheric emission, we show that aberration and curvature of photon trajectories as well as Shapiro time delay significantly affect the phase delay between radio and high-energy light curves, although the characteristic pulse profile that defines pulsar emission is kept.
Key words: radiation mechanisms: thermal / radiation mechanisms: non-thermal / relativistic processes / stars: neutron / gamma rays: stars
© Q. Giraud and J. Pétri 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
In 1967, Jocelyn Bell observed a radio source that with extreme regularity displayed an emission peak every 1.337 s. This radio source, called pulsar for pulsating star, was later identified as a neutron star by Hewish et al. (1968). It is the collapsed core of a giant star, stabilised by neutron degeneracy pressure. A neutron star typically has a diameter of 20 km and a weight of 1.5 times the mass of the Sun (Özel & Freire 2016). When simple arguments about angular momentum and the magnetic flux conservation are followed, this stellar remnant also has a very high rotation speed with periods between 1 ms and 20 s. It also harbours the strongest known magnetic field in the Universe, which is at about the quantum critical value of 4.4 × 109 T or even higher.
Neutron stars are surrounded by a plasma formed of electron-positron pairs produced by photo-disintegration in a strong magnetic field at the surface of the star (Ruderman & Sutherland 1975). This plasma corotates with the neutron star, by the action of the electromagnetic field, up to a limit called the light cylinder, where the plasma corotation speed equals the speed of light, c (Goldreich & Julian 1969), and is denoted by
where Ω is the rotation rate of the neutron star. Beyond this limit, the magnetic field lines are assumed to be open, that is, instead of joining the two magnetic poles, they leave one pole to infinity. To explain the characteristic emission of a pulsar, several models of neutron star magnetospheres have been developed. They require empty gaps, allowing for an electric field parallel to the magnetic field lines, which is responsible for particle acceleration and radiation. The most popular models include the polar cap (Ruderman & Sutherland 1975), the outer gap Cheng et al. (1986), and the slot gap (Arons 1983; Dyks & Rudak 2003) with possible extension to the striped wind (Kirk et al. 2002; Pétri 2011). Charged particles accelerated by this electrical field are responsible for the pulsar emission, generating radio and high-energy emission by inverse Compton scattering, synchrotron radiation, or curvature radiation. This last is the focus of our paper. The pulse that is periodically detected by an observer is simply a consequence of the stellar magnetic field geometry combined with its rotation.
Pulsars, especially accreting pulsars, can also present two hot spots, located at the magnetic north and south poles, where matter falls onto the neutron star surface, with a thermal emission mainly in the X-ray band (around 100 eV). This thermal emission from the hot spots is a valuable indicator for the magnetic field topology on its surface. Recent observations from NICER by Bilous et al. (2019) showed evidence for a multipolar component on the surface. This clearly adds some complexity to the pulsar magnetosphere picture, especially for millisecond pulsars, for which the multipolar magnetic field strength even at the light cylinder has not decayed much compared to the dipolar part. Because of their size, neutron stars are highly compact. This is defined by the ratio between their actual radius R and their Schwarzschild radius, which is defined by
with M the mass of the star and G the gravitational constant, Rg being the gravitational radius of the star. Typically, this ratio is about Rs/R = 0.5. This extreme compactness causes non-negligible relativistic effects on the electromagnetic field structure, as shown by Rezzolla et al. (2001), Pétri (2013, 2014, 2016) and propagation of photons emitted in the vicinity of the neutron star. In order to determine how this affects terrestrial observations of pulsars, we simulated the trajectory of photons in the gravitational field of a neutron star using ray-tracing techniques. These techniques are mostly divided into two methods. A direct integration of the equation of motion in the prescribed metric has been implemented by Vincent et al. (2011). It allows for ray-tracing in a generic metric that is not necessarily analytical. Another approach performs the integration analytically in a Schwarzschild or Kerr metric, leading to elliptical integrals, as were found by Rauch & Blandford (1994). This second technique is less general than the previous one, but we found it much more accurate and faster than solving second-order differential equations derived from the geodesic equations. We also included the calculation of the time of flight of the photon (Shapiro delay), as in Bogdanov et al. (2007), to properly compute the non-thermal magnetospheric emission and the thermal hot-spot emission as received by an distant observer.
There are currently more than 2000 identified pulsars, and although these stellar remnants are particularly known for their typical pulsed radio emission (Lyne & Manchester 1988), the Fermi large area telescope (Fermi/LAT) confirmed the existence of pulsation in the gamma-ray domain (Abdo et al. 2013) for more than 250 of these pulsars. This gamma-ray activity gives us an insight into the pulsar magnetosphere, especially into where the emission sites for high-energy emission are located, because they must be well above the polar cap in order to avoid too strong magnetic photon absorption in the magnetic field close to the critical value of 4.4 × 109 T (Daugherty & Harding 1996). For a more complete introduction on the topic, we refer to Pétri (2018). The gamma-ray peaks show sharp features that are interpreted as caustic effects produced by aberration and retardation effects (Morini 1983; Dyks et al. 2004). Because radio and gamma-rays are not released at the same location, a phase alignment between both pulses is usually rarely seen, except for some millisecond pulsars, suggesting that radio and gamma-rays are produced at nearly the same sites. Moreover, Venter et al. (2012) claimed that the emission altitude is about 30% of the light cylinder radius rL. Distinguishing between the different models such as the polar caps, the two-pole caustics, and the outer gaps requires a careful analysis of their respective features. Watters et al. (2009) therefore computed a comprehensive atlas of pulsar light curves, followed by Venter et al. (2009) and later by Pierbattista et al. (2015, 2016). An atlas like this constrains the pulsar geometry, obliquity, and line-of-sight inclination. Variations of these models introduced altitude-limited outer gaps and slot gaps or low-altitude slot gaps to improve the light-curve fitting, most importantly for millisecond pulsars (Abdo et al. 2010; Venter et al. 2012).
In this paper we self-consistently include general-relativistic effects such as light bending and Shapiro time delay to compute radio and high-energy pulse profiles. We employ semi-analytical solutions for the electromagnetic field around a rotating dipole in a slowly rotating neutron star metric (Pétri 2017), generalising the classical Deutsch solution (Deutsch 1955) to realistic neutron stars treated as compact objects. As a starting exercise, we re-explore thermal radiation from hot spots onto the neutron star surface using simple assumptions. Details are given in the appendix. In Sect. 2 we recall the magnetospheric and emission models, and we also explain the photon-trajectory integration techniques in Schwarzschild space-time. In Sect. 3 we test our algorithm by computing single-photon trajectories as well as some images of the neutron star surface as seen by a distant observer. Finally, high-energy as well as radio emission maps are investigated in depth in Sect. 4. Possible frame-dragging effects for the fastest rotating pulsars are sketched in Sect. 5. Conclusions are drawn in Sect. 6.
2. Emission model
The emission model we used in our computations has been thoroughly described in Pétri (2018). However, for completeness, we recall the components required below.
1. Description of the emission sites according to the magnetic field topology. As a starting point, a rotating magnetic dipole in vacuum is employed in general relativity (GR). Excellent semi-analytical expressions are computed in Pétri (2017). Frame-dragging is negligible, and therefore the Schwarzschild metric prevails as the background gravitational field.
2. Prescription for particle composition and radiation. Particles usually follow magnetic field lines in the corotating frame, emitting mostly curvature photons along the local direction of field lines.
3. Non-thermal radiation processes also include synchrotron and inverse Compton emission as possible mechanisms for broad-band radiation, however.
4. Thermal surface emission from the heating of the polar caps, which is mainly seen in X-rays.
5. Light bending and Shapiro time delay induced by the stellar gravitational field. It is taken into account to produce sky maps.
These items are discussed in the following paragraphs. We conclude this section by discussing the numerical algorithm we used to produce our pulsar light-curves.
2.1. Electromagnetic topology
Since the work of Deutsch (1955), an exact analytical expression for a magnetic dipole rotating in vacuum is known. The general-relativistic extension to his solution was found by Pétri (2017), using a semi-analytical radial expansion into rational Chebyshev functions, which led to generalised spherical Hankel functions for outgoing waves and is denoted by 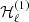 . When the metric tends to Minkowski space-time, they reduce to the standard spherical Hankel functions
. When the metric tends to Minkowski space-time, they reduce to the standard spherical Hankel functions 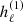 (Arfken & Weber 2005). Rezzolla et al. (2001) and Rezzolla & Ahmedov (2004) found similar expressions about general-relativistic rotating dipoles in vacuum without numerical integration.
(Arfken & Weber 2005). Rezzolla et al. (2001) and Rezzolla & Ahmedov (2004) found similar expressions about general-relativistic rotating dipoles in vacuum without numerical integration.
In general relativity, c/Ω is not equal to the light-cylinder radius rL because Ω is not the actual rotation rate of the neutron star as seen by a local observer in a gravitational field. The light-cylinder radius in Schwarzschild space-time rL is properly defined by the location where the corotation speed reaches the speed of light for a local observer, whose own clock ticks with proper time dτ = α dt, where 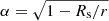 is the lapse function. There the speed of light is reached for r Ω = α c, leading to corrections to the light-cylinder radius that are given to second-order accuracy by
is the lapse function. There the speed of light is reached for r Ω = α c, leading to corrections to the light-cylinder radius that are given to second-order accuracy by
We used this value for the light-cylinder radius in general relativity. Polar cap shapes and separatrix locations were computed according to this expression. The difference between 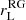 and rL is prominent only for millisecond pulsars for which
and rL is prominent only for millisecond pulsars for which 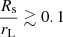 .
.
2.2. Emission sites
2.2.1. Polar cap
We studied two different types of emission that can originate from the polar caps of the pulsar. An isotropic thermal emission that does not depend on the electromagnetic field topology, such as for the black-body X-ray emission from hot spots on the stellar surface, and a non-thermal radio emission tangent to the particle motion along the magnetic field lines. The latter corresponds to the traditionally accepted view about coherent radio emission from pulsars, although it is assumed this emission takes place several stellar radii above the polar cap, up to about 10% of rL for slowly rotating pulsars (Mitra & Li 2004; Mitra et al. 2016), while the origin of radio emission in millisecond pulsars is still an open question. Our simulations are most appropriate for millisecond pulsars for which general-relativistic effects must be taken into account.
2.2.2. Slot gap
In this second picture, high-energy emission takes place along the last open field line surface, or separatrix, in what is called a slot gap (Arons 1983). This region of emission far from the star is needed to avoid strong magnetic photon absorption processes in a too strong magnetic field (Erber 1966). It is admitted that the emission is highest on the separatrix and decreases monotonically beyond this surface. Our model assumes either that emission takes places only on an infinitely thin layer along the separatrix or in a layer of thickness prescribed by the user.
2.3. Radiation properties and aberration
Particles produce photons in several ways. However, to compute a light curve,a generic emission process is enough. We do not treat broadband spectra and polarisation here; a generic emission process is sufficient for our main focus: the shape of the light curves.
The distribution of the pitch angle for particles in the comoving frame was assumed to be isotropic, resulting in an emissivity that follows the same pattern. Emissivity in the inertial frame was obtained by performing a Lorentz boost from the rest frame to the observer frame, the rest frame that not necessarily is the corotating frame.
The line of sight of the distant observer makes an angle ζ with respect to the z axis such that its direction points towards the unit vector
In several models, particles are assumed to follow magnetic field lines in the corotating frame with an isotropic distribution function in the rest frame of the fluid. The aberration formula was originally used by Dyks & Rudak (2003) to switch from the corotating frame to the observer frame. It is given by the usual textbook expression between two observers moving with constant relative velocity v with respect to each other.
To construct light curves from the pulsar magnetospheric emission, we accounted for the fact that when we consider the photon trajectory, we leave the rotating pulsar frame of reference for a static frame of reference attached to the observer. This results in the aberration phenomenon described above. To simulate aberration effects properly, we replaced n′ the unit vector of the propagation direction at the emission position of the photon in the pulsar rotating frame by its counterpart n in the observer frame.
Starting with the Minkowskian metric, the components of the two unit vectors directed along the photon trajectory are affiliated by the Lorentz transformation, given by
where 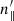 and n∥ are the components of n′ and n that are parallel to the relative velocity β = v/c, β being the normalised velocity vector of the rotating frame, which in the case of the pulsar, is equal to
and n∥ are the components of n′ and n that are parallel to the relative velocity β = v/c, β being the normalised velocity vector of the rotating frame, which in the case of the pulsar, is equal to 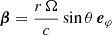 .
. 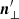 and n⊥ are the components perpendicular to β, and
and n⊥ are the components perpendicular to β, and 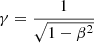 is the Lorentz factor. With the Doppler factor η defined by
is the Lorentz factor. With the Doppler factor η defined by
we obtain the usual flat space-time aberration formula such that
These quantities are not equal to the Lorentz factor and velocity measured by a local observer when gravity is included; they are coordinate quantities, not physical quantities. In a general-relativistic case, we can still use the aberration formula Eq. (7) to find n from n′, but we need to substitute β by βRG and γ by γRG such that
These are indeed the velocity and Lorentz factor as measured by a local observer for whom the flat space-time aberration formula is locally valid.
2.4. Ray-tracing in Schwarzschild metric
The radiating electromagnetic field we used was extracted from semi-analytical general-relativistic expressions. To be consistent, we have to include the relativistic effects in our investigation that will affect photons in the vicinity of the neutron star: light bending, Shapiro time delay, and gravitational redshift. As we haven’t included spectral properties of pulsar emission in our work, this study will focus on light-bending and time-delay only.
There are different approaches for ray-tracing around compact objects such as black holes or neutron stars (Vincent et al. 2011; Psaltis & Johannsen 2012; Chan et al. 2013). The method we used consists of analytically integrating the photon trajectory to obtain an integral that can be computed using any quadrature method. Although this method is not applicable to a general metric because its equation integrals are not amenable to closed formulas, it as been proven to be effective for both Scharwszchild (Pétri 2018) and Kerr (Rauch & Blandford 1994) metrics because of its speed and accuracy for large distances. This makes it particularly helpful in this work, where we had to compute millions of photon paths.
Frame-dragging effects around neutron stars are not relevant for the electrodynamics, especially for the electromagnetic field induced by a rotating magnet in vacuum, as shown by Pétri (2018). Rotation of space-time can even be reasonably neglected for millisecond pulsars. We therefore assumed that Schwarzschild space-time faithfully depicts the gravitational field around pulsars, independently of their rotation rate. We therefore do not discuss the frame-dragging phenomenon in this article. We focus on the Schwarzschild metric to describe the space-time geometry around a massive object, such as a neutron star. In spherical Boyer-Lindquist coordinates (r, θ, ϕ), the massive object is represented by only one free parameter, the Schwarzschild radius Rs,
In this metric, the trajectory of a photon is always contained within a plane defined by the location of the mass M and the initial propagation direction of that photon n. Therefore we can use a two-dimensional projection of the Schwarzschild metric that identifies the plane of the trajectory to the equatorial plane θ = π/2, leading to
r and ϕ are the polar coordinates of the photon in the plane of the trajectory. Within this induced metric, the two coordinates, distance to the origin r and angle ϕ, as used by Gonthier & Harding (1994), are related by the equation for the trajectory as
with ϕ0 and r0 the coordinates of the emission point, b the impact parameter defined as
and ψ the angle between the radial direction and the photon-emission direction n. The plus and minus sign in front of the integral apply to receding dr/dt > 0 and approaching dr/dt < 0 photons, respectively. To be able to determine the position of the photon at infinity, we replaced r in Eq. (11) by the Binet transformation 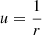 , so that when r → ∞, we have u = 0, and the integral (11) becomes
, so that when r → ∞, we have u = 0, and the integral (11) becomes
with 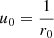 . We note the reversal of sign in front of the integral with respect to Eq. (11). More precisely, Eq. (13) has a positive sign when the photon falls on the origin of the gravitational field and a minus sign when it leaves towards infinity (and inversely for Eq. (11)).
. We note the reversal of sign in front of the integral with respect to Eq. (11). More precisely, Eq. (13) has a positive sign when the photon falls on the origin of the gravitational field and a minus sign when it leaves towards infinity (and inversely for Eq. (11)).
When the impact parameter is lower than a certain critical value given by 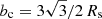 (Kraus 1998), the photon falls on the origin where the star is located. In certain cases, for b > bc, the photon approaches the star in a first stage, reaches a reversal point, and then recedes towards infinity. At this turning point, the radial coordinate of the photon trajectory reaches its minimum, which is equal to rmin. Formally, this is the root of the third-order polynomial in u defined by
(Kraus 1998), the photon falls on the origin where the star is located. In certain cases, for b > bc, the photon approaches the star in a first stage, reaches a reversal point, and then recedes towards infinity. At this turning point, the radial coordinate of the photon trajectory reaches its minimum, which is equal to rmin. Formally, this is the root of the third-order polynomial in u defined by
These equations only give the position of the photon in the plane adapted to the trajectory. For a general orientation of this plane in a full three-dimensional space, we applied three rotations to bring the photon trajectory into this adapted frame by using the Euler angles. These rotations are recalled in Appendix A.
The time coordinate of the photon was computed in the same way as for the trajectory. It is found with another integral given by Pechenick et al. (1983) and reads
with t0 the time coordinate of the date when the photon is emitted. We again used the Binet substitution 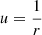 to rewrite it as
to rewrite it as
We integrate the Eqs. (13) and (16) throughout using the Clenshaw-Curtis quadrature that has been explained in depth in Press (2007). It uses fast Fourier-transform techniques that employ cosine transforms to perform Chebyshev interpolation and integration.
3. Test of the photon-trajectory integrations
Before we applied the code to realistic pulsar magnetospheres, we tested our integration scheme against simple cases such as photon trajectories in the equatorial plane and the image of a neutron star as perceived by a distant observer. The study of those two cases already provides a interesting insight of the effect that the gravitational field can have on the pulsar’s emission.
3.1. Single-photon motion in the equatorial plane
Because of the spherical symmetry of the Schwarzschild metric, it is always possible to reduce the particle motion to a plane such that θ = π/2. Photon trajectories around neutron stars are then of four kinds, depending on their receding or approaching motion and depending on whether they are captured by the horizon (in order to explore all the possibilities, we included the Schwarzschild black hole case). We distinguish
(i) photons produced at the surface that leave the star, going to infinity,
(ii) photons produced at the surface that leave the star, but return to it,
(iii) photons coming from infinity that approach the star to hit its surface, and
(iv) photons coming from infinity that approach the star, are deflected, and then return to infinity.
Typical examples of cases (i), (ii), and (iv) are shown in Fig. 1. Case (iii) is similar to case (i), except that the photon travels in the opposite direction. The Schwarzschild radius is normalised to Rs = 2 and depicted by the black circle. Case (i) in Fig. 1 shows a photon leaving the star from its surface. This type of trajectories is easily computed because the radius monotonically increases with the polar angle ϕ. This is seen by inspection of Fig. 2, which shows a mono-valued function ϕ(r). Deflection of light in the vicinity of a compact object must be handled more carefully because the photon first approaches the star with decreasing radius r, but at the turning point, it recedes to infinity by again increasing its radial coordinate r (case (iv)). Such a trajectory is shown in Fig. 1. The approaching part is coloured in light blue and the receding part in dark blue. Therefore the function ϕ(r) is multi-valued and must be treated appropriately by cutting it into two parts that are separated by the shortest distance to the centre of the star rmin, as shown in Fig. 2. The integration constants in the integral formulation of the trajectory are chosen to smoothly join both parts of the motion at the reversal point. The shortest distance rmin is found by analytically solving for the root of the third-order polynomial Eq. (14). A last check was performed for trajectories that are not expected in neutron stars but are useful for black holes. In Fig. 1, a photon emerging from the horizon is strongly deflected and then returns inside the horizon, shown as the red curve. It has an impact parameter b < bc and is therefore always captured by the horizon (case (ii)). Here the trajectory also shows a turning point associated not with a shortest distance, but with a largest distance rmax, which is also found by finding the root of Eq. (14). The polar angle function ϕ(r) is again multi-valued and must be separated in receding and returning parts, as shown in Fig. 2 with in red line. Care must be taken to smoothly join both parts of the trajectory at the turning point, which corresponds to rmax.
 |
Fig. 1. Some possible trajectories for a photon travelling around a Schwarzschild radius. Case (i) is shown in green, case (ii) in red, and case (iv) in blue. |
 |
Fig. 2. Evolution of the polar angular coordinate ϕ with respect to the radial coordinate r corresponding to the paths shown in Fig. 1. The function ϕ(r) is double-valued for trajectories showing turning points. |
3.2. Image distortion of a neutron star
To show how the gravitational field of a neutron star affects the trajectory of photons, we simulated the image seen by a distant observer of the neutron star surface. To do this, we spread emission points all around its surface, located at twice the Schwarzschild radius R = 2 Rs, which means a compactness of the neutron star of typically K = Rs/R = 0.5. Each point was separated from its neighbour by a difference of several degrees in colatitude Δθ and longitude Δϕ. The image of this surface was obtained for flat space-time associated with the Minkowski metric by tracing a line towards a hypothetical screen, a plane perpendicular to the line of sight of a distant observer.
In the general-relativistic case, we searched with a root-finding function for the emission angle θ in the interval ![$ [-\frac{\pi}{2},\frac{\pi}{2}] $](/articles/aa/full_html/2020/07/aa37979-20/aa37979-20-eq32.gif) , for which the angle ϕ(r) given by Eq. (13) is the same as the position of the observer at infinity (here we took ϕobs = 0 as the position of the observer), then we computed the impact parameter b. This impact parameter b is also the distance between the photon trajectory and a parallel line that comes from the origin when general-relativistic effects are negligible (Kraus 1998). At large distance r ≫ Rs, the impact point of the photon on the screen therefore is at a distance b from the projection of the centre of the star on the line that is the intersection of the screen and the plane containing the trajectory of the photon.
, for which the angle ϕ(r) given by Eq. (13) is the same as the position of the observer at infinity (here we took ϕobs = 0 as the position of the observer), then we computed the impact parameter b. This impact parameter b is also the distance between the photon trajectory and a parallel line that comes from the origin when general-relativistic effects are negligible (Kraus 1998). At large distance r ≫ Rs, the impact point of the photon on the screen therefore is at a distance b from the projection of the centre of the star on the line that is the intersection of the screen and the plane containing the trajectory of the photon.
We compared Minkowskian to general-relativistic images for several line-of-sight inclination angles ζ and report the case ζ = 30° in Fig. 3. General-relativistic effects enlarge the image seen by a distant observer. The important point is that a larger portion of the stellar surface is visible because of light-bending by the gravitational field of the star. This allows photons emitted from regions behind the star that are normally hidden in the Minkowskian metric to reach the observer. These effects disappear progressively when the compactness decreases, as shown in Fig. 4, where the same image is found, but for a compactness K = 0.25 (i.e. a radius of the star that is equal to eight times its gravitational radius). The apparent radius of the neutron star, noted R∞, is deduced from the impact parameter. Photons can only leave the star if |ψ| < π/2, therefore the apparent radius measured at spatial infinity immediately follows as
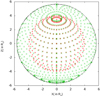 |
Fig. 3. Surface of the neutron star for a flat space-time (in red) and with general-relativistic effects (in green) for a compactness of K = 0.5 and an observer located in a direction of ζ = 30°. The black circle of radius R∞ is also shown for reference. |
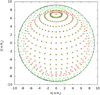 |
Fig. 4. Surface of the neutron star for a flat space-time (in red) and with general-relativistic effects (in green) for a compactness of K = 0.25 and an observer located in a direction of ζ = 30°. The black circle of radius R∞ is also shown for reference. |
R is the radial coordinate labelling the boundary of the neutron star. High compactnesses imply large apparent radii R∞, which have strong implications for the measured flux, temperature, and hot-spot area. This is beyond the scope of this work, however.
4. Magnetospheric emission
We will know apply the Schwarzschild metric and the corresponding ray-tracing techniques to simulations of the magnetospheric emission of the pulsar. This section describes the generalisation of the work presented in Pétri (2018) by including the Shapiro time-delay in addition to the light-bending and general-relativistic electromagnetic field.
4.1. Geometry of the magnetic field and Shapiro time-delay
To simulate the magnetospheric emission of a pulsar, we considered a model with gaps in the co-rotating plasma located along the last closed magnetic field lines and above the polar cap (Ruderman & Sutherland 1975; Harding et al. 2008). We traced the magnetic field lines of the neutron star using the generalisation of the Hankel function as presented in Pétri (2018). As particles are accelerated inside the gaps, we can simulate the emission of photons by curvature radiation, assuming that they are emitted tangentially to the last closed magnetic field lines as viewed from the corotating frame. To have an idea of what a distant observer will perceive from this emission, we computed the coordinates of the photon when it impacts on a celestial sphere centred on the neutron star with a radius large enough (for concreteness, set to 1000 times the light cylinder radius) to moderate the influence of the gravitational field so that photons move on straight lines to good accuracy when hitting this sphere.
We compared the sky maps in two limiting cases of space-time metrics In the Minkowskian case, we traced the tangent lines to the last closed field lines, and then added a phase shift to take the photon time of flight into account, the phase being the longitudinal coordinate on the celestial sphere while in the relativistic case, these maps were obtained by integrating Eqs. (13) and (16). The reported differences between the flat space-time and the Schwarzchild metric are due to differences in the geometry of the magnetic field lines between the two cases, as shown in Fig. 5 for the perpendicular rotator, the curvature of the photon trajectory according to general relativity, and the time delay generated by the curvature of space-time that is called the Shapiro time-delay. In Figs. 6–9 we show the effect of these different factors on the photon impact on the celestial sphere for the special case χ = 60°. For each of these figures, the null phase ϕ = 0 is defined as the date when the observer receives a photon from the magnetic north pole, that is, around the line of sight ζ = 60°. We now detail the merit of aberration, retardation, and light-bending in the construction of light curves and sky maps. In Fig. 6 we show the change in the photon direction angle when aberration and retardation are added in Minkowskian geometry. Aberration remains weak as long as photons are produced well within the light-cylinder. This is shown by the colour scale, where the deviation at the polar caps the deviation. However, when the light-cylinder is approached, the corotation drastically shifts the propagation direction, and retardation effects become strong.
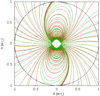 |
Fig. 5. Magnetic field lines of the pulsar in the Minkowskian case (in red) and in the relativistic case (in green) in the equatorial plane when the magnetic axis is perpendicular to the rotation axis and with (in black) the light cylinder. |
 |
Fig. 6. Projection of the Minkowskian magnetic field lines without photon-bending but with the time of flight and aberration effects in Minkowskian geometry. The colour scale depicts the angle in degrees between the emission direction of the photon at production site and its final direction projected onto the celestial sphere due to aberration and retardation. |
 |
Fig. 7. Projection of the GR magnetic field lines with light-bending, aberration, and Shapiro delay included. The colour scale depicts the angle in degrees between the emission direction of the photon at production site and its final direction projected onto the celestial sphere. |
 |
Fig. 8. Projection of the GR magnetic field lines with photon-bending and Shapiro delay. The colour scale depicts the time delay between the photon and a reference time (that of the photon emitted at the magnetic axis) expressed as a fraction of the phase. |
 |
Fig. 9. Projection of the GR magnetic field lines with photon-bending, Shapiro delay, and aberration. The colour scale depicts the difference between the Shapiro time delay and the Minkowskian time delay expressed as a fraction of the phase. |
Figure 7 shows the change in the photon direction from its emission site to infinity when all GR effects are included. The change in angle remains very similar to the Minkowskian case. The reason is that photons are emitted almost radially outwards with small angles ψ defined by the impact parameter b in Eq. (12). When ψ ≪ 1, the light-bending induced by space-time curvature is weak, which explains the good agreement between GR and Minkowskian cases. However, the shape of the polar cap is slightly modified by GR and becomes larger as a result of the combined effect of light-bending and magnetic field distortion. For an off-centred dipole or more generally non-dipolar fields showing a large angle between field lines and radial direction close to the surface, we expect larger discrepancies between Minkowskian and GR radiative properties.
Figure 8 shows the time-of-flight difference between a reference photon taken to be at the magnetic axis and an arbitrary photon emitted locally tangentially to magnetic field lines, normalised to a full period. The advance in time of photons coming from the neighbourhood of the light cylinder is almost 16%. This number comes from the delay of an almost straight-line propagation of photons from the surface to the light-cylinder, which is given by Pétri (2011) and expressed as
The approximation is valid for slow rotators with R ≪ rL.
Finally, Fig. 9 shows the error in the photon arrival time when the Shapiro delay is replaced by the Minkowskian time-of-flight approximation. There is a minimum additional time of about 5% of the period in the vicinity of the light-cylinder up to 8% of the period near the surface. We conclude that the Shapiro delay amounts to 3% difference in the arrival time of radio pulses with respect to high-energy gamma-ray pulses. The difference is most prominent at the surface where gravity has a strong influence on photon motion. Concretely, when the Shapiro delay is taken into account, we can expect an additional time lag between low-altitude radio photons and high-altitude gamma-rays of 3% of the period compared to flat space-time.
4.2. High-energy sky maps
Sky maps are a good mean to synthesise the effect of the viewing angle ζ on the pulse profile. Figures 10 and 11 show typical examples comparing flat to curved space-time, respectively, with obliquities χ ∈ {30° ,60° ,90° }, with a relevant sample of light curves assuming an inclination of the line of sight of ζ ∈ {30° ,60° ,90° }. These maps are drawn following the same procedure as for the maps of photon impacts on the celestial sphere in Sect. 4.1, but the colour code describes the intensity (more precisely, the number of photons) of the perceived radiation and the aberration effect describe in Sect. 2.3 is added. The sky maps are synchronised with the reception of the radio-pulse profile at the magnetic axis (taking to be phase zero in the plot). Comparing plots from Figs. 10 and 11, we conclude that GR tends to smear the light curves and to decrease the peak intensity levels. As summarised in Table 1, the decrease is significant for the perpendicular rotator, but it almost disappears for almost aligned rotators. This is partly due to light-bending, which spreads the photons across a broader solid angle, and additional delays induced by the Shapiro delay contribute as well. The individual pulses are very sharp because we assumed emission only from the last closed magnetic surface. More realistically, we expect a widening of the pulse profiles associated with the thickness of this surface, similar to Dyks et al. (2004) and Bai & Spitkovsky (2010), for instance. We show this effect in the following figures. However, no physical constraint is known so far to estimate the size of this layer, except maybe by fitting to gamma-ray light curves of a sample of Fermi pulsars (Abdo et al. 2013). In all cases, the pulses become narrower and extremely sharp for perpendicular rotators.
 |
Fig. 10. Emission maps for different obliquities χ (from top to bottom: 90°, 60°, and 30°) for the Minkowskian case with light curves for some several values of the inclination angle ζ (from left to right: 90°, 60°, and 30°). Maximum intensity in black and minimum intensity in white. |
 |
Fig. 11. Emission maps for different obliquities χ (from top to bottom: 90°, 60°, and 30°) for the relativistic case with light curves for some several values of the inclination angle ζ (from left to right: 90°, 60°, and 30°). Maximum intensity in black and minimum intensity in white. |
Highest intensity in high energy for various angles between the magnetic axis and the rotation axis.
The sky maps were realised assuming an infinitely thin emission layer along the last closed magnetic field lines. For a more realistic approach to the emission, we also considered a thick layer with intensity-weighted emission according to a Gaussian centred on the polar cap rim θpc with a typical spread of 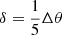 such that the weight function was set to
such that the weight function was set to
This layer encompasses magnetic field lines that cross the surface of the neutron star at a point where the difference in colatitude with the polar cap is at maximum Δθ, where Δθ was set to 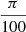 . For each photon emitted along these lines, we attributed a value to its intensity proportional to the Gaussian function w in Eq. (19). The resulting sky maps are presented in Fig. 12 for Minkowskian space-time and in Fig. 13 for general-relativistic space-time. Table 2 summarises the highest intensity in several configurations.
. For each photon emitted along these lines, we attributed a value to its intensity proportional to the Gaussian function w in Eq. (19). The resulting sky maps are presented in Fig. 12 for Minkowskian space-time and in Fig. 13 for general-relativistic space-time. Table 2 summarises the highest intensity in several configurations.
 |
Fig. 12. Emission maps for different obliquities χ (from top to bottom: 90°, 60°, and 30°) for the Minkowskian case with light curves for some values of the inclination angle ζ (from left to right: 90°, 60°, and 30°) with a thick emission layer. Maximum intensity in black and minimum intensity in white. |
 |
Fig. 13. Emission maps for different obliquities χ (from top to bottom: 90°, 60°, and 30°) for the relativistic case with light curves for some values of the inclination angle ζ (from left to right: 90°, 60°, and 30°) with a thick emission layer. Maximum intensity in black and minimum intensity in white. |
Highest intensity in high energy for various angles between the magnetic axis and the rotation axis for a thick emission layer.
Some of the fine double-peaked profiles of a thin layer are now smeared out into a broader single peak as a result of the finite thickness. This is clearly visible for cases (χ = 90° ,ζ = 90° ) and (χ = 30° ,ζ = 60° ), regardless of whether it is for flat or curved space-time.
4.3. Radio sky maps
Pulsar radio emission originates from above the polar caps, well within the light cylinder, where the magnetic field lines are still almost dipolar. To simulate this low-frequency radiation, we spread emission points across the entire polar cap surface, in an area delimited by the last closed field lines. These points were placed between the magnetic north and south poles and at each intersection between the stellar surface and one of the last closed field lines. The spacing between these points was chosen to have a homogeneous density on the polar caps. Expressed in the frame oriented along the magnetic moment, fixing a value for the longitude, the latitude θ of each of these points indexed by an integer i ∈ [0...N] is determined by the formula
This approximation is valid for θpc ≪ 1. θmp is the latitude of the magnetic pole (0° and 180° for each pole in the frame oriented along the magnetic moment), θpc is the latitude of the point where the last closed field line crosses the stellar surface, and N is the number of points we desire between the pole and the rim of the polar cap. The square-root dependence is introduced to maintain a constant surface density of sampling points and avoid an artificial concentration around the magnetic poles. The sampling has to maintain the elementary solid angle dΩ = d(cosθ) dϕ constant. We then shot single photons from each of these points and computed their impact on the celestial sphere, taking all propagation effects into account. Figure 14 shows an example of this sampling for N = 50 points between the centre and the rim of one polar cap for an orthogonal rotator.
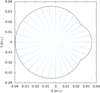 |
Fig. 14. Example of a point distribution (blue) inside the polar cap (black). The magnetic axis, located at the origin, is perpendicular to the rotation axis. |
To have realistic radio pulse profiles that are similar to the observed profiles, we attributed to every received photon a weight depending on its initial position to simulate sky maps with Gaussian radio intensity profiles, such that the weight is given by
with the width of the Gaussian controlled by σpc chosen equal to 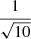 . With these parameters, we obtained the emission maps shown in Fig. 15 for Minkowski space-time and in Fig. 16 for Schwarzschild space-time. Here again, GR smears the pulse profile and moderates the maximum intensity, as reported quantitatively in Table 3.
. With these parameters, we obtained the emission maps shown in Fig. 15 for Minkowski space-time and in Fig. 16 for Schwarzschild space-time. Here again, GR smears the pulse profile and moderates the maximum intensity, as reported quantitatively in Table 3.
 |
Fig. 15. Radio emission for different angles χ of the magnetic axis (from top to bottom: 90°, 60°, and 30°) for the Minkowskian case with light curves for some several values of the inclination angle ζ. Maximum intensity in black and minimum intensity in white. |
 |
Fig. 16. Radio emission for different angles χ of the magnetic axis (from top to bottom: 90°, 60°, and 30°) for the relativistic case with light curves for some several values of the inclination angle ζ. Maximum intensity in black and minimum intensity in white. |
Highest intensity in the radio band for different angles between the magnetic axis and the rotation axis.
4.4. Multi-wavelength light curves
Finally, in order to better compare the full effect of GR on pulsar emission, we plot several representative multi-wavelength light curves extracted from the sky maps presented in Sects. 4.2 and 4.3, which are the light curves of the pulsar for different angles between the line of sight and the rotation axis. In Figs. 17–20, we plot these light curves for one value of the line-of-sight inclination angle for both radio and high-energy emission (in arbitrary units normalising the peak intensity for a better visibility of the pulses). We chose appropriate angles to show the plethora of differences expected between Minkowski and GR, although we do not claim to be exhaustive. In Fig. 17, we used (χ = 90° ,ζ = 90° ). Pulse profile shapes in radio as well as in gamma-rays are well preserved, however, because the additional Shapiro time-delay of the radio pulse profile slightly reduces the time lag between gamma-ray and radio in the relativistic case by a few percent of the period, as seen by comparing the blue and orange curves. In Fig. 18, we used (χ = 60° ,ζ = 60° ). The gamma-ray peak in the relativistic, although very narrow, there shows a different profile than in the Minkowski case. The radio profile does not vary much. In Fig. 19, we used (χ = 45° ,ζ = 50° ). The gamma-ray peak shows a complex profile; the separation of the two most prominent peaks increases in the relativistic case. Again, the radio profile is not changed. This shows a difference in the pulse shape in radio and high-energy emission that depends on the viewing geometry. In the last example of Fig. 20, where (χ = 30° ,ζ = 60° ), when the line of sight grazes the rim of the polar cap, the radio profiles are very different because the Schwarzschild metric broadens the pulses, as the figure shows.
 |
Fig. 17. Radio and high-energy light curves for χ = 90° and ζ = 90°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission is shown in orange for a flat space-time and in blue for the relativistic case. |
 |
Fig. 18. Radio and high-energy light curves for χ = 60° and ζ = 60°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission is shown in orange for a flat space-time and in blue for the relativistic case. |
 |
Fig. 19. Radio and high-energy light curves for χ = 45° and ζ = 50°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission is shown in orange for a flat space-time and in blue for the relativistic case. |
 |
Fig. 20. Radio and high-energy light curves for χ = 30° and ζ = 60°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission is shown in orange for a flat space-time and in blue for the relativistic case. |
Figure 21–24 show the multi-wavelength light curves when the separatrix has a given thickness as expressed by Eq. (19). The sharp gamma-ray peaks are now smeared by the finite transversal size of the emitting layer. The time lag between radio and gamma-ray is not affected, but the gamma-ray pulse profiles and intensities can change drastically. This study therefore shows the sensitivity of the geometry of the emission sites when light curves are computed for the purpose of comparing them with those of gamma-ray pulsars. Some of the fine double gamma-ray peak pulses have disappeared, as in Fig. 21, and only a single pulse is left that is located at the same phase. Some weak gamma-ray pulses are now far more intense, for instance, around phase 0.2 in Fig. 22, which is to be compared with Fig. 18. They become as bright as the other peak. Some other sharp peaks merged into a single peak, for example, around phase 0.4 in Fig. 23. The same merging is observed in Fig. 24.
 |
Fig. 21. Radio and high-energy light curves for χ = 90° and ζ = 90°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission from a thick layer is shown in orange for a flat space-time and in blue for the relativistic case. |
 |
Fig. 22. Radio and high-energy light curves for χ = 60° and ζ = 60°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission from a thick layer is shown in orange for a flat space-time and in blue for the relativistic case. |
 |
Fig. 23. Radio and high-energy light curves for χ = 45° and ζ = 0°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission from a thick layer is shown in orange for a flat space-time and in blue for the relativistic case. |
 |
Fig. 24. Radio and high-energy light curves for χ = 30° and ζ = 60°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission from a thick layer is shown in orange for a flat space-time and in blue for the relativistic case. |
The additional time lag between radio and gamma-ray pulses can be estimated by the following simple argument. We consider photons produced at two emission heights, labelled r1 and r2. For photons propagating in the radial direction, integration in the Schwarzschild metric leads to a time lag Δt21 between pulse 2 and pulse 1 normalised to the period P such that
This lag is independent of the distance to the observer. The first term on the right-hand side corresponds to the time of flight in flat space-time, whereas the second term on the right-hand side is due to the space-time curvature and is identified as the Shapiro delay. This delay is shown in Fig. 25 for several spin parameters defined by a = R/rL and a compactness K = 0.5. We assumed that photon 2 was emitted from the surface r2 = R and varied the location of the first photon r1. As expected, the time lag is highest for fast-spinning and compact neutron stars; it reaches an additional delay of several percent with respect to flat space-time. Interestingly, the Shapiro time-delay in principle increases logarithmically with distance without bounds. If the high-energy photons are emitted well outside the light-cylinder, as is claimed for the striped wind model, this delay can be increased by about a factor two at 10 rL.
 |
Fig. 25. Shapiro time-delay Δt21/P for several spin parameters a = R/rL = {10−3, 10−2, 10−1} in red, green, and blue for a compactness K = 0.5 and assuming that one photon is emitted from a height R and 10 R, shown as the solid and dashed line, respectively. |
To conclude our work, we briefly discuss the possible effect of a rotating metric on the light-curve profiles and time lag between radio and gamma-ray pulses. We give some estimates of the corrections that this additional frame-dragging causes.
5. Discussion
The stationary gravitational field of a relativistically rotating star mainly produces two additional effects compared to Newtonian gravity: curvature of physical three-dimensional space, and dragging of inertial frames. They are related to the mass M and angular momentum J of the star, respectively. This translates into two parameters without dimension, the compactness K and the spin a/Rg, which are defined by
We assumed a homogeneous and uniform density inside the star with a moment of inertia I = 2/5 M R2. For normal pulsars with period above 100 ms, the spin can safely be ignored because a ≲ 10−2. Even for millisecond pulsars, Pétri (2017) showed that frame-dragging does not affect the electromagnetic field geometry. The effect of a stationary axisymmetric metric induced by stellar rotation is irrelevant for pulsar magnetospheric emission. By investigating semi-analytically general-relativistic rotating multipolar electromagnetic fields, Pétri (2017) found no noticeable discrepancies in the magnetic field geometry between a Schwarzschild and a slowly rotating neutron star metric for R/rL ≲ 0.1. Consequently, the difference in light curves between the Schwarzschild metric and a rotating metric will be smaller than between flat and Schwarzschild space-times. Moreover, frame-dragging decreases with radius r as 1/r3, therefore it can only be felt by photons that are emitted close to the stellar surface by the fastest-rotating millisecond pulsars with periods P ≲ 5 ms, thus with a ≳ 0.1. Furthermore, to complicate the study even more, multipolar magnetic fields are certainly present for millisecond pulsars and are required to understand their complex pulse profile structure. Consequently, rotating metrics are surely important, but so are the non-dipolar surface fields for these particular millisecond pulsars.
In order to better assess the corrections required by the rotating space-time, we solved the photon trajectories in the equatorial plane of a Kerr black hole (Kerr 1963). Quantitative results are shown for the light-bending in Fig. 26 and for the Shapiro time-delay in Fig. 27 in the equatorial plane of the Kerr metric for a neutron star with a compactness K = Rs/R = 0.5 and an observer at a distance D = 103 Rg. Some photon orbits remain in the equatorial plane with θ = π/2. Their equations of motion depend on an affine parameter σ such that d/dσ = r2 d/ds and
 |
Fig. 26. Photon light-bending for a Kerr metric with spin parameter a and a compactness K = 0.5, assuming photons emitted from close to the surface at r = 4 Rg. The impact parameter b is normalised to Rg. |
 |
Fig. 27. Shapiro time-delay for a Kerr metric with spin parameter a and a compactness K = 0.5, assuming photons emitted from close to the surface at r = 4 Rg. The impact parameter b is normalised to Rg. The observer is located at D = 103 Rg. |
see for instance Misner et al. (1973). We can then determine the trajectory by integration of dϕ/dr and the time delay by integration of dt/dr, as in the Schwarzschild case, see Eqs. (13) and (16). The normalised spin parameter varies between −1 and 1, and the impact parameter b is in the range b ∈ [0, 4 Rg]. For slow rotation, as expected, the differences between Schwarzschild and Kerr are very small.
All the sky maps and light curves we presented here show a north-south symmetry, which means that a pulsar with obliquity χ produces the same emission pattern as another pulsar with an obliquity π − χ, the only difference is a shift of 180° in phase ϕ. This shift is irrelevant to observations, however, because an absolute phase cannot be defined. This symmetric behaviour has been found in the flat Deutsch solution, and it remains for its extension to the Schwarzschild metric, which is by definition spherically symmetric. This property is preserved when we consider an axisymmetrically rotating star as described for instance approximately by the rotating black hole metric or by the slowly rotating neutron star metric (Hartle & Thorne 1968). These metrics are also axially symmetric and preserve the north-south symmetry. Therefore they will not affect the sky maps and the emission properties remain indistinguishable between a pulsar with obliquity χ and its complementary with obliquity π − χ. This situation is reminiscent of the computation of the pulsed emission when we switch from a static dipole to a rotating dipole (Deutsch) in flat space-time. The symmetry in the former magnetic field geometry is preserved in the latter field structure. Only a structure like an off-centred dipole can break the north-south symmetry (Kundu & Pétri 2017), which leads to different asymmetrical polar cap shapes and light curves.
6. Conclusion
We numerically investigated the effects of the gravitational field of a neutron star on its image and its magnetospheric emission by curvature radiation. We demonstrated that the gravitational field affects its emission as observed by a distant observer, according to general relativity. We noted a slight shift in phase between Minkowskian and GR space-time when multi-wavelength pulse profiles were considered. The effects arebarely perceptible, however, except for millisecond pulsars.
In future developments of our model, we plan to simulate phase-resolved spectra focusing on the gravitational redshift and polarisation of emitted photons. Frame-dragging can be added by replacing the Schwarzschild metric by the Kerr metric. Other radiation mechanisms such as synchrotron and inverse Compton emission will be considered for a more complete approach of relativistic effects on the properties of pulsar radiation. When the model is fully complete and self-consistently includes all GR effects, we will apply it to some pulsars that are simultaneously detected in radio and in the high-energy MeV/GeV band, as reported by the second Fermi catalogue, see Abdo et al. (2013).
Acknowledgments
This work has been partly supported by CEFIPRA grant IFC/F5904-B/2018. We also acknowledge the High Performance Computing center of the University of Strasbourg for supporting this work by providing scientific support and access to computing resources. Part of the computing resources were funded by the Equipex Equip@Meso project (Programme Investissements d’Avenir) and the CPER Alsacalcul/Big Data.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 712, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Atwood, W. B., et al. 2013, ApJS, 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Arfken, G. B., & Weber, H. J. 2005, Mathematical Methods for Physicists, 6th edn. (Boston: Elsevier) [Google Scholar]
- Arons, J. 1983, ApJ, 266, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Spitkovsky, A. 2010, ApJ, 715, 1270 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2002, ApJ, 566, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Bilous, A. V., Watts, A. L., Harding, A. K., et al. 2019, ApJ, 887, L23 [CrossRef] [Google Scholar]
- Bogdanov, S., Rybicki, G. B., & Grindlay, J. E. 2007, ApJ, 670, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, C.-K., Psaltis, D., & Özel, F. 2013, ApJ, 777, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Ho, C., & Ruderman, M. 1986, ApJ, 300, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Daugherty, J. K., & Harding, A. K. 1996, ApJ, 458, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Deutsch, A. J. 1955, Ann. Astrophys., 18, 1 [NASA ADS] [Google Scholar]
- Dyks, J., & Rudak, B. 2003, ApJ, 598, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Dyks, J., Harding, A. K., & Rudak, B. 2004, ApJ, 606, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Erber, T. 1966, Rev. Mod. Phys., 38, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Gonthier, P. L., & Harding, A. K. 1994, ApJ, 425, 767 [CrossRef] [Google Scholar]
- Harding, A. K., Stern, J. V., Dyks, J., & Frackowiak, M. 2008, ApJ, 680, 1378 [NASA ADS] [CrossRef] [Google Scholar]
- Hartle, J. B., & Thorne, K. S. 1968, ApJ, 153, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Hewish, A., Bell, S. J., Pilkington, J. D. H., Scott, P. F., & Collins, R. A. 1968, Nature, 217, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Kerr, R. P. 1963, Phys. Rev. Lett., 11, 237 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kirk, J. G., Skjæraasen, O., & Gallant, Y. A. 2002, A&A, 388, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, U. 1998, Rel. Astrophys., 66 [CrossRef] [Google Scholar]
- Kundu, A., & Pétri, J. 2017, MNRAS, 471, 3359 [CrossRef] [Google Scholar]
- Lyne, A. G., & Manchester, R. N. 1988, MNRAS, 234, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Misner, C. W., Thorne, K. S., Wheeler, J. A., & Kaiser, D. I. 1973, Gravitation (Princeton, NJ: Princeton University Press) [Google Scholar]
- Mitra, D., & Li, X. H. 2004, A&A, 421, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mitra, D., Basu, R., Maciesiak, K., et al. 2016, ApJ, 833, 28 [CrossRef] [Google Scholar]
- Morini, M. 1983, MNRAS, 202, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Pechenick, K. R., Ftaclas, C., & Cohen, J. M. 1983, ApJ, 274, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Pierbattista, M., Harding, A. K., Grenier, I. A., et al. 2015, A&A, 575, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierbattista, M., Harding, A. K., Gonthier, P. L., & Grenier, I. A. 2016, A&A, 588, A137 [CrossRef] [EDP Sciences] [Google Scholar]
- Poutanen, J., & Gierliński, M. 2003, MNRAS, 343, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H. 2007, Numerical Recipes the Art of Scientific Computing (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Psaltis, D., & Johannsen, T. 2012, ApJ, 745, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J. 2011, MNRAS, 412, 1870 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J. 2013, MNRAS, 433, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J. 2014, MNRAS, 439, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J. 2016, MNRAS, 455, 3779 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J. 2017, MNRAS, 472, 3304 [CrossRef] [Google Scholar]
- Pétri, J. 2018, MNRAS, 477, 1035 [CrossRef] [Google Scholar]
- Rauch, K. P., & Blandford, R. D. 1994, ApJ, 421, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., & Ahmedov, B. J. 2004, MNRAS, 352, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., Ahmedov, B. J., & Miller, J. C. 2001, MNRAS, 322, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. A., & Sutherland, P. G. 1975, ApJ, 196, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venter, C., Harding, A. K., & Guillemot, L. 2009, ApJ, 707, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Venter, C., Johnson, T. J., & Harding, A. K. 2012, ApJ, 744, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Viironen, K., & Poutanen, J. 2004, A&A, 426, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vincent, F. H., Paumard, T., Gourgoulhon, E., & Perrin, G. 2011, Class. Quant. Grav., 28, 225011 [NASA ADS] [CrossRef] [Google Scholar]
- Watters, K. P., Romani, R. W., Weltevrede, P., & Johnston, S. 2009, ApJ, 695, 1289 [NASA ADS] [CrossRef] [Google Scholar]
- Özel, F., & Freire, P. 2016, ARA&A, 54, 401 [Google Scholar]
Appendix A: Trajectory of a photon in three dimensions
As the trajectory of a photon in the Schwarzschild metric is always contained in a plane, we can trace its path in space by first tracing it into a two-dimensional plane chosen to be the equatorial plane and then use the Euler rotation matrix to switch back to the full three-dimension space.
Introducing the usual three Euler angles as the precession α, the nutation β, the proper rotation γ, and the corresponding rotation matrices along the z-axis
then along the new x′-axis
and finally, along the new z″-axis
the Euler rotation matrix is given by
First we assume a new frame where a point is located by its coordinates x′, y′, and z′ and where the emission point of a photon and its initial direction of propagation are contained in the plane z′ = 0. To obtain the coordinate of a point, such as the emission point, in the new frame from the points in the initial frame (x, y and z), we use the relation deduced from the Euler rotation matrix (A.4) such that
By calling p the intersection point of the plane z = 0 and the initial direction of propagation of the photon, A is the angle between the x-axis and a line passing through the origin and p, and B is the angle between the plane z = 0 and the initial direction of propagation of the photon. After tracing the trajectory of the photon in the plane z′ = 0, we deduce the coordinates in space, in the initial frame, of any point of the trajectory by using the reciprocal transformation given by
This unfortunately only works for spherically symmetric space-times. For rotating metrics, we would have to directly perform full three-dimensional integrations.
Appendix B: Thermal flux from the polar caps
A first interesting application of ray-tracing around neutron stars concerns its thermal X-ray emission from rotating hot spots located around the magnetic poles on the stellar surface. This emission is mostly seen in X-rays and is useful to constrain the stellar mass-radius ratio M/R and therefore its compactness. In this section, we compute sky maps of X-ray light curves similar to the sky maps employed for pulsed high-energy magnetospheric emission. We take general-relativistic effects in a Schwarzschild space-time fully into account: light bending, redshift, and Shapiro delay.
The polar caps, that is, the regions delimited by the last closed field lines when they cross the neutron star surface, are thought to be hot spots that emit like a black body with a temperature of about 100 eV, which therefore is mainly observed in X-rays. The flux received by a distant observer from these two hots pots, assuming a pure dipole, is affected by general-relativistic effects induced by the mass of the neutron star. We simulated the flux emitted by the polar caps. We compared the results for a distant observer when the observer is located in a flat space-time and in the Schwarzchild metric.
Following the notations of Bogdanov et al. (2007), we introduce several angles such as the angle α between the rotation axis and the magnetic axis, the angle ξ between the hot-spot velocity vector and the direction of the line of sight, expressed by
and the angle i between the rotation axis and the direction of the line of sight. Lastly, φ is the pulsar phase. The expression of the observed flux per unit frequency ν emitted by each polar cap then reads
where I(θ) is the intensity of the emission from one polar cap of surface area dS. For the remainder of this section, we admit an isotropic emission pattern with a constant intensity I(θ) that does not depend on θ. η is the Doppler factor measured by a local observer and is expressed as
with its local three-velocity along the eφ axis
where P is the pulsar rotation period. The Lorentz factor is simply related to this three-velocity by
Considering ψ as the polar cap position, that is, the angle between the magnetic axis and the line of sight (Viironen & Poutanen 2004; Poutanen & Gierliński 2003), we found
The plus sign corresponds to the primary polar cap, and the minus sign to the antipodal polar cap (or secondary pole). ψ is equal to ϕ(u) in Eq. (13) when ϕ0 = 0 and r → ∞ (i.e. when u is null), so that we can find θ from Eqs. (13) and (B.6). We compute the received flux using Eq. (B.2). Thus
With Eq. (11), we compute 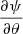 and obtain
and obtain
or by the usual change of variable with u = 1/r,
with the impact parameter derivative given by
When ψ → 0, we use the asymptotic limit 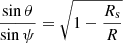 such that the flux simplifies to
such that the flux simplifies to
In the Minkowskian flat space-time, there is no light-bending effect, that is, cosψ = cosθ, and the received flux reduces to
In all cases, the received flux must be considered as null if θ is not in the interval ![$ [-\frac{\pi}{2};\frac{\pi}{2}] $](/articles/aa/full_html/2020/07/aa37979-20/aa37979-20-eq69.gif) because photons cannot travel through the star (the other cases when
because photons cannot travel through the star (the other cases when ![$ \theta \not \in [-\frac{\pi}{2};\frac{\pi}{2}] $](/articles/aa/full_html/2020/07/aa37979-20/aa37979-20-eq70.gif) correspond to photons pointing towards the centre of the star through the crust and must be discarded).
correspond to photons pointing towards the centre of the star through the crust and must be discarded).
The neutron star flux as measured on Earth is the sum of the flux emitted from the two polar caps. However, we need to add a delay to the actual phase in order to take the time of flight of the photon in the Schwarzschild metric into account. In Minkowski space-time, this is simply the time delay produced by the distance between the centre of the star and the observer, divided by the speed of light c plus the retarded time given by Roemer delay that is due to the finite propagation speed of light,
with nobs the unit vector directed towards the observer, starting from the emission point. However, in general relativity, the time of flight must be modified in order to include the Shapiro delay following Eq. (16).
Fully self-consistent and general-relativistic light curve computations require light-bending, gravitational redshift, and Shapiro delay. All these effects are now presented in several sky maps. In all situations, the observer is placed at large distances where gravitational effects can be neglected. Typically, we set its distance to D = 104 R, where general-relativistic effects caused by the gravitational field of the neutron star are expected to remain lower than 10−3. The neutron star obliquity is set to χ = 45°.
Figure B.1 shows the flux received for the Minkowskian metric, where all the relativistic effects have been removed. A full period is normalised to phase equal to one, and the highest flux is also normalised. An S-shaped black stripe with vanishing flux clearly separates the two hot spots in the diagram. The two emission regions are well separated in the phase-inclination of the line-of-sight plane. In general relativity, the situation is much less clear, as we show in the sky maps of Fig. B.2, which represent the flux received from a neutron star of compactness Rs/R = 0.5. Both hot spots are visible for a much longer period, with significant overlapping emission.
 |
Fig. B.1. Flux received from the two polar caps by a distant observer with an angle of χ = 45° between the magnetic axis and the rotation axis in the Minkowskian case. |
 |
Fig. B.2. Flux received from the two polar caps by a distant observer with an angle of χ = 45° between the magnetic axis and the rotation axis in the relativistic case. |
Compared to flat space-time, general-relativistic effects produce a more homogeneous distribution of the flux with respect to the phase, essentially because of light-bending, which we have discussed in Sect. 3.2. The pulse profiles are smeared out. We also note a shift in the phase of the minimum flux received in the Minkowskian case compared to the relativistic case, see Fig. B.7. In the GR case, the second pole becomes apparent, which is not the case in the Minkowskian case. We kept the information about the absolute intensity in order to show the decrease in flux that is induced by GR with respect to flat space-time. This shift is independent of a time delay induced by the curvature of the light ray, as we show in Figs. B.3–B.4, where we did not add the shift in phase due to the photon time of flight.
 |
Fig. B.3. Flux received in the Minkowskian case for a line of sight and a magnetic axis that form an angle of 45° with the rotation axis. The emission from each of the polar caps is shown as the dotted line, the sum of the two is shown in red, and the sum without the flight time is plotted in purple. |
 |
Fig. B.4. Flux received in the relativistic case for a line of sight and a magnetic axis that form an angle of 45° with the rotation axis. The emission from each of the polar cap is shown as the dotted line, the sum of the two is shown in red, and the sum without the flight time is plotted in purple. |
This shift between the minima of flux received is due to the addition of the two fluxes from each polar cap because in the Schwarzschild metric, the hot spots are visible for a longer time for one phase because of the light-bending, as explained in Sect. 3.2.
The time of flight affects the pulse profiles because several photons can pile up at a time or be smeared in time. Compared to the profile shown in Fig. B.4, where the highest intensity exceeds 2.5 × 10−6, the maximum of intensity is slightly lower than 2.5 × 10−6 when Shapiro delay is removed.
A last comparison is performed in Fig. B.5, where we show sky maps without time-of-flight effects in the Minkowskian case. In Fig. B.6, we show this for general relativity. In GR, we note a change in the phase region where the flux is lowest, around phase ϕ = 0.2 and phase ϕ = 0.6. Accurate pulse profile modelling therefore requires a careful analysis of the Shapiro delay for a realistic investigation of the neutron star surface emission.
 |
Fig. B.5. Flux received from the two polar gap by a distant observer with an angle of 45° between the magnetic axis and the rotation axis in the minkowskian case without flight time. |
 |
Fig. B.6. Flux received from the two polar gaps by a distant observer with an angle of 45° between the magnetic axis and the rotation axis in the relativistic case without flight time. |
In order to increase computational speed or to perform analytical work, an approximate expression is used for light-bending, as reported by Beloborodov (2002). It replaces the integral Eq. (13) by the simpler expression
This expression, although simple, is precise enough for realistic neutron star compactnesses. In Fig. B.7, we compute the flux expected from the Beloborodov approximation.
 |
Fig. B.7. Flux received in the relativistic case, with approximation (B.14), for a line of sight and a magnetic axis that form an angle of 45° with the rotation axis. The emission from each of the polar caps is shown as the dotted line, the sum of the two is shown in red, the relativistic case is plotted in purle, and the Minkowskian case is presented in blue. |
The difference between Minkowskian and GR is substantial, as is seen for instance for the orthogonal rotator in the equatorial plane, Fig. B.8. It shows the very good agreement between Beloborodov (2002) and GR computations.
 |
Fig. B.8. Flux received from the two polar caps for a line of sight and a magnetic axis perpendicular to the rotation axis in a flat space-time (red), in the relativistic case (green), and with the Beloborodov approximation (blue). |
All Tables
Highest intensity in high energy for various angles between the magnetic axis and the rotation axis.
Highest intensity in high energy for various angles between the magnetic axis and the rotation axis for a thick emission layer.
Highest intensity in the radio band for different angles between the magnetic axis and the rotation axis.
All Figures
 |
Fig. 1. Some possible trajectories for a photon travelling around a Schwarzschild radius. Case (i) is shown in green, case (ii) in red, and case (iv) in blue. |
| In the text | |
 |
Fig. 2. Evolution of the polar angular coordinate ϕ with respect to the radial coordinate r corresponding to the paths shown in Fig. 1. The function ϕ(r) is double-valued for trajectories showing turning points. |
| In the text | |
 |
Fig. 3. Surface of the neutron star for a flat space-time (in red) and with general-relativistic effects (in green) for a compactness of K = 0.5 and an observer located in a direction of ζ = 30°. The black circle of radius R∞ is also shown for reference. |
| In the text | |
 |
Fig. 4. Surface of the neutron star for a flat space-time (in red) and with general-relativistic effects (in green) for a compactness of K = 0.25 and an observer located in a direction of ζ = 30°. The black circle of radius R∞ is also shown for reference. |
| In the text | |
 |
Fig. 5. Magnetic field lines of the pulsar in the Minkowskian case (in red) and in the relativistic case (in green) in the equatorial plane when the magnetic axis is perpendicular to the rotation axis and with (in black) the light cylinder. |
| In the text | |
 |
Fig. 6. Projection of the Minkowskian magnetic field lines without photon-bending but with the time of flight and aberration effects in Minkowskian geometry. The colour scale depicts the angle in degrees between the emission direction of the photon at production site and its final direction projected onto the celestial sphere due to aberration and retardation. |
| In the text | |
 |
Fig. 7. Projection of the GR magnetic field lines with light-bending, aberration, and Shapiro delay included. The colour scale depicts the angle in degrees between the emission direction of the photon at production site and its final direction projected onto the celestial sphere. |
| In the text | |
 |
Fig. 8. Projection of the GR magnetic field lines with photon-bending and Shapiro delay. The colour scale depicts the time delay between the photon and a reference time (that of the photon emitted at the magnetic axis) expressed as a fraction of the phase. |
| In the text | |
 |
Fig. 9. Projection of the GR magnetic field lines with photon-bending, Shapiro delay, and aberration. The colour scale depicts the difference between the Shapiro time delay and the Minkowskian time delay expressed as a fraction of the phase. |
| In the text | |
 |
Fig. 10. Emission maps for different obliquities χ (from top to bottom: 90°, 60°, and 30°) for the Minkowskian case with light curves for some several values of the inclination angle ζ (from left to right: 90°, 60°, and 30°). Maximum intensity in black and minimum intensity in white. |
| In the text | |
 |
Fig. 11. Emission maps for different obliquities χ (from top to bottom: 90°, 60°, and 30°) for the relativistic case with light curves for some several values of the inclination angle ζ (from left to right: 90°, 60°, and 30°). Maximum intensity in black and minimum intensity in white. |
| In the text | |
 |
Fig. 12. Emission maps for different obliquities χ (from top to bottom: 90°, 60°, and 30°) for the Minkowskian case with light curves for some values of the inclination angle ζ (from left to right: 90°, 60°, and 30°) with a thick emission layer. Maximum intensity in black and minimum intensity in white. |
| In the text | |
 |
Fig. 13. Emission maps for different obliquities χ (from top to bottom: 90°, 60°, and 30°) for the relativistic case with light curves for some values of the inclination angle ζ (from left to right: 90°, 60°, and 30°) with a thick emission layer. Maximum intensity in black and minimum intensity in white. |
| In the text | |
 |
Fig. 14. Example of a point distribution (blue) inside the polar cap (black). The magnetic axis, located at the origin, is perpendicular to the rotation axis. |
| In the text | |
 |
Fig. 15. Radio emission for different angles χ of the magnetic axis (from top to bottom: 90°, 60°, and 30°) for the Minkowskian case with light curves for some several values of the inclination angle ζ. Maximum intensity in black and minimum intensity in white. |
| In the text | |
 |
Fig. 16. Radio emission for different angles χ of the magnetic axis (from top to bottom: 90°, 60°, and 30°) for the relativistic case with light curves for some several values of the inclination angle ζ. Maximum intensity in black and minimum intensity in white. |
| In the text | |
 |
Fig. 17. Radio and high-energy light curves for χ = 90° and ζ = 90°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission is shown in orange for a flat space-time and in blue for the relativistic case. |
| In the text | |
 |
Fig. 18. Radio and high-energy light curves for χ = 60° and ζ = 60°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission is shown in orange for a flat space-time and in blue for the relativistic case. |
| In the text | |
 |
Fig. 19. Radio and high-energy light curves for χ = 45° and ζ = 50°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission is shown in orange for a flat space-time and in blue for the relativistic case. |
| In the text | |
 |
Fig. 20. Radio and high-energy light curves for χ = 30° and ζ = 60°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission is shown in orange for a flat space-time and in blue for the relativistic case. |
| In the text | |
 |
Fig. 21. Radio and high-energy light curves for χ = 90° and ζ = 90°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission from a thick layer is shown in orange for a flat space-time and in blue for the relativistic case. |
| In the text | |
 |
Fig. 22. Radio and high-energy light curves for χ = 60° and ζ = 60°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission from a thick layer is shown in orange for a flat space-time and in blue for the relativistic case. |
| In the text | |
 |
Fig. 23. Radio and high-energy light curves for χ = 45° and ζ = 0°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission from a thick layer is shown in orange for a flat space-time and in blue for the relativistic case. |
| In the text | |
 |
Fig. 24. Radio and high-energy light curves for χ = 30° and ζ = 60°. The radio emission is plotted in red for a flat space-time and in green for the relativistic case, and the high-energy emission from a thick layer is shown in orange for a flat space-time and in blue for the relativistic case. |
| In the text | |
 |
Fig. 25. Shapiro time-delay Δt21/P for several spin parameters a = R/rL = {10−3, 10−2, 10−1} in red, green, and blue for a compactness K = 0.5 and assuming that one photon is emitted from a height R and 10 R, shown as the solid and dashed line, respectively. |
| In the text | |
 |
Fig. 26. Photon light-bending for a Kerr metric with spin parameter a and a compactness K = 0.5, assuming photons emitted from close to the surface at r = 4 Rg. The impact parameter b is normalised to Rg. |
| In the text | |
 |
Fig. 27. Shapiro time-delay for a Kerr metric with spin parameter a and a compactness K = 0.5, assuming photons emitted from close to the surface at r = 4 Rg. The impact parameter b is normalised to Rg. The observer is located at D = 103 Rg. |
| In the text | |
 |
Fig. B.1. Flux received from the two polar caps by a distant observer with an angle of χ = 45° between the magnetic axis and the rotation axis in the Minkowskian case. |
| In the text | |
 |
Fig. B.2. Flux received from the two polar caps by a distant observer with an angle of χ = 45° between the magnetic axis and the rotation axis in the relativistic case. |
| In the text | |
 |
Fig. B.3. Flux received in the Minkowskian case for a line of sight and a magnetic axis that form an angle of 45° with the rotation axis. The emission from each of the polar caps is shown as the dotted line, the sum of the two is shown in red, and the sum without the flight time is plotted in purple. |
| In the text | |
 |
Fig. B.4. Flux received in the relativistic case for a line of sight and a magnetic axis that form an angle of 45° with the rotation axis. The emission from each of the polar cap is shown as the dotted line, the sum of the two is shown in red, and the sum without the flight time is plotted in purple. |
| In the text | |
 |
Fig. B.5. Flux received from the two polar gap by a distant observer with an angle of 45° between the magnetic axis and the rotation axis in the minkowskian case without flight time. |
| In the text | |
 |
Fig. B.6. Flux received from the two polar gaps by a distant observer with an angle of 45° between the magnetic axis and the rotation axis in the relativistic case without flight time. |
| In the text | |
 |
Fig. B.7. Flux received in the relativistic case, with approximation (B.14), for a line of sight and a magnetic axis that form an angle of 45° with the rotation axis. The emission from each of the polar caps is shown as the dotted line, the sum of the two is shown in red, the relativistic case is plotted in purle, and the Minkowskian case is presented in blue. |
| In the text | |
 |
Fig. B.8. Flux received from the two polar caps for a line of sight and a magnetic axis perpendicular to the rotation axis in a flat space-time (red), in the relativistic case (green), and with the Beloborodov approximation (blue). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



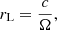
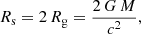
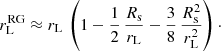
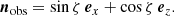
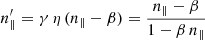
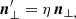
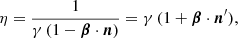
![$$ \begin{aligned} {\boldsymbol{n}} = \frac{1}{\eta } \left[ {\boldsymbol{n}}^{\prime } + \gamma \left( \dfrac{\gamma }{\gamma +1} \, ({\boldsymbol{\beta }} \cdot {\boldsymbol{n}}^{\prime }) + 1 \right) {\boldsymbol{\beta }} \right] . \end{aligned} $$](/articles/aa/full_html/2020/07/aa37979-20/aa37979-20-eq17.gif)
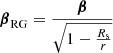
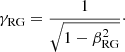
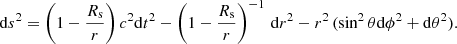
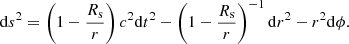
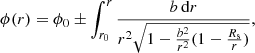
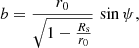
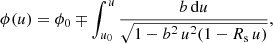
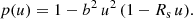
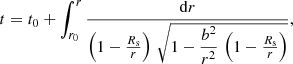
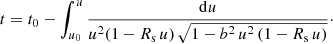
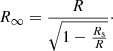
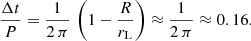
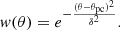
![$$ \begin{aligned} \theta _i - \theta _{\rm mp}= \arccos \left[ 1 - \left( 1 - \cos \theta _{\rm pc} \right) \, \frac{i}{N} \right] \approx \theta _{\rm pc} \, \sqrt{\frac{i}{N}}\cdot \end{aligned} $$](/articles/aa/full_html/2020/07/aa37979-20/aa37979-20-eq38.gif)
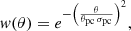
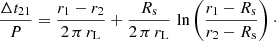
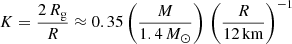
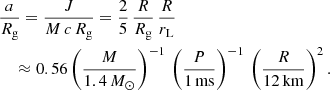
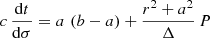
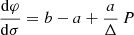
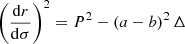
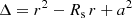
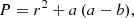
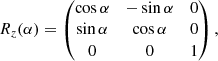
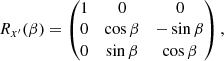
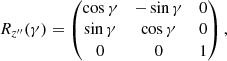
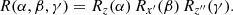
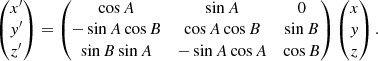

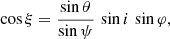
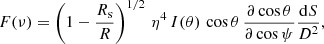
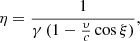
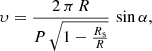
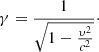
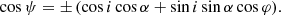
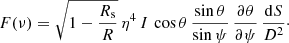
![$$ \begin{aligned} \dfrac{\partial \psi }{\partial \theta } = \int _{R}^{\infty } \frac{b^{\prime }(\theta ) \, \mathrm{d}r}{r^{2} \left[ 1 - \dfrac{b(\theta )^{2}}{r^{2}} \, \left(1-\frac{R_{\rm s} }{r}\right) \right]^{3/2}} , \end{aligned} $$](/articles/aa/full_html/2020/07/aa37979-20/aa37979-20-eq63.gif)
![$$ \begin{aligned} \dfrac{\partial \psi }{\partial \theta } = \int _{0}^{u} \frac{b^{\prime }(\theta )\,\mathrm{d}u}{\left[1-b(\theta )^{2} \, u^{2} \, (1-u \,R_{\rm s} )\right]^{3/2}} , \end{aligned} $$](/articles/aa/full_html/2020/07/aa37979-20/aa37979-20-eq64.gif)