| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 25 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202040020 | |
| Published online | 19 October 2021 | |
Frequency-resolved radio and high-energy emission of pulsars
Université de Strasbourg, CNRS, Observatoire Astronomique de Strasbourg, UMR 7550, 67000 Strasbourg, France
e-mail: quentin.giraud@astro.unistra.fr
Received:
30
November
2020
Accepted:
9
August
2021
Context. Pulsars are detected as broadband electromagnetic emitters from the radio wavelength up to high and very high energy in the MeV, the GeV and sometimes even in the TeV range. Multiwavelength phase-resolved spectra and light curves offer an unrivaled opportunity to understand their underlying radiation mechanisms and to localize their emission sites and therefore the particle acceleration regions.
Aims. In this paper we compute pulsar multiwavelength phase-resolved light curves and spectra, assuming that both curvature and synchrotron radiation operate from inside the magnetosphere of a rotating vacuum magnet. Radio emission arises from dipolar regions above the polar caps, whereas gamma-ray energy emanates from the slot gaps in the vicinity of the separatrix between closed and open field lines.
Methods. By integrating particle trajectories within the slot gaps, we compute energy-dependent photon sky maps in the radio band (MHz−GHz) and in the gamma-ray band (from MeV to GeV) for mono-energetic distribution functions of leptons.
Results. We obtained many details of the energy-dependent light curves and phase-resolved spectra from the radio wavelength up to the gamma-ray energies. Choosing Lorentz factors of γ ≈ 30 for the secondary plasma responsible for the radio emitting particles and γ ≈ 107 for the primary beam producing gamma-ray-emitting particles limited by radiation reaction, we found realistic spectra that account for the wealth of multiwavelength pulsar observations.
Key words: radiation mechanisms: non-thermal / relativistic processes / stars: neutron / gamma rays: stars
© Q. Giraud and J. Pétri 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Neutron stars are mainly observed as pulsars, emitting regular pulses in the whole electromagnetic spectrum from the radio, through the optical and X-rays, up to gamma rays. Although it is well established that a pulsar’s surroundings must be populated with electron-positron pairs, the localization and dynamics of efficient particle acceleration and radiation sites are still poorly understood. Nevertheless, several attempts to design such regions, at least geometrically, have been proposed, such as the outer gaps (Cheng et al. 1986), the slot gaps (Arons 1983), and the polar caps (Ruderman & Sutherland 1975). By computing light curves from these locations, it is then possible to compare the merit of each site and test their ability to reproduce the observed light curves (Dyks & Rudak 2003; Dyks et al. 2004). The presence of a plasma partially or completely screening the electric field shows up in distortions of the light curves from a vacuum rotator compared to a force-free model (Bai & Spitkovsky 2010). Often in the vacuum field investigations, widely used in the literature, the associated accelerating electric fields are not taken into account self-consistently. We should, however, mention the work of Kalapotharakos et al. (2012a); Kalapotharakos et al. (2014), who used resistive plasma models with low conductivity to mimic near-vacuum electromagnetic fields. They also produced sky maps and light curves that take the accelerating electric field into account.
Watters et al. (2009) compiled an atlas of geometric light curves for young pulsars that show the essential characteristics of gamma-ray pulse profiles depending on viewing angle and obliquity. Romani & Watters (2010) then designed a tool to constrain the magnetospheric structure from these gamma-ray light curves. Venter et al. (2009) investigated the special population of millisecond gamma-ray pulsars, showing that two-pole caustics and outer gap models are favored (see also Pierbattista et al. 2015, 2016 for a large sample of pulsars fit with several emission models and Johnson et al. 2014 for a similar study on millisecond pulsars). Harding et al. (2011) produced atlases of two-pole caustics and outer gap emission models in a force-free and vacuum-retarded dipole field geometry to compare light curve features in symmetric and asymmetric slot gap cavities. Obviously, more constraints can be obtained from simultaneous radio and gamma-ray fitting (see for instance the work by Pétri 2011), assuming gamma-ray emission from the striped wind and radio emission from the polar caps.
The second Fermi gamma-ray pulsar catalog (Abdo et al. 2013) contains plenty of information about gamma-ray pulsar spectra and light curves. The gamma-ray peak separation clusters around Δ ≈ 0.5, and the radio peak usually leads the first gamma-ray peak but with some outliers. Force-free or ideal magnetohydrodynamic computations are unable to self-consistently accelerate particles and localize the emission site. Some kind of dissipation of the electromagnetic field is required in order to produce a signal detectable on Earth. So dissipation within the magnetosphere and/or wind must occur, but the precise mechanism and its efficiency are difficult to predict from first principles. Nevertheless, some dissipative magnetospheres, called force-free-inside-dissipative-outside (FIDO) magnetospheres and introduced by Kalapotharakos et al. (2012b), were used by Brambilla et al. (2015) for computing the phase-averaged and phase-resolved γ-ray spectra of eight of the brightest Fermi pulsars. They used billions of test particle trajectories to compute curvature radiation spectra in realistic fields of 107 − 109 T. Based on this work, Kalapotharakos et al. (2017) constrained the dissipation mechanism by looking at curvature radiation in the equatorial current sheet outside the light cylinder, using the spectral data of the Fermi space observatory large area telescope (Fermi/LAT). This allowed limits to be placed on the strength of the accelerating electric field. They used test particle integration in the radiation reaction limit regime in the global force-free dissipative magnetosphere, which is basically a fluid description that avoids the stringent strong field constrain faced by particle-in-cell (PIC) codes. In such a way, they were able to deduce spectra for realistic pulsar field strengths and periods. Nevertheless, starting from PIC simulations, Kalapotharakos et al. (2018) recently found a relation between the particle injection rate and the spin-down luminosity. This work shows the fruitful feedback between simulations and observations conducted to extract useful information about the nature of the particle acceleration and dissipation of the relativistic magnetized flow. Harding (2016) and Venter et al. (2018) gave recent reviews of the successful interplay between magnetospheric modeling and gamma-ray observations.
Further attempts to fit particular pulsars were carried out by other groups. For instance, Takata et al. (2007) and Hirotani (2008) used the vacuum-retarded dipole to model the outer gap of the Crab pulsar. Du et al. (2011) performed computations in the annular gap context for the Vela pulsar, and Du et al. (2012) did so for the Crab pulsar. Several millisecond pulsars were also fit by Du et al. (2013) using a static dipole. Recently, the impact of general-relativistic effects on pulsar light curves has been investigated by Pétri (2018), followed by some improvements made by Giraud & Pétri (2020), including the Shapiro delay.
The observed radio characteristics rely both on the electromagnetic field geometry and its underlying emission sites and on the particle dynamics within these gaps. The main source of electron-positron pairs in a pulsar magnetosphere arises from magnetic photo-absorption in ultra-strong magnetic fields as those present on the neutron star surface. Primary particles are accelerated to high Lorentz factors, γ ≈ 107, emitting curvature photons that themselves disintegrate into a secondary plasma made of pairs, relaxing to a lower energy of about γ ≈ 102 via synchrotron cooling on a very short timescale. Synchrotron emission from the secondary and higher generations is believed to produce optical and X-ray emission in pulsars (Romani 1996; Harding et al. 2008).
Muslimov & Harding (2003) showed that the dynamics of particle acceleration and cascading extends up to several stellar radii starting from the surface around the slot gap inner boundary. In a subsequent paper, Muslimov & Harding (2004) showed that the accelerating electric field in the slot gap remains almost constant at high altitude above the polar cap, enabling particles to reach a Lorentz factor on the order of 107.
Dyks & Rudak (2002) show that the rotation of a magnetic dipole generates an asymmetric magnetic photo-absorption above the polar caps due notably to the electric component, as already pointed out by Daugherty & Lerche (1975). Lee et al. (2010) computed the optical depth of gamma-ray photon absorption in the strong magnetic field of a neutron star, including rotation, aberration, and general relativistic effects; they found a minimum escape altitude of several stellar radii, and even several hundred kilometers for the Crab pulsar, depending on photon energy. Story & Baring (2014) improved their study by implementing near-threshold effects in the pair creation.
The acceleration of the primary beam in the vacuum gaps is quickly balanced by radiative cooling from curvature emission or resonant inverse Compton scattering on thermal X-ray from the surface. Depending on the cooling mechanism, the particle distribution function becomes almost mono-energetic, peaking at a maximum Lorentz of either about 107 (Daugherty & Harding 1989) for the former or 105 − 106 for the latter (Sturner et al. 1995). The secondary pair plasma generated by these processes get energy of about 50 − 100, according to Daugherty & Harding (1982).
Self-consistent computations of pair cascades in polar caps have been performed by several groups in the past (Timokhin 2010; Timokhin & Arons 2013; Timokhin & Harding 2015, 2019; Harding & Muslimov 2011; Harding & Kalapotharakos 2015). It is an important topic in its own right, but our purpose is not to dig into the details of such microphysics. We are instead interested in the observational signature of simple primary and secondary particle distribution functions. A much more detailed discussion of some of the used approximations and results can be found in the recent and up-to-date work by Harding et al. (2018).
The radiative properties of pulsars are usually explained with the existence of two populations of leptons, which differ in their energy and spacial distribution functions. For simplicity, two mono-energetic or two power law distributions can be considered. As is well known for pair creation physics, the low-energy population appears as a result of gamma-ray photon absorption in the strong stellar magnetic field. Such absorption is very sensitive to the geometry, namely to the angle spanned between the photon propagation and the magnetic field direction. Nevertheless, close to the surface where the magnetic field remains mainly dipolar, we expect, to a good approximation, the absorption process to be axisymmetric with respect to the magnetic moment. The origin of the two populations stems from their acceleration dynamics. The primary particles are accelerated in vacuum gaps sustained by strong parallel electric fields, whereas secondary and higher generations are produced by photon disintegrations and evolve in an almost fully screened electric field environment, disfavoring efficient acceleration to very high energies.
In our previous work, we focused our attention on the shape of the pulses emitted in the radio and gamma ray, explicitly showing the impact of gravitation on the geometry of the profiles and on the phase shift between the main radio pulse and the first gamma-ray pulse. We did not take into account the frequency characteristics of this emission, assuming it to be curvature radiation, which is a function of the point of emission and more particularly of the curvature of the field lines. But questions remain regarding their frequency distribution (for the radio and gamma-ray spectrum) and how the shape of the pulses evolves as a function of frequency or energy. This paper answers these questions by providing precise quantitative results if the emission comes from curvature and synchrotron radiation along the magnetic field lines in a flat space-time geometry. The outline of our paper is as follows. In Sect. 2 we present our magnetosphere model and the associated radiation mechanisms. Next, in Sect. 3, we show detailed results of high-energy spectra and light curves from the slot gap models, localizing the sites of efficient gamma-ray photon production that depends on the magnetic inclination angle and line of sight. In Sect. 4 the same approach is used to study the radio spectra and light curves, which depend on the geometry. Conclusions and possible extensions are summarized in Sect. 5.
2. Magnetospheric emission model
2.1. A coherent multiwavelength model
Multiwavelength modeling of radio-loud gamma-ray pulsars is usually limited to the joint computation of only one radio and one gamma-ray light curve. Although this strategy already makes it possible to constrain the geometrical parameters of the magnetosphere (Pétri 2011, Benli et al. 2021, Pétri & Mitra 2021) this is hardly satisfactory because the pulse profiles evolve as a function of frequency or energy. A detailed multifrequency investigation that coherently includes the calculation of radio and gamma-ray spectra (from, e.g., the curvature and synchrotron radiation) proves to be much more constraining and will allow the geometry of the field lines, the altitude of the photon production sites, the distribution functions of the emitting particles, and the associated light curves to be physically and quantitatively linked.
In this paper, this detailed view of broadband electromagnetic emission processes is discussed in depth. To do so, we start with a reminder of the method of calculation of the properties of the curvature and synchrotron emission, their power and characteristic frequency, applied to the pulsar magnetosphere. Then we determine the high-energy spectrum around the GeV, thus in the Fermi/LAT band, as well as some characteristic light curves to conclude on the spectra and radio pulse profiles.
2.2. Magnetosphere structure
We use the analytical expression of the electromagnetic field of a rotating dipole in vacuum as first given by Deutsch (1955). Charged particles are accelerated in gaps where the plasma present in the pulsar’s magnetosphere is not dense enough to screen the component of the electric field parallel to the magnetic field lines. In our model, those gaps are either located along the last closed magnetic field lines from the star surface up to the light cylinder, also called slot gaps (Arons 1983), or above the polar caps delimited by the last closed magnetic field lines in the polar gaps (Ruderman & Sutherland 1975). We also assume that radio and gamma-ray emission are produced by the acceleration of charged particles in those gaps through curvature radiation or decaying into the fundamental Landau level via synchrotron emission. We therefore recall the essential feature of these emission mechanisms.
The location of our emission sites follows the standard polar cap–slot gap picture (see Fig. 1). In our simulations, the radio emission starts at the stellar surface but this is due to the fact that we used a stellar radius of 0.1 rL, which is actually the estimated height of radio emission according to radio polarization data for young pulsars. For those pulsars, the surface lies well within the light cylinder R ≪ rL but using R = 0.1 rL in our computations is a good compromise between speed and accuracy. As exposed in the introduction, several groups studied the pair cascade formation around the polar caps. Some plasma instability produces bunches of pairs such as a soliton emitting coherent radio waves (Mitra 2017). The development of the instability requires time therefore space, in agreement with the expected height of h ≈ 0.1 rL.
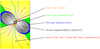 |
Fig. 1. Schematic view of several well-studied emission sites, such as the polar cap, slot gap, outer gap, and striped wind. |
The slot gaps shown in Fig. 1 cross the null surfaces depicted by thick straight lines, null surfaces that separate regions with opposite charge density in the force-free picture. So it seems difficult to understand how particles of the same charge can be continuously accelerated along such slot gaps. The point is that the electrodynamics within these gaps differ significantly from the force-free view. Indeed, slot gaps are regions near the last open field lines free of electron-positron pairs. Particle acceleration in these gaps is slower than in the polar cap for instance and the pair formation front is shifted to higher altitude, actually close to the light cylinder. Therefore, the parallel electric field E∥ is not screened, keeping the same sign all along the particle trajectories. This unscreening effect has been confirmed by a careful investigation of the slot gap electrodynamics by Muslimov & Harding (2003). Moreover Muslimov & Harding (2004) showed that the parallel accelerating electric field E∥ within these gaps tends to a constant value at high altitude above the stellar surface. Electrons are therefore accelerated to high Lorentz factors about 107 while emitting curvature photons from deep within the magnetosphere up to the light cylinder. Low and high altitude approximations found in these aforementioned works have been stuck together to a single analytical formula by Barnard (2021) for multi-TeV fitting of the Vela pulsar (Harding et al. 2018).
Primary particles accelerated within the polar caps produce gamma rays propagating in an opaque medium because of magnetic photo-absorption. They are converted into leptonic pairs and are therefore not directly detectable on Earth but are indirectly detectable via the pulsar wind and its nebula. Indeed, the first Fermi/LAT observations immediately concluded that gamma rays cannot emanate from the polar caps. Only low-energy photons can propagate through the strong magnetic field without being attenuated. Gamma rays necessarily come from higher altitudes within the magnetosphere, for instance in a slot gap, that is a thin region separating the closed field lines from the open field lines. In this interface, the electric field does not increase sharply to efficiently produce pairs contrary to the polar caps. Particles are accelerated all along the slot gaps, emitting gamma rays not absorbed by the weaker magnetic field.
2.3. Curvature radiation
The calculation of the frequency of curvature radiation is deduced from the radius of curvature ρ of the particle trajectory along the magnetic field lines, which is equal to the radius of curvature of these field lines in the corotating frame. The characteristic curvature frequency ωcurv is (Jackson 2001)
beyond which the particle no longer radiates significantly. Specifically, the shape of the curvature radiation spectrum for a particle with Lorentz factor γ is given in Jackson (2001) by
where K5/3 is the modified Bessel function of order 5/3 (Arfken & Weber 2005).
A trajectory or line in space has a curvature as well as a twist. Locally, at a point of this curvature, we associate a trihedron (T, N, M), also called Frenet’s frame, with the tangent T, normal N, and binormal M to the particle trajectory. The curvature κ indicates the change in the tangent vector T and the torsion τ indicates the variation in the osculating plane at the same point. In summary the Frenet formulas giving the variations in the basis vectors of the trihedron are
ds being the curvilinear abscissa along the trajectory. Torsion does not intervene in the calculation of the particle curvature radiation. The curvature itself is thus deduced from the derivative of the tangent T = B/B to the field lines as a function of the curvilinear abscissa s along these field lines. The curvature radius ρ is the inverse of the curvature κ of the magnetic field that is the derivative of the tangent T to the magnetic field line with respect to the curvilinear abscissa ds, so we have
We recall that the variation in the curvilinear abscissa ds is related to the variations in the coordinates of the trajectory dxi by ds2 = γik dxi dxk in any spatial geometry given by the spatial metric γik, which is the spatial projection of the space-time metric gik with respect to a given observer. In Minkowski’s space-time in Cartesian coordinates, this expression simplifies to dxi = (dx, dy, dz) and ds2 = dx2 + dy2 + dz2.
In our model, we assume that the particles follow the field lines in the reference frame corotating with the star, the frequency of the curvature radiation 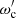 is therefore that of the rotating frame of reference (1). In order to find the frequency of the radiation emitted by our rotating pulsar and measured by a distant inertial observer at rest ωc, we must take into account the Doppler effect and perform a Lorentz transformation from the corotation frame to the inertial frame of the observer. This is equivalent to multiplying Eq. (1) by a Doppler factor η due to the neutron star rotation. We thus have
is therefore that of the rotating frame of reference (1). In order to find the frequency of the radiation emitted by our rotating pulsar and measured by a distant inertial observer at rest ωc, we must take into account the Doppler effect and perform a Lorentz transformation from the corotation frame to the inertial frame of the observer. This is equivalent to multiplying Eq. (1) by a Doppler factor η due to the neutron star rotation. We thus have 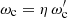 with the Doppler factor generally put in the form
with the Doppler factor generally put in the form
n being the unit vector giving the initial direction of propagation of the photon (tangent to the magnetic field line) as seen in the observer’s frame of reference and taking into account the aberration and β the corotation velocity. So n is given by the equation
where γ is the Lorentz factor of the particle accelerated in the electromagnetic field or the primary or secondary beam. The power radiated by this particle is given by
with e the elementary charge and ϵ0 the vacuum permittivity.
For curves of known geometry, this curvature can be determined analytically, as for example for a static dipole for which the equation of the field lines is known, the lines being themselves each contained in a plane. For a rotating dipole such as the Deutsch dipole or in general relativity, it is not possible to obtain an analytical expression of this curve. It must be estimated numerically by approximating the derivative (4).
Concretely, this curvature is calculated by measuring the variation ΔT of the vector tangent T to the magnetic field lines as one moves along them by a value Δs of the curvilinear abscissa s small enough that the finite difference represents a good approximation of the derivative. Typically a fraction of the radius of the star Δs ≲ R* is sufficient. We then replace κ in Eq. (4) by a discretized version. We calculate this derivative vector field by measuring the variation in the tangent vector T along a field line by varying the curvilinear abscissa s
In order to minimize discretization errors, we chose a method with centered finite differences. Knowing the local radius of curvature and the value of the magnetic field at the point of emission in the rotating frame of reference, we switch back to the spectrum of the curvature radiation in the inertial frame of reference by imposing an energy distribution function for the photon emitting leptons. The simplest situation consists in taking a mono-energy distribution of particles although a general particle population is possible.
2.4. Synchrotron radiation
Synchrotron radiation is a special case of curvature radiation where particles follow circular trajectories. This emission arises from leptons created in high Landau levels and decaying quickly to the fundamental state where the perpendicular momentum is minimal. The particle will then emit at the characteristics frequency
with the synchrotron power Psyn such that
Φ being the pitch angle of the particle. In our simulations, we assumed that particles are born with pitch angles Φ ≈ π/2. The synchrotron spectrum has a similar form as (2), only replacing ωcurv by ωsyn.
2.5. Particle population
The shape of the light curves and spectra strongly depends on the energy distribution of the radiating particles. Current models of acceleration of primary particles and creation of secondary and higher generation of pairs (tertiary, quaternary, etc.) predict a peak of the Lorentz factor around γ ≈ 106 − 107 for primaries and around γ ≈ 10 − 100 for others (Beskin et al. 1993). Although our approach is easily adapted to any particle distribution function, in this work we only consider mono-energetic particles either in the primary beam or in the secondary beam. The primary particles are responsible for the high-energy emission in the GeV band in the slot gap while the secondary particles from the cascades produce the radio emission from the polar caps.
In a more realistic picture, the particle distribution function significantly deviates from a mono-energetic one, the radiation being linearly additive, the calculation of the spectra and light curves will follow the same linear addition scheme of the individual mono-energetic contributions with respective weights corresponding to the weights imposed by the particle distribution function. For example, for a population containing N1 particles of energy γ1 and N2 particles of energy γ2, the total emission will be N1 times that of the mono-energy spectrum at γ1 to which we superimpose N2 times that of the mono-energy spectrum at γ2. A continuous distribution is then subdivided into several intervals of mono-energetic particles and the entire spectrum can be reconstructed. Our results therefore serve as a building block for the most general distribution function obtained by a post-treatment of mono-energetic distribution functions.
We now review the results for the high-energy mono-energetic and radio spectra: For each of the two cases, we have assumed that at each emission point, located along the last magnetic field lines with a curvilinear spacing Δℓ between each point, there is emission by curvature radiation considered to emanate from particles with Lorentz factors γ fixed for each wavelength. We assume that there is no emission for points located more than 95% of the light-cylinder radius Rcyl from the center of the star.
The classical estimation of the maximum Lorentz factor attainable by particles in the electromagnetic field takes into account their braking by radiation reaction in order to compensate the acceleration by the parallel electric field E∥ present in the gaps. The precise value of this field is strongly dependent on the dynamics within the gaps. By equating the radiated power (7) and the power provided by this electric field e E∥ c, the Lorentz factor becomes
In our vacuum model, E∥ ≈ 1012 V m−1 corresponds to the upper limit, that of the Deutsch field where the electric field is not screened at all. In reality, this value is much lower but the maximum Lorentz factor only varies with 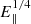 , so it is not very sensitive to a large variation in this parallel electric field.
, so it is not very sensitive to a large variation in this parallel electric field.
It is currently well accepted that the pulsar magnetosphere contains at least two different populations of particles flowing out along open magnetic field lines. The first component is made of primary particles accelerated by the strong parallel electric field in vacuum gaps up to Lorentz factors about γ ≈ 107 and with a particle density number close to the corotation density of np ≈ 2 ε0 Ω ⋅ B/e. These primary particles emit gamma-ray photons decaying into a secondary flow made of electron-positron pairs (Erber 1966) with Lorentz factor in the range γ ≈ 102 − 103 and a multiplicity factor of κ ≈ 103 − 105 (Daugherty & Harding 1982). The typical energy of curvature photons produced by each beam will therefore vary by several orders of magnitude. The radio emission is generated by the dense secondary beam whereas the high-energy emission (in the MeV and GeV energy range) is generated by the ultra-relativistic but much less dense primary beam.
In our model, we assumed a simple mono-energetic population, we typically set γg = 107 for the gamma-ray emission coming from the slot gaps whereas for the radio emission from the polar caps we take γr = 30. We also compute spectra for particles locally reaching the radiation reaction limit and possessing Lorentz factors constrained locally by Eq. (11).
Accurate simulations of pair cascades only rarely show the resultant particle distribution functions. A notable exception is given by Arendt & Eilek (2002) showing that the secondary pair plasma is well represented by a relativistic Jüttner-Synge distribution with typical temperature kB T = m c2 in its rest frame. Earlier work by Sturner et al. (1995) focused on magnetic inverse Compton pair cascade from a primary mono-energetic particle distribution but they only showed photon spectra. Medin & Lai (2010) computes pair spectra and found almost mono-energetic distribution functions sensitive to the period and surface magnetic field and peaking around several tenths or hundreds of MeV. Timokhin & Harding (2015) detailed the localization of secondary particle production, finding a larger spread in energy down to the rest mass energy (see also Harding & Muslimov 2011; Harding & Kalapotharakos 2015 for detailed pair plasma spectra and the associated curvature, synchrotron, and inverse Compton emission applied to the Crab and some other pulsars).
2.6. Emissivity
First of all, the calculation of the spectra we present in the following does not take into account the range of frequencies at which photons are emitted. We approximate the spectrum by a Dirac distribution centered on the characteristic frequency ωc (being the curvature or synchrotron frequency) and whose intensity corresponds to the total power of the integrated radiation on all frequencies of the true continuous spectrum (7) or (10). In other words, the spectrum is approximated in the corotating frame by
Each point on a field line emits photons at a single frequency given by the local characteristic frequency 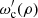 (1) or (9) associated with the local curvature of this same field line. The number of photons to consider is proportional to the total emitted power. A Lorentz transform bring all these quantities into the observer inertial frame. This contrasts sharply with our previous work (Giraud & Pétri 2020) where each position on a given field line produced only one photon of indeterminate energy. In this paper, we remove the ambiguity on frequency by incorporating details of the emission mechanism, frequency and power. Emissivity will no longer be constant along a field line but will vary according to the local curvature.
(1) or (9) associated with the local curvature of this same field line. The number of photons to consider is proportional to the total emitted power. A Lorentz transform bring all these quantities into the observer inertial frame. This contrasts sharply with our previous work (Giraud & Pétri 2020) where each position on a given field line produced only one photon of indeterminate energy. In this paper, we remove the ambiguity on frequency by incorporating details of the emission mechanism, frequency and power. Emissivity will no longer be constant along a field line but will vary according to the local curvature.
In a forthcoming step, we will consider using the full expression of the curvature radiation spectrum given by Eq. (2). Finally, in another possible extension, the most realistic situation takes into account a particle distribution function depicted by a power law such that the number of particles of Lorentz factor between γ and γ + dγ is given by
where p is the spectral index of the power law, the minimum Lorentz factor being γmin and a the maximum value being γmax. This particle distribution function produces another power law for the curvature emissivity jcurv such that
There is thus a simple relationship between the spectral index of the power distribution of particles and photons. Beyond the cutoff frequency associated with γmax the emissivity falls exponentially according to 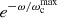 . Below the cutoff frequency associated with γmin the emissivity decreases according to another power law independent of the particle distribution and scaling as
. Below the cutoff frequency associated with γmin the emissivity decreases according to another power law independent of the particle distribution and scaling as 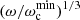 . In between these two limits, the photon spectral index is related to particle power-law distribution p. The same method applies to the synchrotron radiation although with a different relation between particle and photon index.
. In between these two limits, the photon spectral index is related to particle power-law distribution p. The same method applies to the synchrotron radiation although with a different relation between particle and photon index.
2.7. Aberration, retardation, and seep-back effects
The radio and high-energy emission of pulsars originate at high altitude in the magnetosphere, and well above the surface for young pulsars of period P ≳ 100 ms (Mitra 2017). The corotation of these emission sites at relativistic velocities imparts unique characteristics to the pulsar profiles by impacting the relationship between the geometry of the emitting zones and their observational signature.
Phillips (1992) has detailed the impact of several important effects on the arrival time of pulses of all kinds. We considered two emission zones located at an altitude of r1 and r2 > r1, respectively. For photons moving radially away from the neutron star, the delay introduced by the difference in path to be traveled becomes a phase shift for the observer
The dragging of the photon production areas by the rotation of the pulsar causes a projection of the direction of propagation of the photons in the direction of rotation due to aberration by a value of
For both emission sites, this introduces an additional time delay of
Finally, the rotation of the dipole curves the field lines in the opposite direction of rotation. Shitov (1983) gave a simple expression for this sweep-back effect, such that the delay induced amounts to
The total delay ΔtΣ is then the sum of each of these contributions ΔtΣ = Δta + Δtr + ΔtB.
We now discuss in some detail the high-energy and radio light curves and spectra for mono-energetic particle distribution functions applied to the polar cap and slot gap models of a vacuum rotating dipole.
3. High-energy emission
We are interested in the high-energy emission as measured in the Fermi/LAT (Large Area Telescope) band, between 100 MeV and 100 GeV. This Fermi/LAT telescope has detected nearly 300 gamma-ray pulsars all showing very similar spectra peaking around several GeV (Abdo et al. 2013). Our long lasting aim is to compare our predicted light curves and spectral modeling with a whole population of young and millisecond radio-loud gamma-ray pulsars. This section details the bottom line to construct general light curves and spectra from the slot gaps knowing the particle distribution function.
3.1. Thin slot gap
The locus of the last open field lines taking their root at the polar caps generates a two-dimensional surface enclosed within the light cylinder and known as the separatrix. It is sustained by a current sheet separating the dead magnetosphere with closed field lines from the active zone supported by open field lines. In an ideal plasma picture, this current sheet is infinitely thin, representing a discontinuity in the solution. In reality, due to some microphysics dynamics within the plasma, we expect this current sheet to spread around this separatrix with a depth that depends on the plasma condition (temperature, density, magnetic field strength). Therefore, in a first stage, we assumed an ideally infinitely thin gap and in a second stage we release this assumption by using a thick slot gap picture by introducing a typical scale height transverse to this surface.
3.1.1. Sky maps and light curves
We start with the sky map in Fig. 2, which shows an example of the photon energy distribution received by a distant observer from the slot gaps, in logarithmic scale, the energy Ec = ℏ ωc being obtained by multiplying the frequency of the observed radiation ωc (including Doppler and aberration effects) by Planck reduced constant ℏ. The parameters used assume an inclination angle of χ = 60° and a Lorentz factor γ = 107 for the particles accelerated in these cavities, which are typical values quoted for example in Becker et al. (2009) and in Beskin et al. (1993). For each point on the map marked by the phase and inclination of the line of sight (ϕ, ζ), in fact an area of size 0.5° ×0.5°, only the energy of the most energetic photons at that point is displayed. This map therefore reveals the GeV photon production efficiency for each couple of phase-inclination (ϕ, ζ) parameters, but without giving any indication of the actual shape of the spectra for each phase and each angle of the line of sight. We will detail these characteristics later.
 |
Fig. 2. Sky map showing the photon peak energies, in logarithmic scale, depending on the phase and line of sight for an obliquity χ = 60°. |
Knowing the power of curvature radiation Pcurv in (7) we calculate the number of photons emitted by each emission point along the magnetic field lines. In gamma rays, because of the large span in energy range, we decided to cut the energy bands into evenly spaced intervals on a logarithmic scale. Each decade is cut into two intervals so that the successive values follow a geometric progression of reason r = 101/2 ≈ 3.16. The intervals are thus of the form [rn, rn + 1] E0 with n a positive integer and E0 a characteristic energy set by default to E0 = 1 GeV. The following intervals are therefore chosen to represent the emission maps thus made for different obliquities χ, as well as some associated light curves for different line of sight inclinations ζ: from 1 to 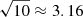 GeV as in Fig. 3, from
GeV as in Fig. 3, from 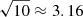 to 10 GeV as in Fig. 4, from 10 to
to 10 GeV as in Fig. 4, from 10 to 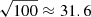 GeV as in Fig. 5 and from
GeV as in Fig. 5 and from 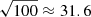 to 100 GeV as Fig. 6. Each of these maps takes into account only photons within a certain energy range, which are chosen as a geometric sequence as explained before. Most of the emission is concentrated between 3.16 and 10 GeV with a few high-energy emission points that can rise above 31.6 GeV. This feature will be detailed in the next paragraph about the spectra, demonstrating that most of the emitted photons are within the frequency range [3, 10] GeV with only a restricted area in the sky map that emits photons with an energy greater than 30 GeV.
to 100 GeV as Fig. 6. Each of these maps takes into account only photons within a certain energy range, which are chosen as a geometric sequence as explained before. Most of the emission is concentrated between 3.16 and 10 GeV with a few high-energy emission points that can rise above 31.6 GeV. This feature will be detailed in the next paragraph about the spectra, demonstrating that most of the emitted photons are within the frequency range [3, 10] GeV with only a restricted area in the sky map that emits photons with an energy greater than 30 GeV.
 |
Fig. 3. Sky maps with photon energies in [1, 3.16] GeV for obliquities χ = {90° ,60° ,30° } from top to bottom. Some light curves are shown for several inclination angles, ζ = {90° ,60° ,30° }. |
Looking at these maps, only two regions stand out with very high-energy photons, around 50 GeV, near the points (ϕ = 0.1, ζ = 90° ) and (ϕ = 0.6, ζ = 90° ). These areas are at high altitude, close to the light cylinder. The rest of the emission seems to show comparatively little variation in energy with the phase or inclination of the line of sight. The results of these maps are a nontrivial combination of the field line curvature, which varies non-monotonically with altitude (see Fig. 7), and the Doppler factor that produces a blueshift or a redshift according to the line of sight geometry (see Fig. 8). As a result, the most energetic photons are repelled toward the light cylinder, but only in regions for which the Doppler factor produces a blueshift, that is, for particles moving along the field lines in the same direction as the direction of rotation (see Fig. 9), particles moving in the opposite direction producing redshifted photons of lower energy.
 |
Fig. 7. Curvature radius depending on the position in the slot gaps for χ = 90° (projection on the xOy plane). The unit of length is the light-cylinder radius Rcyl. |
 |
Fig. 8. Doppler factor depending on the position in the slot gaps (projection on the xOY plane) for χ = 90°. |
 |
Fig. 9. Photon energy depending on the position in the slot gaps (projection on the xOy plane) for χ = 90°. |
3.1.2. Spectra
Looking at the spectra offers another perspective of pulsar multiwavelength emission properties. We began by studying the spectra of a thin slot gap without taking into account the weight assigned to each photon as a function of the radiated power (7).
Figure 10 represents the phase- and line-of-sight-averaged spectra from these gaps for different obliquities: χ = {30° ,60° ,90° }. We find a distribution consistent with what we saw in Fig. 2 for a obliquity χ = 60° (green curve) with very few photons on the highest energies side, above 50 GeV and a high concentration of photons in the center of the spectrum, around a few GeV. The range of the spectrum also varies significantly with the inclination of the magnetic dipole.
 |
Fig. 10. Phase- and line-of-sight-averaged spectra for obliquity χ = {30° ,60° ,90° } shown, respectively, in solid blue, green, and red lines without curvature radiation power weights. |
Nevertheless, from an observational as well as from a more realistic point of view, it is preferable not to average on the line of sight inclination angles since a particular observer only sees the part of the sky map in Fig. 2 corresponding to a fixed angle ζ (i.e., a horizontal line in this plot). An example of the variation in the phase-integrated spectrum (i.e., over the whole period of the pulsar) for χ = 60° is shown in Fig. 11 for different values of the line of sight inclination ζ = {30° ,60° ,90° } again respectively in sold blue, green, and red lines. We notice a great disparity in the shape and the limits of the spectra depending on the obliquity χ although the peak in the spectra remains at approximately the same energy, around 4 GeV. The smallest obliquity χ = 30° shows the tightest spectrum with an energy interval restricted to the band [3, 7] GeV. A higher obliquity with χ = 60° moves this lower limit to about 1 GeV while the upper limit increases to 8−9 GeV. In addition, a double-peak spectrum appears, with one peak at low energy around 1.5 GeV and the other remaining at 4 GeV. We show later that taking into account the curvature radiation power (7) eliminates this second low-energy peak. An even higher obliquity of χ = 90° shifts the spectrum in the opposite direction, toward the higher energies with a lower limit of 4 GeV and an upper limit of 30 GeV. As a conclusion, the observer line of sight strongly impacts the received phase-averaged spectrum. The behavior of these spectra is a direct consequence of the geometry of the field lines, their visibility by the observer, and the aberration and Doppler effects.
 |
Fig. 11. Phase-integrated spectra for χ = 60° and a line of sight inclination ζ = {30° ,60° ,90° } shown, respectively in solid blue, green, and red lines without curvature radiation weights. |
The sky map in Fig. 2 and the spectra in Figs. 10 and 11 have been made on the assumption that for each emission point along the last closed magnetic field line a single photon is emitted, that is, by applying the same procedure as in Giraud & Pétri (2020) and the successive points being separated by a certain length Δs along the field line and arbitrarily fixed by the numerical integration code. A more realistic view must take into account the effectiveness of this curvature radiation (i.e., its power spectrum). Indeed, since we know the radius of curvature of the magnetic field lines at each point, we can deduce the power radiated by a particle accelerated along them using Eq. (7). For the moment, we have not indicated the density of particles in the emitting regions, so we cannot calculate a precise flux detected on Earth, but we can give as an indication the distribution E dN/dE in energy of photons produced by the curvature radiation. The units remain arbitrary; we write them in UA.
Taking the same approach as above, examples of spectra are shown in Fig. 12. As only one value of the Lorentz factor is used, these spectra show rather abrupt decreases and increases in intensity as a function of frequency. As in the spectrum of Fig. 10, a weak flux of photons is produced with an energy above 50 GeV and a strong flux of photons for an energy in the vicinity of 5 GeV. Taking into account the modulation of the intensity of the spectrum as a function of the locally radiated power does not change the frequency range of the emitted photons. This is why the lower and upper limits of the spectra are identical in Figs. 10 and 12. Indeed, the radiated power changes the number of photons produced but not their energy.
As in Fig. 10, these spectra are averaged over the phase and line of sight inclination. A real observer will only measure the spectrum associated with a fixed value of the line of sight ζ. Following the same procedure as for Fig. 12, another example of a phase-integrated spectrum taking into account the power of curvature radiation is shown in Fig. 13 for χ = 60° and for different lines of sight ζ = {30° ,60° ,90° }, respectively in solid blue, green, and red lines. The limits of the spectra remain identical to those of Fig. 11 since the energy of the radiated photons does not change, only their number is modified by taking into account the curvature radiation power. The spectrum in blue for ζ = 30° is very similar to its counterpart without taking into account the power. On the other hand, for ζ = 60° in green, the low-energy peak has disappeared to show only an intense peak around 4−8 GeV, in the form of a plateau. Finally, for ζ = 90°, the high-energy component around 30 GeV stands out very clearly and becomes comparable to the component around 4−8 GeV. This example underlines the importance of the radiated power on the weighting of the real spectrum of a pulsar. It is not enough to simply count the photons emitted in isolation at each point.
Applying these methods for curvature radiation, we are able to compute phase-resolved spectra for a given magnetic axis inclination χ and line of sight ζ depicting a particular observer. Performing this calculation, the phase-integrated spectra have been divided into 10 regular phase intervals Δϕ each of length equal to 10% of the period thus Δt = 0.1 P or Δϕ = 36°. Figure 14 shows an example of phase-resolved spectra according to this breakdown of the period. The phases correspond to the regular intervals from [0.0.1] to [0.9, 1.0]. For the first phase interval, we already see a strong variation in the shape of the spectrum for a line of sight inclined at ζ = 90°, represented by the red curves. Photon energy rises to over 30 GeV in the range [0.0.1] and falls below 9 GeV in the next range [0.1.0.2]. These variations are much less noticeable at lower inclinations of χ = 30°, the blue curves on our spectra, and χ = 60°, the green curves. In the phase interval [0.2, 0.3] all the spectra shrink significantly with a narrow energy peak around 5 GeV regardless of the inclination ζ on the left curve. Then the spectrum widens again slightly toward the higher energies on the interval [0.3, 0.4]. The separation of these spectra becomes more and more visible in the following phases, for example in [0.4, 0.5]. Energies above 30 GeV dominate again for ζ = 90° in the [0.5, 0.6] phase while the other two spectra widen toward the low energies. The separation of the spectra becomes very clear again in phase [0.6, 0.7]. At the next phase in [0.7, 0.8], the spectra converge more and more to refocus around 7 GeV. This trend continues over the next phase intervals, [0.8, 0.9] and [0.9, 1], with a disappearance of the pulsation for ζ = 60° in phase [0.9, 1.0] because it corresponds to the location of the polar cap shadow, visible in Fig. 2, where emission is disappearing.
 |
Fig. 14. Phase-resolved spectra for the phase ϕ in regular intervals of length 0.1 and subdivided into [0.1 k, 0.1 (k + 1)] with k ∈ [0…9] and χ = 60°, and with ζ = {30° ,60° ,90° } shown, respectively, in blue, green, and red for a thin slot gap. |
We note that the maximum intensity of the spectrum is not very sensitive to the phase interval. Whatever the inclination and phase considered, the maximum of the spectra is between 1 and 10 in our arbitrary units. Only the inclination of ζ = 60° seems to show a strong amplitude or even a disappearance of the signal for some given phase intervals.
3.1.3. Spectra with variations in the Lorentz factor
In the above picture, we assumed a very simple injection spectrum of primary electrons into the slot gap and for secondary leptons injected into the polar cap. Leptons had fixed Lorentz factors in the slot gap with γ = 107. However, their energy depends on the local curvature radius along magnetic field lines, thus depending on the location within the magnetosphere, following Eq. (11). We therefore performed a second set of simulations by varying the primary particle Lorentz factor according to the radiation reaction limit imposed by Eq. (11). We plotted the spectra of the precedent section taking the maximum Lorentz factor for the accelerated particle γmax depending on the curvature radius ρ of the magnetic field lines with a value of E∥ fixed at 1012 V m−1 (see for instance Figs. 15–17, where we observe a shift in the spectra to lower energies because the Lorentz factor has diminished by at least one order of magnitude; see also Fig. 18, which shows the Lorentz factor for emission points inside the slot gaps). Figure 19 clearly highlights that the highest energy photons emerge from close to the light cylinder. The color map of the perceived photons energy depending on the location concentrates all these photons in the leading part of the gap.
 |
Fig. 16. Phase-integrated spectra for χ = 60° and a line of sight inclination ζ = 30° ,60° ,90° shown, respectively, in solid blue, green, and red lines for a Lorentz factor depending on the curvature radius. |
 |
Fig. 17. Phase-resolved spectra for the phase ϕ in regular intervals of length 0.1 and subdivided into [0.1 k, 0.1 (k + 1)] with k ∈ [0…9] and χ = 60°, and with ζ = {30° ,60° ,90° } shown, respectively, in blue, green, and red for a thin slot gap and a Lorentz factor depending on the curvature radius. |
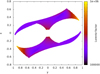 |
Fig. 18. Lorentz factor depending on the position in the slot gaps (projection on the xOy plane) for χ = 90° as calculated using Eq. (11). |
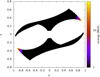 |
Fig. 19. Photon energy depending on the position in the slot gaps (projection on the xOy plane) for χ = 90° for a Lorentz factor depending on the curvature radius. |
The sky maps evolve according to these trends, and we have to choose a lower energy band to retrieve approximately the same light curve for the same geometries. Figures 20–23 show the impact on the sky maps for curvature radiation when the Lorentz factor depends on the curvature radius.
 |
Fig. 20. Sky maps with photon energies in [1, 10] eV for obliquities χ = {90° ,60° ,30° } from top to bottom for a Lorentz factor depending on the curvature radius. Some light curves are shown for several inclination angles, ζ = {90° ,60° ,30° }. |
3.1.4. Spectra with synchrotron radiation
Synchrotron radiation of electrons and positrons is unavoidable in the strong magnetic field of a neutron star. We therefore also added to those previous spectra the contribution of synchrotron emission from particles accelerated along the last closed magnetic field lines, considering only the peak frequency of the synchrotron spectra. Figures 24–26 show some examples where a new spectral component is added at higher energy, in the GeV range.
Because synchrotron emission is most efficient in strong field regions, this radiation emanated from the vicinity of the polar caps as easily recognized by inspection of Fig. 27 showing the photon energy map.
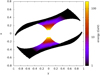 |
Fig. 27. Photon energy depending on the position in the slot gaps (projection on the xOy plane) for χ = 90° only for synchrotron radiations. |
The corresponding sky maps are shown in Figs. 28–31 with appropriate energy ranges. Most of the emission is visible in the GeV to tenths of GeV.
 |
Fig. 28. Sky maps with photon energies in [0.1, 31.6] eV for obliquities χ = {90° ,60° ,30° } from top to bottom for a Lorentz factor depending on the curvature radius plus synchrotron radiations. Some light curves are shown for several inclination angles, ζ = {90° ,60° ,30° }. |
3.2. Thick slot gap
Thin slot gaps are idealized regions of infinitely small thickness producing very sharp gamma-ray peaks due to caustics effects (Morini 1983). Until now we only considered emission along the last closed field lines, neglecting a possible thickness of the current sheet. However, because of the plasma and radiation dynamics within these gaps, we expect an emission layer of finite thickness to form. Therefore, in this paragraph we consider slot gaps relying not only on last closed field lines but also on field lines in their vicinity, some crossing the light cylinder, being open lines, and some staying within the light cylinder, being closed lines. Therefore, in order to tend to a more realistic description of the pulsar high-energy emission from slot gaps, we added in our simulations emission coming from magnetic field lines slightly above or slightly below the last closed field lines.
Sky maps and spectra shown in this paragraph have been realized assuming a thick layer of emission along the last closed magnetic field lines. The power radiated by particles is multiply by a Gaussian weight wg so the emission is maximum along the last closed field lines and decrease when there is an increase in distance between the line where the emission take place and the last closed field line. The colatitude of the last closed field line foot point on the stellar surface being marked by θpc and the colatitude of any field line by θ, in the coordinate system aligned with the magnetic field axis, the Gaussian weight is written as
We take δ = Δθ/5 with an angular distance between two successive magnetic foot points at the same longitude φ equal to Δθ = π/100.
3.2.1. Sky maps and light curves
The sky map of the highest photon energy is shown in Fig. 32 for thick slot gaps and an obliquity χ = 60°. This figure must be compared with Fig. 2 for a thin gap. Now the most energetic photons are still located around the same phase and line of sight inclination with maximum energy around 100 GeV, but as expected the spreading of the current sheet extends the visibility region of high-energy radiation in this sky map. The shadows of the polar caps have almost disappeared because their location overlaps with thick slot gap emission pattern.
 |
Fig. 32. Sky map showing the photon peak energies, in logarithmic scale, depending on the phase and line of sight for an obliquity χ = 60°. |
Equivalently, Figs. 33–36 represent the sky maps for thick slot gaps for different energy ranges, the same as those shown in Figs. 3–6, and different χ inclinations of the magnetic axis. Due to the finite thickness of the gap, the light curves broaden in relation to the transverse size of the slot gaps. At any energies, the bright part of the sky maps has enlarged to a significant part of the full sky. Moreover, the light curves show complex multi pulse profiles varying with energy. However, as already stated before, these sky maps and light curves samples serve as building blocks for the elaboration of more realistic and complete radiation patterns in pulsar magnetospheres. The particle distribution function and the full curvature spectrum must be taken into account. This is why we postponed a meaningful comparison with radio and gamma-ray observations for future works.
3.2.2. Spectra
The emission spectra and maps computed in the previous section have been made with an infinitely thin emission area along the last open field lines. Figure 37 shows the spectrum of the high-energy emission for an emission area of a given thickness, using the same method as that used to draw the sky maps in Fig. 12. According to this spectrum, when a thickness transverse to the emission area is included, additional radiation is received including lower and higher photon energies than those of a thin gap. To the spectrum of the infinitely thin zone are thus added other spectra from neighboring field lines but whose curvature varies slightly, increasing or decreasing according to the nature of the field line: open or closed, which will obviously lead to variations in the radiated power and energy of the radiation. The differences in the shape of the spectra in Figs. 12 and 37 can also be partly explained by the modulation of intensity under the influence of the Gaussian factor that we introduced via the weight (19) and which has also been used here. Thus for each point of impact on the celestial sphere, the measured intensity is the power radiated by the particle multiplied by this Gaussian function.
Figure 38 represents the evolution of the high-energy spectra over different phase intervals for an inclination χ = 60° and several fixed values of the observation angle ζ. It is the same as in Fig. 14 but for thick slot gaps. The emission is visible for all observation angles and for all phases unlike the spectra obtained for radiation without thickness of the emission zone, notably for the phase [0.9, 1], because, as seen in Fig. 34, high-energy emission is received at the phase of the polar cap shadow.
Figure 39 represents the evolution of the shape of the light curve observed for χ = ζ = 60° for different energies, the light curves being normalized by its maximum in each plot. It highlights the variety of pulse shape and width depending on the observed energy range.
 |
Fig. 39. Light curves for χ = ζ = 60° for different energy intervals: in red [1, 3.16] GeV, in green [3.16, 10] GeV, in blue [10, 31.6] GeV, and in violet [31.6, 100] GeV. |
We next determined from which altitude in the magnetosphere of the pulsar this high-energy pulsed emission originates.
3.2.3. Spectra with variations in the Lorentz factor
Using Eq. (11), we plotted the spectra of the precedent section for a Lorentz factor depending on the curvature radius of the magnetic field lines, including the magnetic field lines below and above the last closed field lines for a thick slot gap (see Figs. 40–42).
 |
Fig. 40. Same as Fig. 12 but with a Lorentz factor depending on the curvature radius for a thick slot gap. |
 |
Fig. 41. Phase-integrated spectra for χ = 60° and a line of sight inclination ζ = 30° ,60° ,90° respectively in blue, green and red solid lines for a thick slot gap and a Lorentz factor depending on the curvature radius. |
 |
Fig. 42. Phase resolved spectra for the phase ϕ in regular intervals of length 0.1 and subdivided into [0.1 k, 0.1 (k + 1)] with k ∈ [0…9] with χ = 60° and ζ = {30° ,60° ,90° } respectively in blue, green and red for a thick slot gap and a Lorentz factor depending on the curvature radius. |
Figures 43–46 show the sky maps observed for curvature radiation when the Lorentz factor depends on the curvature radius for a thick slot gap.
 |
Fig. 43. Sky maps with photon energies in [1, 10] eV for obliquities χ = {90° ,60° ,30° } from top to bottom for a Lorentz factor depending on the curvature radius with a thick slot gap. Some light curves are shown for several inclination angles, ζ = {90° ,60° ,30° }. |
3.2.4. Spectra with synchrotron radiation
To the previous spectra we added the contribution of synchrotron radiation from particle accelerated along the magnetic field lines in the gap: along the last closed magnetic field lines and the lines below and above them in order to depict a certain thickness of the emitting region. Figures 47–49 quantify the impact of varying field lines on the phase-averaged and phase-resolved spectra. The photon energy range widens again because of more freedom in the curvature radius depending on the field line considered.
Figures 50–53 show the composite sky maps observed with both kind of emission (curvature radiation and synchrotron) with a thick slot gap for different energy bands.
 |
Fig. 50. Sky maps with photon energies in [0.1, 31.6] keV for obliquities χ = {90° ,60° ,30° } from top to bottom for a Lorentz factor depending on the curvature radius for curvature radiation plus synchrotron radiations (with a Lorentz factor γ = 30). Some light curves are shown for several inclination angles, ζ = {90° ,60° ,30° }. |
3.3. Altitude of emission
Since the frequency of the curvature radiation emitted within the slot gaps has been calculated and since the position of the emission points along the last field lines is known, we can deduce from which altitude in the magnetosphere the energy of the radiation originates. Figures 54–56 show this distribution for an infinitely thin emission zone and for different inclinations of the magnetic axis, respectively of χ = 30°, 60°, and 90°. Each of these maps represents the points of impact on the celestial sphere of photons emitted between two different altitudes separated by a distance equivalent to one times the radius of the star R⋆. The altitude of this spherical corona is plotted from R⋆ to the light cylinder of radius 10 R⋆. The color code of these figures reflects the energy observed for the photons at the origin of each point of impact. Thus each of these three figures is presented with the arrangement shown in Table 1 for the range of the position r of the photon emission point.
 |
Fig. 54. Sky maps of photon energy for an inclination χ = 30°. Each map represents the contribution from a piece of the magnetosphere: those located in a spherical shell of thickness R⋆ whose altitude is increased by R⋆ to the next map. |
These plots emphasize that the most energetic photons are emitted far away from the star surface and therefore close to the light cylinder, which could also indicate that the last closed magnetic field lines are more curved at larger distances from the neutron star. It shows that these points are located in the remotest parts of the magnetosphere and that their high energy may be due to the magnetic field being dragged by the rotation of the neutron star, which generates a large curvature of the magnetic field lines. The large curvature of the magnetic field lines responsible for the high-energy photons is shown in Fig. 7 where the radius of curvature of the field lines calculated at each emission point is shown (the smaller the radius of curvature, the greater the curvature). However, only the high-energy emission points have a small radius of curvature, if the higher-energy emission areas are located in the upper part of the magnetosphere, this may also be due to the Doppler effect caused by the rotation of the pulsar. The Doppler factor η given by Eq. (5) is indeed larger for emission points located at a high altitude from the neutron star because their linear velocity β is larger. Figure 8 gives a map of the emission points with the Doppler factor calculated for each of them, this factor is more important near the high-energy emission points. High-energy emission near the light cylinder therefore requires a favorable combination of two effects: the curvature of the magnetic field lines and the blueshifting Doppler factor.
4. Radio emission
There is still no consensus on the radio mechanism operating in pulsar magnetospheres. Coherent emission is a strong constrain but we do not model such complex plasma processes. We only want to check whether the curvature photon frequency could lie in the gigahertz band as observed in radio pulsars. With our magnetic field geometry, we found that secondary particles with γ = 30 enables us to match this requirement. This is less than what comes out from several works about pair cascading, leading to higher values of γ = 102 − 103. Therefore, some other mechanisms, such as radio photon scattering or absorption, should be included to get a more realistic picture. However, this outstanding problem is out of the scope of the present paper.
As is well known, the radio emission in the polar caps is caused by the acceleration of secondary pairs, that is, particles generated by magnetic photon absorption in the strong magnetic field of the pulsar (Erber 1966), producing an avalanche of leptons. The Lorentz factor of these secondary particles is on the order of γ = 102, as stated in Beskin et al. (1993). In what follows, we choose a mono-energetic distribution function with Lorentz factor γ = 30 in order to obtain frequencies calculated with Eq. (7) in the observational window of radio pulsars.
In order to avoid a sharp on-off boundary within the polar cap, not reflecting the real radio profiles, a weight is assigned to each photon emitted from the polar cap according to the angular distance θ of these points from the magnetic pole, so that the emission profile resembles a Gaussian function. The technique is similar to the introduction of a thickness in the slot gaps described in the previous section. Thus, when plotting the emission maps and the associated light curves, the intensity received over a 0.5 × 0.5 degree zone of the celestial sphere will not increase by one unit for each photon received. Instead it increases by a weighted intensity I taking into account the Gaussian shape for photons. Photons coming from the north polar cap are weighted according to
and a similar expression holds for the south polar cap. The parameter 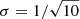 controls the width of the Gaussian shape, the angles θ and θpc being, respectively, the colatitude of the emission point and of the rim of the polar cap in a coordinated system oriented according to the magnetic axis. The Gaussian factor seen in Eq. (20) is used in order to keep pulses of Gaussian shapes and maximum emission at the center of the polar cap.
controls the width of the Gaussian shape, the angles θ and θpc being, respectively, the colatitude of the emission point and of the rim of the polar cap in a coordinated system oriented according to the magnetic axis. The Gaussian factor seen in Eq. (20) is used in order to keep pulses of Gaussian shapes and maximum emission at the center of the polar cap.
We generated a random but homogeneous distribution of 108 points inside both polar caps as depicted in Fig. 57. To obtain such a distribution, the colatitude θ of the emission points in the spherical coordinate system oriented along the magnetic axis (where the colatitude θmp of the north and south pole are, respectively, 0° and 180°) is determined through the formula
 |
Fig. 57. Distribution of 108 radio emission points inside the “north” polar cap at the surface of the neutron star for a perpendicular rotator, showing an almost uniform distribution. |
with θpc the latitude of the point where the last closed field line crosses the stellar surface and X a random number in [0, 1]. The longitude φ of the emission point is determined by introducing another random number Y in [0, 1] such that
where Δφ = 2 π/Nφ is the polar angle between two neighboring points of a polar cap rim and Nφ the number of point samples in the longitudinal direction.
4.1. Sky maps
We then determined the radio emission maps as a function of frequency in order to study the evolution of the pulse shape as measured by a distant observer. Figures 58–60 show examples of sky maps and a corresponding sample of light curves obtained for an emission volume in the range r ∈ [2, 3] R⋆ above the polar caps for different frequency intervals. We note that the frequency interval breakdown is not the same for the different obliquities χ because the spectra do not have the same range or the same upper and lower limits. The choice of frequencies has been optimized to make the intensity maps stand out best.
 |
Fig. 58. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 30°. From top to bottom, these maps shows emission frequencies within [30, 120] MHz, [120, 210] MHz, and [210, 300] MHz. |
 |
Fig. 59. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 60°. From top to bottom, these maps shows emission frequencies within [200, 270] MHz, [270, 340] MHz, and [340, 410] MHz. |
 |
Fig. 60. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 90°. From top to bottom, these maps shows emission frequencies within [330, 450] MHz, [450, 570] MHz, and [570, 690] MHz. |
These maps reveal a narrowing of the pulse profile toward the high frequencies since these photons come from the deepest regions of the magnetosphere. There is also an east-west asymmetry in these profiles between the rising and falling ramps. Sometimes two pulses are observed in the profile, sometimes only one. It should be stressed that these results are only preliminary and that any comparison with observations will have to take into account a particle energy distribution in the form of a power law and not simply a mono-energetic distribution as done in the present work, (see the particle distribution function discussion in Sect. 2). The characteristic curvature frequency must also be replaced by the continuous curvature spectrum centered on this typical frequency. This will make the frequency variation in the pulse profile smoother and the transition between the frequency bands more continuous. After this further step, however left as a future work, detailed comparison with existing multiwavelength observations can be performed.
According to these maps, especially those in Fig. 60, low frequencies are emitted rather at the edge of the area while the higher-frequency components are emitted toward the center of the area. This may seem counter-intuitive since for a static dipole, the center of the pulse, corresponding to the magnetic axis, is a straight line of zero curvature and therefore of zero frequency and power. In other words, within the static limit, there is no emission at the center of the cap. Frequencies and power increase with increasing angular distance from the axis. But for a rotating dipole, as for example in the Deutsch solution we use in the present study, the magnetic field undergoes a sweep-back effect that curves all field lines, even the one associated with the magnetic axis. To be able to visualize this curvature, Figs. 61–63 represent maps of the radii of curvature, measured in units of Rcyl, at the point of photon emission for χ = 30° ,60°, and 90°, respectively, and for two emission heights, on the left for [2, 3] R* and on the right for [4, 5] R*. The fact that the highest frequencies are toward the center of the polar caps is therefore a consequence of the magnetic field line curvature induced by the stellar rotation. The radius of curvature on the field lines from the polar caps is minimal in the case of the perpendicular rotator with χ = 90° and reaches 0.032 Rcyl. It increases when the magnetic axis joins the rotation axis (i.e., when χ decreases). For example, for χ = 30° this minimum radius is 0.05 Rcyl and moves outside the center of the cap. At the same time the maximum curvature radius increases significantly when the rotator is close to the aligned configuration. It is only 0.048 Rcyl for χ = 90° and reaches up to 0.35 Rcyl for χ = 30°, which is an increase of almost one order of magnitude. The photons produced will be much less energetic in this latter case. Within the limit of a perfectly aligned rotator χ = 0°, the radius of curvature becomes infinite at the center of the cap, on the magnetic axis, and the curvature radiation is extinguished at its center.
 |
Fig. 61. Maps of curvature radii in units of Rcyl for an inclination χ = 30°, on the top for an altitude in [2, 3] R⋆, on the bottom for [4, 5] R⋆ above the polar caps. |
The altitude at which photons are produced and their detachment from the magnetosphere in the direction of the observer is not precisely constrained by the observations. The radio polarization data provide some indication for young pulsars, but the error bar remains appreciable. There is therefore some freedom in the choice of the height of the emission sites above the polar ice caps. For this reason we have also drawn emission maps and light curves for an altitude in the range [3, 4] R⋆, as shown in Figs. 64–66 for the same frequency intervals above the polar caps.
 |
Fig. 64. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 30°. From top to bottom, these maps shows emission frequencies within [30, 120] MHz, [120, 210] MHz, and [210, 300] MHz. |
 |
Fig. 65. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 60°. From top to bottom, these maps shows emission frequencies within [200, 270] MHz, [270, 340] MHz, and [340, 410] MHz. |
 |
Fig. 66. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 90°. From top to bottom, these maps shows emission frequencies within [330, 40] MHz, [450, 570] MHz, and [570, 690] MHz. |
Pushing the emission altitude further away from the star causes a spreading of the radio pulse profile since the field lines are divergent. This is reflected in the fact that high altitudes produce the lowest frequencies in relation to wider pulses while low altitudes produce the highest frequencies in relation to narrower pulses, in accordance with the radius-to-frequency mapping model. But in our case, we dispense with the static dipole to take into account all the effects due to the rotation of the magnetic field, the effects of signal aberration and delay.
In order to facilitate the visualization of the evolution of the radio pulses as a function of frequency, the shape of a light curve has been plotted in Fig. 67 according to the frequency interval considered, here those obtained with an emission area between r ∈ [2, 3] R⋆ above the polar caps and for an inclination χ = 60° of the magnetic axis and ζ = 120° of the line of sight. The maximum of the blue profile in the range [340, 410] MHz is ahead of the green profile in the range [270, 340] MHz, which in turn is ahead of the red pulse in the range [200, 270] MHz. This phase lead is significant since it represents 5 to 10% of the pulsar period. It is the consequence of the curvature of the magnetic field lines in the retrograde direction with respect to the stellar rotation and of the production of the high-frequency photons at low altitude, where the field lines are less curved compared to the low-frequency photons produced at higher altitudes, where the field lines are more curved due to the sweep-back effect (Eq. (18)). This effect depends on the ratio (R*/Rcyl): It is negligible for young pulsars but its observational signature should be perceptible for the fastest millisecond pulsars.
 |
Fig. 67. Radio light curves for χ = 60°, ζ = 120° and an emission zone r ∈ [2, 3] R⋆: in red for frequencies in the interval [200, 270] MHz, in green for [270, 340] MHz, and in blue for [340, 410] MHz. |
The phase shift can be estimated from Eqs. (15), (17), and (18) in Sect. 2.7. The maximum offset thus calculated (for a photon emitted at 1 R⋆ above the surface and another emitted at 2 R⋆ and always with χ = 60°) is on the order of 4% of the phase. These effects are therefore not sufficient to explain the shift in the radio emission peak in Fig. 67, but they can certainly play a role in the radio emission observed in these emission areas.
4.2. Spectra
As for the high-energy radiation, Fig. 68 shows the radio spectrum for different values of the obliquity χ of the magnetic field. The points of emission for this spectrum are located on the stellar surface and with the same spatial distribution as shown in Fig. 57.
 |
Fig. 68. Radio emission spectrum, in blue for χ = 30°, in green for χ = 60°, and in red for χ = 90°. |
Figure 68 reveals that the frequency range of the radio emission depends strongly on the angle χ, because the curvature of magnetic field lines is more pronounced for the perpendicular rotator χ = 90° compared to a nearly aligned rotator χ = 30°. Indeed, it is for a magnetic axis perpendicular to the rotation axis that the radio frequencies are the highest, and since the magnetic polar caps are in the equatorial plane, the magnetic field lines passing through them are strongly swept back, and therefore curved by the rotation of the pulsar. The magnetic field lines are curved backward, in the opposite direction of the rotation as shown by Shitov (1983), delaying the radio signal by an amount ΔtB given by Eq. (18). The Doppler effect also contributes partly since the corotation speed vcp = r Ω sin χ is more significant for the perpendicular rotator because of the longer lever arm of length r sin χ. The amplitude of this Doppler effect is related to βcp = (r/Rcyl) sin χ. Generally speaking, the characteristic radio frequency νradio depends on the ratio (r/Rcyl) and on sin χ. Therefore, the range of radio waves around νradio behaves as an increasing function of sin χ. On the other hand, this shift in the radio spectrum toward higher frequencies is attenuated for rotators slower than those studied within this paper. Indeed, for young pulsars, of period P greater than about P > 100 ms, the ratio between the neutron star radius and the light-cylinder radius is much smaller than one, (r/Rcyl)≪1, hence producing a less perceptible variation in frequency as a function of sin χ.
In the above proposed image, the photons escape directly from the star’s surface. In our simulations, the period of rotation of the pulsar is limited to 2 ms because of the prohibitive computing time for a star of larger period. The neutron star surface is fixed at a radius 0.1 Rcyl. Nevertheless, for slow pulsars, this radius of 0.1 Rcyl corresponds to the average real altitude of radio emission (it is in fact a little lower, on the order of 0.05 Rcyl; see for instance Mitra 2017). The width of the pulses as well as the delay between the radio peak and the first gamma-ray peak thus remains realistic despite the overly high period. However, the assumption that radio emission is produced at a fixed altitude is not entirely correct. Indeed, it is known that the highest frequencies are generated at lower altitudes because of the radio-to-frequency mapping. It will therefore be necessary to include an additional degree of freedom for the true position of the emission sites by introducing, for example, an interval of variable altitudes as was done in the high-energy band.
The panels in Fig. 69 show the radio spectrum for different values of the obliquity χ, when the emission area is located above the polar caps, in the range r ∈ [1, 2] R⋆ on the left part and in the range r ∈ [3, 4] R⋆ on the right part. Compared to Fig. 68, the emission no longer occurs in a given radius r but for an entire range of radii r ∈ [r1, r2]. The emission is no longer integrated on a surface (the polar cap) but in a whole three-dimensional volume. The result is a wider range of values of radii of curvature and consequently a wider radio emission spectrum, regardless of the value of χ. This spread is maximum for χ = 30° and less for other values of the inclination of the magnetic axis such as 60° and 90°. Shifting the emission volume to a higher altitude produces an additional spread of the spectrum, which can be seen by comparing the left and right plots in Fig. 69. We conclude from these spectra that the farther the radio emission zone from the surface of the neutron star, the wider the frequency range of the received radio radiation. This phenomenon is very important for the smallest inclination investigated, namely for χ = 30°.
 |
Fig. 69. Radio emission spectra for a region located in the range [1, 2] R⋆ on the top, and in the range [3, 4] R⋆ on the bottom, in blue for χ = 30°, in green for χ = 60°, and in red for χ = 90°. |
This broadening of the spectra is due to the fact that our emission zones above the polar caps possess a certain thickness and is therefore the result of the variation in the curvature of magnetic field lines. However, other phenomena may affect the shape of these spectra, such as the geometry of the field lines, which is certainly varying with altitude, or also the Doppler factor, which depends on the instantaneous rotation speed v = Ω ∧ r = r Ω sin θ eφ and increases with altitude due to the corotation of the magnetosphere with the neutron star.
5. Conclusion
We studied some of the main emission mechanisms taking place within the pulsar magnetosphere, namely synchrotron and curvature radiation from the slot gap and polar cap inside the light cylinder. We showed detailed radio and high-energy light curves and spectra in the Fermi/LAT band. Using realistic values of the Lorentz factors for primary and secondary beams, our spectra fall into the right windows. We computed phase-resolved spectra and found that the spectral energy distribution depends on the phase interval. Also, the averaged radio spectra significantly depend on the pulsar obliquity, whereas the high-energy part seemed much less sensitive to the geometry.
In order to get a more complete view of this emission, it might be useful to add inverse Compton scattering to future simulations, as well as other models with different emission zones, such as outer gaps or the striped wind. The calculation of the spectra will also gain in realism if the mono-energetic particle distribution function is replaced by a power law distribution function and the δ approximation of the curvature spectrum by its spectral energy density.
The polarization of the pulsed emission could also be added to our simulations of radio and high-energy emission. In the radio domain, this polarization already makes it possible to shift the emission sites at high altitude for slow pulsars with periods above 100 ms. The imminent observation of the polarization in X-rays with the Imaging X-ray Polarimetry Explorer (IXPE; Weisskopf et al. 2016) will bring a new strong constraint on the high-energy part of the spectrum, determining its location either inside the light cylinder within the magnetosphere or outside within the wind.
Finally, a discussion of these results in relation to pulsar multiwavelength observations should constrain many dynamical parameters of the relativistic plasma by comparing, for example, the light curves as well as the radio and gamma-ray spectra for pulsars detected simultaneously in these two energy bands.
Acknowledgments
This work has been partly supported by CEFIPRA grant IFC/F5904-B/2018 and ANR-20-CE31-0010. We also acknowledge the High Performance Computing center of the University of Strasbourg for supporting this work by providing scientific support and access to computing resources. Part of the computing resources were funded by the Equipex Equip at Meso project (Programme Investissements d’Avenir) and the CPER Alsacalcul/Big Data.
References
- Abdo, A. A., Ajello, M., Allafort, A., et al. 2013, ApJS, 208, 17 [Google Scholar]
- Arendt, P. N., Jr., & Eilek, J. A. 2002, ApJ, 581, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Arfken, G. B., & Weber, H. J. 2005, Mathematical Methods for Physicists, 6th edn. (Boston: Elsevier) [Google Scholar]
- Arons, J. 1983, ApJ, 266, 215 [CrossRef] [Google Scholar]
- Bai, X.-N., & Spitkovsky, A. 2010, ApJ, 715, 1282 [Google Scholar]
- Barnard, M. 2021, PhD Thesis, North-West University, Potchefstroom, South Africa [Google Scholar]
- Becker, W., Burton, W. B., Cesarsky, C. J., et al. 2009, in Neutron Stars and Pulsars (Berlin, Heidelberg: Springer-Verlag), Astrophys. Space Sci. Lib., 357 [CrossRef] [Google Scholar]
- Benli, O., Pétri, J., & Mitra, D. 2021, A&A, 647, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beskin, V. S., Gurevich, A. V., & Istomin, Y. N. 1993, Physics of the Pulsar Magnetosphere (Cambridge: Cambridge University Press) [Google Scholar]
- Brambilla, G., Kalapotharakos, C., Harding, A. K., & Kazanas, D. 2015, ApJ, 804, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Ho, C., & Ruderman, M. 1986, ApJ, 300, 500 [CrossRef] [Google Scholar]
- Daugherty, J. K., & Harding, A. K. 1982, ApJ, 252, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Daugherty, J. K., & Harding, A. K. 1989, ApJ, 336, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Daugherty, J. K., & Lerche, I. 1975, Astrophys. Space Sci., 38, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Deutsch, A. J. 1955, Ann. Astrophys., 18, 1 [NASA ADS] [Google Scholar]
- Du, Y. J., Han, J. L., Qiao, G. J., & Chou, C. K. 2011, ApJ, 731, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Du, Y. J., Qiao, G. J., & Wang, W. 2012, ApJ, 748, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Du, Y. J., Qiao, G. J., & Chen, D. 2013, ApJ, 763, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Dyks, J., & Rudak, B. 2002, A&A, 393, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dyks, J., & Rudak, B. 2003, ApJ, 598, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Dyks, J., Harding, A. K., & Rudak, B. 2004, ApJ, 606, 1125 [Google Scholar]
- Erber, T. 1966, Rev. Mod. Phys., 38, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Giraud, Q., & Pétri, J. 2020, A&A, 639, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harding, A. K. 2016, J. Plasma Phys., 82, 635820306 [CrossRef] [Google Scholar]
- Harding, A. K., & Kalapotharakos, C. 2015, ApJ, 811, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, A. K., & Muslimov, A. G. 2011, ApJ, 743, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, A. K., Stern, J. V., Dyks, J., & Frackowiak, M. 2008, ApJ, 680, 1378 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, A. K., DeCesar, M. E., Miller, M. C., Kalapotharakos, C., & Contopoulos, I. 2011, ArXiv e-prints [arXiv:1111.0828] [Google Scholar]
- Harding, A. K., Kalapotharakos, C., Barnard, M., & Venter, C. 2018, ApJ, 869, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Hirotani, K. 2008, ApJ, 688, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. D. 2001, Electrodynamique classique: Cours et exercices d’electromagnétisme (Paris: Dunod) [Google Scholar]
- Johnson, T. J., Venter, C., Harding, A. K., et al. 2014, ApJS, 213, 6 [Google Scholar]
- Kalapotharakos, C., Harding, A. K., Kazanas, D., & Contopoulos, I. 2012a, ApJ, 754, L1 [Google Scholar]
- Kalapotharakos, C., Kazanas, D., Harding, A., & Contopoulos, I. 2012b, ApJ, 749, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Kalapotharakos, C., Harding, A. K., & Kazanas, D. 2014, ApJ, 793, 97 [Google Scholar]
- Kalapotharakos, C., Harding, A. K., Kazanas, D., & Brambilla, G. 2017, ApJ, 842, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Kalapotharakos, C., Brambilla, G., Timokhin, A., Harding, A. K., & Kazanas, D. 2018, ApJ, 857, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, K. J., Du, Y. J., Wang, H. G., et al. 2010, MNRAS, 405, 2103 [Google Scholar]
- Medin, Z., & Lai, D. 2010, MNRAS, 406, 1379 [NASA ADS] [Google Scholar]
- Mitra, D. 2017, JApA, 38, 52 [NASA ADS] [Google Scholar]
- Morini, M. 1983, MNRAS, 202, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Muslimov, A. G., & Harding, A. K. 2003, ApJ, 588, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Muslimov, A. G., & Harding, A. K. 2004, ApJ, 606, 1143 [CrossRef] [Google Scholar]
- Phillips, J. A. 1992, ApJ, 385, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Pierbattista, M., Harding, A. K., Grenier, I. A., et al. 2015, A&A, 575, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierbattista, M., Harding, A. K., Gonthier, P. L., & Grenier, I. A. 2016, A&A, 588, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pétri, J. 2011, MNRAS, 412, 1870 [Google Scholar]
- Pétri, J. 2018, MNRAS, 477, 1035 [Google Scholar]
- Pétri, J., & Mitra, D. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202141272 [Google Scholar]
- Romani, R. W. 1996, ApJ, 470, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Romani, R. W., & Watters, K. P. 2010, ApJ, 714, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. A., & Sutherland, P. G. 1975, ApJ, 196, 51 [Google Scholar]
- Shitov, Y. P. 1983, Sov. Astron., 27, 314 [NASA ADS] [Google Scholar]
- Story, S. A., & Baring, M. G. 2014, ApJ, 790, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Sturner, S. J., Dermer, C. D., & Michel, F. C. 1995, ApJ, 445, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Takata, J., Chang, H., & Cheng, K. S. 2007, ApJ, 656, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Timokhin, A. N. 2010, MNRAS, 408, 2092 [NASA ADS] [CrossRef] [Google Scholar]
- Timokhin, A. N., & Arons, J. 2013, MNRAS, 429, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Timokhin, A. N., & Harding, A. K. 2015, ApJ, 810, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Timokhin, A. N., & Harding, A. K. 2019, ApJ, 871, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Venter, C., Harding, A. K., & Guillemot, L. 2009, ApJ, 707, 800 [Google Scholar]
- Venter, C., Harding, A. K., & Grenier, I. 2018, ArXiv e-prints [arXiv:1802.00204] [Google Scholar]
- Watters, K. P., Romani, R. W., Weltevrede, P., & Johnston, S. 2009, ApJ, 695, 1289 [Google Scholar]
- Weisskopf, M. C., Ramsey, B., O’Dell, S. L., et al. 2016, Results Phys., 6, 1179 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Schematic view of several well-studied emission sites, such as the polar cap, slot gap, outer gap, and striped wind. |
| In the text | |
 |
Fig. 2. Sky map showing the photon peak energies, in logarithmic scale, depending on the phase and line of sight for an obliquity χ = 60°. |
| In the text | |
 |
Fig. 3. Sky maps with photon energies in [1, 3.16] GeV for obliquities χ = {90° ,60° ,30° } from top to bottom. Some light curves are shown for several inclination angles, ζ = {90° ,60° ,30° }. |
| In the text | |
 |
Fig. 4. Same as Fig. 3 but for photon energies between [3.16, 10] GeV. |
| In the text | |
 |
Fig. 5. Same as Fig. 3 but for photon energies between [10, 31.6] GeV. |
| In the text | |
 |
Fig. 6. Same as Fig. 3 but for photon energies between [31.6, 100] GeV. |
| In the text | |
 |
Fig. 7. Curvature radius depending on the position in the slot gaps for χ = 90° (projection on the xOy plane). The unit of length is the light-cylinder radius Rcyl. |
| In the text | |
 |
Fig. 8. Doppler factor depending on the position in the slot gaps (projection on the xOY plane) for χ = 90°. |
| In the text | |
 |
Fig. 9. Photon energy depending on the position in the slot gaps (projection on the xOy plane) for χ = 90°. |
| In the text | |
 |
Fig. 10. Phase- and line-of-sight-averaged spectra for obliquity χ = {30° ,60° ,90° } shown, respectively, in solid blue, green, and red lines without curvature radiation power weights. |
| In the text | |
 |
Fig. 11. Phase-integrated spectra for χ = 60° and a line of sight inclination ζ = {30° ,60° ,90° } shown, respectively in solid blue, green, and red lines without curvature radiation weights. |
| In the text | |
 |
Fig. 12. Same as Fig. 10 but with curvature radiation power included. |
| In the text | |
 |
Fig. 13. Same as Fig. 11 but with curvature radiation power included. |
| In the text | |
 |
Fig. 14. Phase-resolved spectra for the phase ϕ in regular intervals of length 0.1 and subdivided into [0.1 k, 0.1 (k + 1)] with k ∈ [0…9] and χ = 60°, and with ζ = {30° ,60° ,90° } shown, respectively, in blue, green, and red for a thin slot gap. |
| In the text | |
 |
Fig. 15. Same as Fig. 12 but with a Lorentz factor depending on the curvature radius. |
| In the text | |
 |
Fig. 16. Phase-integrated spectra for χ = 60° and a line of sight inclination ζ = 30° ,60° ,90° shown, respectively, in solid blue, green, and red lines for a Lorentz factor depending on the curvature radius. |
| In the text | |
 |
Fig. 17. Phase-resolved spectra for the phase ϕ in regular intervals of length 0.1 and subdivided into [0.1 k, 0.1 (k + 1)] with k ∈ [0…9] and χ = 60°, and with ζ = {30° ,60° ,90° } shown, respectively, in blue, green, and red for a thin slot gap and a Lorentz factor depending on the curvature radius. |
| In the text | |
 |
Fig. 18. Lorentz factor depending on the position in the slot gaps (projection on the xOy plane) for χ = 90° as calculated using Eq. (11). |
| In the text | |
 |
Fig. 19. Photon energy depending on the position in the slot gaps (projection on the xOy plane) for χ = 90° for a Lorentz factor depending on the curvature radius. |
| In the text | |
 |
Fig. 20. Sky maps with photon energies in [1, 10] eV for obliquities χ = {90° ,60° ,30° } from top to bottom for a Lorentz factor depending on the curvature radius. Some light curves are shown for several inclination angles, ζ = {90° ,60° ,30° }. |
| In the text | |
 |
Fig. 21. Same as Fig. 28 but for photon energies between [10, 100] eV. |
| In the text | |
 |
Fig. 22. Same as Fig. 28 but for photon energies between 100 eV and 1 keV. |
| In the text | |
 |
Fig. 23. Same as Fig. 28 but for photon energies between [1, 10] keV. |
| In the text | |
 |
Fig. 24. Same as Fig. 15 but with synchrotron radiation in addition to curvature radiation. |
| In the text | |
 |
Fig. 25. Same as Fig. 16 but with synchrotron radiation in addition to curvature radiation. |
| In the text | |
 |
Fig. 26. Same as Fig. 17 but with synchrotron radiation in addition to curvature radiation. |
| In the text | |
 |
Fig. 27. Photon energy depending on the position in the slot gaps (projection on the xOy plane) for χ = 90° only for synchrotron radiations. |
| In the text | |
 |
Fig. 28. Sky maps with photon energies in [0.1, 31.6] eV for obliquities χ = {90° ,60° ,30° } from top to bottom for a Lorentz factor depending on the curvature radius plus synchrotron radiations. Some light curves are shown for several inclination angles, ζ = {90° ,60° ,30° }. |
| In the text | |
 |
Fig. 29. Same as Fig. 28 but for photon energies between 31.6 eV and 10 keV. |
| In the text | |
 |
Fig. 30. Same as Fig. 28 but for photon energies between 10 keV and 3.16 GeV. |
| In the text | |
 |
Fig. 31. Same as Fig. 28 but for photon energies between 3.16 GeV and 1 TeV. |
| In the text | |
 |
Fig. 32. Sky map showing the photon peak energies, in logarithmic scale, depending on the phase and line of sight for an obliquity χ = 60°. |
| In the text | |
 |
Fig. 33. Same as Fig. 3 but for thick slot gaps. |
| In the text | |
 |
Fig. 34. Same as Fig. 4 but for thick slot gaps. |
| In the text | |
 |
Fig. 35. Same as Fig. 5 but for thick slot gaps. |
| In the text | |
 |
Fig. 36. Same as Fig. 6 but for thick slot gaps. |
| In the text | |
 |
Fig. 37. Same as Fig. 12 but for a thick emission region. |
| In the text | |
 |
Fig. 38. Same as Fig. 14 but for a thick slot gap. |
| In the text | |
 |
Fig. 39. Light curves for χ = ζ = 60° for different energy intervals: in red [1, 3.16] GeV, in green [3.16, 10] GeV, in blue [10, 31.6] GeV, and in violet [31.6, 100] GeV. |
| In the text | |
 |
Fig. 40. Same as Fig. 12 but with a Lorentz factor depending on the curvature radius for a thick slot gap. |
| In the text | |
 |
Fig. 41. Phase-integrated spectra for χ = 60° and a line of sight inclination ζ = 30° ,60° ,90° respectively in blue, green and red solid lines for a thick slot gap and a Lorentz factor depending on the curvature radius. |
| In the text | |
 |
Fig. 42. Phase resolved spectra for the phase ϕ in regular intervals of length 0.1 and subdivided into [0.1 k, 0.1 (k + 1)] with k ∈ [0…9] with χ = 60° and ζ = {30° ,60° ,90° } respectively in blue, green and red for a thick slot gap and a Lorentz factor depending on the curvature radius. |
| In the text | |
 |
Fig. 43. Sky maps with photon energies in [1, 10] eV for obliquities χ = {90° ,60° ,30° } from top to bottom for a Lorentz factor depending on the curvature radius with a thick slot gap. Some light curves are shown for several inclination angles, ζ = {90° ,60° ,30° }. |
| In the text | |
 |
Fig. 44. Same as Fig. 28 but for photon energies between [10, 100] eV. |
| In the text | |
 |
Fig. 45. Same as Fig. 28 but for photon energies between 100 eV and 1 keV. |
| In the text | |
 |
Fig. 46. Same as Fig. 28 but for photon energies between [1,10] keV. |
| In the text | |
 |
Fig. 47. Same as Fig. 15 but with synchrotron radiation in addition to curvature radiation. |
| In the text | |
 |
Fig. 48. Same as Fig. 16 but with synchrotron radiation in addition to curvature radiation. |
| In the text | |
 |
Fig. 49. Same as Fig. 17 but with synchrotron radiation in addition to curvature radiation. |
| In the text | |
 |
Fig. 50. Sky maps with photon energies in [0.1, 31.6] keV for obliquities χ = {90° ,60° ,30° } from top to bottom for a Lorentz factor depending on the curvature radius for curvature radiation plus synchrotron radiations (with a Lorentz factor γ = 30). Some light curves are shown for several inclination angles, ζ = {90° ,60° ,30° }. |
| In the text | |
 |
Fig. 51. Same as Fig. 50 but for photon energies between [31.6 keV, 10 MeV]. |
| In the text | |
 |
Fig. 52. Same as Fig. 50 but for photon energies between [0.01, 3.16] GeV. |
| In the text | |
 |
Fig. 53. Same as Fig. 50 but for photon energies between [3.16, 1000] GeV. |
| In the text | |
 |
Fig. 54. Sky maps of photon energy for an inclination χ = 30°. Each map represents the contribution from a piece of the magnetosphere: those located in a spherical shell of thickness R⋆ whose altitude is increased by R⋆ to the next map. |
| In the text | |
 |
Fig. 55. Same as Fig. 54 but with an inclination χ = 60°. |
| In the text | |
 |
Fig. 56. Same as Fig. 54 but with an inclination χ = 90°. |
| In the text | |
 |
Fig. 57. Distribution of 108 radio emission points inside the “north” polar cap at the surface of the neutron star for a perpendicular rotator, showing an almost uniform distribution. |
| In the text | |
 |
Fig. 58. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 30°. From top to bottom, these maps shows emission frequencies within [30, 120] MHz, [120, 210] MHz, and [210, 300] MHz. |
| In the text | |
 |
Fig. 59. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 60°. From top to bottom, these maps shows emission frequencies within [200, 270] MHz, [270, 340] MHz, and [340, 410] MHz. |
| In the text | |
 |
Fig. 60. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 90°. From top to bottom, these maps shows emission frequencies within [330, 450] MHz, [450, 570] MHz, and [570, 690] MHz. |
| In the text | |
 |
Fig. 61. Maps of curvature radii in units of Rcyl for an inclination χ = 30°, on the top for an altitude in [2, 3] R⋆, on the bottom for [4, 5] R⋆ above the polar caps. |
| In the text | |
 |
Fig. 62. Same as Fig. 61 but for an inclination χ = 60°. |
| In the text | |
 |
Fig. 63. Same as Fig. 61 but for an inclination χ = 90°. |
| In the text | |
 |
Fig. 64. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 30°. From top to bottom, these maps shows emission frequencies within [30, 120] MHz, [120, 210] MHz, and [210, 300] MHz. |
| In the text | |
 |
Fig. 65. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 60°. From top to bottom, these maps shows emission frequencies within [200, 270] MHz, [270, 340] MHz, and [340, 410] MHz. |
| In the text | |
 |
Fig. 66. Radio sky maps and some light curves for an emission emanating from an altitude r ∈ [2, 3] R⋆ for an obliquity χ = 90°. From top to bottom, these maps shows emission frequencies within [330, 40] MHz, [450, 570] MHz, and [570, 690] MHz. |
| In the text | |
 |
Fig. 67. Radio light curves for χ = 60°, ζ = 120° and an emission zone r ∈ [2, 3] R⋆: in red for frequencies in the interval [200, 270] MHz, in green for [270, 340] MHz, and in blue for [340, 410] MHz. |
| In the text | |
 |
Fig. 68. Radio emission spectrum, in blue for χ = 30°, in green for χ = 60°, and in red for χ = 90°. |
| In the text | |
 |
Fig. 69. Radio emission spectra for a region located in the range [1, 2] R⋆ on the top, and in the range [3, 4] R⋆ on the bottom, in blue for χ = 30°, in green for χ = 60°, and in red for χ = 90°. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



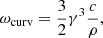
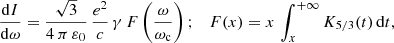
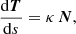
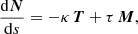
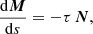
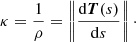
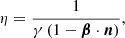
![$$ \begin{aligned} {\boldsymbol{n}} = \frac{1}{\eta }\left[{\boldsymbol{n}}\prime +\gamma \left(\dfrac{\gamma }{\gamma +1}({\boldsymbol{\beta }} \cdot {\boldsymbol{n}}\prime )+1\right){\boldsymbol{\beta }}\right] , \end{aligned} $$](/articles/aa/full_html/2021/10/aa40020-20/aa40020-20-eq10.gif)
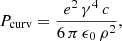
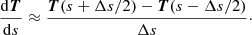
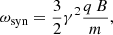
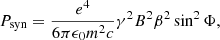
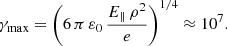
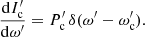
![$$ \begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}\gamma } \propto \gamma ^{-p} \qquad \mathrm{with} \qquad \gamma \in [\gamma _{\rm min},\gamma _{\rm max}], \end{aligned} $$](/articles/aa/full_html/2021/10/aa40020-20/aa40020-20-eq19.gif)
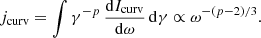
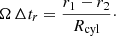
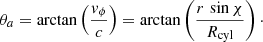
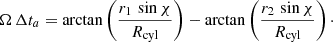
![$$ \begin{aligned} \Omega \,\Delta t_B = 1.2\,\sin ^2\chi \,\left[\left(\frac{r_2}{R_{\rm cyl}}\right)^3-\left(\frac{r_1}{R_{\rm cyl}}\right)^3\right]\cdot \end{aligned} $$](/articles/aa/full_html/2021/10/aa40020-20/aa40020-20-eq26.gif)
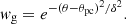
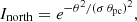
![$$ \begin{aligned} \theta - \theta _{\rm mp} = \arccos \left[1 - \left(1 - \cos \theta _{\rm pc} \right) \, X \right], \end{aligned} $$](/articles/aa/full_html/2021/10/aa40020-20/aa40020-20-eq34.gif)