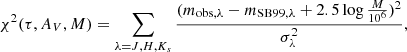EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 639 (July 2020) A&A, 639 (2020) A28 Full HTML
Open Access
Issue
A&A
Volume 639, July 2020
Article Number A28
Number of page(s) 10
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202037755
Published online 03 July 2020

© N. T. Lam et al. 2020

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

The interaction of galaxies, even if it does not end in merging, generally triggers extreme star formation. This is evidenced prominently in (ultra)luminous infrared galaxies ((U)LIRGs), where the star formation rate (SFR) can exceed 1000 times the one of a quiescent galaxy like the Milky Way. These objects radiate most of their energy in the infrared (IR; log(LIR/L⊙) >  11), as the dust of the dense star-forming clouds is heated by the ultraviolet (UV) light. Its major sources are luminous massive stars dominating the starburst activity (Sanders & Mirabel 1996). Found in abundance in (U)LIRGs are very young (< 100 Myr), massive (≳104 M⊙), and dense (≳103 M⊙ pc−1 at core) stellar clusters called super star clusters (SSCs). They play a fundamental role in star formation history throughout the universe, yet their global characteristics and evolution are not well constrained due to a limited number of nearby samples. Notably, their connection with the globular clusters, which are thought to be their remnants, has not been established in detail (Portegies Zwart et al. 2010). Although extensive surveys of LIRGs do exist (e.g., the Great Observatories All-sky LIRG Survey (GOALS); Armus et al. 2009), studying their SSC populations remains challenging because of the large distances. For instance, the GOALS sample in Haan et al. (2011) has a median distance of ∼140 Mpc. To resolve, or at least separate SSC complexes in the near IR with ground-based telescopes, adaptive optics (AO) is usually required. The goal of this paper is precisely to exploit AO-assisted near-IR images of the LIRG IRAS 17138-1017, in order to study its SSC population in terms of luminosity function, age distribution, spatial distribution, extinction, and dust content with the help of a radiative transfer code, as well as theoretical evolutionary tracks. The question of the possible effect of hot dust emission in the K band and the way it can affect the location of SSCs on the color–color diagram (C–CD) is examined in particular.

Our target IRAS 17138-1017 is a late-stage merger (Stierwalt et al. 2014), deeply extincted LIRG (Depoy et al. 1988), with log(LIR/L⊙) = 11.42 at a luminosity distance of 75.9 Mpc (Sanders et al. 2003). Although optical spectroscopy (Yuan et al. 2010) and spectral energy distribution (SED) fitting (Herrero-Illana et al. 2017) suggest some active galatic nucleus (AGN) activities, mid-IR tracers (Herrero-Illana et al. 2017) and X-ray observations (Ricci et al. 2017; Torres-Albà et al. 2018) confirm the domination of starburst in IRAS 17138-1017, as originally proposed by Depoy et al. (1988) based on multiwavelength observations. Herrero-Illana et al. (2017) also suggested the existence of a 23.0 Myr starburst, along with a star formation rate (SFR) of 58.8 M⊙ yr−1, consistent with other indicators. Several highly extinct supernovae have been detected in IRAS 17138-1017 (e.g. Kankare et al. 2008; Kool et al. 2018), as expected for a core-collapse supernova (CCSN) rate of 0.75 SN yr−1 (Herrero-Illana et al. 2017). The SSC population in IRAS 17138-1017 has been characterized in B and I band by Miralles-Caballero et al. (2011), in Ks band by Randriamanakoto et al. (2013a,b), and in BIKs bands all together by Randriamanakoto (2015) as part of their survey of local LIRGs. In this paper, we present an in-depth study of the SSC population in IRAS 17138-1017 with AO images in J, H and Ks bands, using multiconjugate adaptive optics that allow wide field imaging.

2. Observations and data reduction

We observed IRAS 17138-1017 in J, H, and Ks bands on 15 April 2014 (PID: GS-2014A-Q-21; PI: Olivier Lai), using GSAOI, the Gemini South Adaptive Optics Imager (McGregor et al. 2004; Carrasco et al. 2012) fed by GeMS, the Gemini Multi-Conjugate Adaptive Optics System (Rigaut et al. 2014; Neichel et al. 2014). The GSAOI detector consists of 2 × 2 mosaic Rockwell HAWAII-2RG 2048 × 2048 arrays, covering a 85″ × 85″ field of view with a pixel scale of 0.02″. In total, 20, 12, and 8 frames of 120s were obtained in J, H, and Ks bands, respectively, following a 2 × 2 dithering pattern with 15″ × 20″ offsets. The observations used five sodium laser guide stars (LGSs) to correct for the atmospheric distortion and three natural guide stars (NGSs) to compensate for the tip-tilt and plate-scale modes. A temporary misalignment in the Laser Guide Star Wave-Front Sensor (LGSWFS) from November 2013 to June 2014 causing point-spread function (PSF) distortions was reported (e.g. Monty et al. 2018). However, since a software patch was introduced in February 2014, our data only suffers from limited degradation.

Firstly, nonlinear correction, flat division, and sky subtraction were performed on the raw data with the standard IRAF/PYRAF package for Gemini’s GSAOI (Tody et al. 1986, 1993). To correct for the distortion and subsequently align and stack the images, we used DISCO-STU1, a standalone utility provided by Gemini. The static distortion was calculated from a lookup table taking the telescope pointing and instrument position angle into account, while the variable distortion was determined by matching sources between images. After stacking, bad pixels were rejected, and pixels received inverse-variance-weighted average values. Finally, we resampled and rescaled the J and H band images to match the Ks band image using the IRAF tasks GEOMAP and GEOTRAN. The world coordinate system (WCS) was calibrated with the IRAF task CCMAP. Using field stars from the 2MASS catalogue (Skrutskie et al. 2006), we obtain an average astrometric error of 0.2″. The final trimmed images in J, H and Ks are displayed in Fig. 1.

thumbnail Fig. 1.

GeMS/GSAOI images of IRAS 17138-1017 in J (left), H (middle), and Ks (right) plotted in square root scale. The field of view is 32″ × 32″ and the horizontal bar represents 1 kpc at the estimated distance of IRAS 17138-1017.

3. Construction of the super star cluster catalog

3.1. Source extraction

We identified cluster candidates using STARFINDER (Diolaiti et al. 2000), a code developed for the analysis of crowded fields in AO images. An empirical PSF template was first constructed from several bright, non-saturated stars in the subfield, then decontaminated by a preliminary detection at 5σ level. Post-processing including circular masking, principal component extraction, halo smoothing and normalisation were applied. Finally, the sources were iteratively extracted twice at 3σ level. The correlation thresholds were set at 0.7 for J and Ks bands, and 0.8 for H band. These parameters were tuned to recover the faintest objects while limiting spurious detections. After cross-matching all three bands, we detect 109 objects in total with 15 mag ≤ mKs <  22 mag. Most of them exist in the central region of the galaxy. However, several sources in the outer parts may still be true SSCs belonging to some tidal tails. Section 3.3 details how we proceed to discriminate between actual SSCs and possible foreground field stars or background galaxies to obtain a final sample that would be populated by SSCs with a fair degree of confidence.

3.2. Point-spread function photometry

For high background variation and crowding, aperture photometry of extragalactic clusters is prone to contamination from neighboring sources and nebular emission (Bastian et al. 2014), while PSF photometry performs more robustly, as already demonstrated with GeMS/GSAOI by Turri et al. (2017). Thus, we used the photometric measurements from STARFINDER provided together with the extracted sources. The instrumental photometric errors were calculated from the variance associated with the science data, with median values in J, H, and Ks of 0.05 mag, 0.03 mag, and 0.04 mag, respectively. Chavez et al. (2019) estimate photometric zero points for Gemini’s GeMS/GSAOI at various epochs of observation, including the one when the present images were recorded. However, those zero points were derived from standard star observations under natural seeing conditions, and they give colors that are clearly strongly biased when applied to our dataset. We thus preferred to establish zero points directly from multiple non-saturated 2MASS stars within the original fields instead, using the 2MASS calibration (Skrutskie et al. 2006). The corresponding errors for J, H, and Ks band zero points are 0.04 mag, 0.09 mag, and 0.11 mag. Finally, we corrected the foreground Galactic extinction using the Fitzpatrick (1999) reddening law and Schlafly & Finkbeiner (2011) measurements from the NASA/IPAC Extragalactic Database (NED).

3.3. Cluster selection

To evaluate the potential contamination from foreground stars and background galaxies, we analyzed a nearby control field of the same area in which 42 objects are detected. This is not consistent with the theoretical expectation, since in a field of view of 32″ × 32″ at the same galactic coordinates of IRAS 17138-1017 and in the apparent K-band magnitude range of 15 mag ≤ mK <  22 mag, the Besançon model (Robin et al. 2003) expects negligible Milky Way star count (< 1), while the GALAXYCOUNT program (Ellis & Bland-Hawthorn 2007) estimates 12 ± 4 galaxies only, assuming completeness of detection. Now, we cannot exclude a local density that is actually higher than predicted, especially when GALAXYCOUNT is based on galaxy surveys without AO correction, and thus are less sensitive to low surface brightness. Moreover, Ellis & Bland-Hawthorn (2007) also advise using their models with caution for star-counting observations with unknown numbers of galaxies. In fact, the Hubble Source Catalog version 2 (Whitmore et al. 2016) contains all of these objects and even some additional sources in this field. Nevertheless, we visually inspected and removed 42 sources outside the galaxy at a median distance of 10.7″ corresponding to ∼3.9 kpc to minimize contamination, and we also excluded the nucleus (identified unambiguously on the SINFONI velocity map of Piqueras López et al. 2012), leaving us with 66 SSC candidates. The consistency of the catalog is later confirmed in the (H − Ks) versus (J − H) C–CD (Fig. 2) through comparison with the control field, which reveals clearly distinct locations of both samples. The objects in the control field are well grouped in the area expected for field galaxies, as illustrated by the red stars, which corresponds to the average and standard deviation of near-IR colors of the sample of 100 galaxies from the 2MASS survey, studied by Jarrett et al. (2003). About the same area of the (J − H) versus (H − K) diagram is found in Fig. 5 of Foster et al. (2008). However, we notice some variations in the colors of these objects in other nearby control fields, which may be related to the existence of a local galaxy cluster, as mentioned above, and is beyond the scope of our study. Table 1 lists the final sample of detected SSCs with their coordinates, their derived extinctions, ages, and masses as described in the next section, and finally the J, H, and Ks magnitudes with their instrumental uncertainties. For comparison, Randriamanakoto et al. (2013b) detect 60 SSCs in Ks band with photometric errors σm ≤ 0.25 and a 50% completeness limit of mK = 20.0, while Randriamanakoto (2015) detects 104 SSCs in B, I and Ks bands with photometric errors σm ≤ 0.35 in each filter.

thumbnail Fig. 2.

Color–color diagram (J − H) versus (H − Ks) for the selected sample of SSCs (black dots). The theoretical stellar evolution track given by SB99 is shown for solar metallicity as the solid magenta line. The reddening vector corresponding to AV = 1 is shown. The red stars are the sources detected in the control field, and the cross corresponds to the average color indices of the sample of 100 galaxies from the 2MASS survey, studied by Jarrett et al. (2003), with the length of the arms being equal to the standard deviations of those indices. The black cross represents the median errors of the cluster colors.

Table 1.

Catalog of SSC candidates in IRAS 17138-1017.

4. Analyses and results

4.1. Color and magnitude distributions

The (H − Ks) versus (J − H) C–CD of selected clusters is presented in Fig. 2. For comparison, we also plot an evolutionary track calculated using Starburst99 (SB99, Leitherer et al. (1999, 2014)) with the following setup: a simple stellar population (SSP) of 106 M⊙ with a Kroupa et al. (2008) initial mass function (IMF) ranging from 0.1 M⊙ to 100 M⊙ and a solar metallicity (Z = 0.014). We assume the Calzetti et al. (2000) extinction law for starburst galaxies with RV = 4.05 and draw on the C–CD the corresponding reddening vector. With respect to the sources in the control field, the sample occupies a well-separated area in the upper-right region of the diagram, and by comparison with the evolutionary track, we can safely assume that most of the sources are highly extinct. However, some of them (the ones with rather large (H − Ks) colors) cannot be directly de-reddened to match the evolutionary model, since the line parallel to the reddening vector does not cross the theoretical track. Although we think that a large fraction of those peculiar sources do not correspond to an erroneous photometry, but to an additional reddening different from the one due to dust extinction, as discussed in Sect. 5, we consider them as outliers in the de-reddening process that we use. In any case, it appears that for the vast majority of the SSCs we detected, the age is clearly below 5 Myr, as discussed in more detail below.

We also calculated the reddening-independent color index Q = (H − Ks)−E(H − Ks)/E(J − H) × (J − H), which does not depend on the extinction AV, for both the actual data and the theoretical evolutionary track. As demonstrated by Santos et al. (2013), this type of color index is a powerful tool for age diagnostics of young star clusters. A color–magnitude diagram (C–MD) using this index and the absolute de-reddened Ks-band magnitude is shown in Fig. 3 with the same evolutionary track and extinction vector as in the C–CD. This confirms that most of the clusters are very young. Age-reddening degeneracy occurs on both diagrams on the most evolved part of the evolutionary track, because on this portion (i) the track is practically parallel to the reddening vector, and (ii) there are several foldings of the track, so that the lines parallel to the reddening vector may cross the track on several locations, however the impact is weak, because as we already stated, the majority of SSCs are young. We note that in the upper part of the diagram (close to the SB99 track shifted by ∼ − 2 mag), corresponding to the brightest SSCs, the distribution of points tends to be more uniform along the Q axis, as if the brightest SSCs were more evenly distributed along an age sequence than the fainter ones. This could translate into the fact that the most massive SSCs are less subjected to disruption (see discussion in the next section).

thumbnail Fig. 3.

Color–magnitude Q versus Ks diagram using the absolute Ks magnitude and the Q index, which in principle is not affected by the extinction. The same theoretical stellar evolution track as in Fig. 2 is shown. The black cross represents the median errors of the cluster colors and magnitudes.

4.2. Age, mass, and extinction calculation

To derive the age (τ), mass (M), and extinction (AV) of each cluster, we looked for the age and extinction that minimize the quantity (cf., Parmentier et al. 2003):

(1)

where Cobs and CSB99 are the de-reddened colors from the observations and from the SB99 model, respectively, and σC are the estimated errors of the observed colors, using age steps of 0.1 Myr and AV steps of 0.05 mag. Cluster masses were estimated from extinction-corrected J, H, and Ks-band luminosities, assuming mass-to-light ratios from the model, then the median value among the three bands was adopted. We calculated the effects of each band’s photometric errors on the estimated parameters separately, then quadratically summed the resulting increments or decrements to determine the corresponding upper or lower variances of the parameters.

For validation, we also performed a semi-independent SED fitting taking into account cluster masses by minimizing the following quantity (cf., Bik et al. 2003; Anders et al. 2004):

(2)

where mobs, λ and mSB99, λ are the de-reddened apparent magnitudes from the observations and the SB99 model, respectively, and σλ are the photometric errors, using the same age and AV steps as for the color fitting and mass steps of 0.01 dex. The two methods provide consistent results, as shown in Fig. 4, except for one distinct outlier visible in the age plot. For the analyses below, we excluded the peculiar sources that cannot be directly de-reddened to match the evolutionary model (including the outlier above), leaving us with 54 cluster candidates.

thumbnail Fig. 4.

Comparison between the three quantities age, mass and extinction derived for each cluster using color fitting versus the same quantities derived from SED fitting.

Table 1 gives the estimated extinctions, ages, masses and apparent magnitudes of the final sample with the associated instrumental errors.

4.3. Age distribution and star formation history

Figure 5 plots the age distribution of the clusters as an histogram with bins of 0.1 dex in age. We identify two clear peaks at τ = 2.8 and 4.5 Myr. Although rapid changes in the energy distributions and colors of clusters have been known to cause similar statistical artefacts (e.g., Bik et al. 2003; Bastian et al. 2005), in our case, we believe they are real physical patterns given the very fine age steps of 0.1 Myr in our models. The ages corresponding to both peaks are consistent with Randriamanakoto (2015) who find a broad distribution peaking around 6 Myr and extending to younger ages, but that does not separate into two peaks. Nevertheless, comparisons are limited because they use larger age steps and cannot break the age-extinction degeneracy with BIKs-data only. These two peaks in age are particularly prominent, indicating that two very recent bursts occurred and in fact dominate the detected population of SSCs. Such young ages for starbursts are not often observed, but have been measured in a few other galaxies, for instance in M51 where Gieles et al. (2005) find two peaks: one being at 5.5 Myr, or in the dwarf merger ESO 185-IG13 (Adamo et al. 2011a) where the histogram peaks at 3 Myr.

thumbnail Fig. 5.

Age distribution of SSCs in IRAS 17138-1017. The error bars assume Poisson uncertainties.

Figure 6 shows the estimated masses of the clusters versus their ages. The bimodal distribution on the two bursts is especially clear on this plot. Disruption of clusters by interaction with giant molecular clouds (GMCs) in their vicinity has been the subject of many works and debates (Longmore et al. 2014; Adamo et al. 2018). The characteristic disruption time generally follows the relation tdis ≈ t4(Mcl/104 M⊙)0.62 (e.g., Boutloukos & Lamers 2003; de Grijs et al. 2003), where t4 is the disruption time of a 104 M⊙ cluster, which depends on the specific conditions of the galaxy, especially the surface density of molecular clouds. For the non-LIRG star-forming galaxy M51, Gieles et al. (2005) derived a disruption time tdis ≈ 100.0 (Mcl/104 M⊙)0.62 Myr. If the law is universal, no SSC less massive than 104 M⊙ and with an age older than 0.1 Gyr would be detectable in IRAS 17138-1017. This is in fact what we observe, but the lowest mass we detect would also be compatible with t4 = 6 Myr. However in a subsequent paper, Gieles et al. (2006) proposed a more detailed relation where the surface density of GMCs is taken into account, since it may vary by large amounts from one galaxy to another. They find that 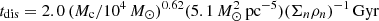, where the surface density of individual GMC (Σn) and the global GMC density (ρn) are scaled to the solar neighborhood. To reach t4 = 6 Myr, we need an increase of the product Σnρn of 300 with respect to the solar neighborhood, a value that is not exceptional in an LIRG galaxy. For instance, ALMA observations of the LIRG IRAS 13120-5453 reveal a surface density Σn = 2.0 × 104 M⊙ pc−2 (Privon et al. 2017) which, if combined with a density of GMC twice that of the solar neighborhood (ρn = 0.03 M⊙ pc−3, Solomon et al. 1987), would provide this factor. IRAS 17138-1017 is well known for its very high obscuration (Depoy et al. 1988, this work). This is also demonstrated by the detection of the most extinct supernovae so far, with AV = 15.7 mag for SN2008cs (Kankare et al. 2008), supporting such high value of Σn. Finally, Piqueras López et al. (2016) find that the star formation rate per unit surface, ΣSFR of IRAS 17138-1017 is the second highest in a sample of 17 LIRGs and ULIRGs. Considering the well-established Kennicutt-Schmidt law ΣSFR ∝ (Σgas)1.4 ± 0.15, this is an additional hint of a high Σn.

thumbnail Fig. 6.

Cluster age-mass plane for the sample of SSCs in IRAS 17138-1017. The blue dash line marks the age of 3.7 Myr splitting two bursts.

We also calculated the cluster formation efficiency (CFE or Γ), defined by Bastian (2008) as the fraction of stellar mass formed in bound clusters Γ = CFR/SFR, where CFR is the cluster formation rate, meaning the total cluster mass in a certain age range divided by the corresponding time interval, and SFR is the star formation rate of the host galaxy during that period. Adopting an SFR of 44.7 M⊙ yr−1 derived from the IR luminosity (Kennicutt 1998) and an age range between 1 and 10 Myr, we obtain Γ ≈ 33.4%. Given the similar SFR, Randriamanakoto (2015) found a value of 17% for the age range between 10 and 100 Myr. These values are consistent with the ones observed for starburst galaxies (Adamo et al. 2018, and references therein) and could be evidence of infant mortality: clusters are disrupted quickly during the first 10 Myr due to the gas expulsion process (Lada & Lada 2003). Our Γ value and the ΣSFR of 8.9 M⊙ yr−1 kpc2 measured by Piqueras López et al. (2016) are also in agreement with the Γ–ΣSFR relation established by Kruijssen (2012). Nevertheless, our estimation of Γ at an early age should only be viewed as an upper limit, due to the possible inclusion of unbound associations in our catalog (Kruijssen & Bastian 2016).

4.4. Extinction

To further examine the relation between the cluster age and extinction as shown in Fig. 7, in Fig. 8 we plot the histograms of AV splitting the SSCs into two groups corresponding to the identified bursts, meaning younger or older than 3.7 Myr. In particular, the bottom plot showing the relative distribution of extinction in each population reveals a clear tendency to have fewer extinct SSCs in the most recent burst, with more than 60% of the SSCs having AV <  5, while the 4.5 Myr burst has more than 60% of the SSCs with AV >  5. Nevertheless, the two most extinct SSCs belong to the young burst. The intuitive idea that “the younger an SSC is, the more embedded it should be”, is not confirmed here. Given the narrow time period between the two bursts, it might be that the first generation had consumed or expelled a part of the interstellar medium (ISM) so that the next generation was born in a less dense medium. Another tentative explanation could be that the most recent burst was triggered by the first one and occurred in a less dense component of the GMC within the galaxy, which had not collapsed at the moment of the first burst.

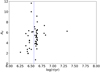thumbnail Fig. 7.

Age versus extinction for the sample of SSCs. The blue dash line marks the age of 3.7 Myr separating the two identified bursts.

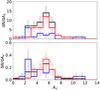thumbnail Fig. 8.

Frequency distribution of the extinction. The black line represents the entire sample, and the blue and red lines correspond to the populations of the 2.8 Myr burst and 4.5 Myr burst, respectively. Top: absolute numbers. Bottom: relative numbers. The error bars assume Poisson uncertainties.

4.5. Luminosity and mass functions

Figures 9 and 10, respectively, plot the intrinsic (de-reddened) Ks-band cluster luminosity function (CLF) and the cluster mass function (CMF) of IRAS 17138-1017, expressed as the number of objects per bin of 1 mag and 0.5 dex of mass, respectively. Each of them can be approximated by a power-law distribution (plotted as the dashed line on each figure) in the forms of dN/dL ∝ Lα and dN/dM ∝ Mβ, with α = −1.44 and β = −1.58. For clusters with age τ ≤ 3.7 Myr, we obtain α = −1.28 and β = −1.48. Clusters with age τ >  3.7 Myr have α = −1.55 and β = −1.67. As can be seen on the plots, the flattening of the young age CLF and CMF is caused by a spike of heavy (6.5 ≤ log(M/M⊙) <  7) and bright (−18 <  MKs ≤ −17) SSCs.

thumbnail Fig. 9.

Luminosity function (dN/dL versus MKs) of the entire sample of SSCs (black) and for the subsamples of age τ ≤ 3.7 Myr (blue) and age τ ≥ 3.7 Myr (red), in bins of 1 mag. The black, blue, and red dash lines are corresponding linear regressions. The error bars assume Poisson uncertainties.

thumbnail Fig. 10.

Mass function of the entire sample of SSCs (black) and for the subsamples of age τ ≤ 3.7 Myr (blue) and age τ >  3.7 Myr (red), in bins of 0.5 dex. The black, blue, and red dash lines are corresponding linear regressions. The error bars assume Poisson uncertainties.

In general, these values of the CLF are at the lower end of the observed range (α  ≈   − 1.87 ± 0.3) for SSCs in ULIRGs and LIRGs (including blue compact dwarves) (Randriamanakoto et al. 2013b; Vavilkin 2011; Miralles-Caballero et al. 2011; Adamo et al. 2010a, 2011a,b). For comparison, normal spiral galaxies, or even star-forming galaxies though not yet LIRGs exhibit significantly steeper distribution, where α ≈ −2.2 ± 0.3 (Elmegreen & Efremov 1997; Gieles et al. 2006; Bastian 2008; Haas et al. 2008; Larsen 2009). However, many authors might not de-redden their estimated magnitudes when the effect of extinction could be significant and lead to CLFs deviating from power law (Megeath 1996). For IRAS 17138-1017, without de-reddening we find that α = −1.57, which matches the Randriamanakoto et al. (2013b) values of α = −1.53 and −1.64 for constant and variable bin widths, respectively.

In terms of the CMF, our indices are shallower than the canonical β ≈ −2 found in the literature (Krumholz et al. 2019), as well as the average value of β = −1.95 ± 0.11 for LIRGs in the GOALS survey (Linden et al. 2017), yet they still fall in the observed range. Starburst galaxies at large distances tend to have flatter CMFs, which might result from a blending effect (Krumholz et al. 2019). For comparison, Randriamanakoto (2015) obtained values of β = −1.86 for clusters younger than 30 Myr, and β = −1.61 for clusters of ages between 30 Myr and 1 Gyr in IRAS 17138-1017, but she also warned of an overestimation of cluster masses and the age-extinction degeneracy.

Because IRAS 17138-1017 is distant, the mass and luminosity functions are only significant for the SSCs more massive than ∼3.0 ×  105 M⊙, which is the range used to fit the power law. Comparison with the CLFs or CMFs of nearby galaxies is thus meaningful only for this range. The observed slopes of both CLF and CMF are linked to the shape of the underlying IMF and to the evolution and disruption of the SSC population. The relatively flatter luminosity distribution of IRAS 17138-1017, with respect to other LIRGs may again be an evidence for the disruption of lower mass SSCs due to tidal shock heating by dense gas, as proposed by Kruijssen et al. (2012). This cruel cradle effect could be more efficient here than in similar galaxies because of its high surface density of GMCs.

Several studies have pointed out that the CMF tends to be steeper than the power law at the high-mass end due to a truncation effect (Adamo et al. 2018). At first sight, such a steepening seems to be present in Fig. 8, the two last bins of the CMF being well below the power law. However, this is actually not significant, due to the very low number of SSCs in those bins.

4.6. Spatial distribution

Figure 11 shows the Ks image of IRAS 17138-1017 with the detected SSCs superimposed and colored in accordance with their ages. There is a clear tendency to find the younger SSCs closer to the center. This can be confirmed by plotting the number of SSCs in successive rings on Fig. 12: the youngest burst mainly populates the central region (R <  1.25 kpc) rather than the more peripheral one. The spatial distribution of the SSCs is also consistent with the cruel cradle effect: older clusters are able to survive early disruption because they have escaped into more quiescent regions, only young clusters are present in the gas-rich environments (Kruijssen et al. 2012).

thumbnail Fig. 11.

Locations of the SSCs on the Ks image of IRAS 17138-1017. The colors of the open circles indicate the age category (blue for age τ ≤ 3.7 Myr burst and red for age τ >  3.7 Myr).

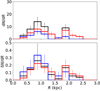thumbnail Fig. 12.

Number of SSCs per ring of increasing diameters centered on the nucleus. The black line represents the entire sample, the blue and red lines correspond to the populations of the 2.8 Myr burst and 4.5 Myr burst, respectively. Top: absolute numbers. Bottom: relative numbers in each category.

Figure 13 plots the relation between the masses of the clusters and their distances to the galactic center. In general, the cluster mass decreases as the galactocentric distance increases. Pflamm-Altenburg et al. (2013), Sun et al. (2016), Randriamanakoto et al. (2019) also find a similar relation for the most massive clusters in their samples, yet Sun et al. (2016) showed that it is mostly caused by size-of-sample effects, and they supported the stochastic cluster formation scenario. We find this trend pertaining to the entire sample of SSCs and less likely affected by any size-of-sample effect. Adamo et al. (2015) also showed that the cluster formation efficiency Γ declines over galactocentric distance in M83, following the Γ − ΣSFR relation of Kruijssen (2012). A radial decrease of ΣSFR is also observed in IRAS 17138-1017 (Piqueras López et al. 2016). We conclude that the formation of star clusters depends on the host galaxy environment.

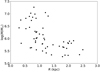thumbnail Fig. 13.

Mass-galactocentric radius relation for the sample of SSCs.

5. Modeling super star clusters with the radiative transfer code MontAGN

Until now, to interpret observations, most cluster studies assumed that evolutionary models such as SB99 can fairly simulate the spectra of SSCs at different ages. However, we have seen that in several cases it is not possible to de-redden the cluster colors along the reddening vector to reach a point on the evolutionary track. Many other authors also face similar problems without definitive explanations, particularly outliers in color space or near-IR excesses in SED fitting (e.g. Grosbøl & Dottori 2008, 2012; Reines et al. 2008a,b; Adamo et al. 2010a, 2011a,b). For instance, the presence of evolved stellar populations was hypothesized to cause extra reddening (e.g. Grosbøl & Dottori 2008, 2012). However using the COLIBRI code (Pastorelli et al. 2019) with an accurate processing of the thermally-pulsing asymptotic giant branch (TP-AGB) phase, we find that a 1 Gyr synthetic stellar population only produces (H − K) = 0.06. Low spatial resolution and large photometric aperture may also introduce nebular emission and nearby stellar contamination into the near-IR flux, resulting in redder colors (Bastian et al. 2014), yet our study should not be susceptible. Other proposed mechanisms include nebular emission (e.g. Reines et al. 2010; Adamo et al. 2010b) and hot dust emission (e.g. Adamo et al. 2010a, 2011a,b). In our study, SB99 only considers the stellar and nebular emission and no other sources of radiation. Because SSCs are formed within dense cocoons of gas and dust, we expected some contribution of the hot dust emission at least in the K-band. In addition, we wondered whether scattered radiation in a highly clumpy medium might lead to a different behavior of the extinction with respect to the wavelength rather than classical reddening laws representing point sources behind a screen. This may be a concern for SSCs, because a significant portion of the light scattered in the cocoon is also collected in the beam2. To quantify the role of these two effects, we generated a series of simulations using the radiative transfer code MontAGN developed by our team (Grosset et al. 2018).

5.1. Model description

To simulate embedded SSCs in the IR, we developed additional features for our three-dimensional radiative transfer code MontAGN (Monte Carlo for Active Galactic Nuclei), which was originally designed for the study of AGNs (Grosset et al. 2016, 2018; Marin et al. 2016). We added polycyclic aromatic hydrocarbons (PAHs) as a component of the ISM following the absorption and emission scheme of Draine & Li (2007), with the absorption cross sections from Siebenmorgen et al. (2014). We also introduced the fractal dust distribution to simulate the hierarchically clumpy ISM within the cluster (Elmegreen 1997). The algorithm followed Mathis et al. (2002). (1) Initially, we selected N random cells in the simulation grid. (2) For each previously selected cell, we selected N other random cells within a distance of S/2L along each Cartesian axis. We recursively selected NH cells in total. Here, S is the grid size, L is the fractal length giving the fractal dimension D = logLN, and H is the number of hierarchical levels. (3) We shifted each cell by multiples of S on three Cartesian axes until it was inside the grid. (4) We only kept cells inside the predefined envelope and filled appropriate dust densities. Our code provides matching results (Lam et al. 2019) to the SSC models from Whelan et al. (2011).

Our SSC models consist of a central point source enshrouded in a spherical dust envelope, with the outer radius fixed at 50 pc. The inner radius increases as the cluster evolves, similarly to Whelan et al. (2011). The source radiates an SB99 spectrum with the following parameters: a 106 M⊙ SSP with a Kroupa et al. (2008) IMF (0.1 M⊙–100 M⊙), Geneva evolutionary tracks (Ekström et al. 2012) at solar metallicity (Z = 0.014), and an instantaneous starburst. The dust envelope has a mass composition of 75% silicate, 13.33% ortho-graphite, 6.67% para-graphite, and 5% PAH (Draine 2011) with a classical MRN grain size distribution (Mathis et al. 1977). Apart from a smooth distribution, 50% of the dust is distributed fractally. We adopted N = 32, D = 2.6, H = 5 for the hierarchically clumpy distribution, a standard dust-to-gas ratio of 0.01 as suggested by Whelan et al. (2011), and a representative star-forming efficiency (SFE) of 33% following Banerjee & Kroupa (2017). The SFE sets the mass of residual ISM and thus of dust, after stars have been formed.

5.2. Results and discussions

Figure 14 displays the SEDs for several sets of parameters where combinations of the inner radius of the envelope and the age are considered. We can see that the models with thin envelopes leak out significant star light and are much brighter in the visible than in the near IR, which is not the case for IRAS 17138-1017. They must be disregarded for this reason. The dust thermal emission in Ks-band is lower than the total flux by at least two orders of magnitude in all considered cases, which is negligible. The same conclusion also applies to the scattered radiation because most of the grains have very low albedo values. We find that the extra reddening brought by thermal and scattered photons is ΔKs = −0.015 at maximum. Figure 15 plots the corresponding points on the C–CD, derived by integrating the flux in each filter band. We also show the reddening vector conforming to the Calzetti et al. (2000) extinction law for starburst galaxies like in Fig. 2, but it is for comparison purposes only and not used in the numerical code. Nevertheless, the colors can be de-reddened along this vector without significant deviations in the estimated ages. As a consequence, the extra reddening could not be explained by the thermal emission or scattered radiation. Assuming good uncertainty estimates, an extra source of reddening affecting a small number of SSCs has yet to be identified.

thumbnail Fig. 14.

Spectral energy distributions obtained with MontAGN for various sets of age τ and inner radius Rin of the dust envelope. The thick lines represent the total flux, the dotted lines indicate the dust emission, and the dashed lines indicate the stellar emission. The position of the Ks-band is denoted.

thumbnail Fig. 15.

Color–color diagram (J − H) versus (H − Ks) for the simulated SSCs with various conditions of age and inner radius of the dust envelope. The same theoretical track and reddening vector as in Fig. 2 are shown.

6. Conclusions

The excellent quality of the AO-assisted near-IR images in J, H, and Ks obtained with GeMS on Gemini allows us to identify 54 SSCs in the LIRG IRAS 17138-1017 and to extract their photometry. Most of them appear highly extinct compared to an evolutionary track provided by SB99. Using the Calzetti et al. (2000) extinction law to directly de-redden the clusters and derive their ages, we show that most of them are very young and distributed in two narrow bins of ages of around 2.8 and 4.5 Myr. Thus, IRAS 17138-1017 is a noticeably interesting object for studying the actual IMF of SSCs since disruption could not have played a significant role at those ages. Their luminosity and mass functions follow the classical power-law behavior, however with somewhat shallower slopes than are usually observed in LIRGs. This is a possible indication of the cruel cradle effect: lower mass SSCs are produced less efficiently in an environment with a high surface density of GMCs (Kruijssen et al. 2012), a very likely characteristic of IRAS 17138-1017 where the most extinct SNe have been observed. The SSCs belonging to the youngest starburst episode primarily gather near the central area, while the older ones from the 4.5 Myr starburst are scattered along the spiral arms. In addition, the extinction of the 2.8 Myr SSCs is generally lower than the 4.5 Myr episode, yet some highly extinct SSCs are found in the first group. Even though being separated by only 2 Myr, the two episodes appear to be distinct, probably triggered by different causes and in different populations of molecular clouds. By comparing the observed photometry with the output from realistic radiative transfer models of young SSCs, we conclude that hot dust emission, as well as scattered photons in the Ks band remain negligible even for the thickest envelopes.

2

To illustrate this, we can consider hypothetical dust grains with a very high albedo (say 0.95): the extinction efficiency Qext would be totally dominated by the scattering term Qsca. However, most of the light from the source would be collected in a beam encompassing the cocoon.

Acknowledgments

The authors would like to thank the referee for helpful comments and suggestions. This study is based on observations obtained at the Gemini Observatory processed using the Gemini IRAF package, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), National Research Council (Canada), CONICYT (Chile), Ministerio de Ciencia, Tecnología e Innovación Productiva (Argentina), Ministério da Ciência, Tecnologia e Inovação (Brazil), and Korea Astronomy and Space Science Institute (Republic of Korea). IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation. PyRAF is a product of the Space Telescope Science Institute, which is operated by AURA for NASA. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is funded by the National Aeronautics and Space Administration and operated by the California Institute of Technology. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This research made use of Astropy (http://www.astropy.org), a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018) and Matplotlib, a 2D graphics package used for Python for application development, interactive scripting, and publication-quality image generation across user interfaces and operating systems (Hunter 2007).

References

  1. Adamo, A., & Bastian, N. 2018, in The Lifecycle of Clusters in Galaxies, ed. S. Stahler, Astrophys. Space Sci. Libr., 424, 91 [Google Scholar]
  2. Adamo, A., Östlin, G., Zackrisson, E., et al. 2010a, MNRAS, 407, 870 [NASA ADS] [CrossRef] [Google Scholar]
  3. Adamo, A., Zackrisson, E., Östlin, G., & Hayes, M. 2010b, ApJ, 725, 1620 [NASA ADS] [CrossRef] [Google Scholar]
  4. Adamo, A., Östlin, G., Zackrisson, E., & Hayes, M. 2011a, MNRAS, 414, 1793 [NASA ADS] [CrossRef] [Google Scholar]
  5. Adamo, A., Östlin, G., Zackrisson, E., et al. 2011b, MNRAS, 415, 2388 [NASA ADS] [CrossRef] [Google Scholar]
  6. Adamo, A., Kruijssen, J. M. D., Bastian, N., Silva-Villa, E., & Ryon, J. 2015, MNRAS, 452, 246 [NASA ADS] [CrossRef] [Google Scholar]
  7. Anders, P., Bissantz, N., Fritze-v Alvensleben, U., & de Grijs, R. 2004, MNRAS, 347, 196 [NASA ADS] [CrossRef] [Google Scholar]
  8. Armus, L., Mazzarella, J. M., Evans, A. S., et al. 2009, PASP, 121, 559 [NASA ADS] [CrossRef] [Google Scholar]
  9. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  11. Banerjee, S., & Kroupa, P. 2017, A&A, 597, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bastian, N. 2008, MNRAS, 390, 759 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bastian, N., Gieles, M., Lamers, H. J. G. L. M., Scheepmaker, R. A., & de Grijs, R. 2005, A&A, 431, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bastian, N., Adamo, A., Schirmer, M., et al. 2014, MNRAS, 444, 3829 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bik, A., Lamers, H. J. G. L. M., Bastian, N., Panagia, N., & Romaniello, M. 2003, A&A, 397, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Boutloukos, S. G., & Lamers, H. J. G. L. M. 2003, MNRAS, 338, 717 [NASA ADS] [CrossRef] [Google Scholar]
  17. Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
  18. Carrasco, E. R., Edwards, M. L., McGregor, P. J., et al. 2012, in Adaptive Optics Systems III, SPIE Conf. Ser., 8447, 84470N [CrossRef] [Google Scholar]
  19. Chavez, J., Carrasco Damele, E. R., & Thomas-Osip, J. 2019, Am. Astron. Soc. Meeting Abstr., 233, 170.01 [Google Scholar]
  20. de Grijs, R., Bastian, N., & Lamers, H. J. G. L. M. 2003, MNRAS, 340, 197 [NASA ADS] [CrossRef] [Google Scholar]
  21. Depoy, D. L., Wynn-Williams, C. G., Hill, G. J., & Becklin, E. E. 1988, AJ, 95, 398 [CrossRef] [Google Scholar]
  22. Diolaiti, E., Bendinelli, O., Bonaccini, D., et al. 2000, A&AS, 147, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Draine, B. T. 2011, in EAS Publications Series, eds. C. Joblin, & A. G. G. M. Tielens, 46, 29 [CrossRef] [EDP Sciences] [Google Scholar]
  24. Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
  25. Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Ellis, S. C., & Bland-Hawthorn, J. 2007, MNRAS, 377, 815 [NASA ADS] [CrossRef] [Google Scholar]
  27. Elmegreen, B. G. 1997, ApJ, 477, 196 [NASA ADS] [CrossRef] [Google Scholar]
  28. Elmegreen, B. G., & Efremov, Y. N. 1997, ApJ, 480, 235 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
  30. Foster, J. B., Román-Zúñiga, C. G., Goodman, A. A., Lada, E. A., & Alves, J. 2008, ApJ, 674, 831 [NASA ADS] [CrossRef] [Google Scholar]
  31. Gieles, M., Bastian, N., Lamers, H. J. G. L. M., & Mout, J. N. 2005, A&A, 441, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Gieles, M., Portegies Zwart, S. F., Baumgardt, H., et al. 2006, MNRAS, 371, 793 [NASA ADS] [CrossRef] [Google Scholar]
  33. Grosbøl, P., & Dottori, H.. 2008, A&A, 490, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Grosbøl, P., & Dottori, H. 2012, A&A, 542, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Grosset, L., Marin, F., Gratadour, D., et al. 2016, SF2A-2016: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, 57 [Google Scholar]
  36. Grosset, L., Rouan, D., Gratadour, D., et al. 2018, A&A, 612, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Haan, S., Surace, J. A., Armus, L., et al. 2011, AJ, 141, 100 [NASA ADS] [CrossRef] [Google Scholar]
  38. Haas, M. R., Gieles, M., Scheepmaker, R. A., Larsen, S. S., & Lamers, H. J. G. L. M. 2008, A&A, 487, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Herrero-Illana, R., Pérez-Torres, M., Rand Riamanakoto, Z., et al. 2017, MNRAS, 471, 1634 [CrossRef] [Google Scholar]
  40. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  41. Jarrett, T. H., Chester, T., Cutri, R., Schneider, S. E., & Huchra, J. P. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kankare, E., Mattila, S., Ryder, S., et al. 2008, ApJ, 689, L97 [NASA ADS] [CrossRef] [Google Scholar]
  43. Kennicutt, R. C., Jr 1998, ARA&A, 36, 189 [Google Scholar]
  44. Kool, E. C., Ryder, S., Kankare, E., et al. 2018, MNRAS, 473, 5641 [CrossRef] [Google Scholar]
  45. Kroupa, P. 2008, in Pathways Through an Eclectic Universe, eds. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 3 [Google Scholar]
  46. Kruijssen, J. M. D. 2012, MNRAS, 426, 3008 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kruijssen, J. M. D., & Bastian, N. 2016, MNRAS, 457, L24 [CrossRef] [Google Scholar]
  48. Kruijssen, J. M. D., Maschberger, T., Moeckel, N., et al. 2012, MNRAS, 419, 841 [NASA ADS] [CrossRef] [Google Scholar]
  49. Krumholz, M. R., McKee, C. F., & Bland -Hawthorn, J. 2019, ARA&A, 57, 227 [NASA ADS] [CrossRef] [Google Scholar]
  50. Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
  51. Lam, N. T., Grosset, L., Rouan, D., & Gratadour, D. 2019, in Astronomical Society of thePacific Conference Series. eds. K. Werner, C. Stehle, T. Rauch, & T. Lanz, ASP Conf. Ser., 519, 273 [Google Scholar]
  52. Larsen, S. S. 2009, A&A, 494, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
  54. Leitherer, C., Ekström, S., Meynet, G., et al. 2014, ApJS, 212, 14 [NASA ADS] [CrossRef] [Google Scholar]
  55. Linden, S. T., Evans, A. S., Rich, J., et al. 2017, ApJ, 843, 91 [CrossRef] [Google Scholar]
  56. Longmore, S. N., Kruijssen, J. M. D., Bastian, N., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 291 [Google Scholar]
  57. Marin, F., Grosset, L., Goosmann, R., et al. 2016, SF2A-2016: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, 103 [Google Scholar]
  58. Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
  59. Mathis, J. S., Whitney, B. A., & Wood, K. 2002, ApJ, 574, 812 [NASA ADS] [CrossRef] [Google Scholar]
  60. McGregor, P., Hart, J., Stevanovic, D., et al. 2004, in Ground-basedInstrumentation for Astronomy, eds. A. F. M. Moorwood, & M. Iye, SPIE. Conf. Ser., 5492, 1033 [NASA ADS] [CrossRef] [Google Scholar]
  61. Megeath, S. T. 1996, A&A, 311, 135 [Google Scholar]
  62. Miralles-Caballero, D., Colina, L., Arribas, S., & Duc, P.-A. 2011, AJ, 142, 79 [NASA ADS] [CrossRef] [Google Scholar]
  63. Monty, S., Puzia, T. H., Miller, B. W., et al. 2018, ApJ, 865, 160 [NASA ADS] [CrossRef] [Google Scholar]
  64. Neichel, B., Rigaut, F., Vidal, F., et al. 2014, MNRAS, 440, 1002 [NASA ADS] [CrossRef] [Google Scholar]
  65. Parmentier, G., de Grijs, R., & Gilmore, G. 2003, MNRAS, 342, 208 [NASA ADS] [CrossRef] [Google Scholar]
  66. Pastorelli, G., Marigo, P., Girardi, L., et al. 2019, MNRAS, 485, 5666 [NASA ADS] [CrossRef] [Google Scholar]
  67. Pflamm-Altenburg, J., González-Lópezlira, R. A., & Kroupa, P. 2013, MNRAS, 435, 2604 [NASA ADS] [CrossRef] [Google Scholar]
  68. Piqueras López, J., Colina, L., Arribas, S., Alonso-Herrero, A., & Bedregal, A. G. 2012, A&A, 546, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Piqueras López, J., Colina, L., Arribas, S., Pereira-Santaella, M., & Alonso-Herrero, A. 2016, A&A, 590, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
  71. Privon, G. C., Aalto, S., Falstad, N., et al. 2017, ApJ, 835, 213 [NASA ADS] [CrossRef] [Google Scholar]
  72. Randriamanakoto, Z. 2015, Ph.D. Thesis, Department of Astronomy, University of Cape Town, Private Bag X3, Rondebosch 7701, South Africa [Google Scholar]
  73. Randriamanakoto, Z., Escala, A., Väisänen, P., et al. 2013a, ApJ, 775, L38 [NASA ADS] [CrossRef] [Google Scholar]
  74. Randriamanakoto, Z., Väisänen, P., Ryder, S., et al. 2013b, MNRAS, 431, 554 [CrossRef] [Google Scholar]
  75. Randriamanakoto, Z., Väisänen, P., Ryder, S. D., & Ranaivomanana, P. 2019, MNRAS, 482, 2530 [CrossRef] [Google Scholar]
  76. Reines, A. E., Johnson, K. E., Goss, W. M. 2008a, AJ, 135, 2222 [CrossRef] [Google Scholar]
  77. Reines, A. E., Johnson, K. E., & Hunt, L. K. 2008b, AJ, 136, 1415 [NASA ADS] [CrossRef] [Google Scholar]
  78. Reines, A. E., Nidever, D. L., Whelan, D. G., & Johnson, K. E. 2010, ApJ, 708, 26 [NASA ADS] [CrossRef] [Google Scholar]
  79. Ricci, C., Bauer, F. E., Treister, E., et al. 2017, MNRAS, 468, 1273 [NASA ADS] [Google Scholar]
  80. Rigaut, F., Neichel, B., Boccas, M., et al. 2014, MNRAS, 437, 2361 [NASA ADS] [CrossRef] [Google Scholar]
  81. Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] [Google Scholar]
  83. Sanders, D. B., Mazzarella, J. M., Kim, D. C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
  84. Santos, J. F. C., Dottori, H., & Grosbøl, P. 2013, A&A, 553, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
  86. Siebenmorgen, R., Voshchinnikov, N. V., & Bagnulo, S. 2014, A&A, 561, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [Google Scholar]
  88. Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [NASA ADS] [CrossRef] [Google Scholar]
  89. Stierwalt, S., Armus, L., Charmandaris, V., et al. 2014, ApJ, 790, 124 [NASA ADS] [CrossRef] [Google Scholar]
  90. Sun, W., de Grijs, R., Fan, Z., & Cameron, E. 2016, ApJ, 816, 9 [CrossRef] [Google Scholar]
  91. Tody, D. 1986, in Instrumentation in Astronomy VI, ed. D. L. Crawford, SPIE Conf. Ser., 627, 733 [NASA ADS] [CrossRef] [Google Scholar]
  92. Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, eds. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 173 [Google Scholar]
  93. Torres-Albà, N., Iwasawa, K., Díaz-Santos, T., et al. 2018, A&A, 620, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Turri, P., McConnachie, A. W., Stetson, P. B., et al. 2017, AJ, 153, 199 [CrossRef] [Google Scholar]
  95. Vavilkin, T. 2011, PhD Thesis, Department of Physics& Astronomy, Stony Brook University, Stony Brook, NY 11794-3800, USA [Google Scholar]
  96. Whelan, D. G., Johnson, K. E., Whitney, B. A., Indebetouw, R., & Wood, K. 2011, ApJ, 729, 111 [NASA ADS] [CrossRef] [Google Scholar]
  97. Whitmore, B. C., Allam, S. S., Budavári, T., et al. 2016, AJ, 151,134 [NASA ADS] [CrossRef] [Google Scholar]
  98. Yuan, T. T., Kewley, L. J., & Sanders, D. B. 2010, ApJ, 709, 884 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Catalog of SSC candidates in IRAS 17138-1017.

In the text

All Figures

thumbnail Fig. 1.

GeMS/GSAOI images of IRAS 17138-1017 in J (left), H (middle), and Ks (right) plotted in square root scale. The field of view is 32″ × 32″ and the horizontal bar represents 1 kpc at the estimated distance of IRAS 17138-1017.
In the text
thumbnail Fig. 2.

Color–color diagram (J − H) versus (H − Ks) for the selected sample of SSCs (black dots). The theoretical stellar evolution track given by SB99 is shown for solar metallicity as the solid magenta line. The reddening vector corresponding to AV = 1 is shown. The red stars are the sources detected in the control field, and the cross corresponds to the average color indices of the sample of 100 galaxies from the 2MASS survey, studied by Jarrett et al. (2003), with the length of the arms being equal to the standard deviations of those indices. The black cross represents the median errors of the cluster colors.
In the text
thumbnail Fig. 3.

Color–magnitude Q versus Ks diagram using the absolute Ks magnitude and the Q index, which in principle is not affected by the extinction. The same theoretical stellar evolution track as in Fig. 2 is shown. The black cross represents the median errors of the cluster colors and magnitudes.
In the text
thumbnail Fig. 4.

Comparison between the three quantities age, mass and extinction derived for each cluster using color fitting versus the same quantities derived from SED fitting.
In the text
thumbnail Fig. 5.

Age distribution of SSCs in IRAS 17138-1017. The error bars assume Poisson uncertainties.
In the text
thumbnail Fig. 6.

Cluster age-mass plane for the sample of SSCs in IRAS 17138-1017. The blue dash line marks the age of 3.7 Myr splitting two bursts.
In the text
thumbnail Fig. 7.

Age versus extinction for the sample of SSCs. The blue dash line marks the age of 3.7 Myr separating the two identified bursts.
In the text
thumbnail Fig. 8.

Frequency distribution of the extinction. The black line represents the entire sample, and the blue and red lines correspond to the populations of the 2.8 Myr burst and 4.5 Myr burst, respectively. Top: absolute numbers. Bottom: relative numbers. The error bars assume Poisson uncertainties.
In the text
thumbnail Fig. 9.

Luminosity function (dN/dL versus MKs) of the entire sample of SSCs (black) and for the subsamples of age τ ≤ 3.7 Myr (blue) and age τ ≥ 3.7 Myr (red), in bins of 1 mag. The black, blue, and red dash lines are corresponding linear regressions. The error bars assume Poisson uncertainties.
In the text
thumbnail Fig. 10.

Mass function of the entire sample of SSCs (black) and for the subsamples of age τ ≤ 3.7 Myr (blue) and age τ >  3.7 Myr (red), in bins of 0.5 dex. The black, blue, and red dash lines are corresponding linear regressions. The error bars assume Poisson uncertainties.
In the text
thumbnail Fig. 11.

Locations of the SSCs on the Ks image of IRAS 17138-1017. The colors of the open circles indicate the age category (blue for age τ ≤ 3.7 Myr burst and red for age τ >  3.7 Myr).
In the text
thumbnail Fig. 12.

Number of SSCs per ring of increasing diameters centered on the nucleus. The black line represents the entire sample, the blue and red lines correspond to the populations of the 2.8 Myr burst and 4.5 Myr burst, respectively. Top: absolute numbers. Bottom: relative numbers in each category.
In the text
thumbnail Fig. 13.

Mass-galactocentric radius relation for the sample of SSCs.
In the text
thumbnail Fig. 14.

Spectral energy distributions obtained with MontAGN for various sets of age τ and inner radius Rin of the dust envelope. The thick lines represent the total flux, the dotted lines indicate the dust emission, and the dashed lines indicate the stellar emission. The position of the Ks-band is denoted.
In the text
thumbnail Fig. 15.

Color–color diagram (J − H) versus (H − Ks) for the simulated SSCs with various conditions of age and inner radius of the dust envelope. The same theoretical track and reddening vector as in Fig. 2 are shown.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.