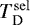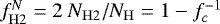| Issue |
A&A
Volume 639, July 2020
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202037602 | |
| Published online | 06 July 2020 | |
H I filaments are cold and associated with dark molecular gas
HI4PI-based estimates of the local diffuse CO–dark H2 distribution★
1
Argelander-Institut für Astronomie,
Auf dem Hügel 71,
53121
Bonn,
Germany
e-mail: pkalberla@astro.uni-bonn.de
2
Tartu Observatory, University of Tartu,
61602
Tõravere,
Tartumaa,
Estonia
Received:
28
January
2020
Accepted:
30
April
2020
Context. There are significant amounts of H2 in the Milky Way. Due to its symmetry H2 does not radiate at radio frequencies. CO is thought to be a tracer for H2; however, CO is formed at significantly higher opacities than H2. Thus, toward high Galactic latitudes significant amounts of H2 are hidden and are called CO–dark.
Aims. We demonstrate that the dust-to-gas ratio is a tool for identifying locations and column densities of CO–dark H2.
Methods. We adopt the hypothesis of a constant E(B−V)∕NH ratio, independent of phase transitions from H I to H2. We investigate the Doppler temperatures TD, from a Gaussian decomposition of HI4PI data, to study temperature dependences of E(B−V)∕NHI.
Results. The E(B−V)∕NHI ratio in the cold H I gas phase is high in comparison to the warmer phase. We consider this as evidence that cold H I gas toward high Galactic latitudes is associated with H2. Beyond CO–bright regions, for TD ≤ 1165 K we find a correlation (NHI + 2NH2)∕NHI ∝−logTD. In combination with a factor XCO = 4.0 × 1020 cm−2 (K km s−1)−1 this yields NH∕E(B−V) ~ 5.1 to 6.7 × 1021 cm−2 mag−1 for the full sky, which is compatible with X-ray scattering and UV absorption line observations.
Conclusions. Cold H I with TD ≤ 1165 K contains on average 46% CO–dark H2. Prominent filaments have TD ≤ 220 K and typical excitation temperatures Tex ~ 50 K. With a molecular gas fraction of ≥61% they are dominated dynamically by H2.
Key words: ISM: clouds / ISM: structure / ISM: molecules / dust, extinction
FITS files for Figs. 11–13 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/639/A26
© ESO 2020
1 Introduction
The ISM is a multiphase medium and a major part consists of neutral atomic and molecular gas that is highly intermixed with interstellar dust (Draine 2003). The most abundant atomic and molecular constituents of the gas are H I and H2. H I is easy to observe but H2 is homonuclear; it has no permanent electrical dipole moment, and therefore rotational or vibrational transitions are not observable at radio frequencies (Carruthers 1970). Space-based far-UV spectrographs are needed for H2 observations (Spitzer & Zabriskie 1959). These pencil-beam observations are involved, and therefore supplementing data from secondary tracers is often used to deduce the spatial and density distribution of the H2. Because of its rather high abundance and low excitation temperature, CO is considered to be a standard tracer for molecular hydrogen. H2 interacts with CO via collisions (Bolatto et al. 2013), and therefore the CO line intensities and shapes are quantitative measures for the H2 volume density and kinetic gas temperature. However, CO is formed at higher opacities and significantly lower gaseous temperatures than H2 (Bolatto et al. 2013, their Fig. 1). Consequently, a major fraction of H2 in the local ISM is not associated with CO. We call molecular hydrogen CO–dark when the CO does not trace it at all or the actual H2 content exceeds the amount expected from the observed CO and the standard XCO factor (Bolatto et al. 2013).
The only direct observational probes of H2 in the diffuse ISM are the far-UV electronic transitions in the Lyman and Werner bands (Spitzer & Zabriskie 1959). To observe these lines space-based spectrographs are needed, like that on board the Copernicus orbital observatory or the Far Ultraviolet Spectroscopic Explorer (FUSE). Pioneering work was done by Savage et al. (1977) and Bohlin et al. (1978), but only data at a few hundred positions are available and the molecular gas fractions 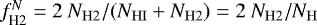 for the diffuse medium in the range 2 × 1019 < NH < 2 × 1021 cm−2 are particularly uncertain; we refer to Fig. 1 and further discussions of the review by Snow & McCall (2006). These observation of H2 toward high Galactic latitudes indicate that major amounts of the molecular gas are CO–dark. In addition, cross-correlation studies between different tracers of the total gas and the H I column density imply the existence of CO–dark H2 (e.g., Reach et al. 1998; Planck Collaboration XIX 2011; Strong & Mattox 1996; and Grenier et al. 2005).
for the diffuse medium in the range 2 × 1019 < NH < 2 × 1021 cm−2 are particularly uncertain; we refer to Fig. 1 and further discussions of the review by Snow & McCall (2006). These observation of H2 toward high Galactic latitudes indicate that major amounts of the molecular gas are CO–dark. In addition, cross-correlation studies between different tracers of the total gas and the H I column density imply the existence of CO–dark H2 (e.g., Reach et al. 1998; Planck Collaboration XIX 2011; Strong & Mattox 1996; and Grenier et al. 2005).
To estimate the amount of H2 located away from CO–bright or even star-forming regions, the tight correlation between the dust and gas is of key interest. The dust far-infrared radiation (IFIR) and its optical extinction (E(B−V)) are both closely correlated with NH and must scale linearly with it Liszt (2014a,b). Using the linear correlation between NHI and the optical extinction E(B−V) (Schlegel et al. 1998) toward the low extinction regions of the high Galactic latitude sky, Lenz et al. (2017) deduce NHI ∕E(B−V) = 8.8 × 1021 cm−2 mag−1 at HI4PI angular resolution. With that value, they derive a new map of interstellar reddening covering 39% of the sky. They need to restrict their approach to NHI < 4 × 1020 cm−2 to prevent opacity effects or phase transitions from degrading the linear correlation.
Our aim here is to go beyond that limit in NHI. We do that by accounting for the CO–dark H2. In the diffuse ISM we show that a phase transition from H I to H2 does not have an immediate feedback on the physical properties of the dust. We adopt the hypothesis that the dust extinction still scales linearly to NH even when H2 is forming in the diffuse ISM. When H2 is formed the H I emission gets dimmer, but the optical extinction remains unchanged. We use in the following E(B−V) (Schlegel et al. 1998) and NHI from HI4PI (HI4PI Collaboration 2016) as observables, and when needed perform a consistency check with the IFIR versus NH correlation. The difference between the dust traced NH and the observed NHI is the (dark) amount of 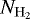 . Because we restrict our investigation to high Galactic latitudes (|b|≳10°), this minimizes the confusion with high mass star-forming regions. Our approach is certainly not straightforwardly applicable to these regions.
. Because we restrict our investigation to high Galactic latitudes (|b|≳10°), this minimizes the confusion with high mass star-forming regions. Our approach is certainly not straightforwardly applicable to these regions.
Toward the high Galactic latitude sky we find in the literature some spread in (NH ∕E(B−V)). Using soft X-ray scattering Predehl & Schmitt (1995) find NH∕E(B−V) = 5.55 × 1021 cm−2 mag−1. At optical and UV wavelength Savage et al. (1977) and Bohlin et al. (1978) determined NH ∕E(B−V) = 5.8 × 1021 cm−2 mag−1 using Lyα and NH2 absorption against early-type stars. At radio wavelength Liszt (2014a) deduces NHI ∕E(B−V) = 8.3 × 1021 cm−2 mag−1 from the LAB survey and Lenz et al. (2017) find NHI ∕E(B−V) = 8.8 × 1021 cm−2 mag−1 from HI4PI data. These observations have differences of many orders of magnitude in wavelengths and also in the probed spatial volumes and densities, but the NHI∕E(B−V) ratio is found to be remarkably constant. This implies that the gas-to-dust ratio is not a function of the physical state of the gaseous phase (e.g., gas temperatureTgas, volume density nH, or chemical composition ΨH). These quantities change with time, but toward the high Galactic latitude sky on the large angular scales probed by single dish H I surveys, we know that the physical conditions can be very closely approximated by a hydrostatic equilibrium ansatz (Kalberla 2003). The relevant parameter is only the column density of hydrogen nuclei NH. This quantity remains constant even during a phase transition from H I to H2.
Here we perform a cross-correlation analysis of neutral atomic gas (H I) and the interstellar reddening E(B−V) toward the high Galactic latitude sky. Toward these regions of interest we identify those portions of the diffuse ISM which contain CO–dark H2. We adopt the hypothesis that the dust-to-gas ratio is constant, or more precisely that the optical extinction scales linearly with the column density of the hydrogen nuclei. If this assumption is valid, the Galactic foregrounds can be quantitatively evaluated throughout the whole high Galactic latitude sky.
In Sect. 2 we investigate the correlation of the interstellar reddening with the H I gas temperature, extracted from a Gaussian decomposition of the HI4PI survey. In Sect. 3 we show a tight correlation of the H I gas temperaturealong the major axis of ISM filaments, which implies that the cold neutral medium (CNM) is host to the CO–dark H2. Due to its low but sufficient fraction of ionization (Crutcher et al. 2010, their Fig. 1), the CNM is already closely interwoven with the magnetic lines of forces. In Sect. 4 we put our findings in a perspective to the debate on caustics in the ISM, and we focus on the question of whether the NH ∕E(B−V) ratio might depend on the gas temperature of the CNM. We finish in Sect. 5 with a brief summary and some conclusions.
2 E(B–V)/NHI dependences on H I temperatures
The temperature of a gaseous medium is characterized by thermal motions. For H I gas in equilibrium this kinetic temperature is related to the spin temperature, which is the excitation temperature of the hyperfine levels evaluated according to the Boltzmann equation (Field 1959). The 21 cm transition is usually collisionally excited, and the spin temperature of the gas is a measure of the kinetic temperature. To measure the spin temperatures it is necessary to determine the 21 cm lines in both emission and absorption. This requires sufficiently strong background sources and needs careful considerations for radiative transfer effects along the line of sight (e.g., Heiles & Troland 2003a; Murray et al. 2018a). These investigations are elaborate and are limited in practice to a small number of positions; for the millennium Arecibo 21 cm absorption-line survey, only 79 continuum sources were available (Heiles & Troland 2003a) and for the 21-SPONGE H I absorption line survey 57 lines of sight were available (Murray et al. 2018a).
We use a Gaussian decomposition of the HI4PI survey and characterize the temperature of an H I cloud by its Doppler temperatures TD = 21.86 δv2 (Payne et al. 1980, Eq. (8)). Here δv2 is the observed FWHM line width corrected for instrumental broadening. Under typical conditions TD is a measure for an upper limit of the kinetic temperature Tkin (Field 1959; Field et al. 1969); a coupling of the λ–21 cm excitation temperature and local gas motions is only possible toward strong Ly–α environments (Liszt 2001).
There is no unique use of the term Doppler temperature in the literature. In the case of absorption lines Li & Goldsmith (2003) use the expression equivalent temperature. Heiles & Troland (2003a) define a parameter Tk,max to describe the kinetic temperature of a component without nonthermal broadening without naming Tk,max in a particular way. Nevertheless, this parameter is important for our understanding of the dynamical state of the ISM. Observed line widths result from intrinsic thermal broadening (representing kinetic temperatures Tkin) and turbulent motions, causing the observed line broadening. This broadening, essentially resulting from a convolution of thermal and turbulent motions along the line of sight, is described by the characteristic turbulent Mach number (Heiles & Troland 2003b, Sect. 6.2.4):
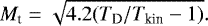 (1)
(1)
Cold neutral medium clouds tend to be turbulent and supersonic, and high Mach numbers are common (Heiles & Troland 2003b, Fig. 12). In the CNM there is a well-defined median magnetic field, and Heiles & Troland (2005) conclude that turbulence and magnetism are in approximate equipartition with a characteristic turbulent Mach number Mt = 3.7 at a median CNM kinetic temperature of 50 K. Energy equipartition between magnetic and kinetic energy implies B2 ∕(4π) ∝ nHδv2 for a hydrogen volume density nH (Crutcher 1999; Basu 2000; Hennebelle & Inutsuka 2019), hence B2 ∝ nHTD.
The practical advantage of using Doppler temperatures is that TD can easily be determined from Gaussian components at any observed position. This allows in particular a systematic determination of Doppler temperatures along or across filaments that is not possible with absorption data. The CNM in filamentary structures shows a well-defined log-normal distribution with a median TD = 223 K, corresponding to Mt = 3.7 for the above-mentioned thermal temperature of 50 K (Kalberla & Haud 2018, Sect. 5.11). For a turbulent ISM that can be described by a characteristic Mach number according to Eq. (1), TD may therefore be considered as a temperature measure. Uncertainties arise from unknown variations in Mt.
2.1 Basic numerical strategies
To study the dust-to-gas ratio we consider a constant ratio R = E(B−V)∕NH, a cornerstone assumption according to Liszt (2014b). Differently from all previous investigations, we primarily do not study this ratio for integrated reddening or column densities along the line of sight. In general, E(B−V) and NH may originate from several clouds or layers along the line of sight. We assume that H2 forms out of the H I phase and variations of the dust-to-gas ratio are due to phase transitions from one phase to the other. Decomposing the observed H I line profile into n Gaussian components, we describe this configuration as
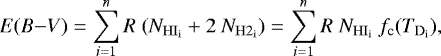 (2)
(2)
and assign to each individual H I cloud i a conversionfactor 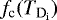 to take H2 associated with this H I cloud into account. The observed H I may exist as a mixture of the cold, warm, and lukewarm neutral medium (CNM, WNM, and LNM, respectively), in general with several such components along the line of sight. However it is expected that H2 is associated only with cold H I (McKee & Ostriker 1977; Wolfire et al. 2003, 2010); this motivates us to assume that there is a temperature dependence of the correction factor fc (TD). In the simplest case, as assumed here, fc(TD) may be independent of E(B−V).
to take H2 associated with this H I cloud into account. The observed H I may exist as a mixture of the cold, warm, and lukewarm neutral medium (CNM, WNM, and LNM, respectively), in general with several such components along the line of sight. However it is expected that H2 is associated only with cold H I (McKee & Ostriker 1977; Wolfire et al. 2003, 2010); this motivates us to assume that there is a temperature dependence of the correction factor fc (TD). In the simplest case, as assumed here, fc(TD) may be independent of E(B−V).
To determine 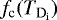 we need to develop a strategy for solving Eq. (2). We aim to tackle this iteratively by inserting general accepted initial estimates from the literature (see next subsection), and then improving the solution step by step.
we need to develop a strategy for solving Eq. (2). We aim to tackle this iteratively by inserting general accepted initial estimates from the literature (see next subsection), and then improving the solution step by step.
Let us assume that we have some reasonable estimate 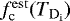 . At a given position we separate the Gaussian components (if present) in a selected range
. At a given position we separate the Gaussian components (if present) in a selected range 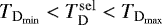 . For H I outside this
. For H I outside this 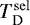 range we obtain the partial extinction as a sum of extinctions for m ≤ n components
range we obtain the partial extinction as a sum of extinctions for m ≤ n components
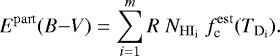 (3)
(3)
For the selected Doppler temperature 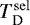 the observed column density is
the observed column density is 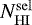 with a corresponding extinction (E(B−V) − Epart(B−V)). The H I based dust-to-gas ratio is
with a corresponding extinction (E(B−V) − Epart(B−V)). The H I based dust-to-gas ratio is
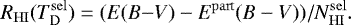 (4)
(4)
When we have several components at similar Doppler temperatures we treat them as a single component with 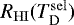 . This is equivalent to the assumption that these components have the same ratio
. This is equivalent to the assumption that these components have the same ratio 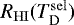 .
.
Relating 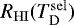 of the selected component to the cornerstone ratio
of the selected component to the cornerstone ratio
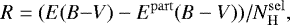 (5)
(5)
we have in agreement with Eq. (2)
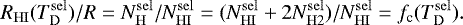 (6)
(6)
Thus, we use systematic deviations of the observed dust-to-gas ratio RHI from the cornerstone ratio R to estimate the associated H2. Applying this recipe to all observed positions in our sample we derive distributions for RHI (TD) as function of the selected Doppler temperatures 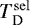 . In principle the problem in deriving fc(TD) is that we need to start from scratch,
. In principle the problem in deriving fc(TD) is that we need to start from scratch, 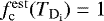 . Uncertainties in
. Uncertainties in 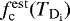 propagate through Eq. (3). We need to reiterate on Eq. (3), successively improving
propagate through Eq. (3). We need to reiterate on Eq. (3), successively improving 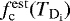 . This task is considerably simplified by taking some reasonable initial conditions into account.
. This task is considerably simplified by taking some reasonable initial conditions into account.
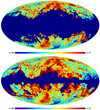 |
Fig. 1 E(B−V)∕NHI in regions used for the determination of the dust-to-gas ratio. Masked regions, including the Magellanic Clouds, are shown in blue. Top: E(B−V)∕NHI defined for canonical thin H I gas with NHI ≤ 4 × 1020 cm−2 and E(B−V) ≤ 0.08 mag (Lenz et al. 2017). Bottom: E(B−V)∕NHI outside CO–bright regions. Units are 10−27 cm2, scaling and color-coding are as in Fig. 4 for the mean corrected E(B− V)∕NH dust-to-gas ratio within a 2σ range. |
2.2 Bootstrap, initial constraints
To simplify a solution of Eq. (3) we make use of several previously published results and adopt some broadly accepted assumptions:
- 1.
E(B−V)∕NHI is well defined for NHI≲4 × 1020 cm−2 and E(B−V)≲0.08 mag (e.g., Savage et al. 1977; Liszt 2014a,b; Lenz et al. 2017). We limit our first attempts to solve Eq. (2) for this range referred to in the following as canonical thin gas, see Fig. 1 top. This is the case considered by Lenz et al. (2017, Fig. 9), and we use their ratio of R = E(B−V)∕NHI = (1.113 ± 0.002) × 10−22 cm2 mag as the cornerstone dust-to-gas ratio.
- 2.
E(B−V)∕NHI is best defined toward high latitudes; a significant onset of H2 formation is expected in the range 20°≳|b|≳8° (Liszt 2014a,b; Dame et al. 2001). We avoid |b|≲8° since there are no sight lines with small E(B−V) in this range.
- 3.
It appears well established that the molecular hydrogen fraction
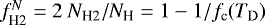 for the WNM should be negligible (McKee & Ostriker 1977; Wolfire et al. 2003). Initially we define fc (TD) = 1 for the WNM.
for the WNM should be negligible (McKee & Ostriker 1977; Wolfire et al. 2003). Initially we define fc (TD) = 1 for the WNM. - 4.
The H2 distribution may be CO–dark (Grenier et al. 2005). There is a fundamental difference between H2 associated with CO in dense molecular clouds (CO–bright H2) and H2 outside such clouds where the gas-phase carbon resides in C or C+ (CO–dark H2) (Wolfire et al. 2010). We exclude CO–bright regions with observed CO emission. To generate CO–masked regions for exclusion, we identify the areas by using the type 2 product from the Planck legacy data release1. We smooth these data heavily with a 5° Gaussian beam and mask all data for CO emission above a level of 0.2 K. Our CO mask covers 25.9% of the sky, compared to Planck Collaboration XI (2014) who used, without smoothing, a sky fraction with significant CO emission in excess of 0.15 K km s−1 (about 18% of the sky). We mask additional regions that are affected by the Magellanic Clouds to avoid outliers in the dust-to-gas ratio by contamination from these sources, see Fig. 1 bottom.
- 5.
H I gas at high velocities contains insignificant amounts of dust (Wakker & van Woerden 1997; Miville-Deschênes et al. 2005; Lenz et al. 2017). The main body of the dust-bearing gas is associated with velocities |vLSR|≲90 km s−1 and we use this velocity range.
- 6.
Single-dish H I data may suffer from unknown optical depth effects. We consider corrections as proposed by Lee et al. (2015) and Murray et al. (2018b) by multiplying observed column densities by a factor f = log10(NHIobs∕1020) × (0.26 ± 0.02) + (0.91 ± 0.02) or alternatively by f = log10(NHIobs∕1020) × (0.19 ± 0.02) + (0.89 ± 0.02) (Nguyen et al. 2018).
During iterations, after obtaining a reasonable accurate solution of Eq. (3) some of these estimates and constraints can be released. We discuss this later in context.
2.3 Databases
We use HI4PI H I data decomposed into Gaussian components as described by Kalberla & Haud (2018). This decomposition is limited by the blending of the obtained Gaussians, and in most cases the decomposition toward a single line of sight is not unique (Sect. 4.1 of Haud 2000). However, it is feasible to deduce a reliable Gaussian decomposition by accounting not for isolated line profiles, but for larger neighboring regions. This enables us to find a coherent solution for the whole area of interest and yields more statistically independent Gaussian components for corresponding lines of sight.
The largest groups of blended Gaussians in each profile from the unmasked region of the sky in the bottom panel of Fig. 1 contain on average 5.7 Gaussians. The uniqueness and stability of our decompositions of the profiles, represented by six blended Gaussians, has been examined in Sect. 4.2 of Haud (2000). The results of the modeling of the decomposition process demonstrate that the blending is mostly a problem for broad HI lines, while the CNM with its sharply defined narrow lines allows unique clues. As we are mostly discussing the cold gas here, we consider the used decomposition results appropriate for the present statistical study.
The interstellar reddening E(B−V) data are from Schlegel et al. (1998)2. We resample this data set to a homogeneous HEALPix grid (Górski et al. 2005) with nside = 1024 and apply the correction 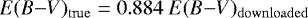 (Schlafly & Finkbeiner 2011), consistent with the scaling used by Lenz et al. (2017). Our analysis is in all cases done on a HEALPix grid with nside = 1024. We use the tool ud_grade from the HEALPix software distribution3 for up- or downgrading. The H I data have a FWHM resolutions of 10.′8 for the northern sky (Winkel et al. 2016) and 14.′5 for the southern (Kalberla & Haud 2019). Column densities are accurate to 2.5% (Winkel et al. 2016). The E(B−V) data have a resolutions close to 7′ for a HEALPix grid with nside = 512 and are assumed to be accurate to 16% (Schlegel et al. 1998).
(Schlafly & Finkbeiner 2011), consistent with the scaling used by Lenz et al. (2017). Our analysis is in all cases done on a HEALPix grid with nside = 1024. We use the tool ud_grade from the HEALPix software distribution3 for up- or downgrading. The H I data have a FWHM resolutions of 10.′8 for the northern sky (Winkel et al. 2016) and 14.′5 for the southern (Kalberla & Haud 2019). Column densities are accurate to 2.5% (Winkel et al. 2016). The E(B−V) data have a resolutions close to 7′ for a HEALPix grid with nside = 512 and are assumed to be accurate to 16% (Schlegel et al. 1998).
2.4 Fitting fc (TD)
We use a limited sample of selected Doppler temperatures 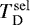 to determine the dust-to-gas ratios
to determine the dust-to-gas ratios 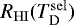 according to Eq. (4) across the sky. Our approach is iterative: initial estimates of fc (TD) were restricted to the canonical thin sample; later we released constraints as far as possible. Here we demonstrate our results for the final fc(TD) fit from Eq. (7).
according to Eq. (4) across the sky. Our approach is iterative: initial estimates of fc (TD) were restricted to the canonical thin sample; later we released constraints as far as possible. Here we demonstrate our results for the final fc(TD) fit from Eq. (7).
The top panel of Fig. 2 displays the log-normal distributions for 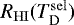 for a range of Doppler temperatures,
for a range of Doppler temperatures, 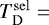 50, 100, 200, 400, and 800K. For decreasing TD the ratios
50, 100, 200, 400, and 800K. For decreasing TD the ratios 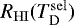 shift to higher values. In the top panel of Fig. 2 we display for comparison the ratios E(B−V)∕NHI for the total reddening and integrated column densities for all data with |b| > 20° (black) and the canonical sample according to Lenz et al. (2017) (red dashed). Extending the sample to a larger fraction of the sky leads to an extended asymmetric wing of E(B−V)∕NHI for |b| > 20°. Most of the H I gas belongs to the WNM, the dust-to-gas ratio for this part is unaffected. Deviations in E(B−V)∕NHI are caused by the CNM. The
shift to higher values. In the top panel of Fig. 2 we display for comparison the ratios E(B−V)∕NHI for the total reddening and integrated column densities for all data with |b| > 20° (black) and the canonical sample according to Lenz et al. (2017) (red dashed). Extending the sample to a larger fraction of the sky leads to an extended asymmetric wing of E(B−V)∕NHI for |b| > 20°. Most of the H I gas belongs to the WNM, the dust-to-gas ratio for this part is unaffected. Deviations in E(B−V)∕NHI are caused by the CNM. The 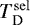 -selected
-selected 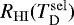 samples arescaled up in amplitude, but belong to the extended wing of the black E(B−V)∕NHI distribution. The amplitudes of the selected
samples arescaled up in amplitude, but belong to the extended wing of the black E(B−V)∕NHI distribution. The amplitudes of the selected 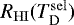 distributions reflect the frequency distribution of components with different Doppler temperatures or line widths (Kalberla & Haud 2018, Fig. 4). CNM components with TD ~ 220 K are most frequent (Kalberla et al. 2016, Fig. 13).
distributions reflect the frequency distribution of components with different Doppler temperatures or line widths (Kalberla & Haud 2018, Fig. 4). CNM components with TD ~ 220 K are most frequent (Kalberla et al. 2016, Fig. 13).
We use the 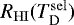 distributions to determine fc(TD) according toEq. (6); this is simply the factor needed to shift each log-normal distribution in Fig. 2, top, to the canonical R-value, the geometrical mean of the canonical E(B−V)∕NHI distribution (red). For each of the log-normal distributions we determine a mean correction factor
distributions to determine fc(TD) according toEq. (6); this is simply the factor needed to shift each log-normal distribution in Fig. 2, top, to the canonical R-value, the geometrical mean of the canonical E(B−V)∕NHI distribution (red). For each of the log-normal distributions we determine a mean correction factor 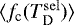 from the geometrical mean of the
from the geometrical mean of the 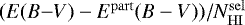 distribution by fitting a Gaussian. After a few iterations it became clear that this correction can be approximated astonishingly well by only two regression lines, linear fits for log(TD) :
distribution by fitting a Gaussian. After a few iterations it became clear that this correction can be approximated astonishingly well by only two regression lines, linear fits for log(TD) :
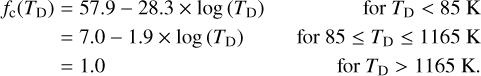 (7)
(7)
This best fit result to these two linear regressions is found by selecting all positions outside CO–bright regions. The convergence of the fitting process is slow, with oscillations around a single dominant pole but decreasing amplitudes for the deviations between two successive iterations. After seven unconstrained iterations we decided to terminate this process by using the mean of two successive iterations as a penalty. We display in Fig. 3 our final result. The solid lines represent the two derived regressions; we also plot the bracketing results from the last two iterations (green and red crosses). The dashed line gives the combined fc(TD)-solution according to Eq. (7) that we use in the following.
In the middle and lower panels of Fig. 2 we display with the same color-coding as on top the CNM distributions of 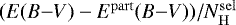 after applying the fc (TD)-correction from Eq. (7). In addition we display the E(B−V)∕NH distributions (black) calculated from total reddening and integrated hydrogen column densities after application of the fc (TD)-correction. The results in the middle panel are for |b| > 20°, at the bottom for all-sky but excluding CO–bright regions (see Fig. 1). For both panels the CNM distributions are centered close to the canonical R = E(B−V)∕NHI = 1.113 × 10−22 cm2 mag. The E(B−V)∕NH distribution in the bottom panel has a nearly Gaussian shape, without the extended wings seen in the upper panels. This is our best fit result; the range |b| > 20° still contains some contaminations from CO–bright regions.
after applying the fc (TD)-correction from Eq. (7). In addition we display the E(B−V)∕NH distributions (black) calculated from total reddening and integrated hydrogen column densities after application of the fc (TD)-correction. The results in the middle panel are for |b| > 20°, at the bottom for all-sky but excluding CO–bright regions (see Fig. 1). For both panels the CNM distributions are centered close to the canonical R = E(B−V)∕NHI = 1.113 × 10−22 cm2 mag. The E(B−V)∕NH distribution in the bottom panel has a nearly Gaussian shape, without the extended wings seen in the upper panels. This is our best fit result; the range |b| > 20° still contains some contaminations from CO–bright regions.
During the iteration procedure it became clear that fc(TD) can be consistently deduced by dropping the major constraints considered in Sect. 2.2. Constraints on column densities or interstellar extinction (items 1 and 2) are not necessary. It is very important, however, to distinguish between CO–dark and CO–bright regions (item 4); it even appears necessary to extend the mask for the CO–bright parts of the sky spatially by smoothing the observed CO emission heavily. The selection of the velocity range (item 5) has a very limited impact on the fit results. It is not necessary to distinguish H I phases (item 3); the fc (TD) solution according to Eq. (7) applies only to TD≲1165 K. This limit may serve as a new definition for CNM gas; however, the numerical value is not very well defined from the fit. It is also not a sharp limit because the onset of the fc (TD)-correction is only gradual at TD≲1165 K. The border between CNM and LNM was defined previously by Kalberla & Haud (2018, Fig. 7) as the Doppler temperature where the frequency distribution for CNM and LNM Gaussians is equal. This new limit of 1165 K would be a definition of the highest temperature where a transition from H I to H2 is observable.
An excess of E(B−V)∕NH may be affected by saturation of the H I emission due to self-absorption or optical depth effects. Fukui et al. (2015) investigated these effects and, from the analysis of Planck/IRAS data toward high galactic latitudes, derived 2–2.5 times higher H I densities than under the optical thin assumption. They suggested that optically thick H I gas may dominate CO–dark gas in the Milky Way. Contrary to their results, we find that optical depth corrections according to Sect. 2.2 item 6 affect the ratio 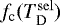 on average by 5% for a correction according to Lee et al. (2015) and by 1% for the correction proposed by Nguyen et al. (2018). Both corrections are too small to explain systematical changes in the gas-to-dust ratio. Similarly, Liszt (2014b) concludes that optical depth corrections are too small to have any significant effect on the derived NHI ∕E(B−V) ratio. More recently Murray et al. (2018b), using GALFA-H I data, confirm that excess dust emission in the local ISM cannot be dominated by optically thick H I in the local ISM. Tang et al. (2016) investigated the physical properties of CO–dark molecular gas traced by C+. Their sample of 36 sources close to the Galactic plane should be most sensitive to optical depth effects, but they find that the H I optical depth can vary in a wide parameter range without significantly affecting the global relations between the CO–dark gas fraction
on average by 5% for a correction according to Lee et al. (2015) and by 1% for the correction proposed by Nguyen et al. (2018). Both corrections are too small to explain systematical changes in the gas-to-dust ratio. Similarly, Liszt (2014b) concludes that optical depth corrections are too small to have any significant effect on the derived NHI ∕E(B−V) ratio. More recently Murray et al. (2018b), using GALFA-H I data, confirm that excess dust emission in the local ISM cannot be dominated by optically thick H I in the local ISM. Tang et al. (2016) investigated the physical properties of CO–dark molecular gas traced by C+. Their sample of 36 sources close to the Galactic plane should be most sensitive to optical depth effects, but they find that the H I optical depth can vary in a wide parameter range without significantly affecting the global relations between the CO–dark gas fraction 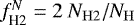 , and H I excitation temperature. Tang et al. (2016) conclude that the molecular gas must be the dominant component regardless of individual excitation temperatures, optical depth, and the lack of CO emission. Deriving excitation temperatures Tex for an optical depth of 1, these authors find a relation
, and H I excitation temperature. Tang et al. (2016) conclude that the molecular gas must be the dominant component regardless of individual excitation temperatures, optical depth, and the lack of CO emission. Deriving excitation temperatures Tex for an optical depth of 1, these authors find a relation 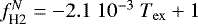 . This trend, in agreement with results from Rachford et al. (2009), implies
. This trend, in agreement with results from Rachford et al. (2009), implies 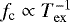 , broadly consistent with Eq. (7).
, broadly consistent with Eq. (7).
Optical depth corrections derived by different groups (Lee et al. 2015; Murray et al. 2018b; Nguyen et al. 2018) are rather uncertain; we show, that a single parameter dependence of fc (TD)-correction according to Eq. (6) is sufficient to minimize systematic fluctuations in the E(B−V)∕NHI ratio over the full high Galactic latitude sky. Even toward the CO–bright highest HI column density star-forming regions, a radiation transfer calculation for H I is feasible, which Li & Goldsmith (2003) demonstratein great detail. Our analyses are toward the high Galactic latitude sky, away from CO–bright or even star-forming regions. Thus, opacity effects are avoided by selecting CO–dark regions of the sky. Section 3 comprises compelling evidence that toward high Galactic latitudes the typical filamentary CNM structures show up with low Doppler temperatures TD ≲220 K and FWHM of δvLSR≲3 km s−1 and negligible optical depth effects.
 |
Fig. 2 Probability distribution functions for Gaussian components with selected Doppler temperatures
|
 |
Fig. 3 Hydrogen column density correction factor fc(TD) from an all-sky fit, excluding positions in CO–bright regions. The crosses show fit results from the last iterations, the solid lines the regressions from Eq. (7), the dashed red line the adopted complete solution. |
 |
Fig. 4 Left: E(B−V)∕NHI (top), E(B−V)∕NH with the fc(TD) correction Eq. (7) (middle), and E(B−V)∕NHtot including a correction for XCO = 4.0 × 1020 cm−2 (K km s−1)−1 (bottom). Units are 10−22 cm2 mag, displayed are data around the mean within a 2σ range on both sides. For a comparison of E(B−V)∕NHI after restricting the data to the canonical thin gas and to CO–bright regions we refer to Fig. 1. Right: τ353 ∕NHI (top), τ353∕NH (middle), and τ353∕NHtot (bottom). Units are 10−27 cm2, also displayed are data within 2σ around the mean. |
2.5 Spatial distribution of E(B–V)/NH
We use the fc(TD) relation according to Eq. (7) to derive an all-sky relationship between gas and interstellar reddening. We calculate for each position the ratios E(B−V)∕NHI and E(B−V)∕NH to generate maps of the spatial distribution of these ratios. For E(B−V)∕NH we determine an average of (1.0 ± 0.2) 10−22 cm2 mag from a fit of the E(B−V)∕NH distribution displayed in black in the bottom panel of Fig. 2.
Figure 4, left, shows the derived maps. While in the top panel only NHI is accounted for, in the middle panel the hydrogen column density NH is shown according to the correction Eq. (7). We scale the color-coding to display a 2σ range around the average E(B−V)∕NH. The bottom panel serves as reference; we use the canonical XCO factor to determine the total column density NHtot using 12CO as tracer of the CO–bright NH2. We use CO data from Dame et al. (2001)4 to calculate this part of the H2 distribution but a straightforward subtraction of the CO–bright NH2 leads to unsatisfactory results. First we notice that the CO–bright H2 cannot be determined by simply usinga constant XCO factor. The second problem is that a straightforward subtraction of a CO–bright H2 component leads to an obvious spatial mismatch between observed and modeled CO–bright H2 distribution. Figure 5 can help demonstrate the problems. From top to bottom we show attempts to model the CO–bright H2 distribution with various smoothing kernels. We aim to derive the properties of the diffuse CO–dark H2 but a best possible fit of the CO–bright H2 is beyond the scope of this publication.
For a reasonable solution we find that the CO data from Dame et al. (2001) need to be smoothed to a resolution of about 2° (Fig. 5, middle). The original survey data were constructed from several different CO surveys with a grid spacing of 0. °125. Surveys with half beamwidth spacing were smoothed with a Gaussian with FWHM of 0. °125. For the lambda data product the original Dame et al. (2001) data with a resolution ranging from 0. °125 to 0. °5 were interpolated to a HEALPix grid with nside = 512, appropriate for a comparison with E(B−V) data on the same grid. The implication from the noisy performance of the unsmoothed CO data (Fig. 5, top) is that the spatial distributions of CO and H2 in CO–bright regions must be different. A significant part of the H2 appears to be distributed around dense molecular gas cores; we refer to the model proposed by Wolfire et al. (2010) and Fig. 1 of Seifried et al. (2020). We apply a factor XCO = 4.0 × 1020 cm−2 (K km s−1)−1 to calculate the CO–bright H2. This factor is high, but still in the range 1.7 < XCO < 4.2 × 1020 cm−2 (K km s−1)−1 determined by several authors from extinction data (Bolatto et al. 2013, Table 1). The bottom left panel of Fig. 4 shows that such a determination of the CO-associated H2 leads to an improved ratio for 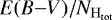 , but there are significant deviations from an average dust-to-gas ratio. It is obvious that the CO–bright H2 cannot be derived by using a unique XCO factor. We conclude that a determination of the E(B−V)∕NH ratio is currently safe outside CO–bright regions, but probably also to the full sky with only a few restrictions.
, but there are significant deviations from an average dust-to-gas ratio. It is obvious that the CO–bright H2 cannot be derived by using a unique XCO factor. We conclude that a determination of the E(B−V)∕NH ratio is currently safe outside CO–bright regions, but probably also to the full sky with only a few restrictions.
An independent estimate for the FIR opacity caused by the dust is given by Planck maps of the optical depth τ353 at 353 GHz (Planck Collaboration XIX 2011; Planck Collaboration Int. XLVIII 2016). We used the optical depth map from the Planck Collaboration Int. XLVIII (2016) data release5 and calculated the ratios τ353∕NHI, τ353 ∕NH, and τ353 ∕NHtot. The results are shown on the right side of Fig. 4. We used again a scaling of the color-coding such that a 2σ range around the average τ353∕NH is displayed. We determine an average of (7.10 ± 1.7) 10−27 cm2. The maps in the left and right panels of Fig. 4 should be comparable, but we find some striking large-scale differences, existing both for raw and corrected H I data, indicating that there are unaccounted for systematic uncertainties.
Column densities for individual positions from H I surveys have typical uncertainties on a 2.5% level (Winkel et al. 2016), but there are no additional uncertainties on large scales. We conclude that at least some of the systematic deviations from the mean must come from the extinction data. For the dust-to-gas ratio E(B−V)∕NH using the data from Schlegel et al. (1998) we derive outside CO–bright regions a relative scatter of 21%. This compares to a scatter of 24% for τ353 ∕NH. According to Schlegel et al. (1998) some of the E(B−V) data are known to contain fluctuations of ± 15% amplitude that are coherent over scales of 10°. These may be real variations from gas to dust, or they may trace some unresolved instrumental or systematical problems such as shortcomings in the temperature corrections (Schlafly et al. 2010). For a comparison between E(B−V) and τ353 we refer to Planck Collaboration XI (2014, Sect. 7.3, Fig. 26). At a resolution of 6.′1 and for NHI < 2 1020 cm−2, the ratio E(B−V)∕τ353 is constant within a scatter of 7%. Smoothing both data sets to a resolution of 30′ the ratio E(B−V)∕τ353 shows local variations larger than 30% all over the sky. This database is no longer available for download. Using the optical depth map from Planck Collaboration Int. XLVIII (2016), currently available in the official distribution (see footnote 5), we obtain an all-sky rms scatter of 23% for the nside = 1024 databases and 20% after 30′ smoothing.
Systematical large-scale deviations from the average dust-to-gas ratio cause a significant fraction of the scatter of 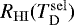 and
and 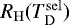 in Fig. 2 and also uncertainties in fitting an fc(TD) correction to the H I data. It is hard to estimate how far regression parameters in Eq. (7) are affected by such systematical problems. Our estimate of the CO–bright H2 distribution is strongly affected by remaining enhancements in the gas-to-dust ratio near the Galactic plane, see Fig. 4 bottom. Here we have an additional problem with variations caused by expected uncertainties in XCO. We decided not to apply a fit to large-scale enhancements in E(B−V)∕NHtot.
in Fig. 2 and also uncertainties in fitting an fc(TD) correction to the H I data. It is hard to estimate how far regression parameters in Eq. (7) are affected by such systematical problems. Our estimate of the CO–bright H2 distribution is strongly affected by remaining enhancements in the gas-to-dust ratio near the Galactic plane, see Fig. 4 bottom. Here we have an additional problem with variations caused by expected uncertainties in XCO. We decided not to apply a fit to large-scale enhancements in E(B−V)∕NHtot.
 |
Fig. 5 Galactic plane excerpts for E(B−V)∕NHtot with a correction for XCO = 4.0 × 1020 cm−2 (K km s−1)−1 as in Fig. 4 (bottom left), but with different smoothing kernels S: (from top to bottom) S with FWHMof 0°, 1°, 2°, 3°, and 4°. |
2.6 The NH/E(B-V) ratio after fc (TD) correction
Dependences of the H I determined NH∕E(B−V) ratio on various selection criteria have been discussed in great detail by Liszt (2014a,b), and by Lenz et al. (2017) who concluded that it is possible to derive any NHI ∕E(B−V) value between those of Bohlin et al. (1978) and Liszt (2014b) depending simply on the range of column densities comprised by the fit. In the following we want to check whether this situation has improved after application of the fc (TD) correction.
We calculate all-sky ratios corresponding to the panels on the left side of Fig. 4. In the top panel of Fig. 6 we display a 2D histogram of NHI∕E(B−V) from HI4PIas observed. In the middle panel we show the distribution of NH ∕E(B−V) after application of fc(TD). We mask CO–bright regions, thus this histogram is valid for all diffuse H2 regions that are not affected by additional H2 that might be associated with CO. In the bottom panel of Fig. 6 we show a 2D histogram using all-sky H I and CO–dark as well as estimated CO–bright H2, as shown in Fig. 4, bottom left.
The 2D histograms in logarithmic scale from Fig. 6 can be directly compared to Fig. 1, bottom right panel, in Lenz et al. (2017). Remarkable is the absence of the increase in scatter reported by Lenz et al. (2017) above NHI ≥ 4 × 1020cm−2 in our corrected data. The maximum number of components is around NHI ≃ 5 × 1020 cm^-2, and here we see a slight bending in the gas-to-dust ratio. Even above this value the linear correlation remains very well defined.
Using all-sky data without any constraints we obtain NH ∕E(B−V) ~ 5.1 × 1021cm−2mag−1. Excluding latitudes |b|≤ 8° we get NH∕E(B−V) ~ 6.7 × 1021cm−2mag−1. Both results are affected by systematic errors, but bracket the previous determination NH ∕E(B−V) ~ 5.8 × 1021cm−2mag−1 by Bohlin et al. (1978). They are also consistent with the more recent determination NH ∕E(B−V) = (6.45 ± 0.06) 1021cm−2mag−1 by Zhu et al. (2017) who considered X-ray observations of a large sample of Galactic sightlines.
 |
Fig. 6 All-sky 2D histograms for the E(B−V) vs. NHI (top) and NH (bottom) after applying the fc(TD) correction. Middle: data in CO–bright regions were disregarded. The color-coding represents pixel counts. |
3 The nature of H I filaments
Data presented by H I observers led recently to a picture of the neutral ISM with the CNM distributed into cold, small-scale anisotropic structures, preferentially aligned along the magnetic field and associated with dust (e.g., Heiles & Troland 2005; Clark et al. 2014, 2019; Kalberla et al. 2016; Kalberla & Haud 2020). Supporting evidence for low temperatures at the position of filaments was recently reported from Na I absorption measurements of 50 985 quasar spectra by Peek & Clark (2019). The interpretation that filamentary structures are cold is questioned frequently, however. Small-scale structure in H I channel maps is often assumed to originate from velocity caustics, caused by the turbulent velocity field, rather than from real density structures (e.g., Lazarian & Pogosyan 2000; Lazarian & Yuen 2018; Yuen et al. 2019). In this context we need to discuss the structure of H I in filaments, in particular the distribution of temperatures and velocities and their relation to FIR emission.
3.1 TD along the bones of H I filaments
We use Doppler temperature thresholds to demonstrate their response to FIR emission observed with Planck at 857 GHz6. The median Doppler temperature of the CNM at high Galactic latitudes is 220 K (Clark et al. 2014; Kalberla et al. 2016; Kalberla & Haud 2019). We use this value to mask the observed 857 GHz emission at each position where an H I Gaussian component with a Doppler temperaturebelow this temperature threshold is found. The masking is repeated by changing the temperature threshold by a factor of 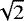 , hence we use upper TD limits of 155, 220, and 311 K. Results from this masking are shown in Fig. 7. For a threshold of 155 K only prominent filaments are masked; a threshold of 220 K affects most of the filaments, and with an upper limit of 311 K just a few weak and diffuse filaments survive the masking. Thus, cold filamentary CNM structures at high Galactic latitudes mark enhanced FIR emission at 857 GHz; lower TD values are observed at the position of the most pronounced filaments. Filamentary structures get more diffuse at higher TD values, implying a 3D structure with lowest temperatures at the bones (or centers) of the filaments within a warmer and more diffuse environment. These results probably imply that most of the filamentary H I structures are caused by fibers (Clark et al. 2014)rather than sheets as advocated previously by Heiles & Crutcher (2005).
, hence we use upper TD limits of 155, 220, and 311 K. Results from this masking are shown in Fig. 7. For a threshold of 155 K only prominent filaments are masked; a threshold of 220 K affects most of the filaments, and with an upper limit of 311 K just a few weak and diffuse filaments survive the masking. Thus, cold filamentary CNM structures at high Galactic latitudes mark enhanced FIR emission at 857 GHz; lower TD values are observed at the position of the most pronounced filaments. Filamentary structures get more diffuse at higher TD values, implying a 3D structure with lowest temperatures at the bones (or centers) of the filaments within a warmer and more diffuse environment. These results probably imply that most of the filamentary H I structures are caused by fibers (Clark et al. 2014)rather than sheets as advocated previously by Heiles & Crutcher (2005).
 |
Fig. 7 Far-IR emission at 857 GHz as observed by Planck, original data at top left. To indicate upper limits for Tkin, positionswith CNM Doppler temperatures below thresholds of 155, 220, and 311 K (topright, bottom left, and bottom right) are masked. The color scale represents log(I857/MJy sr−1). |
 |
Fig. 8 Histogram of the 2D density distribution of FIR emission intensities at 857 GHz and H2 column densities for TD < 1165 K outside CO–bright regions, covering 65% of the sky. The color-coding represents pixel counts. |
3.2 Far-IR emission from cold H I filaments
The masking shown in Fig. 7 can be repeated for dust emission observed with Planck at other frequencies and demonstrates unambiguously that CNM and FIR filaments are associated with each other. We interpret this correlation as an indication for the presence of diffuse CO–dark H2. Figure 8 displays a 2D histogram derived for the distribution of CO–dark H2 according toEq. (7) and FIR emission in filaments at 857 GHz. There is a clear trend of FIR intensities I857 increasing progressively with increasing H2 column densities. It was noted previously by Clark et al. (2019) and Kalberla & Haud (2020) that the I857 ∕N ratio increases significantly with the intensity of H I small-scale structures. We find that the H2 is correlated with the CNM (Eq. (7)) and at the same time with dust (Figs. 7 and 8). This way cold H I is linked to dust filaments, but only for TD < 1165 K, in the presence of diffuse H2. Filamentarystructures associated with warmer H I are not observed (see Fig. 13 in Kalberla et al. 2016).
3.3 Internal velocity structure of H I filaments
The majority of the structures visible in Fig. 7 are located in the plane of the sky, otherwise we would not be able to recognizetheir filamentary structure. Clark (2018) and Clark & Hensley (2019) derived 3D Stokes parameter maps to constrain the coherence of these 3D structures and the orientation of the filaments and their relation to the interstellar magnetic field. Figure 7 suggests that dust, giving rise to FIR emission, and H2 as the coldest constituents are located in the centers (the bones) of the filaments. The warmer H I appears to be distributed around the bones.
To characterize this situation we use the simplified model of H I distributed as a tube, encapsulating dust and H2. In the case of caustics (Lazarian & Pogosyan 2000; Lazarian & Yuen 2018; Yuen et al. 2019) velocities along the line of sight are constant. If however the filaments are density structures that are not exactly in dynamical equilibrium,we may have the chance to observe two boundary layers around the central bone containing H2 and dust. We check our Gaussian data by searching at each position for two narrow Gaussian components that might be related to each other. First we determine the velocity v0 for the component with the lowest Doppler temperature TD. Next we search at the same position for the Gaussian component with the lowest velocity deviation |v1 − v0| that satisfies the condition TD < 1165 K. ΔvLSR = v1 − v0 then definesthe velocity difference between the two boundary layers or skins along the line of sight.
For 54% of all positions we obtain two closely related narrow Gaussian components. Our results are displayed inFig. 9. The 2D histogram shows a highly symmetric butterfly diagram with well-defined velocity differences indicating pairs of closely related CNM components along the line of sight. For TD > 85 K we fit |ΔvLSR| = −6.1 + 3.8 × log (TD). At a characteristic Doppler temperatureTD ~ 220 K this implies a component separation ΔvLSR ~ 2.8 km s−1. In comparison to δvLSR = 3.17 km s−1, the velocity width of the Gaussian with TD = 220 K, this velocity shift is sufficient to exclude errors from line blending. Also for other values TD ≳85 K line blending is unimportant. The distribution of the ΔvLSR values on the sky is mostly random without preference for positive or negative ΔvLSR values.
Interpreting ΔvLSR as being caused by turbulent motions, we can deconvolve for the line broadening to estimate the excitation temperature as 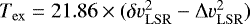 . For a median Doppler temperature TD ~ 220 K we obtain the characteristic excitation temperature Tex ~ 48.5 K. Similar for TD ~ 155 K filaments (Fig. 7, top right) we get Tex ~ 47 K. These estimates are in excellent agreement with the median Tex ~ 50 K derived by Heiles & Troland (2005). We conclude that the H I filaments are cold and at least some of this CNM is encapsulating the H2, consistent with the finding in Sect. 3.1 that filaments are 3D structures with the lowest temperatures interior at the bones.
. For a median Doppler temperature TD ~ 220 K we obtain the characteristic excitation temperature Tex ~ 48.5 K. Similar for TD ~ 155 K filaments (Fig. 7, top right) we get Tex ~ 47 K. These estimates are in excellent agreement with the median Tex ~ 50 K derived by Heiles & Troland (2005). We conclude that the H I filaments are cold and at least some of this CNM is encapsulating the H2, consistent with the finding in Sect. 3.1 that filaments are 3D structures with the lowest temperatures interior at the bones.
 |
Fig. 9 Histogram of the 2D density distribution of the internal velocity structure perpendicular to the bones of H I filaments. ΔvLSR is defined in the velocity domain as the deviation of the nearest Gaussian component relative to the component with the lowest TD. |
4 Discussion
In Sect. 2.2 we apply some commonly adapted assumptions to determine the initial estimates to solve Eq. (2). After quantifying fc(TD) iteratively it became apparent, that these standard assumptions can be released without losing the statistical significance of the results. More important is our finding that after the application of a fc (TD) correction according to Eq. (7) the commonly applied restriction to high latitudes or to regions with E(B−V)∕NHI and NHI ≲4 × 1020 cm−2 and E(B−V)≲0.08 mag can be released. The fc(TD) correction is also applicable toward regions with significant amounts of H2. However, weneed to exclude those regions with bright CO emission from the fitting. Inferring the molecular gas contribution from H I in regions with CO emission does not lead to a reliable presentation of the data without considering additional H2 associated with CO in these regions (Fig. 1 bottom). As a result the fc (TD) correction isapplicable to at least 74% of the sky, quite an improvement to the validity limitations of the previous H I-based determinations of the dust-to-gas relation (Lenz et al. 2017). We find that only 8.8% of the sky are unaffected by the fc (TD) correction. We also tried to determine the H2 distribution within CO–bright regions. We apply a factor XCO = 4.0 × 1020 cm−2 (K km s−1)−1 to calculate the H2 in CO–bright regions. The application of a constant XCO factor is only a rough estimate and only partly successful. However, we found no indications that the fc (TD) conversion in this range could be invalid, thus this correction appears to be valid in general for all diffuse H2 regions.
4.1 The CO-dark gas fraction
Our fc(TD) correction is applicable to an H2 component of the ISM that is termed CO–dark gas by Grenier et al. (2005). This is H2 outside CO dominated regions. For this diffuse molecular gas the carbon is in the form of C or C+ and not CO (Wolfire et al. 2010). Our approach allows us to quantify the atomic and molecular gas from the diffuse atomic gas, via the diffuse molecular, up to the translucent cloud regime (Snow & McCall 2006). The fc (TD) correction according to Eq. (7) implies a moderate onset of H2 formation for H I Doppler temperatures TD≲1165 K. In consequence, the fc(TD) term leads to a notable presence of H2 already in the canonical thin regions described in Sect. 2.2, item 1. Small-scale H I structures are filamentary and have a median Doppler temperature of TD ~ 220 K (Clark et al. 2014; Kalberla et al. 2016; Kalberla & Haud 2018). In this case fc (TD) = 2.55, thus the fraction for the CO–dark H2 interior to the CNM 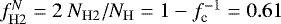 . These CNM structures are clearly dominated by H2. Filaments with TD≲220 K cover 64% of the sky. The bones of these filaments, which we characterize according to Sect. 3.1 or Fig. 7 as TD≲155 K, have
. These CNM structures are clearly dominated by H2. Filaments with TD≲220 K cover 64% of the sky. The bones of these filaments, which we characterize according to Sect. 3.1 or Fig. 7 as TD≲155 K, have 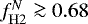 and cover 48% of the sky, thus in the central parts of the filaments the CO–dark molecular gas is enhanced. Only a few CNM clouds have TD≲85 K, but these clouds are local condensations at prominent filamentary structures. For TD ~ 50 K about 90% of the column density is molecular, but only at 9% of the sky positions. H I Dopplertemperatures are upper limits to kinetic temperatures, hence clouds with TD ≲85 K are exceptionally cold in comparison to the average H2 rotational temperatures of 80 K determined by Savage et al. (1977) for diffuse H2. We conclude that H I filaments and in particular their bones are cold, typically with Tex ~ 50 K, and associated with CO–dark molecular gas. Figure 9 implies that most of the H2 is encapsulated within the H I.
and cover 48% of the sky, thus in the central parts of the filaments the CO–dark molecular gas is enhanced. Only a few CNM clouds have TD≲85 K, but these clouds are local condensations at prominent filamentary structures. For TD ~ 50 K about 90% of the column density is molecular, but only at 9% of the sky positions. H I Dopplertemperatures are upper limits to kinetic temperatures, hence clouds with TD ≲85 K are exceptionally cold in comparison to the average H2 rotational temperatures of 80 K determined by Savage et al. (1977) for diffuse H2. We conclude that H I filaments and in particular their bones are cold, typically with Tex ~ 50 K, and associated with CO–dark molecular gas. Figure 9 implies that most of the H2 is encapsulated within the H I.
Figure 10 displays 2D histograms of the frequency distribution for all Gaussian components with CNM molecular gas fractions 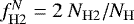 against the fractional E(B−V) for each of these clouds. We use several different selection criteria. Already in the case of the canonical thin regions with NHI ≤ 4 × 1020 cm−2 and E(B−V) ≤ 0.08 mag we find appreciable fractions
against the fractional E(B−V) for each of these clouds. We use several different selection criteria. Already in the case of the canonical thin regions with NHI ≤ 4 × 1020 cm−2 and E(B−V) ≤ 0.08 mag we find appreciable fractions 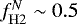 , similar to the CO–masked gas, resulting in the all-sky case in a slightly lower
, similar to the CO–masked gas, resulting in the all-sky case in a slightly lower 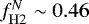 . The implication is that CO–dark gas must be less abundant in the CO–masked regions. Calculating the distribution there shows that the
. The implication is that CO–dark gas must be less abundant in the CO–masked regions. Calculating the distribution there shows that the 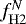 ratio drops significantly for very obscured regions. CO–dark H2 gas is depleted in CO-rich regions since the CO–dark part lies outside the dominant CO region (Wolfire et al. 2010). Numerical simulations by Seifried et al. (2020) show that the dark gas fraction scales inversely with the amount of well-shielded gas for E(B−V)≳0.5. This is the range where we find a considerable drop in the dark gas fraction, on average
ratio drops significantly for very obscured regions. CO–dark H2 gas is depleted in CO-rich regions since the CO–dark part lies outside the dominant CO region (Wolfire et al. 2010). Numerical simulations by Seifried et al. (2020) show that the dark gas fraction scales inversely with the amount of well-shielded gas for E(B−V)≳0.5. This is the range where we find a considerable drop in the dark gas fraction, on average 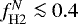 (Fig. 10, bottom right).
(Fig. 10, bottom right).
Summing up all CNM components with TD≲1165 K we obtain an all-sky fraction of 46% for the CO–dark H2 gas; excluding CO dominated regions we get 49.6%. Accounting for all gas in our local vicinity, including the WNM, we find a molecular gas fraction of 18%, consistent with a fraction of 17%, determined by Savage et al. (1977). This average molecular gas fraction compares to fractions between 1 and 30% for cirrus clouds reported by Gillmon & Shull (2006). Our results are somewhat higher than the value of 27% that can be inferred from Wolfire et al. (2010).
All of the 2D histograms for the NH∕E(B−V) ratio in Fig. 6 show a bending of the slope of the distributions at a column density 5 × 1020cm−2. This effect was first observed by Savage et al. (1977) and attributed to a systematic change in the molecular gas fraction at this column density. We find that the onset of H2 formation is not limited to a threshold in column density. Only the Doppler temperature of the gas is important, and Fig. 10 (top left) is explained by the fact that a significant fraction of this gas does not reach low Doppler temperatures.
Figure 10 indicates that the fraction 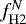 must be relatively constant for the bulk of the CNM components. The investigations by Wolfire et al. (2010) appear to be consistent with this finding. They use a different definition for the molecular gas fraction, but their conclusion is that the fraction of molecular mass in the dark component is remarkably constant and insensitive to the incident ultraviolet radiation field strength and the internal density distribution, and the mass of the molecular cloud. Our empirical fc (TD) correction is based on a statistical investigation over a large number of positions. We can only claim that the fc (TD) correction is valid on average. If however the molecular gas fraction is as insensitive to environmental conditions as claimed by Wolfire et al. (2010), the correction can faithfully be applied even to individual CNM clouds.
must be relatively constant for the bulk of the CNM components. The investigations by Wolfire et al. (2010) appear to be consistent with this finding. They use a different definition for the molecular gas fraction, but their conclusion is that the fraction of molecular mass in the dark component is remarkably constant and insensitive to the incident ultraviolet radiation field strength and the internal density distribution, and the mass of the molecular cloud. Our empirical fc (TD) correction is based on a statistical investigation over a large number of positions. We can only claim that the fc (TD) correction is valid on average. If however the molecular gas fraction is as insensitive to environmental conditions as claimed by Wolfire et al. (2010), the correction can faithfully be applied even to individual CNM clouds.
We display in Fig. 11 a map of the CO–dark gas for |vLSR|≤ 8 km s−1. This velocity range is most closely representative of filamentary structures in our local vicinity (Kalberla et al. 2016, Sect. 5.13). We see that most of the CO–dark molecular gas is organized in filaments. For a comparison with the total amount of H I and CO–dark H2 in the velocity range |vLSR|≤ 90 km s−1 see Fig. 12. Except for CO–bright regions, which were disregarded here because of the uncertain XCO correction, this map may be helpful to supplement interstellar reddening maps. Figure 13 displays our estimate of the total H I, CO–dark and CO–bright gas distribution in the Milky Way. Figures 11–13 demonstrate our current estimates on the distribution of diffuse H2 and the total neutral hydrogen in the Milky Way, without and with CO–bright H2. The significance of these results needs to be evaluated.
 |
Fig. 10 2D histograms of the CNM molecular gas fractions |
4.2 H2 power spectra
The H2 distribution displayed in Fig. 11 is linked to the H I distribution via Eq. (7). This implies that the diffuse H2 is embedded in the H I. The H I filaments that host the H2 must necessarily be density structures in conflict with the interpretation of filaments as velocity caustics (Lazarian & Pogosyan 2000; Lazarian & Yuen 2018; Yuen et al. 2019). We can use HI4PI data to estimate the power distribution of the diffuse molecular H2 at large scales. Our data processing is the same as described by Kalberla & Haud (2019) except that we restrict our analysis to the diffuse CO–dark H2. We select Gaussian components according to their Doppler temperatures and central velocities. Figure 14 shows the power spectra for three velocity windows: |vLSR| < 25, 8, and 1 km s−1. On top we display spectra for |b| > 20°, on the bottom are all-sky data. These spectra are shallow in comparison to the CNM power spectra shown in Figs. 1 and 23 of Kalberla & Haud (2019). The diffuse H2 is embedded in the CNM and the colder the H I, the more pronounced are intermittent small-scale structures with transitions to H2. The relations between hierarchical scaling of successive structures in a turbulent medium have been described by She & Leveque (1994). A 3D incompressible flow is considered as a hierarchy of structures, the most singular structures are assumed to be filaments. Accordingly high intensity structures are understood as filaments with a Hausdorff dimension of one. Reducing the dimension implies a reduction of the power law index. The expected energy spectrum of turbulence is accordingly E(k) ∝ k−5∕3−0.03.
Figure 14 indicates that most of the H2 structures are local; |vLSR| < 8 km s−1 contains a significant fraction of the power. H2 structures extracted for |vLSR| < 1 km s−1 are the best examples with the highest signal-to-noise ratio (S/N) for an all-sky distribution of intermittent filamentary structures. The corresponding power spectra with fitted power law indices − 1.79≳γ≳ − 1.9 are significantly shallower than − 2.14≳γ≳ − 2.37 for the CNM Kalberla & Haud (2019, Fig. 1). These results support the conjecture by She & Leveque (1994), who find that the nature of these asymptotic flow structures is a specific property of the three-dimensional incompressible flows and that only filamentary structures seem to be mechanically stable. In the case of the diffuse ISM, phase transitions increase intermittency, therefore affecting the properties of the turbulent flow. Spectral indices for the H I distribution in narrow velocity channels were found to depend on Doppler temperatures, and Kalberla et al. (2016, 2017) and Kalberla & Haud (2020) interpret this as an indication that the turbulent flow is affected by phase transitions. The coupling of linear density structures to the Galactic magnetic field (Clark & Hensley 2019) appears in addition to support the hierarchy of structures in the ISM that approach Hausdorff dimensions of one for filamentary structures.
Figure 15 compares power spectra selecting different neutral hydrogen species, H I, H, and H2 (CO–dark gas only) from our model calculations. As in Fig. 14 we selected components with Doppler temperatures TD < 1165 K at |vLSR| < 1 km s−1. We compare power spectra at high latitudes (top) and all-sky (bottom). The column density spectra for NH = NHI + 2 NH2 (blue) have the highest power, as expected since this is the total amount of all neutral hydrogen. The (2 NH2) power spectra (black) have within the uncertainties power law slopes that are identical to the NH power spectra and are straight up to high multipoles l ~ 400. The high power tails of the H I spectra (red) bend up at l≳300. Comparing these H I spectra with Kalberla & Haud (2019, Fig. 1) indicates systematic differences. The turn-over of these CNM power spectra with deviations from a fitted straight power law is ever earlier at l≳100. Furthermore, those CNM power spectra are significantly steeper (− 2.14≳γ≳ − 2.37) than the H I spectra from Fig. 15 constrained by TD < 1165 K (− 1.70≳γ≳ − 1.83).
In addition to power spectra with Doppler temperatures TD < 1165 K, we plot in Fig. 15 (2 NH2) power spectra for TD < 85 K (orange); this is for the steep branch from Eq. (7) and Fig. 3. Even though the H2 clumps from the coldest CNM are located along H2 filaments, most of the filamentary structures are broken and this sample of H2 clumps approaches a random distribution for objects with a Hausdorff dimension of zero. In agreement with the conjecture by She & Leveque (1994), these power spectra are very shallow. These power spectra are straight up to l≲500. Deviations, caused by optical depth effects, are not recognizable.
For an interpretation of all these different power spectra we need to take into account that different ISM phases (WNM, LNM, CNM, and H2) are related to each other. A complete description of these phases demands that all cross-correlations between the phases need to be taken into account (Kalberla & Haud 2019, Eq. (4)). A detailed treatment of the cross-correlations is beyond the scope of the current publication, but we may safely conclude that the (2 NH2) power spectra (black) in Fig. 15 have the best-defined self-similar straight power spectra for the cold ISM in the intermediate range of scales up to l≲400. We argued in Sect. 2.4 that the definition for Gaussian CNM components (Kalberla &Haud 2019) is broadly consistent with an upper limit of Doppler temperatures TD ≲1165 K. However, from the outstanding properties of the (2 NH2) spectral power distributions from Fig. 15 it appears appropriate to consider this limit as relevant for phase transitions that lead to significant filamentary H2 structures. This threshold should not be considered as a canonical value; instead, it is a weighted mean comprising a best fit value for all physical conditions considered by us over 74% of the sky outside CO–bright regions.
A comparable upper limit TD ~ 1100 K was found for Doppler temperatures of filamentary features derived by unsharp masking of HI4PI data by Kalberla et al. (2016, Sect. 5.11). At a Mach number of 3.7 it is consistent with an upper limit of Tkin ~ 220 K for the kinetic temperature as expected for a stable CNM phase (Wolfire et al. 2003). An upper TD limit for fc (TD) is not in conflict with phase transitions out of the WNM but it implies that the H I must first cool down to the CNM before H2 molecules can form.
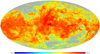 |
Fig. 11 Distribution of CO–dark H2 in the velocity range |vLSR|≤ 8 km s−1 from the HI4PI survey. The scale is logarithmic, NH units are cm−2. |
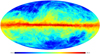 |
Fig. 12 Distribution of H I and diffuse CO–dark H2 in the velocity range |vLSR|≤ 90 km s−1. The scale is logarithmic, NH units are cm−2. |
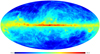 |
Fig. 13 Distribution of H I, CO–dark and estimated CO–bright H2 in the velocity range |vLSR|≤ 90 km s−1. The scale is logarithmic, NH units are cm−2. |
 |
Fig. 14 Power spectra for the derived column density distributions of the diffuse H2 at |vLSR| < 25, 8, and 1 km s−1 at high latitudes (top) and all-sky (bottom). The power indices γ were fitted for multipoles 10 < l < 300; the vertical line indicates the upper limit in l. |
5 Summary and conclusion
We use Doppler temperatures TD from a Gaussian decomposition of HI4PI data to study temperature dependences of E(B−V)∕NHI. This ratio increases with − log (TD), and we interpret this trend with the presence of unaccounted molecular hydrogen: E(B−V)∕NHI≳E(B−V)∕(NHI + 2 NH2). Systematic changes of E(B−V)∕NHI allow the definition of a temperature dependent correction under the assumption of a constant E(B−V)∕(NHI + 2 NH2) ratio.
This empirical fc(TD) correction (Eq. (7)) allows us to estimate the dark molecular gas content in the CNM. We find evidence of H2 at temperatures TD≲1165 K; on average the diffuse molecular gas fraction in CNM clouds outside CO–bright regions is 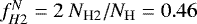 . Filamentary H I structures with TD≲220 K are cold with Tex≲50 K, are with
. Filamentary H I structures with TD≲220 K are cold with Tex≲50 K, are with 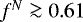 dominated by H2, and are associated with dust. According to Clark & Hensley (2019) they are aligned with the magnetic field, representing magnetically coherent regions of space. All these filaments have column densities below the limit log (NH∕cm-2) ~ 21.7 where the preferential orientation of the magnetic field along the filaments switches to being perpendicular to the NH contours (Planck Collaboration Int. XXXV 2016). We find evidence that the central parts of the filaments, the bones, have the lowest temperatures and increased molecular gas fractions
dominated by H2, and are associated with dust. According to Clark & Hensley (2019) they are aligned with the magnetic field, representing magnetically coherent regions of space. All these filaments have column densities below the limit log (NH∕cm-2) ~ 21.7 where the preferential orientation of the magnetic field along the filaments switches to being perpendicular to the NH contours (Planck Collaboration Int. XXXV 2016). We find evidence that the central parts of the filaments, the bones, have the lowest temperatures and increased molecular gas fractions 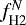 . The H I encapsulates the H2. Applying the fc(TD) correction leads to a significant reduction of systematic deviations in the E(B−V)∕(NHI + 2 NH2) ratio at high Galactic latitudes. Extending the TD correction to CO–bright regions is possible with some limited success for a factor XCO = 4.0 × 1020 cm−2 (K km s−1)−1.
. The H I encapsulates the H2. Applying the fc(TD) correction leads to a significant reduction of systematic deviations in the E(B−V)∕(NHI + 2 NH2) ratio at high Galactic latitudes. Extending the TD correction to CO–bright regions is possible with some limited success for a factor XCO = 4.0 × 1020 cm−2 (K km s−1)−1.
Our empirical correction is based on statistical investigations, covering 74% of the sky; thus, the validity is limited to an on-average correction. However theoretical investigations by Wolfire et al. (2010) indicate that the H2 content is insensitive to environmental conditions. If this is really the case, our corrections may be universal and can be used to predict the foreground attenuation affecting our view to the distant universe. It appears worth trying this because, as they say, the proof of the pudding is in the eating, and we provide the necessary data7.
 |
Fig. 15 Power spectra, comparing column density distributions for H I, H, and H2 (CO–dark) at |vLSR| < 1 km s−1 for Doppler temperatures TD < 1165 K and TD < 85 K at high latitudes (top) and all-sky (bottom). The power indices γ were fitted for multipoles 10 < l < 300; the vertical line indicates the upper limit in l. |
Acknowledgements
We thank the referee for careful reading and constructive criticism. U.H. acknowledges the support by the Estonian Research Council grant IUT26-2, and by the European Regional Development Fund (TK133). HI4PI is based on observationswith the 100-m telescope of the MPIfR (Max-Planck-Institut für Radioastronomie) at Effelsberg and the Parkes Radio Telescope, which is part of the Australia Telescope and is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. This research has made use of NASA’s Astrophysics Data System. Some of the results in this paper have been derived using the HEALPix package. We also used the Karma package by R.E. Gooch.
References
- Basu, S. 2000, ApJ, 540, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Carruthers, G. R. 1970, Space Sci. Rev., 10, 459 [CrossRef] [Google Scholar]
- Clark, S. E. 2018, ApJ, 857, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S. E., & Hensley, B. S. 2019, ApJ, 887, 136 [CrossRef] [Google Scholar]
- Clark, S. E., Peek, J. E. G., & Putman, M. E. 2014, ApJ, 789, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S. E., Hill, J. C., Peek, J. E. G., et al. 2015, Phys. Rev. Lett., 115, 241302 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S. E., Peek, J. E. G., & Miville-Deschênes, M.-A. 2019, ApJ, 874, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M., Wandelt, B., Heiles, C., et al. 2010, ApJ, 725, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B. 1959, ApJ, 129, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B., Goldsmith, D. W., & Habing, H. J. 1969, ApJ, 155, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Fukui, Y., Torii, K., Onishi, T., et al. 2015, ApJ, 798, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Gillmon, K., & Shull, J. M. 2006, ApJ, 636, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Grenier, I. A., Casandjian, J.-M., & Terrier, R. 2005, Science, 307, 1292 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Haud, U. 2000, A&A, 364, 83 [NASA ADS] [Google Scholar]
- Heiles, C., & Crutcher, R. 2005, Cosmic Magnetic Fields (Berlin: Springer), 137 [Google Scholar]
- Heiles, C., & Troland, T. H. 2003a, ApJS, 145, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Troland, T. H. 2003b, ApJ, 586, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Troland, T. H. 2005, ApJ, 624, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Inutsuka, Shu-ichiro. 2019, Front. Astron. Space Sci., 6, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M., & Dame, T. M. 2015, ARA&A, 53, 583 [NASA ADS] [CrossRef] [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W. 2003, ApJ, 588, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., & Haud, U. 2018, A&A, 619, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., & Haud, U. 2019, A&A, 627, A112 [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., & Haud, U. 2020, A&A, submitted [arXiv:2003.01454] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Kerp, J., Haud, U., et al. 2016, ApJ, 821, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Kerp, J., Haud, U., & Haverkorn, M. 2017, A&A, 607, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazarian, A., & Pogosyan, D. 2000, ApJ, 537, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Yuen, K. H. 2018, ApJ, 853, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, D., Hensley, B. S., & Doré, O. 2017, ApJ, 846, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M.-Y., Stanimirović, S., Murray, C. E., Heiles, C., & Miller, J. 2015, ApJ, 809, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Li, D., & Goldsmith, P. F. 2003, ApJ, 585, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Liszt, H. 2001, A&A, 371, 698 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H. 2014a, ApJ, 780, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Liszt, H. 2014b, ApJ, 783, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Miville-Deschênes, M.-A., Boulanger, F., Reach, W. T., et al. 2005, ApJ, 631, L57 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F.,& Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, C. E., Stanimirović, S., Goss, W. M., et al. 2018a, ApJS, 238, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, C. E., Peek, J. E. G., Lee, M.-Y., et al. 2018b, ApJ, 862, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, H., Dawson, J. R., Miville-Deschênes, M.-A., et al. 2018, ApJ, 862, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Payne, H. E., Terzian, Y., & Salpeter, E. E. 1980, ApJ, 240, 499 [CrossRef] [Google Scholar]
- Peek, J. E. G., & Clark, S. E. 2019, ApJ, 886, L13 [CrossRef] [Google Scholar]
- Peek, J. E. G., Babler, B. L., Zheng, Y., et al. 2018, ApJS, 234, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIX. 2011, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVIII. 2016, A&A, 596, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXIX. 2016, A&A, 586, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXV. 2016, A&A, 586, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Predehl, P., & Schmitt, J. H. M. M. 1995, A&A, 500, 459 [Google Scholar]
- Rachford, B. L., Snow, T. P., Destree, J. D., et al. 2009, ApJS, 180, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Reach, W. T., Wall, W. F., & Odegard, N. 1998, ApJ, 507, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., Bohlin, R. C., Drake, J. F., et al. 1977, ApJ, 216, 291 [NASA ADS] [CrossRef] [Google Scholar]
- She, Z.-S., & Leveque, E. 1994, Phys. Rev. Lett., 72, 336 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Finkbeiner, D. P., Schlegel, D. J., et al. 2010, ApJ, 725, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Seifried, D., Haid, S., Walch, S., et al. 2020, MNRAS, 492, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L., & Zabriskie, F. R. 1959, PASP, 71, 412 [CrossRef] [Google Scholar]
- Strong, A. W., & Mattox, J. R. 1996, A&A, 308, L21 [NASA ADS] [Google Scholar]
- Tang, N., Li, D., Heiles, C., et al. 2016, A&A, 593, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakker, B. P., & van Woerden, H. 1997, ARA&A, 35, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Winkel, B., Kerp, J., Flöer, L., et al. 2016, A&A, 585, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Yuen, K. H., Hu, Y., Lazarian, A., & Pogosyan, D. 2019, ArXiv e-prints [arXiv:1904.03173] [Google Scholar]
- Zhu, H., Tian,W., Li, A., et al. 2017, MNRAS, 471, 3494 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 E(B−V)∕NHI in regions used for the determination of the dust-to-gas ratio. Masked regions, including the Magellanic Clouds, are shown in blue. Top: E(B−V)∕NHI defined for canonical thin H I gas with NHI ≤ 4 × 1020 cm−2 and E(B−V) ≤ 0.08 mag (Lenz et al. 2017). Bottom: E(B−V)∕NHI outside CO–bright regions. Units are 10−27 cm2, scaling and color-coding are as in Fig. 4 for the mean corrected E(B− V)∕NH dust-to-gas ratio within a 2σ range. |
| In the text | |
 |
Fig. 2 Probability distribution functions for Gaussian components with selected Doppler temperatures
|
| In the text | |
 |
Fig. 3 Hydrogen column density correction factor fc(TD) from an all-sky fit, excluding positions in CO–bright regions. The crosses show fit results from the last iterations, the solid lines the regressions from Eq. (7), the dashed red line the adopted complete solution. |
| In the text | |
 |
Fig. 4 Left: E(B−V)∕NHI (top), E(B−V)∕NH with the fc(TD) correction Eq. (7) (middle), and E(B−V)∕NHtot including a correction for XCO = 4.0 × 1020 cm−2 (K km s−1)−1 (bottom). Units are 10−22 cm2 mag, displayed are data around the mean within a 2σ range on both sides. For a comparison of E(B−V)∕NHI after restricting the data to the canonical thin gas and to CO–bright regions we refer to Fig. 1. Right: τ353 ∕NHI (top), τ353∕NH (middle), and τ353∕NHtot (bottom). Units are 10−27 cm2, also displayed are data within 2σ around the mean. |
| In the text | |
 |
Fig. 5 Galactic plane excerpts for E(B−V)∕NHtot with a correction for XCO = 4.0 × 1020 cm−2 (K km s−1)−1 as in Fig. 4 (bottom left), but with different smoothing kernels S: (from top to bottom) S with FWHMof 0°, 1°, 2°, 3°, and 4°. |
| In the text | |
 |
Fig. 6 All-sky 2D histograms for the E(B−V) vs. NHI (top) and NH (bottom) after applying the fc(TD) correction. Middle: data in CO–bright regions were disregarded. The color-coding represents pixel counts. |
| In the text | |
 |
Fig. 7 Far-IR emission at 857 GHz as observed by Planck, original data at top left. To indicate upper limits for Tkin, positionswith CNM Doppler temperatures below thresholds of 155, 220, and 311 K (topright, bottom left, and bottom right) are masked. The color scale represents log(I857/MJy sr−1). |
| In the text | |
 |
Fig. 8 Histogram of the 2D density distribution of FIR emission intensities at 857 GHz and H2 column densities for TD < 1165 K outside CO–bright regions, covering 65% of the sky. The color-coding represents pixel counts. |
| In the text | |
 |
Fig. 9 Histogram of the 2D density distribution of the internal velocity structure perpendicular to the bones of H I filaments. ΔvLSR is defined in the velocity domain as the deviation of the nearest Gaussian component relative to the component with the lowest TD. |
| In the text | |
 |
Fig. 10 2D histograms of the CNM molecular gas fractions |
| In the text | |
 |
Fig. 11 Distribution of CO–dark H2 in the velocity range |vLSR|≤ 8 km s−1 from the HI4PI survey. The scale is logarithmic, NH units are cm−2. |
| In the text | |
 |
Fig. 12 Distribution of H I and diffuse CO–dark H2 in the velocity range |vLSR|≤ 90 km s−1. The scale is logarithmic, NH units are cm−2. |
| In the text | |
 |
Fig. 13 Distribution of H I, CO–dark and estimated CO–bright H2 in the velocity range |vLSR|≤ 90 km s−1. The scale is logarithmic, NH units are cm−2. |
| In the text | |
 |
Fig. 14 Power spectra for the derived column density distributions of the diffuse H2 at |vLSR| < 25, 8, and 1 km s−1 at high latitudes (top) and all-sky (bottom). The power indices γ were fitted for multipoles 10 < l < 300; the vertical line indicates the upper limit in l. |
| In the text | |
 |
Fig. 15 Power spectra, comparing column density distributions for H I, H, and H2 (CO–dark) at |vLSR| < 1 km s−1 for Doppler temperatures TD < 1165 K and TD < 85 K at high latitudes (top) and all-sky (bottom). The power indices γ were fitted for multipoles 10 < l < 300; the vertical line indicates the upper limit in l. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.