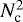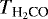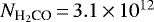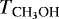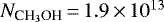| Issue |
A&A
Volume 639, July 2020
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202037533 | |
| Published online | 23 July 2020 | |
Simulating the circumstellar H2CO and CH3OH chemistry of young stellar objects using a spherical physical-chemical model
1
Institute of Physics, University Kassel,
Heinrich-Plett Str. 40,
34132
Kassel,
Germany
e-mail: fuchs@physik.uni-kassel.de
2
Max-Planck-Institut for Extraterrestrial Physics (MPE),
Giessenbachstraße 1,
85748
Garching, Germany
3
Laboratory for Astrophysics, Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden, The Netherlands
4
Max-Planck-Institut for Radio Astronomy (MPIfR),
Auf dem Hügel 69,
53121
Bonn, Germany
Received:
20
January
2020
Accepted:
20
April
2020
Context. Young stellar objects (YSOs) and their environments are generally geometrically and dynamically challenging to model, and the corresponding chemistry is often dominated by regions in non-thermal equilibrium. In addition, modern astrochemical models have to consider not only gas-phase reactions, but also solid-state reactions on icy dust grains. Solving the geometrical, physical, and chemical boundary conditions simultaneously requires a high computational effort and still runs the risk of false predictions due to the intrinsically non-linear effects that can occur. As a first step, solving problems of reduced complexity is helpful to guide more sophisticated approaches.
Aims. The objective of this work is to test a model that uses shell-like structures (i.e., assuming a power-law number density and temperature gradient of the environment surrounding the YSO) to approximate the geometry and physical structure of YSOs, that in turn utilizes an advanced chemical model that includes gas-phase and solid-state reactions to model the chemical abundances of key species. A special focus is set on formaldehyde (H2CO) and methanol (CH3OH) as these molecules can be traced in the gas phase but are produced on icy dust grains. Furthermore, this kind of molecule is believed to be key to understanding the abundance of more complex species. We compare the influence of the geometry of the object on the molecular abundances with the effect induced by its chemistry.
Methods. We set up a model that combines a grain-gas phase chemical model with a physical model of YSOs. The model ignores jets, shocks, and external radiation fields and concentrates on the physical conditions of spherically symmetric YSOs with a density and temperature gradient derived from available spectral energy distribution observations in the infrared. In addition, new observational data are presented using the APEX 12 m and the IRAM 30 m telescopes. Formaldehyde and methanol transitions have been searched for in three YSOs (R CrA-IRS 5A, C1333-IRAS 2A, and L1551-IRS 5) that can be categorized as Class 0 and Class 1 objects, and in the pre-stellar core L1544. The observed abundances of H2CO and CH3OH are compared with those calculated by the spherical physical-chemical model.
Results. Compared to a standard “ρ and T constant” model, i.e., a homogeneous (flat) density and temperature distribution, using number density and temperature gradients results in reduced abundances for the CO hydrogenation products formaldehyde and methanol. However, this geometric effect is generally not large, and depends on the source and on the molecular species under investigation. Although the current model uses simplified geometric assumptions the observed abundances of H2CO and CH3OH are well reproduced for the quiescent Class 1 object R CrA-IRS 5A. Our model tends to overestimate formaldehyde and methanol abundances for sources in early evolutionary stages, like the pre-stellar core L1544 or NGC 1333-IRS 2A (Class 0). Observational results on hydrogen peroxide and water that have also been predicted by our model are discussed elsewhere.
Key words: astrochemistry / molecular processes / stars: protostars / ISM: molecules
© ESO 2020
1 Introduction
It is interesting to reflect on the origin of the chemical content of our solar environment that allowed the creation of life-supporting molecular species, and it is widely believed that the study of the chemistry of young stellar objects (YSOs) will bring us closer to a basic understanding of this topic. Today these YSOs can be studied in great detail using images from the Hubble space telescope (Padgett et al. 1999) or other observatories (Lucas et al. 1997; Close et al. 1997). The images show that these objects can be full of substructures on various scales, resulting in dynamically complex patterns. Depending on the age and history of such an object it can be thought of as consisting of an extended envelope, an accretion disk with a protostar located at its center, cavities, a jet and possibly shock regions, and pronounced interaction zones with central and external radiation fields. Here, in different regions different chemical processes may take place. Molecules are often used as chemical probes for these regions, which can also provide information about the local physical conditions like density and temperature (Bruderer et al. 2009a). In this work we are particularly interested in a chemical network that enables the emergence of complex organic molecules (COMs) and the associated formation of water. It is believed that chemical reactions on grain surfaces and in cryogenic solids (ices) play an important role in the formation of precursor molecules of water and of COMs, like H2CO or CH3OH (Garrod et al. 2008; Du et al. 2012; Lee et al. 2019). A truly faithful model that takes into account multi-dimensional geometric aspects and a chemistry that in some regions is far from a thermal equilibrium is computationally very demanding and, due to the complexity of this task and to non-linear effects that can occur, not necessarily of superior predictive power. The challenges are therefore twofold. On the one hand, an underlying geometry must be realistic enough but not too complex to be comprehensible; on the other hand, complex chemical processes must be modeled sufficiently correctly, i.e., also including gas-grain interactions. Early models of star forming regions assumed a fixed density and temperature (Leung et al. 1984), but quickly models were developed that also considered space-dependent chemistry (e.g., Caselli et al. 1993; Millar et al. 1997) or were adapted to observations under the assumption of spherical symmetry with 1D physical parameters (Doty et al. 2002; Stäuber et al. 2005). Bruderer et al. (2009a,b) introduced a 2D axisymmetric chemical model of YSO envelopes. The model we present here is not of the latterkind. It works with a simplified geometric model that we consider sufficient for our purpose, i.e., it concentrates on the envelope of YSOs, regions that can be considered equivalent to our outer solar system region extending to the Oort cloud where premordial comets originate. Our model assumes spherically symmetric YSOs with a density and temperature gradient based upon spectral energy distributions (SEDs) derived from infrared observations (Robitaille et al. 2007; Kristensen et al. 2012). There have been other in-depth studies and tests of models of YSOs, some of which also used power-law density models (Hogerheijde et al. 2010). Other studies focused more on the dynamical aspects or photon-induced chemistry (Stäuber et al. 2005; Bruderer et al. 2009a). Our chemical model is based on the work of Du et al. (2012) and includes gas-phase and solid-state reactions.
Compared to the gas-phase only a few molecules have been identified as solid components in cosmic ices, with H2O, CO, CH3OH, H2CO, HCOOH, CO2, NH3, and NH being typical examples (Tielens & Hagen 1982; Whittet et al. 1996; Boogert et al. 2015). Thus, not only is water ice (and presumably the precursor hydrogen peroxide) formed on cold grains, formaldehyde (H2CO) and methanol (CH3OH) ices have also been observed (Boogert et al. 2008; Bottinelli et al. 2010). In the laboratory the underlying hydrogenation reaction chain has been investigated on carbon monoxide (CO) interstellar ice analogs (Fuchs et al. 2009; Hiraoka et al. 2002; Watanabe & Kouchi 2002). Starting with solid CO, atomic hydrogen (H) addition leads to the intermediate HCO and subsequently to H2CO. With ongoing hydrogenation, formaldehyde can further react to the intermediate H3CO resulting in CH3OH fractions in the ice. Depending on the initial ice content (e.g., the amount of solid CO and O2), the production of HOOH and H2O, and of H2CO and CH3OH, can proceed simultaneously. In some recent work abstraction reactions along this chain were shown to provide additional pathways in the formation of H2CO in CO ices, and to molecules larger than methanol, like glycol aldehyde, ethylene glycol, and glycerol (Chuang et al. 2016; Fedoseev et al. 2017). Carbon monoxide and molecular oxygen accrete on the grains at about the same temperature, but the abundance of CO is much higher. In the laboratory the hydrogenation of mixed CO and O2 ices results in H2CO and CH3OH, as well as HOOH and H2O, but also in the formation of CO2 via the reactive intermediate HOCO, which links the CO and O2 hydrogenation chains (see Fig. 2 in Ioppolo et al. 2011). The reaction efficiencies of CO+H and O2 +H seem to be comparable, but depend on the initial CO/O2 ratio. For this reason we also include HOOH and H2O in this work as their formation scheme is connected to that of H2CO and CH3OH. However, in contrast to formaldehyde and methanol, HOOH has not been identified in interstellar ices via infrared absorption observations, but only as a gas-phase species via (sub)millimeter emission observations (Bergman et al. 2011; Smith et al. 2011; Fuchs et al. 2020). Du et al. (2012) included a desorption mechanism in their model based on the release of excess energy during the solid-state molecule formation, as did Chuang et al. (2018) for reactive desorption processes of CO hydrogenation products (see also Cazaux et al. 2016; Minissale et al. 2016). Our aim is to estimate molecular abundances of key molecules like H2CO and CH3OH in the gas phase (which are assumed to have formed in the solid phase during the early phases of YSOs) by combining the results of the chemical model from Du et al. (2012) with the assumption of a spherical gradient distribution of the density and temperature. Using our combined physical-chemical model (see Sect. 2) we present in Sect. 5 predictions of H2CO and CH3OH abundances in the close-by YSOs L1551-IRS 5, R CrA-IRS 5A, and NGC 1333-IRAS 2A, and in the pre-stellar core L1544 (Sects. 3 and 4) and compare them with astronomically derived values (Sect. 6).
being typical examples (Tielens & Hagen 1982; Whittet et al. 1996; Boogert et al. 2015). Thus, not only is water ice (and presumably the precursor hydrogen peroxide) formed on cold grains, formaldehyde (H2CO) and methanol (CH3OH) ices have also been observed (Boogert et al. 2008; Bottinelli et al. 2010). In the laboratory the underlying hydrogenation reaction chain has been investigated on carbon monoxide (CO) interstellar ice analogs (Fuchs et al. 2009; Hiraoka et al. 2002; Watanabe & Kouchi 2002). Starting with solid CO, atomic hydrogen (H) addition leads to the intermediate HCO and subsequently to H2CO. With ongoing hydrogenation, formaldehyde can further react to the intermediate H3CO resulting in CH3OH fractions in the ice. Depending on the initial ice content (e.g., the amount of solid CO and O2), the production of HOOH and H2O, and of H2CO and CH3OH, can proceed simultaneously. In some recent work abstraction reactions along this chain were shown to provide additional pathways in the formation of H2CO in CO ices, and to molecules larger than methanol, like glycol aldehyde, ethylene glycol, and glycerol (Chuang et al. 2016; Fedoseev et al. 2017). Carbon monoxide and molecular oxygen accrete on the grains at about the same temperature, but the abundance of CO is much higher. In the laboratory the hydrogenation of mixed CO and O2 ices results in H2CO and CH3OH, as well as HOOH and H2O, but also in the formation of CO2 via the reactive intermediate HOCO, which links the CO and O2 hydrogenation chains (see Fig. 2 in Ioppolo et al. 2011). The reaction efficiencies of CO+H and O2 +H seem to be comparable, but depend on the initial CO/O2 ratio. For this reason we also include HOOH and H2O in this work as their formation scheme is connected to that of H2CO and CH3OH. However, in contrast to formaldehyde and methanol, HOOH has not been identified in interstellar ices via infrared absorption observations, but only as a gas-phase species via (sub)millimeter emission observations (Bergman et al. 2011; Smith et al. 2011; Fuchs et al. 2020). Du et al. (2012) included a desorption mechanism in their model based on the release of excess energy during the solid-state molecule formation, as did Chuang et al. (2018) for reactive desorption processes of CO hydrogenation products (see also Cazaux et al. 2016; Minissale et al. 2016). Our aim is to estimate molecular abundances of key molecules like H2CO and CH3OH in the gas phase (which are assumed to have formed in the solid phase during the early phases of YSOs) by combining the results of the chemical model from Du et al. (2012) with the assumption of a spherical gradient distribution of the density and temperature. Using our combined physical-chemical model (see Sect. 2) we present in Sect. 5 predictions of H2CO and CH3OH abundances in the close-by YSOs L1551-IRS 5, R CrA-IRS 5A, and NGC 1333-IRAS 2A, and in the pre-stellar core L1544 (Sects. 3 and 4) and compare them with astronomically derived values (Sect. 6).
2 Physical-chemical shell model
2.1 Physical parameters
In our approach the results of the chemical calculations done by Du et al. (2012) are used in a physical model of astronomical sources that show spherical symmetry with a power-law number density and temperature gradient ρN (r) ~ r−p and T(r) ~ r−b, with p and b being specific source parameters as listed in Table 1 and r ≥ rstart > 0 given in [AU]1. Here rstart defines the distance to the star from which substantial contributions to molecule formation are expected. This will be discussed later in more detail. In the model the highest densities and temperatures can be found close to the central protostar, which then decrease as a function of the distance r to the central object (except for the source L1544 where the temperature is nearly constant or lowest at the center, and the model had to be adjusted accordingly). The values for the physical model were mainly taken from Kristensen et al. (2012) and are based on dust emission observations and subsequent analysis of the SED using the DUSTY code (Ivezic & Elitzur 1997; see also similar earlier work by Schöier et al. 2002). DUSTY is a 1D spherically symmetric dust radiative transfer code. For our model we used the source parameters p and q and the innermost radius rin (which is defined asthe radius where T = 250 K) to calculate the density and temperature at a given radius within the YSO envelope. Here q is a source-specific proportionality factor (ρN = q ⋅ r−p), as given in Table 1. No structures other than the envelope (i.e., jet outflows or non-symmetrical contributions) are considered (see Fig. 1). More specifically, for CrA-IRS 5A the values given in Lindberg & Jørgensen (2012) have also been used to calculate the temperature gradient; for the pre-stellar core L1544 the parameters were taken from Caselli et al. (2002).
Physical parameters of observed objects.
 |
Fig. 1 Sketch of the applied physical model geometry for protostellar objects. The integrated region (blue-edged hollow sphere) excluding the innermost and outermost parts is the region used for the calculations. The envelope of the object exceeds rend and has a diameter larger than 104 AU. The jet and disk have not been taken into account in our model. |
2.2 Chemical model
The chemical model used is completely based on the work by Du et al. (2012) and has been described there in detail (see also Du & Parise 2011). In brief, the gas phase chemistry is based on the UMIST RATE06 network2 (Woodall et al. 2007). In total 284 gas phase species connected via 3075 gas phase reactions were included, but species containing Fe, Na, Mg, and Cl were excluded. The initial conditions are the same as in Stantcheva & Herbst (2004)3. To model the gas-grain chemistry the hybrid moment equation (HME) approach was used (see Du & Parise 2011). The cosmic-ray ionization rate used is 1.36 × 10−17 s−1 (canonical value; see Woodall et al. 2007). In total, 151 surface reactions and 56 surface species were taken into account (Allen & Robinson 1977; Tielens & Hagen 1982; Hasegawa et al. 1992), with binding energies of surface species based on Hasegawa & Herbst (1993) and Garrod (2008b). In particular, the ice-borne molecules H2CO, CH3OH, HOOH, and H2O are includedand their corresponding surface reaction routes are briefly outlined below.
The hydrogenation of CO results in the formation of H2CO and CH3OH via
![\begin{equation*} \text{CO} \xrightarrow[]{\text{H}} \text{HCO} \xrightarrow[]{\text{H}} \text{H$_2$CO} \xrightarrow[]{\text{H}} \text{H$_3$CO} \xrightarrow[]{\text{H}} \text{CH$_3$OH} \end{equation*}](/articles/aa/full_html/2020/07/aa37533-20/aa37533-20-eq2.png)
and is based on laboratory work by Fuchs et al. (2009), Hiraoka et al. (2002), and Watanabe & Kouchi (2002). We also included the solid-state formation of water on grain surfaces in the model (Cuppen et al. 2010).
There are critical parameters, namely the source age, density, and temperature, that largely determine the accuracy of our predictions. Unfortunately, in the case of the very critical age dependence exact numbers are often not at hand and only the general stage classification (Class 0 or 1) is available. Therefore, we estimated the effect of the source age on the abundance and temperature uncertainty by varying the source age as input parameter.
Using the input parameters in Table 1, our model predicts the abundance ratio A = [X]∕[hydrogen] and number density ρX of each molecule X of interest at a given radius to the central star. An example is shown in Fig. 2, where the used model values are shown for the hydrogen density and temperature (top graph) along the distance axis for the source R CrA-IRS 5A. The model output data is shown in the graph below, with the number densities of H2CO, CH3OH, H2O and HOOH. As can be seen, these molecules are only formed in a shell-like region around the star with a void region at the center and a fall-off at larger radii. The innermost region (i.e., the first few hundred AUs where a disk structure may or may not exist depending on the age of the source) is not considered; instead, we focus on the surrounding still in-falling material of the YSO (see Table 2).
The total number of molecules is calculated by integrating ρX over the source volume and subsequently the column density Nc is determined4. The integration starts at a distance rstart from the star at which significant molecule production occurs; see Fig. 1. The reason for this limitation (rstart) is that, especially for more evolved sources like Class 1 YSOs, at the very center of these objects the geometry is not centro-symmetric but disk-like. Thus, our gradient density law (and temperature law) fails in the inner region and would overestimate the number densities. The chosen starting distance is source and molecule (X) dependent and can, in addition to the hydrogen density, mainly be chosen by suitable temperature Tstart conditions at the distance rstart from the center. Obviously, there is no clear cut-off condition for the integration limits, and numbers have been chosen based on reasonable estimates, as outlined below. In addition, the calculations over large volumes proved to be very time consuming, and thus we worked with two different data sets. Table 2 lists the used integration limits, with set A resulting in a wide shell-like region around the star that also includes the very inner region (here the inner region reaches 100 K and the outer 10 K); set B is a much smaller subregion of A in which the targeted molecules are produced most abundantly (with temperatures between 35 and 15 K). The model values of set B can be achieved in much less time than those of set A, but they are still very close to those of set A. For example, as can be seen from the absolute particle numbers N(X)total, 92 ± 3.6% of H2CO and 98 ± 0.5% of CH3OH is already contained in region B. Thus, in most cases it is sufficient to do the analysis for region B alone. The reason why region B already includes the most particles of our investigated species is as follows. When looking at the conditions for HOOH (rather than for H2CO or CH3OH) we see that at temperatures above 30 K the HOOH production is strongly reduced as O2 cannot freeze out on the grain surfaces, and thus no efficient surface-based hydrogenation can take place. Since at 35 K the HOOH production nearly ceases completely, we chose the corresponding inner radius (rstart) as the starting point for the integration (i.e., for case B). For H2CO and CH3OH the appropriate cut-off temperature is even lower, and accordingly a larger rstart(X) value than rstart(HOOH) could in principle be used. However, for the sake of comparability, we use the smaller value rstart(HOOH) for all species for a given source in set B. In that way the integration range always includes the regions that are essential for all discussed species. In the calculations the region around the central object has been divided into shells with each region having a certain hydrogen density and temperature. Our model does not allow the mixing of particles between these shells. The chemistry of the shells is determined individually, and by assuming a steady transition between these zones the overall content of molecules is calculated. In Fig. 2 the case of R CrA-IRS 5A is displayed. We use rstart ≈ 680 AU for all investigated species, with the local temperature being 35 K. The upper integration limit is rend ≈ 4200 AU corresponding to 15 K temperature where the mobility of particles on the grain surfaces is already strongly reduced.
Finally, the column density Nc(X) is calculated by putting the total number of species X within the given integration range (corresponding to a certain volume) in proportion to the cross section of the calculated sphere. We calculated two types of column densities, which are indicated by superscripts 1 and 25 : 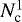 (X) is calculated using all molecules within the radii rstart and rend (i.e., N(X)total divided by
(X) is calculated using all molecules within the radii rstart and rend (i.e., N(X)total divided by  ) and is the overall average column density;
) and is the overall average column density; 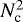 (X) is the column density along the line of sight of the telescope with a main beam lobe of θmb = 25′′ (i.e., at typical main beam diameters of APEX 12 m at 242 GHz, and IRAM 30 m at 97 GHz; see Fig. 3). In Table 3 the results of the calculation are listed assuming that the age of the source is accurately determined. No uncertainties are given. The differences in the given column densities between sets A and B result in the much larger cross section of set A compared to set B, whereas the absolute particle number in both cases is nearly identical. A more useful number for observations with radio telescopes is the column density
(X) is the column density along the line of sight of the telescope with a main beam lobe of θmb = 25′′ (i.e., at typical main beam diameters of APEX 12 m at 242 GHz, and IRAM 30 m at 97 GHz; see Fig. 3). In Table 3 the results of the calculation are listed assuming that the age of the source is accurately determined. No uncertainties are given. The differences in the given column densities between sets A and B result in the much larger cross section of set A compared to set B, whereas the absolute particle number in both cases is nearly identical. A more useful number for observations with radio telescopes is the column density  (X), which corresponds to the main beam lobe of the telescope (θmb) and is calculated by the integration of the number density within the cylindrical volume defined by θmb (
(X), which corresponds to the main beam lobe of the telescope (θmb) and is calculated by the integration of the number density within the cylindrical volume defined by θmb ( diameter d) that stretches along the line of sight as shown in Fig. 3. As θmb is a function of the wavelength we only give a representative value for θmb = 25′′ in Table 3. It can be seen that the differences between
diameter d) that stretches along the line of sight as shown in Fig. 3. As θmb is a function of the wavelength we only give a representative value for θmb = 25′′ in Table 3. It can be seen that the differences between  (X) of the set A and B are negligible and that
(X) of the set A and B are negligible and that 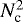 (X) is close to the value
(X) is close to the value 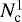 (X) for set B, as is expected.
(X) for set B, as is expected.
Parameters used in the shell model and resulting mean temperature and density of hydrogen.
 |
Fig. 2 Shell model of R CrA-IRS 5A. Top: temperature (solid red) and hydrogen density (dashed green) are given as a function of the distance to the central star. Bottom: number density n of the molecules H2CO, CH3OH, H2O and HOOH is shown (light green, dark green, blue and purple, respectively). The region at low radii (gray area at left) has been excluded from the abundance calculations of the species. |
Shell model results for H2CO and CH3OH.
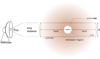 |
Fig. 3 Cylindrical region used to calculate the column density |
2.3 First tests
Our model reproduces the values by Du et al. (2012) for the known source ρ Oph A with constant ρ and T nearly exactly, and is thus consistent with the previous study of this source.
Comparison with “flat” model
In a second step, we investigated what effect the gradients of the H2 density and temperature (i.e., our geometrical assumptions) have on the molecule abundances. To do this, we compared the results of our “gradient” model given in Table 3 with the abundance values that were calculated using a constant density and temperature over the assumed source size. In the flat model we used the hydrogen mean temperature, number density, and absolute particle numbers given in Table 2. This means that in both calculations the chemical network is the same, only the physical parameters ρ and T are different. Thus, instead of having a hydrogen density gradient in our chemical calculations a constant density 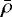 was used for all radii and a constant average temperature
was used for all radii and a constant average temperature 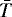 . Naturally, this resulted in a different outcome of the investigated molecular species (see Table 4). In all cases, except L1544 where the gradient model is not used anyway, the molecule abundances of H2CO and CH3OH in a gradient model were lower by 14–100% depending on the examined molecule and source compared to the flat model. In the case of HOOH and H2O (not shown in the table) we saw differences of up to 800%, i.e., the hydrogen peroxide and water abundance can be strongly overestimated in the flat model compared to a gradient model. This means that using the gradient model generally results in more conservativeabundances, and consequently reduces the amount of objects that seem suitable for observations when compared with the standard ρ and T constant model. Nevertheless, it seems worthwhile mentioning that even in the worst case this geometric effect is not large (not even an order of magnitude) and cannot account for large discrepancies between modeled and observed abundances.
. Naturally, this resulted in a different outcome of the investigated molecular species (see Table 4). In all cases, except L1544 where the gradient model is not used anyway, the molecule abundances of H2CO and CH3OH in a gradient model were lower by 14–100% depending on the examined molecule and source compared to the flat model. In the case of HOOH and H2O (not shown in the table) we saw differences of up to 800%, i.e., the hydrogen peroxide and water abundance can be strongly overestimated in the flat model compared to a gradient model. This means that using the gradient model generally results in more conservativeabundances, and consequently reduces the amount of objects that seem suitable for observations when compared with the standard ρ and T constant model. Nevertheless, it seems worthwhile mentioning that even in the worst case this geometric effect is not large (not even an order of magnitude) and cannot account for large discrepancies between modeled and observed abundances.
Results for H2CO and CH3OH from the flat model based on constant densities and constant temperatures.
The age uncertainty problem
Our model is sensitive to the age of the investigated object. In each of the sublayers (shells) the chemistry evolves separately in time according to the age of the object. The geometry does not change during this time evolution, and is only given by the geometric parameters fixed in Table 1. This scenario greatly simplifies the problem and most likely does not correspond to reality; however, due to the strongly increased complexity a simultaneous co-evolutionof physical and chemical parameters was not realized in our model. Unfortunately, the age of the sources is very often not known to high precision, which results in a large uncertainty of the calculated values. To estimate the resulting uncertainties we varied the ages of the sources as given in Table 1 by ±30% (see Table 5). In our model, the changes in the absolute particle numbers N(X)total and column densities 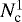 (X) and
(X) and 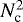 (X) are different when assuming 30% less or 30% more time for the object, an asymmetry that also exists for a flat model and which reflects the complicated chemical evolution with time (see Fig. 1 in Du et al. 2012). The resulting uncertainties are large, i.e., on the order of the mean value itself.
(X) are different when assuming 30% less or 30% more time for the object, an asymmetry that also exists for a flat model and which reflects the complicated chemical evolution with time (see Fig. 1 in Du et al. 2012). The resulting uncertainties are large, i.e., on the order of the mean value itself.
Results of robustness test for object age using an age variation ±30% to estimate column density uncertainties for H2CO and CH3OH.
Recommended values
For convenience and to ease comparison, the recommended model values for Nc and T are summarized in Table 8 along with the results of our observations which are discussed in Sect. 5. As can be seen, the recommended values are close to those of set B and C in Table 3. The uncertainty values are estimated from variations in the source age and boundary conditions (i.e., using the more conservative values of set B, and temperature changes of ± 1 K (i.e., ~10% of absolute value).
3 Astronomical sources
Based on anextensive list of pre- and protostellar objects (e.g., Kristensen et al. 2012; Mottram et al. 2014), we selected those sources that are the most promising candidates to test our new physical-chemical model and that are within reach of either the APEX 12 m or the IRAM 30 m telescope, namely R CrA-IRS 5A, NGC 1333-IRAS 2A, L1551-IRS 5, and L1544. The selected sources have in common that water has been detected towards these objects and that the predicted amount of HOOH in these sources is enough to be detected.Observational details of all four investigated sources are given in Fuchs et al. (2020). Here we briefly summarize the H2CO and CH3OH observationsof these sources that have been published prior to this work.
L1544 (pre-stellar core)
This object is a starless low-mass star forming region in the constellation Taurus (Crapsi et al. 2005, 2007). There have been previous investigations of formaldehyde (H2CO) by Tafalla et al. (1998) and Young et al. (2004) and methanol (CH3OH; Jiménez-Serra et al. 2016; Punanova et al. 2018). Both molecules have been detected in this source. L1544 can be modeled with a simple flat temperature and density distribution according to Caselli et al. (2002).
NGC 1333-IRS 2A (Class 0)
NGC 1333-IRS 2A is a typical Class 0 object (Brinch et al. 2009) located in the constellation Perseus. It is a binary system with an associated molecular jet and bow shock (Sandell et al. 1994). Observations of H2CO and CH3OH have been performed by Maret et al. (2004, 2005), Jørgensen et al. (2005), and Bottinelli et al. (2007). Due to the complex structure we decided to investigate three separate spatial regions of this source: IRS 2A-1 (center position), IRS 2A-2 (off-center), and IRS 2A-1 (in center line to north–south outflow).
R CrA-IRS 5A (Class 1)
The source IRS 5 (Taylor & Storey 1984) is located in Corona Australis close to the star R CrA. Formaldehyde and methanol have been detected in this source by Lindberg et al. (2015).
L1551-IRS 5 (Class 1)
The close-by young stellar object L1551 is a Class 1 source with a core binary system in the Taurus molecular cloud complex (Osorio et al. 2003; Lee et al. 2014; Ainsworth et al. 2016). This object is associated with molecular outflows and shock regions (Snell et al. 1980). H2CO (Sandqvist & Bernes 1980; Duncan et al. 1987) and CH3OH (White et al. 2006) have been detected in this source.
4 Observations and data reduction
The observations were performed using the APEX 12 m and IRAM 30 m telescopes (see Fuchs et al. 2020 for observational and data analysis details). In brief, in September 2015 we used the APEX 12 m telescope at three selected wavelengths between 0.9 mm and 1.3 mm for observations on R CrA-IRS 5A and NGC 1333-IRAS 2A6. The observations using the IRAM 30 m telescope at the Pico del Veleta in Spain towards L1551-IRS 5 and L1544 were done in August 20167 at four selected wavelengths between 1.3 and 3.3 mm. L1551 has been investigated in position switching mode as well as in frequency switching mode, whereas L1544 has been observed in frequency switching mode only. The basic data reduction and processing was done using the Continuum and Line Analysis Single-dish Software (CLASS) from the GILDAS8 software package. The observations were analyzed using two methods. In the first method we used the measured integrated line intensities to produce a population diagram (alias Boltzmann plot or rotational diagram) of each detected molecule to extract the respective total column density NC and rotational temperatureTrot. The second method utilizes the eXtended CASA Line Analysis Software Suite (XCLASS)9 by Möller et al. (2017) and in particular the myXCLASS program to model our data. Similar to the above-mentioned method myXCLASS assumes local thermodynamic equilibrium (LTE), and thus the two methods give quantities that can be directly compared with each other.
Observational results at H2CO frequency positions.
5 Observational results and analysis
This work focuses on the analysis of molecular emission from species relevant to test our shell model (see Sect. 2), namely H2CO and CH3OH10, and the observational results are listed in Tables 6 and 7, respectively. Other molecular lines that we detected towards these sources within the covered band passes are not discussed further; for example, in R CrA-IRS 5A we identified lines from 13 CO, SO, NO, c-C3H2, CN isotopologues, DCN, and HCCNC.
Observational results at CH3OH frequency positions.
5.1 H2CO observations
Formaldehyde is a very common molecule in YSOs and has been observed in all four sources (see Table 6). A list of astronomically relevant formaldehyde transitions including some spectroscopic parameters is given in Table A.1. All rotational diagrams used in the following analysis of H2CO (and also of CH3OH) are summarized in Fig. B.4.
R CrA-IRS 5A
The observed spectra are shown in Fig. 4. Each line can be fitted well using the Gaussian line profile method. The analysis of these lines allows us to determine the temperature and column density to be around T = 27–28 K and NC = 4–5 × 1013 cm−2. Here, the rotational diagram method and myXCLASS results agree well. Previously, the source was investigated by Lindberg et al. (2015) with 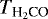 = 29.8 ± 2.4 K and NC= 3.7 × 1013 cm−1, which is in fair agreement with our results.
= 29.8 ± 2.4 K and NC= 3.7 × 1013 cm−1, which is in fair agreement with our results.
NGC 1333-IRAS 2A
This source reveals a rather complicated structure that becomes clear from its H2CO spectra11. Formaldehyde has been observed at all three spatial positions (see Fig. B.1 (A) positions 1–3). For all three positions the 218.2 GHz H2CO (30,3 − 20,2) line can be well reproduced using three Gaussian lines fitted simultaneously. We did not analyze the line profile further, in the sense of using non-LTE, velocity gradient, or other models that take into account the internal structure of this kind of sources. Only in position 2 could the other two H2CO lines (at 218.48 and 218.76 GHz) be observed using two Gaussian lines per observed feature. In our analysis (see Table 6) we only made use of the vlsr = 7.34 km s−1 component. For the central position this results in Trot ≈130 ± 100 K versus TmyXCLASS ≈ 70 K12 using the rotational diagram and myXCLASS, respectively, and NC, rot = 2.6 × 1013 cm−2 and NC, myXCLASS = 1.6 × 1013 cm−2. Previous studies by Maret et al. (2004) came to similar results concerning the column denisty (i.e., Nthin = 3 × 1013 cm−2) using a rotational diagram. However, their analysis used Trot = 24 K, and with corrections for optical opacity they got NC = 1 × 1014 cm−2. Furthermore, they also analyzed the H2CO lines using their large velocity gradient (LVG) code13 (i.e., under non-LTE conditions) which resulted in Tgas = 70 K and NC = 5 × 1013 cm−2, which is close to our value.
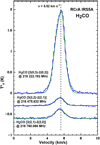 |
Fig. 4 H2CO emission lines towards R CrA-IRS 5A. |
Comparison between observational results and model predictions.
L1551-IRS 5
Also for this source the line profile of H2CO reveals a more complex structure of the source (see Fig. B.2 (A)). From the partial similarity of the line profiles of H2CO and CH3OH to those discussed for CO in L1551 by Snell et al. (1980) it seems like we also probed part of a molecular outflow in the southwest region of L1551-IRS 5 and associated shock regions. Thus, each of the lines at 145.6 and 150.5 GHz was fitted using two Gaussian lines. Five other transitions of H2CO that also liein the observed frequency region could not be detected. Our analysis resulted in T = 19 K and NC = 2 × 1012 cm−2 for the rotational diagram method, and T=17 K and NC = 2 × 1012 cm−2 using myXCLASS. Early H2CO observations by Sandqvist & Bernes (1980) using 6 cm, 2 cm, and 2 mm H2CO emissions from the L1551 region resulted in decreasing temperatures from 23 (center region) to 10 K (cloud periphery) and NC, average = 5 × 1013 cm−2. Later McCauley et al. (2011) re-analyzed H2CO towards IRS5 using the National Radio Astronomy Observatory (NRAO) Green Bank Telescope at 28.9 and 48.2 GHz. They used LVG analysis and assumed a temperature of TK ≈ 100 K resulting in NC ≈ 3−4 × 1013 cm−2. Due to the use of different telescopes, frequencies, and slightly different source center positions a comparison between our results and these results is not straightforward.
L1544
The spectra of this source have been measured in frequency switching mode only (see Fig. B.3 (A)). Compared to the other sources the line widths are narrow (~ 0.6 km s−1) and our analysis resulted in a temperature of T = 12–13 K, which is equal to or slightly higher than previous data with T ≈ 10−12.5 K (e.g., Tafalla et al. 1998; Caselli et al. 2002). In Young et al. (2004)14 the temperature is assumed to increase from 7 (core) to 13 K (periphery). Our inferred column density of NC = 1−2 × 1012 cm−2 is very low. Young et al. (2004)15 indicated a strong depletion effect at the inner core of the source, and previous models of L1544 by Aikawa et al. (2003)16 also showed a strong depletion of gas-phase H2CO on 0–4000 AU scales.
5.2 CH3OH observations
In all our observed sources the existence of methanol could be confirmed as summarized in Table 7. The results are listed in Table 8. Relevant spectroscopic information of CH3OH transitions can be found in Table A.1.
R CrA-IRS 5A
The CH3OH 42,2 –31,2 transition at218.4 GHz could be clearly detected (see Fig. 5) and fitted using a Gaussian line shape, whereas the non-detection of the 81,7−80,8 transition at 318.3 GHz was used to infer the temperature and column density to be T ≈16 K (rotational diagram) with NC = 5−7 × 1013 cm−2 17. Lindberg et al. (2015) measured CH3OH in this source having T = 18 ± 3 K and NC = 3.7 × 1013 cm−2, which is close to our observed values.
NGC 1333-IRAS 2A
Three transitions of methanol could be detected towards position 1 (central position), see Fig. B.1 (B). At the other positions only faint signals at the 42,2−31,2 transition were detected and none at the other frequencies, thus only the position 1 data could be used to deduce reliable T and NC values. Unlike the H2CO signal, it is not clear whether the methanol signal of this source originates from a simple or more complex environment. The spectra can be fitted using a simple Gaussian profile. Using our LTE rotational diagram approach, we estimate T to be around 70 ± 45 K with NC ≈ (9 ± 5) × 1013 cm−2. When using myXCLASS and assuming our model value temperature of 18 K18 we get NC ≈ 4 × 1013 cm−2. Maret et al. (2005) found CH3OH at 101 ± 16 K in this source with NC = (3.4 ± 0.6) × 1014 cm−2 19.
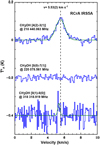 |
Fig. 5 CH3OH transitions towards R CrA-IRS 5A. |
L1551-IRS 5
In this source two transitions of CH3OH at 145 GHz could be observed (see Fig. B.2 (B)). Similar to the H2CO lines discussed earlier, the CH3OH line profile reveals internal source dynamics. Five transitions remained undetected. For the analysis only the 7 km s−1 component was used. The rotational diagram analysis results in T ≈ 4 K and NC = 1 × 1013 cm−2 20. The myXCLASS method results in T ≈ 7 K and NC = 6 × 1012 cm−2. Previous observations by Buckle & Fuller (2000) also resulted in very low temperatures of T ≈ 3.72(76) K, but with a higher column density of NC = 7.69(78) × 1013 cm−2. White et al. (2006) modeled the L1551-IRS 5 as a circumbinary torus assuming methanol temperatures below 20 K and expected NC between 1 and 2 × 1013 cm−2 for radii larger than 4000 AU starting from the IRS 5 center.
L1544
In this calm source we detected three narrow (FWHM of 0.4–0.5 km s−1) methanol lines around146.1 GHz in the frequency switching mode (see Fig. B.3 (B)). No lines could be seen at the two other CH3OH frequency positions (i.e., at 143.9 and 146.4 GHz). The rotational diagram analysis and the myXCLASS analysis result in T ≈7 K and NC≈ 3 × 1013 cm−2. Bizzocchi et al. (2014) observed methanol at Tex = 6 ± 3 K with NC = (1.9 ± 1.9) × 1013 cm−2 using an LTE approach and also made a non-LTE analysis resulting in NC = (2.7 ± 0.6) × 1013 cm−2. Vastel et al. (2014) reported values of Tk = 10 K with Nt = 3 × 1013 cm−2 using non-LTE LVG analysis. Thus, the previous methanol values derived by other groups and our values are in good agreement.
In summary, the H2CO and CH3OH data resulting from the new observations presented here and those available from the literature are found to be in good agreement. With the new observations, a set of well-defined data was obtained, which was used for our comparative studies. However, for sources such as NGC 1333-IRAS 2A and L1551-IRS 5, where earlier data did not yield consistent temperaturevalues for the molecules investigated here, no significant improvement could be achieved, as originally hoped for.
6 Discussion
The results of the observations are summarized and compared to the predicted values by our physical chemical shell model in Table 8.
R CrA-IRS 5A (Class 1)
This source proved to be well suited for our applied shell model. The spectra are not dominated by internal source dynamics (e.g., outflows) and allow a straightforward analysis. The observed and predicted column densities of H2CO and CH3OH agree within a few 1013 cm−2. The measured temperatures of CH3OH agree within 2–3 K with the predicted ≈18 K. However, the H2CO temperature shows a deviation of Tobs(27−28 K) − Tmodel(18 K) ≈ 10 K of yet unknown reason. In a simple gradient model, H2CO is much warmer than our model predicts, which corresponds to a formaldehyde distribution much closer to the protostar than expected (around 1000 AU). However, we cannot simply assume a higher H2CO temperature in our model without further consequences for other species such as CH3OH. An as-yet-unknown H2CO specific heating mechanism may be at play, but this is beyond our model assumptions, and thus remains incomprehensible. As can be seen when comparing the modeled values in Tables 4 and 8 for H2CO, the gradient model column density value is better by about a factor two with respect to the flat model value, whereas the temperatures are nearly identical for both models and show the same deviation with respect to the observed temperature. However, for CH3OH the flat model tends to be closer to the observed column density.
NGC 1333-IRAS 2A (Class 0)
Because of the inner structure and dynamics, the deviation between the modeled shell structure and the observed geometry is stronger than in any other of the sources investigated here. To compare the observations with the model, certain assumptions (like the restriction to the vlsr = 7.34 km s−1 component of the multi-peak molecular transition lines) had to be made. The observed column densities of H2CO and CH3OH (≈1013 cm−2) are not in agreement with the predicted value (≈1014 cm−2). Even so, it should be noted that the gradient model column density value is closer to observations than the flat model value. On first sight, our observed high temperatures for formaldehyde (> 69 K) or methanol (≈69 K), which are partly in agreement with previous works, show that there may be a discrepancy between our assumed temperature profile based on SED observations, which basically reflects the dust conditions in this source and the gas-phase species investigated here. However, the temperature assignment remains difficult, as can be seen from the work of Maret et al. (2004) where temperatures vary between 24 and 70 K for H2CO depending on the analysis method (e.g., using non-LTE analysis methods). In addition, our model does not indicate why the dust and gas-phase temperature should be decoupled. For this source the predictions of the gradient and flat model do not deviate much for H2CO and are equally off with respect to the observed temperature and column density. However, for the CH3OH column density the gradient model is slightly closer to the observations.
L1551-IRS 5 (Class 1)
In this source we have a mixed situation when comparing the observations and the model results. In our analysis we restricted ourselves to the narrow vlsr = 7.0 km s−1 component of the lines21. H2CO shows a depletion with observed column densities as low as a few 1012 cm−2 compared to the predicted NT = 5 × 1013 cm−2. The derived rotational temperatures of formaldehyde (≈17–19 K) are close to the predicted 19 K of the model. Similar to NGC 1333-IRAS 2A the spectra reveal dynamical and most likely non-LTE processes within this source. The column density of methanol is predicted by the model with an order of magnitude difference, which is not very accurate, as is the temperature (ΔTobs-model ≈ 11–14 K). The observed very low temperatures of CH3OH of 3.6–6.7 K contrast with the assumed mean temperature of 18 K from the model. For both, H2CO and CH3OH, the column densities of the gradient model are closer to observations than the flat model values.
L1544 (pre-stellar core)
Previous work by Tafalla et al. (1998) suggests that this source contains molecules at low temperatures. Constrained by their data we used our model to predict the H2CO and CH3OH abundances. The H2CO observations confirmed the low temperature, but the model predicted an order of magnitude higher column density for H2CO in the gas-phase than observed. At the same time the observed column density of CH3OH fits nicely tothe model values, although the temperature is off by a factor of two and close to the assumed inner core temperature by Young et al. (2004) and the 6 K value reported by Bizzocchi et al. (2014). It is not clear why the observations show a depletion of H2CO (at least for the observed transitions) and not for CH3OH. When trying to model different physical parameters, for example density and temperature gradient within reasonable values, it is not possible to explain the discrepancies between the observed and the model abundance. Even when assuming other source ages than 5 × 104 yr within a range of 1 × 104 yr to 1 × 105 yr the observed abundances of H2CO and CH3OH cannot be modeled consistently.
7 Conclusions
A new physical model has been developed and tested that assumes a simple spherical geometry with a density and temperature gradient and combines this with a chemical model (Du et al. 2012) including gas-grain interactions. As test species we used the ice-borne molecules H2CO and CH3OH, but also provided model data for HOOH and H2O, which are discussed elsewhere (Fuchs et al. 2020). Four astronomical sources were chosen in which formaldehyde, methanol, and also water have already been detected.
Our model is most reliable when the source is not dominated by jets or shock regions (which we intentionally did not include in the model) and when the source is not too young. It works well for the quiescent Class 1 object R CrA-IRS 5A. For the young pre-stellar core L1544 no jets and shocks are at play, and our predictions are nearly independent of its geometry. However, the H2CO depletion and the discrepancy between the modeled and observed temperatures of CH3OH show that our chemical model is imprecise when applied to this source (opposed to the L1544 model from Aikawa et al. 2003 which is specifically designed for collapsing pre-stellar cores). For sources (Class 0 and Class 1) with contributions of outflows or shock regions (e.g., NGC 1333-IRAS 2A-1 and L1551-IRS 5) the model is not well suited.
From a theoretical point of view, the applied shell model is an improvement compared to the previously used flat model when modeling objects with spherical gradient distributions of density and temperature, like YSOs of Class 0-1. Our model yields smaller column densities and abundances for H2CO and CH3OH in comparison to a flat model with a constant H2 density and temperature. The geometry effect does not usually change the expected column densities dramatically, i.e., by orders of magnitude, but rather by factors between 2 and 8. This still means that a better signal-to-noise ratio (S/N) is needed, i.e., longer integration times have to be considered. Our new gradient model results are generally closer to the observational results when compared to those predicted by the flat model.
Acknowledgements
We thank the APEX 12 m and IRAM 30 m staff for their excellent support. We thank Peter Schilke, Thomas Möller and Álvaro Sánchez-Monge for their kind introduction to myXCLASS.
Appendix A Additional tables
Selection of relevant transitions of H2CO, and CH3OH for cold environments in the (80–320 GHz) submm region.
Appendix B Additional figures
 |
Fig. B.1 Molecuar transitions towards NGC 1333-IRAS 2A position 1–3. (A) H2CO and (B) CH3OH. |
 |
Fig. B.2 Observations towards L1551-IRS 5 using position switching mode. (A) and (B) show H2CO and CH3OH transitions taken in position switching mode, respectively. |
 |
Fig. B.3 Molecular transitions towards L1544 (frequency switching mode): (A) H2CO and (B) CH3OH. |
 |
Fig. B.4 Rotational diagrams of H2CO (left) and CH3OH (right) emission from (A) R CrA-IRS 5A, (B) NGC 1333-IRAS 2A, (C) L1551-IRS 5, and (D) L1544. |
References
- Aikawa, Y., Ohashi, N., & Herbst, E. 2003, ApJ, 593, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Ainsworth, R. E., Coughlan, C. P., Green, D. A., et al. 2016, MNRAS, 462, 2904 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, M., & Robinson, G. W. 1977, ApJ, 212, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Araya, E. D., Dieter-Conklin, N., Goss, W. M., & Andreev, A. 2014, ApJ, 784, 129 [CrossRef] [Google Scholar]
- Bergman, P., Parise, B., Liseau, R., et al. 2011, A&A, 531, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bizzocchi, L., Caselli, P., Spezzano, S., & Leonardo, E. 2014, A&A, 569, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boogert, A. C. A., Pontoppidan, K. M., Knez, C., et al. 2008, ApJ, 678, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Boogert, A. C. A., Gerakines, P. A., & Whittet, D. C. B. 2015, ARA&A, 53, 541 [Google Scholar]
- Bottinelli, S., Ceccarelli, C., Williams, J. P., & Lefloch, B. 2007, A&A, 463, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bottinelli, S., Boogert, A. C. A., Bouwman, J., et al. 2010, ApJ, 718, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Brinch, C., Jorgensen, J. K., & Hogerheijde, M.R. 2009, A&A, 502, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruderer, S., Doty, S. D., & Benz, A. O. 2009a, ApJS, 183, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Bruderer, S., Benz, A. O., Doty, S. D., et al. 2009b, ApJ, 700, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Buckle, J. V., & Fuller, G. A. 2000, ESA SP 445, 339 [Google Scholar]
- Caselli, P., Hasegawa, T. I., & Herbst, E. 1993, ApJ, 408, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002, ApJ 565, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Keto, E., Bergin, E. A., et al. 2012, ApJ, 759, L37 [Google Scholar]
- Caux, E., Kahane, C., Castets, A., et al. 2011, A&A, 532, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazaux, S., Minissale, M., Dulieu, F., & Hocuk, S. 2016, A&A, 585, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., Baluteau, J.-P., Walmsley, M., et al. 2002, A&A, 383, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chuang, K.-J., Fedoseev, G., Ioppolo, S., et al. 2016, MNRAS, 455, 1702 [Google Scholar]
- Chuang, K.-J., Fedoseev, G., Qasim, D., et al. 2018, ApJ, 853, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Close, L.M., Roddier, F., Northcott, M. J., et al. 1997, ApJ, 478, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, M. C., & Tafalla, M. 2007, A&A, 470, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuppen, H. M., Ioppolo, S., & Linnartz, H. 2010, Phys. Chem. Chem. Phys., 12, 12077 [NASA ADS] [CrossRef] [Google Scholar]
- Doty, S.D., van Dishoeck, E. F., van derTak, F. F. S., & Boonman, A. M. S. 2002, A&A, 389, 446 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Du, F., & Parise, B. 2011, A&A, 530, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Du, F., Parise, B., & Bergman, P. 2012, A&A, 538, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, R. A., Forster, J. R., Gardner, F. F., & Whiteoak, J. B. 1987, MNRAS, 224, 721 [CrossRef] [Google Scholar]
- Fedoseev, G., Chuang, K.-J., Ioppolo, S., et al. 2017, ApJ, 842, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, G. W., Cuppen, H. M., Ioppolo, S., et al. 2009, A&A, 505, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuchs, G. W., Witsch, D., Herberth, D., et al. 2020, A&A, 636, A114 [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T. 2008, A&A, 491, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., Widicus Weaver, S. L., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Hiraoka, K., Sato, T., Sato, S., et al. 2002, ApJ, 577, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Hogerheijde, M. R., & Sandell, G. 2000, ApJ, 534, 880-893 [NASA ADS] [CrossRef] [Google Scholar]
- Ioppolo, S., van Boheemen, Y., Cuppen, H. M., et al. 2011, MNRAS, 413, 2281 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezic, Z., & Elitzur, M. 1997, MNRAS, 287, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Vasyunin, A. I., Caselli, P., et al. 2016, ApJ, 830, L6 [Google Scholar]
- Jørgensen, J. K., Hogerheijde, M. R., van Dishoeck, E. F., et al. 2004, A&A, 413, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jørgensen, J.K., Bourke, T.L., Myers, P.C., et al. 2005, ApJ, 632, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Kristensen, L. E., van Dishoeck, E. F., Bergin, E. A., et al. 2012, A&A, 542, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, J.-E., Lee, J., Lee, S., et al. 2014, ApJS, 214, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-E., Lee, S., Baek, G., et al. 2019, Nat. Astron., 3, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, C. M., Herbst, E., & Huebner, W. F. 1984, ApJS, 56, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lindberg, J. E., & Jørgensen, J. K. 2012, A&A, 548, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindberg, J. E., Jørgensen, J. K., Watanabe, Y., et al. 2015, A&A, 584, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucas, P. W., & Roche, P. F. 1997, MNRAS, 286, 895 [NASA ADS] [Google Scholar]
- Maret, S., Ceccarelli, C., Caux, E., et al. 2004, A&A, 416, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maret, S., Ceccarelli, C., Tielens, A. G. G. M., et al. 2005, A&A, 442, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCauley, P. I., Mangum, J. G., & Wootten, A. 2011, ApJ, 742, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Minissale, M., Dulieu, F., Cazaux, S., & Hocuk, S. 2016, A&A, 585, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millar, T. J., Macdonald, G. H., & Gibb, A. G. 1997, A&A, 325, 1163 [Google Scholar]
- Möller, T., Endres, C., & Schilke, P. 2017, A&A, 598, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mottram, J. C., Kristensen, L. E., van Dishoeck, E. F., et al. 2014, A&A, 572, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., & Lewen, F. 2017, J. Mol. Spectr., 331, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Osorio, M., D’Alessio, P., Muzerolle, J., et al. 2003, ApJ, 586, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Padgett, D. L., Brandner, W., Stapelfeldt, K. R., et al. 1999, ApJ, 117, 1490 [Google Scholar]
- Palmer, P., Zuckerman, B., Buhl, D., & Snyder, L. E., et al. 1969, ApJ, 156, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., Delitsky, M. L., et al. 1998, J. Quant. Spectr. Rad. Transf, 60, 883 [Google Scholar]
- Punanova, A., Caselli, P., Feng, S., et al. 2018, ApJ, 855, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., & Wood, K. 2007, ApJS, 169, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Sandell, G., Knee, L. B. G., Aspin, et al. 1994, A&A, 285, L1 [Google Scholar]
- Sandqvist, Aa., & Bernes, C. 1980, A&A, 89, 187 [Google Scholar]
- Schmalzl, M., Visser, R., Walsh, C., et al. 2014, A&A, 572, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, R. G., Charnley, S. B., Pendleton, Y. J., et al. 2011, ApJ, 743, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Snell, R. L., Loren, R. B., & Plambeck, R. L. 1980, ApJ, 239, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., Jørgensen, J. K., van Dishoeck, E. F., & Blake, G. A. 2002, A&A, 390, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stantcheva, T., & Herbst, E. 2004, A&A, 423, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stäuber, P., Doty, S. D., van Dishoeck, E. F., & Benz, A. O. 2005, A&A, 440, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Mardones, D., Myers, P. C., et al. 1998, ApJ, 504, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, K. N. R., & Storey, J. W. V. 1984, MNRAS, 209, 5 [Google Scholar]
- Tielens, A. G. G. M., & Hagen, W. 1982, A&A, 114, 245 [Google Scholar]
- Vastel, C., Ceccarelli, C., Lefloch, B., & Bachiller, R. 2014, ApJ, 795, L2 [Google Scholar]
- Watanabe, N., & Kouchi, A. 2002, AJ, 571, L173 [Google Scholar]
- White, Glenn J., Fridlund, C. W. M., Bergman, P., et al. 2006, ApJ, 651, L41 [CrossRef] [Google Scholar]
- Whittet, D. C. B., Schutte, W. A., Tielens, A. G. G. M., et al. 1996, A&A, 315, L357 [Google Scholar]
- Woodall, J., Agúndez, M., Markwick-Kemper, A., & Millar, T. 2007, A&A, 466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, L.-H., & Lovas, F. J. 1997, J. Phys. Chem. Ref. Data, 26, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L.-H., Fisher, J., Lees, R. M., et al. 2008, J. Mol. Spectr., 251, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Young, K. E., Lee, J.-E., Evans II, N. J., et al. 2004, ApJ, 614, 252 [NASA ADS] [CrossRef] [Google Scholar]
The term, and the values, of rin and rout in Table 1 are taken from the references given in the table and are used to determine the constants q, p, a, and b. The term rstart, and also the later introduced term rend, is specific to our model and is not the same as rin and rout. The definition of rstart and rend is explained later in the text. In brief, rstart and rend set the integration limits of our model, i.e., they define the region that is considered.
See Stantcheva & Herbst (2004) Table 1 for initial fractional abundances.
Opposed to the column density, the total number of particles is an intrinsic source parameter independent of the line of sight. This number is useful when comparing different models, such as homogeneous and non-homogeneous density and temperature distribution models; see Sect. 2.3.
GILDAS is a software provided and maintained by the Institute de Radioastronomie Millimétrique (IRAM): http://www.iram.fr/IRAMFR/GILDAS
The spectroscopic data of these molecules are based on the following works: for H2CO see Müller & Lewen (2017) and references therein, for CH3OH see Xu et al. (2008) and references therein.
In position 2 (southeast) and position 3 (north) the H2CO line is also partly seen in absorption. Absorption features of H2CO at radio wavelengths were seen as early as 1969 (see Palmer et al. 1969) and are still in use as diagnostic tool (see Araya et al. 2014). In our case the absorption happens against the radio continuum at the mentioned source positions. As can be seen, the absorption can only be detected for the transition at 218.222 GHz which has a low-lying Elow = 10.5 K. For transitions with higher lying Elow, such as the 218.475 GHz and 218.760 GHz transitions with Elow = 57.6 K, no absorption can be observed.
For the fit three lines are used with two lines having the same Eup energy (218.475 and 218.760 GHz; see Table A.1). The rotational diagram uses the average position between these two lines to fit the temperature (which results in a large uncertainty on the temperature). Contrary to this, myXCLASS fits the temperature by using the more intensive of the two lines, and thus calculates the upper limit for T and NC.
See Ceccarelli et al. (2002) for their model implementation.
See Fig. 15 in Young et al. (2004) where they used an energetics code for a model of L1544.
Using myXClass it was not possible to uniquely determine the CH3OH temperature. Thus, in Table 8 we used the model temperature 18 K to determine NC (myXClass).
They also found that their measured temperature is very high, and discussed this in their work; see Maret et al. (2005) Sect. 4.1.
All Tables
Parameters used in the shell model and resulting mean temperature and density of hydrogen.
Results for H2CO and CH3OH from the flat model based on constant densities and constant temperatures.
Results of robustness test for object age using an age variation ±30% to estimate column density uncertainties for H2CO and CH3OH.
Selection of relevant transitions of H2CO, and CH3OH for cold environments in the (80–320 GHz) submm region.
All Figures
 |
Fig. 1 Sketch of the applied physical model geometry for protostellar objects. The integrated region (blue-edged hollow sphere) excluding the innermost and outermost parts is the region used for the calculations. The envelope of the object exceeds rend and has a diameter larger than 104 AU. The jet and disk have not been taken into account in our model. |
| In the text | |
 |
Fig. 2 Shell model of R CrA-IRS 5A. Top: temperature (solid red) and hydrogen density (dashed green) are given as a function of the distance to the central star. Bottom: number density n of the molecules H2CO, CH3OH, H2O and HOOH is shown (light green, dark green, blue and purple, respectively). The region at low radii (gray area at left) has been excluded from the abundance calculations of the species. |
| In the text | |
 |
Fig. 3 Cylindrical region used to calculate the column density |
| In the text | |
 |
Fig. 4 H2CO emission lines towards R CrA-IRS 5A. |
| In the text | |
 |
Fig. 5 CH3OH transitions towards R CrA-IRS 5A. |
| In the text | |
 |
Fig. B.1 Molecuar transitions towards NGC 1333-IRAS 2A position 1–3. (A) H2CO and (B) CH3OH. |
| In the text | |
 |
Fig. B.2 Observations towards L1551-IRS 5 using position switching mode. (A) and (B) show H2CO and CH3OH transitions taken in position switching mode, respectively. |
| In the text | |
 |
Fig. B.3 Molecular transitions towards L1544 (frequency switching mode): (A) H2CO and (B) CH3OH. |
| In the text | |
 |
Fig. B.4 Rotational diagrams of H2CO (left) and CH3OH (right) emission from (A) R CrA-IRS 5A, (B) NGC 1333-IRAS 2A, (C) L1551-IRS 5, and (D) L1544. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.