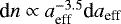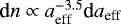| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202037943 | |
| Published online | 23 June 2020 | |
Self-scattering of non-spherical dust grains
The limitations of perfect compact spheres
1
Department of Physics and Astronomy, University College London,
Gower Street,
London
WC1E 6BT,
UK
e-mail: f.kirchschlager@ucl.ac.uk
2
Max Planck Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg,
Germany
e-mail: bertrang@mpia.de
Received:
12
March
2020
Accepted:
27
April
2020
Context. The understanding of (sub-)millimetre polarisation has made a leap forward since high-resolution imaging with the Atacama Large (sub-)Mm Array (ALMA) became available. Amongst other effects, self-scattering (i.e. the scattering of thermal dust emission on other grains) is thought to be the origin of millimetre polarisation. This opens the first window to a direct measurement of dust grain sizes in regions of optically thick continuum emission as it can be found in protoplanetary discs and star-forming regions. However, the newly derived values of grain sizes are usually around ~100 μm and thus one order of magnitude smaller than those obtained from more indirect measurements, as well as those expected from theory (~1 mm).
Aims. We see the origin of this contradiction in the applied dust model of current self-scattering simulations: a perfect compact sphere. The aim of this study is to test our hypothesis by investigating the impact of non-spherical grain shapes on the self-scattering signal.
Methods. We applied discrete dipole approximation simulations to investigate the influence of the grain shape on self-scattering polarisation in three scenarios: an unpolarised and polarised incoming wave under a fixed and a varying incident polarisation angle.
Results. We find significant deviations of the resulting self-scattering polarisation when comparing non-spherical to spherical grains. In particular, tremendous deviations are found for the polarisation signal of grains when observed outside the Rayleigh regime, that is for >100 μm sized grains observed at the 870 μm wavelength. Self-scattering by oblate grains produces higher polarisation degrees compared to spheres, which challenges the interpretation of the origin of observed millimetre polarisation. A (nearly) perfect alignment of the non-spherical grains is required to account for the observed millimetre polarisation in protoplanetary discs. Furthermore, we find conditions under which the emerging scattering polarisation of non-spherical grains is flipped in orientation by 90°.
Conclusions. These results show clearly that the perfect compact sphere is an oversimplified model, which has reached its limit. Our findings point towards a necessary re-evaluation of the dust grain sizes derived from (sub-)millimetre polarisation.
Key words: polarization / scattering / protoplanetary disks / circumstellar matter / stars: pre-main sequence / techniques: polarimetric
© ESO 2020
1 Introduction
In recent years, the field of polarisation at millimetre wavelengths has gone through remarkable developments. Polarisation became a powerful and versatile tool to probe not only magnetic fields (Lazarian & Hoang 2007; Bertrang et al. 2017; Bertrang & Wolf 2017) but also grain sizes (Kataoka et al. 2015), radiation fields (Lazarian & Hoang 2007; Tazaki et al. 2017), and grain porosity (Kirchschlager et al. 2019). Particularly, the ability to measure dust grain sizes pushed the protoplanetary disc community’s interest in self-scattering. The number of cutting-edge polarisation observations obtained with the Atacama Large (sub-)millimetre Array (ALMA) is continuously growing for both protoplanetary discs (e.g. Kataoka et al. 2017; Stephens et al. 2017; Dent et al. 2019; Harrison et al. 2019) and star-forming regions (e.g. Bacciotti et al. 2018; Sadavoy et al. 2019). Prior to the discovery of self-scattering, dust grain sizes were deduced only indirectly by relying on various assumptions on optical dust properties (“spectral index method”; e.g. Miyake & Nakagawa 1993; Carrasco-González et al. 2019. However, the grain sizes that are inferred from self-scattering are challenging the understanding of grain growth: the newly derived grain sizes (~100 μm) are one order of magnitude smaller than those derived from the spectral index (Beckwith et al. 1990) and those expected from theory (~1 mm). In this paper, we explore our hypothesis concerning the cause of this contradiction: the oversimplified dust model of a perfect compact sphere that is applied in current self-scattering models (e.g. Kataoka et al. 2017; Dent et al. 2019). The result of this study has an impact on the interpretation of basic dust properties and, as such, can be applied to various astrophysical environments such as protoplanetary discs, star-forming regions, or the interstellar medium.
In general, continuum radiation is intrinsically polarised as grains are elongated (e.g. Lazarian & Hoang 2007; Bertrang et al. 2017; Bertrang & Wolf 2017; Kirchschlager et al. 2019; Guillet et al. 2020). In the specific case of optically thick continuum emission, the intrinsically polarised dust emission is scattered at other dust grains (self-scattering). In this paper, we investigate the impact of the shape of perfectly aligned grains on the self-scattering signal, including the intrinsic polarisation of the wave before the scattering event.
In Sect. 2 we describe our non-spherical dust grain model and the method to calculate the optical properties of non-spherical dust grains. We present the results for self-scattering without intrinsic polarisation on oblate dust grains in Sect. 3 and for the self-scattering of intrinsically polarised radiation in Sect. 4. We discuss our findings in Sect. 5 and conclude with a summary in Sect. 6.
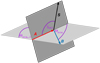 |
Fig. 1 Sketch of a general scattering event on an oblate dust grain, including the incidence direction A, the scattering direction B and the symmetry axis S of the oblate grain. The angles γaxi, Θsca, and Θsca,2 determine the scattering plane and the plane defined by A and S. |
2 Dust model and methods
In our study we considered oblate dust grains with short semi-axis b and long semi-axis c. We varied the axis ratio c∕b in the set {1.0,1.1,1.3,1.5,1.7,2.0}, where c∕b = 1.0 represents a spherical grain. We also varied the effective radius of the oblate grains, which is the radius of a volume-equivalent solid sphere and is given as 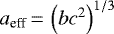 . The particles are compact so the porosity is
. The particles are compact so the porosity is  .
.
To calculate the optical properties of irregularly shaped particles we used the code DDSCAT1 (version 7.3;Draine & Flatau 1994, 2013), which is based on the theory of discrete dipole approximation (DDA; Purcell & Pennypacker 1973). The three-dimensional particle shape is replaced by a corresponding spatial distribution of N discrete dipoles on a cubic grid and the optical properties are then calculated for this dipole distribution. The DDSCAT is well tested and is applicable for most particle shapes and structures but is limited by an upper value for the ratio of grain size aeff to wavelength λ (see e.g. Draine & Goodman 1993; Draine & Flatau 1994; Kirchschlager & Wolf 2013). In our study, we used N = 145 850 dipoles, which corresponds to an upper limit of aeff∕λ ≲ 1.5.
In order to describe a scattering event on an elongated dust grain, three axes are important: the axis parallel to the direction of the incidence radiation, A, the axis parallel to the direction of the scattered radiation, B, and the symmetry axis of the grain, S (Fig. 1). The incidence direction A and the symmetry axis S span the angle γaxi. For γaxi = 90°, the symmetry axis S is perpendicular to the incidence direction A. The scattering direction is defined by the two scattering angles Θsca and Θsca,2, where the former is the angle between the incidence direction A and the scattering direction B, and Θsca,2 is the angle between the scattering plane (defined by A and B) and the plane defined by A and S.
The polarisation degree of the incident and scattered radiation are Pini and Psca, respectively, and the angle of polarisation of the incident radiation is γini. For γini = 0°, the incident polarisation orientation is parallel to the long semi-axis c of the oblategrain (perpendicular to S). The polarisation degree Psca of the scattered radiation is positive when the polarisation orientation is perpendicular to the scattering plane, and Psca is negative when it is coplanar to it. A transition from positive to negative polarisation is accompanied by a 90° flip of the polarisation orientation that is known as polarisation reversal (e.g. Daniel 1980; Kirchschlager & Wolf 2014; Brunngräber & Wolf 2019).
We calculated the optical properties for different grain sizes aeff, axis ratios c∕b, and scattering angles Θsca and Θsca,2. The dust material is astronomical silicate (Draine 2003a,b) and the wavelength amounts to 870 μm, which represents the ALMA waveband B7. The incidence angle is set to γaxi = 90° so that the incident radiation shines on the edge of the oblate grain and incoming photons “see” an ellipsoidally geometric cross section of the oblate grain with semi-axis b and c. We investigate the scattering along two orientations of the scattering plane, Θsca,2 = 90° (grain symmetry axis S perpendicular to the scattering plane, Fig. 2, left) and Θsca,2 = 0° (S coplanar to scattering plane, Fig. 2, right)2.
In Sects. 3 and 4 the results are presented for dust grains with effective radii aeff = 100 μm and aeff = 150 μm. We chose these grain sizes as they lie within the Rayleigh regime (100 μm), meaning the grain size is much smaller than the wavelength (2πaeff∕λ < 1), or is already in the Mie regime (150 μm) where the mean grain size approaches the wavelength.
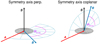 |
Fig. 2 Orientation of the two considered scattering planes (blue grid). Left: grain symmetry axis S is perpendicular to scattering plane (Θsca,2 = 90°). Right: symmetry axis S is coplanar to scattering plane (Θsca,2 = 0°). |
3 Scattering on non-spherical dust grains
We begin with a simplified setup in which an unpolarised incoming wave scatters at a non-spherical grain (for a polarised incoming wave, see Sect. 4). We present this scenario for a single-sized grain as well as a grain size distribution, and compare our results to the case of self-scattering on spherical grains.
3.1 Scattering elements of single-sized grains
The scattering matrix elements S11 and (−S12) of dust grains with effective radius aeff = 100 μm and aeff = 150 μm are shown in Fig. 3 as a function of the scattering angle Θsca and the axis ratio c∕b. For the case of scattering on the 100 μm grains (Fig. 3, left) perpendicular to the symmetry axis S (Θsca,2 = 90°), S11 and (−S12) increase with increasing axis ratio c∕b when the scattering angles are below ~120°. This indicates an enhanced forward scattering of oblate grains. For larger scattering angles, the impact of the axis ratio on the scattering matrix elements is small. For the case in which the symmetry axis S is coplanar to the scattering plane (Θsca,2 = 0°), (−S12) shows an opposite trend compared to the scattering perpendicular to S while S11 is mostly unaffected. The angular averaged value of S11 for Θsca,2 = 90° is slightly larger than for Θsca,2 = 0°, which implies a higher scattering efficiency (Csca) along the long axis compared to the short axis (cf. Cho & Lazarian 2007). Compared to the 100 μm grains, the values of S11 of the 150 μm grains (Fig. 3, right) increase by a factor of six and indicate a rising scattering behaviour at scattering angles larger than 90° (backward scattering enhancement). The values of (−S12) roughly increase by a factor of four and show a stronger dependence on the grain axis ratio for scattering angles larger than ~ 120°. The significant differences in the scattering behaviour of 150 μm grains compared to that of 100 μm grains is representative for grains >100 μm, illustrating that they are beyond the Rayleigh regime, that is, they are in the Mie regime at an observing wavelength of λ = 870 μm.
 |
Fig. 3 Scattering matrix elements S11 and (− S12) of oblate grains as a function of the scattering angle Θsca and differentaxis ratios c∕b, for thetwo scattering planes perpendicular and coplanar to the grain’s symmetry axis (Θsca,2 = 90° and 0°, respectively). The grain size is aeff = 100 μm (Rayleigh regime; left) and aeff = 150 μm (Mie regime; right). |
 |
Fig. 4 Degree of polarisation Psca by scattering on oblate dust grains as a function of the scattering angle Θsca and differentaxis ratio c∕b, for thetwo scattering planes perpendicular and coplanar to the grain’s symmetry axis (Θsca,2 = 90° and 0°, respectively). The polarisation Pini of the incident radiation is zero and the grain size aeff = 100 μm (left) and aeff = 150 μm (right). The grey-shaded region indicates negative scattering polarisations, which imply a reversal of the polarisation orientation. |
3.2 Linear polarisation of single-sized grains
The degree of linear polarisation by scattering,
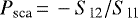 (1)
(1)
(e.g. Bohren & Huffman 1983), reveals quantitative differences between oblate and spherical 100 μm grains (Fig. 4, left). The scattered wave perpendicular to the symmetry axis S (Θsca,2 = 90°) possesses a polarisation that increases with increasing axis ratio c∕b, in particular for scattering angles below 100° but also for large angles (Θsca ≳ 150°). This implies that both forward and backward scattering have an enhanced polarisation fraction in the case of oblate dust grains. The peak polarisations amount to 100% for all axis ratios and occur at Θsca~110°. For the case in which the symmetry axis S is coplanar to the scattering plane (Θsca,2 = 0°), the scattering polarisation decreases with increasing axis ratio. Negative scattering polarisations at small (Θsca ≲ 60°−90°) and large scattering angles (Θsca ≳ 150°) occur in combination with a 90 degree flip of the polarisation orientation. The peak polarisation is also 100% for all axis ratios but shifts from Θsca ~ 110° for spherical grains to ~130° for oblate grains (c∕b = 2.0).
The scattering polarisations at Θsca = 0° and Θsca = 180° of both scattering planes are equal to each other for reasons of symmetry equal. The different polarisation signs in Fig. 4 (and also in Figs. 7 and 8) at these scattering angles result from the 90° rotation of the reference system.
For grain size distributions of spherical grains composed of a mixture of silicate, water ice, and organics, Kataoka et al. (2015) show that maximum polarisation strongly drops from 100 to ≪ 10% when the maximum grain size is increased from 100 to 300 μm (for a wavelength of 870 μm). The significant changes in scattering polarisation when increasing the grain size can also be seen for non-spherical silicates (Fig. 4, right, for aeff = 150 μm). These grains are already in the Mie regime. The peak polarisation as well as the corresponding scattering angle Θsca at which the maximum polarisation occurs depend on the grain axis ratio c∕b. For scattering perpendicular to the symmetry axis S (Θsca,2 = 90°), the peak polarisation only reaches values up to 55%, increases with axis ratio if c∕b ≤ 1.3, and decreases for larger axis ratios. The scattering angle of the peak polarisation is shifted from Θsca~90° for spherical grains to 0° for oblate grains (c∕b = 2.0). For the case that S is coplanar to the scattering plane (Θsca,2 = 0°), the scattering polarisation monotonically decreases with increasing axis ratio. As a consequence, the scattering polarisation of oblate grains with c∕b = 2.0 is negative for nearly all scattering angles except around the peak polarisation. The scattering angle of the peak polarisation shifts from Θsca ~ 90° for spherical grains to 110° for oblate grains (c∕b = 2.0).
In conclusion, spherical grains in the Rayleigh regime (2πaeff∕λ < 1) show quantitative differences compared to oblate grains, but they are still a convenient representative. However, for self-scattering on larger grains (Mie regime) the spherical dust model shows significant qualitative deviations and has to be clearly distinguished from that of non-spherical grains. Moreover, when the wavelength is no longer fixed but increased, the Rayleigh regime is shifted to larger and larger grain sizes (see e.g. Appendix A).
3.3 Circular polarisation of single-sized grains
Finally, we also studied the amount of circular polarisation,
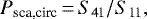 (2)
(2)
of scattered, initially unpolarised radiation on oblate grains. Similar to spherical grains, Psca,circ is negligible for all considered scattering angles, axis ratios, and grain radii as the scattering matrix element |S41| is at least six orders of magnitude below |S11|. The reason for this is the symmetric orientation of the symmetry axis (γaxi = 90°) and the scattering planes (Θsca,2 = 0° and 90°). Non-orthogonal or non-parallel orientations of the axes cause significant circular polarisations even for initially unpolarised radiation (e.g. Gledhill & McCall 2000). Moreover, a significant circular polarisation is also expected if the incoming wave is intrinsically polarised (see Sect. 4.3).
3.4 Linear polarisation of a grain size distribution
The linear polarisation Psca by scattering on single-sized spherical grains shows a strong wavelength dependence for 2πaeff∕λ > 1 with a high frequency and strong oscillations (see e.g. Fig. 2 in Brunngräber & Wolf 2019). The oscillations enable negative scattering polarisations with a reversal of the polarisation orientation. For a fixed wavelength, polarisation oscillations also occur as a function of grain size. We expect that the oscillations could cancel out for an ensemble of different grain sizes or a continuous distribution of grain sizes as the contribution of positive and negative (or the contribution of parallel and perpendicular) scattering polarisations annihilates each other (e.g. Kirchschlager et al. 2019)3.
In order to study the scattering polarisation of grain size distributions of oblate dust grains, we calculated the optical properties for 1000 grain sizes aeff, which are logarithmically equidistantly distributed in the interval [5 nm, 1 mm]. The grain axis ratio and wavelength are fixed to c∕b = 1.5 and λ = 870 μm, respectively.Subsequently, the scattering polarisation is calculated for a size distribution 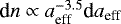 with minimum radius amin = 5 nm, while the maximum grain size is variedbetween 10 μm and 1 mm, and the peak polarisation (maximum polarisation as a function of scattering angle Θsca) is determined (Fig. 5). We assume that all grains are perfectly aligned as otherwise the contributions of differently aligned grains would mitigate each other or even cancel each other out.
with minimum radius amin = 5 nm, while the maximum grain size is variedbetween 10 μm and 1 mm, and the peak polarisation (maximum polarisation as a function of scattering angle Θsca) is determined (Fig. 5). We assume that all grains are perfectly aligned as otherwise the contributions of differently aligned grains would mitigate each other or even cancel each other out.
We distinguish between the scattering plane perpendicular and coplanar to the symmetry axis S (see Fig. 2). For both, the peak polarisation is 100% and the scattering angle of the peak polarisation Θsca ~ 90° when the maximum grain size amax is small compared to the wavelength (Rayleigh regime). The polarisation changes significantly for grain sizes slightly larger than amax = 100 μm as they are already in the Mie regime: the peak polarisation of scattering perpendicular to S (Θsca,2 = 90°) drops to ~35% for amax = 150 μm, and shows some moderate variations for larger sizes before converging to a constant polarisation degree of ~ 29% at grain sizes up to 1 mm. The peak polarisation of the scattering plane coplanar to S (Θsca,2 = 0°) even drops to approximately − 70% for amax = 120 μm and converges to approximately − 21% for larger grain sizes, and the peak polarisation is flipped in orientation by 90° for all size distributions with amax ≳ 110 μm.
We also calculated the scattering polarisation for a size distribution of spherical dust grains using DDA (Fig. 5). The polarisation degrees of the spherical grains are larger than that of scattering along the short axis (coplanar scattering) and smaller than that of scattering along the long axis (perpendicular to symmetry axis S). The scattering polarisation of the spherical grains is 10% for small grains and starts decreasing to ~0−10% when amax ≳ 100 μm, which is comparable to the result of Kataoka et al. (2015). We note that Kataoka et al. (2015) used a different dust composition made of silicate, water ice, and organics.
Independent of the grain axis ratio or scattering plane, the scattering angle of the peak polarisation shows strong oscillations and discontinuous jumps due to the occurrence of multiple polarisation maxima for grain sizes larger than ~ 100 μm. The scattering angles of the peak polarisation significantly deviate from Θsca = 90° and cover the full interval from 0° to 180°. We also plotted in Fig. 5 the scattering polarisation at Θsca = 90°, which shows absolute differences of up to 30% compared to the peak polarisation values.
Furthermore, we calculated the scattering polarisation of grain size distributions for the different ALMA wavebands B6, B5, B4, B3, B2, and B1 (λ = 1.3 mm, 1.5 mm, 2.1 mm, 3.1 mm, 4mm and 7 mm; see Appendix A). The Rayleigh limit is linearly shifted with wavelength to larger maximum grain sizes while the differences between the polarisation degree and orientation of spherical and non-spherical grains are preserved.
Figure 6 shows the product of the scattering polarisation Psca and the albedo ω = κsca∕(κabs + κsca) where κabs and κsca are the absorption and scattering mass opacity of the grain size distributions, respectively. Contrary to the scattering polarisation, the albedo is almost zero for amax ≪ λ∕2π and increases with increasing grain size. Following the approach of Kataoka et al. (2015) for spherical grains, the product of albedo and scattering polarisation,ω Psca, defines a window function for the grain sizes that contribute to the scattering polarisation: only grain size distributions with maximum radii amax ~ λ∕2π have both a significant scattering polarisation and albedo and dominate the polarisation signal at (sub-)millimetre wavelengths. The window functions of non-spherical (Fig. 6, left and right) and spherical (Fig. 6, centre) dust grains are very similar to each other for maximum sizes smaller than or comparable to λ∕2 π, indicating that grains of at least ~λ∕2π in size are required to account for polarisation levels of a few percent detected in several (sub-) millimetre observations. Furthermore, the window functions of non-spherical and spherical dust grains peak at the same grain radii and the peak polarisations increase with increasing wavelength.
The crucial differences between the window functions of non-spherical and spherical dust grains appear when the grain size approaches the wavelength. The amount of scattering polarisation of spherical grains drops to a much lower value than for non-spherical grains (Fig. 5). A significant polarisation persists for large oblate grains that contribute to the self-scattering signal. Consequently, the grain sizes inferred from self-scattering observations are increased to values significantly larger than ~λ∕2π when considering non-spherical grains. The self-scattering of non-spherical grains helps to reconcile the existing discrepancy between grain sizes inferred from self-scattering and more indirect measurements as well as those expected from theory (e.g. Beckwith et al. 1990). The potential detection of a polarisation reversal in the self-scattering signals gives further information about whether the scattering is predominantly along the short or long axis of the spheroidal grains.
Higher polarisation degrees can be realised by, amongst other causes, larger grain axis ratios c∕b. Thus, self-scattering on non-spherical dust grains allows for higher polarisation fractions than usually known from scattering on spherical grains. This is an important result as high polarisation values observed in discs have usually been interpreted as being produced bythe polarised emission of elongated grains and not by self-scattering.
The presented results assume perfect grain alignment (all grain axes point into the same direction). The mean of the scattering polarisation of the two scattering planes (Θsca,2 = 90° and 0°) of non-spherical grains is comparable to the scattering polarisation of spherical grains. Though an appropriate calculation of the scattering polarisation of randomly orientated dust grains needs more than two scattering planes, this already indicates that the oblate grains need to be well or nearly perfectly aligned in order to reveal the different self-scattering behaviour. Realistic grain alignment processes depend strongly on the surrounding gas and radiation conditions as well as on magnetic field strengths, which is well beyond the scope of this study and has to be postponed to future investigations.
 |
Fig. 5 Scattering polarisation Psca for a size distribution of oblate (red and blue) and spherical dust grains (black) as a function of the maximum grain size amax. We show the peak polarisation of the scattering interval [0°, 180°] (solid lines) as well as the polarisation at Θsca = 90°
(dotted lines). The size distribution follows |
 |
Fig. 6 Albedo ω
times scattering polarisation Psca
for a grain size distribution |
 |
Fig. 7 Degree of polarisation Psca by scattering on non-spherical (oblate) dust grains as a function of the scattering angle Θsca and the polarisation Pini of the incident radiation. The incident polarisation orientation is fixed to γini = 0° (perpendicular to the symmetry axis S) and the grain axis ratio is c∕b = 1.5. The grain size is aeff = 100 μm (left) and aeff = 150 μm (right). Thescattering polarisation of an initially unpolarised wave on spherical grains is shown for comparison (black dotted lines). |
4 Self-scattering of intrinsically polarised waves
In this section the self-scattering of intrinsically polarised radiation is investigated. As the optical properties of the grains at which the incoming wave gets scattered are unaffected by the polarisation state of the incident radiation, the scattering matrix elements from Sect. 3 can be reused and intrinsic polarisation is realised by adjusting the Stokes vector of the incoming wave (see Appendix B). As in Sect. 3 the scattering polarisations for aeff = 100 μm and aeff =150 μm grains are investigated as representatives for grains within the Rayleigh or Mie regime. To study the impact on the scattering polarisation, we varied the incident polarisation degree in Sect. 4.1 and the incident polarisation orientation in Sect. 4.2. Circular polarisation is discussed in Sect. 4.3.
4.1 Scattering as a function of the incident polarisation degree Pini
We fix the grain axis ratio to c∕b = 1.5 and the polarisation angle of the incident radiation to γini = 0° so that the incident polarisation is orientated perpendicular to the symmetry axis S (parallel to the long axis of the oblate grains). The emission of non-spherical dust grains is intrinsically polarised (e.g. Cho & Lazarian 2007). In Kirchschlager et al. (2019), we show that a grain axis ratio of c∕b = 1.5 results in a maximum intrinsic polarisation degree of ~35%. Polarisation by emission is a potential source for the polarisation Pini of the incident radiation in an upcoming scattering event. In the following, we gradually increase the polarisation degree of the incident radiation, Pini, from 0 to 35% and calculate the emerging scattering polarisation Psca (Fig. 7).
For initially unpolarised radiation, the orientation of the scattering polarisation is perpendicular to the scattering plane. Thus, the scattering polarisation is directed parallel to the symmetry axis S if the scattering is in the plane perpendicular to S (Θsca,2 = 90°). Increasing the incident polarisation Pini of the incident wave evokes a scattering polarisation component perpendicular to S. Orthogonal contributions cancel each other out and the scattering polarisation parallel to S decreases with increasing Pini. Consequently, intrinsically polarised radiation reduces the scattering polarisation when S is perpendicular to the scattering plane. For 100 μm grains (Fig. 7, left) and backward scattering angles (Θsca ≳ 150°), the orientation of the scattering polarisation can change by 90° if the incident polarisation is higher than Pini ≥ 30%. For 150 μm grains (Fig. 7, right), the polarisation flip occurs for angles Θsca ≳ 100° and incident polarisations Pini ≥ 15%.
The trends are inversed when the symmetry axis S is coplanar to the scattering plane (Θsca,2 = 0°) where the orientations of both the incident and the scattered polarisation are perpendicular to S. For 100 μm grains (Fig. 7, left) the absolute amount of scattering polarisation is reduced for scattering angles Θsca ≲ 60°−90° and Θsca ≳ 150° (which means depolarisation), while it is increased for scattering angles around the peak polarisation (60°−90° ≲ Θsca ≲ 150°). For 150 μm grains (Fig. 7, right), the absolute amount of scattering polarisation is reduced for scattering angles Θsca ≲ 30°−70° and Θsca ≳ 120°, while it is increased for scattering angles 30°−70° ≲ Θsca ≲ 120°.
The scattering polarisation of aeff = 100 μm and aeff = 150 μm grains show further significant differences. The scattering polarisation phase functions of the 150 μm grains are more asymmetric and the peak polarisations are smaller and shifted to smaller scattering angles (Θsca ~ 70−90°). Moreover, the degree of the peak polarisation decreases with increasing intrinsic polarisation Pini, while it is constant (Psca = 100%) for 100 μm grains.
 |
Fig. 8 Same as in Fig. 7, but for a fixed incident polarisation degree Pini = 35% and differentpolarisation orientations γini of the incident radiation. The scattering polarisation of an initially unpolarised wave on spherical grains aswell as on oblate grains is shown for comparison (black solid and dotted lines). Left: grain size aeff = 100 μm. Right: aeff = 150 μm. |
4.2 Scattering as a function of the orientation γini of incident polarisation
In general, the polarisation angle of the incident radiation could have a random orientation with respect to the orientation of the non-spherical scattering grain, and we investigate in this section the influence of several different polarisation directions of the incident radiation. We gradually increased the initial polarisation angle from γini = 0° to 90° with a step width of 22.5° while the incident polarisation degree is fixed to Pini = 35%, and calculated the scattering polarisation Psca (Fig. 8).
Changing the polarisation angle γini of the incident radiation has the opposite effect to an increase of the incident polarisation degree (Sect. 4.1). With increasing polarisation angle γini, the proportion of incident polarisation that is perpendicular to the symmetry axis S mitigates and the proportion parallel to S rises. Consequently, an increase of the incident polarisation angle up to 90° enhances the scattering polarisation in the case of Θsca,2 = 90° and reduces it for Θsca,2 = 0°. For γini = 45°, the parallel and perpendicular components of the incident polarisation are equal and the resulting scattering polarisation is that of initially unpolarised radiation (cf. black solid line and red squares in Fig. 8). Larger incident polarisation angles (γini > 45°) cause an amount of scattered polarisation that is higher than that for initially unpolarised radiation. Incident polarisation angles larger than 90° lead to the contrary effect as the proportion of the incident polarisation perpendicular to S rises again.
The differences between aeff = 100 μm and aeff = 150 μm grains are comparable to the differences when changing the incident polarisation degree (Sect. 4.1). The scattering polarisation phase functions of the 150 μm grains are more asymmetric and the peak polarisations are smaller, shifted to smaller scattering angles, and decrease with increasing polarisation angle γini of the incident radiation.
To summarise, the highest amounts of linear polarisation by scattering on oblate dust grains can be reached when the incident polarisation is high and is directed parallel to the grain symmetry axis S. As this effect increases with the axis ratio of the grains, scattering of intrinsic polarised radiation on non-spherical grains allows higher polarisation fractions than in the case of spherical grains. On the other hand, the incident polarisation can lead to a depolarisation for most of the scattering angles when the proportion of incident polarisation perpendicular to S is larger than the component parallel to it. Moreover, a 90° flip of the orientation of the scattering polarisation can occur at certain scattering angles.
4.3 Circular polarisation
Several observations of circumstellar environments have found high values of circular polarisation that might originate from dust scattering (Whitney & Wolff 2002). In Sect. 3.3 we discussed the zero circular polarisation of scattering of unpolarised,incident radiation on oblate dust grains. Gledhill & McCall (2000) showed that scattered light is significantly circularly polarised when the symmetry of the scattering event is broken. Besides a change of the orientation of the symmetry axis or the scattering planes, this is realised when the incoming wave is initially linearly polarised. In order to break the symmetry, the incident polarisation orientation has to be misaligned with both the symmetry axis S and the scattering plane. Consequently, we find that the scattered radiation is circularly polarised when γini ≠0° or ≠ 90° (Fig. 9). At γini = 45°, the circular polarisation is maximum with absolute values of Psca,circ ~ 6% (aeff = 100 μm; Fig. 9, left) and ~32% (aeff = 150 μm; Fig. 9, right). A flip from left- to right-handed circular polarisation occurs for all polarisation phase functions.
5 Discussion
In Sects. 3 and 4 we saw that non-spherical grain shapes have a significant effect on scattering and in particular the emerging scattering polarisation. While the deviations between spherical and oblate grains of sizes below 100 μm are mostly confined on forward and backwards scattering angles, larger grains with aeff > 100 μm show significant deviations in scattering polarisation values, polarisation peaks, and polarisation orientations when oblate grains are taken into account. This clearly reveals the different scattering behaviour of spherical and non-spherical grains once the grain sizes are beyond the Rayleigh regime and enter the Mie regime. Besides single-sized grains, grain size distributions with maximum sizes above 100 μm also show a clear dependence on the particle shape. In the literature, the interpretation of polarisation observations is commonly based on a perfect spherical, compact dust model. However, our results show that the grain sizes derived from self-scattering on spherical grains give the Rayleigh limit of the observation wavelength not the actual grain size. Therefore, the grain sizes deduced from self-scattering polarisation as discussed in current literature have to be re-evaluated in order to avoid misleading conclusions.
Scattering of non-spherical grains allows the production of higher polarisation fractions. As polarisation values larger than ~ 5% detected in observations have usually been interpreted as being produced by polarised emission of aligned grains, this raises questions about the origin of the polarisation and thus also about the inferred dust properties.
The scattering on non-spherical grains also shows significant circular polarisation. Contrary to spherical grains, single-scattering is sufficient to circularly polarise the scattered radiation (e.g. 33% for aeff = 150 μm grains) unless the grain symmetry axis is symmetrically arranged to the polarisation orientation of the incoming wave. Therefore, upcoming observations of circular polarisation have the potential to unveil the presence of non-spherical grains in protoplanetary discs.
We have seen further that an initial polarisation of the incoming wave can lead either to higher scattering polarisation degrees or to depolarisation, depending on the orientation of the non-spherical dust grain relative to the incident wave and on the scattering plane, as well as on the incident polarisation degree and incident polarisation orientation. The incoming wave can be polarised due to intrinsic polarisation (polarisation by emission) of the non-spherical grains. For a wavelength of λ = 870 μm and an effective radius of aeff = 100 μm, the direction of the intrinsic polarisation is perpendicular to the symmetry axis S (Kirchschlager et al. 2019). If we assume perfect alignment of oblate grains in a protoplanetary disc (due to radiation or magnetic fields), this leads to the scenario shown in Fig. 7.
The higher polarisation fractions compared to spherical grains will be visible in protoplanetary discs or star-forming regions when the dust grains are well aligned. However, due to non-perfect alignment of the grains or multiple scattering, the polarisation state of both the incoming and the scattered wave might deviate. A prediction whether oblate grains cause depolarisation or larger scattering polarisation degrees is ambitious and has to be moved to sophisticated radiative transfer simulations that include grain alignment processes (e.g. Bertrang et al. 2017; Bertrang & Wolf 2017). Moreover, the presence of different dust materials and grain shapes (including prolate grains) in a disc will potentially affect the outcome as well.
Non-spherical dust grains will also emit polarised radiation, which adds to the polarised signal of the scattering. For the convenience and clarity of the presentation, we focused on polarisation by scattering here and did not consider the superposition of scattering and emission, which can have polarisation efficiencies at comparable levels. Future investigations will have to include not only self-scattering by oblate grains with radiation transfer in complex magnetic field geometry, but also polarised emission by aligned grains. These calculations will have to be done in the Mie regime for self-scattering and for polarised emission (Guillet et al. 2020), and not in the Rayleigh regime as is usually done.
 |
Fig. 9 Same as Fig. 8, but for circular polarisation Psca,circ. Left: grain size aeff = 100 μm. Right: aeff = 150 μm. |
6 Conclusions
We have investigated polarisation by single-scattering on non-spherical dust grains. The polarisation degree as well as the polarisation orientation of the incoming wave were modified in order to study different scenarios.
We found that the scattering polarisation of oblate dust grains significantly deviates from that of compact spheres, both for incoming polarised and unpolarised radiation. In the Mie regime (e.g. for grain sizes > 100 μm at wavelengths λ = 870 μm) the deviations between spherical and oblate grains are tremendous and the usage of spherical grains when interpreting polarisation observations is deficient.
Considering non-spherical grains in self-scattering simulations has the potential to explain polarisation observations with grains significantly larger than ~λ∕2π. Thus, the grain sizes derived from self-scattering simulations using non-spherical, perfectly aligned grains can be larger than those from simulations using spherical grains. Self-scattering by oblate, aligned grains produces higher polarisation fractions compared to spheres. This calls into question whether high polarisation values (≳ 5%) observed in protoplanetary discs or star-forming regions are produced by polarised emission, as usually assumed, or by self-scattering.
Scattering of intrinsically polarised waves can lead to either depolarisation or amplification of the scattering polarisation, including polarisation flips. The exact results depend strongly on the grain alignment processes in protoplanetary discs, as well as on disc and dust properties. Finally, we found that circular polarisation is a promising method for the verification of the presence of non-spherical grains and to unveil further dust parameters.
Acknowledgements
We thank the anonymous referee for their constructive comments. FK was supported by European Research Council Grant SNDUST ERC-2015-AdG-694520. G.H.M.B acknowledges funding from the European Research Council under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 757957).
Appendix A Linear polarisation as a function of wavelength
We calculated the scattering polarisation for grain size distribution  for the different ALMA wavebands B6, B5, B4, B3, B2, and B1 (λ = 1.3, 1.5, 2.1, 3.1, 4 and 7 mm, respectively). The minimum effective radius of the grain is amin = 5 nm while the maximum grain size is variedbetween 10 μm and 1 mm (Fig. A.1). The Rayleigh regime is linearly shifted with wavelength λ to larger maximum grain sizes while the scattering polarisation differences between spherical and non-spherical grains are preserved.
for the different ALMA wavebands B6, B5, B4, B3, B2, and B1 (λ = 1.3, 1.5, 2.1, 3.1, 4 and 7 mm, respectively). The minimum effective radius of the grain is amin = 5 nm while the maximum grain size is variedbetween 10 μm and 1 mm (Fig. A.1). The Rayleigh regime is linearly shifted with wavelength λ to larger maximum grain sizes while the scattering polarisation differences between spherical and non-spherical grains are preserved.
 |
Fig. A.1 Same as Fig. 5, only for the ALMA wavebands B6, B5, B4, B3, B2, and B1 (λ = 1.3 mm, 1.5 mm, 2.1 mm, 3.1 mm, 4 mm, 7 mm, resp.). |
Appendix B Scattering formalism
The scattering properties of a dust grain are described by its 4 × 4 scattering matrix, which is a function of grain size, wavelength, material, dust grain shape (e.g. elongicity), and morphology (e.g. porosity), as well as the scattering angles Θsca and Θsca,2. Scattered radiation is characterised by the Stokes vector (Isca, Qsca, Usca, Vsca), which is the product of the scattering matrix and the Stokes vector (Iini, Qini, Uini, Vini) of the incident wave. For oblate dust grains (in contrast to compact spheres), all scattering matrix elements can have a significant contribution. The Stokes vector of the scattered radiation is then given by
 (B.1)
(B.1)
The linear polarisation degree and the polarisation orientation of the scattered/incident radiation are then
 (B.2)
(B.2)
where l = 1 if Qsca/ini < 0, and l = 0 otherwise.
For a special orientation of the grain relative to the incoming wave (e.g. γaxi = 90°, Θsca,2 = 0° or 90°), Eq. (B.1) can be simplified in a similar manner to the way in which spherical grains and scattered linear and circular polarisation are calculated by Eqs. (1) and (2), respectively.
In order to realise a linearly polarised, incoming wave with polarisation degree Pini and polarisation orientation γini = 0°, 22.5°, 45°, 67.5°, and 90°, we set the Stokes vector of the incident radiation to (1, Pini, 0, 0), 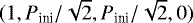 , (1, 0, Pini, 0),
, (1, 0, Pini, 0), 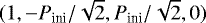 , and (1, −Pini, 0, 0), respectively.
, and (1, −Pini, 0, 0), respectively.
References
- Bacciotti, F., Girart, J. M., Padovani, M., et al. 2018, ApJ, 865, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, S. V. W., Sargent, A. I., Chini, R. S., & Guesten, R. 1990, AJ, 99, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Bertrang, G. H.-M., & Wolf, S. 2017, MNRAS, 469, 2869 [NASA ADS] [CrossRef] [Google Scholar]
- Bertrang, G. H.-M., Flock, M., & Wolf, S. 2017, MNRAS, 464, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Bohren, C. F., & Huffman, D. R. 1983, Absorption and Scattering of Light by Small Particles, eds. Bohren, C. F., & Huffman, D. R. (Hoboken: John Wiley & Sons) [Google Scholar]
- Brunngräber,R., & Wolf, S. 2019, A&A, 627, L10 [CrossRef] [EDP Sciences] [Google Scholar]
- Carrasco-González, C., Sierra, A., Flock, M., et al. 2019, ApJ, 883, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, J., & Lazarian, A. 2007, J. Korean Astron. Soc., 40, 113 [CrossRef] [Google Scholar]
- Daniel, J.-Y. 1980, A&A, 87, 204 [NASA ADS] [Google Scholar]
- Dent, W. R. F., Pinte, C., Cortes, P. C., et al. 2019, MNRAS, 482, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003a, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003b, ApJ, 598, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Flatau, P. J. 1994, J. Opt. Soc. Am. A, 11, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Flatau, P. J. 2013, ArXiv e-prints [arXiv:1305.6497] [Google Scholar]
- Draine, B. T., & Goodman, J. 1993, ApJ, 405, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Gledhill, T. M., & McCall, A. 2000, MNRAS, 314, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Guillet, V., Girart, J. M., Maury, A. J., & Alves, F. O. 2020, A&A 634, L15 [CrossRef] [EDP Sciences] [Google Scholar]
- Harrison, R. E., Looney, L. W., Stephens, I. W., et al. 2019, ApJ, 877, L2 [CrossRef] [Google Scholar]
- Kataoka, A., Muto, T., Momose, M., et al. 2015, ApJ, 809, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, A., Tsukagoshi, T., Pohl, A., et al. 2017, ApJ, 844, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Kirchschlager, F., & Wolf, S. 2013, A&A, 552, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirchschlager, F., & Wolf, S. 2014, A&A, 568, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirchschlager, F., Bertrang, G. H. M., & Flock, M. 2019, MNRAS, 488, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Hoang, T. 2007, MNRAS, 378, 910 [Google Scholar]
- Miyake, K., & Nakagawa, Y. 1993, Icarus, 106, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Purcell, E. M., & Pennypacker, C. R. 1973, ApJ, 186, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Sadavoy, S. I., Stephens, I. W., Myers, P. C., et al. 2019, ApJS, 245, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, I. W., Yang, H., Li, Z.-Y., et al. 2017, ApJ, 851, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Tazaki, R., Lazarian, A., & Nomura, H. 2017, ApJ, 839, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Whitney, B. A., & Wolff, M. J. 2002, ApJ, 574, 205 [NASA ADS] [CrossRef] [Google Scholar]
We note that the mutual obliteration of polarised signals of grains of different radii is the reason for the relatively smooth polarisation pattern in Fig. 3 in Kataoka et al. (2015) where polarisation is displayed as a function of the maximum radius of a size distribution of spherical grains.
All Figures
 |
Fig. 1 Sketch of a general scattering event on an oblate dust grain, including the incidence direction A, the scattering direction B and the symmetry axis S of the oblate grain. The angles γaxi, Θsca, and Θsca,2 determine the scattering plane and the plane defined by A and S. |
| In the text | |
 |
Fig. 2 Orientation of the two considered scattering planes (blue grid). Left: grain symmetry axis S is perpendicular to scattering plane (Θsca,2 = 90°). Right: symmetry axis S is coplanar to scattering plane (Θsca,2 = 0°). |
| In the text | |
 |
Fig. 3 Scattering matrix elements S11 and (− S12) of oblate grains as a function of the scattering angle Θsca and differentaxis ratios c∕b, for thetwo scattering planes perpendicular and coplanar to the grain’s symmetry axis (Θsca,2 = 90° and 0°, respectively). The grain size is aeff = 100 μm (Rayleigh regime; left) and aeff = 150 μm (Mie regime; right). |
| In the text | |
 |
Fig. 4 Degree of polarisation Psca by scattering on oblate dust grains as a function of the scattering angle Θsca and differentaxis ratio c∕b, for thetwo scattering planes perpendicular and coplanar to the grain’s symmetry axis (Θsca,2 = 90° and 0°, respectively). The polarisation Pini of the incident radiation is zero and the grain size aeff = 100 μm (left) and aeff = 150 μm (right). The grey-shaded region indicates negative scattering polarisations, which imply a reversal of the polarisation orientation. |
| In the text | |
 |
Fig. 5 Scattering polarisation Psca for a size distribution of oblate (red and blue) and spherical dust grains (black) as a function of the maximum grain size amax. We show the peak polarisation of the scattering interval [0°, 180°] (solid lines) as well as the polarisation at Θsca = 90°
(dotted lines). The size distribution follows |
| In the text | |
 |
Fig. 6 Albedo ω
times scattering polarisation Psca
for a grain size distribution |
| In the text | |
 |
Fig. 7 Degree of polarisation Psca by scattering on non-spherical (oblate) dust grains as a function of the scattering angle Θsca and the polarisation Pini of the incident radiation. The incident polarisation orientation is fixed to γini = 0° (perpendicular to the symmetry axis S) and the grain axis ratio is c∕b = 1.5. The grain size is aeff = 100 μm (left) and aeff = 150 μm (right). Thescattering polarisation of an initially unpolarised wave on spherical grains is shown for comparison (black dotted lines). |
| In the text | |
 |
Fig. 8 Same as in Fig. 7, but for a fixed incident polarisation degree Pini = 35% and differentpolarisation orientations γini of the incident radiation. The scattering polarisation of an initially unpolarised wave on spherical grains aswell as on oblate grains is shown for comparison (black solid and dotted lines). Left: grain size aeff = 100 μm. Right: aeff = 150 μm. |
| In the text | |
 |
Fig. 9 Same as Fig. 8, but for circular polarisation Psca,circ. Left: grain size aeff = 100 μm. Right: aeff = 150 μm. |
| In the text | |
 |
Fig. A.1 Same as Fig. 5, only for the ALMA wavebands B6, B5, B4, B3, B2, and B1 (λ = 1.3 mm, 1.5 mm, 2.1 mm, 3.1 mm, 4 mm, 7 mm, resp.). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.