| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201937431 | |
| Published online | 11 June 2020 | |
How galaxies populate haloes in very low-density environments
An analysis of the halo occupation distribution in cosmic voids
1
Instituto de Astronomía Teórica y Experimental, CONICET-UNC, Laprida 854, X5000BGR Córdoba, Argentina
e-mail: german.alfaro@unc.edu.ar
2
Observatorio Astronómico de Córdoba, UNC, Laprida 854, X5000BGR Córdoba, Argentina
Received:
30
December
2019
Accepted:
9
April
2020
Context. Evidence shows that properties of dark matter haloes may vary with large-scale environment. Studying the halo occupation distribution in cosmic voids makes it possible to obtain useful information that can shed light on the subject. The history of the formation of the haloes and galaxies residing in these regions is likely to differ from the global behaviour given their extreme environment.
Aims. Our goal is to characterise the halo occupation distribution in the interior of cosmic voids and compare with the general results to unveil the way galaxies populate haloes in simulated galaxy catalogues.
Methods. We used two publicly accessible simulated galaxy catalogues constructed with different methods: a semi-analytical model and a hydrodynamic simulation. In both cases, we identified cosmic voids, and we measured the halo occupation distribution inside these regions for different absolute magnitude thresholds. We compared these determinations with the overall results, and we studied the dependence of different characteristics of the voids. We also analysed the stellar content and the formation time of the haloes inside voids and confronted the general halo population results.
Results. Inside the voids, we find a significantly different halo occupation distribution with respect to the general results. This is present in all absolute magnitude ranges explored. We obtain no signs of variation related to void characteristics, indicating that the effects depend only on the density of the large-scale environment. Additionally, we find that the stellar-mass content also differs within voids that host haloes with less massive central galaxies (∼10%), as well as satellites with significantly lower stellar-mass content (∼30%). Finally, we find a slight difference between the formation times of the younger haloes in voids than the average population. These characteristics indicate that haloes populating voids have had a different formation history, inducing significant changes on the halo occupation distribution.
Key words: large-scale structure of Universe / galaxies: halos / galaxies: statistics / methods: statistical / methods: data analysis
© ESO 2020
1. Introduction
The current paradigm for structure formation in the Universe assumes galaxies forming by baryon condensation within the potential wells that define the collisionless collapse of dark matter haloes (White & Rees 1978). However, the diversity of astrophysical mechanisms involved in the process of galaxy formation and evolution does not allow us to unambiguously determine how galaxies occupy haloes. Thus, understanding the links between galaxies and the dark matter haloes in which they reside is one of the keys to comprehending the formation and evolution of large structures.
Several works show that the halo occupation distribution (HOD) is a powerful tool to connect galaxies and dark matter haloes. The HOD describes the probability distribution P(N|Mhalo) that a virialised halo of mass Mhalo contains N galaxies with some specified characteristic (e.g. Jing et al. 1998; Ma & Fry 2000; Peacock & Smith 2000; Seljak 2000: Scoccimarro et al. 2001; Berlind & Weinberg 2002; Cooray & Sheth 2002; Berlind et al. 2003; Zheng et al. 2005; Yang et al. 2007; Rodriguez et al. 2015). Moreover, many authors have proposed the use of the HOD to constrain models of galaxy formation and evolution (e.g. Benson et al. 2000; Berlind et al. 2003; Kravtsov et al. 2004; Zentner et al. 2005; Zehavi et al. 2011) and cosmological models (e.g. Van Den Bosch et al. 2003; Zheng & Weinberg 2007).
Generally, the HOD approach assumes that the halo population depends only on their mass, a first approximation that has been amply analysed. Some examples of this include the works of Pujol & Gaztañaga (2014), who found that HOD cannot reconstruct the galaxy bias for low-mass haloes in several semi-analytic models, as well as the Pujol et al. (2017) analysis of the influence of local density in HOD – also in semi-analytic models. In the latter, the authors highlight HOD as a better predictor of galaxy bias than halo mass, while on the other hand, Berlind et al. (2003) studied the environmental variations of the HOD in hydrodynamical cosmological simulations, revealing no significant dependence. However, Zehavi et al. (2018), Artale et al. (2018), and Bose et al. (2019) explored the dependence of halo occupation on the large-scale environment for some semi-analytic and hydrodynamical simulations, finding some relevant signs of correlation.
As it is well known, the cosmic web that forms the large-scale structure of the Universe contains regions with large mass density fluctuations concerning the mean background density, with cosmic voids corresponding to the lowest density regions. There are several precise definitions of cosmic voids, where the differences of these definitions account for a diversity of derived void properties such as their topology or the inner mass content (Colberg et al. 2008; Cautun et al. 2018). Nevertheless, all the definitions agree that these regions comprise most of the volume of the Universe, but only contain a small fraction of the galaxy populations (Pan et al. 2012).
The extremely low densities, plus the expansion of the void, make gravitational interactions between galaxies less frequent, a fact that affects the growth and fate of the structure. These characteristics make cosmic voids ideal regions to study aspects of the formation and evolution of galaxies unlikely to be observed elsewhere. The influence of these extremely low-density environments on their member galaxies may be reflected in different dynamical and astrophysics properties compared to galaxies populating higher density regions. Void galaxies tend to be blue, faint, and of late-type morphologies (Rojas et al. 2004; Hoyle et al. 2005, 2012; Patiri et al. 2006; Ceccarelli et al. 2008), generally exhibiting young stellar populations and intense star formation activity (Rojas et al. 2005). Thus, void galaxies are expected to have a significantly different dynamical and astrophysical evolution. In this context, the possible dependence of HOD on the environment should be most clearly seen inside cosmic voids.
In previous work, Ruiz et al. (2019) found a significantly low amplitude of the galaxy-galaxy correlation function for galaxy samples inside cosmic voids. As analysed by Cooray & Sheth (2002), the galaxy power spectrum can be expressed in terms of the HOD. Thus, given that the correlation function is straightforwardly associated with the power spectrum (Peebles 1980), HOD is also expected to differ when measured inside the cosmic voids. In this work, we use the same cosmic void definition as Ruiz et al. (2019), which considers spherical regions where the integrated density contrast does not exceed a given threshold value Δlim. In the literature, see for instance Ruiz et al. (2015b) and references therein, this parameter varies between −0.8 and −0.9, so that inside void boundaries, there is at most 20% to 10% the mean density of the Universe.
This paper is organised as follows. In Sect. 2, we describe the simulated galaxy catalogues obtained from both a semi-analytic model and a hydrodynamical simulation. We also describe the algorithms to identify cosmic voids and the void catalogues obtained. In Sect. 3, we describe the methodology used to determine the HOD inside cosmic voids. In Sect. 4, we present the results of the HOD measurements inside the voids in both catalogues. In this section, we also explore the dependence of the results on void properties such as Δlim, void size, and the surrounding void environment. In Sect. 5, we study the halo stellar mass distribution as a function of the total dark matter halo mass. In Sect. 6, we compare the halo formation time inside voids with the overall results. Finally, in Sect. 7, we present our summary and conclusions.
2. Data
In this section, we present the simulated galaxy catalogues used in this work. We also present a brief description of the void-identification algorithm used and the final void catalogues obtained.
2.1. Simulated galaxy catalogues
We use two simulated galaxy catalogues, one based on a semi-analytic approach and one extracted from a hydrodynamic simulation.
2.1.1. The MDPL2-SAG galaxy catalogue
The MDPL2-SAG1 catalogue is part of the MultiDark-Galaxies catalogues (Knebe et al. 2018), publicly available at the CosmoSim2 and Skies & Universes3 databases. This catalogue was constructed by applying the semi-analytic model of galaxy formation and evolution SAG to the dark matter haloes of the MDPL2 cosmological simulation.
The SAG model (Semi-Analytic Galaxies, Cora et al. 2018) includes all the main physical processes involved in the formation and evolution of galaxies, such as star formation, supernova feedback, radiative cooling of the hot gas, chemical enrichment of gas and galaxies, growth of supermassive black holes, feedback by AGN, starbursts via disc instabilities, and galaxy mergers. For readers interested in a complete description of the several physical processes present in the SAG model and the details of its implementation, we refer them to Cora (2006), Lagos et al. (2008), Tecce et al. (2010), Padilla et al. (2014), Ruiz et al. (2015a), Gargiulo et al. (2015), Cora et al. (2018, 2019), and Collacchioni et al. (2018).
The MDPL2 simulation (Riebe et al. 2013; Klypin et al. 2016), which is also available at the CosmoSim database, counts with 38403 dark matter particles in a comoving box of 1000 h−1 Mpc on a side, which translates as a particle mass resolution of 1.51 × 109 h−1 M⊙. The cosmological parameters adopted correspond to a flat ΛCDM scenario consistent with Planck results (Planck Collaboration XVI 2014): Ωm = 0.307, Ωb = 0.048, σ8 = 0.823, h = 0.678 and n = 0.96.
The haloes and sub-haloes used to populate the simulation with galaxies were identified with the Rockstar Halo Finder (Behroozi et al. 2013a), and the merger trees were constructed with ConsistentTrees (Behroozi et al. 2013b).
From the complete MDPL2-SAG catalogue at z = 0, we selected all galaxies with absolute magnitudes in the r-band Mr − 5 log10(h) ≤ − 16, stellar masses M⋆ ≥ 5 × 108 h−1 M⊙ and host haloes with masses M200c ≥ 5 × 1010 h−1 M⊙, where M200c corresponds to the mass enclosed within over-density of 200 times the critical density of the Universe. The final catalogue comprises 41986893 galaxies.
2.1.2. The TNG300 galaxy catalogue
The TNG300 simulation is part of the IllustrisTNG4 suite of hydrodynamical simulations of galaxy formation in cosmological volumes (Marinacci et al. 2018; Naiman et al. 2018; Nelson et al. 2018; Pillepich et al. 2018a; Springel et al. 2018). Particularly, the TNG300 counts with 25003 dark matter particles and 25003 gas particles in a cubic comoving box of 205 h−1 Mpc on a side, which results in a dark matter and baryonic mass resolutions of 3.98 × 107 h−1 M⊙ and 7.44 × 106 h−1 M⊙, respectively. The cosmological model adopted is a flat ΛCDM with parameters also in agreement with Planck results (Planck Collaboration XIII 2016): Ωm = 0.3089, Ωb = 0.0486, σ8 = 0.8159, h = 0.6774 and n = 0.9667. The simulation was evolved using the moving mesh code AREPO (Springel 2010) and includes not only all the relevant processes of galaxy formation, but also a detailed magneto-hydrodynamical implementation (see Weinberger et al. 2017; Pillepich et al. 2018b for a complete description of the physical processes implemented).
We selected all galaxies from the snapshot at z = 0 with Mr − 5 log10(h) ≤ − 15 and host haloes with masses M200c ≥ 1010 h−1 M⊙. There are 657040 galaxies in the final catalogue.
2.2. Void identification and void catalogues
In both MDPL2-SAG and TNG300 galaxy catalogues, cosmic voids were identified using the algorithm presented in Ruiz et al. (2015b). Briefly, the identification starts estimating the density field via a Voronoi tessellation of the galaxy catalogues, which are used as tracers. For each Voronoi cell, we can compute a density given by ρcell = 1/Vcell, Vcell being the volume of the cell, and define a density contrast as 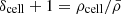 , where
, where 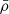 is the mean density of tracers. All Voronoi cells that satisfy δcell < −0.5 are selected as a centre of an under-dense region, and for those centres, we select all-spherical volumes with an integrated density contrast Δ(Rvoid) ≤ Δlim as void candidates, where Rvoid is the void radius, and Δlim is a density contrast threshold, usually chosen as −0.8 or −0.9 (which means 20% or 10% of the mean density of tracers, respectively). For each of those void candidates, the computation of Δ is repeated several times in randomly displaced centres near the previous ones, accepting a new centre only if the new void radius is larger than the older one. This random walk procedure is performed in order to obtain void candidates centred as closely as possible in the true minimum of the density field. The final step of the identification removes overlapping void candidates by keeping the largest voids that do not superpose with any other candidate.
is the mean density of tracers. All Voronoi cells that satisfy δcell < −0.5 are selected as a centre of an under-dense region, and for those centres, we select all-spherical volumes with an integrated density contrast Δ(Rvoid) ≤ Δlim as void candidates, where Rvoid is the void radius, and Δlim is a density contrast threshold, usually chosen as −0.8 or −0.9 (which means 20% or 10% of the mean density of tracers, respectively). For each of those void candidates, the computation of Δ is repeated several times in randomly displaced centres near the previous ones, accepting a new centre only if the new void radius is larger than the older one. This random walk procedure is performed in order to obtain void candidates centred as closely as possible in the true minimum of the density field. The final step of the identification removes overlapping void candidates by keeping the largest voids that do not superpose with any other candidate.
In both catalogues used in this work, we selected all galaxies with Mr − 5 log10(h) ≤ − 20 as tracers to identify voids, obtaining 12791 voids for MDPL2-SAG and 301 voids for TNG300. In Fig. 1, we show the radii distribution for both catalogues (MDPL2-SAG in red and TNG300 in green) and in Table 1 we show the relevant numbers of the void catalogues obtained.
 |
Fig. 1. Radii distribution of cosmic voids identified in MDPL2-SAG (red) and TNG300 (green) catalogues using Δlim = −0.9. |
Properties of the comic voids identified in MDPL2-SAG and TNG300 catalogues.
It can be seen that the TNG300 void radii are smaller than those in MDPL2-SAG. This is due to the fact that the TNG300 catalogue has a larger number density of tracers in this luminosity range than the MDPL2-SAG catalogue (see Table 1). To study the impact of the volume number density of galaxies and voids, in the Appendix A, we test our results using samples of voids limited by size, in order to obtain the same void number densities in both catalogues (Appendix A.1), and using void catalogues identified with equal density-tracer numbers (Appendix A.2). Furthermore, the results found in this work (Sects. 4–6) remain unchanged.
Taking into account that observational works usually consider HOD as a function of a fixed absolute limiting magnitude, Mlim, and aiming for a future comparison with real data, here we show the results obtained with a fixed luminosity threshold. To complete the description of the void samples of each catalogue, in Table 1 we present the number of voids in each sample and sub-sample considered.
3. Analysis of HOD in voids
In this section, we describe the methodology adopted to measure the HOD, and in particular, inside cosmic voids. We studied the mean number of galaxies in haloes of a given mass, ⟨N|Mhalo⟩, being Mhalo = M200c for both catalogues. In order to compute this quantity, we used the available membership information of galaxies to associate them with their host dark matter haloes. In this case, the HOD is just obtained by binning in halo mass and computing the average number of galaxies in each bin.
To compute HOD inside cosmic voids, we followed the procedure described above, but only took into account the haloes that are completely enclosed within void boundaries. Therefore, we removed all haloes that have galaxies beyond the void radius from our samples.
We compared the overall HOD results with those computed only using haloes inside voids. In all cases, to compute the variance obtained in HOD calculations, we used the jackknife technique. For this purpose, we separated the sample of haloes into 50 equal sub-samples, and we computed HOD variations when we did not consider each one of these sub-samples in the measurements. We also tested the results using 10, 100, 150, and 1000 sub-samples in the jackknife procedure, finding that, for 50 or more sub-samples, the variance values stabilise.
In order to explore possible HOD dependence on void parameters, we explored the results obtained as a function of Δlim, void radius and void-type classification according to their environment (see Sect. 4). We also compared the stellar mass content of haloes residing inside voids with that derived for the total halo sample. This comparison provides further information to understand the environmental dependence of the relation between halo total stellar mass and number of galaxies.
4. Results
In this section, we presented the results of the HOD measurements inside the voids in both catalogues and explored their dependence on void properties.
4.1. Dependence on Δlim
Cosmic voids are defined as spherical regions where the integrated over-density is below a certain threshold value Δlim. This parameter is fundamental since it is the only free parameter in our identification algorithm. We identify voids with integrated density contrast Δlim = −0.5, − 0.6, − 0.7, − 0.8, and −0.9. Within these structures, we measured the HOD in each void sample and compared the results with the global HOD obtained for the total haloes sample.
In Fig. 2, we show the dependence of HOD with Δlim in both MDPL2-SAG and TNG300 catalogues. The overall HOD is presented with black lines, while red lines correspond to the HOD inside cosmic voids. As it can be seen, there is a clear dependence of the mean number of galaxies on the over-density threshold used to identify the voids. This dependence is stronger in the case of MDPL2-SAG, however, TNG300 follows the same trend. By using less restricted Δlim values, the HOD inside the voids becomes similar to that obtained in the complete catalogue. This dependence is in agreement with previous results presented by Zehavi et al. (2018), Artale et al. (2018), and Bose et al. (2019), who found evidence of occupancy variation when considering halo sub-samples taking into account their large-scale environment. However, it is worth mentioning some important differences between their approach and our analysis. These authors characterize the environment using spherical volumes (Artale et al. 2018; Bose et al. 2019) or a Gaussian smoothing (Zehavi et al. 2018), both with a fixed scale of 5 h−1 Mpc, and determine the local density for each dark matter halo. These criteria are substantially different to our spherical void definition, which involves large-scale under-densities with a fixed integrated-density contrast, Δlim. A consequence of this definition is that, by construction, our voids have a lack of high-mass haloes, so the internal void HOD is limited to a certain halo mass. This can be seen in Fig. 2, where the maximum halo mass that is achieved decreases with Δlim. For these reasons, given that the methodology and the halo mass ranges of HOD are different, a direct comparison between our results and those presented by Zehavi et al. (2018), Artale et al. (2018), and Bose et al. (2019) is not straightforward. As a final remark, in Fig. 2, it can be seen that beyond halo masses of ∼1012 h−1 M⊙, the environmental differences become significant, reaching factors as large as 2 for Δlim = −0.9.
 |
Fig. 2. HODs measured for galaxies with Mr − 5 log10(h) ≤ − 17 in MDPL2-SAG (left) and TNG300 (right) catalogues. Upper panels: resulting HOD for the complete catalogues (black squares – solid lines) and for haloes inside cosmic voids (red triangles – dashed lines) identified with different values of Δlim, as indicated in the key. Bottom panels: ratio between HOD inside voids and the HOD in the complete catalogues. The error bars are computed using the standard jackknife procedure. |
Since this work aims to study the behaviour of HOD in very low-density environments, we decided to use voids identified with Δlim = −0.9. This selection is also justified by the fact that values of Δlim = −0.8 and −0.9 (which represent 20% and 10% of the mean density of tracers, respectively) are widely used in spherical void finder algorithms in the literature (e.g. Padilla et al. 2005; Ceccarelli et al. 2006; Colberg et al. 2008).
4.2. HOD inside voids
Once Δlim value was fixed as −0.9, we compared the overall HOD with measurements inside voids for different r-band absolute magnitude thresholds. This was done in order to analyse a possible dependence of the variation in the number of satellites in haloes inside voids with luminosity.
In Fig. 3, we compare the HOD inside voids and the overall results obtained on each catalogue for different absolute magnitude limits. The HOD inside voids is shown in red dashed lines, and the overall HOD in black solid lines. The ratio between both is presented at the bottom of each panel. As it can be seen, for all magnitude thresholds (Mr − 5 log10(h) = − 17 to −20, from up to bottom), HOD inside voids is systematically lower for halo masses higher than ∼1012 h−1 M⊙, and it achieves differences up to ∼50%. It is important to note that, for small halo masses, there are no significant differences in the HOD inside voids with respect to the general behaviour. This can be interpreted by considering the formation of the first-ranked galaxy of haloes nearly independently of the environment, but with the satellite population differing due to their slower formation and accretion in the extreme low-density environment of cosmic voids. This result is in general agreement with Bose et al. (2019), who explored the HOD in a TNG300 simulation.
 |
Fig. 3. HOD in MDPL2-SAG and TNG300 catalogues for different luminosity thresholds. Left column: results for MDPL2-SAG and right column: TNG300 catalogue, for magnitude limits Mr − 5log(h) ranging from −17 to −20, from top to bottom. Black solid lines represent the overall HOD, meanwhile red dashed lines the HOD measured inside voids. For each magnitude bin and catalogue, the ratio between both HODs are shown at the bottom of each panel. The uncertainties are calculated by the standard jackknife procedure. |
We further studied HOD as a function of number density cuts instead of luminosity thresholds, avoiding possible differences arising in the assignment of galaxy luminosities in the two simulated datasets. The results are given in Appendix A.2, where it can be seen that the differences between void and global environment remain the same as in Fig. 3 using luminosity thresholds.
We also checked for systematic effects associated with the boundary, given that HOD is computed in spherical volumes. This was accomplished by randomising void centre positions and recalculating HOD in these new volumes. For these randomly placed spherical volumes, we recovered the HOD behaviour of the overall halo sample, providing confidence in our results.
4.3. Dependence on voids radius
So far, we have seen that there is a clear distinction between the HOD inside cosmic voids as compared to the overall behaviour. In this section, we explore a possible dependence on a fundamental parameter of our void sample, namely the void radius.
We divided our samples into several void radius bins and computed the mean HOD in the different radius bins. We define four void sub-samples: Rvoid < 10 h−1 Mpc, 10 h−1 Mpc < Rvoid < 15 h−1 Mpc, 15 h−1 Mpc < Rvoid < 20 h−1 Mpc, and 20 h−1 Mpc < Rvoid. In Fig. 4, we show the results of this analysis. For simplicity, we only present the results for two absolute magnitude thresholds for each galaxy catalogue, MDPL2-SAG on left panels and TNG300 on the right. The adopted absolute magnitude cuts are labelled on each panel. We notice that the results are consistent for all studied ranges of absolute magnitudes. In the figure, each sub-sample is represented by a different colour, as indicated in the key figure (upper-left panel).
 |
Fig. 4. HOD in MDPL2-SAG and TNG300 catalogues for different void radii. Left column: results for MDPL2-SAG and right column: TNG300 catalogue, for Rvoid < 10 h−1 Mpc (orange), 10 h−1 Mpc < Rvoid < 15 h−1 Mpc (purple), 15 h−1 Mpc < Rvoid < 20 h−1 Mpc (blue), and 20 h−1 Mpc < Rvoid (green). Each panel corresponds to a different magnitude limit Mr − 5 log10(h) ranging from −17 to −20. The uncertainties are calculated following the standard jackknife procedure. |
As it can be clearly seen, within uncertainties, there is not a significant dependence of the HOD behaviour on void radius Rvoid. This is somewhat expected, because, given our void definition, up to Rvoid, all voids have the same integrated density contrast independently of their size.
4.4. Dependence on the void’s large-scale environment
Another way to classify cosmic voids is to use their large-scale environment. According to Ceccarelli et al. (2013), voids can be classed as R-types and S-types, where the former are surrounded by large-scale under-dense regions, and the others are embedded into over-dense regions. This is expressed on void profiles, and we use the maximum value of Δ between [2Rvoid, 3Rvoid] to classify them. A void is classified as S-type if the value of Δ is positive, while if Δ is negative, the void is labelled as R-type. Paz et al. (2013) showed that this classification implies that the region surrounding an R-type void is in expansion, and for S-type voids, it is in contraction.
In this section, we analyse the possibility that these dynamical differences can produce an imprint on the HOD behaviour within the void region. In Fig. 5, we show the results of this analysis. For simplicity, only HOD measurements for one absolute magnitude threshold are given for each catalogue, however, the results are similar for the whole range of limiting magnitudes studied. R-type voids are presented in yellow triangles and S-types in green circles. As occurred with void sizes (Sect. 4.3), we find no substantial difference in the HOD between both void sub-samples.
 |
Fig. 5. HOD in TNG300 and MDPL2-SAG catalogues for different voids classification taking into account their large-scale environment. Upper panel: results for TNG300 and lower panel: MDPL2-SAG catalogue, for R-type voids (yellow) and S-type voids (green). We show as example only two magnitude limits: Mr − 5 log10(h) = − 17 for TNG300 and Mr − 5 log10(h) = − 20 for MDPL2-SAG. The uncertainties are calculated following the standard jackknife procedure. |
From these results, we conclude that the effects that drive the changes of the HOD shape inside the voids are present in all cases, independently of void size or surrounding large-scale environment. Here again, we highlight the consistency between the semi-analytic model and the hydro-dynamical simulation results.
5. Stellar mass content
HOD results obtained in the previous sections indicate that, for a dark matter halo with a given mass above ∼1012 h−1 M⊙, the number of galaxies decreases if the halo resides inside a cosmic void. In this section, we aim to investigate if galaxies in cosmic voids show a different stellar mass content than average. The standard scheme is that the galaxy population can be divided into a central halo galaxy and their satellites. We follow this approach in our analysis.
In order to obtain comparable quantities to those obtained before, we computed the mean stellar mass content for galaxies in haloes of a given mass: ⟨M⋆|Mhalo⟩. This quantity was calculated for both the central galaxy and the satellite population considering all galaxies with Mr − 5 log10(h) < − 17.
Figure 6 shows the ⟨M⋆|Mhalo⟩ results for MDPL2-SAG and TNG300 catalogues on the right and left panels, respectively. As can be seen in the upper panels, central galaxies in voids (red triangles) have a similar stellar content to the general population of central (dark squares) for both catalogues, meanwhile, satellite galaxies inside voids (light red triangles) show significantly lower values of M⋆ concerning the general behaviour of satellite galaxies (grey squares). These results can be clearly seen in the bottom panels, where the ratio M⋆, void/M⋆, all is around ∼10% for central galaxies (red dashed lines), and ∼30% for satellite galaxies (light red dotted lines).
 |
Fig. 6. Stellar mass content in central and satellite galaxies for MDPL2-SAG (left) and TNG300 (right) catalogues. Upper panels: ⟨M⋆|Mhalo⟩ as a function of the halo mass for galaxies inside voids (triangles) and all galaxies (squares). Bottom panels: ratio between M⋆ for galaxies in voids and the overall population. Dashed lines correspond to central galaxies and dotted lines to the satellite population. Error bars are computed using the standard jackknife procedure. |
It is important to note that HOD and stellar mass content results are consistent for both galaxy catalogues, and to point out that a halo inside a cosmic void has fewer galaxies, and also each galaxy has a lower stellar mass content. These two main results are schematised in Fig. 7.
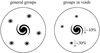 |
Fig. 7. Schematic representation of our main results. Haloes inside cosmic voids have a lower number of member galaxies, which also have a lower stellar mass content (∼10% for central galaxies and ∼30% for satellites), for a fixed halo mass and luminosity threshold. |
6. Halo time-formation in voids
In order to explore possible causes of the differences in the HOD inside cosmic voids, we studied, in both MDPL2-SAG and TNG300 halo catalogues, the distribution of zform, defined as the redshift at which half of the maximum of the halo mass has been accreted onto the halo for the first time. To this aim, we followed the formation history of each halo to determine its maximum mass and the redshift at which it reached half of this value. We expect that the distribution of this parameter inside voids may differ to that in the complete catalogue, and that this different merging history of the haloes populating voids may be responsible for its distinct HOD.
Figure 8 shows the cumulative fraction of zform for MDPL2-SAG (solid lines) and TNG300 (dashed lines) haloes. In both cases, the distributions of zform in voids differ from the global behaviour in the same fashion, showing haloes inside voids (red lines) reaching half of their maximum mass at slightly lower redshifts than elsewhere (black lines). For this analysis, we selected zform as the interpolated redshift between the two closest snapshots where haloes achieve 50% of their maximum mass. These results are consistent with those obtained in previous sections and provide hints that haloes within cosmic voids have a particular formation history with respect to other environments.
 |
Fig. 8. Cumulative fraction of the formation redshift of haloes, zform, for MDPL2-SAG (solid lines) and TNG300 (dashed lines) catalogues. Both panels show the distribution for haloes inside voids (red lines) and all haloes (black lines). |
7. Summary and conclusions
The HOD links the galaxies with their host dark matter halo. In this work, we studied its behaviour in the extremely low-density environments of cosmic voids. For this purpose, we used two simulated galaxy catalogues derived from the MDPL2-SAG semi-analytic model and the TNG300 hydrodynamic simulation. Although these catalogues have different galaxy luminosity functions, void-density tracers, and are built from very different tools, the results obtained for both catalogues are entirely consistent with each other, meaning that the conclusions and discussions addressed in this section apply suitably to the two datasets.
Following our definition of voids, we find a clear dependence of HOD on the environment. The differences increase as the value of the Δlim parameter lowers (more empty voids). However, we found that haloes with masses lower than ∼1012 h−1 M⊙ lack variations in HOD, indicating that for these haloes, the formation of the central galaxies is nearly independent of the large-scale environment density. For larger masses, haloes in sub-dense regions need more mass than average to increase their number of satellite galaxies.
In this work, we used a threshold over-density parameter Δlim = −0.9 to define voids, a usually adopted value that presents the greater differences concerning the global HOD. Our void measurements show that for different ranges of absolute magnitudes, the HOD is always below the overall results. However, the HOD in voids shows no dependence on void radius nor void large-scale environment. By definition, the interior regions of our voids always present the same integrated mass density, so that the lack of HOD dependence on the other parameters suggests that their primary dependence is on the large-scale density where haloes and galaxies reside.
The lower HOD values inside the voids correspond to a smaller number of satellite galaxies per halo. The results of Sect. 5 also show that the average stellar mass per satellite is smaller by ∼30%. Central galaxies are more similar, although their stellar mass is smaller by ∼10%. We conclude that the extreme low-density environment of voids affects the accretion of satellite galaxies generating a population more severely, with fewer satellites and with lower average stellar mass.
Finally, the results of Sect. 6 show that the haloes in voids exhibit lower zform values, so void haloes are younger and may have undergone fewer interactions and mergers with other haloes. This fact could partially explain their difficulty in hosting satellite galaxies.
Acknowledgments
We kindly thank the referee for his/her very useful comments and suggestions that helped to improve this paper. This work was partially supported by Agencia Nacional de Promoción Científica y Tecnológica (PICT 2015-3098, PICT 2016-1975), the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET, Argentina) and the Secretaría de Ciencia y Tecnología de la Universidad Nacional de Córdoba (SeCyT-UNC, Argentina). The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) and the Partnership for Advanced Supercomputing in Europe (PRACE, www.prace-ri.eu) for funding the MultiDark simulation project by providing computing time on the GCS Supercomputer SuperMUC at Leibniz Supercomputing Centre (LRZ, www.lrz.de). The CosmoSim database used in this paper is a service by the Leibniz-Institute for Astrophysics Potsdam (AIP). The MultiDark database was developed in cooperation with the Spanish MultiDark Consolider Project CSD2009-00064. The IllustrisTNG project used in this work (TNG300) have been run on the HazelHen Cray XC40-system at the High Performance Computing Center Stuttgart as part of project GCS-ILLU of the Gauss centres for Supercomputing (GCS).
References
- Artale, M. C., Zehavi, I., Contreras, S., & Norberg, P. 2018, MNRAS, 480, 3978 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Wu, H.-Y. 2013a, ApJ, 762, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., Wu, H.-Y., et al. 2013b, ApJ, 763, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, A., Cole, S., Frenk, C., Baugh, C., & Lacey, C. G. 2000, MNRAS, 311, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Berlind, A. A., & Weinberg, D. H. 2002, ApJ, 575, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Berlind, A. A., Weinberg, D. H., Benson, A. J., et al. 2003, ApJ, 593, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bose, S., Eisenstein, D. J., Hernquist, L., et al. 2019, MNRAS, 490, 5693 [CrossRef] [Google Scholar]
- Cautun, M., Paillas, E., Cai, Y.-C., et al. 2018, MNRAS, 476, 3195 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, L., Padilla, N. D., Valotto, C., & Lambas, D. G. 2006, MNRAS, 373, 1440 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, L., Padilla, N., & Lambas, D. G. 2008, MNRAS, 390, L9 [NASA ADS] [Google Scholar]
- Ceccarelli, L., Paz, D., Lares, M., Padilla, N., & Lambas, D. G. 2013, MNRAS, 434, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Colberg, J. M., Pearce, F., Foster, C., et al. 2008, MNRAS, 387, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Collacchioni, F., Cora, S. A., Lagos, C. D. P., & Vega-Martínez, C. A. 2018, MNRAS, 481, 954 [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cora, S. A. 2006, MNRAS, 368, 1540 [Google Scholar]
- Cora, S. A., Vega-Martínez, C. A., Hough, T., et al. 2018, MNRAS, 479, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Cora, S. A., Hough, T., Vega-Martínez, C. A., & Orsi, Á. A. 2019, MNRAS, 483, 1686 [Google Scholar]
- Gargiulo, I. D., Cora, S. A., Padilla, N. D., et al. 2015, MNRAS, 446, 3820 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, H., Zheng, Z., Zehavi, I., et al. 2015, MNRAS, 453, 4368 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., Rojas, R. R., Vogeley, M. S., & Brinkmann, J. 2005, ApJ, 620, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., Vogeley, M. S., & Pan, D. 2012, MNRAS, 426, 3041 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, Y., Mo, H., & Börner, G. 1998, ApJ, 494, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Yepes, G., Gottlöber, S., Prada, F., & Heß, S. 2016, MNRAS, 457, 4340 [NASA ADS] [CrossRef] [Google Scholar]
- Knebe, A., Stoppacher, D., Prada, F., et al. 2018, MNRAS, 474, 5206 [Google Scholar]
- Kravtsov, A. V., Berlind, A. A., Wechsler, R. H., et al. 2004, ApJ, 609, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. d. P., Cora, S. A., & Padilla, N. D. 2008, MNRAS, 388, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C.-P., & Fry, J. N. 2000, ApJ, 543, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Marinacci, F., Vogelsberger, M., Pakmor, R., et al. 2018, MNRAS, 480, 5113 [NASA ADS] [Google Scholar]
- Naiman, J. P., Pillepich, A., Springel, V., et al. 2018, MNRAS, 477, 1206 [CrossRef] [Google Scholar]
- Nelson, D., Pillepich, A., Springel, V., et al. 2018, MNRAS, 475, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Padilla, N. D., Ceccarelli, L., & Lambas, D. G. 2005, MNRAS, 363, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Padilla, N. D., Salazar-Albornoz, S., Contreras, S., Cora, S. A., & Ruiz, A. N. 2014, MNRAS, 443, 2801 [Google Scholar]
- Pan, D. C., Vogeley, M. S., Hoyle, F., Choi, Y.-Y., & Park, C. 2012, MNRAS, 421, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Patiri, S. G., Prada, F., Holtzman, J., Klypin, A., & Betancort-Rijo, J. 2006, MNRAS, 372, 1710 [NASA ADS] [CrossRef] [Google Scholar]
- Paz, D., Lares, M., Ceccarelli, L., Padilla, N., & Lambas, D. G. 2013, MNRAS, 436, 3480 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J., & Smith, R. 2000, MNRAS, 318, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1980, The Large-scale Structure of the Universe (Princeton: Princeton University Press) [Google Scholar]
- Pillepich, A., Nelson, D., Hernquist, L., et al. 2018a, MNRAS, 475, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Springel, V., Nelson, D., et al. 2018b, MNRAS, 473, 4077 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pujol, A., & Gaztañaga, E. 2014, MNRAS, 442, 1930 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pujol, A., Hoffmann, K., Jiménez, N., & Gaztañaga, E. 2017, A&A, 598, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riebe, K., Partl, A. M., Enke, H., et al. 2013, Astron. Nachr., 334, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodriguez, F., Merchán, M., & Sgró, M. A. 2015, A&A, 580, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rojas, R. R., Vogeley, M. S., Hoyle, F., & Brinkmann, J. 2004, ApJ, 617, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas, R. R., Vogeley, M. S., Hoyle, F., & Brinkmann, J. 2005, ApJ, 624, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz, A. N., Paz, D. J., Lares, M., et al. 2015a, MNRAS, 448, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz, A. N., Cora, S. A., Padilla, N. D., et al. 2015b, ApJ, 801, 139 [Google Scholar]
- Ruiz, A. N., Alfaro, I. G., & Garcia Lambas, D. 2019, MNRAS, 483, 4070 [NASA ADS] [CrossRef] [Google Scholar]
- Scoccimarro, R., Sheth, R. K., Hui, L., & Jain, B. 2001, ApJ, 546, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U. 2000, MNRAS, 318, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2010, MNRAS, 401, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Pakmor, R., Pillepich, A., et al. 2018, MNRAS, 475, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Tecce, T. E., Cora, S. A., Tissera, P. B., Abadi, M. G., & Lagos, C. D. P. 2010, MNRAS, 408, 2008 [NASA ADS] [CrossRef] [Google Scholar]
- Van Den Bosch, F. C., Yang, X., & Mo, H. 2003, MNRAS, 340, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberger, R., Springel, V., Hernquist, L., et al. 2017, MNRAS, 465, 3291 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., van den Bosch, F. C., et al. 2007, ApJ, 671, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2011, ApJ, 736, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Contreras, S., Padilla, N., et al. 2018, ApJ, 853, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Zentner, A. R., Berlind, A. A., Bullock, J. S., Kravtsov, A. V., & Wechsler, R. H. 2005, ApJ, 624, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z., & Weinberg, D. H. 2007, ApJ, 659, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z., Berlind, A. A., Weinberg, D. H., et al. 2005, ApJ, 633, 791 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Impact of number density in HOD determinations
As described in Sect. 2.2, by imposing the same absolute magnitude cut in both galaxy catalogues, and given the differences in the luminosity functions, we obtain galaxy samples with different number densities. As a consequence, HODs are measured in galaxy populations with different number densities. Besides, voids identified using these galaxy tracers also have different number densities as a function of void sizes. In this appendix, we explore the consequences in HOD measurements when we impose the same number density in both simulations on void and galaxy catalogues.
A.1. Equal number density of voids limiting by void radius
Figure A.1 shows the volume number density of voids as a function of radius for TNG300 (green) and MDPL2-SAG (red). In the inset figure, we also present the radii distribution for both void catalogues. As can be seen, the number densities of voids in both catalogues are different. However, it is clear from the figure that if we take voids with Rvoid ∼ 13 h−1 Mpc, both samples are not only similar in density, but also complete in void sizes.
 |
Fig. A.1. Volume number density of voids as a function of void sizes. Green and red curves correspond to TNG300 and MDPL2-SAG catalogues, respectively. The inset figures show the size distributions for both catalogues. |
To analyse both the effects of differences in galaxy number density, and the lack of completeness on our HOD measurements, in Fig. A.2 we give HOD measurements inside voids for the complete sample (circles) and that obtained considering only voids with Rvoid > 13 h−1 Mpc (triangles). We performed this comparison for the TNG300 (right panels) and MDPL2-SAG (left panels) catalogues for two absolute magnitude thresholds, Mr − 5 log10(h) = − 18 and −20 shown in the upper and lower panels, respectively. It can be seen, by restricting the number density of voids, cutting by void radius does not produce a significant change in the HOD determination. We conclude that both the lack of completeness of small voids, and the differences in the number density of voids between the catalogues, do not significantly affect the results of our work.
 |
Fig. A.2. HOD in MDPL2-SAG and TNG300 catalogues for the complete samples of voids (triangles) and voids with Rvoid > 13 h−1 Mpc (circles). Left column: results for MDPL2-SAG and right column: TNG300. Top panels: limit magnitude Mr − 5 log10(h) = − 18 and bottom panels: Mr − 5 log10(h) = − 20. The uncertainties are calculated following the standard jackknife procedure. |
A.2. Equal number density of galaxies and voids
As mentioned above, we identified voids and calculated the HOD using the same absolute magnitude thresholds. However, we can perform this analysis with the same number density of tracers to obtain a similar number density distribution of voids.
In Fig. A.3, we show the volume number density of voids as a function of the radius when the void identification is restricted to the same number density of tracers, ng = 6.37 × 10−3 h3 Mpc−3, for both catalogues. The green curve corresponds to TNG300 and the red one to MDPL2-SAG. The inset in the figure shows the radii distribution for both void samples. As can be seen, these results differ from those presented in Fig. A.1. As expected, both void catalogues now show the same volume number density and size distribution in the complete range of Rvoid.
 |
Fig. A.3. Same as Fig. A.1 but for voids identified using the same number density of tracers. Again, green and red curves correspond to TNG300 and MDPL2-SAG catalogues, respectively, and the inset shows the size distributions of voids. |
Figure A.4 shows the comparison between the HOD inside voids (red dashed lines) with the overall results (black solid lines) for the MDPL2-SAG (left panels) and TNG300 (right panels) catalogues. Small bottom panels show the ratio between HOD in voids and HOD in the complete sample. It is clear that the results are completely consistent with those obtained in the main part of this work, where we used fixed absolute magnitude cuts. It is worth mentioning that the same behaviour is obtained for other equal number density cuts. We believe that it is simpler to use a luminosity threshold to compare the simulations and observational data as well, so our main studies were performed under this prescription.
 |
Fig. A.4. HOD in MDPL2-SAG (left) and TNG300 (right) catalogues for two thresholds of number density of galaxies, ng = 31.42 × 10−3 h3 Mpc−3 (top panels) and ng = 6.37 × 10−3 h3 Mpc−3 (bottom panels). Black solid lines represent the overall HOD, meanwhile red dashed lines represent the HOD measured inside the voids. For each number density and catalogue, the ratio between both HODs are shown at the bottom of each panel. Quoted uncertainties were calculated through the standard jackknife procedure. |
Using these new void catalogues, we used two cuts in number density of galaxies: ng = 31.42 × 10−3 h3 Mpc−3 and 6.37 × 10−3 h3 Mpc−3. This corresponds to the number density of galaxies for Mr = −18 and Mr = −20, respectively, from the Sloan Digital Sky Survey (Guo et al. 2015).
All Tables
All Figures
 |
Fig. 1. Radii distribution of cosmic voids identified in MDPL2-SAG (red) and TNG300 (green) catalogues using Δlim = −0.9. |
| In the text | |
 |
Fig. 2. HODs measured for galaxies with Mr − 5 log10(h) ≤ − 17 in MDPL2-SAG (left) and TNG300 (right) catalogues. Upper panels: resulting HOD for the complete catalogues (black squares – solid lines) and for haloes inside cosmic voids (red triangles – dashed lines) identified with different values of Δlim, as indicated in the key. Bottom panels: ratio between HOD inside voids and the HOD in the complete catalogues. The error bars are computed using the standard jackknife procedure. |
| In the text | |
 |
Fig. 3. HOD in MDPL2-SAG and TNG300 catalogues for different luminosity thresholds. Left column: results for MDPL2-SAG and right column: TNG300 catalogue, for magnitude limits Mr − 5log(h) ranging from −17 to −20, from top to bottom. Black solid lines represent the overall HOD, meanwhile red dashed lines the HOD measured inside voids. For each magnitude bin and catalogue, the ratio between both HODs are shown at the bottom of each panel. The uncertainties are calculated by the standard jackknife procedure. |
| In the text | |
 |
Fig. 4. HOD in MDPL2-SAG and TNG300 catalogues for different void radii. Left column: results for MDPL2-SAG and right column: TNG300 catalogue, for Rvoid < 10 h−1 Mpc (orange), 10 h−1 Mpc < Rvoid < 15 h−1 Mpc (purple), 15 h−1 Mpc < Rvoid < 20 h−1 Mpc (blue), and 20 h−1 Mpc < Rvoid (green). Each panel corresponds to a different magnitude limit Mr − 5 log10(h) ranging from −17 to −20. The uncertainties are calculated following the standard jackknife procedure. |
| In the text | |
 |
Fig. 5. HOD in TNG300 and MDPL2-SAG catalogues for different voids classification taking into account their large-scale environment. Upper panel: results for TNG300 and lower panel: MDPL2-SAG catalogue, for R-type voids (yellow) and S-type voids (green). We show as example only two magnitude limits: Mr − 5 log10(h) = − 17 for TNG300 and Mr − 5 log10(h) = − 20 for MDPL2-SAG. The uncertainties are calculated following the standard jackknife procedure. |
| In the text | |
 |
Fig. 6. Stellar mass content in central and satellite galaxies for MDPL2-SAG (left) and TNG300 (right) catalogues. Upper panels: ⟨M⋆|Mhalo⟩ as a function of the halo mass for galaxies inside voids (triangles) and all galaxies (squares). Bottom panels: ratio between M⋆ for galaxies in voids and the overall population. Dashed lines correspond to central galaxies and dotted lines to the satellite population. Error bars are computed using the standard jackknife procedure. |
| In the text | |
 |
Fig. 7. Schematic representation of our main results. Haloes inside cosmic voids have a lower number of member galaxies, which also have a lower stellar mass content (∼10% for central galaxies and ∼30% for satellites), for a fixed halo mass and luminosity threshold. |
| In the text | |
 |
Fig. 8. Cumulative fraction of the formation redshift of haloes, zform, for MDPL2-SAG (solid lines) and TNG300 (dashed lines) catalogues. Both panels show the distribution for haloes inside voids (red lines) and all haloes (black lines). |
| In the text | |
 |
Fig. A.1. Volume number density of voids as a function of void sizes. Green and red curves correspond to TNG300 and MDPL2-SAG catalogues, respectively. The inset figures show the size distributions for both catalogues. |
| In the text | |
 |
Fig. A.2. HOD in MDPL2-SAG and TNG300 catalogues for the complete samples of voids (triangles) and voids with Rvoid > 13 h−1 Mpc (circles). Left column: results for MDPL2-SAG and right column: TNG300. Top panels: limit magnitude Mr − 5 log10(h) = − 18 and bottom panels: Mr − 5 log10(h) = − 20. The uncertainties are calculated following the standard jackknife procedure. |
| In the text | |
 |
Fig. A.3. Same as Fig. A.1 but for voids identified using the same number density of tracers. Again, green and red curves correspond to TNG300 and MDPL2-SAG catalogues, respectively, and the inset shows the size distributions of voids. |
| In the text | |
 |
Fig. A.4. HOD in MDPL2-SAG (left) and TNG300 (right) catalogues for two thresholds of number density of galaxies, ng = 31.42 × 10−3 h3 Mpc−3 (top panels) and ng = 6.37 × 10−3 h3 Mpc−3 (bottom panels). Black solid lines represent the overall HOD, meanwhile red dashed lines represent the HOD measured inside the voids. For each number density and catalogue, the ratio between both HODs are shown at the bottom of each panel. Quoted uncertainties were calculated through the standard jackknife procedure. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


