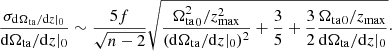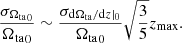| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201937358 | |
| Published online | 17 June 2020 | |
Letter to the Editor
Turnaround density as a probe of the cosmological constant
1
Department of Physics and Institute for Theoretical and Computational Physics, University of Crete, 70013 Heraklio, Greece
e-mail: pavlidou@physics.uoc.gr
2
Institute of Astrophysics, Foundation for Research and Technology – Hellas, Vassilika Vouton, 70013 Heraklio, Greece
3
Department of Astronomy and Astrophysics and KICP, University of Chicago, Chicago, IL 60637, USA
Received:
19
December
2019
Accepted:
20
April
2020
Spherical collapse predicts that a single value of the turnaround density, meaning the average matter density within the scale on which a structure detaches from the Hubble flow, characterizes all cosmic structures at the same redshift. It was recently shown by Korkidis et al. that this feature persists in complex non-spherical galaxy clusters that have been identified in N-body simulations. Here we show that the low-redshift evolution of the turnaround density constrains the cosmological parameters and it can be used to derive a local constraint on ΩΛ, 0 alone, independent of Ωm, 0. The turnaround density thus offers a promising new method for exploiting upcoming large cosmological datasets.
Key words: cosmological parameters / large-scale structure of Universe / galaxies: clusters: general
© ESO 2020
1. Introduction
Despite the many successes of concordance ΛCDM cosmology, increasingly accurate cosmological datasets are starting to reveal tensions (see e.g., Bernal et al. 2016; Zhao et al. 2017; Hildebrandt et al. 2017; Joudaki et al. 2017; Charnock et al. 2017; Motloch & Hu 2018; Planck Collaboration VI 2020; Riess et al. 2018, 2019; Raveri & Hu 2019; Adhikari & Huterer 2019; Handley 2019; Di Valentino et al. 2020a,b). Additionally, our evidence for the existence of vacuum energy, whether it is in the form of a cosmological constant Λ or not, remains indirect, with different datasets constraining primarily the relation between the present-day values of the matter and Λ density parameters (Ωm, 0 and ΩΛ, 0, respectively), rather than ΩΛ, 0 alone. This is in contrast to Ωm, 0, to which certain datasets (e.g., cluster abundances, baryon acoustic oscillations) are almost exclusively sensitive, independently of the value or sheer existence of ΩΛ, 0. This periodically leads to a critical revisiting of the strength of the evidence that ΩΛ, 0 ≠ 0 (Kolb et al. 2006; Buchert & Räsänen 2012; Nielsen et al. 2016; Dam et al. 2017; Colin et al. 2019; Kang et al. 2020), which is also fuelled by the lack of generally accepted fundamental-physics-driven candidates for the nature of vacuum energy. In this context, unexplored probes of the cosmological parameters can provide new insights for the cosmological model.
In recent years, considerable attention has been paid to the properties of cosmic structures on the largest scales as a means of locally probing cosmology and alternative theories of gravity (e.g., Cuesta et al. 2008; Tavio et al. 2008; Tiret & Combes 2008; Pavlidou & Tomaras 2014; Pavlidou et al. 2014; Diemer & Kravtsov 2014; Stark et al. 2017; Baxter et al. 2017; Adhikari et al. 2018; Walker et al. 2019). The turnaround radius (the scale on which a cosmic structure detaches from the Hubble flow) has been the focus of many such studies (Pavlidou et al. 2014; Tanoglidis et al. 2015, 2016; Lee & Li 2017; Bhattacharya et al. 2017; Nojiri et al. 2018; Capozziello et al. 2019; Santa & Enea Romano 2019; Lopes et al. 2019; Wong 2019). The turnaround radius can be measured kinematically in any galaxy cluster as the boundary between the cluster and the expanding Universe. Spherical collapse predicts that all structures turning around at some cosmic epoch share a characteristic average density within the turnaround radius, that is, the turnaround density, ρta. Korkidis et al. (2020) have used N-body simulations to show that a single turnaround radius also meaningfully describes simulated galaxy clusters with realistic shapes and that the average matter density within that turnaround radius has a narrow distribution around a characteristic value for clusters of all masses, which is consistent with the predictions of spherical collapse.
The turnaround density is sensitive to the presence of a cosmological constant Λ. Once the effect of Λ becomes dominant over the gravitational self-attraction of matter, it halts structure growth (Busha et al. 2003, 2005; Pavlidou & Tomaras 2014; Tanoglidis et al. 2015). As a consequence, in an ever-expanding Universe with Λ, not all overdensities are destined to eventually detach from the Hubble flow (e.g., Pavlidou & Fields 2005), and ρta has a hard lower bound of 2ρΛ = 2(Λc2/8πG) (Pavlidou & Tomaras 2014). The evolution of ρta thus changes between early and late cosmic times in a cosmology-revealing manner. In ΛCDM, at early times, when matter dominates, ρta falls as a−3, where a = (1 + z)−1 is the scale factor of the Universe (see e.g., Peebles 1980; Padmanabhan 1993; and Sect. 2). At late times, when Λ dominates, ρta → 2ρΛ ∝ a0 (Fig. 1, upper panel, black solid line). In contrast, in an open matter-only Universe, ρta decreases without bound, as a−3 while matter dominates, and as a−2 when curvature takes over (Fig. 1, upper panel, red dashed line). For the present cosmic epoch, concordance ΛCDM predicts that ρta ∝ a−1.5 (Fig. 1, upper panel, dotted black line), which is already shallower than the asymptotic late-time behavior of a matter-only Universe. It is therefore reasonable to expect that a measurement of the evolution of ρta with redshift could provide evidence for the existence of Λ. This result is independent of the early-times behavior of ρta (universal for all cosmologies), so observations at low redshifts would be sufficient to establish it. The turnaround density could thus provide a ‘local’ probe of the cosmological parameters, demonstrating the existence of dark energy by using its effect on scales that are much smaller than the observable universe and by using structures located at low redshifts.
 |
Fig. 1. Upper panel: evolution with scale factor a of ρta in units of the present-day critical density, ρc, 0. Black solid line: flat ΛCDM cosmology with Ωm, 0 = 0.315 (Planck Collaboration VI 2020). Red dashed line: matter-only open cosmology, with Ωm, 0 = 0.315, ΩΛ, 0 = 0. Black dotted line: present-day (a = 1) tangent to the black solid line, with slope ρta ∼ a−1.5, shallower than the asymptotic behavior of an ΩΛ, 0 = 0 Universe. Lower panel: evolution of ρta with redshift z, for Ωm, 0 = 0.315 and different values of ΩΛ, 0. The magenta shaded box shows the accuracy that can be achieved by measuring ρta in 100 clusters at z = 0.3 with fractional uncertainty of 50% in each, and is indicative of the discriminating power of such an experiment. |
In this Letter, we explore the type of constraints that could be placed on the cosmological parameters, Ωm, 0 and ΩΛ, 0, by using measurements of the present-day value of the turnaround density, ρta, 0, and of its present-day rate of change with redshift, dρta/dz|0. For the predictions of the concordance ΛCDM model, we use the 2018 Planck cosmological parameters (Planck Collaboration VI 2020): Ωm, 0 = 0.315, ΩΛ, 0 = 1 − Ωm, 0, H0 = 67.4 km s−1 Mpc−1. This choice has no qualitative effect on our conclusions.
2. Evolution of ρta
We consider a spherical shell of evolving radius Rs that is destined to eventually turn around, surrounding a single spherical perturbation in an otherwise homogeneous and isotropic Universe. We consider the background Universe on a scale R large enough so that the perturbation negligibly alters its expansion properties.
The evolution of both the background Universe and the shell is described by a Friedmann equation, each with a different curvature constant κ. We consider shells that turn around late enough so that their turnaround radius is much larger than their size at matter-radiation equality and, therefore, we only consider the matter, curvature, and cosmological constant contributions to the Friedmann equation. For the background Universe we write:
From Eq. (1), we can obtain κU in terms of the present-day value of the Hubble parameter, H0 = Ṙ|0/Ṙ0 (quantities with subscript 0 refer to z = 0):
We define the present-day critical density, 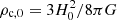 , and the background-Universe scale factor, a = R/R0 = 1/(1 + z) (so that a = 1 today and ρm = ρm, 0a−3). Then, substituting in (1) yields the Friedmann equation in its most frequently encountered form,
, and the background-Universe scale factor, a = R/R0 = 1/(1 + z) (so that a = 1 today and ρm = ρm, 0a−3). Then, substituting in (1) yields the Friedmann equation in its most frequently encountered form,
where 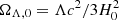 . For the spherical shell around the perturbation, we write:
. For the spherical shell around the perturbation, we write:
In this case, we obtain κs by considering the state of the shell at its time of turnaround, ata1. Then, Ṙs is equal to zero; Rs is equal to the turnaround radius, Rs, ta; and the mass density enclosed by Rs is equal to the turnaround density ρta at ata:
Substituting in (4), defining the shell scale factor as = Rs/Rs, ta (so that as = 1 at the time of turnaround and 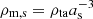 ), and measuring densities in units of the background-Universe critical density ρc, 0 yields:
), and measuring densities in units of the background-Universe critical density ρc, 0 yields:
where Ωta = ρta/ρc, 0. Ωta is a function of ata, which, in turn, depends on the initial overdensity within the shell: initially denser perturbations turn around earlier. Dividing Eq. (6) by Eq. (3) and taking the positive square root (since for as ≤ 1 both Universe and perturbation expand) we obtain:
The turnaround density Ωta as a function of turnaround time ata can be obtained by integrating the perturbation scale factor, as, from 0 to 1 and the Universe scale factor, a, from 0 to ata:
The result of this integration is plotted in the upper panel of Fig. 1 for a flat ΛCDM cosmology, with Ωm, 0 = 0.315 (black solid line) and an open CDM universe with Ωm, 0 = 0.315 and ΩΛ, 0 = 0 (red dashed line). The present-day slope of the scaling is shown with the dotted line. Remarkably, the present cosmic epoch coincides with the era of transition between asymptotic behaviors. For this reason, Ωta(z) curves for different values of ΩΛ, 0 deviate from each other very quickly, already at low z, as shown in the lower panel of Fig. 1.
In principle, two exact measurements of Ωta at two different redshifts would uniquely determine Ωm, 0 and ΩΛ, 0. Alternatively, if Ωta is measured at some redshift (e.g., z = 0, ata = 1), then Eq. (8) yields a constraint on the relative values of Ωm, 0 and ΩΛ, 0. A measurement of the present-day value of Ωta is most sensitive to the value of Ωm, 0 (see Fig. 2, red contours; we also note in the lower panel of Fig. 1 that different values for ΩΛ, 0 yield very similar present-day Ωta when Ωm, 0 remains the same).
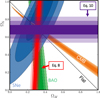 |
Fig. 2. Constraints on Ωm, 0 and ΩΛ, 0 from the cosmic microwave background (CMB, orange contours, WMAP, Komatsu et al. 2011), supernovae (blue contours, Union 2 SN Ia compilation, Amanullah et al. 2010), and baryon acoustic oscillations (green contours, SDSS, Eisenstein et al. 2005; from Amanullah et al. 2010, Fig. 10). The red and purple contours correspond to projected 1, 2, and 3σ constraints implied by Eqs. (8) and (10), respectively, using a presumed high-accuracy measurement of the evolution of Ωta at the low-redshift Universe (∼42 000 galaxy clusters at z ≤ 0.3, with an individual-cluster Ωta uncertainty of 50%, see Sect. 3), yielding a 1.5% accuracy estimate of Ωta0 and a 3.5% estimate of dΩta/dz|0. We have assumed that Ωta evolves with z as predicted by flat Ωm, 0 = 0.315, ΛCDM cosmology. At this level of accuracy, ΩΛ, 0 > 0 could be established at a 14σ confidence level from the turnaround density data alone. |
The lower panel of Fig. 1 shows that the present-day value of the rate of change of Ωta with z for a given value of Ωm, 0 is very sensitive to ΩΛ, 0. This implies that dΩta/dz|0 would be a useful cosmological observable. We can obtain a prediction for dΩta/data|0 = −dΩta/dz|0 by differentiating Eq. (8) with respect to ata:
For the present cosmic epoch (ata = 1) Eq. (9) becomes
independent of Ωm, 0.
If a measurement is then made of Ωta in a sufficient number of clusters at a range of (low) redshifts, then both the slope dΩta/dz|0 and the intercept Ωta0 of the scaling can be derived. A constraint on ΩΛ, 0 alone can thus be obtained from Eq. (10) (see Fig. 2, purple contours).
3. Possible constraints on cosmological parameters
Here we present a simplified estimate of the potential accuracy of a measurement of Ωta0 and dΩta/data|0, and of the associated inference of the cosmological parameters Ωm, 0 and ΩΛ, 0, under the following three assumptions. 1. Errors are dominated by statistical uncertainties. 2. Ωta(z) behaves approximately linearly with z in the low redshift range we will consider. 3. The redshift distribution of measured clusters follows2 dn/dz ∝ z2.
We can obtain an estimate of the uncertainties in dΩta/dz|0 and Ωta0 by considering the errors in the slope and intercept of a linear regression fit to Ωta(z)≈Ωta0 + (dΩta/dz|0)z of a sample of n measurements of (zi, Ωtai) in individual galaxy clusters with z ≤ zmax. In each cluster, Ωtai is measured with some uncertainty σΩta, i. In linear regression, the standard error of the slope, σdΩta/dz|0, is ![$ \sqrt{\left(\sum\nolimits_{i=1}^n \epsilon_i^2/n\right)/\left[(n-2)\mathrm{Var}(z)\right]} $](/articles/aa/full_html/2020/06/aa37358-19/aa37358-19-eq14.gif) , where ϵi are the regression residuals and Var(z) the variance of the independent variable.
, where ϵi are the regression residuals and Var(z) the variance of the independent variable. 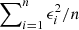 is equal to
is equal to 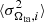 . If Ωta in all clusters can be measured with the same fractional accuracy f, then
. If Ωta in all clusters can be measured with the same fractional accuracy f, then ![$ \sum\nolimits_{i=1}^n \epsilon_i^2/n = \langle f^2\Omega_{\mathrm{ta}}^2(z)\rangle= f^2 \langle \left[{\Omega_{\mathrm{ta}}}_0+(\mathrm{d}\Omega_{\mathrm{ta}}/\mathrm{d}z|_0)z\right]^2 \rangle $](/articles/aa/full_html/2020/06/aa37358-19/aa37358-19-eq17.gif) . To calculate both the latter average and Var(z), we use dn/dz ∼ z2. Finally, dividing by dΩta/dz|0, we obtain the fractional uncertainty of the slope:
. To calculate both the latter average and Var(z), we use dn/dz ∼ z2. Finally, dividing by dΩta/dz|0, we obtain the fractional uncertainty of the slope:
The error of the intercept is related to that of the slope through 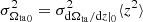 . Calculating the latter average and using Eq. (11), we obtain:
. Calculating the latter average and using Eq. (11), we obtain:
Measurements of Ωta in individual clusters will likely have a relatively poor accuracy (f ∼ 0.5)3. If concordance ΛCDM cosmology holds, then Ωta0 = 3.71 (Eq. (8)) and dΩta/dz|0 = −dΩta/data|0 = 5.67 (Eq. (10)). If then Ωta were measured in the ∼42 000 clusters with zmax = 0.3 and M200 > 0.6 × 1014 M⊙ in the 14 000 square degrees of the Sloan Digital Sky Survey (SDSS) III (Wen et al. 2012) with f = 0.5, we could obtain an estimate of Ωta0 with an uncertainty of ∼1.5%, and an estimate of dΩta/dz|0 with an uncertainty of ∼3.5%. These would yield the constraints on Ωm, 0 and ΩΛ, 0 shown in Fig. 2 with the red (Eq. (8)) and purple (Eq. (10)) contours. The projected measurement of ΩΛ, 0 shown features a 7% accuracy, corresponding to a 14σ confidence level that ΩΛ, 0 > 0. In Fig. 3, we have combined the constraints from Eqs. (8) and (10) to obtain confidence levels on the values of Ωm, 0 and ΩΛ, 0, assuming all uncertainties to be Gaussian and ignoring nonlinear corrections to the low-redshift behavior of Ωta(z).
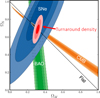 |
Fig. 3. Red and pink contours: projected 1, 2, and 3σ confidence intervals on Ωm, 0 and ΩΛ, 0 from turnaround density data only, obtained by combining the constraints from Eqs. (8) and (10) shown in Fig. 2. As in Fig. 2, the contours are over-plotted on Fig. 10 of Amanullah et al. (2010) showing constraints from supernovae (blue), the CMB (orange), and baryon acoustic oscillations (green). |
4. Discussion
Equation (10) being independent of Ωm, 0 is a nontrivial feature, not shared by any of the currently used probes of the cosmological parameters, which makes the evolution of ρta especially attractive as a direct, local probe of ΩΛ, 0. The CMB primarily probes the geometry of the Universe, so the confidence region on the Ωm, 0 − ΩΛ, 0 plane that can be directly derived from it resembles a negative-slope strip (Fig. 2, orange), and it is only in combination with other probes (e.g., weak lensing, or baryon acoustic oscillations) that the CMB reveals a clear preference for ΩΛ, 0 ∼ 0.7 (e.g., Spergel et al. 2003; Planck Collaboration VI 2020). Cluster abundances and baryon acoustic oscillations on the other hand are primarily sensitive to Ωm, 0 (as is the present-day value of the turnaround density) and by themselves reveal very little about the existence of a cosmological constant (Fig. 2, green and red). This is why observational evidence in support of the currently accepted Ωm, 0 ∼ 0.3 predated the general adoption of a non-zero cosmological constant (e.g., Davis et al. 1985; Bahcall & Cen 1993; Cole et al. 1995). Finally, type Ia supernovae, which, as standard candles, probe the cosmological parameters by mapping the redshift dependence of the luminosity distance, only constrain the relative values of Ωm, 0 and ΩΛ, 0 if they are observed in the low-redshift Universe. This constraint is a diagonal positive-slope strip on the Ωm, 0 − ΩΛ, 0 plane (Perlmutter et al. 1997). The slope of this strip changes with increasing redshift and, thus, only by extending supernovae observations to high redshifts (z ∼ 1) can a measurement of both Ωm, 0 and ΩΛ, 0 be obtained (Goobar & Perlmutter 1995). By contrast, through Eq. (10) we can estimate ΩΛ, 0 today, with no reference to Ωm, 0, using the effect of Λ on galaxy-cluster scales rather than on the Universe as a whole, and based on low-redshift observations alone.
We note that the independence of Eq. (10) from Ωm, 0 holds only at z = 0. Producing an estimate of ΩΛ, 0 using Eq. (10) requires measuring the present-day slope and intercept of Ωta(z), ideally within a redshift range where Ωta grows linearly with z. When data from higher redshifts are used, nonlinear terms will introduce some dependence between the ΩΛ, 0 and Ωm, 0 estimates, which, however, can be quantified based on Eq. (8). In practice, once measurements of Ωta are obtained, a nonlinear fit will be performed on the predicted Ωta(z) parameterized by Ωm, 0 and ΩΛ, 0 (see lower panel of Fig. 1), which will yield a measurement of both cosmological parameters (similar to the contours of Fig. 3). For the range z ≤ 0.3 considered in Sect. 3, the deviation of Ωta(z) from its linear approximation around z = 0 is < 10% for any value of ΩΛ, 0: small, but not subdominant compared to the statistical uncertainties that can be achieved using the large number of available clusters out to this distance. For this reason, the predicted shapes of the constraints from Ωta(z) in Fig. 2 should be viewed as approximations.
The technique discussed here depends on independent measurements of Ωta in different structures and it does not require completeness of the sample of clusters used. For this reason, the same result can be obtained with measurements in only a fraction of the z ≤ 0.3 SDSS clusters, if the sample is optimized in terms of its redshift distribution. There is also margin for improvement in the accuracy of the measurement of Ωta in individual clusters, for example, by applying quality cuts based on the absence of massive neighbors (Korkidis et al. 2020), mass cuts (Köhlinger et al. 2015), or galaxy-number cuts (Karachentsev & Nasonova 2010; Lee 2018). About 500 well-selected z < 0.3 clusters, uniformly distributed over redshift, with Ωta measured with 25% accuracy in each, would be enough to establish ΩΛ, 0 > 0 at the 5σ level.
In estimating the potential accuracy of constraints on Ωm, 0 and ΩΛ, 0, we assumed all uncertainties to be statistical. However, before any statement on cosmology can be made based on measurements of Ωta(z), systematic errors have to be carefully considered as well. For the proof-of-principle calculation of Sect. 2 we used the model of spherical collapse of a single structure in an otherwise uniform and isotropic background universe. Although Korkidis et al. (2020) have shown that the predictions of spherical collapse for Ωta persist in N-body simulations, they have also reported a small systematic shift towards higher values of Ωta due to effects that oppose gravity in realistic cosmic structures (primarily tidal forces from massive neighbors and, to a much smaller extent, rotation; see also Bhattacharya & Tomaras 2019). Whether this shift evolves with redshift, and how, remains to be explored through simulations.
Measuring ρta in a single cluster requires separate measurements of the cluster turnaround radius, Rta, and of the cluster mass, Mta, within Rta; then the turnaround density is simply obtained from 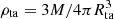 . The quantities Rta and Mta might also suffer from systematic biases in their measurement that also have to be quantified and accounted for, using both mock observations of simulated structures and cross-calibration of measurements using different techniques. The uncertainty of a single measurement of ρta is dominated by that of Rta, which, in turn, can be obtained from observations of peculiar velocities with respect to the Hubble flow of cluster member galaxies, provided these galaxies have distances measured by some indicator other than redshift. Estimates of the turnaround radius have been attempted in several nearby structures (Karachentsev & Kashibadze 2005; Lee 2018), including the Virgo cluster (Karachentsev & Nasonova 2010) and the Fornax-Eridanus complex (Nasonova et al. 2011). Although deriving cosmological parameters from these measurements requires a careful consideration of the uncertainties involved, which is beyond of scope of this work, it is worth noting that these measurements are consistent with Planck-parameter concordance ΛCDM.
. The quantities Rta and Mta might also suffer from systematic biases in their measurement that also have to be quantified and accounted for, using both mock observations of simulated structures and cross-calibration of measurements using different techniques. The uncertainty of a single measurement of ρta is dominated by that of Rta, which, in turn, can be obtained from observations of peculiar velocities with respect to the Hubble flow of cluster member galaxies, provided these galaxies have distances measured by some indicator other than redshift. Estimates of the turnaround radius have been attempted in several nearby structures (Karachentsev & Kashibadze 2005; Lee 2018), including the Virgo cluster (Karachentsev & Nasonova 2010) and the Fornax-Eridanus complex (Nasonova et al. 2011). Although deriving cosmological parameters from these measurements requires a careful consideration of the uncertainties involved, which is beyond of scope of this work, it is worth noting that these measurements are consistent with Planck-parameter concordance ΛCDM.
Deriving Ωta from ρta in general requires an assumption on the value of H0 = h × 100 km s−1 Mpc−1. However, many techniques for the measurement of cluster masses and cluster radii are themselves calibrated on the local expansion of the Universe (i.e., they yield masses in h−1 M⊙ and radii in h−1 Mpc). Estimates of Ωta obtained from such measurements are independent of h.
Extending such analyses to a large number of structures will require the measurement of a large number of cluster masses, redshifts, and independent distance estimates of member galaxies. However, these measurements are already considered of high cosmological significance and large-scale campaigns to obtain them are planned or underway. In this context, the turnaround density provides a promising new way to analyze and exploit upcoming large cosmological datasets.
This is equivalent to assuming distances ∝z and a constant number density of clusters in the nearby Universe. Such a distribution approximates well the redshift distribution of clusters in e.g., Wen et al. (2012) out to z ∼ 0.2. For higher redshifts the number of clusters in Wen et al. (2012) grows more slowly with z, which for a fixed number of clusters results in tighter constraints.
This comes from a typical uncertainty of ∼30% in the cluster mass measurement (e.g., Köhlinger et al. 2015), an uncertainty of ∼10% in the turnaround radius (comparable to what has been claimed for nearby clusters, e.g., Karachentsev & Kashibadze 2005; Karachentsev & Nasonova 2010), and a ∼25% halo-to-halo scatter seen in N-body simulations (Korkidis et al. 2020).
Acknowledgments
We thank A. Zezas, K. Tassis, I. Papadakis, V. Charmandaris, N. Kylafis, and I. Papamastorakis for valuable discussions, and an anonymous referee for their careful review and constructive comments. GK acknowledges support from the European Research Council under the European Union’s Horizon 2020 research and innovation program, under grant agreement no 771282.
References
- Adhikari, S., & Huterer, D. 2019, JCAP, 2019, 036 [CrossRef] [Google Scholar]
- Adhikari, S., Sakstein, J., Jain, B., Dalal, N., & Li, B. 2018, JCAP, 2018, 033 [NASA ADS] [CrossRef] [Google Scholar]
- Amanullah, R., Lidman, C., Rubin, D., et al. 2010, ApJ, 716, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, N. A., & Cen, R. 1993, ApJ, 407, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Baxter, E., Chang, C., Jain, B., et al. 2017, ApJ, 841, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Bernal, J. L., Verde, L., & Riess, A. G. 2016, JCAP, 2016, 019 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, S., & Tomaras, T. N. 2019, ArXiv e-prints [arXiv:1911.06228] [Google Scholar]
- Bhattacharya, S., Dialektopoulos, K. F., Enea Romano, A., Skordis, C., & Tomaras, T. N. 2017, JCAP, 2017, 018 [CrossRef] [Google Scholar]
- Buchert, T., & Räsänen, S. 2012, Annu. Rev. Nucl. Part. Sci., 62, 57 [Google Scholar]
- Busha, M. T., Adams, F. C., Wechsler, R. H., & Evrard, A. E. 2003, ApJ, 596, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Busha, M. T., Evrard, A. E., Adams, F. C., & Wechsler, R. H. 2005, MNRAS, 363, L11 [NASA ADS] [Google Scholar]
- Capozziello, S., Dialektopoulos, K. F., & Luongo, O. 2019, Int. J. Mod. Phys. D, 28, 1950058 [CrossRef] [Google Scholar]
- Charnock, T., Battye, R. A., & Moss, A. 2017, Phys. Rev. D, 95, 123535 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Fisher, K. B., & Weinberg, D. H. 1995, MNRAS, 275, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Colin, J., Mohayaee, R., Rameez, M., & Sarkar, S. 2019, A&A, 631, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuesta, A. J., Prada, F., Klypin, A., & Moles, M. 2008, MNRAS, 389, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Dam, L. H., Heinesen, A., & Wiltshire, D. L. 2017, MNRAS, 472, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Efstathiou, G., Frenk, C. S., & White, S. D. M. 1985, ApJ, 292, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Diemer, B., & Kravtsov, A. V. 2014, ApJ, 789, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Di Valentino, E., Melchiorri, A., & Silk, J. 2020a, ArXiv e-prints [arXiv:2003.04935] [Google Scholar]
- Di Valentino, E., Melchiorri, A., & Silk, J. 2020b, Nat. Astron., 4, 196 [CrossRef] [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Goobar, A., & Perlmutter, S. 1995, ApJ, 450, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Handley, W. 2019, ArXiv e-prints [arXiv:1908.09139] [Google Scholar]
- Hildebrandt, H., Viola, M., Heymans, C., et al. 2017, MNRAS, 465, 1454 [Google Scholar]
- Joudaki, S., Mead, A., Blake, C., et al. 2017, MNRAS, 471, 1259 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, Y., Lee, Y.-W., Kim, Y.-L., Chung, C., & Ree, C. H. 2020, ApJ, 889, 8 [Google Scholar]
- Karachentsev, I. D., & Kashibadze, O. G. 2005, ArXiv e-prints [arXiv:astro-ph/0509207] [Google Scholar]
- Karachentsev, I. D., & Nasonova, O. G. 2010, MNRAS, 405, 1075 [NASA ADS] [Google Scholar]
- Köhlinger, F., Hoekstra, H., & Eriksen, M. 2015, MNRAS, 453, 3107 [NASA ADS] [Google Scholar]
- Kolb, E. W., Matarrese, S., & Riotto, A. 2006, New J. Phys., 8, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Korkidis, G., Pavlidou, V., Tassis, K., et al. 2020, A&A, in press, https://doi.org/10.1051/0004-6361/201937337 [Google Scholar]
- Lee, J. 2018, ApJ, 856, 57 [CrossRef] [Google Scholar]
- Lee, J., & Li, B. 2017, ApJ, 842, 2 [CrossRef] [Google Scholar]
- Lopes, R. C. C., Voivodic, R., Abramo, L. R., & Sodré, L., Jr. 2019, JCAP, 2019, 026 [CrossRef] [Google Scholar]
- Motloch, P., & Hu, W. 2018, Phys. Rev. D, 97, 103536 [CrossRef] [Google Scholar]
- Nasonova, O. G., de Freitas Pacheco, J. A., & Karachentsev, I. D. 2011, A&A, 532, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nielsen, J. T., Guffanti, A., & Sarkar, S. 2016, Sci. Rep., 6, 35596 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nojiri, S., Odintsov, S. D., & Faraoni, V. 2018, Phys. Rev. D, 98, 024005 [CrossRef] [Google Scholar]
- Padmanabhan, T. 1993, Structure Formation in the Universe (Cambridge: Cambridge University Press) [Google Scholar]
- Pavlidou, V., & Fields, B. D. 2005, Phys. Rev. D, 71, 043510 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlidou, V., & Tomaras, T. N. 2014, JCAP, 2014, 020 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlidou, V., Tetradis, N., & Tomaras, T. N. 2014, JCAP, 2014, 017 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1980, The Large-scale Structure of the Universe (Princeton: Princeton University Press) [Google Scholar]
- Perlmutter, S., Gabi, S., Goldhaber, G., et al. 1997, ApJ, 483, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, in press, https://doi.org/10.1051/0004-6361/201833910 [Google Scholar]
- Raveri, M., & Hu, W. 2019, Phys. Rev. D, 99, 043506 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018, ApJ, 855, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., & Scolnic, D. 2019, ApJ, 876, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Santa, C., & Enea Romano, A. 2019, ArXiv e-prints [arXiv:1905.07620] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, A., Miller, C. J., & Huterer, D. 2017, Phys. Rev. D, 96, 023543 [NASA ADS] [CrossRef] [Google Scholar]
- Tanoglidis, D., Pavlidou, V., & Tomaras, T. N. 2015, JCAP, 2015, 060 [CrossRef] [Google Scholar]
- Tanoglidis, D., Pavlidou, V., & Tomaras, T. 2016, ArXiv e-prints [arXiv:1601.03740] [Google Scholar]
- Tavio, H., Cuesta, A. J., Prada, F., Klypin, A. A., & Sanchez-Conde, M. A. 2008, ArXiv e-prints [arXiv:0807.3027] [Google Scholar]
- Tiret, O., & Combes, F. 2008, A&A, 483, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, S., Simionescu, A., Nagai, D., et al. 2019, Space Sci. Rev., 215, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, Z. L., Han, J. L., & Liu, F. S. 2012, ApJS, 199, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, C. C. 2019, ArXiv e-prints [arXiv:1910.10477] [Google Scholar]
- Zhao, G.-B., Raveri, M., Pogosian, L., et al. 2017, Nat. Astron., 1, 627 [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Upper panel: evolution with scale factor a of ρta in units of the present-day critical density, ρc, 0. Black solid line: flat ΛCDM cosmology with Ωm, 0 = 0.315 (Planck Collaboration VI 2020). Red dashed line: matter-only open cosmology, with Ωm, 0 = 0.315, ΩΛ, 0 = 0. Black dotted line: present-day (a = 1) tangent to the black solid line, with slope ρta ∼ a−1.5, shallower than the asymptotic behavior of an ΩΛ, 0 = 0 Universe. Lower panel: evolution of ρta with redshift z, for Ωm, 0 = 0.315 and different values of ΩΛ, 0. The magenta shaded box shows the accuracy that can be achieved by measuring ρta in 100 clusters at z = 0.3 with fractional uncertainty of 50% in each, and is indicative of the discriminating power of such an experiment. |
| In the text | |
 |
Fig. 2. Constraints on Ωm, 0 and ΩΛ, 0 from the cosmic microwave background (CMB, orange contours, WMAP, Komatsu et al. 2011), supernovae (blue contours, Union 2 SN Ia compilation, Amanullah et al. 2010), and baryon acoustic oscillations (green contours, SDSS, Eisenstein et al. 2005; from Amanullah et al. 2010, Fig. 10). The red and purple contours correspond to projected 1, 2, and 3σ constraints implied by Eqs. (8) and (10), respectively, using a presumed high-accuracy measurement of the evolution of Ωta at the low-redshift Universe (∼42 000 galaxy clusters at z ≤ 0.3, with an individual-cluster Ωta uncertainty of 50%, see Sect. 3), yielding a 1.5% accuracy estimate of Ωta0 and a 3.5% estimate of dΩta/dz|0. We have assumed that Ωta evolves with z as predicted by flat Ωm, 0 = 0.315, ΛCDM cosmology. At this level of accuracy, ΩΛ, 0 > 0 could be established at a 14σ confidence level from the turnaround density data alone. |
| In the text | |
 |
Fig. 3. Red and pink contours: projected 1, 2, and 3σ confidence intervals on Ωm, 0 and ΩΛ, 0 from turnaround density data only, obtained by combining the constraints from Eqs. (8) and (10) shown in Fig. 2. As in Fig. 2, the contours are over-plotted on Fig. 10 of Amanullah et al. (2010) showing constraints from supernovae (blue), the CMB (orange), and baryon acoustic oscillations (green). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



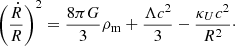
![$$ \begin{aligned} \kappa _Uc^2 = - R_0^2 \left[H_0^2 - \frac{8\pi G}{3} \rho _{\rm m,0} - \frac{\Lambda c^2}{3} \right]\cdot \end{aligned} $$](/articles/aa/full_html/2020/06/aa37358-19/aa37358-19-eq2.gif)
![$$ \begin{aligned} \left(\frac{\dot{a}}{a}\right)^2 = H_0^2 \left[ \Omega _{\rm m,0} a^{-3} + \Omega _{\Lambda ,0} +(1-\Omega _{\rm m,0}-\Omega _{\Lambda ,0})a^{-2}\right], \end{aligned} $$](/articles/aa/full_html/2020/06/aa37358-19/aa37358-19-eq4.gif)
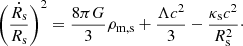
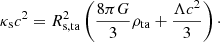
![$$ \begin{aligned} \left(\frac{\dot{a_{\rm s}}}{a_{\rm s}}\right)^2 = H_0^2 \left[\Omega _{\rm ta} a_{\rm s}^{-3} + \Omega _{\Lambda ,0} -(\Omega _{\rm ta}+\Omega _{\Lambda ,0})a_{\rm s}^{-2}\right], \end{aligned} $$](/articles/aa/full_html/2020/06/aa37358-19/aa37358-19-eq9.gif)
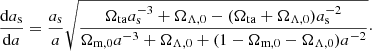
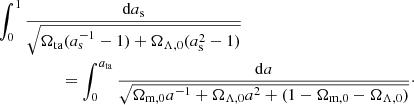
![$$ \begin{aligned}&-\frac{1}{2}\frac{\mathrm{d}\Omega _{\rm ta}}{\mathrm{d}a_{\rm ta}}\int _0^1 \frac{\mathrm{d}a_{\rm s} (a_{\rm s}^{-1}-1)}{\left[\Omega _{\rm ta}(a_{\rm s}^{-1}-1) + \Omega _{\Lambda ,0}(a_{\rm s}^2-1)\right]^{3/2}}\nonumber \\&\qquad \qquad \qquad =\frac{1}{\sqrt{\Omega _{\rm m,0} a_{\rm ta}^{-1} + \Omega _{\Lambda ,0} a_{\rm ta}^2 +(1-\Omega _{\rm m,0} -\Omega _{\Lambda ,0})}}\cdot \end{aligned} $$](/articles/aa/full_html/2020/06/aa37358-19/aa37358-19-eq12.gif)
![$$ \begin{aligned} -\frac{1}{2}\left.\frac{\mathrm{d}\Omega _{\rm ta}}{\mathrm{d}a_{\rm ta}}\right|_0 \int _0^1 \frac{\mathrm{d}a_{\rm s} (a_{\rm s}^{-1}-1)}{\left[{\Omega _{\rm ta}}_0 (a_{\rm s}^{-1}-1) + \Omega _{\Lambda ,0}(a_{\rm s}^2-1)\right]^{3/2}} =1, \end{aligned} $$](/articles/aa/full_html/2020/06/aa37358-19/aa37358-19-eq13.gif)