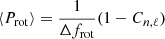| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201936555 | |
| Published online | 11 June 2020 | |
KIC 8975515: A fast-rotating (γ Dor – δ Sct) hybrid star with Rossby modes and a slower δ Sct companion in a long-period orbit
1
Núcleo de Astronomía, Facultad de Ingeniería y Ciencias, Universidad Diego Portales, Av. Ejército Libertador 441, Santiago, Chile
e-mail: anya.samadi@mail.udp.cl
2
Research Institute for Applied Physics and Astronomy, University of Tabriz, PO Box 51664, Tabriz, Iran
3
Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussel, Belgium
4
Department of theoretical Physics and Astrophysics, Physics Faculty, University of Tabriz, PO Box 51664, Tabriz, Iran
Received:
22
August
2019
Accepted:
16
April
2020
Aims. KIC 8975515 is a double-lined spectroscopic binary system with hybrid nature. Regular monitoring with the échelle spectrograph HERMES show that both components have matching atmospheric properties (Teff ∼ 7400 K), and that one of them is a fast rotator (v sin i = 162 versus 32 km s−1). Our aim is to study the Kepler light curve in order to determine the frequencies of the pulsations, to search for regular spacing patterns in the Fourier spectrum, if any, and to discuss their origin in the context of binarity and fast rotation.
Methods. In this paper, we study the properties of the stellar pulsations based on a careful analysis of the Fourier spectrum. This was done by performing repeated frequency-search analyses with successive prewhitenings of all the significant frequencies detected in the spectrum. Moreover, we searched for regular period spacing among the g modes as well as frequency splitting among the g and p modes in frequency.
Results. In the low-frequency regime, one series of prograde g modes and four series of retrograde r modes, were detected. The r modes are well-distributed with respect to the harmonics of the rotational frequency of the fast-rotating star frot = 1.647 d−1. The dominant g mode is f2 = 2.37 d−1. The strongest p mode is f1 = 13.97 d−1. We identified two multiplets of regularly split p modes with the mean values of 0.42 d−1 and 1.65 d−1. In addition, we also identified a few incidences of mode coupling (between f1 and a g or r mode).
Conclusions. We detected five series of retrograde r and prograde g modes as well as two multiplets of p modes with rotational frequency splitttings related to both components of KIC 8975515. We identified the fast-rotating component as a hybrid pulsator with r modes, and the slowly-rotating component as a δ Sct pulsator.
Key words: techniques: photometric / techniques: spectroscopic / binaries: spectroscopic / stars: variables: δ Scuti / asteroseismology / stars: rotation
© ESO 2020
1. Introduction
Asteroseismology is a formidable tool in astrophysics, which allows us to investigate the interior structure of stars based on phenomena observed at their surface. This knowledge is essential for a detailed understanding of both stellar structure and stellar evolution. For γ Dor and δ Scuti variables, which are two subgroups of classical A- and F-type pulsators, are intriguing objects with regard to their stellar interior. They are located at the cross section of the Cepheid instability strip and the main sequence. The first subgroup comprises the γ Dor variables of spectral type A7-F5. They have masses, M, from 1.5 to 1.8 M⊙ and temperatures, Teff, from 6700 to 7400 K (Catelan & Smith 2015). Their pulsations are mainly due to low-degree (ℓ ≪ 4) high-radial order (20 ≲ n ≲ 120) gravity (g) modes (Van Reeth et al. 2016; Saio et al. 2018), which occur in the radiative zones close to the stellar core. The fact that these modes are excited in the deep stellar interior provides us with important information about the chemical gradient of the different layers. As a result of the excited high-radial order g modes (Shibahashi 1979; Tassoul 1980), the occurrence of deviations from a uniform period spacing reveals the chemical inhomogeneities of the near-core convective structures (Miglio et al. 2008). The typical period of their pulsation modes lies in the range from 0.3 to 3 days. Studying the pulsations of γ Dor stars with intermediate to fast rotation provides information on their differential rotation, the angular momentum transport between the layers (e.g., Ouazzani et al. 2017; Li et al. 2019a,b), and other physical processes from the different excitation layers.
Van Reeth et al. (2016) detected the first observational evidence of r modes (global Rossby waves), alongside g modes, for γ Dor stars with significant rotation. Recently, Li et al. (2019b) reported the detection of both r and g mode period spacing patterns for 82 γ Dor stars. In the absence of considerable stellar rotation, toroidal motions associated with r modes cannot provide any compression or expansion. Hence, the stellar atmospheres neither undergo any restoring force nor any light variations. However, in the rapidly rotating regime, the toroidal motions get coupled with spheroidal motions and they present themselves as temperature perturbations. Furthermore, the coupling of spheroidal motions provides excitation to the r modes by the κ mechanism (e.g., DA white dwarfs in Saio 1982; Berthomieu & Provost 1983). We note that r modes appear at lower frequencies than the (prograde) g mode frequencies and their period spacings form a retrograde pattern (Van Reeth et al. 2016; Saio et al. 2018; Li et al. 2019b). Saio et al. (2018) show that r modes of azimuthal order m appear at frequencies lower than m times the rotational frequency.
The second subgroup, involving the δ Sct variables include intermediate-mass, pre-main sequence (Zwintz et al. 2014), main sequence (Aerts et al. 2010), or post-main sequence (Breger 2007) stars in the classical instability strip. They are slightly hotter than γ Dor stars with masses, M, from 1.5 to 2.5 M⊙ and temperatures, Teff, from 6900 to 8900 K. Their pulsation periods range from 0.01 d to 0.25 d (15 min to 6 h) (Aerts et al. 2010; Catelan & Smith 2015). This group pulsates in radial and nonradial, low-degree (ℓ = 1−3) and low-overtone (n = 0, 1, 2, 3, …) p modes (Aerts et al. 2010; Sánchez Arias et al. 2017). The p modes are excited near the surface and reflect the physical properties of the stellar envelope.
Based on theoretical computations, Xiong et al. (2016) show that the δ Sct and the γ Dor pulsators may describe a single, larger instability strip. In the region where both theoretical instability strips overlap, we expect to find hybrid behavior (Balona & Dziembowski 2011; Xiong et al. 2016). This is clearly seen in the observational color-magnitude diagrams, for example, from Kepler (Bradley et al. 2015). Hybrid stars must have both detectable g modes (in the low(er)-frequency range) and detectable p modes (in the high(er)-frequency range) in their Fourier spectrum.
The mode driving mechanism(s) for hybrid stars (γ Dor/δ Sct or δ Sct/γ Dor) is not well-understood. For all the classical pulsators located in the Cepheid instability strip, for example, the δ Sct stars, the κ mechanism is believed to be the major excitation mechanism (Handler 1999; Houdek et al. 1999; Balona et al. 2015). Furthermore, turbulent pressure may also contribute in driving p modes in δ Sct stars (Houdek 2000; Antoci et al. 2014). Whereas, for γ Dor stars, convective flux blocking at the bottom of the convection zone is thought to drive the pulsations (Guzik et al. 2000; Dupret et al. 2004, 2005). The study by Xiong et al. (2016) shows that for the hot δ Sct and γ Dor stars, the (radiative) κ mechanism is the main driving force for both p and g modes, whereas, for the cool δ Sct and γ Dor stars, it is the coupling of convection and oscillations that excites or damps the pulsations. The much larger instability strip described by Xiong et al. (2016) extends well beyond the borders of the classical instability strips of the γ Dor and the δ Sct stars, respectively (e.g., Handler 1999; McNamara 2000; Dupret et al. 2004). Indeed, from an observational perspective, the width of the δ Sct instability strip was shown to extend beyond the theoretical edges (Bowman & Kurtz 2018). Murphy et al. (2019) derived a new empirical instability strip that is much wider, and somewhat hotter, than the theoretical ones (e.g., Handler 1999).
The detection of pulsations in binary systems not only provides an additional tool to derive stellar parameters in an independent way, but it is also the perfect laboratory to check the influence of binarity (e.g., eccentricity, tidal effects Samadi-Ghadim et al. 2018a; Guo et al. 2017, mass transfer Mkrtichian et al. 2018, chemical peculiarities Kolbas et al. 2015, the presence of a third body Samadi-Ghadim et al. 2010; Gies et al. 2015, etc.) on stellar structure, stellar evolution, and the excited oscillation modes. Based on various surveys, the fraction of multiple systems in a population, MF, among the intermediate-mass stars is 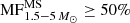 (Duchêne & Kraus 2013). Moreover, the observed frequency of spectroscopic binaries among field intermediate-mass stars is in the range of 30−45% (Duchêne & Kraus 2013). Thus, we may expect that a significant fraction of the γ Dor and δ Sct stars resides in binary or multiple systems. Recently more than 2200 Kepler main-sequence A- and F-type stars were studied using the pulsation timing method in search of binarity across a narrow interval in (log) period allowed by the method (Murphy et al. 2018). These authors detected a binary fraction of 13.9 ± 2.1% among the studied sample. In comparison, Lampens et al. (2018) report an extensive multiepoch spectroscopic survey of 50 Kepler hybrid pulsators for which they derived a multiplicity fraction of at least 27%.
(Duchêne & Kraus 2013). Moreover, the observed frequency of spectroscopic binaries among field intermediate-mass stars is in the range of 30−45% (Duchêne & Kraus 2013). Thus, we may expect that a significant fraction of the γ Dor and δ Sct stars resides in binary or multiple systems. Recently more than 2200 Kepler main-sequence A- and F-type stars were studied using the pulsation timing method in search of binarity across a narrow interval in (log) period allowed by the method (Murphy et al. 2018). These authors detected a binary fraction of 13.9 ± 2.1% among the studied sample. In comparison, Lampens et al. (2018) report an extensive multiepoch spectroscopic survey of 50 Kepler hybrid pulsators for which they derived a multiplicity fraction of at least 27%.
Stellar pulsation studies exploiting the most precise photometric data from space missions to date, such as CoRoT (Baglin et al. 2006), Kepler (K2; Koch et al. 2010), and TESS (Ricker et al. 2015), have become very fruitful as these missions provide light curves of unprecedented accuracy with errors on the order of a few μmag (i.e., few parts per million). These space missions allowed for the detection of several hundreds of hybrid γ Dor-δ Sct pulsators exhibiting both types of modes simultaneously, albeit with very low amplitudes. For a detailed historical review of the discoveries, we refer to Qian et al. (2019). We briefly review a few extensive studies concerning systems with hybrid pulsations here. Examples of such studies are: KIC 4544587, an eccentric eclipsing binary system with an orbital period Porb = 2.19 days (Hambleton et al. 2013); KIC 10080943, a double-lined spectroscopic binary with Porb = 15.34 days (Schmid et al. 2015; Keen et al. 2015); KIC 9592855, a post-mass-transfer eclipsing binary with Porb = 1.2 days (Guo et al. 2017); KIC 4150611, a quintuplet system where the primary is a triplet (Hełminiak et al. 2017); and KIC 6048106, an Algol-type eclipsing binary with Porb = 1.56 days (Lee 2016; Samadi-Ghadim et al. 2018a,b). In addition, Derekas et al. (2019) discovered the double-lined spectroscopic binary KIC 5709664, by using the phase modulation (PM) method (Murphy et al. 2014) and the fitting of radial velocity data, with both r- and p-modes.
In this paper, we focus our attention on a Kepler (candidate) hybrid pulsating star recently discovered as a double-lined, long-period, high mass-ratio, spectroscopic binary system (SB2), KIC 8975515. Our goal is to detect the pulsation frequencies and to characterize the pulsations using the photometric Kepler data. The properties of the Kepler light curves are described in Sect. 2. We describe our methodology for the pulsation study in Sect. 3. The details and results of the frequency analyses for both the high- and the low-frequency regions are presented in Sect. 4. We discuss all the results brought together in Sect. 5. Finally, in Sect. 6, we present a summary and our main conclusions.
2. Photometric observations from the Kepler mission
KIC 8975515, a bright Kepler object with Kp = 9.515 mag, was observed during the quarters Q0−Q17 in long-cadence mode (LC with a sampling of 29.42 min). There are four months of observations in short-cadence (SC) mode that are available with a sampling of 58.85 s from the quarters Q2.3, Q5.1, Q5.2, and Q5.3. Altogether, 1470.46 days (fres = 0.00068 d−1)1 of LC and 121.79 d of SC (fres = 0.00821 d−1) data are available. For the light curves, we took the Kepler original flux and its error for all quarters from the Kepler Asteroseismic Science Operations Centre (KASOC). We first converted the flux to magnitude and then applied a polynomial fit to each quarter. The fit was then subtracted from the original data in order to smooth the trends in each quarter. We finally concatenated the light curves of all quarters and removed the outliers manually. The “detrended” light curve in LC mode was used for this pulsation study.
A close-up view of the light variations of KIC 8975515 is shown in Fig. 1 for both LC and SC sampling modes. The relative magnitude varies with a semi-amplitude of 1 mmag on average.
 |
Fig. 1. Close-up view of the light variations of KIC 8975515. The vertical axis displays the relative magnitude (mag), while the horizontal axis displays the Barycentric Kepler Julian Date (BKJD = BJD – 2454833.0) in days. Panel a: an 11 day interval of the long-cadence (LC) light curve from Q6. Panel b: same time interval of the short-cadence (SC) light curve. |
KIC 8975515 was first studied and reported as an A- and F-type hybrid star by Uytterhoeven et al. (2011). We list the information available from the Kepler input catalog in Table 1, which as derived with the assumption of single star. Moreover, Gaia DR2 (Gaia Collaboration 2018a, 2018b) measured a parallax of ϖ = 2.506 ± 0.0387 mas for this target. The projected rotational velocities are those from Lampens et al. (2018). The orbital parameters, such as Porb, the eccentricity, e, and the mass ratio, q, (the ratio of aA sin i (Table 11) as well as a2 sin i (Table 8) reported by Lampens et al. 2018) showing that q ∼ 0.8 indicate that the system consists of two stars of an almost similar mass in a long-period, eccentric orbit. The updated values in Table 1 are from Lampens et al. (priv. comm.).
Information on KIC 8975515 from surveys and databases.
3. Methodology of the pulsation study
Our approach is based on the Lomb-Scargle periodogram (Lomb 1976; Scargle 1982). We calculated the periodogram of the observed light curves up to the Nyquist frequency (both LC and SC samplings with fNYLC = 24.65 d−1 and fNYSC = 734.07 d−1). The signal-to-noise ratio (S/N) of each frequency was calculated in a box-size of 2 d−1. The prewhitening method is from Vaníček (1971). We consider a frequency to be significant only if S/N ≥ 4, based on the criterion of Breger et al. (1993). For detailed information on the frequency analysis and the prewhitening methods, along with the error determination, see Samadi-Ghadim et al. (2018a). We consider two frequencies to be resolved if their difference is larger than the resolution frequency, fres = 1/T, which is 0.00068 d−1 for the LC light curve. This procedure has provided us with a list of prewhitened frequencies of an acceptable S/N and amplitude. We refer to them as “significant” frequencies and we check the possible origin (whether they can be due to pulsations or caused by some other mechanism). During the frequency analysis, we also checked whether any significant frequency is a linear combination of the previous frequencies of the highest S/N and larger amplitudes (i.e., having a larger than mean S/N and a mean amplitude of the previously prewhitened g modes).
According to asymptotic theory of stellar pulsations (Shibahashi 1979; Tassoul 1980), regular period spacing may occur for the high-radial order g modes, n ≫ l, in which n and ℓ are the radial order and the degree of the mode, respectively. In contrast, for the p modes, regular splitting may occur because of the rotation. For genuine hybrid stars, we can expect to see these regularities in the period and frequency domains for the g modes and in the frequency domain for the p modes. The regular period spacings, for the g and p modes, can be affected by rotation or chemical inhomogeneties (Bouabid et al. 2013; Li et al. 2019b).
4. Frequency analysis
Figure 2 shows the Fourier spectrum both for the LC and SC Kepler light curves. The full Fourier spectrum is shown in pink, while the significant frequencies are presented in black. In the case of SC observations, the illustration (panel b in Fig. 2) shows a close-up view of the frequency range (0−25 d−1) where some significant frequencies show up. Clearly, both LC and SC frequency spectra present almost the same features. For the current study, we used the LC light curve with the longest time base. The list of detected significant frequencies is presented in Table A.2. It is sorted according to decreasing amplitude. In total, we resolved 331 frequencies.
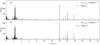 |
Fig. 2. Fourier spectrum of KIC 8975515 (pink). Panel a: frequency spectrum associated with LC observations (pink) and the significant frequencies with S/N ≥ 4.0 in a box size of 2 d−1 (black). Panel b: same as (a) but for the SC observations (referring to the quarters Q2.3 as well as Q5.1, 5.2, and 5.3). There is no significant frequency between 25 and 50 d−1 and we clipped it off from the illustration. |
Interestingly, we can see that the dominant modes pertain to both the low- and the high-frequency regions. Indeed, the dominant frequency in the high-frequency region, f1 = 13.97236 ± 0.00001 d−1, has an amplitude of A1 = 268 ± 5 μmag, while the most significant frequency in the g mode region, f2 = 2.37418 ± 0.00001 d−1, occurs with a very similar amplitude, A2 = 265 ± 5 μmag.
Next, we searched for the frequencies that are combinations of the most significant frequencies, that is, “parent” frequencies. The parent frequencies were chosen among low-frequency modes up to 3.3 d−1 and both have an amplitude and S/N that are higher than the corresponding mean values (i.e., Amean = 13 μmag and S/Nmean = 14.9) of the detected frequencies. Accordingly, we selected 24 frequencies as parent frequencies. Furthermore, we searched for the combination of 13.97 d−1 with any low-frequency mode to reveal the high frequencies which might appear as the coupling of f1 and g modes. This can help to detect low- and high-frequency modes originating from the same star. Generally, a combination frequency has a smaller amplitude than that of both parent frequencies and the difference between this linear combination (of the parent frequencies) and the candidate combination frequency should match within a tolerance of the resolution frequency (e.g., Zhang et al. 2018). The results are reported in Table A.2 and we indicate the parent frequencies with a check mark under the column “P”. The subscript “*” means that the detected frequency is not a unique combination of parent frequencies. Moreover, the frequencies that are a possible harmonic of any parent frequency are also reported in Table A.2.
4.1. The high-frequency region
A quick look at Fig. 2 and a close-up view of the high-frequency section of Fig. 3b shows that the p modes are very sparsely distributed and extend to 22 d−1, unlike the distribution of the g modes (Sect. 4.2). The significant frequencies have amplitudes ranging from A = 1 to 268 μmag.
 |
Fig. 3. Regular frequency spacing for p modes. Panels a1, a2: frequency splittings and their deviation from mean frequency splitting (Table 2). Panels b1, b2: associated frequencies of the detected multiplets of significant frequencies (black) and the full frequency spectrum (pink). |
Because of nonlinear effects, the combination of the g modes, fg, and the dominant p mode (fpmax) may generate some coupled frequency peaks in the form of fpmax ± fg (Kurtz et al. 2014). We found f303 (11.96 d−1) to be a combination of f1 and f16 (2.79 d−1), which is a prograde g mode. On the other hand f285 (12.29 d−1) is a combination of f1 and f18, which is a retrograde mode. Similarly f94 (10.59 d−1) is a combination of f1 with another retrograde mode (f35). We refer to these frequencies with “MC” in Table A.2. We ran a Monte Carlo simulation and found that each combination has about 2% probability of occurring by random chance.
We detected two different types of multiplets: doublets and triplets with the (semi-)regular frequency spacing of Δfmean• = 0.419 ± 0.020 d−1 (magenta in Fig. 3) and Δfmean◼ = 1.654 ± 0.018 d−1 (blue in Fig. 3), located on either side of f1, though not involving f1. The quoted error is the standard deviation. Table 2 lists the associated frequencies in d−1 and the Δf value between each couple of them where ϵΔf equals 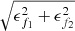 . Figure 3, presents the associated frequencies (lower panel) and their Δf values (upper panel), which are distinguishable by two different colors and symbols, respectively. We detected one frequency in the g mode region f200 (1.6467 ± 0.0001 d−1), which is equal to the larger frequency splitting within the errors (1.654 ± 0.018 d−1). However, there are other groups of frequencies in the interval (6.72 to 8.63 d−1) that are either a combination of prograde g modes (f156, f262) or a combination of prograde g and retrograde r modes (f145, f28, and f281). We suggest that the larger frequency splitting is related to the fast rotating companion and the smaller one is related to the slowly rotating one. We present arguments in favor of this in Sect. 5.
. Figure 3, presents the associated frequencies (lower panel) and their Δf values (upper panel), which are distinguishable by two different colors and symbols, respectively. We detected one frequency in the g mode region f200 (1.6467 ± 0.0001 d−1), which is equal to the larger frequency splitting within the errors (1.654 ± 0.018 d−1). However, there are other groups of frequencies in the interval (6.72 to 8.63 d−1) that are either a combination of prograde g modes (f156, f262) or a combination of prograde g and retrograde r modes (f145, f28, and f281). We suggest that the larger frequency splitting is related to the fast rotating companion and the smaller one is related to the slowly rotating one. We present arguments in favor of this in Sect. 5.
We present the échelle diagram (Fig. 4) for all the significant high frequencies, using the large mean frequency splitting from Table 2. Panel a in Fig. 4 shows the frequency modulo of the mean frequency splitting associated with the slowly rotating star frot = 0.419 d−1. Similarly in panel b, we show the modes with detected regular splittings versus modulo frot = 1.654 d−1, which we associated to the fast-rotating star.
 |
Fig. 4. Échelle diagram of p modes with (quasi-)regular frequency spacing from the Fourier spectrum of KIC 8975515 (Table 2). Symbol size refers to the amplitude of the p modes. Color coding and symbols are similar to Fig. 3. The symbol size is associated with the mode amplitudes. Panel a: frequency modulo of the mean rotational frequency spacing value associated with the slowly-rotating star, 0.419 d−1 (magenta circles), was plotted twice. Panel b: frequency modulo of the mean rotational frequency spacing value associated with the fast-rotating star, 1.654 d−1 (blue squares), was plotted twice. |
4.2. The low-frequency region
We carefully investigated the period spectrum in search of any regular period spacing pattern. The upper panel in Fig. 5 shows different patterns of period spacing ΔΠ that are either prograde (blue squares) or retrograde (green triangles and cyan circles). Their associated periods and frequencies with similar colors are illustrated in the middle and lower panels, respectively. The period spacings and their deviation from the mean value, ϵΔΠ, are reported in Tables 3 and A.1. For the prograde pattern in the frequency interval (2.19 to 2.90) d−1, ΔΠ decreases from 577 to 97 s with an increasing period. Its mean period spacing equals ΔΠmean◼ = 264 ± 132 s; the error is the standard deviation. There are several frequencies that are a combination of parent prograde g modes and they do indeed fit in the pattern very well e.g., in the interval (2.40 to 2.47) d−1. In addition, in the frequency interval (2.68 to 2.70) d−1, we detected a group of frequencies of much lower ΔΠmean⬧ = 73 ± 13 s that are well separated from the precited prograde pattern. We show them with magenta diamonds in Fig. 5 (for the frequencies see Table 3). The retrograde modes in the frequency interval (3.24 to 4.79) d−1 have ΔΠmean• = 226 ± 137 s (cyan circles in Fig. 5). However, some of these modes (in Table A.1) are also combinations of prograde g modes (Saio et al. 2018). These combinations are listed in Table A.2. For these modes, ΔΠ increases from 20 to 491 s with an increasing period. The second group of retrograde modes was detected in the range of (1.66 to 2.15) d−1 (Fig. 5). Though the lower periods show a decreasing period spacing, we consider them to be part of the same group as discussed in Sect. 5. The list of frequencies and their period spacing values are reported in Table A.1. We note that ΔΠ in this pattern first decreases from 268 to 123 s and then increases from 28 to 565 s and its overall average is ΔΠmean▴ = 162 ± 130 s. Similar to previous groups of retrograde modes some of these modes are also a combination of prograde g modes (Table A.2). Furthermore, we detected two more period spacing patterns (retrograde see Sect. 5) with a smaller number of detected modes than other detected modes. These modes are in the frequency intervals of (1.58 to 1.64) d−1 and (5.82 to 6.18) d−1. They are illustrated with olive green pluses and orange stars, respectively, in Fig. 5. Their ΔΠ values and errors are reported in Table A.1. Their average period spacing values are ΔΠmean+ = 272 ± 45 s and ΔΠmean* = 148 ± 65 s, respectively. We suggest that all detected group of modes except the prograde g modes are r modes that are excited because of the fast rotation. We discuss this in detail in Sect. 5. However, several frequencies occur at very low frequencies in the intervals (0.1 and 0.95) d−1 and (1.25 to 1.55) d−1. These modes are either a linear combination of prograde g modes (nfgi − mfgj, n, m = 1, 2, and (i, j) as index of the g modes) or prograde g modes and retrograde r modes f8, f24, and f35 (fgi − frj, i, and j represent the g and r modes). Furthermore, a few frequencies are lower than 0.1 d−1. There are also a few significant frequencies in the frequency interval (4.96 to 5.82) d−1. These frequencies are either a combination of prograde g modes (nfgi + mfgj) or a combination of prograde g and r modes (afgi + bfrj and a, b = 1, 2). The combinations are listed in Table A.2.
 |
Fig. 5. Panel a: period spacing patterns for r and g modes on the period spectrum of KIC 8975515 (LC). Panel b: associated frequencies for the detected g and r modes in panel a (Tables 3 and A.1) are shown with pointed-lines in the same color in panel a. The frequencies in black are the significant modes and the full periodogram of KIC 8975515 is plotted in light pink. |
Detected g modes in the Fourier spectrum of KIC 8975515 (long-cadence observations).
5. Discussion
5.1. The high-frequency modes
In the region (7 to 23.5) d−1, we detected two kinds of multiplets that occur at both sides of the dominant frequency f1 (13.97 d−1), with frequency spacings Δfmean = 1.65 and 0.42 d−1. Both regular patterns, which appear in the form of doublets and triplets, are not perfectly symmetrical which could be indicative of second-order rotational effects (Saio 1981). To the first-order approximation, we have (Saio et al. 2015):
where Cn, ℓ is the Ledoux constant (Ledoux 1951). For the p modes, the Ledoux constant Cn, ℓ is zero, and the rotation period is not related to the mode degree ℓ. Consequently, the rotation period that corresponds to the 1.65 d−1 and 0.42 d−1 splitting equals Prot = 0.604 d and Prot = 2.385 d, respectively. We note that f200 (1.647 ± 0.0001 d−1) might be the rotation frequency of the fast-rotating star. The R value in Table 1 was obtained from blended photometry; however, we know that both components have similar atmospheric properties, thus we may consider the value as a reasonable estimate for each component of the system. If we consider the radius R = 2.197 R⊙ as an estimation of the radius for one of the components, we obtain equatorial velocities of Veq ∼ 182 km s−1 and ∼46 km s−1 and irot ∼ 63° and ∼44° for the fast- and slowly-rotating stars, based on 1.65 d−1 and 0.42 d−1 splittings, respectively. The consistency between the spectroscopic projected rotational velocity and the one estimated from Δfmean indicates that both components of the system may have p modes that are excited.
The three identified combinations of f1 with either one of the prograde g modes or one of the retrograde r modes (mode couplings) suggest that f1, the prograde g, and the retrograde r modes are excited in the fast-rotating component. Furthermore, f1 is the most dominant frequency and a singlet in the p mode region.
The échelle diagram of the detected p modes that belong to regular patterns shows that the ridges including the modes with different regular frequency splittings (0.42 and 1.65 d−1) cross each other. This fact reveals that these modes originate from different companion stars (e.g., Li et al. 2018).
5.2. Regular period spacings of the g modes
Figure 5 illustrates that the excited low-frequency modes include both prograde and retrograde modes. According to Saio et al. (2018) (Sect. 1), we may expect the r modes to appear as groups of low-frequency modes at frequencies that are slightly lower than m times the rotational frequency, mfrot, for intermediate to fast-rotating stars. For KIC 8975515, we indeed found a close connection between the identified retrograde modes and the regular frequency spacing Δfmean◼ = 1.654 ± 0.018 d−1 detected in the high-frequency region. The same conclusion holds for the two small series of frequencies with few modes (the stars and pluses in Fig. 5). The retrograde modes that appear are in distinct period and frequency regions, which are separated by the harmonics with respect to the harmonics of the (large) rotation frequency (f200 = 1.647 ± 0.0001 d−1). Hence, we associated these modes to r modes and assigned an azimuthal order m to them according to their position with respect to the type 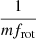 boundaries. For instance, the r modes that are excited at the frequencies lower than 1.65 d−1 (from 1.54 to 1.64 d−1) were assigned to m = 1, and m = 3 r modes appear up to the period limit
boundaries. For instance, the r modes that are excited at the frequencies lower than 1.65 d−1 (from 1.54 to 1.64 d−1) were assigned to m = 1, and m = 3 r modes appear up to the period limit 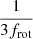 from (3.35 to 4.94) d−1. However, a few modes with a period spacing (73 ± 13 s) that is much lower than all other detections are not located in an expected region following such an interpretation. Thus, we cannot determine their origin and we did not detect any of them to be in regularly split patterns that could be associated to the rotational frequency of either component (or one of the components).
from (3.35 to 4.94) d−1. However, a few modes with a period spacing (73 ± 13 s) that is much lower than all other detections are not located in an expected region following such an interpretation. Thus, we cannot determine their origin and we did not detect any of them to be in regularly split patterns that could be associated to the rotational frequency of either component (or one of the components).
As expected from the models (e.g., Saio et al. 2018), the odd and even r modes display different structures. For example, for r modes m = 3, the period spacing first increases from 71 s to 215 s and then decreases steeply to 69 s (periods from 0.216 to 0.223 d). In the immediately following period interval, the retrograde pattern starts with ΔP values increasing from 225 up to 491 s. However, no modes were detected beyond this range as evidence of the (expected) steep decrease of ΔP close to the period limit (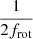 ). Beyond this period limit, the series of prograde g modes (m = −2) appear. In conclusion, we show that an overwhelming majority of the detected low-frequency modes are located in period intervals, which are largely delimited by integer multiples of the rotation frequency of the fast-rotating star. This observational fact supports the conclusion that these r and g modes have the same origin as the series of p modes with Δfmean = 1.65 d−1, that is, they originate from the fast-rotating companion star.
). Beyond this period limit, the series of prograde g modes (m = −2) appear. In conclusion, we show that an overwhelming majority of the detected low-frequency modes are located in period intervals, which are largely delimited by integer multiples of the rotation frequency of the fast-rotating star. This observational fact supports the conclusion that these r and g modes have the same origin as the series of p modes with Δfmean = 1.65 d−1, that is, they originate from the fast-rotating companion star.
6. Summary
We analyzed a four-year long dataset observed in long-cadence mode by the Kepler mission in order to study the pulsations of KIC 8975515. This target consists of a fast-rotating and a slowly-rotating companion star (i.e., v sin i of 162 ± 2 km s−1 and 32 ± 1 km s−1) of otherwise similar masses and atmospheric properties. They form a SB2 system in a long-period and eccentric orbit. Binarity in combination with fast rotation of one of the companions along with hybrid pulsations makes this object of high asteroseismic interest.
The detailed pulsation analysis shows that the most dominant modes in the low- and high-frequency regime have about the same power. Concerning the low-frequency region of the frequency spectrum, the significant pulsation frequencies occur in the range of 1.58−6.18 d−1. We detected five regular period spacing patterns in this regime including a series of prograde g modes and four series of r modes (m = 1, 2, 3, and 4), which are well located in the frequency intervals delimited by the harmonics of the rotational frequency for the fast-rotating star.
We detected two types of combination frequencies in the lower-frequency region, which are either a combination of prograde g modes or a combination of a g and an r mode. Both types appear at frequencies that are lower than m = 1 up to 0.1 d−1 and in between the m = 3 and m = 4 r modes. Some combinations also appear in the intermediate range from 6.72 to 8.63 d−1. Concerning the high-frequency regime, the most dominant p mode f1 (i.e., 13.97 d−1) appears as a singlet between two groups of regularly split modes (20 modes between 7.24 and 21.17 d−1) with Δfrot equal to 0.419 ± 0.020 d−1 and 1.656 ± 0.018 d−1.
We interpreted both groups of p modes to be multiplets of rotationally split p modes since their mean frequency spacings are in agreement with the estimated rotation velocity of each component. In addition, we detected the presence of the low frequency f200 = 1.647 ± 0.001 d−1 whose value clearly agrees with the largest mean frequency spacing supporting the interpretation that it represents the rotation frequency of the fast-rotating star. Furthermore, we identified three combinations of f1 with either one of the prograde g modes or one of the retrograde r modes, among the p modes. This indicates that f1 has the same origin as the prograde g and the retrograde r modes, that is, they all originate from the fast-rotating component. Finally, the échelle diagram of all the detected p mode frequencies versus each one of the mean spacings reveals that the modes associated with the different multiplets are located along crossing ridges, thus each multiplet comes from a different companion star. Once all of these conclusions are put together, along with the fact that the regions where the r and g modes appear as distinct groups with respect to the harmonics of the detected (fast) rotation frequency (f200), show that we can identify the origin of most of the modes detected in KIC 8975515.
In summary, we propose, on the basis of the presented study, that the fast-rotating component is a hybrid (γ Dor – δ Sct) pulsator, which also shows r modes of azimuthal order m = 1, 2, 3, and 4, which are naturally excited because of the fast rotation. Whereas the slow-rotating companion is a δ Sct pulsator with regularly (rotationally) split p modes.
Acknowledgments
The authors thank the Kepler team efforts to provide and present all the observational data and light curves for the public. The authors also appreciate and thank the KASOC team for presenting corrected light curves to the community. The authors acknowledge, the enlightening discussions with Prof. Donald W. Kurtz from Jeremiah Horrocks Institute, University of Central Lancashire, Dr. Giovanni M. Mirouh from Astrophysics Research Group, Faculty of Engineering and Physical Sciences, University of Surrey and Prof. Omar Gustavo Benvenuto from Universidad Nacional de La Plata, Buenos Aires, Argentina. A. S. also thanks Paul Van Cauteren from the Humain Observatory (ROB) for his continuous support. We also acknowledge the anonymous referee for very useful comments on the paper. We acknowledge the financial support of ALMA-CONICYT grant number 31170029 for this research. Furthermore, P.J. acknowledges partial financial support of FONDECYT Iniciación grant number 11170174.
References
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Springer Science+Business Media B.V.) [Google Scholar]
- Antoci, V., Cunha, M., Houdek, G., et al. 2014, ApJ, 796, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006, in The CoRoT Mission Pre-Launch Status – Stellar Seismology and Planet Finding, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, ESA Spec. Publ., 1306, 33 [Google Scholar]
- Balona, L. A., & Dziembowski, W. A. 2011, MNRAS, 417, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L. A., Daszyńska-Daszkiewicz, J., & Pamyatnykh, A. A. 2015, MNRAS, 452, 3073 [NASA ADS] [CrossRef] [Google Scholar]
- Berthomieu, G., & Provost, J. 1983, A&A, 122, 199 [NASA ADS] [Google Scholar]
- Bouabid, M.-P., Dupret, M.-A., Salmon, S., et al. 2013, MNRAS, 429, 2500 [NASA ADS] [CrossRef] [Google Scholar]
- Bowman, D. M., & Kurtz, D. W. 2018, MNRAS, 476, 3169 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, P. A., Guzik, J. A., Miles, L. F., et al. 2015, AJ, 149, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M. 2007, Commun. Asteroseismol., 150, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
- Catelan, M., & Smith, H. A. 2015, Pulsating Stars (Wiley-VCH) [CrossRef] [Google Scholar]
- Derekas, A., Murphy, S. J., Dálya, G., et al. 2019, MNRAS, 486, 2129 [CrossRef] [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Dupret, M.-A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2004, A&A, 414, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dupret, M. A., Grigahcène, A., Garrido, R., et al. 2005, MNRAS, 360, 1143 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018a, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Katz, D., et al.) 2018b, A&A, 616, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gies, D. R., Matson, R. A., Guo, Z., et al. 2015, AJ, 150, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Z., Gies, D. R., & Matson, R. A. 2017, ApJ, 851, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Guzik, J. A., Kaye, A. B., Bradley, P. A., Cox, A. N., & Neuforge, C. 2000, ApJ, 542, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Hambleton, K. M., Kurtz, D. W., Prša, A., et al. 2013, MNRAS, 434, 925 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Handler, G. 1999, MNRAS, 309, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Hełminiak, K. G., Ukita, N., Kambe, E., et al. 2017, A&A, 602, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houdek, G. 2000, in Convective Effects on p-Mode Stability in δ Scuti Stars, eds. M. Breger, & M. Montgomery, ASP Conf. Ser., 210, 454 [Google Scholar]
- Houdek, G., Balmforth, N. J., Christensen-Dalsgaard, J., & Gough, D. O. 1999, A&A, 351, 582 [NASA ADS] [Google Scholar]
- Keen, M. A., Bedding, T. R., Murphy, S. J., et al. 2015, MNRAS, 454, 1792 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Kolbas, V., Pavlovski, K., Southworth, J., et al. 2015, MNRAS, 451, 4150 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Saio, H., Takata, M., et al. 2014, MNRAS, 444, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Lampens, P., Frémat, Y., Vermeylen, L., et al. 2018, A&A, 610, A17 [CrossRef] [EDP Sciences] [Google Scholar]
- Ledoux, P. 1951, ApJ, 114, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. W. 2016, ApJ, 833, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Bedding, T. R., Li, T., et al. 2018, MNRAS, 476, 470 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, G., Bedding, T. R., Murphy, S. J., et al. 2019a, MNRAS, 482, 1757 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., & Antoci, V. 2019b, MNRAS, 487, 782 [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, D. H. 2000, in Delta Scuti and Related Stars, eds. M. Breger, & M. Montgomery, ASP Conf. Ser., 210, 373 [NASA ADS] [Google Scholar]
- Miglio, A., Montalbán, J., Noels, A., & Eggenberger, P. 2008, MNRAS, 386, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Mkrtichian, D. E., Lehmann, H., Rodríguez, E., et al. 2018, MNRAS, 475, 4745 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, S. J., Bedding, T. R., Shibahashi, H., Kurtz, D. W., & Kjeldsen, H. 2014, MNRAS, 441, 2515 [Google Scholar]
- Murphy, S. J., Moe, M., Kurtz, D. W., et al. 2018, MNRAS, 474, 4322 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, S. J., Hey, D., Van Reeth, T., & Bedding, T. R. 2019, MNRAS, 485, 2380 [NASA ADS] [CrossRef] [Google Scholar]
- Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., et al. 2017, MNRAS, 465, 2294 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S.-B., Shi, X.-D., Zhu, L.-Y., et al. 2019, Res. Astron. Astrophys., 19, 064 [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H. 1981, ApJ, 244, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H. 1982, ApJ, 256, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., Kurtz, D. W., Takata, M., et al. 2015, MNRAS, 447, 3264 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., Bedding, T. R., Kurtz, D. W., et al. 2018, MNRAS, 477, 2183 [Google Scholar]
- Samadi-Ghadim, A., Jassur, D. M. Z., Nassiri, S., et al. 2010, New Astron., 15, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Samadi-Ghadim, A., Lampens, P., & Jassur, D. 2018a, Acta Astron., 68, 425 [Google Scholar]
- Samadi-Ghadim, A., Lampens, P., & Jassur, D. 2018b, MNRAS, 474, 5549 [CrossRef] [Google Scholar]
- Sánchez Arias, J. P., Córsico, A. H., & Althaus, L. G. 2017, A&A, 597, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schmid, V. S., Tkachenko, A., Aerts, C., et al. 2015, A&A, 584, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shibahashi, H. 1979, PASJ, 31, 87 [NASA ADS] [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Uytterhoeven, K., Moya, A., Grigahcène, A., et al. 2011, A&A, 534, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaníček, P. 1971, Ap&SS, 12, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xiong, D. R., Deng, L., Zhang, C., & Wang, K. 2016, MNRAS, 457, 3163 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X. B., Fu, J. N., Luo, C. Q., Ren, A. B., & Yan, Z. Z. 2018, ApJ, 865, 115 [Google Scholar]
- Zwintz, K., Fossati, L., Ryabchikova, T., et al. 2014, Science, 345, 550 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Appendix A: Additional tables
Detected r modes in the Fourier spectrum of KIC 8975515, which are located at lower frequencies equal to two and three times (m = 1, 2, 3) the observational rotational frequency frot = 1.65 d−1 (Fig. 3 and Table 2) associated with the fast-rotating star (v sin i = 162 km s−1).
Detected frequencies with acceptable signal-to-noise ratio (S/N) from the Fourier spectrum of KIC 8975515 (long-cadence observations, LC).
All Tables
Detected g modes in the Fourier spectrum of KIC 8975515 (long-cadence observations).
Detected r modes in the Fourier spectrum of KIC 8975515, which are located at lower frequencies equal to two and three times (m = 1, 2, 3) the observational rotational frequency frot = 1.65 d−1 (Fig. 3 and Table 2) associated with the fast-rotating star (v sin i = 162 km s−1).
Detected frequencies with acceptable signal-to-noise ratio (S/N) from the Fourier spectrum of KIC 8975515 (long-cadence observations, LC).
All Figures
 |
Fig. 1. Close-up view of the light variations of KIC 8975515. The vertical axis displays the relative magnitude (mag), while the horizontal axis displays the Barycentric Kepler Julian Date (BKJD = BJD – 2454833.0) in days. Panel a: an 11 day interval of the long-cadence (LC) light curve from Q6. Panel b: same time interval of the short-cadence (SC) light curve. |
| In the text | |
 |
Fig. 2. Fourier spectrum of KIC 8975515 (pink). Panel a: frequency spectrum associated with LC observations (pink) and the significant frequencies with S/N ≥ 4.0 in a box size of 2 d−1 (black). Panel b: same as (a) but for the SC observations (referring to the quarters Q2.3 as well as Q5.1, 5.2, and 5.3). There is no significant frequency between 25 and 50 d−1 and we clipped it off from the illustration. |
| In the text | |
 |
Fig. 3. Regular frequency spacing for p modes. Panels a1, a2: frequency splittings and their deviation from mean frequency splitting (Table 2). Panels b1, b2: associated frequencies of the detected multiplets of significant frequencies (black) and the full frequency spectrum (pink). |
| In the text | |
 |
Fig. 4. Échelle diagram of p modes with (quasi-)regular frequency spacing from the Fourier spectrum of KIC 8975515 (Table 2). Symbol size refers to the amplitude of the p modes. Color coding and symbols are similar to Fig. 3. The symbol size is associated with the mode amplitudes. Panel a: frequency modulo of the mean rotational frequency spacing value associated with the slowly-rotating star, 0.419 d−1 (magenta circles), was plotted twice. Panel b: frequency modulo of the mean rotational frequency spacing value associated with the fast-rotating star, 1.654 d−1 (blue squares), was plotted twice. |
| In the text | |
 |
Fig. 5. Panel a: period spacing patterns for r and g modes on the period spectrum of KIC 8975515 (LC). Panel b: associated frequencies for the detected g and r modes in panel a (Tables 3 and A.1) are shown with pointed-lines in the same color in panel a. The frequencies in black are the significant modes and the full periodogram of KIC 8975515 is plotted in light pink. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.