EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 636 (April 2020) A&A, 636 (2020) A18 Full HTML
Free Access
Issue
A&A
Volume 636, April 2020
Article Number A18
Number of page(s) 11
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201937087
Published online 08 April 2020

© ESO 2020

1. Introduction

The physical properties of dust are directly linked to those of the given interstellar medium (ISM) in which it is found. The dust is not only heated by the interstellar radiation field (ISRF) but it is also affected by other mechanisms at play in the ISM, which can lead to a change in its physical properties and even the destruction of a particular dust grain type. The following processes dominate the evolution of the dust content and the grain size distribution (Hirashita 2015): (i) dust stellar production; (ii) dust destruction by supernova (SN) shocks in the ISM via sputtering; (iii) grain growth via accretion of metals in the gas phase and (iv) coagulation1; as well as (v) grain disruption or fragmentation (shattering). All these processes impact large and small grains differently: (i) supernovae (SNe) and asymptotic giant branch (AGB) stars are predicted to supply mostly large grains2 (Nozawa et al. 2007; Ventura et al. 2012; Bevan et al. 2017; Gall et al. 2014; Priestley et al. 2019); (ii) dust destruction by sputtering affect both large and small grains, with thermal sputtering in SN shocks mostly affecting smaller grains and non-thermal sputtering affecting large grains (Hu et al. 2019); (iii) grain growth via accretion is favoured when the number of small grains is large, as small grains have a larger surface-to-volume ratio (Hirashita 2012); (iv) grain growth via coagulation occurs in the dense ISM and moves the grain size distribution towards larger grain sizes (Ormel et al. 2009); and (v) fragmentation associated with shattering creates a large number of small grains (Jones et al. 1996).

As a result of all these mechanisms, smoothed particle hydrodynamic (SPH) simulations (see e.g. Aoyama et al. 2017) show that the dust grain size distribution evolves as the galaxy evolves; therefore, the evolution of the total dust mass and the grain size distribution in galaxies are closely related (see also Asano et al. 2013a; Mattsson 2016). At t <  0.1 Gyr, the grain size distribution is dominated by large grains (with radius a ≳ 0.1 μm) produced by stars; as the galaxy evolution proceeds, shattering occurs and a large number of small grains (a ≲ 0.01 μm) are formed. Grain growth starts to be an important mechanism and a bump at a ∼ 0.01 μm appears between 1 and 10 Gyr. The increase of small grains favours the coagulation of small grains into larger ones and, consequently, the bump is moved towards larger grains at 5−10 Gyr (Asano et al. 2013a, 2014). The extinction curve strongly depends on the physical and optical properties of dust grains (Salim & Narayanan 2020; Hirashita & Murga 2020), therefore understanding how the grain size distribution evolves can shed light on the origin of the differences in the extinction curves among galaxies at high and low redshifts. In particular, since grain growth has the potential to change the grain size distribution, the shape of the extinction curve will change as a result of grain growth (Hirashita 2012; Asano et al. 2014).

At the moment, there are only a few studies incorporating the evolution of the grain size distribution. Asano et al. (2013a) suggest that shattering produces a large abundance of very small grains (VSGs) and, therefore, it enhances the efficiency of grain growth. Hirashita (2015) (see also Hirashita & Aoyama 2019) propose a two-size approximation of large (a ≳ 0.03 μm) and small (a ≲ 0.03 μm) grains, finding that the ratio of small to large grains is directly linked to accretion, shattering, and coagulation processes. Aoyama et al. (2017) use this approximation to produce, for the first time, hydrodynamical simulations of a galaxy with dust formation and destruction that includes large and small grains. They are able to trace the evolution of the grain size distribution along the evolution of the galaxy and infer the evolution of the dust extinction curves across time (Hou et al. 2017).

Modelling the evolution of each dust grain with a particular size is a very expensive computing task. Hirashita (2015) proposes a two-size approximation of the grain size distribution that alleviates the computing cost while retaining a description of the main features of the evolution of the grain size distribution (see also Aoyama et al. (2020) and Hirashita & Aoyama (2019) for a recent analysis, including a more sophisticated functional form of the grain size distribution). This approach has been very recently applied to cosmological simulations, leading to a breakthrough in the field (Aoyama et al. 2017, 2018; McKinnon et al. 2018; Hirashita & Aoyama 2019; Hou et al. 2017, 2019; Gjergo et al. 2018). Aoyama et al. (2020) have been able to follow the full dust grain size distribution for a single galaxy and have confirmed the results provided by the two grain size approximation. Snapshots of the simulations at young ages seems to explain the extinction curves in high-redshift quasars (Hou et al. 2017). These SPH simulations need to be confronted by observational data, but so far no observational constrains have been available. Comparing the results from the simulations with the observations presented here will allow us to test the assumptions adopted in the simulations.

We present here a systematic study of the radial variations of the abundance of the different grain types over the galactic disc of three galaxies with different morphological types: M 101(SABcd) and NGC 628(SAcd), which are two more massive spiral galaxies, and M 33(SAc), which is a less massive spiral galaxy. In the future, we plan to extend this study to a larger sample of galaxies covering a wider morphological range. We have derived ratios of small to large grains at different galactocentric distances covering a wide range in metallicity (12 + log(O/H) ∼ 7.8−8.8). The variation of the relative abundance of the different grain types within the galactic discs sets up restrictions on the results of the SPH simulations which incorporate dust formation and destruction within a two-grain size formalism. We make a step forward in applying the same fitting methodology to a wide sample of galaxies from the KINGFISH (Kennicutt et al. 2011) and Dwarf Galaxy Survey (DGS, Madden et al. 2013) and compare the observational results with the recent cosmological simulations. These comparisons provide an observational benchmark for future simulations.

In Sect. 2, we present the data and fitting technique applied to the observations. The results of the fitting across the disc of our three galaxy sample is compared with the SPH simulations of a single galaxy in Sect. 3. In Sect. 4, we compare the predictions of cosmological simulations with the results from fitting the integrated spectral energy distributions (SEDs) of a large sample of galaxies. We discuss the main agreements and disagreements between the observations and simulations in Sect. 5. Conclusions are presented in Sect. 6.

2. Data and SED fitting

In this study, we analyse the data in two different ways: one based on a spatially resolved analysis for three individual galaxies and the other based on an analysis of the integrated SED of a sample of galaxies. The first approach allows us to study how the relative contributions of the different grain types changes with metallicity and radius within the galactic disc; the second approach provides information about the relative grain size distributions of galaxies as a whole and, therefore, it is useful when comparing the results of the evolution of the grain size distribution in a cosmological volume. In this last approach, we have included galaxies from two different surveys in order to cover a wide range of morphological types, along with other physical properties of galaxies, such as metallicity, mass, and star formation rate (SFR).

2.1. Spatially resolved studies

We used infrared data from the KINGFISH collaboration (Kennicutt et al. 2011) for M 101 and NGC 628 and from HerM33es (Kramer et al. 2010) for M 33 to derive dust mass maps over the discs of these galaxies. We fit the infrared spectral energy distributions from 3.6 μm to 500 μm at each location of the disc of these spiral galaxies on a pixel-by-pixel basis. We take only those pixels with reliable SEDs, that is, pixels with fluxes in all bands from 3.6 μm to 500 μm with values over three times the standard deviation of the background value in each filter. We applied another mask to cover a wide area of the disc with diffuse and star-forming regions while avoiding low surface brightness areas that would lead to unreliable fits.

We used the classical Desert et al. (1990) dust model, which consists of three different grain populations: polycyclic aromatic hydrocarbons (PAHs), VSGs, and big silicate grains (BGs), and assumed an ISRF with the shape as the solar neighbourhood given in Mathis et al. (1983). The fitting procedure uses a Bayesian approach (see Fig. 1 for a schematic representation of the procedure). We first created a library of models with different values of the input parameters, covering a wide range of possible solutions for each galaxy. Convolution of the modelled SEDs with the corresponding filter bandpass of our observations allows us to obtain the fluxes in each band for each model in the library. With the observed and modelled fluxes, we computed the χ2 value associated to each model. We then built up the probability density function to obtain the best parameter value and its uncertainty. The fitting procedure gives us not only the dust mass but also the relative mass fraction for each grain type, as well as the scale factor of the ISRF. With this information, we created maps of the dust abundance for each grain type across the discs of our three-galaxy sample. Using HI and CO observations, we also produced gas-to-dust mass ratio maps of the disc of each individual galaxy. A detailed explanation of the fitting procedure and the derivation of the gas-to-dust mass ratio maps is presented in Vílchez et al. (2019) for M 101 and NGC 628 and Relaño et al. (2018) for M 33.

thumbnail Fig. 1.

Schematic representation of the SED fitting procedure performed in this study. Nparam is the number of free parameters assumed in the models: relative mass fraction of PAHs, VSGs, and BGs, the scale factor of the ISRF, and a scale factor to describe the contribution of the old stellar population to the NIR-continuum. PDF is the probability density function obtained assuming an uniform prior distribution of the initial parameters. Fmod (band), and Fobs (band) are the corresponding modelled and observed fluxes in each band.

2.2. Integrated SEDs of a galaxy sample

We applied the same fitting procedure to the integrated SEDs of the KINGFISH (Kennicutt et al. 2011) and DGS (Madden et al. 2013) surveys. The integrated photometry of the KINGFISH and DGS is presented in Dale et al. (2017) and Rémy-Ruyer et al. (2015), respectively. To avoid contamination of spurious fits, we only took galaxies with detections in all bands, eliminating uncompleted SEDs and SEDs with upper limits. The strategy for the fitting procedure is the same as the one performed for the disc of M 101, NGC 628, and M 33, but we changed the range for the ISRF scale to provide better coverage of the possible solutions in the case of integrated galaxies. Furthermore, we removed galaxies with fits of residuals in the 24 μm and 70 μm bands above 35%.

The dust model of Desert et al. (1990) assumes that PAHs are grains with radii (0.4–1.2) × 10−3 μm, VSGs correspond to grains with radii of (1.2–15) × 10−3 μm and that BGs are grains with radii larger than 15 × 10−3 μm. The separation in sizes implies that, in comparison with the simulations, small grains are PAHs and VSGs, whereas large grains correspond to silicate BGs in our observations. Despite of the existence of new dust models that are more sophisticated than the classical one proposed in Desert et al. (1990), we decided to apply the latter model for the present study. The main reason is for its simplicity and the small number of free parameters, compared to the more sophisticated recent dust models (e.g. Draine & Li 2007; Compiègne et al. 2011; Jones et al. 2013). In Relaño et al. (2016) we compared the dust models of both Desert et al. (1990) and Compiègne et al. (2011) and found that they both agree in reproducing the relative abundance of VSG and BG grains.

3. Comparison with SPH simulations of a single galaxy

Aoyama et al. (2017) and Hou et al. (2017) performed GADGET-3 SPH simulations (originally explained by Springel 2005) of an isolated galaxy incorporating dust evolution mechanisms. The simulations are based on those provided by the low-resolution model of AGORA simulations (Kim et al. 2014), with a spatial scale of ∼80 pc. An initial disc is created as a characteristic model of galaxies at z ∼ 1. The old stellar populations are dynamically collisionless star particles that build the initial mass of the disc and bulge. The initial physical parameters of the simulated galaxy are shown in Table 1 in Aoyama et al. (2017), with initial stellar and gas distributions described in Kim et al. (2014). Once the galaxy is built with the initial disc, star formation occurs following the prescription given in Eq. (2) of Aoyama et al. (2017), which parameterises the SFR in terms of the gas density. Each new created star particle is seen as a single stellar population with Chabrier ( 2003) initial mass function (IMF) and carries information on the stellar mass, metallicity, and formation time.

Dust is produced by the metals ejected by SNe and the metal enrichment is assumed to occur ∼4 Myr after the star formation. Dust production by AGB stars is not included in these simulations. The amount of dust produced by AGB stars is still under debate, as is the question of how the dust yields from AGB stars depend on other physical parameters, such as metallicity, star formation history, or the internal parameters of stars (e.g. Nanni et al. 2018, 2019). Contribution to the dust budget from AGB stars can exceed the amount of dust produced by SNe at later ages, with a higher contribution of AGB stars at lower metallicity (e.g. Fig. 3 in Valiante et al. 2009). However, accurate dust budget calculations done in the Magellanic Clouds (Srinivasan et al. 2016; Zhukovska & Henning 2013), where stars can be individually observed, suggest that the amount of dust observed in the ISM is higher than the cumulative dust mass produced by AGB stars during cosmic time scales. Therefore, we consider that excluding AGB star dust production in the simulation does not substantially impact the results of the simulations. Future observational facilities are needed to estimate with greater accuracy the amount of dust produced by AGB stars in galaxies located at a further distance than the Magellanic Clouds (e.g. Boyer et al. 2015).

The simulations adopt the two-grain size distribution approximation presented in Hirashita (2015), separating the grain size distribution into small and large grains at a ∼ 0.03 μm (with a being the grain radius). The separation is justified on the basis of a full calculation of the grain size distribution performed by Asano et al. (2013a), who showed that the processes dominating the small grain abundance create a bump in the size distribution at small grain sizes, while dust production by stars creates a bump in the large grain size regime. The separation between these two bumps is at a ≃ 0.03 μm. The Desert et al. (1990) dust model assumes a separation between small and large grains of a = 0.015 μm, which is similar to the separation limit of the two grain size approximation and also separates the two bumps predicted by the analysis of the full grain size distribution. The time evolution of the dust abundances is followed in each gas particle and includes stellar dust production, SN destruction, grain disruption by shattering in the diffuse ISM, and grain growth by coagulation and accretion in the dense ISM. The simulations assume a solar metallicity of Z⊙ = 0.02 and, therefore, for consistency, we assume the same value for the observations presented here. We refer the reader to Aoyama et al. (2017) for a full description on how each process is incorporated into the simulations, along with the dependencies of the time scales, and we refer to Hou et al. (2017) for a study of the extinction curves predicted by these simulations.

3.1. Radial profiles of the dust mass

We first compared the radial variation of the dust content predicted by the simulations with the results from the observations. Figure 2 shows the radial profiles of the dust mass surface density obtained from the observations, as well as predictions of the simulations at different time steps of the galaxy evolution. The data points show the mean value within elliptical rings of 0.1 R25 width and the error bars represent the variation of the dust mass surface density in each ring. In general, the dust mass surface density decreases towards the outer parts of the galaxy. The decrement is more pronounced for M 101 and NGC 628 than for M 33, as the first two galaxies show higher metallicity values in their centres and more pronounced metallicity gradients: 12 + log(O/H) = 8.72−0.83 R/R25 for M 101; (Croxall et al. 2016), 12 + log(O/H) = 8.84−0.49 R/R25 for NGC 628 (Berg et al. 2015); and 12 + log(O/H) = 8.50−0.38 R/R25 for M 33 (Bresolin 2011).

thumbnail Fig. 2.

Radial profile of the dust mass surface density for M 101 (top), NGC 628 (middle), and M 33 (bottom) compared to the profiles provided by the simulations performed by Aoyama et al. (2017) and Hou et al. (2017). Dust production in stellar ejecta, dust destruction by SN shocks, grain growth by accretion and coagulation, as well as shattering, are taking into account in the simulations.

The model at 0.3 Gyr shows very low dust masses compared to the observations, while models at later ages, namely 1−10 Gyr, fit at least part of the disc of the galaxies. The simulations predict, however, high dust masses and steeper radial gradients in the centre of the galaxy at all ages, which does not agree with the mild gradients across the whole disc obtained from the observations. The discrepancy might be produced by the assumptions in the initial conditions of the simulations. Dust is produced in the simulations by the metals ejected from the core-collapse SNe. The SN rate depends on the IMF and the SFR prescription assumed in the simulations. The SFR is parameterised in terms of the gas density (see Eq. (2) in Aoyama et al. 2017) and therefore the metal enrichment is influenced by the initial gas distribution of the galactic disc. The fact that in the centre of the galaxies the simulations do not describe properly the observations would indicate that the gas distribution of the simulated galaxy does not completely reproduce the exact gas distribution of our three galaxies. Indeed, the simulated galaxy has a large bulge, while none of these galaxies show signatures of large bulges in their centres: Sheth et al. (2010) classified NGC 628 and M 101 as galaxies hosting a pseudobulge and Corbelli & Walterbos (2007) did not find any kinematical signature of a bulge in M 33. We should point out here that our goal in the present paper is not to perform a SPH simulation of each individual galaxy, but to provide a global observational comparison that tests the results and provide clues for possible caveats of the simulations. Some galaxies in the KINGFISH survey present signatures of central bulges (e.g. NGC 4536 and NGC 1291, Salo et al. 2015). In the future, we plan to extend our spatially resolved study to a larger number of galaxies from the KINGFISH survey, covering a broader range of morphologies. In this way, we will be able to test whether our interpretation of the disagreement of the radial profile between data and simulations is correct and verify whether galaxies with a larger bulge indeed fit the simulations better.

3.2. Dust to gas mass ratio versus metallicity and radius

In Fig. 3, we show how the dust-to-gas mass ratio (Dtot) derived from our observations compares to the SPH simulations. In the right panels, we show the radial variation of Dtot (normalised to R25), and in the left panels we show the variation of Dtot as a function of metallicity. The observed data points have been derived using the gas-to-dust mass maps obtained previously in Vílchez et al. (2019) for M 101 and NGC 628, and Relaño et al. (2018) for M 33. We integrate these maps in elliptical rings of 0.1 R25 width and take the mean value as the representative value for the gas-to-dust mass ratio in each ring. Each data point in Fig. 3 is, therefore, the inverse of the mean value of each elliptical ring and the error bar represents the corresponding variation within the ring. The metallicity in each ring (scaled to Z⊙ = 0.02) has been obtained using the metallicity gradients derived from spectroscopic observations for each galaxy: Croxall et al. (2016) for M 101, Berg et al. (2015) for NGC 628, and Bresolin (2011) for M 33 (see previous section).

thumbnail Fig. 3.

Comparison of the variation of the dust-to-gas mass ratio (Dtot) with metallicity (left) and galactocentric radius (right) for M 101 (top), NGC 628 (middle), and M 33 (bottom) with the SPH simulations of an isolated galaxy performed by Aoyama et al. (2017) and Hou et al. (2017). Thick lines represent mean values for each model in the simulation and the coloured areas cover the 25 and 75 percentile of the particle distribution. A solar metallicity of Z⊙ = 0.02 has been adopted for our observations for consistency with the solar metallicity assumed in the simulations.

Models at 0.3 Gyr are not presented in these figures as they are not able to reproduce our observations. This seems plausible as these galaxies are already older than 0.3 Gyr: Lin et al. (2013) and Sánchez-Blázquez et al. (2014) estimate ages for the stellar population of the disc of τ ∼ 6−7 Gyr for M 101 and τ ∼ 3−6 Gyr for NGC 628; while for M 33, Javadi et al. (2017) show that the oldest star formation epoch occurred at τ ≈ 3−6 Gyr, with a second epoch ≈200−300 Myr ago, reaching a level of almost four times the SFR of the earlier epoch.

The agreement between Dtot derived from observations and the predictions of the simulations is good at high metallicities and in the central parts of the galaxies, but at low metallicities, the observed Dtot is always higher than the values predicted by the simulations. Since the dust mass surface density is not well reproduced by the observations, the fact that Dtot follows the behaviour of the observations in the central parts of the galaxies indicates that the gas mass fraction assumed in the simulations might be too high. An excess in the gas mass has already been suggested in Hou et al. (2019), as their simulations seem to produce a few times higher gas-to-stellar mass ratio than the observed ratio derived in Saintonge et al. (2017). There is also an excess of the simulated gas mass compared to the results of the ALFALFA survey presented in Maddox et al. (2015).

In the lower metallicity range, corresponding to the outer parts of M 101 and M 33, the observed Dtot is not well reproduced by the SPH simulations. Only the behaviour of Dtot in NGC 628, which has a relatively high molecular gas mass fraction across its disc and does not reach as low levels of metallicity as the other two galaxies, seems to agree with the simulations. The simulations seem to fail to explain the Dtot behaviour at low metallicities and low dense gas fractions.

The comparison between simulations and observations is better in the Dtot versus radius relation (Fig. 3, right panels) than in the relation with metallicity (Fig. 3, left panels). This is expected as binning in metallicity follows exactly the metal enrichment of each particle in the simulations, which is subject to the initial conditions of the simulation: SFR, IMF, and initial gas distribution in the disc, as well as the metal yields assumed in the simulations (see Kim et al. 2014 for details). In our observations, we assume a metallicity radial gradient derived from optical spectroscopic data where the electron temperature had previously been obtained (see Sect. 3.1). In this sense, we are not taking into account possible azimuthal metallicity variations within the disc and each radial bin has a single metallicity defined by the metallicity gradient. However, it is expected that these azimuthal variations, when present, are not above ∼0.1 dex, typically. The fact that the simulations are able to adequately reproduce the radial trends of the observations, and not the metallicity, might indicate that azimuthal variations in metallicity predicted by the simulations are large and significantly affected by the initial conditions.

3.3. Small to large grain ratio versus metallicity and radius

We present in Fig. 4 the ratio between the total mass of the small grains and large grains, DS/DL, as a function of metallicity (left panels) and radius (right panels). The data points were obtained integrating the DS/DL maps derived from the SED fitting. Each point corresponds to the mean value in each ring with error bars representing the dispersion of the values within each ring. The thick lines show the predictions of the SPH simulations at different time steps of the galaxy evolution, and coloured areas show the dispersion in the models.

thumbnail Fig. 4.

Comparison of the variation of the small-to-large grain mass ratio (DS/DL) with metallicity (left) and galactocentric radius (right) for M 101 (top panels), NGC 628 (middle panels), and M 33 (bottom panels) with the SPH simulations of an isolated galaxy performed by Aoyama et al. (2017) and Hou et al. (2017). Thick lines represent mean values for each model and the coloured areas cover the 25 and 75 percentile of the particle distribution. A solar metallicity of Z⊙ = 0.02 was adopted.

Within each galaxy, DS/DL seems to be independent of the metallicity and radius, especially in M 101. However, in M 33 we see a mild steady radial decline, although at the 1σ level and in NGC 628, the ratio tends to drop towards the inner, high-metallicity parts of the galaxy, with a central value clearly lower than the rest of the disc. Interestingly, the outer parts of M 101 reach the same low metallicity as M 33, but they still present a constant and higher DS/DL than M 33. The model at 1 Gyr reproduces the drop of the ratio at low metallicity in the outer parts of M 33, while models of 3−10 Gyr better describe the trend for M 101 and NGC 628. This is in agreement with the fact that M 33 is expected to be a younger (and more flocculent) galaxy (Javadi et al. 2017) than M 101 and NGC 628 (Lin et al. 2013; Sánchez-Blázquez et al. 2014).

The radial profile of DS/DL (right panels in Fig. 4) gives a few hints about which dominant mechanism influences the evolution of the dust at each galactocentric radius. As has already been shown in Hirashita (2015), stars mainly form large grains and coagulation enhances the large grain fraction; the small grain fraction is enhanced by shattering in the diffuse medium and accretion of gas phase metals onto dust. On the other hand, shock destruction in SNe will make both large and small grain fractions to decrease. Time scales for each mechanism depend on different physical quantities: the accretion time scale is inversely proportional to metallicity and the fraction of dense gas, while the coagulation time scale depends only on the fraction of dense gas as well as on the amount of small grains. Shattering mainly occurs in diffuse areas with densities below a certain threshold (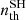 = 1 cm−3, Aoyama et al. 2017). Its time scale is therefore related to the SN rate (and thus to SFR), as the shock destruction time scale.

We explain the radial behaviour of DS/DL for our three galaxies in comparison with the results of the simulations and the radial profiles of the SFR and the molecular gas fraction for each galaxy. These are presented in Fig. 5. The SFR has been derived for each galaxy using FUV (GALEX) and total infrared (TIR) luminosities, and the prescription given in Hao et al. (2011):

(1)

thumbnail Fig. 5.

Radial profile of the SFR (left) and molecular gas fraction (right) (normalised to R25) for NGC 628 (red squares), M 101 (black circles) and M 33 (green diamonds). SFRs were derived using FUV (GALEX) and TIR luminosities (see Eq. (1)). The molecular gas fraction was derived from HI and CO observations assuming a XCO factor inversely proportional to the metallicity (see Vílchez et al. 2019, for more details). The elliptical rings have a width of 0.1 R25. Data points and coloured areas correspond respectively to the mean value and the dispersion for each ring.

with LFUV and LTIR in erg s−1. The TIR luminosity was derived using all the bands included in the SED fitting and the parameterisation of Boquien et al. (2011).

The molecular gas fraction was obtained from HI and CO observations assuming a XCO factor inversely proportional to the metallicity (see Vílchez et al. 2019; Relaño et al. 2018 for more details). We make the proxy that the molecular gas fraction describes the dense gas fraction of the galaxy, which seems plausible as the molecular gas is in general the densest gas in the ISM.

There is a drop of DS/DL in the central parts of NGC 628, where the metallicity and the molecular gas fraction are high (see middle panels of Fig. 5). In these central areas, dust is growing via accretion and Dtot is increasing (see both panels of Fig. 3) with metallicity. The critical metallicity, as defined by Asano et al. (2013b), has been reached and the molecular gas fraction is quite high, which are the conditions for accretion to take place. However, in the most inner parts, at R ≤ 0.3 R25, coagulation is taking over and a high fraction of large grains is forming, causing DS/DL to decrease. The coagulation time scale depends inversely on the abundance of small grains and the dense gras fraction (e.g. Eq. (22) in Aoyama et al. 2017) and both quantities are high in the central parts of NGC 628: small grains are initially abundant due to accretion and the molecular gas fraction is above fmol ≥ 0.7.

The behaviour of DS/DL for M 33 is completely different from NGC 628. The ratio increases in the inner region (although at 1σ level) and shows a drop in the outer R ≥ 0.3 R25 part of the disc. Only the model at 1 Gyr shows an increase of DS/DL in the central parts of the galaxy, corresponding to early phases where the high SFR produces high dust formation by stellar sources in the form of large grains but also shattering is dominant, and therefore, an effective conversion of large grains into small grains is happening. Shattering is produced by large grains colliding in shocks in the diffuse ISM. The shattering time scale is inversely dependent on the large grain abundance and the gas density. M 33 presents a significant increase of the SFR in the central areas while the molecular gas fraction is relatively low (fmol ≤ 0.6, Fig. 5), which makes shattering the most favourable process in these regions.

The radial trend of DS/DL for M 101 is relatively constant. In the central areas (R ≤ 0.2 R25) the metallicity is high and the molecular gas fraction is above 0.7. Accretion is occurring in the central areas but the effect might well be balanced by coagulation, whose time scale inversely depends on the dense gas fraction, and shattering as SFR increases significantly in the central R ≤ 0.4 R25 areas (left panel Fig. 5). In the outer parts of M 101, the dense gas fraction drops significantly, the metallicity is also low and therefore, accretion and coagulation are not expected to be significant. The balance between stellar dust production in the form of large grains and shattering would keep DS/DL constant.

4. Comparison with cosmological simulations

In this section we extend the comparison of DS/DL to a large galaxy sample. We derive a value of DS/DL for each galaxy using the integrated SED and compare the results with the predictions of cosmological simulations. Hou et al. (2019) and Aoyama et al. (2018) performed SPH simulations and followed the evolution of the dust properties within a cosmological volume. They assumed the two grain size approximation from Hirashita (2015) and dust reprocessing in the ISM: grain destruction by SN shocks, grain disruption by shattering in the diffuse ISM, and grain growth by coagulation and accretion. Unlike the single galaxy simulations performed by Aoyama et al. (2017), the cosmological simulations made by Hou et al. (2019) and Aoyama et al. (2018) do include dust formation by AGB stars, in addition to dust formation by SNe. Dust grains are additionally destroyed by sputtering in hot gas (> 106 K) regions in the circumgalactic medium. While Aoyama et al. (2018) did not include AGN feedback and focused more in the overall dust properties of the cosmological volumen, Hou et al. (2019) included AGN feedback and studied the dust scaling relations in galaxies as well as the evolution of the grain size distribution. Here we compare our results with the predictions of Hou et al. (2019).

In the top panel of Fig. 6, we show the mean value of DS/DL (black thick line) of the simulated galaxy distribution as a function of the metallicity. The coloured area represents the 1σ limit of the galaxy distribution. For low-metallicity galaxies, log(Z/Z⊙) ∼ − 2, dust is mainly produced by stars and shattering is the only source of small grains. At a higher metallicity (−2 ≤ log(Z/Z⊙) ≤ −1), accretion becomes efficient and DS/DL start to increase significantly. At −1 ≤ log(Z/Z⊙) ≤ −0.5, coagulation becomes efficient and a balance between the amount of small grains created by accretion and shattering, and the large grains created via coagulation is achieved. The result is a constant DS/DL in this metallicity range. At higher metallicities, log(Z/Z⊙) ≥ −0.5, coagulation dominates against accretion and shattering and, therefore, the ratio decreases with increasing Z. In the bottom panel of Fig. 6 we show the variation of DS/DL as a function of the stellar mass of the galaxy. The simulations present a similar behaviour as in the top panel, which reflects the fact that the simulations generally reproduce the expected mass–metallicity correlation (see Fig. 2 in Hou et al. 2019). In the middle panel of Fig. 6, a mild trend of low DS/DL at higher specific SFR (sSFR) is observed. The trend is however modulated by the metallicity, as it can be seen in the full galaxy distribution shown in Fig. 6c of Hou et al. (2019).

thumbnail Fig. 6.

Comparison of DS/DL with metallicity (top), sSFR (middle) and stellar mass (bottom) obtained from cosmological simulations from Hou et al. (2019) and the results obtained from SED modelling for the KINGFISH (black dots) and DGS (blue asteriscs). SFRs were derived for KINGFISH galaxies using the updated FUV (GALEX) and TIR luminosities given in Dale et al. (2017), while the SFR for the DGS were taken from Rémy-Ruyer et al. (2015) who used Hα and TIR. Stellar masses for both samples were obtained using the prescription given in Eskew et al. (2012).

We compared the trends predicted by the cosmological simulations in Fig. 6 with the DS/DL derived from fitting the integrated SEDs of the KINGFISH and DGS galaxies. In general, there is a relatively good agreement between DS/DL predicted by the simulations and those derived from the SED fitting. In the top panel of Fig. 6 we see that, despite some KINGFISH and DGS galaxies having a high DS/DL, most of the galaxies fall within the relation found by the cosmological simulations.

The trend of DS/DL versus sSFR (middle panel of Fig. 6) is reproduced well overall by the KINGFISH galaxies, except for 7 galaxies having log(DS/DL) above ∼−0.3. Almost all the DGS shows higher DS/DL values than the simulated ones at a given sSFR. It seems the simulations are not able to completely trace the evolution of the large and small grains for the DGS galaxies. It is possible that the dwarf galaxies, with more porous ISM and harder radiation fields than the normal spirals, might process the dust grains in a different way, enhancing the mechanisms such as shattering that convert large grains into small ones (e.g. Chastenet et al. 2017; Galliano et al. 2018).

Finally, the simulations are not able to trace the behaviour of DS/DL versus stellar mass (bottom panel of Fig. 6) of the KINGFISH and DGS galaxies; most of the galaxies present higher DS/DL values than those predicted by the simulations within two orders of magnitude in stellar mass. Moreover, there is trend of constant DS/DL at high stellar mass, which does not agree with the steep decrement of DS/DL predicted by the simulations at high stellar mass. The steep decrement of DS/DL could be related to the AGN feedback model included in the simulations. AGN feedback is added to suppress the metal enrichment and explain the deficit of galaxies in the high mass end of the stellar mass function (see Fig. 1 in Hou et al. 2019). As the accretion time scale depends on the inverse of the metallicity, a decrement of metallicity in massive galaxies would lead to less accretion, and therefore less dust mass in the form of small grains. Besides, if these simulated galaxies still have a high dense gas fraction, coagulation can also be important and more dust in the form of large grains would be expected. Since the simulations overpredict the dust-to-gas mass ratio in massive galaxies (see Fig. 4b in Hou et al. 2019), increasing the accretion efficiency would move the dust-to-gas mass ratio further away from the observations, and therefore a higher dense gas fraction in the simulated galaxies would be probably the best possible explanation.

The trend of DS/DL as a function of metallicity, sSFR and stellar mass predicted by the simulations and derived from the observations is, in general, in reasonable agreement considering that we are comparing galaxies with different morphological types and at different evolutionary states and physical conditions of the ISM. This comparison reinforces the general trends and results of the cosmological simulations in tracking the evolution of the dust grain size distribution. It also provides certain clues about the possible limitations and caveats in the assumptions and initial conditions adopted in the simulations.

5. Discussion

The work presented here demonstrates a set of observational results that can be used to test the validity of the assumptions of the relevant simulations and models. We find agreements and disagreements between the observations and simulations. In some cases, the disagreements are due to a poor match of the observational sample with the physical conditions assumed in the simulations; while in others, the comparison might reveal problems with the simulations themselves. In the latter case, the comparison to the observations might serve as a guide for further improvements in future simulations. In this section, we discuss these agreements and disagreements in greater detail.

5.1. Disagreement between observations and simulations

The main disagreements between observations and simulations for the spatially resolved studies in our comparison are: (i) flatter observational dust radial profiles than those predicted by the simulations and (ii) higher Dtot derived from the observations at low metallicities. For integrated galaxies, the behaviour of the observed DS/DL as a function of sSFR and stellar mass is not well reproduced by the simulations.

Some of the discrepancies are due to physical causes as our observed galaxies do not resemble completely the galaxy types assumed in the simulations. In the case of spatially resolved studies, the simulations predict higher central dust surface densities and steeper radial gradients than those provided by the observations. This reflects the difference of the initial conditions adopted by the single galaxy SPH simulations, which assume a galaxy with a large bulge. None of our galaxies show evidence of large bulges in their centres; our set of galaxies are late-types rather than earlier prominent bulge types assumed to describe the initial conditions in the SPH simulations. In a similar way, when comparing the integrated SEDs of the DGS galaxies to cosmological simulations, we find that the physical properties of the ISM for low-metallicity galaxies of the DGS is not well reproduced by the simulations, which are more adequate for describing higher metallicity galaxies. In order to properly describe the DGS galaxies, a harder ISRF and a more porous ISM would have to be included in the simulations. This would most likely improve the agreement in the comparison of DS/DL versus sSFR and metallicity with the observations.

Other discrepancies shown in this study are related to the limitations of the assumptions in the simulations. For spatially resolved studies, the discrepancy in the dust mass surface density in the central parts of the galaxy and the agreement in the Dtot in the same areas indicate that the gas mass fraction assumed in the simulations might be too high. This discrepancy has been already suggested by previous studies (Saintonge et al. 2017; Maddox et al. 2015). In addition, observed radial gradients of Dtot agree better with simulations than the observed behaviour of Dtot as a function of metallicity, which shows that simulations predict larger azimuthal variations in metallicity than what it is typically observed. Finally, AGB stars are not taken into account within the frame work of the SPH simulations of a single galaxy of Aoyama et al. (2017) and Hou et al. (2017). If the expected contribution of the AGB stars to the dust budget is higher at low metallicities, as it has been suggested previously (e.g. Valiante et al. 2009), this would affect the outer parts of the galaxies and might make the gradient of Dtot versus metallicity to agree better with the observations.

For the case of integrated galaxies, the observational behaviour of the DS/DL ratio as a function of the stellar mass is not well reproduced by the cosmological simulations, especially in the higher stellar mass range. The discrepancy might be related to the prescription for AGN feedback assumed in the cosmological simulations, which is able to reproduce the deficit of galaxies in the high mass end of the stellar mass function but predicts lower metallicities. Environments with low metallicity would lead to less accretion and less dust mass in the form of small grains. Therefore, the prescription for AGN feedback underpredicts the DS/DL ratio for the most massive galaxies.

5.2. Agreements and conclusions on dust evolution

For spatially resolved observations there is a general agreement of the radial relations of Dtot and DS/DL ratio between observations and simulations. The spatially resolved studies of the three different galaxies reveal that the evolution of the dust is not well described by one single parameter. Coagulation, accretion, and shattering affect the DS/DL ratio, but the time scales of these processes also depend on other physical parameters such as metallicity, SFR, and fmol. Therefore, the DS/DL ratio, in combination with the SFR and fmol, can be used to indicate the main mechanism that is responsible for the evolution of the interstellar dust. Based on this scenario, we can interpret radial profiles of these parameters for our three galaxies and derive the most important mechanism in the dust evolution at different galactocentric distances. While in the most central regions of NGC 628, there is evidence that coagulation is taking over other mechanisms, in M 101, accretion seems to be in equilibrium with coagulation and shattering. This is not the case with M 33, where in the central areas, shattering is shown to be the most favourable mechanism regulating the evolution of the interstellar dust.

The integrated values of DS/DL for the galaxy sample considered in this study show a general agreement with the predictions of the variation of this ratio with metallicity. Most of the observational ratios from the KINGFISH galaxy sample lie within the limits predicted by the simulations and within a metallicity range where a combination of accretion, coagulation, and shattering is driving the evolution of the interstellar dust, thus confirming that the simulations describe the dust evolution in this type of galaxies well.

6. Conclusions

In this paper, we study how the total mass of the small and large grains varies across the disc of a set of spiral galaxies with different masses. This observational information is needed for a comparison and validation of the recent SPH simulations, which include the evolution of the grain size distribution. We also study the variation of DS/DL ratio for a large galaxy sample and compare it with the predictions of the recent cosmological simulations.

Using the results provided by fitting the observed SED at each location of the disc of a set of three spiral galaxies: NGC 628, M 101, and M 33, we were able to derive the relative abundance of each grain type across the individual galactic discs. We applied the same fitting procedure to the KINGFISH and DGS galaxies and compared the DS/DL ratio derived from the fitting with the predictions of the cosmological simulations. Our main conclusions are the following:

  • The radial profile of the dust mass surface density provided by the simulations of a single galaxy shows higher values than the observations in the centres of the galaxies. The simulated dust mass distribution at ages of 1−10 Gyr agrees reasonably well at larger galactocentric distances. The differences in the central parts might be related to the initial conditions of the galactic disc assumed by the simulations.

  • The agreement between Dtot derived from observations and the predictions of the simulations is good at high metallicities and in the central parts of the galaxies. For low metallicities, the agreement is worse, which most likely is due to the fact that the metallicity variations predicted by the simulations are large and they are also affected by the initial conditions assumed by the simulations.

  • The behaviour of the DS/DL ratio as a function of radius and metallicity shows different trends for each galaxy, revealing the importance of the main mechanism regulating dust evolution. For NGC 628 the ratio declines in the central parts, which shows that coagulation is important in these areas. For M 33 the ratio increases towards the central parts, presenting evidence that shattering is the main mechanism affecting the dust evolution. For M 101, the ratio is constant across the whole disc, which suggests that in this galaxy, there is a balance between accretion and shattering forming small grains and coagulation and star formation as the main producers of large grains.

  • We compare the DS/DL ratio derived from the integrated SEDs of KINGFISH and DGS galaxies with the results of the cosmological simulations performed by Hou et al. (2019). In general, the agreement between predictions from the simulations and results from the SED fitting is quite reasonable. Simulations seem to do well in explaining the behaviour of DS/DL as a function of metallicity. The behaviour of DS/DL versus stellar mass for both galaxy samples is not well reproduced by the simulations, especially at the high stellar mass end.

Here we present, for the first time, a comparison of the dust-to-gas mass ratio and small-to-large grain mass ratio predicted by SPH simulations of a single galaxy, including the evolution of the grain size distribution with the results provided after fitting the observational SEDs. The comparison lends observational support to the results provided by the simulations. A detailed simulation of each individual galaxy is out of the scope of this paper. Cosmological simulations, including the evolution of the grain size distribution, can make use of this study’s observational data to test their results and improve their assumptions.

1

In case (iii) the dust mass increases, while it stays fixed in case (iv).

2

It is unclear whether the size distribution of grains formed in SN is representative of the grains ejected in the ISM after passage through the reverse shock (Bianchi & Schneider 2007; Marassi et al. 2015, 2019; Bocchio et al. 2016).

Acknowledgments

The authors would like to thank the referee, Prof. Takeuchi, for the very constructive comments that helped to improve the first version of the paper. MR and UL acknowledges support by the research projects AYA2014-53506-P and AYA2017-84897-P from the Spanish Ministerio de Economía y Competitividad and Junta de Andalucía Grant FQM108; support from the European Regional Development Funds (FEDER) is acknowledged. KCH is supported by the IAEC-UPBC joint research foundation (Grant No. 257) and Israel Science Foundation (Grant No. 1769/15). JVM acknowledges financial support from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award to the Instituto de Astrofísica de Andalucía (SEV-2017-0709). MR and UL thank to the Computational service PROTEUS at the Instituto Carlos I. This work was partially supported by the Spanish Ministerio de Economía y Competitividad under Grants AYA2016-79724-C4-4-P and AYA2016-79724-C4-3-P, and excellence project PEX2011-FQM-7058 of Junta de Andalucía (Spain). This research made use of APLpy, an open-source plotting package for Python hosted at http://aplpy.github.com of TOPCAT & STIL: Starlink Table/VOTable Processing Software of Matplotlib, a suite of open-source python modules that provide a framework for creating scientific plots.

References

  1. Aoyama, S., Hou, K.-C., Shimizu, I., et al. 2017, MNRAS, 466, 105 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aoyama, S., Hou, K.-C., Hirashita, H., Nagamine, K., & Shimizu, I. 2018, MNRAS, 478, 4905 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aoyama, S., Hirashita, H., & Nagamine, K. 2020, MNRAS, 491, 3844 [NASA ADS] [Google Scholar]
  4. Asano, R. S., Takeuchi, T. T., Hirashita, H., & Nozawa, T. 2013a, MNRAS, 432, 637 [NASA ADS] [CrossRef] [Google Scholar]
  5. Asano, R. S., Takeuchi, T. T., Hirashita, H., & Inoue, A. K. 2013b, Earth Planets Space, 65, 213 [NASA ADS] [CrossRef] [Google Scholar]
  6. Asano, R. S., Takeuchi, T. T., Hirashita, H., & Nozawa, T. 2014, MNRAS, 440, 134 [NASA ADS] [CrossRef] [Google Scholar]
  7. Berg, D. A., Skillman, E. D., Croxall, K. V., et al. 2015, ApJ, 806, 16 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bevan, A., Barlow, M. J., & Milisavljevic, D. 2017, Mem. Soc. Astron. It., 88, 397 [NASA ADS] [Google Scholar]
  9. Bianchi, S., & Schneider, R. 2007, MNRAS, 378, 973 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bocchio, M., Marassi, S., Schneider, R., et al. 2016, A&A, 587, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Boquien, M., Calzetti, D., Combes, F., et al. 2011, AJ, 142, 111 [NASA ADS] [CrossRef] [Google Scholar]
  12. Boyer, M. L., McQuinn, K. B. W., Barmby, P., et al. 2015, ApJS, 216, 10 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bresolin, F. 2011, ApJ, 730, 129 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chastenet, J., Bot, C., Gordon, K. D., et al. 2017, A&A, 601, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Corbelli, E., & Walterbos, R. A. M. 2007, ApJ, 669, 315 [NASA ADS] [CrossRef] [Google Scholar]
  18. Croxall, K. V., Pogge, R. W., Berg, D. A., Skillman, E. D., & Moustakas, J. 2016, ApJ, 830, 4 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dale, D. A., Cook, D. O., Roussel, H., et al. 2017, ApJ, 837, 90 [NASA ADS] [CrossRef] [Google Scholar]
  20. Desert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
  21. Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
  22. Eskew, M., Zaritsky, D., & Meidt, S. 2012, AJ, 143, 139 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gall, C., Hjorth, J., Watson, D., et al. 2014, Nature, 511, 326 [NASA ADS] [CrossRef] [Google Scholar]
  24. Galliano, F., Galametz, M., & Jones, A. P. 2018, ARA&A, 56, 673 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gjergo, E., Granato, G. L., Murante, G., et al. 2018, MNRAS, 479, 2588 [NASA ADS] [CrossRef] [Google Scholar]
  26. Hao, C.-N., Kennicutt, R. C., Johnson, B. D., et al. 2011, ApJ, 741, 124 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hirashita, H. 2012, MNRAS, 422, 1263 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hirashita, H. 2015, MNRAS, 447, 2937 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hirashita, H., & Aoyama, S. 2019, MNRAS, 482, 2555 [NASA ADS] [CrossRef] [Google Scholar]
  30. Hirashita, H., & Murga, M. S. 2020, MNRAS, 492, 3779 [CrossRef] [Google Scholar]
  31. Hou, K.-C., Hirashita, H., Nagamine, K., Aoyama, S., & Shimizu, I. 2017, MNRAS, 469, 870 [NASA ADS] [CrossRef] [Google Scholar]
  32. Hou, K.-C., Aoyama, S., Hirashita, H., Nagamine, K., & Shimizu, I. 2019, MNRAS, 485, 1727 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hu, C.-Y., Zhukovska, S., Somerville, R. S., & Naab, T. 2019, MNRAS, 487, 3252 [NASA ADS] [CrossRef] [Google Scholar]
  34. Javadi, A., van Loon, J. T., Khosroshahi, H. G., et al. 2017, MNRAS, 464, 2103 [NASA ADS] [CrossRef] [Google Scholar]
  35. Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
  36. Jones, A. P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Kennicutt, R. C., Calzetti, D., Aniano, G., et al. 2011, PASP, 123, 1347 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kim, J.-H., Abel, T., Agertz, O., et al. 2014, ApJS, 210, 14 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kramer, C., Buchbender, C., Xilouris, E. M., et al. 2010, A&A, 518, L67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Lin, L., Zou, H., Kong, X., et al. 2013, ApJ, 769, 127 [NASA ADS] [CrossRef] [Google Scholar]
  41. Madden, S. C., Rémy-Ruyer, A., Galametz, M., et al. 2013, PASP, 125, 600 [NASA ADS] [CrossRef] [Google Scholar]
  42. Maddox, N., Hess, K. M., Obreschkow, D., Jarvis, M. J., & Blyth, S. L. 2015, MNRAS, 447, 1610 [NASA ADS] [CrossRef] [Google Scholar]
  43. Marassi, S., Schneider, R., Limongi, M., et al. 2015, MNRAS, 454, 4250 [NASA ADS] [CrossRef] [Google Scholar]
  44. Marassi, S., Schneider, R., Limongi, M., et al. 2019, MNRAS, 484, 2587 [NASA ADS] [CrossRef] [Google Scholar]
  45. Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
  46. Mattsson, L. 2016, Planet. Space Sci., 133, 107 [NASA ADS] [CrossRef] [Google Scholar]
  47. McKinnon, R., Vogelsberger, M., Torrey, P., Marinacci, F., & Kannan, R. 2018, MNRAS, 478, 2851 [NASA ADS] [CrossRef] [Google Scholar]
  48. Nanni, A., Marigo, P., Girardi, L., et al. 2018, MNRAS, 473, 5492 [NASA ADS] [CrossRef] [Google Scholar]
  49. Nanni, A., Groenewegen, M. A. T., Aringer, B., et al. 2019, MNRAS, 487, 502 [NASA ADS] [CrossRef] [Google Scholar]
  50. Nozawa, T., Kozasa, T., Habe, A., et al. 2007, ApJ, 666, 955 [NASA ADS] [CrossRef] [Google Scholar]
  51. Ormel, C. W., Paszun, D., Dominik, C., & Tielens, A. G. G. M. 2009, A&A, 502, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Priestley, F. D., Barlow, M. J., & De Looze, I. 2019, MNRAS, 485, 440 [NASA ADS] [CrossRef] [Google Scholar]
  53. Relaño, M., Kennicutt, R., Lisenfeld, U., et al. 2016, A&A, 595, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Relaño, M., De Looze, I., Kennicutt, R. C., et al. 2018, A&A, 613, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2015, A&A, 582, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Saintonge, A., Catinella, B., Tacconi, L. J., et al. 2017, ApJS, 233, 22 [Google Scholar]
  57. Salim, S., & Narayanan, D. 2020, ARA&A, submitted [arXiv:2001.03181] [Google Scholar]
  58. Salo, H., Laurikainen, E., Laine, J., et al. 2015, ApJS, 219, 4 [NASA ADS] [CrossRef] [Google Scholar]
  59. Sánchez-Blázquez, P., Rosales-Ortega, F., Diaz, A., & Sánchez, S. F. 2014, MNRAS, 437, 1534 [NASA ADS] [CrossRef] [Google Scholar]
  60. Sheth, K., Regan, M., Hinz, J. L., et al. 2010, PASP, 122, 1397 [NASA ADS] [CrossRef] [Google Scholar]
  61. Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
  62. Srinivasan, S., Boyer, M. L., Kemper, F., et al. 2016, MNRAS, 457, 2814 [NASA ADS] [CrossRef] [Google Scholar]
  63. Valiante, R., Schneider, R., Bianchi, S., & Andersen, A. C. 2009, MNRAS, 397, 1661 [NASA ADS] [CrossRef] [Google Scholar]
  64. Ventura, P., di Criscienzo, M., Schneider, R., et al. 2012, MNRAS, 424, 2345 [NASA ADS] [CrossRef] [Google Scholar]
  65. Vílchez, J. M., Relaño, M., Kennicutt, R., et al. 2019, MNRAS, 483, 4968 [NASA ADS] [CrossRef] [Google Scholar]
  66. Zhukovska, S., & Henning, T. 2013, A&A, 555, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Figures

thumbnail Fig. 1.

Schematic representation of the SED fitting procedure performed in this study. Nparam is the number of free parameters assumed in the models: relative mass fraction of PAHs, VSGs, and BGs, the scale factor of the ISRF, and a scale factor to describe the contribution of the old stellar population to the NIR-continuum. PDF is the probability density function obtained assuming an uniform prior distribution of the initial parameters. Fmod (band), and Fobs (band) are the corresponding modelled and observed fluxes in each band.
In the text
thumbnail Fig. 2.

Radial profile of the dust mass surface density for M 101 (top), NGC 628 (middle), and M 33 (bottom) compared to the profiles provided by the simulations performed by Aoyama et al. (2017) and Hou et al. (2017). Dust production in stellar ejecta, dust destruction by SN shocks, grain growth by accretion and coagulation, as well as shattering, are taking into account in the simulations.
In the text
thumbnail Fig. 3.

Comparison of the variation of the dust-to-gas mass ratio (Dtot) with metallicity (left) and galactocentric radius (right) for M 101 (top), NGC 628 (middle), and M 33 (bottom) with the SPH simulations of an isolated galaxy performed by Aoyama et al. (2017) and Hou et al. (2017). Thick lines represent mean values for each model in the simulation and the coloured areas cover the 25 and 75 percentile of the particle distribution. A solar metallicity of Z⊙ = 0.02 has been adopted for our observations for consistency with the solar metallicity assumed in the simulations.
In the text
thumbnail Fig. 4.

Comparison of the variation of the small-to-large grain mass ratio (DS/DL) with metallicity (left) and galactocentric radius (right) for M 101 (top panels), NGC 628 (middle panels), and M 33 (bottom panels) with the SPH simulations of an isolated galaxy performed by Aoyama et al. (2017) and Hou et al. (2017). Thick lines represent mean values for each model and the coloured areas cover the 25 and 75 percentile of the particle distribution. A solar metallicity of Z⊙ = 0.02 was adopted.
In the text
thumbnail Fig. 5.

Radial profile of the SFR (left) and molecular gas fraction (right) (normalised to R25) for NGC 628 (red squares), M 101 (black circles) and M 33 (green diamonds). SFRs were derived using FUV (GALEX) and TIR luminosities (see Eq. (1)). The molecular gas fraction was derived from HI and CO observations assuming a XCO factor inversely proportional to the metallicity (see Vílchez et al. 2019, for more details). The elliptical rings have a width of 0.1 R25. Data points and coloured areas correspond respectively to the mean value and the dispersion for each ring.
In the text
thumbnail Fig. 6.

Comparison of DS/DL with metallicity (top), sSFR (middle) and stellar mass (bottom) obtained from cosmological simulations from Hou et al. (2019) and the results obtained from SED modelling for the KINGFISH (black dots) and DGS (blue asteriscs). SFRs were derived for KINGFISH galaxies using the updated FUV (GALEX) and TIR luminosities given in Dale et al. (2017), while the SFR for the DGS were taken from Rémy-Ruyer et al. (2015) who used Hα and TIR. Stellar masses for both samples were obtained using the prescription given in Eskew et al. (2012).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.