| Issue |
A&A
Volume 635, March 2020
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201937324 | |
| Published online | 06 March 2020 | |
High-precision polarimetry of nearby stars (d < 50 pc)
Mapping the interstellar dust and magnetic field inside the Local Bubble★
1
Department of Physics and Astronomy, University of Turku,
Turku, Finland
e-mail: piirola@utu.fi
2
FINCA, University of Turku,
20014
Turku, Finland
3
Department of Astronomy and Astrophysics, University of Chicago,
Chicago
IL
60637, USA
4
Graduate School of Science, Tohoku University,
Aoba-ku,
Sendai
980-8578, Japan
5
Leibniz-Institut für Sonnenphysik,
79104
Freiburg, Germany
6
Greenhill observatory, School of Natural Sciences, University of Tasmania,
Private Bag 37,
Hobart,
TAS 7001, Australia
Received:
16
December
2019
Accepted:
27
January
2020
Context. We investigate the linear polarization produced by interstellar dust aligned by the magnetic field in the solar neighborhood (d < 50 pc). We also look for intrinsic effects from circumstellar processes, specifically in terms of polarization variability and wavelength dependence.
Aims. We aim to detect and map dust clouds which give rise to statistically significant amounts of polarization of the starlight passing through the cloud, and to determine the interstellar magnetic field direction from the position angle of the observed polarization.
Methods. High-precision broad-band (BV R) polarization observations are made of 361 stars in spectral classes F to G, with detection sensitivity at the level of or better than 10−5 (0.001%). The sample consists of 125 stars in the magnitude range 6–9 observed at the 2.2 m UH88 telescope on Mauna Kea, 205 stars in the magnitude range 3–6 observed at the Japanese (Tohoku) T60 telescope on Haleakala, and 31 stars in the magnitude range 4–7 observed at the 1.27 m H127 telescope of the Greenhill Observatory, Tasmania. Identical copies of the Dipol-2 polarimeter are used on these three sites.
Results. Statistically significant (>3σ) polarization is found in 115 stars, and >2σ detection in 178 stars, out of the total sample of 361 stars. Polarization maps based on these data show filament-like patterns of polarization position angles, which are related to both the heliosphere geometry, the kinematics of nearby clouds, and the Interstellar Boundary EXplorer ribbon magnetic field. From long-term multiple observations, a number (~20) of stars show evidence of intrinsic variability at the 10−5 level. This can be attributed to circumstellar effects (e.g., debris disks and chromospheric activity). The star HD 101805 shows a peculiar wavelength dependence, indicating size distribution of scattering particles different from that of a typical interstellar medium. Our high signal-to-noise measurements of nearby stars with very low polarization also provide a useful dataset for calibration purposes.
Key words: techniques: polarimetric / dust, extinction / ISM: magnetic fields / ISM: structure / circumstellar matter / stars: activity
Tables 6 and 7 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/635/A46.
© ESO 2020
1 Introduction
In the course of polarization studies of astrophysical objects that require very high signal-to-noise ratio (S/N; see Berdyugin et al. 2016, 2018), we observed samples of nearby stars (d < 50 pc) in order to determine and subtract the instrumental polarization produced by the telescope. This is achieved with a typical uncertainty of 2−3 × 10−6 (ppm) for each run, normally spanning intervals of between several days and one month. To avoid intrinsic effects as much as possible, stars of spectral types F-G were selected. These calibration measurements are crucial for each of the research programs, but they also provide a valuable database of the minute amounts of polarization in each of the observed stars. The individual stellar data points can in turn be used to map the interstellar magnetic field and dust content along the path that the observed starlight has traversed.
While the interstellar magnetic field (ISMF) structure and dust content are relatively well understood from the polarization maps based on measurements of stars at larger distances – d > 50 pc up to the kiloparsec ranges (see e.g., Berdyugin et al. 2014) – the very low dust content and therefore low degree of polarization within the Local Bubble have prevented detailed polarization studies until the recent development of extremely high-S/N polarimeters, with 10−6−10−5 detection sensitivity (see e.g., Bailey et al. 2010, 2015; Piirola et al. 2014; Cotton et al. 2017, 2019).
Encouraged by the successful implementation of our high-precision polarimeter (Dipol-2), and the availability of sufficient amounts of observing time from remotely operated telescopes at good observing sites, we have initiated a dedicated program for deriving the structure of the very local magnetic field from stellar polarization data. The need for a survey of optical polarizations that trace the local interstellar magnetic field became clear with the discovery by Interstellar Boundary EXplorer (IBEX) of an arc (or “ribbon”) of energetic neutral atoms whose center traces the direction of the ISMF shaping the heliosphere (McComas et al. 2009; Schwadron et al. 2009).
Target stars for this program were selected from objects in the HIPPARCOS catalog (Perryman et al. 1997). Channels devoid of nearby suitable target objects were found in the HIPPARCOS data in many locations, indicating either an irregular distribution of dust or an irregular distribution of suitable target stars. Some earlier results from our nearby star observationshave been included in the studies by Frisch et al. (2015a,b), tracing the structure of the very local ISMF.
In the present paper we give a detailed description of our current dataset and discuss the results based on the polarization map obtained. The statistical significance of the detections is addressed. It is also interesting to look for evidence of intrinsic polarization variability in some of the stars observed. Examples are given of particular wavelength dependence found, suggesting effects from a circumstellar debris disk.
Summary of observations.
2 Observations
We carried out observations in 2014–2019 at three telescopes, the 2.2 m UH88 telescope on Mauna Kea, the Tohoku 60 cm telescope (T60) on Haleakala, and the University of Tasmania (UTAS) 1.27 m (H127) telescope at Greenhill Observatory, Tasmania. Observations were made with the simultaneous three-color (BV R) polarimeter Dipol-2 (Piirola et al. 2014). Identical copies of the instrument are used at each of the three sites. At UH88 and T60 the observations were carried out in remote operation mode. Some additional data on the stars in our sample were obtained at the Nordic Optical Telescope (NOT) and William Herschel Telescope (WHT) at ORM, La Palma, A summary of the observations is given in Table 1.
The polarimeter, Dipol-2, is capable of making simultaneous measurements in three passbands, B, V, and R (see Figs. 1 and 2, and Table 2), with high sensitivity. The detection limit of polarization is at the level of 10−5, which is set in practice by photon noise. An important asset of the instrument is that the sky background polarization is directly (optically) eliminated. The perpendicularly polarized components of sky are superimposed by the plane parallel calcite beam splitter, and sky polarization is thereby canceled (Piirola 1973). This is essential, as the polarized flux from scattered skylight can exceed the signal from the target by orders of magnitude, particularly in bright Moon conditions. Dipol-2 has been found to be a very stable and reliable instrument as demonstrated recently by detection of the variable polarization at the 0.1% level from the massive binaries HD 48099 (Berdyugin et al. 2016) and λ Tauri (Berdyugin et al. 2018).
The Dipol-2 polarimetry routine consists of cycles of 16 exposures at different orientations of the superachromatic half-wave retarder (22.5° steps), corresponding to a full (360°) rotation of the retarder. Each group of four successive exposures gives one independent measurement of the normalized Stokes parameters q = pcos2θ and u = psin2θ, where p is the degree of linear polarization and θ the position angle of the maximum electric vector, in the equatorial frame of reference. Accordingly, one cycle gives four independent measurements of q and u.
For the highest S/N measurements it is advantageous to strongly defocus images to spread light over a very large number of pixels. In this way we can expose up to 108 electrons in one stellar image without saturating the CCD pixels. Even if there are minor shifts in the position of the two perpendicularly polarized images of the target, the vast majority of the pixels remain the same over the full measurement cycle (16 exposures). Minor imperfections in the flat field are eliminated in the reductions, because the ratio of the o- and e- beam transmission, and efficiency, if constant, is automatically canceled in the reduction algorithm. This provides inherently very stable instrument and detection sensitivity better than 10−5 (<10 ppm) in ~1 h for sufficiently bright stars. Moreover, the Dipol-2 polarimeter is photon noise limited down to these very low polarization signal levels.
In order to reduce the photon noise to the required (10−5) level, the total telescope time used for the nightly observation of each star was 0.5–1.5 h, depending on the brightness of the star. With a typical single exposure time of 1–3 s, the total number of individual observations of the normalized Stokes parameters q and u for one star was usually in the range 128–256. This provides very good statistical error estimates for the nightly average points of q and u for each star.
Standard CCD reduction procedures (bias and dark subtraction, flat fielding) were applied prior to extracting the fluxes from the double images of the target formed on the CCD by the polarizing calcite beam splitter. A special centering algorithm and subframing procedures were used to facilitate the processing of a large number – up to several hundred – of exposures at the same time. In computing the mean values of q and u we applied a “2σ” iterative weighting algorithm. The initial mean and standard deviation were obtained by applying equal weights to all points. Subsequently, on each step, individual points deviating by more than two standard deviations from the mean (d > 2σ) were given a lower weight proportional to the inverse square of the error estimate, ex. The value ex = σ for d < 2σ was assumed to increase linearly from ex = 1σ to 3σ with d increasing from 2σ to 3σ. Points with d > 3σ were rejected. The procedure converges fast and values of mean and standard deviation are obtained within a few iterations. Under normal conditions, 6–8% of individual points deviated by more than 2σ and were given lower weight (W < 1). The remaining 92–94% of points were equally weighted (W = 1). The weighting procedure helps to suppress effects from transient clouds, moments of bad seeing, cosmic ray events, and so on.
The simultaneous polarization measurements in the three (BV R) passbands provided by Dipol-2 are very useful for studying the wavelength dependence of polarization. Indeed they also improve the efficiency. There is only a small amount of internal absorption in the dichroic beam splitters used to separate the color passbands.
In the case of the extremely low polarization values found in the stars inside the Local Bubble, the S/N in each of the wavelength bands (BV R) may not be sufficient to obtain useful data for constraining the wavelength dependence of interstellar polarization, and thereby the aligned grain size distribution. In such cases, and because of the relatively flat shape of the IS polarization curve in the optical part of the spectrum, itis meaningful to compute “broad-band” (400–800 nm) polarization values by weighted averaging of the normalized Stokes parameters q and u obtained in the B, V, and R passbands to improve the S/N and the statistical significance of the detection for very weak polarization signals.
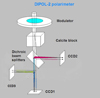 |
Fig. 1 Scheme of the Dipol-2 polarimeter. Rotatable superachromatic λ/2 retarder plate modulates the relative intensities of the two polarized beams produced by the calcite crystal, with an amount proportional to the degree of linear polarization of the incoming radiation. Two dichroic mirrors split the light into three passbands: blue, visible, and red. The fluxes of the two polarized stellar images in each band are measured with three highly sensitive cooled CCD detectors. |
 |
Fig. 2 Dipol-2 polarimeter with the front cover removed, showing (from top) the polarization modulator unit (retarder plate and the calcite plate), the dichroics unit dividing the light onto three CCDs: the blue (right), the visible (bottom), and the red (left). |
Equivalent wavelengths and full widths at half maximum (FWHM) of the Dipol-2 passbands.
Instrumental polarization of the UH88 telescope in the B, V, and R passbands, in units of 10−6 (ppm), for the observing runs in 2014–2016.
3 Results and discussion
3.1 Instrumental polarization
Because of the very small degree of polarization produced by the interstellar dust in the Solar vicinity, it is crucial to determine and subtract the effects of the telescope optics and the instrument itself from the measured polarization. This is done by observing nearby stars which can be assumed to be almost unpolarized thanks to their proximity to us and freedom from intrinsic polarization effects ensured by the selection of the spectral type (F-G main sequence stars).
However, we cannot assume that any single star has zero polarization within the strict limits required for the present work. Therefore, we always observe a sample of at least 15–20 stars in different parts of the sky and determine the instrumental polarization as the average of the q and u from the sample. In this way, weak effects of interstellar polarization in each of the observed stars tend to cancel out, because the ISMF direction varies strongly in different parts of the sky. Possible intrinsic (circumstellar or photospheric) effects are also likely to be randomly oriented within the sample.
In Tables 3–5 we list the values of the instrumental polarization, qt and ut, obtained for the UH88, T60, and H127 telescopes, respectively, for each run carried out. Statistical uncertainties are typically in the range 2− 3 × 10−6, and the values for each telescope do not change significantly from one run to another. This is reassuring, since samples in different parts of the sky are used for different runs (seasons), and possible residual effects from interstellar polarization appear to be small. Obviously, there are slow long-term drifts and small jumps from mirror cleaning or other effects from the telescope optics.
We excluded stars with significant detected polarizations from the instrumental polarization computation, and applied a simple iterative procedure to calculate the average q and u from the sample to provide qt and ut in each of the BV R passbands separately. These values, qt and ut, are then subtracted from the observed q and u in each passband for all of the observed stars. The telescopes we use for the present work (UH88, T60, and H127) are equatorially mounted, which is convenient in the sense that the telescope polarization does not rotate on the sky. It only gives a constant shift in (q, u).
The superachromatic half-wave plates we use have very good efficiency throughout the whole wavelength range of the Dipol-2 passbands (400–800 nm). Nevertheless, we observed high polarization standard stars to check for the polarization scale calibration, and for the zero-point of position angles.
In each run, at least two different large polarization standards were observed, typically both at the beginning and at the end of the run. The stars HD 25443, HD 161056, HD 204827, BD+25 727, and BD+59 389 were used for this purpose. We found evidence of small calibration coefficients (1.02–1.04) needed in the V and R passbands. Though these differences can be partially due to systematic errors in the published values (Hsu & Breger 1982; Turnshek et al. 1990; Schmidt et al. 1992), we applied the corrections to bring our data into the system commonly used by other investigators. In any case, for the very small polarization degrees found in the present study, these scale corrections are entirely negligible.
Instrumental polarization of the T60 telescope in the B, V, and R passbands, in units of 10−6 (ppm), for the observing runs in 2014–2018.
Instrumental polarization of the H127 telescope in the B, V, and R passbands, in units of 10−6 (ppm), for the observing runs in 2017 and 2018.
3.2 Broad-band (400–800 nm) polarization
Tables 6–8 list the broad-band polarizations computed by weighted averaging of the normalized Stokes parameters q and u obtained in the B, V, and R bands at the UH88, T60, and H127 telescopes, respectively. Statistically significant (> 3σ) polarizations are detected in 115 out of the 361 stars observed.
It is interesting to note the differences in the fraction of > 3σ detections at the different telescopes. At the UH88 about one-third of the stars (43 of 125) show measurable polarization, whereas at the T60 the fraction is about one-quarter (49 of 205). This may be partially due to the fact that at UH88 we generally observed somewhat fainter stars at larger distances, and the effects from interstellar dust are therefore probably stronger. When identifying the target stars, the fainter magnitudes achievable with UH88 also made it possible to pick more reddened stars for a given distance compared to stars selected for T60. The data from H127 show the largest fraction of polarized stars, namely approximately two-thirds (23 of 31). This clearly indicates that the average dust content is larger in the direction of the H127 sample of stars (Southern hemisphere, 04h < α < 12h, −77° < δ < −4°).
Figures 3 and 4 show polarization maps based on the broad-band data plotted in the Galactic (l, b) and Equatorial coordinates. The general view may be slightly complicated, but there are several interesting features showing well-aligned polarization vectors. Some of them resemble “arc” or “loop”-like structures. One prominent example can be seen in the aforementioned region of the H127 sample of southern stars (200° < l < 315°, −75° < b < 0°). Further observations would be useful to establish the polarization features in this interesting region in greater detail. We also note that the uncertainty of the instrumental polarization determination is somewhat larger for the H127 sample, particularly for the second run (Table 5), due to significant amounts of polarization in most of the observed stars.
When comparing our map with earlier published data on nearby star polarization by Cotton et al. (2017), we can see similarities in the position angle patterns, particularly near the longitudes l ~ 0° and l = 260°−315°, even though the samples of observed stars are entirely different and also extend in the study of these authors to longer distances (d > 50 pc) than in our data.
The polarization position angle patterns (Figs. 3 and 4) suggest that the polarizing dust grains are aligned along magnetic filaments, some with spatial extents greater than 90°. Combined with data from several literature sources, Frisch et al. (2015a) found that the position angles for stars in the longitude range l = 315° − 60° reveal a filament in the direction toward the heliosphere nose region, as defined by the flow of interstellar neutral gas through the heliosphere (l ~ 4°, b ~ 15°). Our data (Fig. 3) also clearly show a filament in the opposite direction (l ~ 180°, b ~−15°) corresponding to the (spatially broader) region of the heliosphere tail.
High-sensitivity measurements of the polarizations of nearby stars provide the only methodology capable of connecting the ambient ISMF with the ISMF shaping the heliosphere (Frisch et al. 2015a). The interstellar magnetic field shaping the heliosphere was discovered to be traced by a “ribbon” of energetic neutral atoms (ENAs) formed by charge-exchange between interstellar neutral hydrogen atoms and plasma near the heliopause that separates solar and interstellar plasma (McComas et al. 2009). Modeling of the magnetic field creating the IBEX ribbon (Zirnstein et al. 2016) yields an ISMF direction toward l = 26°, b = 50°. The newly discovered filament (Figs. 3 and 5) that is centered near l = 240°, b = −42° roughly follows the direction of the IBEX ribbon ISMF. Several stars in this filament are within 20 pc, and the nearest star, HD 33262, is 12 pc away. These new polarization data firmly place the filament within the cluster of local interstellar clouds flowing past the Sun and extending to the solar location (Frisch et al. 2011). The new filament is also aligned with the projected interface between two of these local clouds, Dorados and the Blue Cloud, which have boundaries parallel to each other and the polarization filament, and have quasi-perpendicular velocities through the Local Standard of Rest (Frisch et al., in prep.).
Efforts to evaluate the correspondence between polarization strengths and interstellar column densities for nearby stars have been unsuccessful because of the low column densities and unknown levels of ionization in the gas (Frisch et al. 2015b). Extended regions withstars lacking significant polarizations are also found, which can indicate very low dust content, nearby depolarization screens, or regions at the poles of the magnetic field.
The star HD 83683 in the T60 data shows much stronger polarization than the others: P(%) = 0.0602 ± 0.0011, θeq = 125.2° ± 0.5°. This star is in the direction of a known nearby dust cloud (l ~ 220°, b ~ 43°) inside the Local Bubble (Meyer et al. 2006; Peek et al. 2011). Fitting the Serkowski law (Serkowski 1973) to the polarization data in the B, V, and R bands yields: pmax = 0.0649 ± 0.0008%, λmax = 0.706 ± 0.017 μm. Polarization peaking in the red wavelengths indicates size distribution of scattering particles which are somewhat greater than the average in the interstellar medium.
The star HD 101805 in the H127 data (Table 8) shows larger polarization than other stars in the sample (p = 0.0223 ± 0.0011%), most likely due to a contribution of circumstellar origin (Sect. 3.3).
In the UH88 data, the star HD 126679 (l ~ 335°, b ~ 42°) shows higher polarization, P = 0.0595 ± 0.0008%, θeq = 16.4° ± 0.4°, but the wavelength dependence looks normal interstellar (λmax = 0.501 ± 0.060 μm, pmax = 0.0623 ± 0.0012%).
Figure 6 shows the dependence of observed polarization with distance. Due to the fact that the degree of polarization is always positive, for small polarizations the observational errors bias the polarization towards higher values. Statistically, this can be corrected by 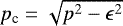 , where p is the observed degree of polarization and ɛ its error (see Serkowski 1962). For p < ɛ, we adopt pc = 0. The upper boundary of the points in Fig. 6 gives a dependence of maximum polarization with distance, p d−1 ~ 2.9 ppm pc−1. A linear fit to all points gives p d−1 = 0.37 ± 0.14 ppm pc−1. This is much less than the value 1.64 ± 0.30 ppm pc−1 derived by Cotton et al. (2017) from a sample of southern hemisphere stars. The majority of observed points in Fig. 6 lie well below the upper boundary, indicating very low contents of interstellar dust. There are large regions on the sky with no detectable polarization (see also Figs. 3 and 4) up to distances d = 40−50 pc. The viewing angle between the ISMF and the line of sight also contributes to the low observed polarization.
, where p is the observed degree of polarization and ɛ its error (see Serkowski 1962). For p < ɛ, we adopt pc = 0. The upper boundary of the points in Fig. 6 gives a dependence of maximum polarization with distance, p d−1 ~ 2.9 ppm pc−1. A linear fit to all points gives p d−1 = 0.37 ± 0.14 ppm pc−1. This is much less than the value 1.64 ± 0.30 ppm pc−1 derived by Cotton et al. (2017) from a sample of southern hemisphere stars. The majority of observed points in Fig. 6 lie well below the upper boundary, indicating very low contents of interstellar dust. There are large regions on the sky with no detectable polarization (see also Figs. 3 and 4) up to distances d = 40−50 pc. The viewing angle between the ISMF and the line of sight also contributes to the low observed polarization.
Broad-band (400–800 nm) polarimetric data of nearby stars observed at the H127 telescope.
 |
Fig. 3 Polarization map based on the observed sample of nearby stars (d < 50 pc), plotted in Galactic coordinates. The length of the bars is proportional to the degree of polarization and the orientation gives the direction of the maximum electric vector. Regions with aligned polarization vectors can be seen, suggesting filament-type structures. Two different polarization scales are used for clarity, as indicated in the bottom of the panel. For low observed degrees of polarization, p < 2σ (no detection), only a cross with bar lengths, σ, is plotted. |
 |
Fig. 4 Polarization map based on the sample of nearby stars (d < 50 pc), plotted in Equatorial coordinates. Two different polarization scales are used for clarity, as indicated in the bottom of the panel. For low observed degrees of polarization, p < 2σ (no detection), only a cross with bar lengths, σ, is plotted. The dotted line shows the Galactic equator. |
 |
Fig. 5 Polarization position angles (bars) of a magnetic filament that is roughly parallel to the interstellar magnetic field shaping the heliosphere are plotted for stars within 20 (red) and 40 (blue) parsecs. Stars with p∕ep less than 1.95 are plotted as dots. The green dashed line indicates the direction of the ISMF shaping the heliosphere as determined from the center of the IBEX ribbon of ENAs (see Sect. 3.2). Data are plotted in Galactic coordinates (l, b). |
 |
Fig. 6 Observed degree of polarization, pc, corrected for the positive bias (see Sect. 3.2), plotted vs. distance, d. Upper boundary gives the relation, pc ~ 2.9 ppm pc−1, and linear fitto all points (dashed line), pc = 0.37 ± 0.14 ppm pc−1. |
Evidence of intrinsic polarization in the star HD 101805 from a peculiar wavelength dependence.
Stars with multiple observations from the H127 telescope.
Broad-band (400–800 nm) polarimetric data of nearby stars observed at the WHT telescope.
Broad-band (400–800 nm) polarimetric data of nearby stars observed at the NOT telescope.
3.3 Evidence of intrinsic effects from wavelength dependence and/or variability of polarization
Three-color (BV R) polarimetric data obtained for the star HD 101805 (Table 9) show polarization increasing from p = 0.0172 ± 0.0019% in the R-band to p = 0.0314 ± 0.0018% in the B-band. This suggests a contribution from small scattering particles (Rayleigh-type scattering) in a circumstellar dust and/or gas envelope. Further studies of the circumstellar environment of HD 101805 would be desirable.
For the majority of the nearby stars (d < 50 pc) observed, the degree of polarization in the B, V, and R passbands isvery low, and constraining the properties of interstellar or circumstellar dust by the wavelength dependence is difficult.
We observed several stars on more than one night. Multiple observations give the possibility to look for variability on long time intervals from weeks to years. As an initial approach we have adopted a criterium for picking up candidates for variable polarization: we choose stars that show a standard deviation of the normalized Stokes parameters q and u of more than twice what is expected from the errors of the nightly points. Table A.11 lists measurements of stars that show give evidence of variable polarization from the data obtained at the T60 telescope. The majority of our multiple observations were made with T60.
From the total of 205 stars observed at T60 there are 18 stars showing a standard deviation of q and u of more than twice what is expected from the errors of the nightly points (Table A.11). A few stars show (> 3σ) night-to-night changes. The clearest examples are HD 19373, HD 58855, and HD 205289, where either the q or u parameter is found to deviate significantly from the mean values at the 2–3 × 10−5 level. Still, the evidence for variability is rather marginal, and polarization variations exceeding 10−5 do not appear to be common in inactive F-G main sequence stars. More observations are needed to find evidence for possible periodicity or other systematic time variability.
In our data from the H127 telescope there are five stars observed more than once (Table 10). None of these stars show statistically significant deviations of q and u from their mean values, that is, variations are <2σ.
We have additional polarization data from observations made at the WHT telescope, and at the NOT telescope, at ORM, La Palma. The copy of Dipol-2 polarimeter used at the WHT is the one currently at H127. At the NOT a new version (Dipol-UF) is used. This instrument is equipped with high-speed readout EMCCD cameras; otherwise the instrument principle is similar to that of Dipol-2.
The star HD 6715 shows somewhat stronger polarization, p(%) = 0.0036 ± 0.0009, in our measurements at the WHT (Table 11) than observed at the UH88 (Table 6), p(%) = 0.0007 ± 0.0009, indicating possible intrinsic effects. The polarized star HD 132307 observations at WHT and UH88 are in agreement within the errors.
The stars observed at the NOT (Table 12) were already measured at the T60 telescope (Table 7). The results are in good agreement. The star HD 191195 gives a > 3σ detection at both telescopes: p(%) = 0.0042 ± 0.0010, θ = 80.7° ± 7.0°, and p(%) = 0.0039 ± 0.0008, θ = 68.2° ± 5.6°, at the T60 and the NOT, respectively.
 |
Fig. 7 Polarization map of northern Galactic latitude (b > 0°) nearby stars (d < 50 pc), shown for comparison with earlier published results of more distant stars (Fig. 8). The polarizations for the peculiar stars HD 83683 and HD 126679 are not shown here. |
 |
Fig. 8 Polarization map of northern Galactic latitude stars in the distance range 100 pc < d < 500 pc. We note that the polarization scale is compressed by a factor of ~70 compared with that in Fig. 7, and only stars with b > 30° are plotted (from Berdyugin et al. 2014). |
3.4 Comparison of polarization maps at high northern Galactic latitudes for the nearby and distant stars
Figure 7 gives a polarization map for the nearby stars at northern Galactic latitudes, for comparison with earlier results for more distant stars (Berdyugin et al. 2014). The most prominent feature seen in the northern (b > 30°) high-latitude polarization map for the distant (d ≥ 100 pc) stars is a giant “arc” or “loop” between the longitudes 270° and 45°, with the center at l = 330° (Fig. 8). There is a striking difference between the longitude range l = 240°−(360°)−60° (top panel of Fig. 8), where polarizations are strong and well aligned, and the range l = 60°−240° (bottom panel of Fig. 8), where polarizations are much smaller and no clear alignment patterns are visible.
The number of observed nearby stars in Fig. 7 is small, but comparison with Fig. 8 shows similar features: larger polarizations in l = 240°−(360°)−0°, and smaller values in l = 60°−240°. There is also evidence for the “arc” structure seen in the top panel. Accordingly, local magnetic field structures seen in the distance range 100 –500 pc also appear at closer distances. This result is consistent with a position of the Sun inside the Local Bubble where more nearby interstellar dust is found in the Galactic center hemisphere than in the anti-center hemisphere (Frisch & Dwarkadas 2017).
4 Conclusions
We collected an extensive high-S/N polarization dataset of 361 nearby stars (d < 50 pc). Polarization maps based on these data show patterns of aligned polarization vectors, correlating with known nearby dust clouds.
The polarization position angles show that the very local ISMF is arranged into distinct magnetic filaments, some with spatial extents greater than 90°. These magnetic filaments provide a new perspective on the structure of local interstellar clouds that are historically identified primarily by cloud kinematics. There are large regions on the sky with no detectable polarizations (p < 10−5), up to distances d = 40−50 pc, which indicates very low dust content in these areas, particularly on the northern sky. A linear fit to our sample gives a relation for the average dependence of the degree of polarization versus distance, p d−1 = 0.37 ± 0.14 ppm pc−1. This is smaller by a factor of about four than values found for representative regions in the southern hemisphere (Cotton et al. 2017). However, the scatter is large and the values for individual stars in our dataset are in the range 0 < p d−1 < 2.9 ppm pc−1. Beyond this, there are a few outliers. The extreme case is HD 83683 which is located in a known nearby dust cloud and has p d−1 = 14.8 ± 0.2 ppm pc−1.
From long-term multiple observations a number (~20) of stars show marginal evidence of intrinsic variability at the 10−5 level. Three stars show statistically significant (>3σ) night-to-night changes. These can be attributed to circumstellar effects (e.g., debris disks, chromospheric activity). The star HD 101805 shows a peculiar wavelength dependence with a steep gradient, indicating size distribution of scattering particles different from that of typical interstellar medium.
Comparison of polarization maps at the high northern Galactic latitudes for distant (100 pc < d < 500 pc) and nearby stars (d < 50 pc) reveals similar features of polarization patterns, that is, local magnetic field structures seen in the distance range d = 100–500 pc also extend to and appear at closer distances. Our high-S/N measurements of intrinsically inactive F-G stars in the magnitude range 3.8 < V < 9.1, with very low polarization, also provide a useful dataset for calibration purposes.
Acknowledgements
This work was supported by the ERC Advanced Grant Hot- Mol ERC-2011-AdG-291659 (www.hotmol.eu). Dipol-2 was built in the cooperation between the University of Turku, Finland, and the Kiepenheuer Institut für Sonnenphysik, Germany, with the support by the Leibniz Association grant SAW-2011-KIS-7. We are grateful to the Institute forAstronomy, University of Hawaii for the observing time allocated for us on the UH88 and T60 telescopes, and to the University of Tasmania (UTAS) for the observing time at the H127 telescope. The Nordic Optical Telescope (NOT), and the William Herschel Telescope (WHT) are operated in the Spanish Observatorio del Roque de los Muchachos (ORM) of the Instituto de Astrophysica de Canarias (IAC). Greenhill Observatory is supported by the University of Tasmania Foundation. The H127 telescope is funded in part by grant LE110100055 from the Australian Research Council. The work of P.F. was funded by the IBEX mission as part of NASA’s Explorer Program (80NSSC18K0237) and the IMAP mission as a part of NASA’s Solar Terrestrial Probes Program (80GSFC19C0027).
Appendix A Additional table
Stars showing evidence of polarization variability from the observations at the T60 telescope.
References
- Bailey, J., Lucas, P. W., & Hough, J. H. 2010, MNRAS, 405, 2570 [NASA ADS] [Google Scholar]
- Bailey, J., Kedziora-Chudczer, L., Cotton, D. V., et al. 2015, MNRAS, 449, 3064 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugin, A., Piirola, V., & Teerikorpi, P. 2014, A&A, 561, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugin, A., Piirola, V., Sadegi, S., et al. 2016, A&A, 591, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugin, A., Piirola, V., Sakanoi, T., Kagitani, M., & Yoneda, M. 2018, A&A, 611, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cotton, D. V., Marshall, J. P., Bailey, J., et al. 2017, MNRAS, 467, 873 [NASA ADS] [Google Scholar]
- Cotton, D. V., Marshall, J. P., Frisch, P. C., et al. 2019, MNRAS, 483, 3636 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, P., & Dwarkadas, V. V. 2017, Handbook of Supernovae, Effect of Supernovae on the Local Interstellar Material (Berlin: Springer), 2253 [Google Scholar]
- Frisch, P. C., Redfield, S., & Slavin, J. D. 2011, ARA&A, 49, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, P. C., Andersson, B. G., Berdyugin, A., et al. 2015a, ApJ, 805, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, P. C., Berdyugin, A., Piirola, V., et al. 2015b, ApJ, 814, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Hsu, J. C., & Breger, M. 1982, ApJ, 262, 732 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Allegrini, F., & Bochsler, P., et al. 2009, Science, 326, 959 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Meyer, D. M., Lauroesch, J. T., Heiles, C., Peek, J. E. G., & Engelhorn, K. 2006, ApJ, 650, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Peek, J. E. G., Heiles, C., Peek, K. M. G., Meyer, D. M., & Lauroesch, J. T. 2011, ApJ, 735, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 500, 501 [NASA ADS] [Google Scholar]
- Piirola, V. 1973, A&A, 27, 383 [NASA ADS] [Google Scholar]
- Piirola, V., Berdyugin, A., & Berdyugina, S. 2014, Proc. SPIE, 9147, 91478I [Google Scholar]
- Schmidt, G. D., Elston, R., & Lupie, O. L. 1992, AJ, 104, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Schwadron, N. A., Bzowski, M., & Crew, G. B. 2009, Science, 326, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Serkowski, K. 1962, Adv. Astron. Astrophys., 1, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Serkowski, K. 1973, IAU Symp., 52, 145 [NASA ADS] [Google Scholar]
- Turnshek, D. A., Bohlin, R. C., Williamson, R. L., I., et al. 1990, AJ, 99, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Zirnstein, E. J., Heerikhuisen, J., Funsten, H. O., et al. 2016, ApJ, 818, L18 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Equivalent wavelengths and full widths at half maximum (FWHM) of the Dipol-2 passbands.
Instrumental polarization of the UH88 telescope in the B, V, and R passbands, in units of 10−6 (ppm), for the observing runs in 2014–2016.
Instrumental polarization of the T60 telescope in the B, V, and R passbands, in units of 10−6 (ppm), for the observing runs in 2014–2018.
Instrumental polarization of the H127 telescope in the B, V, and R passbands, in units of 10−6 (ppm), for the observing runs in 2017 and 2018.
Broad-band (400–800 nm) polarimetric data of nearby stars observed at the H127 telescope.
Evidence of intrinsic polarization in the star HD 101805 from a peculiar wavelength dependence.
Broad-band (400–800 nm) polarimetric data of nearby stars observed at the WHT telescope.
Broad-band (400–800 nm) polarimetric data of nearby stars observed at the NOT telescope.
Stars showing evidence of polarization variability from the observations at the T60 telescope.
All Figures
 |
Fig. 1 Scheme of the Dipol-2 polarimeter. Rotatable superachromatic λ/2 retarder plate modulates the relative intensities of the two polarized beams produced by the calcite crystal, with an amount proportional to the degree of linear polarization of the incoming radiation. Two dichroic mirrors split the light into three passbands: blue, visible, and red. The fluxes of the two polarized stellar images in each band are measured with three highly sensitive cooled CCD detectors. |
| In the text | |
 |
Fig. 2 Dipol-2 polarimeter with the front cover removed, showing (from top) the polarization modulator unit (retarder plate and the calcite plate), the dichroics unit dividing the light onto three CCDs: the blue (right), the visible (bottom), and the red (left). |
| In the text | |
 |
Fig. 3 Polarization map based on the observed sample of nearby stars (d < 50 pc), plotted in Galactic coordinates. The length of the bars is proportional to the degree of polarization and the orientation gives the direction of the maximum electric vector. Regions with aligned polarization vectors can be seen, suggesting filament-type structures. Two different polarization scales are used for clarity, as indicated in the bottom of the panel. For low observed degrees of polarization, p < 2σ (no detection), only a cross with bar lengths, σ, is plotted. |
| In the text | |
 |
Fig. 4 Polarization map based on the sample of nearby stars (d < 50 pc), plotted in Equatorial coordinates. Two different polarization scales are used for clarity, as indicated in the bottom of the panel. For low observed degrees of polarization, p < 2σ (no detection), only a cross with bar lengths, σ, is plotted. The dotted line shows the Galactic equator. |
| In the text | |
 |
Fig. 5 Polarization position angles (bars) of a magnetic filament that is roughly parallel to the interstellar magnetic field shaping the heliosphere are plotted for stars within 20 (red) and 40 (blue) parsecs. Stars with p∕ep less than 1.95 are plotted as dots. The green dashed line indicates the direction of the ISMF shaping the heliosphere as determined from the center of the IBEX ribbon of ENAs (see Sect. 3.2). Data are plotted in Galactic coordinates (l, b). |
| In the text | |
 |
Fig. 6 Observed degree of polarization, pc, corrected for the positive bias (see Sect. 3.2), plotted vs. distance, d. Upper boundary gives the relation, pc ~ 2.9 ppm pc−1, and linear fitto all points (dashed line), pc = 0.37 ± 0.14 ppm pc−1. |
| In the text | |
 |
Fig. 7 Polarization map of northern Galactic latitude (b > 0°) nearby stars (d < 50 pc), shown for comparison with earlier published results of more distant stars (Fig. 8). The polarizations for the peculiar stars HD 83683 and HD 126679 are not shown here. |
| In the text | |
 |
Fig. 8 Polarization map of northern Galactic latitude stars in the distance range 100 pc < d < 500 pc. We note that the polarization scale is compressed by a factor of ~70 compared with that in Fig. 7, and only stars with b > 30° are plotted (from Berdyugin et al. 2014). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


