| Issue |
A&A
Volume 635, March 2020
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201936993 | |
| Published online | 17 March 2020 | |
Statistical mass function of prestellar cores from the density distribution of their natal clouds
1
Department of Applied Physics, Faculty of Applied Mathematics, Technical University,
8 Kliment Ohridski Blvd.,
1000 Sofia, Bulgaria
e-mail: savadd@tu-sofia.bg
2
University of Sofia, Faculty of Physics,
5 James Bourchier Blvd.,
1164 Sofia, Bulgaria
3
Universität Heidelberg, Zentrum für Astronomie, Institut für Theoretische Astrophysik,
Albert-Ueberle-Str. 2,
69120 Heidelberg, Germany
4
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482 Potsdam, Germany
Received:
25
October
2019
Accepted:
3
February
2020
The mass function of clumps observed in molecular clouds raises interesting theoretical issues, especially in its relation to the stellar initial mass function (IMF). We propose a statistical model of the mass function of prestellar cores (CMF), formed in self-gravitating isothermal clouds at a given stage of their evolution. The latter is characterized by the mass-density probability distribution function (ρ-PDF), which is a power-law with slope q. The different molecular clouds are divided into ensembles according to the PDF slope and each ensemble is represented by a single spherical cloud. The cores are considered as elements of self-similar structure typical for fractal clouds and are modeled by spherical objects populating each cloud shell. Our model assumes relations between size, mass, and density of the statistical cores. Out of these, a core mass-density relationship ρ ∝ mx is derived where x = 1∕(1 + q). We find that q determines the existence or nonexistence of a threshold density for core collapse. The derived general CMF is a power law of slope − 1 while the CMF of gravitationally unstable cores has a slope (−1 + x∕2), comparable with the slopes of the high-mass part of the stellar IMF and of observational CMFs.
Key words: ISM: clouds / ISM: structure / methods: statistical
© ESO 2020
1 Introduction
Star formation is a complex, multi-scale process in the interstellar medium. Its final stages occur in the densest cloudy regions, consisting mostly of molecular gas with densities n ≳ 102 cm−3 (Klessen & Glover 2016, and the references therein). This gas is as cold as T ~ 10−30 K and its thermodynamical state could be considered as approximately isothermal. Interplay between gravity, turbulence, thermal pressure and magnetic fields takes place at various scales (from thousands of astronomical units to tens of parsecs) within these cold zones in star-forming regions. The nonthermal motions are mostly supersonic and are considered as a signature of hierarchical and chaotic collapse at all scales (Vázquez-Semadeni et al. 2007; Ballesteros-Paredes et al. 2011, 2018), accretion-driven turbulence (Klessen & Hennebelle 2010), and/or momentum and/or energy deposition into the clouds by supernova explosions (Dib et al. 2006; Padoan et al. 2016) and other mechanisms. Although this physical picture is very complex, the gas dynamics at the advanced evolutionary stages of the cloud are dominated by gravity. However, the onset of a multi-scale collapse is not only determined in the densest regions. The process rather starts at Galactic scales (Ibáñez-Mejía et al. 2016; Elmegreen 2018) and continues to cascade down to smaller scales and denser regions. When gravity becomes the dominant acting force, a power-law tail (PLT) is expected to develop at the high-density part of the probability density function of mass- (ρ-PDF) and column-density (N-PDF). The latter has been observed in a number of studies of star-forming regions (Kainulainen et al. 2009; Schneider et al. 2015a,b). The PLT of the ρ-PDF has been found in numerical simulations (e.g., Klessen 2000; Dib & Burkert 2005; Kritsuk et al. 2011; Collins et al. 2012) and explanations of this phenomenon have been presented based on theoretical considerations (Elmegreen 2011, 2018; Girichidis et al. 2014; Guszejnov, Hopkins & Grudić 2018; Donkov & Stefanov 2018). Almost all of these studies are dedicated to the investigation of dense molecular gas, while Elmegreen (2018) supposes that PLTs should also be observed at larger scales comparable with the Galactic scale height.
Gas structures that correspond to spatial scales within the PLT range could be transient or collapsing depending on the local Jeans mass. It has been shown from simple hierarchical considerations that the mass function of such condensations dN∕d logm should possess a slope of − 1 (Fleck 1996), because each small spatial scale at the hierarchy bottom is included in each large scale at the top. Such a slope is typical for fractals, whose dynamics are determined by a steady state (Elmegreen & Falgarone 1996). In the case where one tightens the scope of consideration to collapsing structures only, a Salpeter slope of approximately − 1.3 (Salpeter 1955) might be expected (Hennebelle & Chabrier 2008).
In this study, we aim to model the mass function of prestellar cores (CMF) generated in molecular clouds (MCs) which are characterized by a pure power-law ρ-PDF. A statisticalapproach is justified since both the CMF and the PDF are statistical descriptions of star-forming regions. In many regions the high-mass slope of the derived CMF turns out to be indistinguishable within the 1σ uncertainty due to limited size of the used sample (e.g., Alves et al. 2007; Reid & Wilson 2006; Enoch et al. 2008; Ikeda & Kitamura 2009; Polychroni et al. 2013). On the other hand, the diversity of ρ-PDFs, as testified by numerous simulations of star-forming regions, is large (Klessen 2000; Dib & Burkert 2005; Kritsuk et al. 2011; Collins et al. 2012; Federrath & Klessen 2013; Girichidis et al. 2014). To deal with this issue, we divide MCs into ensembles according to the PDF slope and each ensemble is represented by a single spherical cloud. The cores are considered as elements of self-similar structure typical for fractal clouds and are modeled by spherical objects populating each cloud shell. Their mass function is derived from basic relations between core quantities whereas statistics for the cores are obtained from the ρ-PDF.
Our approach is presented in detail in Sect. 2. We model the prestellar cores as abstract, homogeneous objects (simply referred to as cores) which obey appropriate assumptions, reflecting the basic properties of real condensations. Starting from these assumptions and from the properties of the ρ-PDF, we derive a mass–density relationship that our statistical cores should obey. Then, in Sect. 3, we derive the general CMF withinthis framework. The conditions for core collapse are analyzed in Sect. 4 and then the mass function of unstable cores is derived (Sect. 5). We discuss two issues with the applicability of the model in Sect. 6 and conclude with a summary of the study in Sect. 7. To help the reader, a list of frequently used symbols and notations is provided in Table 1.
Frequently used notations.
2 Setting of the model
2.1 Cloud model and its PDF
We use the abstract model of molecular clouds that was introduced in Donkov et al. (2017, hereafter, DVK17). The basic properties and assumptions are summarized below. A spherical cloud with mass density profile ρ(ℓ) is considered. The scales ℓ0 ≪ ℓ ≤ ℓc are defined simply as radii measured from the center of the sphere to a given density level, where ℓc is the size of the entire cloud and ℓ0 is the size of its homogeneous inner part. Thus the scales are derived from the volume-weighted ρ-PDF p(s):
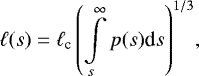 (1)
(1)
where s = ln(ρ∕ρn) is the logarithmic density with the average density of the entire cloud 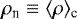 chosen as a normalization unit. Using this definition, the size of the homogeneous inner part ℓ0 ≪ℓ is neglected tosimplify the calculations. The upper integration limit is taken to be infinity, that is, the density in the cloud inner part corresponds to very large densities compared to the density at the edge of the cloud. Thus, ℓ(s) is the radius of the sphere, corresponding to density level ρ. This radius is not related to the size of any contiguous object delineated on MC intensity maps or through clump extraction techniques. It contains implicitly the physics of the considered MC through the ρ-PDF. Li & Burkert (2016) use a similar definition aimed to simplify the cloud structure in their model.
chosen as a normalization unit. Using this definition, the size of the homogeneous inner part ℓ0 ≪ℓ is neglected tosimplify the calculations. The upper integration limit is taken to be infinity, that is, the density in the cloud inner part corresponds to very large densities compared to the density at the edge of the cloud. Thus, ℓ(s) is the radius of the sphere, corresponding to density level ρ. This radius is not related to the size of any contiguous object delineated on MC intensity maps or through clump extraction techniques. It contains implicitly the physics of the considered MC through the ρ-PDF. Li & Burkert (2016) use a similar definition aimed to simplify the cloud structure in their model.
The cloud is taken as representative of the so-called MC class of equivalence, introduced in DVK17. Figure 1 schematically illustrates the concept. By assumption, all class members are characterized by single ρ-PDF, single cloud size (ℓc), single size (ℓ0) and density (ρ0) of the cloud inner part and density at the edge of the cloud (ρc). In this study, we also add the assumption that the cloud is isothermal, with temperature T. We point out that individual class members could widely differ in their morphology and physics. The MC class of equivalence is conceived here as a statistical ensemble. Its average (abstract) member possesses spherical symmetry and isotropy and is statistically representative of the behavior of any single class member.
In this study, we consider a ρ-PDF that consistsonly of a PLT with a slope q < −1:
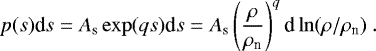 (2)
(2)
Here, As is the normalization constant and can be obtained from the condition 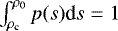 . From this, one obtains:
. From this, one obtains:
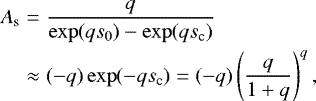 (3)
(3)
making use of a formula for 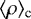 obtained in DVK17. From the reasonable assumption that ρc ≡ ρ(ℓc) ≪ ρ0, the averaged density of the entire cloud becomes a simple function of the density of the edge of the cloud and the ρ-PDF slope q:
obtained in DVK17. From the reasonable assumption that ρc ≡ ρ(ℓc) ≪ ρ0, the averaged density of the entire cloud becomes a simple function of the density of the edge of the cloud and the ρ-PDF slope q:
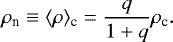 (4)
(4)
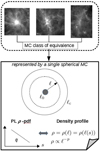 |
Fig. 1 Concept of the MC class of equivalence (after Donkov et al. 2017). |
2.2 Assumptions about the core population
Within the presented cloud model of DVK17, we now implement assumptions about the population of prestellar cores in MCs of a given class of equivalence. These include relations between core mass, density, and size; and a rule for statistical weighting of cores according to their densities which is needed to derive the core mass function in Sect. 3.
2.2.1 Relations for statistical cores
The prestellar cores are modeled by abstract statistical objects referred to hereafter as “cores”. These are homogeneous spheres with mass m and size (radius) l. The cloud shell, corresponding to log-density range [s, s + ds] at a given density level ρ = ρn exp(s), is populated by |dNρ| cores1.
We postulate a natural relation between core density, mass, and size:
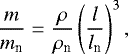 (5)
(5)
as well a commonly adopted core mass–size relation of power-law type:
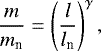 (6)
(6)
where mn, ρn, and ln are normalization units. The second relation is studied in many works on core populations as the exponent γ is often taken to be constant (independent on the scale). In the proposed model we adopt the assumption of self-similarity in turbulent fractal clouds, that is, that the core mass–size relation should reflect the general cloud structure in terms of abstract scales: M(ℓ) ∝ ℓγ. Then, in case of a purely power-law ρ-PDF, the mass scaling exponent is a function of its slope only (see Sect. 3.2 in DVK17):
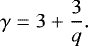 (7)
(7)
Combining the assumed relations between core quantities (Eqs. (5)–(6)), one can derive the following mass–density relation for the cores:
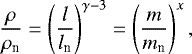 (8)
(8)
is called the structure parameter. We point out that the existence of a power-law mass–density relation for core populations is supported by the main scenarios of core formation and/or evolution. If the cores have formed via purely turbulent fragmentation, it is derived from a combination of the velocity scaling law with shock-front conditions (Padoan & Nordlund 2002). In gravoturbulent scenarios, the core mass–density relation is an outcome of energy balance (virial-like relations) at different spatial scales (Donkov et al. 2012). Donkov et al. (2011) substantiated this relation theoretically, estimating the range of values of the structure parameter x from equipartitions between various forms of energy in evolved MCs. Figure 2 illustrates how the basic elements of the proposed model are linked.
Numerical estimates of the exponents in those relations are useful for reference in the considerations hereafter. Typical slopes − 4 ≤ q ≤−1.5 for evolving PLTs (Kritsuk et al. 2011; Collins et al. 2011; Girichidis et al. 2014) yield − 0.33 ≥ x ≥−2, 2.25 ≥ γ ≥ 1.
One has some freedom to choose the normalization units in relations (5) and (6). A widely used choice of normalization unit of density in numerical simulations is the mean density of the box. In this work, following DVK17, we opt for the mean cloud density (Eq. (4)):
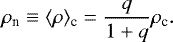 (10)
(10)
Regarding the normalization unit of size, it is natural to set it to be comparable to the core sizes, that is, in a broad range of scales belowthe cloud size. For simplicity we take:
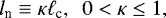 (11)
(11)
where κ = const(ℓ) is a model parameter. The meaning of κ is clarified further throughout Sects. 3–5. The normalization unit of mass mn is obtained from the condition of mass conservation at a given scale ℓ (see Sect. 2.2.2).
By use of the normalization units, we define logarithmic variables for mass, size, and volume as follows:
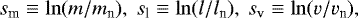 (12)
(12)
where v = (4π∕3)l3 is the core volume and 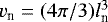 is the volume normalization unit. Now one is able to derive from the density PDF (Eq. (2)) statistical distributions of core masses, sizes, and volumes which are power-law functions with exponents depending on q and on the structure parameter x. This is donein Appendix A.1. We note here only that
is the volume normalization unit. Now one is able to derive from the density PDF (Eq. (2)) statistical distributions of core masses, sizes, and volumes which are power-law functions with exponents depending on q and on the structure parameter x. This is donein Appendix A.1. We note here only that
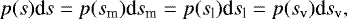 (13)
(13)
due to the one-to-one correspondence between the density, mass, size, and volume of the cores.
 |
Fig. 2 Sketch of the model setting which shows the statistical link between the density distribution in the cloud and the core population. The double-ended arrows denote one-to-one correspondence between quantities. The concepts introduced in this work (in regard to the DVK17 model) are shaded in gray. |
2.2.2 Weighting of cores according to their density
The key issue in our model is how to weight the contributions of statistical cores with different densities to the total statistics. If 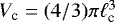 is the total volume of the cloud, we postulate that the volume dVs = −Vcp(s)ds of the shell, corresponding log-density range [s, s + ds], is equal to the sum of volumes of the cores it contains. Hence, if d Nρ is the contribution of a shell with density ρ to the total number of cores, we get:
is the total volume of the cloud, we postulate that the volume dVs = −Vcp(s)ds of the shell, corresponding log-density range [s, s + ds], is equal to the sum of volumes of the cores it contains. Hence, if d Nρ is the contribution of a shell with density ρ to the total number of cores, we get:
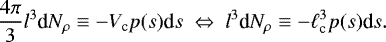 (14)
(14)
We note that dNρ is negative, since the total number of cores Nρ down to a given density threshold ρ decreases as the density increases up to ρ0. The same holds for the volume dVs. We note that Vs ≡ Vℓ.
One must check whether the volume and mass are conserved at a given scale ℓc ≥ ℓ ≫ ℓ0 (i.e., at given density threshold ρc ≤ ρ ≪ ρ0). The volume of a scale ℓ is calculated in a straightforward manner:
![\[ V_{\ell}=\frac{4\pi}{3}\ell^3. \]](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq20.png)
To calculate the mass of the scale Mℓ, we invoke the scaling relations for mass and density profile for a given scale in case of a power-law PDF, derived in DVK17:
![\begin{align*}&M_{\ell}=M_{\textrm{c}}\left(\frac{\ell}{\ell_{\textrm{c}}}\right)^{\gamma},\nonumber\\[5pt] &\rho=\rho_{\textrm{c}}\left(\frac{\ell}{\ell_{\textrm{c}}}\right)^{-p}, \end{align*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq21.png) (15)
(15)
where p is the density profile exponent and 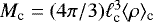 is the total mass of the cloud. A simple relation between p and the slope of the high-density power-law part of the ρ-PDF in spherically symmetric clouds has been derived analytically: p = −3∕q (Federrath & Klessen 2013; Girichidis et al. 2014). Using this relation and combining Eqs. (4), (9), and (15), one obtains:
is the total mass of the cloud. A simple relation between p and the slope of the high-density power-law part of the ρ-PDF in spherically symmetric clouds has been derived analytically: p = −3∕q (Federrath & Klessen 2013; Girichidis et al. 2014). Using this relation and combining Eqs. (4), (9), and (15), one obtains:
![\begin{eqnarray*}M_{\ell} &=&M_{\textrm{c}}\left(\frac{\ell}{\ell_{\textrm{c}}}\right)^{\gamma}=M_{\textrm{c}}\left(\frac{\rho}{\rho_{\textrm{c}}}\right)^{-\gamma/p} \nonumber\\[5pt] ~&=&M_{\textrm{c}}\left(\frac{\rho}{\rho_{\textrm{n}}}\right)^{1+q}\left(\frac{q}{1+q}\right)^{1+q}~. \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq23.png) (16)
(16)
On the other hand, the volume and the mass of a given scale ℓ can be calculated as sums of the volumes and masses of the cores populating this scale, respectively. Taking into account that V0 ≪ Vℓ and using Eq. (14), one obtains for the volume:
![\begin{eqnarray*} &&\hspace*{-6pt}\sum_{\rho}^{\rho_0} \frac{4\pi}{3}l^3 |\Delta N_{\rho}|= \int_{\rho}^{\rho_0}-\frac{4\pi}{3}l^3 \textrm{d}N_{\rho}\nonumber\\[5pt] &&\qquad\quad\ \ \ \ \ \quad=\int_{\rho}^{\rho_0} V_{\textrm{c}}p(s)\textrm{d}s=\int_{\rho}^{\rho_0} -\textrm{d}V_s \simeq V_{\ell}.\nonumber \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq24.png)
This simply means that the volume conservation is trivial, since the cores are accounted for in Eq. (14) through their volumes. In view of the model setup ρc ≤ ρ ≪ ρ0, for the mass one obtains accordingly:
![\begin{eqnarray*} \begin{aligned} \sum_{\rho}^{\rho_0} m |\Delta N_{\rho}|&= \int_{\rho}^{\rho_0} m l^{-3} \ell_{\textrm{c}}^3 p(s)\textrm{d}s~ \nonumber\\[3pt] &=\frac{m_{\textrm{n}}}{l_{\textrm{n}}^3} \ell_{\textrm{c}}^3 \int_{\rho}^{\rho_0} \frac{m}{m_{\textrm{n}}} \left(\frac{l}{l_{\textrm{n}}}\right)^{-3} p(s)\textrm{d}s \nonumber\\[3pt] &=\frac{m_{\textrm{n}}}{l_{\textrm{n}}^3} \ell_{\textrm{c}}^3 \int_{\rho}^{\rho_0} \left(\frac{\rho}{\rho_{\textrm{n}}}\right) p(s)\textrm{d}s \nonumber \\[3pt] &\simeq m_{\textrm{n}} \left(\frac{\ell_{\textrm{c}}}{l_{\textrm{n}}}\right)^3 \left(\frac{q}{1+q}\right)^{1+q}\left(\frac{\rho}{\rho_{\textrm{n}}}\right)^{1+q} \nonumber \\[3pt] &=\frac{m_{\textrm{n}}}{\kappa^3}\left(\frac{q}{1+q}\right)^{1+q}\left(\frac{\rho}{\rho_{\textrm{n}}}\right)^{1+q}~. \nonumber \end{aligned} \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq25.png)
Equating the above expression for Mℓ and formula (16), we derive an expression for the mass normalization unit mn which links it to the parameter κ (Eq. (11)):
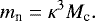 (17)
(17)
This formula leads (in view of Eq. (5)) to an important relation for the cores:
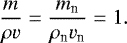 (18)
(18)
Some statistical quantities of the cores and their relations are derived in Appendix A.2 by use of the formulae obtained in Sect. 2.2. Now one is able to calculate two quantities which are measures of the total number of cores above a given density level (Nρ) and in the entire cloud (Nc):
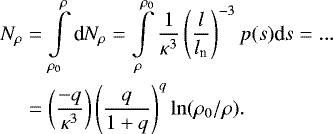 (19)
(19)
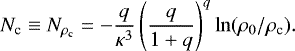 (20)
(20)
The latter quantity is useful for assessment of the conditions for core collapse (Sect. 4).
3 The core mass function
In this section, we derive the CMF within the framework of the presented model. The statistical contribution of cores in a given shell [s, s + ds] is calculated in Sect. 2.2.2 (Eq. (14)): 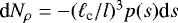 . Due to the one-to-one correspondence between core density and core mass, we have d Nm = dNρ and p(s)ds = p(sm)dsm (cf. Eq. (13)). Therefore,
. Due to the one-to-one correspondence between core density and core mass, we have d Nm = dNρ and p(s)ds = p(sm)dsm (cf. Eq. (13)). Therefore,
![\[ \frac{\textrm{d}N_{\textrm{m}}}{\textrm{d}\ln\left(\frac{m}{m_{\textrm{n}}}\right)}= -\left(\frac{\ell_{\textrm{c}}}{l}\right)^3 p(s_{\textrm{m}}). \]](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq31.png)
After some algebraic operations and by use of Eqs. (11) and (9) one obtains:
![\[ (\ell_{\textrm{c}}/l)^3=(\ell_{\textrm{c}}/l_{\textrm{n}})^3 (l_{\textrm{n}}/l)^3=(1/\kappa)^3(m/m_{\textrm{n}})^{-3/\gamma}. \]](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq32.png)
Now, replacing p(sm) with 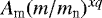 from Eq. (A.1) and in view of the relation − 3∕γ + xq = 0 (cf. Eq. (6)), we obtain a differential core mass distribution:
from Eq. (A.1) and in view of the relation − 3∕γ + xq = 0 (cf. Eq. (6)), we obtain a differential core mass distribution:
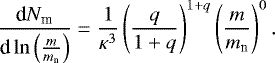 (21)
(21)
This is still not a formula for the CMF because one has to take into account the fractal structure of the cloud. In other words, the r.h.s. of Eq. (21) must be weighted with respect to the number of scales at density level ρ which are contained in the entire MC. This weighting corresponds to the physical picture of a steady state in the cloud as the material is accreted through the cloud boundary and is transferred downwards through all scales. Therefore, for a given scale ℓ with mass Mℓ, the weighting coefficient should be Mc∕Mℓ. Making use of Eqs. (15) and (8)–(10), one obtains
![\[ \frac{M_{\textrm{c}}}{M_{\ell}}=\left(\frac{\ell}{\ell_{\textrm{c}}}\right)^{-\gamma}=\left(\frac{\rho}{\rho_{\textrm{c}}}\right)^{\gamma/p}=\left(\frac{q}{1+q}\right)^{\gamma/p}\left(\frac{m}{m_{\textrm{n}}}\right)^{x\gamma/p}, \]](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq35.png)
and for the exponents: γ∕p = −(1 + q) and xγ∕p = −1. This yields a formula for the CMF:
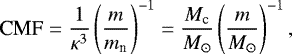 (22)
(22)
where the conversion to solar units is made using Eq. (17): 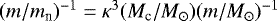 .
.
The derived CMF does not depend on κ (formula (22)), that is, the latter behaves as a free parameter as long one considers the cores as substructures in a fractal (self-similar) cloud. Indeed, this result recovers the mass spectrum in the interstellar medium modeled as a scale-invariant hierarchy of density fluctuations (Fleck 1996). As shown by Elmegreen & Falgarone (1996, see Sect. 4 there), the slope − 1 is to be expected considering a large sample of clouds – the fractal dimension of the whole ensemble equals the mass–size exponent γ which yields a CMF that is independent of the physical conditions in an individual cloud. The construction of statistical ensemble proposed in DVK17 and in this work is consistent with their conclusion. From the point of view of observations, the total clump population in star-forming regions, which is extracted by use of various clump-finding techniques, displays shallower or similar slopes if the CMF is fitted by one power-law function (Heithausen et al. 1998; Kramer et al. 1998; Li et al. 2007; Pekruhl et al. 2013). On the other hand, if the CMF is fitted by two power-law functions, the slope of the high-mass part is comparable to or steeper than that of the stellar initial mass function (IMF; see Veltchev et al. 2013 and references therein). Some numerical simulations (e.g., Dib et al. 2008a,b) indicate also that the slope should steepen when high-density cores are selected.
4 Conditions for core collapse
Now we analyze the ability of cores of a given density ρ to collapse. We introduce the Jeans mass at density ρ in the form
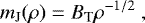 (23)
(23)
where 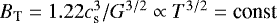 , due to the assumption of isothermality of the cloud. Recalling the derived core mass–density relationship (Eq. (8)), for the mass of cores at density level ρ, one obtains:
, due to the assumption of isothermality of the cloud. Recalling the derived core mass–density relationship (Eq. (8)), for the mass of cores at density level ρ, one obtains: 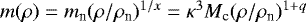 . For the ratio of the core mass to the local Jeans mass, this yields:
. For the ratio of the core mass to the local Jeans mass, this yields:
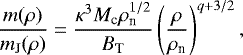
which is transformed by use of Eq. (11) to:
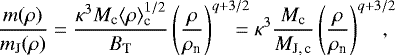 (24)
(24)
where 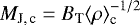 is the Jeans mass for the entire cloud. The coefficient (κ3Mc∕MJ, c) of this power-law relationship is a function of the global cloud parameters only. In particular, the parameter κ (formula (11)) is related through Eq. (20) to the total number of cores and the characteristics of the ρ-PDF:
is the Jeans mass for the entire cloud. The coefficient (κ3Mc∕MJ, c) of this power-law relationship is a function of the global cloud parameters only. In particular, the parameter κ (formula (11)) is related through Eq. (20) to the total number of cores and the characteristics of the ρ-PDF:
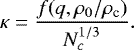 (25)
(25)
For typical PDF slopes − 3 ≤ q ≤−1.5 and density contrasts 102 ≲ (ρ0∕ρc) ≲ 103 (corresponding to a well-resolved PLT in simulations), the numerator in the expression above is a slightly varying function with values of between 1 and 2. Thus, κ3 reflects mainly the total number of cores and its reciprocal quantity 1∕κ3 can be interpreted as a measure of how fragmented the cloud is (index of MC fragmentation). An appropriate (constant) value of κ is to be determined from Nc (Fig. 3).
When considering the gravitational fragmentation of the cloud, as opposed to simply fractal density distributions, κ is no longer a free parameter because additional physical processes play a role, such as the competition between gravitational collapse and thermal pressure. As shown in the following section, gravitational instability modifies the construction of the CMF.
Setting m∕mJ ≥ 1 as a condition for core collapse, one arrives from Eq. (24) at three different scenarios for star formation in the cloud. These are illustrated in Fig. 4 where κ is calculated from Eq. (25) for the given slope and Nc:
– q + 3∕2 = 0 ⇔ q = −3∕2.
This slope corresponds to a well-developed PLT at an advanced evolutionary stage in self-gravitating media (Kritsuk et al. 2011; Girichidis et al. 2014). In this special case evidently all cores in the cloud will be either gravitationally stable or unstable, depending on the Jeans content of the cloud Mc ∕MJ, c and on the index of MC fragmentation 1∕κ3:
![\[ m/m_{\textrm{J}}=\kappa^3 M_{\textrm{c}}/M_{\textrm{J,\,c}}. \]](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq45.png)
In a sub-Jeans cloud, all cores will dissolve without any star formation. The increase of fragmentation in super-Jeans clouds is unfavorable for core collapse. A low index of fragmentation (1∕κ3 = 25.4) would lead to the prediction of ubiquitous core collapse even in a moderately super-Jeans cloud (solid line in Fig. 4, top left). Vice versa, in the case of highly fragmented MCs with 1∕κ3 = 244.1 (Fig. 4, top right) a ubiquitous core collapse would take place only if the Jeans content is very high (say, Mc ≳ 102MJ, c).
This case is an illustrative example of how the fragmentation of the cloud determines the effectiveness of local collapse. Of course, not all possible values of κ would have a physical meaning; Fig. 4 is intented to present simply the total general picture. Comparison of the model with samples of real clouds can impose constraints on the index of fragmentation.
– q + 3∕2 > 0 ⇔ − 1 > q > −3∕2.
In a given cloud with some fixed index of fragmentation, the ratio m∕mJ increases with the core density ρ. This is the case of a threshold core density for star formation, ρthres, whereby all cores with ρ ≥ ρthres will collapse. The more Jeans masses contained in the cloud, the lower the threshold (thick dashed line in Fig. 4, top). However, shallow slopes − 1 > q > −3∕2 appear rarely in simulated self-gravitating clouds; usually for restricted time-spans at their late evolutionary stages (Veltchev et al. 2019).
– q + 3∕2 < 0 ⇔ q < −3∕2.
Steeper ρ-PDF slopes are typical at earlier stages of self-gravitating media as testified from ρ-PDFs derived from numerical simulations (Kritsuk et al. 2011; Collins et al. 2012; Veltchev et al. 2019). A PLT with q ≲ −3 is barely distinguishable from the wing of a lognormal distribution. As seen in Fig. 4 (top, thin dashed lines), there is an upper threshold density ρthres, up in this case, for a given cloud and some fixed index of fragmentation, that is, only cores with ρ ≤ ρthres, up will collapse. This result is counter-intuitive at first glance but it stems from the obtained core mass–density relationship m ∝ ρ1∕x (Eq. (8)). More massive cores are less dense (Fig. 4, bottom) and, since x > −2 for q < −3∕2, core mass grows faster with decreasing density than the local Jeans mass does.
 |
Fig. 3 Relationship between the parameter κ and the total number of detected cores (Eq. (25)), for different choices of the ρ-PDF slope and density contrast. |
5 Mass function of unstable cores
A natural assumption for dynamically evolving clouds is that the formed cores are constantly replenished. On this assumption, Clark et al. (2007) argue that the core mass function should be weighted by a coefficient accounting for dynamics of unstable cores:
![\[ \left(\frac{\tau_{\textrm{ff}}(\rho)}{\tau_{\textrm{ff}}(\langle\rho\rangle_{\textrm{c}})}\right)^{-1}=\left(\frac{\langle\rho\rangle_{\textrm{c}}}{\rho}\right)^{-1/2}=\left(\frac{m}{m_{\textrm{n}}}\right)^{x/2}, \]](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq46.png)
where τff(ρ) and 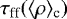 are the free-fall times for a core of density ρ and for the entire MC, respectively. Those authors consider a CMF which is a combination of two power-law functions, while in our statistical framework the CMF resulting from fractal hierarchical structure is a single power law (Eq. (22)). We assume thatonly unstable cores fitting the criteria derived in the previous section will eventually collapse. To obtain their CMF, one should apply free-fall times weighting to the r.h.s. of Eq. (22) and obtain:
are the free-fall times for a core of density ρ and for the entire MC, respectively. Those authors consider a CMF which is a combination of two power-law functions, while in our statistical framework the CMF resulting from fractal hierarchical structure is a single power law (Eq. (22)). We assume thatonly unstable cores fitting the criteria derived in the previous section will eventually collapse. To obtain their CMF, one should apply free-fall times weighting to the r.h.s. of Eq. (22) and obtain:
 |
Fig. 4 Conditions for core collapse for different total numbers of cores (columns) and PDF slopes. Top: function m∕mJ (Eq. (24)) projected on the plain “core density vs. cloud mass”. Lines denote the condition m∕mJ = 1; the domains of unstable cores for the three exemplary values of q are shown with arrows. An isothermal Jeans mass within the cloud MJ, c for T = 30 K is adopted. Bottom: mass–density relationship for cores (Eq. (8)) where the mass is given in units of the total mass of the cloud. The density contrast in the cloud is fixed at (ρ0 ∕ρc)= 103. |
 (26)
(26)
Probability distribution function slopes of − 4 ≤ q ≤−1.5 yield CMF slopes Γ = −1 + x∕2 in the range − 1.17 and − 2 (cf. Eq. (9)). Interestingly, the latter includes the classical Salpeter value − 1.33 of the stellar IMF. Similar CMF slopes have been found in a number of observational studies (Table 2). We point out as well that the slope Γ depends implicitly on time through the slope of the ρ-PDF (Eq. (9)). The latter is expected to become shallower in evolving self-gravitating clouds (Girichidis et al. 2014) which would lead to steepening of the CMF of unstable cores.
In the case q = −3∕2 and given that all cores are unstable (see the comment in the previous section), one obtains a steep CMF with Γ =−2. The cases with q < −3∕2 correspond to the typical PDFs in evolving self-gravitating clouds. The upper core density threshold ρthres, up corresponds to a minimal mass of collapsing cores which serves as the characteristic mass Mch separating the regimes of noncollapsing and collapsing cores. In that way, the model predicts a CMF in evolving self-gravitating clouds that is a combination of two power laws with slopes:
![\begin{eqnarray*}\Gamma&=&-1, m<M_{\textrm{ch}}\nonumber\\[3pt] \Gamma&=&-1+\frac{x}{2}, m\ge M_{\textrm{ch}}. \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq49.png) (27)
(27)
We note that the characteristic mass Mch is to be calculated from the condition m(ρ) ≥ mJ(ρ) (Eq. (24)). The coefficient in the latter can be transformed by use of Eq. (25) to:
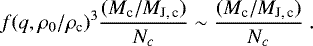 (28)
(28)
Thus, the modeled characteristic mass depends on global cloud parameters: the PDF slope q (through the structure parameter x) and the cloud’s Jeans content per core. The larger the latter quantity for a fixed q, the lower the value of Mch. We note that the cloud’s Jeans content per core could also take values below unity since MJ, c may exceed local Jeans masses substantially. Comparison of formulae (25), (26), and (28) shows how κ affects the characteristic mass. This could give additional opportunities to constrain the values of parameter κ from observational and/or numerical studies.
In Fig. 5 we compare the CMF of unstable cores from our model with high-mass CMFs from observations of clumps in several star-forming regions (Table 2). In all but one of those works most or all of the sampled cores have been assessed as gravitationally bound. For plausible values of the Jeans content per core 0.5 ≤ (Mc∕MJ, c)∕Nc ≤ 20, we find good consistency with CMFs derived from dust-extinction and dust-emission studies, with slopes Γ close to the Salpeter value. In those cases the modeled Mch is constrained within an order-of-magnitude range, with mean values of about 2− 3 solar masses.
6 Discussion
6.1 Time constraints on the model’s applicability
Basic presupposition of our model is a power-law ρ-PDF with constant slope which is independent of the spatial scale. In view of the definition of scales (formula (1)), this translates into the requirement in which the ρ-PDF is not subject to noticeable and/or stochastic changes in the considered time frame. This leads to some constraints on evolutionary time or phase of the system. Well developed PLTs of PDFs are clearly distinguishable from lognormal wings and are to be expected in self-gravitating clouds at evolutionary times ≳ 0.2τff (Klessen 2000; Girichidis et al. 2014; Kritsuk et al. 2011; Collins et al. 2012). A recent analysis of ρ-PDF PLTs in simulated self-gravitating clumps shows that the slope |q| decreases smoothly within periods of 0.2−2.5τff, depending on the Jeans content, the initial velocity field, and the type of turbulence driving, and suffers fast variations as it approaches the limiting value of ~1.5 (Veltchev et al. 2019). Also taking into account the zone of agreement in the CMF-parameter space between observations and our model (see Fig. 5), we claim that the latter is best applicable at early phases of cloud collapse. These early phases are characterized by slopes − 2 ≳ q ≳−4 and a temporary delay of the collapse due to stabilizing agents like magnetic field and thermal pressure (see discussion in Girichidis et al. 2014). This physical picture is conceptually consistent with the result of our model: formation of massive, low-density but super-Jeans cores which are subject to further fragmentation leading to protostellar objects.
Parameters of high-mass parts of observational CMFs in some SF regions.
 |
Fig. 5 Parameters of modeled mass functions of unstable cores (open symbols) compared with those of the high-mass part of observational CMFs (filled symbols; the numbers correspond to the data in Table 2). Vertical solid lines denote the range of characteristic masses generated by varying (Mc ∕MJ, c)∕Nc from 0.5 (large symbols) to 20.0 (small symbols). The domain of PLTs which can be distinguished from a lognormal wing (q ≳ −4) is shown with a vertical dashed line and an arrow. See text. |
6.2 Relation to other core mass function models
Essentially, the presented model aims to reproduce the general CMF which is to be expected from turbulent or gravoturbulent fragmentation of dense clouds into condensations of different shapes and densities modeled through statistical cores. In that sense, the model is similar to the approach of Padoan & Nordlund (2002) who also derive the CMF slope through weighting over the scales in the fractal cloud (cf. their Sect. 5 with Sect. 3 in this paper). In their purely self-similar consideration, the obtained CMF slope is also − 1, with no dependence on the fractal dimension of the cloud, that is, on the local physical conditions. The main difference between ours and the model of Padoan & Nordlund (2002) is that we assume a purely power-law PDF (characteristic of dense protocluster clumps) in contrast to the lognormal PDF in their treatment.
The model setting of Padoan & Nordlund (2002) has been extended and upgraded to further follow the dynamical evolution of prestellar cores formed through initial cloud fragmentation. For instance, Dib et al. (2007) investigate how the process of coalescence of cores in the inner part of MCs affects the time-evolution of the CMF and its transition to the stellar IMF. Dib et al. (2010) take into account the internal structure of cores in terms of density profile and mass–density relationship whereas the core radius depends on the core mass and position in the cloud. These latter authors introduce a time-dependent accretion onto the cores which also depends on their location and leads to significant modification of the CMF in the course of cloud evolution. Alternatively, Dib et al. (2013) make use of the same set of initial conditions in the cloud and study the evolution of cores without accretion but implementing the kinetic energy input by stellar winds from massive newly formed stars. Our model is comparable to the above-mentioned studies only in terms of the initial cloud fragmentation but without preference to any particular physical mechanism. The only assumption on the further core evolution is that unbound cores eventually dissolve while their bound peers contract and are being replenished. In regard to the mass function of unstable cores, the presented model follows the approach of Clark et al. (2007) who show that the initial (shallow) CMF should be corrected to account for the different free-fall times of cores and thus its slope would become similar to that of the Salpeter value of the stellar IMF or steeper.
All models referred to above aim to connect the CMF with the stellar IMF although they do not discuss the origin of the CMF itself. The goal of this paper is not to reproduce the high-density slope of the IMF from the CMF. The treatment of the latter issue would require implementation of more physical processes, such as disk fragmentation or core merging, also taking into account their variation in the star-forming environments. Rather, sticking to the statistical approach of DVK17, we extend their study on possible links between general structure of MCs and characteristics of their fragments (cores) which eventually give birth to stars.
6.3 Comparison with observational mass functions of prestellar cores
From an observational point of view, the proposed CMF model is applicable to MCs with large PLTs on their column–density distributions. The sole constraint stemming from the model is that the mean column densities of the extracted cores (regardless of the extraction method) are within the PLT range. Therefore, considering only the PLT, the column-density PDF translates – under the model assumption of spherical symmetry – to a power-law density PDF (see DVK17).
The range − 2 ≥ q ≥−4 (leading to CMF slopes − 1.5 ≤ Γ ≤−1.17) of good consistency of our model with observational CMFs (Fig. 5) corresponds to values of the mass scaling index γ between 1.5 and 2.25 (formula (15)). Such a range of γ is entirely consistent with the general structure of Galactic molecular clouds as studied in different tracers: molecular-line emissions, dust continuum, and dust extinction. For instance, Lombardi et al. (2010) found γ ≲ 2 for a sample of clouds with a substantial range of masses, and therefore defined by different choices of column–density threshold. Kauffmann et al. (2010) derived a mass–size relationship with γ = 1.7 for cloud fragments of sizes 1−4 pc in several nearby star-forming regions. The size and mass ranges in those studies also fit well with the ones calculated from our model for a typical density contrast ρ0 ∕ρc = 103 and various values of the cloud’s Jeans content: 0.6−2 pc and 102−103 M⊙, respectively.
The theoretical position of the characteristic mass2 is a complex issue which is widely discussed in the literature. Considerations of Jeans collapse in turbulent medium show that Mch depends only on global cloud parameters like sound speed and sonic scale, even when the assumption of isothermality is not valid (see Hopkins 2012; Guszejnov & Hopkins 2015, and references therein). On the other hand, from simulations of supersonic isothermal turbulence, Schmidt et al. (2010) derive CMFs of unstable cores with characteristic mass depending on the Jeans length in the numerical box and on (resolution) effects stemming from the applied clump-finding algorithm. The variation of Mch from our model (determined by the quantity (28)) is qualitatively comparable to their result. If the Jeans content of the cloud Mc ∕MJ, c is comparable to or exceeds within an order of magnitude the number of extracted cores Nc, the characteristic mass is consistent with observational works.
7 Summary
We propose a statistical model of the CMF generated at a given point of evolution of self-gravitating isothermal clouds. The latter are represented by abstract spherical objects characterized by single size, density profile, density contrast, and parameters of the cloud core. The ρ-PDF in the cloud is assumed to be purely power law, with slope q. The statistical prestellar cores are homogeneous spheres that populate cloud shells as determined by the corresponding log-density ranges.
The basic assumptions of the model are power-law relations between core density, mass, and size, and self-similarity typical for fractal clouds. The main parameters are the total number of cores Nc (alternatively, the index of cloud fragmentation 1∕κ3) and the cloud mass in Jeans masses Mc∕MJ, c (Jeans content of the cloud).
Our results are as follows:
- 1.
The CMF in general is a power law of slope Γ = −1. The found slope is to be expected if one considers the cores as hierarchical objects in a fractal cloud. Such a slope is in general agreement with a number of studies of the total clump population in star-forming regions.
- 2.
Regarding the conditions for core collapse, the model yields three scenarios, conditioned by the PDF slope q:
-
q = −3∕2 (well developed PLT at advanced evolutionary stages): all cores are either stable or unstable, depending on Nc and the Jeans content of the cloud.
-
− 1 > q > −3∕2: all cores above some threshold density collapse.
-
q < −3∕2: all cores below some threshold density collapse. These are less dense but massive objects, which are possibly subject to further fragmentation.
-
- 3.
The derived time-weighted CMF of gravitationally unstable cores is a power law of slope Γ = −1 + x∕2 where x = 1∕(1 + q) and q ≤−3∕2. This gives good agreement with high-mass parts of observational CMFs for PDF slopes − 2 ≥ q ≥−4 which characterize earlier phases of cloud collapse. The CMF of the total population in these cases is a combination of two power laws as the characteristic mass separates the regimes of noncollapsing and collapsing (high-mass) cores.
Acknowledgements
We are grateful to our anonymous referee for the critical and careful reading of the manuscript and for the valuable suggestions. S.D. acknowledges support by the Bulgarian National Science Fund under Grant N 12/11 (20.12.2017). T.V. acknowledges support by the DFG under grant KL 1358/20-1 and additional funding from the Ministry of Education and Science of the Republic of Bulgaria, National RI Roadmap Project DO1-277/16.12.2019, as well from the Scientific Research Fund of the University of Sofia, Grant #80-10-68/19.04.2018. P.G. acknowledges funding from the European Research Council under ERC-CoG grant CRAGSMAN-646955. R.S.K. thanks funding from the DFG in the Collaborative Research Center (SFB 881) “The Milky Way System” (subprojects B1, B2, and B8) and in the Priority Program SPP 1573 “Physics of the Interstellar Medium” (grant numbers KL 1358/18.1, KL 1358/19.2).
Appendix A Statistical properties of cores
A.1 Distributions of mass, size, and volume
Those distributions are derived by:
![\begin{eqnarray*}\begin{aligned} \hspace*{-2pt}p(s_{\textrm{m}})\textrm{d}s_{\textrm{m}} &= A_{\textrm{m}}\exp(qxs_{\textrm{m}})\textrm{d}s_{\textrm{m}}&~ \\[4pt] \hspace*{-2pt}&= A_{\textrm{m}} \left(\frac{m}{m_{\textrm{n}}}\right)^{qx} \textrm{d}\ln\left(\frac{m}{m_{\textrm{n}}}\right)~,&A_{\textrm{m}}=xA_{\textrm{s}}, \end{aligned} \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq51.png) (A.1)
(A.1)
![\begin{eqnarray*}\begin{aligned} \hspace*{-2pt}p(s_{\textrm{l}})\textrm{d}s_{\textrm{l}} &=A_{\textrm{l}}\exp\left(q\frac{3x}{1-x}s_{\textrm{l}}\right)\textrm{d}s_{\textrm{l}}&~ \\[4pt] \hspace*{-2pt}&= A_{\textrm{l}} \left(\frac{l}{l_{\textrm{n}}}\right)^{q\frac{3x}{1-x}} \textrm{d}\ln\left(\frac{l}{l_{\textrm{n}}}\right)~,&A_{\textrm{l}}=\frac{3x}{1-x}A_{\textrm{s}}, \end{aligned} \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq52.png) (A.2)
(A.2)
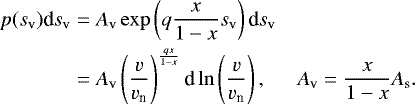 (A.3)
(A.3)
We note that Eqs. (A.1)–(A.3) rely on the assumption that the power-law ρ-PDF is preserved at all scales compared to the core sizes. Indeed, this follows implicitly from the two assumptions(Eqs. (5)–(6)), combined with the relation between the slope q of the ρ-PDF and the structure parameter x (Eq. (9)).
A.2 Averaged quantities
The averaged core mass, density, volume, and size over the entire cloud are obtained by use of the formulae obtained in Sect. 2.2. According to the method of calculation, two types of averaging are distinguished: arithmetic and geometric (logarithmic). The obtained relations between the averaged quantities (Eqs. (A.8), (A.9) and (A.14)) could serve as tools to probe the applicability of the model for selected observed or simulated medium.
A.2.1 Arithmetic averaged quantities
The arithmetic average of core density is:
![\begin{eqnarray*}\begin{aligned} \overline{\left(\frac{\rho}{\rho_{\textrm{n}}}\right)}_{\textrm{ar}} &= A_{\textrm{s}} \int\limits_{\rho_{\textrm{c}}}^{\rho_0} \left(\frac{\rho}{\rho_{\textrm{n}}}\right) \left(\frac{\rho}{\rho_{\textrm{n}}}\right)^{q} \textrm{d}\ln\left(\frac{\rho}{\rho_{\textrm{n}}}\right) =... \\[3pt] & = \left(\frac{q}{q+1}\right) \left(\frac{\rho_{\textrm{c}}}{\rho_{\textrm{n}}}\right) \bigg[\frac{(\rho_0/\rho_{\textrm{c}})^{1+q}-1}{(\rho_0/\rho_{\textrm{c}})^{q}-1}\bigg]\simeq 1. \end{aligned} \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq54.png) (A.4)
(A.4)
This is atrivial result because  and
and 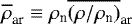 .
.
The arithmetic average of core mass is:
![\begin{eqnarray*}\begin{aligned} \overline{\left(\frac{m}{m_{\textrm{n}}}\right)}_{\textrm{ar}} &= A_{\textrm{m}} \int\limits_{\rho_{\textrm{c}}}^{\rho_0} \left(\frac{m}{m_{\textrm{n}}}\right) \left(\frac{m}{m_{\textrm{n}}}\right)^{qx} \textrm{d}\ln\left(\frac{m}{m_{\textrm{n}}}\right) \\[2pt] & = \left(\frac{qx}{qx+1}\right) \left(\frac{m_{\textrm{c}}}{m_{\textrm{n}}}\right) \left[\frac{(\rho_0/\rho_{\textrm{c}})^{\frac{1}{x}+q}-1}{(\rho_0/\rho_{\textrm{c}})^{q}-1}\right]\\[3pt] &\simeq \left(\frac{q}{2q+1}\right)\left(\frac{m_{\textrm{c}}}{m_{\textrm{n}}}\right) =\!\left(\frac{q}{2q+1}\right) \left(\frac{1+q}{q}\right)^{1+q}, \end{aligned} \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq57.png) (A.5)
(A.5)
where at the last step we make use of 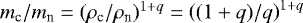 (cf. Eqs. (8), (11) and (9)).
(cf. Eqs. (8), (11) and (9)).
The arithmetic average of core volume is:
![\begin{eqnarray*}\begin{aligned} \overline{\left(\frac{v}{v_{\textrm{n}}}\right)}_{\textrm{ar}} &= A_{\textrm{v}} \int\limits_{\rho_{\textrm{c}}}^{\rho_0} \left(\frac{v}{v_{\textrm{n}}}\right) \left(\frac{v}{v_{\textrm{n}}}\right)^{q\frac{x}{1-x}} \textrm{d}\ln\left(\frac{v}{v_{\textrm{n}}}\right) =...\\[3pt] &= \left(\frac{q\frac{x}{1-x}}{1+q\frac{x}{1-x}}\right) \left(\frac{v_{\textrm{c}}}{v_{\textrm{n}}}\right) \left[\frac{(\rho_0/\rho_{\textrm{c}})^{\frac{1-x}{x}+q}-1}{(\rho_0/\rho_{\textrm{c}})^{q}-1}\right] \\[3pt] & \simeq \frac{1}{2} \left(\frac{v_{\textrm{c}}}{v_{\textrm{n}}}\right) = \frac{1}{2} \left(\frac{1+q}{q}\right)^{q}~, \end{aligned} \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq59.png) (A.6)
(A.6)
where atthe last step we make use of 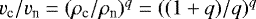 .
.
Furthermore, the arithmetic average of the size reads:
![\begin{eqnarray*}\begin{aligned} \overline{\left(\frac{l}{l_{\textrm{n}}}\right)}_{\textrm{ar}} &= A_{\textrm{l}} \int\limits_{\rho_{\textrm{c}}}^{\rho_0} \left(\frac{l}{l_{\textrm{n}}}\right) \left(\frac{l}{l_{\textrm{n}}}\right)^{q\frac{3x}{1-x}} \textrm{d}\ln\left(\frac{l}{l_{\textrm{n}}}\right) =... \\[3pt] & = \left(\frac{q\frac{3x}{1-x}}{1+q\frac{3x}{1-x}}\right) \left(\frac{l_{\textrm{c}}}{l_{\textrm{n}}}\right) \left[\frac{(\rho_0/\rho_{\textrm{c}})^{\frac{1-x}{3x}+q}-1}{(\rho_0/\rho_{\textrm{c}})^{q}-1}\right] \\[3pt] & \simeq \frac{3}{4} \left(\frac{l_{\textrm{c}}}{l_{\textrm{n}}}\right) = \frac{3}{4} \left(\frac{1+q}{q}\right)^{q/3}, \end{aligned} \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq61.png) (A.7)
(A.7)
where at the last step we make use of 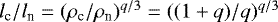 .
.
Eventually we define the arithmetic average quantities as follows: 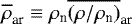 ,
, 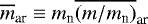 ,
, 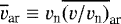 and
and 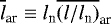 . From the Eqs. (A.4)–(A.7) are derived the relations:
. From the Eqs. (A.4)–(A.7) are derived the relations:
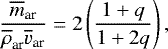 (A.8)
(A.8)
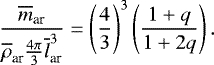 (A.9)
(A.9)
We highlight the difference between the last two formulas. In contrast, the analogous relations derived for the corresponding geometric averaged quantities turned out to be equal (see the end of the following section).
A.2.2 Geometric (logarithmic) averaged quantities
The geometric average of core density is defined:
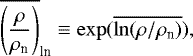
Subsequently, after some calculations one obtains:
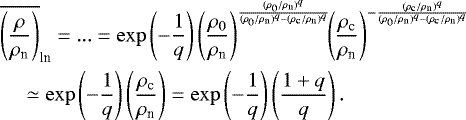 (A.10)
(A.10)
The geometric average of core mass is defined in an analogous way:
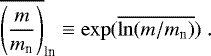
The use of the relationship ln(m∕mn) = (1∕x)ln(ρ∕ρn) and, hence, 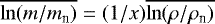 simplifies the calculation of the averaged core mass:
simplifies the calculation of the averaged core mass:
![\begin{eqnarray*}\overline{\left(\frac{m}{m_{\textrm{n}}}\right)}_{\textrm{ln}}= \left[\overline{\left(\frac{\rho}{\rho_{\textrm{n}}}\right)}_{\textrm{ln}}\Bigg]^{1/x}\simeq \Bigg[\exp\left(-\frac{1}{q}\right) \left(\frac{1+q}{q}\right)\right]^{1/x}. \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq74.png) (A.11)
(A.11)
The geometric average core volume and size are defined and calculated analogously:
![\begin{eqnarray*}\begin{aligned} \overline{\left(\frac{v}{v_{\textrm{n}}}\right)}_{\textrm{ln}} & \equiv \exp(\overline{\ln(v/v_{\textrm{n}})})= \left[\overline{\left(\frac{\rho}{\rho_{\textrm{n}}}\right)}_{\textrm{ln}}\right]^{\frac{1-x}{x}} \\[6pt] & \simeq \left[\exp\left(-\frac{1}{q}\right) \left(\frac{1+q}{q}\right)\right]^{\frac{1-x}{x}}, \end{aligned} \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq75.png) (A.12)
(A.12)
![\begin{eqnarray*}\begin{aligned} \hspace*{-2pt}\overline{\left(\frac{l}{l_{\textrm{n}}}\right)}_{\textrm{ln}}& \equiv \exp(\overline{\ln(l/l_{\textrm{n}})})= \left[\overline{\left(\frac{\rho}{\rho_{\textrm{n}}}\right)}_{\textrm{ln}}\right]^{\frac{1-x}{3x}} \\[7pt] & \simeq \left[\exp\left(-\frac{1}{q}\right) \left(\frac{1+q}{q}\right)\right]^{\frac{1-x}{3x}}. \end{aligned} \end{eqnarray*}](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq76.png) (A.13)
(A.13)
Eventually we define the geometric averaged quantities as follows: 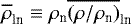 ,
, 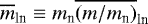 ,
, 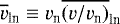 and
and 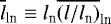 . From Eqs. (A.10)–(A.13) we derive a relationship between geometric averaged density, mass, volume, and size of the cores:
. From Eqs. (A.10)–(A.13) we derive a relationship between geometric averaged density, mass, volume, and size of the cores:
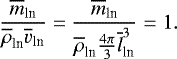 (A.14)
(A.14)
References
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballesteros-Paredes, J., Hartmann, L., Vázquez-Semadeni, E., Heitsch, F., & Zamora-Avilés, M. 2011, MNRAS, 411, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Ballesteros-Paredes, J., Vázquez-Semadeni, E., Palau, A., & Klessen, R. S. 2018, MNRAS, 479, 2112 [NASA ADS] [Google Scholar]
- Clark, P., Klessen, R., & Bonnell, I. 2007, MNRAS, 379, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, D., Padoan, P., Norman, M. L., & Xu, H. 2011, ApJ, 731, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, D., Kritsuk, A., Padoan, P., et al. 2012, ApJ, 750, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., & Burkert, A. 2005, ApJ, 630, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Bell, E., & Burkert, A. 2006, ApJ, 638, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Kim, J., & Shadmehri, M. 2007, MNRAS, 381, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Brandenburg, A., Kim, J., Gopinathan, M., & André, P. 2008a, ApJ, 678, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Galván-Madrid, R., Kim, J., & Vázquez-Semadeni, E. 2008b, in SF2A-2008: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, C. Charbonnel, eds. F. Combes, R. Samadi, 309 [Google Scholar]
- Dib, S., Shadmehri, M., Padoan, P., et al. 2010, MNRAS, 405, 401 [NASA ADS] [Google Scholar]
- Dib, S., Gutkin, J., Brandner, W., & Basu, S. 2013, MNRAS, 436, 3727 [NASA ADS] [CrossRef] [Google Scholar]
- Donkov, S., & Stefanov, I. 2018, MNRAS, 474, 5588 [NASA ADS] [CrossRef] [Google Scholar]
- Donkov, S., Veltchev, T., & Klessen, R. S. 2011, MNRAS, 418, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Donkov, S., Veltchev, T., & Klessen, R. S. 2012, MNRAS, 423, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Donkov, S., Veltchev, T., & Klessen, R. S. 2017, MNRAS, 466, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 2011, ApJ, 731, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. 2018, ApJ, 854, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B., & Falgarone, E. 1996, ApJ, 471, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M., Evans, N. J., Sargent, A., Glenn, J. 2008, ApJ, 684, 1240 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Fleck, R. C., Jr. 1996, ApJ, 458, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Giannini, T., Elia, D., Lorenzetti, D., et al. 2012, A&A, 539, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girichidis, P., Konstandin, L., Whitworth, A. P., & Klessen, R. S. 2014, ApJ, 781, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Guszejnov, D., & Hopkins, Ph. 2015, MNRAS, 450, 4137 [NASA ADS] [CrossRef] [Google Scholar]
- Guszejnov, D., Hopkins, Ph., & Grudić, M. 2018, MNRAS, 477, 5139 [NASA ADS] [CrossRef] [Google Scholar]
- Heithausen, A., Bensch, F., Stutzki, J., Falgarone, E., & Panis, J. 1998, A&A, 331, L65 [NASA ADS] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2008, ApJ, 684, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, Ph. 2012, MNRAS, 423, 2037 [NASA ADS] [CrossRef] [Google Scholar]
- Ibáñez-Mejía, J., Mac Low, M.-M., Klessen, R. S., & Baczynski, C. 2016, ApJ, 824, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ikeda, N., & Kitamura, Y. 2009, ApJ, 705, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Ikeda, N., & Kitamura, Y. 2011, ApJ, 732, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, J., Pillai, T., Shetty, R., Myers, P., & Goodman, A. 2010, ApJ, 716, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S. 2000, ApJ, 535, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S.,& Glover, S. C. O. 2016, in Star Formation in Galaxy Evolution: Connecting Numerical Models to Reality, Saas-Fee Advanced Course, (Berlin: Springer-Verlag), 43, 85 [Google Scholar]
- Klessen, R. S.,& Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramer, C., Stutzki, J., Rohrig, R., & Corneliussen, U. 1998, A&A, 329, 249 [NASA ADS] [Google Scholar]
- Kritsuk, A., Norman, M., & Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G.-X., & Burkert, A. 2016, MNRAS, 461, 3027 [NASA ADS] [CrossRef] [Google Scholar]
- Li, D., Velusamy, T., Goldsmith, P., & Langer, W. 2007, ApJ, 655, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. 2010, A&A, 519, 7 [Google Scholar]
- Motte, F., André, Ph., & Neri, R. 1998, A&A, 336, 150 [Google Scholar]
- Padoan, P., & Nordlund, A. 2002, ApJ, 576, 870 [Google Scholar]
- Padoan, P., Pan, L., Haugbølle, T., & Nordlund, Å. 2016, ApJ, 822, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Pekruhl, S., Preibisch, T., Schuller, F., & Menten, K. 2013, A&A, 550, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polychroni, D., Schisano, E., Elia, D., et al. 2013, ApJ, 777, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M., & Wilson, C. 2006, ApJ, 650, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. 1955, ApJ, 121, 161 [Google Scholar]
- Schmidt, W., Kern, S., Federrath, C., & Klessen, R. S. 2010, A&A 516, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Girichidis, P., et al. 2015a, MNRAS, 453L, 41 [Google Scholar]
- Schneider, N., Csengeri, T., Klessen, R., et al. 2015b, A&A, 578, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tachihara, K., Onishi, T., Mizuno, A., & Fukui, Y. 2002, A&A, 385, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vázquez-Semadeni, E., Gómez, G., Jappsen, A., et al. 2007, ApJ, 657, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Veltchev, T., Donkov, S., & Klessen, R. S. 2013, MNRAS, 432, 495 [Google Scholar]
- Veltchev, T. V., Girichidis, Ph., Donkov, S., et al. 2019, MNRAS, 489, 788 [NASA ADS] [CrossRef] [Google Scholar]
The absolute value is to be taken since the total number of cores, 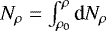 , decreases with increasing density threshold ρ (see Sect. 2.2.2).
, decreases with increasing density threshold ρ (see Sect. 2.2.2).
All Tables
All Figures
 |
Fig. 1 Concept of the MC class of equivalence (after Donkov et al. 2017). |
| In the text | |
 |
Fig. 2 Sketch of the model setting which shows the statistical link between the density distribution in the cloud and the core population. The double-ended arrows denote one-to-one correspondence between quantities. The concepts introduced in this work (in regard to the DVK17 model) are shaded in gray. |
| In the text | |
 |
Fig. 3 Relationship between the parameter κ and the total number of detected cores (Eq. (25)), for different choices of the ρ-PDF slope and density contrast. |
| In the text | |
 |
Fig. 4 Conditions for core collapse for different total numbers of cores (columns) and PDF slopes. Top: function m∕mJ (Eq. (24)) projected on the plain “core density vs. cloud mass”. Lines denote the condition m∕mJ = 1; the domains of unstable cores for the three exemplary values of q are shown with arrows. An isothermal Jeans mass within the cloud MJ, c for T = 30 K is adopted. Bottom: mass–density relationship for cores (Eq. (8)) where the mass is given in units of the total mass of the cloud. The density contrast in the cloud is fixed at (ρ0 ∕ρc)= 103. |
| In the text | |
 |
Fig. 5 Parameters of modeled mass functions of unstable cores (open symbols) compared with those of the high-mass part of observational CMFs (filled symbols; the numbers correspond to the data in Table 2). Vertical solid lines denote the range of characteristic masses generated by varying (Mc ∕MJ, c)∕Nc from 0.5 (large symbols) to 20.0 (small symbols). The domain of PLTs which can be distinguished from a lognormal wing (q ≳ −4) is shown with a vertical dashed line and an arrow. See text. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



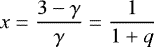
![\[ \overline{\ln\left(\frac{\rho}{\rho_{\textrm{n}}}\right)}= A_{\textrm{s}} \int\limits_{\rho_{\textrm{c}}}^{\rho_0} \ln\left(\frac{\rho}{\rho_{\textrm{n}}}\right) \left(\frac{\rho}{\rho_{\textrm{n}}}\right)^{q} \textrm{d}\ln\left(\frac{\rho}{\rho_{\textrm{n}}}\right). \]](/articles/aa/full_html/2020/03/aa36993-19/aa36993-19-eq70.png)