EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 635 (March 2020) A&A, 635 (2020) A172 Full HTML
Free Access
Issue
A&A
Volume 635, March 2020
Article Number A172
Number of page(s) 11
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201936992
Published online 30 March 2020

© ESO 2020

1. Introduction

Black hole (BH) spins are fundamental physical parameters that preserve information about the formation, evolution, and the mass accretion rate history of supermassive black holes (SMBHs) residing in the centers of galaxies (Volonteri et al. 2005; Volonteri 2010). The determination of the BH spin has been addressed by three different X-ray data analysis methods (for further details see Reynolds & Fabian 2008). However, the majority of the spin measurements in active galactic nuclei (AGN) have been constrained by fitting the X-ray spectra with a model including a reprocessed (“reflected”) component from the accretion disk. The reflection spectrum encodes information about the magnitude of the spin via the location of the innermost stable circular orbit (ISCO). Currently, there are more than two dozen BH spin measurements with robust results, and a large number of them have high spin values (Reynolds 2019). Due to the clear observational features, the reflection method is one of the most preferred BH spin estimation methods. Although, some observational challenges could affect the constraining of the spin, such as obtaining a sufficiently high signal-to-noise X-ray spectrum, assessing the effect of absorption and emission features on the continuum, as well as weakness of the inner disk Fe Kα line in sources seen at low inclination angles (Laor 2019).

The magnitude of the spin of SMBHs in AGN plays an important role in constraining relativistic jet production models. Magnetic fields can extract the rotational energy of a spinning BH via the Blandford-Znajek mechanism that launches jets (Blandford & Znajek 1977). The so-called spin paradigm attempts to explain the wide radio-loudness distribution (Sikora et al. 2007) solely in terms of differences in the BH spin (Blandford 1999; Wilson & Colbert 1995; Tchekhovskoy et al. 2010). The existence of highly-spinning black holes in radio-quiet AGN does not fit well with this paradigm (e.g., Walton et al. 2013; Reynolds 2014). Hence, the production of powerful relativistic jets might not depend exclusively on high spins but also on the role of another parameter in the Blandford-Znajek mechanism, namely magnetic flux threading the black hole. For instance, Sikora & Begelman (2013) propose that the accretion history of a BH may determine whether high enough magnetic flux is accumulated in the BH to launch powerful jets. This latter model is sometimes called the “magnetic flux paradigm”. The magnetic flux, together with the BH spin determines the jet power – hence the wide range of jet powers would not only depend on the range of spins but also on the accretion history of the source. The most powerful jets, which have power that is comparable to the accretion power of the system, can be explained by the magnetically arrested disk (MAD; Narayan et al. 2003; Tchekhovskoy et al. 2011; McKinney et al. 2012) scenario in which the magnetic flux threading a BH is at the maximum value allowed by the accretion rate.

The study of the distribution of BH spins in radio-quiet and radio-intermediate AGN can potentially help to distinguish between the two paradigms. Flat-spectrum radio-intermediate quasars (RIQ) are especially interesting sources in this respect since it has been suggested that they are beamed counterparts of radio-quiet quasars (Falcke et al. 1996a,b) and since their compact radio cores, in principle, allow the jet magnetic flux to be measured with very long baseline interferometry (VLBI) by using the core-shift effect (e.g., Pushkarev et al. 2012; Zamaninasab et al. 2014).

III Zw 2 (also known as Mrk 1501 and PG 0007+106; z = 0.089) is a radio-intermediate source in the Palomar-Green (PG) survey of quasars (Schmidt & Green 1983), but its luminosity corresponds to a Seyfert galaxy type I (Khachikian & Weedman 1974). It hosts a supermassive black hole with a mass on the order of 108 − 109 M⊙ (Salvi et al. 2002; Hao et al. 2005; Vestergaard & Peterson 2006; Grier et al. 2012) and an Eddington ratio of ∼0.1 (Inoue et al. 2007). A study for a period of 25 years has shown significant variability (an order of magnitude) from radio to X-ray wavelengths (Salvi et al. 2002). Recently, two gamma-ray flaring episodes have been detected by Fermi-LAT, which correlate well with optical and radio emission (Liao et al. 2016). High-resolution radio observations of III Zw 2 have shown a compact radio core with a flat spectrum and a relativistic, although not very highly relativistic, jet that moves at an apparent superluminal speed of 1.3−2.7c (Falcke et al. 1999; Brunthaler et al. 2000, 2005; Lister et al. 2019). In addition, III Zw 2 has a weak extended radio emission (Brunthaler et al. 2005) that continues to the kiloparsec scale (Cooper et al. 2007).

Previous X-ray spectral studies of III Zw 2 have reported a significant, broad Fe Kα line emission in the EPIC spectra of the XMM-Newton observation in 2000 (Salvi et al. 2002; Piconcelli et al. 2005; Jiménez-Bailón et al. 2005). Salvi et al. (2002) found that the best-fit model includes a reflection component (PEXRAV) with an iron line at 6.45 keV (EW ∼ 0.87 keV). Further studies on the Fe Kα line emission have been performed by Gonzalez et al. (2018) based on the archival data from XMM-Newton in 2000 and Suzaku in 2011. They modeled the spectra with a reflection component (XILLVER; García & Kallman 2010; García et al. 2011, 2013) and provided interpretations as to the nature of the reflector emitting the line. Based on the best fit results, they interpreted that the XMM-Newton spectrum can be explained by reflection from a highly-ionized accretion disk, while the Suzaku spectrum is more consistent with a reflection from a cold torus. A highly spinning black hole was assumed throughout their study. However, no spin estimate based on the observations has previously been reported for III Zw 2.

In this work, we aim to estimate, for the first time, the BH spin using the X-ray spectra of III Zw 2. In Sect. 2, we present our new X-ray observations from XMM-Newton and NuSTAR missions, archival data from XMM and Suzaku, and the corresponding data reduction procedures used to obtain the calibrated data products. In Sect. 3, we describe the results of the spectral analysis that includes the model fitting of the data with phenomenological models to estimate the photon indices and black body temperature as well as testing a warm absorber model. Subsequently, we fit a model including a reflection component to two data sets: the XMM-Newton observation of 2000 and our joint broadband XMM-Newton+NuSTAR observations of 2017. We modeled these spectra with a reflection model RELXILL (Dauser et al. 2010, 2014, 2016; García et al. 2014), which allowed us to resolve the reflection spectrum fully, and thus we are able to give an estimate of the BH spin. In Sect. 4, we summarize our main results, which include the observation of a soft excess component on the XMM-2000 and 2017 data sets as well as the Fe Kα line profile. Jointly fitting the combined 2000 and 2017 spectra with RELXILL suggests that III Zw 2 harbors a fast-rotating black hole. In addition, we discuss some of the caveats of this work as well as future prospects.

2. Observations and data reduction

NuSTAR observations with the supporting XMM-Newton observations are currently the only set of instruments that provide the necessary sensitivity and bandpass to study the accretion processes of AGN in detail. The hard X-ray band of NuSTAR is used to study the reflection features of the iron line region and Compton reflection hump, and the soft X-ray band of XMM-Newton is used to support the study of the reflection features in the iron line region and the soft excess.

We observed III Zw 2 simultaneously with XMM-Newton and NuSTAR on 2017 December 11. In Table 1, XMM-Newton exposures are given for the EPIC-pn camera for the 0.2−10 keV band with a mean countrate of 8.74 ± 0.02 counts s−1 (1000 s bin time). NuSTAR exposures are given for the two focal plane modules (FPM) in the 3−79 keV band. The mean countrates for the 7000 s bin lightcurves for both detectors are 0.590 ± 0.004 and 0.607 ± 0.004 counts s−1.

Table 1.

X-ray observations of III Zw 2 used in this paper.

2.1. XMM-Newton

In this work, we only analyze the EPIC-pn source spectra due to the higher sensitivity compared to the MOS cameras. The 2017 observation of III Zw 2 with the EPIC-PN camera was executed in the Prime Small window mode with a thin filter for a total duration of 41 ks and an exposure time of 26 ks. To obtain the spectra, we processed the EPIC-PN data using the HEASOFT package version 6.24 and the XMM-Newton Scientific Analysis System (SAS version 17.0.0) and followed the guidelines on the mission website1. High-level science products were obtained using the XMMEXTRACTOR tool. For the light curve and spectral extraction, large background flaring was subtracted with the task TABGTIGEN by creating a good time interval file with a background countrate threshold of 0.4 count s−1. No pile-up corrections were applied as the countrate during the observation is well below the small window pile-up threshold (25 count s−1). The energy band used for the spectral analysis ranges from 0.23 to 10 keV.

2.2. NuSTAR

The calibration and product extraction of the NuSTAR data were performed by following the standard guidelines2. We used the NUPIPELINE script to obtain calibrated event files for the FPMA and FPMB detectors. Subsequently, we used the NUPRODUCTS script to extract the instrumental responses, the source spectra from a 30″ circular area centered on the source, and the background spectra from a 60″ circular area from a source-free region. We also include the correction of South-Atlantic anomaly (SAA) effect on the background rates. The exclusion of SAA passages was carried out by using the following parameters: SAACALC = 3, SAAMODE = optimized, and TENTACLE = yes. For the spectral fitting, we used both FPM spectra in the energy range of 3−50 keV with a constant in the model to account for any differences in the normalization between the two detectors.

2.3. Archival X-ray data

In addition, we analyzed all of the available X-ray observations of III Zw 2, which were conducted in the past in comparable resolution in the soft X-ray domain, namely an XMM-Newton observation from 2000 and a Suzaku observation from 2011 (see Table 1). We reduced the XMM data of the 2000 observation similarly to the 2017 data (see above). For the Suzaku 2011 observation, we used the available data products from the XIS0 and XIS3 CCD cameras.

2.4. Radio data

The 37 GHz radio observations of III Zw 2 covering 1986−2019 were made with the 13.7 m diameter Metsähovi radio telescope in Finland (see Fig. 5, which shows the radio flux curve from 1997 to 2019). The detection limit of the telescope at 37 GHz is on the order of 0.2 Jy under optimal conditions. Data points with a signal-to-noise ratio (S/N) < 4 are handled as nondetections. The flux density scale is set by observations of DR 21. Sources NGC 7027, 3C 274, and 3C 84 are used as secondary calibrators. A detailed description of the data reduction and analysis is given in Teräsranta et al. (1998). The error estimate in the flux density includes the contribution from the measurement root mean square (rms) and the uncertainty of the absolute calibration.

3. Spectral analysis and results

This work is mainly devoted to the spectral analysis of the X-ray data by fitting models to the observed source spectra for the epochs listed in Table 1. The analysis of the X-ray spectra was performed with ISIS3 (Interactive Spectral Interpretation System, package version 1.6.2−41; Houck & Denicola 2000). Before fitting, we grouped the spectra such that each energy bin has S/N ≥ 10. The fit quality was estimated using χ2 statistics and the uncertainties associated with the model parameters are shown at the 90% confidence level.

Figure 1 displays the X-ray spectra of III Zw 2 from the XMM-2000, Suzaku-2011, and XMM+NuSTAR-2017 observations. Overall, the spectral shape stays similar with a clear change in the flux level between the 2000 and 2017 observations. On the contrary, the Suzaku-2011 spectrum shows a change in the spectral shape with a different power-law index and stronger absorption.

thumbnail Fig. 1.

Multiepoch folded spectra of III Zw 2 for the observations in 2000, 2011, and 2017.

We first fit the spectra with a phenomenological model, consisting of an absorbed power-law component (PHABS × POWERLAW; hereafter PL). We did not fixed the value of the neutral hydrogen column density (NH) as it was done in previous studies (Salvi et al. 2002; Jiménez-Bailón et al. 2005; Piconcelli et al. 2005; Gonzalez et al. 2018) in order to allow its possible variability over time (the Galactic value is NH ∼ 5 × 1020 cm−2; Kalberla et al. 2005) and to take any variability in an additional, intrinsic absorption component into account.

Figure 2a shows the data/model ratio (residuals) of the PL model in the range 0.2−10 keV for all epochs. A prominent soft X-ray excess (0.2−1 keV) is observed in the XMM-2017 spectrum similar to the 2000 data (Gonzalez et al. 2018). The existence of a soft excess in the Suzaku-2011 spectrum is difficult to ascertain due to a flatter spectrum, higher absorption, and a limited low energy response. The Suzaku-2011 spectrum appears to be significantly more absorbed with the NH differing by a factor of at least two compared to the other epochs (see Fig. 1). Additionally, the spectrum presents a lower photon index (Γ ∼ 1.58).

thumbnail Fig. 2.

Data-to-model ratio of (a) an absorbed power-law model and (b) an absorbed power-law+black-body radiation model for all epochs. The vertical dashed-line marks the position of the Fe Kα line.

A prominent excess between 5−7 keV is observed in the XMM-2000 residuals, indicating a contribution from the Fe Kα line (Salvi et al. 2002; Jiménez-Bailón et al. 2005; Gonzalez et al. 2018). Interestingly, such an excess appears to also be present in the Suzaku-2011 residuals; however, it is less prominent and statistically less significant. In contrast to these findings, the XMM+NuSTAR-2017 residuals show no significant Fe Kα line.

Based on the reduced χ2 values shown in Table 2, it is clear that pure power-law models are not suitable to describe the XMM/NuSTAR data. Here, we point out that since the Suzaku-2011 data have a limited low energy response, they cannot be used to place any constraints on the soft excess. Thus, we conclude that the PL model can sufficiently explain the Suzaku-2011 spectrum and we do not fit any subsequent models to the data.

Table 2.

Parameters for the best-fit models for all the datasets.

Secondly, we added a black body component to model the soft excess (hereafter PL+BB). The residuals of these fits for all epochs are shown in Fig. 2b. We find that PL+BB model fits the XMM+NuSTAR-2017 and the XMM-2000 data sets much better. The spectral fitting results are displayed in Table 2.

The black body temperatures of the best fitting PL+BB models range between 136 and 192 eV, which are consistent with the values reported by Piconcelli et al. (2005) and Gierliński & Done (2004). These values are much higher than the maximum temperature of the standard accretion disk (∼10 eV), which means that we cannot attribute the black body component to the thermal emission from the accretion disk. Such a large temperature of the soft excess has also been reported for several other AGN, including radio-quiet PG quasars as well as narrow line Seyfert 1 galaxies (NLS1s; Ai et al. 2010, and references therein). However, no correlation between the soft excess temperature and the black hole masses (as low as 106 M⊙) has been found for the large majority of the sources with the exception of radio-loud NLS1s (Yuan et al. 2010).

Above, we show that a black body(-like) component is needed to fit the spectrum of III Zw 2 well. The physical interpretation of the soft excess is a long-standing issue, which has been addressed by different models. These include, for instance, the Comptonization of accretion disk photons to soft X-ray energies (Ai et al. 2010, and references therein), the reflection and absorption of photons in partially ionized material (Done & Nayakshin 2007; Done et al. 2007), and magnetic reconnection on the surface of the disk accelerating nonthermal electrons, which then scatter photons via inverse Compton to soft-excess energies (Zhong & Wang 2013).

Phenomenological models including a black body component serve as a crude proxy for these physical scenarios and as such we cannot rule them out. However, individually testing a variety of such models is beyond the scope of this paper since our goal is to constrain the spin value of the central black hole in III Zw 2. In the rest of the paper, we thus concentrate on modeling the spectra within a relativistic reflection scenario that can naturally explain both the soft excess and the excess around 6.4 keV. For completeness purposes, we first shortly discuss a warm absorber model, which is a commonly proposed alternative to reflection models for explaining the observed AGN X-ray spectra.

3.1. Warm absorber model

Even if the spectra of III Zw 2 do not exhibit any strong absorption edges when compared to other sources (see Porquet et al. 2004), we also investigate a scenario where so-called warm absorber (WA; model ZXIPCF) might be present. Thus, we fit the data with a model where partially ionized absorbing material partially covers the power-law continuum source (hereafter WA*PL) as well as with the same model including a black body emitter (hereafter WA*(PL+BB)).

The results of the fits are shown in Table 2. These models produce an improvement to the fit statistics compared to the PL and PL+BB models for the XMM-2000 spectrum. While both models can effectively fit the excess around 6.4 keV, they do not fit the soft excess well (see residuals in Figs. 3a,b; bottom panels). As for the 2017 spectrum, the WA*PL model only produces a slight improvement over the PL model, and the residuals show a clear pattern in the soft X-rays similar to the PL model fit (Fig. 3a; upper panel). The WA*(PL+BB) model produces a better fit, but essentially it is very similar to the PL+BB model (with some additional reprocessing in a cool gas), so the WA cannot be the physical interpretation used to explain the soft excess in this case. The implied black-body temperature is again high and comparable to the values obtained previously without a warm absorber (see Table 2). We have also tried to fit the spectra with a power-law model modified by two warm absorbers; however, this model does not produce a significant improvement to the previous single warm absorber models fit to the 2000 spectrum, that is, we find a similar fit quality. While a double warm absorber model can improve the single warm absorber power-law fit (with χ2/d.o.f. = 589.4/458) to the 2017 spectrum, it does not fit the data above 30 keV well.

thumbnail Fig. 3.

Data-to-model ratio of (a) a power-law continuum model with partial covering of a partially ionized absorber and (b) the same as in (a), but with black body emission included.

Considering that the 2000 and 2017 spectra have a similar spectral shape overall, albeit with a different X-ray flux, and that there is a sign of a broad Fe Kα line in the 2000 spectrum, we investigate a disk reflection scenario to estimate the black hole spin of III Zw 2 in the next section. As we will see, the reflection model can explain both the soft excess emission and the blurred Fe Kα line within a single physical scenario.

3.2. Reflection model

To explore physical conditions around the supermassive black hole in III Zw 2, we employed the relativistic reflection model, RELXILL4 (García et al. 2014; Dauser et al. 2014), to fit the data. RELXILL models the irradiation (in coronal geometry) of the accretion disk by an emitter with a broken power law spectrum and a radial emissivity profile. It combines the reprocessed emission from the disk with the relativistic broadening effects on the emission features. For high-quality data, the model allows for the estimation of a number of parameters, such as the disk ionization parameter (ξ), the iron abundance (AFe), the reflection fraction (R), the inclination angle (θ), and the black hole spin (a). For the disk irradiation profile, we fixed the power-law indices to β1 = 5, β2 = 3 and the break radius to Rbr = 4 Rg, corresponding to a low height of the primary X-ray source from the disk (Dauser et al. 2013). The energy cutoff of the primary spectrum was set to 300 keV. Additionally, the gas density in the accretion disk is assumed to be 1015 cm−3 (García et al. 2016).

To constrain the spin, an assumption about the disk inclination limits has been made based on the results of previous works. It is well known that III Zw 2 has a radio jet exhibiting superluminal motion (Brunthaler et al. 2000; Lister et al. 2019). The maximum jet viewing angle of 41° was estimated from the apparent superluminal motion by Brunthaler et al. (2000). In addition to this limit, various other estimates of the jet inclination can be derived from radio observations. Hovatta et al. (2009) reported a jet inclination angle of 35° based on the flux variability time scale in the Metsähovi 37 GHz monitoring data and the apparent jet speed measured by the MOJAVE Survey (Lister et al. 2019). Liodakis et al. (2018) used a similar technique with the 15 GHz flux variability data from the Owens Valley Radio Observatory monitoring program and report a jet inclination angle of 22.1° with lower and upper limits of 0.9° and 23.5°, respectively. Furthermore, the one-sidedness of the jet in III Zw 2 can be used to place an upper limit of 53° on the jet inclination based on the required ratio of the Doppler boosting factors for the jet and the counter-jet5. Taken together, the upper limit of 41° for the jet inclination appears well-motivated. We assume that the jet is launched perpendicular to the accretion disk and, thus, we also set the maximum limit for the disk inclination to 41°.

We first fit the 2000 and 2017 data sets individually, then jointly. Results of the individual fits are shown in Table 3. The confidence limits were calculated simultaneously for all free model parameters. We find that the RELXILL models produce a similar fit quality as the warm absorber models for the 2000 data set and the black body component models for the 2017 data set.

Table 3.

RELXILL and RELXILLLP (i.e., lamp-post) model parameters.

Assuming that the reflection component causes the soft excess, we obtain a very large spin for the 2017 data set. Due to the large spin and a low reflection fraction, the modeled iron line is heavily broadened and rather inconspicuous in the 2017 data set, while in the 2000 data set the line is more visible due to increased reflection fraction (by a factor of two). We also explored the scenario where a change in the location of the illuminating source to the accretion disk explains the time variable spectral features. For this, we fit the data with the lamp-post scenario (RELXILLLP). In this model, we allow the height (h) of the primary radiating source to vary freely. However, we find no significant differences in the heights between the two epochs. The lower limits of the spin values that were produced by either the RELXILL or RELXILLLP models are significantly different for the first epoch.

We also attempted to fit the XMM-2000 and XMM+NuSTAR-2017 data sets with the reflection model affected by a warm absorber (hereafter WA*RELXILL). The 2000 spectrum can be well fit (χ2/d.o.f. = 134.2/131) with this model similar to the non-WA reflection model, so we do not find any significant improvement in the fits. The lower limit of the spin is, however, affected when including the warm absorber in the fit of XMM-2000 data (a ≥ 0.46). While the WA*RELXILL can model the soft excess of the 2017 spectrum well, it fails to fit the hard X-ray component (> 30 keV). This is in accordance with the results by Risaliti et al. (2013), who found for a much higher S/N spectrum of NGC 1365 that partial covering absorption models can effectively fit the data up to 10 keV; but they deviate from the data at higher energies.

In addition, we performed a joint fit to the combined 2000 and 2017 data sets with the RELXILL model. A joint-fit consists of linked and unlinked parameters. Linked parameters are values which we assume do not change in human timescales, such as the BH spin, the disk inclination, the ionization parameter and the iron abundance. Since we have not found any significant differences in the neutral hydrogen column density for the two XMM-epochs (see Table 2), we let this also be a linked parameter. The unlinked parameters, such as the power-law photon index, normalization, and the reflection fraction, were allowed to vary independently.

The best fit produces a nearly maximal spin of a ≥ 0.98 with the disk inclination pegged to the maximum allowed value of 41° (see Table 4). Additionally, the values of the other parameters appear to be similar to the values obtained in Table 3. The joint-fit model of the multi-epoch spectra is shown in Fig. 4. Here, we note that we have also studied cases, where the inclination angle is fixed to lower values (see Table A.1), such as 22° (Liodakis et al. 2018) and 35° (Hovatta et al. 2009) with a clear impact being to the value of iron abundance, the ionization parameter, and the reflection fraction. As a sanity check, we also fit the data allowing the irradiation profile parameters to vary freely. The model converges at steep power-laws (β1 = 8.8 and β2 = 3.1 with Rbr = 2.8 Rg) as is expected if the reflection comes from the inner accretion disk. The increase in the number of free parameters leads to a fit that is slightly better statistically (χ2/d.o.f. = 669.5/595), but it does not properly reproduce the hard X-ray part of the spectrum. Therefore, we favor the fit where the irradiation profile is kept fixed.

thumbnail Fig. 4.

Joint-fit of the combined 2000 and 2017 data sets with the RELXILL model (blue line). The data-to-model ratio is shown in the lower panel. The model fits the iron line as a heavily broadened and asymmetric feature, indicating emission from very close to the black hole event horizon.

Table 4.

RELXILL joint-fit parameters of the combined XMM-2000 and XMM+NuSTAR 2017 spectra.

We note that the RELXILL model is able to fit both spectra well by only varying the reflection factor, power-law index, and normalization. On the other hand, as shown in Fig. 1, the X-ray flux has clearly increased in the 0.23−10 keV range for over 17 years. One possible explanation for the increased X-ray luminosity is the change in the mass accretion rate by a factor of ∼2.

Since the best fit of the combined data set in Table 4 gives an inclination at the upper edge of the allowed range, we have extended our analysis by fitting the RELXILL model to the data that also have a wide range of assumed disk inclinations. The results of these fits to the combined 2000+2017 data set are shown in Appendix A (see Table A.1). By letting the inclination vary freely, it settles on θ = 55 ° ±2°. For this model, the black hole spin is higher than 0.99. The overall fit quality as a function of inclination shows a clear valley around ∼50°. Both low (≲20°) and high (≳60°) inclination cases produce a poor fit to the iron line.

Finally, we extended the analysis to examine the quality of the fit for a wide range of spin values. The results are displayed in Table B.1. The minimum χ2 value is found at the very high (positive) black hole spin (a = 0.992). Overall, we find a lower fit quality when the spin is set to values ≤0.9. In addition, low positive and all negative spin values show a strong tendency toward very large disk inclinations (hitting the upper limit of 80°), subsolar iron abundances, and low reflection fractions for both epochs. Given the limits to the jet inclination angle derived from the radio observations, and the fact that III Zw 2 is a type 1 AGN with prominent broad emission lines (Marziani et al. 2003), we consider it rather unlikely that the disk inclination would be so high. We discuss this further in the next section.

4. Summary and discussion

We study the X-ray spectrum of III Zw 2 for three different X-ray observations made in 2000, 2011, and 2017. To explore the presence of a soft X-ray component and an Fe Kα line in the data, we first applied phenomenological power-law models. These results have shown a visible soft-excess component in the 2000 (Gonzalez et al. 2018) and 2017 data sets. In addition, a prominent iron line has been observed in the XMM-2000 data (Salvi et al. 2002; Piconcelli et al. 2005; Gonzalez et al. 2018). We study whether the soft excess and the iron line can be fit with a reflection model.

The black hole spin of III Zw 2 was constrained by applying the relativistic reflection model RELXILL. We estimated the BH spin using two different methods: by fitting the data separately and by combining the two observation epochs (2000 and 2017) under the joint-fit approach. In both methods, we set an upper limit of 41° for the disk inclination. Fitting the 2000 spectrum alone produces a lower limit for the spin of a ≥ 0.78, while the 2017 spectrum gives a ≥ 0.98. Since the BH spin is not expected to change in a time scale of years, a joint-fit is considered as a preferable method to determine the spin of III Zw 2. The joint fit favors a large spin value with a lower limit, a ≥ 0.98. We note that the quoted lower limits correspond to the statistical uncertainty of the fit, and they do not take any systematic effects into account. While systematics are difficult to assess, we can use the results of Bonson & Gallo (2016) as a guideline. Those authors have studied the ability of the standard fitting procedure to recover the correct model parameters from a large number of simulated Seyfert 1 spectra. Their results indicate that spin can be measured with confidence to an accuracy of about ±0.1 for high spin cases (a >  0.8), especially if the measured spectrum extends up to 70 keV. Finally, we note that large spin values (0.85 <  a <  0.92) have been also reported by Gnedin et al. (2012). Their results are based on spectropolarimetric observations combined with the jet kinetic power and assuming a large disk inclination angle of 60°.

The estimation of the black hole spin by fitting a relativistic reflection model has naturally a number of caveats, which we discuss below.

  • It is possible that the X-ray spectrum is affected by intervening partially ionized absorbing material. If this is the case, the magnitude and the shape of the reflected component would be different from what is assumed here depending on the amount of absorption and this could affect our results presented above. While we cannot exclude such a warm absorber model, it requires an additional black body component of an unspecified origin in order to fit the data. Therefore, here, we favor the reflection scenario as it is able to fit the data within a single physical scenario without adding phenomenological components.

  • Since the black hole spin in our model fits is sensitive to the assumed disk inclination, it is important to have external constraints for it. Throughout this work we assume that the accretion disk is perpendicular to the jet and the jet viewing angle is constant. The alignment of the jet with the angular momentum vector of the disk is the simplest assumption and it has some observational support from the measurements of the X-ray binary system XTE J1550−564 (Steiner & McClintock 2012). Recent general relativistic magneto-hydrodynamic simulations of tilted accretion disks around black holes have shown that the disk and the jet are generally well-aligned (Liska et al. 2018). However, the Bardeen-Petterson effect can align the jet and the disk with the black hole spin axis at small radii (less than a few Rg) rapidly compared to the viscous time scale in which the whole disk-jet system aligns with the black hole spin axis (Liska et al. 2019a). This can temporarily leave the outer jet misaligned with respect to the inner accretion disk. It is not clear how large this misalignment can be, but, for example, the simulations performed by Liska et al. (2019b) indicate ≲15° difference even when the disk is originally tilted by 60° with respect to the black hole spin axis. Hence, while we cannot exclude the possibility that the inner disk inclination differs from the jet inclination, misalignment of tens of degrees seems unlikely.

  • The jet direction may not stay constant over time. While a precessing jet has been suggested for III Zw 2 based on the quasi-periodic variations in its radio flux curves (Li et al. 2010), the measured jet kinematics rule out a large precession angle. Namely, there are three emission features which were ejected into the VLBI jet of III Zw 2 during the past 20 years and which have robust kinematics measurements. All of them are moving in the same direction with the position angles of their motion differing less than ∼8° (Brunthaler et al. 2000, 2005; Lister et al. 2019)

  • We find no prominent Fe Kα line emission in the 2017 spectrum. This behavior seems to be well explained by a heavy broadening of the iron line due to a high spin and a variable reflection fraction, which might be a signature of a change in the disk and/or corona geometry during a flare event or during a post-flare event, leading to decreased illumination in the disk. However, 37 GHz radio observations of III Zw 2 show that the source was in a very low radio state in 2000 and 2017. The epochs are highlighted in Fig. 5.

  • We do not discard the possibility of X-ray emission from the jet, which is known to dominate the radio emission from III Zw 26. This emission might have swamped the iron line and contaminated the continuum spectrum in 2017. However, we note that the power law photon indices in 2000 and 2017 model fits are on average close to 1.8, which is similar to what was found in radio-quiet quasars (Piconcelli et al. 2005) associated with the Comptonized hot corona of the disk (Landt et al. 2008). On the contrary, the spectrum in 2011 is highly absorbed with a photon index close to 1.6 that is similar to that of radio-loud quasars (Piconcelli et al. 2005). Thus, we suggest that the 2011 spectrum has an additional X-ray contribution from the jet, which is most likely due to Synchrotron-Self Compton emission. In addition to this, it is interesting to note that the Suzaku observation in 2011 coincides with the rising part of a small radio flare at 37 GHz, while the 2000 and 2017 X-ray observations coincide with very low radio flux states that are indicative of a low jet contribution (see Fig. 5). Thus, here, we suggest that in general a good strategy would be to perform X-ray observations when these types of sources are in their lowest radio state. This may indicate a suitable condition for the detection of the reflection component.

thumbnail Fig. 5.

37 GHz radio observations of III Zw 2 obtained at the Metsähovi Radio Observatory. The red arrows indicate the epochs when X-ray observations were performed.

If the observed excesses below 1 keV and at 5−7 keV in the spectrum of III Zw 2 are due to inner disk reflection, our modeling indicates a nearly maximally spinning black hole for this source. This result is the same whether using our initial assumption on the maximum disk inclination (41°) or allowing the disk inclination to vary freely (see Table A.1). While the limit of a ≥ 0.98 corresponds to statistical uncertainties only and does not include systematic effects, such as the finite thickness of the accretion disk (Taylor & Reynolds 2018), our results do favor a fast-spinning BH in a source that belongs to a group of radio-intermediate quasars, which have been suggested to be relativistically beamed counterparts of radio-quiet quasars (Falcke et al. 1996b). If the jet in III Zw 2 is indeed intrinsically weak, this suggests that spin is not the only parameter driving the vast differences in jet production efficiencies of accreting black holes.

Since the radio emission from the extended jet in III Zw 2 is very weak compared to its beamed core emission (Falcke et al. 1996a; Cooper et al. 2007) and since its optical emission is dominated by the accretion disk (Chen et al. 2012), we can estimate the intrinsic radio-loudness of III Zw 2 by simply scaling the observed radio-loudness by δ−2.5, where δ is the relativistic Doppler factor and we have assumed a continuous jet with a spectral index of −0.5 (Hovatta et al. 2014). The range of reported radio-loudness in III Zw 2 is 150−200 (Falcke et al. 1996b; Sikora et al. 2007) and the Doppler factor estimates range from ∼2 to ≳6 (Hovatta et al. 2009; Liao et al. 2016; Liodakis et al. 2018). This gives a rough estimate that the intrinsic radio-loudness in III Zw 2 is in the range of 2−35, which indeed would place it in or close to the radio-quiet group.

The next step will be to measure the jet’s magnetic flux with VLBI observations. The prediction of the magnetic flux paradigm is that III Zw 2 – with its fast spinning black hole – should have magnetic flux well below the MAD-limit in order to explain the relatively low jet efficiency (Sikora & Begelman 2013).

5

In 2004.4, there was an ejection of a new jet emission feature that had a speed of βapp = 1.36 (Lister et al. 2019). This jet feature is well-separated from the core in the MOJAVE 15 GHz VLBA image taken on August 9, 2007. We measured the surface brightness ratio between the approaching jet and the counter-jet at a distance of 1.2 mas from the VLBI core. Since there is no detectable emission on the counter-jet side, we used three times the image’s rms noise of 0.23 mJy beam−1 as an upper limit. The resulting lower limit of the brightness ratio RB is 64 and the corresponding upper limit of the jet inclination is 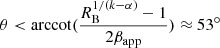θ < arccot ( R B 1 / ( k − α ) − 1 2 β app ) ≈ 53 ° $ \theta < \mathrm{arccot} (\frac{R_{\mathrm{B}}^{1/(k-\alpha)}-1}{2\beta_{\mathrm{app}}}) \approx 53^\circ $, where k = 3 for a transient jet feature and spectral index α is assumed to have the canonical value of −0.7.

6

Liao et al. (2016) even propose that the spectral energy distribution of III Zw 2 can be well-fit by a single-zone, leptonic blazar model during the rapid γ-ray flare in 2009.

Acknowledgments

We thank Stefanie Komossa for her valuable suggestions and comments during the writing of this paper. We also thank the anonymous referee for useful comments that helped to improve the manuscript. This work was supported by the Academy of Finland under the project “Physics of Black Hole -Powered Jets” (project numbers 274477, 284495, and 312496). This publication makes use of data obtained at the Metsähovi Radio Observatory, operated by the Aalto University in Finland. Data and/or software have been provided by the High Energy Astrophysics Science Archive Research Center (HEASARC), which is a service of the Astrophysics Science Division at NASA/GSFC and the High Energy Astrophysics Division of the Smithsonian Astrophysical Observatory. This research has also made use of data obtained from the Suzaku satellite, a collaborative mission between the space agencies of Japan (JAXA) and the USA (NASA). This research has made use of data from the MOJAVE database that is maintained by the MOJAVE team (Lister et al. 2018). K. I. I. K. was supported by the Academy of Finland project 320085.

References

  1. Ai, Y. L., Yuan, W., Zhou, H. Y., Wang, T. G., & Zhang, S. H. 2010, ApJ, 727, 31 [Google Scholar]
  2. Blandford, R. D. 1999, in Astrophysical Discs – An EC Summer School, eds. J. A. Sellwood, & J. Goodman, ASP Conf. Ser., 160, 265 [NASA ADS] [Google Scholar]
  3. Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bonson, K., & Gallo, L. C. 2016, MNRAS, 458, 1927 [NASA ADS] [CrossRef] [Google Scholar]
  5. Brunthaler, A., Falcke, H., Bower, G. C., et al. 2000, A&A, 357, L45 [NASA ADS] [Google Scholar]
  6. Brunthaler, A., Falcke, H., Bower, G. C., et al. 2005, A&A, 435, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Chen, L., Cao, X., & Bai, J. M. 2012, ApJ, 748, 119 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cooper, N. J., Lister, M. L., & Kochanczyk, M. D. 2007, ApJS, 171, 376 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dauser, T., Wilms, J., Reynolds, C. S., & Brenneman, L. W. 2010, MNRAS, 409, 1534 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dauser, T., Garcia, J., Wilms, J., et al. 2013, MNRAS, 430, 1694 [NASA ADS] [CrossRef] [Google Scholar]
  11. Dauser, T., Garcia, J., Parker, M. L., Fabian, A. C., & Wilms, J. 2014, MNRAS, 444, L100 [NASA ADS] [CrossRef] [Google Scholar]
  12. Dauser, T., García, J., & Wilms, J. 2016, Astron. Nachr., 337, 362 [NASA ADS] [CrossRef] [Google Scholar]
  13. Done, C., & Nayakshin, S. 2007, MNRAS, 377, L59 [NASA ADS] [Google Scholar]
  14. Done, C., Gierliński, M., Sobolewska, M., & Schurch, N. 2007, in The Central Engine of Active Galactic Nuclei, eds. L. C. Ho, & J. W. Wang, ASP Conf. Ser., 373, 121 [NASA ADS] [Google Scholar]
  15. Falcke, H., Patnaik, A. R., & Sherwood, W. 1996a, ApJ, 473, L13 [NASA ADS] [CrossRef] [Google Scholar]
  16. Falcke, H., Sherwood, W., & Patnaik, A. R. 1996b, ApJ, 471, 106 [NASA ADS] [CrossRef] [Google Scholar]
  17. Falcke, H., Bower, G. C., Lobanov, A. P., et al. 1999, ApJ, 514, L17 [NASA ADS] [CrossRef] [Google Scholar]
  18. García, J., & Kallman, T. R. 2010, ApJ, 718, 695 [NASA ADS] [CrossRef] [Google Scholar]
  19. García, J., Kallman, T. R., & Mushotzky, R. F. 2011, ApJ, 731, 131 [NASA ADS] [CrossRef] [Google Scholar]
  20. García, J., Dauser, T., Reynolds, C. S., et al. 2013, ApJ, 768, 146 [NASA ADS] [CrossRef] [Google Scholar]
  21. García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [NASA ADS] [CrossRef] [Google Scholar]
  22. García, J. A., Fabian, A. C., Kallman, T. R., et al. 2016, MNRAS, 462, 751 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gierliński, M., & Done, C. 2004, MNRAS, 349, L7 [NASA ADS] [CrossRef] [Google Scholar]
  24. Gnedin, Y. N., Afanasiev, V. L., Borisov, N. V., et al. 2012, Astron. Rep., 56, 573 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gonzalez, A. G., Waddell, S. G. H., & Gallo, L. C. 2018, MNRAS, 475, 128 [NASA ADS] [CrossRef] [Google Scholar]
  26. Grier, C. J., Peterson, B. M., Pogge, R. W., et al. 2012, ApJ, 755, 60 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hao, C. N., Xia, X. Y., Mao, S., Wu, H., & Deng, Z. G. 2005, ApJ, 625, 78 [NASA ADS] [CrossRef] [Google Scholar]
  28. Houck, J. C., & Denicola, L. A. 2000, in Astronomical Data Analysis Software and Systems IX, eds. N. Manset, C. Veillet, & D. Crabtree, ASP Conf. Ser., 216, 591 [NASA ADS] [Google Scholar]
  29. Hovatta, T., Valtaoja, E., Tornikoski, M., & Lähteenmäki, A. 2009, A&A, 494, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Hovatta, T., Aller, M. F., Aller, H. D., et al. 2014, AJ, 147, 143 [NASA ADS] [CrossRef] [Google Scholar]
  31. Inoue, H., Terashima, Y., & Ho, L. C. 2007, ApJ, 662, 860 [NASA ADS] [CrossRef] [Google Scholar]
  32. Jiménez-Bailón, E., Piconcelli, E., Guainazzi, M., et al. 2005, A&A, 435, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Khachikian, E. Y., & Weedman, D. W. 1974, ApJ, 192, 581 [NASA ADS] [CrossRef] [Google Scholar]
  35. Landt, H., Padovani, P., Giommi, P., Perri, M., & Cheung, C. C. 2008, ApJ, 676, 87 [NASA ADS] [CrossRef] [Google Scholar]
  36. Laor, A. 2019, Nat. Astron., 3, 374 [NASA ADS] [CrossRef] [Google Scholar]
  37. Li, H. Z., Xie, G. Z., Dai, H., et al. 2010, New Astron., 15, 254 [NASA ADS] [CrossRef] [Google Scholar]
  38. Liao, N.-H., Xin, Y.-L., Fan, X.-L., et al. 2016, ApJS, 226, 17 [NASA ADS] [CrossRef] [Google Scholar]
  39. Liodakis, I., Hovatta, T., Huppenkothen, D., et al. 2018, ApJ, 866, 137 [NASA ADS] [CrossRef] [Google Scholar]
  40. Liska, M., Hesp, C., Tchekhovskoy, A., et al. 2018, MNRAS, 474, L81 [NASA ADS] [CrossRef] [Google Scholar]
  41. Liska, M., Tchekhovskoy, A., Ingram, A., & van der Klis, M. 2019a, MNRAS, 487, 550 [NASA ADS] [CrossRef] [Google Scholar]
  42. Liska, M., Hesp, C., Tchekhovskoy, A., et al. 2019b, MNRAS, submitted [arXiv:1901.05970] [Google Scholar]
  43. Lister, M. L., Aller, M. F., Aller, H. D., et al. 2018, ApJS, 234, 12 [NASA ADS] [CrossRef] [Google Scholar]
  44. Lister, M. L., Homan, D. C., Hovatta, T., et al. 2019, ApJ, 874, 43 [NASA ADS] [CrossRef] [Google Scholar]
  45. Marziani, P., Sulentic, J. W., Zamanov, R., et al. 2003, ApJS, 145, 199 [NASA ADS] [CrossRef] [Google Scholar]
  46. McKinney, J. C., Tchekhovskoy, A., & Blandford, R. D. 2012, MNRAS, 423, 3083 [NASA ADS] [CrossRef] [Google Scholar]
  47. Narayan, R., Igumenshchev, I. V., & Abramowicz, M. A. 2003, PASJ, 55, L69 [NASA ADS] [Google Scholar]
  48. Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2005, A&A, 432, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Porquet, D., Reeves, J. N., O’Brien, P., & Brinkmann, W. 2004, A&A, 422, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Pushkarev, A. B., Hovatta, T., Kovalev, Y. Y., et al. 2012, A&A, 545, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Reynolds, C. S. 2014, Space Sci. Rev., 183, 277 [Google Scholar]
  52. Reynolds, C. S. 2019, Nat. Astron., 3, 41 [NASA ADS] [CrossRef] [Google Scholar]
  53. Reynolds, C. S., & Fabian, A. C. 2008, ApJ, 675, 1048 [NASA ADS] [CrossRef] [Google Scholar]
  54. Risaliti, G., Harrison, F. A., Madsen, K. K., et al. 2013, Nature, 494, 449 [NASA ADS] [CrossRef] [Google Scholar]
  55. Salvi, N. J., Page, M. J., Stevens, J. A., et al. 2002, MNRAS, 335, 177 [NASA ADS] [CrossRef] [Google Scholar]
  56. Schmidt, M., & Green, R. F. 1983, ApJ, 269, 352 [NASA ADS] [CrossRef] [Google Scholar]
  57. Sikora, M., & Begelman, M. C. 2013, ApJ, 764, L24 [NASA ADS] [CrossRef] [Google Scholar]
  58. Sikora, M., Stawarz, Ł., & Lasota, J.-P. 2007, ApJ, 658, 815 [NASA ADS] [CrossRef] [Google Scholar]
  59. Steiner, J. F., & McClintock, J. E. 2012, ApJ, 745, 136 [NASA ADS] [CrossRef] [Google Scholar]
  60. Taylor, C., & Reynolds, C. S. 2018, ApJ, 855, 120 [NASA ADS] [CrossRef] [Google Scholar]
  61. Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2010, ApJ, 711, 50 [NASA ADS] [CrossRef] [Google Scholar]
  62. Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2011, MNRAS, 418, L79 [NASA ADS] [CrossRef] [Google Scholar]
  63. Teräsranta, H., Tornikoski, M., Mujunen, A., et al. 1998, A&AS, 132, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [NASA ADS] [CrossRef] [Google Scholar]
  65. Volonteri, M. 2010, in Accretion and Ejection in AGN: A Global View, eds. L. Maraschi, G. Ghisellini, R. Della Ceca, & F. Tavecchio, ASP Conf. Ser., 427, 3 [NASA ADS] [Google Scholar]
  66. Volonteri, M., Madau, P., Quataert, E., & Rees, M. J. 2005, ApJ, 620, 69 [NASA ADS] [CrossRef] [Google Scholar]
  67. Walton, D. J., Nardini, E., Fabian, A. C., Gallo, L. C., & Reis, R. C. 2013, MNRAS, 428, 2901 [NASA ADS] [CrossRef] [Google Scholar]
  68. Wilson, A. S., & Colbert, E. J. M. 1995, ApJ, 438, 62 [NASA ADS] [CrossRef] [Google Scholar]
  69. Yuan, W., Liu, B. F., Zhou, H., & Wang, T. G. 2010, ApJ, 723, 508 [NASA ADS] [CrossRef] [Google Scholar]
  70. Zamaninasab, M., Clausen-Brown, E., Savolainen, T., & Tchekhovskoy, A. 2014, Nature, 510, 126 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  71. Zhong, X., & Wang, J. 2013, ApJ, 773, 23 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Different disk inclination values

Below we show the best-fit parameters for RELXILL models that have different fixed disk inclination values as well as for the freely varying, nonconstrained inclination case. The joint-fit with RELXILL is given to the combined 2000 and 2017 spectra. We use the same fixed values for the irradiation profile and disk radius parameters as described in Sect. 3.2. The joint-fits of the iron line region are displayed in Fig. A.1.

thumbnail Fig. A.1.

RELXILL fits of the high-energy edge of the iron line of the combined 2000 and 2017 data sets for the different inclination angles shown in Table A.1. The figure shows the 3−9 keV part of the spectrum. At lower angles, the model fits of the iron line are skewed toward the left side whereas at higher angles the fits display a linear tendency with a change in the slope. The models around the line resemble a broadened and asymmetric feature when the disk inclination lies, for instance, between 40 and 55°.

Table A.1.

RELXILL joint-fit results for different disk inclinations.

Appendix B: Different spin values

Below we show the RELXILL fits of the combined 2000 and 2017 data sets. The best-fit parameters are displayed for different fixed spin values. The disk inclination and the other parameters vary freely.

Table B.1.

RELXILL joint-fit results for different spin values.

All Tables

Table 1.

X-ray observations of III Zw 2 used in this paper.

In the text
Table 2.

Parameters for the best-fit models for all the datasets.

In the text
Table 3.

RELXILL and RELXILLLP (i.e., lamp-post) model parameters.

In the text
Table 4.

RELXILL joint-fit parameters of the combined XMM-2000 and XMM+NuSTAR 2017 spectra.

In the text
Table A.1.

RELXILL joint-fit results for different disk inclinations.

In the text
Table B.1.

RELXILL joint-fit results for different spin values.

In the text

All Figures

thumbnail Fig. 1.

Multiepoch folded spectra of III Zw 2 for the observations in 2000, 2011, and 2017.
In the text
thumbnail Fig. 2.

Data-to-model ratio of (a) an absorbed power-law model and (b) an absorbed power-law+black-body radiation model for all epochs. The vertical dashed-line marks the position of the Fe Kα line.
In the text
thumbnail Fig. 3.

Data-to-model ratio of (a) a power-law continuum model with partial covering of a partially ionized absorber and (b) the same as in (a), but with black body emission included.
In the text
thumbnail Fig. 4.

Joint-fit of the combined 2000 and 2017 data sets with the RELXILL model (blue line). The data-to-model ratio is shown in the lower panel. The model fits the iron line as a heavily broadened and asymmetric feature, indicating emission from very close to the black hole event horizon.
In the text
thumbnail Fig. 5.

37 GHz radio observations of III Zw 2 obtained at the Metsähovi Radio Observatory. The red arrows indicate the epochs when X-ray observations were performed.
In the text
thumbnail Fig. A.1.

RELXILL fits of the high-energy edge of the iron line of the combined 2000 and 2017 data sets for the different inclination angles shown in Table A.1. The figure shows the 3−9 keV part of the spectrum. At lower angles, the model fits of the iron line are skewed toward the left side whereas at higher angles the fits display a linear tendency with a change in the slope. The models around the line resemble a broadened and asymmetric feature when the disk inclination lies, for instance, between 40 and 55°.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.