| Issue |
A&A
Volume 635, March 2020
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201936297 | |
| Published online | 17 March 2020 | |
A diagnostic diagram for γ Doradus variables and slowly pulsating B-type stars
1
LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, Univ. Paris Diderot, Sorbonne Paris Cité, 5 Place Jules Janssen, 92195 Meudon, France
2
Department of Astronomy, School of Science, The University of Tokyo, 7–3–1 Hongo, Bunkyo-ku, Tokyo 113–0033, Japan
e-mail: takata@astron.s.u-tokyo.ac.jp
3
Astronomical Institute, Graduate School of Science, Tohoku University, Sendai 980–8578, Japan
4
IRAP, Université de Toulouse, CNRS, UPS, CNES, 14 Avenue Édouard Belin, 31400 Toulouse, France
5
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
6
STAR Institute, Université de Liège, Allée du 6 Août 19, 4000 Liège, Belgium
Received:
12
July
2019
Accepted:
3
February
2020
Pulsating variables of γ Doradus type (γ Dor) and slowly pulsating B-type (SPB) stars are found on and near the main sequence with typical periods varying between one and several days, making them rather hard to detect from the ground. It is only with space missions such as CoRoT and Kepler that we became truly capable of determining their oscillation frequencies with enough precision to perform in-depth analyses. Here we present an efficient and easy-to-implement seismic tool, in which the frequency (ν) and the square root of the frequency difference (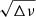 ) are plotted against each other as the abscissa and the ordinate, respectively. This allows us to immediately (1) perform mode identification; (2) estimate the average rotation rate and the characteristic period of gravity modes; and (3) recognise certain physical effects, including buoyancy glitches and avoided crossings. This diagnostic tool can only be applied to prograde sectoral g modes. To validate the tool presented here, we used stellar models and also applied it to three γ Dor (KIC 12066947, KIC 5608334 and KIC 4846809) and one SPB star (KIC 3459297), all observed with Kepler. Furthermore, we show that the rotation rates determined using this new tool are consistent with the results of previous studies.
) are plotted against each other as the abscissa and the ordinate, respectively. This allows us to immediately (1) perform mode identification; (2) estimate the average rotation rate and the characteristic period of gravity modes; and (3) recognise certain physical effects, including buoyancy glitches and avoided crossings. This diagnostic tool can only be applied to prograde sectoral g modes. To validate the tool presented here, we used stellar models and also applied it to three γ Dor (KIC 12066947, KIC 5608334 and KIC 4846809) and one SPB star (KIC 3459297), all observed with Kepler. Furthermore, we show that the rotation rates determined using this new tool are consistent with the results of previous studies.
Key words: asteroseismology / stars: oscillations / stars: rotation / methods: data analysis
© M. Takata et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Gamma Doradus (γ Dor) stars are a class of pulsating variable stars located on and near the main sequence with spectral types from late-A to early-F. The corresponding mass range is between 1.4 and 2.0 M⊙1. They show multi-periodic variability with amplitudes of ≲0.1 mag and periods of about one day. The average measured projected rotational velocity, v sin i, is ∼70−100 km s−1, which indicates that the surface rotation rate is of the same order as the pulsation periods. This means that rotation significantly affects the low-frequency oscillation modes in these stars, making them perfect objects for the study of how rotation affects the internal structure and evolution of these stars.
There has been substantial progress in the understanding of γ Dor stars, thanks to space missions such as CoRoT (Baglin et al. 2006) and Kepler (Borucki et al. 2010), which delivered long and continuous observations with unprecedented precision of a vast number of stars. Contrary to ground-based data, space observations do not suffer from daily aliasing issues, which pose a serious problem when studying pulsating stars with periods close to one day. It is only thanks to multiple years of data from Kepler that oscillation periods in γ Dor stars have finally been resolved, leading to a true revolution in the study of these stars (e.g. Van Reeth et al. 2015). While Kepler data have revealed a significant number of oscillation modes in many cases, their exact identification is absolutely crucial for in-depth analyses.
Oscillation frequencies in rapid rotators are fundamentally different from those of slow rotators. For the latter, the rotation can be regarded as a small perturbation and so the average internal rotation rate can be estimated by measuring the rotational splittings in the frequency spectrum (Cowling & Newing 1949; Ledoux 1951). In the case of rapid rotators, the period versus period-spacing (P–ΔP) diagram is known to provide useful information about the mode identification and the internal rotation rate (e.g. Bouabid et al. 2013; Ouazzani et al. 2017). The asymptotic formula of the period spacing (Ballot et al. 2012) serves as a useful theoretical basis for extracting information from the frequency spectrum. Nevertheless, the estimation of the rotation rates of these stars is not a simple task. Van Reeth et al. (2016), for example, use a large grid of evolutionary models with an assumed range of rotation rates to find the best-fitting parameters for their sample of stars, including the rotation rates. On the other hand, Christophe et al. (2018) propose a model-independent method based on the discrete Fourier transform. The basic idea is that the pulsation periods will be evenly spaced even when the star is rapidly rotating if the period coordinate is stretched appropriately. Li et al. (2019) developed a different model-independent method in the same theoretical framework as Van Reeth et al. (2016) and Christophe et al. (2018), which is described in detail in Sect. 2.1. Li et al. (2020) then applied the method to as many as 611 γ Dor stars in the Kepler field. The central problem of all the methods mentioned above is the parameter sweep in a multidimensional space, which is generally time-consuming and computationally intense.
In this paper, we show that the internal rotation rate of γ Dor and slowly pulsating B-type (SPB) stars can be estimated in a model-independent way by using a simple linear relation between the oscillation frequency and the square-root of the frequency difference. This method can only be applied to prograde sectoral g modes, which is fortunate as observations (e.g. Saio et al. 2018a; Li et al. 2019) show that γ Dor stars predominantly pulsate in these modes. We confine ourselves to single stars in this paper because tidal effects in binaries (or multiple systems) could complicate the picture significantly. Prograde sectoral g modes consist of the waves that propagate in the same longitudinal direction as the rotation, with large amplitudes confined to the equatorial region. Their main restoring force is buoyancy, while the Coriolis force plays an essential role in the equatorial confinement. These modes, which are found in γ Dor stars, are also excited in SPB stars (Waelkens 1991; Salmon et al. 2014). These stars are known as gravity-mode pulsators on the main-sequence with the mass between 3−9 M⊙. The second most dominant component in the frequency spectrum of γ Dor stars is that of r modes (Papaloizou & Pringle 1978; Van Reeth et al. 2016; Saio et al. 2018b), which appear at lower frequencies than prograde sectoral g modes. Rossby (r) modes are mostly composed of toroidal waves (Rossby waves) in each spherical (or equipotential) layer, which are restored by the Coriolis force. The (phase) propagation of the modes is opposite to the rotation in the longitudinal direction (in the co-rotating frame), while the wave motions in adjacent layers are weakly coupled with each other through the influence of the buoyancy. Observations suggest that these modes are detected not only in γ Dor stars, but also in other various types of stars, including chemically peculiar stars and accreting white dwarfs (Saio 2018, 2019).
The structure of this paper is as follows: the method is described in detail in Sect. 2. It is then applied to (a) synthetic model frequencies and (b) observed frequencies of four stars in Sect. 3. Section 4 is devoted to discussions and conclusion.
2. Method
2.1. Theoretical framework
The present study focuses on eigenmodes of stellar oscillations, specifically, prograde sectoral g modes that have been detected in γ Dor and SPB stars. These modes have significantly longer periods than the dynamical time scale of the star and they are strongly affected by the Coriolis force. This is because their rotation periods are of the same order as the oscillation periods. These properties imply that the modes are composed of gravito-inertial waves, which are waves that are subject to the influence of both buoyancy and Coriolis forces.
The equations that govern the low-frequency eigenmodes of linear adiabatic oscillation in rapidly and uniformly2 rotating stars can be formulated to a good level of precision in the framework of the traditional approximation of rotation (Eckart 1960). We neglect (1) the perturbation to the gravitational potential (the Cowling approximation after Cowling 1941), (2) the centrifugal deformation (the assumption of spherical symmetry of the equilibrium structure), and (3) the horizontal component of the rotation vector. The derived equations are separable in the spherical coordinates (r, θ, ϕ), with the direction of θ = 0 aligned with the rotation axis. While the ϕ parts of the eigenfunctions are described by the sinusoidal function, eimϕ, where m is the integral index called the azimuthal order, the θ parts come from the solution of the Laplace tidal equation (the Hough function). On the other hand, the radial parts of the governing equations are of the same form as those of the spheroidal modes of non-rotating stars under the Cowling approximation. The only difference from the non-rotating case is that the term ℓ(ℓ + 1), where ℓ is the spherical degree, is replaced with the eigenvalue λℓ, m of the Laplace tidal equation. Assuming further that the radial wavelength of the oscillation is much shorter than the local scale height of the equilibrium structure, we may apply the asymptotic analysis (e.g. Vandakurov 1967) to derive the condition for the eigenfrequency of the low-frequency modes as
where the meanings of the symbols are given as follows: kr is the radial wave number of the oscillation; r1 and r2 represent the inner and outer boundaries of the region where the constituent waves are propagative; n is the radial (integral) order of modes; α is the phase shift introduced at the inner and outer boundaries of the propagative region. The expression for the radial wave number kr is given by
Here N(r) is the Brunt–Väisälä frequency, which is a function of the radius r, and νco is the cyclic frequency of the oscillation in the co-rotating frame. The eigenvalue λℓ, m(s) depends on not only ℓ and m, but also the spin parameter s, which is defined by
The index ℓ (spherical degree) of λℓ, m(s) means that λℓ, m(s)→ℓ(ℓ+1) as s → 0, while the angular part of the eigenfunctions cannot be described by any single spherical harmonic for s ≠ 0. In other words, the ℓ of eigenmodes in rotating stars indicates the degree of spherical harmonics that specify the angular dependence only in the limit of no rotation. We note that νco is related to the oscillation frequency in the inertial frame, ν, by
In this paper, we adopt the convention that positive (negative) values of m correspond to prograde (retrograde) modes. Equation (1) implies that the oscillation period in the co-rotating frame is given by
in which the parameter P0 is defined by
Equation (5) is in general an implicit expression because s depends on νco. In the absence of rotation, the series of high-order gravity modes with a given spherical degree ℓ are equidistantly spaced by a constant period spacing of  provided that the composition profiles have no steep gradient, and that the dependence of r1 and r2 on the frequency is negligible. Although the spectrum of the low-frequency oscillations in rapidly-rotating stars does not show constant period spacings, the parameter P0 still characterises the structure of the spectrum through Eq. (5). In this sense, P0 can be regarded as a characteristic period of the gravity-mode oscillations3.
provided that the composition profiles have no steep gradient, and that the dependence of r1 and r2 on the frequency is negligible. Although the spectrum of the low-frequency oscillations in rapidly-rotating stars does not show constant period spacings, the parameter P0 still characterises the structure of the spectrum through Eq. (5). In this sense, P0 can be regarded as a characteristic period of the gravity-mode oscillations3.
2.2. Prograde sectoral g modes and the  diagram
diagram
We derive the relation between the frequency and the square root of the frequency difference for prograde sectoral g modes with a given m. Supposing that there is a list of (observed or synthetic) frequencies sorted in the ascending order with the radial orders nk (k = 1, 2, …) and the same m, we can take the difference of Eq. (5) multiplied by  between the (k + 1)th and kth frequencies to obtain
between the (k + 1)th and kth frequencies to obtain
in which Δkq generally means the difference in q between the (k + 1)th and kth frequencies in the list, except for Δkn = −(nk + 1 − nk) (≥1). When we derive Eq. (7), we assume that r1, r2 and α are independent of the frequency. For the prograde sectoral g modes, which have ℓ = m > 0, there is an approximate relation for large s,
(e.g. Bildsten et al. 1996; Townsend 2003). The accuracy of Eq. (8) is depicted in Fig. 1. We may further introduce the linearisation relation,
 |
Fig. 1. Relative differences in the square roots of the eigenvalues of the Laplace tidal equation |
under the assumption of  , where Δkν = νk + 1 − νk and
, where Δkν = νk + 1 − νk and  , with νk being the kth frequency in the list. With the help of Eqs. (8) and (9), we can reduce Eq. (7) to
, with νk being the kth frequency in the list. With the help of Eqs. (8) and (9), we can reduce Eq. (7) to
In Eq. (10), Δkν (the difference between the two adjacent frequencies) and  (the average frequency of the two) are both observables that are computed from the same pair of mode frequencies, while m, Δkn, P0 and νrot are not known in advance. With estimates of m and Δkn, we can construct a diagram, based on only the two observables, in which the abscissa and the ordinate are given by
(the average frequency of the two) are both observables that are computed from the same pair of mode frequencies, while m, Δkn, P0 and νrot are not known in advance. With estimates of m and Δkn, we can construct a diagram, based on only the two observables, in which the abscissa and the ordinate are given by  and
and  , respectively. We call this the diagram of ν versus
, respectively. We call this the diagram of ν versus  , or simply the ν–
, or simply the ν– diagram. Although mode identification (i.e., the knowledge of Δkn) is not always straightforward, this tool can be used to constrain Δkn of these prograde modes as described in Sect. 3. According to Eq. (10), each pair of the two adjacent frequencies should correspond to a point of a common straight line in the diagram. The slope and the abscissa intercept (the intersection point with the horizontal line of
diagram. Although mode identification (i.e., the knowledge of Δkn) is not always straightforward, this tool can be used to constrain Δkn of these prograde modes as described in Sect. 3. According to Eq. (10), each pair of the two adjacent frequencies should correspond to a point of a common straight line in the diagram. The slope and the abscissa intercept (the intersection point with the horizontal line of  ) of the linear fit are given by
) of the linear fit are given by  and νrot, respectively. Using this result inversely, we can estimate νrot and P0 by plotting the modes in the diagram and fitting them with a straight line. The simplest procedure is to perform linear least-squares fitting under the assumption that the errors of each point are uncorrelated with each other. This assumption is acceptable for rough estimates. However, as shown in the Appendix A, Δkν and Δk + 1ν are correlated with each other since they both depend on νk + 1.
and νrot, respectively. Using this result inversely, we can estimate νrot and P0 by plotting the modes in the diagram and fitting them with a straight line. The simplest procedure is to perform linear least-squares fitting under the assumption that the errors of each point are uncorrelated with each other. This assumption is acceptable for rough estimates. However, as shown in the Appendix A, Δkν and Δk + 1ν are correlated with each other since they both depend on νk + 1.
2.3. Revised method of estimating νrot and P0
The formula given by Eq. (10) can be improved by discarding the two approximations that are given by Eqs. (8) and (9). The revised formula can directly be obtained from Eq. (7) as
in which
The correction factor fk, which is a function of νrot, is practically close to 1 because Eqs. (8) and (9) are generally good approximations. This property can be utilised to construct the following iterative procedure to obtain better estimates of νrot and P0:
-
set fk to
 and perform the least-squares fitting based on Eq. (11) to estimate
and perform the least-squares fitting based on Eq. (11) to estimate  and
and  (cf. Appendix A); this step is called iteration 1.
(cf. Appendix A); this step is called iteration 1. -
calculate fk by substituting
 into Eq. (12), and perform the least-squares fitting again to estimate
into Eq. (12), and perform the least-squares fitting again to estimate  and
and  based on Eq. (11); this step is called iteration 2.
based on Eq. (11); this step is called iteration 2. -
repeat the same procedure as step 2 to obtain
 and
and  from
from  (iteration i + 1) for i = 2, 3, … until both of
(iteration i + 1) for i = 2, 3, … until both of  and
and  are small enough.
are small enough.
We use the numerical values of λm, m(s) to evaluate Eq. (12).
2.4. Error estimates
The errors in νrot and P0 obtained by the procedure in Sect. 2.3 can originate from (1) the observational errors in the frequency measurement and (2) the systematic errors in Eq. (11), which arise from differential rotation, steep chemical composition gradient (discussed in Sect. 3.1), and deviation from the traditional approximation of rotation in the asymptotic limit. Because the relative errors in the frequencies of γ Dor and SPB stars in the Kepler data are typically of the order of 10−5 or below, we regard that the dominant uncertainties come from (2). In order to estimate the systematic errors accurately, we need a detailed comparison between the frequencies computed under the traditional approximation of rotation in the asymptotic limit and those determined by two-dimensional computations that take full account of the effects of the rapid rotation. We leave this expensive comparison to future work, however, for a first approximation, we determine uncertainties in νrot and P0 from the residual sum of squares of the least-squares fitting. These estimates are based on the assumptions that (a) the uncertainties in the frequencies are not correlated and that (b) they follow a Gaussian distribution with the same standard deviation. For the sake of simplicity, we assume that there is no error correlation, but we do point out that the systematic errors in Eq. (11) are likely to be highly correlated. We set the default confidence level to 99% for the uncertainties in the estimates of νrot and P0. More details are given in Appendix A.
3. Results
As described in Sect. 1, the ν– diagram method was developed based on Kepler observations. It indicates that most of the observed frequencies in γ Dor stars can be identified as prograde sectoral g modes and r modes. Therefore, we first address these two types of modes in this section, while the other types are discussed in Sect. 3.3.2.
diagram method was developed based on Kepler observations. It indicates that most of the observed frequencies in γ Dor stars can be identified as prograde sectoral g modes and r modes. Therefore, we first address these two types of modes in this section, while the other types are discussed in Sect. 3.3.2.
Since analysing γ Dor and SPB stars requires very similar techniques, in this section we choose to concentrate on the former, while the latter is discussed in Appendix B.
3.1. Tests based on models
We construct the ν– diagrams and estimate νrot and P0 for the following three models of γ Dor stars (all having the same mass of 1.86 M⊙), which are described in detail in Christophe et al. (2018): (1) Model A (with smooth profiles of chemical composition); (2) Model B (with steep gradients of the chemical composition profiles just above the convective core); (3) Model A with differential rotation (DR) (νrot = 15 μHz and 7 μHz in the convective core and the envelope, respectively). For each model, we used the same set of eigenfrequencies as Christophe et al. (2018), that is, those of prograde sectoral g modes with m = 1 and the g mode radial orders between −50 and −20. All mode frequencies were computed with the ACOR oscillation code (Ouazzani et al. 2012, 2015). For the sake of simplicity, we took only the spherically-symmetric part of the centrifugal deformation into account. In Figs. 2–4 we show the ν–
diagrams and estimate νrot and P0 for the following three models of γ Dor stars (all having the same mass of 1.86 M⊙), which are described in detail in Christophe et al. (2018): (1) Model A (with smooth profiles of chemical composition); (2) Model B (with steep gradients of the chemical composition profiles just above the convective core); (3) Model A with differential rotation (DR) (νrot = 15 μHz and 7 μHz in the convective core and the envelope, respectively). For each model, we used the same set of eigenfrequencies as Christophe et al. (2018), that is, those of prograde sectoral g modes with m = 1 and the g mode radial orders between −50 and −20. All mode frequencies were computed with the ACOR oscillation code (Ouazzani et al. 2012, 2015). For the sake of simplicity, we took only the spherically-symmetric part of the centrifugal deformation into account. In Figs. 2–4 we show the ν– diagrams for these models. The corresponding estimates of νrot and P0 are summarised in Table 1.
diagrams for these models. The corresponding estimates of νrot and P0 are summarised in Table 1.
 |
Fig. 2. ν versus |
Estimates of νrot and P0 for the three theoretical models from the synthetic eigenfrequencies of the prograde sectoral g modes with the azimuthal order of m = 1.
The ν– diagrams in Figs. 2–4 clearly show that all the open circle symbols are well aligned and fit a straight line. This confirms that Eq. (10) is a good approximation in all of the models. In models (1) and (2), the spin parameter of the eigenmodes ranges between 1 and 3, for which Eq. (8) is accurate to only about 10–20% (see Fig. 1). The inaccuracy of Eq. (8) results in the deviation of fk in Eq. (12) from 1. This is the main reason for the differences between the dashed and solid lines in Figs. 2 and 3 or, equivalently, the differences between the outputs of iteration 1 and the converged values for these two models (see Table 1).
diagrams in Figs. 2–4 clearly show that all the open circle symbols are well aligned and fit a straight line. This confirms that Eq. (10) is a good approximation in all of the models. In models (1) and (2), the spin parameter of the eigenmodes ranges between 1 and 3, for which Eq. (8) is accurate to only about 10–20% (see Fig. 1). The inaccuracy of Eq. (8) results in the deviation of fk in Eq. (12) from 1. This is the main reason for the differences between the dashed and solid lines in Figs. 2 and 3 or, equivalently, the differences between the outputs of iteration 1 and the converged values for these two models (see Table 1).
The converged values for the rotation rate based on the iterative linear least-squares fitting described in Sect. 2.3 are generally consistent with the results based on the discrete Fourier transform (DFT) map developed by Christophe et al. (2018), as shown in Table 1. Although the differences between the converged estimates and the true values are generally small, the true values of νrot and P0 are found outside the given confidence intervals for all cases, which indicates that the unaccounted systematic errors of Eq. (11) can be significantly larger than the uncertainties derived here.
As an example of the unaccounted error sources, we may list the steep gradients in the chemical composition profiles just above the convective core in model (2). This cannot be treated by the standard asymptotic analysis because it assumes that the wavelength of the oscillation is much shorter than the scale height of the equilibrium structure. The corresponding variation in the Brunt–Väisälä frequency (buoyancy glitch) is known to cause a wavy structure in the period spacing (e.g. Miglio et al. 2008; Bouabid et al. 2013; Kurtz et al. 2014). Such an oscillatory behaviour in ΔP caused by a glitch can also be found in  as shown in Fig. 3.
as shown in Fig. 3.
The case of model (3) (see Fig. 4) can be used to check what happens if the method is applied to the case of differential rotation, although the uniform rotation is assumed in the (standard) traditional approximation of rotation. Broadly speaking, we find no critical difference from Fig. 2 because most of the points are aligned. This is, at first glance, consistent with the argument in Appendix E, which claims that the effect of weak differential rotation (in the radial direction) can be taken into account only by replacing the uniform rotation frequency by its average weighted by N/r over the propagation region. However, the weak differential rotation cannot be assumed for model (3) since the variation between 7 and 15 μHz is large. This means that for a strongly differentially rotating star, we cannot simply interpret the derived νrot, even though the value of 11.80 ± 0.04 μHz for model (3) is clearly within the range of values in the model.
 |
Fig. 4. Same as Fig. 2, but for model (3). This model includes differential rotation. A detailed explanation of the symbols and the dotted line labelled |
It is remarkable that our method allows us to highlight the two avoided crossings in Fig. 4 at a frequency of ∼15.5 μHz and ∼17.5 μHz, respectively. It should be noted that methods using the traditional approximation framework cannot account for this phenomenon. This is shown by the filled circles deviating from the solid line (base line). Since these points cannot be interpreted in the framework developed in Sect. 2, we simply discard them in the fitting to estimate νrot and P0. Lee & Saio (1989) demonstrated that an avoided crossing can be caused by the horizontal component of the rotation vector, which is neglected in the traditional approximation of rotation. However, there may be other reasons too. In principle, it can occur due to any neglected terms that make the governing equations variable-inseparable into the radial and angular parts. In the case of differential rotation, those that include the gradient of the rotation frequency can also induce the avoided crossing.
Another important difference in model (3) is that some modes are missing, meaning that not all modes are of consecutive radial order. More specifically, the open diamonds aligned with the blue dotted line labelled “ ” in Fig. 4 correspond to the jumps in the radial order n with Δkn = 2. This demonstrates that this method allows us to not only determine νrot and P0 but also Δkn. When a point is found on the line that has the same abscissa intercept as the base line but a slope steeper than the base line by factor of
” in Fig. 4 correspond to the jumps in the radial order n with Δkn = 2. This demonstrates that this method allows us to not only determine νrot and P0 but also Δkn. When a point is found on the line that has the same abscissa intercept as the base line but a slope steeper than the base line by factor of  (with j = 2, 3, …), we may interpret this as a missing j−1 radial order(s) with Δkn = j. With the value of Δkn, we can calculate the left-hand side of Eq. (10), which can be used in the fitting. This correction factor of
(with j = 2, 3, …), we may interpret this as a missing j−1 radial order(s) with Δkn = j. With the value of Δkn, we can calculate the left-hand side of Eq. (10), which can be used in the fitting. This correction factor of  is indicated by each of the vertical cyan lines in Fig. 4. We only use the open circles in Fig. 4 to estimate νrot and P0.
is indicated by each of the vertical cyan lines in Fig. 4. We only use the open circles in Fig. 4 to estimate νrot and P0.
We apply the same method and construct the ν– diagram for r modes of model (1) (see Fig. 5). In sharp contrast to Fig. 2, these modes are not distributed along a straight line with a positive slope. This very clear difference can be used to distinguish r modes from prograde sectoral g modes. Thus, the diagram is also useful for mode identification in this respect.
diagram for r modes of model (1) (see Fig. 5). In sharp contrast to Fig. 2, these modes are not distributed along a straight line with a positive slope. This very clear difference can be used to distinguish r modes from prograde sectoral g modes. Thus, the diagram is also useful for mode identification in this respect.
 |
Fig. 5. Diagram of ν versus |
3.2. Application to real stars
3.2.1. KIC 12066947
The first γ Dor star analysed here is KIC 12066947. The observed frequencies and the Lomb-Scargle periodogram are provided in Table A.1 and Fig. 6 of Christophe et al. (2018), respectively. All peaks were extracted using the Aarhus University ECHO (Extraction of CoHerent Oscillations) pipeline described in Antoci et al. (2019). Analyses show that the extracted frequencies are separated in two clusters, Cluster A between 20 and 24 μHz and Cluster B between 27 and 35 μHz.
The ν– diagram in Fig. 6 is constructed using 14 frequencies in Cluster B, which could be identified as m = 1 modes. It can be seen that except for one peak, all modes follow the three lines that are displayed. The solid line is the base line, while the two dotted lines labelled “
diagram in Fig. 6 is constructed using 14 frequencies in Cluster B, which could be identified as m = 1 modes. It can be seen that except for one peak, all modes follow the three lines that are displayed. The solid line is the base line, while the two dotted lines labelled “ ” and “
” and “ ” indicate slopes that are larger than the base line by factors
” indicate slopes that are larger than the base line by factors  and
and  , respectively.
, respectively.
 |
Fig. 6. ν versus |
This is consistent with the interpretation that these frequencies are those of the prograde sectoral g modes. The outlier at  is discarded when we perform the least-squares fitting, which converges after three iterations. Table 2 provides the converged estimates of νrot and P0 with their 99% and 1σ confidence intervals. These results are consistent with those of Van Reeth et al. (2016) and Christophe et al. (2018) within 1σ, while those of Li et al. (2019) are within 99% confidence intervals. We note that the uncertainties of Li et al. (2019) are smaller than the others because they include not only prograde sectoral g modes but also r modes in their analysis.
is discarded when we perform the least-squares fitting, which converges after three iterations. Table 2 provides the converged estimates of νrot and P0 with their 99% and 1σ confidence intervals. These results are consistent with those of Van Reeth et al. (2016) and Christophe et al. (2018) within 1σ, while those of Li et al. (2019) are within 99% confidence intervals. We note that the uncertainties of Li et al. (2019) are smaller than the others because they include not only prograde sectoral g modes but also r modes in their analysis.
Estimates of νrot and P0 for KIC 12066947.
The ν– diagram constructed using the frequencies in Cluster A is shown in Fig. 7. It is clear that we fail to observe the modes showing the expected pattern for prograde sectoral g modes. We therefore conclude that these peaks are those of other modes, which is consistent with Van Reeth et al. (2016) who identify these as r modes (cf. Fig. 5).
diagram constructed using the frequencies in Cluster A is shown in Fig. 7. It is clear that we fail to observe the modes showing the expected pattern for prograde sectoral g modes. We therefore conclude that these peaks are those of other modes, which is consistent with Van Reeth et al. (2016) who identify these as r modes (cf. Fig. 5).
 |
Fig. 7. ν versus |
3.2.2. KIC 5608334
Saio et al. (2018a) study KIC 5608334, which shows remarkable frequency groups (fg) in the amplitude spectrum (cf. Fig. 3 in the paper). We adopted their mode identification of the four frequency groups, fg1–fg4, as the prograde sectoral g modes with m = 1−4, respectively. From 192 frequencies that are determined with the ECHO pipeline of Antoci et al. (2019) and listed in Table A.1 of Saio et al. (2018a), we first excluded those with amplitudes smaller than 5 ppm (all of which belong to fg3 and fg4). We chose to do so because the small peaks show significant outliers in the ν– diagram, which may imply that many of them do not correspond to prograde sectoral g modes or additional effects such as glitches are present. The physical origin of them should be examined in a separate study. In addition, if multiple frequencies are found in a very narrow frequency range for all of fg1–fg4 (cf. Fig. 4 of Saio et al. 2018a), we chose only the one with the highest amplitude and discarded the rest. The number of the remaining frequencies is 79 in total, and is equal to 24, 30, 14 and 11 for fg1–fg4, respectively. We then constructed the ν–
diagram, which may imply that many of them do not correspond to prograde sectoral g modes or additional effects such as glitches are present. The physical origin of them should be examined in a separate study. In addition, if multiple frequencies are found in a very narrow frequency range for all of fg1–fg4 (cf. Fig. 4 of Saio et al. 2018a), we chose only the one with the highest amplitude and discarded the rest. The number of the remaining frequencies is 79 in total, and is equal to 24, 30, 14 and 11 for fg1–fg4, respectively. We then constructed the ν– diagrams for each frequency group, which are shown in Figs. 8–11. Table 3 provides the corresponding results of the least-squares fitting, where only the open circles in Figs. 8–11 were used.
diagrams for each frequency group, which are shown in Figs. 8–11. Table 3 provides the corresponding results of the least-squares fitting, where only the open circles in Figs. 8–11 were used.
 |
Fig. 8. ν versus |
Estimates of νrot and P0 for KIC 5608334.
There are a few possible physical reasons for the discarded points, which are indicated by filled circles in Figs. 8 and 9: they might originate from an avoided crossing (as in Fig. 4) or from a contamination of other types of frequencies (e.g. those of tesseral modes or combination frequencies) than those of the prograde sectoral g modes. These outliers are caused by the frequencies with small amplitudes: they disappear if we exclude those with amplitudes smaller than 100 and 20 ppm in fg1 and fg2, respectively. We observe a small deviation of some of the open circles from the base lines in Figs. 8–11. It is possible that they also originate from an avoided crossing or the influence of the nonlinear mode interaction, as discussed in Saio et al. (2018a). Although the estimates of νrot and P0 for fg1–fg4 are completely consistent with each other within the errors, we cannot conclude uniform rotation only from these results because the theoretical model of Saio et al. (2018a) indicates that there is little difference in the propagation cavity of the modes for the different groups, so the estimates for fg1–fg4 correspond to essentially the same physical quantities. Based on these considerations, the last row of Table 3 gives the estimates in the case where all the points with open circles in Figs. 8–11 are simultaneously taken into account in the fitting.
Saio et al. (2018a) estimate the internal rotation rate of the star as 2.20 d−1 (25.5 μHz) by comparing the observed period spacings with theoretical models by eye. Considering the roughness of their estimate, we regard the small deviation in our results outlined in Table 3 as non-significant. Saio et al. (2018a) also note an isolated peak at 2.2397 d−1 (25.922 μHz) in the frequency spectrum, which could be due to rotational modulation. If this is indeed the case, the derived surface rotation rate agrees well with the average internal rotation rate in Table 3 (cf. Appendix E). Li et al. (2020) also analyse this star, but based only on peaks belonging to fg1. They obtain νrot = 26.0 ± 0.1 μHz (2.25 ± 0.01 d−1) and P0 = (4.4 ± 0.2)×103 s. These are completely consistent with our results in Table 3.
3.3. Applicability of the method
3.3.1. Slow rotation
While the fundamental approximation of the present analysis,  (cf. Eq. (8)), can be justified only when the spin parameter satisfies s ≫ 1, we show in Appendix C that in principle the ν–
(cf. Eq. (8)), can be justified only when the spin parameter satisfies s ≫ 1, we show in Appendix C that in principle the ν–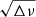 diagram method may also work for s ≲ 1. However, we should stress that it is essential not to use the approximation of
diagram method may also work for s ≲ 1. However, we should stress that it is essential not to use the approximation of  in the case of slow rotation, but to utilise the realistic values shown in Fig. 1.
in the case of slow rotation, but to utilise the realistic values shown in Fig. 1.
3.3.2. Mode identification
As described above, the ν– diagram allows us to distinguish prograde sectoral g modes from r modes (cf. Sect. 3.1), however other types of modes may complicate the mode identification process. In this section, we discuss possible issues that may influence mode identification.
diagram allows us to distinguish prograde sectoral g modes from r modes (cf. Sect. 3.1), however other types of modes may complicate the mode identification process. In this section, we discuss possible issues that may influence mode identification.
Retrograde modes with ℓ = 1 and m = −1 behave differently from the prograde modes when plotted in both, the ν– as well as the P–ΔP diagrams (cf. Bouabid et al. 2013). More specifically, the sign of the slope is different: negative for retrograde and positive for prograde modes in the ν–
as well as the P–ΔP diagrams (cf. Bouabid et al. 2013). More specifically, the sign of the slope is different: negative for retrograde and positive for prograde modes in the ν– diagram.
diagram.
One relevant question may refer to how we discriminate prograde sectoral g modes with different azimuthal order m. We believe that this is not a real problem. As in the case of KIC 5608334 (Saio et al. 2018a), these modes with different m usually appear in different groups in the frequency spectrum, with smaller amplitudes for the group with higher frequencies. Since the effect of the geometrical cancellation is more significant for the modes with larger m, we may identify those groups as the modes with m = 1, 2, … in the order of frequency. In particular, if there is only one group observed, and the ν– diagram confirms that it consists of the prograde sectoral g modes, it is quite likely that the group is that of m = 1 modes.
diagram confirms that it consists of the prograde sectoral g modes, it is quite likely that the group is that of m = 1 modes.
Some possible confusion can be caused by the zonal modes (m = 0), which are claimed to be observed in rare cases (cf. Van Reeth et al. 2016; Li et al. 2020). In Fig. 12 we show the ℓ = 1 zonal modes of model (1) in the ν– diagram. We clearly observe very similar alignment of the points on a straight line to that in Fig. 2. If we erroneously identify these as prograde sectoral g modes with m = 1, we obtain the rotation rate of νrot = 3.6 μHz (0.31 d−1), which is quite different from the true value of 7 μHz (0.60 d−1). This example shows that it is dangerous to apply the method blindly. We therefore suggest for the mode identification to use the information about the amplitude in addition to the ν–
diagram. We clearly observe very similar alignment of the points on a straight line to that in Fig. 2. If we erroneously identify these as prograde sectoral g modes with m = 1, we obtain the rotation rate of νrot = 3.6 μHz (0.31 d−1), which is quite different from the true value of 7 μHz (0.60 d−1). This example shows that it is dangerous to apply the method blindly. We therefore suggest for the mode identification to use the information about the amplitude in addition to the ν– diagram. This point is demonstrated in a particular case. Van Reeth et al. (2015) detect two series of period spacings in KIC 4846809 (see Fig. 15 of the paper), in which the shorter-period (higher-frequency) series have significantly larger amplitudes. Both series cannot be prograde sectoral g modes, because frequencies in the higher-frequency group (with higher azimuthal order, m) are more likely to have smaller amplitudes due to the more severe effect of the geometrical cancellation. We therefore argue that the higher-frequency (shorter-period) series of KIC 4846809 corresponds to the prograde sectoral g modes with m = 1, which can be confirmed in the ν–
diagram. This point is demonstrated in a particular case. Van Reeth et al. (2015) detect two series of period spacings in KIC 4846809 (see Fig. 15 of the paper), in which the shorter-period (higher-frequency) series have significantly larger amplitudes. Both series cannot be prograde sectoral g modes, because frequencies in the higher-frequency group (with higher azimuthal order, m) are more likely to have smaller amplitudes due to the more severe effect of the geometrical cancellation. We therefore argue that the higher-frequency (shorter-period) series of KIC 4846809 corresponds to the prograde sectoral g modes with m = 1, which can be confirmed in the ν– diagram shown in Fig. 13. This identification is consistent with Van Reeth et al. (2016). The lower frequencies (longer periods) series cannot be identified by our method completely, while Van Reeth et al. (2016) regard them as zonal modes.
diagram shown in Fig. 13. This identification is consistent with Van Reeth et al. (2016). The lower frequencies (longer periods) series cannot be identified by our method completely, while Van Reeth et al. (2016) regard them as zonal modes.
 |
Fig. 12. Diagram of ν versus |
 |
Fig. 13. Diagram of ν versus |
Other types of modes, such as ℓ = 2 and m = ±1, can also introduce confusion similar to that caused by the zonal modes. They appear as a series with a negative slope in the P–ΔP diagram, which translates into one with a positive slope in the ν– diagram. However, they are unlikely to have much larger amplitude than prograde sectoral g modes when the stellar rotation is fairly high and are, apparently, identified in only few stars (Li et al. 2020). Such exceptional cases should carefully be investigated in a separate study.
diagram. However, they are unlikely to have much larger amplitude than prograde sectoral g modes when the stellar rotation is fairly high and are, apparently, identified in only few stars (Li et al. 2020). Such exceptional cases should carefully be investigated in a separate study.
Having considered all of the above, we may propose a general procedure for mode identification as follows:
1. The first step is to identify frequency groups, each composing a cluster in the frequency spectrum of a given star. If this is not possible, it may be the case that the star rotates slowly and that frequency splittings may be identified.
2. If one or more groups are present, mode identification is required. From a practical point of view, it seems to be a good initial guess that the group with the largest amplitude corresponds to the prograde sectoral g modes of m = 1. For these modes we expect to observe larger amplitudes because the geometrical cancellation effect is significantly smaller in comparison to other types of modes. We may find an exception for r modes but only if the star rotates rapidly, or more precisely if the spin parameter satisfies s ≳ 1 (Saio et al. 2018a).
3. If the modes of the first group do not align in the ν– diagram and show a positive slope consistent with prograde sectoral g modes, then the frequency group with the second-largest amplitudes should be examined.
diagram and show a positive slope consistent with prograde sectoral g modes, then the frequency group with the second-largest amplitudes should be examined.
4. This process should be repeated until prograde sectoral g modes with m = 1 are found (or all of the frequency groups have been checked). If there are two (or more) frequency groups with similar amplitudes at each step, we may assume that the one with the highest frequency originates from the prograde sectoral g modes with m = 1.
5. Once the identification of the first group is successful (i.e. m = 1), one may look for m = 2, 3, … modes that should be located around the frequencies of the first group multiplied by m.
We regard this procedure as a general guideline that is applicable to the majority of the stars. The further details of the mode identification should be examined carefully based on a large sample of stars.
4. Discussion and conclusion
We propose the ν– diagram as an asteroseismic tool to estimate the average rotation rate (νrot) and the characteristic period of the gravity-mode oscillations (P0) of γ Dor and SPB stars from the frequencies of the prograde sectoral g modes. Our method is endorsed by the fact that the prograde sectoral g modes are most commonly observed in (rapidly rotating) γ Dor stars and SPB stars (e.g. Van Reeth et al. 2015; Pápics et al. 2017). Although the method is based on the same asymptotic formula of the low-frequency oscillation under the traditional approximation of rotation as in previous works (Van Reeth et al. 2016; Christophe et al. 2018; Li et al. 2019, 2020), the biggest advantage here is in its efficiency and simplicity. It is easy to get rough estimates of νrot and P0 by plotting the diagram and applying a linear fit, which the majority of the modes follow ideally. The estimates of νrot and P0 can be derived from the abscissa intercept and (the square of) the slope of the line, respectively. If no clear alignment is visible, it is unlikely that the observed frequencies correspond to prograde sectoral g modes. The diagram thus also allows us to perform mode identification. In addition, this tool can also be used to discuss the physics of oscillation modes including the buoyancy glitch (Fig. 3) and the avoided crossing (Fig. 4). The first rough estimates of νrot and P0 can be improved by just a linear least-squares fitting with a few iterations. It should be stressed that the method is free from any time-intensive parameter search in two- (or more) dimensional space. There is no need to constrain the ranges of any parameters in advance or give any initial guesses. These properties are important, especially when analysing a large sample of stars.
diagram as an asteroseismic tool to estimate the average rotation rate (νrot) and the characteristic period of the gravity-mode oscillations (P0) of γ Dor and SPB stars from the frequencies of the prograde sectoral g modes. Our method is endorsed by the fact that the prograde sectoral g modes are most commonly observed in (rapidly rotating) γ Dor stars and SPB stars (e.g. Van Reeth et al. 2015; Pápics et al. 2017). Although the method is based on the same asymptotic formula of the low-frequency oscillation under the traditional approximation of rotation as in previous works (Van Reeth et al. 2016; Christophe et al. 2018; Li et al. 2019, 2020), the biggest advantage here is in its efficiency and simplicity. It is easy to get rough estimates of νrot and P0 by plotting the diagram and applying a linear fit, which the majority of the modes follow ideally. The estimates of νrot and P0 can be derived from the abscissa intercept and (the square of) the slope of the line, respectively. If no clear alignment is visible, it is unlikely that the observed frequencies correspond to prograde sectoral g modes. The diagram thus also allows us to perform mode identification. In addition, this tool can also be used to discuss the physics of oscillation modes including the buoyancy glitch (Fig. 3) and the avoided crossing (Fig. 4). The first rough estimates of νrot and P0 can be improved by just a linear least-squares fitting with a few iterations. It should be stressed that the method is free from any time-intensive parameter search in two- (or more) dimensional space. There is no need to constrain the ranges of any parameters in advance or give any initial guesses. These properties are important, especially when analysing a large sample of stars.
The method proposed in this paper depends on the eigenvalue of the Laplace tidal equation of the prograde sectoral g modes being approximately equal to the square of the azimuthal order, m2, if the spin parameter s is much larger than 1 (cf. Fig. 1). This implies that the mode frequencies are nearly independent of νrot in the co-rotating frame (cf. Eq. (5)). This is because the dispersion relation of the constituent waves (internal equatorial Kelvin waves) is independent of νrot when s ≫ 1 and also because they propagate only along the equator in the same limit. More details about the physical properties of the modes, which may be called Kelvin g modes, are discussed in Appendix D. While the mode frequencies are insensitive to νrot in the co-rotating frame, we may infer νrot from those in the inertial frame through the advection effect induced by rotation (Doppler shift), which is represented by the second term on the right-hand side of Eq. (4). The ν– diagram allows us to represent this effect graphically.
diagram allows us to represent this effect graphically.
While it is standard to assume that the rotation rate is constant in the traditional approximation of rotation, this is not necessary in the asymptotic limit. In the case where the rotation rate weakly depends on the radius, the obtained estimate of νrot should be interpreted as the average of the internal rotation rate weighted by N/r (the Brunt–Väisälä frequency divided by the radius), as is proposed by Ouazzani et al. (2019) and justified in Appendix E.
We confirm that the estimate of νrot is highly correlated with that of P0 (cf. Van Reeth et al. 2016; Christophe et al. 2018): the correlation coefficient a, which is defined in Eq. (A.29), satisfies a ≥ 0.98 in most cases presented in this paper. Such high values can be understood based on the ν– diagram. Supposing we have obtained the best-fit line on the diagram, if we slightly increase (or decrease) the abscissa intercept (νrot) from the best-fit value and perform a linear fit under this constraint, the slope of the fitted line (
diagram. Supposing we have obtained the best-fit line on the diagram, if we slightly increase (or decrease) the abscissa intercept (νrot) from the best-fit value and perform a linear fit under this constraint, the slope of the fitted line ( ) is necessarily steeper (or shallower) than the best-fit line because all the points in the diagram are located in the upper right side of the abscissa intercept (the domain of ν/m > νrot and
) is necessarily steeper (or shallower) than the best-fit line because all the points in the diagram are located in the upper right side of the abscissa intercept (the domain of ν/m > νrot and  ). The reason for the high correlation coefficient is that we take only prograde sectoral g modes into account. We can, in principle, reduce the correlation by including other types of modes, if available (cf. Li et al. 2019). In this context, a natural extension of the present method would be to include the other types of modes by deriving similar formulae to Eq. (11).
). The reason for the high correlation coefficient is that we take only prograde sectoral g modes into account. We can, in principle, reduce the correlation by including other types of modes, if available (cf. Li et al. 2019). In this context, a natural extension of the present method would be to include the other types of modes by deriving similar formulae to Eq. (11).
We adopt conservative estimates of the formal uncertainties in the present analysis, corresponding to 99% confidence intervals calculated based on the goodness of the fit. Nevertheless, Table 1 shows evidence that these values can significantly underestimate the true uncertainties. This is probably a common problem in any method based on the asymptotic frequency formula under the traditional approximation of rotation and it should be examined in detail in a future work. In order to evaluate the total uncertainty, it is necessary to improve Eq. (11), which is the fundamental relation of the present work. This can be done by taking into account additional physical effects, including centrifugal deformation, correction to the traditional approximation of rotation, higher-order terms in the asymptotic frequency formula, and the possible steep variation of the chemical composition profiles just outside the convective core.
For more details about the history of γ Dor stars we refer the reader to Saio et al. (2018a). Although the prototype was discovered in 1963 (Cousins & Warren 1963), the class of γ Dor pulsators was established only three decades later (Balona et al. 1994).
Christophe et al. (2018) and Ouazzani et al. (2019) introduce P0 as the buoyancy radius.
Acknowledgments
We thank NASA and the Kepler team for their revolutionary data. M. T. thanks B. Mosser and his colleagues for their support and hospitality at the Paris Observatory, where this project started. The anonymous referee is acknowledged for valuable remarks, which helped improving this paper. M. T. is partially supported by JSPS KAKENHI Grant Number JP18K03695. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant agreement no.: DNRF106). S. J. A. J. S. is funded by the Wallonia-Brussels Federation ARC grant for Concerted Research Actions.
References
- Antoci, V., Cunha, M. S., Bowman, D. M., et al. 2019, MNRAS, 490, 4040 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, in 36th COSPAR Scientific Assembly, COSPAR Meeting, 36 [Google Scholar]
- Ballot, J., Lignières, F., Prat, V., Reese, D. R., & Rieutord, M. 2012, in Progress in Solar/Stellar Physics with Helio- and Asteroseismology, eds. H. Shibahashi, M. Takata, & A. E. Lynas-Gray, ASP Conf. Ser., 462, 389 [NASA ADS] [Google Scholar]
- Balona, L. A., Krisciunas, K., & Cousins, A. W. J. 1994, MNRAS, 270, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L., Ushomirsky, G., & Cutler, C. 1996, ApJ, 460, 827 [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bouabid, M.-P., Dupret, M.-A., Salmon, S., et al. 2013, MNRAS, 429, 2500 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S., & Lebovitz, N. R. 1964, ApJ, 140, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Christophe, S., Ballot, J., Ouazzani, R.-M., Antoci, V., & Salmon, S. J. A. J. 2018, A&A, 618, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cousins, A. W. J., & Warren, P. R. 1963, Mon. Notes Astron. Soc. S. Afr., 22, 65 [NASA ADS] [Google Scholar]
- Cowling, T. G. 1941, MNRAS, 101, 367 [NASA ADS] [Google Scholar]
- Cowling, T. G., & Newing, R. A. 1949, ApJ, 109, 149 [Google Scholar]
- Cox, J. P. 1980, Theory of Stellar Pulsation, Princeton Series in Astrophysics (Princeton: Princeton University Press) [CrossRef] [Google Scholar]
- Dziembowski, W. A., Daszyńska-Daszkiewicz, J., & Pamyatnykh, A. A. 2007, MNRAS, 374, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Eadie, W. T., Drijard, D., James, F. E., Roos, M., & Sadoulet, B. 1971, Statistical Methods in Experimental Physics (Amsterdam: North Holland Publishing Co.) [Google Scholar]
- Eckart, C. 1960, Hydrodynamics of Oceans and Atmospheres (New York: Pergamon Press) [Google Scholar]
- Gill, A. 1982, Atmosphere-ocean Dynamics (New York: Academic Press) [Google Scholar]
- Gough, D. O. 1993, in Astrophysical Fluid Dynamics – Les Houches 1987, eds. J. P. Zahn, & J. Zinn-Justin (Amsterdam: North Holland Publishing Co.), 399 [Google Scholar]
- Gough, D. O., & Sekii, T. 2002, MNRAS, 335, 170 [Google Scholar]
- Goupil, M. J., Mosser, B., Marques, J. P., et al. 2013, A&A, 549, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurtz, D. W., Saio, H., Takata, M., et al. 2014, MNRAS, 444, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, P. 1951, ApJ, 114, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, U., & Saio, H. 1989, MNRAS, 237, 875 [NASA ADS] [Google Scholar]
- Lee, U., & Saio, H. 1997, ApJ, 491, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., & Antoci, V. 2019, MNRAS, 487, 782 [Google Scholar]
- Li, G., Van Reeth, T., Bedding, T. R., et al. 2020, MNRAS, 491, 3586 [NASA ADS] [CrossRef] [Google Scholar]
- Longuet-Higgins, M. S. 1968, Philos. Trans. R. Soc. London A, 262, 511 [Google Scholar]
- Mathis, S. 2009, A&A, 506, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miglio, A., Montalbán, J., Noels, A., & Eggenberger, P. 2008, MNRAS, 386, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Ouazzani, R.-M., Dupret, M.-A., & Reese, D. R. 2012, A&A, 547, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouazzani, R.-M., Roxburgh, I. W., & Dupret, M.-A. 2015, A&A, 579, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., et al. 2017, MNRAS, 465, 2294 [NASA ADS] [CrossRef] [Google Scholar]
- Ouazzani, R. M., Marques, J. P., Goupil, M. J., et al. 2019, A&A, 626, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaloizou, J., & Pringle, J. E. 1978, MNRAS, 182, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Pápics, P. I., Tkachenko, A., Van Reeth, T., et al. 2017, A&A, 598, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saio, H. 2018, ArXiv e-prints [arXiv:1812.01253] [Google Scholar]
- Saio, H. 2019, MNRAS, 487, 2177 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., Bedding, T. R., Kurtz, D. W., et al. 2018a, MNRAS, 477, 2183 [Google Scholar]
- Saio, H., Kurtz, D. W., Murphy, S. J., Antoci, V. L., & Lee, U. 2018b, MNRAS, 474, 2774 [NASA ADS] [CrossRef] [Google Scholar]
- Salmon, S. J. A. J., Montalbán, J., Reese, D. R., Dupret, M.-A., & Eggenberger, P. 2014, A&A, 569, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Ap&SS, 316, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Thomson, W. 1863, Philos. Trans. R. Soc. London, 153, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Thomson, W. 1880, Proc. R. Soc. Edinb., 10, 92 [Google Scholar]
- Townsend, R. H. D. 2003, MNRAS, 340, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015, ApJS, 218, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Reeth, T., Mombarg, J. S. G., Mathis, S., et al. 2018, A&A, 618, A24 [NASA ADS] [EDP Sciences] [Google Scholar]
- Vandakurov, Y. V. 1967, AZh, 44, 786 [NASA ADS] [Google Scholar]
- Waelkens, C. 1991, A&A, 246, 453 [NASA ADS] [Google Scholar]
Appendix A: Linear least-squares fitting with correlated errors
A.1. Simplifying assumptions
Here we describe the method of estimating νrot and P0 with their uncertainties based on Eq. (11) in detail. We paid special attention to the treatment of the error correlation. The following three assumptions are made for the sake of simplicity: (1) the errors {ϵk} of the mode frequencies {νk} follow a Gaussian distribution with the same (but unknown) standard deviation, σ, and those of different modes are not correlated with each other; supposing that the number of the mode frequencies is K + 1, and that ϵ indicates the (K+1)-element vector whose kth element is equal to ϵk, this assumption implies
in which vT, E(a) and Ik generally mean the transpose of v, the expected value of a and the identity matrix of size k, respectively; (2) because the relation  holds for any data sets we use in this paper, the frequency errors affect only the vertical position of the modes (symbols) in the ν–
holds for any data sets we use in this paper, the frequency errors affect only the vertical position of the modes (symbols) in the ν– diagram; (3) since fk, which is defined by Eq. (12), is generally close to 1, the frequency errors have negligible impact on fk.
diagram; (3) since fk, which is defined by Eq. (12), is generally close to 1, the frequency errors have negligible impact on fk.
A.2. Formulation in the vector form
We assume for the moment that the K + 1 mode frequencies have consecutive radial orders and the same azimuthal order m, so that there are K relations in the form of Eq. (11). This assumption is not essential (cf. the second paragraph of Appendix A.3). Neglecting the second- and higher-order terms in {ϵk}, we may rewrite those relations as
in which e represents the error term caused by {ϵk}. The definitions of the symbols in Eq. (A.2) are given as follows: the kth element of the K-element vector y is given by
the K × 2 matrix X is defined by
the 2-element vector θ is provided by
the kth element of the K-element vector e is given by
in which
We note that e can be expressed by
where K × K diagonal matrix H and K × (K+1) matrix Q are defined by
and
respectively.
A.3. Error correlation
The variance-covariance matrix of the error vector e can be calculated from Eqs. (A.1) and (A.8) as
in which C0 = HQQTH. We separate C0 from C because C0 can be calculated from the mode frequencies, whereas σ is unknown. The fact that C is a tridiagonal matrix means that any two successive elements of e are correlated with each other. The inverse of C can be expressed by
in which the (i, j) element of  is given by
is given by
It has so far been assumed that the K relations in the form of Eq. (11) are all included in the analysis. We may have neglected some of them because they produced outliers in the ν– diagram. The possible reasons include avoided crossings, which cannot be described by the traditional approximation of rotation, and contamination of other types of modes than the prograde sectoral g modes. In this case, the expression of C (and its inverse) should be modified accordingly. For example, if we discard the kth element of Eq. (A.2) for 1 < k < K, the remaining relations are separated into two groups, one with the 1, …, (k − 1)th elements and the other with the (k + 1), …, Kth elements. Since ek − 1 is not correlated with ek + 1 (cf. Eq. (A.6)), there is no error correlation between the two groups. The modified expression of
diagram. The possible reasons include avoided crossings, which cannot be described by the traditional approximation of rotation, and contamination of other types of modes than the prograde sectoral g modes. In this case, the expression of C (and its inverse) should be modified accordingly. For example, if we discard the kth element of Eq. (A.2) for 1 < k < K, the remaining relations are separated into two groups, one with the 1, …, (k − 1)th elements and the other with the (k + 1), …, Kth elements. Since ek − 1 is not correlated with ek + 1 (cf. Eq. (A.6)), there is no error correlation between the two groups. The modified expression of  is composed of two diagonal blocks both in the form of Eq. (A.13) with K replaced by the block size, which is equal to k − 1 and K − k for the first and second blocks, respectively. This treatment can easily be generalised as follows: supposing that the relations are separated into J different groups with no error correlation,
is composed of two diagonal blocks both in the form of Eq. (A.13) with K replaced by the block size, which is equal to k − 1 and K − k for the first and second blocks, respectively. This treatment can easily be generalised as follows: supposing that the relations are separated into J different groups with no error correlation,  should be composed of J diagonal blocks in the form of Eq. (A.13). Based on this, it is possible to include the mode frequencies with different azimuthal order m in the analysis because the errors of any two relations with different m in the form of Eq. (11) are not correlated with each other. The different values of m correspond to different diagonal blocks of
should be composed of J diagonal blocks in the form of Eq. (A.13). Based on this, it is possible to include the mode frequencies with different azimuthal order m in the analysis because the errors of any two relations with different m in the form of Eq. (11) are not correlated with each other. The different values of m correspond to different diagonal blocks of  , and each can generally consist of multiple diagonal blocks in the form of Eq. (A.13).
, and each can generally consist of multiple diagonal blocks in the form of Eq. (A.13).
A.4. Linear least-squares fitting
The problem of the linear least-squares fitting in the presence of error correlation is discussed in the literature (e.g. Eadie et al. 1971; Gough & Sekii 2002). The key idea is to multiply Eq. (A.2) by an appropriate K × K regular matrix from the left side so that any two elements of the resultant error vector are not correlated with each other. Once the error correlation disappears, we can adopt the standard procedure of the least-squares fitting. The procedure can be rewritten in terms of the original variables. In fact, we should find such θ that minimises
for given y, X and  . The solution is given by
. The solution is given by
where A is a 2 × 2 matrix defined by
Vector  is the best linear unbiased estimator of θ, whose variance-covariance matrix is provided by
is the best linear unbiased estimator of θ, whose variance-covariance matrix is provided by
On the other hand, the residual sum of squares divided by K − 2 yields the minimum variance unbiased estimator of σ2,
The corresponding estimator of νrot is naturally found to be
Neglecting the second- and higher-order terms in {ϵk}, we can show that  is unbiased. Its variance is accordingly calculated as
is unbiased. Its variance is accordingly calculated as
The uncertainty in  can be estimated based on the fact that
can be estimated based on the fact that
follows Student’s t-distribution with K − 2 degrees of freedom. Here,  stands for the standard error of
stands for the standard error of  defined by
defined by
The q% confidence interval of νrot is provided by
in which t0 is such a value that the probability of |t| ≤ t0 is equal to q/100. Alternatively, t0 can be set (for K > 4) to
which corresponds to one standard deviation.
The way of estimating P0 is analogous. All we need to do is replace the expressions for the estimator, its variance and the standard error with
and
respectively.
Finally, the covariance and the correlation coefficient between  and
and  can be computed as
can be computed as
and
respectively.
Appendix B: Application to SPB stars
In this section, we apply the ν– diagram method to SPB stars. First we validate the method based on a typical evolutionary model, and then apply it to KIC 3459297.
diagram method to SPB stars. First we validate the method based on a typical evolutionary model, and then apply it to KIC 3459297.
B.1. Validation based on a model
As in the case of Model A for γ Dor stars (cf. Sect. 3.1), we use the stellar evolution code CLES (Scuflaire et al. 2008) to construct a 4 M⊙ model of an SPB star. The model parameters are summarised in Table B.1. The details on how this model is calculated are the same as in Model A (cf. Christophe et al. 2018), however we note that turbulent diffusion is included to approximate the effect of rotationally-induced mixing, which smoothes the chemical composition profiles outside the convective core. The eigenfrequencies of the prograde sectoral g modes with m = 1 are computed using the ACOR oscillation code (Ouazzani et al. 2012, 2015) with a uniform rotation frequency of 7 μHz (0.60 d−1). The range of radial orders is between −50 and −18. The results are shown in Fig. B.1.
 |
Fig. B.1. Diagram of ν versus |
Parameters of a typical evolutionary model of an SPB star.
We confirm that also in the case of an SPB star all modes follow a nearly perfect linear trend, which is similar to model (1) shown in Fig. 2. Our estimates for the rotational frequency νrot and the characteristic period P0 are provided in Table B.2. Strictly speaking, these estimates are slightly smaller than the true values by 0.9% and 4% for νrot and P0, respectively, which is similar to the case of Model A listed in Table 1. We find that this is an intrinsic limitation of the method, which relies on the asymptotic formula under the traditional approximation of rotation. Nevertheless, since the two parameters are recovered reasonably well, we consider that the method can be applied to not only γ Dor stars, but SPB stars as well.
Estimates of νrot and P0 for the evolutionary model of an SPB star, the parameters of which are summarised in Table B.1.
B.2. KIC 3459297
We use the frequencies of KIC 3459297 that are listed in Table A.2 of Christophe et al. (2018). While those frequencies distribute in three separate groups (cf. Fig. 8 of Christophe et al. 2018), we ignore the lowest-frequency group below 1.5 μHz because it probably originates from instrumental effects or the artefacts introduced during data analysis. The group between 9 and 14 μHz and that between 23 and 31 μHz are referred to as fg1 and fg2, with 24 and 8 frequencies, respectively. We identify the frequencies in fg1 and fg2 as those of prograde sectoral g modes with m = 1 and m = 2, respectively.
The ν– diagram is shown in Fig. B.2. As in the case of KIC 5608334, which is discussed in Sect. 3.2.2, we discard four frequencies (10.219, 10.354, 11.233 and 24.903 μHz) from the list because there is another frequency very close to each of them with higher amplitude. We also exclude the two red points in Fig. B.2 in the νrot and P0 fitting because they do not follow the same linear trend as the other modes. These peaks might indicate the presence of a buoyancy glitch (cf. Fig. 3) or an avoided crossing (cf. Fig. 4).
diagram is shown in Fig. B.2. As in the case of KIC 5608334, which is discussed in Sect. 3.2.2, we discard four frequencies (10.219, 10.354, 11.233 and 24.903 μHz) from the list because there is another frequency very close to each of them with higher amplitude. We also exclude the two red points in Fig. B.2 in the νrot and P0 fitting because they do not follow the same linear trend as the other modes. These peaks might indicate the presence of a buoyancy glitch (cf. Fig. 3) or an avoided crossing (cf. Fig. 4).
 |
Fig. B.2. Diagram of ν versus |
The estimates for νrot and P0 are given in Table B.3, where the second and third row are obtained by using the peaks in fg1 and fg2, respectively. Our results (fifth and sixth row of Table B.3) clearly reproduce the values published by Pápics et al. (2017) and Christophe et al. (2018). Pápics et al. (2017) identify the frequencies in fg2 as those of prograde sectoral g modes with m = 2, whereas Christophe et al. (2018) do not take those frequencies into account. In Fig. B.2 we show that the blue symbols corresponding to the modes in fg2 follow a similar linear trend as the red circles (m = 1 modes), supporting the mode identification of Pápics et al. (2017). The estimates for νrot are consistent within 2σ among the three independent analyses.
Estimates of νrot and P0 for KIC 3459297.
Appendix C: Case of slow rotation
The method to determine νrot and P0 based on the ν– diagram is inspired by the approximate expression for the eigenvalue of the Laplace tidal equation, λ, which is given by Eq. (8). Because this relation is accurate only when the spin parameter s is much larger than 1, it is important to check whether the same method can be applied even for (0≤)s ≲ 1, which implies the case of slow rotation.
diagram is inspired by the approximate expression for the eigenvalue of the Laplace tidal equation, λ, which is given by Eq. (8). Because this relation is accurate only when the spin parameter s is much larger than 1, it is important to check whether the same method can be applied even for (0≤)s ≲ 1, which implies the case of slow rotation.
For this purpose, we reduce the rotation frequency of model (1) (cf. Sect. 3.1) from 7 μHz to 3 μHz, and calculate the frequencies of prograde sectoral g modes with m = 1 and radial orders between −31 and −17. The corresponding range of the spin parameter is between 0.70 and 0.37.
Figure C.1 shows the ν– diagram for this slowly-rotating model (Model As). Although Eq. (8) is not very accurate for these modes (cf. Fig. 1), we still observe that all modes follow the linear trend in the diagram. We thus cannot find any qualitative difference from the fast-rotating case in Fig. 2.
diagram for this slowly-rotating model (Model As). Although Eq. (8) is not very accurate for these modes (cf. Fig. 1), we still observe that all modes follow the linear trend in the diagram. We thus cannot find any qualitative difference from the fast-rotating case in Fig. 2.
 |
Fig. C.1. Diagram of ν versus |
Table C.1 provides the estimates for νrot and P0, which are larger than the true values by only 3% and 0.5%, respectively. Comparing these results with the case of fast rotation in Table 1, we find the following: (1) larger relative uncertainties for the case of slow rotation by about an order of magnitude for νrot and multiple factors for P0; (2) larger differences between the outputs of the initial and last iterations in spite of the similar number of iterations necessary for the convergence (5 and 6 for model (1) and Model As, respectively). The reason for point (1) is the difference in the number of frequencies that are considered in the analyses. If we extend, to include all the modes between n = −17 and n = −52, the uncertainties of νrot and P0 are reduced to values similar to model (1). Point (2) is simply because the deviation from Eq. (8) is more significant. We may still regard that this approximation remains reasonably good even in the limit of slow rotation. In fact, the limiting value of ![$ \sqrt{\lambda} = \sqrt[4]{m \left(m+1\right)} $](/articles/aa/full_html/2020/03/aa36297-19/aa36297-19-eq134.gif) for the non-rotating case is different from the approximation of
for the non-rotating case is different from the approximation of  by only about 20% for m = 1. Therefore, the factor fk given by Eq. (12) changes during iterations by maximum this amount. This property helps the iterative procedure to be robust. However, in the case of slow rotation it is crucial to use the accurate numerical values of λ, which are shown in Fig. 1, rather than its approximate form of m2 for s ≫ 1. A failure to do so will impact the accuracy of νrot and P0.
by only about 20% for m = 1. Therefore, the factor fk given by Eq. (12) changes during iterations by maximum this amount. This property helps the iterative procedure to be robust. However, in the case of slow rotation it is crucial to use the accurate numerical values of λ, which are shown in Fig. 1, rather than its approximate form of m2 for s ≫ 1. A failure to do so will impact the accuracy of νrot and P0.
Estimates of νrot and P0 for Model As.
The method also works for a slow rotation because the asymptotic formula for the oscillation frequencies under the traditional approximation of rotation (cf. Eq. (5)) can be justified even in the limit of |s| ≪ 1. In fact, it can generally be shown that, for |s| ≪ 1, λ is given by
(Longuet-Higgins 1968), from which we can derive
Equation (C.2) is the standard formula of the rotational splitting for the high-order g modes in the case of very slow rotation (cf. Cowling & Newing 1949; Ledoux 1951). Of course, it is more practical in that case to use the rotational splittings rather than the ν– method to determine νrot, while P0 can be measured directly from the period spacing.
method to determine νrot, while P0 can be measured directly from the period spacing.
In conclusion, we find no serious problem in applying the method of the ν– diagram to the case of slow rotation if prograde sectoral g modes are properly identified.
diagram to the case of slow rotation if prograde sectoral g modes are properly identified.
Appendix D: Physics of the prograde sectoral g modes
D.1. Constituent waves
Prograde sectoral g modes are composed of internal equatorial Kelvin waves when the spin parameter s is much larger than 1 (cf. Townsend 2003). This can be understood from the common physical properties between the Kelvin waves and the prograde sectoral g modes, which are described in meteorology and oceanography literature (e.g. Gill 1982). These waves are trapped in the equatorial region, with their displacement predominantly parallel to the equator. Their horizontal propagation is in the same longitudinal direction as the rotation, while they also propagate in the radial direction because of the buoyancy force. Unlike the other gravito-inertial waves, they are restored only by the buoyancy force, whereas the Coriolis force does not influence the wave propagation except for controlling the range of the equatorial confinement by contributing to the force balance (geostrophic balance) in the latitudinal direction. This explains why the dispersion relation does not depend on the rotation rate. Having understood the preceding properties, we may call the prograde sectoral g modes: “Kelvin g modes”. We note that Kelvin modes are sometimes referred to as f modes, oscillation modes of non-rotating stars that consist of surface gravity waves (e.g. Chandrasekhar & Lebovitz 1964; Cox 1980). There should be no confusion between the two types of Kelvin modes of totally different physical characters. The Kelvin waves in the rotating case originate from Thomson (1880), while Thomson (1863) studies the oscillation modes of a liquid sphere (a homogeneous incompressible spherical body), which correspond to the surface gravity modes.
D.2. Variation in λ
When there is no rotation (with the spin parameter of s = 0), the Laplace tidal equation is reduced to the standard associated Legendre differential equation, so that we obtain the eigenvalue of λm, m = m(m+1) for the prograde sectoral g modes. As demonstrated in the previous studies (e.g. Bildsten et al. 1996; Lee & Saio 1997), λm, m monotonically decreases as s becomes large, and is asymptotically equal to m2 as s → ∞.
We may interpret the transition from λm, m = m(m+1) for s = 0 to λm, m = m2 for s → ∞ as being caused by the change in the geometry. When s = 0, the system is totally spherically symmetric, so that the horizontal propagation of the waves can reach all over the (two-dimensional) sphere. From a mathematical point of view, the eigenvalue, m(m+1), is that of the angular part of the Laplace operator, whereas it is physically determined by the quantisation condition that the constituent waves are in phase before and after travelling around the sphere (e.g. Gough 1993). On the other hand, the propagation region of the waves degenerates towards the equator (one-dimensional sphere) in the limit of s → ∞. In addition, the geostrophic balance forces the latitudinal (θ) component of the displacement to be zero, leaving only the longitudinal (ϕ) component. Therefore, only the longitudinal waves along the equator are allowed. The eigenvalue of λm, m = m2 can again be obtained by the quantisation condition, which requires the same phase of the waves before and after going around the equator. We can formally show that the Laplace tidal equation for p′ (the Eulerian perturbation to the pressure) is reduced to −m2p′= − λp′, which means
at the equator (θ = π/2) under the condition of the geostrophic balance. Equation (D.1) is equivalent to the spatial part of the wave equation at the equator.
D.3. Contribution of the spheroidal and toroidal components
We may discuss the decrease in λ as s increases from a different point of view than the one in Appendix D.2.
We first note that λ can be regarded as a measure of the divergence of the horizontal components of the displacement,
in which ξθ and ξϕ are the θ and ϕ components of the horizontal displacement ξh, respectively. Under the traditional approximation of rotation, the angular dependence of the eigenfunctions is described by the Hough functions, Θ(cos θ), which are the solutions of the Laplace tidal equation. Based on this, the following can be shown:
where Ξh indicates the (common) radial dependence of ξθ and ξϕ. The denominator on the right-hand side of Eq. (D.3) is just a normalisation factor.
Next, we may suppose to express ξh by a sum of two parts, the spheroidal and toroidal components, which are linear combinations of the terms in the form of
and
respectively. Here, Yℓ, m(θ, ϕ) is a spherical harmonic of degree ℓ and azimuthal order m, while er, eθ and eϕ indicate the unit vectors in the r, θ and ϕ directions, respectively. Given that ξh is expanded into the series, we may regard that λ is fixed by an average of the contribution of each term in the both components, specified by Eqs. (D.4) and (D.5). In the absence of rotation, the eigenfunction, ξh, is contributed by only one term of the spheroidal component, which satisfies
We can thus understand λ = ℓ(ℓ+1) in this case. Although the toroidal component also contributes to ξh when s ≠ 0, ∇h ⋅ ξh has no sensitivity to the component (divergence free). From these considerations, we may interpret that the gradual decrease in λ as s increases is caused by the decaying contribution of the spheroidal components to ξh, which implies the growing contribution of the toroidal components.
Appendix E: Differential rotation
In the description of stellar oscillations under the traditional approximation of rotation, it is usually assumed that the rotation rate, νrot, inside the stars is uniform. However, if we assume that the wavelength of the oscillations is much shorter than the scale height of the equilibrium structure, which can be justified for the low-frequency oscillations of γ Dor and SPB stars, we can show that the effect of weak differential rotation on the pulsation frequencies ν is negligibly small (cf. Dziembowski et al. 2007; Mathis 2009; Van Reeth et al. 2018).
Under the assumptions that νrot is a function of only the radius, r, and that the scale height of the variation in νrot is much longer than the wavelength of the oscillations, we can show that the form of the eigenmode condition, given by Eq. (1), remains the same. The only differences are found in that the oscillation frequency in the rotating frame, νco, and the spin parameter, s, in Eq. (2) are not constant, but dependent on r through the r-dependence of νrot. We may thus formulate the (leading-order) change in the eigenfrequency, δν, due to the variation of νrot in the radial direction. Neglecting the frequency dependence of r1 and r2 in Eq. (1), we can derive
Here, δνrot means the deviation of νrot from some constant value, νrot, 0, while ⟨f⟩ generally indicates the average of f defined by
We note that s and the partial derivative of λℓ, m in Eq. (E.1) are evaluated for νrot = νrot, 0. Because the choice of νrot, 0 is arbitrary (so far as δνrot remains small), we can particularly set νrot, 0 = ⟨νrot⟩, for which we find ⟨δνrot⟩ = 0 and hence δν = 0 for any modes from Eq. (E.1). Thus, the oscillation frequency spectrum is not changed for any different rotation profiles if their averages ⟨νrot⟩ are the same. In other words, the mode frequencies are sensitive to only the average ⟨νrot⟩, and insensitive to any variation around it. We can thus interpret the estimate of the (uniform) rotation rate inferred from the oscillation frequencies as ⟨νrot⟩. According to the evolutionary models of γ Dor and SPB stars, the weight function N/r generally gets larger in the deeper layers, takes a maximum just outside the convective core with a sharp peak (due to steep gradients in the distribution of the chemical compositions), and drops to essentially zero in the convective core. Therefore, the average ⟨νrot⟩ is mainly weighted in the layers near but outside the convective core. The rotation frequency of slow rotators that is inferred from high-order g modes is essentially the same average, ⟨νrot⟩ (e.g. Goupil et al. 2013).
All Tables
Estimates of νrot and P0 for the three theoretical models from the synthetic eigenfrequencies of the prograde sectoral g modes with the azimuthal order of m = 1.
Estimates of νrot and P0 for the evolutionary model of an SPB star, the parameters of which are summarised in Table B.1.
All Figures
 |
Fig. 1. Relative differences in the square roots of the eigenvalues of the Laplace tidal equation |
| In the text | |
 |
Fig. 2. ν versus |
| In the text | |
 |
Fig. 3. Same as Fig. 2, but for model (2) (Model B). |
| In the text | |
 |
Fig. 4. Same as Fig. 2, but for model (3). This model includes differential rotation. A detailed explanation of the symbols and the dotted line labelled |
| In the text | |
 |
Fig. 5. Diagram of ν versus |
| In the text | |
 |
Fig. 6. ν versus |
| In the text | |
 |
Fig. 7. ν versus |
| In the text | |
 |
Fig. 8. ν versus |
| In the text | |
 |
Fig. 9. Same as Fig. 8, but for fg2 (m = 2). |
| In the text | |
 |
Fig. 10. Same as Fig. 8, but for fg3 (m = 3). |
| In the text | |
 |
Fig. 11. Same as Fig. 8, but for fg4 (m = 4). |
| In the text | |
 |
Fig. 12. Diagram of ν versus |
| In the text | |
 |
Fig. 13. Diagram of ν versus |
| In the text | |
 |
Fig. B.1. Diagram of ν versus |
| In the text | |
 |
Fig. B.2. Diagram of ν versus |
| In the text | |
 |
Fig. C.1. Diagram of ν versus |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.








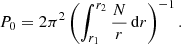

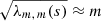





![$$ \begin{aligned} f_k \left(\nu _{\mathrm{rot} }\right) = \left[ \frac{-1}{m \Delta _k \nu } \Delta _k\left( \frac{\sqrt{\lambda _{m,\,m}\left(s\right)}}{\nu _{\mathrm{co} }} \right) \right]^{\frac{1}{2}} \left( \nu _{k + \frac{1}{2}} - m \nu _{\mathrm{rot} } \right). \end{aligned} $$](/articles/aa/full_html/2020/03/aa36297-19/aa36297-19-eq27.gif)
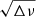



















![$$ \begin{aligned} \left( C_0^{-1} \right)_{i, j} = \frac{i j}{h_i h_j} \left[ \frac{1}{\max \left(i,\,j\right)} - \frac{1}{K+1} \right] \quad (i,\,j = 1,\,2,\,\ldots ,\,K) . \end{aligned} $$](/articles/aa/full_html/2020/03/aa36297-19/aa36297-19-eq98.gif)









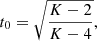










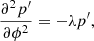





![$$ \begin{aligned} \delta \nu = \frac{2}{s} \left[ 1 + \frac{m s}{2} - \left( 1 + \frac{1}{2}\, \frac{\partial \ln \lambda _{\ell ,\,m}}{\partial \ln s} \right)^{-1} \right] \left\langle \delta \nu _{\mathrm{rot} } \right\rangle . \end{aligned} $$](/articles/aa/full_html/2020/03/aa36297-19/aa36297-19-eq146.gif)
