| Issue |
A&A
Volume 634, February 2020
|
|
|---|---|---|
| Article Number | A3 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201937065 | |
| Published online | 28 January 2020 | |
LOFAR radio search for single and periodic pulses from M 31
1
ASTRON, The Netherlands Institute for Radio Astronomy, Postbus 2, 7990 Dwingeloo, The Netherlands
e-mail: leeuwen@astron.nl
2
Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 Amsterdam, The Netherlands
3
SKA Organisation, Jodrell Bank Observatory, Lower Withington, Macclesfield, Cheshire SK11 9DL, UK
4
Astro Space Center of the Lebedev Physical Institute, Profsoyuznaya Str. 84/32, Moscow 117997, Russia
5
Department of Physics, McGill University, 3600 Rue University, Montréal, QC H3A 2T8, Canada
6
McGill Space Institute, McGill University, 3550 Rue University, Montréal, QC H3A 2A7, Canada
7
Jodrell Bank Center for Astrophysics, School of Physics and Astronomy, University of Manchester, Manchester M13 9PL, UK
Received:
5
November
2019
Accepted:
25
November
2019
Bright short radio bursts are emitted by sources at a wide range of distances: from the nearby Crab pulsar to remote fast radio bursts (FRBs). FRBs are likely to originate from distant neutron stars, but our knowledge of the radio pulsar population has been limited to the Galaxy and the Magellanic Clouds. In an attempt to increase our understanding of extragalactic pulsar populations and their giant-pulse emission, we employed the low-frequency radio telescope LOFAR to search the Andromeda galaxy (M 31) for radio bursts emitted by young Crab-like pulsars. For direct comparison we also present a LOFAR study on the low-frequency giant pulses from the Crab pulsar; their fluence distribution follows a power law with slope 3.04 ± 0.03. A number of candidate signals were detected from M 31, but none proved persistent. FRBs are sometimes thought of as Crab-like pulsars with exceedingly bright giant pulses; based on our sensitivity, we can rule out that M 31 hosts pulsars that are more than an order of magnitude brighter than the Crab pulsar if their pulse scattering follows that of the known FRBs.
Key words: pulsars: general / pulsars: individual: B0531+21 / galaxies: individual: M 31
© ESO 2020
1. Introduction
Millisecond-duration radio signals map out an ever-increasing volume of our Universe. Already based on the first pulsar, Hewish et al. (1968) deducted a distance of ∼65 pc from the interstellar dispersion. The distance scale next stepped through three more prefixes: 60 kpc for Small Magellanic Cloud pulsars (McConnell et al. 1991), 972 Mpc for FRB121102 (luminosity distance; Tendulkar et al. 2017), and ∼17 Gpc for FRB160102 (Bhandari et al. 2018). In this way, pulsars chart out the densities of our Galaxy, and fast radio bursts (FRBs) cover the Universe.
A gap remains around the 1 Mpc mark, however. Targeted pulsar and fast-transient observations of our neighbor galaxy M 31, at 785 ± 25 kpc (McConnachie et al. 2005), may provide these lacking insights. Advantages of an M 31 search are the relative proximity, together with a sight line away from both the Galactic and M 31 plane, suggesting modest dispersion measures (DMs). The star formation rate over the last > 107 yr is only about half that of the Milky Way for M 31 (Yin et al. 2009), which is less favorable.
In addition to measuring electron densities, extragalactic pulsar detections could sample the intergalactic magnetic field, reveal the most luminous part of the extragalactic population, and enable comparisons of pulsar populations between galaxies. These necessarily bright pulsars could also fill in the currently existing luminosity gap, which spans ten orders of magnitude, between known pulsars and FRBs, about which very little is known. For these reasons, nearby galaxies were previously searched for fast transients and pulsars (see Mikhailov & van Leeuwen 2016, and references therein). None of these searches were successful; but for M 31, Rubio-Herrera et al. (2013) carried out a search with the Westerbork Synthesis Radio Telescope (WSRT) at 328 MHz and discovered six bursts at the same DM of 54.7 pc cm−3. To be firmly associated with Andromeda, the source needs a DM that exceeds the sum of the foreground Galactic and intergalactic medium (IGM) DMs. Using an IGM density of nIGM = 0.16 m−3 (Yao et al. 2017) the IGM between the Milky Way and M 31 would contribute only 0.13 pc cm−3, which would not significantly influence the total. The model designed by Yao et al. (2017) to simulate the Galactic electron density predicts that the maximum Milky Way contribution in this line of sight is 61 pc cm−3. The model of Cordes & Lazio (2002) expects 68 pc cm−3. The uncertainties in these models, however, especially at high Galactic latitudes, can exceed a factor of 2 (Deller et al. 2019). Thus the source may be at the outer edge of the Milky Way or at the outer edge of M 31; and following it up was a main motivation for our work here.
We report on an M 31 search, for which we used LOFAR (van Haarlem et al. 2013). LOFAR searches benefit from the high sensitivity and an observing frequency that covers the pulsar flux density peak (Stappers et al. 2011). M 31 is the highest ranked extragalactic-search candidate for LOFAR (van Leeuwen & Stappers 2010). We compare our M 31 single-pulse results with those for a Galactic giant-pulse emitter, the Crab pulsar1. Section 2 covers observations and data analysis and Sect. 3 the search results. In Sect. 4 we compare the required M 31 pulsar flux density distribution to that of the Crab pulsar. We discuss these results and conclude in Sects. 5 and 6.
2. Observations and data analysis
The two observations, carried out in 2011 (for 1 h) and 2014 (for 4 h), used the High Band Antennas (HBAs) of the central LOFAR “superterp”. Its high filling factor allows for coherent surveying at the highest possible speed (Stappers et al. 2011; Coenen et al. 2014). Further background on the observations and analysis is available in Mikhailov 2018 (henceforth M18). The main observing characteristics include the use of a pointing grid of about 100 tied-array beams that covers M 31, M 32, and M 110 (Fig. 1); a central frequency around 150 MHz, and bandwidth of 29 and 78 MHz for the two observations, respectively; plus a ∼1 ms sampling time and 12 kHz spectral resolution. Data were beamformed, cleaned from basic radio frequency interference (RFI), processed into 8-bit Stokes-I filterbank data using the standard LOFAR pulsar pipeline (Alexov et al. 2010), and stored in the LOFAR Long Term Archive (LTA2, Renting & Holties 2011).
 |
Fig. 1. Combination of our 2011 beam pattern with the localization distribution of the DM = 54.7 pc cm−3 candidate from Rubio-Herrera et al. (2013) in blue. The overall outline and beam numbers over the 2011 observation are shown; the 25 absent beams failed initial processing. Because observations were taken around transit, the beams are close to circular. The size of the blue ellipses indicates the S/N of the DM = 54.7 pc cm−3 single-pulse detection in the WSRT subbeam at that location. In the background we show the H I peak brightness map at 60 arcsec and 6 km s−1 resolution, as observed with WSRT (Braun et al. 2009). The 91 tied-array beams pattern from 2014 is overlaid on a 10 h LOFAR imaging observation of M 31, adopted from M18. |
Data were next dedispersed over a range of trial DMs, determined using the PRESTO (Ransom 2001) dedispersion plan optimizer. The Galactic DM contribution toward M 31 has been modeled (Yao et al. 2017) to be ∼60 pc cm−3 on average, with a foreground gradient over our beam pattern of about ∼7 pc cm−3, increasing toward lower Galactic latitude. The relatively face-on inclination limits the dispersion caused in M 31 itself: DMs of about several hundred pc cm−3 are expected (cf. Sect. 5.2).
The 2011 observations were searched from 0−1000 pc cm−3 in 30 000 trials with increasing spacing of 0.01−0.1 pc cm−3. For our observing setup, the intra-channel dispersion smearing for DM = 1000 pc cm−3 is about 30 ms (M18), and for DMs above this, the signal-to-noise ratio (S/N) of narrow bursts decreases further. Following the discovery of high-DM FRBs, the 2014 data were searched up to 2500 pc cm−3 in 45 000 trials. For the limited computing time, we retain sensitivity to very bright high-DM events there, caused by uncertainties in the DM contributions of the IGM and M 31 itself, or from background FRBs unrelated to M 31 (cf. FRB131104; Ravi et al. 2015). While earlier searches for FRBs with LOFAR and the MWA have not been successful (cf. Karastergiou et al. 2015; Sokolowski et al. 2018; ter Veen et al. 2019), FRBs have been detected down to 400 MHz (CHIME/FRB Collaboration 2019), where some are narrow and unscattered even at the bottom of the band. This suggests that a detection at LOFAR frequencies could be possible, and would inform us further on the FRB emission properties.
The 2011 data were initially searched for single-pulse emission on the Hydra cluster in Manchester. Data were transferred there from the LOFAR LTA over a bandwidth-on-demand 1−10 Gbps network. Search output data were partially inspected.
All 2011 and 2014 data were transferred to the Dutch national supercomputer Cartesius3. There, we performed dedispersion and periodicity and single-pulse searches using PRESTO (Ransom 2001) over the course of about 325 000 core-hours of Cartesius computing time4. All periodic candidates that were relatively slow (P > 20 ms) and of high significance (PRESTO-reported reduced χ2 > 2) were inspected by eye. There were ∼25 000. We also inspected all ∼20 000 single-pulse candidates of pulse width W < 100 ms and with an S/N higher than 10σ.
3. Search results
3.1. 2011 observations
The DM = 54.7 pc cm−3 bursts identified in Rubio-Herrera et al. (2013) were recorded in a wide-field WSRT mode called 8gr8 (Janssen et al. 2009). This created eight tied-array beams, each offset within the grating response of the linear WSRT array. This allows for searches over the full field of view of the primary beams of the 25m dish. The method could only localize this intermittent source to several bands on the sky, as shown in blue in Fig. 1, and reports the two most likely regions at (RA, Dec) = (00h 46m 29s, +41°26′) and (00h 44m 46s, +41°41′). In our 2011 setup these two locations fall in beams 21 and 68.
All data were blindly searched on the Dutch supercomputer Cartesius. We used the LOTAAS single-pulse search pipeline (Sanidas et al. 2019), which is based on PRESTO, to remove RFI and identify individual pulses up to widths of 100 ms. We inspected the single-pulse and periodic output both by eye and with the LOTAAS single-pulse (Michilli & Hessels 2018; Michilli et al. 2018) and periodic (Lyon et al. 2016) machine-learning classifiers.
No single pulses were found that appeared in both the initial search of the 50−60 pc cm−3 dispersion-measure range and in the full search. Of the noteworthy periodic candidates seen in the 2011 data (cf. M18), none were redetected in the 2014 observations. Overall, no significant single-pulse or periodic candidates were identified.
3.2. 2014 Observations
A similar blind search through the 2014 data found no convincing pulsar signals from M 31, M 32, or M 110. A close inspection of even low-significance single-pulse detections around DM = 54.7 pc cm−3 was unable to confirm the Rubio-Herrera et al. (2013) candidate.
We derive the LOFAR upper limits following from these non-detections using the radiometer-equation based method described in Sect. 3.2 of Kondratiev et al. (2016) and detailed in M18. Our sky noise estimate includes the continuum contribution from M 31 itself. For the periodicity search (ps), our estimated sensitivity Smin, ps reached in the full four hours for an S/N = 10σ event, assuming a 10% pulse duty cycle, is 1.3 ± 0.7 mJy; where we followed Kondratiev et al. (2016) in estimating the uncertainty of LOFAR flux density measurements at 50%.
We derive the single-pulse search flux density limit using Eq. (3) from Mikhailov & van Leeuwen (2016), based on Cordes & McLaughlin (2003). For a short single pulse of width w = 1 ms, the minimum detectable flux density Smin, sps is 15 ± 8 Jy. Our minimum detectable fluence for a pulse of width w is thus 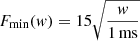 Jy ms.
Jy ms.
4. Comparison of giant pulses from the Crab pulsar to the M 31 search
Based on this sensitivity, could we detect bright giant pulses (GPs) from young neutron stars in the Andromeda galaxy? To determine this, we compare our results against the brightest known specimen, the Crab pulsar. Below we derive its LOFAR fluence distributions. This is relevant for determining the odds of detecting bright super-giant pulses (Cordes 2004; Cordes & Wasserman 2016) in our searches of M 31.
4.1. Crab pulsar at LOFAR frequencies
Earlier multi-frequency studies of Crab GPs spanned the radio spectrum from 20 MHz with the LWA to 15 GHz with the Effelsberg telescope (for an overview, see M18). The 430 MHz Arecibo Crab observations by McLaughlin & Cordes (2003) suggest that one GP/h could be seen out to 1 Mpc. M 31 is closer than this, but is outside the Arecibo declination range.
To determine whether LOFAR could detect Crab-like GPs from M 31, we used it to observe the Crab pulsar5. The setup was similar to Sect. 2, but with 21 core stations in “complex voltage” mode (Stappers et al. 2011) and using coherent dedispersion with CDMT (Bassa et al. 2017a).
We flux calibrated the data following Bilous et al. (2016). The contribution from the nebula to the station-beam noise was included through the Haslam et al. (1982) 408 MHz map. Furthermore, because our tied-array beam covers ∼about one-fourth of the Crab Nebula, we added one-fourth of 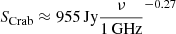 (Bietenholz et al. 1997) to the background noise budget.
(Bietenholz et al. 1997) to the background noise budget.
Using this approach, we determined the peak flux density and fluence of all single pulses in our hour of data. Over a downsampling range of 5−500 ms, we identified 4000 pulses whose pulse-integrated S/Ns exceeded 5σ (a fluence of ∼250 Jy ms). Figure 2 shows an example of the occurrence of multiple pulses within a 1 s window.
 |
Fig. 2. One second of LOFAR data containing multiple Crab giant pulses. Dashed lines indicate the same phase as the onset of the highest pulse. Giant pulses occur at the main and inter-pulse phase. |
The distribution of GP fluence, between our lower limit of 250 Jy ms and the brightest detected pulse of 1.1 × 104 Jy ms, versus rate is shown in Fig. 3. We estimated the slope with the maximum likelihood, following Crawford et al. (1970). For this power-law fit, the index α = 3.04 ± 0.03. We note that this is the fit to the differential energy distribution (as plotted in Fig. 3), not to the cumulative distribution, which is equally often reported in the literature. Thus, α = 3.04 ± 0.03 describes the slope of the probability density function p(F)∝F−α as in Karuppusamy et al. (2012), not for the index we shall here call β, which describes the probability distribution 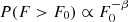 as in Sallmen et al. (1999); the relation between the two is that β = α − 1 = 2.04. This measurement falls within the range of determinations of the power-law index α at other frequencies (see Karuppusamy et al. 2012 and Table 4.2 in M18).
as in Sallmen et al. (1999); the relation between the two is that β = α − 1 = 2.04. This measurement falls within the range of determinations of the power-law index α at other frequencies (see Karuppusamy et al. 2012 and Table 4.2 in M18).
 |
Fig. 3. Crab fluence distribution as measured in the same setup as the LOFAR M 31 search, together with the power-law best fit. The measurement error σ on the fluence values is indicated in the bottom left corner. |
4.2. GPs in M 31
Using this fluence distribution and rate, we determine whether we could have detected 1-ms wide Crab-like GPs from M 31. For a pulsar like this, our minimum detectable fluence Fmin = Sw = 15 Jy ms. The faintest possible detectable GP from M 31 would have to be FCrab, M 31 = Fmin × (DM 31/DCrab)2 ∼ 2.3 × 106 Jy ms if it were as close as the Crab. When we extrapolate the 1 h histogram in Fig. 3, the 4 h observation toward M 31 the fluence FCrab, 4 h of brightest detected pulse would be around 1.1 × 104 × 41/3.04 = 1.7 × 104 Jy ms. This is about 100× dimmer than our limiting minimum sensitivity from M 31.
The scattering medium to M 31 is much less clumped than toward the Crab pulsar, however, and possibly contains no nebula. This means intrinsically short-duration Crab-like GPs (5 μs in Sallmen et al. 1999) from M 31 might invoke little scattering. This is seen over even longer distances in FRBs (cf. Fig. 5 of Cordes et al. 2016). When we assume an average DM for sources in M 31 of 150 pc cm−3 (cf. Sect. 5.2), this FRB relation suggests a scattering time of ∼10−5 ms at 1 GHz. When we scale as ν−3.5, the scattering time at LOFAR frequencies is about 10 μs. For a pulsar like this to have been detected, its 10 μs GP from M 31 would have to exceed that of the Crab by a factor  . Our non-detection thus tells us that there are no pulsars in M 31 beamed at Earth that follow scattering similar to FRBs and emit GPs that are an order of magnitude brighter per unit time than the Crab pulsar.
. Our non-detection thus tells us that there are no pulsars in M 31 beamed at Earth that follow scattering similar to FRBs and emit GPs that are an order of magnitude brighter per unit time than the Crab pulsar.
5. Discussion
5.1. Neutron-star formation in M 31
We did not detect any astrophysical periodic or single pulses from the Andromeda galaxy. We first discuss the implications on whether neutron stars are expected there.
The total star formation rate (SFR) of M 31 has been stable over the last few tens of Myr, at ∼1 M⊙ yr−1 (Williams 2003). This is about twice lower than the SFR in our Milky Way, which is 1.9 ± 0.4 M⊙ yr−1 (Chomiuk & Povich 2011). The SFR is important because it maps linearly to the neutron-star birth rate (cf. Eq. (6) in Keane & Kramer 2008).
The neutron-star low-mass X-ray binaries (e.g., Stiele et al. 2011; Pastor-Marazuela et al. 2019) and X-ray pulsars (Esposito et al. 2016; Rodríguez Castillo et al. 2018) in M 31 are clearly evidence for the presence of neutron stars in the Andromeda galaxy. Further support is provided by its supernova remnants. In our Galaxy, 295 are known (Green 2014). A similar number, 156, are identified in M 31 (Lee & Lee 2014). Overall, the radio pulsar population in M 31 may be somewhat smaller than that in our Milky Way, but other neutron-star detections suggest that active pulsars are present.
5.2. Dispersion measure contributions from M 31
The electron content of M 31 may contribute significantly to the pulse dispersion, which would reduce the detectability especially for sources located on its far side. To investigate the scale of this effect, we modified the electron-density model designed by Yao et al. (2017)6 for our Galaxy to describe M 31. In our own Galaxy, the Earth and the pulsars are both embedded inside the medium. Pulsars in M 31 are observed from outside this galaxy, and we aim to estimate the dispersion smearing to its mid-plane. This integration over the full line of sight means that the exact value of the electron density and disk scale height by themselves do not strongly influence the outcome. From the M 31 mass and major-axis length, we derived the densities and scale heights. We modeled the gaseous disk using an electron density that doubles from the center out to a radius of 12 kpc and then falls off with a hyperbolic secant squared sech2(x) scale length of 8 kpc (Chemin et al. 2009). This is different from the Milky Way, whose thin- and thick-disk electron densities were modeled to be constant out to 4 and 15 kpc, respectively, and then to fall off at 1.2 and 2.5 kpc length scales (Yao et al. 2017).
From our model and the orientation of the Andromeda galaxy in the sky, we determined the dispersion measure over our survey field toward sources in the M 31 mid-plane (Fig. 4). The Galactic foreground of ∼60 pc cm−3 covers the entire field. In about 20% of the field we expect twice this value. In 10% the expected DM > 180 pc cm−3. All modeled dispersion measures fall within the search space. The intra-channel smearing for the highest DM (> 180 pc cm−3) region is 5 ms, of about two samples in the 2011 data and ten samples in the 2014 data. This is sufficiently low to suggest that the deleterious effects of the M 31 dispersion are limited and are not a reason for our non-detections.
 |
Fig. 4. Expected total dispersion measure for sources in the mid-plane of M 31. The Galactic foreground is visible throughout. The 91 tied-array beam pattern from the 2014 observation is shown in outline. |
5.3. Future LOFAR work
The feasibility of detecting Crab-like pulsars from Andromeda depends on the rate and luminosity of their giant pulses (Fig. 3). For the telescope sensitivity of our current setup, we can extrapolate from this rate to the required wait-time for a detectable pulse, which is 13 times stronger than the brightest expected pulse in our 4 h observation (cf. Sect. 4.2). If the high flux-density tail of this GP distribution is described by the same overall power law, the wait would be 4 h × 133.04 = 1 × 105 h for a burst that is bright enough. These results strongly depend on the as yet unknown super-giant pulse population (Cordes 2004).
A campaign that first improves the luminosity limits may be challenging, but considering the steep power law, it may be more realistic than simply waiting longer. A factor of 4 in sensitivity could be attained by coherently adding not the current 6, but all 24 LOFAR core stations. An order of magnitude more tied-array beams would have to be searched, but these could be preferentially positioned on the M 31 disk to maximize discovery potential in a given total observing time. Based on the power-law slope of 3.04, the remaining factor of 3 could be overcome through an observing campaign 33.04 times longer than our current 4 hr, that is, ∼100 h. An attempt like this could invest in more computationally-intensive semi-coherent dedispersion to limit intra-channel smearing (see, e.g., CDMT code and results, Bassa et al. 2017a,b; Maan et al. 2018). Because GPs are intrinsically of ns−μs duration, reducing the dispersive and sampling effects that dilute this signal into the background increases the search sensitivity.
5.4. Other future surveys and follow up
Because of its large angular size (the LOFAR observations were almost 4° across), attempts to more deeply search M 31 for transients are only possible with wide-field and/or high-survey-speed instruments. Apertif, the successor to the system used by Braun et al. (2009) and Rubio-Herrera et al. (2013, cf. Sect. 3.1), can encompass M 31 in a single pointing at 1.4 GHz and has a powerful time-domain search backend (Oosterloo et al. 2009; van Leeuwen 2014; Maan & van Leeuwen 2017).
In single-pulse searches of the type we focused on in this paper, the Square Kilometre Array Mid can detect Crab-like pulsars from over a Mpc (Keane et al. 2015).
Arguably, the telescope most likely to find the first pulsars in M 31 is the Five-hundred-meter Aperture Spherical Telescope (FAST; Smits et al. 2009; Li & Pan 2016). Its sensitivity is high (1250 m2 K−1; Table 1, Dewdney et al. 2013), and M 31 is one the few galaxies of interest within its declination range.
6. Conclusions
We obtained some of the deepest pulsar search observations of M 31, but did not detect any new pulsars. We observed the Crab pulsar with the same LOFAR setup. We detected thousands of giant pulses, and measured a power-law index of the pulse-brightness probability density function of 3.04 ± 0.03. We extrapolated this distribution to the longer observation of and larger distance to M 31. Any pulsar there that outshines the Crab by an order of magnitude, and whose single pulses are scattered the same way as FRBs, would have been detected by us. We conclude that no such super-Crab beamed at Earth exists in the Andromeda galaxy.
The comparison is additionally fitting given the mythological struggle involving Andromeda and the sea monster as told by Ovidius (8).
Project data are public at https://lta.lofar.eu/
Acknowledgments
We thank Marten van Kerkwijk for making available digitize.py, Jason Hessels and Ben Stappers for input at the proposal and observing stage, and Anya Bilous, Cees Bassa, Jean-Mathias Grießmeier and Michael Kramer for comments on the manuscript. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement n. 617199, and from the Netherlands Research School for Astronomy (NOVA4-ARTS). D. M. is a Banting Fellow. This paper is based on data obtained with the International LOFAR Telescope (ILT) under project code LC0_035. LOFAR (van Haarlem et al. 2013) is the Low Frequency Array designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, that are owned by various parties (each with their own funding sources), and that are collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefitted from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Université d’Orléans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, The Netherlands; The Science and Technology Facilities Council, UK; Ministry of Science and Higher Education, Poland. This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative. Computing time was provided by NWO Physical Sciences (project n. 15310).
References
- Alexov, A., Hessels, J., Mol, J. D., Stappers, B., & van Leeuwen, J. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K. I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 193 [NASA ADS] [Google Scholar]
- Bassa, C. G., Pleunis, Z., & Hessels, J. W. T. 2017a, Astron. Comput., 18, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Bassa, C. G., Pleunis, Z., Hessels, J. W. T., et al. 2017b, ApJ, 846, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Bhandari, S., Keane, E. F., Barr, E. D., et al. 2018, MNRAS, 475, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Bietenholz, M. F., Kassim, N., Frail, D. A., et al. 1997, ApJ, 490, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bilous, A. V., Kondratiev, V. I., Kramer, M., et al. 2016, A&A, 591, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braun, R., Thilker, D. A., Walterbos, R. A. M., & Corbelli, E. 2009, ApJ, 695, 937 [Google Scholar]
- Chemin, L., Carignan, C., & Foster, T. 2009, ApJ, 705, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- CHIME/FRB Collaboration (Amiri, M., et al.) 2019, Nature, 566, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Chomiuk, L., & Povich, M. S. 2011, AJ, 142, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Coenen, T., van Leeuwen, J., Hessels, J. W. T., et al. 2014, A&A, 570, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cordes, J. M. 2004, in Milky Way Surveys: The Structure and Evolution of our Galaxy, eds. D. Clemens, R. Shah, & T. Brainerd, ASP Conf. Ser., 317, 211 [NASA ADS] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002, ArXiv e-prints [arXiv:astro-ph/0207156] [Google Scholar]
- Cordes, J. M., & McLaughlin, M. A. 2003, ApJ, 596, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Wasserman, I. 2016, MNRAS, 457, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., Wharton, R. S., Spitler, L. G., Chatterjee, S., & Wasserman, I. 2016, ArXiv e-prints [arXiv:1605.05890] [Google Scholar]
- Crawford, D. F., Jauncey, D. L., & Murdoch, H. S. 1970, ApJ, 162, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., Goss, W. M., Brisken, W. F., et al. 2019, ApJ, 875, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Dewdney, P. E., Turner, W., Millenaar, R., et al. 2013, http://www.skatelescope.org/wp-content/uploads/2013/03/SKA-TEL-SKO-DD-001-1_BaselineDesign1.pdf [Google Scholar]
- Esposito, P., Israel, G. L., Belfiore, A., et al. 2016, MNRAS, 457, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 2014, Bull. Astron. Soc. India, 42, 47 [NASA ADS] [Google Scholar]
- Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
- Hewish, A., Bell, S. J., Pilkington, J. D. H., Scott, P. F., & Collins, R. A. 1968, Nature, 217, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Janssen, G. H., Stappers, B. W., Braun, R., et al. 2009, A&A, 498, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karastergiou, A., Chennamangalam, J., Armour, W., et al. 2015, MNRAS, 452, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Karuppusamy, R., Stappers, B. W., & Lee, K. J. 2012, A&A, 538, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keane, E. F., & Kramer, M. 2008, MNRAS, 391, 2009 [NASA ADS] [CrossRef] [Google Scholar]
- Keane, E., Bhattacharyya, B., Kramer, M., et al. 2015, Advancing Astrophysics with the Square Kilometre Array (AASKA14), 40 [CrossRef] [Google Scholar]
- Kondratiev, V. I., Verbiest, J. P. W., Hessels, J. W. T., et al. 2016, A&A, 585, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, J. H., & Lee, M. G. 2014, ApJ, 786, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Li, D., & Pan, Z. 2016, Radio Sci., 51, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Lyon, R. J., Stappers, B. W., Cooper, S., Brooke, J. M., & Knowles, J. D. 2016, MNRAS, 459, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Maan, Y., Bassa, C., van Leeuwen, J., Krishnakumar, M. A., & Joshi, B. C. 2018, ApJ, 864, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Maan, Y., & van Leeuwen, J. 2017, XXXIInd General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS), Montreal, QC, 2 [Google Scholar]
- McConnachie, A. W., Irwin, M. J., Ferguson, A. M. N., et al. 2005, MNRAS, 356, 979 [NASA ADS] [CrossRef] [Google Scholar]
- McConnell, D., McCulloch, P. M., Hamilton, P. A., et al. 1991, MNRAS, 249, 654 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, M. A., & Cordes, J. M. 2003, ApJ, 596, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Michilli, D., & Hessels, J. W. T. 2018, Astrophysics Source Code Library [record ascl:1806.013] [Google Scholar]
- Michilli, D., Hessels, J. W. T., Lyon, R. J., et al. 2018, MNRAS, 480, 3457 [NASA ADS] [CrossRef] [Google Scholar]
- Mikhailov, K. 2018, PhD Thesis, University of Amsterdam, The Netherlands [Google Scholar]
- Mikhailov, K., & van Leeuwen, J. 2016, A&A, 593, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oosterloo, T., Verheijen, M. A. W., van Cappellen, W., et al. 2009, Wide Field Astronomy & Technology for the Square Kilometre Array, 70 [Google Scholar]
- Ovidius, P. N. 2008, in Metamorphoses, ed. A. Golding (London: W. Seres) [Google Scholar]
- Pastor-Marazuela, I., Webb, N. A., Wojtowicz, D., & van Leeuwen, J. 2019, A&A, submitted [Google Scholar]
- Ransom, S. M. 2001, PhD Thesis, Harvard University, USA [Google Scholar]
- Ravi, V., Shannon, R. M., & Jameson, A. 2015, ApJ, 799, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Renting, G. A., & Holties, H. A. 2011, in Astronomical Data Analysis Software and Systems XX, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 49 [NASA ADS] [Google Scholar]
- Rodríguez Castillo, G. A., Israel, G. L., Esposito, P., et al. 2018, ApJ, 861, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Rubio-Herrera, E., Stappers, B. W., Hessels, J. W. T., & Braun, R. 2013, MNRAS, 428, 2857 [NASA ADS] [CrossRef] [Google Scholar]
- Sallmen, S., Backer, D. C., Hankins, T. H., Moffett, D., & Lundgren, S. 1999, ApJ, 517, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Sanidas, S., Cooper, S., Bassa, C. G., et al. 2019, A&A, 626, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smits, R., Lorimer, D. R., Kramer, M., et al. 2009, A&A, 505, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sokolowski, M., Bhat, N. D. R., Macquart, J. P., et al. 2018, ApJ, 867, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Stappers, B. W., Hessels, J. W. T., Alexov, A., et al. 2011, A&A, 530, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stiele, H., Pietsch, W., Haberl, F., et al. 2011, A&A, 534, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tendulkar, S. P., Bassa, C. G., Cordes, J. M., et al. 2017, ApJ, 834, L7 [NASA ADS] [CrossRef] [Google Scholar]
- ter Veen, S., Enriquez, J. E., Falcke, H., et al. 2019, A&A, 621, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, J. 2014, in The Third Hot-wiring the Transient Universe Workshop, eds. P. R. Wozniak, M. J. Graham, A. A. Mahabal, & R. Seaman, 79 [Google Scholar]
- van Leeuwen, J., & Stappers, B. W. 2010, A&A, 509, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, B. F. 2003, AJ, 126, 1312 [NASA ADS] [CrossRef] [Google Scholar]
- Yao, J. M., Manchester, R. N., & Wang, N. 2017, ApJ, 835, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Yin, J., Hou, J. L., Prantzos, N., et al. 2009, A&A, 505, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1. Combination of our 2011 beam pattern with the localization distribution of the DM = 54.7 pc cm−3 candidate from Rubio-Herrera et al. (2013) in blue. The overall outline and beam numbers over the 2011 observation are shown; the 25 absent beams failed initial processing. Because observations were taken around transit, the beams are close to circular. The size of the blue ellipses indicates the S/N of the DM = 54.7 pc cm−3 single-pulse detection in the WSRT subbeam at that location. In the background we show the H I peak brightness map at 60 arcsec and 6 km s−1 resolution, as observed with WSRT (Braun et al. 2009). The 91 tied-array beams pattern from 2014 is overlaid on a 10 h LOFAR imaging observation of M 31, adopted from M18. |
| In the text | |
 |
Fig. 2. One second of LOFAR data containing multiple Crab giant pulses. Dashed lines indicate the same phase as the onset of the highest pulse. Giant pulses occur at the main and inter-pulse phase. |
| In the text | |
 |
Fig. 3. Crab fluence distribution as measured in the same setup as the LOFAR M 31 search, together with the power-law best fit. The measurement error σ on the fluence values is indicated in the bottom left corner. |
| In the text | |
 |
Fig. 4. Expected total dispersion measure for sources in the mid-plane of M 31. The Galactic foreground is visible throughout. The 91 tied-array beam pattern from the 2014 observation is shown in outline. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


