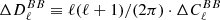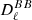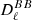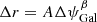| Issue |
A&A
Volume 634, February 2020
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 6 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201833504 | |
| Published online | 17 February 2020 | |
Absolute calibration of the polarisation angle for future CMB B-mode experiments from current and future measurements of the Crab nebula
1
IRAP, Université de Toulouse, CNRS, CNES, UPS, Toulouse, France
e-mail: jonathan.aumont@irap.omp.eu
2
Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble Alpes, CNRS, 53 av. des Martyrs, Grenoble, France
3
Institut de RadioAstronomie Millimétrique (IRAM), Granada, Spain
4
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
Received:
26
May
2018
Accepted:
15
January
2020
A tremendous international effort is currently dedicated to observing the so-called primordial B modes of the cosmic microwave background (CMB) polarisation. If measured, this faint signal, caused by the primordial gravitational wave background, would be evidence of the inflation epoch and quantify its energy scale, providing a rigorous test of fundamental physics far beyond the reach of accelerators. At the unprecedented sensitivity level that the new generation of CMB experiments aims to reach, every uncontrolled instrumental systematic effect will potentially result in an analysis bias that is larger than the much sought-after CMB B-mode signal. The absolute calibration of the polarisation angle is particularly important in this context because any associated error will end up in leakage from the much larger E modes into B modes. The Crab nebula (Tau A), with its bright microwave synchrotron emission, is one of the few objects in the sky that can be used as absolute polarisation calibrators. In this paper we review the currently best constraints on its polarisation angle from 23 to 353 GHz at typical angular scales for CMB observations from WMAP, XPOL, Planck, and NIKA data. These polarisation angle measurements are compatible with a constant angle of −88.26° ±0.27° (assuming that systematic errors are independent between frequencies and that the experiments fully capture the extent of the Crab nebula). We study the uncertainty on this mean angle under different considerations for combinations of the individual measurement errors. For each of the cases, we study the potential effect on the CMB B-mode spectrum and on the recovered r parameter through a likelihood analysis. We find that current constraints on the Crab polarisation angle, assuming it is constant through microwave frequencies, allow us to calibrate experiments with an accuracy enabling the measurement of r ∼ 0.01. On the other hand, even under the most optimistic assumptions, current constraints will lead to an important limitation for the detection of r ∼ 10−3. New realistic measurement of the Crab nebula can change this situation by strengthening the assumption of the consistency across microwave frequencies and reducing the combined error.
Key words: cosmic background radiation / ISM: supernova remnants / polarization
© J. Aumont et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The polarisation of the cosmic microwave background (CMB) anisotropies offers a powerful way to investigate the early Universe. In particular, primordial gravitational waves (tensor perturbations) arising from an early inflationary epoch (Guth 1981; Linde 1982) could be responsible for a specific pattern in the CMB polarisation, the so-called CMB “primordial B modes” (Polnarev 1985; Kamionkowski et al. 1997; Seljak & Zaldarriaga 1997). Therefore, the detection of the primordial CMB B modes would constitute an evidence for inflation and would open a window to new physics. However, they are expected to be much fainter (more than an order of magnitude, hence much more difficult to detect) than the CMB E-mode polarisation anisotropies that are produced by scalar (density) perturbations at recombination (Hu & White 1997; Hu & Dodelson 2002). The CMB polarisation E modes have been accurately measured by the Planck satellite (Planck Collaboration XI 2016), and their spectrum is about a factor of 100 fainter than the power spectrum of the CMB temperature anisotropies (Planck Collaboration XI 2016).
In the past decade the quest for the CMB polarisation B modes has become one of the main aims of observational cosmology, leading to very active instrumental developments and to a large number of CMB experiments (e.g. BICEP2 Collaboration 2014; Polarbear Collaboration 2014; Keisler et al. 2015; Louis et al. 2017). The goal of these experiments is to measure the tensor-to-scalar ratio r, which is given by the relative amplitude of the primordial tensor and scalar perturbations and is directly related to the energy scale of inflation. Recently, BICEP2, Keck Array and Planck Collaborations (2015) and BICEP2 and Keck Array Collaborations (2016) set a 95% upper limit for the detection of the tensor-to-scalar ratio of r < 0.07.
Future CMB experiments aiming at measuring the primordial B modes target r values ranging from 10−2 to 10−4 (e.g. Aumont et al. 2016; Henderson et al. 2016; Rubiño-Martín et al. 2012; Grayson et al. 2016; Arnold et al. 2014; Benson et al. 2014; Essinger-Hileman et al. 2014; Lazear et al. 2014; Bergman et al. 2018; Abazajian et al. 2016; COrE Collaboration 2011; Suzuki et al. 2018). Although great efforts are made to reach a signal this low by constantly improving instrumental sensitivity, residual foreground emission and instrumental systematic effects might limit the final results. The former has been widely discussed in the literature (see Amblard et al. 2007; Betoule et al. 2009; Errard et al. 2016, and references therein).
In terms of instrumental systematic effects, one of the main challenges for future ground-based, balloon-borne, and satellite CMB polarisation experiments is the accurate calibration of the absolute polarisation angle. The most common strategy to accurately take these calibration errors into account in CMB experiments is self-calibration by minimising the 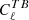 and
and 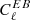 spectra, for which no cosmological signal is expected from standard cosmology parity-invariant physical processes. Nevertheless, non-standard cosmological mechanisms can produce non-vanishing
spectra, for which no cosmological signal is expected from standard cosmology parity-invariant physical processes. Nevertheless, non-standard cosmological mechanisms can produce non-vanishing 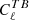 and
and 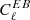 (referred to as cosmic birefringence, due e.g. to cosmological pseudo-scalar field, chiral gravity, primordial magnetic field, see e.g. Gluscevic & Kamionkowski 2010; Planck Collaboration Int. XLIX 2016; Planck Collaboration XIX 2016) that next-generation CMB experiments would like to characterise. Galactic foreground (Planck Collaboration Int. XXX. 2016) and uncontrolled systematics can also produce non-zero TB and EB spectra that need to be taken into account before these quantities are minimised. In this context, it might be interesting to use a sky calibration source for the absolute polarisation angle, in order to preserve the
(referred to as cosmic birefringence, due e.g. to cosmological pseudo-scalar field, chiral gravity, primordial magnetic field, see e.g. Gluscevic & Kamionkowski 2010; Planck Collaboration Int. XLIX 2016; Planck Collaboration XIX 2016) that next-generation CMB experiments would like to characterise. Galactic foreground (Planck Collaboration Int. XXX. 2016) and uncontrolled systematics can also produce non-zero TB and EB spectra that need to be taken into account before these quantities are minimised. In this context, it might be interesting to use a sky calibration source for the absolute polarisation angle, in order to preserve the 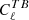 and
and 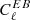 spectra for science and foreground and systematics assessment.
spectra for science and foreground and systematics assessment.
This sky calibration could thus be achieved using observations of well-known polarised sources such as the Crab nebula (Tau A) (see e.g. Keating et al. 2013; Kaufman et al. 2016), which is the brightest polarised astrophysical object in the microwave sky at angular scales of a few arcminutes.
The Crab nebula is a plerion-type supernova remnant emitting a highly polarised synchrotron signal (Weiler & Panagia 1978; Michel et al. 1991) from radio to millimetre wavelengths (Macías-Pérez et al. 2010). A recent study by Ritacco et al. (2018) has demonstrated that the Crab nebula synchrotron emission from radio to millimetre wavelengths is well characterised by a single power law both in temperature and polarisation, which would indicate that a single population of relativistic electrons is responsible for the emission of the nebula. As a consequence, the degree and angle of polarisation of the Crab nebula are expected to be constant across frequencies in this range, making the Crab nebula a potential polarisation standard.
In this paper we study in detail the current constraints on the Crab polarisation angle and discuss how they can be used to perform an absolute calibration of the polarisation angle of CMB experiments. We then derive the expected systematic uncertainties on the measured tensor-to-scalar ratio r. The purpose of our paper is to present the potential performances of an absolute calibration of the polarisation angle that would rely on the existing and future measurements of the Crab nebula polarisation alone, in contrast to what CMB experiments could achieve with TB and EB minimisation.
The paper is organised as follows: in Sect. 2 we review the currently best constraints on the Crab nebula microwave polarisation angle from 23 to 353 GHz. In Sect. 3 we discuss several cases corresponding to different assumptions that can be made on these measurement uncertainties, in order to obtain the combined error on the Crab nebula polarisation angle. We derive in Sect. 4 the spurious CMB B-mode signal coming from E to B mixing if the Crab nebula were to be used as a calibrator for the absolute polarisation angle with these uncertainties. Sect. 5 presents a likelihood analysis in order to express the miscalibration errors in terms of biases on the measurement of the tensor-to-scalar ratio r, and we finally discuss our conclusions in Sect. 6.
2. Crab polarisation angle measurements
Ritacco et al. (2018) provided a compendium of the Crab nebula polarisation angle measurement in Galactic coordinates ψGal from 23 to 353 GHz. It introduces the NIKA measurement at 150 GHz and recomputes the Planck-HFI angles (100, 143, 217 and 353 GHz) in a improved analysis with respect to Planck Collaboration XXVI (2016), based on the Planck 2018 maps (Planck Collaboration III 2020). Ritacco et al. (2018) also included measurements by WMAP (23, 33, 44, 61, and 94 GHz, Weiland et al. 2011), XPOL (90 GHz, Aumont et al. 2010), and Planck-LFI (Planck Collaboration XXVI 2016). In the following, we choose to forego taking the POLKAWiesemeyer et al. (2014) data point presented in Ritacco et al. (2018) into account, which is a clear outlier. Despite the diversity of the instrumental spatial resolutions of the measurements we consider, we assume that the different flux integration techniques that were used when the polarisation angle was computed capture the extent of the Crab nebula and efficiently reject the background emission.
The ψGal values presented in Ritacco et al. (2018) are reported in Table 1, together with their associated statistical and systematic uncertainties. For Planck-HFI, we consider several calibration errors. We refer to the pre-flight errors on the absolute calibration of the polarisation angle (Rosset et al. 2010) as the ground calibration error. These absolute calibration errors were later refined at 100, 143, and 217 GHz in Planck Collaboration Int. XLVI (2016) using self-calibration, that is, 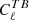 and
and 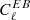 minimisation, for which no cosmological signal is expected in the absence of parity-violating processes (although Galactic signals could produce a non-zero
minimisation, for which no cosmological signal is expected in the absence of parity-violating processes (although Galactic signals could produce a non-zero 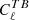 or
or 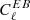 signal, Planck Collaboration Int. XXX. 2016). For each Planck-HFI polarised band, we sum in quadrature the fitted angle and its 1σ error from Appendix A.6 of Planck Collaboration Int. XLVI (2016), and consider this value as the self-calibration error on the absolute calibration of the polarisation angle. We note that the potential presence of cosmic birefringence or foregrounds with significant
signal, Planck Collaboration Int. XXX. 2016). For each Planck-HFI polarised band, we sum in quadrature the fitted angle and its 1σ error from Appendix A.6 of Planck Collaboration Int. XLVI (2016), and consider this value as the self-calibration error on the absolute calibration of the polarisation angle. We note that the potential presence of cosmic birefringence or foregrounds with significant 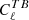 or
or 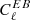 would make this error an overestimate; our approach is conservative in this sense. In the present work, we refer to these errors as TB and EB, respectively. No TB and EB errors were assessed for the 353 GHz channel, so that we always assign this channel measurement with the Planck-HFI ground uncertainty.
would make this error an overestimate; our approach is conservative in this sense. In the present work, we refer to these errors as TB and EB, respectively. No TB and EB errors were assessed for the 353 GHz channel, so that we always assign this channel measurement with the Planck-HFI ground uncertainty.
Compendium of the sub-millimetre Crab nebula polarisation angle measurements in Galactic coordinates for WMAP (Weiland et al. 2011), XPOL (Aumont et al. 2010), Planck-LFI (Planck Collaboration XXVI 2016), and Planck-HFI and NIKA (Ritacco et al. 2018).
The Crab polarisation angle values in Table 1 are compatible with a constant angle from 23 to 353 GHz (Fig. 1), computed as the inverse-noise weighted average considering the cst-PlanckGround systematic uncertainties (see Sect. 3),
 |
Fig. 1. Measurements of the Crab nebula polarisation angles from Table 1 for WMAP (blue diamonds), XPOL (green square), Planck-LFI (purple circles), Planck-HFI (red triangles), and NIKA (yellow crosses). Statistical error bars |
where 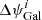 and Δ
and Δ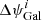 are the individual measurements and their errors are presented in Table 1. The
are the individual measurements and their errors are presented in Table 1. The 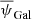 value differs slightly from the one reported in Ritacco et al. (2018) because we excluded the outlying POLKA measurement from the present analysis.
value differs slightly from the one reported in Ritacco et al. (2018) because we excluded the outlying POLKA measurement from the present analysis.
To derive this 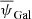 value, we considered that for each individual measurement the total error ΔψGal is the quadratic sum of the statistical error
value, we considered that for each individual measurement the total error ΔψGal is the quadratic sum of the statistical error 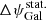 and the systematic error
and the systematic error 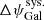 . In the following, we assume that the systematic errors
. In the following, we assume that the systematic errors 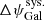 are uncorrelated between our data points. This argument is optimistic because many systematic errors might be correlated (calibration errors, Galactic background, etc...). Taking these correlations into account requires dedicated studies of these correlations, which are not comprehensively available. This therefore goes beyond the scope of the present paper.
are uncorrelated between our data points. This argument is optimistic because many systematic errors might be correlated (calibration errors, Galactic background, etc...). Taking these correlations into account requires dedicated studies of these correlations, which are not comprehensively available. This therefore goes beyond the scope of the present paper.
3. Combined uncertainty on the Crab polarisation angle
In order to use the Crab nebula sub-millimetre polarisation angle 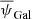 as an absolute angle calibrator for CMB measurements, we are interested in the constraints on its uncertainty ΔψGal, assessed from the measurements presented in Sect. 2. Given the relatively small number of measurements and the variety of instruments, observing conditions, and data processing, there is no unique way to combine them all into a single result with a well-defined uncertainty. We therefore propose and tested several combinations of these measurements to assess the combined uncertainty ΔψGal:
as an absolute angle calibrator for CMB measurements, we are interested in the constraints on its uncertainty ΔψGal, assessed from the measurements presented in Sect. 2. Given the relatively small number of measurements and the variety of instruments, observing conditions, and data processing, there is no unique way to combine them all into a single result with a well-defined uncertainty. We therefore propose and tested several combinations of these measurements to assess the combined uncertainty ΔψGal:
-
max: We do not assume that the Crab polarisation angle ψGal is constant from 23 to 353 GHz and take the combined error ΔψGal as the maximum difference between the inverse-noise weighted mean
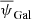 and an individual measurement (the NIKA measurement). The combined error is in this max case ΔψGal = 3.96° (237.7 arcmin).
and an individual measurement (the NIKA measurement). The combined error is in this max case ΔψGal = 3.96° (237.7 arcmin). -
stddev: We take the standard deviation among the individual measurements to be the combined error on the Crab polarisation angle, without assuming this angle to be constant. In this stddev case, the combined error is ΔψGal = 1.24° (74.6 arcmin). We note that this combined error is consistent with what would be expected from the measurements errors and is not dominated by intrinsic inter-frequency variations.
-
cst-PlanckGround: We assume that the Crab polarisation angle ψGal is constant between 23 and 353 GHz. The combined error is thus taken as the error on the inverse-noise weighted mean. In the cst-PlanckGround case, we take the pre-flight assessment of the error on the absolute calibration angle (Rosset et al. 2010) as being the dominant systematic error
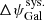 for Planck-HFI. The combined error is in this case ΔψGal = 0.27° (15.9 arcmin).
for Planck-HFI. The combined error is in this case ΔψGal = 0.27° (15.9 arcmin). -
cst-PlanckEB: As for the cst-PlanckGround case, the Crab polarisation angle is assumed constant. The difference with the cst-PlanckGround case is that we use the
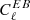 minimisation assessment of the error
minimisation assessment of the error 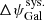 for the 100, 143, and 217 GHz Planck-HFI channels (Planck Collaboration Int. XLVI 2016). For the other experiments and for the Planck-HFI 353 GHz channel, the cst-PlanckGround errors are used. The resulting combined error in that case is ΔψGal = 0.19° (11.5 arcmin).
for the 100, 143, and 217 GHz Planck-HFI channels (Planck Collaboration Int. XLVI 2016). For the other experiments and for the Planck-HFI 353 GHz channel, the cst-PlanckGround errors are used. The resulting combined error in that case is ΔψGal = 0.19° (11.5 arcmin). -
cst-PlanckTB: This is the same as cst-PlanckEB, but with the
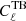 minimisation
minimisation 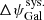 (Planck Collaboration Int. XLVI 2016). The resulting combined error is ΔψGal = 0.16° (9.4 arcmin).
(Planck Collaboration Int. XLVI 2016). The resulting combined error is ΔψGal = 0.16° (9.4 arcmin). -
cst-PlanckTB+future: This is the same as cst-PlanckTB, but adding two future measurements points with a total error
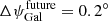 each. The combined error, assuming a constant polarisation angle for the Crab, in this case is ΔψGal = 0.11° (6.3 arcmin).
each. The combined error, assuming a constant polarisation angle for the Crab, in this case is ΔψGal = 0.11° (6.3 arcmin).
We note that in the cst-PlanckEB, cst-PlanckTB and cst-PlanckTB+future cases we used the systematic errors assessed from the 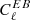 or
or 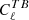 minimisations of the Planck-HFI channels only as descriptors of the systematic errors on the polarisation angle. We used this assessment of the systematic errors on the polarisation angle because they better reflect the in-flight capabilities of Planck-HFI as opposed to the pre-flight measurements in Rosset et al. (2010). We did not use polarisation angle values from the
minimisations of the Planck-HFI channels only as descriptors of the systematic errors on the polarisation angle. We used this assessment of the systematic errors on the polarisation angle because they better reflect the in-flight capabilities of Planck-HFI as opposed to the pre-flight measurements in Rosset et al. (2010). We did not use polarisation angle values from the 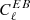 and
and 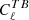 minimisation in this paper. The values of the combined error ΔψGal on the Crab polarisation angle
minimisation in this paper. The values of the combined error ΔψGal on the Crab polarisation angle 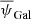 for the different cases presented above are summarised in Table 2.
for the different cases presented above are summarised in Table 2.
4. E − B mixing from absolute polarisation angle miscalibration
A miscalibration of the absolute polarisation angle by ΔψGal will lead to a mixing of E and B modes. In the CMB and because 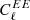 is much larger than
is much larger than 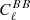 , this is often referred to as an “E to B leakage” and reads (e.g. Rosset et al. 2010)
, this is often referred to as an “E to B leakage” and reads (e.g. Rosset et al. 2010)
where 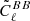 is the effectively measured
is the effectively measured 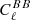 spectrum and Δ
spectrum and Δ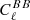 is the corresponding spurious bias component. The E to B leakage is therefore constrained by the error on the absolute angle calibration. Unlike some other systematic effects specific to polarisation, it does not depend on the scan pattern of the observation and therefore cannot be mitigated.
is the corresponding spurious bias component. The E to B leakage is therefore constrained by the error on the absolute angle calibration. Unlike some other systematic effects specific to polarisation, it does not depend on the scan pattern of the observation and therefore cannot be mitigated.
When the Crab nebula is used as a calibrator, the uncertainty on its polarisation angle ΔψGal sets a lower limit on the calibration error, and this affects the magnitude of the corresponding B modes bias. Figure 2 shows the bias Δ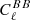 for the different combinations of experimental uncertainties presented in Sect. 2. When we relax the assumption of a constant Crab polarisation angle from 23 to 353 GHz (max and stddev), the spurious B-mode signal from E − B mixing exceeds the primordial signal for r = 10−3 at all angular scales. When we assume the Crab polarisation angle to be constant (cst-PlanckTB+future, cst-PlanckTB, cst-PlanckEB and cst-PlanckGround), the biases range from ∼3 to ∼30% of the primordial tensor signal for ℓ < 10, from ∼20 to more than 100% at ℓ ∼ 100 and exceed the signal in all cases for ℓ > 250.
for the different combinations of experimental uncertainties presented in Sect. 2. When we relax the assumption of a constant Crab polarisation angle from 23 to 353 GHz (max and stddev), the spurious B-mode signal from E − B mixing exceeds the primordial signal for r = 10−3 at all angular scales. When we assume the Crab polarisation angle to be constant (cst-PlanckTB+future, cst-PlanckTB, cst-PlanckEB and cst-PlanckGround), the biases range from ∼3 to ∼30% of the primordial tensor signal for ℓ < 10, from ∼20 to more than 100% at ℓ ∼ 100 and exceed the signal in all cases for ℓ > 250.
5. Likelihood analysis
We quantified the effect of the absolute polarisation angle miscalibration by considering its effect on the recovery of the tensor-to-scalar ratio r from CMB B-mode measurements. This was made in a likelihood analysis on the r parameter from simulated 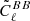 measurements in the presence of a spurious signal Δ
measurements in the presence of a spurious signal Δ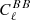 (ΔψGal) from the E − B leakage caused by the miscalibration of the polarisation angle.
(ΔψGal) from the E − B leakage caused by the miscalibration of the polarisation angle.
In each simulation, we considered a 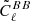 measurement for r = 0 and ΔψGal ≠ 0, reading
measurement for r = 0 and ΔψGal ≠ 0, reading 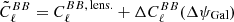 . The lensing-only
. The lensing-only 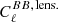 spectrum was computed from the Planck Collaboration XIII (2016)ΛCDM cosmology and the Δ
spectrum was computed from the Planck Collaboration XIII (2016)ΛCDM cosmology and the Δ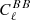 (ΔψGal) E − B mixing component comes from Eq. (2). In each simulation, we randomly drew the ΔψGal miscalibration from a Gaussian distribution having a 1σ dispersion corresponding to the error in each of the cases presented in Sect. 3. The log-likelihood log (ℒ(r)) = χ2(r)/2 then reads
(ΔψGal) E − B mixing component comes from Eq. (2). In each simulation, we randomly drew the ΔψGal miscalibration from a Gaussian distribution having a 1σ dispersion corresponding to the error in each of the cases presented in Sect. 3. The log-likelihood log (ℒ(r)) = χ2(r)/2 then reads
where 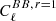 is the Planck Collaboration XIII (2016)ΛCDM cosmology tensor mode spectrum for r = 1, and σtot is the quadratic sum of the cosmic variance and the 1σE − B mixing residual term. The cosmic variance was computed for fsky = 0.5, assuming a 10% residual after delensing.
is the Planck Collaboration XIII (2016)ΛCDM cosmology tensor mode spectrum for r = 1, and σtot is the quadratic sum of the cosmic variance and the 1σE − B mixing residual term. The cosmic variance was computed for fsky = 0.5, assuming a 10% residual after delensing.
The likelihood function was computed on 10 000 Monte Carlo simulations. For each simulation, we built the posterior on r from Eq. (3) and fit the bias Δr with respect to r = 0. The 10 000 biases follow a typical χ2 distribution. We sorted these Δr biases and derived the value Δr(95 % C.L.), which is defined as the r value for which 95 % of the simulations have a smaller Δr. This was made in three regimes of multipole range: for a typical ground-based experiment targeting the recombination bump (ℓmin = 30, ℓmax = 300), a satellite experiment with a large beam that only has access to the reionisation bump (ℓmin = 2, ℓmax = 30), and a satellite experiment with access to both the reionisation and recombination bumps (ℓmin = 2, ℓmax = 300).
Neither foregrounds nor their residuals were modelled in this simple analysis, in order to focus on the effect of the polarisation angle miscalibration. In addition to assuming a perfect component separation, we therefore assumed that the miscalibration E − B mixing residual from foregrounds was also perfectly removed. This is a good approximation at first order because the E − B mixing term does not change the foreground frequency dependence, remaining a second-order effect in the residuals after component separation.
The Δr(95 % C.L.) values are presented in Fig. 3 for the recombination and reionisation bumps. The spurious B-mode polarisation from E − B mixing is more penalised at high-ℓ, resulting in higher r biases for the recombination bump than for the reionisation bump or both bumps together. The two cases considered in Sect. 3, where we did not assume a spectrally constant polarisation for the Crab nebula (max and stddev), lead to biases on the r posterior that are of the order of r = 10−2 or larger. In the cases where we assumed that the Crab polarisation angle is constant (cst-PlanckGround, cst-PlanckEB, cst-PlanckTB, and cst-PlanckTB+future), the biases on r range from r ∼ 10−4 to r ∼ 3 × 10−3. For the detection of r = 10−2, the currently best combined uncertainty on the Crab polarisation angle (cst-PlanckTB case) would lead to a potential 95% C.L. bias of ∼10% at the recombination bump and ∼4% at the reionisation bump. With respect to r = 10−3, the current limits would lead to a 100% bias at the recombination bump and 40% at the lowest ℓ multipoles. Considering new measurements of the Crab polarisation angle, as in the cst-PlanckTB+future case, the bias could be decreased to negligible values for the measurement of r = 10−2 and down to ∼10 and ∼30% of r = 10−3 for the reionisation and recombination bumps, respectively.
 |
Fig. 2. Left panel: |
 |
Fig. 3. Likelihood posterior on r biases (with respect to an input signal of r = 0) for the different cases of combined calibration errors (presented in Sect. 2) from 10 000 Monte Carlo simulations as a function of the combined error on the angle ΔψGal in degrees. They are computed independently for the recombination bump (30 < ℓ < 300, squares), the reionisation bump (2 < ℓ < 30, diamonds), and the combination of both (2 < ℓ < 300, crosses). The best-fit |
Based on Eq. (2), we expect that the bias on r due to E − B mixing from an incorrect calibration of the absolute polarisation angle would scale as 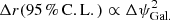 . We fitted the biases on r from our likelihood analysis by power laws of the form Δr(95 % C.L.) = A · (ΔψGal.)β (see Fig. 3). We find for the reionisation bump (A, β)2 < ℓ < 30 = (0.007, 1.90), for the recombination bump, (A, β)30 < ℓ < 300 = (0.020, 1.84), and for the combination of both (A, β)2 < ℓ < 300 = (0.011, 1.96).
. We fitted the biases on r from our likelihood analysis by power laws of the form Δr(95 % C.L.) = A · (ΔψGal.)β (see Fig. 3). We find for the reionisation bump (A, β)2 < ℓ < 30 = (0.007, 1.90), for the recombination bump, (A, β)30 < ℓ < 300 = (0.020, 1.84), and for the combination of both (A, β)2 < ℓ < 300 = (0.011, 1.96).
6. Conclusion and discussion
We here studied a compendium of the best constraints on the Crab nebula polarisation angle to date, from 23 to 353 GHz (Weiland et al. 2011; Aumont et al. 2010; Planck Collaboration XXVI 2016; Ritacco et al. 2018) to derive the combined uncertainty on this angle under different assumptions. We explored the effect that an uncertainty like this has on the measurement of the CMB B-mode primordial signal through the bias it generates on the estimation of the r parameter when the Crab nebula is used as a calibrator for the absolute polarisation angle of an experiment. No other source of r biases was considered in this work.
We find that in order to prevent biases larger than r = 10−2, we must assume that the Crab polarisation angle is constant across microwave frequencies. This is a fair hypothesis because current studies, including Ritacco et al. (2018), are compatible with a single synchrotron component being responsible for the Crab nebula microwave emission. Nevertheless, the current measurement systematic errors and dispersion are large, and future constraints might be needed to strengthen these constraints.
When we assume the Crab polarisation angle as constant from 23 to 353 GHz and consider the ground calibration errors for the Planck-HFI measurements, the combined uncertainty on ψGal leads to potential biases on r of the order of 3 × 10−3 at the recombination bump and ∼10−3 at the reionisation bump. Our estimates address the absolute polarisation angle calibration uncertainty. The consequent biases would thus be applicable to any experiment, regardless of its sensitivity, and they jeopardize the measure primordial CMB B modes around r = 10−3, as currently targeted by ongoing and near-future projects.
The Planck-HFI uncertainty on the Crab polarisation angle measurements can be narrowed by considering the errors coming from the 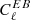 and
and 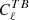 minimisations. In the latter case, the r bias arising from the incorrect calibration of the absolute polarisation angle is ∼4 × 10−4 at the recombination bump and ∼10−4 at the reionisation bump. However, these minimisations make the assumption that the Planck-HFI
minimisations. In the latter case, the r bias arising from the incorrect calibration of the absolute polarisation angle is ∼4 × 10−4 at the recombination bump and ∼10−4 at the reionisation bump. However, these minimisations make the assumption that the Planck-HFI 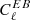 and
and 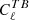 are not contaminated by Galactic components or systematic effects beyond the calibration of the instrumental absolute polarisation angle.
are not contaminated by Galactic components or systematic effects beyond the calibration of the instrumental absolute polarisation angle.
The present study suggests that the error on r caused by the absolute polarisation angle calibration would be mitigated when additional measurements of the Crab polarisation angle were added. We find that when we add two future measurements with total uncertainties of 0.2° to the current observations, the bias on r from miscalibration decreases to ∼4 × 10−4 at the recombination bump and ∼10−4 at the reionisation bump. These values are acceptable for an experiment targeting r = 10−3, especially one with access to large angular scales, such as the LITEBIRD experiment. However, these new measurements will not only be needed to reduce the statistical uncertainty on the Crab nebula polarisation angle. They are also required to definitively assess its stability across the microwave frequency. The XPOL (Thum et al. 2008) and NIKA2 (Calvo et al. 2016) instruments might enable such measurements at 90 and 260 GHz.
We combined measurements of the Crab nebula polarisation angle from experiments that observed with a wide range of angular resolutions. By directly comparing these measurements, we assumed that aperture photometry (or similar techniques) captures the entire emission from the Crab, and that the measurements are not contaminated by other sources of emission. Naturally, an additional complication in using the Crab nebula as an absolute polarisation angle calibrator for any given CMB experiment will come from the uncertainties in the knowledge of the instrumental polarised beams. The effect of an incorrect beam modelling, including side-lobes, requires a case-by-case analysis and goes beyond the scope of this paper. Another source of uncertainties in the combination comes from Faraday rotation effects that are proportional to the square of the observing wavelength. For the Crab nebula the rotation measure has been estimated to be RM = −24.54 ± 0.21 rad m−2 (Weiland et al. 2011; Bietenholz & Kronberg 1991). This corresponds to about 0.24° at 23 GHz. When Faraday rotation in the existing Crab nebula measurements is accounted for, the average polarisation angle is −88.19° ±0.33°. This is just one-sixth of the current uncertainties lower than the value quoted in Eq. (1). In future studies Faraday rotation should be accounted for at low frequencies in more detail to meet the required precision.
The polarisation efficiency is another crucial instrumental parameter that has to be characterised by an experiment aiming at measuring the CMB B modes. The Crab polarised intensity could be used as a calibrator for this parameter. Nevertheless, unlike the polarisation angle, the Crab polarised intensity is not constant across frequencies (Ritacco et al. 2018). Therefore the expected final polarisation efficiency calibration uncertainty is limited by frequency extrapolation of the Crab nebula emission. Moreover, the uncertainty on the annual fading of the Crab synchrotron emission will affect the calibration of the polarisation efficiencies, while it is not expected to influence the determination of the polarisation angle.
Acknowledgments
We thank the Planck Collaboration for allowing us to use the 2018 Planck maps in advance of public release to obtain integrated flux densities in intensity and polarisation in the Crab nebula. We thank Douglas Scott for useful comments on the paper. We thank Ricardo Genova-Santos for very useful comments and references on Faraday rotation effects.
References
- Abazajian, K. N., Adshead, P., Ahmed, Z., et al. 2016, ArXiv e-prints [arXiv:1610.02743] [Google Scholar]
- Amblard, A., Cooray, A., & Kaplinghat, M. 2007, Phys. Rev. D, 75, 083508 [NASA ADS] [CrossRef] [Google Scholar]
- Arnold, K., Stebor, N., Ade, P. A. R., et al. 2014, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII, Proc. SPIE, 9153, 91531F [CrossRef] [Google Scholar]
- Aumont, J., Conversi, L., Thum, C., et al. 2010, A&A, 514, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aumont, J., Banfi, S., Battaglia, P., et al. 2016, ArXiv e-prints [arXiv:1609.04372] [Google Scholar]
- Benson, B. A., Ade, P. A. R., Ahmed, Z., et al. 2014, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII, Proc. SPIE, 9153, 91531P [CrossRef] [Google Scholar]
- Bergman, A. S., Ade, P. A. R., Akers, S., et al. 2018, J. Low Temp. Phys., 193, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Betoule, M., Pierpaoli, E., Delabrouille, J., Le Jeune, M., & Cardoso, J.-F. 2009, A&A, 503, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- BICEP2 Collaboration 2014, Phys. Rev. Lett., 112, 241101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- BICEP2 and Keck Array Collaborations 2016, Phys. Rev. Lett., 116, 031302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- BICEP2, Keck Array and Planck Collaborations 2015, Phys. Rev. Lett., 114, 101301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bietenholz, M. F., & Kronberg, P. P. 1991, ApJ, 368, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Calvo, M., Benoît, A., Catalano, A., et al. 2016, J. Low Temp. Phys., 184, 816 [NASA ADS] [CrossRef] [Google Scholar]
- COrE Collaboration 2011, ArXiv e-prints [ArXiv:1102.2181] [Google Scholar]
- Errard, J., Feeney, S. M., Peiris, H. V., & Jaffe, A. H. 2016, J. Cosmology Astropart. Phys., 3, 052 [Google Scholar]
- Essinger-Hileman, T., Ali, A., Amiri, M., et al. 2014, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII, Proc. SPIE, 9153, 91531I [CrossRef] [Google Scholar]
- Gluscevic, V., & Kamionkowski, M. 2010, Phys. Rev. D, 81, 123529 [NASA ADS] [CrossRef] [Google Scholar]
- Grayson, J. A., Ade, P. A. R., Ahmed, Z., et al. 2016, Proc. SPIE, 9914, 17 [Google Scholar]
- Guth, A. H. 1981, Phys. Rev. D, 23, 347 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Henderson, S. W., Allison, R., Austermann, J., et al. 2016, J. Low Temp. Phys., 184, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Dodelson, S. 2002, ARA&A, 40, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & White, M. 1997, New A Rev., 2, 323 [Google Scholar]
- Kamionkowski, M., Kosowsky, A., & Stebbins, A. 1997, Phys. Rev. Lett., 78, 2058 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufman, J., Leon, D., & Keating, B. 2016, Int. J. Modern Phys. D, 25, 1640008 [NASA ADS] [CrossRef] [Google Scholar]
- Keating, B. G., Shimon, M., & Yadav, A. P. S. 2013, ApJ, 762, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Keisler, R., Hoover, S., Harrington, N., et al. 2015, ApJ, 807 [Google Scholar]
- Lazear, J., Ade, P. A. R., Benford, D., et al. 2014, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII, Proc. SPIE, 9153, 91531L [NASA ADS] [CrossRef] [Google Scholar]
- Linde, A. D. 1982, Phys. Lett. B, 108, 389 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Louis, T., Grace, E., Hasselfield, M., et al. 2017, J. Cosmol. Astropart. Phys., 2017 [Google Scholar]
- Macías-Pérez, J. F., Mayet, F., Aumont, J., & Désert, F.-X. 2010, ApJ, 711, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, F. C., Scowen, P. A., Dufour, R. J., & Hester, J. J. 1991, ApJ, 368, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XI. 2016, A&A, 594, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIX. 2016, A&A, 594, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVI. 2016, A&A, 594, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration III. 2020, A&A, in press, https://doi.org/10.1051/0004-6361/201832909 [Google Scholar]
- Planck Collaboration Int. XXX. 2016, A&A, 586, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVI. 2016, A&A, 596, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLIX. 2016, A&A, 596, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polarbear Collaboration 2014, ApJ, 794 [Google Scholar]
- Polnarev, A. 1985, Sov. Astron., 29, 607 [NASA ADS] [Google Scholar]
- Ritacco, A., Macías-Pérez, J. F., Ponthieu, N., et al. 2018, A&A, 616, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosset, C., Tristram, M., Ponthieu, N., et al. 2010, A&A, 520, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubiño-Martín, J. A., Rebolo, R., Aguiar, M., et al. 2012, in Ground-based and Airborne Telescopes IV, Proc. SPIE, 8444, 84442Y [CrossRef] [Google Scholar]
- Seljak, U., & Zaldarriaga, M. 1997, Phys. Rev. Lett., 78, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, A., Ade, P. A. R., Akiba, Y., et al. 2018, J. Low Temp. Phys., 193, 1048 [NASA ADS] [CrossRef] [Google Scholar]
- Thum, C., Wiesemeyer, H., Paubert, G., Navarro, S., & Morris, D. 2008, PASP, 120, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Weiland, J. L., Odegard, N., Hill, R. S., et al. 2011, ApJS, 192 [CrossRef] [Google Scholar]
- Weiler, K. W., & Panagia, N. 1978, A&A, 70, 419 [NASA ADS] [Google Scholar]
- Wiesemeyer, H., Hezareh, T., Kreysa, E., et al. 2014, PASP, 126, 1027 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Compendium of the sub-millimetre Crab nebula polarisation angle measurements in Galactic coordinates for WMAP (Weiland et al. 2011), XPOL (Aumont et al. 2010), Planck-LFI (Planck Collaboration XXVI 2016), and Planck-HFI and NIKA (Ritacco et al. 2018).
All Figures
 |
Fig. 1. Measurements of the Crab nebula polarisation angles from Table 1 for WMAP (blue diamonds), XPOL (green square), Planck-LFI (purple circles), Planck-HFI (red triangles), and NIKA (yellow crosses). Statistical error bars |
| In the text | |
 |
Fig. 2. Left panel: |
| In the text | |
 |
Fig. 3. Likelihood posterior on r biases (with respect to an input signal of r = 0) for the different cases of combined calibration errors (presented in Sect. 2) from 10 000 Monte Carlo simulations as a function of the combined error on the angle ΔψGal in degrees. They are computed independently for the recombination bump (30 < ℓ < 300, squares), the reionisation bump (2 < ℓ < 30, diamonds), and the combination of both (2 < ℓ < 300, crosses). The best-fit |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



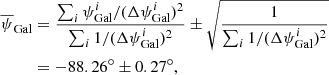
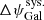
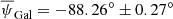
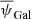
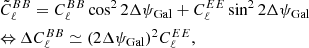
![$$ \begin{aligned} 2\log \left(\mathcal{L} (r)\right)&=\chi ^2(r)\nonumber \\&=\sum _{\ell \in [\ell _{\rm min},\ell _{\rm max}]}\frac{\left(\tilde{C}_\ell ^{BB}-r\cdot C_\ell ^{BB,\,r=1}-C_\ell ^{BB,\,\mathrm{lens.}}\right)^2}{\sigma _{\rm tot.}^2}\nonumber \\&=\sum _{\ell \in [\ell _{\rm min},\ell _{\rm max}]}\frac{\left(\Delta C_\ell ^{BB}(\Delta \psi _{\rm Gal})-r\cdot C_\ell ^{BB,\,r=1}\right)^2}{\sigma _{\rm tot.}^2}, \end{aligned} $$](/articles/aa/full_html/2020/02/aa33504-18/aa33504-18-eq55.gif)