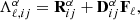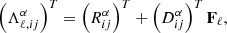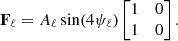| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 10 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202346829 | |
| Published online | 29 November 2023 | |
COSMOGLOBE DR1 results
II. Constraints on isotropic cosmic birefringence from reprocessed WMAP and Planck LFI data
1
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029 Blindern, 0315 Oslo, Norway
e-mail: j.r.eskilt@astro.uio.no
2
Imperial Centre for Inference and Cosmology, Department of Physics, Imperial College London, Blackett Laboratory, Prince Consort Road, London SW7 2AZ, UK
3
Dipartimento di Fisica, Università degli Studi di Milano, Via Celoria, 16, Milano, Italy
4
Instituto de Física, Universidade de São Paulo, C.P. 66318, CEP: 05315-970, São Paulo, Brazil
5
Department of Astrophysical Sciences, Princeton University, 4 Ivy Lane, Princeton, NJ 08540, USA
6
Department of Physics and Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, BC V6T1Z1, Canada
7
David A. Dunlap Department of Astronomy & Astrophysics, University of Toronto, 50 St. George Street, Toronto, ON M5S 3H4, Canada
8
Dunlap Institute for Astronomy & Astrophysics, University of Toronto, 50 St. George Street, Toronto, ON M5S 3H4, Canada
9
Waterloo Centre for Astrophysics, University of Waterloo, Waterloo, ON N2L 3G1, Canada
10
Department of Physics, Indian Institute of Technology (BHU), Varanasi 221005, India
11
Indian Institute of Astrophysics, Koramangala II Block, Bangalore 560034, India
12
Laboratoire Astroparticule et Cosmologie (APC), Université Paris, CNRS, 10 rue Alice Domon et Léonie Duquet, 75013 Paris, France
13
Department of Physics, University of California, Berkeley, Berkeley, CA 94720, USA
Received:
7
May
2023
Accepted:
27
June
2023
Cosmic birefringence is a parity-violating effect that might have rotated the plane of the linearly polarized light of the cosmic microwave background (CMB) by an angle β since its emission. This angle has recently been measured to be nonzero at a statistical significance of 3.6σ in the official Planck PR4 and 9-year WMAP data. In this work, we constrain β using the reprocessed BEYONDPLANCK LFI and COSMOGLOBE DR1 WMAP polarization maps. These novel maps have both lower systematic residuals and a more complete error description than the corresponding official products. Foreground EB correlations could bias measurements of β, and while thermal dust EB emission has been argued to be statistically nonzero, no evidence for synchrotron EB power has been reported. Unlike the dust-dominated Planck HFI maps, the majority of the LFI and WMAP polarization maps are instead dominated by synchrotron emission. Simultaneously constraining β and the polarization miscalibration angle, α, of each channel, we find a best-fit value of β = 0.35° ±0.70° with LFI and WMAP data only. When including the Planck HFI PR4 maps, but fitting β separately for dust-dominated, β> 70 GHz, and synchrotron-dominated channels, β≤70 GHz, we find β≤70 GHz = 0.53° ±0.28°. This differs from zero with a statistical significance of 1.9σ, and the main contribution to this value comes from the LFI 70 GHz channel. While the statistical significances of these results are low on their own, the measurement derived from the LFI and WMAP synchrotron-dominated maps agrees with the previously reported HFI-dominated constraints, despite the very different astrophysical and instrumental systematics involved in all these experiments.
Key words: cosmic background radiation / cosmology: observations
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The standard model of cosmology, Λ cold dark matter (CDM), predicts no parity-violating physics on cosmological scales. There are, however, extensions of the standard model that allow it, one example being an ultra-light axion-like field, ϕ, that couples to the electromagnetic field tensor, Fμν,
where ℒ is the Lagrangian density, gγϕ is a coupling constant, and 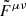 is the Hodge dual of Fμν (see, for instance, a recent review by Komatsu 2022). This term effectively causes the plane of the linear polarization of electromagnetic waves to rotate as they propagate through empty space (Carroll et al. 1990; Carroll & Field 1991; Harari & Sikivie 1992). The predicted rotation angle, β, as a function of the direction of the line of sight,
is the Hodge dual of Fμν (see, for instance, a recent review by Komatsu 2022). This term effectively causes the plane of the linear polarization of electromagnetic waves to rotate as they propagate through empty space (Carroll et al. 1990; Carroll & Field 1991; Harari & Sikivie 1992). The predicted rotation angle, β, as a function of the direction of the line of sight, 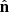 , is
, is
where ηo and ηe are the conformal times at observation and emission of the photons, respectively, and r ≡ ηo − ηe is the conformal distance from the observer to the emitter.
The cosmic microwave background (CMB) is the oldest polarized light in the Universe and therefore among our most sensitive probes of a light axion-like field. Raw CMB polarization measurements are typically provided in terms of the Stokes parameters, Q and U, that measure two orthogonal modes of linear polarization in a given coordinate system. When using such measurements to constrain cosmic birefringence, it is convenient to transform them into coordinate-independent E and B modes following Kamionkowski et al. (1997) and Seljak & Zaldarriaga (1997). In this representation, cosmic birefringence rotates the intrinsic E and B modes emitted at the last scattering surface into the Eo and Bo modes we observe today (Lue et al. 1999). Assuming that the cosmic birefringence angle is isotropic and adopting the convention that a positive β defines a clockwise rotation of the plane of linear polarization on the sky, these rotations are given as
Defining the angular power spectrum as 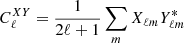 , one can show that (Feng et al. 2005)
, one can show that (Feng et al. 2005)
The last term is the intrinsic EB power spectrum of the CMB, which is predicted to be zero in ΛCDM, and we accordingly neglect it in this work.
No instrument is perfect. All polarization-sensitive CMB detectors have an intrinsic miscalibration angle, α, which represents the difference between the true polarization angle of the detector and that assumed in the analysis. This angle induces a spurious rotation of the plane of the polarized electromagnetic waves and is therefore, for a single frequency channel, fully degenerate with β. To account for this instrumental systematic in an estimate of cosmic birefringence, one needs to replace the β in Eq. (4) with α + β. The calibration uncertainty in α will then induce a corresponding systematic uncertainty in β.
A novel method for breaking the α + β degeneracy was introduced by Minami et al. (2019) and Minami & Komatsu (2020a), who proposed exploiting the differing multipole behavior between CMB and polarized foreground emission to self-calibrate the miscalibration angles. In this approach, an important assumption is that cosmic birefringence would have a negligible impact on the photons originating from our Galaxy, while substantially impacting only the CMB photons that have traveled much farther. Minami & Komatsu (2020b) applied this method to the Planck Public Release 3 (PR3) polarization data and find a best-fit value of β = 0.35° ±0.14°, which nominally disfavors β = 0° at a statistical significance of 2.4σ.
This analysis on the High Frequency Instrument (HFI) channels was further improved by Diego-Palazuelos et al. (2022), who applied the same method to the Planck Public Release 4 (PR4) data, often called “NPIPE” (Planck Collaboration Int. LVII 2020). This data set has a higher signal-to-noise ratio than PR3 due to the inclusion of more data, and it has lower systematic uncertainties. The updated analysis yielded a birefringence angle constraint of β = 0.30° ±0.11°, corresponding to a 21% smaller uncertainty than the original analysis.
Neither of these measurements explicitly accounted for the intrinsic EB correlation in polarized thermal dust emission, as it has not been directly measured. Planck did, however, detect parity-odd dust TB correlations (Planck Collaboration XI 2020). The origin of the measured TB correlations has been hypothesized to be due to a misalignment between local magnetic fields and dust filaments (Huffenberger et al. 2020; Clark et al. 2021), which would also give rise to an intrinsic EB power spectrum of dust emission.
Using an ansatz inspired by the filamentary model of Clark et al. (2021), Diego-Palazuelos et al. (2022) find that the statistical significance of the cosmic birefringence increases to 3.3σ with β = 0.36° ±0.11°. However, they also note that this model slightly affects the value of β as a function of sky fraction.
In a follow-up paper, one of the authors of our work included the rest of the Planck polarization data by incorporating the Planck Low Frequency Instrument (LFI) bands of Planck PR4 (Eskilt 2022). These frequencies are dominated by synchrotron emission, for which no evidence of an intrinsic EB correlation has been presented to date (Martire et al. 2022; Rubino-Martin et al. 2023). A positive measurement of β using synchrotron-dominated maps alone could suggest that  is not the cause of the recent nonzero measurements of isotropic cosmic birefringence. Indeed, even without including the filamentary dust EB model for the HFI channels and assuming
is not the cause of the recent nonzero measurements of isotropic cosmic birefringence. Indeed, even without including the filamentary dust EB model for the HFI channels and assuming  , the inclusion of the LFI maps alone increased the statistical significance of a nonzero cosmic birefringence angle to 3.3σ at β = 0.33° ±0.10°.
, the inclusion of the LFI maps alone increased the statistical significance of a nonzero cosmic birefringence angle to 3.3σ at β = 0.33° ±0.10°.
The strongest constraint on synchrotron EB comes from Planck and WMAP (Martire et al. 2022), where the authors modeled 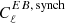 as a constant and
as a constant and 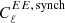 as a power law in multipole space in the range 30 ≲ ℓ ≲ 300. They report that
as a power law in multipole space in the range 30 ≲ ℓ ≲ 300. They report that 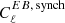 is consistent with zero at a range of sky fractions, and they find the ratio
is consistent with zero at a range of sky fractions, and they find the ratio 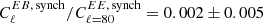 at fsky = 0.94. But as
at fsky = 0.94. But as 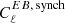 was modeled as being constant in multipole space, one should be careful to extrapolate this bound to higher multipoles, and hence, an upper bound on the foreground bias on β is hard to quantify and could be large.
was modeled as being constant in multipole space, one should be careful to extrapolate this bound to higher multipoles, and hence, an upper bound on the foreground bias on β is hard to quantify and could be large.
Eskilt (2022) also analyzed the frequency behavior of the birefringence signature and find that it is consistent with being frequency-independent, which is precisely the prediction of an ultra-light axion that couples to electromagnetism. At the same time, an explanation based on the Faraday rotation of magnetic fields is disfavored because of its strong frequency dependence, β ∝ 1/ν2, where ν is frequency. Recently, Eskilt et al. (2023) have shown that the signal is not consistent with early dark energy coupling to photons.
An analysis of possible systematic effects that could bias measurements of β in the HFI channels was performed by Diego-Palazuelos et al. (2023). The authors show that the positive measurement of β is robust against beam leakage, intensity-to-polarization leakage, and cross-polarization effects. However, they warn that foreground EB could potentially bias a birefringence measurement, as also reported by Diego-Palazuelos et al. (2022).
Finally, Eskilt & Komatsu (2022) also included the 9-year WMAP measurements between 23 and 94 GHz in the cosmic birefringence analysis. Even though the WMAP observations have a low signal-to-noise ratio with respect to β by themselves, cross-correlating these channels with LFI and HFI channels provides slightly smaller error bars on β. Specifically, the baseline result yielded 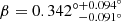 using nearly full-sky data, which is a 3.6σ measurement of a nonzero birefringence angle. They also find a consistent result, β = 0.37° ±0.14°, with a much larger mask, for which thermal dust EB correlations have been argued to be mostly positive (Clark et al. 2021; Diego-Palazuelos et al. 2022).
using nearly full-sky data, which is a 3.6σ measurement of a nonzero birefringence angle. They also find a consistent result, β = 0.37° ±0.14°, with a much larger mask, for which thermal dust EB correlations have been argued to be mostly positive (Clark et al. 2021; Diego-Palazuelos et al. 2022).
As of today, there are no other useful public CMB satellite polarization data available to include in this particular analysis framework, and even the amount of ground-based or suborbital data is limited. The reason for this is that the estimator developed by Minami et al. (2019) and Minami & Komatsu (2020a) requires a sufficient amount of polarized foreground emission to break the degeneracy between α and β, but ground-based telescopes tend to point their instruments away from foreground-dominated parts of the sky to maximize their CMB sensitivity. In addition, none of the public ground-based telescope data can guarantee a miscalibration angle that is small compared to β ∼ 0.3°. Therefore, we expect little to be gained from including these data sets as they are now (see, however, Cornelison et al. 2022 for accounts of recent attempts at calibrating the BICEP3 instrument to achieve a precision of < 0.1°).
While the amount of new data is currently limited, systematic uncertainties from both astrophysical foregrounds and instrumentation remain an important issue regarding these cosmic birefringence measurements. In that respect, we note that there has been a major effort in the community to build a single coherent end-to-end CMB Bayesian analysis framework that simultaneously accounts for instrumental, astrophysical, and cosmological parameters. This work originally started within the Planck Collaboration (Planck Collaboration X 2016) as an effort to establish a coherent model of the astrophysical sky through Bayesian analysis. This method was later generalized to also account for instrumental effects by the BEYONDPLANCK Collaboration (BeyondPlanck Collaboration 2023, and references therein), who also used this novel framework to derive Planck LFI sky maps with lower systematic residuals than the official products (Basyrov et al. 2023).
COSMOGLOBE1 is a global open science initiative that aims to simultaneously apply this framework to all available state-of-the-art data sets and build one coherent model of the radio, microwave, and submillimeter sky based on all these observations. The first major COSMOGLOBE data release (called DR1) is described in a suite of four papers and includes the first joint end-to-end processing of the WMAP and Planck LFI data sets. The main results, as defined by frequency maps and preliminary astrophysical and cosmological results, are summarized by Watts et al. (2023a); perhaps the most striking outcome from this work is a set of WMAP polarization maps with significantly lower large-scale instrumental systematics than the official products.
Our paper focuses on birefringence measurements from the reprocessed COSMOGLOBE WMAP and BEYONDPLANCK LFI maps. Not only are these maps cleaner in terms of instrumental effects than previous products, but most of their particular frequencies are also dominated by polarized synchrotron emission. A constraint on cosmic birefringence derived from WMAP and LFI alone is therefore intrinsically interesting because it will be associated with very different astrophysical uncertainties than the previous results from HFI and thermal dust-dominated maps. A third advantage of the new products is that they are associated with a large ensemble of posterior-based samples, each corresponding to a different realization of instrumental systematic uncertainties. This novel product allows for a much more complete uncertainty estimation than previous traditional pipelines. In particular, the WMAP maps produced by Watts et al. (2023a) significantly improve the statistical treatment of poorly constrained transmission imbalance modes, and they allow for a direct unbiased estimate of the polarized sky without explicit post-processing.
The rest of the paper is organized as follows. Section 2 describes the BEYONDPLANCK and COSMOGLOBE data sets, and Sect. 3 gives a brief review of the cosmic birefringence methodology. We present our main results in Sect. 4, and we draw conclusions in Sect. 5.
2. BEYONDPLANCK and COSMOGLOBE data
In this paper, we focus primarily on the reprocessed COSMOGLOBE DR1 WMAP (Watts et al. 2023a), BEYONDPLANCK LFI (BeyondPlanck Collaboration 2023), and Planck PR4 HFI (Planck Collaboration Int. LVII 2020) polarization sky maps, although we also analyze some combinations of the legacy 9-yr WMAP (Bennett et al. 2013) and Planck PR4 LFI (Planck Collaboration Int. LVII 2020) data. The BEYONDPLANCK and COSMOGLOBE products are derived using the end-to-end Gibbs sampler implemented in the Commander32 code base (Galloway et al. 2023). This method draws samples for each band’s calibration and noise parameters while conditioning on a sky model. Then the sky model is sampled while conditioning on the same calibration and noise parameters. This iterative process maps out the joint posterior distribution, accounting for correlations between instrumental and sky parameters in a statistically coherent framework (see, e.g., Geman & Geman 1984; Brilenkov et al. 2023, for further discussion of the Gibbs sampling methodology and philosophy).
As discussed by Basyrov et al. (2023), the reprocessed LFI maps resulting from this procedure provide better control of gain uncertainty than the PR3 and PR4 analyses. For these reasons, we consider the BEYONDPLANCK Commander3 approach to yield the most accurate and best characterized Planck LFI maps to date. In particular, the 44 GHz map, which was plagued by null test failures even after the PR4 analysis, is now of sufficient quality to be used for cosmological analyses. For example, Colombo et al. (2023) and Paradiso et al. (2023) used these maps to make robust measurements of the large-scale polarized CMB and reionization optical depth τ.
The BEYONDPLANCK project was a pathfinder that focused specifically on Planck LFI. Now COSMOGLOBE aims to apply this unified framework to jointly analyze as many state-of-the-art data sets as possible. The first major application to a new data set is WMAP, as first described by Watts et al. (2023b). The WMAP experiment (Bennett et al. 2013) observed the microwave sky with ten polarization-sensitive differencing assemblies at multiple frequencies, including K-band (23 GHz), Ka-band (33 GHz), Q-band (41 GHz), V-band (61 GHz), and W-band (94 GHz). As presented in a companion paper by Watts et al. (2023a), a joint analysis of WMAP and Planck LFI time-ordered data within the COSMOGLOBE framework has now yielded maps that are essentially free of poorly measured transmission imbalance modes, resulting in the best consistency between Planck LFI and WMAP to date.
COSMOGLOBE DR1 provides updated maps for both WMAP and LFI, and in principle, we could therefore have used also the COSMOGLOBE DR1 LFI maps in the current birefringence analysis. However, as noted by Minami & Komatsu (2020b) and Diego-Palazuelos et al. (2022), it is generally advantageous to exploit only cross-correlation spectra in order to maximize the overall signal-to-noise ratio of the estimator in question. Since the BEYONDPLANCK data release provides half-mission split maps for all LFI channels, while COSMOGLOBE DR1 currently only provides co-added full-mission maps (Basyrov et al. 2023), we used the BEYONDPLANCK half-mission LFI maps in the following. Furthermore, Watts et al. (2023a) show that the COSMOGLOBE LFI maps are very similar to the BEYONDPLANCK LFI maps, differing only by 1−2 μK on large angular scales. Specifically, for LFI we used 200 half-mission BEYONDPLANCK Gibbs samples for each channel, while for WMAP we used the first 200 samples of the first COSMOGLOBE DR1 main chain3 (Watts et al. 2023a). This Gibbs chain only sampled the V-band and W-band maps once every two and four Gibbs iterations, respectively, due to the high cost of map making for these bands, resulting in a total of 100 V-band samples and 50 W-band samples to be processed in the following.
For Planck HFI, we used the latest official Planck PR4 products for all frequency channels. In terms of ancillary data, we used the official beam profiles provided by the WMAP and Planck Collaborations (Bennett et al. 2013; Planck Collaboration IV 2016).
3. Method
In this section we provide a brief review of the methodology introduced and developed by Minami et al. (2019), Minami & Komatsu (2020a) and Diego-Palazuelos et al. (2022). As noted above, the fundamental assumption of Minami et al. (2019) is that cosmic birefringence would have a negligible impact on polarized foreground emission from our own Galaxy and significantly impacts only the CMB photons that have traveled for almost 14 billion years. The plane of linear polarization of the foreground emission is therefore rotated only by the miscalibration angle α, while the CMB photons are rotated by α + β. We can therefore write the observed E and B modes as
where “fg”, “CMB”, and “n” denote the foreground, CMB, and noise components, respectively.
We define the ensemble-averaged power spectrum as 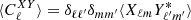 . When computing this for the observed E and B modes defined in Eq. (5), one finds (Minami et al. 2019)
. When computing this for the observed E and B modes defined in Eq. (5), one finds (Minami et al. 2019)
This equation allows us to break the degeneracy between α and β by using the polarized foreground emission to calibrate α. However, α might be biased if we do not include the intrinsic EB correlations of the foreground emission. The 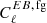 was not directly measured for synchrotron or dust, but there is substantial indirect evidence that it is nonzero, at least for dust (Clark et al. 2021; Diego-Palazuelos et al. 2022; Vacher et al. 2023).
was not directly measured for synchrotron or dust, but there is substantial indirect evidence that it is nonzero, at least for dust (Clark et al. 2021; Diego-Palazuelos et al. 2022; Vacher et al. 2023).
This paper focuses on synchrotron-dominated channels, in part because there has been no detection of a nonzero EB correlation for this component (Martire et al. 2022; Rubino-Martin et al. 2023). In the following, we therefore assume that 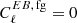 for synchrotron channels, while for dust-dominated channels, we adopt the filamentary thermal dust model for estimating the EB correlation as explained below.
for synchrotron channels, while for dust-dominated channels, we adopt the filamentary thermal dust model for estimating the EB correlation as explained below.
Lambda CDM predicts no parity violation at the last scattering surface; hence, we set 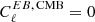 . One could wonder if the recent measurements of cosmic birefringence could be explained by this term. However, Fujita et al. (2022) conclude that primordial chiral gravitational waves, which give rise to intrinsic EB correlations of the CMB, cannot cause a cosmic birefringence measurement of β ∼ 0.3° due to an overproduction of BB power relative to observational constraints.
. One could wonder if the recent measurements of cosmic birefringence could be explained by this term. However, Fujita et al. (2022) conclude that primordial chiral gravitational waves, which give rise to intrinsic EB correlations of the CMB, cannot cause a cosmic birefringence measurement of β ∼ 0.3° due to an overproduction of BB power relative to observational constraints.
By extending the analysis to multiple frequency channels, labeled i and j, respectively, one can show that (Minami & Komatsu 2020a)
and
where
The different frequencies in these expressions may actually be different frequency channels from either the same or different experiments, or they may be different splits of the same frequency channel, for instance half-mission maps (e.g., Planck Collaboration II 2020). In the latter case, we assume that both split maps have the same miscalibration angle αi, while in the former case, we assume that they are different.
In addition, we allow β to depend on data sets, and we denote the corresponding birefringence angle βi. This allows us to derive independent constraints on cosmic birefringence by specific frequency channels, while still being able to exploit information in complementary channels to constrain foreground contributions and the miscalibration angles. Thus, a given result will be characterized by an overall analysis configuration that defines which data sets are included in the overall analysis, as well as a specification of which channels are used to constrain β.
Equations (7) and (8) can be combined into one equation as follows,
where, for now, we set the foreground EB correlation to zero. We combine the equations for all combinations of (i, j) into vectors, and define both a vector of observed spectra, ![$ \boldsymbol{C}^{\rm o}_\ell = \left[C^{E_i E_j,\, {\rm o}}_\ell, C^{B_i B_j,\, {\rm o}}_\ell, C^{E_i B_j,\, {\rm o}}_\ell\right]^T $](/articles/aa/full_html/2023/11/aa46829-23/aa46829-23-eq29.gif) as well as a vector of beam-smoothed theoretical ΛCDM spectra,
as well as a vector of beam-smoothed theoretical ΛCDM spectra, ![$ \boldsymbol{C}^{\Lambda {\rm CDM}}_\ell = \left[C^{E_i E_j, \,\Lambda {\rm CDM}}_\ell, C^{B_i B_j, \,\Lambda {\rm CDM}}_\ell\right]^T $](/articles/aa/full_html/2023/11/aa46829-23/aa46829-23-eq30.gif) . In all these expressions, we exclude intra-channel auto-correlations (i, i) in order to avoid noise biases.
. In all these expressions, we exclude intra-channel auto-correlations (i, i) in order to avoid noise biases.
We next wanted to constrain αi and βi using Eq. (13) for different combinations of (i, j). In practice, we reorganized these equations into a vector 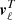 , which can now be written in the following matrix form,
, which can now be written in the following matrix form,
where
This vector has an associated covariance matrix that reads (Minami et al. 2019; Minami 2020; Minami & Komatsu 2020a)
where we take the covariance of the observed spectra to be
and fsky is the fraction of sky used for the analysis. As in previous works, we avoided including terms of the form 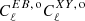 on the right-hand side of Eq. (17) due to the large statistical fluctuations of
on the right-hand side of Eq. (17) due to the large statistical fluctuations of 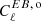 (Minami & Komatsu 2020a).
(Minami & Komatsu 2020a).
As discussed by Minami et al. (2019) and Minami & Komatsu (2020a), it is reasonable to assume 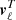 to be approximately Gaussian distributed, and one can then define the following likelihood,
to be approximately Gaussian distributed, and one can then define the following likelihood,
where 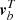 depends on αi and βi while Mb only depends on αi. We additionally binned both the vector and covariance matrix over Δℓ to reduce statistical fluctuations,
depends on αi and βi while Mb only depends on αi. We additionally binned both the vector and covariance matrix over Δℓ to reduce statistical fluctuations,
To actually derive the posterior distribution for these parameters with either one or multiple channel-dependent β, we used the publicly available Markov chain Monte Carlo sampler emcee (Foreman-Mackey et al. 2013), coupled to this likelihood. We adopted uniform priors on both αi and βi in the following.
The observed power spectra were computed using PolSpice4 (Chon et al. 2004). We applied a mask similar to in previous work (Diego-Palazuelos et al. 2022; Eskilt & Komatsu 2022) that removes pixels in which the intensity of the carbon-monoxide (CO) line is stronger than 45 KRJ km s−1. We also excluded polarized point sources using the official Planck point source masks. We define the effective sky fraction coverage as (Hivon et al. 2002; Challinor & Chon 2005)
Here, Npix is the number of pixels and wi is the weight of the apodized mask at pixel i.
Unlike previous LFI-based analyses that used the official Planck half-mission maps for 30 and 44 GHz and detector split maps for 70 GHz (Planck Collaboration Int. LVII 2020; Eskilt 2022; Eskilt & Komatsu 2022), we used BEYONDPLANCK half-mission maps for all channels in this paper, since no BEYONDPLANCK detector split maps are available at this time (BeyondPlanck Collaboration 2023). The second Planck half-mission split map has a few unobserved regions of the sky, which are masked. Because of this, we find that the sky fraction drops from fsky = 0.92, as used in previous work (Diego-Palazuelos et al. 2022; Eskilt & Komatsu 2022), to fsky = 0.90.
We employed CAMB5 (Lewis et al. 2000) to compute the theoretical ΛCDM power spectra, using the cosmological parameters from Planck 2018 (Planck Collaboration VI 2020). We smoothed these spectra with the Planck PR4 and 9-year WMAP beam transfer function matrices, 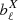 , respectively, together with the HEALPix6 (Gorski et al. 2005) pixel window functions, wpix, ℓ, such that
, respectively, together with the HEALPix6 (Gorski et al. 2005) pixel window functions, wpix, ℓ, such that
To include the effect of EB correlations from thermal dust emission, we adopted the ansatz proposed by Diego-Palazuelos et al. (2022), which was inspired by the work of Clark et al. (2021). Specifically, we related the dust EB power spectrum to the Planck measured dust TB and TE correlations as follows (Planck Collaboration XI 2020),
Here Aℓ ≥ 0 is represented as four free parameters in the multipole ranges 51 ≤ ℓ ≤ 130, 131 ≤ ℓ ≤ 210, 211 ≤ ℓ ≤ 510, and 511 ≤ ℓ ≤ 1490 with flat positive priors, while ψℓ is the misalignment angle between local magnetic fields and the long axis of filamentary structures averaged over some multipole range. The misalignment angle is given by Clark et al. (2021)
We found ψℓ by smoothing the observed TB and TE spectra from the Planck PR4 353 GHz channel for the sky mask used in the analysis. We applied the ψℓ from 353 GHz channel to all dust-dominated maps, namely the HFI channels and the W-band from WMAP. To incorporate this model into the analysis, we followed Diego-Palazuelos et al. (2022) and Eskilt & Komatsu (2022) by defining the matrices
where
These modified matrices Aℓ and Bℓ replace the A and B matrices in Eqs. (14) and (16). It should be noted that we did not apply this dust EB model to cross-correlations that include at least one synchrotron-dominated map. More specifically, we make the assumption that 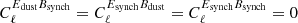 .
.
To derive the final constraints, we modified the publicly available code7 presented by Eskilt & Komatsu (2022) to include the BEYONDPLANCK and COSMOGLOBE channels rather than the 9-yr WMAP and LFI PR4 maps. Although the main focus of this paper is to measure cosmic birefringence from synchrotron-dominated maps, we also performed a joint analysis with the HFI channels, which are all dust-dominated, and we also included the WMAP W-band, which, with the new COSMOGLOBE DR1 processing, appears usable for cosmological analysis (Watts et al. 2023a).
Following previous analyses (Minami & Komatsu 2020b; Diego-Palazuelos et al. 2022; Eskilt 2022; Eskilt & Komatsu 2022), we used the multipole range ℓmin ≤ ℓ ≤ ℓmax, where ℓmin = 51 and Δℓ = 20. For all of LFI and WMAP-based analyses, we used ℓmax = 990, and when also including HFI data, we extended the upper range to ℓmax = 1490.
We applied this machinery to each individual sample in the BEYONDPLANCK and COSMOGLOBE frequency map ensembles, and not the corresponding posterior mean maps. This allowed us to propagate both systematic and statistical uncertainties to the final error budgets for α and β. We find the distribution of β to be closely approximated by a Gaussian distribution, and we therefore found the combined uncertainty of β over Gibbs samples by adding the two terms in quadrature, 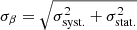 , where
, where 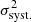 is the variance measured between Gibbs samples and
is the variance measured between Gibbs samples and 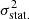 is the white noise uncertainty for a single realization.
is the white noise uncertainty for a single realization.
4. Results
4.1. WMAP+LFI analysis
We first present results derived from Planck LFI and WMAP only, both as processed by the BEYONDPLANCK and COSMOGLOBE framework. We begin with the case of fitting one global birefringence angle, β, across all frequencies. Markov chain trace plots for this case are shown in Fig. 1, in which panels from top to bottom show WMAP-only, LFI-only, and WMAP-plus-LFI results. The scatter in the central values from sample to sample illustrates the systematic uncertainties due to variations in instrumental and astrophysical parameters, while the statistical error bars (indicated as gray 1σ bands) are due to uncorrelated instrumental noise. We find these to be indistinguishable from sample to sample. Since the W channel is only processed every fourth main Gibbs iteration in the COSMOGLOBE DR1 data set (Watts et al. 2023a), we also performed this measurement only every fourth Gibbs iteration for WMAP. Overall, we see in this figure that the systematic uncertainties account for a relatively small fraction of the total scatter for WMAP, primarily due to the higher white noise level, while they are more important for the LFI and combined analyses, which have higher signal-to-noise ratios. We report our results using the mean, the statistical uncertainty, and the systematic uncertainty throughout.
 |
Fig. 1. Measurements of cosmic birefringence over Gibbs iterations. The black line shows β with a gray 1σ band. The dashed lines show the central value of the measurement made with the corresponding 9-yr WMAP or Planck PR4 maps, which we find to have the same white noise uncertainty as a single COSMOGLOBE or BEYONDPLANCK realization. |
The solid line in Fig. 1 indicates β = 0°, while the dotted line shows β = 0.34°, corresponding to the best-fit joint analysis of Planck PR4 and WMAP 9-yr result (Eskilt & Komatsu 2022). The dashed lines show the corresponding measurements from the 9-yr WMAP and PR4 LFI data sets in each panel. Their statistical error bars are similar to the measurement from COSMOGLOBE and BEYONDPLANCK and not shown. We note that the 9-yr WMAP gives a similar result to the COSMOGLOBE WMAP channels, while the BEYONDPLANCK LFI measurements of β are roughly 1σ higher than the same measurements from Planck PR4 LFI data. This is likely due to the fact that BEYONDPLANCK fixed the null test failures that plagued the official Planck LFI channels.
We conservatively discard the first ten samples in each Markov chain as burn-in, but note that we have not seen any effect that indicates a significant nonstationary period. Averaging over all post-burn-in samples, we find β = 0.81° ±2.40° (stat.) ±0.42° (syst.) for WMAP; β = 0.47° ±0.93° ±0.36° for LFI; and β = 0.35° ±0.66° ±0.23° for the joint analysis of both LFI and WMAP. These results are tabulated in Table 1, where the statistical and systematic uncertainties are added in quadrature.
Summary of posterior mean cosmic birefringence angles, β, as derived for various data combinations.
We also show the combined measurements in Fig. 2, where the histograms show the scattering of the central values, while the red and blue lines show the measurements with the statistical and total uncertainty, respectively. Here we note that the instrumental systematic uncertainties of β are much lower than statistical uncertainties from noise for both WMAP and LFI. Specifically, we find σsyst./σstat. = 39% for LFI and σsyst./σstat. = 17% for WMAP. At the same time, the total uncertainties are too large to shed independent light on the HFI-based result of β ∼ 0.35°.
 |
Fig. 2. Probability density of the measurements from Fig. 1. The black histograms show the scatter in the central values, and the red lines show the statistical uncertainties. The blue lines show the total uncertainties. The black dotted line shows β = 0.34°. |
The corresponding miscalibration angles, α, are tabulated in Table 2 and plotted in Fig. 3. Overall, we see that these are generally consistent with zero, with the WMAP K-band showing the largest deviation at 2.6σ for the WMAP+LFI-only analysis. However, this result is not robust with respect to data selection.
 |
Fig. 3. Miscalibration angles measured in WMAP (red) and Planck LFI (blue). The semi-transparent lines show the measurements equivalent to the lower panels of Figs. 1 and 2, while the opaque lines correspond to the β measurement in Fig. 7. The error bars include both statistical and systematic uncertainties. |
Summary of posterior mean miscalibration angles, α, for each Planck LFI and WMAP frequency channel, using either only LFI and WMAP data for fitting the model (second column) or LFI and WMAP plus HFI data (third column).
4.2. LFI+HFI analysis
Next, we performed a joint analysis between the BEYONDPLANCK LFI and Planck PR4 HFI maps. In this analysis, we include the dust filamentary model for HFI, and we sample jointly two cosmic birefringence angles βi, eleven miscalibration angles αi, and four dust amplitude parameters Aℓ. Since we are including more data and the dust filamentary model for dust EB is computationally more expensive, we sample β for every fifth Gibbs iteration. Figure 4 shows the resulting constraints on β separately for the LFI and the HFI channels.
 |
Fig. 4. Probability density of cosmic birefringence for every fifth Gibbs iteration of the BEYONDPLANCK LFI maps. This is analyzed jointly with the Planck PR4 HFI detector split maps. One birefringence angle is additionally sampled for the LFI channels and another for the HFI channels. The error bars include both statistical and systematic uncertainties from LFI. The dashed vertical line shows β = 0°, and the dotted line shows β = 0.34°. |
We note that we only have access to one set of maximum-likelihood Planck PR4 HFI maps, and it is therefore harder to assess the impact of instrumental systematic effects than it is with the BEYONDPLANCK and COSMOGLOBE maps. However, Diego-Palazuelos et al. (2023) considered a wide range of effects, and found these to have a limited impact on β.
We find βLFI = 0.52° ±0.34° ±0.13°, which gives a combined uncertainty of 0.37°. This corresponds nominally to a nonzero birefringence angle of 1.4σ. To understand which channels drive this value, we fit β individually for each LFI channel. This is shown in terms of posterior distributions in Fig. 5, and posterior summary statistics are tabulated in Table 1. As usual, we additionally sampled a separate birefringence angle for HFI, βHFI, miscalibration angles, αi, and dust EB amplitudes, Aℓ, which are not shown.
 |
Fig. 5. Same as Fig. 4, except one β is sampled individually for the 30, 44, and 70 GHz channels. One β is additionally sampled for HFI but not shown. We show the total uncertainties from both LFI systematics and statistical uncertainties. |
In Fig. 5 we see that the positive value is dominated by the 70 GHz channel, with β70 = 0.85° ±0.42° ±0.13°, which corresponds to a total uncertainty of 0.44°. This formally disfavors β = 0° at a statistical significance of 1.9σ. In contrast, the 30 and 44 GHz channels show no evidence for a positive value, but their uncertainties are also significantly larger, with posterior summary values of β30 = −0.07° ±0.69° ±0.29° and β44 = 0.10° ±0.70° ±0.25°, respectively. We also note that, while β44 and β70 are consistent with the Planck PR4 LFI analysis described by Eskilt (2022), which used a similar mask, the 30 GHz channel measurement from BEYONDPLANCK data has dropped by more than 1σ as compared to the Planck PR4 LFI maps.
One might wonder if the large measurement of β in the 70 GHz channel could be caused by polarized dust EB emission. This channel contains more polarized synchrotron than dust emission, but the latter is not negligible as the channel is close to the foreground minimum where synchrotron and dust emission are roughly equal (Planck Collaboration IV 2018). We did not apply our dust filamentary model to this channel, but we note that from earlier work the birefringence angle always increases when accounting for this effect (Diego-Palazuelos et al. 2022), and therefore the quoted value of β70 represents a conservative lower limit.
For the HFI channels, we find βHFI = 0.22° ±0.11° ±0.02°, where the systematic uncertainty indicates only the variation due to LFI marginalization. This value is slightly lower than previously reported values, and parts of this is likely due to the somewhat more conservative mask used in the current analysis, due to missing pixels in the half-mission split (Diego-Palazuelos et al. 2022; Eskilt 2022; Eskilt & Komatsu 2022). We also find that the 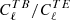 power ratio is higher in the 353 GHz channel at smaller multipoles for the mask used in this work. This is a tracer of polarized dust emission that is known to be highly mask-dependent (Clark et al. 2021; Diego-Palazuelos et al. 2022), and this might suggest a larger dust EB amplitude that might not be fully encapsulated by the dust model. Diego-Palazuelos et al. (2022) showed that the dust filamentary model is mostly able to mitigate the effect of dust, but one would still expect a slight weakening of the signal of β for masks with a sky coverage around fsky ≲ 0.90.
power ratio is higher in the 353 GHz channel at smaller multipoles for the mask used in this work. This is a tracer of polarized dust emission that is known to be highly mask-dependent (Clark et al. 2021; Diego-Palazuelos et al. 2022), and this might suggest a larger dust EB amplitude that might not be fully encapsulated by the dust model. Diego-Palazuelos et al. (2022) showed that the dust filamentary model is mostly able to mitigate the effect of dust, but one would still expect a slight weakening of the signal of β for masks with a sky coverage around fsky ≲ 0.90.
4.3. WMAP+LFI+HFI analysis
Finally, we analyzed the combination of all three main data sets, namely the COSMOGLOBE WMAP, BEYONDPLANCK LFI, and Planck PR4 HFI channels. The main results from this analysis are summarized in Fig. 6, where β is measured separately for WMAP, LFI, and HFI. Only every 16th Gibbs sample is processed in this analysis, due to a high computational cost.
 |
Fig. 6. Same as Fig. 4 but jointly with the COSMOGLOBE WMAP channels for every 16th Gibbs iteration. An additional β is sampled for the WMAP channels. |
For WMAP, we find that βWMAP = −0.12° ±0.46° ±0.06°, where the systematic error term denotes the systematic uncertainties arising only from LFI and WMAP, and not HFI. For LFI, we find βLFI = 0.53° ±0.31° ±0.08°, which is inconsistent with β = 0° at a 1.6σ statistical significance. Finally, for HFI we find βHFI = 0.26° ±0.10° ±0.01°. We note that even though the central value of βWMAP itself is negative, the addition of the WMAP channels slightly increases the statistical significance of both βLFI and βHFI by providing more information through cross-correlations.
To further probe the impact of channels that are dominated by either synchrotron or thermal dust emission, we split β into two groups; one for synchrotron-dominated channels, β≤70 GHz, and another for thermal dust-dominated channels, β> 70 GHz. The results from this calculation are summarized in Fig. 7 and Table 1.
 |
Fig. 7. Same as Fig. 6 but we sample β separately for synchrotron-dominated channels, β≤70 GHz, and dust-dominated channels, β> 70 GHz. |
For the synchrotron-dominated channels, we find β≤70 GHz = 0.53° ±0.27° ±0.06°, which disfavors β = 0° at a 1.9σ statistical significance. This signal is mostly driven by the 70 GHz channel. However, as noted above, the addition of WMAP does increase the statistical significance of βLFI, which, with the exception of the W-band, belong to the channels with frequency ≤70 GHz.
While the dust filamentary model of Clark et al. (2021) is not applicable to synchrotron emission, it is possible that a different mechanism gives rise to an intrinsic synchrotron EB power spectrum. Negative synchrotron EB correlations would bias β to be larger and could be the cause of the signal. Another possibility is EB correlations between polarized synchrotron and dust emission. Knowing that synchrotron and dust emission are correlated (Choi & Page 2015; Planck Collaboration XI 2020), we cannot rule out the existence of 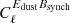 or
or 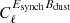 . Lastly, the dust-dominated channels yield β> 70 GHz = 0.23° ±0.10° ±0.01°.
. Lastly, the dust-dominated channels yield β> 70 GHz = 0.23° ±0.10° ±0.01°.
Finally, we compute one global β angle for the joint analysis of all three data sets. These results are listed in Table 1, and compared with those found in earlier analyses (Diego-Palazuelos et al. 2022; Eskilt & Komatsu 2022). Joint analysis of β is driven by the HFI channels, so the signal is sensitive to dust EB, which is modeled with the dust filamentary ansatz. The discrepancy of β between the left and right columns of the lower half of Table 1 is most likely due to the masking sensitivity of the filamentary dust model.
5. Conclusions
We have analyzed the reprocessed BEYONDPLANCK LFI and COSMOGLOBE WMAP polarization maps with respect to isotropic cosmic birefringence. These channels shed new light on the previously reported measurement of a nonzero birefringence angle, β, from Planck HFI, as they both have very different systematics from HFI and are dominated by synchrotron emission, for which no significant EB correlations have been measured (Martire et al. 2022; Rubino-Martin et al. 2023). While there has been no direct measurement of the EB correlations of thermal dust emission, there are indications of its existence (Huffenberger et al. 2020; Clark et al. 2021).
The uncertainty on β from LFI and WMAP alone is too large to allow robust independent evidence for cosmic birefringence, with a best-fit combined value of β = 0.35° ±0.70°, where the error bar includes both systematic and statistical uncertainties. This uncertainty is more than six times larger than that for HFI alone. However, when performing a joint analysis with Planck PR4 HFI, which provides additional valuable information regarding the foregrounds and miscalibration angles, we do find a value of β = 0.53° ±0.28° in the synchrotron-dominated maps that include channels up to and including 70 GHz. This is positive at a statistical significance of 1.9σ and is consistent with the 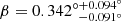 from the joint analysis of the public 9-year WMAP and Planck PR4 data (Eskilt & Komatsu 2022).
from the joint analysis of the public 9-year WMAP and Planck PR4 data (Eskilt & Komatsu 2022).
The measurement from the synchrotron-dominated channels is driven by the 70 GHz channel, which is notable for at least two reasons. Firstly, this channel has the lowest foreground contribution of any channel considered in this line of work. Secondly, it is the LFI channel with the highest sensitivity and lowest instrumental systematics, which is why it has formed the basis of almost all cosmological results from LFI.
We have assumed that 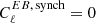 in our analyses as it has been found to be statistically consistent with zero (Martire et al. 2022), but we still cannot rule out synchrotron EB as the cause of a signal in the LFI and WMAP channels. As discussed in Minami et al. (2019) and Diego-Palazuelos et al. (2022), we can parameterize the foreground EB as
in our analyses as it has been found to be statistically consistent with zero (Martire et al. 2022), but we still cannot rule out synchrotron EB as the cause of a signal in the LFI and WMAP channels. As discussed in Minami et al. (2019) and Diego-Palazuelos et al. (2022), we can parameterize the foreground EB as 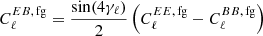 , where γℓ is the effective foreground rotation. If it is independent of multipole, γℓ = γ, and |γ|≪1, the bias on β will be γ, meaning that we do not measure β but β − γ if we neglect foreground EB in the analysis. Assuming
, where γℓ is the effective foreground rotation. If it is independent of multipole, γℓ = γ, and |γ|≪1, the bias on β will be γ, meaning that we do not measure β but β − γ if we neglect foreground EB in the analysis. Assuming 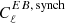 is constant in multipole space, Martire et al. (2022) found the ratio
is constant in multipole space, Martire et al. (2022) found the ratio 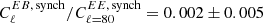 when fsky = 0.94, which, together with
when fsky = 0.94, which, together with 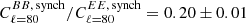 , we find γℓ = 80 = 0.07° ±0.18°. We note that γℓ > 0 would bias the observed β to be smaller than its real value (the total bias would be some average of γℓ over the multipoles). But with the unrealistic assumption that
, we find γℓ = 80 = 0.07° ±0.18°. We note that γℓ > 0 would bias the observed β to be smaller than its real value (the total bias would be some average of γℓ over the multipoles). But with the unrealistic assumption that 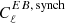 is constant and does not decay for higher multipoles, one should be careful at extrapolating γℓ. Hence, we cannot rule out synchrotron EB as the cause of the signal in the LFI and WMAP maps.
is constant and does not decay for higher multipoles, one should be careful at extrapolating γℓ. Hence, we cannot rule out synchrotron EB as the cause of the signal in the LFI and WMAP maps.
Nor can we rule out possible correlations between the E and B modes of synchrotron and dust emission, namely 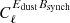 and
and 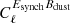 , which we have not found reported constraints on in the literature. This could bias our measurements since we also measure birefringence in synchrotron channels through cross-power spectra with the dust-dominated HFI channels.
, which we have not found reported constraints on in the literature. This could bias our measurements since we also measure birefringence in synchrotron channels through cross-power spectra with the dust-dominated HFI channels.
While our analysis suggests that the current instrumental model adopted in the COSMOGLOBE framework does not play a dominant role regarding the final uncertainties, accounting for typically only about 10% of the total uncertainty, it is important to emphasize that the polarization angle has not yet been sampled over directly in this framework. Adding support for that degree of freedom could be important for decreasing these uncertainties further, for instance using Tau A as a calibration source at the map level. This should be considered a high-priority issue for next-generation processing for both Planck and WMAP.
Future CMB experiments should, however, focus their efforts on precise on-ground calibrations of their polarization angles, which is no longer possible for WMAP and Planck. Negligible miscalibration angles make this analysis more robust against foreground EB as we do not have to break the α + β degeneracy (see Cornelison et al. 2022, where the authors achieve a polarization angle uncertainty of < 0.1° for BICEP3).
If cosmic birefringence is demonstrated to be of cosmological origin, it would be a revolutionary window on high-energy physics and cosmology (Agrawal et al. 2022; Fujita et al. 2021; Komatsu 2022) and could possibly shed light on the dark sector of the Universe.
Available at https://cosmoglobe.uio.no
Acknowledgments
We are grateful to Patricia Diego-Palazuelos and Eiichiro Komatsu for useful discussions and feedback. Planck is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states and led by Principal Investigators from France and Italy, telescope reflectors provided through a collaboration between ESA and a scientific consortium led and funded by Denmark, and additional contributions from NASA (USA). The current work has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement numbers 819478 (ERC; Cosmoglobe) and 772253 (ERC; bits2cosmology). In addition, the collaboration acknowledges support from RCN (Norway; grant no. 274990). Softwares: PolSpice (Chon et al. 2004), healpy (Gorski et al. 2005; Zonca et al. 2019), Matplotlib (Hunter 2007), NumPy (Harris et al. 2020), CAMB (Lewis et al. 2000), emcee (Foreman-Mackey et al. 2013).
References
- Agrawal, P., Nee, M., & Reig, M. 2022, J. High Energy Phys., 10, 141 [CrossRef] [Google Scholar]
- Basyrov, A., Suur-Uski, A.-S., Colombo, L. P. L., et al. 2023, A&A, 675, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., et al. 2013, ApJS, 208, 20 [Google Scholar]
- BeyondPlanck Collaboration (Andersen, K. J., et al.) 2023, A&A, 675, A1 [Google Scholar]
- Brilenkov, M., Fornazier, K. S. F., Hergt, L. T., et al. 2023, A&A, 675, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carroll, S. M., & Field, G. B. 1991, Phys. Rev. D, 43, 3789 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, S. M., Field, G. B., & Jackiw, R. 1990, Phys. Rev. D, 41, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Challinor, A., & Chon, G. 2005, MNRAS, 360, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, S. K., & Page, L. A. 2015, JCAP, 12, 020 [Google Scholar]
- Chon, G., Challinor, A., Prunet, S., Hivon, E., & Szapudi, I. 2004, MNRAS, 350, 914 [Google Scholar]
- Clark, S. E., Kim, C.-G., Hill, J. C., & Hensley, B. S. 2021, ApJ, 919, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Colombo, L. P. L., Eskilt, J. R., Paradiso, S., et al. 2023, A&A, 675, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cornelison, J., Vergès, C., Ade, P. A. R., et al. 2022, Proc. SPIE Int. Soc. Opt. Eng., 12190, 121901X [NASA ADS] [Google Scholar]
- Diego-Palazuelos, P., Eskilt, J. R., Minami, Y., et al. 2022, Phys. Rev. Lett., 128, 091302 [NASA ADS] [CrossRef] [Google Scholar]
- Diego-Palazuelos, P., Martínez-González, E., Vielva, P., et al. 2023, JCAP, 01, 044 [CrossRef] [Google Scholar]
- Eskilt, J. R. 2022, A&A, 662, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eskilt, J. R., & Komatsu, E. 2022, Phys. Rev. D, 106, 063503 [NASA ADS] [CrossRef] [Google Scholar]
- Eskilt, J. R., Herold, L., Komatsu, E., et al. 2023, Phys. Rev. Lett., 131, 121001 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, B., Li, H., Li, M., & Zhang, X. 2005, Phys. Lett. B, 620, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fujita, T., Murai, K., Nakatsuka, H., & Tsujikawa, S. 2021, Phys. Rev. D, 103, 043509 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, T., Minami, Y., Shiraishi, M., & Yokoyama, S. 2022, Phys. Rev. D, 106, 103529 [CrossRef] [Google Scholar]
- Galloway, M., Andersen, K. J., Aurlien, R., et al. 2023, A&A, 675, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geman, S., & Geman, D. 1984, IEEE Trans. Pattern Anal. Mach. Intell., 6, 721 [CrossRef] [Google Scholar]
- Gorski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
- Harari, D., & Sikivie, P. 1992, Phys. Lett. B, 289, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hivon, E., Gorski, K. M., Netterfield, C. B., et al. 2002, ApJ, 567, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Huffenberger, K. M., Rotti, A., & Collins, D. C. 2020, ApJ, 899, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kamionkowski, M., Kosowsky, A., & Stebbins, A. 1997, Phys. Rev. Lett., 78, 2058 [Google Scholar]
- Komatsu, E. 2022, Nat. Rev. Phys., 4, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [Google Scholar]
- Lue, A., Wang, L.-M., & Kamionkowski, M. 1999, Phys. Rev. Lett., 83, 1506 [NASA ADS] [CrossRef] [Google Scholar]
- Martire, F. A., Barreiro, R. B., & Martínez-González, E. 2022, JCAP, 04, 003 [CrossRef] [Google Scholar]
- Minami, Y. 2020, Prog. Theor. Exp. Phys., 2020, 063E01 [CrossRef] [Google Scholar]
- Minami, Y., & Komatsu, E. 2020a, Prog. Theor. Exp. Phys., 2020, 103E02 [CrossRef] [Google Scholar]
- Minami, Y., & Komatsu, E. 2020b, Phys. Rev. Lett., 125, 221301 [NASA ADS] [CrossRef] [Google Scholar]
- Minami, Y., Ochi, H., Ichiki, K., et al. 2019, Prog. Theor. Exp. Phys., 2019, 083E02 [CrossRef] [Google Scholar]
- Paradiso, S., Colombo, L. P. L., Andersen, K. J., et al. 2023, A&A, 675, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IV. 2016, A&A, 594, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2016, A&A, 594, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IV. 2018, A&A, 641, A4 [Google Scholar]
- Planck Collaboration II. 2020, A&A, 641, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2020, A&A, 641, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. LVII. 2020, A&A, 643, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubino-Martin, J. A., Guidi, F., Génova-Santos, R. T., et al. 2023, MNRAS, 519, 3383 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U., & Zaldarriaga, M. 1997, Phys. Rev. Lett., 78, 2054 [Google Scholar]
- Vacher, L., Aumont, J., Boulanger, F., et al. 2023, A&A, 672, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watts, D. J., Basyrov, A., Eskilt, J. R., et al. 2023a, A&A, 679, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watts, D. J., Galloway, M., Ihle, H. T., et al. 2023b, A&A, 675, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zonca, A., Singer, L. P., Lenz, D., et al. 2019, J. Open Source Softw., 4, 1298 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of posterior mean cosmic birefringence angles, β, as derived for various data combinations.
Summary of posterior mean miscalibration angles, α, for each Planck LFI and WMAP frequency channel, using either only LFI and WMAP data for fitting the model (second column) or LFI and WMAP plus HFI data (third column).
All Figures
 |
Fig. 1. Measurements of cosmic birefringence over Gibbs iterations. The black line shows β with a gray 1σ band. The dashed lines show the central value of the measurement made with the corresponding 9-yr WMAP or Planck PR4 maps, which we find to have the same white noise uncertainty as a single COSMOGLOBE or BEYONDPLANCK realization. |
| In the text | |
 |
Fig. 2. Probability density of the measurements from Fig. 1. The black histograms show the scatter in the central values, and the red lines show the statistical uncertainties. The blue lines show the total uncertainties. The black dotted line shows β = 0.34°. |
| In the text | |
 |
Fig. 3. Miscalibration angles measured in WMAP (red) and Planck LFI (blue). The semi-transparent lines show the measurements equivalent to the lower panels of Figs. 1 and 2, while the opaque lines correspond to the β measurement in Fig. 7. The error bars include both statistical and systematic uncertainties. |
| In the text | |
 |
Fig. 4. Probability density of cosmic birefringence for every fifth Gibbs iteration of the BEYONDPLANCK LFI maps. This is analyzed jointly with the Planck PR4 HFI detector split maps. One birefringence angle is additionally sampled for the LFI channels and another for the HFI channels. The error bars include both statistical and systematic uncertainties from LFI. The dashed vertical line shows β = 0°, and the dotted line shows β = 0.34°. |
| In the text | |
 |
Fig. 5. Same as Fig. 4, except one β is sampled individually for the 30, 44, and 70 GHz channels. One β is additionally sampled for HFI but not shown. We show the total uncertainties from both LFI systematics and statistical uncertainties. |
| In the text | |
 |
Fig. 6. Same as Fig. 4 but jointly with the COSMOGLOBE WMAP channels for every 16th Gibbs iteration. An additional β is sampled for the WMAP channels. |
| In the text | |
 |
Fig. 7. Same as Fig. 6 but we sample β separately for synchrotron-dominated channels, β≤70 GHz, and dust-dominated channels, β> 70 GHz. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



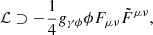
![$$ \begin{aligned} \beta (\hat{\mathbf{n }}) =\frac{1}{2} g_{\gamma \phi }\left[\phi (\eta _{\mathrm{o}})-\phi (\eta _{\mathrm{e}},r\hat{\mathbf{n }})\right], \end{aligned} $$](/articles/aa/full_html/2023/11/aa46829-23/aa46829-23-eq4.gif)
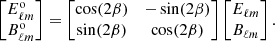
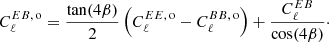
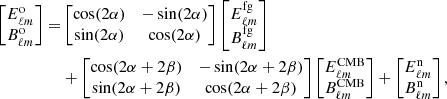
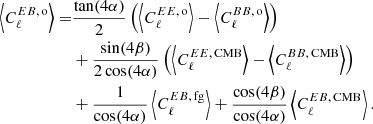
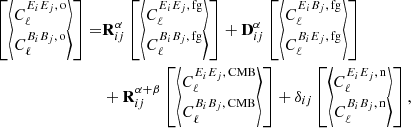
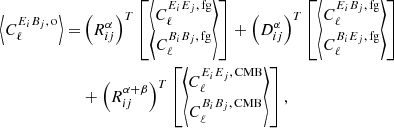
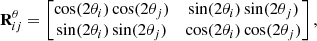
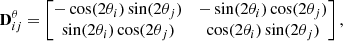
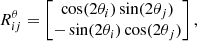
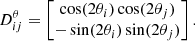
![$$ \begin{aligned} \left\langle C_\ell ^{E_iB_j,\, \mathrm{o}}\right\rangle =&\left(R^{\alpha }_{ij}\right)^T\left(\mathbf R ^{\alpha }_{ij}\right)^{-1} \begin{bmatrix} \left\langle C_\ell ^{E_iE_j,\, \mathrm{o}}\right\rangle \\ \left\langle C_\ell ^{B_iB_j,\, \mathrm{o}}\right\rangle \end{bmatrix}\nonumber \\&+\bigg [\left(R^{\alpha +\beta }_{ij}\right)^T-\left(R^{\alpha }_{ij} \right)^T\left(\mathbf R ^{\alpha }_{ij}\right)^{-1} \mathbf R ^{\alpha +\beta }_{ij}\bigg ]\begin{bmatrix} \left\langle C_\ell ^{E_iE_j,\, \mathrm{CMB}}\right\rangle \\ \left\langle C_\ell ^{B_iB_j,\, \mathrm{CMB}}\right\rangle \end{bmatrix}, \end{aligned} $$](/articles/aa/full_html/2023/11/aa46829-23/aa46829-23-eq28.gif)
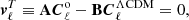
![$$ \begin{aligned}&\mathbf A _{ij} = \begin{bmatrix}- \left(R^{\alpha }_{ij}\right)^T\left(\mathbf R ^{\alpha }_{ij}\right)^{-1}, 1\end{bmatrix},\\&\mathbf B _{ij} = \left[\left(R^{\alpha +\beta }_{ij}\right)^T-\left(R^{\alpha }_{ij}\right)^T \left(\mathbf R ^{\alpha }_{ij}\right)^{-1}\mathbf R ^{\alpha +\beta }_{ij}\right].\nonumber \end{aligned} $$](/articles/aa/full_html/2023/11/aa46829-23/aa46829-23-eq33.gif)
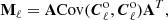
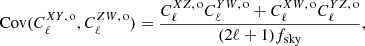
![$$ \begin{aligned} \ln \mathcal{L} = -\frac{1}{2} \left[\sum _{b} \boldsymbol{v}^T_{b} \mathbf M ^{-1}_b \boldsymbol{v}_{b} + \ln \mathbf M _b\right], \end{aligned} $$](/articles/aa/full_html/2023/11/aa46829-23/aa46829-23-eq39.gif)
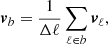
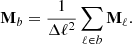
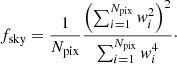
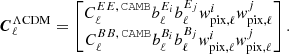
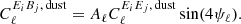
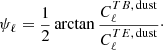
![$$ \begin{aligned}&\mathbf A _{\ell , ij} = \left[-\left(\Lambda ^{\alpha }_{\ell , ij}\right)^T \left(\mathbf {\Lambda} ^{\alpha }_{\ell , ij}\right)^{-1},\, 1\right],\\&\mathbf B _{\ell , ij} =\left[\left(R^{\alpha +\beta }_{ij}\right)^T-\left(\Lambda ^{\alpha }_{\ell , ij}\right)^T\left(\mathbf \Lambda ^{\alpha }_{\ell , ij}\right)^{-1}\mathbf R ^{\alpha +\beta }_{ij}\right],\nonumber \end{aligned} $$](/articles/aa/full_html/2023/11/aa46829-23/aa46829-23-eq48.gif)