| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201936099 | |
| Published online | 06 December 2019 | |
Optimization of surface flux transport models for the solar polar magnetic field
Eötvös Loránd University, Department of Astronomy, Budapest, Hungary
e-mail: k.petrovay@astro.elte.hu, m.talafha@astro.elte.hu
Received:
13
June
2019
Accepted:
10
October
2019
Context. The choice of free parameters in surface flux transport (SFT) models describing the evolution of the large-scale poloidal magnetic field of the Sun is critical for the correct reproduction of the polar magnetic flux built up during a solar cycle, which is known to be a good predictor of the amplitude of the upcoming cycle.
Aims. For an informed choice of parameters it is important to understand the effects of and interplay among the various parameters and to optimize the models for the polar magnetic field.
Methods. Here we present the results of a large-scale systematic study of the parameter space in an SFT model where the source term representing the net effect of tilted flux emergence was chosen to represent a typical, average solar cycle as described by observations.
Results. Comparing the results with observational constraints on the spatiotemporal variation of the polar magnetic field, as seen in magnetograms for the last four solar cycles, we mark allowed and excluded regions in the 3D parameter space defined by the flow amplitude u0, the magnetic diffusivity η and the decay time scale τ, for three different assumed meridional flow profiles.
Conclusions. Without a significant decay term in the SFT equation (i.e., for τ > 10 yr) the global dipole moment reverses too late in the cycle for all flow profiles and parameters, providing independent supporting evidence for the need of a decay term, even in the case of identical cycles. An allowed domain is found to exist for τ values in the 5–10 yr range for all flow profiles considered. Generally higher values of η (500–800 km2 s−1) are preferred though some solutions with lower η are still allowed.
Key words: Sun: magnetic fields / Sun: photosphere
© ESO 2019
1. Introduction
Synoptic maps of the line-of-sight component of the large-scale solar magnetic field have been available on a regular basis since the 1970s. Most of this large-scale flux resides in unipolar areas where one polarity prevails among the magnetic network elements (Stix 2004). High-resolution observations indicate that this field is mostly concentrated in numerous thin, strong flux tubes that are vertically aligned (as illustrated e.g. in Fig. 2 of Orozco Suárez et al. 2007), so the true photospheric field is assumed to be radial, and its amplitude on the solar surface, B(λ, ϕ) can be derived by a deprojection of the line-of-sight field as a function of heliographic latitude λ and longitude ϕ. A possible smaller contribution to the large-scale field from a slight polarity imbalance in the small-scale mixed polarity internetwork fields would not alter this situation, as the orientation of this field is more isotropic but on average still symmetric around the radial direction.
In order to interpret the evolution of the photospheric field on these synoptic maps, surface flux transport (SFT) models were developed in the 1980s (Sheeley et al. 1983). The models described the evolution of B by an advective-diffusive transport equation, advection being ascribed to differential rotation and poleward meridional flow, and diffusion attributed to the mixing action of supergranular flows; a source term was included to represent flux emergence in the form of newly appearing bipolar active regions (ARs). This early age of SFT model development, as reviewed by Sheeley (2005), mostly focused on the overall reproduction of the evolution of the large-scale field during a period of about one solar cycle (Cycle 21, for which data were available at the time). These models demonstrate that the reversal of the polar field and of the solar dipole moment at the middle of activity cycles, followed by the build-up of a new poloidal field in the late phases of the cycle originate from the systematic latitude-dependent tilt of ARs relative to the azimuthal direction (Joy’s law): as this imparts a meridional component to the AR magnetic field, each AR gives a contribution to the global solar dipole moment and these contributions gradually change the Sun’s polar magnetic field, after the magnetic fields of the trailing parts of decayed active regions are transported to the poles.
Interest in SFT models increased again in the 2000s when they were used for the reconstruction of the long-term variation of the total solar magnetic flux and open flux, with a view to reconstruct coronal and interplanetary conditions (Wang et al. 2000). The long-term solar record clearly indicates that solar cycles vary in amplitude in a manner that appears to be random. As these explorations have run SFT models for many solar cycles, it has become clear (Schrijver et al. 2002) that such variations in cycle amplitude will, for reasons explained in the previous paragraph, result in a random walk of the unsigned amplitude of the solar dipole moment from one cycle to the next, until it reaches values well exceeding the typical total contribution for ARs in a cycle, so that polar reversal would cease, quenching the dynamo. As a workaround, Schrijver et al. (2002) suggested the introduction of a sink or decay term of the form −B/τ in the transport equation, tentatively interpreted as an unobserved process (U-loop emergence). The decay term was more convincingly interpreted as a simplistic phenomenological representation of a 3D effect by Baumann et al. (2006) who argued that, owing to the high aspect ratio of the solar convective zone, the decay timescale of the field due to vertical diffusion should be two orders of magnitude shorter than the decay time scale of horizontal diffusion, implying τ = 5 − 10 years. While it has later been suggested that downward directed pumping in the subsurface layers may suppress vertical diffusion, this has not been convincingly demonstrated, nor did it solve the dipole moment drift problem. Intercycle variations in the meridional flow (Wang et al. 2002) or in Joy’s law (Cameron et al. 2010) have also been suggested to solve the dipole moment drift problem, though the suggested variations are still disputed and the time periods studied were relatively short.
A third period of increased activity in SFT modelling started around 2010, with the increased interest in solar cycle prediction following the abrupt change of the long-term level of solar activity with Cycle 24 (Pesnell 2008). As it was realized that the best physical precursor of the amplitude of an upcoming solar cycle was the amplitude of the Sun’s polar magnetic field at the start of the cycle (Petrovay 2010), the next logical step was the use of SFT models to describe the buildup process of this polar field, in the hope of extending the temporal range of cycle prediction.
Any SFT model needs to make assumptions concerning an ill-constrained function, the effective meridional flow profile u(θ), as well as three free parameters: the flow amplitude u0, the diffusivity η and the decay time scale τ. Other choices, such as differential rotation or the form of the source, are much better constrained by observations. For applications where an exact quantitative reproduction of the evolving magnetic field is important the appropriate choice of parameters will be especially crucial. The determination of model parameters is a complex issue, to be discussed in some detail in Sect. 2 below. We will argue that a calibration of SFT models to correctly reproduce the characteristics of the evolution of the polar magnetic field and of the solar dipole moment is the method that best fits the objectives of solar cycle prediction. This argument provides the motivation of the research presented in the rest of the paper. In Sect. 3 we determine the criteria that the SFT model of a “typical” or “ideal” solar cycle should satisfy to qualify as a good representation of the actual evolution of the solar polar magnetic fields. Then, in Sect. 4 we perform a systematic study on a large grid of SFT models with different parameter sets and with an idealized, yet realistic source term representing a “typical” cycle. Comparing the results with the preset criteria we mark out allowed and excluded domains in the parameter space. Results of this analysis are discussed in Sect. 5. Section 6 concludes the paper.
2. Motivation
Two general approaches have been taken in the choice of parameter values and flow profiles in SFT models: direct measurements and internal calibrations of the model.
Direct measurements of the meridional flow have been made by numerous researchers using three different methods: Doppler shifts of spectral lines, (e.g., Hathaway 1996), helioseismic inversions, (e.g., Schad et al. 2011), and local correlation tracking of moving magnetic flux concentrations (e.g., Iida 2016). While a general review of these efforts is far beyond the scope of this paper, we can safely say that, despite some claims to the contrary, the results can hardly be considered concordant. There is not even agreement regarding the latitude range where the overall meridional flow peaks. To cite just a few recent results: in a time–distance helioseismic analysis Chen & Zhao (2017) find that the polewards surface flow peaks at latitudes of 50 − 60°, whereas Imada & Fujiyama (2018) report a peak near 45° from magnetic feature tracking, while Zhao et al. (2014) find that the flow peaks at a latitude of ∼15°. Part of the reason for the discrepancy is the very significant cycle dependence of the flow, following a migrating pattern associated with torsional oscillations (Lin & Chou 2018).
Determinations of the surface differential rotation based on correlation tracking show that small-scale, short-term correlation tracking leads to results that strongly deviate from the more rigid rotation of large-scale, long-lived magnetic patterns (Wilcox et al. 1970; Wang & Sheeley 1994). This suggests that small-scale, short-term tracking studies are of limited use for the determination of the transport properties of large-scale fields. A study of the effect of transport processes in the deep convective zone on surface patterns by Petrovay & Szakály (1999) also showed that the evolution of the large-scale surface field is strongly influenced or even dominated by subsurface processes, rather than by the flows localized to the surface. Similar conclusions were reached recently by Whitbread et al. (2019) who find that the apparent diffusion of surface magnetic fields resulting from AR decay cannot be represented by the nominal surface value of the diffusivity unless these fields are somehow disconnected from the magnetic field in the deep convective zone. All this may well explain why direct determinations of the magnetic diffusivity generally tend to yield lower values than internal calibrations of SFT models (see Table 6.2 in Schrijver & Zwaan 2000).
In the face of this state of the affairs, internal calibrations of the SFT model seem to be the preferable way to follow in the determination of parameters. Parameter studies and optimization attempts have been made previously by several authors. The first more extensive parameter study of the SFT model was performed by Baumann et al. (2004) who considered the effect of varying each parameter, one at a time, in a model without a decay term, with a fixed form of the meridional flow profile and a simplified source term. More recently, a 3 × 3 model grid in the (u0, η) plane was presented by Virtanen et al. (2017) with a source term taken from observations and the resulting butterfly diagram was qualitatively compared to the observed pattern.
Lemerle et al. (2015) and Whitbread et al. (2017) searched for an optimal combination of parameters (including flow profile) using the PIKAIA optimization algorithm. These latter studies were the first to apply a quantitative criterium (the “merit function” of the algorithm) to judge the goodness of the fit between a model result and observations. The merit used in those studies was essentially the χ2 difference between observed and simulated magnetic butterfly diagrams. These two studies differed in the time period considered and in the way the source term was constructed from observational data, as well as in some further details, but their results were in general comparable. Depending on model details, Whitbread et al. (2017) find that acceptable values of u0, η and τ can fall in the ranges 7–22 m s−1, 220–800 km2 s−1 and 2.5–30 year, respectively. At the same time, the characteristics of polar fields were not particularly faithfully reproduced in the optimized solution. This is due to the fact that the polar area covers a small fraction of the solar surface, having little weight in the determination of the merit applied.
However, as discussed above in the Introduction, the ability to correctly reproduce the polar magnetic field is critical if SFT models are to be applied for solar cycle prediction purposes (as opposed to a general reproduction of observed magnetic butterfly diagrams). Therefore, in the present work we perform another SFT model parameter study where the merit is based on a good quantitative reproduction of the spatiotemporal variation of solar polar magnetic fields. Furthermore, while PIKAIA is an extremely powerful tool, it offers little physical insight and yields only limited information on the extent of the allowed domain in parameter space. Therefore, another difference relative to previous work is that instead of using an optimization algorithm or a more limited systematic study, here we perform a detailed mapping of the 3D parameter space defined by (u0, η, τ) for several alternative meridional flow profiles. This extensive mapping of the parameter space is supported by our choice to employ a source term representing an idealized cycle (as discussed below in more detail) instead of constructing the source based on the observation of a particular solar cycle.
3. Observational constraints and choice of merit
The amplitude of the Sun’s poloidal magnetic field at sunspot minimum is known to be a good predictor of the amplitude of the subsequent solar cycle (Petrovay 2019). SFT models offer a way to to extend the temporal scope of this cycle precursor, provided they are optimized to best reproduce the observed variation of the solar poloidal field. In order to determine what are the salient features of this variation, to be reproduced in the models, in Fig. 1 we show the temporal variation of two measures of the poloidal field, contrasted with the variation of the sunspot number. In line with standard practice in solar physics (e.g. in determining sunspot cycle maxima and minima), all curves have been smoothed with a 13-month sliding window. The solid black line shows the smoothed amplitude of the polar magnetic field strength measured at Wilcox Solar Observatory (WSO) averaged over 55–90° latitudes along the central meridian over both poles. The geometry is illustrated in Fig. 1 of Svalgaard et al. (1978). It is thus approximately given by
where 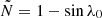 and λ0 = 55° is the lowest latitude of the polemost pixel. The factor 1.8 accounts for magnetograph saturation, (cf. Svalgaard et al. 1978). The plotted line is the average of the unsigned amplitude at the two poles.
and λ0 = 55° is the lowest latitude of the polemost pixel. The factor 1.8 accounts for magnetograph saturation, (cf. Svalgaard et al. 1978). The plotted line is the average of the unsigned amplitude at the two poles.
 |
Fig. 1. Hemispherically averaged polar field amplitude from the WSO data set (black solid) and the global axial dipole moment (red dot-dashed) as a function of time. The monthly sunspot number series (blue dashed) is shown for comparison, with an arbitrary rescaling. All curves were smoothed with a 13-month sliding window. Times of sunspot minima are marked by the dashed vertical lines. Global dipole amplitudes were obtained by courtesy of Jie Jiang and represent the average of values computed for all available data sets at the given time (Jiang et al. 2018). |
Also shown is an alternative measure of the amplitude of the poloidal field component, the axial dipole coefficient, i.e. the amplitude of the coefficient of the 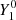 term in a spherical harmonic expansion of the distribution of the radial magnetic field strength over the solar disk:
term in a spherical harmonic expansion of the distribution of the radial magnetic field strength over the solar disk:
where 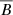 denotes the azimuthally averaged radial magnetic field. In solar physics literature this dipole coefficient is normally referred to as the solar (axial) dipole moment. Dipole moment, as usually defined in physics, has a different dimension but it is indeed proportional to D.
denotes the azimuthally averaged radial magnetic field. In solar physics literature this dipole coefficient is normally referred to as the solar (axial) dipole moment. Dipole moment, as usually defined in physics, has a different dimension but it is indeed proportional to D.
The behavior of the curves in Fig. 1 shows that the times of dipole reversal are usually rather sharply defined, (in the sense dipole moment values below, say, 10% of the peak are only observed in time intervals that are much shorter than the cycle period). Based on the plotted data the overall dipole is found to reverse 3.44 ± 0.18 years after the minimum, while the WSO field characterizing the polar contribution to the dipole reverses after 4.33 ± 0.36 years. The formal 1σ errors here correspond to the standard deviations calculated for the 4 observed reversals – admittedly a very low number. The low scatter in these values suggests that the cycle phase of polar dipole reversal may be a sensitive test of SFT and dynamo models.
In contrast to reversal times, maxima of the dipole amplitude are much less well defined (occurring 7.27 ± 1.38 and 8.33 ± 1.08 years after minimum for the two curves). The curves display broad, slightly slanting plateaus covering about 3–5 years (Iijima et al. 2017); the dipole amplitude at the time of solar minimum is still typically 84 ± 12% (global dipole) and 90 ± 6% (polar fields) of its maximal value, reached years earlier.
A further well-known empirical result is that around solar minimum the poloidal field has a “topknot” structure (a field distribution that is much more concentrated toward the poles than a dipole configuration, Sheeley et al. 1989). Owing to the limited resolution and projection effects, the latitude dependence of this field can only be determined indirectly, exploiting the annual variation of the tilt of the solar axis relative to the line of sight and comparing the resulting modulation in the longitudinal field with fits of the form B ∼ sinnλ. As discussed in detail by Petrie (2015), various determinations of n have yielded values in the range 8–9. As in our models the field profiles are not necessarily well fitted by sinnλ we characterize the extent of the topknot with the latitude λ1/2 where B drops to half its value at the pole. The observational constraints indicating that n > 7 imply λ1/2 > 65°. The upper limit may be less well defined due to the limited resolution; so here we adopt λ1/2 < 75° – a rather generous value compared to the 69° that corresponds to n = 10.
These empirical limits on polar field variation are summarized in Table 1. For use in solar cycle prediction based on the polar precursor method we require that SFT models of a “typical” solar cycle must satisfy the listed five constraints. In view of the rather high uncertainty in the value of the mean related to the very low number of observed cycles, in our parameter study we will we extend the allowed domain to ±2σ. (Note that, as σ is the standard deviation of the data, the uncertainty of the mean is only half that -so our study actually allows for a generous ±4σ uncertainty in the value of the mean).
Observational constraints on the variation of the poloidal field in a typical cycle.
We reiterate that these values have been determined for the last four solar cycles (21–24), Fig. 1, after smoothing the data with a 13-month sliding window, and the errors given in Table 1 are standard deviations calculated for the four cycles 21–24. For example, the reversal times of the WSO field amplitudes for the individual cycles, counted from the last minimum, are 4.50, 3.92, 4.08, and 4.83 years, while for the dipole moment values they were 3.42, 3.27, 3.33, and 3.75 years, respectively. For λ1/2 the nominal values shown in the table correspond to a fiducial ±2σ interval of 65°–75°, adopted as discussed above.
4. Model
As our intention here is to model “typical” or “average” solar cycles, our source function will not consist of individual ARs but a smooth distribution representing the probability distribution of the emergence of preceding (p) and following (f) polarities on the solar surface. By its nature this source is then axially symmetric, so our whole SFT model will be reduced to one dimension:
where R is the solar radius and S is the source representing flux emergence.
4.1. Meridional flow
For the meridional flow we consider three different profiles that have been used in SFT or dynamo models for cycle prediction (Fig. 2).
 |
Fig. 2. Meridional flow profiles applied in the study. |
Flow 1: a simple sinusoidal profile
This profile was used e.g. by Dikpati et al. (2006) and Cameron & Schüssler (2007), with u0 = 14.5 m s−1, η = 300 km2 s−1 and τ = 5.6 yr.
Flow 2: a sinusoidal profile with a dead zone around the poles,
This profile was used by van Ballegooijen et al. (1998) and in numerous papers by the MPS/Beijing group (Cameron et al. 2010; Jiang et al. 2014; Jiang & Cao 2018), with λ0 = 75°, u0 = 11 m s−1, η = 250 km2 s−1 and τ = ∞.
Flow 3: a profile peaking at high latitudes,
This profile was used by Lemerle & Charbonneau (2017). 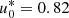 is a normalization factor defined so that u0 gives the maximum meridional flow velocity, like in the other profiles.
is a normalization factor defined so that u0 gives the maximum meridional flow velocity, like in the other profiles.
4.2. Source term
Our source term is a smooth distribution representing the probability distribution of the emergence of p- and f- polarities on the solar surface. Similar to the approach of Dikpati et al. (2006) and Cameron & Schüssler (2007), we represent the source by a pair of rings of opposite magnetic polarity:
where k = ±1 is a factor alternating between even and odd cycles. Am is an arbitrary amplitude that depends on the flow profile (0.003, 0.015 and 0.0005 for our three profiles, respectively) used to ensure that the resulting polar field amplitude roughly agrees with observations (even though the amplitudes produced in this linear model are not used as a merit in the optimization). The latitudinal profile S2[λ;λ0(t),δλ] is a Gaussian with a fixed full width at half-maximum of 2δλ = 6°, migrating equatorward during the course of a cycle:
The latitudinal separation of the rings comes as a consequence of Joy’s law:
while their trajectory over the course of a cycle is given by a quadratic fit derived by Jiang et al. (2011) from many observed solar cycles:
where P = 11 year is the cycle period.
Finally, the time profile of solar activity in a typical cycle was determined by Hathaway et al. (1994) from the average of many cycles as
with a = 0.00185, b = 48.7, c = 0.71, where tc is the time since the last cycle minimum.
In addition to the quadratic source term described above, an alternate form of the source term was also considered, to check the sensitivity of the results on this choice. The alternate form had a linear trajectory instead of Eq. (10) and a constant latitudinal separation of 1° between the flux rings, while in other respects it was identical to the above.
4.3. Model grid
For each choice of meridional flow profile and source function we computed 1105 models with different parameter combinations. u0 was allowed to vary between 5 and 20 m s−1 in steps of 2.5; η varied from 50 to 750 km2 s−1 in steps of 50, while τ varied from 2 to 10 years in steps of 1 year, and two additional values (τ = 20 and τ = 100) were also considered, the latter value being effectively equivalent to a negligible decay term in Eq. (3). The transport equation was solved with a simple explicit code, making sure that the resolution ensures flux conservation to an acceptable degree so as not to appreciably influence the results. A latitudinal grid spacing of 0.5° and a timestep of 6 h was found to suffice in most cases. Our code is made available on GitHub1 to ensure reproducibility of the results. Starting from an arbitrary (dipole) initial state, the calculations were run for 20 solar cycles, until very nearly steady oscillations set in. At that point we evaluated whether a given model complies with the imposed observational constraints listed in Table 1.
4.4. Parameter maps
Figures 3–5 show examples of a “good” and a “bad” solution. The left-hand panels of Figs. 3 and 4 present the time variation of the actual value of the polar magnetic field strength B(θ = 0), the value measured by WSO (Eq. (1)) and the global dipole moment (Eq. (2)). The right-hand panels in these figures, in turn, display the latitudinal profiles of B at solar minimum and at the instants when the measures of polar field amplitude plotted in the left panels take their maxima. Figure 5 displays the spatiotemporal variation of B against time and latitude, i.e. the magnetic butterfly diagram characterizing these simulations.
 |
Fig. 3. Example of a solution satisfying all observational constraints on the polar magnetic field: temporal variation and latitudinal profiles for u0 = 10 m s−1, η = 600 km2 s−1 and τ = 7 yr (Flow 1). Time variations of various quantities are shown in the left panel: in the label of the dotted curve B refers to the field amplitude at the pole; vertical dashed lines mark the reversals of the WSO polar field. Right panel: latitudinal profile of the magnetic field at various instants as indicated; vertical dashed lines mark the latitudes where B equals half its value at the poles at cycle minimum. |
 |
Fig. 4. Example of a solution at odds with several observational constraints on the polar magnetic field: temporal variation and latitudinal profiles. for u0 = 12.5 m s−1, η = 500 km2 s−1 and τ = 5 yr (Flow 2). Notations as in Fig. 3. |
 |
Fig. 5. Butterfly diagrams (plots of the field strength against time and latitude) of the example solutions shown in Figs. 3 and 4. |
While at first sight similar, these plots indicate that in the second case the polar topknot is too broad and the polar reversal occurs too early in comparison with the observational constraints listed in Sect. 3, imposed with a generous limit of 2σ (or 4σ in terms of the uncertainty of the mean, cf. discussion in Sect. 3).
For the two cases plotted, λ1/2 takes the value 71° and 64°, respectively, while the WSO field is reversed 4.0 and 3.4 years after the minimum. Comparing this with the values in Table 1, both values fall within the allowed ±2σ interval in the first case, while both fall outside it in the second. The second set of parameter is therefore discarded as incompatible with the observational constraints on the polar field, while the first model is admissible by all five constraints.
Such comparisons can be performed for each parameter combination in our model grids, and as a result, admitted and discarded domains in the 3D (u0, η, τ) parameter space can be identified. In order to visualize these domains, we construct 2D maps of slices of the parameter space with fixed values of τ. In these 2D maps the allowed domain is shown unmasked, in more vivid colors, while the excluded domain is shown through a semitransparent dotted grey mask, in pale colors. One set of such maps for flow profile 2 at τ = 100 yr is shown in Fig. 6, where the colored panels represent the first three merit parameters listen in Table 1 on the u0–η plane. The allowed domains are shown combined in the middle right panel, the darkest gray showing the domain allowed by all three criteria.
 |
Fig. 6. Set of maps of the u0–η parameter plane for the case of τ = 100 yr, flow type 2. Colour coded maps show the distribution of three merit variables, with the excluded domain masked out (less vivid hues and dotted). Allowed domains are shown combined in grey in the bottom right panel. Units are m s−1 for u0, km2 s−1 for η, years for time and degrees for latitude. |
The last two merit criteria related to the global dipole moment are not included in this plot partly for clarity and partly because these criteria were found to be most sensitive to τ, so in slices taken at fixed values of τ either the allowed or the excluded domain tends to cover the whole plane. This is separately borne out in Fig. 7 where slices of the 3D parameter space orthogonal to the slices in Fig. 6 are shown, mapping the distribution of the merit parameters associated with the dipole moment. It is apparent that these parameters are indeed mainly controlled by τ: for shorter values of τ the global field decays faster, so it reverses earlier and declines more significantly from its maximum to the end of the cycle.
 |
Fig. 7. Set of maps of the u0–τ parameter plane for the case of η = 500 (top), and of the η–τ plane for u0 = 10, showing allowed and excluded domains for the dipole reversal time (left) and ratio of dipole moment at cycle minimum to the maximal dipole moment (right). Units are m s−1 for u0, km2 s−1 for η and years for τ. |
5. Discussion
One immediate conclusion from these studies follows directly from our above mentioned observation that the time variation of the dipole moment primarily depends on τ. In fact we find that for higher values of τ, i.e. without a significant decay term in the transport equation, the global dipole moment invariably reverses too late in the cycle. This is seen in Fig. 7; the equivalent plots look similar also for other flow types and other values of u0 or η.
In contrast to this, we find that a range of shorter decay times exists where, with our realistic source function, all five merit criteria can be satisfied in some part of the parameter space. This range of τ lies somewhere between 5 and 10 years for all three flow types considered (though exact limits of the range depend on the flow profile).
All this can be taken as evidence for the need for a decay term in the transport equation for the realistic modelling of the time variation of the global dipole moment in an average cycle. As in our models intercycle variations are not present, this line of evidence is independent from the drift in dipole moment that originally motivated the introduction of the decay term (Schrijver et al. 2002 – cf. discussion in Sect. 1 above).
For the allowed solution with τ in the range 5–10 years, higher diffusivity values (500 km2 s−1 and above) are generally favoured, i,e. the bulk of the allowed domain lies here. In the case of the flow with a polar dead zone (flow type 2, Fig. 8) the value of u0 generally also needs to be high (≳15 m s−1) or the topknot becomes too broad; however, a narrow band of allowed solutions along a line of constant η/u0 ratio also exists.
From this, the parameter combination u0 = 11 m s−1 and η = 250 km2 s−1 used by Cameron et al. (2010) or Jiang & Cao (2018) stands out as admissible with a τ value of about 8 years, while for τ ≳ 10 it produces too late dipole reversals in the “average” cycle studied here.
Turning our attention now to the pole-reaching flows (types 1 and 3), we find that the allowed domain that exists in the range τ ≃ 5 − 9 invariably lies in the top left part of our parameter plane, i.e. combinations with higher diffusivity and lower flow speed are preferred. This is mainly due to the topknot width constraint: it was already shown by Sheeley et al. (1989) that the topknot width for pole-reaching flows scales with η/u0, thus becoming too broad for higher values of this parameter.
In particular, with the flow profile obtained in the 2 × 2D dynamo model of Lemerle & Charbonneau (2017) polar fields will only show fully solar-like behavior for η/u0 ≳ 150 (e.g. for u0 ≳ 5 m s−1η ≳ 700 km2 s−1) and τ ∼ 5 − 9 yr. In contrast, the values u0 = 17 km s−1, η = 600 km2 s−1 and τ = 10 yr, resulting from their globally optimized solution, yield a too narrow topknot and a delayed dipole reversal (Fig. 9). The reason why this parameter set was obtained by Lemerle & Charbonneau (2017) as an optimized solution clearly lies in their different choice of merit and their combined optimization of an SFT model and a coupled dynamo model, instead of using a source term modeled on observations.
Overall, the admitted domain is found to be the most extensive for a simple sinusoidal flow profile with τ ≃ 7 (Fig. 10). In this case, practically the whole upper left half of the u0–η plane is allowed. Taken by themselves, then, the polar field constraints considered in this paper would suggest the use of this simple flow model for cycle prediction purposes with a η/u0 ratio exceeding about 50.
As mentioned at the end of Sect. 4.2, for comparison we also considered a less realistic choice of the source function, with a linear decrease in AR latitudes during the cycle and no accompanying variation in the tilt. Results for this case are available from the GitHub repository. It was found that there exist no parameter combinations where all five merit criteria can be simultaneously satisfied in this case. This shows that satisfying our criteria is non-trivial, and the very existence of admissible solutions indirectly supports the correctness of our choice for the source function.
6. Conclusion
In this paper we mapped the parameter space of surface flux transport models from the point of view of the spatiotemporal variation of the polar field resulting with a source term representing an average solar cycle, marking the allowed domain compatible with observational constraints. In Sect. 2 we argued that other methods of constraining parameter space are less well suited for applications of SFT to solar cycle prediction.
A key finding of this work was that without a significant decay term in the SFT equation (i.e., for τ > 10 yr) the global dipole moment reverses too late in the cycle for all flow profiles and parameters. This provides independent supporting evidence for the need of the inclusion of a decay term in SFT models even for identical cycles.
The question may arise whether this conclusion is related to our use of a rather restricted range (about ±4 months) allowed for the dipolar moment reversal time, derived from the average of all available observational datasets. Indeed, considering individual datasets, the dipole reversal often deviates by several months (in rare cases by even a year) from the averaged set. However, our parameter maps for the dipole moment reversal time (e.g., Fig. 7) show that for τ = 100 no reasonable extension of the allowed range can account for the delay in the dipole reversal time which in these cases well exceeds two years in all cases. We further note that anecdotal evidence exists in the literature for cases where the dipole reversal time of one individual cycle was apparently well reproduced in SFT models without a decay term (DeVore et al. 1985; Wang et al. 1989; Jiang & Cao 2018). While none of these studies was comprehensive enough to draw general conclusions beyond the particularities of a given cycle, the roots of this apparent puzzle clearly need to be understood. It is worth noting that recently Virtanen et al. (2017) also confirmed the need for a decay term in order to attain polar reversal in Cycle 24.
Turning now to models with a decay term, an allowed domain was found to exist for τ values in the 5–10 yr range for all flow profiles considered. Generally higher values of η (500–800) are preferred, though some solutions with lower η are still allowed. The admitted domain was found to be the most extensive for a simple sinusoidal flow profile with τ ≃ 7 (Fig. 10): in this case, practically the whole upper left half of the u0–η plane is allowed. Taken by themselves, then, the polar field constraints considered in this paper would suggest the use of this simple flow model with the η/u0 ratio exceeding about 50.
It may be worth comparing these results with those of Whitbread et al. (2017), who used the PIKAIA algorithm to optimize the SFT models for different regimes. The flow profile used in these models differed from our profiles and was relatively closest to our profile 2. The properties of the source also differed and the merit criterion was to optimize overall agreement with observed magnetograms, rather than with the polar field. Their results, summarized in their Table 1, indicate admissible ranges for u0 and η comparable to our results for flow type 2; however, their preferred ranges for τ are shorter than ours, in the range 1.5–6 years, except for one configuration of the source term where significantly higher values were admitted. It is to be noted that, as we discussed in Sect. 3 above, the neglect of 3D transport processes renders SFT modelling an essentially phenomenological approach to the description of magnetic flux transport where the effective flows, diffusivities or decay times yielding a good fit to observations do not necessarily correspond to their actual values on the solar surface. In view of this it may not come as a big surprise that optimization for different merit functions may lead to different results. The choice of parameters will simply need to be adapted to the objectives of the modelling.
A plausible further extension of this work would admit intercycle variations in cycle amplitudes and periods, focusing on how SFT parameter choices influence the interplay of stochastic and nonlinear effects.
Acknowledgments
This research was supported by the Hungarian National Research, Development and Innovation Fund (grant no. NKFI K-128384) and by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 739500.
References
- Baumann, I., Schmitt, D., Schüssler, M., & Solanki, S. 2004, A&A, 426, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baumann, I., Schmitt, D., & Schüssler, M. 2006, A&A, 446, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, R., & Schüssler, M. 2007, ApJ, 659, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R. H., Jiang, J., Schmitt, D., & Schüssler, M. 2010, ApJ, 719, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, R., & Zhao, J. 2017, ApJ, 849, 144 [Google Scholar]
- DeVore, C., Sheeley, Jr., N., Boris, J., Young, Jr., T., & Harvey, K. 1985, Aust. J. Phys., 38, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Dikpati, M., De Toma, G., & Gilman, P. A. 2006, Geophys. Res. Lett., 33, L05102 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H. 1996, ApJ, 460, 1027 [Google Scholar]
- Hathaway, D. H., Wilson, R. M., & Reichmann, E. J. 1994, Sol. Phys., 151, 177 [Google Scholar]
- Iida, Y. 2016, J. Space Weather Space Clim., 6, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iijima, H., Hotta, H., Imada, S., Kusano, K., & Shiota, D. 2017, A&A, 607, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Imada, S., & Fujiyama, M. 2018, ApJ, 864, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., & Cao, J. 2018, J. Atmos. Sol. Terrest. Phys., 176, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Schüssler, M. 2011, A&A, 528, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, J., Hathaway, D., Cameron, R., et al. 2014, Space Sci. Rev., 186, 491 [Google Scholar]
- Jiang, J., Wang, J.-X., Jiao, Q.-R., & Cao, J.-B. 2018, ApJ, 863, 159 [Google Scholar]
- Lemerle, A., & Charbonneau, P. 2017, ApJ, 834, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Lemerle, A., Charbonneau, P., & Carignan-Dugas, A. 2015, ApJ, 810, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C.-H., & Chou, D.-Y. 2018, ApJ, 860, 48 [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., del Toro Iniesta, J. C., et al. 2007, ApJ, 670, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Pesnell, W. D. 2008, Sol. Phys., 252, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Petrie, G. J. D. 2015, Liv. Rev. Sol. Phys., 12, 5 [CrossRef] [Google Scholar]
- Petrovay, K. 2010, Liv. Rev. Sol. Phys., 7, 6 [Google Scholar]
- Petrovay, K. 2019, ArXiv e-prints [arXiv:1907.02107] [Google Scholar]
- Petrovay, K., & Szakály, G. 1999, Sol. Phys., 185, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Schad, A., Timmer, J., & Roth, M. 2011, ApJ, 734, 97 [Google Scholar]
- Schrijver, C. J., & Zwaan, C. 2000, Solar and Stellar Magnetic Activity (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Schrijver, C. J., De Rosa, M. L., & Title, A. M. 2002, ApJ, 577, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Sheeley, Jr., N. R. 2005, Liv. Rev. Sol. Phys., 2, 5 [Google Scholar]
- Sheeley, N., Boris, J., Young, T., DeVore, C., & Harvey, K. 1983, Symposium-International Astronomical Union (Cambridge: Cambridge University Press), 102, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Sheeley, Jr., N. R., Wang, Y.-M., & DeVore, C. R. 1989, Sol. Phys., 124, 1 [Google Scholar]
- Stix, M. 2004, The Sun: An Introduction (Berlin: Springer) [Google Scholar]
- Svalgaard, L., Duvall, Jr., T., & Scherrer, P. 1978, Sol. Phys., 58, 225 [Google Scholar]
- van Ballegooijen, A., Cartledge, N., & Priest, E. 1998, ApJ, 501, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, I. O. I., Virtanen, I. I., Pevtsov, A. A., Yeates, A., & Mursula, K. 2017, A&A, 604, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y.-M., Nash, A., & Sheeley, Jr., N. 1989, ApJ, 347, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y. M., & Sheeley, Jr., N. R. 1994, ApJ, 430, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M., Lean, J., & Sheeley, Jr., N. 2000, Geophys. Res. Lett., 27, 505 [Google Scholar]
- Wang, Y.-M., Sheeley, Jr., N. R., & Lean, J. 2002, ApJ, 580, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Whitbread, T., Yeates, A. R., Muñoz-Jaramillo, A., & Petrie, G. J. D. 2017, A&A, 607, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitbread, T., Yeates, A. R., & Muñoz-Jaramillo, A. 2019, A&A, 627, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilcox, J. M., Schatten, K. H., Tanenbaum, A. S., & Howard, R. 1970, Sol. Phys., 14, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J., Kosovichev, A. G., & Bogart, R. S. 2014, ApJ, 789, L7 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Observational constraints on the variation of the poloidal field in a typical cycle.
All Figures
 |
Fig. 1. Hemispherically averaged polar field amplitude from the WSO data set (black solid) and the global axial dipole moment (red dot-dashed) as a function of time. The monthly sunspot number series (blue dashed) is shown for comparison, with an arbitrary rescaling. All curves were smoothed with a 13-month sliding window. Times of sunspot minima are marked by the dashed vertical lines. Global dipole amplitudes were obtained by courtesy of Jie Jiang and represent the average of values computed for all available data sets at the given time (Jiang et al. 2018). |
| In the text | |
 |
Fig. 2. Meridional flow profiles applied in the study. |
| In the text | |
 |
Fig. 3. Example of a solution satisfying all observational constraints on the polar magnetic field: temporal variation and latitudinal profiles for u0 = 10 m s−1, η = 600 km2 s−1 and τ = 7 yr (Flow 1). Time variations of various quantities are shown in the left panel: in the label of the dotted curve B refers to the field amplitude at the pole; vertical dashed lines mark the reversals of the WSO polar field. Right panel: latitudinal profile of the magnetic field at various instants as indicated; vertical dashed lines mark the latitudes where B equals half its value at the poles at cycle minimum. |
| In the text | |
 |
Fig. 4. Example of a solution at odds with several observational constraints on the polar magnetic field: temporal variation and latitudinal profiles. for u0 = 12.5 m s−1, η = 500 km2 s−1 and τ = 5 yr (Flow 2). Notations as in Fig. 3. |
| In the text | |
 |
Fig. 5. Butterfly diagrams (plots of the field strength against time and latitude) of the example solutions shown in Figs. 3 and 4. |
| In the text | |
 |
Fig. 6. Set of maps of the u0–η parameter plane for the case of τ = 100 yr, flow type 2. Colour coded maps show the distribution of three merit variables, with the excluded domain masked out (less vivid hues and dotted). Allowed domains are shown combined in grey in the bottom right panel. Units are m s−1 for u0, km2 s−1 for η, years for time and degrees for latitude. |
| In the text | |
 |
Fig. 7. Set of maps of the u0–τ parameter plane for the case of η = 500 (top), and of the η–τ plane for u0 = 10, showing allowed and excluded domains for the dipole reversal time (left) and ratio of dipole moment at cycle minimum to the maximal dipole moment (right). Units are m s−1 for u0, km2 s−1 for η and years for τ. |
| In the text | |
 |
Fig. 8. Same as Fig. 6 for the case of τ = 7, flow type 2. |
| In the text | |
 |
Fig. 9. Same as Fig. 6 for the case of τ = 10, flow type 3. |
| In the text | |
 |
Fig. 10. Same as Fig. 6 for the case of τ = 7, flow type 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



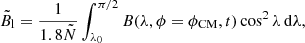
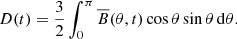
![$$ \begin{aligned} \frac{\partial B}{\partial t} =&\frac{1}{R\cos {\lambda }}\frac{\partial }{\partial \lambda }\left[Bu(\lambda )\cos {\lambda }\right] \nonumber \\&+\frac{\eta }{R^2\cos {\lambda }} \frac{\partial }{\partial \lambda }\left(\cos {\lambda }\frac{\partial B}{\partial \lambda }\right) -\frac{B}{\tau } + S(\lambda ,t) \end{aligned} $$](/articles/aa/full_html/2019/12/aa36099-19/aa36099-19-eq6.gif)
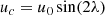
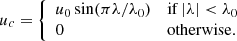
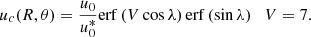
![$$ \begin{aligned} S(\lambda ,t)=&kA_m S_1(t) S_2\left[\lambda ;\lambda _0(t)-\Delta \lambda (t),\delta \lambda \right] \nonumber \\&-kA_m S_1(t) S_2\left[\lambda ;\lambda _0(t)+\Delta \lambda (t),\delta \lambda \right] \nonumber \\&+kA_m S_1(t) S_2\left[\lambda ;-\lambda _0(t)-\Delta \lambda (t),\delta \lambda \right] \nonumber \\&-kA_m S_1(t) S_2\left[\lambda ;-\lambda _0(t)+\Delta \lambda (t),\delta \lambda \right] \end{aligned} $$](/articles/aa/full_html/2019/12/aa36099-19/aa36099-19-eq11.gif)
![$$ \begin{aligned} S_2(\lambda ;\lambda _0,\delta \lambda ) = \exp \left[-(\lambda -\lambda _0)^2/2\delta \lambda ^2\right]. \end{aligned} $$](/articles/aa/full_html/2019/12/aa36099-19/aa36099-19-eq12.gif)
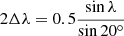
![$$ \begin{aligned} \lambda _0\,[^\circ ] = 26.4 - 34.2 (t/P) + 16.1(t/P)^2 \end{aligned} $$](/articles/aa/full_html/2019/12/aa36099-19/aa36099-19-eq14.gif)
![$$ \begin{aligned} S_1(t)= at^{3}_{c}/[\exp (t^{2}_{c}/b^{2})- c] \end{aligned} $$](/articles/aa/full_html/2019/12/aa36099-19/aa36099-19-eq15.gif)