| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 18 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201936006 | |
| Published online | 27 November 2019 | |
KiDS-SQuaD
II. Machine learning selection of bright extragalactic objects to search for new gravitationally lensed quasars⋆
1
Institute of Astronomy, V. N. Karazin Kharkiv National University, 35 Sumska Str., Kharkiv, Ukraine
e-mail: vld.khramtsov@gmail.com
2
Institute of Radio Astronomy of the National Academy of Sciences of Ukraine, 4 Mystetstv Str., Kharkiv, Ukraine
e-mail: alexey.v.sergeyev@gmail.com
3
INAF – Osservatorio Astronomico di Capodimonte, Salita Moiariello, 16, 80131 Napoli, Italy
e-mail: chiara.spiniello@gmail.com
4
European Southern Observatory, Karl-Schwarschild-Str. 2, 85748 Garching, Germany
5
INAF – Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
6
School of Physics and Astronomy, Sun Yat-sen University, 2 Daxue Road, Tangjia, Zhuhai, Guangdong 519082, PR China
7
DARK, Niels Bohr Institute, Copenhagen University, Lyngbyvej 2, 2100 Copenhagen, Denmark
8
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
9
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
10
INAF – Osservatorio Astronomico di Padova, Via dell’Osservatorio 5, 35122 Padova, Italy
11
Shanghai Astronomical Observatory (SHAO), Nandan Road 80, Shanghai 200030, PR China
12
College of Physics of Jilin University, Qianjin Street 2699, Changchun 130012, PR China
Received:
3
June
2019
Accepted:
8
October
2019
Context. The KiDS Strongly lensed QUAsar Detection project (KiDS-SQuaD) is aimed at finding as many previously undiscovered gravitational lensed quasars as possible in the Kilo Degree Survey. This is the second paper of this series where we present a new, automatic object-classification method based on the machine learning technique.
Aims. The main goal of this paper is to build a catalogue of bright extragalactic objects (galaxies and quasars) from the KiDS Data Release 4, with minimum stellar contamination and preserving the completeness as much as possible. We show here that this catalogue represents the perfect starting point to search for reliable gravitationally lensed quasar candidates.
Methods. After testing some of the most used machine learning algorithms, decision-tree-based classifiers, we decided to use CatBoost, which was specifically trained with the aim of creating a sample of extragalactic sources that is as clean of stars as possible. We discuss the input data, define the training sample for the classifier, give quantitative estimates of its performances, and finally describe the validation results with Gaia DR2, AllWISE, and GAMA catalogues.
Results. We built and made available to the scientific community the KiDS Bright EXtraGalactic Objects catalogue (KiDS-BEXGO), specifically created to find gravitational lenses but applicable to a wide number of scientific purposes. The KiDS-BEXGO catalogue is made of ≈6 million sources classified as quasars (≈200 000) and galaxies (≈5.7 M) up to r < 22m. To demonstrate the potential of the catalogue in the search for strongly lensed quasars, we selected ≈950 “Multiplets”: close pairs of quasars or galaxies surrounded by at least one quasar. We present cutouts and coordinates of the 12 most reliable gravitationally lensed quasar candidates. We showed that employing a machine learning method decreases the stellar contaminants within the gravitationally lensed candidates, comparing the current results to the previous ones, presented in the first paper from this series.
Conclusions. Our work presents the first comprehensive identification of bright extragalactic objects in KiDS DR4 data, which is, for us, the first necessary step towards finding strong gravitational lenses in wide-sky photometric surveys, but has also many other more general astrophysical applications.
Key words: gravitational lensing: strong / methods: data analysis / surveys / catalogs / quasars: general / galaxies: general
The KiDS Bright EXtraGalactic Objects (KiDS-BEXGO) catalogue is also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/632/A56
© ESO 2019
1. Introduction
Modern deep and wide-field sky photometric surveys offer an unprecedented opportunity to collect large amounts of data for statistical studies of the nearby and far-away universe. Over the last decade, they have provided new insights into the structure of our own Galaxy as well as of the extragalactic objects at all scales, from giant galaxies to faint and compact stellar systems. Deep surveys allow us to trace the mass assembly of galaxy clusters and to map the intracluster light components (globular clusters, dwarf galaxies, and diffuse light). They have also opened the time domain leading to a new understanding of the transient phenomena in the universe.
One of the fields where large sky surveys can be of precious help is strong gravitational lensing and in particular in finding new lensed quasars. Strong gravitationally lensed quasars are very rare objects: one quasar in ∼103.5 is expected to be strongly lensed for i-band-limiting magnitude deeper than i ≈ 21m (see e.g. Fig. 3 and Sect. 3.1 in Oguri & Marshall 2010). However, it was clear upon their first discovery (Walsh et al. 1979) that these systems are extremely useful tools for observational cosmology and extragalactic astrophysics (see e.g. the review by Kochanek 2006).
When a quasar is strongly lensed by a galaxy, it results in multiple images of the same source, accompanied by arcs or rings that map the lensed host of the quasar. The light curves of different images are offset by measurable time delays that depend on the cosmological distances to lens and source and on the gravitational potential of the lens (Refsdal 1964). This in turn enables one-step measurements of the expansion history of the Universe (primarily H0, Suyu et al. 2014) and the dark matter halos of massive lens galaxies (Keeton & Moustakas 2009; Zackrisson & Riehm 2010; Gilman et al. 2018; Liao et al. 2018).
In addition to the deflection caused by the lens, the light of the quasar can also be deflected by the gravitational field of other low-mass bodies moving along the line-of-sight (10−6 < m/M⊙ < 103, e.g. single stars, brown dwarfs, planets, globular clusters, etc.). This microlensing phenomenon provides a quantitative handle on the stellar content of the lens galaxies (Schechter & Wambsganss 2002; Bate et al. 2011; Oguri et al. 2014), and can simultaneously provide constraints on the inner structure of the source quasar, namely accretion disk size, thermal profile, and the geometry of the broad-line region (Anguita et al. 2008; Sluse et al. 2011; Motta et al. 2012; Guerras et al. 2013; Braibant et al. 2014). Finally, compared with galaxy–galaxy lenses, lensed quasars are detectable down to smaller image-separations, thereby ensuring more complete coverage of the lens mass range.
Unfortunately, progress in these fields has been limited by the paucity of confirmed systems. This is why in the last decade enormous effort has been devoted, in conjunction with the advent of deep wide-field sky photometric surveys, to the search for new lenses. These surveys offer an unprecedented opportunity to search for strong gravitational lenses on a much larger portion of the sky (Oguri et al. 2006; Treu et al. 2015; Lemon et al. 2017; Rusu et al. 2019; Agnello et al. 2018a,b; Agnello & Spiniello 2019). However, it is necessary to develop and use sophisticated automated methods (e.g. Decision Trees, Quinlan 1986, Naïve Bayes, Duda & Hart 1973, Neural Networks, Rumelhart et al. 1986, Support Vector Machines, Vapnik 1995; Cortes & Vapnik 1995) to process the very large amount of data that the surveys provide.
Obviously, the first step to find gravitationally lensed quasars is to classify objects, selecting extragalactic objects among millions of sources, while minimizing stellar contamination as much as possible. More generally speaking, the identification of extragalactic objects, quasars, and galaxies at all redshifts is an all-important task that can help to answer to a wide range of astrophysical and cosmological questions, such as the relationship between active galactic nuclei (AGNs) and host galaxies or the cosmic evolution of super massive black holes or the formation and evolution of galaxies (Driver et al. 2009) across cosmic time (Kauffmann & Haehnelt 2000; Haehnelt & Kauffmann 2000; Wyithe & Loeb 2003; Hopkins et al. 2006; Shankar et al. 2009; Shen et al. 2009).
Machine learning (ML) methods have proven to be very effective in identifying and classifying extragalactic sources (e.g. Eyer & Blake 2005; Elting et al. 2008; Kim et al. 2011; Gieseke et al. 2011; Kovács & Szapudi 2015; Brescia et al. 2015; Peters et al. 2015; Krakowski et al. 2016, 2018; Viquar et al. 2018; Khramtsov & Akhmetov 2018; Nolte et al. 2019; Bai et al. 2019) with respect to any manual colour cut. A specific type of classifiers, the ensembles of decision trees, were shown to be advantageous in the identification of extragalactic sources, and in particular quasars (Ball et al. 2006; Carrasco et al. 2015; Hernitschek et al. 2016; Schindler et al. 2017, 2018; Sergeyev et al. 2018; Jin et al. 2019; Nakoneczny et al. 2019). They allow the user to explore, with a little human intervention and affordable computing time, large datasets, thus selecting candidates with less stringent pre-selection criteria, maximizing the precision (recovery rate), and minimizing the stellar contamination.
More specifically, ML methods to search for strong gravitational lenses have also been developed, although we note that the large majority of them are built to find galaxy–galaxy lenses, rather than lensed quasars, using a deep learning approach (e.g. Cabanac et al. 2007; Paraficz et al. 2016; Lanusse et al. 2018; Metcalf et al. 2018; Petrillo et al. 2017, 2019a,b; but see also Agnello et al. 2015; Krone-Martins et al. 2018; Jacobs et al. 2019 for lensed quasars).
It is very important to note that at the catalogue-level lensed quasars can be either point-like sources (and hence must be reliably separated from stars), or single extended objects. Indeed, when the deflector gives a non-negligible contribution to the light of the whole system or the multiple images are blended together, the lensing system produces an “extended”, single match in a photometric catalogue, rather than many “point-like” matches. Therefore, the first step towards finding strong gravitationally lensed quasars is to select both galaxies and quasars, possibly discarding all the galactic objects. This is indeed the main focus of this paper, which is the second of the KiDS Strongly lensed QUAsar Detection (KiDS-SQuad) project, and presents an ML classifier specifically designed to remove stellar contaminants from a catalogue of bright extragalactic sources in the Kilo Degree Survey (KiDS, de Jong et al. 2013).
This paper is organized as follows. In Sect. 1 we introduce the search for gravitationally lensed quasars in KiDS. In Sect. 2 we give a general overview of the catalogues and data we use. In Sect. 3 we discuss the method to classify objects and isolate extragalactic ones using optical and infrared deep photometry, and we introduce and describe our own classification pipeline. In Sect. 4 we present the main result of this pipeline: the catalogue of Bright EXtraGalactic Objects from KiDS DR4 – KiDS-BEXGO, as well as different validation tests based on external data to assess the performance of the classifier. Finally, in Sect. 5 we focus on “Multiplets”: close pairs of quasars, or galaxies surrounded by at least one quasar (within 5″), which represent the best strong gravitationally lensed quasar candidates. We present our conclusions and future perspectives in Sect. 6. In addition, we present in the appendix a direct comparison of three different machine learning methods that we tested, all based on decision trees.
The KiDS Strongly lensed QUAsar Detection project. The KiDS survey (de Jong et al. 2013; Kuijken et al. 2019) is ideal to identify and classify objects and to search for strong gravitational lenses thanks to its high spatial resolution (0.2″ pixel−1, Capaccioli & Schipani 2011), excellent (for ground observation standards) seeing quality (mean r-band FWHM ≈ 0.70), depth (25m in r-band), and wide footprint (1350 deg2 have been covered and the data will be released with DR5). Taking advantage of these characteristics of the survey, we recently started the KiDS-SQuaD project presented in Spiniello et al. (2018, hereafter Paper I).
With KiDS-SQuaD, we are carrying out a systematic census of lensed quasars with the final goal being to build a statistically relevant sample of lenses, covering a wide range of parameters (geometrical configurations, deflector masses and morphologies, redshifts, and nature of the sources). This would enable us to study the dark matter halos of lens galaxies up to z ∼ 1 (Schechter & Wambsganss 2002; Bate et al. 2011; Suyu et al. 2014) as well as the quasar-host galaxy co-evolution up to z ∼ 2 (Rusu et al. 2014; Agnello et al. 2016; Ding et al. 2017), to put constraints on the inner structure of the quasar accretion disk (size and thermal profile; e.g. Anguita et al. 2008; Motta et al. 2012) and on the broad-line-region geometry (e.g. Sluse et al. 2011; Guerras et al. 2013; Braibant et al. 2014), and finally to gather precise cosmography (e.g. Suyu et al. 2014, 2017).
The power of KiDS in the object-classification challenge has already been demonstrated in Nakoneczny et al. (2019, hereafter N19) who built and released a catalogue of quasars from KiDS DR3 (440 deg2), classified with a random forest supervised ML model, trained on Sloan Digital Sky Survey DR14 (SDSS DR14, Abolfathi et al. 2018) spectroscopic data. The approach we undertake in this paper is similar to the one presented in N19, as we also use KiDS data as input and SDSS as a training sample, although we fine-tune and customize our pipelines to be more suitable for the search of lensed quasars. Moreover, the biggest difference between these works is that now we have available photometry in nine bands. In fact, the optical data in KIDS are now (starting from DR4, Kuijken et al. 2019) complemented by infrared data from the VISTA Kilo-degree INfrared Galaxy (VIKING) survey, covering the same KiDS area in the Z, Y, J, H, and Ks near-infrared bands (Edge et al. 2013). Thus, the KiDS × VIKING photometric dataset provides a unique deep, wide coverage in nine bands (u, g, r, i, Z, Y, J, H, Ks), which has proven to be extremely effective in separating quasars from stars using photometric characteristics (e.g. Carrasco et al. 2015). Indeed, one of the limitations of the first paper of this series was the manual optical colour selection we used to select quasar-like objects. In the approach taken in this first publication, the number of final lensed quasar candidates highly depends on the selection criteria that are somehow arbitrary and often calibrated on previous findings. Moreover, generally, this number is of the order of 10 ÷ 30 sources per deg2, making the necessary second step of visual inspection very difficult and long. To avoid manual arbitrary cuts and to deal with the larger amount of data coming from the fourth and fifth KiDS Data Release (Kuijken et al. 2019), and above all from new deep, wide-field surveys such as Euclid (Laureijs et al. 2011) or LSST (Ivezić & LSST Science Collaboration 2013), we developed a method based on ML, which we present here. This automatic method allows us to more efficiently pinpoint extragalactic systems while eliminating as much stellar contamination as possible.
Although, as already stated, many ML classifiers have been developed and released, we decided to build our own pipeline in order to be able to fully customize the characteristics and parameters of the algorithm. As we explain in detail in this paper, we require high completeness and purity, in an attempt to build a catalogue of extragalactic objects that is as clean from stars as possible, and at the same time as complete as possible. Therefore, developing our own tool and releasing the resulting catalogue is the best possible choice.
2. Data overview
2.1. The input catalogue from KiDS DR4
The KiDS survey (de Jong et al. 2013) is one of the European Southern Observatory (ESO) public surveys carried on with the VLT Survey Telescope (VST, Capaccioli & Schipani 2011; Capaccioli et al. 2012). Starting from DR4 (Kuijken et al. 2019), KiDS optical photometric data, covering 1350 deg2 in u, g, r, i bands, are complemented with infrared data from the VISTA Kilo-Degree Infrared Galaxy Survey (VIKING, Edge et al. 2013), covering the same region on sky in five near-infrared bands (Z, Y, J, H, Ks). Typical magnitude limits for each of the nine bands are 24.2, 25.1, 25.0, 23.6, 22.7, 22.0, 21.8, 21.1, 21.2 (AB magnitudes, 5σ in 2″ aperture), with seeing generally below 1.0″ (Wright et al. 2019; Kuijken et al. 2019). Throughout this paper we make use of extinction-corrected Gaussian Aperture and PSF (GAaP, Kuijken 2008; Kuijken et al. 2015) magnitudes.
We started from the r-band catalogue, which is the one with the best seeing (0.7″, on average), and we selected 9 596 412 sources with r < 22m and good aperture-matched photometry measured in each of the other eight bands (we removed all the sources with MAGERR_GAAP > 1m in each of the band). Limiting the classification to only bright objects is necessary to avoid any extrapolation to uncovered regions in the space of features. We therefore only consider the magnitude range covered by spectroscopically confirmed objects from the Sloan Digital Sky Survey Data Release 14 (SDSS DR14, Abolfathi et al. 2018) that we use as a training sample. The histogram of the r-band magnitude distribution for the whole KIDS DR4 and for the spectroscopically confirmed objects that we use as a training sample is shown in Fig. 1.
 |
Fig. 1. Histogram of the r magnitude distribution for the full KiDS DR4 catalogue (blue) and the SDSS × KiDS training sample (red). |
The same approach (using the same magnitude threshold) has already been tested and was successfully used for KiDS-DR3 in N19. Finally, as we describe in more detail below, we also use the magnitude-dependent parameter CLASS_STAR for the source classification. This has already proven to be a very important feature in N19.
2.2. The training sample from SDSS DR14
To provide accurate classification, one needs to use a large sample of objects with known true classes. Such data can be obtained from spectroscopic surveys. For our purpose, following the approach of N19, we used the SDSS DR141 catalogue.
The SDSS DR14 catalogue contains 4 311 571 spectroscopically confirmed objects, classified based on their spectra in three main classes: galaxies (2 546 963 objects), quasars (824 548 objects), and stars (940 060 objects). We preserve this structure in our classification, setting up a three-label classification system, which we describe in detail in Sect. 3.
We assume that a quasar (hereafter, QSO) is a point-like source2 with QSO class and QSO or BROADLINE subclass; a normal galaxy (hereafter, GALAXY) is an extended source that has a GALAXY class label without STARFORMING, BROADLINE, or STARBURST BROADLINE subclasses. The star labelling in SDSS does not have subclasses; therefore we simply assume that the source is a star (hereafter, STAR) if it is classified as such in the catalogue.
We cross-matched the SDSS DR14 full catalogue with the catalogue of bright sources from KiDS DR4 described above (r < 22m) using a 1.0 arcsec radius and obtaining in this way a training sample of 183 048 sources; some of these sources however have dubious spectroscopic classification.
Careful cleaning is very important for our scientific purpose, but an automatic masking procedure, eliminating all the dubious cases and often applied in classification pipelines to reach the highest possible pureness, is not appropriate here. In fact, this kind of masking might cause the loss of interesting objects with complex morphology and photometric properties, which can indeed be very good lens candidates3. We therefore paid particular attention to the cleaning procedure, carrying it out manually and interactively.
In particular, we used this first “unpolished” training sample to train the classifiers (which we describe in the following section). We then visually inspected all the misclassified objects (of the order of a few hundred)4. Interestingly, during inspection, we discovered that SDSS DR14 indeed contains a few objects with incorrect labels.
Among these, we identified a few white dwarf and compact galaxies labelled as QSO, blended sources where one of the components is a star or stars projected into a galaxy. Since classifiers trained on such a dataset can inherit these mistakes, we removed the sources for which the true class did not fit with its imaging and/or spectral properties. The whole classification pipeline was iterated a few times, testing the cleaning also with different classifiers (see following section). We note that the total number of removed sources does not exceed a few percent of the training sample, but that the classification results before and after this iterative cleaning procedure are not identical, with the classifier learned with the “clean” training sample producing better results in terms of pureness.
Finally, we test the impact of changing the threshold we choose on the photometric errors of each single band to get a better handle on the importance of our assumptions in building the input catalogue and the best training sample for it. In particular, we tested three different upper limits for the errors on the magnitudes of the training sample: 1m, 0.5m and 0.3m. Also, in this case, we trained the classifiers three times with three different training sets made of objects passing these three thresholds and then we compared the performances. We found negligible differences in purity and completeness (at the 0.1% level) in the classification of the training sample. Finally, we also compared the predictions for the whole input catalogue obtained using the three different training samples, finding again no significant differences in the distribution of the sources among the classes. We therefore decided to use the training sample with the largest number of objects and the same error threshold as the input catalogue (1m).
In conclusion, after removing the sources (i) with bad spectroscopic redshift estimation (for which zWarning > 0), (ii) missing one or more of the nine optical–infrared magnitudes, (iii) with high photometric errors (> 1m in each filter) and (iv) that are accidental duplicates retrieved after our cross-matching procedure, we ended up with 121 375 sources, of which 24 307 sources classified as STAR, 12 152 sources classified as QSO, and 84 917 sources labelled as GALAXY. This catalogue, hereafter named SDSS × KiDS, is used in Sect. 3.3 as a training sample for the classifiers.
3. Classification
Since stars, quasars, and galaxies have different photometric characteristics, it is in principle possible to separate them on the basis of their (optical and infrared) colours.
3.1. Feature selection
Our first task was to define a feature space for the objects using the nine magnitudes (u, g, r, i, Z, Y, J, H, Ks) provided by KiDS and VIKING. Even though there are only eight independent colours, some colour combinations may be more distinctive, and so we chose to examine all 36 pairwise magnitude combinations. We also added the KiDS r-band CLASS_STAR parameter to the feature set. This corresponds to the “stellarity” of a source, which is a continuous measure of whether the object is extended (CLASS_STAR = 0) or point-like (CLASS_STAR = 1) and has proven to be a very powerful feature in the classification (e.g. N19). As shown in Fig. 8 of de Jong et al. (2013), the CLASS_STAR parameter depends on the signal-to-noise ratio (S/N) and is an effective way to separate stars from galaxies only for data with S/N > 50 in r-band. Therefore, an alternative way to select the input data to classify, which would probably also allow investigation of fainter magnitudes, might be to put a cut in the S/N rather than on the r-band magnitude. Nakoneczny et al. (2019) showed that, although magnitudes contribute less to classification than colours and stellarity index, the output based on colours only was different from that using also magnitudes. In this respect, we note that the five infrared bands from VIKING strengthen the separation of stars from quasars and galaxies and thus allow us to follow a physically motivated and model-driven approach that consider only colours in the classification.
Colours and stellarity values of the sources correspond to the coordinates in the thirty-seven-dimensional feature space, in which the classification has been performed.
Our chosen three-class labelling (stars, quasars, galaxies) yields the purest identification of quasars, compared to the two-class scheme (stars and quasars together as point-like, and galaxies as extended sources) or the four-class scheme (stars, quasars, regular galaxies, and galaxies with strong emission lines). Also, we stress that a two-class problem, which only separates stars from extragalactic sources, is not adequate for our scientific purposes. It is true that to find gravitationally lensed quasars, we need a catalogue that contains both galaxies and quasars, but we need a combined morphological and photometric selection in order to identify different combinations of objects (quasar pairs, quasar+star alignments, lenses) that are blended into extended objects by the survey pipelines (see Sect. 5).
3.2. Choice of tree-based method
In the following sections, we describe the classification algorithm and calibration strategy that we use to build our catalogue, which was the end product of a large series of tests and experiments we carried out, also using different classification schemes, as detailed in the Appendix A. We tested three different classifiers, all based on decision trees (Random Forests and two different Gradient Boosting approaches). In the end, we chose the CatBoost (Dorogush et al. 2018; Prokhorenkova et al. 2018) scheme, out of the two Gradient Boosting (GB, Friedman 2000) ensemble algorithms that we tested, because it provided the best performance during the training process, which is described below.
In general, GB is an ensemble algorithm that constructs a learner by fitting in an iterative way the gradients of the prediction residuals from the previously constructed weak learners, typically decision trees (gradient boosting decision trees (GBDTs)). In particular, CatBoost is a novel, fast, scalable, high-performance open-source GBDT library5. Compared to other GBDT algorithms, CatBoost has the advantage of using Ordered Boosting (Prokhorenkova et al. 2018) to curb the overfitting problem, as we highlight in Appendix A. To our knowledge, this is the first application of the CatBoost algorithm to an astronomical task.
3.3. Fine-tuning and learning process
In order to quantify the performance of a classifier, one needs to define a set of validation data and the type of learning with respect to the training-to-validation division. We therefore split the validation into two groups: out-of-fold (OOF) and hold-out. The hold-out sample consists of a random subsample of the initial training data which will be used only for the final performance quantification. The remaining part of the initial sample is used to train the classifiers with a k-fold cross-validation procedure. This is a common method to train classifiers and directly compare classification algorithms. Briefly, one divides the training sample into k randomly partitioned disjoint equal parts. The classification algorithm then trains on k − 1 parts and the remaining one is used as validating data. This process is repeated k times, each time using one of the k disjoint subsamples as validating data and obtaining a prediction from it. The combination of these k predictions forms the so-called OOF sample. Similarly, to obtain the prediction on the new data, the k predictions from each of the fold models are averaged together. A schematic view of the learning process is visualized in Fig. 2.
 |
Fig. 2. Schematic view of the learning via ten-fold cross validation procedure and validation with the OOF and the hold-out samples drawn from the initial training sample. |
Starting from the SDSS × KiDS sample of 121 376 sources, we randomly selected 20% of it as hold-out sample and use the remaining 80% as OOF training sample in the cross-validation process6. We stress that among the classifiers that we tested, CatBoost returned the best performance both on the hold-out and OOF samples.
Before training can take place, the classifier has a list of hyper-parameters that have to be tuned to reach the highest possible classification quality. This is true for each of the different classifiers that we tested. For this purpose, we performed an optimal hyperparameter search on 60% of the initial training sample via three-fold cross-validation with a “BayesSearch” for CatBoost7.
While tuning the wide range of hyperparameters for CatBoost, we noticed that the most influential ones were the max_depth and the early_stopping parameters. We selected max_depth = 8 and early_stopping = 150 after BayesSearch, with a maximum number of trees of 3500.
Moreover, we applied a weighting criterion to the loss function for the CatBoost model to further decrease the contaminants by stars in the extragalactic objects catalogue (see Appendix A.1 for more details).
After this hyperparameter fine-tuning, we finally trained CatBoost with the same training and validation data and with a ten-fold cross-validation (see Fig. 2). The result of the performance for the final CatBoost model (after the fine-tuning) is presented as confusion matrices in Fig. 3 for both the OOF sample (top) and the hold-out sample (bottom). Using the weighting for stars and galaxies, we saw a significant improvement in the purity of the quasar sample; in fact, by comparing the confusion matrices before and after re-weighting the loss function (see appendix), one can see that the rate of stars misclassified as quasars decreased from ≈0.60% to ≈0.30%. CatBoost lost only < 1.50% of the quasars, thus only marginally decreasing the resulting completeness of this class.
 |
Fig. 3. Confusion matrices for the final version of CatBoost, after weighting the loss function, performed on the OOF sample (top panel) and the hold-out sample (bottom panel). |
3.4. Feature importance
Another notable result that we can get with CatBoost is the relative importance of each feature in the classification procedure. Feature importance, calculated with a decision tree, shows the frequency with which a certain feature occurs in the tree. In such a way, the higher frequency is directly related to the higher feature contribution to separate the sources, that is the importance of a given feature. An excellent example of this kind of analysis, together with a full description of the feature importance technique is presented in D’Isanto et al. (2018). Figure 4 shows the ten most informative features for all of the CatBoost models, trained one by one via ten-fold cross-validation. Among these, the CLASS_STAR is certainly the most important one, followed by H − Ks, u − g, g − r, and J − Ks. This is in perfect agreement with a number of results in the literature, for example using u − g and g − r colour diagram it is possible to separate low-redshift quasars from stars (Abraham et al. 2012; Carrasco et al. 2015). These features, together with the stellarity, are also the most important ones in other ML-based classifiers (e.g. N19). Furthermore, quasars at z ≈ 2.5 and z ≈ 5.6 may be recovered using the K-band information in the colour space (Chiu et al. 2007). Finally, it is well known and also intuitively easy to understand that morphological information (described here by the CLASS_STAR feature) allows one to clearly select galaxies, dividing them from stars and quasars at least in the relatively bright magnitude range that we consider (r < 22m).
 |
Fig. 4. Importance of the ten most significant features, calculated with CatBoost in each of the ten folds. The dispersion of importance for each feature is represented by a horizontal tick at each bar. |
The upper panel of Fig. 5 shows the number of quasars, stars, and galaxies from the full initial training sample as a function of their r-band magnitude (in the AB reference system). The bottom panel of the same figure shows instead the percentage of objects that have been misclassified by our algorithm (contaminators). The maximum rate of star-contaminators per bin of r-band magnitude in the quasars catalogue is ≤0.6% and is expected at the faint end of the sample (r ≈ 22m). Instead, the stars misclassified as galaxies span over the full optical r magnitude range and do not exceed 0.1%.
 |
Fig. 5. Upper panel: histogram of the r magnitudes for the three classes of training sources (top panel). Bottom panel: rate at which stars are misclassified as quasars (red curve) or as galaxies (black curve) as a function of their r magnitude. The plot is produced for the full initial training sample. |
Finally, we checked the contamination rate against the S/N in the u-band, which is the noisiest one for KiDS, finding that the relative contamination of stars decreases at each magnitude bin by ∼2% when we only consider objects with S/N > 100.
For the input data, whose distribution in the feature space should be similar to that of the training set, we expect a contamination of 0.3% from stars and 0.1% from galaxies in the sample of quasars, and 0.1% from stars and 0.6% from quasars in the sample of galaxies. We therefore conclude that the algorithm is in principle able to correctly classify up to 97.5% of all the bright quasars, and up to 99.8% of the galaxies from the KiDS DR4 input catalogue. These estimations are ideal and do not necessarily reflect the real situation, because they are only based on the training sample, which is a much smaller and simpler sample than the full catalogue. A more realistic estimate of the quality of our extragalactic catalogue in terms of purity and completeness can be obtained using external data to validate the resulting sample of classified sources, as we do in Sect. 4.
We stress that, for our final scientific purpose of finding gravitationally lensed quasars, the most crucial point is to be able to clean any sample of stellar contaminants. It is indeed of fundamental importance to separate stars from quasars to as greater degree as possible, both being point-like sources.
Since the KiDS DR4 input catalogue consists mostly of galaxies, there will be a non-negligible number of galaxies contaminating the quasars sample. However, as we explain in more detail in Sect. 5, strong lenses can be classified as GALAXY, if the deflector gives a non-negligible contribution to the light and/or the multiple images of quasars are not deblended, or they can be identified as multiple quasars. In the first case, the whole system will result in one extended object whose colours are a mixture of typical galaxy and quasar colours. This is the main reason why we build and inspect a catalogue containing all the extragalactic sources (QSO + GALAXY) looking then for “Multiplets”: objects with nearby (within 5″) companions. In particular, we select sources classified as GALAXY with at least one nearby QSO companion, to find lenses belonging to former group, and sources classified as QSO with at least one QSO companion, to find lenses belonging to the latter group.
4. The Bright EXtraGalactic Objects catalogue in KiDS DR4 (KiDS-BEXGO)
For each object in the KiDS DR4 input catalogue, the classifier returns three numbers representing the probability of belonging to each of the three classes of objects: pSTAR, pGALAXY, pQSO. In general, we assume that a source belongs to a given class when the probability of being in that class is the highest. With this simple assumption, starting from the input 9.6 million sources in the KiDS DR4 catalogue, we retrieved: 186 037 (2%) quasars, 3 716 137 (39%) stars, and 5 694 238 (59%) galaxies. Using a more severe threshold instead, namely considering that an object belongs to a class when the corresponding probability is > 0.8, we obtain: 5 665 586 (59%) “sure” galaxies, 3 660 368 (38%) “sure” stars, and 145 653 (1.5%) “sure” quasars, plus 122 306 objects (1.3%) with “unsure” classification. We note that for the classification of objects in the final catalogue we stick to the original assumption that a source belongs to the class with the largest probability, without applying any further threshold, since “unsure” extragalactic sources (with pGALAXY ≈ pQSO) could very well be good lens candidates where the deflector and the quasar images are blended and all give a contribution to the light of the system. However, since the levels of completeness and purity depend on the chosen probability, and different scientific cases might require different levels, we provide in Table 1 the number of objects classified in each subsample for five different thresholds. Furthermore, Fig. 6 shows the confusion matrices obtained for the OOF training sample for the four highest probability levels (0.8, 0.9, 0.95, 0.99) and the completeness rate as a function of the probability threshold for the three classes.
Number of objects for each class using different probability threshold to define class belonging.
 |
Fig. 6. Upper panel: confusion matrices for the final version of CatBoost performed on the OOF sample using different thresholds of probability in the object classification (see text for more details). Bottom panel: completeness rate of the OOF sample as a function of the adopted probability threshold for each class. |
Finally, Fig. 7 provides a visualization of the class distribution of the objects in the output catalogue. Each corner of the triangular density plot represents the maximum probability of belonging to a given class. Objects within the region delimited by dotted lines are “sure” according to the threshold given above (p > 0.8).
 |
Fig. 7. Density plot of the final distribution of sources among the classes in the output catalogue. The triangle corners show the maximum probability of belonging to a given family (right QSO, left GALAXY, up STAR), and colours indicate number of objects. Dashed lines correspond to the p = 0.8 threshold. |
In Sect. 5, we only focus on the objects with pQSO > pSTAR or pGALAXY > pSTAR that form the KiDS-BEXGO catalogue used for the gravitational lens searches. Here, instead, we discuss three of the many possible validation procedures, for one or more classes of objects, performed using external data (from the Gaia astrometric survey, from the AllWISE infrared catalogue, and from the GAMA survey). Using an external dataset to validate catalogues obtained with ML techniques is a rather standard procedure, as already shown in for example Khramtsov et al. (2018), where the PMA (Akhmetov et al. 2017) catalogue of proper motions was used to validate the purity of a sample of galaxies.
Given the results presented in the tests below, together with predictions on the hold-out sample, we are confident that our ML classifier is able to minimize the stellar contamination in the BEXGO catalogue, which is the first, most crucial step when searching for gravitationally lensed quasars within very large catalogues.
4.1. Astrometric validation with Gaia
The latest data release of Gaia, DR2 (Gaia Collaboration 2018a), measured five astrometric parameters (positions α, δ, proper motions μα, μδ, and parallaxes 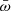 ) for 1.3 billion sources, covering the whole celestial sphere up to G < 21m8. The systematical errors in Gaia DR2, estimated with ≈500 000 quasars, do not exceed 0.03 mas (Gaia Collaboration 2018b). Thus, the Gaia DR2 provides an excellent means to test the purity of our catalogue, especially for quasars.
) for 1.3 billion sources, covering the whole celestial sphere up to G < 21m8. The systematical errors in Gaia DR2, estimated with ≈500 000 quasars, do not exceed 0.03 mas (Gaia Collaboration 2018b). Thus, the Gaia DR2 provides an excellent means to test the purity of our catalogue, especially for quasars.
One of the main observational properties of quasars that can be used to validate the sample of candidates classified as such is the fact that they have proper motions of only a few micro-arcseconds since they very distant sources (Bachchan et al. 2016).
We cross-matched the KiDS DR4 sample of 9.5 million classified sources with the Gaia DR2 catalogue using a 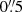 radius, and retrieved a sample of sources with defined astrometric parameters, of which 52 636 were classified as QSO, 2 369 414 were classified as STAR, and 25 346 – as GALAXY. We then checked the proper motions and parallaxes of all the objects classified as quasars and with a match in Gaia to test the assumption that quasars are indeed zero-proper-motion and zero-parallax sources within the systematic errors. The results of this test are shown in Fig. 8. The behaviour of the proper-motion components is consistent with the estimated contamination of stars within the quasar subsample of the KiDS DR4 catalogue (Fig. 5). In fact, at the faintest magnitudes (G > 20.5m), the proper-motion components deviate strongly due to larger contamination from stars. At very bright magnitudes (G > 17.5m), the standard deviation of the mean of the proper motions and parallaxes is also large, but this is due to a relatively small amount of sources in this magnitude bin rather than to star contamination. It is also important to note that the parallax (right plot of Fig. 8) is biased for the sample of extragalactic sources towards the value of −0.029 mas reported in Lindegren et al. (2018).
radius, and retrieved a sample of sources with defined astrometric parameters, of which 52 636 were classified as QSO, 2 369 414 were classified as STAR, and 25 346 – as GALAXY. We then checked the proper motions and parallaxes of all the objects classified as quasars and with a match in Gaia to test the assumption that quasars are indeed zero-proper-motion and zero-parallax sources within the systematic errors. The results of this test are shown in Fig. 8. The behaviour of the proper-motion components is consistent with the estimated contamination of stars within the quasar subsample of the KiDS DR4 catalogue (Fig. 5). In fact, at the faintest magnitudes (G > 20.5m), the proper-motion components deviate strongly due to larger contamination from stars. At very bright magnitudes (G > 17.5m), the standard deviation of the mean of the proper motions and parallaxes is also large, but this is due to a relatively small amount of sources in this magnitude bin rather than to star contamination. It is also important to note that the parallax (right plot of Fig. 8) is biased for the sample of extragalactic sources towards the value of −0.029 mas reported in Lindegren et al. (2018).
 |
Fig. 8. Median right ascension (green curve, left) and declination (black curve, left) of the proper motion components, and parallax (red curve, right) for the KiDS DR4 QSO sample as a function of the GaiaG magnitude. The coloured areas represent the standard deviation of the mean σ/N, where σ is the standard deviation and N is the number of quasars in each bin. The black horizontal line in the right plot represents the parallax zero-point (equals to −0.029 mas, Lindegren et al. 2018). |
Given the mean, median, and standard deviation of the proper motion components and of the parallax of the astrometric parameters reported in Table 2, we can conclude that the sample of KiDS DR4 quasars mainly consists of motionless sources. A more detailed astrometric analysis, providing a more quantitative estimation of the rate of contaminating stars, cannot be produced without accurate modelling and the involvement of other external datasets, which goes beyond the purposes of this paper.
Basic statistics of the astrometric parameters of all the objects in the KiDS output catalogue classified as quasars and with a match in Gaia DR2.
To assess the purity of the galaxy sample, we use the very simple argument that, by construction, Gaia should contain no galaxies at all (Robin et al. 2012). Thus none of the objects with high pGALAXY should have a match in Gaia DR2. This is, of course, only a rough approximation since there might be a number of galaxies that Gaia still measures, such as for example objects with bright cores. From the cross-match with Gaia, we find ≈25 000 objects classified as GALAXY. We note that among these only 1784 objects have CLASS_STAR > 0.5, and thus can be point-like sources in KiDS, misclassified by our algorithm, or very compact galaxies below the KiDS resolution.
In Fig. 9 we show the distribution of the CLASS_STAR parameter for each class of objects in the full KiDS DR4 catalogue. Assuming that galaxies are all extended objects, we would expect to find in KiDS no objects classified as GALAXY with CLASS_STAR > 0.5. However, there are objects that are point-like according to their CLASS_STAR value but that have been classified as GALAXY by our algorithm on the basis of their colours. The number of point-like galaxies from Fig. 9 is larger than a couple of thousand, as predicted by the cross-match with Gaia. This slight disagreement might be explained by the better resolution of Gaia (Krone-Martins et al. 2018): these sources might be seen as point-like in KiDS, but are extended and thus not identified in Gaia. Despite this, the majority of GALAXY sources with a Gaia match are indeed extended objects in KiDS, or sources near to a bright star. This was directly verified on a random sample of ≈5000 objects via the SDSS DR14 Navigate Tool9, and then also by checking the KiDS r-band images, finding bright features (e.g. cores, regions in arms, etc.) for most of the sources that could be resolved only for galaxies with significant angular size.
 |
Fig. 9. Distribution of the CLASS_STAR parameter for the sources classified as GALAXY (black), QSO (red), or STARS (blue). |
4.2. Validation of galaxies with GAMA
To validate the pureness and completeness of the subsample of galaxies within the BEXGO catalogue, we cross-matched it with spectroscopically confirmed galaxies from the Galaxy And Mass Assembly Survey Data Release 3 (GAMA DR3, Baldry et al. 2018). In particular, following the suggestions given on the GAMA website, we retrieved all the objects10 with redshifts z > 0.05 and with a high “normalised” redshift quality (nQ > 1). We matched these ≈208k sources with our final catalogue of classified objects from KiDS, finding 105 334 systems in common. Among these, 105 018 were indeed classified as GALAXY from CatBoost and 104 970 have a pGALAXY ≥ 0.8. Thus, only 0.3% of the common objects have been misclassified (123 as STARS and 181 QSO). Although we are aware that this test is not definitive and that it is not straightforward to directly translate the relative number of contaminants into a percentage of pureness of the final galaxy catalogue, it shows that, at least for this small but representative sample of galaxies, our CatBoost classifiers perform well.
4.3. Validation of quasars with mid-infrared data from WISE
Mid-infrared (MIR) colours are a very effective way to separate quasars from stars and passive galaxies, since while the latter two show approximately zero MIR colours, quasars emit strongly in these bands (Elvis et al. 1994; Stern et al. 2005; Assef et al. 2013). As largely demonstrated by a number of published works, including Paper I, it is possible to separate quasars from stars and galaxies using a combination of infrared colour and magnitudes cuts (e.g. the two-colour criteria of Lacy et al. 2004; Stern et al. 2005; Donley et al. 2012 with Spitzer11 data; the two-colour criteria in Jarrett et al. 2011; Mateos et al. 2012; or the one-colour criteria of Stern et al. 2012; Assef et al. 2013). We note that in general it is harder to validate the purity of galaxies in the same way since stars overlap with (non-active) galaxies in this dimension (see e.g. Fig. 12 in Wright et al. 2010).
Here, we decided to use the single infrared colour cut [3.6] μm − [4.5] μm > 0.8 proposed by Stern et al. (2012) using data from the Wide-field Infrared Survey Explorer, WISE (Wright et al. 2010), the NASA space mission that aims at mapping the whole sky in four MIR bands: W1, W2, W3, W4 (3.6, 4.5, 12 and 22 μm respectively). This criterion can separate quasars from stars and galaxies with a purity of ≈95%, but allows one to select systems only up to z ≈ 3.5 (Guo et al. 2018). Moreover, we caution the reader that a sample selected with this criterion can be contaminated by brown dwarfs which have similar colours. The more elaborate two-colour criterion of Mateos et al. (2012) allows one to reduce this contamination, but it requires reliable measurements in the W3 band, which would significantly decreases the total number of matched sources in our case.
Finally, we wish to clarify that in this paper the WISE data are only used as validation for the quasar catalogue but not for the lens search. As a matter of fact, the bottle-neck of the search for gravitationally lenses performed in Paper I was indeed the overly severe WISE colour pre-selection. In case the lens and the source are blended in WISE and the deflector gives a large contribution to the light, the colours of this effective source may no longer be quasar-like and may move indeed toward lower W1 − W2 values. These objects were not retained in our previous study. Here we rely on a more solid and trustworthy way to classify objects, our ML-based classifier, and thus we do not need to apply any cut, nor do we need to require a match with WISE to build our candidates list.
We cross-matched the SDSS training sample as well as the catalogue of all the classified objects with the AllWISE (Cutri et al. 2013) data release using a 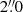 radius. The resulting sample consists of 114 773 quasars, 3 289 858 galaxies, and 2 020 768 stars for the classified objects and of 8 879 quasars, 78 816 galaxies, and 13 249 stars for the SDSS × KiDS training sample.
radius. The resulting sample consists of 114 773 quasars, 3 289 858 galaxies, and 2 020 768 stars for the classified objects and of 8 879 quasars, 78 816 galaxies, and 13 249 stars for the SDSS × KiDS training sample.
Figure 10 shows the histograms of the distribution of the W1 − W2 colour for the KIDS DR4 objects classified in the three classes (left panels), and for the corresponding training sample (right panel), colour coded by their classification family: red for QSO, black for GALAXY, and blue for STARS. In general, the distribution of the full catalogue shows a similar distribution to that of the training sample, with the peak of the QSO subsample shifted toward larger W1 − W2 values (W1 − W2 > 0.8), as expected. We note however that the distributions of the full catalogue are much broader than the distributions of the corresponding training sample, especially towards larger W1 − W2 values, both in negative and in positive. This is particularly true for the GALAXY and STAR classes. This might indicate a lower purity for these families and consequently a larger contamination level in the QSO family, or a lack in the training sample of particular classes of objects (e.g. active galaxies). As we show in the previous section, the purity of the objects classified as GALAXY seems to be relatively high. Therefore, we speculate that one of the reasons for the slight disagreement between the distribution of galaxies from the training sample and from the output BEXGO catalogue in the W1 − W2 space might simply arise from the fact that the SDSS galaxies are generally more luminous than the KiDS ones.
 |
Fig. 10. Left panel: distribution of the W1 − W2 colour for the classified KiDS DR4, colour coded according to their classification family (red for QSO, black for GALAXY, blue for STAR). Right panel: distribution of the W1 − W2 colour for the train samples. A fair agreement can be found between corresponding classes, although the distribution for the full catalogues is generally broader than that of the training samples. In both panels, the peak of the QSO distribution is shifted towards larger W1 − W2 with respect to the GALAXY and STARS, as expected. |
More and deeper investigations will be performed into purity and completeness in the forthcoming papers of the KiDS-SQuaD series. Nevertheless, we are confident that our automatic classifier allows us to obtain a catalogue of quasars and galaxies with very little stellar contamination. In fact, as we show in Sect. 5, the contamination is much less than that obtained in Paper I, where we rely on simple and manual optical and infrared colour cuts. We stress again that our final goal has been to create an automatic and effective method to build a catalogue of extragalactic objects with the smallest possible contamination from stars. This is the first necessary step in searching for strong gravitationally lensed quasars. We believe that these three validation steps with external data demonstrate that we have succeeded in our goal and therefore can now use the newly created catalogue to search for lens candidates.
5. Searching for gravitationally lensed quasars
Strong gravitationally lensed quasars are valuable but very rare objects that can provide direct and purely gravitational probes of cosmology and extragalactic astrophysics. Generally speaking, we can separate lensed quasars into three families: (i) systems where the quasar images dominate (mainly low-separation couples/quadruplets with a faint deflector in between), (ii) objects where the deflector is a bright, usually red, massive galaxy that dominates the light budget of the system, and finally (iii) systems where both lens and source give a non-negligible contribution to the light. In the last two cases, CatBoost will most probably return multiple matches, of which at least one will be classified as extended (GALAXY), while in the former one it will classify them as multiple QSO. However, we note that in cases where the separation between the quasar components is too small, the objects might not be resolved in the KiDS catalogue, and thus might result in a single match from our algorithm. Indeed, most of the known low-separation gravitationally lensed quasars discovered in the SDSS are identified as “single” galaxies (only in a few cases as a single quasar), since the poor resolution does not allow the multiple components to be deblended. Of course, the better image resolution of KiDS helps in this case, but some lenses with very low separation are blended also in KiDS. This is why it is of crucial importance to have a catalogue of extragalactic objects that is as clean from stellar contamination as possible and as complete and efficient as possible in selecting and classifying galaxies and quasars.
5.1. Recovery of known lens systems
To demonstrate our statement that lensed quasars are not always classified as (multiples, nearby) QSO by ML-based algorithms that work in a magnitude-colour space, and at the same time to highlight the importance of having an extragalactic catalogue, we carried out a test on the recovery of known lenses, as already done in Paper I.
We started from the same list of ≈260 confirmed lensed quasars that we used in Paper I and updated it with new systems recently discovered in wide-sky surveys (Agnello et al. 2018a,b; Ostrovski et al. 2018; Anguita et al. 2018; Lemon et al. 2018; Spiniello et al. 2019). The cross-match between the full KIDS DR4 catalogue of objects with r < 22m and the list of known lensed quasars (288 systems) gave us 17 known lenses. All of them have been retrieved in the KiDS-BEXGO catalogue, 10 classified as QSO and 7 as GALAXY (one of them with a pQSO ≈ 0.45). In 8 cases the lenses returned multiple matches (see Sect. 5.2). These 17 known lenses are reported in Table 3, together with the probability of belonging to each class. We do not explicitly report their right ascensions and declinations in separate columns because their IDs already contain the J2000 coordinates in the usual “hhmmss.ss ± ddmmss.ss” format.
Known lenses in the KIDS DR4 footprint.
Based on this simple and qualitative test, it appears clear that selecting only quasars would allow one to find only lens systems where the contribution to the light from the quasars is much larger than the contribution of the deflector. Selecting only QSO we would retrieve roughly 65% of the known lensed quasar population – 11 out of 17 systems.
Finally, although this goes beyond the scope of this paper, we note that another important advantage of having an extragalactic source catalogue (rather than one containing only quasars) is that it offers the possibility to search for galaxy–galaxy gravitational lenses. This type of gravitationally lensed object allows the detailed investigation of mass distribution in massive galaxies up to z ∼ 1, especially when combined with dynamics (Koopmans et al. 2006, 2009; Spiniello et al. 2011, 2015). Morphological and photometric criteria can be used to find this kind of lens: one should look for red extended objects (GALAXY with red colours) with the presence of blue extended objects (GALAXY with blue colours) within small circular apertures. We will work in this direction in a forthcoming paper, possibly using automatic ML-based routines (e.g. Petrillo et al. 2017, 2019a,b) and already available catalogues of luminous red galaxies in the Kilo Degree Survey (e.g. Vakili et al. 2019).
5.2. Looking for Multiplets
Starting from the KiDS-BEXGO catalogue of 5 880 276 objects, we retrieve only systems belonging to the following distinct groups:
(1) “QSO-Multiplets”: sources classified as QSO and with at least one nearby QSO companion (within a 5″ circular aperture radius) with similar colours, and (2) “GALAXY-Multiplets”: sources classified as GALAXY and surrounded by at least one object classified as QSO within a 5″ circular aperture radius12.
This simple procedure allowed us to obtain 347 unique objects for the first group and 611 unique objects for the second. These 958 objects were then visually inspected independently by four researchers in our team that also graded them from “0” to “4”, with “4” being a “sure” lens. Among these, some where already known lenses, some are probably binary quasars, and some are simply contaminants appearing as close-by companions because of sky projection. Nevertheless, we found many very promising lens candidates, objects that at least two people graded with a score higher than or equal to “2”. We present the 12 candidates with mean grade ≥2.5 in Table 4 (divided into the two types of Multiplets). We publicly release their coordinates to facilitate spectroscopic follow-up, which is the last necessary step for unambiguous confirmation.
Most reliable gravitationally lensed quasar candidates found with the “Multiplets” method described in the text.
The gri-combined KiDS cutouts of these 12 candidates are shown in Fig. 11. The first two rows show candidates belonging to the GALAXY-Multiplets family while the bottom row shows QSO-Multiplets candidates. In the former group, the deflector gives a much larger contribution to the light, as can be clearly seen from the images. KiDSJ0008−3237 seems to be a very reliable galaxy–galaxy candidate, while KiDSJ0215−2909, definitively among the most promising objects, might be a fold-quadruplet similar to the one recently found in the VST-ATLAS Survey, WISE 025942.9−163543 (Schechter et al. 2018) and very useful for cosmography studies (time-delay measurement of H0; see e.g. “The H0 Lenses in COSMOGRAIL’s Wellspring”13 results).
 |
Fig. 11. 12 best candidates, both of GALAXY-Multiplets type (first two rows) and of QSO-Multiplets type (bottom row). The cutouts show gri combined KiDS images of 10″ × 10″ in size. The coordinates of the candidates are given in Table 4. |
We note that of the 17 known lenses, only 8 have been selected as Multiplets (2 as QSO-Multiplets and 6 as GALAXY-Multiplets). The other 9 systems have not been deblended in the KiDS catalogue, and thus only have one single match in our classification scheme. These numbers are perfectly in line with the results obtained in Paper I where we found that the “Multiplets” method alone allowed the recovery of ∼40% of the known lenses. In a forthcoming paper of this series fully dedicated to the lens search, we will perform a more careful candidate selection, also based on improved colour and magnitude criteria, to select objects with similar colours and applying the Blue and Red Offsets of Quasars and Extragalactic Sources (BaROQuES) scripts to the full BEXGO catalogue, which were already successful tested in Paper I.
We finally note that we re-discovered a very promising quadruplet: KIDS0239−3211 that was presented in an AAS research note (Sergeyev et al. 2018) and was found by the first application of our ML-based classifier14. The same system was first detected by Hartley et al. (2017) using image-based Support Vector Machine classifier and then by Petrillo et al. (2019b) using convolutional neural networks; but since they did not release the coordinates in their paper, we re-discover it in a completely independent way.
5.3. Comparison with Paper I
We cross-match the list of all the lens candidates found in Paper I with the BEXGO catalogue. We find that among the 210 objects we found in Spiniello et al. (2018), 148 are recovered in the extragalactic objects catalogue (≈45% classified as QSO and ≈55% as GALAXY) and 66 are also selected as Multiplets. Of the 62 remaining objects, 33 have r > 22m and therefore were discarded at the input catalogue creation stage, and 29 were classified as STAR by CatBoost; these 29 stars indeed also have a match in Gaia, and all of them have non-negligible proper motions and parallaxes. Finally, among the DR3 candidates that were not found in the DR4 KiDS-BEXGO, four were spectroscopically followed-up and turned out to be stars15. These numbers nicely demonstrate that the employment of the ML-based classifier further helps in decreasing the risk of stellar contamination within gravitationally lensed quasar candidates.
Of the seven known lenses that we recovered in Paper I, six are again recovered. We only lose the nearly identical quasar (NIQ) couple QJ0240−343 (Tinney 1995; Tinney et al. 1997) behind the Fornax dwarf spheroidal galaxy, because it has r magnitude of r = 22.17m and therefore did not satisfy our initial conditions.
6. Results and conclusions
In this second paper of the KiDS-SQuaD project we present a new ML-based classifier to identify extragalactic objects in a search for lensed quasars within the KiDS DR4 data. The technique adopted in this paper has become relatively standard in the extragalactic community to classify objects in multi-band photometric surveys (Gieseke et al. 2011; Kovács & Szapudi 2015; Brescia et al. 2015; Carrasco et al. 2015; Peters et al. 2015; Krakowski et al. 2016, 2018; Viquar et al. 2018; Khramtsov & Akhmetov 2018; Barrientos et al. 2018; Nolte et al. 2019; Bai et al. 2019; Nakoneczny et al. 2019), which provide a very large amount of data.
A similar approach has also been already tested on the Kilo Degree Survey by Nakoneczny et al. (2019), who presented a ML-based pipeline to classify objects into three classes (stars, galaxies and quasars) and successfully applied it to the KiDS DR3 (de Jong et al. 2017). Our work, although extending from their findings, has been developed within a different framework, i.e. the search for lensed quasars, and it differs from N19 in many aspects, from the assumption that quasars are point-like sources to the cleaning procedure, optimization, and fine-tuning aimed at minimizing stellar contamination in the catalogue of extragalactic objects. Finally, here we also add infrared data, using deep photometry in nine bands (instead of four), which further helps to isolate stars.
Here we provide a general summary of the archived results of this paper, highlighting the main main steps that we undertook and the results that we achieved.
We used the large potential of ML methods on broad optical–infrared photometric data from the KiDS DR4 survey. We identified the CatBoost ad the best possible classifiers for our purposes, comparing and quantifying the performance of some of the most used classifiers based on decision trees on the same training sample. The result of this direct comparison is presented in Appendix A. Moreover, we performed ad-hoc customization and fine-tuning of the parameters of CatBoost, to reach the required levels of purity and completeness and to avoid overfitting problems.
We used a set of 121 376 spectroscopic confirmed objects from the SDSS DR14, after applying a careful cleaning procedure and also visually inspecting the ambiguous cases when necessary. We splitted the training dataset into hold-out and out-of-fold parts, to asses the performance (in terms of completeness and purity) of the CatBoost algorithm. We then defined (and solved) a three-class problem (STAR, GALAXY, QSO), working with a simple basic assumption made for the classification: quasars and stars are point-like sources, while galaxies are extended. We therefore used the CLASS_STAR parameter – a “stellarity” index from the KiDS catalogue – which turned out to be the most important feature in our classification algorithm (as in N19), together with optical and infrared colours.
We applied CatBoost on all the data from KiDS DR4 with magnitude brighter than r = 22m and reliable photometry measured in each of the nine bands. For each input source, the classifier calculated the probability of belonging to the three different classes of objects: pSTAR, pGALAXY, pQSO. We assumed that a source belongs to a given class when the probability of being in that class is the highest but we also studied the variation in completeness and purity as a function of the probability threshold used to assign an object to a given class.
We collected all the objects that were not classified as stars, building the KiDS-BEXGO catalogue, which we then validated using external data (Gaia DR2, AllWISE and GAMA).
We firstly showed the potential of the KiDS-BEXGO catalogue in the gravitationally lensed quasar search, with a simple test on the recovery of known, confirmed lenses. We proved, in this way, that our method of selecting extragalactic sources (not only quasars) is a necessary condition to discover as many new systems as possible. Secondly, we used the KiDS-BEXGO catalogue to search for new, undiscovered gravitationally lensed quasars, looking for objects with nearby companions and obtained a list of 958 “Multiplets” (347 QSO and 611 GALAXY) that we visually inspected. We found 12 very reliable lens candidates, for which we release coordinates and show KiDS gri-combined images.
Finally, we showed the improvement in terms of stellar contamination of the final list of candidates that we obtain with respect to what was obtained in Paper I.
In this paper we focussed on the ML classifier and on building the catalogue of bright extragalactic objects, which can be useful for a broad series of scientific goals, but at the same time we highlighted the need for different methods to search for lens candidates within the catalogue (e.g. the BaROQuES) and direct image analysis (DIA). These methods will be investigated and applied to BEXGO in Paper III, already in preparation (Sergeyev et al., in prep.), where we will present a systematic and automated way to select reliable candidates from the KiDS-BEXGO catalogue, as well as the first results from the ongoing spectroscopic follow-up campaigns. In particular, we will apply the BaROQuES scripts to our catalogue and will also exploit the full potential of the DIA (see Paper I for more details) to get precise astrometry and fit the photometry of our most reliable candidates. Finally, in the future, we aim to improve the classification model, working in a larger, more complex feature space, and to develop a more detailed classification scheme, for example splitting the classification of galaxies into late and early types, given that massive early types are more likely acting as deflectors due to the fact that on average they are more massive.
SDSS DR14 is the second release of the Sloan Digital Sky Survey IV phase (Blanton et al. 2017) and it includes data from all previous SDSS data releases.
We used the Navigate SDSS visual tool (http://skyserver.sdss.org/dr14/en/tools/chart/navi.aspx) to inspect misclassified sources.
https://catboost.ai/, developed by Yandex researchers and engineers https://yandex.com/company/
This limit corresponds to r ≈ 21m for quasars at z ≤ 3, (Proft & Wambsganss 2015).
Acknowledgments
The authors wish to thank Maciej Bilicki for the interesting discussion and the very constructive comments that helped in improving the final manuscript. CS has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie actions grant agreement No 664931. CT acknowledges funding from the INAF PRIN-SKA 2017 program 1.05.01.88.04. KK acknowledges support by the Alexander von Humboldt Foundation. JTAdJ is supported by the Netherlands Organisation for Scientific Research (NWO) through grant 621.016.402. HYS acknowledges the support from the Shanghai Committee of Science and Technology grant No. 19ZR1466600. This work is based on data products from observations made with ESO Telescopes at the La Silla or Paranal Observatories under programme ID(s) 177.A-3016(A), 177.A-3016(B), 177.A-3016(C), 177.A-3016(D), 177.A-3016(E), 177.A-3016(F), 177.A-3016(G), 177.A-3016(H), 177.A-3016(I), 177.A-3016(J), 177.A-3016(K), 177.A-3016(L), 177.A-3016(M), 177.A-3016(N), 177.A-3016(O), 177.A-3016(P), 177.A-3016(Q), 177.A-3016(S), 177.A-3017(A), 177.A-3018(A), 060.A-9038(A), 094.B-0512(A), and on data products produced by Target/OmegaCEN, INAF-OACN, INAF-OAPD and the KiDS production team, on behalf of the KiDS consortium. OmegaCEN and the KiDS production team acknowledge support by NOVA and NWO-M grants. Members of INAF-OAPD and INAF-OACN also acknowledge the support from the Department of Physics & Astronomy of the University of Padova, and of the Department of Physics of Univ. Federico II (Naples). This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, and NEOWISE, which is a project of the Jet Propulsion Laboratory/California Institute of Technology. WISE and NEOWISE are funded by the National Aeronautics and Space Administration. This publication makes use of data products from the Sloan Digital Sky Survey IV. Funding for SDSS IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This work has made use of data from Galaxy and MAss Assemby Survey. GAMA is a joint European-Australasian project based around a spectroscopic campaign using the Anglo-Australian Telescope. The GAMA input catalogue is based on data taken from the Sloan Digital Sky Survey and the UKIRT Infrared Deep Sky Survey. Complementary imaging of the GAMA regions is being obtained by a number of independent survey programmes including GALEX MIS, VST KiDS, VISTA VIKING, WISE, Herschel-ATLAS, GMRT and ASKAP providing UV to radio coverage. GAMA is funded by the STFC (UK), the ARC (Australia), the AAO, and the participating institutions. The GAMA website is http://www.gama-survey.org/
References
- Abolfathi, B., Aguado, D., Aguilar, G., et al. 2018, ApJS, 235, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Abraham, S., Philip, N., Kembhavi, A., Wadadekar, Y. G., & Sinha, R. 2012, MNRAS, 419, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Agnello, A., & Spiniello, C. 2019, MNRAS, 489, 2525 [NASA ADS] [CrossRef] [Google Scholar]
- Agnello, A., Kelly, B. C., Treu, T., & Marshall, P. J. 2015, MNRAS, 448, 1446 [NASA ADS] [CrossRef] [Google Scholar]
- Agnello, A., Sonnenfeld, A., Suyu, S. H., et al. 2016, MNRAS, 458, 3830 [NASA ADS] [CrossRef] [Google Scholar]
- Agnello, A., Schechter, P. L., Morgan, N. D., et al. 2018a, MNRAS, 475, 2086 [NASA ADS] [CrossRef] [Google Scholar]
- Agnello, A., Lin, H., Kuropatkin, N., et al. 2018b, MNRAS, 479, 4345 [NASA ADS] [CrossRef] [Google Scholar]
- Akhmetov, V., Fedorov, P., Velichko, A., & Shulga, V. 2017, MNRAS, 469, 763 [NASA ADS] [Google Scholar]
- Anguita, T., Schmidt, R. W., Turner, E. L., et al. 2008, A&A, 480, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anguita, T., Schechter, P. L., Kuropatkin, N., et al. 2018, MNRAS, 480, 5017 [NASA ADS] [Google Scholar]
- Assef, R. J., Stern, D., Kochanek, C. S., et al. 2013, ApJ, 772, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Bachchan, R. K., Hobbs, D., & Lindegren, L. 2016, A&A, 589, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bai, Y., Liu, J., Wang, S., & Yang, F. 2019, AJ, 157, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Liske, J., Brown, M. J. I., et al. 2018, MNRAS, 474, 3875 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, N. M., Brunner, R. J., Myers, A. D., & Tcheng, D. 2006, ApJ, 650, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Barrientos, F., Pichara, K., Troncoso, P., et al. 2018, VST in the Era of the Large Sky Surveys, 9 [Google Scholar]
- Bate, N. F., Floyd, D. J. E., Webster, R. L., & Wyithe, J. S. B. 2011, ApJ, 731, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M., Bershady, M., Abolfathi, B., et al. 2017, AJ, 154, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Braibant, L., Hutsemékers, D., Sluse, D., Anguita, T., & García-Vergara, C. J. 2014, A&A, 565, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Breiman, L. 2001, Mach. Learn., 45, 5 [CrossRef] [Google Scholar]
- Brescia, M., Cavuoti, S., & Longo, G. 2015, MNRAS, 450, 3893 [NASA ADS] [CrossRef] [Google Scholar]
- Cabanac, R. A., Alard, C., Dantel-Fort, M., et al. 2007, A&A, 461, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrasco, D., Barrientos, L., Pichara, K., et al. 2015, A&A, 584, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capaccioli, M., & Schipani, P. 2011, The Messenger, 146, 2 [NASA ADS] [Google Scholar]
- Capaccioli, M., Schipani, P., de Paris, G., et al. 2012, Science from the Next Generation Imaging and Spectroscopic Surveys, 1 [Google Scholar]
- Chen, T., & Guestrin, C. 2016, Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 785 [Google Scholar]
- Chiu, K., Richards, G., Hewett, P., & Maddox, N. 2007, MNRAS, 375, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Cortes, C., & Vapnik, V. 1995, Mach. Learn., 20, 273 [Google Scholar]
- Cutri, R., Wright, E., Conrow, T., et al. 2013, Explanatory Supplement to the AllWISE Data Release Products, Tech. rep. [Google Scholar]
- D’Isanto, A., Cavuoti, S., Gieseke, F., & Polsterer, K. 2018, A&A, 616, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, J. T. A., Verdoes Kleijn, G. A., Kuijken, K. H., & Valentijn, E. A. 2013, Exp. Astron., 35, 25 [Google Scholar]
- de Jong, J. T. A., Verdoes Kleijn, G. A., Erben, T., et al. 2017, A&A, 604, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ding, X., Treu, T., Suyu, S. H., et al. 2017, MNRAS, 465, 4634 [NASA ADS] [CrossRef] [Google Scholar]
- Donley, J. L., Koekemoer, A. M., Brusa, M., et al. 2012, ApJ, 748, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Dorogush, A. V., Ershov, V., & Gulin, A. 2018, ArXiv e-prints [arXiv:1810.11363] [Google Scholar]
- Driver, S. P., Norberg, P., Baldry, I. K., et al. 2009, Geophys., 50, 12 [Google Scholar]
- Duda, R. O., & Hart, P. E. 1973, Pattern Classification and Scene Analysis (J. Wiley & Sons) [Google Scholar]
- Edge, A., Sutherland, W., Kuijken, K., et al. 2013, The Messenger, 154, 32 [NASA ADS] [Google Scholar]
- Elting, C., Bailer-Jones, C. A. L., & Smith, K. W. 2008, Am. Inst. Phys. Conf. Ser., 1082, 9 [NASA ADS] [Google Scholar]
- Elvis, M., Wilkes, B. J., McDowell, J. C., et al. 1994, ApJS, 95, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Eyer, L., & Blake, C. 2005, MNRAS, 358, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, J. H. 2000, Ann. Stat., 29, 1189 [Google Scholar]
- Gaia Collaboration (Brown, A., et al.) 2018a, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Mignard, F., et al.) 2018b, A&A, 616, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieseke, F., Polsterer, K. L., Thom, A., et al. 2011, 2010 Ninth International Conference on Machine Learning and Applications, 352 [Google Scholar]
- Gilman, D., Birrer, S., Treu, T., Keeton, C. R., & Nierenberg, A. 2018, MNRAS, 481, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Guerras, E., Mediavilla, E., Jimenez-Vicente, J., et al. 2013, ApJ, 778, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, S., Qi, Z., Liao, S., et al. 2018, A&A, 618, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartley, P., Flamary, R., Jackson, N., Tagore, A. S., & Metcalf, R. B. 2017, MNRAS, 471, 3378 [NASA ADS] [CrossRef] [Google Scholar]
- Haehnelt, M. G., & Kauffmann, G. 2000, MNRAS, 318, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Hernitschek, N., Schlafly, E., Branimir, S., et al. 2016, ApJ, 817, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., Robertson, B., & Springel, V. 2006, ApJS, 163, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž, & LSST Science Collaboration 2013, LSST Science Requirements Document, http://ls.st/LPM-17 [Google Scholar]
- Jacobs, C., Collett, T., Glazebrook, K., et al. 2019, MNRAS, 484, 5330 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Cohen, M., Masci, F., et al. 2011, ApJ, 735, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, X., Zhang, Y., & Zhang, J. 2019, MNRAS, 485, 4539 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., & Haehnelt, M. 2000, MNRAS, 311, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Keeton, C. R., & Moustakas, L. A. 2009, ApJ, 699, 1720 [NASA ADS] [CrossRef] [Google Scholar]
- Khramtsov, V., & Akhmetov, V. 2018, Proceedings of a IEEE XIIIth International Scientific and Technical Conference “CSIT”, 72 [Google Scholar]
- Khramtsov, V., Akhmetov, V., & Fedorov, P. 2018, A&A, submitted [Google Scholar]
- Kim, D.-W., Protopapas, P., Byun, Y.-I., et al. 2011, ApJ, 735, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, A., & Szapudi, I. 2015, MNRAS, 448, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Krakowski, T., Małek, K., Bilicki, M., et al. 2016, A&A, 596, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krakowski, T., Małek, K., Bilicki, M., Siudek, M., & Pollo, A. 2018, Polish Astron. Soc., 7, 252 [Google Scholar]
- Kochanek, C. S. 2006, in Gravitational Lensing: Strong, Weak and Micro, eds. G. Meylan, P. Jetzer, & P. North (Berlin: Springer-Verlag) [Google Scholar]
- Koopmans, L. V. E., Treu, T., Bolton, A. S., Burles, S., & Moustakas, L. A. 2006, ApJ, 649, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmans, L. V. E., Bolton, A., Treu, T., et al. 2009, ApJ, 703, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Krone-Martins, A., Delchambre, L., Wertz, O., et al. 2018, A&A, 616, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuijken, K. 2008, A&A, 482, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuijken, K., Heymans, C., Hildebrandt, H., et al. 2015, MNRAS, 454, 3500 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K., Heymans, C., Dvornik, A., et al. 2019, A&A, 625, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacy, M., Storrie-Lombardi, L. J., Sajina, A., et al. 2004, ApJS, 154, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Lanusse, F., Ma, Q., Li, N., et al. 2018, MNRAS, 473, 3895 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Liao, K., Ding, X., Biesiada, M., Fan, X.-L., & Zhu, Z.-H. 2018, ApJ, 867, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Hernandez, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemon, C. A., Auger, M. W., McMahon, R. G., & Koposov, S. E. 2017, MNRAS, 472, 5023 [NASA ADS] [CrossRef] [Google Scholar]
- Lemon, C., Auger, M., McMahon, R., & Ostrovski, F. 2018, MNRAS, 479, 5060 [NASA ADS] [CrossRef] [Google Scholar]
- Mansour, Y. 1997, Proceedings of the 14th International Conference on Machine Learning, 195 [Google Scholar]
- Mateos, S., Alonso-Herrero, A., Carrera, F. J., et al. 2012, MNRAS, 426, 3271 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, B. 1975, Biochim. Biophys. Acta (BBA)– Protein Struct., 405, 442 [CrossRef] [Google Scholar]
- Metcalf, R. B., Meneghetti, M., Avestruz, C., et al. 2018, A&A, 625, A119 [Google Scholar]
- Motta, V., Mediavilla, E., Falco, E., & Muñoz, J. A. 2012, ApJ, 755, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Nakoneczny, S., Bilicki, M., Solarz, A., et al. 2019, A&A, 624, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nolte, A., Wang, L., Bilicki, M., Holwerda, B., & Biehl, M. 2019, Neurocomputing, 342, 172 [CrossRef] [Google Scholar]
- Oguri, M., & Marshall, P. J. 2010, MNRAS, 405, 2579 [NASA ADS] [Google Scholar]
- Oguri, M., Inada, N., Pindor, B., et al. 2006, AJ, 132, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Rusu, C. E., & Falco, E. E. 2014, MNRAS, 439, 2494 [NASA ADS] [CrossRef] [Google Scholar]
- Ostrovski, F., Lemon, C., Auger, M., et al. 2018, MNRAS, 473, L116 [NASA ADS] [CrossRef] [Google Scholar]
- Paraficz, D., Courbin, F., Tramacere, A., et al. 2016, A&A, 592, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peters, C. M., Richards, G. T., Myers, A. D., et al. 2015, ApJ, 811, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Petrillo, C. E., Tortora, C., Chatterjee, S., et al. 2017, MNRAS, 472, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Petrillo, C. E., Tortora, C., Chatterjee, S., et al. 2019a, MNRAS, 482, 807 [NASA ADS] [Google Scholar]
- Petrillo, C. E., Tortora, C., Vernardos, G., et al. 2019b, MNRAS, 484, 3879 [NASA ADS] [CrossRef] [Google Scholar]
- Proft, S., & Wambsganss, J. 2015, A&A, 574, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prokhorenkova, L., Gusev, G., Vorobev, A., Dorogush, A. V., & Gulin, A. 2018, Adv. Neural Inf. Process. Syst., 31, 6638 [Google Scholar]
- Quinlan, J. R. 1986, Mach. Learn., 1, 81 [Google Scholar]
- Refsdal, S. 1964, MNRAS, 128, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Rumelhart, D. E., Hinton, G. E., & Williams, R. J. 1986, Parallel Distributed Processing: Explorations in the Microstructure of Cognition (Cambridge, MA, USA: MIT Press), 1, 318 [Google Scholar]
- Robin, A., Luri, X., Reylé, C., et al. 2012, A&A, 543, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rusu, C. E., Oguri, M., Minowa, Y., et al. 2014, MNRAS, 444, 2561 [NASA ADS] [CrossRef] [Google Scholar]
- Rusu, C. E., Berghea, C. T., Fassnacht, C. D., et al. 2019, MNRAS, 486, 4987 [NASA ADS] [Google Scholar]
- Shankar, F., Weinberg, D. H., & Miralda-Escudé, J. 2009, ApJ, 690, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Strauss, M. A., Ross, N. P., et al. 2009, ApJ, 697, 1656 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. L., & Wambsganss, J. 2002, ApJ, 580, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. L., Anguita, T., Morgan, N. D., Read, M., & Shanks, T. 2018, Res. Notes AAS, 2, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Schindler, J.-T., Fan, X., McGreer, I. D., et al. 2017, ApJ, 851, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Schindler, J.-T., Fan, X., McGreer, I. D., et al. 2018, ApJ, 863, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Sergeyev, A., Spiniello, C., Khramtsov, V., et al. 2018, Res. Notes AAS, 2, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Sluse, D., Schmidt, R., Courbin, F., et al. 2011, A&A, 528, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spiniello, C., Koopmans, L. V. E., Trager, S. C., Czoske, O., & Treu, T. 2011, MNRAS, 417, 3000 [NASA ADS] [CrossRef] [Google Scholar]
- Spiniello, C., Koopmans, L. V. E., Trager, S. C., et al. 2015, MNRAS, 452, 2434 [NASA ADS] [CrossRef] [Google Scholar]
- Spiniello, C., Agnello, A., Napolitano, N. R., et al. 2018, MNRAS, 480, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Spiniello, C., Sergeyev, A., Marchetti, L., et al. 2019, MNRAS, 485, 5086 [NASA ADS] [Google Scholar]
- Stern, D., Eisenhardt, P., Gorjian, V., et al. 2005, ApJ, 631, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, D., Assef, R. J., Benford, D. J., et al. 2012, ApJ, 753, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Treu, T., Hilbert, S., et al. 2014, ApJ, 788, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Bonvin, V., Courbin, F., et al. 2017, MNRAS, 468, 2590 [Google Scholar]
- Treu, T., Agnello, A., & Strides Team 2015, Am. Astron. Soc., 225, 318.04 [NASA ADS] [Google Scholar]
- Tinney, C. G. 1995, MNRAS, 277, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Tinney, C. G., Da Costa, G. S., & Zinnecker, H. 1997, MNRAS, 285, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Vakili, M., et al. 2019, MNRAS, in press [Google Scholar]
- Vapnik, V. 1995, The Nature of Statistical Learning Theory (New York, USA: Springer-Verlag) [Google Scholar]
- Viquar, M., Basak, S., Dasgupta, A., Agrawal, S., & Saha, S. 2018, ArXiv e-prints [arXiv:1804.05051] [Google Scholar]
- Walsh, D., Carswell, R. F., & Weymann, R. J. 1979, Nature, 279, 381 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, A. H., Hildebrandt, H., Kuijken, K., et al. 2019, A&A, 632, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyithe, J. S. B., & Loeb, A. 2003, ApJ, 595, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Zackrisson, E., & Riehm, T. 2010, Adv. Astron., 2010, 478910 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Testing different classifiers
The main result of the main body of the paper is a catalogue of bright objects from KiDS DR4 that we classified into three families, STAR, QSO, and GALAXY, using a ML-based classifier that uses the GB algorithm.
In order to choose the best possible algorithm for our purposes, we tested two different approaches (and three diffrent methods) based on ensembles of decision trees, namely the GB (Friedman 2000) and RF (Breiman 2001) algorithms. Here in this appendix, we provide a more detailed description of the classifiers, their main characteristics, and their strength and weakness points in order to provide a better understanding of the differences and similarities between them and to finally justify our final choice.
The general classification problem can be simply explained considering a training dataset (D) with n samples and m features for each sample with defined label yi: D = {xi, yi} where  . The goal is then to create an approximation function F : x → y.
. The goal is then to create an approximation function F : x → y.
The two GB algorithms mentioned above follow two different approaches of ensemble learning, that could be propagated not only on the decision trees. We describe them in details in the following sections. We focus instead on the RF method in the following section.
A.1. Gradient Boosting decision trees
XGBoost (Chen & Guestrin 2016 and CatBoost Dorogush et al. 2018; Prokhorenkova et al. 2018) are two GB (Friedman 2000) algorithms that implement two different schemes for calculating gradients.
Let us consider the ensemble of K trees, where the predicted score for an input x is given by the sum of the values predicted by the individual K trees: 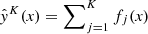 , where fj is the output of the jth decision tree.
, where fj is the output of the jth decision tree.
Building the (K + 1)th decision tree minimizes an objective function 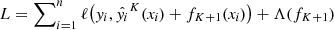 , where
, where 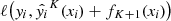 depends on the first (and, possibly, second) deviation of the loss function
depends on the first (and, possibly, second) deviation of the loss function 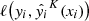 , and Λ(fK + 1) is a regularization function that penalizes the complexity of the (K + 1)th tree to prevent overfitting. To build a (K + 1)th decision tree, the algorithm starts with a single decision node and iteratively tries to add a best split for each node, until a stop criterion on tree growth is satisfied.
, and Λ(fK + 1) is a regularization function that penalizes the complexity of the (K + 1)th tree to prevent overfitting. To build a (K + 1)th decision tree, the algorithm starts with a single decision node and iteratively tries to add a best split for each node, until a stop criterion on tree growth is satisfied.
XGBoost estimates the gradient value for all of the objects in a leaf and calculates the average gradient to determine the best split for each node. In this way, the gradient is estimated via the same data points, on which the current decision tree was built on. In general, such splitting procedure leads to the gradient bias, due to the repeated usage of the same objects through all iterations, and, as result, to an overfitting problem (Prokhorenkova et al. 2018).
CatBoost, the chosen algorithm for this paper, in its turn implements the splitting technique called Ordered Boosting (Prokhorenkova et al. 2018), which overcomes this problem. With Ordered Boosting, the gradients are calculated not for all of the objects but for the shuffled training dataset (so-called random permutations), wherein the gradients are calculated for the objects before a given j + 1 object. In such a way, the gradient for the j + 1 object is calculated based on a prediction of the model, learnt by previous samples in a shuffled dataset.
One of the limitations of the GBDT algorithms is the existence of a wide range of parameters that have to be tuned to get the highest classification quality; CatBoost also confers an advantage in this respect, because it performs well without hyperparameter tuning.
For our task, the most influential hyperparameters that have to be tuned in GBDT algorithms are:
-
learning_rate – the rate of gradient descent;
-
min_split_loss – the minimum loss reduction required to split a node of the tree;
-
max_depth – the maximum depth of the decision trees;
-
min_child_weight – the minimum number of samples in the node of the decision tree required to make a split;
-
max_delta_step – the maximum step controlling convergence during gradient descent;
-
colsample_bytree – the subsample ratio of the features during building each decision tree;
-
subsample – the subsample ratio of the training objects
In particular, we noticed that the parameters that mostly affected the learning quality for our training dataset were learning_rate (greater values correspond to a sharper gradient descent, that is good for learning acceleration, but can lead to missing the loss minimum), and max_depth (greater values correspond to a large complexity of the trees, and can lead to overfitting).
Moreover, GB algorithms usually allow the use of a stop criterion, responsible for the termination of the learning when an overfitting occurs (the so-called, early_stopping parameter). It is expressed via the number of constructed trees, after which the quality of the metric no longer increases. Usually this parameter ranges between 10 and 1000 trees, depending on learning_rate. If the early stopping criterion is met, the GB algorithm accepts the number of trees, satisfied to the best score. Paying particular attention to the early_stopping parameter is the best way to avoid as much overfitting as possible. To quantify, how the quality of the classification changes over the iterations, for XGBoost and CatBoost, it is necessary to define a quality metric. Defining this metric allows one to express the changing of the classification quality against the complexity of the GBDT algorithm and can be easily used to control the overfitting. Widely used quality metrics are accuracy, precision, recall, and F1-score; however, these metrics are sensitive to the imbalance in number of training sources among different classes. Therefore, we decided to use Matthews correlation coefficient (MCC, Matthews 1975) which is instead insensitive to this imbalance.
Finally, a good way to decrease the number of stars and galaxies classified by the algorithm as quasars is to apply a weight to the loss function of these two classes. In fact, this trick, applied to CatBoost, helped us in the paper to improve the final purity of the quasar selection with a minimal decrease in the completeness of the training set. In particular, we weighted the loss function for the STAR and GALAXY samples in the following way:
where wi = 1 if source is a QSO and wi = 4 if source is STAR or GALAXY.
A.2. Random Forest
Another method of ensemble learning with decision trees is based on the use of an RF (Breiman 2001) algorithm. This was the choice adopted in KiDS DR3 by N19. The basic idea of RF is that a set of decision trees can fit a robust classifier by averaging their decisions.
From the performance side, the RF constructs a large number of decision trees and then uses the majority vote among them. The main pipeline of the single decision tree includes the following steps: (1) generation of different samples from the training set with the same size, but using random subsets of all the objects. The repetition of some objects among different subsamples is required to make the sample complete (so-called, random subsample with replacement); (2) let the decision tree learn on the “random subsample with replacement”, generated at step (1), but using randomly selected 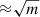 features.
features.
The RF therefore consists of many learning processes, each performed on a single decision tree using different random subsamples with replacement and randomly selected features. The single prediction of a class for given objects is thus a simple average on the predictions of all constructed decision trees (bootstrap bagging method). The big advantage of RF is that it uses both the bootstrap bagging method (averaging prediction of the estimators learnt with random subsamples with replacement) and the learning of each estimator with a random subset of features. These procedures prevent overfitting and in most of the cases help to improve the classification performance and to increase the generalization ability of the RF.
The principal hyperparameters that are required for the RF fitting on the training dataset are:
-
n_estimators – the number of decision trees;
-
max_features – the maximum number of features to be used in the node;
-
max_depth – the maximum depth of the decision trees;
-
min_samples_split – the minimum number of samples in the node of the decision tree required to make a split;
-
min_samples_leaf – the minimum number of samples required to be in the leaf node (the end node in which the splitting finishes) of each tree;
-
class_weight – weights associated with each class (is required in the case of imbalance training sample).
The number of estimators and the maximum depth (and/or minimum number of samples in the node) are mandatory hyperparameters. Moreover, fine-tuning of the parameters 3, 4, and 5 is crucial to avoid overfitting. For instance, setting the values of these parameters to their common values of {∞,2, 1} respectively will lead to overfitting most of the time. In fact, if the depth of the decision tree is too high, and the minimum number of sample required to be in the leaf node is too small, and each single object in the training will have its own class characterized by its features. This will then make it impossible to classify new, unknown objects, although the accuracy of classification of the training set will be equal to about 100% (Mansour 1997). Therefore, to reduce overfitting, one has to limit the maximum depth of the decision trees (usually set to 3−20, depending on the amount and topology of the features), and/or the minimum number of samples in the nodes.
A.3. Performance of the classification algorithms
To directly compare the performance of the three algorithms that we tested, we used confusion matrices. These show the relative number of predicted objects in each of the three classes with respect to the number of true classes. The confusion matrices for RF, XGBoost, and CatBoost are shown in Fig. A.1. As we can see, RF provides the highest completeness for quasars (≈98.8%), but with a contamination of ≈0.8% from stars and ≈0.1% from galaxies; XGBoost shows the greatest purity of quasar selection, but with a very low completeness (only ≈75.8% quasars were classified as quasars).
 |
Fig. A.1. Confusion matrices for the RF (left), XGBoost (central) and CatBoost (right) predictions on OOF sample (top panels) and hold-out sample (bottom panels). |
For the GALAXY class, CatBoost and RF provide very similar completeness (higher than XGBoost), with a very low contamination from stars (< 0.1%) but CatBoost gives a much greater contamination from QSO (≈0.25%).
As one can see, RF and CatBoost show very similar results. To better understand which was the best choice for our scientific purposes, we decided to compare the difference between the MCC value received for the training sample and the one received for the OOF sample, for each of the algorithms. Usually, a large difference between these two scores (training and validation) indicates an overfitting in the model, that is the classifier loses its ability to classify sources, that are not presented in the training sample, and consequently is only able to classify correctly training data. For the RF, we received the following MCC values for training and OOF samples respectively: 0.9925 and 0.9892 (with a difference of 0.0033). For CatBoost the MCC equals 0.9901 for training data and 0.9894 for the OOF sample. Therefore, in this case, the difference (0.0007) is almost five times smaller.
In conclusion, CatBoost is more able to generalize good results on an unseen dataset. It also maintains the purity and completeness of the quasar selection at a very high level and maximizes the completeness of the sample of galaxies. At the same time, CatBoost also removes the greatest amount of stellar contamination. For all of these reasons, CatBoost was chosen as the optimal classifier for our purposes.
All Tables
Number of objects for each class using different probability threshold to define class belonging.
Basic statistics of the astrometric parameters of all the objects in the KiDS output catalogue classified as quasars and with a match in Gaia DR2.
Most reliable gravitationally lensed quasar candidates found with the “Multiplets” method described in the text.
All Figures
 |
Fig. 1. Histogram of the r magnitude distribution for the full KiDS DR4 catalogue (blue) and the SDSS × KiDS training sample (red). |
| In the text | |
 |
Fig. 2. Schematic view of the learning via ten-fold cross validation procedure and validation with the OOF and the hold-out samples drawn from the initial training sample. |
| In the text | |
 |
Fig. 3. Confusion matrices for the final version of CatBoost, after weighting the loss function, performed on the OOF sample (top panel) and the hold-out sample (bottom panel). |
| In the text | |
 |
Fig. 4. Importance of the ten most significant features, calculated with CatBoost in each of the ten folds. The dispersion of importance for each feature is represented by a horizontal tick at each bar. |
| In the text | |
 |
Fig. 5. Upper panel: histogram of the r magnitudes for the three classes of training sources (top panel). Bottom panel: rate at which stars are misclassified as quasars (red curve) or as galaxies (black curve) as a function of their r magnitude. The plot is produced for the full initial training sample. |
| In the text | |
 |
Fig. 6. Upper panel: confusion matrices for the final version of CatBoost performed on the OOF sample using different thresholds of probability in the object classification (see text for more details). Bottom panel: completeness rate of the OOF sample as a function of the adopted probability threshold for each class. |
| In the text | |
 |
Fig. 7. Density plot of the final distribution of sources among the classes in the output catalogue. The triangle corners show the maximum probability of belonging to a given family (right QSO, left GALAXY, up STAR), and colours indicate number of objects. Dashed lines correspond to the p = 0.8 threshold. |
| In the text | |
 |
Fig. 8. Median right ascension (green curve, left) and declination (black curve, left) of the proper motion components, and parallax (red curve, right) for the KiDS DR4 QSO sample as a function of the GaiaG magnitude. The coloured areas represent the standard deviation of the mean σ/N, where σ is the standard deviation and N is the number of quasars in each bin. The black horizontal line in the right plot represents the parallax zero-point (equals to −0.029 mas, Lindegren et al. 2018). |
| In the text | |
 |
Fig. 9. Distribution of the CLASS_STAR parameter for the sources classified as GALAXY (black), QSO (red), or STARS (blue). |
| In the text | |
 |
Fig. 10. Left panel: distribution of the W1 − W2 colour for the classified KiDS DR4, colour coded according to their classification family (red for QSO, black for GALAXY, blue for STAR). Right panel: distribution of the W1 − W2 colour for the train samples. A fair agreement can be found between corresponding classes, although the distribution for the full catalogues is generally broader than that of the training samples. In both panels, the peak of the QSO distribution is shifted towards larger W1 − W2 with respect to the GALAXY and STARS, as expected. |
| In the text | |
 |
Fig. 11. 12 best candidates, both of GALAXY-Multiplets type (first two rows) and of QSO-Multiplets type (bottom row). The cutouts show gri combined KiDS images of 10″ × 10″ in size. The coordinates of the candidates are given in Table 4. |
| In the text | |
 |
Fig. A.1. Confusion matrices for the RF (left), XGBoost (central) and CatBoost (right) predictions on OOF sample (top panels) and hold-out sample (bottom panels). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} L=\frac{1}{\sum _{i=1}^n w_i} \sum _{i=1}^n w_i [\ell \big (y_i, \hat{y_i}^K(\boldsymbol{{x}}_{\boldsymbol{{i}}}) + f_{K+1}(\boldsymbol{{x}}_{\boldsymbol{{i}}})\big )+\Lambda (f_{K+1})] , \end{aligned} $$](/articles/aa/full_html/2019/12/aa36006-19/aa36006-19-eq10.gif)