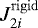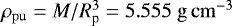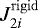| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201935938 | |
| Published online | 04 December 2019 | |
Understanding Jupiter’s deep interior: the effect of a dilute core
State Key Laboratory of Lunar and Planetary Sciences, Macau University of Science and Technology, Macao,
PR China
e-mail: ddni@must.edu.mo
Received:
23
May
2019
Accepted:
4
November
2019
Context. The Juno spacecraft has significantly improved the accuracy of low-order even gravitational harmonics. It has been demonstrated that a dilute core is helpful to interpret Juno’s gravity measurements. However, introducing a dilute core adds a new degree of freedom to Jupiter’s interior models in addition to the uncertainties in the equations of state for hydrogen and helium.
Aims. We present four-layer structure models for Jupiter where a dilute core region is added above a central compact core of rocks. The effect of the dilute core on the structure and composition of Jupiter is investigated in detail. Combined with current knowledge of Jupiter’s composition and thermal state, we aim to obtain information on the dilute core. Also, we investigate the effect of equations of state for hydrogen and helium on the predictions of the core mass and heavy element abundance.
Methods. In the four-layer structure model, the heavy element abundances in the outer two envelopes and the mass of the compact core were adjusted to reproduce Jupiter’s equatorial radius as well as Juno’s gravity observations. Different dilute core configurations were constructed in terms of its size and composition and different equations of state for hydrogen and helium were used in interior structure calculations. Optimized calculations were then performed to investigate the effect of dilute cores and equations of state on Jupiter’s internal structure and composition.
Results. It is found that the absolute values of J6 and J8 tend to decrease as helium becomes more depleted in the dilute core region. Most interior structure calculations seem to prefer an inward decrease of the helium mass fraction from the metallic envelope to the dilute core region. We also show that the core mass and heavy element abundance in Jupiter are dependent upon the rock-to-ice ratio in the dilute core region, the temperature jump from the molecular to metallic envelope, and the equations of state for hydrogen and helium. The resulting heavy-element mass in the core is generally larger than the three-layer structure models owing to the heavy elements dissolved in the dilute core region, and the global heavy-element abundance is in good agreement with the available dilute-core predictions.
Key words: planets and satellites: individual: Jupiter / planets and satellites: interiors / planets and satellites: composition
© ESO 2019
1 Introduction
The Juno spacecraft has measured Jupiter’s gravitational field to high precision through precise Doppler tracking in its polar orbit around Jupiter, compared with the previous values detected by Pioneer 10 and 11 and by Voyager 1 and 2 (Folkner et al. 2017; Bolton et al. 2017; Iess et al. 2018). These new gravity data have improved our knowledge of Jupiter’s interior. The even gravity harmonics are affected by the shape and internal structure of Jupiter in its hydrostatic equilibrium under the effect of rotational distortion. To accurately describe the shape and internal structure of Jupiter, various interior models with new ingredients, such as two-layer and three-layer structure models, have been established by several groups (Guillot & Morel 1995; Guillot 1999; Hubbard 1999, 2013; Anderson & Schubert 2007; Kaspi et al. 2010; Nettelmann et al. 2012; Helled et al. 2015; Vazan et al. 2015; Kong et al. 2016; Wahl et al. 2017; Ni 2018; Guillot et al. 2018; Debras & Chabrier 2019). Most of these models describe the internal structure of Jupiter via the physical laws of nature given an empirical or simulated equation of state (EOS), such as polytropic EOSs, EOSs obtained using the free-energy minimization method (Saumon et al. 1995), and ab initio EOSs (Nettelmann et al. 2008, 2012; French et al. 2012; Becker et al. 2014; Militzer et al. 2008; Militzer & Hubbard 2013; Chabrier et al. 2019). The EOSs describe the microscopic properties of planetary matter and play an important role in calculating the structure and evolution of planets, in spite of uncertainties in the hydrogen–helium phase separation (Hubbard et al. 2002; Saumon & Guillot 2004; Fortney & Nettelmann 2010; Miguel et al. 2016, 2018; Militzer et al. 2016; Debras & Chabrier 2019). Juno’s gravity measurements have demonstrated small values for high-order even gravitational harmonics with respect to the heavy-element abundance measured by the Galileo entry probe (Wahl et al. 2017; Debras & Chabrier 2019). In order to reconcile the calculated gravitational harmonics with these small values of J4 to J8, Wahl et al. (2017) proposed a dilute core model where heavy elements are dissolved in a hydrogen–helium mixture and expanded outward through a portion of Jupiter. Alternatively, these latter authors modified the abundances of helium and heavy elements in the outer molecular envelope to be lower than those measured by the Galileo entry probe. Stimulated by dilute cores, the three-layer structure models for Jupiter have been generalized into four-layer structure models by introducing a dilute core region above central compact cores. Guillot et al. (2018) compared the effective even harmonics 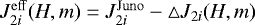 with the ones obtained from interior models assuming rigid rotation to explore the rotation of Jupiter’s deep interior. It is found that Jupiter’s deep interior exhibits an almost rigid-body rotation and Jupiter’s atmospheric zonal flow extends to a depth H of 2000−3500 km. Debras & Chabrier (2019) established new models of Jupiter which satisfy both Juno’s gravity data and the outer helium and heavy element abundances from Galileo, showing a considerable entropy increase between the outer and inner envelopes and an inward decreasing abundance of heavy elements in the inner envelope.
with the ones obtained from interior models assuming rigid rotation to explore the rotation of Jupiter’s deep interior. It is found that Jupiter’s deep interior exhibits an almost rigid-body rotation and Jupiter’s atmospheric zonal flow extends to a depth H of 2000−3500 km. Debras & Chabrier (2019) established new models of Jupiter which satisfy both Juno’s gravity data and the outer helium and heavy element abundances from Galileo, showing a considerable entropy increase between the outer and inner envelopes and an inward decreasing abundance of heavy elements in the inner envelope.
Significant progress has been made in understanding the interior of Jupiter based on Juno’s gravity data in particular for the presence of dilute cores. However, little is known about the dilute cores in Jupiter, since measured gravitational harmonics only provide information on its exterior. Wahl et al. (2017) investigated the effect of dilute cores on zonal gravitational harmonics J4 to J8 with respect to compact cores. In this study, we consider various dilute core configurations and construct four-layer structure models based on current observations of Jupiter’s shape and gravity field and on current simulated results of EOSs. Great attention is paid to the element abundance in the dilute core region and its effect on the internal structure of Jupiter. In Sect. 2, we describe four-layer structure models and specify dilute cores for Jupiter. The gravitational harmonics are calculated in terms of the fifth-order theory of figures and the newly detected data from Juno corrected by the dynamical contribution of Kaspi et al. (2018) are used to constrain the internal structure of Jupiter. In Sect. 3, the physical EOSs for pure hydrogen and pure helium are presented and the additive volume rule is presented to generate the EOS for mixtures of hydrogen, helium, and heavy elements. Section 4 presents various dilute core configurations and interior model predictions. The effects of dilute cores on the internal structure of Jupiter are discussed in detail together with the sensitivity of the predictions to the EOSs adopted in the interior models. Finally, the main results of this work are summarized in Sect. 5.
2 Four-layer structure interior models for Jupiter
In this workwe consider Jupiter’s interior models following the approach described in detail by Guillot (1999), Guillot et al. (2018), and Galanti et al. (2019). The radial structure of Jupiter is assumed to consist of four layers: (1) a homogeneous molecular hydrogen atmosphere in which helium is depleted, (2) a homogeneous metallic hydrogen envelope in which helium is enriched, (3) a dilute core region composed of metallic hydrogen, helium, and enriched heavy elements, and (4) an isothermal central compact core of rocks. The heavy elements, composed of ices and rocks, are assumed to be either water for ices or a mixture of silicates as “dry sand” for rocks (Vazan et al. 2015). The outer two layers are divided by the molecular-to-metallic transition of hydrogen. It has been suggested that the separation between these two layers in Jupiter corresponds to a narrow region of H/He phase separation, where helium is depleted in the upper layer and becomes enriched in the lower layer. The pressure P1−2 for the H/He phase transition ranges from 1.0 to 4.0 Mbar in terms of the immiscibility calculations of Morales et al. (2013). The hydrogen–helium immiscibility region would bring in a convective barrier into Jupiter’s interior, which stabilizes the composition difference between the molecular and metallic layers and reduces the heat transport from the deeper interior (Hubbard & Militzer 2016; Militzer et al. 2016). Owing to helium rain on Jupiter, the upper atmosphere of molecular hydrogen has a smaller helium mass fraction (Y1) than the lower metallic-hydrogen envelope (Y2), and the heavy-element abundances are different in these two layers (denoted by Z1 and Z2). There is also a possible jump in temperature ΔT1−2 across the interface between these two layers besides the discontinuities in density and entropy (Guillot et al. 2018). The mass fractions of helium and heavy elements in the dilute core region are denoted by Y3 and Z3 respectively. There is an increase in the heavy element abundance for the dilute core region. That is, ΔZ2−3 = Z3 − Z2 > 0. The onset of the dilute core region is described with the pressure Pdil (Pdil > P1−2). The helium abundance in the upper atmosphere Y1 is constrained by the Galileo observations Y1∕(1 − Z1) = 0.238 ± 0.005 (von Zahn et al. 1998), and the mean helium mass fraction in Jupiter Y∕(1 − Z) should be equal to its value in the protosolar nebula Yproto∕(1 − Zproto) = 0.277 ± 0.006 (Serenelli & Basu 2010; Guillot et al. 2018). Figure 1 illustrates a schematic diagram of Jupiter’s four-layer structure.
One of the main constraints in understanding the origin and evolution of a planet is its internal structure. Recent evolution models of Jupiter with primordial composition gradients have brought in a current-state structure of Jupiter which is consistent with available observational constraints (Vazan et al. 2016, 2018). Jupiter’s evolution model with a steep primordial composition gradient suggested that the outer envelope becomes adiabatic and enriched with heavy elements via convective mixing while the deep interior becomes non-adiabatic with a staircase composition structure (Vazan et al. 2018). If helium rain is considered in the latter stages of evolution, the region of the outer convective envelope would be separated into two homogeneous envelopes with different compositions. The staircase composition structure in the deep interior is physical, but the exact treatment of the staircases is a relatively complex task. The compact core plus a dilute core region can be regarded as a straightforward approximation for the staircase structure.
Measured gravitational harmonics provide information on the external levels of a planet and gravitational harmonics with higher orders show a higher sensitivity to the outermost part of a planet (Guillot 2005). Therefore, the element abundances in the outer two layers are generally constrained by the measured gravitational harmonics from Juno. In computational practice, there is counter-balance correlation between the abundances of helium and heavy elements, Y and Z, making it difficult to explicitly determine both of them at the same time. Following the works of Guillot & Morel (1995), Saumon & Guillot (2004), Miguel et al. (2016, 2018), and Guillot et al. (2018), only the heavy-element abundances, Z1 and Z2, are adjusted to reproduce Juno’s gravity data. The existence of a core in Jupiter and its physical properties are of great importance to test giant-planet formation theories and are associated with the heavy element abundances in the outer envelopes (Helled 2012). The mass of the central compact core Mcore is therefore also inferred in terms of Juno’s gravity data (Guillot & Morel 1995; Saumon & Guillot 2004; Miguel et al. 2016, 2018; Guillot et al. 2018).
The element abundances in the dilute core region, Y3 and Z3, are poorly constrained by Juno’s gravity measurements and therefore they are adopted beforehand within a wide range (Guillot et al. 2018). Special attention should be paid to the interface between the metallic envelope and the dilute core region where the density jump Δρ2−3 = ρdil(Pdil) − ρmet(Pdil) cannot be negative. For this reason, the compositions Y3 and Z3 in the dilutecore region should be chosen with caution, following the requirement
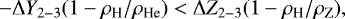 (1)
(1)
where ΔY2−3 and ΔZ2−3 separately stand for a jump in the mass fractions of helium and heavy elements, and ρH, ρHe, and ρZ, are the densities of hydrogen, helium, and heavy elements at the interface, respectively. In the dilute core region, water is in a liquid phase and can be fully dissolved into the metallic hydrogen (Wilson & Militzer 2012a). Silica, as a proxy for rocks, is also found to be dissolved into the metallic hydrogen at the central conditions of Jupiter (Wilson & Militzer 2012b), giving an active response to the existence of eroded or eroding cores in Jupiter. In view of this, one free parameter frock, called the rock mass fraction in heavy elements, is introduced for the dilute core region to take into account the rocks dissolved from the central rocky core.
The interior structure calculations are performed by solving the equations of hydrostatic equilibrium, thermodynamic equilibrium, mass conservation, and energy conservation (Guillot & Morel 1995). The outer boundary condition at 1 bar is set as T = 165 ± 5 K based on Voyager and Galileo measurements (Lindal et al. 1981). Our numerical model is established on the code CEPAM (Guillot et al. 2018; Guillot & Morel 1995). We make no change regarding the numerical methods involved but some modifications for the above four-layer structure model. First, a dilute core region is added where the heavy elements are composed of ice and rock, and a large ensemble of dilute core configurations are constructed in terms of its size and composition Pdil, Y3, Z3, and frock ; details can be found in Appendix A. Second, the optimization procedure is extended using three adjustable parameters Z1, Z2, and Mcore, rather than the original two parameters Z1 and Mcore.
The concentric MacLaurin spheroid (CMS) method and theory of figures (ToF) have been used to calculate the self-consistent shape and gravity field of rotating liquid planets (Hubbard 2013; Hubbard & Militzer 2016; Nettelmann 2017; Debras & Chabrier 2018; Militzer et al. 2019). The CMS method shows better accuracy but requires a larger amount of computation with respect to the ToF (Hubbard 2013; Debras & Chabrier 2018). The accuracy of the ToF to fourth order has been explored by Nettelmann (2017) and is sufficient to infer the internal structure of Jupiter from Juno’s gravity data. In view of a large ensemble of possible dilute core configurations and a number of iterations necessary to fit Juno’s gravitational harmonics, we decide to employ the ToF to fifth order (ToF5) and develop new ToF5 subroutines within the CEPAM based on the work of Zharkov & Trubitsyn (1975). The level surfaces are given by the figure functions s2i (s) in the form
![\begin{eqnarray*}r(s,\theta)\;{=}\;s\Bigg{[}1+\sum_{i{=}0}^{5}s_{2i}(s)P_{2i}(\cos\theta)\Bigg{]}, \end{eqnarray*}](/articles/aa/full_html/2019/12/aa35938-19/aa35938-19-eq3.png) (2)
(2)
and the gravitational zonal harmonic coefficients are weighted integrals over the internal density distribution ρ(r, θ),
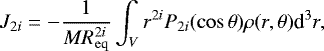 (3)
(3)
where Req is the equatorial radius of the planet. Using the computed figure functions s2i (s) and abbreviating the level surface as r = s(1 + ∑), one can evaluate the even zonal harmonics from Eq. (3) as (Guillot et al. 2018)
![\begin{eqnarray*}J_{2i}&=&-\frac{3}{2}\bigg{(}\frac{R_{\textrm{p}}}{R_{\mathrm{eq}}}\bigg{)}^{2i}\int_{-1}^{1}\textrm{d}\cos\theta~P_{2i}(\cos\theta)\int_{0}^{1}\textrm{d}x~\nonumber \\[4pt] &&\times\, x^{2i+2}\bigg{(}1+\sum\bigg{)}^{2i+2}\eta(x)\bigg{(}\frac{\textrm{d}r}{\textrm{d}s}\bigg{)}, \end{eqnarray*}](/articles/aa/full_html/2019/12/aa35938-19/aa35938-19-eq5.png) (4)
(4)
where Rp is the mean radius of the planet, x is the scaled mean radius, x = s∕Rp, η(x) is the normalized density distribution,and (dr∕ds) is the derivative of r with respectto s obtained from Eq. (2). In Appendix B, the ToF5 implementation is checked and the comparison with the CMS method is presented. The accuracy of the ToF5 is found to be sufficient to infer Jupiter’s interior from Juno’s gravity data.
The even gravity harmonics are contributed from a rigidly rotating planet 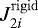 and differentially rotating zonal flows ΔJ2i, since the dynamical flows affect the internal density distribution. The rigid-rotation contribution is obtained bysubtracting the flow-induced contribution from Juno’s gravity data of Iess et al. (2018),
and differentially rotating zonal flows ΔJ2i, since the dynamical flows affect the internal density distribution. The rigid-rotation contribution is obtained bysubtracting the flow-induced contribution from Juno’s gravity data of Iess et al. (2018), 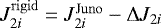 . The flow-induced even gravity harmonics by Kaspi et al. (2018) are adopted in this work and the resulting rigid-rotation contribution
. The flow-induced even gravity harmonics by Kaspi et al. (2018) are adopted in this work and the resulting rigid-rotation contribution 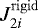 is used for reference (Debras & Chabrier 2019). Table 1 shows Juno’s even gravity harmonics, which are decomposed into the dynamical and static parts, ΔJ2i and
is used for reference (Debras & Chabrier 2019). Table 1 shows Juno’s even gravity harmonics, which are decomposed into the dynamical and static parts, ΔJ2i and 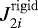 .
.
 |
Fig. 1 Schematic four-layer structure of Jupiter. There is a temperature jump ΔT1−2 between the molecular and metallic hydrogen envelopes owing to a thin helium rain layer and the onset of the dilute core region is described with the pressure Pdil. |
3 Equations of state
Interior models of Jupiter require the input of the hydrogen–helium EOSs, namely the density as a function of temperature, pressure and composition. There are various EOSs available based on different methods and considerations (Guillot & Morel 1995; Saumon & Guillot 2004; Miguel et al. 2016, 2018). Saumon et al. (1995) presented the EOSs for hydrogen and helium using the free-energy minimization technique within the chemical picture, namely SCvH. Along with the progress in computer capacity and numerical techniques, EOSs have also been calculated from ab initio simulations within the physical picture since 2006 (Nettelmann et al. 2008, 2012; French et al. 2012; Becker et al. 2014; Militzer et al. 2008; Militzer & Hubbard 2013; Chabrier et al. 2019). Recently, Chabrier et al. (2019, CMS19) presented new EOSs for pure fluid hydrogen and helium as well as dense hydrogen–helium mixtures, where ab initio simulations for intermediate density are combined with semi-analytical calculations for low density and high density. Based on the works of Miguel et al. (2016, 2018) and Chabrier et al. (2019), we choose to use four different EOSs for hydrogen and helium in this work: the ab initio EOS REOS3b for which the zero point of the specific internal energy in the REOS.3 tables of Becker et al. (2014) is changed to coincide in the ideal gas regime with the SCvH EOS; the ab initio EOS MH13+SCvH which is extracted from the tables of Militzer & Hubbard (2013, MH13) for hydrogen–helium mixtures using the SCvH EOS; the newly available EOS CMS19 of Chabrier et al. (2019); and the SCvH EOS of Saumon et al. (1995). The SCvH EOS seems to be incompatible with available shock compression data (Miguel et al. 2016, 2018), but has been widely used in the previous interior models of Jupiter. Here it is still used as a comparison and test of the present calculations. For a minor amount of heavy elements, we choose to use the EOS of dry sand in SESAME for rocks and the SESAME EOS 7154 of water for ices (Lyon & Johnson 1992; Guillot & Morel 1995; Saumon & Guillot 2004). For mixtures of hydrogen, helium, and heavy elements, the EOS is generated using the separate EOSs for pure species in terms of the additive volume rule. The density for the mixture is therefore approximated at any given pressure P, temperature T, and X∕Y∕Z composition as
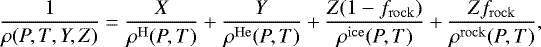 (5)
(5)
where frock is the rock mass fraction in heavy elements as defined in Sect. 2.
Jupiter’s gravity harmonics J2i, decomposed into the dynamical and static parts, ΔJ2i and 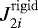 .
.
4 Model results
The heavy element abundances Z1 and Z2 as well as the compact core mass Mcore are adjusted to reproduce Jupiter’s equatorial radius Req and even low-order gravitational harmonics J2, J4, J6. The optimization procedure for the observational constraints is performed by minimizing the following function (Guillot & Morel 1995; Saumon & Guillot 2004):
![\begin{equation*}\chi^{2}(Z_{1},Z_{2},M_{\mathrm{core}})=\frac{1}{4}\left[\left(\frac{R_{\mathrm{eq}}^{\mathrm{cal.}}-R_{\mathrm{eq}}^{\mathrm{obs.}}}{\sigma_{R_{\mathrm{eq}}}}\right)^{2} +\sum_{i=1}^{3}\left(\frac{J_{2i}^{\mathrm{cal.}}-J_{2i}^{\mathrm{obs.}}}{\sigma_{J_{2i}}}\right)^{2}\right], \end{equation*}](/articles/aa/full_html/2019/12/aa35938-19/aa35938-19-eq11.png) (6)
(6)
where σq denotes the observational uncertainties of the quantity q. Some model parameters are not explicitly determined at present, such as the pressure P1−2 and temperature jump ΔT1−2 of the H/He phase transition. The pressure P1−2 for the H/He phase transition affects Jupiter’s internal structure, which has been widely investigated by several groups (Nettelmann et al. 2012; Becker et al. 2014; Miguel et al. 2016, 2018). The P1−2 effect is beyond the scope of this work and is fixed at P1−2 = 2.0 Mbar in our calculations. The change ΔT1−2 in temperature resulting from the H–He phase separation is uniformly varied from 0 to 800 K. The objective of the present paper is to explore the effect of dilute cores on Jupiter’s internal structure based on current knowledge of Jupiter’s composition and thermal state. In order to consider all possible dilute core configurations, four quantities characterizing the size and composition of dilute cores, Pdil, Y3, Z3, and frock, are chosen within a broad range. We impose the following constraints on them: (i) the jump ΔZ2−3 in the heavy element abundance from the metallic envelope to the dilute core region ranges from 0 to 0.2. The variation ΔY2−3 in the helium mass fraction is not larger than 0.2. Furthermore, they should follow the rule Eq. (1) in order to avoid the density decrease towards the center. (ii) The helium mass fraction Y2 in the metallic envelope is correlated with Y3 in the dilute core region by the requirement that the mean helium mass fraction in Jupiter should be equal to its value in the protosolar nebula. In accordance with helium rain in Jupiter, the resulting helium mass fraction Y2 should be larger than that in the above layer. That is, Y2 > Y1. (iii) The onset of the dilute core region Pdil is uniformly varied from 6 to 26 Mbar. (iv) The rock mass fraction frock is allowed to vary from 0 to 1.0 for the dilute core region. We note that Jupiter’s “core” is considered to be a central compact core plus a dilute core region. Therefore, the heavy element mass in the core is expressed as 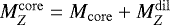 , while the heavy element mass in the envelopes is given by
, while the heavy element mass in the envelopes is given by 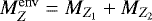 .
.
 |
Fig. 2 Mass of heavy elements in the core and in the molecular and metallic envelopes predicted with different rock fractions frock in the dilute core region. Full and half solid points show the results for two different EOSs of hydrogen and helium, respectively:REOS3b (full solid) and MH13+SCvH (half solid). |
4.1 Rockfractions in the dilute core region
First, let us focus on the effect of the rock mass fraction frock on Jupiter’sinterior models. In the dilute core region, the mass fractions of ices and rocks are given as Zice = Z3(1 − frock) and Zrock = Z3frock, respectively.Figure 2 shows the dependence of Jupiter’s internal structure on the rock fraction frock for both ab initio EOSs of hydrogen and helium: REOS3b and MH13+SCvH. With increasing rock fraction, the heavy element mass in the core 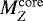 becomes smaller and the heavy element mass in the envelope
becomes smaller and the heavy element mass in the envelope 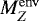 also becomes smaller for the same
also becomes smaller for the same 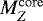 . It seems that increasing the rock fraction tends to lower heavy element abundance in Jupiter. Miguel et al. (2016, 2018) investigated the effect of the EOSs for heavy elements on Jupiter’s interior using three different EOSs: water NIST, water SESAME, and dry sand SESAME. As the EOS for heavy elements is changed from water SESAME to dry sand SESAME, corresponding to the change of frock from 0.0 to 1.0, theselatter authors found that both masses of the core and heavy elements become lower. Our results presented here are consistent with theirs. In order to gain a clear insight into the other effects on Jupiter’s internal structure, the rock fraction is fixed at frock = 0.45 for the dilute core region in the following calculations unless otherwise specified.
. It seems that increasing the rock fraction tends to lower heavy element abundance in Jupiter. Miguel et al. (2016, 2018) investigated the effect of the EOSs for heavy elements on Jupiter’s interior using three different EOSs: water NIST, water SESAME, and dry sand SESAME. As the EOS for heavy elements is changed from water SESAME to dry sand SESAME, corresponding to the change of frock from 0.0 to 1.0, theselatter authors found that both masses of the core and heavy elements become lower. Our results presented here are consistent with theirs. In order to gain a clear insight into the other effects on Jupiter’s internal structure, the rock fraction is fixed at frock = 0.45 for the dilute core region in the following calculations unless otherwise specified.
Jupiter’s gravity harmonics J2i and model values of some selected interior models.
4.2 Jupiter’s internal structure and even gravity harmonics
In view of the unprecedented precision of Juno’s gravity data and the dynamical uncertainties of differentially rotating zonal flows, we allow the model solutions to deviate from the measured values within ~30σ, corresponding to χ2 ≤ 103. In all, 1887 solutions are calculated for REOS3b, 1681 solutions for MH13+SCvH, 825 solutions for CMS19, and 386 solutions forSCvH. Figure 3 shows the gravity harmonics obtained with various models in the Ji − Ji+2 plans, compared with Juno’s static gravity harmonics 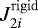 .
.
Table 2 shows Jupiter’s gravity harmonics J2i and model values of some representative interior models. All the models are able to match Juno’s J2 value. The REOS3b model shows good agreement with Juno’s J2, J4, and J6 values. The REOS3b EOS has a higher temperature profile than the MH13+SCvH EOS, corresponding to a lower density of hydrogen–helium mixtures (Miguel et al. 2016, 2018). The larger heavy element abundances in the envelopes are therefore required to reach Jupiter’s mean density. The MH13+SCvH and CMS19 models show similar results for Jupiter’s gravity harmonics, but the CMS19 adiabat has a higher density in the ~Mbar region than the previous EOSs (Chabrier et al. 2019). This leads to a small fraction of heavy elements in Jupiter’s interior. The SCvH model reproduces Juno’s J2 and J4 values and exhibits a small compact core together with high envelope metallicity. Figure 4 shows the profiles of temperatureand specific entropy as a function of scaled mass for the REOS3b model. The central temperature is more than 20 000 K and the temperature jump appears from the molecular to metallic envelopes. We note that the deep interior could exhibit a higher temperature than what we consider here. This is because the dilute core region may be nonadiabatic owing to large composition gradients, reducing the outward heat transport. Indeed, the evolution calculation of Vazan et al. (2018) suggested that some temperature jumps emerge in the deep interior and the central temperature is as high as 30 000 K. The specific entropy is decreased towards the central compact core. This is due to an increase of the heavy element abundance.
Figure 5 illustrates the density profiles as a function of scaled radius for three REOS3b models: with a central compact core of Mcore = 6.2 M⊕ (black solid lines), Mcore = 2.8 M⊕ (red dashed lines), and Mcore = 0.1 M⊕ (blue dotted lines). The density values are normalized by a constant density of 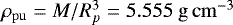 in the figure. The even gravitational harmonics tightly constrain the external part of a planet, and so there are minor differences in the outer region x = 0.6−1.0. Proceeding towards the deeper interior, the differences become obvious owing to different dilute core configurations adopted in the interior models. The loss of the central compact core is balanced either by a higher heavy-element abundance in the dilute core region or byan expansion of the dilute core region.
in the figure. The even gravitational harmonics tightly constrain the external part of a planet, and so there are minor differences in the outer region x = 0.6−1.0. Proceeding towards the deeper interior, the differences become obvious owing to different dilute core configurations adopted in the interior models. The loss of the central compact core is balanced either by a higher heavy-element abundance in the dilute core region or byan expansion of the dilute core region.
 |
Fig. 3 Jupiter’s gravity harmonics obtained with various models in the Ji−Ji+2 planes. The model solutions are shown as open points according to different EOSs used in the interior models and Juno’s static gravity harmonics |
 |
Fig. 4 Temperature (black solid) and specific entropy (red dashed) vs. scaled mass for the selected REOS3b model shown in Table 2. |
 |
Fig. 5 Density profiles of three REOS3b models: black solid, red dashed, and blue dotted curves correspond to different central compact cores of Mcore = 6.2, 2.8, 0.1 M⊕, respectively. For the sake of clarity, the density values are normalized by a constant density
|
4.3 Jupiter’s element abundance in the dilute core region
The helium mass fraction Y2 in the metallic envelope is correlated with the helium mass fraction Y3 in the dilute core region, as shown in Appendix A. This correlation can be used to reveal the helium mass fraction in the dilute core region. Figure 6 illustrates the helium mass fractions in the metallic envelope and in the dilute core region, which are derived with four different EOSs for hydrogen and helium and various dilute core sizes Pdil. The resulting Y2 values are constrained by the existence of helium rain in Jupiter Y2 > Y1, and the resulting Y3 values are constrained by the requirement (Eq. (1)) that the density increases from the metallic envelope to the dilute core region under the balance between ΔZ2−3 and ΔY2−3. As the heavy element abundance is increased in the dilute core region, the optimization solutions of REOS3b and MH13+SCvH prefer an inward decrease of the helium mass fraction Y3 < Y2, the CMS19 solutions are comparable between Y3 < Y2 and Y3 > Y2, and the SCvH solutions all lie in the area of Y3 < Y2. Furthermore, a smaller dilute core, corresponding to a larger Pdil value, showsa steeper slope in Y3∕Y2, suggesting more helium variations in the dilute core region.
In the four-layer structure models, the key parameters such as the heavy element abundances in the outer two envelopes (Z1 and Z2) and the mass of the central compact core (Mcore) are adjusted to match the observational constraints. As the dilute core configuration is varied in both size (Pdil) and composition (ΔY2−3 and ΔZ2−3), the resulting values of these three quantities show small variations for a given equatorial radius Req and low-order harmonics. There is a trade-off between these three quantities and the dilute core configuration. Therefore, as the dilute core configuration is varied, the low-order gravitational harmonics make no noticeable variation. But the high-order harmonics are dependent upon the dilute core configuration because they are more sensitive to any change in the outmost part of a planet (Guillot 2005). As one would expect, the high-order harmonics (> J4) would exhibit smaller variations when the dilute core region gets reduced by increasing the Pdil value. We pay most attention to the effect of the dilute core composition on the high-order harmonics. For the sake of clarity, the change in the heavy element abundance is fixed at ΔZ2−3 = 0.09 and the change in the helium fraction ΔY2−3 is varied between −0.10 and 0.20. Figure 7 shows the dependence of the high-order harmonics J6, J8, and J10 on the composition of the dilute core region with different EOSs for hydrogen and helium. The figure applies to ΔZ2−3 = 0.09, but would remain very similar for the other ΔZ2−3 values. Wahl et al. (2017) discussed two possible interpretations of the low absolute values of J4 to J8 : a dilute core by increasing the density in the metallic region and a lower density through a portion of the outer molecular envelope by increasing the entropy; the latter effect is more considerable than the former. The SCvH interior models yield larger absolute values of J6, J8, and J10 compared with the static harmonics 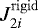 . This is due to the higher density in the outmost envelope resulting from a large amount of heavy elements in the molecular envelope. For all four cases of REOS3b, MH13+SCvH, CMS19, and SCvH, the absolute values of J6 and J8 generally show a decreasing tendency as helium becomes more depleted in the dilute core region. The variation of J10 is much less considerable than for J6 and J8 and the uncertainty of
. This is due to the higher density in the outmost envelope resulting from a large amount of heavy elements in the molecular envelope. For all four cases of REOS3b, MH13+SCvH, CMS19, and SCvH, the absolute values of J6 and J8 generally show a decreasing tendency as helium becomes more depleted in the dilute core region. The variation of J10 is much less considerable than for J6 and J8 and the uncertainty of 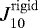 is quite large. To gain further insight into such a decreasing tendency, we take the optimization solutions using REOS3b for example. The masses of the compact core and the heavy elements in the envelope are illustrated in Fig. 8 as a function of ΔY2−3. As can be seen, the mass of the compact core tends to increase with decreasing ΔY2−3 values and meanwhile the heavy element mass is reduced in the outer envelope. This leads to a lower density in the outer envelope. As a consequence, the absolute values of the high-order harmonics are decreased with decreasing ΔY2−3 values.
is quite large. To gain further insight into such a decreasing tendency, we take the optimization solutions using REOS3b for example. The masses of the compact core and the heavy elements in the envelope are illustrated in Fig. 8 as a function of ΔY2−3. As can be seen, the mass of the compact core tends to increase with decreasing ΔY2−3 values and meanwhile the heavy element mass is reduced in the outer envelope. This leads to a lower density in the outer envelope. As a consequence, the absolute values of the high-order harmonics are decreased with decreasing ΔY2−3 values.
4.4 Jupiter’s core and mass of heavy element
The interior models are constructed using four different EOSs for hydrogen and helium, as mentioned in Sect. 3. It should be noted that each interior model proceeds with the same boundary conditions, the same model assumptions, and the same variation space of model parameters. It is of great interest to investigate the effect of EOSs on the predictions of the four-layer structure models. Figure 9 shows the sensitivity of Jupiter’s internal structure to the EOSs for hydrogen and helium adopted in the model. As can be seen, the interior model predictions show a clear dependence on the adopted EOSs, where four different EOSs correspond to different areas of 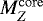 and
and 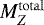 almost without overlays. For MH13+SCvH, the heavy element mass in the core
almost without overlays. For MH13+SCvH, the heavy element mass in the core 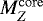 spans over the range of 6.5−27.0 M⊕ and the global heavy element abundance Zglobal is estimatedas five to six times solar fraction. These results are in good agreement with the MH13 predictions of 6−25 M⊕ and five to six times solar fraction suggested by Wahl et al. (2017). For REOS3b,
spans over the range of 6.5−27.0 M⊕ and the global heavy element abundance Zglobal is estimatedas five to six times solar fraction. These results are in good agreement with the MH13 predictions of 6−25 M⊕ and five to six times solar fraction suggested by Wahl et al. (2017). For REOS3b, 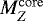 spans over a wider range of 7−32 M⊕ and Zglobal is as high as seven times solar fraction. They are also consistent with the Model S predictions of Wahl et al. (2017), where the REOS3 EOS was used in the dilute core model and Jupiter’s interior was evaluated as
spans over a wider range of 7−32 M⊕ and Zglobal is as high as seven times solar fraction. They are also consistent with the Model S predictions of Wahl et al. (2017), where the REOS3 EOS was used in the dilute core model and Jupiter’s interior was evaluated as 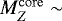 19 M⊕ and Zglobal ~ 7.12 times solar fraction. Results of SCvH show an even larger amount of heavy elements in the interior of Jupiter. The core mass of SCvH is almost contributed from the heavy elements in the dilute core region, exhibiting a small central compact core between 0 and 1 M⊕. Results of CMS19 show a small Zglobal value of two to three times solar fraction and a small core mass
19 M⊕ and Zglobal ~ 7.12 times solar fraction. Results of SCvH show an even larger amount of heavy elements in the interior of Jupiter. The core mass of SCvH is almost contributed from the heavy elements in the dilute core region, exhibiting a small central compact core between 0 and 1 M⊕. Results of CMS19 show a small Zglobal value of two to three times solar fraction and a small core mass 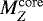 of 3−12 M⊕. This is because the CMS19 adiabat generally has a higher density (pressure) in the ~Mbar region with respect to the other EOSs (Chabrier et al. 2019), considerably reducing the metallicity in Jupiter. The
of 3−12 M⊕. This is because the CMS19 adiabat generally has a higher density (pressure) in the ~Mbar region with respect to the other EOSs (Chabrier et al. 2019), considerably reducing the metallicity in Jupiter. The 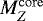 values presented here are generally larger than the results of the three-layer structure models by Miguel et al. (2016, 2018). This is not particularly surprising since the core mass
values presented here are generally larger than the results of the three-layer structure models by Miguel et al. (2016, 2018). This is not particularly surprising since the core mass 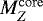 in this study contains the heavy element mass in the dilute core region in addition to the central compact core.
in this study contains the heavy element mass in the dilute core region in addition to the central compact core.
Figure 10 shows the effect of temperature jumps ΔT1−2 from the molecular to metallic envelope on the internal structure of Jupiter. As ΔT1−2 is increased from 200 to 800 K, a larger amount of heavy elements is allowed in the interior of Jupiter. A larger temperaturejump causes the deep interior to become hotter and exhibit lower densities. Such a density deficit is compensated by adding more heavy elements in the deep interior. Moreover, convection in the deep interior could be suppressed owing to large composition gradients (Vazan et al. 2018). This results in a hotter dilute core than what we consider here. As expected, the hotter interior would allow a larger amount of heavy elements, and therefore the global heavy element abundance in Jupiter could be larger than the results shown in Fig. 9.
 |
Fig. 6 Helium mass fractions in the metallic hydrogen envelope and in the dilute core region derived with four different EOSs for hydrogen and helium: REOS3b (top left panel), MH13+SCvH (top right panel), CMS19 (bottom left panel),and SCvH (bottom-right panel). The results are displayed according to different dilute core sizes Pdil. |
5 Summary
Juno’s gravity field observations have been shown to be of high precision for even gravitational harmonics (Iess et al. 2018) and a dilute core has been proposed to reconcile the calculated gravitational harmonics with Juno’s gravity observations (Wahl et al. 2017; Guillot et al. 2018; Debras & Chabrier 2019). Introducing a dilute core adds a degree of freedom to Jupiter’s interior models. In this paper, we examine the effect of a dilute core on the internal structure of Jupiter within the four-layer structure model. The heavy element abundances in the outer two envelope and the mass of the central compact core are adjusted to reproduce Jupiter’s equatorial radius as well as Juno’s observations J2, J4, and J6 corrected by the dynamical contributions of Kaspi et al. (2018). Different dilute core configurations are constructed in terms of its size and composition (Pdil, Y3, Z3, and frock) and the dependence of interior model predictions on the dilute core is investigated. Also, four different equations of state (EOSs) for hydrogen and helium (REOS3b, MH13+SCvH, CMS19, and SCVH) are used based on the works of Miguel et al. (2016, 2018) and Chabrier et al. (2019) and the effect of EOSs on the internal structure of Jupiter is explored.
The heavy elements in dilute core region are assumed to be composed of ices and rocks, while the compact core is only composed of rocks. We first examined the effect of the rock fraction frock in the dilute core region. With increasing rock fraction, it is found that both the heavy element masses in the core 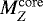 and in the envelopes
and in the envelopes 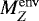 become smaller, suggesting a lower global amount of heavy elements. The helium mass fraction Y2 in the metallic envelope is correlated with the helium mass fraction Y3 in the dilute core region by the requirement that the mean helium mass fraction in Jupiter is equal to its value in the protosolar nebula. The solutions of REOS3b and MH13+SCvH seem to prefer an inward decrease of the helium mass fraction Y3 < Y2 and the SCvH solutions all suggest a helium depletion in the dilute core region. Indeed, a smaller dilute core allows more helium depletion in the dilute core region. As helium becomes more depleted in the dilute core region, the mass of the compact core is found to be increased and the heavy element mass is decreased in the outer envelopes, which results in a lower density in a portion of the molecular envelope. As a result, the absolute values of J6 and J8 generally show a decreasing tendency with decreasing ΔY2−3 values for a fixed heavy element enrichment.
become smaller, suggesting a lower global amount of heavy elements. The helium mass fraction Y2 in the metallic envelope is correlated with the helium mass fraction Y3 in the dilute core region by the requirement that the mean helium mass fraction in Jupiter is equal to its value in the protosolar nebula. The solutions of REOS3b and MH13+SCvH seem to prefer an inward decrease of the helium mass fraction Y3 < Y2 and the SCvH solutions all suggest a helium depletion in the dilute core region. Indeed, a smaller dilute core allows more helium depletion in the dilute core region. As helium becomes more depleted in the dilute core region, the mass of the compact core is found to be increased and the heavy element mass is decreased in the outer envelopes, which results in a lower density in a portion of the molecular envelope. As a result, the absolute values of J6 and J8 generally show a decreasing tendency with decreasing ΔY2−3 values for a fixed heavy element enrichment.
The heavy element mass in the core 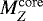 is contributed from the central compact core Mcore and the heavy elements
is contributed from the central compact core Mcore and the heavy elements 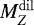 dissolved in the dilute core region; this mass is dependent on the EOS for hydrogen and helium adopted in interior structure calculations. The models using MH13+SCvH yield
dissolved in the dilute core region; this mass is dependent on the EOS for hydrogen and helium adopted in interior structure calculations. The models using MH13+SCvH yield 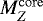 between 6.5 and 27.0 M⊕ and the global heavy element fraction of five to six times solar fraction. The models using REOS3b yield
between 6.5 and 27.0 M⊕ and the global heavy element fraction of five to six times solar fraction. The models using REOS3b yield 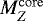 between 7 and 32 M⊕ and global Z of about seven times solar fraction. The models using SCvH yield
between 7 and 32 M⊕ and global Z of about seven times solar fraction. The models using SCvH yield 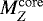 between 5 and 30 M⊕ and a globalZ as high as seven to eight times solar fraction, but exhibit a small central compact core between 0 and 1 M⊕. These results showgood agreement with the dilute core predictions of Wahl et al. (2017). The models using CMS19 yield a small core mass
between 5 and 30 M⊕ and a globalZ as high as seven to eight times solar fraction, but exhibit a small central compact core between 0 and 1 M⊕. These results showgood agreement with the dilute core predictions of Wahl et al. (2017). The models using CMS19 yield a small core mass 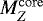 between 3 and 12 M⊕ and a small global Z as low as two to three times solar fraction. This is because the CMS19 adiabat generally has a higher density in the ~Mbar region as compared with the other EOSs (Chabrier et al. 2019), considerably reducing the metallicity in Jupiter. The mass predictions of heavy elements are also related to the temperature jumps ΔT1−2 from the molecular to metallic envelope. As the temperature jump is increased, the deep interior exhibits lower densities, which are compensated by adding a larger amount of heavy elements. Therefore, the temperature jump ΔT1−2 tends to an increase of the heavy element mass in Jupiter’s interior. We note that convection in the deep interior could be suppressed owing to large composition gradients (Vazan et al. 2018), leading to a hotter dilute core. As a result, a larger amount of heavy elements could be allowed with respect to the present calculations.
between 3 and 12 M⊕ and a small global Z as low as two to three times solar fraction. This is because the CMS19 adiabat generally has a higher density in the ~Mbar region as compared with the other EOSs (Chabrier et al. 2019), considerably reducing the metallicity in Jupiter. The mass predictions of heavy elements are also related to the temperature jumps ΔT1−2 from the molecular to metallic envelope. As the temperature jump is increased, the deep interior exhibits lower densities, which are compensated by adding a larger amount of heavy elements. Therefore, the temperature jump ΔT1−2 tends to an increase of the heavy element mass in Jupiter’s interior. We note that convection in the deep interior could be suppressed owing to large composition gradients (Vazan et al. 2018), leading to a hotter dilute core. As a result, a larger amount of heavy elements could be allowed with respect to the present calculations.
The optimization solutions of REOS3b, MH13+SCvH, and CMS19 show a smaller value for the heavy element abundance Z1 in the outer molecular envelope, while the SCvH models yield a larger value of Z1, as compared with the Galileo entry probe of Z1 ≈ 0.017. Further, the decrease in Z1 is more significant in the case of MH13+SCvH and CMS19. One possible explanation is that the ab initio EOSs might overestimate the density in the low-pressure region (Wahl et al. 2017). Better knowledge of the EOSs for hydrogen, helium, and hydrogen–helium mixtures would be helpful to solve this puzzle. Alternatively, there could be a considerable entropy increase between the outer and inner envelopes and an inward decreasing abundance of heavy elements in the inner envelope for Jupiter (Debras & Chabrier 2019). For the first time in history, the Juno spacecraft probed Jupiter’s deep troposphere down to 200 bars using its microwave radiometer (MWR) instrument. In anticipation of new observational MWR results, the interior modeling effort will be assisted by better knowledge of the metallicity in the outermost region, because it serves as the outer boundary condition of Jupiter’s interior models and shows close correlation with Jupiter’s gravitational zonal harmonics.
 |
Fig. 7 High-order gravitational harmonics as a function of the change ΔY2−3 in the helium mass fraction from the metallic envelope to the dilute core region, where the change in the heavy element abundance is fixed at ΔZ2−3 = 0.09. The pink rectangle shows the uncertainty of the static gravitational harmonics
|
 |
Fig. 8 Optimization solutions obtained with REOS3b vs. the change in the helium mass fraction from the metallic envelope to the dilute core region: the mass of the central compact core (left panel) and the heavy-element mass in the envelopes (right panel). The results are shown according to different dilute core sizes Pdil. |
 |
Fig. 9 Mass of heavy elements in the core and total heavy element mass in Jupiter predicted with different EOSs for hydrogen and helium. Horizontal lines denote the global mass fraction of heavy elements in units of the solar abundance of heavy elements. |
 |
Fig. 10 Mass of heavy elements in the core and in the molecular and metallic envelopes predicted with different temperature jumps ΔT1−2 from the molecular to metallic envelope. The different colors are for different ΔT1−2 values as appears in the legend and the different points are for three different EOSs of hydrogen and helium: REOS3b (full solid), MH13+SCvH (top-half solid symbols), and CMS19 (lower-half solid symbols). |
Acknowledgements
D.N greatly appreciates T. Guillot for valuable suggestions and helpful discussions. D.N also appreciates Y. Miguel for providing data regarding REOS3b. This work is supported by the Science and Technology Development Fund, Macau SAR (File No. 0005/2019/A1) and the National Natural Science Foundation of China (Grant No. 11761161001).
Appendix A Dilute cores in the four-layer structure model
The pressure Pdil is employed to characterize the size of the dilute core region, which is implemented in the CEPAM code as the pressure P1−2 for the hydrogen molecular-to-metallic transition. The element abundances in the dilute core region, Y3 and Z3, are adoptedbeforehand within a wide range (Guillot et al. 2018). The helium mass fraction Y3 is closely correlated with the helium mass fraction Y2 in the metallic envelope because the mean helium mass fraction in Jupiter Y∕(1 − Z) should be equal to its value in the protosolar nebula Yproto∕(1 − Zproto) = 0.277 ± 0.006 (Serenelli & Basu 2010; Guillot et al. 2018). Using the Galileo observations Y1 ∕(1 − Z1) = 0.238 ± 0.005 (von Zahn et al. 1998) and the heavy element abundances Z1 and Z2, one can express the correlation as
![\begin{eqnarray*}Y_{2}&\;{=}\;&\frac{Y_{\mathrm{proto}}(1-Z_{2})}{(1-Z_{\mathrm{proto}})}+\left[\frac{Y_{\mathrm{proto}}(1-Z_{1})}{(1-Z_{\mathrm{proto}})}-Y_{1}\right]\left(\frac{1-m_{1-2}}{m_{1-2}-M_{\mathrm{core}}}\right) \nonumber \\[5.5pt] &&-\left[\frac{Y_{\mathrm{proto}}\Delta Z_{2-3}}{(1-Z_{\mathrm{proto}})}+\Delta Y_{2-3}\right]\left(\frac{m_{\mathrm{dil}}-M_{\mathrm{core}}}{m_{1-2}-M_{\mathrm{core}}}\right), \end{eqnarray*}](/articles/aa/full_html/2019/12/aa35938-19/aa35938-19-eq37.png) (A.1)
(A.1)
where ΔY2−3 = Y3 − Y2, ΔZ2−3 = Z3 − Z2, m1−2 and mdil are, respectively, the masses inside the interfaces P1−2 and Pdil. For the heavy element abundance Z3, it is relevant to note that the rock mass fraction frock is introduced to take into account the rocks dissolved from the central rocky core. That is, the rocks are mixed with the ices in proportion of Zrock = frockZ3.
Appendix B Theory of figures to fifth order compared with CMS
We present some tests for the implementation of the ToF to fifth order (ToF5) in this paper. Tables B.1 and B.2 show the comparison for a linear density model and a polytrope of index one, respectively. The CMS results of Hubbard (2013) and Nettelmann (2017) are also shown for comparison. We can see that the results of this work agree well with the CMS-512 results in particular for higher order harmonics. The offset in J4 is smaller than the dynamical contribution of Kaspi et al. (2018) and the offsets in J6 to J10 are all within Juno’s uncertainties.
Results for linear density model.
Results for polytrope of index one.
Nettelmann (2017) converted the ToF-based density profile as a function of the mean radius s to a density profile as a function of the equatorial radius r using the figure functions s2i(s) and recalculated the gravitational harmonics using the CMS method. Recently, Militzer et al. (2019) proposed an acceleration technique for the CMS method. Next, we evaluate the offset between the ToF5 and accelerated CMS methods. First, we perform the accelerated CMS calculation for one ToF-based density profile and compare the calculated gravitational harmonics. The accelerated CMS method is then used to fit Juno’s gravitational harmonics instead of ToF5. The resulting gravitational harmonics and model values are compared with the ToF5 results in Table B.3. Their offsets are further compared with the 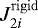 error bar including both Juno and dynamics uncertainties. The differences between the ToF5-fit and CMS results could be attributed to the conversion from mean to equatorial radii or the error of grid discretization (Guillot et al. 2018). For the ToF5-fit and CMS-fit results with the same J2 value, one can see that the offset in J4 × 106 is smaller than the error bar of
error bar including both Juno and dynamics uncertainties. The differences between the ToF5-fit and CMS results could be attributed to the conversion from mean to equatorial radii or the error of grid discretization (Guillot et al. 2018). For the ToF5-fit and CMS-fit results with the same J2 value, one can see that the offset in J4 × 106 is smaller than the error bar of 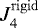 and the offsets in higher order harmonics are even smaller than the error bar by about one order of magnitude. Furthermore, the effect on the heavy element abundances in Jupiter’s interior is negligible with respect to the other uncertainties. As can be seen, the heavy element abundance in the envelopes is reduced by 0.0003 at most while the core mass is only increased by 0.03−0.04 Earth mass. With these in mind, the ToF5 is accurate enough to infer Jupiter’s interior from Juno’s gravity data.
and the offsets in higher order harmonics are even smaller than the error bar by about one order of magnitude. Furthermore, the effect on the heavy element abundances in Jupiter’s interior is negligible with respect to the other uncertainties. As can be seen, the heavy element abundance in the envelopes is reduced by 0.0003 at most while the core mass is only increased by 0.03−0.04 Earth mass. With these in mind, the ToF5 is accurate enough to infer Jupiter’s interior from Juno’s gravity data.
Comparison of the CEPAM-ToF5 and accelerated CMS results for two representative models.
References
- Anderson, J. D., & Schubert, G. 2007, Science, 317, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, A., Lorenzen, W., Fortney, J., & Nettelmann, N. 2014, ApJS, 215, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, S. J., Adriani, A., Adumitroaie, V., et al. 2017, Science, 356, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Mazevet, S., & Soubiran, F. 2019, ApJ, 872, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Debras, F., & Chabrier, G. 2018, A&A, 609, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Debras, F., & Chabrier, G. 2019, ApJ, 872, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Folkner, W. M., Iess, L., Anderson, J. D., et al. 2017, Geophys. Res. Lett., 44, 4694 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., & Nettelmann, N. 2010, Space Sci. Rev., 152, 423 [NASA ADS] [CrossRef] [Google Scholar]
- French, M., Becker, A., Lorenzen, W., et al. 2012, ApJS, 202, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Galanti, E., Kaspi, Y., Miguel, Y. 2019, Geophys. Res. Lett., 46, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 1999, Planet. Space Sci., 47, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 2005, Ann. Rev. Earth Planet. Sci., 33, 493 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Guillot, T., & Morel P. 1995, A&AS, 109, 109 [NASA ADS] [Google Scholar]
- Guillot, T., Miguel, Y., Militzer, B., et al. 2018, Nature, 555, 227 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Helled, R. 2012, ApJ, 748, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Helled, R., Galanti, E., & Kaspi, Y. 2015, Nature, 520, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B. 1999, Icarus, 137, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B. 2013, ApJ, 768, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B., & Militzer, B. 2016, ApJ, 820, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B., Burrows, A., & Lunine, J. I. 2002, ARA&A, 40, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Iess, L., Folkner, W. M., Durante, D., et al. 2018, Nature, 555, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, Y., Hubbard, W. B., Showman, A. P., & Flierl, G. R. 2010, Geophys. Res. Lett., 37, L01204 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, Y., Galanti, E., Hubbard, W. B., et al. 2018, Nature, 555, 223 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kong, D., Zhang, K., & Schubert, G. 2016, ApJ, 826, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Lindal, G. F., Wood, G. E., Levy, G. S., et al. 1981, J. Geophys. Res., 86, 8721 [NASA ADS] [CrossRef] [Google Scholar]
- Lyon, S. P., & Johnson, J. D. 1992, LANL Rep. LA-UR-92-3407 (Los Alamos: LANL) [Google Scholar]
- Miguel, Y., Guillot, T., & Fayon, L. 2016, A&A, 596, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miguel, Y., Guillot, T., & Fayon, L. 2018, A&A, 618, C2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Militzer, B., & Hubbard, W. B. 2013, ApJ, 774, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Militzer, B., Hubbard, W. B., Vorberger, J., Tamblyn, I., & Bonev, S. A. 2008, ApJ, 688, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Militzer, B., Soubiran, F., Wahl, S. M., & Hubbard, W. 2016, J. Geophys. Res. Planets, 121, 1552 [NASA ADS] [CrossRef] [Google Scholar]
- Militzer, B., Wahl, S. M., & Hubbard, W. 2019, ApJ, 879, 78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morales, M. A., Hamel, S., Caspersen, K., & Schwegler, E. 2013, Phys. Rev. B, 87, 174105 [NASA ADS] [CrossRef] [Google Scholar]
- Nettelmann, N. 2017, A&A, 606, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nettelmann, N., Holst, B., Kietzmann, A., French, M., & Redmer, R. 2008, ApJS, 683, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Nettelmann, N., Becker, A., Holst, B., & Redmer, R. 2012, ApJ, 750, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Ni, D. 2018, A&A, 613, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saumon, D., & Guillot, T. 2004, ApJ, 609, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Serenelli, A. M., & Basu, S. 2010, ApJ, 719, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Vazan, A., Helled, R., Kovetz, A., & Podolak, M. 2015, ApJ, 803, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Vazan, A., Helled, R., Podolak, M., & Kovetz, A. 2016, ApJ, 829, 118 [Google Scholar]
- Vazan, A., Helled, R., & Guillot, T. 2018, A&A, 610, L14 [Google Scholar]
- von Zahn, U., Hunten, D. M., & Lehmacher, G. 1998, J. Geophys. Res. Planets, 103, 22815 [CrossRef] [Google Scholar]
- Wahl, S. M., Hubbard, W. B., Militzer, B., et al. 2017, Geophys. Res. Lett., 44, 4649 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, H. F., & Militzer, B. 2012a, ApJ, 745, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, H. F., & Militzer, B. 2012b, Phys. Rev. Lett., 108, 111101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zharkov, V. N., & Trubitsyn, V. P. 1975, AZh, 52, 599 [NASA ADS] [Google Scholar]
- Zharkov, V. N., & Trubitsyn, V. P. 1978, Physics of Planetary Interiors (Pachart Publishing House) [Google Scholar]
All Tables
Jupiter’s gravity harmonics J2i, decomposed into the dynamical and static parts, ΔJ2i and 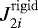 .
.
Jupiter’s gravity harmonics J2i and model values of some selected interior models.
Comparison of the CEPAM-ToF5 and accelerated CMS results for two representative models.
All Figures
 |
Fig. 1 Schematic four-layer structure of Jupiter. There is a temperature jump ΔT1−2 between the molecular and metallic hydrogen envelopes owing to a thin helium rain layer and the onset of the dilute core region is described with the pressure Pdil. |
| In the text | |
 |
Fig. 2 Mass of heavy elements in the core and in the molecular and metallic envelopes predicted with different rock fractions frock in the dilute core region. Full and half solid points show the results for two different EOSs of hydrogen and helium, respectively:REOS3b (full solid) and MH13+SCvH (half solid). |
| In the text | |
 |
Fig. 3 Jupiter’s gravity harmonics obtained with various models in the Ji−Ji+2 planes. The model solutions are shown as open points according to different EOSs used in the interior models and Juno’s static gravity harmonics |
| In the text | |
 |
Fig. 4 Temperature (black solid) and specific entropy (red dashed) vs. scaled mass for the selected REOS3b model shown in Table 2. |
| In the text | |
 |
Fig. 5 Density profiles of three REOS3b models: black solid, red dashed, and blue dotted curves correspond to different central compact cores of Mcore = 6.2, 2.8, 0.1 M⊕, respectively. For the sake of clarity, the density values are normalized by a constant density
|
| In the text | |
 |
Fig. 6 Helium mass fractions in the metallic hydrogen envelope and in the dilute core region derived with four different EOSs for hydrogen and helium: REOS3b (top left panel), MH13+SCvH (top right panel), CMS19 (bottom left panel),and SCvH (bottom-right panel). The results are displayed according to different dilute core sizes Pdil. |
| In the text | |
 |
Fig. 7 High-order gravitational harmonics as a function of the change ΔY2−3 in the helium mass fraction from the metallic envelope to the dilute core region, where the change in the heavy element abundance is fixed at ΔZ2−3 = 0.09. The pink rectangle shows the uncertainty of the static gravitational harmonics
|
| In the text | |
 |
Fig. 8 Optimization solutions obtained with REOS3b vs. the change in the helium mass fraction from the metallic envelope to the dilute core region: the mass of the central compact core (left panel) and the heavy-element mass in the envelopes (right panel). The results are shown according to different dilute core sizes Pdil. |
| In the text | |
 |
Fig. 9 Mass of heavy elements in the core and total heavy element mass in Jupiter predicted with different EOSs for hydrogen and helium. Horizontal lines denote the global mass fraction of heavy elements in units of the solar abundance of heavy elements. |
| In the text | |
 |
Fig. 10 Mass of heavy elements in the core and in the molecular and metallic envelopes predicted with different temperature jumps ΔT1−2 from the molecular to metallic envelope. The different colors are for different ΔT1−2 values as appears in the legend and the different points are for three different EOSs of hydrogen and helium: REOS3b (full solid), MH13+SCvH (top-half solid symbols), and CMS19 (lower-half solid symbols). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.