| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A70 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201936351 | |
| Published online | 23 October 2019 | |
Exploring the conditions for forming cold gas giants through planetesimal accretion
1
Lund Observatory, Department of Astronomy and Theoretical Physics, Lund University,
Box 43,
221 00
Lund,
Sweden
e-mail: anders@astro.lu.se
2
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
e-mail: bitsch@mpia.de
Received:
20
July
2019
Accepted:
20
September
2019
The formation of cold gas giants similar to Jupiter and Saturn in orbit and mass is a great challenge for planetesimal-driven core accretion models because the core growth rates far from the star are low. Here we model the growth and migration of single protoplanets that accrete planetesimals and gas. We integrated the core growth rate using fits in the literature to N-body simulations, which provide the efficiency of accreting the planetesimals that a protoplanet migrates through. We take into account three constraints from the solar system and from protoplanetary discs: (1) the masses of the terrestrial planets and the comet reservoirs in Neptune’s scattered disc and the Oort cloud are consistent with a primordial planetesimal population of a few Earth masses per AU, (2) evidence from the asteroid belt and the Kuiper belt indicates that the characteristic planetesimal diameter is 100 km, and (3) observations of protoplanetary discs indicate that the dust is stirred by weak turbulence; this gas turbulence also excites the inclinations of planetesimals. Our nominal model built on these constraints results in maximum protoplanet masses of 0.1 Earth masses. Ignoring constraint (1) above, we show that even a planetesimal population of 1000 Earth masses, corresponding to 50 Earth masses per AU, fails to produce cold gas giants (although it successfully forms hot and warm gas giants). We conclude that a massive planetesimal reservoir is in itself insufficient to produce cold gas giants. The formation of cold gas giants by planetesimal accretion additionally requires that planetesimals are small and that the turbulent stirring is very weak, thereby violating all three above constraints.
Key words: planets and satellites: formation / planet–disk interactions / planets and satellites: gaseous planets
© ESO 2019
1 Introduction
The catalogue of exoplanets is growing continuously. The observed planets can be broadly divided into an inner population of planets, orbiting within a few astronomical units (AU) from the star, and an outer population on more distant orbits (see Winn & Fabrycky 2015, for a recent review of the exoplanet populations). Planets from the inner population, that is, hot and warm gas giants, super-Earths, and terrestrial planets, are relatively straightforward to form in computer simulations, because the rates of accreting planetesimals and pebbles so close to the star are high (Coleman & Nelson 2014; Lambrechts et al. 2019), and because the inner edge of the protoplanetary disc can stop migrating trains of protoplanets (Masset et al. 2006; Cresswell & Nelson 2006).
Planets in the outer population are far more challenging for planet formation theories because growth rates are lower there and no general migration barriers exist so far away from the edge of the protoplanetary disc. While gas-giant planets similar to Jupiter in our solar system orbit 15% of solar-type stars out to a few AU from the star (Mayor et al. 2011), the occurrence rate drops to 3–6% on ~5 AU orbits (Rowan et al. 2016). Direct-imaging surveys find occurrence rates in the range of 1–6% on orbits beyond 20 AU (Vigan et al. 2017).
Gas giants in cold orbits (which we define here to be broadly the regions beyond 2–3 AU) are therefore generally rare, but a significant fraction of the giant planets found in the inner population (hot and warm gas giants) were likely scattered there from their primordial cold orbits (Dawson & Murray-Clay 2013; Buchhave et al. 2018, see also the review by Davies et al. 2014). The overall occurrence rate of gas giants increases rapidly with the metallicity of the star (Udry & Santos 2007; Buchhave et al. 2012), which make cold gas giants excellent probes of the effect of the planetary growth rate (which is proportional to the metallicity) on the outcome of planet formation. Cold gas giants also pose the strongest necessity for rapid planetary growth because growth timescales of more than a few million years will preclude the accretion of gas onto the core.
In this paper we study core formation by accretion of planetesimals. This is the classical mode of core accretion (Pollack et al. 1996), although many studies employing N-body methods have questioned whether planetesimal accretion is able to form the cores of cold gas giants before the gaseous protoplanetary disc dissipates (Thommes et al. 2003; Levison et al. 2010; Coleman & Nelson 2014). Here we formulate a similar concern based on studying the growth tracks of single migrating protoplanets. We base our models on three constraints from the solar system and protoplanetary discs for (1) the total planetesimal mass, (2) the characteristic planetesimal size, and (3) the strength of the inclination stirring by the turbulent gas.
The formation environment of exoplanets, in terms of the diameters and total mass of the primordial planetesimal populations that contributed to core accretion, is relatively poorly constrained. Observations of very young stars in the embedded class 0 phase (e.g. Tychoniec et al. 2018) show that the protoplanetary discs in this phase are often very massive (containing up to several tens of percent of the mass of the central star) and compact (from a few ten AU down to a few AU in size). These young stars also display high accretion rates in the range between 10−7 and 10−6 M⊙ yr−1 (Hartmann et al. 2016). These masses and accretion rates are consistent with models of the formation of a protostar and a surrounding protoplanetary disc by the collapse of a giant molecular cloud core. The angular momentum transport and mass accretion is driven by gravitational instabilities and spiral arms in these earliest phases of star formation and disc evolution (Dullemond et al. 2006). If planetesimals form very efficiently during these earliest stages of protoplanetary disc evolution, then young protoplanetary discs could form several hundred or even a few thousand Earth masses (ME) of planetesimals. A gravitationally unstable disc converting 1% of its gas surface density into planetesimals would produce approximately 50 ME of planetesimals per AU. Alternatively, pebble pile-ups in the inner regions of the disc could produce very large amounts of planetesimals over timescales of millions of years (Dra̧żkowska & Dullemond 2018) if a significant fraction of the inwards-drifting pebbles are converted into planetesimals.
The remnant planetesimal populations in the solar system nevertheless provide us with a possibility of probing the properties of the primordial planetesimals that formed around the young Sun. Terrestrial planet formation simulations successfully form Earth and Venus analogues starting from protoplanets with a total mass of a few ME (Raymond et al. 2009; Izidoro & Raymond 2018), more than an order of magnitude lower than the above scenario of a very massive planetesimal population would predict. Adding more mass than this to the terrestrial planet zone instead results in the formation ofa population of migrating super-Earths (Ogihara et al. 2015).
A part of the primordial planetesimal population beyond Neptune now resides in Neptune’s scattered disc and in the Oort cloud. Brasser (2008) found that a primordial planetesimal population of approximately 35 ME outside of Neptune is consistent with the inferred mass of the outer Oort cloud (~ 1 ME). This value, a few ME per AU, is again at least an order of magnitude below what would be produced if planetesimals formed at the self-gravitating stage of the protoplanetary disc.
The planetesimal mass per AU in the 5–10 AU region could in principle have been one to two orders of magnitude higher than what is inferred from interior and exterior regions, perhaps as the result of planetesimal formation by pebble pile-ups exterior of the water ice line (Dra̧żkowska & Dullemond 2018). However, simulations of the early migration history of Jupiter show that ~ 1 ME of planetesimals is scattered in front of Jupiter and parked in the asteroid belt (Raymond & Izidoro 2017; Pirani et al. 2019), when a standard planetesimal population comparable to that of the minimum mass solar nebula is assumed (Hayashi 1981). Scaling these models to a much more massive planetesimal population would imply injection of 50 ME or more of planetesimals into the asteroid belt, which would raise the question of how this enormous amount of planetesimals could subsequently have been removed (Petit et al. 2001).
The birth sizes of planetesimals are also well constrained in the solar system. The size distribution of asteroids in the main belt is consistent with formation of bodies of a characteristic size of 100 km (Bottke et al. 2005; Morbidelli et al. 2009) and subsequent growth of larger bodies (up to Ceres mass or even to the mass of protoplanets) by accretion of millimeter-sized pebbles (Johansen et al. 2015). The shallow size distribution below the characteristic asteroid size, top-heavy with the differential number of asteroids per mass unit d N∕dM ∝ M−1.6, is consistent with the initial mass function of planetesimals produced by the streaming instability (Johansen et al. 2015; Simon et al. 2016; Abod et al. 2019), but could also arise from accretion of planetesimals of initially 100 m in size (Weidenschilling 2011). A general pathway to form such small planetesimals is still unknown (Johansen et al. 2014). The size distribution between 10 and 100 km of cold classical Kuiper belt objects has a similar shape to planetesimals formed by the streaming instability, followed by a shallow exponential tapering at sizes above 100 km (Schäfer et al. 2017). The absence of craters from impactors of sizes below 1 km on Pluto, Charon, and the cold classical Kuiper belt object MU69 (Singer et al. 2019; Stern et al. 2019) and the high binary fraction of cold classical Kuiper belt objects (Nesvorný et al. 2019) give further evidence of the formation of large planetesimals from gravitationally bound pebble clumps (Johansen et al. 2014).
The inclination of the planetesimal population is another important parameter in setting the efficiency of planetesimal accretion. Planetesimal inclinations are mainly stirred by mutual scattering and by gravitational torques from the turbulent gas (Ida et al. 2008). Recent measurements of the scale height of the dust layer in protoplanetary discs are consistent with a weak turbulence with a diffusion coefficient between 10−4 and 10−3 (Pinte et al. 2016; Dullemond et al. 2018). We show that even these levels of turbulence stir the planetesimals to inclinations of about 0.01, which reduces the core growth rate significantly compared to models neglecting turbulent stirring.
Using these combined constraints in our model for core growth by planetesimal accretion, we demonstrate that protoplanets reach a maximum mass of 0.1 ME after three million years of disc evolution. If we ignore the constraints from the solar system on the total planetesimal population and allow planetesimals to form at the self-gravitating stage, yielding a total planetesimal mass of nearly 1000 ME (approximately 50 ME per AU), then our model produces hot and warm gas giants, but no cold objects similar to Jupiter and Saturn in mass and orbit. We show that we must additionally lower the characteristic planetesimal size as well as the turbulent stirring level by a factor 10 each to be able to form cold gas giants.
The paper is organised as follows. In Sect. 2 we review numerical studies of core growth by planetesimal accretion. Particularly, we focus on the large literature that exists on N-body simulations demonstrating that the formation of Jupiter’s core is slowed down significantly by gap formation in the planetesimal population and by the oligarchic growth of multiple bodies competing for planetesimals. In Sect. 3 we present the equations that we solve in order to produce growth tracks of protoplanets that migrate and accrete planetesimals and gas in an evolving protoplanetary disc. The results are presented in Sect. 4. Our main finding is that a planetesimal population of 1000 ME is insufficient to form cold gas giants and that the planetesimal sizes and the turbulent stirring must additionally be significantly lower than their nominal values in order to form analogues of Jupiter and Saturn. We summarise and discuss our results in Sect. 5. In Appendix A we present a pebble-driven planet formation model, based on constraints from observations of pebbles in protoplanetary discs and experiments on dust coagulation, to give perspective to the planetesimal-driven planet formation model considered in the main paper.
2 Core growth with planetesimals
We start byreviewing in this section the literature that exists on the formation of cold gas giants, similar to Jupiter in mass and orbit, by planetesimal accretion. We focus on papers that concern N-body simulations because they capture the radial transport of planetesimals in connection with gap formation in the planetesimal population, for instance, and the oligarchic growth of multiple protoplanets.
Simulations of core formation can broadly be categorised into four quadrants in the space spanned by single or multiple in one direction and migrating or non-migrating along the other: (1) single non-migrating protoplanets, (2) single migrating protoplanets, (3) multiple non-migrating protoplanets, and (4) multiple migrating protoplanets. We review the literature on these four quadrants in the next subsections.
2.1 Single non-migrating protoplanets
Tanaka & Ida (1997) simulated the dynamics of a single protoplanet in an ocean of smaller planetesimals. They observed that the planetesimals scattered by the protoplanet circularise by gas drag beyond the reach of the protoplanet. The growth of the protoplanet during gap formation was explored in Rafikov (2001). Using Eq. (25) of Rafikov (2001), we calculate that a gap is opened when the protoplanet has achieved a mass roughly between that of the Moon and that of Mars in the 5–10 AU regions. Very small planetesimals are able to penetrate into the gap by radial drift, but they must be smaller than a few kilometers to drift fast enough to penetrate. A phase of rapid gas accretion would also allow the core to access the small planetesimals trapped at the gap edges (Shiraishi & Ida 2008; Zhou & Lin 2007), but such rapid growth is generally not obtained during core formation, and particularly not at the early stages of core growth.
2.2 Multiple non-migrating protoplanets
Already Tanaka & Ida (1997) suggested that the problem of gap formation could be alleviated by the simultaneous growth of multiple protoplanets. Terrestrial planet formation simulations show that such an oligarchic growth phase is a robust outcome of planetesimal accretion (Kokubo & Ida 2000). Oligarchic growth in the giant planet region was simulated by Thommes et al. (2003), neglecting planetary migration from the gas torque. The oligarchic growth shows no strong gap formation. Nevertheless, Thommes et al. (2003) required a surface density of 200 kg m−2 in planetesimals of 10 km in size at 5 AU (translating into approximately 24 ME per AU) to form cores of 5 ME there. Modern solar abundances yield a total condensible solids fraction of Z ≈ 1.5% (Lodders 2003), but a large fraction of the oxygen will be bound in supervolatile CO rather than water (Bitsch et al. 2019) and hence will not contribute to the planetesimal mass outside of the water-ice line. With conservative value for the relative mass bound in planetesimals of Zpla ≈ 0.5, the successful models of Thommes et al. (2003) require the gas surface density of a gravitationally unstable disc with self-gravity parameter Q ≈ 1. Levison et al. (2010) instead considered the growth of four initially massive protoplanets, but observed that these simply scattered a joint gap in the population of planetesimals of 100 km in size. This result highlights that placing protoplanets within a limited spatial interval can strongly reduce the mutual feeding of the protoplanets in the oligarchic growth picture and instead leads to the transport of planetesimals to beyond the reach of the protoplanets.
2.3 Single migrating protoplanets
The accretion rate of a migrating protoplanet was considered by Ward & Hahn (1995) and by Tanaka & Ida (1999). At slow migration (and/or small planetesimals experiencing short gas drag timescales), the protoplanet becomes a shepherd as the planetesimals are pushed in front of the protoplanet. This process is similar to the gap formation observed in Tanaka & Ida (1997). Fast migration instead turns the protoplanet into a predator that plows through the planetesimals while accreting a small fraction of them. This accretion regime is the focus of this paper because the case of a single migrating protoplanet can be easily compared to similar models where core growth is driven by pebble accretion (Bitsch et al. 2015; Bitsch & Johansen 2017; Johansen et al. 2019). A second motivation for studying single protoplanets rather than oligarchic growth is the possibility that a few large protoplanets form at ice lines and hence have a major head start in the accretion process, thus avoiding to compete for planetesimals with other protoplanets (Schoonenberg & Ormel 2017; Dra̧żkowska & Alibert 2017; Liu et al. 2019).
2.4 Multiple migrating protoplanets
Coleman & Nelson (2014) simulated oligarchic growth including migration and found that the gas giants that form in the simulations had all migrated to the inner regions of the protoplanetary disc. In other experiments they showed that gas giants must start their formation beyond 20 AU in the protoplanetary disc in order to have migration space in which to accrete gas. This necessity for forming the cores of gas giants very far from the Sun was also found in pebble accretion models (Bitsch et al. 2015; Ndugu et al. 2018; Johansen et al. 2019). Pirani et al. (2019) proposed that the asymmetric distributions of leading versus trailing Jupiter trojans is due to the capture of the trojans while Jupiter was migrating rapidly inwards from its formation region beyond 20 AU.
2.5 Small planetesimals?
N-body simulations have demonstrated that the formation of cold gas giants is very hard in all four quadrants of the multiplicity-migration space described above. Rafikov (2004) considered the possibility that planetesimals are either born small or fragment to small sizes. Such small planetesimals (with sizes smaller than 1 km) have low scale heights (and are hence more easily captured by the protoplanet) and penetrate planetesimal gaps formed by protoplanet scattering. The penetration by small planetesimals through the scattering gap may be the reason why some statistical approaches to the planetesimal population are able to form a Jupiter-planet on a 5 AU orbit in models neglecting migration and oligarchic growth (D’Angelo et al. 2014).
Evidence from the solar system nevertheless suggests a characteristic planetesimal size of 100 km (as we discussed in the introduction). In the gravitationally unfocused case, the collision timescale of planetesimals with number density npla, physical cross section σpla, radius Rpla, internal density ρ∙, and relative speed between the planetesimals δv is
![\begin{eqnarray*} t_{\textrm{coll}} &=& \frac{1}{n_{\textrm{pla}} \sigma_{\textrm{pla}} \delta v} \approx \frac{R_{\textrm{pla}} \rho_{\bullet}}{\Sigma_{\textrm{pla}} \Omega} \nonumber \\[5pt] &=& 50.3\,\textrm{Myr}\,f_{\textrm{pla}}^{-1} \left(\frac{R_{\textrm{pla}}}{50\,\textrm{km}} \right) \left(\frac{\rho_{\bullet}}{2 \times 10^3\,\textrm{kg\,m}^{-3}} \right) \left(\frac{r}{10\,\textrm{AU}} \right)^{5/2}. \end{eqnarray*}](/articles/aa/full_html/2019/11/aa36351-19/aa36351-19-eq1.png) (1)
(1)
Here we assumed a planetesimal surface density of Σpla = 10 kg m−2fpla[r∕(10 AU)]−1 (corresponding to a constant 2.4 ME of planetesimals per AU). Even a very massive planetesimal disc with fpla = 10 would have a collision timescale of 1–5 Myr in the 5–10 AU region. Moreover, the characteristic planetesimal size of 100 km observed in the modern solar system indicates that the primordial planetesimal population did not undergo an extensive fragmentation process to smaller and more easily accreted planetesimals.
2.6 Regions of zero migration?
By injecting artificial regions of zero-migration in the cold regions of the protoplanetary disc that trap protoplanets and planetesimals, Coleman & Nelson (2016) showed that this approach allows the formation of cold Jupiters through planetesimal accretion in the outer disc. Their models successfully produced cold Jupiters because protoplanets and planetesimals gathered in these convergence zones. However, the mechanism for the emergence of long-lived zero-migration zones in the formation region of cold gas giants is not clear, but it might be related to pressure bumps that arise in non-ideal magnetohydrodynamics (MHD) simulations of protoplanetary discs (Flock et al. 2015; Riols & Lesur 2019).
3 Governing equations
The main focus of our paper is the simulation of the growth of single migrating protoplanets by planetesimal accretion. Our approach is similar to that of Johansen et al. (2019), who presented core growth tracks for cores accreting small pebbles alone, but we ignore the contribution of pebbles to core accretion here. We compare the results obtained here to those of pebble-driven core accretion models in the conclusions (and in Appendix A).
3.1 Planetesimal accretion
We followed the parametrisations of Tanaka & Ida (1999), based on analytical fits to N-body simulations,for the planetesimal accretion rate. We briefly summarise these equations here. The equations are normalised with respect to the local dynamics near the protoplanet orbiting at a distance r from the star. Distances are thus normalised by the Hill radius RH of the protoplanet, while times are normalised by the synodic period TK ∕hp. Here TK is the Keplerian period and ![$h_{\textrm{p}} = R_{\textrm{H}} / r = [M/(3 M_{\star})]^{1/3}$](/articles/aa/full_html/2019/11/aa36351-19/aa36351-19-eq2.png) is the reduced Hill radius. The physical radius of the protoplanet is given by
is the reduced Hill radius. The physical radius of the protoplanet is given by 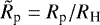 in these units. We ignored the contribution of the gas envelope to the cross section of the protoplanet because the cross section would increase significantly only above a core mass of 5 ME for our nominal planetesimal radii of 50 km (D’Angelo et al. 2014) and because the accretion rate only scales as the square root of the effective capture radius for the relevant planetesimal inclinations considered here (see Eq. (10)).
in these units. We ignored the contribution of the gas envelope to the cross section of the protoplanet because the cross section would increase significantly only above a core mass of 5 ME for our nominal planetesimal radii of 50 km (D’Angelo et al. 2014) and because the accretion rate only scales as the square root of the effective capture radius for the relevant planetesimal inclinations considered here (see Eq. (10)).
The migration timescale is calculated as
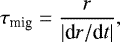 (2)
(2)
where r is the semi-major axis of the protoplanet and dr∕dt is the migration speed (see Sect. 3.3 below). The normalised migration timescale is given by
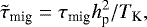 (3)
(3)
where TK = 2π∕Ω is the orbital period. This normalisation is a consequence of the radial position equation ṙ = vr = r∕τmig.
The gas drag timescale of the planetesimals is
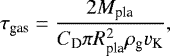 (4)
(4)
where Mpla is the planetesimal mass, CD is the drag coefficient, ρg is the gas density, and vK is the Keplerian speed of the protoplanet. We set CD = 0.5 for simplicity; this non-linear drag regime is valid for planetesimals larger than a few kilometers (Weidenschilling 1977). The normalised gas-drag timescale, which enters the damping equations for eccentricity and inclination, is then given by
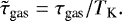 (5)
(5)
Tanaka & Ida (1999) found a critical migration timescale for shepherding,
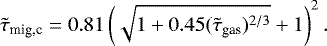 (6)
(6)
Protoplanets with 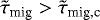 are considered to be shepherds and stop their accretion of planetesimals. These shepherding bodies nevertheless continue to migrate into regions of higher gas density, which in turn increases the gas drag on the planetesimals and hence reinforces the shepherding behaviour (the run-away shepherding effect).
are considered to be shepherds and stop their accretion of planetesimals. These shepherding bodies nevertheless continue to migrate into regions of higher gas density, which in turn increases the gas drag on the planetesimals and hence reinforces the shepherding behaviour (the run-away shepherding effect).
The accretion rate of the protoplanet is given by
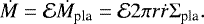 (7)
(7)
Here 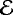 is the accretion efficiency and Ṁpla is the flux of planetesimals that cross the orbit of the migrating protoplanet. The migration speed is parameterised through the inverse of the normalised migration timescale,
is the accretion efficiency and Ṁpla is the flux of planetesimals that cross the orbit of the migrating protoplanet. The migration speed is parameterised through the inverse of the normalised migration timescale,
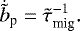 (8)
(8)
The accretion efficiency is then parameterised as
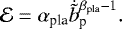 (9)
(9)
The parameters αpla and βpla are fits to numerical simulations. Tanaka & Ida (1999) found the expressions

Here ĩ0 is the inclination of the planetesimalpopulation, divided by hp to convert this into Hill sphere units.
3.2 Planetesimal inclinations
Tanaka & Ida (1999) showed that a protoplanet easily excites the eccentricities of the planetesimals that it migrates towards, but the inclination of a planetesimal is hardly changed prior to the first scattering by the protoplanet. Therefore the planetesimal inclination is an important parameter in the accretion rate. We mainly set the inclination from the balance between the stirring by the turbulent gas and damping by gas drag, but for our experiments with a very or extremely weak turbulent stirring, we also included the inclination excitation by mutual planetesimal scatterings (see below).
Ida et al. (2008) used a non-dimensional parameter γ to quantify the stirring by the turbulent gas and find the equilibrium eccentricity through
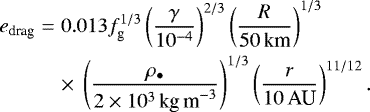 (12)
(12)
Here fg is the gas surface density profile relative to the minimum mass solar nebula (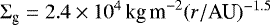 is used as a reference value by Ida et al. 2008). We set i0 = edrag because turbulent density fluctuations appear to excite eccentricities and inclinations equally well (Yang et al. 2012).
is used as a reference value by Ida et al. 2008). We set i0 = edrag because turbulent density fluctuations appear to excite eccentricities and inclinations equally well (Yang et al. 2012).
The turbulent stirring parameter γ that appears in Eq. (12) gives the scaling factor of the random-walk excitation of the planetesimal eccentricity. Ida et al. (2008) suggested that γ ~ αt (where αt here denotes the turbulent diffusion coefficient, in contrast to the α value that controls the viscous evolution of the protoplanetary disc), or 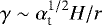 (where H∕r is the disc aspect ratio). Observations of the thickness of the dust layer in the protoplanetary disc around the young star HL Tau suggest a turbulent diffusion coefficient of a few times 10−4 (Pinte et al. 2016), but the interpretation depends on the assumed Stokes number of the sedimented pebbles. The radial scale height of pebble ringsobserved in the Disk Substructures at High Angular Resolution Project (DSHARP) indicates a diffusion coefficient ~ 10−3 (Dullemond et al. 2018). The physical origin of this weak turbulence is unknown; the vertical shear instability and active surface layer turbulence both yield turbulent diffusion coefficients in excess of 10−3 in the mid-plane (Stoll & Kley 2016; Yang et al. 2018). We here assumed a relatively low value of γ = 10−4 as the nominal value because this is consistent with observations and likely represents a lower limit to the realistic span of values. This value of γ also yields planetesimal inclinations similar those measured in simulations of the stirring of planetesimals in the dead zone by density waves propagating down from turbulent surface layers (Gressel et al. 2012). However, in Sect. 4.3 we show the change in our results when we adopt even lower values of the stirring coefficient.
(where H∕r is the disc aspect ratio). Observations of the thickness of the dust layer in the protoplanetary disc around the young star HL Tau suggest a turbulent diffusion coefficient of a few times 10−4 (Pinte et al. 2016), but the interpretation depends on the assumed Stokes number of the sedimented pebbles. The radial scale height of pebble ringsobserved in the Disk Substructures at High Angular Resolution Project (DSHARP) indicates a diffusion coefficient ~ 10−3 (Dullemond et al. 2018). The physical origin of this weak turbulence is unknown; the vertical shear instability and active surface layer turbulence both yield turbulent diffusion coefficients in excess of 10−3 in the mid-plane (Stoll & Kley 2016; Yang et al. 2018). We here assumed a relatively low value of γ = 10−4 as the nominal value because this is consistent with observations and likely represents a lower limit to the realistic span of values. This value of γ also yields planetesimal inclinations similar those measured in simulations of the stirring of planetesimals in the dead zone by density waves propagating down from turbulent surface layers (Gressel et al. 2012). However, in Sect. 4.3 we show the change in our results when we adopt even lower values of the stirring coefficient.
Ida et al. (2008) also argued that the highest eccentricity induced by mutual planetesimal scatterings is reached when the random velocity becomes comparable to the escape speed because this situation favours collisions over strong scattering. The resulting eccentricity only depends on the planetesimal escape speed and on the Keplerian speed,
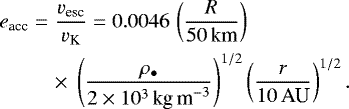 (13)
(13)
Our nominal value of γ = 10−4 in Eq. (12) therefore represents the lower end of the range where mutual scatterings are less important than turbulent stirring, for a planetesimal radius of 50 km. We therefore ignored for simplicity inclination excitation by planetesimal scatterings for the main simulations in Sect. 4, but we included it for consistency in our experiments with lower values of γ presented in Sect. 4.3.
3.3 Planetary migration
We used a combined expression for planetary migration that captured the nominal type I migration of low-mass cores and the transition to migration modified by gap formation (based on Kanagawa et al. 2018). This migration prescription and its consequences for planet formation are discussed in Ida et al. (2018) and in Johansen et al. (2019). The migration is proportional to the gas surface density and initially to the planetary mass, but the migration rate drops as the inverse of the planetary mass after the protoplanet reaches a gap-opening mass of approximately 20 ME. The turbulent viscosity, which determines the gap-opening mass, was set to a low value of αt = 10−4.
3.4 Gas accretion
Johansen et al. (2019) allowed gas accretion to commence after the core reached the pebble isolation mass; here we instead assumed that a core mass of 10 ME marks the transition to gas accretion. This simplified approach guarantees a core mass that is comparable to those inferred from the giant planets in the solar system (Guillot 2005; Wahl et al. 2017), while it allows us emphasise the core formation process rather than the physics of gas accretion. The expressions that we use for the gas accretion rate are discussed in detail in Ida et al. (2018) and Johansen et al. (2019). We chose a low opacity in the gas envelope to facilitate rapid gas accretion; the gas accretion timescale of a Jupiter-mass planet is generally a few hundred thousand years in this model.
3.5 Evolution of the protoplanetary disc
The protoplanetary disc is evolved as a standard viscous α disc with α = 0.01. The disc surface density profile follows a (negative) power law out to a characteristic radius beyond which the profile is exponentially tapered. We used analytical expressions for the evolution of the mass accretion rate onto the star and of the characteristic disc radius, anchored by choosing the initial gas mass flux onto the star, Ṁ0, and the final gas mass flux after 3 Myr of disc evolution, Ṁ3, after which the protoplanetary disc is assumed to photoevaporate. The choice of the final accretion rate effectively sets the initial characteristic disc size; a high value of Ṁ3 implies a large initial disc size and vice versa (see Johansen et al. 2019).
We ignored viscous heating of the protoplanetary disc, motivated by simulations showing that this heating is weak in discs accreting by magnetic stresses (Mori et al. 2019). We therefore considered only stellar irradiation to set the fixed gas temperature profile, using the irradiated temperature profile given in Ida et al. (2016). This temperature approach yields a disc aspect ratio H∕r = 0.024 at 1 AU that increases with distance as a power law of index 2∕7. The smooth disc profile precludes any regions of outwards migration in the disc, but such regions are limited to the inner few AU from the star in any case (unless the turbulent viscosity is high, see Cossou et al. 2014; Bitsch & Johansen 2016) and hence do not affect the growth tracks for cold gas giants, which are the focus of this paper.
4 Growth of single migrating protoplanets
4.1 Accretion efficiency
We start by calculating the efficiency of accreting planetesimals of 50 km in radius (100 km in diameter) using the Tanaka & Ida (1999) parametrisation for two different values of the turbulent stirring (weak stirring with γ = 10−4 and very weak stirring withγ = 10−5) as a function of the distance from the star and the mass of the protoplanet in Fig. 1. The planetesimal inclinations were calculated taking only the turbulent stirring by the gas into account. The results are shown for three values of the stellar gas accretion rate, Ṁ = 10−6 M⊙ yr−1, Ṁ = 10−7 M⊙ yr−1, and Ṁ = 10−8 M⊙ yr−1. We considered here a very large disc size, such that Ṁ is inwards and constant out to 100 AU. We recall that we ignored viscous heating; the inclusion of viscous heating would heat the inner regions of the protoplanetary disc and hence decrease the migration rate, which would in turn make the protoplanets more prone to shepherding. The considered accretion rates represent an evolutionary sequence in which the accretion rate decreases with increasing age of the protoplanetary disc. The stellar accretion rate affects the planetesimal accretion efficiency mainly through the gas surface density, which in turn scales the migration rate and the inclination of the planetesimals in equilibrium between turbulent stirring and gas damping.
The accretion efficiency for planetesimals of 50 km in radiuslies in the range between 0.0001 and 0.03 in the region of giant planet formation in the solar system (the region between 5 and 20 AU in distance from the star and 1 and 10 ME in mass is marked with dotted lines in the plots). Lowering the turbulent stirring coefficient to γ = 10−5 increases the efficiency by approximately a factor three. This increase comes mainly from 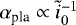 (Eq. (10) for
(Eq. (10) for 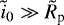 ) and ĩ0 ∝ γ2∕3 (Eq. (12)), which combine to make
) and ĩ0 ∝ γ2∕3 (Eq. (12)), which combine to make 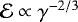 (Eq. (9)). This scaling slightly overpredicts the actual increase when lowering γ from 10−4 to 10−5 because of saturation effects in Eq. (10) towards the 2D limit. The efficiency increases with decreasing stellar mass accretion rate because more slowly migrating protoplanets accrete a larger fraction of the planetesimal flux.
(Eq. (9)). This scaling slightly overpredicts the actual increase when lowering γ from 10−4 to 10−5 because of saturation effects in Eq. (10) towards the 2D limit. The efficiency increases with decreasing stellar mass accretion rate because more slowly migrating protoplanets accrete a larger fraction of the planetesimal flux.
The transition from predator to shepherd is marked with a thick red line in Fig. 1. This transition depends on the gas drag timescale and on the migration speed. The transition to shepherding generally occurs at around 1 AU from the star in the final decade of core growth (M ≈ 1–10 ME). Cores with lower mass transition to shepherding farther out.
 |
Fig. 1 Accretion efficiency of a protoplanet accreting planetesimals of radius 50 km and for weak turbulent stirring (γ = 10−4, left plots) and very weak turbulent stirring (γ = 10−5, right plots) as a function of the distance from the star and the protoplanet mass. The three rows show the accretion efficiency for three different increasing (top to bottom) values of the mass accretion rate through the disc; the gas surface density in turn defines the equilibrium inclination of the planetesimals and the transition of the protoplanet from an accreting predator (exterior of the red line) to a non-accreting shepherd (interior of the red line). The parameter region of core formation in the solar system (the box made by 5 and 20 AU and by 1 and 10 ME) is marked with dashed lines. The accretion efficiency beyond 5 AU lies at a value of a few percent or lower for the case of weak turbulent stirring, while lowering the turbulent stirring to γ = 10−5 increases the efficiency by approximately a factor 3. The efficiency overall increases with decreasing gas accretion through the disc because more slowly migrating planets accrete a higher fraction of the planetesimals that they migrate through (even though the planetesimal inclinations increase slightly as the gas drag is reduced). |
4.2 Growth map
We calculated a large number of growth tracks, defined by the starting position r0 and starting time t0 of the protoplanet. We started the protoplanets at a mass of 10−3 ME, a value thatmay even be reached by the most massive planetesimals formed by the streaming instability (Liu et al. 2019). We considered four different combinations of the beginning and final stellar accretion rate: (Ṁ0, Ṁ3) = (10−7, 3 × 10−9), (10−6, 10−8), (10−6, 3 × 10−9), and (10−6, 10−9). The planetesimals were assumed to form at t = 0 following the primordial gas surface density profile. With a planetesimal metallicity of Zpla = 0.01, these protoplanetary disc models contain 187 ME, 965 ME, 432 ME, and 208 ME of planetesimals, respectively. The planetesimals were assumed to be 50 km in radius and the turbulent stirring coefficient was chosen at its nominal value of γ = 10−4 for all four growth maps.
The growth maps in Fig. 2 indicate the final mass of the planets in continuous colours and the final positions as white contour lines. The final mass decreases for protoplanets starting at later times because the time left for growing the planet is shorter. Protoplanets starting their growth close to the star or late in the disc evolution migrate slowly enough to become planetesimal shepherds; hence the final mass drops to zero at late starting times. The yellow line marks the size of the protoplanetary disc and the red contours show the self-gravity parameter Q = csΩ∕(πGΣg) (Safronov 1960; Toomre 1964), where cs is the sound speed of the gas, Ω is the Keplerian frequency, and Σg is the gas surface density.
The protoplanetary disc model shown in the upper left corner contains approximately twice the mass in planetesimals of the minimum mass solar nebula (Hayashi 1981), consistent with the constraints on the primordial planetesimal populations discussed in the introduction. This model entirely fails to form any gas giants. Because the planetesimal accretion efficiency is at most a few percent, the total planetesimal mass of ≈187 ME is insufficient to form a core of 10 ME. The most massive protoplanets grow to approximately 0.1 ME (comparable to Mars) in this model.
When the initial mass accretion rate is increased by a factor 10 to 10−6 M⊙ yr−1, the model shown in the upper right corner of Fig. 2 yields a protoplanetary disc that starts with a self-gravity parameter Q below 1.5 in a large region from 3 to 30 AU. The disc initially has a characteristic size of 20 AU, beyond which the power-law gas surface density transitions to an exponential tapering. This model successfully produces gas-giant planets that end in orbits up to 2 AU from the star, but fails to form any analogues of Jupiter and Saturn in the 5–10 AU region.
The two lower plots of Fig. 2 show versions of the protoplanetary disc with an initially high accretion rate, but with smaller initial disc sizes (9 and 4 AU) and lower final accretion rates (Ṁ3 = 3 × 10−9 M⊙ yr−1 and Ṁ3 = 10−9 M⊙ yr−1). The reduction in initial disc size pushes the final positions of the gas giants that are formed even closer to the star. Protoplanets can grow even outside of the initial disc size because we assumed that planetesimals also form at an abundance of 1% relative to the gas in the exponentially tapered regions.
 |
Fig. 2 Growth maps for protoplanet growth by planetesimal accretion, with gas accretion commencing after 10 ME is reached. The maps show the final mass (i.e. the mass reached when the disc has dissipated after 3 Myr) as continuous colours and the final positions as white contour lines as a function of the starting position of the protoplanet and the starting time. We additionally show the size of the protoplanetary disc (yellow line) and the Toomre Q of the gas (red contour lines). The panels show the results for four values of the initial mass accretion rate through the disc and the mass accretion rate after 3 Myr. The instantaneous stellar mass accretion rate is shown on the right axis. Each panel is also labelled with the total mass of the planetesimals in the models; we assume here that 1% of the initial gas surface density profile is converted into planetesimals at t = 0. The nominal model (upper left) achieves protoplanet growth only up to 0.1 ME, approximately the mass of Mars. The three other models, where planetesimals form at the gravitationally unstable phase of protoplanetary disc evolution, successfully form hot and warm gas giants interior of 2 AU, but are not able to form any cold gasgiants in the 5–10 AU region (see inset in the upper right panel). |
4.3 Boosting planetesimal accretion
We tested ways to boost core growth by planetesimal accretion by decreasing the size of the planetesimals, decreasing the migration speed, increasing the initial mass of the protoplanets, and decreasing the inclinations of the planetesimals. We illustrate the growth tracks of protoplanets starting at 5, 10, 15, and 20 AU in Fig. 3 in what we call the massive planetesimal population model (the model at the top right of Fig. 2: initial size of 20 AU, initial stellar accretion rate of 10−6 M⊙ yr−1, and 965 ME of planetesimals) for two different planetesimal sizes (50 and 5 km), for a case where the migration speed is reduced, and for a case with a more massive initial protoplanet. We also overplot the current positions of the giant planets in the solar system. Starting at 5 AU and with planetesimals of 50 km, we can only form Jupiter-mass planets ending in (warm) 1 AU orbits. Starting farther out at 10 AU, smaller planetesimals help in promoting the growth of the protoplanet, but the nominal planetesimal radius of 50 km and the smaller planetesimals with radius 5 km both fail to produce protoplanets beyond 1 ME in mass.
In order to explore the role of the migration rate on the outcome of planet formation, we produced additional growth tracks with the migration multiplied by a reduction factor fmig = 0.2 for all protoplanet masses. We also ignored the transition to shepherding in this experiment because shepherding might be suppressed when multiple protoplanets scatter planetesimals between them (Kokubo & Ida 2000; Thommes et al. 2003). The result is shown with yellow curves in Fig. 3. The reduced migration has a weak positive effect on the growth tracks starting at 5 AU; they now produce gas giants in 2–3 AU orbits. The effect is overall negative farther out, however. Lowering the migration speed leads to a higher efficiency of accreting planetesimals, but the flux of planetesimals that the protoplanets migrates over is also reduced, which reduces the overall growth rate.
In Fig. 3 we show with dash-dotted blue lines the growth tracks when we started with a larger protoplanet mass of Mp,0 = 0.1 ME. These protoplanets experience rapid migration towards the star. This has the positive effect of bringing the protoplanets into the regions of higher accretion efficiency closer to the star, but increasing the protoplanet mass does not help to create giant planets in cold orbits.
We show the final planet mass as a function of the final position forming in the massive planetesimal population model in Fig. 4 for lower values of the turbulent stirring γ. We assumed again that the protoplanetsstart growing immediately at t = 0. We include here the inclination stirring by mutual scattering (Eq. (13)) and by torques from the turbulent gas (Eq. (12), multiplied by 0.5 because i ≈ 0.5e is typical for excitation by scattering). The planetesimal inclination is set as the larger of the two expressions. We tested three values of the turbulent stirring coefficient γ (weak turbulence: γ = 10−4, very weak turbulence: γ = 10−5, and extremely weak turbulence: γ = 10−6) and two planetesimal sizes (50 and 5 km). The outermost Jupiter-mass planet shifts from 2 to 3 AU when the turbulence strength is decreased from weak to very weak or extremely weak. In the latter two cases the inclination is mainly set by the escape speed of the planetesimals. Lowering the planetesimal radius to 5 km permits the formation of Jupiter-mass planets in the 5 AU region when the turbulence is very weak or extremely weak.
 |
Fig. 3 Growth tracks of protoplanets accreting planetesimals of two different radii (blue and red lines), with reduced migration (yellow lines) and starting with a higher protoplanet mass (blue dash-dotted lines). The growth tracks are started at either 5, 10, 15, or 20 AU. We used here the massive planetesimal population model that contains 965 ME of planetesimals formed at t = 0 and assumed that the protoplanets start to grow immediately thereafter. Growth tracks starting at 5 AU generally become warm gas giants, ending in final orbits around 1 AU. Protoplanets starting farther out experience only moderate growth due to the low planetesimal accretion efficiencies there. Lowering the migration rate has a net positive effect for the growth track starting at 5 AU, but the more distant protoplanets experience a decreased growth rate when they migrate more slowly because the flux of planetesimals past migrating the protoplanet is reduced. The more massive protoplanets experience rapid migration towards the regions of high accretion efficiency close to the star, but the adoption of initially more massive protoplanets does not help in forming cold gas giants. |
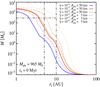 |
Fig. 4 Finalplanetary mass as a function of the final planetary orbit for protoplanets starting to accrete at t = 0 in the massive planetesimal population model with two different planetesimal radii (50 and 5 km) and three values of the turbulent stirring coefficient (10−4, 10−5, and 10−6). The solid blue line (γ = 10−4/Rpla = 50 km) corresponds to a cut at t0 = 0 of the upper right panel of Fig. 2. The planetesimal inclinations are here set as the maximum of the inclinations given by turbulent stirring and by mutual planetesimal scattering. Planetesimals with a nominal radius of 50 km can only form Jupiter-mass planets interior of 3 AU, even when the turbulent stirring is very weak with γ = 10−5 or extremelyweak with γ = 10−6, because of inclination stirring by mutual planetesimal scattering. Lowering the planetesimal radius to 5 km allows the formation of Jupiter analogues when the turbulent stirring coefficient is γ = 10−5 or γ = 10−6. |
 |
Fig. 5 Growth maps for core growth by accretion of 50 km planetesimals that form at either t = 0.1 Myr (top panel) or t = 0.5 Myr (bottom panel). The planetesimal population is given 1% of the gas surface density at the evolution stage of the protoplanetary disc at the chosen formation time. The protoplanets are nevertheless still started at the full range of starting times, even before the planetesimals form. Delaying the formation of planetesimals to t = 0.1 Myr reduces the parameter space for forming hot and warm gas giants significantly, while the delay to 0.5 Myr entirely removes the capability of the protoplanetary disc to form any giant planets. |
4.4 Later planetesimal formation
Iron meteorites are evidence that some planetesimal populations formed very early in the solar system and subsequently melted by heat from the decay of short-lived radioactive elements (Bizzarro et al. 2005; Kleine et al. 2009). However, most meteorites are classified as primitive and undifferentiated and hence likely formed at least 1 Myr after the formation of the Sun, so that melting and differentiation were avoided (Larsen et al. 2016). We therefore explore in Fig. 5 the effect of forming planetesimals at either t = 0.1 Myr or at t = 0.5 Myr. Delaying the formation of planetesimals by 0.1 Myr has no significant effect on the growth map because the protoplanetary disc is still in its pristine phase at this time and forms a massive population of 707 ME of planetesimals. On the other hand, delaying planetesimal formation to 0.5 Myr and forming 307 ME of planetesimals is detrimental to the growth of the protoplanet and entirely removes the possibility of forming gas-accreting cores.
5 Summary and discussion
We have used the fits to N-body simulations of single migrating protoplanets from Tanaka & Ida (1999) to produce growth tracks for protoplanets growing by accreting planetesimals. We assumed that gas accretion is rapid and commences when the core reaches a mass of 10 Earth masses. We evolved the protoplanetary gas disc using the standard viscous approach. The initial disc size was set by defining the beginning stellar accretion rate and the final stellar accretion rate after three million years when we assume that the remaining gas is photoevaporated.
Our nominal parameters for the planetesimal population followed from three constraints that come from studies of the solar system and protoplanetary discs. The first constraint comes from theoretical models of terrestrial planet formation and from the inferred modern populations of planetesimals in Neptune’s scattered disc and in the Oort cloud; these models both indicate a primordial planetesimal population in the solar system of a few Earth masses per AU (Raymond et al. 2009; Brasser 2008; Brasser & Morbidelli 2013). The second constraint is that the characteristic planetesimal diameter in the solar system, inferred from the asteroid belt and from the Kuiper belt (Bottke et al. 2005; Morbidelli et al. 2009; Abod et al. 2019; Singer et al. 2019; Stern et al. 2019), is approximately 100 km; we take this as the nominal birth size of the planetesimals. The stirring of the planetesimal inclinations by the turbulent gas plays a very important role in setting the efficiency of planetesimal accretion. Our third constraint comes from protoplanetary discs; here the turbulent stirring coefficient of dust is inferred to lie in the range between 10−4 and 10−3 (Pinte et al. 2016; Dullemond et al. 2018). We therefore used a nominal value γ = 10−4 for the turbulent stirring coefficient; this value is also consistent with measurements of the planetesimal inclinations in the dead zone of protoplanetary discs (Gressel et al. 2012).
Based on these constraints, we built a nominal protoplanetary disc model where planetesimals formed when the stellar accretion rate is 10−7 M⊙ yr−1 and the disc has an initial size of 40 AU. The disc contains 187 Earth masses of planetesimals, slightly higher than twice the minimum mass solar nebula (Hayashi 1981). However, the protoplanets in this model grow only to a maximum mass of 0.1 Earth masses, similar to the mass of Mars. The same protoplanetary disc model yielded super-Earths and gas-giant planets when the core mass was evolved only through the accretion of a similar amount of small pebbles (Johansen et al. 2019).
We therefore tested another model where the planetesimals formed already at the self-gravitating stage of protoplanetary disc evolution, where the mass accretion onto the star was Ṁ = 10−6 M⊙ yr−1. This instead yielded 965 Earth masses of planetesimals in a protoplanetary disc of an initial size of 20 AU; this enormous mass, corresponding to 50 Earth masses per AU or approximately 13 times the minimum mass solar nebula, is in clear conflict with the inferred primordial population of planetesimals in the solar system (the first constraint above). This model successfully produced hot and cold gas giants, but failed to form any analogues of Jupiter and Saturn in orbit and mass. We experimented with smaller planetesimals and lower values of the turbulent stirring and were finally able to form cold gas giants with a combination of small planetesimals (5 km in radius, violating the second constraint above) and very weak turbulence (γ = 10−5, violating the third constraint above). We conclude that the formation of cold gas giants in the planetesimal accretion scenario requires not only an extremely massive planetesimal population, but also a reduced planetesimal size and a reduced turbulent stirring compared to the nominal values. Our conclusions thus agree with those of Fortier et al. (2013), who also found that the inclinations and sizes of the planetesimal population are key parameters in setting the core growth rate.
Our conclusions about the inability for planetesimal accretion to form cold gas giants under nominal conditions are in line with many studies that have used N-body approaches to core growth by planetesimal accretion, both ignoring migration (Thommes et al. 2003; Levison et al. 2010) and including migration (Coleman & Nelson 2014). We have made many assumptions and simplifications to make the problem tractable. Our most dubious assumption is maybe that there is no interaction between the growing protoplanets. However, this approach allowed us to study the physics of simultaneous growth and migration separately. We also ignored the viscous heating of the protoplanetary disc and potential zones of outwards migration in the inner parts of the protoplanetary disc (Cossou et al. 2014).
It is possible that we miss one or more important piece of physics in the problem of core accretion with planetesimals. Capobianco et al. (2011) followed up on a finding from Levison et al. (2010) showing that some of their simulations starting with four massive protoplanets showed rapid outwards migration of the protoplanets by planetesimal scattering and rapid growth to cores of 10 Earth masses. Coleman & Nelson (2016) instead considered the possibility that the outer regions of the protoplanetary disc are filled with sharp pressure bumps able to concentrate protoplanets and planetesimals and stop migration to the inner disc. It is also possible that planetesimal accretion in nature plays only a minor role for core accretion. Alternatives to the core accretion scenario include the direct collapse of the gas to form gas giants (Helled et al. 2014) and the tidal downsizing of massive gas clumps to form super-Earths (Nayakshin 2017).
The pebble accretion scenario has also been proposed as an alternative to planetesimal accretion (Johansen & Lambrechts 2017; Ormel 2017). The high accretion rates of pebbles have been demonstrated in N-body simulations to naturally form cold gas giants, regardless of whether migration is excluded (Levison et al. 2015) or included (Izidoro et al. 2019; Bitsch et al. 2019). Statistical approaches including pebble accretion and migration have found that pebble accretion can drive the formation of cold gas giants in nominal protoplanetary disc models and for large (drift-limited) and small (constant Stokes number St = 0.01) pebbles (Bitsch et al. 2015; Johansen et al. 2019), provided that the turbulence is weak enough to allow pebbles to sediment and form a relatively thin mid-plane layer with a width of at most 10% of the gas scale height. We present in Appendix A growth maps for pebble accretion demonstrating that it is possible to form cold gas giants by pebble accretion considering a conservative pebble growth model where the pebble sizes are limited by fragmentation and bouncing. The area of parameter space where cold gas giants emerge is nevertheless a strong function of the turbulent diffusion coefficient and the metallicity of the protoplanetary disc. This critical behaviour with metallicity is in good agreement with exoplanet surveys that find an increasing occurrence rate of gas giants beyond solar metallicity (Santos et al. 2004; Johnson et al. 2010; Buchhave et al. 2012).
Protoplanetary discs may very well have high masses in the earliest phases of star formation (Tychoniec et al. 2018), as envisioned in our models with a massive primordial planetesimal population. However, while the formation of 1000 Earth masses of planetesimals is questionable, the growth from the dust to pebbles should be a natural process in these protoplanetary discs. The pebbles that are not captured by the growing protoplanets would then simply be accreted onto the star together with the gas.
Part of the drifting pebbles may also be converted into planetesimals, for example, at the water-ice line (Schoonenberg & Ormel 2017; Dra̧żkowska & Alibert 2017). Lenz et al. (2019) showed that the trapping of drifting pebbles in vortices and pressure bumps could form approximately 100 Earth masses of planetesimals, far less than the 1000 Earth masses needed to drive core growth by planetesimal accretion. Dra̧żkowska & Dullemond (2018), on the other hand, found that several hundred Earth masses of planetesimals can form from pebble pile-ups in a relatively narrow region beyond the water-ice line. A large fraction of this population of planetesimals (~10%) would nevertheless have been pushed into the asteroid belt by the migrating proto-Jupiter (Raymond & Izidoro 2017; Pirani et al. 2019), indicating that planetesimal formation at the water-ice line cannot have been as efficient in the solar system as found in Dra̧żkowska & Dullemond (2018). Photoevaporation provides an additional route to convert hundreds of Earth masses of pebbles into planetesimals out to 1000 AU from the star (Carrera et al. 2017), but such populations of approximately 0.1–1 Earth masses per AU are not in conflict with solar system evidence on the mass of the primordial planetesimal population.
While pebble drift is an advantage because surplus planetary building material is lost, the rapid loss of the pebble population could be detrimental to core growth by pebble accretion. Johansen et al. (2019) nevertheless demonstrated that small pebbles, with Stokes numbers of about 0.01, continue to drift through the disc for more than a million years if the initial protoplanetary disc is large (of approximately 100 AU at the stage when the stellar accretion rate is 10−7 M⊙ yr−1). These small pebbles are brought along with the viscous expansion of the outer regions of the protoplanetary disc and subsequently drizzle in from large distances. Some protoplanetary discs observed in recent ALMA surveys appear to be low mass and compact (Ansdell et al. 2017); such discs may have started out small and rapidly lost most of their pebbles to radial drift. Manara et al. (2018) proposed that the low total mass of solids in relatively old protoplanetary discs implies that planet formation was largely completed within the first million years or sooner; early growth like this may again be explained in the pebble accretion scenario given the potentially very high pebble massfluxes at the earliest stages of protoplanetary disc evolution (Tanaka & Tsukamoto 2019; Johansen et al. 2019).
As a final point, we advocate here using the giant planets in the solar system, combined with constraints from the solar system planetesimal populations and the observed turbulence levels in protoplanetary discs, as a benchmark problem for planet formation models. If a planet formation theory fails to form the solar system giants, given these constraints, then its success at forming any exoplanetary systems is doubtful as well.
Acknowledgements
A.J. thanks the Swedish Research Council (grant 2018-04867), the Knut and Alice Wallenberg Foundation (grants 2012.0150, 2014.0017) and the European Research Council (ERC Consolidator Grant 724687-PLANETESYS) for research support. B.B. thanks the European Research Council (ERC Starting Grant 757448-PAMDORA) for their financial support. The authors would like to thank the anonymous referee for helpful advice that helped improve the original manuscript.
Appendix A Pebble-driven planet formation model
In this appendix we use a similar approach as in the main paper to perform simulations of planet formation through pebble accretion, under constraints set by observations of protoplanetary discs and by dust coagulation experiments. Our approach to calculating the pebble accretion rate is described in detail in Johansen et al. (2019). We used the same protoplanetary disc model as for planetesimal accretion, with the accretion rate starting at 10−6 M⊙ yr−1 and ending at 10−8 M⊙ yr−1 at disc dissipation after 3 Myr. The instantaneous pebble mass flux was fixed at a constant ratio ξ of the gas mass flux onto the star. The pebble flux was assumed to be constant throughout the protoplanetary disc at any given time, until the outer edge of the disc where the flux is damped with the same exponential factor as the gas column density in the viscous accretion disc evolution equations. A constant flux ratio like this could result from slow pebble growth in the outer regions of the protoplanetary discs, so that pebbles grow only from the dust transported inwards by the viscous gas flow at the outer edge of the disc (this model was explored in an appendix of Johansen et al. 2019). An important difference compared to the planetesimal accretion models presented in the main paper is that the pebble column density is set relative to the instantaneous gas mass flux onto the star, while the planetesimals were assumed to form in a massive population at t = 0.
In the spirit of choosing the free parameters according to constraints, we considered pebble sizes based on coagulation experiments. We therefore set the pebble size at a given distance from the star equal to the minimum of the size obtained by fragmentation-limited pebble growth (Birnstiel et al. 2012) and by bouncing-limited pebble growth (Zsom et al. 2010). For fragmentation-limited pebble growth we set the pebble Stokes number according to
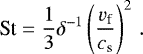 (A.1)
(A.1)
This yields a turbulent collision speed equal to the critical speed for fragmentation, vf. The turbulent viscosity αv sets the collision speed in reality, but we assumed here that the turbulent viscosity is equal to the turbulent diffusion coefficient δ. For the bouncing-limited pebble growth we simply set the pebble radius equal to 1 mm.
The turbulent diffusion coefficient was estimated by Pinte et al. (2016) for the protoplanetary disc around HL Tau from fitting synthetic images to the observations. The best fit was found for a pebble scale height of 1 AU at a distance of 100 AU from the star. At this distance the passively irradiated disc model yields an aspect ratio of H∕r≈ 0.2, assuming a central mass of 0.5 M⊙ (van der Marel et al. 2019) and a temperature of 47 K at 100 AU (Carrasco-González et al. 2019). Hence the dust layer thickness relative to the gas scale height is Hp∕Hg ≈ 0.05. This ratio arises physically entirely from the Stokes number and the turbulent diffusion coefficient through the diffusion-sedimentation equilibrium
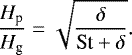 (A.2)
(A.2)
The analysis of Pinte et al. (2016) yielded a turbulent diffusion coefficient slightly higher than 10−4 at 100 AU. Mulders & Dominik (2012) estimated similar values of turbulence by analysing the SED of protoplanetary discs in a range of stellar masses. These values are estimated for the outer regions of protoplanetary discs. Zhang et al. (2018) proposed that a single planet of mass q = 10−4 relative to the central star might be responsible for the two bright rings in the protoplanetary disc around the young star AS 209 if the turbulent viscosity is as low as 10−5 closer to thestar.
 |
Fig. A.1 Stokes number (solid lines) and turbulent diffusion coefficient (dotted lines) for pebble growth limited by fragmentation and bouncing, shown for three different stages of protoplanetary disc evolution. The ratio of the scale height of the pebbles to the scale height of the gas is Hp ∕Hg = 0.1 in the top plot and Hp∕Hg = 0.2 in the bottom plot. The outer regions of the protoplanetary disc have pebble sizes set by fragmentation, yielding a relatively constant Stokes number and diffusion coefficient. The bouncing-limited growth closer to the star gives very low values of the Stokes number and turbulent diffusion coefficient. Overall, the approximately millimeter-sized pebbles obtained in our model agrees with the pebble sizes inferred for the disc around the young star HL Tau (Carrasco-González et al. 2019). |
Knowing the scale height of the mid-plane layer and assuming fragmentation-limited pebble growth yields a combined solution for the Stokes number and the turbulent diffusion coefficient,
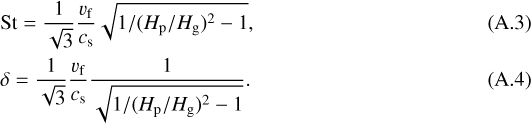
For the regions where growth is bouncing limited, we calculated the Stokes number of the mm-sized pebbles stuck at the bouncing barrier and set the turbulent diffusion coefficient that satisfies Eq. (A.2) through
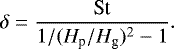 (A.5)
(A.5)
In Fig. A.1 we show the Stokes number and turbulent diffusion coefficient resulting from the pebble growth model. We considered two values for the ratio of the pebble scale height to the gas scale height, Hp ∕Hg = 0.1 and Hp ∕Hg = 0.2. Fragmentation sets the pebble size in the outer regions of the protoplanetary disc. Fragmentation-limited growth generally yields St ~ 0.01 and δ ~ 0.0001, independent of the temporal evolution of the gas. These values are very similar to the assumption of constant St = 0.01 and constant δ = 0.0001 of Johansen et al. (2019). The growth becomes bouncing limited closer to the star. The Stokes number of the millimeter-sized pebbles drops to very low values, St ~ 10−5−10−3. The accretion of such small pebbles by pebble accretion is still poorly understood because their short gas coupling timescales make them sensitive to recycling flows in the Hill sphere and to convection (Popovas et al. 2018, 2019; Rosenthal & Murray-Clay 2019). The planetary growth tracks that we obtain here within a few 10 AU should therefore be interpreted with some caution; we focus in our analysis here on the formation of cold gas giants farther from the star where the Stokes number is higher.
 |
Fig. A.2 Growth maps of protoplanets accreting pebbles and gas for four combinations of the relative pebble mid-plane layer thickness, Hp∕Hg, and the pebble flux relative to the gas, ξ. Cold gas giants form readily from seeds starting in the outer parts of the protoplanetary disc when the mid-plane layer is very thin (top left plot) or the metallicity is higher than the solar value (bottom left plot). However, changing any of these parameters by a factor two increases the pebble accretion timescales enough to quench the formation of gas giants (top right and bottom right plots). Protoplanets only grow to super-Earth masses in these cases. |
We show growth maps for protoplanets accreting pebbles and gas in Fig. A.2 for four combinations of the relative thickness of the pebble mid-plane layer Hp ∕Hg and the pebble flux relative to the gas flux ξ. For Hp∕Hg = 0.05, corresponding to the value inferred for HL Tau (Pinte et al. 2016), and ξ = 0.01 cold gas giants emerge from protoplanets that start to accrete pebbles between 30 and 35 AU (top left panel). Protoplanets forming in the 10–30 AU region migrate enough to become gas giants on warm and hot orbits instead. Doubling the scale-height ratio to Hp ∕Hg = 0.1 (top right panel) quenches the formation of giant planets, with protoplanets now only growing to super-Earth masses. At twice the metallicity (bottom left panel), the cold gas giants reemerge, growing even to super-Jupiter masses. Again doubling the relative scale height to Hp∕Hg = 0.2 reverts the situation to forming only super-Earths (bottom left panel). This transition from super-Earth formation to gas-giant formation at around solar metallicity is consistent with exoplanet surveys (Buchhave et al. 2012). Johansen et al. (2019) further demonstrated that the parameter space for the formation of cold gas giants becomes much smaller for initially smaller protoplanetary discs whose accretion rates drop faster. The formation of gas giants in cold orbits is hard, even for pebble accretion. The fact that the transition from super-Earths to gas giants occurs around solar metallicity can nevertheless be seen as a major agreement between theory and observations.
References
- Abod, C. P., Simon, J. B., Li, R., et al. 2019, ApJ, 883, 192 [Google Scholar]
- Ansdell, M., Williams, J. P., Manara, C. F., et al. 2017, AJ, 153, 240 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., & Johansen, A. 2016, A&A, 590, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., & Johansen, A. 2017, Astrophys. Space Sci. Lib., 445, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., Johansen, A., Lambrechts, M., & Morbidelli, A. 2015, A&A, 575, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Izidoro, A., Johansen, A., et al. 2019, A&A, 623, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bizzarro, M., Baker, J. A., Haack, H., & Lundgaard, K. L. 2005, ApJ, 632, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Durda, D. D., Nesvorný, D., et al. 2005, Icarus, 179, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R. 2008, A&A, 492, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brasser, R., & Morbidelli, A. 2013, Icarus, 225, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Buchhave, L. A., Bitsch, B., Johansen, A., et al. 2018, ApJ, 856, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Capobianco, C. C., Duncan, M., & Levison, H. F. 2011, Icarus, 211, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco-González, C., Sierra, A., Flock, M., et al. 2019, ApJ, 883, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Carrera, D., Gorti, U., Johansen, A., et al. 2017, ApJ, 839, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, G. A. L., & Nelson, R. P. 2014, MNRAS, 445, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, G. A. L., & Nelson, R. P. 2016, MNRAS, 460, 2779 [NASA ADS] [CrossRef] [Google Scholar]
- Cossou, C., Raymond, S. N., Hersant, F., et al. 2014, A&A, 569, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2006, A&A, 450, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., Weidenschilling, S. J., Lissauer, J. J., et al. 2014, Icarus, 241, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, M. B., Adams, F. C., Armitage, P., et al. 2014, Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 787 [Google Scholar]
- Dawson, R. I., & Murray-Clay, R. A. 2013, ApJ, 767, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Dra̧żkowska, J., & Alibert, Y. 2017, A&A, 608, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dra̧żkowska, J., & Dullemond, C. P. 2018, A&A, 614, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Natta, A., & Testi, L. 2006, ApJ, 645, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Birnstiel, T., Huang, J., et al. 2018, ApJ, 869, L46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flock, M., Ruge, J. P., Dzyurkevich, N., et al. 2015, A&A, 574, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortier, A., Alibert, Y., Carron, F., et al. 2013, A&A, 549, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gressel, O., Nelson, R. P., & Turner, N. J. 2012, MNRAS, 422, 1140 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 2005, Ann. Rev. Earth Planet. Sci., 33, 493 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Hartmann, L., Herczeg, G., & Calvet, N. 2016, ARA&A, 54, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Helled, R., Bodenheimer, P., Podolak, M., et al. 2014, Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 643 [Google Scholar]
- Ida, S., Guillot, T., & Morbidelli, A. 2008, ApJ, 686, 1292 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., Guillot, T., & Morbidelli, A. 2016, A&A, 591, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ida, S., Tanaka, H., Johansen, A., et al. 2018, ApJ, 864, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Izidoro, A., & Raymond, S. N. 2018, Handbook of Exoplanets (Berlin: Springer), 142 [Google Scholar]
- Izidoro, A., Bitsch, B., Raymond, S. N., et al. 2019, A&A, submitted [arXiv:1902.08772] [Google Scholar]
- Johansen, A., & Lambrechts, M. 2017, Ann. Rev. Earth Planet. Sci., 45, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Blum, J., Tanaka, H., et al. 2014, Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 547 [Google Scholar]
- Johansen, A., Mac Low, M.-M., Lacerda, P., & Bizzarro, M. 2015, Sci. Adv., 1, 1500109 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Ida, S., & Brasser, R. 2019, A&A, 622, A202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W., et al. 2010, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Kanagawa, K. D., Tanaka, H., & Szuszkiewicz, E. 2018, ApJ, 861, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Kleine, T., Touboul, M., Bourdon, B., et al. 2009, Geochim. Cosmochim. Acta, 73, 5150 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 2000, Icarus, 143, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., Morbidelli, A., Jacobson, S. A., et al. 2019, A&A, 627, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larsen, K. K., Schiller, M., & Bizzarro, M. 2016, Geochim. Cosmochim. Acta, 176, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, C. T., Klahr, H., & Birnstiel, T. 2019, ApJ, 874, 36 [CrossRef] [Google Scholar]
- Levison, H. F., Thommes, E., & Duncan, M. J. 2010, AJ, 139, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Kretke, K. A., & Duncan, M. J. 2015, Nature, 524, 322 [CrossRef] [Google Scholar]
- Liu, B., Ormel, C. W., & Johansen, A. 2019, A&A, 624, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Manara, C. F., Morbidelli, A., & Guillot, T. 2018, A&A, 618, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. S., D’Angelo, G., & Kley, W. 2006, ApJ, 652, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, ArXiv e-prints [arXiv:1109.2497] [Google Scholar]
- Morbidelli, A., Bottke, W. F., Nesvorný, D., et al. 2009, Icarus, 204, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, S., Bai, X.-N., & Okuzumi, S. 2019, ApJ, 872, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G. D., & Dominik, C. 2012, A&A, 539, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nayakshin, S. 2017, PASA, 34, e002 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Li, R., Youdin, A. N., et al. 2019, Nat. Astron., 3, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Ndugu, N., Bitsch, B., & Jurua, E. 2018, MNRAS, 474, 886 [Google Scholar]
- Ogihara, M., Morbidelli, A., & Guillot, T. 2015, A&A, 578, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W. 2017, Formation, Evolution, and Dynamics of Young Solar Systems (Berlin: Springer), 197 [Google Scholar]
- Petit, J.-M., Morbidelli, A., & Chambers, J. 2001, Icarus, 153, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Pinte, C., Dent, W. R. F., Ménard, F., et al. 2016, ApJ, 816, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Pirani, S., Johansen, A., Bitsch, B., et al. 2019, A&A, 623, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Popovas, A., Nordlund, Å., Ramsey, J. P., et al. 2018, MNRAS, 479, 5136 [NASA ADS] [CrossRef] [Google Scholar]
- Popovas, A., Nordlund, Å., & Ramsey, J. P. 2019, MNRAS, 482, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2001, AJ, 122, 2713 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2004, AJ, 128, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Riols, A., & Lesur, G. 2019, A&A, 625, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raymond, S. N., & Izidoro, A. 2017, Icarus, 297, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., O’Brien, D. P., Morbidelli, A., et al. 2009, Icarus, 203, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenthal, M. M., & Murray-Clay, R. A. 2019, ArXiv e-prints [arXiv:1908.06991] [Google Scholar]
- Rowan, D., Meschiari, S., Laughlin, G., et al. 2016, ApJ, 817, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Safronov, V. S. 1960, Ann. Astrophys., 23, 979 [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schäfer, U., Yang, C.-C., & Johansen, A. 2017, A&A, 597, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schoonenberg, D., & Ormel, C. W. 2017, A&A, 602, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shiraishi, M., & Ida, S. 2008, ApJ, 684, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. B., Armitage, P. J., Li, R., et al. 2016, ApJ, 822, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Singer, K. N., McKinnon, W. B., Gladman, B., et al. 2019, Science, 363, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, S. A., Weaver, H. A., Spencer, J. R., et al. 2019, Science, 364, aaw9771 [NASA ADS] [CrossRef] [Google Scholar]
- Stoll, M. H. R., & Kley, W. 2016, A&A, 594, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, H., & Ida, S. 1997, Icarus, 125, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., & Ida, S. 1999, Icarus, 139, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, Y. A., & Tsukamoto, Y. 2019, MNRAS, 484, 1574 [NASA ADS] [CrossRef] [Google Scholar]
- Thommes, E. W., Duncan, M. J., & Levison, H. F. 2003, Icarus, 161, 431 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
- Tychoniec, Ł., Tobin, J. J., Karska, A., et al. 2018, ApJS, 238, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Udry, S., & Santos, N. C. 2007, ARA&A, 45, 397 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel,N., Dong, R., di Francesco, J., et al. 2019, ApJ, 872, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Vigan, A., Bonavita, M., Biller, B., et al. 2017, A&A, 603, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahl, S. M., Hubbard, W. B., Militzer, B., et al. 2017, Geophys. Res. Lett., 44, 4649 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, W. R., & Hahn, J. M. 1995, ApJ, 440, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., & Fabrycky, D. C. 2015, ARA&A, 53, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 2011, Icarus, 214, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, C.-C., Mac Low, M.-M., & Menou, K. 2012, ApJ, 748, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, C.-C., Mac Low, M.-M., & Johansen, A. 2018, ApJ, 868, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S., Zhu, Z., Huang, J., et al. 2018, ApJ, 869, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, J.-L., & Lin, D. N. C. 2007, ApJ, 666, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Zsom, A., Ormel, C. W., Güttler, C., Blum, J., & Dullemond, C. P. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Accretion efficiency of a protoplanet accreting planetesimals of radius 50 km and for weak turbulent stirring (γ = 10−4, left plots) and very weak turbulent stirring (γ = 10−5, right plots) as a function of the distance from the star and the protoplanet mass. The three rows show the accretion efficiency for three different increasing (top to bottom) values of the mass accretion rate through the disc; the gas surface density in turn defines the equilibrium inclination of the planetesimals and the transition of the protoplanet from an accreting predator (exterior of the red line) to a non-accreting shepherd (interior of the red line). The parameter region of core formation in the solar system (the box made by 5 and 20 AU and by 1 and 10 ME) is marked with dashed lines. The accretion efficiency beyond 5 AU lies at a value of a few percent or lower for the case of weak turbulent stirring, while lowering the turbulent stirring to γ = 10−5 increases the efficiency by approximately a factor 3. The efficiency overall increases with decreasing gas accretion through the disc because more slowly migrating planets accrete a higher fraction of the planetesimals that they migrate through (even though the planetesimal inclinations increase slightly as the gas drag is reduced). |
| In the text | |
 |
Fig. 2 Growth maps for protoplanet growth by planetesimal accretion, with gas accretion commencing after 10 ME is reached. The maps show the final mass (i.e. the mass reached when the disc has dissipated after 3 Myr) as continuous colours and the final positions as white contour lines as a function of the starting position of the protoplanet and the starting time. We additionally show the size of the protoplanetary disc (yellow line) and the Toomre Q of the gas (red contour lines). The panels show the results for four values of the initial mass accretion rate through the disc and the mass accretion rate after 3 Myr. The instantaneous stellar mass accretion rate is shown on the right axis. Each panel is also labelled with the total mass of the planetesimals in the models; we assume here that 1% of the initial gas surface density profile is converted into planetesimals at t = 0. The nominal model (upper left) achieves protoplanet growth only up to 0.1 ME, approximately the mass of Mars. The three other models, where planetesimals form at the gravitationally unstable phase of protoplanetary disc evolution, successfully form hot and warm gas giants interior of 2 AU, but are not able to form any cold gasgiants in the 5–10 AU region (see inset in the upper right panel). |
| In the text | |
 |
Fig. 3 Growth tracks of protoplanets accreting planetesimals of two different radii (blue and red lines), with reduced migration (yellow lines) and starting with a higher protoplanet mass (blue dash-dotted lines). The growth tracks are started at either 5, 10, 15, or 20 AU. We used here the massive planetesimal population model that contains 965 ME of planetesimals formed at t = 0 and assumed that the protoplanets start to grow immediately thereafter. Growth tracks starting at 5 AU generally become warm gas giants, ending in final orbits around 1 AU. Protoplanets starting farther out experience only moderate growth due to the low planetesimal accretion efficiencies there. Lowering the migration rate has a net positive effect for the growth track starting at 5 AU, but the more distant protoplanets experience a decreased growth rate when they migrate more slowly because the flux of planetesimals past migrating the protoplanet is reduced. The more massive protoplanets experience rapid migration towards the regions of high accretion efficiency close to the star, but the adoption of initially more massive protoplanets does not help in forming cold gas giants. |
| In the text | |
 |
Fig. 4 Finalplanetary mass as a function of the final planetary orbit for protoplanets starting to accrete at t = 0 in the massive planetesimal population model with two different planetesimal radii (50 and 5 km) and three values of the turbulent stirring coefficient (10−4, 10−5, and 10−6). The solid blue line (γ = 10−4/Rpla = 50 km) corresponds to a cut at t0 = 0 of the upper right panel of Fig. 2. The planetesimal inclinations are here set as the maximum of the inclinations given by turbulent stirring and by mutual planetesimal scattering. Planetesimals with a nominal radius of 50 km can only form Jupiter-mass planets interior of 3 AU, even when the turbulent stirring is very weak with γ = 10−5 or extremelyweak with γ = 10−6, because of inclination stirring by mutual planetesimal scattering. Lowering the planetesimal radius to 5 km allows the formation of Jupiter analogues when the turbulent stirring coefficient is γ = 10−5 or γ = 10−6. |
| In the text | |
 |
Fig. 5 Growth maps for core growth by accretion of 50 km planetesimals that form at either t = 0.1 Myr (top panel) or t = 0.5 Myr (bottom panel). The planetesimal population is given 1% of the gas surface density at the evolution stage of the protoplanetary disc at the chosen formation time. The protoplanets are nevertheless still started at the full range of starting times, even before the planetesimals form. Delaying the formation of planetesimals to t = 0.1 Myr reduces the parameter space for forming hot and warm gas giants significantly, while the delay to 0.5 Myr entirely removes the capability of the protoplanetary disc to form any giant planets. |
| In the text | |
 |
Fig. A.1 Stokes number (solid lines) and turbulent diffusion coefficient (dotted lines) for pebble growth limited by fragmentation and bouncing, shown for three different stages of protoplanetary disc evolution. The ratio of the scale height of the pebbles to the scale height of the gas is Hp ∕Hg = 0.1 in the top plot and Hp∕Hg = 0.2 in the bottom plot. The outer regions of the protoplanetary disc have pebble sizes set by fragmentation, yielding a relatively constant Stokes number and diffusion coefficient. The bouncing-limited growth closer to the star gives very low values of the Stokes number and turbulent diffusion coefficient. Overall, the approximately millimeter-sized pebbles obtained in our model agrees with the pebble sizes inferred for the disc around the young star HL Tau (Carrasco-González et al. 2019). |
| In the text | |
 |
Fig. A.2 Growth maps of protoplanets accreting pebbles and gas for four combinations of the relative pebble mid-plane layer thickness, Hp∕Hg, and the pebble flux relative to the gas, ξ. Cold gas giants form readily from seeds starting in the outer parts of the protoplanetary disc when the mid-plane layer is very thin (top left plot) or the metallicity is higher than the solar value (bottom left plot). However, changing any of these parameters by a factor two increases the pebble accretion timescales enough to quench the formation of gas giants (top right and bottom right plots). Protoplanets only grow to super-Earth masses in these cases. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


