| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 22 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201935622 | |
| Published online | 16 October 2019 | |
Consistent radial velocities of classical Cepheids from the cross-correlation technique★,★★
1
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris,
5 Place Jules Janssen,
92195
Meudon,
France
e-mail: Simon.Borgniet@obspm.fr
2
Université Côte d’Azur, OCA, CNRS, Lagrange, Parc Valrose,
Bât. Fizeau,
06108
Nice Cedex 02,
France
3
European Southern Observatory,
Alonso de Córdova 3107,
Casilla
19001,
Santiago,
Chile
4
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748
Garching,
Germany
5
Embry-Riddle Aeronautical University, Physical Sciences Department,
600 S Clyde Morris Boulevard,
Daytona Beach,
FL
32114,
USA
6
Departamento de Astronomía, Universidad de Concepción,
Casilla 160-C,
Concepción,
Chile
7
Millenium Institute of Astrophysics,
Av. Vicuna Mackenna 4860,
Santiago,
Chile
8
Nicolaus Copernicus Astronomical Centre, Polish Academy of Sciences,
Bartycka 18,
00-716
Warszawa,
Poland
Received:
4
April
2019
Accepted:
5
August
2019
Context. Accurate radial velocities (vrad) of Cepheids are mandatory within the context of Cepheid distance measurements using the Baade-Wesselink technique. The most common vrad derivation method consists in cross-correlating the observed stellar spectra with a binary template and measuring a velocity on the resulting mean profile. Nevertheless, for Cepheids and other pulsating stars, the spectral lines selected within the template as well as the way of fitting the cross-correlation function (CCF) have a direct and significant impact on the measured vrad.
Aims. Our first aim is to detail the steps to compute consistent CCFs and vrad of Cepheids. Next, this study aims at characterising the impact of Cepheid spectral properties and vrad computation methods on the resulting line profiles and vrad time series.
Methods. We collected more than 3900 high-resolution spectra from seven different spectrographs of 64 Classical Milky Way (MW) Cepheids. These spectra were normalised and standardised using a single custom-made process on pre-defined wavelength ranges. We built six tailored correlation templates selecting unblended spectral lines of different depths based on a synthetic Cepheid spectrum, on three different wavelength ranges from 3900 to 8000 Å. Each observed spectrum was cross-correlated with these templates to build the corresponding CCFs, adopted as the proxy for the spectrum mean line profile. We derived a set of line profile observables as well as three different vrad measurements from each CCF and two custom proxies for the CCF quality and amount of signal.
Results. This study presents a large catalogue of consistent Cepheid CCFs and vrad time series. It confirms that each step of the process has a significant impact on the deduced vrad: the wavelength, the template line depth and width, and the vrad computation method. The way towards more robust Cepheid vrad time series seems to go through steps that minimise the asymmetry of the line profile and its impact on the vrad. Centroid or first-moment vrad, that exhibit slightly smaller amplitudes but significantly smaller scatter than Gaussian or biGaussian vrad, should therefore be favoured. Stronger or deeper spectral lines also tend to be less asymmetric and lead to more robust vrad than weaker lines.
Key words: techniques: spectroscopic / techniques: radial velocities / stars: variables: Cepheids / stars: atmospheres
Catalog of radial velocity (and other observables) time series, the cross-correlation functions and our tailored correlation templates are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/631/A37
Partly based on observations made with ESO telescopes at Paranal and La Silla observatories under program IDs: 072.D-0419, 073.D-0136, 091.D-0469(A), 097.D60150(A) and 190.D-0237 for HARPS data; 098.D-0379(A), 0100.D-0397(A) and 0101.D-0551(A) for UVES data; and 073.D-0072(A), 074.D-0008(B), 075.D-0676(A), 084.B-0029(A) and 087.D-0603(A) for FEROS data. Partly based on observations made with the SOPHIE spectrograph at the Observatoire de Haute-Provence (CNRS, France), under program IDs PNPS.FRAN (12B), PNPS.GALL (13A, 14A, 15A), PNPS.KERV (13B, 16B, 17B), and PNPS.BORG (18A). Partly based on observations made with the CORALIE spectrograph on the Euler telescope (Swiss Observatory) at La Silla, Chile, under program numbers 1 and 756. Partly based on observations collected at the Telescope Nazionale Galileo in the framework of the OPTICON proposal 2015B/15 for HARPS-North data.
© S. Borgniet et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Cepheids are essential extra-galactic distance standards because their period of pulsation (P) is tightly correlated with their absolute luminosity, a (mostly empirical) relationship known for more than a century as the Leavitt law, or the Cepheid period-luminosity (P-L) relationship (Leavitt & Pickering 1912). Cepheids have therefore greatly contributed to precision cosmology, and especially to the measurement of the Hubble constant H0 (Freedman & Madore 2010; Riess et al. 2011, 2016; Riess 2018). Their high-amplitude pulsations, which generally follow a relatively clear pattern, also make them targets of choice for spectroscopic studies looking for a better understanding of the stellar structure.
Radial velocities (vrad) of Cepheids have therefore long been of great interest. Firstly, they allow detection and characterisation of Cepheid stellar companions (i.e. single-line spectroscopic binaries or SB1s), which have revealed themselves to be widespread (see e.g. Evans et al. 2015; Anderson et al. 2015, 2016; Gallenne et al. 2013, 2015, 2019, 2018). The most common application of Cepheid vrad is their use forthe measurement of the Cepheid distances through the parallax-of-pulsation method, also known as the Baade–Wesselink (BW) technique (Lindemann 1918; Baade 1926; Wesselink 1946). The BW method allows direct derivation of the distance in a quasi-geometrical way through the ratio of the Cepheid linear radius variation (ΔR, measured spectroscopically) over the angular diameter variation Δθ (see recent examples in e.g. Kervella et al. 2004; Gallenne et al. 2012, 2017; Mérand et al. 2015; Nardetto 2018).
The linear radius variation ΔR is assumed to be proportional to the vrad curve integrated over the pulsation phase. To understand how, it is first necessary to remind ourselves exactly what the radial velocity represents (see also Lindegren & Dravins 2003, on the definition) in the context of a pulsating star and especially a classical Cepheid. Cepheids are radial pulsators with a given photospheric pulsation velocity (vpuls) at a given phase of the pulsation period. The pulsation velocity vpuls is a true physical quantity, whereas we measure the resulting Doppler shift of the received stellar light integrated over the stellar disk and projected on our line of sight. This Doppler shift is measured either on a single spectral line or on the cross-correlation function (CCF) of the full spectrum with a correlation template. Each region of the stellar disk is more or less Doppler-shifted and contributes more or less to the total spectrum depending on its position on the disk and on the limb-darkening. As a consequence, the Doppler shift of the spectrum integrated over the stellar disk (and the corresponding vrad) is mitigated by a certain amount compared to the physical vpuls. This amount is called the projection factor (or p-factor) and it rounds up all the various sources of physical and spectral variability (Burki et al. 1982; Nardetto et al. 2007). It is also the key parameter of classical BW methods as it is fully degenerate with the distance (Mérand et al. 2015).
Another consequence of the radial projection effect is that each line (and therefore the global line profile) of the total Cepheid spectrum is intrinsically asymmetric (Sabbey et al. 1995; Nardetto et al. 2006). This has a strong and variable effect on the measurement of the Doppler shift of the line, depending on the measurement method. Furthermore, it is now common knowledge that Cepheid spectral lines are shifted differently depending on their formation region or depth, that is to say that an atmospheric velocity gradient is present. Thus, the way a Cepheid vrad measurement is affected depends on which spectral lines are used (Nardetto et al. 2007; Anderson 2016). In short, to each vrad measurement corresponds a different p-factor (and thus potentially a different distance estimation). Finally, at a deeper precision level, additional phenomena might introduce uncertainty on the vrad and p-factors: shockwaves (Nardetto 2018), convective blueshift (Nardetto et al. 2008), or cycle-to-cycle variability (Anderson 2016).
Cepheid studies do not always clarify how the vrad were computed. Furthermore and most often, the template used to cross-correlate the spectra is not described or provided, except in very few cases (Brahm et al. 2017). However, given the context developed above, authors should always make clear what spectral lines were used to derive the vrad and how the vrad were computed, as stressed by Anderson (2018).
Here, we present a consistent spectroscopic survey of 64 classical Milky Way (MW) Cepheids. For each target, this includes for each target the CCFs, various line-profile observables, and several vrad time series built from different correlation templates and computation methods. In Sect. 2, we describe our Cepheid sample, the observations performed and the data used in this study. We introduce the principles of our framework and the main outputs in Sect. 3. We then apply our method to derive a consistent set of CCFs, observables, and vrad for our full Cepheid sample. We discuss and characterise the results of the survey in Sect. 4. We finally conclude on the perspectives and possible applications of this survey in Sect. 5.
 |
Fig. 1 Pulsation period (P) distribution of our Cepheid sample. |
2 Surveydescription
2.1 Sample
Our sample is made up of 64 Classical Galactic Cepheids with pulsation periods in the range ~ 2 to ~ 68 days. We provide the full details of our sample in Table A.1. We selected our targets based on the number of available high-resolution spectra (and the number of corresponding distinct observation epochs) that we could recover either from new observations or from spectroscopic archives (see below). We selected only targets with a good enough sampling and coverage (i.e. ≳20%) of the pulsation phase. We show the pulsation period distribution of our sample in Fig. 1. Most of our targets have a period of between a few and 20 days, but we also include a small number of Cepheids with periods up to several tens of days in order to scan the whole Cepheid period range as well as possible.
2.2 Data
We gathered a total of 3919 high-resolution (40 000 ≲ R = λ∕ dλ ≲ 115 000) spectra acquired with seven different echelle spectrographs. These instruments are located in both hemispheres and allow us to cover a wide wavelength range (from the near-ultraviolet (NUV) to the near-infrared (NIR)), depending on their respective characteristics (Table 1).
Spectrographs implemented in this study.
2.2.1 New observations
Here, we detail our new, previously unpublished observations. Our observational strategy was adapted to maximise the pulsation phase coverage for each target.
SOPHIE
From June 2013 to August 2018, we observed 30 northern Cepheids with the fibre-fed SOPHIE spectrograph (Bouchy & Sophie Team 2006)mounted on the 1.93 m telescope at Observatoire de Haute-Provence (France). We acquired 296 spectra in High-Resolution mode (R ~ 75 000). In addition, we gathered 74 spectra in High-Efficiency mode (R ~ 40 000) from the public SOPHIE archive1. Exposure times of a few minutes allowed for a median signal-to-noise ratio (S/N) at 550 nm of 94.
UVES
From September 2016 to August 2018, we used the UVES spectrograph (Dekker et al. 2000) mounted on the UT2 telescope at the Very Large Telescope (Table 1) to carry out an analogous survey of 24 southern Cepheids. We used both UVES blue and red arms (centred at ~437 and ~760 nm, respectively) to expand our wavelength coverage. Given the fast acquisition rate, we acquired several consecutive (up to a dozen) spectra at each epoch and with each arm. We collected overall 981 and 1350 spectra with the blue and red arms of UVES, with a median S/N of 135 and 156, respectively.
HERMES
From July 2014 to August 2018, we acquired 110 additional spectra with the HERMES spectrograph (R ~ 85 000, Raskin et al. 2011) on the Flemish 1.2 m at Roque de los Muchachos (La Palma) Observatory. This allowed us to complete our phase coverage of three targets (V1334 Cyg, FF Aql and W Sgr, see Gallenne et al. 2019, 2018).
2.2.2 Archive data
For other spectrographs, we collected spectra that we have already used in previous studies or that we retrieved from the ESO public archive2.
HARPS
We collected more than 400 archive spectra obtained with the High-Accuracy Radial-velocity Planet Searcher spectrograph mounted on the 3.6 m telescope at La Silla observatory (HARPS, Pepe et al. 2002). The HARPS spectrograph has the highest spectral resolution (R ~ 115 000) and the best vrad precision among all spectrographs currently implemented in our framework (Table 1). This highlights the importance of these data. We already presented most of these spectra in previous studies (Nardetto et al. 2006, 2007, 2009). We retrieved the remaining spectra from the ESO database.
CORALIE
We also gathered almost 500 spectra that we acquired with the CORALIE spectrograph (Queloz et al. 2001a) at La Silla Observatory from 2013 to 2017. We already used some of these spectra in previous studies (see e.g. Gallenne et al. 2019).
HARPS-North
We used 103 high-resolution, high-S/N (≳250) HARPS-North spectra of δ Cep. The HARPS-North spectrograph is mounted on the TNG telescope at La Palma observatory (see Cosentino et al. 2012, and Table 1). We already presented these spectra in a previous study that highlighted their quality (Nardetto et al. 2017).
FEROS
We finally retrieved almost one hundred FEROS spectra from the ESO public database. The FEROS instrument is a fibre-fed spectrograph mounted on the 2.2 m MPG telescope at La Silla Observatory with a spectral resolution of R ~ 48 000 (Kaufer & Pasquini 1998). The FEROS data allowed us mostly to add three medium- to long-period Cepheids to our sample (UZ Cet, AV Sgr and V340 Ara, see Table A.1).
3 Method
3.1 Principle: CCF as the spectrum proxy
Because of the physical characteristics of Cepheids, their location on the Hertzprung–Russell diagram, and their moderate rotation rates, Cepheid spectra typically exhibit hundreds or even thousands of narrow absorption lines. It is subsequently possible to measure the Doppler shift (and hence, the vrad) for specific single lines of different depths (see e.g. Nardetto et al. 2006). However, single-line vrad may differ from one line to another due to velocity gradients or spectral peculiarities. The single-line vrad precision also depends on the spectrum S/N, which might limit its use to high- or very high-S/N spectra (typically with S/N above 75 to 100; see e.g. Nardetto et al. 2006; Meunier et al. 2017).
An efficient approach to derive accurate vrad that are representative of the full spectrum is to use a proxy for the spectrum instead of the spectrum itself. In other words, it consists in building a single global line profile that combines the useful information from all the spectral lines (Doppler shift, depth, width and asymmetry). This description corresponds well to the CCF. Building the CCF consists in cross-correlating the spectrum with a pre-defined template that is successively Doppler shifted (Baranne et al. 1979; Queloz 1995). This template can be a synthetic spectrum (e.g. for the Gaia Radial Velocity Spectrograph, see Katz et al. 2019), a reference built from all spectra (Galland et al. 2005), or, more generally, an adapted binary template (also named a binary mask, see e.g. Queloz 1995; Pepe et al. 2002). The binary designation refers to the fact that the template is equal to one (or > 0) at the wavelengths of the selected spectral lines and is equal to zero everywhere else (spectrum continuum or rejected lines). Hence, the CCF includes the contribution of all the spectral lines included within the correlation template. Therefore, it provides a much higher S/N (and a better vrad accuracy) compared to a single line (Pepe et al. 2002; Anderson 2018). Alternative techniques or mathematical functions such as the spectral broadening function (Rucinski 1992, 1999), the auto-correlation function (Borra & Deschatelets 2017), or the least-square deconvolution method (Britavskiy et al. 2016), have been proposed to characterise Cepheid line profiles. Still, the CCF remains both the easiest and most widely used method to study line profiles of Cepheids and other stellar pulsators (see e.g. Nardetto et al. 2009; Anderson 2018).
Specifically, the CCF built from a binary correlation template allows us to select which spectral lines to take into account in the global line profile and thus in the vrad computation. This is a key factor to consider when trying to build homogeneous Cepheid vrad time series. Given its relative simplicity, its widespread use, and its high interest in terms of line selection and template customisation, we decided to use CCF built from tailored correlation templates within our framework.
3.2 Standardising the spectra
The main inputs of our framework are high-resolution spectra, pre-processed using the dedicated instrument pipelines. These are in a one-dimensional (1D) format (i.e. wavelength versus flux; typically the s1d format produced by ESO spectrograph data reduction systems or DRS), with the spectral orders already re-connected and re-sampled in wavelength. We chose the 1D format because it is a default product of the DRS of all the instruments included in this study, contrary to the 2D (e2ds) format which is not produced for UVES and FEROS to our knowledge. Furthermore, using the spectrum 1D format instead of the 2D format avoids the need to correct for the instrumental response by spectral order (i.e. the blaze function), which would otherwise oblige us to introduce additional processing steps that might be less consistent from instrument to instrument. Given that classical Cepheid spectra typically exhibit thousands of narrow absorption lines, the order-to-order re-connection does not have any significant visual impact on the re-connected spectrum (Fig. 2, top). The wavelength re-sampling typically leads to slightly smaller wavelength steps than the original CCD sampling (typically 0.01–0.02 Å), meaning that the resulting 1D spectra are slightly over-sampled3, which should not introduce any significant uncertainties. With the same view of achieving the greatest consistency of our CCF computation process, we consider that standardising our input spectra is a necessary step given the variety of the included spectrographs. Firstly, we define three wavelength ranges (Δλ) on which the input spectra are cross-correlated. These ranges are fixed and defined to cover as many of the wavelength domains of the implemented spectrographs as possible (Table 1):
- 1.
A green range with Δλ = [4500–6800] Å. This visible range corresponds to a wavelength domain covered by most of the implemented spectrographs. It also roughly corresponds to the wavelengths where spectra of classical Cepheids typically reach the highest flux density.
- 2.
A blue range with Δλ = [3900–4980] Å. We defined this range to specifically cover the wavelength domain of the UVES blue arm.
- 3.
A red range with Δλ = [5700–8800] Å. This range is covered by the UVES red arm, HERMES and FEROS.
Secondly, we extract the continuum from each spectrum and normalise the spectrum following the same process for all spectrographs. Briefly, we build a continuum function or envelope by interpolating between a certain number of points that depends both on the resolution R of the spectrograph and on the absorption line density along the spectrum (Fig. 2). Each interpolation point is carefully computed to be representative of the spectrum’s continuum on the corresponding wavelength slice, by considering the flux value at 99% of the highest intensity over the considered slice while excluding possible cosmics. A similar normalisation process was used and validated by Meunier et al. (2017). Broad deep lines (Hydrogen Balmer and Paschen series, as well as Calcium H and K lines) are excluded from the continuum function building. We simultaneously correct for the remaining cosmics, if any. The spectrum is then normalised by dividing it by this continuum function or envelope. We then correct the spectrum from the barycentric Earth radial velocity (or BERV), if necessary. Finally, we select the spectra to cross-correlate based on their S/N (taken at 5500 Å in the case of the green wavelength range). We empirically put our S/N threshold to 30 to ensure a reasonably good CCF computation.
 |
Fig. 2 Typical input observed spectrum. Top: input HARPS β Dor 1D spectrum (black solid line) on the green wavelength range. The continuum interpolation is displayed in red. Broad deep lines that are excluded from the continuum interpolation are highlighted in grey, and wavelength ranges with strong tellurics arehighlighted in orange. Bottom: normalised spectrum. The red solid line is normalised to unity. On both plots, the insert is a zoom on a 100-Å slice of the spectrum (in blue). |
3.3 Building tailored correlation templates
This step forms the focal point of our approach. Indeed, we use our custom correlation templates to cross-correlate all observed spectra on a given wavelength range regardless of the target and of the spectrograph. We illustrate our template building process in Fig. 3 and we display the main properties of our templates in Table 2. To build our templates, we first generated a reference Cepheid synthetic spectrum over our three wavelength ranges. To do so, we used the radiative transfer PHOENIX code (Hauschildt & Baron 1999, 2010). PHOENIX is a non-local thermodynamic equilibrium (NLTE) atmosphere model code that uses spherically symmetric radiative transfer in the case of giant stars such as Cepheids (Hauschildt et al. 1999). In terms of stellar physics, we adopted solar metallicities, which are suitable for classical MW Cepheids with typical spectral types in the F8–G5 range. We adopted a model with Teff = 5250 K and log g =1. This corresponds to a somewhat colder Cepheid with a slightly smaller log g than the average of our sample (i.e. it roughly corresponds to the average Teff and log g of a P ~ 15- to ~20-day Cepheid; see e.g. Kovtyukh et al. 2005). We chose these Teff and log g values as a compromise between obtaining a reference synthetic Cepheid spectrum with as many unblended spectral lines of different depths as possible and staying close to the average properties of our sample. As a consequence, our adoptedsynthetic spectrum corresponds to a slightly later spectral type than the G2 templates classically used in the literature. We generated our synthetic reference spectrum over our three wavelength ranges with R = 115 000, corresponding to our spectrograph with the highest resolution (HARPS, see Table 1).
From our reference spectrum, we selected the spectral lines to be included within our correlation templates following an approach similar to Hindsley & Bell (1986). First, we considered only lines stronger than 0.1 in relative depth (i.e. with a minimum normalised flux below 0.9), as an arbitrary limit between meaningful lines and the continuum of the spectrum. We then selected the lines to include based on their relative depth, in order to probe lines forming at different optical depths. We considered three line depth ranges (i.e. shallow, intermediate-depth, and deep lines) and we built three corresponding templates on the green wavelength range (weak, medium and deep templates). We selected only unblended lines separated from adjacent lines by more than 0.4 Å for deep and intermediate lines, and by more than 0.7 Å for shallow lines. Finally, we excluded any lines within wavelength ranges around broad non-metalliclines such as the hydrogen Balmer and Paschen series (Anderson 2018), as well as the calcium II H and K lines and the calcium II NIR triplet. We also excluded lines within wavelength ranges corresponding to strong telluric lines, based on inputs from the ESO MOLECFIT tool (Smette et al. 2015) and on high-resolution spectra of Achernar (i.e. a fast-rotating Be dwarf star with very few and extremely broadened stellar lines). For each of these templates, the selected lines were uniformly put at a height of one within the template (i.e. no weighting according to the line depth; see Fig. 3, middle). Thus, we roughly approximate the stellar atmosphere as a three-layer model, each layer being probed by a template. Having lines of the same weight within each template means that the average line depth of the template is roughly equally representative of all the selected lines (Table 2). We tailored these three depth-specific templates (weak, medium, and deep) to have a number of lines of the same order of magnitude, average wavelengths as close as possible and average line depths as different as possible to investigate the specific impact of the template average line depth on the vrad (Sect. 4.6).
Next, we built a fourth template (ALL) including all the lines selected within the three previous templates on the green range. This time we weighted the template lines proportionally to their relative depth within the PHOENIX spectrum (Fig. 3, bottom). Such weighting is typical of the default templates used within the DRS (Pepe et al. 2002). We built this ALL template: (i) to have reference vrad time series based on a template with a higher number of lines (Sect. 4.1); (ii) for comparison with default weighted DRS templates (Sect. 4.5); and (iii) to have a reference for the comparison of our depth-dependent templates (Sect. 4.6). Weighting the lines means that stronger lines have more weight (more impact) than weaker lines within the CCF and vrad computation. Thus, the average line depth of the ALL template is 0.63 (weighted lines) instead of 0.58 without line weighting, while the other template characteristics (mean wavelength, mean line width) do not significantly change. This also allows us to have a fourth template that is more distinct in terms of average depth from the medium template (average depth ~ 0.56, Table 2).
Because of our strict spectral line selection, each of our three depth-specific templates includes ~ 150 to ~ 220 lines only. In contrast, the default DRS templates with a spectral type closest to classical Cepheids (i.e. typically G2-type templates adapted to main sequence dwarfs) include thousands of often blended lines (Anderson 2016). As an example, the HARPS DRS default G2 template considered over our green range includes more than 1700 lines (see Table 2 and Fig. 3, bottom). We also note that such DRS templates have very narrow lines (typical width σℓ < 0.1 Å). In contrast, we fixed our template line width by considering the selected line width at 90% of the continuum within our PHOENIX synthetic Cepheid spectrum, that is, average line widths larger by a factor of between four and six compared to the G2 template. We discuss the rationale for this choice and its impact in more detail in Sect. 4.5. We finally note that our correlation templates are sampled with a fine wavelength step of ~ 0.02 Å, meaning that our template lines typically cover 15 to 25 wavelength pixels.
The distribution of selected lines within our templates generally follows the spectral line density of our reference spectrum (i.e. the line distribution as a function of wavelength), with dips corresponding to telluric or broad line exclusion ranges (Fig. 4). The slightly redder average wavelength of our weak template is induced by the increased line density (i.e. a higher line blending) in the bluer part of our reference spectrum. In addition, we built two other templates including intermediate-depth lines but covering this time our blue and red wavelength ranges. The number of included lines is relatively small, due to either the reduced wavelength span and strong line blending (in the case of the blue range) or the importance of the telluric ranges (in the case of the red range). However, our three medium templates have nearly similar average depths and average wavelengths separated by more than 1000 Å from each other (Table 2), to investigate the potential impact of the template wavelength range on the vrad (Sect. 4.4).
 |
Fig. 3 Building tailored correlation templates. Top: reference synthetic PHOENIX spectrum (solid black line), with assumed limit on the continuum (solid red line). Line depth ranges corresponding to the weak, medium and deep templates are highlighted (in blue, green, and purple shades, respectively). Comparison with three observed Cepheid spectra, shifted in flux for clarity: δ Cep with HARPS-North (ϕ = 0.37, cyan line), β Dor with HARPS (ϕ = 0.33, yellow line), and ℓ Car with HARPS (ϕ = 0.38, orange line). We point out that these spectra have not been Doppler-shifted from the absolute velocities of the stars. Middle: corresponding weak, medium, and deep correlation templates (blue, green, and purple shades, respectively). Bottom: weighted ALL template (red shade). The default G2 template from the HARPS DRS (black shade) is added for comparison (see text). |
Main characteristics of our correlation templates.
 |
Fig. 4 Correlation template transparency T (see Table 2) vs. wavelength for our green λ range. The line density of our reference spectrum is plotted in black and the transparency of our four correlation templates in red, blue,green, and purple (ALL, weak, medium, and deep templates, respectively). The template transparency is equivalent to the selected line density within the template (see text). |
3.4 Characterising the CCF
We cross-correlate each of our reduced spectra with our tailored templates, depending on the spectrograph and the covered wavelength range. We aim at extracting as much information as possible from the CCF, not only the selected Doppler shift or radial velocity. To do so, we use and derive different estimators of the shape of the CCF profile, that we discuss here. We specifically discuss the vrad measurements later in Sect. 3.5. We give more technical details and formulae for the observable derivation in Appendix B. Our various observables are illustrated in Fig. 5 and summarised in Table 3.
 |
Fig. 5 Cross-correlation function, main line profile observables, and vrad (based on a δ Cep HARPS-North spectrum cross-correlated with our medium template on the green range, see text). From left to right and top to bottom: CCF, normalised CCF, normalised CCF Gaussian fit, normalised CCF biGaussian fit. On all plots the CCF is displayed as a black solid line, the CCF continuum as a solid straight red line and the vrad at the CCF minimum as a vertical dotted black line. On the top left plot, the CCF core vrad range (i.e. Δcore) is highlighted in green. On the top right plot, the area covered by the CCF core and used for the EW and RVcc-c integration is highlighted in green. The letters CT and D designate the contrast and depth of the CCF core, respectively (as defined in the text). On the bottom right plot, the FWHMs corresponding to the blue and red parts of our biGaussian model are displayed as a blue and red arrow, respectively. The inserts are zooms in vrad on the CCF core. |
CCF observables considered in this study.
CCF core, wings, and continuum
Cepheid spectra may exhibit strongly asymmetric lines induced by the line-of-sight projection of the pulsation velocity. Given that we exclude most blended lines from our correlation templates (i.e. lines that usually smooth the CCF if taken into account), the typical shape of our CCFs may deviate significantly from that of a Gaussian (Fig. 5, and see e.g. Queloz 1995). First, our CCFs typically exhibit two significant bumps or shoulders on both sides of the CCF core; second, the CCF shape outside of the CCF core is not completely flat. These effects are more noticeable for our CCFs than for CCFs computed with typical DRS templates because we use templates with a relatively small number of lines of variable depth, and because we reject most blended lines. Most often, studies that present CCF profiles show only the CCF core and not the CCF wings. We consider it necessary to take into account both the core and the wings of theCCF for a proper CCF characterisation within our study. We compute our CCFs on an extended vrad grid ranging from −200 to 200 km s−1 in order to adequately sample the full CCF profile. The respective height of the two CCF shoulders depends on the CCF asymmetry and the direction of the Doppler shift, that is the CCF left shoulder is higher (lower) when the spectrum is blueshifted (redshifted; Fig. 5). We define the CCF core as the area centred on the CCF main peak and below the CCF lower shoulder for practicality. The CCF wings include the whole vrad ranges outside of the CCF shoulders, and the CCF pseudo-continuum (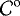 ) is defined as the average value of the CCF wings. The CCF can be normalised by dividing it by the value of
) is defined as the average value of the CCF wings. The CCF can be normalised by dividing it by the value of 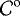 , as done for theinput spectra.
, as done for theinput spectra.
Modelling the CCF
We derive some of our line profile observables through fitting the CCF core by parameterised models. We use here both a classical four-parameter Gaussian model (offset, depth, width, and Doppler shift) and a biGaussian model (offset, depth, asymmetry, and Doppler shift) where we distinguish between the blue and red parts of the CCF core (see more details in Appendix B).
CCF depth and width
We define the CCF core depth (D) as the difference between the maximum and the minimum of the CCF core, which we either measure directly on the CCF or through the Gaussian or biGaussian models. We distinguish this CCF depth from another separate observable that we name here the CCF contrast (CT) and that we define as the difference between our CCF continuum and the minimum of the CCF core (Fig. 5, top right). Our main observable for the CCF width is the full width at half maximum (FWHM) of the CCF core Gaussian model (Fig. 5, bottom left). Finally, we compute the equivalent width (EW) of the CCF core in a similar way as what is commonly done for single spectral lines (see e.g. Kovtyukh et al. 2005). The EW is a mixed proxy of the CCF core depth and width. The variability of the depth and width of the CCF profile is directly related to the various quantities that have a broadening effect on the spectral lines (i.e. the pulsation, but also and mostly the effective temperature Teff, the turbulence, and the Cepheid rotation rate). For example, the FWHM has been used as an estimator of the micro-turbulence velocity (Borra & Deschatelets 2017).
CCF asymmetry
We derive the bisector of the CCF core as a classical way to estimate its asymmetry. Our proxy is the bisector inverse span (BIS, Queloz et al. 2001b), that is, the vrad difference between the top and the bottom of the CCF core bisector (Appendix B). According to authors (Anderson 2016, 2019; Britavskiy et al. 2018), the BIS is a good estimator of the line profile asymmetry of stellar pulsators such as Cepheids. Another asymmetry proxy is the line asymmetry estimator defined by Nardetto et al. (2006) based on the biGaussian model of single spectral lines. By analogy, we derive a similar asymmetry proxy from our CCF biGaussian model through the comparison of the width of the blue and red parts of the CCF core (Fig. 5, bottom right, and see Appendix B).
CCF quality
Depending on the number and the strength of the lines selected within, the correlation template has a direct impact on the global shapeand depth of the resulting CCF. In particular, selecting lines of reduced strength (i.e. shallower lines) reduces the amount of signal contained by the CCF core with respect to the CCF wings. Thus, the reliability and accuracy of the derived vrad and line profile observables will be impacted. Here, we find it necessary to assess the quality of our derived CCF in order to figure how much confidence we can put on our observables. We define the two following criteria (see formulae in Appendix B):
- 1.
A CCF quality factor Q, defined as the ratio of the CCF contrast CT over the CCF short-range vrad variability, that is, the standard deviation of the difference between the original CCF and the CCF smoothed over a given vrad window (CCFsmth in Fig. 5 top left).
- 2.
A CCF S/N (S/NCCF), defined as the ratio of the CCF core depth D over the standard deviation of the CCF wings.
The Q criterion estimates how noisy or dispersed the whole CCF is and how well the CCF core can be distinguished from the CCF wings. This is important with respect to the convergence and reliability of our CCF Gaussian or biGaussian models and our observable automatic computation. In the following, we adopt an arbitrary minimal threshold of Q = 4 for good-quality CCFs (more details in Sect. 4). Baranne et al. (1979) also defined a CCF quality factor, but it was directly dependent on the spectrum exposure time and its photon noise. Here our Q criterion is purely CCF-specific. Defining such a quality criterion helped us to build our line-depth-specific correlation templates. Our second criterion S/NCCF estimates the amount of signal within the CCF core, weighted by the CCF wing global dispersion. We used S/NCCF to derive the uncertainties on some of our CCF-based proxies (see Appendix B).
3.5 Computing the radial velocities
We emphasise here again that any Cepheid (or pulsating star) vrad measurement is somewhat biased with respect to the pulsation-induced asymmetry of the line or CCF profile. We decided here to merely implement three different (and well-known) ways to compute vrad measurements. We did not try to definitely assess which method is to be preferred. Generally speaking, we consider that several different vrad computation methods should always be considered for Cepheids and pulsating stars (Burki et al. 1982).
Centroid vrad
The CCF Doppler shift can be quantified by computing the centroid or barycentric velocity (hereafter RVcc-c, Appendix B). In the same way as done by Nardetto et al. (2006) for single spectral lines, the CCF RVcc-c corresponds to the first moment of the CCF core profile (see Hindsley & Bell 1986, and Fig. 5, top right). Studies of the Cepheid p-factor decomposition have favoured single-line centroid vrad compared to other single-line vrad computation methods as they are independent from rotational and turbulent broadening (Burki et al. 1982; Nardetto et al. 2006). However, they require a high enough S/N.
Gaussian vrad
The most classical and widely used way to compute the vrad is to fit the CCF profile with a Gaussian model (Fig. 5, bottom left). The derived Gaussian radial velocity (hereafter RVcc-g) is less sensitive to scatter in the spectrum than the CCF first moment, and is thus more stable and less dependent on the S/N of the spectrum (Anderson 2018). However, RVcc-g is potentially biased for Cepheids and other stellar pulsators as it accounts badly for the CCF profile asymmetry at high pulsation velocities (Nardetto et al. 2006).
biGaussian vrad
A solution to reproduce more closely the CCF asymmetry is to fit the CCF core with a biGaussian model instead of a simple Gaussian (as first done by Nardetto et al. 2006, for single-line vrad computation) that is, by fitting the blue and red parts of the CCF core profile separately (Fig. 5, bottom right). This gives us a third biGaussian vrad value (hereafter RVcc-2g).
 |
Fig. 6 Normalised δ Cep CCFs (top left plot) and main observables phased along the pulsation period, colour-coded with the phase ϕ, based on δ Cep HARPS-North spectra cross-correlated with our ALL template on our green range. On the bottom left plot, δRV denotes the difference between our Gaussian (RVcc-g) and biGaussian (RVcc-2g) vrad. Measurements are displayed as coloured dots and interpolated spline curves as red solid lines, if any. |
4 Results
4.1 A consistent catalogue
We computed the CCFs, corresponding line profile observable and quality proxy time series, and corresponding vrad time series for our whole 64-Cepheid sample, using our six correlation templates and the input spectra standardised on our three wavelength ranges. This makes up a large homogeneous catalogue of MW Cepheid CCFs and vrad. The full catalogue is available at the CDS, including the CCFs, various time series, and our correlation templates. We display a (small) example of our data (e.g. CCFs, vrad, and line profile observables deduced from δ Cep HARPS-North spectra cross-correlated on the green range with the ALL template) in Fig. 6. The displayed data appear robust and behave as expected along the pulsation phase. The CCF asymmetry proxies (BIS and biGaussian asymmetry) show the same behaviour and are correlated to the difference between biGaussian and Gaussian vrad (in agreement with the results of Anderson 2016). In this example, our CCF quality factor Q is high and nearly constant at all phases, which we show to be a sign of good CCF quality further below (Sect. 4). Our CCF S/NCCF behaves in correlation with the CCF depth, as expected: it is the highest when the CCF is the deepest, that is, when the Cepheid reaches it largest radius. On the contrary, the CCF FWHM is the largest at the end of the contraction phase (Nardetto et al. 2006).
We provide the vrad time series as processed, that is with the corresponding observation Modified Julian Day (MJD) but without any correction done on the vrad, except for the correction from the BERV done on the input spectra themselves if necessary (Sect. 3.2). Thus, we provide the vrad without correcting for a potential binary companion and without removing the absolute star vrad (or systemic velocity). For some of our targets (most of them also being spectroscopic binaries, see below), we have enough data to sample the pulsation phase adequately with several spectrographs. However, the data are not enough for us to clearly estimate instrumental vrad offsets from spectrograph to spectrograph because such offsets are typically of the order of 100 m s−1 or below, that is, very small compared to the Cepheid vrad variability (pulsation- and binary-induced). Some of these instrumental spectrograph-to-spectrograph vrad offsets have previously been measured with very good accuracy (Soubiran et al. 2013; Gallenne et al. 2018). In terms of outliers, we note only a very few vrad problematic data (i.e. that exhibit unexpected offsets for all templates and all methods). Those concern a few CORALIE spectra acquired between MJD 57196 and MJD 57206 (i.e. in mid-June 2015; see Fig. 7, bottom plot).
4.2 Spectroscopic binaries
Most of MW Classical Cepheids have been revealed to be components of binary or even multiple systems (Kervella et al. 2019). Here, we are mainly concerned with single-lined spectroscopic binaries (SB1s), that is, for which the companion signature is noticeable in the derived primary Cepheid vrad. We detected a number of 18 unambiguous SB1s within our Cepheid sample, with 11 other Cepheids exhibiting vrad scatter that hint towards a companion (Table A.1). For some of these binaries, new derivations of the companion orbital parameters were recently performed based on the data presented here in published studies (see Gallenne et al. 2019, 2018, and Fig. 7). We redirect the interested reader towards the latter studies, since Cepheid SB1s are not the focus of the present study. Nonetheless, we propose in Appendix C a new estimation of the companion orbital parameters for two of our SB1 targets (SU Cyg and V496 Aql), to highlight the interest of our new vrad data in combination with previous vrad data. In the following, we did not find it necessary to correct the vrad data for the companion signatures, as we mainly compare the same vrad time series computed in different ways.
4.3 vrad computation method
Here, we investigate the specific impact of the vrad computation method on the Cepheid vrad measurements. We compare the three methods that we implemented here, namely the centroid, Gaussian, and biGaussian vrad (RVcc-c, RVcc-g, and RVcc-2g, respectively). For this comparison, we limit ourselves to vrad measurements made with agiven correlation template on the green range. We select Cepheids with a good sampling of the pulsation curve within theseconstraints only, that is 47 targets. For each of these targets, we compute two linear regressions: (1) of RVcc-g versus RVcc-c measurements and (2) of RVcc-2g versus RVcc-c measurements (Fig. 8). We then study the distribution of the values of the slope of these regressions. We consider that such an approach is safer and more reliable than comparing the peak-to-peak amplitudes of the two vrad time series phased along the Cepheid pulsation period (as done by e.g. Nardetto et al. 2007). Firstly, this allows us to take into account all the vrad measurements (and not only the extremal vrad values), and secondly, it should make the comparison of the two vrad time series less prone to bias induced by shockwaves (Nardetto et al. 2018) or cycle-to-cycle vrad variability (Anderson 2014, 2016) for example, that especially affect the extremal vrad measurements. We use the same approach in the following Sects. 4.4–4.6.
Overall, we find Gaussian vrad to have slightly larger amplitudes than centroid vrad, and biGaussian vrad to have significantly larger amplitudes than both other methods. For the ALL template, we estimate RVcc-g to be larger than RVcc-c by ~ 1% overall, and RVcc-2g to be larger than RVcc-c by ~ 3–4% overall (Fig. 9, left). This agrees with biGaussian vrad being more sensitive to the CCF asymmetry, as found in previous studies (Nardetto et al. 2006; Anderson 2016). This trend seems to be more pronounced:
- 1.
for shallower lines: with our intermediate-line template, we find RVcc-g to be ~1–2% larger than RVcc-c and RVcc-2g to be ~5% larger than RVcc-c overall;
- 2.
for shorter pulsation periods (Fig. 9, right).
Both results agree with shallower lines and corresponding CCFs being more asymmetric than deeper ones (Anderson 2016). We also note that the dispersion of the linear regression slope values is much higher for biGaussian vrad than for Gaussian vrad. The Gaussian model is probably more robust than the biGaussian model because it has one less fitting parameter. If confirmed, it would also mean that a robust p-factor distribution over a large Cepheid sample would be more difficult to obtain with biGaussian vrad than with centroid or Gaussian vrad. To conclude here, we show and confirm the significant impact of the vrad computation method on the deduced CCF vrad time series.
 |
Fig. 7 Combined vrad of FF Aql. Top: centroid vrad (RVcc-c) obtainedwith the ALL template on the green range for four spectrographs, phased (ϕ) along the Cepheid pulsation period and not binary-corrected. Bottom: same, but the vrad have been corrected from the Keplerian orbit of the binary companion. Our best spline curve is displayed as a red solid line. The vrad are corrected only from the Keplerian orbit (no offset correction), based on the orbital parameters recently computed by Gallenne et al. (2019). The red box contains one of our few CORALIE vrad outliers (see text), which we did not take into account to build the spline curve. |
 |
Fig. 8 Comparison of vrad computation methods for FM Aql SOPHIE vrad (green range, medium template). The x-axis corresponds to RVcc-c. Here, RVcc-g and RVcc-2g are displayed as blue diamonds and red dots, respectively. We point out that the uncertainties on all vrad are displayed but are not necessarily visible. The best linear regressions are displayed as cyan and orange solid lines (along with their 1σ uncertainty in same-colour shades), respectively. The black dashed line corresponds to a slope of 1. The bottom insert corresponds to the residuals of the two linear regressions (same colour code). |
4.4 Template wavelength range
Here, we investigate the impact of the wavelength range (Δλ) on which we compute our CCFs on the vrad measurements. To do so, we use the vrad measurements that we obtained based on our three medium templates spanning the three pre-defined wavelength ranges (blue, green, and red). First, to compare green and red CCFs and vrad, we use our three targets observed extensively with FEROS (UZ Sct, V340 Ara and AV Sgr), as well as our three HERMES targets (V1334 Cyg, FF Aql and W Sgr). For these instruments and targets, the same acquired spectra cover both the green and red wavelength ranges, which allows us to make a direct comparison between the corresponding green and red data. Second, to compare our blue and red wavelength ranges, we use our UVES data (24 targets in all, Table A.1), as the corresponding blue and red spectra were acquired at the same observation epochs (thus allowing for a direct comparison). For each target and each UVES arm, we average the successive CCFs obtained at each epoch of observation (see Sect. 2) and we derive the corresponding observables, in order to have the same number of measurements for the blue and red arms.
We look first at the general CCF quality for each wavelength range (Fig. 10). We note that our green and red (intermediate-line template) CCFs exhibit an almost constant average quality factor ⟨ Q⟩ (around 4.5–5). On the contrary, our blue CCFs show a decreased ⟨Q⟩ that is muchmore variable (between −1 and 2, Fig. 10 middle plot). The green and red CCFs exhibit a well-defined and relatively deep core, while the blue CCFs are much more noisy and exhibit a shallower core (Fig. 10, left plot). Overall, we note that our good-quality CCFs have a nearly constant Q above ~4 (see also Fig. 6) independently of their depth. On the contrary, when the ratio between the contrast of the CCF core and the dispersion of the CCF continuum is decreased beyond a certain point, the CCF Q factor starts to decrease (below 4) and becomes significantly variable. This led us to define a CCF quality threshold of Q = 4. When looking at our other proxy S/NCCF, it is more variable: red CCFs exhibit the highest S/NCCF values (between 70 and 130 for intermediate-depth lines, Fig. 10 right plot), while green CCFs have somewhat lower S/NCCF values (in agreement with the respective CCF depths). Finally, blue CCFs show understandably much smaller S/NCCF values (below 40).
This quality difference between blue and red UVES CCFs does not originate in the number of lines included within the respective correlation templates (Table 3). Rather, it originates in the much increased spectral line density on the blue range compared to the red range. Between 3900 and ~ 5000 Å, typical Cepheid spectra are crowded with spectral lines that are often blended with each other. Even if we tried to select only un-blended lines from our synthetic Cepheid spectrum, this line density has nonetheless an impact on our CCFs. Meanwhile, there are much fewer spectral lines on the red range, and these are much more separated from each other. This explains the increased quality of the red CCFs.
Second, we look at the blue and red vrad themselves. For each of the selected targets, we compute the linear regression of the red versus green vrad (FEROS and HERMES targets) or red versus blue vrad (UVES targets). Overall, it is difficult to detect a definitive trend. Nonetheless, the average slope of the linear regression seems to be slightly below 1 (~ 0.97–0.98, see Fig. 11). If confirmed, this would mean that Cepheid vrad amplitudes of variation decrease at larger wavelengths. This would agree with the findings of Nardetto et al. (2009), who reported a linear decrease of the Cepheid vrad peak-to-peak amplitude, based on CCFs computed order-by-order with the HARPS DRS and its classical G2 template. However, we cannot confirm whether or not this trend depends on the Cepheid pulsation period. We emphasise that our result remains to be confirmed given the relatively few number of vrad measurements used to perform the linear regression for each target. In the context of this study, we also consider this wavelength effect (between our different λ ranges) to be small enough to be neglectedwithin a given λ range. Such studies would need to be extended to IR wavelengths in order to be confirmed. Nardetto (2018) did not find a significant difference between the vrad curve amplitude of ℓ Car measured in the optical and on an IR line, respectively.
If considering the zero-point, there is no clear result for our green versus red vrad regressions given that the zero-point value seems to depend on the spectrograph (Fig. 11, top left). When looking at our UVES targets, there seems to be a consistent offset of ~ 1.5–2 km s−1 between the vrad measured with the blue and red arms of UVES. It is not clear whether this is related to the wavelength or to technical differences in the acquisition of the UVES blue and red spectra (Molaro et al. 2008). Finally, we find the BIS amplitude over the Cepheid pulsation period to be slightly increased over our red range compared to our blue or green ranges (Fig. 11, bottom right).
 |
Fig. 9 Left: slope distribution for the RVcc-g vs RVcc-c and RVcc-2g vs RVcc-c linear regressions (in blue and red shades, respectively). Right: same slope values vs. the pulsation period for each target. The computation was made based on our ALL template on our green range. |
 |
Fig. 10 Quality of the CCF vs. wavelength range. Left (top, solid lines): comparison of a green and a red CCF of UZ Sct based on the same FEROS spectrum as well as the comparison of a blue and a red CCF of BG Cru (bottom; dashed lines) based on UVES spectra acquired at the same observation epoch with the blue and red arms of UVES, respectively. The bottom UVES CCFs have been shifted downwards for clarity. Middle: histogram of the CCF quality factor Q averaged over the pulsation period P for each studied Cepheid (green: six FEROS and HERMES targets; blue: 24 UVES blue arm targets; red: 30 FEROS, HERMES, and UVES red arm targets; see text). Right: same, but for the histogram of our S/NCCF proxy averaged over P for each target. |
4.5 Template line width
Here, we investigate the impact of the average line width of a given correlation template (σℓ) on the resulting CCFs and vrad.
4.5.1 Impact of variable line width
We first consider the impact of a variable σℓ for one of our tailored correlation templates, namely the ALL template over the green range. We cross-correlated the 103 HARPS-North spectra of δ Cep with the ALL template for different line widths ranging from ~5 to 140% of the default ALL template line width, that is, σℓ ranging from ~0.03 to ~0.6 Å (Fig. 12). In terms of CCF shape, broadening the template lines has two results: first, it leads to a broadening of the CCF core (i.e. a shallower and wider CCF core); and second, it strongly reduces the noise or dispersion of the CCF wings. Both effects were already predicted by Queloz (1995) for example. The decrease in CCF depth leads to a slight decrease of our CCF Q-factor averaged over the pulsation phase (yet still well over Q = 4). In contrast, the decrease of the CCF wing variability at the same time leads to a strong increase of our S/NCCF criterion up to a maximum for σℓ in the 0.35–0.45 Å range (Fig. 12, top right). This is the main reason for our choice of wider lines in our tailored templates (Sect. 3.3): broadening the template lines allows us to make the CCF core more distinguishable from the CCF wings, even if the CCF core is made shallower. The decrease of the CCF wing variability with an increasing σℓ also allows a more robust CCF Gaussian or biGaussian modelling by making the CCF shape closer to that of a Gaussian (Queloz 1995). We observe the same CCF behaviour as a function of σℓ for our other templates (deep, medium, and weak).
Increasing σℓ (i.e. broadening the CCF) also reduces the CCF asymmetry variability and leads to smaller vrad amplitudes (Fig. 12, middle and bottom right). We consider this to be a positive result as our focus is on increasing the consistency of Cepheid vrad: reducing the CCF asymmetry leads to less asymmetry-dependent (i.e. less variable and more consistent) vrad time series (and thus less variable p-factors). On the contrary, Cepheid studies that focus on specific items such as the atmospheric velocity gradient should therefore use narrow-line templates to exacerbate the CCF asymmetry and enhance its impact on the vrad.
 |
Fig. 11 CCF vrad vs. wavelength range. Top left: red vs. green linear regression for our six targets (see text): the regression slope is plotted vs. the regression zero-point with green diamonds for HERMES targets and green dots for FEROS targets. Top middle: histogram of red vs. blue vrad slope for our UVES targets. Top right: same, but for the vrad zero-point. Bottom left: amplitude of variation over P of the CCF BIS, plotted for our red range vs. our blue or green range, for the same targets as above (left). Bottom middle: distribution of the red vs. blue vrad slope with P for our UVES targets. Bottom right: same as middle, but for the vrad regression zero-point. |
 |
Fig. 12 Cross-correlation function and vrad vs. template average line width σℓ. Left: CCFs resulting from the cross-correlation of one observed δ Cep spectrum (see text) with the ALL template built with a variable σℓ within the range 0.02–0.62 Å (y-axis). The CCFs tested at different σℓ are shown in orange and the CCF corresponding to the default σℓ ~ 0.43 used in this study (Table 2) is shown in red. The CCF corresponding to the same δ Cep spectrum and the G2 HARPS DRS template is showed as a dashed black curve and is shifted vertically for clarity. The four right plots show the behaviour of different CCF observables vs. σℓ (from left to right and top to bottom; in red circles): (i) the CCF Q-factor averaged over the 103 δ Cep spectra; (ii) the same but for the averaged S/NCCF criterion; (iii) the slope of the linear regression to the δ Cep BIS time series at a given σℓ vs. the BIS time series at σℓ ~ 0.43; and (iv) the same but for the RVcc-c time series. On the four plots, the red diamond corresponds to the default σℓ used in this study for the ALL template and the black square corresponds to the G2 HARPS DRS template. |
 |
Fig. 13 HARPS ℓ Car CCFs computed with our four depth-dependent correlation templates on the green λ range. Left: example of the four CCFs corresponding to a same spectrum and our four respective templates. Middle: CCF quality factor Q of ℓ Car vs. pulsation phase (ϕ) for CCFs built based on our four templates (same colour code). Right: same, but for our CCF signal estimator S/NCCF. |
4.5.2 Comparison with the G2 HARPS DRS default template
We subsequently compared our ALL δ Cep CCFs with the CCFs computed from the same spectra but with the classical G2 template from the HARPS DRS. We retrieved the G2 template from the data made available by Brahm et al. (2017) and adapted it to our specifications (i.e. the green wavelength domain and telluric exclusion ranges, Sect. 3.3). Over our green range, the G2 template includes more than 1700 very narrow lines (σℓ ~ 0.08 Å, Table 2); it gives significantly different CCFs with a narrower and deeper core and very flat wings (Fig. 12). The G2 CCF narrow core is induced by the small σℓ, while the flatness of the CCF wings is induced by the many blended lines and the occasional G2 template line mismatches (Queloz 1995, and see Fig. 3). This leads to both a high CCF Q-factor and a high S/NCCF criterion. Given that our templates are specifically tailored for Cepheids (i.e. much less line mismatches) and that our constraints on the line selection aremuch more stringent (no blended lines), our CCF wings are inevitably noisier, justifying our use of wider template lines. On the other hand, the G2 CCFs are much more asymmetric than the CCFs built from our ALL template and exhibit larger vrad amplitudes (Fig. 12).
4.6 Template line depth
Here, we investigate the impact of the average line depth of the correlation template on the resulting Cepheid CCFs and vrad. We looked at our data obtained on our green range only, with the four corresponding templates (weak, medium, deep, and ALL templates), that is, considering a sub-sample of 50 targets.
4.6.1 CCF quality
We look at the CCF quality for each of our four line depth-dependent correlation templates. As expected, the derived CCFs have a deeper core for templates corresponding to deeper lines (i.e. templates with a higher average line depth in Table 2); see Fig. 13 (left). For three of our four templates, we generally find our CCF quality factor Q to be nearly constant during the pulsation phase, with a value of ~4–5 (Figs. 13 and 14). On the contrary, for the weak template, the Q proxy is much smaller (between 0 and 3, Fig. 14 left) and significantly variable during the pulsation (Fig. 13, middle). We consider this as a criterion defining the good quality of a CCF and the reliability of the derived observables. As we already explained in Sect. 4.4, we empirically put a Q = 4 threshold to distinguish between high-quality (Q ≥ 4) and mixed-quality (Q < 4) CCFs and data. Almost all our data derived from the medium, deep, and ALL templates meet our empirical quality threshold, while the data derived from the weak template are below this criterion. We note that even when using narrower lines for the weak template (as detailed in Sect. 4.5 for the ALL template), the derived Q-factors are still below our Q = 4 empirical criterion. To obtain better-quality CCFs from such weak-line templates, we consider that the best solution would be to include more shallow lines, for example by alleviating our constraints on the line selection as described in Sect. 3.3. Finally, we find our S/NCCF parameter to be variable both during the pulsation phase (Fig. 13, right) and as a function of the correlation template used (Fig. 14, middle). Understandably, the S/NCCF values increase both for deeper lines and for templates including more lines.
4.6.2 CCF asymmetry
We used our BIS variable to study the impact of the line depth on the CCF asymmetry. We do not find any clear pattern in terms of BIS amplitude over the pulsation phase ϕ. However, we find the BIS averaged over ϕ to be higher(in absolute values) for the weak template compared to our three other templates (Fig. 14, right). This agrees with shallower lines being more sensitive to the line asymmetry as reported by Anderson (2016).
4.6.3 Radial velocities
We finally look at the impact of the average line depth of the correlation template on the vrad. To do so, we compute for each of our selected targets three linear regressions: weak versus ALL RVcc-c, medium versus ALL RVcc-c, and deep versus ALL RVcc-c, respectively (on the green wavelength range). We selected the centroid vrad method as we derive it directly from the CCF and not from a CCF fit (as for Gaussian and biGaussian vrad that are less robust).We display our results in Fig. 15.
We find that the zero-point of the linear regressions significantly change when going from one template to another. The median offset between deep and ALL vrad time series is marginal (0.07 ± 0.12 km s−1), but the median offsets between medium and ALL vrad and between weak and ALL vrad are significant (− 0.43 ± 0.31 km s−1 and 0.87± 0.46 km s−1, respectively). Such vrad offsets between correlation templates based on lines of different depth could be expected and agree with the findings of Nardetto et al. (2008, 2009); Vasilyev et al. (2017) on the dependency of Cepheid γ-velocities on the spectral lines and their depth. This would need a more in-depth analysis which is beyond the scope of this paper.
In contrast, the slopes of the linear regressions exhibit a significant variability but no clear trend from one template to another. The median slopes are comparable at a 1σ level (1.001 ± 0.028, 1 ± 0.016, and 0.998 ± 0.006 for the weak vs. ALL, medium vs. ALL, and deep vs. ALL regressions, respectively). However, the so-called stellar velocity gradient (between spectral lines of different depths) is expected to have a significant impact on the Cepheid vrad amplitudes, as detailed by Nardetto et al. (2006, 2007) for single lines. Significant differences in terms of CCF asymmetry and vrad were also reported by Anderson (2016) when cross-correlating spectra of ℓ Car with two correlation templates (one weak-line and one strong-line, respectively, both having narrow lines). These authors reported an enhanced asymmetry for weak lines as well as an increased sensitivity or variability of their vrad. We consider that the present lack of significant trend (i.e. of the regression slope as a function of the average template line depth) is at least partially caused by our use of broader template lines (Sect. 4.5), that reduce the asymmetry of the resulting CCFs and decrease the sensitivity of the vrad time series. However, the slope distribution for the weak versus ALL regressions exhibits a much larger dispersion than for the deep versus ALL regressions. This would agree with strong lines showing less asymmetry and leading to more robust vrad.
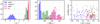 |
Fig. 14 CCF quality and asymmetry vs. correlation template. Left: histograms of the CCF Q factor averaged over the pulsation phase for each target, for our four line depth-dependent templates. Middle: same, but for our CCF S/NCCF proxy (same colour code). Right: amplitude of the BIS during the pulsation phase vs. averaged BIS for each target, for our four templates (same colour code). |
 |
Fig. 15 Comparison of centroid vrad computed with our respective correlation templates on the green range. The figure represents the slope vs. zero-point distribution of the linear regression of the weak (blue), medium (green) and deep (purple) vrad vs. the ALL vrad, respectively. |
5 Conclusions
We carried out a large spectroscopic survey of Classical MW Cepheids based on several thousand high-resolution spectra from seven spectrographs. We detailed the framework that we implemented to derive and characterise Cepheid line profiles and vrad time series as consistently as possible based on the cross-correlation method. Briefly, the main steps of our formalism are the following:
- 1.
normalising and standardising in wavelength all the spectra in the same way;
- 2.
using pre-defined correlation templates with an emphasis on the selected lines, their average depth, and their width;
- 3.
characterising not only the CCF Doppler shift, but its shape, depth, width, asymmetry and amount of extractable signal;
- 4.
deriving the vrad while accounting for the intrinsic CCF asymmetry.
We show that each parameter and each step of the process has a significant impact on the derived Cepheid vrad: the wavelength range on which the spectrum is considered, the correlation template used for the cross-correlation (both in terms of line depth and template line width), and the way of computing the radial velocity have a significant impact on the derived vrad. For Baade-Wesselink studies, this means that significantly different projection factors and distances could be obtained for the same Cepheid, depending on how the former items are treated. Hence, giving at least a minimum of detail on the vrad computation process should be a pre-requisite for such studies. We also emphasise the importance of fully characterising the cross-correlation profile (CCF) through various estimators of its shape, width, depth, asymmetry and the amount of signal within it. We publish both our tailored correlation templates, the derived CCFs, and the various vrad, line profile proxy, and CCF quality proxy time series computed from the CCFs at the CDS. As we show in this study, deriving fully consistent Cepheid vrad from the cross-correlation method is not an easy task. Nevertheless, it seems that the way towards more robust Cepheid vrad (and thus more robust p-factors) is by minimising the asymmetry of the line profile (here, the CCF) and reducing the sensitivity of the resulting vrad to this asymmetry: for example using centroid vrad, favouring stronger lines in cross-correlation templates, or even using templates with somewhat broader lines than usual.
High-resolution spectroscopy of Cepheids has a lot of different applications. Our next objective is to take a fresh look at the computation of the Cepheid effective temperature Teff from spectra. Cepheid Teff exhibit a large variability (of the order of hundreds of Kelvin) over the pulsation phase, which has a significant impact on spectra. We aim at using our Cepheid sample to accurately measure both the absolute average Cepheid Teff and its variation over the pulsation cycle by rehashing pre-existing methods based on the ratio of the depths or EWs of selected line pairs (see e.g. Kovtyukh & Gorlova 2000; Sousa et al. 2010, respectively). Other stellar parameters can be easily derived from Cepheid spectra, such as for example metallic abundances (Luck 2018).
Another possibility is to again use the CCF as the proxy of the spectrum to deduce parameters other than the vrad. An interesting point is to build a model grid of Cepheid CCFs, in the same way as done by Britavskiy et al. (2018) with their grid of synthetic bisectors. In the case of non-pulsating stars, CCF profiles can already be used (instead of the spectra themselves) to derive the Teff, log g and metallicities for example (Malavolta et al. 2017).
Finally, it would be interesting to see if and how the Cepheid CCF formalism that we detailed here can be applied to the data of the Gaia Radial Velocity Spectrograph (RVS, Cropper et al. 2018). The RVS spectra are centred on the Calcium II NIR triplet, on a narrow wavelength band if compared to the spectrographs implemented within this study. They are expected to produce transit vrad measurements with a precision well below 1 km s−1 however, that is, enough to scan the Cepheid vrad pulsation amplitude (Sartoretti et al. 2018; Katz et al. 2019). This would be a great opportunity given that Gaia will observe several thousands of MW Cepheids.
Acknowledgements
The authors acknowledge the support of the French Agence Nationale de la Recherche (ANR) under grant ANR-15-CE31-0012-01 (project UnlockCepheids). W.G. and G.P. gratefully acknowledge support from the Chilean Centro de Astrofisica yTecnologias Afines (CATA) BASAL grant AFB-170002. W.G. also acknowledges support from the Chilean Ministry of Economy,Development and Tourism’s Millennium Science Iniciative through grant IC120009 awarded to the Millenium Institute of Astrophysics (MAS). The research leading to these results has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 695099). The Swiss 1.2 m Euler telescope and the CORALIE spectrograph are supported by the Swiss National Science Foundation. This research is partly based on observations made with the Mercator Telescope, operated on the island of La Palma by the Flemish Community, at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. HERMES is supported by the Fund for Scientific Research of Flanders (FWO), Belgium, the Research Council of K.U. Leuven, Belgium, the Fonds National de la Recherche Scientifique (F.R.S.-FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland, and the Thüringer Landessternwarte, Tautenburg,Germany. This research made use of the SIMBAD and VIZIER databases at the CDS, Strasbourg (France), and NASA’s Astrophysics Data System Bibliographic Services. We made use of the Python programming language (Rossum 1995) and the open source Python packages numpy (van der Walt et al. 2011), scipy (Jones et al. 2001), matplotlib (Hunter 2007), and astropy (Astropy Collaboration 2013). The authors would like to thank the anonymous referee for the useful remarks and points, especially on using the cross-correlation method.
Appendix A Detail ofour Cepheid sample
Details of our Cepheid sample.
Appendix B Details on the computation of CCF, radial velocities, and observables
B.1 CCF computation
We use the crosscorrRV package from the Python AstroLib library 4 to cross-correlate each observed spectrum with a given correlation template. We compute the CCF on a default vrad grid ranging from − 200 to + 200 km s−1 with a 1 km s−1 step. Such a step is of the order of what is commonly done in the DRS of the spectrographs considered in this study (see e.g. Queloz 1995; Baranne et al. 1996), and it is enough to provide precise vrad measurements (e.g. through a CCF Gaussian or biGaussian fit). The crosscorrRV package is an easy-to-use and time-tested framework for cross-correlating 1D spectra with templates. The correlation template is successively Doppler-shifted in wavelength, and then linearly interpolatedat the spectrum wavelength points for the correlation. Given that our correlation templates are sampled with a ~ 0.02 Å step (roughly corresponding to a ~ 1 km s−1 step in terms of vrad and similar to the wavelength step of our input spectra), we do not expect this linear interpolation to modify our template lines and to impact the derived observables.
B.2 Observable computation
CCF continuum and depth
We denote the vrad extension of the CCF core (i.e. the area of the CCF peak located below the CCF lower shoulder, see Fig. 5) as Δcore and we denote the reunion of the CCF wing vrad ranges (i.e. the vrad ranges both left and right of the two CCF shoulders) as Δwings. We thus define the CCF continuum 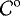 as
as
![\begin{equation*} \mathcal{C}^{\textrm{o}} = \ {\langle} \mathrm{CCF} [\Delta_{\textrm{wings}}] {\rangle}. \end{equation*}](/articles/aa/full_html/2019/11/aa35622-19/aa35622-19-eq4.png) (B.1)
(B.1)
Next, we define the CCF contrast (normalised here by the CCF continuum) as
![\begin{equation*} CT = 1 - \frac{\mathrm{min} \left(\mathrm{CCF} [\Delta_{\textrm{core}}] \right) }{\mathcal{C}^{\textrm{o}}} \end{equation*}](/articles/aa/full_html/2019/11/aa35622-19/aa35622-19-eq5.png) (B.2)
(B.2)
while we define the (normalised) CCF core depth (D) as
![\begin{equation*} D = \frac{\mathrm{max} \left(\mathrm{CCF} [\Delta_{\textrm{core}}] \right) - \mathrm{min} \left(\mathrm{CCF} [\Delta_{\textrm{core}}] \right)}{\mathcal{C}^{\textrm{o}}}. \end{equation*}](/articles/aa/full_html/2019/11/aa35622-19/aa35622-19-eq6.png) (B.3)
(B.3)
CCF core equivalent width
We compute EW through a direct integration of the CCF over Δcore:
![\begin{equation*} \mathrm{EW} = \int_{\Delta_{\textrm{core}}} \! \left(1 - \frac{\mathrm{CCF}[v_{\textrm{rad}}]}{\mathrm{max} (\mathrm{CCF}[\Delta_{\textrm{core}}])}\right) \, \mathrm{d}(v_{\textrm{rad}}). \end{equation*}](/articles/aa/full_html/2019/11/aa35622-19/aa35622-19-eq7.png) (B.4)
(B.4)
The integration is done on a finer vrad grid (vrad step of 50 m s−1) than the CCF computation (see above). The CCF EW is equivalent to the width (in km s−1) of a theoretical rectangle with a height equal to 1 (considering the normalised CCF) and with a surface equal to the area covered by the CCF core.
CCF first moment
To derive the first moment of the CCF core RVcc-c, we compute the cumulated integral of the CCF profile over Δcore, using the same vrad grid as for the CCF EW. Integrating the CCF core including the small area above the lower shoulder and below the higher shoulder does not lead to significant changes to the CCF EW and RVcc-c. The EW values are marginally higher (by ~1–2% or typically 100 m s−1, and the RVcc-c amplitudes increase only marginally, by a few tens of m s−1 (i.e. by a value lower than the typical RVcc-c uncertainties). We adopt the same nomenclature as that of Nardetto et al. (2006, 2009) for the different vrad computation methods applied to the CCF: RVcc-c for the CCF first moment (by analogy with RVc for single-line first moments), RVcc-g for the CCF Gaussian (by analogy with RVg single-line Gaussian models), and so on.
CCF bisector
We compute the CCF bisector by dividing the CCF core into 100 horizontal slices (between the minimum and the maximum of the CCF peak) and by computing the mean vrad for each slice. We then compute the corresponding Bisector Inverse Span (BIS), defined as the vrad span between a top and a bottom domain of the bisector (Queloz et al. 2001b). If denoting Vtop and Vbtm as the mean vrad of these top and bottom BIS domains, we have BIS = Vtop − Vbtm. We use the top and bottom bisector region definition given by Galland et al. (2005): that is, a top region extending from 15 to 46% of the CCF depth D and a bottom region from 57 to 85% of D.
CCF quality proxies
We compute our CCF quality factor Q as
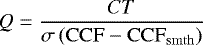 (B.5)
(B.5)
where CT represents the CCF contrast, σ denotes the standard deviation, and CCFsmth represents the CCF smoothed over a vrad range equal to 2.355 × Δcore. We then compute our CCF S/N estimator as
![\begin{equation*} {S/N_{\textrm{CCF}}} = \frac{D}{\sigma \left(\mathrm{CCF} [\Delta_{\textrm{wings}}] \right)}. \end{equation*}](/articles/aa/full_html/2019/11/aa35622-19/aa35622-19-eq9.png) (B.6)
(B.6)
 |
Fig. B.1 Distribution of the mean vrad uncertainties (i.e. averaged over all the vrad measurements for each target), for the vrad computed on the green λ range. Left: ALL template. Right: medium template. The uncertainty distributions are displayed in blue, red, and black shades for RVcc-g, RVcc-2g and RVcc-c, respectively. |
As shown in Sect. 4, Q does not necessarily depend linearly on the CCF contrast CT. It stays on a plateau at ~4–5 for all good-quality CCFs but starts to significantly decrease when the CCF wings become noisy and the CCF core very shallow.
CCF Gaussian fit
We model the profile of the CCF core or main peak (considered over its vrad extension Δcore) with a four-parameter Gaussian function ( ):
):
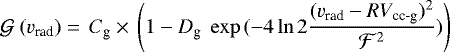 (B.7)
(B.7)
where  g refers to the offset of the Gaussian function, Dg to its (normalised) depth,
g refers to the offset of the Gaussian function, Dg to its (normalised) depth,  to its FWHM, and RVcc-g to the Gaussian vrad.
to its FWHM, and RVcc-g to the Gaussian vrad.
CCF biGaussian fit
As done with the Gaussian model, we fitted the CCF core with a five-parameter biGaussian function ( ):
):
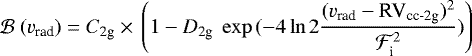 (B.8)
(B.8)
where 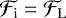 if vrad < RVcc-2g (equivalent to the FWHM of a Gaussian model of the CCF blue wing) and
if vrad < RVcc-2g (equivalent to the FWHM of a Gaussian model of the CCF blue wing) and 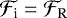 if vrad > RVcc-2g (FWHM of a Gaussian fitted to the CCF red wing). Other parameters (continuum, depth, vrad) are analogous to the Gaussian ones. We point out that our biGaussian model is slightly different from the one used by Nardetto et al. (2006), as the radial velocity RVcc-2g is one of the free parameters. For both the Gaussian and biGaussian fits, we use a non-linear least-square method as implemented in the curve_fit function of the scipy.optimize Python package.
if vrad > RVcc-2g (FWHM of a Gaussian fitted to the CCF red wing). Other parameters (continuum, depth, vrad) are analogous to the Gaussian ones. We point out that our biGaussian model is slightly different from the one used by Nardetto et al. (2006), as the radial velocity RVcc-2g is one of the free parameters. For both the Gaussian and biGaussian fits, we use a non-linear least-square method as implemented in the curve_fit function of the scipy.optimize Python package.
B.3 Uncertainties
While choosing which vrad computation method(s) to use for Cepheids is an important question, computing reliable and realistic uncertainties on the CCF vrad and other line profile observables is also important. Typically, the DRS of high-resolution spectrographs include two main sources of uncertainty on the vrad: (1) the photon noise (proportional to the inverse of the S/N of the spectrum); and (2) the instrumental noise (or read-out noise), corresponding to the instrumental vrad precision and the instrumental stability (Baranne et al. 1996; Pepe et al. 2002). For the best spectrographs (e.g. HARPS), the increased instrumental stability (Table 1) and easily reachable high spectrum S/N mean that vrad uncertainties lower than 1 m s−1 on average can be routinely achieved (Pepe et al. 2018). Such vrad precision is importantin the case of exoplanet surveys around (generally) non-pulsating stars, for which the CCF can be properly fitted with a Gaussian model. However, Cepheids (and other radially pulsating stars) pose a different kind of challenge, due to the Cepheid vrad accuracy being strongly dependent on the correlation template and the vrad computation method used.
We decided here to compute our vrad (and other line profile observable) uncertainties based on our CCFs and their characteristics to remain consistent within our CCF-based framework, instead of using the photon noise of the spectrum. We use S∕NCCF (see above) to estimate the uncertainty on the centroid radial velocity RVcc-c:
![\begin{equation*} \epsilon_{\textrm{cc-c}} = \frac{W}{S/N_{\textrm{CCF}}} \, = \frac{W}{D} \times \sigma \left(\mathrm{CCF} [\Delta_{\textrm{wings}}] \right) \end{equation*}](/articles/aa/full_html/2019/11/aa35622-19/aa35622-19-eq18.png) (B.9)
(B.9)
where W denotes the width of the CCF core at half its depth D. Such a formula is analogous in terms of dimensions to the formulae provided by Queloz (1995); Baranne et al. (1996) for example; it makes the RVcc-c uncertainty directly dependent on the correlation template used to compute the CCF and on the observational pulsation phase. Next, to derive the BIS uncertainty (ɛBIS), we first compute the uncertainties on Vtop and Vbtm as classical errors on the mean (i.e. as the ratio of the bisector vrad dispersion in the defined top and bottom regions over the square root of the number of vrad points in the two respective bisector slices). We then add these two uncertainties quadratically to obtain ɛBIS.
 |
Fig. B.2 Uncertainties vs. pulsation phase. Based on HARPS-North δ Cep spectra cross-correlated with the ALL template on the green λ range. Left: vrad uncertainties vs. pulsationphase (ϕ), for Gaussian, biGaussian and centroid vrad (blue, red and black dots, respectively); right: BIS uncertainties vs. phase. |
 |
Fig. B.3 Comparison between our s1d-based CCF computation and the automatic (e2ds-based) DRS CCF computation (see text). For each plot, the data that we obtain from the cross-correlation of the δ Cep HARPS-North (1D) spectra with the G2 template adapted to our green wavelength range (see Sect. 4.5.2) are plotted against the corresponding observables retrieved from the available DRS data (automatically produced from the 2D spectra and the default G2 template). From top to bottom and left to right: Gaussian vrad, Gaussian FWHM, CCF BIS, and CCF depth. |
For all the observables (vrad, Gaussian FWHM, biGaussian asymmetry, etc) derived from a Gaussian or a biGaussian CCF model, we use the uncertainties derived within the fit, that is, the 1σ uncertainties computed from the square root of the covariance matrix diagonal. These uncertainties describe how closely the Gaussian or biGaussian fit agrees with the modelled CCF. We thus consider it valid to use them within our CCF-based formalism. We compare the derived uncertainties on RVcc-c (ɛcc-c, from our formula), RVcc-g and RVcc-2g (ɛcc-g and ɛcc-2g from the fits) in Fig. B.1. Overall, ⟨ɛcc-2g⟩ is twice larger than ⟨ɛcc-g⟩ (~ 20 m s−1 against ~ 10 m s−1, respectively,for the ALL correlation template), which agrees with the biGaussian model being more sensitive to the asymmetry and somewhat less robust than the Gaussian model. Meanwhile, ⟨ ɛcc-c⟩ is about one order of magnitude larger than ⟨ɛcc-g⟩. We cannot infer anything from this given that our computation formula for ⟨ ɛcc-c⟩ is arbitrary (see above), but we note that the shape of the distribution is similar for ⟨ ɛcc-c⟩ and ⟨ ɛcc-g⟩, which gives us confidence in our formula. Finally, going from a template with more and deeper lines to a template with less and shallower lines leads understandably to an increase of the vrad uncertainties (Fig. B.1).
We also display in Fig. B.2 the vrad and BIS uncertainties versus the pulsation phase for one of our targets (δ Cep). The Gaussian and biGaussian vrad uncertainties are slightly variable with the phase, while the centroid vrad uncertainties (ɛcc-c) are significantly variable (being an order of magnitude larger than the other uncertainties). The ɛcc-c uncertainties do not exhibit the same pattern of variation as ɛcc-g and ɛcc-2g. The BIS uncertainties are significantly variable with ϕ, with ɛBIS being the highest for the largest CCF asymmetry (see Fig. 6). On average, ɛBIS has the same order of magnitude as ɛcc-g or ɛcc-2g. We note that our ɛBIS estimation may be a conservative one as the BIS is a vrad differential measurement (Anderson 2019).
B.4 Comparison with the DRS-based CCF computation
Here, we compare our s1d-based CCF computation and derived observables with the e2ds-based CCF computation performed automatically by the spectrograph DRS. We consider on the one hand the 103 HARPS-North δ Cep (1D) spectra cross-correlated with the DRS G2 template adapted to our green wavelength range (as done in Sect. 4.5.2); and on the other hand the data produced by the HARPS-North DRS based on the original G2 template and the corresponding 2D spectra of δ Cep. The DRS cross-correlates each order of the 2D spectrum with the default G2 template before summing the CCFs over all the orders to obtain the average CCF, which is then fitted by a Gaussian. We display the results in Fig. B.3. For the four compared observables (Gaussian vrad, Gaussian FWHM, BIS and CCF depth), we obtain a Pearson correlation coefficient between 0.99 and 1, showing the robustness of our s1d-based approach. A linear regression of the two Gaussian vrad time series leads to a slope very close to 1 (= 1.006 ± 0.002) and a non-significant zero-point. The differences in terms of CCF depth and FWHM amplitudes remain small (by <2 and <4%, respectively) and probably originate in the fact that the DRS CCF computation is done on a wider wavelength interval than our green range (encompassing all orders, i.e. from ~3900 to ~6900 Å). The larger differences in terms of BIS amplitudes can be explained by the different BIS definitions between this study and the DRS. Overall, this confirms that using the s1d spectra with a S/N lower threshold (Sect. 3.2) is a valid approach.
Appendix C New orbital parameters
We detail here the computation of the companion orbital parameters to two of our Cepheid targets, SU Cyg and V496 Aql. First, we combined for each target our vrad data with previous vrad time series from the literature, to obtain a time baseline roughly of the same order as the orbital period. Next, we used they orbit tool (Ségransan et al. 2011) to simultaneously model the orbital and pulsation curves with Keplerian models. y orbit is based on a Levenberg–Marquardt algorithm that allows to fit vrad data with Keplerian models (among others), after selecting the values with a genetic algorithm. We consider using a Keplerian fit to model the pulsation curve as a valid first approximation in the case of these two Cepheids as they are fundamental pulsators. The orbital parameters are detailed in Table C.1.
New orbital parameters of two binary Cepheids.
SU Cyg
We combined our SOPHIE data with vrad taken from Gorynya et al. (1998). Our best y orbit model corresponds to an orbital period Porb ~ 539 days (or ~1.5 yr), in agreement with Evans et al. (2015), and a ~0.8 high eccentricity. Assuming the primary mass from Evans et al. (2015) and the hipparcos parallax (Table C.1), we deduce a minimal mass of 2 M⊙ and a semi-major axis (sma) of ~2.5 au for the secondary. In comparison, Evans et al. (2015) found a true secondary mass of 3.2 M⊙. Kervella et al. (2019) reported an orbital period of 549 days (i.e. close to our y orbit value) but with an eccentricity twice smaller and a companion true secondary mass of 4.7 M⊙. Our high eccentricity value may be an artefact induced by the Keplerian modelling of an uneven vrad sample.
V496 Aql
We combined our HARPS, SOPHIE, and CORALIE data with vrad taken from Gorynya et al. (1998), Storm et al. (2011) and Groenewegen (2013). Our best model corresponds to an orbital period of 1352 ± 6 days or ~ 3.7 yr, that is, somewhat longer than the 2.9 yr period of Evans et al. (2015). Groenewegen (2013) reported a significantly smaller orbital period (~ 1066 days), but with a null-eccentricity model, which probably explains the difference. Assuming the primary mass of these authors and the Gaia DR2 parallax, we deduce a companion minimal mass of 1.4 M⊙ and a companion sma of ~4.6 au. In comparison, Evans et al. (2015) found a true secondary mass of 1.9 M⊙.
References
- Anderson, R. I. 2014, A&A, 566, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, R. I. 2016, MNRAS, 463, 1707 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, R. I. 2018, in The RR Lyrae 2017 Conference. Revival of the Classical Pulsators: from Galactic Structure to Stellar Interior Diagnostics, eds. R. Smolec, K. Kinemuchi, & R. I. Anderson (Poland: Polish Astronomical Society), 6, 193 [Google Scholar]
- Anderson, R. I. 2019, A&A, 623, A146 [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, R. I., Sahlmann, J., Holl, B., et al. 2015, ApJ, 804, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, R. I., Casertano, S., Riess, A. G., et al. 2016, ApJS, 226, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baade, W. 1926, Astron. Nachr., 228, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Mayor, M., & Poncet, J. L. 1979, Vistas Astron., 23, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borra, E. F., & Deschatelets, D. 2017, MNRAS, 470, 4732 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchy, F., & Sophie Team. 2006, in Tenth Anniversary of 51 Peg-b: Status of and prospects for hot Jupiter studies, eds. L. Arnold, F. Bouchy, & C. Moutou (Paris: Frontier Group), 319 [Google Scholar]
- Brahm, R., Jordán, A., & Espinoza, N. 2017, PASP, 129, 034002 [NASA ADS] [CrossRef] [Google Scholar]
- Britavskiy, N., Pancino, E., Tsymbal, V., et al. 2016, Commmun. Konkoly Observ. Hungary, 105, 105 [Google Scholar]
- Britavskiy, N., Pancino, E., Tsymbal, V., Romano, D., & Fossati, L. 2018, MNRAS, 474, 3344 [CrossRef] [Google Scholar]
- Burki, G., Mayor, M., & Benz, W. 1982, A&A, 109, 258 [NASA ADS] [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, Proc. SPIE, 8446, 84461V [Google Scholar]
- Cropper, M., Katz, D., Sartoretti, P., et al. 2018, A&A, 616, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye & A. F. Moorwood, Proc. SPIE, 4008, 534 [Google Scholar]
- Evans, N. R., Berdnikov, L., Lauer, J., et al. 2015, AJ, 150, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., & Madore, B. F. 2010, ARA&A, 48, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galland, F., Lagrange, A.-M., Udry, S., et al. 2005, A&A, 444, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Kervella, P., Mérand, A., et al. 2012, A&A, 541, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Monnier, J. D., Mérand, A., et al. 2013, A&A, 552, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Mérand, A., Kervella, P., et al. 2015, A&A, 579, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Kervella, P., Mérand, A., et al. 2017, A&A, 608, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Kervella, P., Evans, N. R., et al. 2018, ApJ, 867, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Gallenne, A., Kervella, P., Borgniet, S., et al. 2019, A&A, 622, A164 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gorynya, N. A., Samus’, N. N., Sachkov, M. E., et al. 1998, Astron. Lett., 24, 815 [Google Scholar]
- Groenewegen, M. A. T. 2013, A&A, 550, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 1999, J. Comput. Appl. Math., 109, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 2010, A&A, 509, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., Allard, F., Ferguson, J., Baron, E., & Alexander, D. R. 1999, ApJ, 525, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Hindsley, R., & Bell, R. A. 1986, PASP, 98, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python, online guide [Google Scholar]
- Katz, D., Sartoretti, P., Cropper, M., et al. 2019, A&A, 622, A205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufer, A., & Pasquini, L. 1998, in Optical Astronomical Instrumentation, ed. S. D’Odorico, Proc. SPIE, 3355, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Nardetto, N., Bersier, D., Mourard, D., & Coudé du Foresto, V. 2004, A&A, 416, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Gallenne, A., Remage Evans, N., et al. 2019, A&A, 623, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovtyukh, V. V., & Gorlova, N. I. 2000, A&A, 358, 587 [NASA ADS] [Google Scholar]
- Kovtyukh, V. V., Andrievsky, S. M., Belik, S. I., & Luck, R. E. 2005, AJ, 129, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Leavitt, H. S., & Pickering, E. C. 1912, Harvard Coll. Observ. Circ., 173, 1 [Google Scholar]
- Lindegren, L., & Dravins, D. 2003, A&A, 401, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindemann, F. A. 1918, MNRAS, 78, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E. 2018, AJ, 156, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Malavolta, L., Lovis, C., Pepe, F., Sneden, C., & Udry, S. 2017, MNRAS, 469, 3965 [NASA ADS] [CrossRef] [Google Scholar]
- Mérand, A., Kervella, P., Breitfelder, J., et al. 2015, A&A, 584, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Lagrange, A. M., Mbemba Kabuiku, L., et al. 2017, A&A, 597, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molaro, P., Levshakov, S. A., Monai, S., et al. 2008, A&A, 481, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N. 2018, ArXiv e-prints [arXiv:1801.04158] [Google Scholar]
- Nardetto, N., Mourard, D., Kervella, P., et al. 2006, A&A, 453, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Mourard, D., Mathias, P., Fokin, A., & Gillet, D. 2007, A&A, 471, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Stoekl, A., Bersier, D., & Barnes, T. G. 2008, A&A, 489, 1255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Gieren, W., Kervella, P., et al. 2009, A&A, 502, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Poretti, E., Rainer, M., et al. 2017, A&A, 597, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Poretti, E., Gallenne, A., et al. 2018, A&A, 616, A92 [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Mayor, M., Rupprecht, G., et al. 2002, The Messenger, 110, 9 [NASA ADS] [Google Scholar]
- Pepe, F., Bouchy, F., Mayor, M., & Udry, S. 2018, High-Precision Spectrographs for Exoplanet Research: CORAVEL, ELODIE, CORALIE, SOPHIE and HARPS (Berlin: Springer International Publishing AG), 190 [Google Scholar]
- Queloz, D. 1995, IAU Symp., 167, 221 [Google Scholar]
- Queloz, D., Mayor, M., Udry, S., et al. 2001a, The Messenger, 105, 1 [NASA ADS] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001b, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riess, A. 2018, AAS Meeting Abstract 231, 117.01 [Google Scholar]
- Riess, A. G., Macri, L., Casertano, S., et al. 2011, ApJ, 730, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Rossum, G. 1995, Python Reference Manual (Amsterdam, The Netherlands: Centrum voor Wiskunde en Informatica) [Google Scholar]
- Rucinski, S. M. 1992, AJ, 104, 1968 [NASA ADS] [CrossRef] [Google Scholar]
- Rucinski, S. 1999, ASP Conf. Ser., 185, 82 [Google Scholar]
- Sabbey, C. N., Sasselov, D. D., Fieldus, M. S., et al. 1995, ApJ, 446, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Sartoretti, P., Katz, D., Cropper, M., et al. 2018, A&A, 616, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ségransan, D., Mayor, M., Udry, S., et al. 2011, A&A, 535, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soubiran, C., Jasniewicz, G., Chemin, L., et al. 2013, A&A, 552, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Alapini, A., Israelian, G., & Santos, N. C. 2010, A&A, 512, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Storm, J., Gieren, W., Fouque, P., et al. 2011, VizieR Online Data Catalog: III/53 [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasilyev, V., Ludwig, H.-G., Freytag, B., Lemasle, B., & Marconi, M. 2017, A&A, 606, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wesselink, A. J. 1946, Bull. Astron. Inst. Netherlands, 10, 91 [Google Scholar]
see e.g. for SOPHIE: http://www.obs-hp.fr/guide/sophie/reduction.html
All Tables
All Figures
 |
Fig. 1 Pulsation period (P) distribution of our Cepheid sample. |
| In the text | |
 |
Fig. 2 Typical input observed spectrum. Top: input HARPS β Dor 1D spectrum (black solid line) on the green wavelength range. The continuum interpolation is displayed in red. Broad deep lines that are excluded from the continuum interpolation are highlighted in grey, and wavelength ranges with strong tellurics arehighlighted in orange. Bottom: normalised spectrum. The red solid line is normalised to unity. On both plots, the insert is a zoom on a 100-Å slice of the spectrum (in blue). |
| In the text | |
 |
Fig. 3 Building tailored correlation templates. Top: reference synthetic PHOENIX spectrum (solid black line), with assumed limit on the continuum (solid red line). Line depth ranges corresponding to the weak, medium and deep templates are highlighted (in blue, green, and purple shades, respectively). Comparison with three observed Cepheid spectra, shifted in flux for clarity: δ Cep with HARPS-North (ϕ = 0.37, cyan line), β Dor with HARPS (ϕ = 0.33, yellow line), and ℓ Car with HARPS (ϕ = 0.38, orange line). We point out that these spectra have not been Doppler-shifted from the absolute velocities of the stars. Middle: corresponding weak, medium, and deep correlation templates (blue, green, and purple shades, respectively). Bottom: weighted ALL template (red shade). The default G2 template from the HARPS DRS (black shade) is added for comparison (see text). |
| In the text | |
 |
Fig. 4 Correlation template transparency T (see Table 2) vs. wavelength for our green λ range. The line density of our reference spectrum is plotted in black and the transparency of our four correlation templates in red, blue,green, and purple (ALL, weak, medium, and deep templates, respectively). The template transparency is equivalent to the selected line density within the template (see text). |
| In the text | |
 |
Fig. 5 Cross-correlation function, main line profile observables, and vrad (based on a δ Cep HARPS-North spectrum cross-correlated with our medium template on the green range, see text). From left to right and top to bottom: CCF, normalised CCF, normalised CCF Gaussian fit, normalised CCF biGaussian fit. On all plots the CCF is displayed as a black solid line, the CCF continuum as a solid straight red line and the vrad at the CCF minimum as a vertical dotted black line. On the top left plot, the CCF core vrad range (i.e. Δcore) is highlighted in green. On the top right plot, the area covered by the CCF core and used for the EW and RVcc-c integration is highlighted in green. The letters CT and D designate the contrast and depth of the CCF core, respectively (as defined in the text). On the bottom right plot, the FWHMs corresponding to the blue and red parts of our biGaussian model are displayed as a blue and red arrow, respectively. The inserts are zooms in vrad on the CCF core. |
| In the text | |
 |
Fig. 6 Normalised δ Cep CCFs (top left plot) and main observables phased along the pulsation period, colour-coded with the phase ϕ, based on δ Cep HARPS-North spectra cross-correlated with our ALL template on our green range. On the bottom left plot, δRV denotes the difference between our Gaussian (RVcc-g) and biGaussian (RVcc-2g) vrad. Measurements are displayed as coloured dots and interpolated spline curves as red solid lines, if any. |
| In the text | |
 |
Fig. 7 Combined vrad of FF Aql. Top: centroid vrad (RVcc-c) obtainedwith the ALL template on the green range for four spectrographs, phased (ϕ) along the Cepheid pulsation period and not binary-corrected. Bottom: same, but the vrad have been corrected from the Keplerian orbit of the binary companion. Our best spline curve is displayed as a red solid line. The vrad are corrected only from the Keplerian orbit (no offset correction), based on the orbital parameters recently computed by Gallenne et al. (2019). The red box contains one of our few CORALIE vrad outliers (see text), which we did not take into account to build the spline curve. |
| In the text | |
 |
Fig. 8 Comparison of vrad computation methods for FM Aql SOPHIE vrad (green range, medium template). The x-axis corresponds to RVcc-c. Here, RVcc-g and RVcc-2g are displayed as blue diamonds and red dots, respectively. We point out that the uncertainties on all vrad are displayed but are not necessarily visible. The best linear regressions are displayed as cyan and orange solid lines (along with their 1σ uncertainty in same-colour shades), respectively. The black dashed line corresponds to a slope of 1. The bottom insert corresponds to the residuals of the two linear regressions (same colour code). |
| In the text | |
 |
Fig. 9 Left: slope distribution for the RVcc-g vs RVcc-c and RVcc-2g vs RVcc-c linear regressions (in blue and red shades, respectively). Right: same slope values vs. the pulsation period for each target. The computation was made based on our ALL template on our green range. |
| In the text | |
 |
Fig. 10 Quality of the CCF vs. wavelength range. Left (top, solid lines): comparison of a green and a red CCF of UZ Sct based on the same FEROS spectrum as well as the comparison of a blue and a red CCF of BG Cru (bottom; dashed lines) based on UVES spectra acquired at the same observation epoch with the blue and red arms of UVES, respectively. The bottom UVES CCFs have been shifted downwards for clarity. Middle: histogram of the CCF quality factor Q averaged over the pulsation period P for each studied Cepheid (green: six FEROS and HERMES targets; blue: 24 UVES blue arm targets; red: 30 FEROS, HERMES, and UVES red arm targets; see text). Right: same, but for the histogram of our S/NCCF proxy averaged over P for each target. |
| In the text | |
 |
Fig. 11 CCF vrad vs. wavelength range. Top left: red vs. green linear regression for our six targets (see text): the regression slope is plotted vs. the regression zero-point with green diamonds for HERMES targets and green dots for FEROS targets. Top middle: histogram of red vs. blue vrad slope for our UVES targets. Top right: same, but for the vrad zero-point. Bottom left: amplitude of variation over P of the CCF BIS, plotted for our red range vs. our blue or green range, for the same targets as above (left). Bottom middle: distribution of the red vs. blue vrad slope with P for our UVES targets. Bottom right: same as middle, but for the vrad regression zero-point. |
| In the text | |
 |
Fig. 12 Cross-correlation function and vrad vs. template average line width σℓ. Left: CCFs resulting from the cross-correlation of one observed δ Cep spectrum (see text) with the ALL template built with a variable σℓ within the range 0.02–0.62 Å (y-axis). The CCFs tested at different σℓ are shown in orange and the CCF corresponding to the default σℓ ~ 0.43 used in this study (Table 2) is shown in red. The CCF corresponding to the same δ Cep spectrum and the G2 HARPS DRS template is showed as a dashed black curve and is shifted vertically for clarity. The four right plots show the behaviour of different CCF observables vs. σℓ (from left to right and top to bottom; in red circles): (i) the CCF Q-factor averaged over the 103 δ Cep spectra; (ii) the same but for the averaged S/NCCF criterion; (iii) the slope of the linear regression to the δ Cep BIS time series at a given σℓ vs. the BIS time series at σℓ ~ 0.43; and (iv) the same but for the RVcc-c time series. On the four plots, the red diamond corresponds to the default σℓ used in this study for the ALL template and the black square corresponds to the G2 HARPS DRS template. |
| In the text | |
 |
Fig. 13 HARPS ℓ Car CCFs computed with our four depth-dependent correlation templates on the green λ range. Left: example of the four CCFs corresponding to a same spectrum and our four respective templates. Middle: CCF quality factor Q of ℓ Car vs. pulsation phase (ϕ) for CCFs built based on our four templates (same colour code). Right: same, but for our CCF signal estimator S/NCCF. |
| In the text | |
 |
Fig. 14 CCF quality and asymmetry vs. correlation template. Left: histograms of the CCF Q factor averaged over the pulsation phase for each target, for our four line depth-dependent templates. Middle: same, but for our CCF S/NCCF proxy (same colour code). Right: amplitude of the BIS during the pulsation phase vs. averaged BIS for each target, for our four templates (same colour code). |
| In the text | |
 |
Fig. 15 Comparison of centroid vrad computed with our respective correlation templates on the green range. The figure represents the slope vs. zero-point distribution of the linear regression of the weak (blue), medium (green) and deep (purple) vrad vs. the ALL vrad, respectively. |
| In the text | |
 |
Fig. B.1 Distribution of the mean vrad uncertainties (i.e. averaged over all the vrad measurements for each target), for the vrad computed on the green λ range. Left: ALL template. Right: medium template. The uncertainty distributions are displayed in blue, red, and black shades for RVcc-g, RVcc-2g and RVcc-c, respectively. |
| In the text | |
 |
Fig. B.2 Uncertainties vs. pulsation phase. Based on HARPS-North δ Cep spectra cross-correlated with the ALL template on the green λ range. Left: vrad uncertainties vs. pulsationphase (ϕ), for Gaussian, biGaussian and centroid vrad (blue, red and black dots, respectively); right: BIS uncertainties vs. phase. |
| In the text | |
 |
Fig. B.3 Comparison between our s1d-based CCF computation and the automatic (e2ds-based) DRS CCF computation (see text). For each plot, the data that we obtain from the cross-correlation of the δ Cep HARPS-North (1D) spectra with the G2 template adapted to our green wavelength range (see Sect. 4.5.2) are plotted against the corresponding observables retrieved from the available DRS data (automatically produced from the 2D spectra and the default G2 template). From top to bottom and left to right: Gaussian vrad, Gaussian FWHM, CCF BIS, and CCF depth. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


