| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 7 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201833210 | |
| Published online | 24 August 2018 | |
CRIRES high-resolution infrared spectroscopy of the long-period Cepheid l Carinae⋆
1
Université Côte d’Azur, OCA, CNRS, Lagrange, France
e-mail Nicolas.Nardetto@oca.eu
2
INAF – Osservatorio Astronomico di Brera, Via E. Bianchi 46, 23807 Merate (LC), Italy
3
Fundación Galileo Galilei – INAF, Rambla José Ana Fernandez Pérez 7, 38712 Breña Baja, Spain
4
European Southern Observatory, Alonso de Córdova 3107, 19001Casilla, Santiago, Chile
5
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748Garching b. München, Germany
6
Observatoire Midi-Pyrénées, Laboratoire d’Astrophysique, UMR 5572, Université Paul Sabatier, Toulouse 3, 14 avenue Edouard Belin, 31400 Toulouse, France
7
Departamento de Astronomía, Universidad de Concepción, 160-C Casilla, Concepción, Chile
8
Millenium Institute of Astrophysics, Santiago, Chile
9
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warszawa, Poland
10
LESIA (UMR 8109), Observatoire de Paris, PSL, CNRS, UPMC, Univ. Paris-Diderot, 5 place Jules Janssen, 92195 Meudon, France
11
UMI 3386, Unidad Mixta Internacional Franco-Chilena de Astronomía, CNRS/INSU, France
12
Departamento de Astronomía, Universidad de Chile, Camino El Observatorio, 1515 Las Condes, Santiago, Chile
13
Université de Toulouse, UPS-OMP, Institut de Recherche en Astrophysique et Planétologie, Toulouse, France
14
CNRS, UMR5277, Institut de recherche en Astrophysique et Planétologie, 14 Avenue Edouard Belin, 31400 Toulouse, France
15
Department of Astronomy & Astrophysics, University of Toronto, 50 St. George Street, M5S 3H4 Toronto, ON, Canada
16
Leibniz Institute for Astrophysics, An der Sternwarte 16, 14482 Potsdam, Germany
Received:
11
April
2018
Accepted:
30
May
2018
Context. The dynamical structure of the atmosphere of Cepheids has been well studied in the optical. Several authors have found very interesting spectral features in the J band, but little data have been secured beyond 1.6 μm. However, such observations can probe different radial velocities and line asymmetry regimes, and are able to provide crucial insights into stellar physics.
Aims. Our goal was to investigate the infrared line-forming region in the K-band domain, and its impact on the projection factor and the k-term of Cepheids.
Methods. We secured CRIRES observations for the long-period Cepheid l Car, with a focus on the unblended spectral line NaI 2208.969 nm. We measured the corresponding radial velocities (by using the first moment method) and the line asymmetries (by using the bi-Gaussian method). These quantities are compared to the HARPS visible spectra we previously obtained on l Car.
Results. The optical and infrared radial velocity curves show the same amplitude (only about 3% of difference), with a slight radial velocity shift of about 0.5 ± 0.3 km s−1 between the two curves. Around the minimum radius (phase ≃ 0.9) the visible radial velocity curve is found in advance compared to the infrared one (phase lag), which is consistent with an infrared line forming higher in the atmosphere (compared to the visible line) and with a compression wave moving from the bottom to the top of the atmosphere during maximum outward velocity. The asymmetry of the K-band line is also found to be significantly different from that of the optical line.
Key words: techniques: spectroscopic / stars: oscillations / stars: variables: Cepheids / line: profiles / line: formation
l Car(lowercase l) HD 48410 should not be confused with L Car(uppercase L) HD 90264 or i Car(lowercase i) HD 79447 or I Car(uppercase I) HD 90589 or ι Car(iota) HD 80404. To avoid these misidentifications, ℓ Car (e.g., Nardetto et al. 2009; Anderson et al. 2016) or l Car (e.g., Neilson et al. 2016) have been used instead in the recent literature.
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
For almost a century, the Baade–Wesselink (BW) method is used to derive the distance of Cepheids (Lindemann 1918; Baade 1926; Wesselink 1946). The concept is simple: distances are computed using measurements of the angular diameter over the whole pulsation period along with the stellar radius variations deduced from the integration of the pulsation velocity Vpuls. The pulsation velocity is linked to the observed radial velocity (RV) by the projection factor p = Vpuls/RV (Nardetto et al. 2004, 2017). There are three versions of the BW method corresponding to different ways of determining the angular diameter curve: a photometric version based on infrared surface brightness relations (Fouque & Gieren 1997; Fouqué et al. 2007; Storm et al. 2011a, b); an interferometric version (Lane et al. 2000; Kervella et al. 2004b; Mérand et al. 2005); and a more recent version that combines several photometric bands, velocimetry, and interferometry (SPIPS; Merand et al. 2015). On the other hand, the radial velocity curve is usually derived from optical spectroscopy. This means that the projection factor, which is wavelength-dependent (Nardetto et al. 2009; Neilson et al. 2012), is also calculated in the visible. Infrared spectroscopy can also be used to derive the radius variation, but the projection factor must be calculated consistently, i.e., taking into account both the expected limb darkening of the star in the infrared domain, and the atmospheric velocity gradient as probed by the infrared spectral lines.
On the interferometric side, Cepheids are usually observed at infrared wavelengths, whereas at optical wavelengths the pulsation has actually been resolved for only three stars, β Dor, η Aql (Jacob 2008), and the long-period l Car (Davis et al. 2009). For the latter, the angular diameter curves derived respectively from the infrared surface brightness relation and infrared interferometry are consistent (Kervella et al. 2004a), while it is not the case for the short-period Cepheid δ Cep (Ngeow et al. 2012). Interestingly, a resolved structure around δ Cep has recently been discovered in the visible spectral range using interferometry (Nardetto et al. 2016).
In these three BW approaches an underlying assumption is that the size of the star (i.e., its photosphere, independently of its limb darkening) has the same position whatever the wavelength domain considered. Sasselov & Lester (1990) used the static models from Kurucz (1979) and derived the depth of the photosphere (defined by an optical depth of 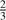 in the continuum) as a function of the wavelength (their Fig. 21). The impact of this effect on the derived distance was estimated to be around 1% or 2% by Nardetto et al. (2011) using a hydrodynamical model of l Car. Another interesting piece of evidence comes from Anderson et al. (2016) who found different motions of l Car by tracing its pulsation with contemporaneous optical velocimetry and infrared interferometry.
in the continuum) as a function of the wavelength (their Fig. 21). The impact of this effect on the derived distance was estimated to be around 1% or 2% by Nardetto et al. (2011) using a hydrodynamical model of l Car. Another interesting piece of evidence comes from Anderson et al. (2016) who found different motions of l Car by tracing its pulsation with contemporaneous optical velocimetry and infrared interferometry.
The dynamical structure of the atmosphere of Cepheids has been well studied in the optical (Sanford 1956; Bell & Rodgers 1964; Karp 1975; Sasselov & Lester 1990; Wallerstein et al. 2015; Nardetto et al. 2006, 2017; Anderson 2014; Anderson et al. 2016), while only a few spectroscopic observations are available in the infrared. At 1.1 μm, Sasselov et al. (1989) used the Fourier Transform Spectrometer (FTS) at the Canada-France-Hawaii Telescope (CFHT) (Maillard & Michel 1982) to monitor two Cepheids, X Sgr (P = 7.013 d) and η Aql (P = 7.177 d). They reported RV curves with systematically larger amplitudes (20–35%) in the infrared than in the optical domain. This result was later confirmed in a subsequent study based on a larger set of infrared spectroscopic data (Sasselov & Lester 1990). In addition, Sasselov & Lester (1994b, c, a) studied the HeI 10830 Å spectral line to model the chromospherical structure of Cepheids.
This paper presents the very first analysis of infrared spectra in the K band (2.2 μm) of the Cepheid l Car. The final goal is to investigate the behavior of the RV curve at such long wavelengths.
2. CRIRES observations of l Car
The cryogenic high-resolution infrared echelle spectrograph CRIRES was located at the Nasmyth focus A of the UT1 of the ESO Very Large Telescope (Kaeufl et al. 2004). It provided a resolving power of up to 100 000 in the spectral range from 1–5.3 μm when used with a 0.2″ slit. The spectra were imaged on a detector mosaic composed of four Aladdin III detectors (4096 × 512 pixel) with a gap of ≃250 pixels between the chips. For all our observations, the spectral range is the same (in nm): [2178–2188], [2191–2201], [2204–2214], [2216–2226].
Our target was the long-period (P = 35.551 d) Galactic Cepheid l Car (HD 84810 HR 3884, variable from V = 3.35 to V = 4.06, G5Iab/b). A detailed investigation of the period rate change over more than a century of observations is given by Breitfelder et al. (2016; +27.283 ± 0.984 s yr−1) and Neilson et al. (2016; +20.23 ± 1.39 s yr−1), who also concluded that l Car does not show evidence of the same enhanced massloss rates measured for δ Cep. However, a compact circumstellar envelope was detected by means of several instruments operating in the infrared (Kervella et al. 2009).
Most of the CRIRES spectra data were secured between April 2 and July 2, 2012. Two spectra were taken in January 2013, and we added two taken in April 2008 (Nardetto et al. 2011). Table 1 reports the log of observations. We used the EsoRex ESO Recipe Execution pipeline to reduce the data. However, the standard wavelength calibration of the spectra based on the thorium-argon lamp was unsuccessful (except for detector 1); therefore, we used the Molecfit ESO sky modeling tool in order to calibrate the data (Smetteet al. 2015; Kausch et al. 2015)1. For this, we compared each observed spectrum with its corresponding atmospheric model generated with Molecfit (including telluric lines) and we derived a mean offset of 10.7 ± 0.3 km s−1. This value was used to calibrate the wavelength of all spectra.
Log and results of the CRIRES observations of l Car.
By using the Atomic Spectra Bibliographic Databases of the National Institute of Standards and Technology (NIST) (Kramida et al. 2016), we were able to identify only one spectral line that was not blended by telluric lines at all phases, i.e., NaI 2208.969 nm (in the wavelength range of detector 3). This line is the second component of a doublet; the first component (NaI 2206.242 nm), albeit within our spectral range of observation, is unfortunately blended by a telluric line, which prevents its analysis (Fig. 1).
 |
Fig. 1. CRIRES spectra corresponding to phase 0.0 are plotted over the four detectors D1–D4. The blue vertical features indicate the telluric lines as identified with the Molecfit ESO sky modeling tool. The atmospheric line indicated on D1 by a red region is blended between phase 0.6–1.0. The NaI doublet appears in D3: the first component (2206.242 nm, red region) is blended, while the second (2208.969 nm, green region) is analyzed in this paper. |
For the first time we explore the spectral region beyond 2.0 μm; the previous studies (Sasselov et al. 1989; Sasselov & Lester 1990) were performed in the 1.08–1.6 μm domain. The line-profile changes are shown in Fig. 2.
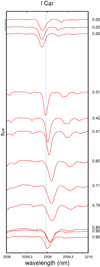 |
Fig. 2. Profile variations in the NaI 2208.969 nm line obtained from the CRIRES spectra of l Car (the reference wavelength is indicated by the blue vertical dotted line). The black vertical line at the top left corresponds to a differential flux of 0.15. The pulsation phases are indicated to the right of each profile. |
From these spectral line profiles, we extract several physical quantities using the methods described in Nardetto et al. (2006). We fit a four-parameter analytic spectral line profile to the data (Eqs. (2) and (3) in Nardetto et al. 2006): the depth of the line, D (quantity without dimension); the wavelength associated with the minimum of the line, λm (in Å); the full width at half maximum (FWHM) in the line (in Å); and the line asymmetry, A (in percentage of the FWHM). All these parameters are listed in Table 1 together with the centroid velocity, RVc, i.e., the first moment of each spectral line profile (Eq. (2) in Nardetto et al. 2006); λm values have been converted into velocities (RVm, not used in this study, but listed for sake of completeness).
3. Comparison between infrared and visible observations
The similarity between the optical and infrared RV curves of Cepheids is not obvious. After the papers in the 1990s mentioned in Sect. 1, our HARPS and CRIRES data of l Car provide one of the few examples currently available with modern instrumentation.
Taking into account the secular period variations (Neilson et al. 2016), we computed a period P = 35.5496 d and a time of maximum brightness Tmax = JD 2456023.533 at the epoch of the CRIRES observations. The CRIRES RVc data (red open squares in Fig. 3) folded with these elements show a time of maximum (receding) RV at BJD 2456053.05 ± 1.0. The uncertainty is mostly due to fixing the real maximum RV phase and consequently the mean RV value. On the other hand, the minimum (approaching) RV is better fixed at BJD 2456025.0 ± 0.5. The minimum RV corresponds to the maximum brightness Tmax, within a narrow phase lag between the two curves (Simon 1984), so the agreement with the Tmax reported above is very satisfactory. We then apply a spline interpolation on these measurements (red solid line).
 |
Fig. 3. CRIRES infrared RV data (NaI 2208.969 nm line, open red squares), HARPS optical RV data (line 605.6 nm, blue open triangles and fitting blue curve), and RVcc−g data (black open circles and fitting black line). |
For comparison purposes, we discuss the HARPS data presented in Nardetto et al. (2009). We used the RVcc−g values, obtained from the Gaussian fit of the cross-correlation function. We computed a period P = 35.5476 d and a Tmax = JD 2453001.573 at the epoch of these observations (January and February 2004). The Tmax value is in excellent agreement with the observed minimum RV, i.e., BJD 2453002.46. We can compare straightforwardly the HARPS (visible) curve with the CRIRES (infrared) curve since the two ephemerides are based on the periods and time of maxima at the time of the respective observations. We also repeated the analysis by computing the phases assuming the same T0 and an average period of 35.5486 d by obtaining very small phase shifts.
To make the comparison, we plot the RVc curve associated with the line 605.6 nm presented in Nardetto et al. (2006) (blue triangles in Fig. 3). We also plot the RVcc−g values and curve used above (black empty circles and black solid line in Fig. 3). We recall (see Nardetto et al. 2009) that the small differences between the RV curve of a line (like RVc for 605.6 nm) and that of the RVcc−g calculated from the whole spectrum is partly due to the fgrad component of the projection factor p, and to the way the RV values are derived (centroid versus Gaussian fit).
The bump seen at phases 0.47, 0.60, and 0.71 in the CRIRES RV might be due to a compression wave traveling in the upper part of the atmosphere (probed by the extended forming regions of infrared lines; see Fig. 21 in Sasselov & Lester 1990) or to small variations in the shapes of the RV curves related to cycle 44 (phases 0.71 and 0.79), cycle 46 (phase 0.47), and cycle 51 (phase 0.60). Such cycle-to-cycle variations are reported in the RV curves of Cepheids (Anderson 2016). We also note that the mean value of the CRIRES curve (red line in Fig. 3) differs by 0.53 ± 0.30 km s−1 from that of the HARPS RVc curve (blue line in Fig. 3). The uncertainty is due to wavelength calibration. Such an offset could be due to the different impact of granulation on the line-forming regions in the optical and infrared. The deeper the line-forming region, the more the mean radial velocity is blueshifted (Vasilyev et al. 2017), which could indicate that the infrared line forms in the upper part of the atmosphere. In order to verify this assumption, we compute the layers (at the maximum radius) corresponding to an optical depth of 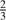 at the center of the lines NaI 2208.969 nm and FeI 605.6 nm from the hydrodynamical model of l Car presented in Nardetto et al. (2007). We found 100% and 20%, respectively (0% corresponds to the photospheric layer, while 100% is the layer at the top of the atmosphere). The core of the NaI 2208.969 nm line thus forms at the top of the atmosphere, conversely to the iron line in the visible.
at the center of the lines NaI 2208.969 nm and FeI 605.6 nm from the hydrodynamical model of l Car presented in Nardetto et al. (2007). We found 100% and 20%, respectively (0% corresponds to the photospheric layer, while 100% is the layer at the top of the atmosphere). The core of the NaI 2208.969 nm line thus forms at the top of the atmosphere, conversely to the iron line in the visible.
We note that the infrared RVc curve has almost the same amplitude as its visible counterpart. This is seen in Fig. 4 where we plot the amplitude of the RVc curve associated with the 17 lines (black dots), including 605.6 nm (blue triangles) of different depths. The infrared line (red squares in Fig. 4) is consistent with the visible RVc amplitudes. For comparison, the amplitude of the RVcc−g (black solid line and circles in Fig. 3) is slightly larger, as already discussed in Nardetto et al. (2017).
 |
Fig. 4. Amplitude of the RVc curves plotted as a function of the line depth for 17 different visible lines (Nardetto et al. 2007; black dots), including the 605.6 nm spectral line (blue triangle), and the infrared line (red square). The horizontal black solid line is the amplitude of velocity associated with RVcc−g. |
Another striking feature of the infrared radial velocity curve is the delay shift with respect to its visible counterpart that can be clearly seen in the descending branch. As proven by the use of different P and T0 values, the shift cannot be explained by the secular changes. The shift observed in the Cepheid l Car is comparable to that observed in RR Lyrae stars by Mathias et al. (1995) between metallic and hydrogen lines in the visible (their Fig. 5), and related to the Van Hoof effect (van Hoof & Struve 1953), i.e., a delay in the velocities associated with the high and low line-forming regions. This effect has also been found in classical and type II Cepheids (Vinko et al. 1998). This can be seen in Fig. 5 where we plot the radius variation associated with visible and infrared lines, respectively. This figure shows that a compression wave moves from the bottom to the top of the atmosphere during maximum outward velocity (phases around 0.9–1.0), which is consistent with Fig. 10 of Sasselov & Lester (1994a) based on a time-dependent model of η Aql. This result seems to indicate, again, that the infrared line-forming region is probably located in the upper part of the atmosphere compared to the optical one, which might also explain why the visible and infrared line asymmetry (A) curves are quite different in shape (Fig. 6). These differences in shape are probably due to different states of temperature and pressure between the bottom and top of the atmosphere, but also to different velocity fields (compression wave traveling).
 |
Fig. 5. Interpolated radial velocity curves of Fig. 3 corrected from their respective velocity offsets and integrated with time in order to plot the radius variation associated with visible and infrared lines as a function of pulsation phase. |
 |
Fig. 6. Infrared (red open squares) and visible (blue open triangles) line asymmetry curves, which are quite different. |
4. Discussion and conclusion
Our analysis of the behavior of the pulsation of l Car in the infrared shows that the RVc curve of the NaI 2208.969 nm has about the same amplitude as the same curve obtained from optical lines, while a delay shift is noticeable in the descending branch (at minimum radius of the star). This observational result at 2.0 μm is different from that observed in the RV curves at 1.1 μm of the Cepheids X Sgr and η Aql, where amplitudes 20–35% larger than the optical values were measured (Sasselov et al. 1989; Sasselov & Lester 1990). The same authors report on a doubling effect in the 1.08 μm line of short-period Cepheids X Sgr, δ Cep, η Aql, and possibly T Mon, but we did not observe it in the 2.2 μm NaI line of the long-period Cepheid l Car (Fig. 2). Low [N/C] and [Na/Fe] ratios are reported in the atmosphere of l Car (Luck & Lambert 2011; Genovali et al. 2015). Such peculiarities can play a role in the occurrence (or not) of atmospheric shockwaves. We recall that we did not find any line doubling in the visible range for δ Cep (Nardetto et al. 2017) or for any Cepheid in our HARPS sample (Nardetto et al. 2006). X Sgr is the only exception and the clear line-doubling was attributed to a double shockwave in the atmosphere (Mathias et al. 2006).
The observed equality between the two amplitudes is physically interesting. In principle, RVc is independent of the width of the spectral line (rotation and micro-turbulence), while it depends on the pulsation velocity (associated with the line-forming region) and the limb-darkening. We refer to the limb darkening within the line and not to the limb darkening in the continuum, which is often used as an approximation of the projection factor decomposition in the visible (Nardetto et al. 2007). Thus, equivalent visible and infrared RVc amplitudes is consistent with similar pulsation velocities and limb darkenings (within the lines). Or conversely, it could indicate that the infrared line region is located in the upper part of the atmosphere as suggested by the hydrodynamical model2, the delay shift (or Van Hoof effect), and the bump around phase 0.7 (dynamical effect or cycle-to-cycle variation). Thus, the pulsation velocity amplitude corresponding to the infrared line-forming region could be larger (compared to visible), which could compensate a weaker limb darkening within the infrared line. In particular, the completely different behavior of the asymmetry of the NaI 2208.969 nm line also seems to indicate that the infrared lines are sensitive to different physical processes with respect to optical lines and/or are formed at a different atmospheric height, which can also modify its RV velocity (Albrow & Cottrell 1996). Eventually, the impact of the granulation on the infrared line-forming region can contribute to the observed velocity shift between optical and infrared lines.
In any case, these results clearly indicate that the differences between infrared and optical high-resolution spectroscopy are a key to better understanding the dynamics of the atmospheres of Cepheids. In particular, it could help in disclosing the true nature of the so-called k-term, i.e., the apparent systematic blueshifted motion at the level of a few km s−1 shown by all Cepheids (e.g., Nardetto et al. 2009; Vasilyev et al. 2017). Simultaneous spectra acquired with new-generation, broadrange echelle spectrographs, like GIANO (Origlia et al. 2014) and its updated version GIARPS (Claudi et al. 2016) at the Telescopio Nazionale Galileo, or CRIRES+ at ESO (Follert et al. 2014), will be particularly helpful in this context.
Thanks to the new and larger CRIRES data set, we realized that two measurements (out of four) presented in Nardetto et al. (2011; spectra at phase 0.27 and 0.78 in their Fig. 3; see also Sect. 4) were critically affected by an artifact in the wavelength calibration that could not be corrected. This led to an incorrect estimate of the infrared radial velocity amplitude and an incorrect line identification, while the general conclusions of the paper remain unchanged. These two measurements are not used in the present study.
Available at http://cdsweb.u-strasbg.fr/
Acknowledgments
Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programme 089.D-0726(A). This research has made use of the SIMBAD and VIZIER3 databases at CDS, Strasbourg (France), and of electronic bibliography maintained by the NASA/ADS system. NN and EP acknowledge the Observatoire de la Côte d’Azur for the one-month grant that allowed EP to work at OCA in June and July 2017. EP acknowledges financial support from PRIN INAF-2014. WG gratefully acknowledges financial support for this work from the BASAL Centro de Astrofisica y Tecnologias Afines (CATA) AFB-170002, and from the Millenium Institute of Astrophysics (MAS) of the Iniciativa Cientifica Milenio del Ministerio de Economia, Fomento y Turismo de Chile, project IC120009. Support from the Polish National Science Center grant MAESTRO 2012/06/A/ST9/00269 is also acknowledged. EP and MR acknowledge financial support from PRIN INAF-2014. NN, PK, AG, and WG acknowledge the support of the French–Chilean exchange program ECOS-Sud/CONICYT (C13U01). BP acknowledges financial support from the Polish National Science Center grant SONATA 2014/15/D/ST9/02248. The authors acknowledge the support of the French Agence Nationale de la Recherche (ANR), under grant ANR-15-CE31-0012-01 (project UnlockCepheids) and the financial support from “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, France.
References
- Albrow, M. D., & Cottrell, P. L. 1996, MNRAS, 278, 337 [NASA ADS] [Google Scholar]
- Anderson, R. I. 2014, A&A, 566, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, R. I. 2016, MNRAS, 463, 1707 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, R. I., Mérand, A., Kervella, P., et al. 2016, MNRAS, 455, 4231 [NASA ADS] [CrossRef] [Google Scholar]
- Baade, W. 1926, Astron. Nachr., 228, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, R. A., & Rodgers, A. W. 1964, MNRAS, 128, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Breitfelder, J., Mérand, A., Kervella, P., et al. 2016, A&A, 587, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claudi, R., Benatti, S., Carleo, I., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, Proc. SPIE, 9908, 99081A [CrossRef] [Google Scholar]
- Davis, J., Jacob, A. P., Robertson, J. G., et al. 2009, MNRAS, 394, 1620 [NASA ADS] [CrossRef] [Google Scholar]
- Follert, R., Dorn, R. J., Oliva, E., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 914719 [CrossRef] [Google Scholar]
- Fouque, P., & Gieren, W. P. 1997, A&A, 320, 799 [NASA ADS] [Google Scholar]
- Fouqué, P., Arriagada, P., Storm, J., et al. 2007, A&A, 476, 73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genovali, K., Lemasle, B., da Silva, R., et al. 2015, A&A, 580, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jacob A. P., 2008, PhD Thesis, University of Sydney, Australia [Google Scholar]
- Kaeufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, in Ground-based Instrumentation for Astronomy, eds. A. F. M., Moorwood, & M. Iye, SPIE Conf. Ser., 5492, 1218 [Google Scholar]
- Karp, A. H. 1975, ApJ, 201, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Fouqué, P., Storm, J., et al. 2004a, ApJ, 604, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Nardetto, N., Bersier, D., Mourard, D., & Coudé du Foresto, V. 2004b, A&A, 416, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Mérand, A., & Gallenne, A. 2009, A&A, 498, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramida, A., Ralchenko, Y., & Reader, J. 2016, in APS Division of Atomic, Molecular and Optical Physics Meeting Abstracts [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lane, B. F., Kuchner, M. J., Boden, A. F., Creech-Eakman, M., & Kulkarni, S. R. 2000, Nature, 407, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Lindemann, F. A. 1918, MNRAS, 78, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., & Lambert, D. L. 2011, AJ, 142, 136 [Google Scholar]
- Maillard, J. P., & Michel, G. 1982, in IAU Colloq. 67: Instrumentation for Astronomy with Large Optical Telescopes, ed. C. M. Humphries, Astrophys. Space Sci. Lib., 92, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Mathias, P., Gillet, D., Fokin, A. B., & Chadid, M. 1995, A&A, 298, 843 [NASA ADS] [Google Scholar]
- Mathias, P., Gillet, D., Fokin, A. B., et al. 2006, A&A, 457, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Kervella, P., Coudé du Foresto, V., et al. 2005, A&A, 438, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merand, A., Kervella, P., Breitfelder, J., et al. 2015, A&A, 584, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Fokin, A., Mourard, D., et al. 2004, A&A, 428, 131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Mourard, D., Kervella, P., et al. 2006, A&A, 453, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Mourard, D., Mathias, P., Fokin, A., & Gillet, D. 2007, A&A, 471, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Gieren, W., Kervella, P., et al. 2009, A&A, 502, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Fokin, A., Fouqué, P., et al. 2011, A&A, 534, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Mérand, A., Mourard, D., et al. 2016, A&A, 593, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Poretti, E., Rainer, M., et al. 2017, A&A, 597, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., Nardetto, N., Ngeow, C.-C., Fouqué, P., & Storm, J. 2012, A&A, 541, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., Engle, S. G., Guinan, E. F., Bisol, A. C., & Butterworth, N. 2016, ApJ, 824, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ngeow, C.-C., Neilson, H. R., Nardetto, N., & Marengo, M. 2012, A&A, 543, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Origlia, L., Oliva, E., Baffa, C., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91471E [Google Scholar]
- Sanford, R. F. 1956, ApJ, 123, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Sasselov, D. D., & Lester, J. B. 1990, ApJ, 362, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Sasselov, D. D., & Lester, J. B. 1994a, ApJ, 423, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Sasselov, D. D., & Lester, J. B. 1994b, ApJ, 423, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Sasselov, D. D., & Lester, J. B. 1994c, ApJ, 423, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Sasselov, D. D., Fieldus, M. S., & Lester, J. B. 1989, ApJ, 337, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, N. R. 1984, ApJ, 284, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Storm, J., Gieren, W., Fouqué, P., et al. 2011a, A&A, 534, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Storm, J., Gieren, W., Fouqué, P., et al. 2011b, A&A, 534, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Hoof, A., & Struve, O. 1953, PASP, 65, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Vasilyev, V., Ludwig, H.-G., Freytag, B., Lemasle, B., & Marconi, M. 2017, A&A, 606, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vinko, J., Remage Evans, N., Kiss, L. L., & Szabados, L. 1998, MNRAS, 296, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G., Albright, M. B., & Ritchey, A. M. 2015, PASP, 127, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Wesselink, A. J. 1946, Bull. Astron. Inst. Neth., 10, 91 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. CRIRES spectra corresponding to phase 0.0 are plotted over the four detectors D1–D4. The blue vertical features indicate the telluric lines as identified with the Molecfit ESO sky modeling tool. The atmospheric line indicated on D1 by a red region is blended between phase 0.6–1.0. The NaI doublet appears in D3: the first component (2206.242 nm, red region) is blended, while the second (2208.969 nm, green region) is analyzed in this paper. |
| In the text | |
 |
Fig. 2. Profile variations in the NaI 2208.969 nm line obtained from the CRIRES spectra of l Car (the reference wavelength is indicated by the blue vertical dotted line). The black vertical line at the top left corresponds to a differential flux of 0.15. The pulsation phases are indicated to the right of each profile. |
| In the text | |
 |
Fig. 3. CRIRES infrared RV data (NaI 2208.969 nm line, open red squares), HARPS optical RV data (line 605.6 nm, blue open triangles and fitting blue curve), and RVcc−g data (black open circles and fitting black line). |
| In the text | |
 |
Fig. 4. Amplitude of the RVc curves plotted as a function of the line depth for 17 different visible lines (Nardetto et al. 2007; black dots), including the 605.6 nm spectral line (blue triangle), and the infrared line (red square). The horizontal black solid line is the amplitude of velocity associated with RVcc−g. |
| In the text | |
 |
Fig. 5. Interpolated radial velocity curves of Fig. 3 corrected from their respective velocity offsets and integrated with time in order to plot the radius variation associated with visible and infrared lines as a function of pulsation phase. |
| In the text | |
 |
Fig. 6. Infrared (red open squares) and visible (blue open triangles) line asymmetry curves, which are quite different. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


