| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A175 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935375 | |
| Published online | 19 November 2019 | |
Stellar mass–halo mass relation for the brightest central galaxies of X-ray clusters since z ∼ 0.65
1
Max Planck institute for extraterrestrial physics, Garching by Munich, Germany
e-mail: erfanian@mpe.mpg.de
2
University of Helsinki, Department of Physics, PO Box 64, 00014 Helsinki, Finland
3
Astrophysics Research Institute, Liverpool John Moores University, IC2, Liverpool Science Park, 146 Brownlow Hill, Liverpool L3 5RF, UK
4
Excellence Cluster Universe, Boltzmannstr. 2, 85748 Garching bei München, Germany
5
INAF/Osservatorio Astronomico di Trieste, Via G. B. Tiepolo 11, 34131 Trieste, Italy
6
Department of Physics, University of Bath, Claverton Down, Bath BA2 7AY, UK
7
School of Astronomy, Institute for Research in Fundamental Sciences (IPM), Tehran 19395-5531, Iran
8
Faculty of Physics, Ludwig-Maximilians-Universität, Scheinerstr. 1, 81679 Munich, Germany
9
Kavli Institute for Particle Astrophysics & Cosmology, Stanford University, PO Box 2450, Stanford, CA 94305, USA
10
SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA
11
IRAP, Université de Toulouse, CNRS, UPS, CNES, Toulouse, France
12
Finnish centre for Astronomy with ESO (FINCA), University of Turku, Quantum, Vesilinnantie 5, 20014 Turku, Finland
13
Helsinki Institute of Physics, University of Helsinki, PO Box 64, 00014 Helsinki, Finland
14
School of Physics and Astronomy, University of St Andrews, North Haugh, St Andrews KY16 9SS, UK
15
Department of Physics and Astronomy, University of Utah, 115 S. 1400 E., Salt Lake City, UT 84112, USA
16
Steward Observatory, University of Arizona, 933 North Cherry Avenue, Tucson, AZ 85721, USA
17
Department of Astronomy and Astrophysics, The Pennsylvania State University, University Park, PA 16802, USA
18
Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA 16802, USA
Received:
26
February
2019
Accepted:
12
July
2019
We present the brightest cluster galaxies (BCGs) catalog for SPectroscoic IDentification of eROSITA Sources (SPIDERS) DR14 cluster program value-added catalog. We list the 416 BCGs identified as part of this process, along with their stellar mass, star formation rates (SFRs), and morphological properties. We identified the BCGs based on the available spectroscopic data from SPIDERS and photometric data from SDSS. We computed stellar masses and SFRs of the BCGs on the basis of SDSS, WISE, and GALEX photometry using spectral energy distribution fitting. Morphological properties for all BCGs were derived by Sersic profile fitting using the software package SIGMA in different optical bands (g,r,i). We combined this catalog with the BCGs of galaxy groups and clusters extracted from the deeper AEGIS, CDFS, COSMOS, XMM-CFHTLS, and XMM-XXL surveys to study the stellar mass–halo mass relation using the largest sample of X-ray groups and clusters known to date. This result suggests that the mass growth of the central galaxy is controlled by the hierarchical mass growth of the host halo. We find a strong correlation between the stellar mass of BCGs and the mass of their host halos. This relation shows no evolution since z ∼ 0.65. We measure a mean scatter of 0.21 and 0.25 for the stellar mass of BCGs in a given halo mass at low (0.1 < z < 0.3) and high (0.3 < z < 0.65) redshifts, respectively. We further demonstrate that the BCG mass is covariant with the richness of the host halos in the very X-ray luminous systems. We also find evidence that part of the scatter between X-ray luminosity and richness can be reduced by considering stellar mass as an additional variable.
Key words: galaxies: evolution / galaxies: clusters: general / galaxies: groups: general / X-rays: galaxies: clusters / galaxies: elliptical and lenticular, cD
© G. Erfanianfar et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
The brightest cluster galaxies (BCGs) are the most luminous galaxies among the member galaxies in a cluster. These galaxies usually reside close to the optical and X-ray centers of galaxy clusters (or groups), depending on the dynamical state of the clusters. Previous studies show that BCGs do not follow the same luminosity function as satellite galaxies (Tremaine & Richstone 1977), suggesting a distinct evolutionary path resulting in a unique set of properties. Moreover, the unique location of these luminous galaxies link their origin and evolution with the evolution of their host clusters, and therefore can provide direct information on the formation history of large-scale structures in the Universe (Conroy et al. 2007).
Although, many pioneering studies have attempted to establish a single scenario for BCG formation (Fabian 1994; Cowie & Binney 1977; Fabian & Nulsen 1977; Ostriker & Hausman 1977; Ostriker & Tremaine 1975; Kormendy 1984; Merritt 1983, 1984), recent studies have generally suggested that no single scenario can fully explain all aspects of BCGs (Brough et al. 2007; Loubser & Sánchez-Blázquez 2012; Jimmy et al. 2013). For instance, BCGs display a very diverse range of mass-to-light ratios, of sizes at a given mass, and spatial distributions of their stellar populations (Von Der Linden et al. 2007; Loubser & Sánchez-Blázquez 2012).
There are many unanswered questions on the formation and evolution of BCGs. In the current paradigm of structure formation in the universe, galaxies form within their cold dark matter halos. These dark matter halos mainly form and evolve by gravity. However, the assembly of the stellar content of galaxies is regulated by the more complex physics of gas cooling, heating, and consumption by star formation as well as merger events. According to numerical simulations and semi-analytical models, BCGs form through a two-fold process. At high redshifts, the stellar mass component of BCGs is initially created through the collapse of cooling gas or gas-rich mergers. The BCGs continue to grow essentially by dissipationless processes such as dry mergers (De Lucia & Blaizot 2007; Naab et al. 2009; Laporte et al. 2012). In general, observations confirm this formation scenario; however, some studies imply that the key mechanism for the evolution of BCGs is feedback rather than merging (e.g., Ascaso et al. 2011).
In order to understand how the hierarchical growth of structures regulates the properties of a galaxy, we should quantify the relation between dark matter halos and the properties of the galaxies they host. Specifically, the stellar mass–halo mass relation provides powerful constraints on the galaxy formation process that any successful model should be able to account for. Moreover, the mass ratio of the stellar mass of BCGs to their host group or cluster reveals how efficiently the baryonic component has been converted into stars. Both direct and indirect methods have been employed to study this relation. Direct measurements of halo mass include X-ray observations, the Sunyaev−Zeldovich effect, galaxy−galaxy lensing, and satellite kinematics within galaxy groups and clusters (e.g., Lin & Mohr 2004; Yang et al. 2007; Hansen et al. 2009; Kravtsov et al. 2004; Gozaliasl et al. 2019). Indirect methods include halo occupation distribution (HOD) modeling (Yang et al. 2003; Leauthaud et al. 2011, 2012; Zehavi et al. 2011; Parejko et al. 2013; Guo et al. 2014), conditional luminosity function modeling (Yang et al. 2009), and abundance matching techniques (Colín et al. 1999; Kravtsov & Klypin 1999; Kravtsov et al. 2004; Tasitsiomi et al. 2004; Vale & Ostriker 2004; van den Bosch et al. 2005; Conroy et al. 2006; Shankar et al. 2006; Vale & Ostriker 2006; Conroy & Wechsler 2009; Behroozi et al. 2010; Guo et al. 2010; Moster et al. 2010; Hearin & Watson 2013; Reddick et al. 2013). In this work, we examine the stellar mass–halo mass relation of BCGs using a sample of X-ray groups and clusters with the widest halo mass range available to date. To this end, we perform a search based on the photometric and spectroscopic redshifts provided by the Sloan Digital Sky Survey (SDSS DR14) to identify BCGs of clusters found in SPectroscoic IDentification of eROSITA Sources–COnstrain Dark Energy with X-ray clusters (SPIDERS-CODEX). We provide properties of galaxies such as stellar mass, star formation rate (SFR), and structural parameters for this BCG sample. This catalog is combined with BCG catalogs extracted from the deeper All-wavelength Extended Groth strip International Survey (AEGIS) (Erfanianfar et al. 2013), Cosmological Evolution Survey (COSMOS) (Finoguenov et al. 2007; George et al. 2011, 2013), ECDFS survey (Erfanianfar et al. 2014), XMM-CFHTLS (Mirkazemi et al. 2015), and XMM-XXL survey (Pierre et al. 2016) to widen the halo mass range probed. The BCGs in all surveys are identified and characterized following identical methods. In Sect. 3 we present the X-ray cluster catalog and optical data that we used in this work. In Sect. 3 we explain the method for determining the various BCG properties. In Sect. 4 we present the stellar mass–halo mass relation. We discuss and summarize our findings in Sect. 5. Throughout, we adopt a (Chabrier 2003) initial mass function (IMF), and a cosmology with H0 = 71 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7. The BCG value-added catalog (VAC) is available through the SDSS website1.
2. Data
Our study is based upon a sample of BCGs drawn from a variety of datasets. The primary sample of this work is that produced from the SDSS SPIDERS-CODEX sample of galaxy clusters; we systematically and objectively identify 416 BCGs from this dataset and present a catalog of the properties of these objects in this paper. We supplement this sample with BCGs drawn from five previous surveys. In this section we describe the basic specifications of the six surveys.
2.1. CODEX–SPIDERS
The SPIDERS-CODEX survey is one of the projects of the Sloan Digital Sky Survey-IV (SDSS-IV; Blanton et al. 2017). The SPIDERS survey (Clerc et al. 2016) obtains spectra of X-ray sources using the SDSS telescope and spectrograph (Gunn et al. 2006; Smee et al. 2013) covering the optical and near-infrared (NIR) at a spectral resolution of approximately 2000. The host groups and clusters in our study are drawn from the catalog of spectroscopically confirmed X-ray detected clusters in the Data Release 14 the SDSS (DR14; Abolfathi et al. 2018).
Galaxy clusters were initially identified via the emission of their hot baryonic component as X-ray extended sources in ROSAT (ROentgen SATellite) and XMM-Newton observations. The initial redshift was assigned to these clusters using the red-sequence method. Spectroscopic redshifts obtained by SPIDERS (DR14) provided confirmation of the clustered nature of these objects and their redshift (up to z ∼ 0.65). The gas properties derived from X-ray observations, such as luminosity and R500, were derived using precise cluster redshifts and these properties provide an estimate of their total mass M200 following Leauthaud et al. (2010) and assuming a standard evolution of scaling relations, i.e., 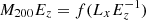 , where Ez = (Ωm(1 + z)3 + ΩΛ)1/2 (median M200 ∼5 × 1014 M⊙) (Clerc et al. 2016). We used only those clusters with a single optical counterpart from this catalog.
, where Ez = (Ωm(1 + z)3 + ΩΛ)1/2 (median M200 ∼5 × 1014 M⊙) (Clerc et al. 2016). We used only those clusters with a single optical counterpart from this catalog.
2.2. AEGIS, COSMOS, and CDFS
A full description of the data available in the AEGIS, COSMO, and CDFS fields is provided in Sect. 2.1 of Erfanianfar et al. (2014). Briefly, all of these fields have been covered by deep Chandra and XMM-Newton observations (Erfanianfar et al. 2014; Finoguenov et al. 2007; George et al. 2011, 2013). In addition to deep X-ray data, all of these surveys take advantage of deep multiwavelength imaging data extending to the radio regime and a dense (optical) spectroscopic sampling. We used clusters and groups in these fields with an assigned identification flag equal to 1 and redshifts below z = 0.65. These criteria add an additional 45 (typically less massive) X-ray groups to our full sample.
2.3. XMM-CFHTLS
The XMM-CFHTLS catalog has been constructed through a series of short XMM-Newton observations of faint RASS (ROSAT all-sky survey) sources in the CFHTLS wide fields (Mirkazemi et al. 2015). We used the T0007 data release of CFHTLS and its corresponding photometric redshift catalog. The photometric redshifts were computed using the methods of Ilbert et al. (2006) and Coupon et al. (2009). The spectroscopic redshifts were derived from a series of Hectospec observations with MMT (Fabricant et al. 2005; Mirkazemi et al. 2015). We also added the spectroscopic data from DR14 SDSS to this sample. We used in total 75 X-ray clusters from XMM-CFHTLS with 0.1 < z < 0.65.
2.4. XMM-XXL
The XXL Survey is the largest area (50 deg2) XMM program to date (Pierre et al. 2016) with the aim of identifying several hundred galaxy clusters along with several tens of thousands of AGNs in the [0.5–2] keV band. We used those clusters which overlap with the W1 field of CFHTLS to take advantage of the photometric and spectroscopic data available in this wide field. In total, this adds 25 (predominantly massive) X-ray clusters from XMM-XXL to our study. Figure 1 shows the M200–redshift relation for the full sample of groups and clusters used in this work.
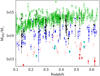 |
Fig. 1. Cluster M200–redshift plane for CODEX-SPIDERS (green cross), AEGIS (cyan filled square), COSMOS (pink diamond), CDFS (point down red triangle), XMM-CFHTLS (point-up blue triangle), and XMM-XXL (black filled circle) surveys used in this work. |
2.5. Data base summary
Our sample of clusters includes 416 from SPIDERS and 110 from the other five cluster surveys. During our analysis we detected two duplications between these surveys. There was one cluster in common between CODEX and CFHTLS and one between CODEX and XMM-XXL. The X-ray properties were consistent. However, we kept those from CFHTLS and XMM-XXL due to deeper X-ray and optical data. The locations in the mass-redshift plane of the 526 unique clusters in our total sample is presented in Fig. 1. The clusters cover redshifts between 0.1 and 0.65.
3. Method
3.1. BCG selection
In many previous studies, BCGs have been identified via visual inspection. However, for a large sample of groups and clusters, it is not an efficient approach. In order to cope with this problem, we selected BCGs based on their photometric and spectroscopic properties. For the CODEX-SPIDERS sample, we considered all clusters from the DR14 cluster catalog that have at least one member with a spectroscopic redshift (Clerc et al. 2016). According to Clerc et al. (2016), in the process of cluster identification, for some X-ray sources, two optical counterparts have been assigned. We did not consider these counterparts in this analysis to exclude any uncertainties they could impose on this work. This sample includes 439 clusters. This catalog contains both X-ray and optical centers. The X-ray center is the center of X-ray sources in the ROSAT observation. Owing to the large RASS survey point spread function (PSF) with a full width half maximum (FWHM) of ∼4 arcmin (Boese 2000), these centers have a relatively large uncertainty associated with them. The second centers in the catalog are the optical centers (Rykoff et al. 2014). The photometry and photometric redshifts of all objects within three virial radii (3 × r200) from the optical center were extracted from SDSS. We only considered those galaxies that have a good photometry flag. Photometric redshifts from DR14 SDSS were substituted for spectroscopic redshifts when available. In order to model the photometric redshifts based on the cModeli magnitude of galaxies (Fig. 2), we used galaxies with spectroscopic redshift at the same distance from the cluster centers. We needed this model to know how to select member galaxies based on their photometric redshifts. We used this model, the optical center, and the redshift of the clusters to identify member galaxies. According to the galaxies’ i-band magnitude and the model, we chose those galaxies that are within 3 × σmodel as member galaxies.
 |
Fig. 2. Relation (Photometric redshifts–Spectroscopic redshifts)/(1 + Spectroscopic redshifts) (Δz) vs. i-band cModel magnitude for a sample of galaxies with both spectroscopic and photometric redshifts in SDSS DR14 (gray dots). The black pluses and black solid line show the dispersion and peak of the Gaussian fitted in each i-band magnitude bin, respectively. There are in total 17 bins. The red dashed lines indicate the model fitted to the dispersions. |
Appendix A demonstrates the reliability of this method in selecting member galaxies based on the photometric redshifts. Using the halo lightcone catalog from the MillenniumXXL simulation, we show that the accuracy of BCG selection based on the photometric redshift of galaxies is ∼88%. In case a spectroscopic redshift has been measured, we consider that galaxy as a cluster member if its redshift falls within 0.01 × (1 + zcluster). After selecting member galaxies with this method, we chose BCGs as the brightest member galaxy inside 1 × r200 from the optical center; 81% of BCGs have both spectroscopic and photometric redshifts. Figure 4 presents the distance of the BCGs from the optical and X-ray centers normalized by R200. Most of the BCGs (79%) reside in ∼0.05 × r200 from optical center. Approximately 92% and 84% of BCGs reside in 0.5 × R200 from optical center and X-ray center, respectively. To produce a homogeneous BCG sample, we selected the BCGs using the same procedure as for CODEX-SPIDERS for all of five other fields (see Fig. 3).
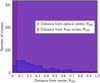 |
Fig. 4. Distance of the BCGs from the optical and X-ray centers normalized by R200. Of the BCGs, 79% reside in ∼0.05 × r200 from optical center, and 92% and 84% of BCGs reside in 0.5 × R200 from optical center and X-ray center, respectively. |
3.2. Stellar mass and star formation rate
We computed the SFR and stellar masses for the BCGs of CODEX-SPIDERS clusters using Le PHARE (PHotometric Analysis for Redshift Estimations; Arnouts et al. 2001; Ilbert et al. 2006), a publicly available code based on a χ2 template fitting procedure. We used Galaxy Evolution Explorer (GALEX) data for the ultraviolet (UV) part of the spectrum. The GALEX instrument provides UV broadband information: far-UV (FUV, 1344–1786 Å) and near-UV (NUV, 1771–2831 Å). For the optical part of the spectrum we used SDSS u, g, r, i, z cModel magnitudes. We also used Wide-Field Infrared Survey Explorer (WISE) forced photometry (Lang et al. 2016) for the infrared part of spectrum.
We followed the procedure described in Ilbert et al. (2009, 2010). First we adjusted the photometric zero points, as explained in Ilbert et al. (2006). Namely, using a χ2 minimization at fixed cluster redshift, we determined for each galaxy the corresponding best-fitting COSMOS templates (included in the package; see Ilbert et al. 2006). Dust extinction was applied to the templates using the Calzetti et al. (2000) law, with E(B − V) in the range 0–0.5 and with a step of 0.1. We applied the systematic zero-point offsets to the observed-frame photometry and computed the SFR and stellar masses using LePHARE, following the recipe of Ilbert et al. (2010). The spectral energy distribution (SED) templates for the computation of mass and SFR were generated with the stellar population synthesis package developed by Bruzual & Charlot (2003, hereafter BC03). We assume a universal IMF from Chabrier (2003) and an exponentially declining SF history, SFR ∝ e−t/τ (with 0.1 < τ < 30 Gyr). The SEDs were generated for a grid of 51 ages (spanning a range from 0.1 Gyr to 13.5 Gyr). We also included emission lines appropriate for the templates as described in Ilbert et al. (2010). We replaced the SFR from SED fitting with those from MPA-JHU VAC. Stellar mass estimates for the other fields in this work were derived through SED fitting by Le PHARE (Ilbert et al. 2010; Erfanianfar et al. 2014; Mirkazemi et al. 2015). Consistent stellar mass estimations are key to prevent potential biases in the analysis of our combined sample.
3.3. Structure parameters
The BCGs in the SPIDERS sample were modeled using GALFIT (Peng et al. 2010) through the Structural Investigation of Galaxies via Model Analysis code (SIGMA), which is the host pipeline that runs GALFIT (Kelvin et al. 2012; see relevant sections in Furnell et al. 2018). An R-based pipeline software previously used in the GAMA (Galaxy And Mass Assembly) survey (Driver et al. 2011), SIGMA provides model light profiles for ∼105 GAMA galaxies in five optical (SDSS−ugriz) and four NIR (UKIRT−YJHK) passbands (see Hill et al. 2011). This pipeline is capable of performing a full fit, including: object extraction through Source Extractor (SExtractor; Bertin & Arnouts 1996), creating a model of the field PSF (PSFEx; Bertin 2011), estimating the local sky about an object, masking external objects and, finally, fitting a two-dimensional light profile through GALFIT. We provide fits for our BCGs in three bands (gri) for three models: a de Vaucouleurs profile (n = 4), a free Sersic profile (1 < n < 20), and a free Sersic + fixed exponential (n = 1) dual-component model (Furnell et al. 2018). Table 1 lists the columns of the CODEX-SPIDES VAC; C1 and C2 refer to the first and second components to a model, for the S+X model; C1 is the Sersic bulge and C2 is the exponential halo.
CODEX-SPIDERS DR14 BCGs value-added catalog.
4. Stellar mass–halo mass relation
In this section, we explore the connection between the stellar mass of BCGs and the halo mass of their host groups or clusters. For this purpose, we divide our sample into two redshift bins (low redshift: 0.1 ≤ z ≤ 0.3 and high redshift: 0.3 < z ≤ 0.65). This is also done in order to take into account different sampling of X-ray luminosity with redshift. First, we compare the stellar mass of BCGs with the halo mass of their host groups and clusters (see Fig. 5). The red and blue shaded points show the individual BCGs and the blue and red lines represent the fitted power-law model. The shaded areas indicate the corresponding 95% confidence levels. The blue and red points with error bars present the geometric mean of BCG stellar masses for a given halo mass. The stellar mass of BCGs and their host halo masses correlate significantly, with Pearson correlation coefficients of 0.7 and 0.4 in the low and high redshift bins, respectively. The two scaling relations agree with each other within their uncertainties. We do not observe any notable redshift evolution in the relation between the central galaxy stellar mass and the host halo mass since z ∼ 0.65. The best power-law fitted model is listed in Table 2. We also report the mean and the corresponding scatters in Table 3. The bins of halo masses are chosen such that each bin includes at least 15 clusters.
 |
Fig. 5. Stellar masses vs. halo masses of the BCGs in our sample. Different symbols represent different surveys. The blue shaded symbols show BCGs with 0.1 ≤ z ≤ 0.3 and the red shaded symbols show BCGs with 0.3 < z ≤ 0.65. The blue dashed and the red dash-dotted lines show the best power-law fits for the low and high redshifts, respectively. The blue and red shaded area around the fitted lines represent 95% confidence levels of the fits. The blue squares and red dots with error bars present the mean of stellar mass of BCGs at a given halo mass. The error bars are their standard errors. The Pearson correlation coefficient is 0.7 for low redshift BCGs and 0.4 for high redshift BCGs. |
Best-fit power-law parameters for the stellar mass–halo mass relation.
Mean of stellar mass of BCGs in a given halo mass.
Figure 6 shows the dispersion in the stellar mass of BCGs at a given halo mass (σlog M*). This scatter is one of the most fundamental aspects of the relationship between the galaxies and their host halos (Wechsler & Tinker 2018). In abundance matching models, we can derive the same stellar mass function from different choices for scatter, but the predicted spatial distribution of galaxies would be different. This directly impacts the clustering of galaxies. As massive halos (Mh > 1012 M⊙) get more clustered, thus galaxies at high masses have the highest sensitivity to this scatter (Wechsler & Tinker 2018). We derive a value of 0.21 and 0.25 for the mean scatter of the stellar mass at a given halo mass at low and high redshifts, respectively. The slightly higher scatter at high redshift is consistent with the larger uncertainties of stellar mass estimates. This is the first time that this scatter is quantified directly using a sample of X-ray groups and clusters over a halo mass range spanning 13 < log(M200/M⊙) < 15.4. Previously, Kravtsov et al. (2018), using a small sample of local clusters, derived a value of (σlog M*)∼0.19. Moreover, Zu & Mandelbaum (2015) obtained a constraint on the scatter at Mh ∼ 1014 M⊙ (σlog M* = 0.18 ± 0.01) using a combination of galaxy clustering and galaxy lensing of z = 0 SDSS galaxies. Current predictions from the semi-analytic and empirical models have consistent scatter in the halo mass range considered in this work (Henriques et al. 2015; Lu et al. 2014; Somerville et al. 2012; Behroozi et al. 2019, see Fig. 8 in Wechsler & Tinker 2018). However, some of hydrodynamical simulations predict a scatter below 0.2 dex at the high-mass end (Khandai et al. 2015; McAlpine et al. 2016; Pillepich et al. 2018). We note that the observed σlog M* constitutes the quadratic sum of intrinsic scatter and measurement uncertainties on stellar masses. A proper understanding of the measurement error in stellar mass is thus required to infer the intrinsic scatter. In this work, we consider as sources of the measurement dispersion both the propagated uncertainties in the photometry and the photometric redshifts based thereupon.
 |
Fig. 6. Scatter in the stellar mass of BCGs at a given halo mass in low and high redshift bins. The scatter is the quadratic sum of intrinsic scatter and measurement scatter of stellar masses. |
Figure 7 presents the measurement scatter of stellar mass in redshift-magnitude space for the CODEX sample. We derive the scatter by propagating the errors in magnitudes based on the magnitude uncertainties in SDSS. Moreover, we include uncertainty induced by the lack of NIR data. We also consider an intrinsic error in stellar mass computation using the SED fitting method, accounting for uncertainties associated with, for example, the adopted functional form for the star formation histories and reddening law (∼0.14 dex see Ilbert et al. 2010). Figure 7 illustrates that the scatter induced by stellar mass measurement is ∼0.19 dex for galaxies with i < 21 and 0.1 ≤ z ≤ 0.65. Taking advantage of deeper photometry and often the existence of NIR data, we would expect a lower scatter in our stellar mass measurement for our other surveys (Erfanianfar et al. 2014). However, since we are working with BCGs, this difference is not significant and does not cause differences in the dispersion of stellar mass of BCGs vs. the mass of their host halos for different surveys (see Fig. 5).
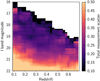 |
Fig. 7. Total measurement scatter in estimating stellar mass in redshift-magnitude space. |
We investigate the relation between the stellar mass to host halo mass ratio of BCGs as a function of halo masses (SHMR; Fig. 8). For comparison, we also show inferences from the literature by Behroozi et al. (2019), i.e., SHMR using empirical models based on evolving galaxies within their dark matter halo histories constrained by galaxy clustering and galaxy-galaxy lensing; Moster et al. (2018), i.e., the parameterized SHMR inferred from abundance matching; Kravtsov & Borgani (2012), i.e., SHMR from observed X-ray clusters at low redshift; Yang et al. (2012), i.e., SHMR from conditional luminosity function modeling; and Coupon et al. (2015), SHMR from HOD modeling. The large blue squares indicate the mean of the stellar masses of BCGs at a given halo mass. A comparison with Behroozi et al. (2019) and Moster et al. (2018) agrees well within the error bars at both low and high redshift. We report the best power-law fitted model in Table 2.
 |
Fig. 8. Stellar-to-halo mass ratio vs. host halo mass of BCGs. The shaded blue areas and the blue squares show the 95% confidence level of the fitted model and the mean of the stellar-to-halo mass ratio of BCGs at a given halo mass, respectively. Their error bars represent the standard error in stellar mass fraction including intrinsic and measurement uncertainties. The red shaded area is the same relation from Behroozi et al. (2010) at z ∼ 0.1 and z ∼ 0.5, respectively. The dash-dotted black line in the left panel shows the Yang et al. (2009) relation at z ∼ 0.1. The gray dashed lines show the Moster et al. (2018) relation. |
5. Stellar mass–richness correlation
As a final test, we investigated the Pearson correlation (normalized covariance) between the richness and the stellar mass of BCGs at a given X-ray luminosity. Figure 9 shows this correlation at low and high redshifts. We only use the CODEX sample, for which measurements of richness are available from redMapper (Rykoff et al. 2014). At least 15 clusters exist in each bin of X-ray luminosity. The error bars are estimated through the Jacknife procedure (Efron 1982). There is a slightly positive richness-BCG mass correlation starting at log LX > 44.5. This correlation becomes stronger at the high luminosity end of our sample. Previously, Furnell et al. (2018), using a sample of massive clusters with 0.05 ≤ z ≤ 0.3, found a weak positive correlation between stellar mass of BCGs and richness of clusters in a given X-ray luminosity. The positive correlation between the stellar mass of BCGs and the richness of clusters implies that the growth of the BCGs and the growth of the host clusters are intimately related. Indeed, the deviation in richness is often associated with higher BCG mass. This positive correlation may also provide clues to the origin of the dispersion of the richness and X-ray luminosities in extremely luminous halos.
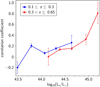 |
Fig. 9. Correlation coefficient for stellar mass of BCGs and the richness of the host halos in a given X-ray luminosity. The error bars are derived using jackknife resampling |
6. Summary and discussion
In this paper, we derived the properties of BCGs of a large sample of X-ray clusters in the CODEX, COSMOS, AEGIS, CFHTLS-XMM, and XMM-XXL surveys with spectroscopic and photometric redshifts. We investigated the distance of the BCGs from the X-ray and optical centers in the CODEX sample. We find BCGs positions agree well with the optical centers (Fig. 4). The BCGs of CODEX clusters and their properties are presented as a VAC of the SDSS DR14 (Abolfathi et al. 2018).
By estimating the stellar masses of BCGs in a consistent manner, we constructed the largest current BCG sample from X-ray halos to study the stellar mass−halo mass relation. Investigating the galaxy–halo connection sheds light on the physical processes regulating galaxy formation. Figure 5 demonstrates that there is a strong correlation between the stellar mass and the halo masses of BCGs. We observe no evolution in this relation since z ∼ 0.65. This result suggests that the mass growth of the central galaxy is controlled by the hierarchical mass growth of the host halo. Thus, in contrast to satellite galaxies, merger events likely play a main role in the mass accretion history of central galaxies with respect to the star formation activity. This interpretation is in agreement with Behroozi et al. (2019), who have reported that the fraction of galaxy buildup due to mergers is a strongly increasing function of mass and nearly all of dwarf galaxy buildup is due to in situ star formation and most of present-day massive galaxy buildup due to mergers.
We also investigated the dispersion around the mean of stellar mass of BCGs at a given halo mass. This scatter is one of the most fundamental aspects of the relationship between galaxies and their host halos. In abundance matching models, we can derive the same stellar mass function from different choices for scatter, but the predicted spatial distribution of galaxies would be different. This distribution impacts the clustering of galaxies directly. As massive halos (Mh > 1012 M⊙) get more clustered, thus galaxies at high masses have the highest sensitivity to this scatter (Wechsler & Tinker 2018). We find an observed constant scatter of 0.21 dex at low redshifts and 0.25 dex at high redshifts. This measurement is consistent with the current predictions from hydrodynamical simulations and with some of the empirical models (Henriques et al. 2015; Lu et al. 2014; Somerville et al. 2012; Behroozi et al. 2019, also see Fig. 8 in Wechsler & Tinker 2018).
As a further step, we quantified the errors in the measurement of stellar masses (Fig. 7). The upper limit mean scatter induced by the stellar mass measurement is ∼0.19 dex for galaxies with imag < 21 and 0.1 ≤ z ≤ 0.65 in the CODEX sample, and less for the other, deeper surveys used in this work. In order to investigate further the connection of the BCGs and their host halos, we investigated the SHMR (Fig. 8). We find a strong agreement with Behroozi et al. (2019), Moster et al. (2018), Yang et al. (2012), and Coupon et al. (2015) at both low and high redshifts.
Finally, we show that the BCG mass is covariant with the number of galaxies hosted by the group or cluster. This positive covariance suggests a connection between the growth of the BCGs and their host halos. The strength of this correlation vanishes for lower luminous systems. This transition in observed covariance indicates a transition in the physical processes that determine the mass of a BCG. Feedback in massive BCGs could be responsible for the loss of this covariance and slightly decouple the growth of the BCGs from the growth of the cluster. We will investigate this correlation in more detail with a larger sample of clusters in RASS-DECaLS in a future study (Erfanianfar et al. in prep.).
Acknowledgments
This paper is partially based on SDSS data. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS website is www.sdss.org. SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut fur Astrophysik Potsdam (AIP), Max-Planck-Institut fur Astronomie (MPIA Heidelberg), Max-Planck-Institut fur Astrophysik (MPA Garching), Max-Planck-Institut fur Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatorio Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autonoma de Mexico, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University. This work also got support from the Excellence Cluster Universe with its data center C2PAP.
Evaluation of the BCG selection method
In order to evaluate the accuracy of our BCG selection in cluster surveys with low spectroscopic incompleteness, we used a halo lightcone catalog from MillenniumXXL simulation (Smith et al. 2017). Smith et al. used the Monte Carlo method to assign galaxies randomly based on their luminosities to dark matter halos, following a HOD (Smith et al. 2017). We used 300 deg2 of this catalog, which encompass 1448 galaxy clusters with virial mass > 1014 M⊙ and 0.1 ≤ z ≤ 0.65. The photometric redshifts are randomly assigned to the galaxies using a Gaussian distribution with standard deviation given by the relation between photometric redshift dispersion and magnitude in the SDSS survey. We selected the member galaxies within one virial radius in projection on the sky and within ±3 times the photometric redshift error around the cluster redshift in redshift space. Since the true BCG is known from the full three-dimensional simulation information, we can assess whether the true BCG is correctly selected. We repeated the procedure of assigning noise to the photometry and finding the BCG 100 times. We find that the BCGs are selected with an accuracy of 90%. As a further step, we also take into account the errors on the luminosity of BCGs in our analysis. In this exercise, we randomly assigned magnitude to the galaxies using Gaussian distribution with standard deviation given by the relation between magnitude error and magnitude in SDSS. We repeated the same procedure as before considering photometric redshift error and luminosity error at the same time to asses the accuracy of selecting of BCGs. This exercise demonstrates that taking into account both uncertainties, the accuracy of selection BCG decreases to 88%. However, in this test, the member galaxies are selected based on photometric redshifts and the result of this test is the lower limits for our observational work.
References
- Abolfathi, B., Aguado, D. S., Aguilar, G., et al. 2018, ApJS, 235, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Vandame, B., Benoist, C., et al. 2001, A&A, 379, 740 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ascaso, B., Aguerri, J. A. L., Varela, J., et al. 2011, ApJ, 726, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Conroy, C., & Wechsler, R. H. 2010, ApJ, 717, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P., Wechsler, R., Hearin, A., & Conroy, C. 2019, MNRAS, 488, 3143 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2011, in Astronomical Data Analysis Software and Systems XX, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 435 [NASA ADS] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Boese, F. G. 2000, A&AS, 141, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brough, S., Proctor, R., Forbes, D. A., et al. 2007, MNRAS, 378, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Clerc, N., Merloni, A., Zhang, Y.-Y., et al. 2016, MNRAS, 463, 4490 [NASA ADS] [CrossRef] [Google Scholar]
- Colín, P., Klypin, A. A., Kravtsov, A. V., & Khokhlov, A. M. 1999, ApJ, 523, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., & Wechsler, R. H. 2009, ApJ, 696, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Wechsler, R. H., & Kravtsov, A. V. 2006, ApJ, 647, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Wechsler, R. H., & Kravtsov, A. V. 2007, ApJ, 668, 826 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Ilbert, O., Kilbinger, M., et al. 2009, A&A, 500, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coupon, J., Arnouts, S., van Waerbeke, L., et al. 2015, MNRAS, 449, 1352 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., & Binney, J. 1977, ApJ, 215, 723 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., Hill, D. T., Kelvin, L. S., et al. 2011, MNRAS, 413, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Efron, B. 1982, The Jackknife, The Bootstrap and Other Resampling Plans (Philadelphia: Society for Industrial and Applied Mathematics) [Google Scholar]
- Erfanianfar, G., Finoguenov, A., Tanaka, M., et al. 2013, ApJ, 765, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Erfanianfar, G., Popesso, P., Finoguenov, A., et al. 2014, MNRAS, 445, 2725 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 1994, ARA&A, 32, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., & Nulsen, P. E. J. 1977, MNRAS, 180, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricant, D., Fata, R., Roll, J., et al. 2005, PASP, 117, 1411 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., Guzzo, L., Hasinger, G., et al. 2007, ApJS, 172, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Furnell, K. E., Collins, C. A., Kelvin, L. S., et al. 2018, MNRAS, 478, 4952 [NASA ADS] [CrossRef] [Google Scholar]
- George, M. R., Leauthaud, A., Bundy, K., et al. 2011, ApJ, 742, 125 [NASA ADS] [CrossRef] [Google Scholar]
- George, M. R., Ma, C.-P., Bundy, K., et al. 2013, ApJ, 770, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Gozaliasl, G., Finoguenov, A., Tanaka, M., et al. 2019, MNRAS, 483, 3545 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Li, C., & Boylan-Kolchin, M. 2010, MNRAS, 404, 1111 [NASA ADS] [Google Scholar]
- Guo, H., Zheng, Z., Zehavi, I., et al. 2014, MNRAS, 441, 2398 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, S. M., Sheldon, E. S., Wechsler, R. H., & Koester, B. P. 2009, ApJ, 699, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Hearin, A. P., & Watson, D. F. 2013, MNRAS, 435, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Henriques, B. M. B., White, S. D. M., Thomas, P. A., et al. 2015, MNRAS, 451, 2663 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, D. T., Kelvin, L. S., Driver, S. P., et al. 2011, MNRAS, 412, 765 [NASA ADS] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Jimmy, Tran, K.-V., Brough, S., et al. 2013, ApJ, 778, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Kelvin, L. S., Driver, S. P., Robotham, A. S. G., et al. 2012, MNRAS, 421, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Khandai, N., Di Matteo, T., Croft, R., et al. 2015, MNRAS, 450, 1349 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J. 1984, ApJ, 287, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., & Borgani, S. 2012, ARA&A, 50, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., & Klypin, A. A. 1999, ApJ, 520, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Berlind, A. A., Wechsler, R. H., et al. 2004, ApJ, 609, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Vikhlinin, A. A., & Meshcheryakov, A. V. 2018, Astron. Lett., 44, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, D., Hogg, D. W., & Schlegel, D. J. 2016, AJ, 151, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Laporte, C. F. P., White, S. D. M., Naab, T., Ruszkowski, M., & Springel, V. 2012, MNRAS, 424, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Leauthaud, A., Finoguenov, A., Kneib, J.-P., et al. 2010, ApJ, 709, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Leauthaud, A., Tinker, J., Behroozi, P. S., Busha, M. T., & Wechsler, R. H. 2011, ApJ, 738, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Leauthaud, A., Tinker, J., Bundy, K., et al. 2012, ApJ, 744, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y.-T., & Mohr, J. J. 2004, ApJ, 617, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Loubser, S. I., & Sánchez-Blázquez, P. 2012, MNRAS, 425, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, Y., Wechsler, R. H., Somerville, R. S., et al. 2014, ApJ, 795, 123 [NASA ADS] [CrossRef] [Google Scholar]
- McAlpine, S., Helly, J. C., Schaller, M., et al. 2016, Astron. Comput., 15, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D. 1983, ApJ, 264, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D. 1984, ApJ, 276, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Mirkazemi, M., Finoguenov, A., Pereira, M. J., et al. 2015, ApJ, 799, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Somerville, R. S., Maulbetsch, C., et al. 2010, ApJ, 710, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2018, MNRAS, 477, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Johansson, P. H., & Ostriker, J. P. 2009, ApJ, 699, L178 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. P., & Hausman, M. A. 1977, ApJ, 217, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. P., & Tremaine, S. D. 1975, ApJ, 202, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Parejko, J. K., Sunayama, T., Padmanabhan, N., et al. 2013, MNRAS, 429, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2010, AJ, 139, 2097 [NASA ADS] [CrossRef] [Google Scholar]
- Pierre, M., Pacaud, F., Adami, C., et al. 2016, A&A, 592, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillepich, A., Nelson, D., Hernquist, L., et al. 2018, MNRAS, 475, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Reddick, R. M., Wechsler, R. H., Tinker, J. L., & Behroozi, P. S. 2013, ApJ, 771, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Rykoff, E. S., Rozo, E., Busha, M. T., et al. 2014, ApJ, 785, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Shankar, F., Lapi, A., Salucci, P., De Zotti, G., & Danese, L. 2006, ApJ, 643, 14 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Smee, S. A., Gunn, J. E., Uomoto, A., et al. 2013, AJ, 146, 32 [Google Scholar]
- Smith, A., Cole, S., Baugh, C., et al. 2017, MNRAS, 470, 4646 [NASA ADS] [CrossRef] [Google Scholar]
- Somerville, R. S., Gilmore, R. C., Primack, J. R., & Domínguez, A. 2012, MNRAS, 423, 1992 [NASA ADS] [CrossRef] [Google Scholar]
- Tasitsiomi, A., Kravtsov, A. V., Wechsler, R. H., & Primack, J. R. 2004, ApJ, 614, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S. D., & Richstone, D. O. 1977, ApJ, 212, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Vale, A., & Ostriker, J. P. 2004, MNRAS, 353, 189 [Google Scholar]
- Vale, A., & Ostriker, J. P. 2006, MNRAS, 371, 1173 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, F. C., Yang, X., Mo, H. J., & Norberg, P. 2005, MNRAS, 356, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Von Der Linden, A., Best, P. N., Kauffmann, G., & White, S. D. M. 2007, MNRAS, 379, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Wechsler, R. H., & Tinker, J. L. 2018, ARA&A, 56, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., & van den Bosch, F. C. 2003, MNRAS, 339, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., van den Bosch, F. C., et al. 2007, ApJ, 671, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., & van den Bosch, F. C. 2009, ApJ, 695, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., van den Bosch, F. C., Zhang, Y., & Han, J. 2012, ApJ, 752, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2011, ApJ, 736, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Zu, Y., & Mandelbaum, R. 2015, MNRAS, 454, 1161 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Cluster M200–redshift plane for CODEX-SPIDERS (green cross), AEGIS (cyan filled square), COSMOS (pink diamond), CDFS (point down red triangle), XMM-CFHTLS (point-up blue triangle), and XMM-XXL (black filled circle) surveys used in this work. |
| In the text | |
 |
Fig. 2. Relation (Photometric redshifts–Spectroscopic redshifts)/(1 + Spectroscopic redshifts) (Δz) vs. i-band cModel magnitude for a sample of galaxies with both spectroscopic and photometric redshifts in SDSS DR14 (gray dots). The black pluses and black solid line show the dispersion and peak of the Gaussian fitted in each i-band magnitude bin, respectively. There are in total 17 bins. The red dashed lines indicate the model fitted to the dispersions. |
| In the text | |
 |
Fig. 3. Same as Fig. 2 but for the AEGIS, COSMOS, CDFS, XMM-CFHTLS, and XMM-XXL fields. |
| In the text | |
 |
Fig. 4. Distance of the BCGs from the optical and X-ray centers normalized by R200. Of the BCGs, 79% reside in ∼0.05 × r200 from optical center, and 92% and 84% of BCGs reside in 0.5 × R200 from optical center and X-ray center, respectively. |
| In the text | |
 |
Fig. 5. Stellar masses vs. halo masses of the BCGs in our sample. Different symbols represent different surveys. The blue shaded symbols show BCGs with 0.1 ≤ z ≤ 0.3 and the red shaded symbols show BCGs with 0.3 < z ≤ 0.65. The blue dashed and the red dash-dotted lines show the best power-law fits for the low and high redshifts, respectively. The blue and red shaded area around the fitted lines represent 95% confidence levels of the fits. The blue squares and red dots with error bars present the mean of stellar mass of BCGs at a given halo mass. The error bars are their standard errors. The Pearson correlation coefficient is 0.7 for low redshift BCGs and 0.4 for high redshift BCGs. |
| In the text | |
 |
Fig. 6. Scatter in the stellar mass of BCGs at a given halo mass in low and high redshift bins. The scatter is the quadratic sum of intrinsic scatter and measurement scatter of stellar masses. |
| In the text | |
 |
Fig. 7. Total measurement scatter in estimating stellar mass in redshift-magnitude space. |
| In the text | |
 |
Fig. 8. Stellar-to-halo mass ratio vs. host halo mass of BCGs. The shaded blue areas and the blue squares show the 95% confidence level of the fitted model and the mean of the stellar-to-halo mass ratio of BCGs at a given halo mass, respectively. Their error bars represent the standard error in stellar mass fraction including intrinsic and measurement uncertainties. The red shaded area is the same relation from Behroozi et al. (2010) at z ∼ 0.1 and z ∼ 0.5, respectively. The dash-dotted black line in the left panel shows the Yang et al. (2009) relation at z ∼ 0.1. The gray dashed lines show the Moster et al. (2018) relation. |
| In the text | |
 |
Fig. 9. Correlation coefficient for stellar mass of BCGs and the richness of the host halos in a given X-ray luminosity. The error bars are derived using jackknife resampling |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


