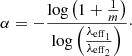| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201936322 | |
| Published online | 23 September 2019 | |
Letter to the Editor
Variability of the near-infrared extinction curve towards the Galactic centre
1
Instituto de Astrofísica de Andalucía (CSIC), Glorieta de la Astronomía s/n, 18008 Granada, Spain
e-mail: fnoguer@iaa.es
2
Centro de Astrobiología (CSIC/INTA), ctra. de Ajalvir km. 4, 28850 Torrejón de Ardoz, Madrid, Spain
3
Centro Astronómico Hispano-Alemán (CSIC-MPG), Observatorio Astronómico de Calar Alto, Sierra de los Filabres, 04550 Gérgal, Almería, Spain
4
Max-Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
Received:
16
July
2019
Accepted:
22
August
2019
Context. Due to the extreme extinction towards the Galactic centre (AV ∼ 30 mag), its stellar population is mainly studied in the near-infrared (NIR) regime. Therefore, a proper analysis of the NIR extinction curve is necessary to fully characterise the stellar structure and population of the inner part of the galaxy.
Aims. We studied the dependence of the extinction index (αλ) in the NIR on the line of sight, wavelength, and extinction.
Methods. We used the GALACTICNUCLEUS imaging survey, a high angular resolution catalogue (0.2″) for the inner part of the Galaxy in JHKs, and studied the spatial variation in the extinction index. We also applied two independent methods based on red clump stars to compute the extinction index between different bands and its variation with wavelength.
Results. We did not detect any significant line-of-sight or extinction variation in α within the studied region in the nuclear stellar disc. The extinction index between JH and HKs differs by 0.19 ± 0.05. We obtained mean values for the extinction indices αJH = 2.43 ± 0.03 and αHKs = 2.23 ± 0.03. The dependence of the extinction index on the wavelength could explain the differences obtained for αλ in the literature since it was assumed constant for the NIR regime.
Key words: Galaxy: nucleus / dust / extinction / Galaxy: center / stars: horizontal-branch
© ESO 2019
1. Introduction
The Galactic centre (GC) is a crucial astrophysical laboratory since it is the closest galactic nucleus and the only one where we can resolve individual stars down to milliparsec scales. Nevertheless, very little is known about its structure and stellar population, due to the strong crowding and the large interstellar extinction (AV ≳ 30 mag, AKs ≳ 2.5 mag, e.g. Scoville et al. 2003; Nishiyama et al. 2008; Fritz et al. 2011; Schödel et al. 2010). Therefore, a proper characterisation of the near-infrared (NIR) extinction law is fundamental to better understand the GC.
It is generally accepted that the extinction curve in the NIR can be approximated by a power law (e.g. Nishiyama et al. 2008; Fritz et al. 2011) of the form Aλ ∝ λ−α, where λ and α are the wavelength and the extinction index, respectively. However, the value of the extinction index has changed significantly in recent decades from values of ∼1.5 (e.g. Rieke & Lebofsky 1985; Draine 1989) to α > 2.0 or even ∼2.5 (e.g. Nishiyama et al. 2006; Stead & Hoare 2009; Gosling et al. 2009; Schödel et al. 2010; Fritz et al. 2011; Alonso-García et al. 2017; Nogueras-Lara et al. 2018a). In addition to this discrepancy, some evidence of a possible variation in the extinction index between the NIR bands JH and HKs has been reported recently (Nogueras-Lara et al. 2018a; Hosek et al. 2018). These different values can lead us to generate an incorrect picture of the inner structure of the galaxy. Namely, a small change in α (∼10−15%) can result in a change in absolute extinction of ∼0.3 mag, which corresponds to a bias in the estimation of distances, based on the distance modulus, of ∼1 kpc (Matsunaga et al. 2016) at the GC distance (∼8 kpc). The situation is even more complicated when inferring the stellar type of a star using NIR photometry, where a small variation correcting the extinction completely changes the type of a star (e.g. Figs. 33 and 34 Nogueras-Lara et al. 2018a).
In this Letter we characterise the extinction curve in the NIR bands JHKs towards the nuclear bulge (NB) using the GALACTICNUCLEUS survey (Nogueras-Lara et al. 2018a, 2019a) and two independent methods based on red clump (RC) stars (e.g. Girardi 2016).
2. Data
We used for this study the GALACTICNUCLEUS survey (Nogueras-Lara et al. 2018a, 2019a). This is a JHKs NIR photometric survey carried out with the HAWK-I camera (Kissler-Patig et al. 2008) located at the ESO VLT unit telescope 4. This survey uses the speckle holography technique described by Schödel et al. (2013) to reach a high angular resolution of 0.2″. The photometry and astrometry are obtained by means of point spread function (PSF) fitting using the StarFinder software package (Diolaiti et al. 2000). The catalogue reaches 5σ detection limits of approximately J = 22, H = 21, and Ks = 20 mag. The photometric uncertainties are less than 0.05 mag at J ≲ 20, H ≲ 17, and Ks ≲ 16 mag. The zero point (ZP) is calibrated using the SIRIUS/IRSF GC survey (e.g. Nagayama et al. 2003; Nishiyama et al. 2006) and its associated uncertainty is ∼0.036 mag in all three bands.
In the study presented in this Letter, we used the J, H, and Ks photometry of 14 different fields of the survey that cover a rectangular region of 90 pc × 20 pc centred on Sgr A* and corresponding to the central part of the NB (Nogueras-Lara et al. 2019b), as shown in Fig. 1.
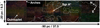 |
Fig. 1. Image of the studied region produced combining the Ks, H, and J bands in red, green, and blue, respectively. Sagittarius A* and the Arches and Quintuplet clusters are indicated by arrows. The black rectangle near the Arches cluster corresponds to a field with incomplete data. The white dashed contours indicate regions dominated by dark clouds. The cross-shaped region corresponds to a low completeness region due to crowding (the nuclear star cluster, NSC). |
3. Colour-magnitude diagrams
Figure 2 depicts the colour-magnitude diagrams (CMD) H versus J − H and Ks versus H − Ks. The highly populated region located at J − H > 2.5 and H − Ks > 1.3 corresponds to the GC stellar population, whereas stars at J − H < 2.5 and H − Ks < 1.3 trace foreground stars probably belonging to three spiral arms (Nogueras-Lara et al. 2018a). The high density regions within the blue dashed trapezoids show the GC RC feature following the reddening vector due to differential extinction. We clearly distinguish a bright and a faint RC, which trace an old stellar population (≳8 Gyr) and stars formed in a younger star formation burst (∼1 Gyr), respectively (Nogueras-Lara et al. 2019b).
 |
Fig. 2. Colour-magnitude diagrams H vs. J − H (upper panel) and Ks vs. H − Ks (lower panel). The RC is marked by the blue dashed parallelograms. The two blue arrows show a double feature in the RC. The black arrow depicts the reddening vector with an extinction AKs = 0.5 mag (computed using α = 2.30 ± 0.08, Nogueras-Lara et al. 2018a). The insets show the RC region with the two features obtained applying GMM and their uncertainties in cyan (see main text). |
4. Extinction index analysis
We analysed the line-of-sight variability and the variation as a function of the wavelength of the extinction index.
4.1. Spatial variability of the extinction index
We employed the method described in Sect. 6.1. of Nogueras-Lara et al. (2018a; the grid method), increasing the area of the region analysed by a factor of ∼10. This method uses RC stars (giant stars in their helium core burning stage) (e.g. Girardi 2016) to compute simultaneously the extinction index and the extinction at a fixed wavelength (λ = 1.61 μm). We used atmosphere models (Kurucz 1993) to compute synthetic magnitudes of the RC stars for the filters used in our observations and minimised the corresponding χ2. We reddened the synthetic stellar models using a grid of extinctions and α (with a step of 0.016 for both of them). To model RC stars we used an effective temperature of 4750 K, log g = +2.5 (Bovy et al. 2014), a radius of 10.0 ± 0.5 R⊙ (e.g. Chaplin & Miglio 2013; Girardi 2016), and twice solar metallicity according to recent work (e.g. Do et al. 2015, 2018; Feldmeier-Krause et al. 2017; Nandakumar et al. 2018; Schultheis et al. 2019), which allowed us to decrease the uncertainty of the results. We also assumed a distance to the GC of 8.0 ± 0.1 kpc with lower uncertainty, averaging the last results obtained by Abuter (2018) and Do et al. (2019). We selected the RC stars shown in the blue dashed parallelograms in Fig. 2. We expected some contamination of the red giant branch bump (RGBB) (see e.g. Nataf et al. 2011; Wegg & Gerhard 2013), but since the intrinsic colour is similar to the RC (Nogueras-Lara et al. 2018b) it does not have a significant influence on our results. We computed the extinction index and A1.61 for all the RC stars detected in all three bands (JHKs) with an uncertainty less than 0.05 mag in all three bands (∼62 000 stars in total). To study the variability of the extinction index with the line of sight, we computed extinction index maps using the results obtained for αJH, αHKs, and αJKs. We defined a pixel size of 1 arcmin and computed the extinction index using a 3σ clipping algorithm for all the RC stars within a pixel. We computed the maps for αJH, αHKs, and αJKs to study the variation with wavelength. We only calculated the extinction index value for a given pixel if more than 80 stars were detected. Figure 3 shows the obtained results for αJH, αHKs, and αJKs. We estimated the statistical uncertainties via the standard deviation of the distribution of the obtained values for each pixel. We found that the uncertainties are below 0.016 for all the maps. The systematic uncertainties were not considered since they change all the pixels for each map in the same way, and we analysed the relative difference between the pixels of the same map.
 |
Fig. 3. Extinction-index maps: (a) JH-map; (b) HKs-map; (c) JKs-map. Cross-shaped pixels indicate that there are not enough stars for a reliable estimate. |
We observed some variation between different pixels, as can be seen in Fig. 3. Nevertheless, we found that the systematic uncertainty of the ZP of the pointings used to produced the catalogue (∼0.036 mag in all three bands) can explain this variation. For this, we recomputed the extinction indices (αJH, αHKs, and αJKs) considering that, for each band independently, the magnitude of the RC stars used is affected by the systematic uncertainty of the ZP. We combined quadratically the obtained extinction index uncertainty for each band and found that the expected variation in the extinction index is ΔαJH = 0.05, ΔαHKs = 0.08, and ΔαJKs = 0.03. We also created histograms of the extinction-index values per pixel. Figure 4 shows the results. The standard deviation of the distributions are below the ZP systematic uncertainties. We conclude that there is no significant variation in the extinction index with the line of sight within the uncertainties of our data. This agrees with the non-variation in the extinction index measured between a region in the GC (Nogueras-Lara et al. 2018a) and two regions in the inner bulge located at a distance of ∼0.4° and ∼0.6° (Galactic north) from Sgr A* (Nogueras-Lara et al. 2018b).
 |
Fig. 4. Histograms of the extinction-index values per pixel: (left) JH-map; (middle) HKs-map; (right) JKs-map. The red line indicates a Gaussian fit. The mean and the standard deviation are specified in the figure. |
We also produced the corresponding maps for the extinction A1.61 and checked that for all the band combinations (JH, HKs, and JKs), we obtained equivalent maps, as was expected since we used stars common to all three bands.
4.2. Unique extinction index in the NIR?
To analyse the variation in the extinction index with wavelength, we created histograms for the values obtained for αJH, αHKs, αJKs, αJHKs and the corresponding extinctions A1.61, for all the stars used in the analysis. The obtained distributions are well fitted by a Gaussian model (Fig. 5). Table 1 summarises the results. The uncertainties refer to systematics and were computed varying independently all the parameters involved in the calculation in their uncertainty ranges, as described in Nogueras-Lara et al. (2018a). We used a different range to estimate the uncertainties only in the case of the distance to the GC and the metallicity of the GC stellar population, where the updated values allowed us to reduce the systematics in comparison to our previous work. The statistical uncertainties were estimated using the error of the mean of the distributions, and are negligible given the number of stars used for the calculation.
 |
Fig. 5. Upper panels: histograms obtained for αJH (left panel) and αHKs (right panel) using the method presented in Sect. 4.1. Lower panels: histograms obtained for A1.61, associated with the calculations using JH and HKs. The red lines show the Gaussian fits to the data. The mean and the standard deviation of each histogram are specified in each panel. |
Our results suggest that the extinction index depends on wavelength in the NIR. We obtained Δα = αJH − αHKs = 0.22 ± 0.13, which supposes a ∼2σ detection of a different extinction index between JH and HKs. We estimated the uncertainty computing the difference between the extinction indices when varying all the parameters specified in Sect. 4.1. The uncertainty is lower than the value obtained simply using the quadratic propagation because the variation in some parameters produces a change in both αJH and αHKs in the same direction.
4.3. Variation in the extinction index with the extinction
The spread of the RC along the reddening vector shown in Fig. 2 is mainly due to differential extinction. In this way, we analysed the variation in αλ with the extinction (A1.61), dividing the RC stars in the CMD into small bins of J − Ks = 0.25. We only used stars detected in all three bands with uncertainties < 0.05 mag. The results are shown in Table 2. The uncertainties are computed as explained in the Sect. 4.1. We found some dependence of αHKs on the extinction, whereas αJH appears to be constant. Nevertheless, we conclude that both extinction indices can be considered constant within the estimated uncertainties. On the other hand, we confirmed the previously computed value of αJH − αHKs ∼ 0.2 that is also observed for different A1.61.
4.4. Slope of the RC features
To check the Δα = αJH − αHKs obtained with the grid method, we studied the slopes of the RC features. We used all the RC stars shown in the blue dashed parallelograms in Fig. 2. Firstly, we divided the RC region in the CMD into small vertical bins to apply the SCIKIT-LEARN python function GaussianMixture (GMM, Pedregosa et al. 2011) to compare a one-Gaussian model with a two-Gaussian model to fit the Ks stellar distribution for each bin (Nogueras-Lara et al. 2018b). Using the Bayesian information criterion (Schwarz 1978) and the Akaike information criterion (Akaike 1974), we found that a double-Gaussian model fits the data better as expected (Rui et al. 2019; Nogueras-Lara et al. 2019b). We computed the slope of both RC features using a jackknife resampling method and calculated the systematic uncertainties varying the bin width, the RC selection, and the width and the number of bins used, as described in Nogueras-Lara et al. (2018b). We repeated the same analysis for the CMDs Ks versus J − Ks and H versus J − H. The secondary RC feature is more sensitive to extinction and completeness problems given that it is fainter than the main feature. For this reason, we removed the last bins in the calculation of the slope of the secondary feature. Moreover, we excluded regions affected by dark clouds (using as reference the J band, as it is more prone to extinction) that can influence the slopes of the features as they could change the relative number of stars in each feature for faint magnitudes. We also masked the central region belonging to the nuclear star cluster (NSC) because it could have a different star formation history and a lower completeness (Nogueras-Lara et al. 2019b). Using the slope of the features, we computed the extinction index by means of Eq. (1) in Nogueras-Lara et al. (2018b):
Here m is the slope of the features in the CMD λeff2 versus λeff1 − λeff2, and λeffi is the effective wavelength. Table 3 summarises the results obtained for each colour.
Extinction index calculation using the slope of the RC.
Combining the values for both clumps, we computed αHKs = 2.29 ± 0.02 and αJH = 2.52 ± 0.09, where the uncertainties were quadratically propagated. We obtained Δα = 0.23 ± 0.09. The uncertainty is even smaller if we just consider the bright RC, Δα = 0.19 ± 0.05, which supposes that the difference in the inter-band extinction index is detected with ∼4σ significance. The results fully agree within the uncertainties with the previous values estimated using a completely independent method.
The extinction indices computed using this method are somewhat higher than those obtained in Sect. 4.1. This could be a consequence of a small shift, within the uncertainties, of the ZP calculation that affects the first method (which is considered in the estimation of the uncertainties) but does not affect the second method. Nevertheless, all the values agree within the uncertainties. Moreover, the ZP uncertainty does not affect the estimation of Δα in the second method. Therefore, we considered the value Δα = 0.19 ± 0.05 as the best estimation.
5. Discussion and conclusion
We have analysed the spatial variability of the extinction index and its dependence on the extinction, A1.61. We find that there is no variation within the uncertainties. Therefore, it is possible to assume a constant α for the studied region of the NB in the NIR. We detected a difference in the extinction index between JH and HKs of Δα = 0.19 ± 0.05, combining the values obtained using two independent methods (Δα = 0.22 ± 0.13 and Δα = 0.19 ± 0.05). We used a weighted average for the calculation and the uncertainty estimation. We also obtain the mean values of the extinction indices αJH = 2.43 ± 0.03 and αHKs = 2.23 ± 0.03, computed combining the results from Tables 1 and 3 (bright feature), and calculating the uncertainties via the difference between values (also coincident with the standard deviation). We did not use a weighted mean given the much lower uncertainties of the values obtained with the slope of the RC, which might lead to a biased result. Comparing our findings with those of previous works, we suggest that some discrepancies towards different extinction-index values could be explained via the direct assumption of having just one single α for JHKs (e.g. Nishiyama et al. 2006; Stead & Hoare 2009; Gosling et al. 2009; Fritz et al. 2011; Alonso-García et al. 2017). This depends on the methodology used. In particular applying the method described in Sect. 4.1, we obtained a value αJHKs = 2.32 ± 0.09, which lies between the two values computed for αJH and αHKs. On the other hand, using the slope of the RC to derive the extinction curve implies that it is necessary to know whether one or more RC features are present in the RC in the CMDs. Moreover, this method is quite dependent on the completeness of the photometry. The slope of the RC feature(s) might change at the faint end if the completeness is not sufficient.
To the best of our knowledge this is the first time that the extinction curve in the GC has been shown not to depend on the line of sight or extinction, and to depend on wavelength. Previous studies always used a uniform extinction curve with different values. The great accuracy of this work has only been possible thanks to the high angular resolution GALACTICNUCLEUS survey.
Acknowledgments
The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement n° [614922]. This work is based on observations made with ESO Telescopes at the La Silla Paranal Observatory under programme IDs 195.B-0283 and 091.B-0418. We thank the staff at ESO for their great efforts and helpfulness. F.N.-L. acknowledges financial support from a MECD pre-doctoral contract, code FPU14/01700. F.N. acknowledges financial support through Spanish grants ESP2015-65597-C4-1-R and ESP2017-86582-C4-1-R (MINECO/FEDER). We acknowledge support from the State Agency for Research of the Spanish MCIU through the Centre of Excellence Severo Ochoa Award of the Instituto de Astrofísica de Andalucía (CSIC) (SEV-2017-0709). N.N. acknowledges support from Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject B8) of the German Research Foundation (DFG).
References
- Akaike, H. 1974, Autom. Control IEEE Trans., 19, 716 [Google Scholar]
- Alonso-García, J., Minniti, D., Catelan, M., et al. 2017, ApJ, 849, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Nidever, D. L., Rix, H.-W., et al. 2014, ApJ, 790, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Diolaiti, E., Bendinelli, O., Bonaccini, D., et al. 2000, A&AS, 147, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Do, T., Kerzendorf, W., Winsor, N., et al. 2015, ApJ, 809, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Do, T., Kerzendorf, W., Konopacky, Q., et al. 2018, ApJ, 855, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Do, T., Hees, A., Ghez, A., et al. 2019, Science, 365, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1989, in Infrared Spectroscopy in Astronomy, ESA SP, 290, 93 [NASA ADS] [Google Scholar]
- Feldmeier-Krause, A., Kerzendorf, W., Neumayer, N., et al. 2017, MNRAS, 464, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, T. K., Gillessen, S., Dodds-Eden, K., et al. 2011, ApJ, 737, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L. 2016, ARA&A, 54, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gosling, A. J., Bandyopadhyay, R. M., & Blundell, K. M. 2009, MNRAS, 394, 2247 [NASA ADS] [CrossRef] [Google Scholar]
- Gravity Collaboration (Abuter, R., et al.) 2018, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hosek, Jr., M. W., Lu, J. R., Anderson, J., et al. 2018, ApJ, 855, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Kissler-Patig, M., Pirard, J.-F., Casali, M., et al. 2008, A&A, 491, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L. 1993, VizieR Online Data Catalog: VI/039 [Google Scholar]
- Matsunaga, N., Feast, M. W., Bono, G., et al. 2016, MNRAS, 462, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Nagayama, T., Nagashima, C., Nakajima, Y., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, Proc. SPIE, 4841, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Nandakumar, G., Ryde, N., Schultheis, M., et al. 2018, MNRAS, 478, 4374 [NASA ADS] [CrossRef] [Google Scholar]
- Nataf, D. M., Udalski, A., Gould, A., & Pinsonneault, M. H. 2011, ApJ, 730, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Nagata, T., Kusakabe, N., et al. 2006, ApJ, 638, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Nagata, T., Tamura, M., et al. 2008, ApJ, 680, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Nogueras-Lara, F., Gallego-Calvente, A. T., Dong, H., et al. 2018a, A&A, 610, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nogueras-Lara, F., Schödel, R., Dong, H., et al. 2018b, A&A, 620, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nogueras-Lara, F., Schödel, R., Gallego-Calvente, A. T., et al. 2019a, A&A, in press, https://doi.org/10.1051/0004-6361/201936263 [Google Scholar]
- Nogueras-Lara, F., Schödel, R., Gallego-Calvente, A. T., et al. 2019b, Nat. Astron., submitted [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Rui, N. Z., Hosek, Jr., M. W., Lu, J. R., et al. 2019, ApJ, 877, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Schödel, R., Najarro, F., Muzic, K., & Eckart, A. 2010, A&A, 511, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schödel, R., Yelda, S., Ghez, A., et al. 2013, MNRAS, 429, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Schultheis, M., Rich, R. M., Origlia, L., et al. 2019, A&A, 627, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [Google Scholar]
- Scoville, N. Z., Stolovy, S. R., Rieke, M., Christopher, M., & Yusef-Zadeh, F. 2003, ApJ, 594, 294 [Google Scholar]
- Stead, J. J., & Hoare, M. G. 2009, MNRAS, 400, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Wegg, C., & Gerhard, O. 2013, MNRAS, 435, 1874 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Image of the studied region produced combining the Ks, H, and J bands in red, green, and blue, respectively. Sagittarius A* and the Arches and Quintuplet clusters are indicated by arrows. The black rectangle near the Arches cluster corresponds to a field with incomplete data. The white dashed contours indicate regions dominated by dark clouds. The cross-shaped region corresponds to a low completeness region due to crowding (the nuclear star cluster, NSC). |
| In the text | |
 |
Fig. 2. Colour-magnitude diagrams H vs. J − H (upper panel) and Ks vs. H − Ks (lower panel). The RC is marked by the blue dashed parallelograms. The two blue arrows show a double feature in the RC. The black arrow depicts the reddening vector with an extinction AKs = 0.5 mag (computed using α = 2.30 ± 0.08, Nogueras-Lara et al. 2018a). The insets show the RC region with the two features obtained applying GMM and their uncertainties in cyan (see main text). |
| In the text | |
 |
Fig. 3. Extinction-index maps: (a) JH-map; (b) HKs-map; (c) JKs-map. Cross-shaped pixels indicate that there are not enough stars for a reliable estimate. |
| In the text | |
 |
Fig. 4. Histograms of the extinction-index values per pixel: (left) JH-map; (middle) HKs-map; (right) JKs-map. The red line indicates a Gaussian fit. The mean and the standard deviation are specified in the figure. |
| In the text | |
 |
Fig. 5. Upper panels: histograms obtained for αJH (left panel) and αHKs (right panel) using the method presented in Sect. 4.1. Lower panels: histograms obtained for A1.61, associated with the calculations using JH and HKs. The red lines show the Gaussian fits to the data. The mean and the standard deviation of each histogram are specified in each panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.