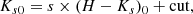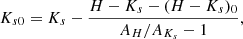| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202140554 | |
| Published online | 16 March 2021 | |
Letter to the Editor
Distance to three molecular clouds in the central molecular zone
1
Max-Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
e-mail: nogueras@mpia.de
2
Instituto de Astrofísica de Andalucía (IAA-CSIC), Glorieta de la Astronomía s/n, 18008 Granada, Spain
3
Université Côte d’Azur, Observatoire de la Côte d’Azur, Laboratoire Lagrange, CNRS, Blvd de l’Observatoire, 06304 Nice, France
Received:
12
February
2021
Accepted:
3
March
2021
Context. The determination of absolute and relative distances of molecular clouds along the line-of-sight towards the central molecular zone (CMZ) is crucial for inferring its orbital structure and dynamics and for understanding star formation in the clouds.
Aims. Recent work has suggested that the G0.253+0.016 cloud (the Brick) does not belong to the CMZ. This motivated us to crosscheck those results, computing the absolute and relative distances to the Brick as well as to another two molecular clouds (the 50 km s−1 and the 20 km s−1 clouds), and discuss their CMZ membership.
Methods. We used the colour magnitude diagrams Ks versus H − Ks to compare stars detected towards the target clouds with stars detected towards three reference regions in the nuclear stellar disc (NSD) and the Galactic bulge. We used red clump (RC) stars to estimate the distance to each region.
Results. We found that all the clouds present a double RC feature. Such a double RC has been reported in previous work for the NSD, but not for the bulge adjacent to it. We exclude the possibility that the different RC features are located at significantly different distances. The obtained absolute and relative distances are compatible with the Galactic centre distance (∼8 kpc).
Key words: Galaxy: nucleus / Galaxy: center / stars: distances / stars: horizontal-branch / dust / extinction
© F. Nogueras-Lara et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
The central molecular zone (CMZ) is an accumulation of dense molecular gas (R ≲ 200 pc) where the gas channelled through the Galactic bar settles in orbits around the Galactic centre (GC; e.g., Morris & Serabyn 1996). It contains ∼3 − 5 × 107 M⊙ of molecular gas (Dahmen et al. 1998; Pierce-Price et al. 2000) and constitutes a star-forming region characterised by extreme conditions, such as a high confining pressure of 106 − 7 K cm−3 (Yamauchi et al. 1990; Spergel & Blitz 1992; Muno et al. 2004) and strong magnetic fields (∼5 mG; Pillai et al. 2015). The CMZ partially overlaps with the nuclear stellar disc (NSD), a distinct disc-like structure of stars (Launhardt et al. 2002) characterised by mainly old stars (> 80% of the stellar mass formed > 8 Gyr ago; Nogueras-Lara et al. 2020a). The presence of young clusters and HII regions highlights recent and ongoing star formation in the NSD, the Galaxy’s most prolific (massive) star-forming region when averaged by its volume (e.g., the Arches and the Quintuplet clusters; Figer et al. 1999, 2002; Schneider et al. 2014). Nevertheless, the currently observed star formation in the CMZ is about an order of magnitude below what is expected based on the amount of dense gas (e.g., Longmore et al. 2013; Kauffmann et al. 2017).
The determination of the absolute and relative distances between the clouds that form part of the CMZ is crucial for inferring its structure and dynamics, as well as for better understanding how star formation proceeds in this environment (e.g., Kruijssen et al. 2015). Its 3D structure has not yet been fully constrained: there are several possible scenarios, including a twisted elliptical ring (Molinari et al. 2011), two spiral arms (e.g., Ridley et al. 2017), and an open gas stream (Kruijssen et al. 2015). In this sense, it is of fundamental interest to distinguish between dark clouds belonging to the CMZ and possible foreground clouds (Longmore et al. 2013).
Observations along the line-of-sight towards the GC are hampered by extreme extinction (AV ≳ 30 mag, AKs ≳ 2.5 mag; e.g., Nishiyama et al. 2008; Schödel et al. 2010; Nogueras-Lara et al. 2018a, 2020b) and crowding. Given these limitations, the majority of stars that can be observed are red giants. In particular, red clump (RC) stars (metal-rich, core helium burning giants; e.g., Girardi 2016) are the dominant and best tracer of the structure in the inner Galaxy and can be used to estimate distances towards the CMZ molecular clouds (e.g., Longmore et al. 2012; Zoccali et al. 2021).
In this Letter, we estimate the distance to three molecular clouds, G0.254+0016 (the ‘Brick’, Longmore et al. 2012), the 50 km s−1 cloud, and the 20 km s−1 cloud (e.g., Kauffmann et al. 2017), and discuss whether they belong to the CMZ. In particular, the recent paper by Zoccali et al. (2021) found that the Brick cloud is not located at the GC, so we aimed at cross-validating their results.
2. Data
To overcome the observational challenges, we used H and Ks photometry from the GALACTICNUCLEUS (GNS) survey (Nogueras-Lara et al. 2018a, 2019a). The GNS survey offers JHKs photometry of the inner GC at high angular resolution (∼0.2″). It also suffers little saturation. Therefore, it offers a high dynamic range and is complete below the RC, which are indispensable features for GC research. Statistical photometric uncertainties are ≲0.04 mag at the RC. The systematic uncertainty of the zero points (ZPs) is 0.04 mag in each band.
For our analysis, we chose circular regions with radii of 1.2′ centred on the coordinates shown in Table 1. Three of the regions are centred on the target clouds, the other three on control regions. The control regions are two low-extinction fields in the NSD and one in the nearby bulge. Figure 1 shows the locations of the regions.
 |
Fig. 1. Target regions over-plotted on a Spitzer/IRAC image at 3.6 μm. |
Target regions.
The Brick field images were of lower than mean quality in the GNS survey. Therefore, the conservative settings of the pipeline were not adequate for this field. For this reason, we performed dedicated point spread function (PSF) fitting photometry using StarFinder (Diolaiti et al. 2000) on the corresponding GNS image.
We estimated the completeness due to crowding (completeness at the magnitudes of interest is not limited by sensitivity in the crowded GC fields) in the same way as it was derived for the GNS survey in Sect. 4.3. of Nogueras-Lara et al. (2019a). Figure 2 shows the colour magnitude diagrams (CMDs) Ks versus H − Ks of the target regions, and the 80% completeness limit is indicated for each of the regions.
 |
Fig. 2. Colour magnitude diagrams Ks vs. H − Ks of the target regions: the 50 km s−1 cloud (panel a), the 20 km s−1 cloud (b), the Brick cloud (c), Control 1 (d), Control 2 (e), and the bulge region (f). The red parallelograms show the RC feature and the cut applied for the foreground population. The insets are zoom-ins on the RC regions where we detect a double RC (Sect. 3.1). The red and orange points correspond to the best fit obtained for the two RC features and indicate the 1σ uncertainties. The dashed orange lines mark the 80% completeness level. |
Given the relatively small size of the target regions, the contamination from the foreground population (stars in the line-of-sight from the Earth to the GC, mainly from the Galactic disc) is not significant. Nevertheless, we excluded stars with H − Ks < 1.3 mag for the regions in the NSD (removing stars belonging to the disc and the bulge; Nogueras-Lara et al. 2020a; Sormani et al. 2020). In the case of the bulge region, we applied a colour cut H − Ks ∼ 1.1 mag, in agreement with previous work (Nogueras-Lara et al. 2018b).
3. Analysis of the RC features
3.1. RC features and star formation
The analysis of the RC features in the CMD can give us insights into the star formation history (SFH) of the studied regions. In particular, the NSD is characterised by a double RC feature associated with its dominant old stellar population (the bright RC) and a significant star formation event that occurred ∼1 Gyr ago (∼5% of the total stellar mass), corresponding to the faint RC (see Fig. 1 in Nogueras-Lara et al. 2020a). On the other hand, the innermost regions of the Galactic bulge are characterised by an alpha-enhanced, metal-rich, old stellar population (e.g., Fulbright et al. 2006, 2007; Babusiaux et al. 2010; Hill et al. 2011; Bensby et al. 2011, 2018; Ness et al. 2013; Johnson et al. 2013; Rojas-Arriagada et al. 2020) that produces a single RC feature (Nogueras-Lara et al. 2018b). Thus, by studying the RC feature for a given cloud it is possible to infer whether the majority of stars in front of the cloud belong to the NSD or to the foreground population (mostly the inner bulge, as in our bulge control field).
We analysed the RC features inside the red parallelograms in Fig. 2. We applied the techniques described in Nogueras-Lara et al. (2018b, 2019b, 2020b) to distinguish between an individual or a double RC in the data. Namely, we divided the features into colour bins (∼0.1 mag, depending on the density of the points for each region) and fitted a single- and a double-Gaussian model to the Ks distribution for each colour bin. We used the Akaike information criterion (AIC; Akaike 1974) to compare both models. We found that a double RC model is favoured in all cases with the exception of the case corresponding to the inner bulge, which is consistent with our previous work on the entire inner GC region (Nogueras-Lara et al. 2020a,b). The inner bulge region only shows a single RC, in agreement with its mainly old stellar population (Nogueras-Lara et al. 2018b). Table 2 shows the distances between features obtained for each case. The statistical uncertainties were estimated using a jackknife resampling method, the systematics were obtained by varying the bin width, and the outlines of the parallelogram were used to select the stars.
Analysis of the RC features.
3.2. Reddening vector and distances
The colour cut applied to our data guarantees the exclusion of stars from the Galactic disc. As pointed out by Zoccali et al. (2021), any RC feature significantly closer to Earth than the GC would manifest itself as an over-density vertically offset from the reddening line fit to the GC RC feature in the CMDs. We estimate that a difference of 1 kpc at the GC distance implies a variation in Ks of ∼0.3 mag. Therefore, the analysed RC features do not include any significant contribution from stars at different distances given that there are not any points significantly outside the general slope trend in the RC features, within the uncertainties. In this way, the slopes of the RC features indicate the direction of the reddening vector and can be translated into the extinction curve (e.g., Nishiyama et al. 2009; Nogueras-Lara et al. 2020b). We obtained the reddening free magnitude for the RC features by computing the corresponding linear fit and following the equation:
where Ks0 is the reddening free magnitude, s is the slope of the reddening vector, (H − Ks)0 = 0.07 ± 0.03 mag is the intrinsic colour of the RC (Nogueras-Lara et al. 2020a), and cut is the intercept of the linear fit.
We applied a linear fit to each of the obtained RC features. Table 2 shows the results, and the uncertainties were estimated as previously explained. Moreover, we considered the contribution of the systematic uncertainty of the ZPs to the uncertainties of the estimated intercepts and added it quadratically to the systematics. The resulting uncertainty of the intercepts is ∼0.1 mag, and it was added quadratically to the systematics. We converted the reddening free magnitudes into distances using the distance modulus and assuming an absolute magnitude of MKs = −1.59 ± 0.04 for RC stars, which was computed by averaging over the values obtained by Groenewegen (2008), Hawkins et al. (2017), and Chan & Bovy (2020). The uncertainty corresponds to the standard deviation of the measurements. We applied a population correction of ΔMK = −0.07 ± 0.07, as explained in Schödel et al. (2010). We only used the bright RC to derive the distances because of the larger uncertainties of the faint RC and the difficulty of determining a proper MKs due to the fact that the RC brightness is very sensitive to age variations for stellar populations ∼1 Gyr (see Fig. 6 in Girardi 2016). The last column of Table 2 shows the results. The uncertainties were obtained by applying the error propagation when computing the distance from the distance modulus.
4. Extinction towards the RC features
We needed to exclude the possibility that the double RCs may be due to populations at different mean distances. Thus, we computed the extinction to each of them, assuming that they correspond to RC stars with the same intrinsic colours. We used the technique explained in Sect. 4.1 of Nogueras-Lara et al. (2018b). Namely, we determined the line that indicates the 50% probability of membership to each of the features within the parallelograms in Fig. 2 using the Gaussian mixture function (Pedregosa et al. 2011). We then created a grid of extinction values (A1.61, extinction at 1.61 μm) in steps of 0.01 mag and calculated the corresponding colour (H − Ks) for RC stars (assuming a Kurucz model for an RC star, as explained in Nogueras-Lara et al. 2018b), applying the extinction curve from Nogueras-Lara et al. (2020b). We compared the colours from the stars in each of the features with the grid to obtain the best fit that minimises a χ2. Table 3 shows the results. The mean extinction values were obtained by applying a Gaussian fit to the A1.61 distributions. The statistical uncertainties correspond to the error of the mean, and the systematics were computed varying all the parameters involved in the calculation (Nogueras-Lara et al. 2018b). We found that the extinctions for both RCs are compatible within the uncertainties. This confirms that the stars are placed at roughly the same distance and that the double RC is due to the SFH.
Extinction towards the RC features.
5. RC fitting
We computed the average reddening free magnitude for the bright RC for each region to estimate its distance. We defined a common selection criterion for all the regions to select the RC stars (H − Ks ∈ [1.3 − 2.0] and delimited by the lines Ks > 1.2(H − Ks) + 12.44 and Ks > 1.2(H − Ks)+13.84). In this way, we avoided any systematic effect related to the star selection. We de-reddened the stars individually by applying the equation (e.g., Nogueras-Lara et al. 2020b):
where Ks0 is the reddening free magnitude, Ks and H are the observed magnitudes, (H − Ks)0 is the intrinsic colour of RC stars (0.07 ± 0.03; e.g., Nogueras-Lara et al. 2020a), and AH/AKs is the extinction curve (1.84 ± 0.03, Nogueras-Lara et al. 2020b).
Figure 3 shows the underlying distributions for the analysed regions where we identified the double RC structure obtained in the previous section. We applied a Gaussian fit to the brightest RC peak, which corresponds to the dominant old stellar population in the NSD. Table 4 shows the obtained results. The statistical uncertainties were negligible given the number of stars. The systematics were estimated considering all the uncertainties of the quantities involved in Eq. (2) and equal to ∼0.13 mag. To compute relative distances, the systematic uncertainties were decreased by ∼25% since only the ZP systematics affect the relative difference.
 |
Fig. 3. Histograms corresponding to the de-reddened RC stars in the analysed regions. The solid lines show a Gaussian fit to the bright RC. The numbers 1 and 2 indicate the double RC features observed in the data. |
Average RC magnitudes and distances.
We found that the distances to the target clouds are compatible, within the uncertainties, with the distances to the control fields as well as with the GC distance of ∼8 kpc (e.g., GRAVITY Collaboration 2018; Do et al. 2019).
6. Discussion and conclusion
In this Letter we computed the distances to three molecular clouds in the CMZ (the 50 km s−1, 20 km s−1, and Brick clouds) and investigated their CMZ membership.
We found that all fields towards the clouds present a double RC with an equal magnitude difference (ΔKs) between both features, indicating similar stellar populations. The ΔKs and the slope of the features agree with previous work for the NSD (ΔKs = 0.44 ± 0.01 mag from Nogueras-Lara et al. 2020a and a slope of 1.19 ± 0.04, obtained by transforming the extinction ratio AH/AKs = 1.84 ± 0.03 from Nogueras-Lara et al. 2020b). Therefore, the stars present in the target molecular clouds are compatible with the extinction curve and the SFH found for the NSD, and therefore also the control regions. If the clouds were located closer to Earth, outside of the NSD, then they should show single RCs, as observed for the inner bulge control field. This indicates that none of the target clouds likely belong to the inner bulge. Moreover, we also computed the distances to the clouds, applying a linear fit to the bright RCs (Eq. (1)), and found that they are compatible with the GC distance of ∼8 kpc.
We investigated the nature of the two RC features by computing the extinction towards each of them. We found that the extinction towards both features is compatible within the uncertainties in all the cases. Therefore, it is very unlikely that they are placed at different distances. However, the Brick was recently claimed to not belong to the CMZ, having a distance from the Sun of 7.20 ± 0.16 ± 0.2 kpc (Zoccali et al. 2021). If this were the case, the stellar population belonging to the NSD according to Zoccali et al. (2021) (in this Letter, the secondary RC) would have a significantly larger extinction given the high amount of gas and dust present in the CMZ. Thus, obtaining similar extinctions for both RC features, and the very similar values in comparison to other regions belonging to the NSD (control regions), indicates that the Brick is likely at the GC distance. Furthermore, the Brick appears to be less transparent in the near infrared than the other analysed clouds (see Fig. 2) due to the fact that it is very unlikely to observe stars beyond it. Hence, observing the features of star formation expected for the NSD places the Brick at the GC.
To further analyse whether the Brick and the other clouds belong to the CMZ, we used the same approach as Zoccali et al. (2021). We assumed reddening free (H − Ks, Ks) values of an RC as inferred from the results obtained for Baade’s window (0.22, 13.2) and plotted the extinction curve from that starting point (Zoccali et al. 2021). If the RC stars in our CMDs lie at the GC, then they should scatter around this reddening line. We assumed the extinction curve used in Zoccali et al. (2021), AKs = 1.308 ± 0.05 × E(H − Ks) (Minniti et al. 2020), and the extinction curve AKs = 1.19 ± 0.04 × E(H − Ks) (Nogueras-Lara et al. 2020b). Figure 4 shows the results. For all the regions, with the exception of the inner bulge region, we found that the bright RC is fitted well by the two reddening lines. The line obtained using the extinction curve from Minniti et al. (2020) is below the other but still compatible within the uncertainties. Only the inner bulge RC is below the lines, probably indicating a different average distance (larger, according to our results). Thus, we concluded that all the regions in the NSD actually belong to the NSD and are within the CMZ, including the Brick cloud.
 |
Fig. 4. Colour magnitude diagrams Ks vs. H − Ks of the target regions: the 50 km s−1 cloud (panel a), the 20 km s−1 cloud (b), the Brick cloud (c), Control 1 (d), Control 2 (e), and the bulge region (f). The red and orange points indicate the detected double feature for the RC. The solid violet line corresponds to the reddening line of RC stars at an 8.2 kpc distance following the extinction curve from Nogueras-Lara et al. (2020b). The dashed blue line shows the extinction curve from Minniti et al. (2020). The black, violet, and blue error bars correspond to the systematics of the data and the two extinction curves, respectively. |
We believe that the three main causes for the disagreement between our result and that of Zoccali et al. (2021) are: (1) It is necessary to consider the double RC features given the SFH in the NSD to avoid the misidentification of any of the clumps. (2) The extinction curve by Minniti et al. (2020) was derived using classical Cepheids in the bulge and the far side of the disc, but none in the GC. Hence, the line-of-sight towards the GC is not adequately covered, implying that possible variations of the extinction curve along the line-of-sight would make this law inappropriate for the GC region. On the other hand, previous work on the NSD (Nogueras-Lara et al. 2019b, 2020b) obtained an extinction curve compatible with the slopes of the analysed RC features; as such, this extinction curve might be more appropriate for studying the CMZ. Our results agree for both extinction curves, but an underestimation of the uncertainties or not considering the double RC features might produce biased results. Calculating the expected position for the RC at the GC distance using both extinction curves gives a difference of ∼0.18 mag for H − Ks = 1.75 mag. Therefore, the Ks distance of ∼0.28 mag measured between the bright RC and the theoretical reddening line by Zoccali et al. (2021) would be reduced to ∼0.1 mag when using the extinction curve by Nogueras-Lara et al. (2020b) (being thus in agreement with the GC distance within the uncertainties). (3) There is an underestimation of the uncertainties. The slope of the extinction curve used is 1.308 ± 0.05. Therefore, to compute the Ks magnitude corresponding to a given H − Ks value, the equation is Ks = 1.308 × (H − Ks)+12.91, where the intercept was computed using the Baade’s window starting point. Thus, the error for a computed Ks value (assuming no uncertainty for the intercept) would be 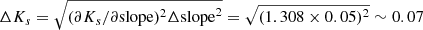 mag. Therefore, after error propagation, that implies a systematic uncertainty of ∼300 pc instead of 200 pc (Zoccali et al. 2021). Additionally, we think that Zoccali et al. (2021) only considered the systematics of the Ks ZP, not that of the H ZP, in their work. Taking both sources of uncertainty into account would increase the uncertainty up to ∼0.1 mag, corresponding to ∼350 pc at a distance of 7.2 kpc (∼400 at 8 kpc).
mag. Therefore, after error propagation, that implies a systematic uncertainty of ∼300 pc instead of 200 pc (Zoccali et al. 2021). Additionally, we think that Zoccali et al. (2021) only considered the systematics of the Ks ZP, not that of the H ZP, in their work. Taking both sources of uncertainty into account would increase the uncertainty up to ∼0.1 mag, corresponding to ∼350 pc at a distance of 7.2 kpc (∼400 at 8 kpc).
Finally, we computed the distance towards all the regions in the NSD de-reddening RC stars, which were selected in a similar way for all regions to avoid selection effects, and found that the distances to all the regions are compatible with one another with an uncertainty of ∼400 pc (Table 4). Therefore, we conclude that the studied clouds are compatible with the GC distance.
Acknowledgments
This work is based on observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 195.B-0283. We thank the staff of ESO for their great efforts and helpfulness. We thank Steven Longmore for useful discussion and comments on the manuscript. F.N.-L. and N.N. gratefully acknowledge support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 138713538 – SFB 881 (“The Milky Way System”, subproject B8). R.S. acknowledges financial support from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award for the Instituto de Astrofísica de Andalucía (SEV-2017-0709). R.S. acknowledges financial support from national project PGC2018-095049-B-C21 (MCIU/AEI/FEDER, UE).
References
- Akaike, H. 1974, Autom. Control IEEE Trans., 19, 716 [Google Scholar]
- Babusiaux, C., Gómez, A., Hill, V., et al. 2010, A&A, 519, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Adén, D., Meléndez, J., et al. 2011, A&A, 533, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., Gould, A., et al. 2018, IAU Symp., 334, 86 [NASA ADS] [Google Scholar]
- Chan, V. C., & Bovy, J. 2020, MNRAS, 493, 4367 [CrossRef] [Google Scholar]
- Dahmen, G., Huttemeister, S., Wilson, T. L., & Mauersberger, R. 1998, A&A, 331, 959 [Google Scholar]
- Diolaiti, E., Bendinelli, O., Bonaccini, D., et al. 2000, A&AS, 147, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Do, T., Hees, A., Ghez, A., et al. 2019, Science, 365, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Figer, D. F., McLean, I. S., & Morris, M. 1999, ApJ, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Figer, D. F., Najarro, F., Gilmore, D., et al. 2002, ApJ, 581, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2006, ApJ, 636, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2007, ApJ, 661, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L. 2016, ARA&A, 54, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2008, A&A, 488, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hawkins, K., Leistedt, B., Bovy, J., & Hogg, D. W. 2017, MNRAS, 471, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, V., Lecureur, A., Gómez, A., et al. 2011, A&A, 534, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, C. I., Rich, R. M., Kobayashi, C., et al. 2013, ApJ, 765, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Pillai, T., Zhang, Q., et al. 2017, A&A, 603, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kruijssen, J. M. D., Dale, J. E., & Longmore, S. N. 2015, MNRAS, 447, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Launhardt, R., Zylka, R., & Mezger, P. G. 2002, A&A, 384, 112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longmore, S. N., Rathborne, J., Bastian, N., et al. 2012, ApJ, 746, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Longmore, S. N., Kruijssen, J. M. D., Bally, J., et al. 2013, MNRAS, 433, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Minniti, J. H., Sbordone, L., Rojas-Arriagada, A., et al. 2020, A&A, 640, A92 [EDP Sciences] [Google Scholar]
- Molinari, S., Bally, J., Noriega-Crespo, A., et al. 2011, ApJ, 735, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M., & Serabyn, E. 1996, ARA&A, 34, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Muno, M. P., Arabadjis, J. S., Baganoff, F. K., et al. 2004, ApJ, 613, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2013, MNRAS, 430, 836 [Google Scholar]
- Nishiyama, S., Nagata, T., Tamura, M., et al. 2008, ApJ, 680, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 696, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Nogueras-Lara, F., Gallego-Calvente, A. T., Dong, H., et al. 2018a, A&A, 610, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nogueras-Lara, F., Schödel, R., Dong, H., et al. 2018b, A&A, 620, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nogueras-Lara, F., Schödel, R., Gallego-Calvente, A. T., et al. 2019a, A&A, 631, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nogueras-Lara, F., Schödel, R., Najarro, F., et al. 2019b, A&A, 630, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nogueras-Lara, F., Schödel, R., Gallego-Calvente, A. T., et al. 2020a, Nat. Astron., 4, 377 [CrossRef] [Google Scholar]
- Nogueras-Lara, F., Schödel, R., Neumayer, N., et al. 2020b, A&A, 641, A141 [EDP Sciences] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Pierce-Price, D., Richer, J. S., Greaves, J. S., et al. 2000, ApJ, 545, L121 [Google Scholar]
- Pillai, T., Kauffmann, J., Tan, J. C., et al. 2015, ApJ, 799, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Ridley, M. G. L., Sormani, M. C., Treß, R. G., Magorrian, J., & Klessen, R. S. 2017, MNRAS, 469, 2251 [Google Scholar]
- Rojas-Arriagada, A., Zasowski, G., Schultheis, M., et al. 2020, MNRAS, 499, 1037 [CrossRef] [Google Scholar]
- Schneider, F. R. N., Izzard, R. G., de Mink, S. E., et al. 2014, ApJ, 780, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Schödel, R., Najarro, F., Muzic, K., & Eckart, A. 2010, A&A, 511, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sormani, M. C., Magorrian, J., Nogueras-Lara, F., et al. 2020, MNRAS, 499, 7 [Google Scholar]
- Spergel, D. N., & Blitz, L. 1992, Nature, 357, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Yamauchi, S., Kawada, M., Koyama, K., et al. 1990, ApJ, 365, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Zoccali, M., Valenti, E., Surot, F., et al. 2021, MNRAS, 502, 1246 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Target regions over-plotted on a Spitzer/IRAC image at 3.6 μm. |
| In the text | |
 |
Fig. 2. Colour magnitude diagrams Ks vs. H − Ks of the target regions: the 50 km s−1 cloud (panel a), the 20 km s−1 cloud (b), the Brick cloud (c), Control 1 (d), Control 2 (e), and the bulge region (f). The red parallelograms show the RC feature and the cut applied for the foreground population. The insets are zoom-ins on the RC regions where we detect a double RC (Sect. 3.1). The red and orange points correspond to the best fit obtained for the two RC features and indicate the 1σ uncertainties. The dashed orange lines mark the 80% completeness level. |
| In the text | |
 |
Fig. 3. Histograms corresponding to the de-reddened RC stars in the analysed regions. The solid lines show a Gaussian fit to the bright RC. The numbers 1 and 2 indicate the double RC features observed in the data. |
| In the text | |
 |
Fig. 4. Colour magnitude diagrams Ks vs. H − Ks of the target regions: the 50 km s−1 cloud (panel a), the 20 km s−1 cloud (b), the Brick cloud (c), Control 1 (d), Control 2 (e), and the bulge region (f). The red and orange points indicate the detected double feature for the RC. The solid violet line corresponds to the reddening line of RC stars at an 8.2 kpc distance following the extinction curve from Nogueras-Lara et al. (2020b). The dashed blue line shows the extinction curve from Minniti et al. (2020). The black, violet, and blue error bars correspond to the systematics of the data and the two extinction curves, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.