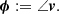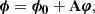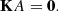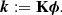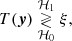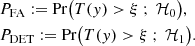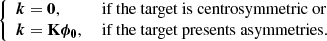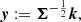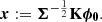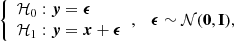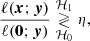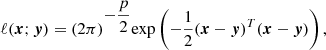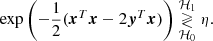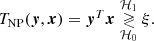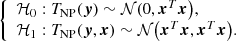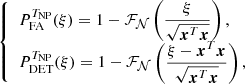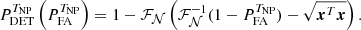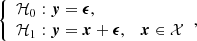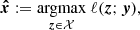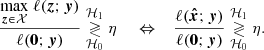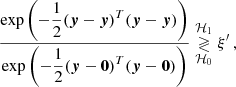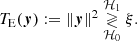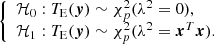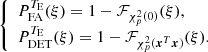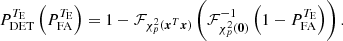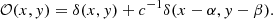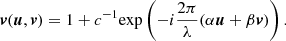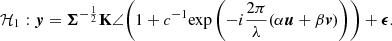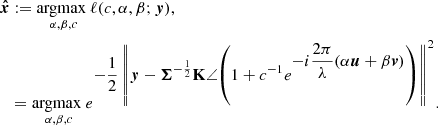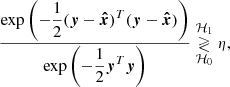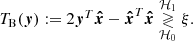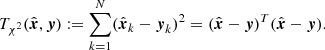| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 10 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201935247 | |
| Published online | 02 October 2019 | |
Kernel-phase detection limits
Hypothesis testing and the example of JWST NIRISS full-pupil images
1
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, France
e-mail: alban.ceau@oca.eu
2
Department of Astronomy, University of Michigan, Ann Arbor, MI 48109, USA
3
Space Telescope Science Institute, Baltimore, MD 21218, USA
Received:
11
February
2019
Accepted:
7
August
2019
Context. The James Webb Space Telescope (JWST) will offer high angular resolution observing capability in the near-infrared with masking interferometry on the Near-Infrared Imager and Slitless Spectrograph (NIRISS), and coronagraphic imaging on the Near-Infrared Camera (NIRCam) and the Mid-Infrared Instrument (MIRI). Full-aperture kernel-phase-based interferometry complements these observing modes by allowing us to probe for companions at small angular resolution while preserving the telescope throughput.
Aims. Our goal is to derive both theoretical and operational contrast-detection limits for the kernel-phase analysis of JWST NIRISS full-pupil observations using tools from hypothesis testing theory. The study is immediately applied to observations of faint brown dwarfs with this instrument, but the tools and methods introduced here are applicable in a wide variety of contexts.
Methods. We construct a statistically independent set of observable quantities from a collection of aberration-robust kernel phases. Three detection tests based on these observable quantities are designed and analysed, all having the property of guaranteeing a constant false-alarm rate for phase aberrations smaller than about one radian. One of these tests, the likelihood ratio or Neyman-Pearson test, provides a theoretical performance bound for any detection test.
Results. The operational detection method considered here is shown to exhibit only marginal power loss with respect to the theoretical bound. In principle, for the test set to a false-alarm probability of 1%, companions at contrasts reaching 103 and separations of 200 mas around objects of magnitude 14.1 are detectable with a probability of 68%. For the brightest objects observable using the full pupil of JWST and NIRISS, contrasts of up to 104 at separations of 200 mas could ultimately be achieved, barring significant wavefront drift. We also provide a statistical analysis of the uncertainties affecting the contrasts and separations that are estimated for the detected companions.
Conclusions. The proposed detection method is close to the ultimate bound and offers guarantees on the probability of making a false detection for binaries, as well as on the error bars for the estimated parameters of the binaries that will be detected by JWST NIRISS. This method is not only applicable to JWST NIRISS but to any imaging system with adequate sampling.
Key words: instrumentation: high angular resolution / methods: data analysis / stars: low-mass / binaries: close / techniques: image processing / methods: statistical
© A. Ceau et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
In the past few years, many nearby brown dwarfs have been discovered thanks to the Wide-field Infrared Survey Explorer (WISE) sky survey (Wright et al. 2010; Cushing et al. 2011; Schneider et al. 2015). These newly discovered objects present an observational challenge due to their intrinsically low luminosities. Some of them have been observed by the Hubble Space Telescope (HST), mostly for proper motion and parallax measurements (e.g. Marsh et al. 2013). While previous studies have searched for companions, they lacked the sensitivity in the optical and the near infrared to achieve high enough contrasts to detect very low-mass companions (e.g. Fontanive et al. 2018). High angular resolution observations are also possible from the ground using either adaptive optics or optical interferometry. Cool dwarfs are however intrinsically faint objects and therefore fall short of the requirements of either technique, unless assisted by laser guide stars (Bernat et al. 2010).
Issues limiting the quality of ground-based observations, such as sky background or atmospheric perturbations, can be alleviated by observing from space. When launched, the James Webb Space Telescope (JWST, Gardner et al. 2006) will be the largest ever space telescope, and will provide unparalleled sensitivity for studying faint, cool dwarfs. With a 6.5 m primary mirror, and an instrument suite covering the 0.6−25.5 μm wavelength range, the theoretical angular resolution of this telescope ranges from 20 to 800 mas. For a nearby object located less than 20 pc away, this translates to the ability to resolve structures present within a few astronomical units (AU) of the central source.
However, even for instruments capable of very high angular resolution, the glare from an object can drown out the light from faint surrounding structures. This issue is usually addressed by using coronagraphy and the instrumentation of the JWST offers several coronagraphs inside the Near-Infrared Camera (NIRCam) and the Mid-Infrared instrument (MIRI), with inner working angles ranging from 300 to 800 mas. To probe the innermost parts of nearby systems, inside the inner working angles of the coronagraphs, interferometry offers a viable alternative. In that scope, onboard JWST, the Near-Infrared Imager and Slitless Spectrograph (NIRISS) offers the aperture masking interferometer (AMI) observing mode (Sivaramakrishnan et al. 2012) with a non-redundant mask (NRM) located in the instrument pupil wheel. The AMI enables the detection of objects with lower contrasts, but at narrower separations compared to what can be achieved by the JWST coronagraphs. The AMI is expected to have sufficient performance to address yet unanswered questions in the fields of active galaxy nuclei (AGNs; Ford et al. 2014), planetary formation, exoplanets (Artigau et al. 2014), and to facilitate follow-ups on astrometry measurements from the Gaia mission, or on ground-based extreme adaptive optics (AO) surveys. In the case of binary point sources in non-coronagraphic modes, contrast ratios as high as 10 mag (104) for the brightest companions at 130 mas can be attained using AMI (Sivaramakrishnan et al. 2012; Greenbaum et al. 2015, 2018).
The AMI achieves its best performance by taking advantage of self-calibrating observable quantities called closure phases (Jennison 1958). This technique, first developed for radio interferometry and later adapted to the optical regime (Baldwin et al. 1986) was adapted to single-dish telescopes using a non-redundant aperture mask. Initially used in seeing-limited observing conditions (Nakajima 1989), the technique eventually took advantage of the development of AO (Tuthill et al. 2006) allowing stabilised longer-exposure modes and providing the ability to observe fainter objects. Non-redundant mask interferometry is now routinely used and has led to a variety of studies (e.g. Sallum et al. 2015; Kraus et al. 2008, 2011).
Kernel phase generalises the idea of closure phase to apertures of arbitrary shapes, and can be reliably used when aberrations are smaller than about one radian (Martinache 2010). This method can therefore be used on images acquired using any instrument onboard JWST, provided that the instrument pupil geometry is accurately modelled. It is therefore useable on full-pupil images as well as on AMI/NRM closure phases. The Kernel method has already been used successfully to uncover new brown dwarf binaries with HST observations, as reported by Pope et al. (2013). Full-aperture kernel phase and AMI closure phase cover the same parameter space but with its lower throughput (∼15%), AMI is suited to the observation of bright targets that would otherwise saturate the instrument, as well as to observations where aberrations are too important to fall into the linear regime covered by the kernel method.
Kernel- and closure phase rely on exploiting the phase of the Fourier transform (also referred to as the complex visibility) of the image. The image must satisfy the Nyquist-sampling requirement (platescale smaller than 0.5 λ/D), although small-grid dithering allows observers to reconstruct a Nyquist-sampled image for other filters. Saturation should be avoided, although recovery is still possible (Laugier et al. 2019). For a filter to be fully exploitable, its shortest wavelength must respect the sampling criterion. For the 6.5 m diameter of the primary mirror of JWST, this means that the filters compatible with a Kernel-phase analysis are:
-
NIRCam in the short wavelength channel (0.6 − 2.3 μm), with a platescale of 31 mas pixel−1: F212N
-
NIRCam in the long wavelength channel (2.4 − 5.0 μm), with a platescale of 63 mas pixel−1: F430M, F460M, F466N, F470N and F480M.
-
NIRISS, with a platescale of 65 mas pixel−1 (STSCI 2018): F430M and F480M.
-
MIRI, with a platescale of 110 mas pixel−1: all filters but F770W and F780W.
Kernel detection limits for NIRCam have been computed by Sallum & Skemer (2019) for the F430M and F480M filters, as well a for NIRISS AMI in those same bands. The present work aims at setting a general statistical framework for the theoretical and operational detection limits of the Kernel approach, with focus on guarantees for the actual false-alarm rate of the implemented detection method. As for the practical results, we investigate various aspects of the detection limits achievable for full-aperture NIRISS observations in the F480M filter.
Section 2 describes how kernel phases are constructed, presents the corresponding statistical model, and introduces three statistical tests that are later used to determine contrast detection limits. Section 3 shows how the method is applied to simulated images by JWST NIRISS. For several objects representative of the Y dwarfs discovered by WISE, this part highlights the need for estimating the noise covariance matrix, compares the performance of proposed detection tests, and analyses the statistical uncertainty resulting in the estimation of the parameters of the detected binaries. For the remainder of this paper, an italicised lowercase letter such as a denotes a real or complex number, a bold lowercase italicised letter such as a denotes a vector, a bold italicised uppercase letter such as A denotes a matrix, and a hat such as 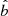 denotes the maximum likelihood estimate (MLE) of an unknown parameter b.
denotes the maximum likelihood estimate (MLE) of an unknown parameter b.
2. Kernel approach and statistical models
2.1. Kernel approach
The kernel framework introduced by Martinache (2010) describes diffraction-dominated images produced by the mostly continuous aperture of a telescope as if they were the interference pattern formed by a discrete array of virtual subapertures laid out on a regular grid of finite step. Although any pupil model can in principle yield kernel phases, using a regularly spaced grid allows the redundancy of the filled aperture to be encoded simply and effectively. The fidelity of the discrete representation of the continuous aperture increases with the density the grid. In practice however, the size of the grid step (s) translates into a cut-off frequency λ/s that is matched to the field of view over which the diffractive signal is recorded. The example of the discrete representation of the JWST entrance aperture along with an image of the theoretical point spread function (PSF) of the original aperture are shown in Fig. 1. The entrance pupil is a combination of the entrance pupil and of an additional pupil-plane mask, CLEARP.
 |
Fig. 1. Left: entrance pupil for JWST. Centre: discrete model of the pupil. The pupil is modelled by an array of subpupils, enabling the use of the kernel method. Right: simulated PSF for NIRISS using the 480M filter, represented using a non-linear colour scale. The coloured arrows represent the directions along which the simulated companions are placed. |
Kernel phases are formed from a linear combination of the phase measured in the Fourier transform of the image. For a given wavelength, the discrete grid describing the original aperture also defines the sampling of the Fourier space via the coordinates and redundancies of the different baselines. The values of the Fourier transform of an image for the selected spatial frequencies are collected in the complex visibility vector v. The phase vector ϕ is defined as the argument of the complex visibility,
In the optical path of a diffraction-limited instrument, unknown and potentially evolving aberrations result in a variable PSF that degrades the image quality. According to Martinache (2010), in the small aberration regime and for simple (i.e. non-coronagraphic) images, a linear model relates the phase ϕ measured in the Fourier space to the true phase of the observed object ϕ0 and to the aberration phase φ present across the aperture:
where A is a phase transfer matrix, encoding how the aberrations in each subaperture will propagate to the Fourier phase of the image. Its properties depend on the discrete representation of the aperture. The discrete model of the aperture of JWST featured in Fig. 1 is made of m = 452 virtual subapertures, placed on a grid with a step size of 20 cm that form n = 1363 distinct baselines, resulting in a full rank phase transfer matrix A of dimensions 1363 × 452. The kernel matrix K is defined as a p × n matrix that verifies
The kernel matrix cancels phase perturbation to the first order (Ireland 2013). With the chosen model, this matrix makes it possible to form a vector of kernel phases k of size (p × 1), with p = 887, defined as:
The kernel matrix K represents the left-nullspace of the transfer matrix A, and is computed from its singular value decomposition. The discrete representation of the aperture, the associated phase transfer matrix A, and the kernel matrix K can be generated using a specially designed Python package called XARA1, which also offers the basic tools to extract kernel phases from images.
2.2. Statistical modelling and hypothesis tests
Given a data image, how likely is it that a companion is present? The present study proposes to tackle this question through statistical hypothesis testing. A hypothesis test compares a test statistic (noted T) to a threshold (ξ), and has the general form
where y is the data under test (obtained from the image) and the test statistic T(y) is a real random variable. In (5), the null hypothesis ℋ0 (noise only) is accepted if T(y) < ξ and the alternative hypothesis ℋ1 (noise + companion) is accepted otherwise. If the distribution of T can be known, the probability of false alarm can be controlled by the value of the test threshold ξ.
The performance of a detection test is given by its probability of false alarm (PFA, the probability that a detection occurs under ℋ0) and its probability of detection (PDET, the probability that a detection occurs under ℋ1):
The power of a test is its PDET at a given PFA: the higher the PDET for a given PFA, the more powerful the test. It can be conveniently represented as a receiver operating characteristic (ROC) curve, PDET as a function of PFA.
Turning back to our detection problem, in the absence of noise the kernel phases can take the values
The noises affecting the images propagate into the Fourier phases and consequently into the kernel phases. As we see in the following section, the noise on the kernels can be modelled by a correlated Gaussian distribution with a covariance denoted Σ. If this matrix is known, we can construct a vector y of “whitened” kernel phases which are decorrelated (hence independent), and similarly a vector x of whitened theoretical kernel phases corresponding to the signature of the target:
This leads to the following statistical hypotheses:
where ϵ is a p × 1 noise vector with independent and identically distributed Gaussian entries (thanks to the whitening), and 𝒩(0, I) denotes the standard normal distribution (the covariance of ϵ is the identity matrix, I).
2.2.1. Known signature in white Gaussian noise
For the problem defined in (10), the most powerful test is the likelihood ratio (LR), or Neyman-Pearson (NP) test (Neyman & Pearson 1933). For this test, the companion signature x must be known. The NP test is defined as
where ℓ(x; y) is the likelihood of the signature x given the data y and η is an adjustable threshold. For the Gaussian white noise considered here, the likelihood is (Scharf & Friedlander 1994)
with p being the length of the kernel phase vector. The likelihood under ℋ0 can be obtained from Eq. (12) by taking x = 0. Combining Eqs. (12) and (11) under ℋ0 and ℋ1 gives the test
Taking the logarithm of Eq. (13) and noting  leads to the test
leads to the test
Hence, the NP test amounts to comparing the dot product of the data with the signature to a threshold. The distribution of TNP can be analytically determined under ℋ0 and ℋ1:
Using 𝒩(0, 1) to denote a standard normal variable and ℱ𝒩 its cumulative distribution function (CDF), PFA and PDET for TNP can be derived using their definitions in Eq. (6) and the distributions in Eq. (15)
which, for the purpose of plotting ROC curves, combine to
This test is the most powerful for the considered model, and serves as the benchmark against which any other detection test can be evaluated.
Implementing the NP test (Eq. (14)) requires knowledge of the target signature x (namely, contrast and position if x corresponds to a companion). In practical situations however, x is often partially or even fully unknown. This leads us to consider the statistical model
where 𝒳 is a space describing some prior information about x. Below, we consider two cases: a completely unknown signature (𝒳 = ℝp) and the signature of a binary with unknown contrast and separation (𝒳 is then the space spanned by all possible binary signatures). A classical approach when some parameters describing the target x are unknown is to inject its MLE (denoted 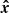 ) in place of x in the LR of Eq. (11). The MLE is defined by
) in place of x in the LR of Eq. (11). The MLE is defined by
and injecting the MLE in the LR leads to the so-called generalised likelihood ratio (GLR) defined as
2.2.2. Completely unknown x signature
If we assume as a worst-case situation that nothing is known about the signature x, we have 𝒳 = ℝp. The likelihood in (12) is maximised for 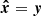 , and injecting this value in Eq. (20) yields
, and injecting this value in Eq. (20) yields
with ξ′ being a threshold. Taking the logarithm of Eq. (21), we obtain the test:
This test uses the measured squared norm of the signal as a test statistic and is called an energy detector (hence TE). Its statistic is distributed as:
Using 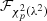 to denote the CDF of a
to denote the CDF of a 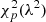 random variable with p degrees of freedom and non-centrality parameter λ, we obtain
random variable with p degrees of freedom and non-centrality parameter λ, we obtain
We note that test TE in Eq. (22) was previously used in the literature, for example by Zwieback et al. and Le Bouquin & Absil (2016; 2012) (although not identified as a GLR), with the PFA reported in Eq. (24).
The expressions above combine into
Indeed, this test does not exploit any prior knowledge of the structure of the object to be detected and can thus be seen as providing a lower bound for the detection performance.
2.2.3. Signature of a binary
Repeated observations of gravitationally interacting multiple systems is the only means by which unambiguous dynamical masses can be determined. Because they make it possible to resolve asymmetries near or even slightly below the diffraction limit, which translates into small orbital distances, NRM closure or kernel phase (Kraus et al. 2008; Huélamo et al. 2011; Lacour et al. 2011) and full-aperture kernel phase (Pope et al. 2013; Laugier et al. 2019) are particularly suited to the observation of unequal-brightness, low-mass binary systems.
At any instant, a binary system is characterised by three parameters: the angular separation ρ of the companion relative to the primary, its position angle θ, and a contrast c, defined here as the luminosity ratio of the primary over the secondary. Our simulations assume that the position angle is measured in the image relative to the axis pointing up (represented by a blue arrow in the right hand panel of Fig. 1), and increases counterclockwise. Actual observations also have to take into account the orientation of the telescope to project the apparent position angle onto the celestial sphere to combine observations at multiple epochs.
As an intermediate step, it is also convenient to use a Cartesian coordinate system in which the location of the secondary is given by (α, β). If the binary system is made of two individually unresolved point sources, its intensity distribution 𝒪 can be modelled as a pair of Dirac distributions:
The complex visibility v associated to this object is the 2D Fourier transform of Eq. (26) (van Cittert 1934; Zernike 1938), that is,
We reiterate that in the alternative hypothesis defined in Eq. (18), 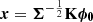 , where ϕ0 = ∠v. This leads to the parametric hypothesis:
, where ϕ0 = ∠v. This leads to the parametric hypothesis:
Under ℋ1, there are three free parameters: α, β, and c, so the MLE is now
Finding the MLE is equivalent to minimising the argument of the exponential. This minimisation cannot be done analytically but numerical methods can be used to compute 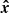 , as explained below. Injecting (29) in (20) gives the test
, as explained below. Injecting (29) in (20) gives the test
equivalent to
We note that this detection problem is similar to “case VII” of Scharf & Friedlander (1994), where the detection procedure also relies on the ML estimation of the signal of interest. In this latter study, however, the signature x is assumed to reside in a linear subspace (independent from the nuisance subspace), which is not the case here.
As mentioned above, the MLE 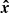 must be found numerically. Figure 2 illustrates, for one realisation of ϵ, an example of the value of the likelihood for a fixed contrast as a function of position angles α and β. It is apparent that the likelihood function is multimodal, so the minimisation strategy must be able to avoid local minima. A brute force search on a finely discretised grid of the parameter space is possible but comes at a large computation cost. Efficient numerical methods for solving multimodal problems exist, such as for instance the Monte Carlo Markov chains method with simulated annealing (Andrieu et al. 2003) or nested sampling (Skilling 2004).
must be found numerically. Figure 2 illustrates, for one realisation of ϵ, an example of the value of the likelihood for a fixed contrast as a function of position angles α and β. It is apparent that the likelihood function is multimodal, so the minimisation strategy must be able to avoid local minima. A brute force search on a finely discretised grid of the parameter space is possible but comes at a large computation cost. Efficient numerical methods for solving multimodal problems exist, such as for instance the Monte Carlo Markov chains method with simulated annealing (Andrieu et al. 2003) or nested sampling (Skilling 2004).
 |
Fig. 2. Map of the likelihood that is maximised in Eq. (29) for a data vector y accounting for a realistic covariance matrix Σ for JWST NIRISS. The companion signature has parameters α = β = 104 mas (red cross) and c = 100. |
Because the distribution of TB involves the unknown distribution of the MLE estimate 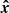 , it cannot be characterised analytically. However, as we see in the following section, this distribution can be estimated by Monte Carlo simulations, allowing us to accurately establish the relationship between the false-alarm probability
, it cannot be characterised analytically. However, as we see in the following section, this distribution can be estimated by Monte Carlo simulations, allowing us to accurately establish the relationship between the false-alarm probability 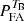 of this test and the threshold ξ in Eq. (31).
of this test and the threshold ξ in Eq. (31).
As an important final remark, we underline that the false-alarm probabilities of the considered tests are independent of the power of the phase perturbations φ (at least as long as the linear model in Eq. (2) holds, that is, for phase perturbation below ≈1 radian). This is clear from expressions (16) and (24) for tests TNP and TE; this is also the case for test TB because the phase perturbation is cancelled by the operator K and does not affect the test statistic. This means that the false-alarm rate of these tests remains constant in case of fluctuating aberrations, which is a desirable feature in practice.
2.2.4. Likelihoods, likelihood ratios, and χ2 intervals
The test statistic TB can be interpreted in terms of χ2-derived intervals as follows. Let 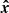 be some model obtained by some fit on data y. The χ2 score corresponding to this fit is
be some model obtained by some fit on data y. The χ2 score corresponding to this fit is
Considering the likelihood in Eq. (12), this shows that if y is Gaussian with mean 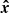 , the score in Eq. (32) is indeed a
, the score in Eq. (32) is indeed a 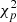 random variable. Now, the test statistics TB can be rewritten as
random variable. Now, the test statistics TB can be rewritten as
which shows that TB can be interpreted as the reduction in the sum of squared residuals when comparing the null hypothesis to the considered model.
For the sake of accurately controlling the false-alarm rate, we note however that Tχ2 in Eq. (32) may not be distributed as a 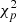 variable because
variable because 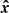 is a random variable. Actually, the true distribution of Tχ2 may not be known analytically, and a Monte Carlo procedure (such as that mentioned in Sect. 2.2.3 for the estimation of the correspondence between the PFA and threshold for TB) is required.
is a random variable. Actually, the true distribution of Tχ2 may not be known analytically, and a Monte Carlo procedure (such as that mentioned in Sect. 2.2.3 for the estimation of the correspondence between the PFA and threshold for TB) is required.
3. Results
The tests with the performance analyses presented in Sect. 2 are very general: considering a different aperture and instrumental noise simply amounts to replacing A, K, and Σ in the equations. We focus now on their specific application to JWST NIRISS full-pupil images (see Table 1).
Detector and targets characteristics used to compute the covariance of the kernel phases extracted from our JWST NIRISS simulated dataset.
3.1. Dataset and considered targets
We applied the three detection tests previously introduced to a series of simulated JWST/NIRISS datasets, replicating the observing scenario of archetypal ultracool Y-type brown dwarfs. While their multiplicity rate is currently unknown, more than 25 such objects have been discovered less than 20 pc away, mostly by the WISE mission (Kirkpatrick et al. 2011). At 20 pc, the theoretical angular resolution of JWST for λ = 4.8 μm translates into an orbital distance of 3 AU: interferometric observations will make it possible to probe within the first few AU of most known Y dwarfs.
JWST NIRISS images of Y dwarfs are simulated to evaluate the performance of the detection tests, using the ami_sim2 package (Greenbaum et al. 2016), corresponding to a 40 min integration on target and a 40 min integration on a perfect calibrator. Frames are simulated in full-pupil mode, using the F480M filter, for two different “W2” magnitudes: 15.4 and 14.1. The W2 magnitude is the apparent magnitude in the band selected by the W2 (λ = 4.6 μm) WISE filter (Wright et al. 2010). For these objects, companions are placed at a single position angle θ = 315° (materialised by the orange arrow in the PSF shown in Fig. 1). The simulated companions lie at separations of ρ = 73 mas (≈0.5λ/D @ λ = 4.8 μm) or ρ = 147 mas (≈λ/D @ λ = 4.8 μm), and have contrasts c = 10, c = 20, c = 50, or c = 100, leading to a total of eight possible signatures.
For any given target, a calibration frame is simulated and we assume no calibration error (stable wavefront, calibrator with the same spectrum and brightness as the Y dwarf). To comply with a real situation, kernel phases are not extracted directly from the simulated image: the frames are recentred, cropped to a size of 64 × 64 pixels and apodized by a super-Gaussian mask (see Eq. (2) of Laugier et al. 2019) of 30 pixels in radius to weigh down the edges of the image.
3.2. Modelling the errors
Two types of errors affect kernel phases and the outcome of the statistical tests described in Sect. 2. First are statistical errors induced by random noises whose overall impact can be captured in the acquisition or the synthesis of a global covariance matrix. Second are systematic errors resulting from the imperfect modelling by the kernel framework of the broadband, long-exposure, and diffractive nature of images. The subtraction of kernel phases acquired on a point source theoretically accounts for this systematic error. However, in practice, wavefront drifts between observations will result in unaccounted-for residual errors referred to as systematic errors (Ireland 2013).
To estimate the potential impact of systematic errors induced by wavefront drift, we rely on Perrin et al. (2018) who predict that over a timescale of two hours, JWST drifts will result at most in a 16 nm rms wavefront across the entire pupil3. We used the ten OPD maps distributed with the webbpsf package, scaled down to correspond to the predicted rms to produce images resulting in ten distinct kernel-phase realisations. The dispersion of kernel phases across these realisations was used to estimate the magnitude of the calibration residual. In the bright target scenario (W2 mag = 14.1) introduced in Sect. 3.1, this calibration residual accounts for about 14 % of the total noise variance. As is shown further below, this systematic error has a small impact when observing faint targets.
3.3. Covariance estimation
Whereas simulated images used in the analysis include all the previously listed noises, experience has shown us that, apart from calibration residuals, the covariance matrix can accurately be estimated using the three dominant noises: photon, readout, and dark current. Figure 3 indeed shows that after whitening by this simpler covariance, the distribution of kernel-phases is indistinguishable from a normal distribution of standard deviation 1.
 |
Fig. 3. Histogram of the values of the whitened kernel phases for the calibration images (orange). Standard, normal distribution (blue). Left-panel: higher flux regime. Right panel: lower flux regime. The distribution of whitened kernel phases obtained in practice is accurately described by the theoretical normal distribution considered in Eq. (10). |
The effect of the whitening is further illustrated in Fig. 4, which shows how previously noise-correlated kernel phases (left panel) are indeed made statistically independent (right panel). The thus-whitened observables can indeed be reliably used as input for the different statistical tests introduced in Sect. 2.2.
 |
Fig. 4. Isocontours of the joint PDF of the 668th and 669th elements of the kernel-phase vector k, k668 and k669, before (left) and after (right) whitening. The PDFs are estimated using 105 noise realisations. |
In practice, the covariance Σ is estimated using Monte Carlo simulations. An accurate estimation requires a number of simulated frames much greater than the total number of kernels; we used 105 frames for 887 kernels in our case.
Calibrated kernel phases are obtained by subtracting the kernel phases of a calibrator from those of the target in order to remove kernel model imperfections. Since the same flux is assumed for both observations, they share the same covariance. The covariance of the calibrated kernel-phase vector is therefore twice the covariance Σest estimated from the MC simulations.
To account for unknown calibration errors reported in NRM-interferometry as well as in full aperture kernel phases that result in a kernel-phase bias, one commonly used solution has been to artificially inflate the experimental variance by adding an additional term whose overall magnitude is adjusted during the model fit (e.g. Martinache et al. 2009). The OPD maps introduced in Sect. 3.2 make it possible to estimate the magnitude of this bias a priori. Proper treatment of the calibration would require the subtraction of an estimate of the calibration term, using either the POISE algorithm of Ireland (2013) or the KL decomposition approach described by Kammerer et al. (2019) that relies on the observation of multiple calibration sources. Here we estimate the impact of an unaccounted-for calibration error on the contrast detection limits by adding the residual determined after analysis of the simulation that included the OPD maps to the diagonal of the covariance. To pursue the possibly covariated effects would require the computation of a distinct covariance matrix from a large number of distinct realisations of telescope drifts. For the faint brown dwarf case that motivates this study, the impact of the calibration error is small, and therefore we chose not to pursue the non-diagonal terms.
3.4. Parameter estimation
Detecting a companion using the operational binary test TB requires the determination of the MLE 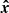 . This requires estimation of the parameters ρ, θ, and c from the whitened kernel phases y in Eq. (28). The distribution of the parameters can be estimated by generating, for each considered signature, a large number of noisy kernel phases and estimating the parameters. In practice, a global optimisation algorithm can be used. For the purpose of making a large number of simulations, we assume that the algorithm has localised the region in which the global minimum is situated (the darkest region in Fig. 2). In this setting, the minimum can be found by a gradient descent algorithm.
. This requires estimation of the parameters ρ, θ, and c from the whitened kernel phases y in Eq. (28). The distribution of the parameters can be estimated by generating, for each considered signature, a large number of noisy kernel phases and estimating the parameters. In practice, a global optimisation algorithm can be used. For the purpose of making a large number of simulations, we assume that the algorithm has localised the region in which the global minimum is situated (the darkest region in Fig. 2). In this setting, the minimum can be found by a gradient descent algorithm.
In the following, we use the algorithm described by Branch et al. (1999), as implemented in scipy.optimize.leastsquares, which uses the local gradient and optimises for the direction descent and step size. The initialisation of the algorithm corresponds to the parameters of the injected companion. This method is suited for the determination of contrast limits thanks to its speed. We checked that we obtained very similar results with a (computationally more expensive) systematic grid search that would typically be used in practice4.
Figure 5 shows the recovered kernel phases as a function of the kernel phases of simulated images for different separation, contrast, and flux regimes. The fit remains relatively consistent for each case, with scatter becoming predictably more important as the S/N decreases (the S/N is affected by the contrast, the separation, and the total flux in the image).
 |
Fig. 5. Kernel phases of the recovered signature (x axis) against the true kernel phases of the injected binary (y axis). Left panel: high flux regime. Right panel: low flux regime. The worst S/N situation (ρ = 73.5 mas, c = 100) is in orange, and the best S/N (ρ = 147 mas, c = 10) is in blue. |
All of the signatures presented in Fig. 6 are detectable by the TB with PFA < 10−3. The shape of the 2D distribution of the estimated separation ρ and contrast c reproduces what was for instance reported by Pravdo et al. (2006) in the context of NRM observations: at angular separations smaller than λ/D, estimates for the contrast and the angular separation are strongly correlated.
 |
Fig. 6. Error on the recovered parameters. Top panels: circles represent the separation and contrasts of the injected signature, and each column represents one flux regime. Bottom panels: error on the estimated angle θ. The parameters ρ and c of each injected signature are represented as coloured circles on the top panels, while θ is fixed at 315° for all signatures. The same colour code is used for every panel, with each colour corresponding to an injected signature. Each dot on the top panel represents the parameters estimated for a single realisation of the noise. |
Figure 6 also shows that two regimes can be distinguished. For a companion at ρ ≈ λ/D (for JWST λ/D = 152 mas @ λ4.80 μm), all parameters are well constrained, while for a companion at ρ < λ/D, the contrast and the angular separation cannot be well constrained simultaneously. In practice, this means that the estimation of the position of a companion using kernel-phases when the expected angular separation is smaller than λ/D can be further constrained by an independent measurement of the luminosity of the companion at a different epoch, when ρ > λ/D. This property can be particularly useful in the case of objects with high eccentricities or inclinations.
A study of the consequences of the uncertainties on parameters and correlations on the orbit that can be fitted using the Kernel method on NIRISS images is out of the scope of this paper; this should be the object of future work, along with recommendations of optimum observing strategies in regards to the uncertainties on measured orbital parameters.
3.5. Detection and contrast performance
Firstly, we validate the theoretical relations predicting the performance of the NP test TNP (Eq. (17)) and of the energy detector TE (Eq. (24)), and determine the actual performance of TB (Eq. (31)). For that purpose, we perform Monte Carlo simulations consisting of 2000 realisations5 of y under ℋ0 and under ℋ1 for a given signature x (cf. Eq. (27)).
All of the detection limits are shown for PFA = 1% and PDET = 68%. In terms more frequently encountered in astronomy publications, this is equivalent to having a 68% chance of making a ≈2.3σ detection.
On each realisation, we perform each of the three tests using the kernels operator K and the covariance matrix Σ estimated as in Sect. 3.3.
Figure 7 presents our results in the form of ROC curves, which provide a graphical representation of the power of each test. It can be seen that the dashed curves representing the theoretical ROCs accurately match the solid lines corresponding to the performance achieved in practice. As expected, TNP appears to be the most powerful of the three tests (this test corresponds to the upper performance bound) and TE the least powerful of the three (this test uses no prior information on the target signature and can be seen as a lower bound). The performance of TB logically lies in between, but much closer to the upper than to the lower bound.
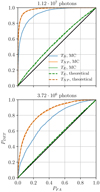 |
Fig. 7. ROC curves of TE (green), TNP (blue), and TB (orange). Theoretical ROC curves for TNP and TE plotted using Eqs. (17) and (24), for a companion at ρ = 200 mas, c = 1200, and θ = 45° off the vertical. Dashed lines correspond to theoretical ROCs, while solid lines represent ROCs obtained by Monte-Carlo simulations. The closer a curve is to the black line on the diagonal, the less powerful the corresponding test. The higher flux regime is represented in the top panel, and the lower flux regime in the bottom panel. The performance of TNP and TE are accurately described by the theoretical expressions in Eqs. (17) and (24). The test TNP presents the highest performance. TB is the next-best-performing test and TE has the lowest performance of the three. We see a clear improvement of the power of all tests as the flux (and thus the S/N) increases. |
The detection limits for the three tests TNP, TE, and TB are represented in Fig. 8 across a range of contrasts and separations, for a fixed position angle θ = 315°. The dashed lines correspond to no wavefront error while the solid lines correspond to 16 nm rms of wavefront error. We can see that the theoretical performance, validated for a single companion signature in Fig. 7, hold true over a large range of contrasts and separations, and that the detection limit of TB remains close to the bound provided by TNP. The dashed and dotted lines correspond to a perfectly stable JWST leading to a perfect calibration of the systematic errors.
 |
Fig. 8. Detection limits at a fixed position angle θ = 315°: below the contours the PDET falls below 68% for a fixed PFA of 1%, represented as a function of the separation and contrast of the companions, for TE (green), TB (blue), and TNP (orange). The dashed lines represent theoretical detection limits for TE and TNP (Eqs. (17) and (24)) and the dotted lines present the limits achieved in the MC simulations. TNP (orange) provides ideal detection limits for a Kernel treatment of a JWST-NIRISS image and the practical test TB (dotted blue) has contrast detection limits within a factor of 2.5 of the theoretical maximum. The solid lines represent the detection limits for TB (blue) and TNP (red) with a calibration residual corresponding to a 16 nm rms wavefront drift. |
The detection limits further depend on θ, because the PSF of JWST NIRISS is not centrosymmetric (as visible in Fig. 1). Fluctuations of these limits are shown in Fig. 9 for three position angles. Figure 9 also indicates the S/N level at the corresponding positions in the image (computed here as the maximal pixel value of a noiseless image with only the companion, divided by the standard deviation of the considered noise), showing that the detection limits follow the overall noise level in the image. Performance wise, the detectable contrast ratios are of the order of 103 at 200 mas, with some variations between the two flux levels considered.
 |
Fig. 9. Detection limits for test TB (Eq. (31)), in the higher flux regime (top panel) and the lower flux regime (bottom panel). The solid lines correspond to contours of PDET = 68% at a fixed PFA = 1%. Detection limits are represented at three different position angles for the companion: 0, 45, and 90° off the vertical, as orientated in the PSF shown in Fig. 1. The relative S/Ns (see text) are indicated by dashed lines. The shot (photon) noise is the main limiting noise in most cases. |
3.6. Mass limits for WISE 1405+5534
WISE 1405+5534 is a Y-type brown dwarf with a W2 magnitude of 14.1 that was used as a reference target to produce the contrast detection limits featured in Fig. 8. The raw observational detection limit curve of contrast as a function of angular separation can be converted into an astrophysical detection limit curve of companion mass as a function of orbital separation.
Whereas the 129 ± 19 mas parallax measured by Dupuy & Kraus (2013) directly allows for the conversion of the angular separation into a projected orbital distance, the contrast to mass conversion requires a model. We use the mass–luminosity relations given by the AMES-Cond model of Baraffe et al. (2003) for an age of 1 Gyr and a mass estimate of 30 MJ for the primary given by Cushing et al. (2011).
The detection limits obtained for WISE 1405+5534 are shown in Fig. 10. At PFA = 1%, and PDET = 68%, a 1 MJ can be detected at separations greater that 1.5 AU. An orbit with this semi major axis would have a period of 40 years, thus a quarter of an orbit could be captured with repeated observations over the expected service life of JWST.
 |
Fig. 10. Detection limits of a possible companion to WISE 1405+5534 at PFA = 1% and PDET = 68%, as a function of contrast (right ordinate axis) or mass (left ordinate axis) and absolute separation in AU. A one-Jupiter-mass object is detectable down to 1.5 AU from the primary. |
3.7. Bright limits
For the faint Y-dwarf targets considered thus far, it may have occurred to the reader that the contrast detection limits are dominated by the effect of the dark current and the readout noise and not by the photon noise of the central object. We wish here to complete the description of the properties of our approach with a bright target scenario that will feature a different behaviour, thus exhibiting the contribution of the photon noise.
The saturation limit for full-pupil JWST NIRISS using the F480M filter and a 64 × 64 pixels subarray size is 7.6 mag. We consider a shorter observation sequence, with a total of 20 min spent on the target of interest and 20 min on a calibrator of similar brightness. The detection limits for this observation using the operational test TB are shown in Fig. 11, at PFA = 1%, and PDET = 68%.
 |
Fig. 11. Detection limits for the brightest target observable without saturation with JWST NIRISS. Solid lines show detection limits for TB at PFA = 1% and PDET = 68% applied to the image with the greatest possible dynamic range, with 20 min total integration time. For the brightest images, the kernel method with the test TB ideally allows detection of contrasts up to 105 beyond 500 mas. The dashed orange line represents detection limits in the presence of a 16 nm wavefront drift. |
Unlike the contrast detection limits obtained on the faint targets, the curves now clearly reveal two different regimes. Up to an angular separation of ≈500 mas, where the photon noise is expected to dominate, the contrast detection decreases as a function of the angular separation. Beyond this point, it reaches a plateau, as the detection is once again dominated by the homogeneous properties of the dark current and the readout noise.
In this bright scenario, calibration errors induced by a drift comparable to what was described in Sect. 3.5 will have a stronger impact on the weak signal of a high-contrast companion. Sallum & Skemer (2019) feature contrast detection limits for NIRCam in a similar scenario that takes calibration errors into account. Under the hypothesis introduced in Sect. 3.2, the calibration error accounts here for 85% of the total noise variance of the kernels and therefore results in a degraded performance by a factor of approximately 10, as shown by the dashed curve in Fig. 11.
4. Conclusion
This paper provides a theoretical and numerical analysis of the performance of various detection tests based on the Kernel method. The approach provides an upper bound for the achievable detection limits, and an operational detection test whose performances are close to the upper bound. Furthermore, the false-alarm rate of these tests is not affected by fluctuating aberrations and can be tuned a priori.
The kernel-based detection approach presented in this paper is not specific to either NIRISS, the 480M band, the full-pupil imaging mode, or to JWST itself. The method only requires weak wavefront perturbations and appropriate sampling (i.e. a small-enough plate scale as compared to λ/D). In particular, the statistical treatment proposed in this study can also be used for NRM data.
For JWST-NIRISS in the F480M band, we have shown that medium-(≈102) to high-(≈103)contrast detections can realistically be achieved for separations down to half of λ/D on ultracool brown dwarf primary targets. In practice, this means that a 80 min observation sequence can allow for the detection of a 1 MJ situated 1.5 AU away from a 30 MJ Y-type brown dwarf at a distance of 8 pc. On brighter targets, kernel-phase analysis combined with the methods presented in this paper can reveal companions at contrasts ≈103 down to 0.3 λ/D.
Detection results presented in this paper rely on up-to-date simulations of JWST-NIRISS frames that take into account all the noises expected to contribute to kernel-phase uncertainties. These results can be affected by several factors that are not yet accounted for, the most critical being probably calibration errors. Instrumental drifts in the range of a few tens of nanometres, as predicted by Perrin et al. (2018), are not expected to significantly degrade performances for Y dwarfs. Another limitation may come from the algorithmic efficiency in determining the MLE 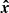 in Eq. (29) for the test TB. Overly coarse grid searches or algorithms too sensitive to local minima will lead to a loss in detection power and to an increased uncertainty for the estimated parameters.
in Eq. (29) for the test TB. Overly coarse grid searches or algorithms too sensitive to local minima will lead to a loss in detection power and to an increased uncertainty for the estimated parameters.
The performance reported in this work can therefore be seen as ideal contrast performance achievable using kernel phases for JWST NIRISS images. The method can in principle be improved upon by exploiting the full information available in the image (present not only in the phase but also, to a lesser extent, in the amplitude of the complex visibility). Even working solely with the phase, the calibration problem can be mitigated by using a more accurate and less idealised representation of the instrument. A significant fraction of the calibration error comes from the use of a necessarily approximate discrete model to represent the continuous phenomenon of diffraction. The results reported in this work were achieved using a dense aperture model to mitigate this discretisation error; however, the representation is not yet optimal. One avenue to improve the overall fidelity for example seems to be to take into account a variable local transmission function to more accurately describe the aperture with the same grid density. The study of the general aperture modelling prescription will be the object of future work.
The XARA package is regularly updated in the context of the KERNEL project.
XARA is available at http://github.com/fmartinache/xara
ami_sim is available at https://github.com/agreenbaum/ami_sim
Perrin et al. (2018) predict that large variations in slew angle will result in the most important variations, as the primary mirror regains thermal equilibrium over the course of days.
Acknowledgments
KERNEL has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement CoG – #683029). We wish to thank Nick Cvetojevic for proof-reading the paper and his contribution to group discussions. The manuscript was also significantly improved following the comments and recommendations from the anonymous referee.
References
- Andrieu, C., de Freitas, N., Doucet, A., & Jordan, M. I. 2003, Mach. Learn., 50, 5 [CrossRef] [Google Scholar]
- Artigau, Ă., Sivaramakrishnan, A., Greenbaum, A. Z., et al. 2014, SPIE Conf. Ser., 9143, 914340 [Google Scholar]
- Baldwin, J. E., Haniff, C. A., Mackay, C. D., & Warner, P. J. 1986, Nature, 320, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernat, D., Bouchez, A. H., Ireland, M., et al. 2010, ApJ, 715, 724 [Google Scholar]
- Branch, M. A., Coleman, T. F., & Li, Y. 1999, SIAM J. Sci. Comput., 21, 442 [CrossRef] [Google Scholar]
- Cushing, M. C., Kirkpatrick, J. D., Gelino, C. R., et al. 2011, ApJ, 743, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Dupuy, T. J., & Kraus, A. L. 2013, Science, 341, 1492 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanive, C., Biller, B., Bonavita, M., & Allers, K. 2018, MNRAS, 479, 2702 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, K. E., McKernan, B., Sivaramakrishnan, A., et al. 2014, AJ, 783, A73 [Google Scholar]
- Gardner, J. P., Mather, J. C., Clampin, M., et al. 2006, Space Sci. Rev., 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Greenbaum, A. Z., Pueyo, L., Sivaramakrishnan, A., & Lacour, S. 2015, ApJ, 798, 68 [Google Scholar]
- Greenbaum, A., Sivaramakrishnan, A., Sahlmann, J., & Thatte, D. 2016, https://github.com/agreenbaum/ami_sim [Google Scholar]
- Greenbaum, A. Z., Pueyo, L., Ruffio, J.-B., et al. 2018, AJ, 155, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Huélamo, N., Lacour, S., Tuthill, P., et al. 2011, A&A, 528, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ireland, M. J. 2013, MNRAS, 433, 1718 [NASA ADS] [CrossRef] [Google Scholar]
- Jennison, R. C. 1958, MNRAS, 118, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Kammerer, J., Ireland, M. J., Martinache, F., & Girard, J. H. 2019, MNRAS, 486, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirkpatrick, J. D., Cushing, M. C., Gelino, C. R., et al. 2011, ApJS, 197, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., Ireland, M. J., Martinache, F., & Lloyd, J. P. 2008, ApJ, 679, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., Ireland, M. J., Martinache, F., & Hillenbrand, L. A. 2011, ApJ, 731, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lacour, S., Tuthill, P., Amico, P., et al. 2011, A&A, 532, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laugier, R., Martinache, F., Ceau, A., et al. 2019, A&A, 623, A164 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Bouquin, J.-B., & Absil, O. 2012, A&A, 541, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsh, K. A., Wright, E. L., Kirkpatrick, J. D., et al. 2013, ApJ, 762, 119 [Google Scholar]
- Martinache, F. 2010, ApJ, 724, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Martinache, F., Guyon, O., Garrel, V., et al. 2009, AIP Conf. Proc., 1158, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, T. 1989, AJ, 97, 1510 [NASA ADS] [CrossRef] [Google Scholar]
- Neyman, J., & Pearson, E. S. 1933, Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci., 231, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, M. D., Pueyo, L., Rajan, A., et al. 2018, in Space Telescopes and Instrumentation 2018: Optical, Infrared, and Millimeter Wave, eds. H. A. MacEwen, M. Lystrup, G. G. Fazio, et al. (SPIE), 1069809, 8 [CrossRef] [Google Scholar]
- Pope, B., Martinache, F., & Tuthill, P. 2013, ApJ, 767, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Pravdo, S. H., Shaklan, S. B., Wiktorowicz, S. J., et al. 2006, ApJ, 649, 389 [Google Scholar]
- Sallum, S., & Skemer, A. 2019, J. Astron. Telesc. Instrum. Syst., 5, 1 [Google Scholar]
- Sallum, S., Follette, K. B., Eisner, J. A., et al. 2015, Nature, 527, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Scharf, L., & Friedlander, B. 1994, IEEE Trans. Sign. Process., 42, 2146 [Google Scholar]
- Schneider, A. C., Cushing, M. C., Kirkpatrick, J. D., et al. 2015, ApJ, 804, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Sivaramakrishnan, A., Lafrenière, D., Ford, K. E. S., et al. 2012, Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, 8442, 84422S [Google Scholar]
- Skilling, J. 2004, AIP Conf. Proc., 735, 395 [Google Scholar]
- STSCI 2018, NIRISS Imaging, Space Telescope Science Institute, James Webb Space Telescope User Documentation [Google Scholar]
- Tuthill, P., Monnier, J., Tanner, A., et al. 2006, Science, 313, 935 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Cittert, P. 1934, Physica, 1, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Zernike, F. 1938, Physica, 5, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Zwieback, S., Liu, X., Antonova, S., et al. 2016, IEEE Trans. Geosci. Remote Sens., 54, 5588 [Google Scholar]
All Tables
Detector and targets characteristics used to compute the covariance of the kernel phases extracted from our JWST NIRISS simulated dataset.
All Figures
 |
Fig. 1. Left: entrance pupil for JWST. Centre: discrete model of the pupil. The pupil is modelled by an array of subpupils, enabling the use of the kernel method. Right: simulated PSF for NIRISS using the 480M filter, represented using a non-linear colour scale. The coloured arrows represent the directions along which the simulated companions are placed. |
| In the text | |
 |
Fig. 2. Map of the likelihood that is maximised in Eq. (29) for a data vector y accounting for a realistic covariance matrix Σ for JWST NIRISS. The companion signature has parameters α = β = 104 mas (red cross) and c = 100. |
| In the text | |
 |
Fig. 3. Histogram of the values of the whitened kernel phases for the calibration images (orange). Standard, normal distribution (blue). Left-panel: higher flux regime. Right panel: lower flux regime. The distribution of whitened kernel phases obtained in practice is accurately described by the theoretical normal distribution considered in Eq. (10). |
| In the text | |
 |
Fig. 4. Isocontours of the joint PDF of the 668th and 669th elements of the kernel-phase vector k, k668 and k669, before (left) and after (right) whitening. The PDFs are estimated using 105 noise realisations. |
| In the text | |
 |
Fig. 5. Kernel phases of the recovered signature (x axis) against the true kernel phases of the injected binary (y axis). Left panel: high flux regime. Right panel: low flux regime. The worst S/N situation (ρ = 73.5 mas, c = 100) is in orange, and the best S/N (ρ = 147 mas, c = 10) is in blue. |
| In the text | |
 |
Fig. 6. Error on the recovered parameters. Top panels: circles represent the separation and contrasts of the injected signature, and each column represents one flux regime. Bottom panels: error on the estimated angle θ. The parameters ρ and c of each injected signature are represented as coloured circles on the top panels, while θ is fixed at 315° for all signatures. The same colour code is used for every panel, with each colour corresponding to an injected signature. Each dot on the top panel represents the parameters estimated for a single realisation of the noise. |
| In the text | |
 |
Fig. 7. ROC curves of TE (green), TNP (blue), and TB (orange). Theoretical ROC curves for TNP and TE plotted using Eqs. (17) and (24), for a companion at ρ = 200 mas, c = 1200, and θ = 45° off the vertical. Dashed lines correspond to theoretical ROCs, while solid lines represent ROCs obtained by Monte-Carlo simulations. The closer a curve is to the black line on the diagonal, the less powerful the corresponding test. The higher flux regime is represented in the top panel, and the lower flux regime in the bottom panel. The performance of TNP and TE are accurately described by the theoretical expressions in Eqs. (17) and (24). The test TNP presents the highest performance. TB is the next-best-performing test and TE has the lowest performance of the three. We see a clear improvement of the power of all tests as the flux (and thus the S/N) increases. |
| In the text | |
 |
Fig. 8. Detection limits at a fixed position angle θ = 315°: below the contours the PDET falls below 68% for a fixed PFA of 1%, represented as a function of the separation and contrast of the companions, for TE (green), TB (blue), and TNP (orange). The dashed lines represent theoretical detection limits for TE and TNP (Eqs. (17) and (24)) and the dotted lines present the limits achieved in the MC simulations. TNP (orange) provides ideal detection limits for a Kernel treatment of a JWST-NIRISS image and the practical test TB (dotted blue) has contrast detection limits within a factor of 2.5 of the theoretical maximum. The solid lines represent the detection limits for TB (blue) and TNP (red) with a calibration residual corresponding to a 16 nm rms wavefront drift. |
| In the text | |
 |
Fig. 9. Detection limits for test TB (Eq. (31)), in the higher flux regime (top panel) and the lower flux regime (bottom panel). The solid lines correspond to contours of PDET = 68% at a fixed PFA = 1%. Detection limits are represented at three different position angles for the companion: 0, 45, and 90° off the vertical, as orientated in the PSF shown in Fig. 1. The relative S/Ns (see text) are indicated by dashed lines. The shot (photon) noise is the main limiting noise in most cases. |
| In the text | |
 |
Fig. 10. Detection limits of a possible companion to WISE 1405+5534 at PFA = 1% and PDET = 68%, as a function of contrast (right ordinate axis) or mass (left ordinate axis) and absolute separation in AU. A one-Jupiter-mass object is detectable down to 1.5 AU from the primary. |
| In the text | |
 |
Fig. 11. Detection limits for the brightest target observable without saturation with JWST NIRISS. Solid lines show detection limits for TB at PFA = 1% and PDET = 68% applied to the image with the greatest possible dynamic range, with 20 min total integration time. For the brightest images, the kernel method with the test TB ideally allows detection of contrasts up to 105 beyond 500 mas. The dashed orange line represents detection limits in the presence of a 16 nm wavefront drift. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.