| Issue |
A&A
Volume 630, October 2019
Rosetta mission full comet phase results
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834907 | |
| Published online | 20 September 2019 | |
Analysis of night-side dust activity on comet 67P observed by VIRTIS-M: a new method to constrain the thermal inertia on the surface
1
Istituto di Astrofisica e Planetologia Spaziali, Istituto Nazionale di Astrofisica, Rome, Italy
e-mail: giovanna.rinaldi@inaf.it
2
Institute of Physics and Astronomy, University of Potsdam, Potsdam, Germany
3
Institute of Planetary Research, DLR, 12489 Berlin, Germany
4
LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Université, Université Paris Diderot,
Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
5
Lunar and Planetary Laboratory, University of Arizona, Tucson,
AZ 85721, USA
6
Università degli Studi di Napoli Parthenope, Dip. di Scienze e Tecnologie,
CDN IC4, 80143 Naples, Italy
7
Department of Physics and Astronomy, University of Padova,
Via Marzolo 8, 35131 Padova, Italy
8
Department of Physics, Oxford University, Oxford, UK
9
INAF – Osservatorio Astrofisico di Arcetri, Firenze, Italy
10
ASI, Via del Politecnico snc,
00133, Rome, Italy
Received:
17
December
2018
Accepted:
28
March
2019
On 2015 July 18, near perihelion at a heliocentric distance of 1.28 au, the Visible InfraRed Thermal Imaging Spectrometer (VIRTIS-M) on board the Rosetta spacecraft had the opportunity of observing dust activity in the inner coma with a view of the night side (shadowed side) of comet 67P/Churyumov-Gerasimenko. At the time of the measurements we present here, we observe a dust plume that originates on the far side of the nucleus. We are able to identify the approximate location of its source at the boundary between the Hapi and Anuket regions, and we find that it has been in darkness for some hours before the observation. Assuming that this time span is equal to the conductive time scale, we obtain a thermal inertia in the range 25–36 W K−1 m−2 s−1/2. These thermal inertia values can be used to verify with a 3D finite-element method (FEM) numerical code whether the surface and subsurface temperatures agree with the values found in the literature. We explored three different configurations: (1) a layer of water ice mixed with dust beneath a dust mantle of 5 mm with thermal inertia of 36 J m−2 K−1 s−0.5; (2) the same structure, but with thermal inertia of 100 J m−2 K−1 s−0.5; (3) an ice-dust mixture that is directly exposed. Of these three configurations, the first seems to be the most reasonable, both for the low thermal inertia and for the agreement with the surface and subsurface temperatures that have been found for the comet 67P/Churyumov-Gerasimenko. The spectral properties of the plume show that the visible dust color ranged from 16 ± 4.8%/100 nm to 13 ± 2.6%/100 nm, indicating that this plume has no detectable color gradient. The morphology of the plume can be classified as a narrow jet that has an estimated total ejected mass of between 6 and 19 tons when we assume size distribution indices between −2.5 and −3.
Key words: comets: general / comets: individual: 67P/Churyumov-Gerasimenko / infrared: planetary systems
© ESO 2019
1 Introduction
Dust activity on the night side (dark side) of comet 67P/ Churyumov-Gerasimenko (hereafter 67P) has been observed by the Optical, Spectroscopic, and Infrared Remote Imaging System (OSIRIS) on board the Rosetta mission (Knollenberg et al. 2016; Shi et al. 2016), and similar activity has been reported on other comets by previous space missions (Farnham et al. 2007; Feaga et al. 2007; Belton et al. 2008; A’Hearn et al. 2011). Some of these activities, which often occur deep in the night side, are classified as outbursts that lead to the formation of short-lived dust jets and plumes. Feaga et al. (2007) suggested that the dust activities observed near sunrise might be triggered by sublimation of water ice and of more volatile ices (super volatiles, such as CO and CO2) that have refrozen and accumulated on the surface during the night. Belton et al. (2008) showed that outbursts occur both in darkness or daylight, suggesting that they are not controlled by direct sunlight but rather by processes in the interior. This conclusion is strengthened by astronomical observations that show no dependence of the occurrence rate of outbursts with heliocentric distance and only a small increase in their occurrence rate post-perihelion relative to pre-perihelion. The post-perihelion activity peak, observed on 67P and other comets, suggests that the thermal environment in the immediate vicinity of the surface, in particular, the lag due to the thermal inertia of the nucleus surface layers, may play a role in triggering the outburst (Gulkis et al. 2015; Spohn et al. 2015). On 2015 March 12, Knollenberg et al. (2016) observed with the OSIRIS Wide Angle Camera (WAC) one prominent event before dawn, when 67P was approachingperihelion. This event was probably due to a mini-outburst coming from the Imhotep region. To explain the mechanism that caused the outburst event, these authors suggested the build-up of high-pressure gas conditions under the devolatilized surface layers. The pressure would increase until it overcame the tensile strength of the surface, at which point the gas pocket erupted, releasing the gas and accelerating the surrounding non-volatile material. This would leave a small pit or depression that exposed fresh volatile material that continued to sublimate. The validity of such a mechanism, which is a strong candidate for explaining the observation we report here, depends on the properties of the surface and subsurface, such as its layering and the thermal inertia profile.
Thermal inertia of comet surfaces has been analyzed for several previous comet missions. Groussin et al. (2013) derived values lower than 250 W K−1 m−2 s−1∕2 (hereafter TIU, Thermal Inertia Units) for comet 103P/Hartley 2 and lower than 45 TIU for comet 9P/Tempel 1 from the temperaturerise on the morning terminator. Similar values have been found by A’Hearn et al. (2011) and Davidsson et al. (2013) for the same comets. For 67P, thermal inertia has been derived from data obtained by the Microwave Instrument on the Rosetta orbiter (MIRO; Gulkis et al. 2007) and from data by the Multipurpose Sensors for Surface and Sub-Surface Science (MUPUS) instrument package at the Philae landing site Abydos (Spohn et al. 2007). Spohn et al. (2007) derived a low value of thermal inertia, in the range between 10 to 80 TIU (Gulkis et al. 2015; Spohn et al. 2015; Schloerb et al. 2015).
The main purpose of the present work is to analyze a specific night-side dust activity observed by the Visual Infrared and Thermal Imaging Spectrometer (VIRTIS; Coradini et al. 2007) and so to obtain an independent constraint on the surface thermal inertia of comet 67P in the correspondence of the active emitting area. The mapping channel VIRTIS-M (VM hereafter) observed this night-side dust emission at a heliocentric distance of 1.28 au, one month before the perihelion passage.
Despite the large number of dust emission observations by Rosetta and other comet missions and hypotheses such as those described above, the mechanism that forms the dust is still unknown. Gas flow must be involved to accelerate the dust away from the surface, and we need a thermal analysis of the conditions to understand their role in generating the night-side activity. Our analysis of the illumination conditions of the likely emitting region provides a new method for inferring the thermal inertia of that region. For this we used the COMSOL Multiphysics 5.3a package1, in particular, the module “Surface-to-Surface Radiation” in combination with MESHLAB2, applied to the shape model SHAP5 (Jorda et al. 2016), taking into account shadowing effects. It is crucial to calculate the illumination conditions to compute the solar energy input to the surface. We investigated whether it is possible for an event to be sustained by a thermal lag in the subsurface and applied a 3D thermophysical model (using the COMSOL Multiphysics module “Heat Transfer in Solids”) in order to evaluate the surface and subsurface temperature of the emitting region. Because we are only interested in the thermal history of the likely emitting region and also because this requires much computational time, the model was applied only to a specific part of the neck region of the nucleus, using the 3D radiation results as boundary condition. We analyzed configurations with and without a dust mantle over the dust-ice mixture for which we considered two different values of thermal conductivity for the dust, in order to compute the dependence of the surface and subsurface temperatures on the thermodynamic parameters such as density, specific heat, and thermal conductivity.
To distinguish between transient events and long-lasting features such as jets (which are stable for more than one comet rotation, as shown by Vincent et al. 2016), we adopted the following criteria: the transient events observed by VM were identified by their light curve (radiance at a given wavelength versus time) characterized by a sudden brightness increase in the coma that is associated with a release of gas and dust over a very short timescale, that is, 5–30 min (Bockelée-Morvan et al. 2017; Rinaldi et al. 2018). The light curve of a transient event can only be derived when the direction of the dust emission is perpendicular to the VM slit, for instance, when the scan occurs along the radial direction of the plume. The VM data are acquired with a temporal scan, as shown in Fig. 1, in which each line corresponds to a given time. This allows us to reconstruct the temporal evolution of the event. However, in the observation analyzed in this work, the dust emission direction is parallel to the VM slit, which prevents us from determining the light curve. Therefore we cannot assess whether the event is an outburst or transient, and we refer to it as a plume.
Section 2 presents a VM observation acquired on 2015 July 18. We study the physical properties of the dust ejecta (Sect. 3), including the radial profile (Sect. 3.1), color (Sect. 3.2), filling factor, and dust mass loss (Sect. 3.3). We analyze the illumination conditions of the likely emitting region and the thermal inertia of that region in Sects. 4–6. In Sect. 7 we investigate the 3D thermophysical model in order to evaluate the surface and subsurface temperature of the emitting region. Conclusions are provided in Sect. 8.
2 Observation and data reduction
The results presented here were derived from data obtained with the VIRTIS experiment on board the Rosetta spacecraft. VIRTIS is composed of two instruments: VIRTIS-H (VH; Drossart et al. 2000), a cross-dispersing point spectrometer providing spectra with high spectral resolution in the range 1.9–5 μm, and VIRTIS-M (VM; Coradini et al. 2007), an imaging spectrometer working in the range 0.25–5 μm by means of two channels, the visible (VIS) and the infrared (IR) channels, which cover the 0.25–1 μm and the 1–5 μm spectral intervals, respectively. Because of the failure in early May 2015 of the cryocooler, which is necessary to operate the IR channel, our analysis is restricted to VIS hyperspectral images. This dataset was continuously acquired forthe entire duration of the mission. The spectra and images used for the analysis were reduced using the VIRTIS calibration pipeline (Ammannito et al. 2006; Filacchione et al. 2006), with additional corrections derived from in-flight data. We removed defective pixels and cosmic-ray strikes using a median filter despiking algorithm, which was employed only in the spatial dimensions of the data and therefore left the spectral data intact.
We here analyze a hyperspectral cube acquired by VM on 2015 July 18, which shows night-side dust activity (Figs. 1 and 2). This image cube was acquired one month before the perihelion passage at a heliocentric distance of 1.28 au and a distance from the comet nucleus of 189 km. The corresponding Field of View (FOV) is about 12 km in the horizontal direction and 6 km in the vertical one, referred to the distance of the comet center to the spacecraft. The spacecraft was approximately on a terminator orbit so that the Sun illuminated one side and the other side was in darkness (Fig. 1).
Figure 2 displays the intensity map of the dust continuum in units of W m−2 sr−1 μm−1. The map is a composite image where the comet nucleus (as an average in the wavelength range 0.45–0.55 μm) is superimposed on the image of the dust continuum averaged in a bandpass of 0.10 μm centered on 0.55 μm. The Sun is at the top of the image, and on the day side, the dust activity shows a predictable behavior that is correlated with the illumination conditions. The dust continuum image displays a narrow, collimated plume that is rather sharply bounded on the image plane. The dust plume is seen to expand as a narrow ejecta projected on the FOV plane. The maximum intensity of the dust plume is 0.098 W m−2 sr−1 μm−1.
Table 1 provides the geometry information for the hyperspectral cube calculated by a routine (Acton 1996) that uses the spacecraft trajectory and orientation stored in SPICE kernels, and the 67P SHAP5 shape model for the comet nucleus (Jorda et al. 2016). The image was acquired line by line by means of a scanning mirror, taking 20 seconds per line. The final image is composed of a sequence of consecutive lines in the vertical direction.
In Table 2 we list all the relevant information obtained from the analysis of our observation, such as dust plume observation time, longitude and latitude of the estimated source region of the dust plume (Sect. 5), radiance level, and color at the maximum of the dust plume emission (Sect. 3.2).
The analysis of the VM dust continuum can be limited by infield stray light when the instrument slit is partially filled by the bright nucleus, and a sizable portion of the incoming photons is spread into the adjacent coma pixels. For the plume studied here, there is no stray light because the nucleus is in the dark, and its signal is therefore close to zero.
 |
Fig. 1 Configuration of the nucleus of the comet and jet with respect to the VIRTIS-M slit (horizontal red line) and its direction (red arrow). The VIRTIS-M data cubes are acquired with a temporal scan in which each line corresponds to a given time (white arrows). The orange thick line shows the Sun direction. The spacecraft is approximately in a terminator orbit with a phase angle of 90°, so that one side of the comet is illuminated by the Sun and the other side is in darkness. |
VIRTIS-M observation analysed in this work.
Dust plume properties in the VIS channel.
3 Properties of night-side dust ejecta
In this section, we analyze the physical properties of the dust plume in terms of radial profile, color, filling factor, and dust mass loss.
3.1 Radial profile
A particular feature of this observation is that the projected radial direction of the dust plume is along the instrument slit (horizontal red line in Fig. 1), spanning more than ten lines in the vertical direction that were acquired in about 3 min. For the first time, we therefore have the possibility to study the radial profile of a dust plume with VM data and to obtain information on the applicability of the fountain model to the cometary coma. In an ideal model, in which spherical continuity is satisfied, the radial column dust particle density profile n(ρ) is expected to follow the expression (Eddington 1910)
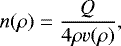 (1)
(1)
where ρ is the distance from the comet center, Q is the production rate of the number of particles of a given size, and v(ρ) is the particle outflow velocity. If there is no acceleration of the particles that are lifted off the surface, the observed scattered light intensity along the FOV should follow a simple 1/ρ profile. Deviations from a 1∕ρ relationship reflect changes in the dust component. Several processes can modify the radiance profiles: dust acceleration or a lateral dust flow can increase the slope, while optical depth effects and extended or secondary sources act to flatten it (Gerig et al. 2018).
In Fig. 3, panel A presents the radial profile of the observed radiance at 0.55 μm, averaged over ten lines, versus ρ. The distance, ρ, is calculatedusing the angular distance of each pixel from the center of the nucleus and the distance of the spacecraft to the center of the comet. According to the description of the shape model by Preusker et al. (2017), this center is defined as the center of mass. The profile is characterized by a steep increase in the first 1 km from the nucleus surface, followed by a smooth decrease for 1 km after maximum was reached. Panel B shows the radiance multiplied by ρ as a means for better visualizing changes in the coma. Beyond 4 km, the profile multiplied by ρ has an approximately constant value, independent of ρ. This is consistent with a cometary coma in a steady state, with constant dust production and outflow speed together with the conservation of dust grains. The decrease observed between 2.8 and 4 km can be explained by dust acceleration. A similar behavior has been reported in other comets by Belton et al. (2013), Tubiana et al. (2015), Knollenberg et al. (2016), and Miles et al. (2016). The vanishing radiance values at distances shorter than 2 km show that the inner parts of the plume are not illuminated by sunlight because of shadowing (see Sect. 5).
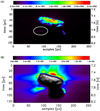 |
Fig. 2 Radiance at 0.55 μm on VIRTIS-M data cube V1_00395824539 acquired on 2015 July 18. Panel A: VM image at 0.55 μm. Panel B: same image, but the coma has been stretched to visualize the plume on the shadowed side (indicated by the oval). The cube details are listed in Table 1. The radiance has units of W m−2 sr−1 μm−1. |
 |
Fig. 3 Top panel: radiance of the radial profile of the dust plume at 0.55 μm on July 18 along the distance from the nucleus center (ρ).Bottom panel: radial profile multiplied by ρ vs. ρ. |
3.2 Color
The dust emitted from a comet in a plume or jet is often characterized by the color, the normalized reflectivity gradient, or reddening, measured in percent/100 nm (Jewitt & Meech 1986), which yields information about the dust scattering properties from which factors such as particle size, shape, and composition can be inferred. The color can be calculated using the values of the reflectance at two or more wavelengths. The reflectance, R, is a dimensionless quantity calculated by dividing the measured scattered light intensity I by the solar incident flux. When we take the wavelength-dependent solar flux from Kurucz (1994), the mean reflectance gradient per 100 nm, r, for a particular wavelength interval becomes
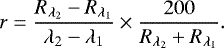 (2)
(2)
The reflectances we used are averages over a narrow bandpass of 10 nm in width centered on 550 nm (λ1) and 750 nm (λ2). This was chosen to optimize the signal-to-noise ratio (S/N) and so minimize the internal error in the color determination. We obtained a 2D color map using the spectrum for each pixel in the image (Fig. 4). The color uncertainties were evaluated with the method used by Rinaldi et al. (2018), by propagating the formal error that is inversely proportional to the S/N. Outside the dust plume, the uncertainty is higher because the radiance and the S/N are both very low (Fig. 2). For this reason, the color fluctuations outside the dust plume region delimited by the contour lines in Fig. 2 are not realistic. Inside the plume, the radiance and the S/N give us an uncertainty of about 15–20%.
The 2D color map does not show evidence of different reddening values with respect to the surrounding coma. In Fig. 4 the black contour lines are the radiance levels at 550 nm. The red color, more than 18%/100 nm, outside the larger contour is noise. The value of the color in the upper part of the dust plume is close to 13 ± 2.6%/100 nm, which is essentially the same as the values below and above, which are around 15–16 ± 4.8%/10 nm. There is no evident color gradient in this dust plume, in contrast to outburst ejectas (Bockelée-Morvan et al. 2017; Rinaldi et al. 2018).
 |
Fig. 4 Panel A: dust continuum image of the July 18 plume at 0.55 μm. Panel B: spatial distribution of the color calculated in the yellow square of the dust image. The black contours are the radiance levels at 0.55 μm. The dust ejecta do not display an evident color gradient, as observed in other outbursts observed by VM (Rinaldi et al. 2018). |
3.3 Filling factor and dust mass loss
In the method applied in Rinaldi et al. (2018), the expression for computing the filling factor is
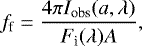 (3)
(3)
where Iobs(a, λ) is the observed scattered light intensity by the instrument (in W m−2 sr−1 μm−1), a is the dust particle radius, Fi (λ) is the incident solar flux, and A = Qsca × p(g), where Qsca is the scattering efficiency and p(g) is the phase function. Rinaldi et al. (2018) assumed a different albedo for the quiescent dust coma and for the outburst dust particles (Bockelée-Morvan et al. 2017; Agarwal et al. 2017) because the color map showed an evident color gradient. For this dust plume the color gradient is weak, and to compute the filling factor, we therefore assumed the quantity wp(g) as albedo, which was calculated by Ciarniello et al. (2015), where w = Qsca∕Qext is the single scattering albedo at 0.55 μm. The extinction efficiency Qext is equal to 1, and so w is just the scattering efficiency Qsca. The value for the quiescent dust coma at 90° of phase angle is 0.04. The value of the filling factor was obtained at the maximum of the plume radiance, where the value is 3.0%.
To calculate the observed dust mass that was ejected, we converted the filling factor to a total ejected dust mass, assuming the differential size distribution of the dust grains (n(a)da), where a is the grain radius, and the particle bulk density (ρbulk):
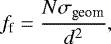 (4)
(4)
where N is the number of particles inside the pixel area d2, and σgeom is the geometrical particle cross section. The mass of material responsible for the VIS dust emission inside the pixel area d2 was computed with the equations reported by Rinaldi et al. (2018):
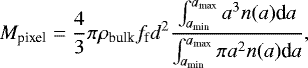 (5)
(5)
where amin and amax are the minimum and maximum grain radii. The minimum and maximum sizes considered in this work are amin = 0.1 μm and amax = 1000 μm, which takes a wide range of particle sizes into account.
In the formulas above, the total observed dust mass that is ejected in the plume is the integral over a large area containing the dust plume. By integrating the mass for each pixel (Mpixel) over the area where signal from the dust plume is present, we can determine the observed total dust mass that is emitted during the event. In our calculations we used a constant bulk density of 795 kg m−3 for all particles (Fulle et al. 2016).
We integrated over a rectangle extending from the closest nucleus boundary, which was chosen to avoid capturing any signal from the nucleus, to the final edge of the plume. The total mass computations are reported in Table 3.
Assuming a typical size distribution taken from the literature on 67P, with size distribution indices between −2.5 and −3 (Vincent et al. 2016), we estimate the observed total mass in the plume to be between 6 and 19 tons.
Observed total ejected dust mass.
4 Illumination conditions
Figure 2 suggests that this dust event originates from the dark side of the neck region. In order to evaluate the illuminationconditions at the observation time, we have to investigate the observation geometry that occurred before, after, and at the
time of the image cube acquisition. To calculate the local illumination at any position on the surface of the comet nucleus, we need to know the orientation of the cometary rotation axis and the rotation period. As in Kömle et al. (2017), we considered the Sun as apoint light source because the distance from the comet is very large compared to the size of the Sun. The position of the Sun in the Cartesian system of the comet is
![\begin{equation*} \left\{\!\! \begin{array}{ll} x_{\textrm{sun}}(t) = r_{\textrm{h}}(t) \cos \theta_{\textrm{sun}}(t) \cos\left(\phi - \frac{2{\pi}t}{P_{\textrm{comet}}}\right)\\\\[-5pt] y_{\textrm{sun}}(t) = r_{\textrm{h}}(t) \cos \theta_{\textrm{sun}}(t) \sin\left(\phi - \frac{2{\pi}t}{P_{\textrm{comet}}}\right)\\\\[-5pt] z_{\textrm{sun}}(t) = r_{\textrm{h}}(t) \sin \theta_{\textrm{sun}}(t), \end{array} \right. \end{equation*}](/articles/aa/full_html/2019/10/aa34907-18/aa34907-18-eq6.png) (6)
(6)
where θsun = −35.22° is the subsolar latitude, ϕ = 164.04° the subsolar longitude, and rh is the heliocentric distance at the time of observation (see Table 1). The shape model adopted in this calculation is SHAP5 (Jorda et al. 2016), adapted to a format that is suitable for the software COMSOL Multiphysics 5.3a3. In particular, we used the COMSOL module “Surface-to-Surface Radiation”.
The hemi-cube method was used to calculate the shadowing effects on the cometary surface (Formisano et al. 2018). In Figs. 5 and 6, we report the illumination conditions at 1.28 au. This corresponds to the heliocentric distance at which the dust plume observed by VIRTIS occurred on 2015 July 18. In Fig. 5 the comet is oriented as in Fig. 2, from two hours before the start time of the observations (7:16 h solar local time) to one hour after. In all the frames shown in Fig. 5, we observe that the neck, which is probably the region from which the dust plume is emitted, is entirely in shadows. For this reason it is interesting to analyze the illumination conditions on the far side of the comet, that is, the side that was not covered by the VM observation discussed here (see Fig. 6). The relevant fact is that even if the neck was not illuminated at the onset of the dust plume, it was illuminated until some hour before the observation starting time, so that the emission event could have been activated well before that time.
To validate our illumination calculation tool, we report in Appendix A the comparison between three images of Rosetta’s Navigation Camera (NavCam) at different times. We also present our illumination results.
 |
Fig. 5 Solar illumination on the comet oriented as in Fig. 2, at 1.28 au on 2015 July 18 from 5:16 h to 8:16 h.The color scale indicates the cosine of the solar incidence above the surface. The time step between the frames is 20 min. |
 |
Fig. 6 Solar illumination on the far side of the comet, i.e., the side that was not covered by the VM observation. The color scale indicates the cosine of the solar incidence above the surface. The time step between the frames is 20 min. |
5 Source location of the dust plume
The calculation of the illumination conditions critically depends on the identification of the probable location of the source of the dust plume event. We selected three regions on the basis of the illumination conditions at different times (see Fig. 7): the first isin the neck at 4:35 h (panel A). The second is located in the head of the comet, at 6:15 h (panel B). Finally, the third region is at the bottom of the neck, at 6:56 h (panel C). To identify the most likely emitting region, we drew the normal (black lines in Fig. 7) to the facets covering those regions, assuming that because the dust plume is a collimated and narrow jet (Fig. 2), the ejected dust particles have been accelerated away from the surface in a direction perpendicular to the surface. By comparing the directions of the normal to the configuration of Fig. 2, it appears that the location we search for is probably that from panel A of Fig. 7, which is mainly in the Anuket region and partially in the Hapi region, as shown in Fig. 8B (red rectangle). Anuket is a consolidated region that is mostly smooth at intermediate and large scales, but with small-scale roughness that gives it a rocky appearance. Its boundary with Hapi is extremely well defined (Thomas et al. 2018), characterized by textural and topographic discontinuities in the local terrain (Vincent et al. 2016; Fornasier et al. 2019). It is tempting to conjecture that the precise location of the source of the dust plume may be at the morphological boundary. As shown in Fig. 9, such areas are characterized by discontinuities in the local terrain that are either textural or topographic, as observed in Vincent et al. (2016) and Fornasier et al. (2019).
 |
Fig. 7 Definition of the normals (black lines) to the possible emitting regions by observing the illumination conditions of Fig. 6 at different local times. The color scale refers to the cosine of the solar incidence. Panel A: emitting region on the neck at 4:35 h (peak illumination), see panel A of Fig. 8. Panel B: another possible emitting region (in the head of the comet) at 6:16 h. Panel C: bottom region at 6:56 h. By observing the normal directions and comparing them with the emission of Fig. 2, the emitting region of panel A seems to be a more likely candidate. |
 |
Fig. 8 Panel A: mean cosine of the solar incidence angle vs. rotation time of the likely emitting region (Fig. 7): the red interval ranges from about 4:35 h to 6:15 h, the time span in which the likely emitting region is illuminated.We selected 4:35 h because it corresponds to the peak of the cosine plot, while 6:15 h corresponds to the moment in which the region starts to move into shadow. The blue interval represents the observation time of the dust plume (7:42–7:48 h). We note that during the dust plume, the emitting region is completely in shadow. Panel B: source region of the night-side dust activity detected by VM. The red rectangle indicates the emitting region calculated with the method described in the first part of Sect. 5, with a latitude ranging from − 30° to +10° and a longitude from 265 to 280°. The green rectangle indicates the source region constrained by measuring the length of the plume shadow. The region is mainly in the Anuket and Hapi regions. |
 |
Fig. 9 OSIRIS NAC image acquired on 2016 June 8 at 15:26:38 h and projected onto the shape model of 67P. A 500 m long fracture in the neck region of comet 67P can be seen at the bottom of this frame along the +280° meridian. |
Geolocalization of the source of the dust plume
In order to constrain the source region better, we measured in the VM image the position and orientation of the plume, and the size of the shadow region. Scattered light from the near-nucleus part of the jet is not observed. This section of the jet indeed lies in the shadow of the large lobe and therefore is not illuminated by sunlight. These geometric properties of the jet can be used to constrain itssource region.
We assumed that the dust particles within the jet escaped perpendicularly to their source region. Using the shape model version SHAP7 (500k facets, Preusker et al. 2017), we derived the plume properties geometrically for nearly 15 000 facets inside the longitude range = [260°, 300°] and latitude range = [−40°, 20°]. We also determined the three parameters mentioned above at the mid-time of the VM observation of the plume (2015-07-18T07:45:00).
The calculations were restricted to the neck regions illuminated 1.75 h before the VM observation. The reference axis was defined as the pointing vector from the nucleus center to the Sun (toward +Y in Fig. 1). The orientation of the plume was defined as the position angle between the plume and the reference axis, the shadow size was defined as thedistance between the intersecting point of the plume vector to the Y-axis and the maximum radiance point along the plume, and the position of the plume is the distancebetween this intersecting point and the nucleus center (which is on the Y-axis). Figure 10 shows scatterplots of the residuals of the three parameters (plume orientation, shadow size, and plume position, in percentage) and the combination score for each facet projected on a longitude-latitude based frame. The residual of the parameter (R) and the identifying score (S) are defined as follows:
 (7)
(7)
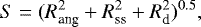 (8)
(8)
where Psim is the derived parameter for the facet, and Pobs is the observed value on the VM image. Rang, Rss, and Rd are the residuals of the plume orientation, shadow length, and jet position in percentage. The measured position angle, shadow length, and position distance are 96.5°, 1.664 km, and 0.379 km, respectively. The possible source regions should have a score close to zero. The score panel in Fig. 10 shows that the jet source is in a very narrow region for which the latitude is between −10° and 0° and the longitude between 275° and 285° (see Table 2 and green rectangle of Fig. 8B).
The narrow source region is in the Anuket region and is characterized by a 500 m long fracture at 283–284° longitude and −7 to +18° latitude. This fracture was spotted early in the Rosetta mission, and was observed in OSIRIS images to evolve over the two years of study. Already by 2014 December, it had extended by about 30 m, which is thought to be linked to the increasing spin rate of the comet before perihelion. Furthermore, in OSIRIS images taken in 2016 June, a newfracture that was at least 150 m long and perhaps extended up to 300 m was identified parallel to the original fracture (Thomas et al. 2018). Thomas et al. (2015) first described the neck – head boundary as probable tension fractions. The fractures and lineaments are dark-looking features with a width of a few meters and are some hundred meters long. They are characterized by sinuous outlines and variable width, suggesting that they are probably the surface expression of tension fractures and outburst sources (Skorov et al. 2016; Höfner et al. 2017).
In Sect. 3.3 we estimated the observed total mass of the dust plume to be between 6 and 19 tons, assuming a typical size distribution with indices between − 2.5 and − 3. The excavated volume lies in the range of 7.5–24 m3, which corresponds to an emitting area of 750–2390 m2 for a vertical thickness of 10 mm (Sect. 7). When we consider the calculated emitting area as a portion of this fracture of a few meters wide (i.e., 5 m), this corresponds to the formation of a 150–478 m long fracture. When we consider thecalculated emitting area as a circular pit, we find a path with a radius of 150–270 m. Pits like this have been observed elsewhere on the comet, possibly caused by sinkhole collapse associated with the formation of previous outbursts (El-Maarry et al. 2015, 2016; Vincent et al. 2016).
 |
Fig. 10 Simulation of the orientation, shadow length, and position of jets originating from the neck regions illuminated 1.75 h before the VIRTIS-M observations. Each point corresponds to the center of a facet in shape model version cg-dlr_ spg-shap7-v1.0, with 500 k facets. In the right panel, the score (see text) is plotted. Values of the score close to zero correspond to the best fit to the observations. |
6 Thermal inertia of 67P
Temperature measurements of the cometary surface show that the inferred thermal inertia is low, so there should be a small thermal lag that can activate a dust and gas emission a few hours after illumination (Groussin et al. 2007, 2013; Schloerb et al. 2015; Tosi et al. 2019). We here propose a new method for inferring the thermal inertia of a particular region of the surface of the comet. Previous methods are generally based on the estimating the thermal inertia from the measured temperature(e.g., Capria et al. 2014) or using daily amplitude of surface soil heat flux and temperature (Wang et al. 2010).
The key requirement is estimating the time span between the starting point, or peak, of the dust plume and the last time that the emittingregion (the border between Hapi and Anuket) is illuminated by the Sun. When we assume that this time span is equal to the conductive timescale, which is defined as
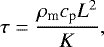 (9)
(9)
where L is the depth of the upper boundary of the ice-dust mixture layer, K is the thermal conductivity, ρm is the mean density and cp is the specific heat, we can derive the thermal conductivity and consequently the thermal inertia. The thermal inertia is deduced using the following equation:
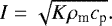 (10)
(10)
We assumed L = 5 mm (Shi et al. 2016; Hu et al. 2017), ρm = 533 kg m−3 (Pätzold et al. 2016) and cp = 1000 J kg−1 K−1 (Kömle et al. 2017). The time span of Eq. (9) can be constrained by observing panel A of Fig. 8, where we show the cosine of the solar incidence angle of the likely emitting region that we previously defined (Fig. 7 A). The red box marks the time span between the peak of the cosine plot (4:35 h) and the moment at which the region starts to move into the shadow (6:15 h). The blue box indicates the observation time of the dust plume (7:42–7:48 h), during which the likely emitting region is not illuminated. When we assume τ = 187 min (start = 4:35 h, stop = 7:42 h), we obtain a thermal conductivity of 1.2 × 10−3 W m−1 K−1 and consequently a thermal inertia of 25 TIU. Conversely, when we assume τ = 90 min (start = 6:15 h, stop = 7:42 h), we obtain a thermal conductivity of 2.5 × 10−3 W m−1 K−1 and a thermal inertia of 36 TIU. The values 25–36 TIU are compatible with the range provided by Gulkis et al. (2015) and Spohn et al. (2015) and also with the estimation provided by several previous comet missions. Our estimate is also compatible with the values found by Marshall et al. (2018), who found a thermal inertia < 80 TIU for the Seth, Ash, and Aten regions. The range of values of thermal conductivity we derived (i.e., 1.2–2.5 × 10−3 W m−1 K−1) is compatible with the values used in the literature in thermophysical modeling (Shi et al. 2016; Hu et al. 2017).
Observing Fig. 8A, we note that when we consider the start time as the moment in which the mean cosine of the solar incidence attains a value of 0.5 (in the increasing part of the plot), the thermal inertia estimate does not change dramatically. In this case, τ ≃ 6 h, and the thermal conductivity being 6 × 10−4 W m−1 K−1, a thermal inertia value of 18 TIU is found. Conversely, if the start time is assumed as the moment in which the mean cosine of the solar incidence is 0.5 in the decreasing part, the time span is about 1 h, and the thermal conductivity derived is 3.7 × 10−3 W m−1 K−1. Consequently, the thermal inertia is about 45 TIU. As a result of this sensitivity analysis, we can extend the thermal inertia range from 20 to 45 TIU, even if 20 TIU would correspond to a value of thermal conductivity that is very low and probably hard to justify.
7 Thermophysical model
We applied a thermophysical model to study the surface and subsurface temperatures of the emitting area between Hapi and Anuket, defined in Fig. 8B, and also to test whether the thermal inertia derived in previous section is compatible with the surface and subsurface temperatures found in the literature. The model was applied only to a small portion (1 × 1 × 5 cm) of the likely emitting region. The integration domain (see Fig. 11) is characterized by a surface area of 1 cm2 and a depth of 4.5 cm, which is larger than the diurnal skin depth (typically a fraction of only a few centimeters). Self-heating between the facets of the surface of the integration domain is taken into account.
 |
Fig. 11 Panel A: computation domain characteristic of the neck region. The top area (surface) is 1 cm2 while the height is chosen larger than the diurnal skin depth, which is on the order of one centimeter. Self-heating between thefacets of the surface is taken into account. Panel B: illustration of the vertical structures assumed in this work. Left panel: dust mantle at the top (5 millimeters) and beneath a mixture of dust and water ice (blue spheres) with thermal inertia 36 TIU (model M1; derived from the method described in Sect. 6) and 100 TIU (model M2). Right panel: no dust mantle, with direct exposure of the dust-ice mixture layer (model M3). |
7.1 Basic equations and boundary conditions
A 3D finite element method was applied using the software COMSOL Multiphysics4 and in particular the module “Heat transfer in Solids”, in combination with the meshing program MESHLAB. We solved the heat equation numerically, and combined it with a mass conservation equation to treat the water vapor emission, with no internal source or thermal convection, as in De Sanctis et al. (2005, 2010), Formisano et al. (2016, 2018, 2019a), Capria et al. (2017).
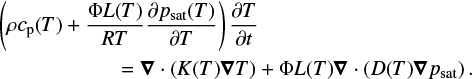 (11)
(11)
In this equation, Φ is the porosity, psat(T) is the saturation pressure, R is the universal gas constant, L(T) is the latent sublimation heat, and D(T) is the gas diffusion coefficient. At the surface the following energy balance was imposed (Formisano et al. 2018, 2019b):
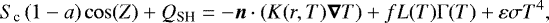 (12)
(12)
where QSH is the self-heating term and takes the mutual radiative interaction between the facets of the surface into account, a is the albedo, Sc is the local irradiation intensity in W m−2, cos (Z) is the cosine of the solar incidence angle, ε is the emissivity (set to 0.97), f is the area fraction covered by ice (if present on the surface), σ is the Stefan-Boltzmann constant, and Γ(T) is the water vapor production rate in kg m−2 s−1 defined by the following formula (Delsemme & Miller 1971):
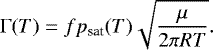 (13)
(13)
Here μ represents the water molar mass and psat(T) is given by Fanale & Salvail (1984):
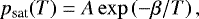 (14)
(14)
where A = 3.56 × 1012 Pa and β =6141.667 K. Local thermodynamic equilibrium was assumed. The term fL(T)Γ(T) is included in Eq. (12) only in the case of ice on the surface. The sublimation rate calculated with Eq. (13) includes the icy area fraction factor as in Hu et al. (2017):
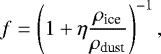 (15)
(15)
where η is the dust-to-ice ratio in mass, ρice is the ice density, and ρdust is the dust density. We note that f = 1 corresponds to a fully icy surface. At the bottom and on the vertical sides of our computational domain we imposed vanishing heat flux, and we assumed an initially constant temperature of 120 K (Kömle et al. 2017) in the whole domain, similar to the value adopted by Hu et al. (2017). The numerical grid of the computation domain shown in Fig. 11 A was chosen automatically by the COMSOL Multiphysics software, based both on the shape of the integration domain and on the physical equations involved.
7.2 Initial configurations
The fraction of the water ice on the surface of a comet seems to be very limited: for comet 67P, an upper limit of < 1% has been estimated (Capaccioni et al. 2015). Sublimation of water ice arises from layers that are made of a mixture of dust and ice, beneath a cover of dust of a few millimeters. The dust-to-ice ratio by mass would be at least 6 (Sierks et al. 2015; Capaccioni et al. 2015; Rotundi et al. 2015; Filacchione et al. 2016).
In this paper we consider three different cases in order to evaluate the dependence of the surface and subsurface temperatures on the physical parameters adopted in this work. The first configuration (model M1) is characterized by a dust mantle of 5 mm with thermal inertia 36 TIU (or equivalently, K = 2.5 × 10−3 W m−1 K−1) above a layer made of a mixture of dust and ice (whose ratio is fixed to 6 for all the configurations). The second configuration (model M2) is similar to the first, but with a thermal inertia of 100 TIU, that is, the thermal conductivity is an order of magnitude greater (2 × 10−2 W m−1 K−1) than in the M1 case. This choice was made in order to show the effects of a high value of the thermal inertia on the surface and subsurface temperatures. The third and last configuration (model M3) represents an extreme case in which the dust-ice mixture is directly exposed without a dust layer. Model M1 uses a value of thermal inertia derived through the method we discussed in Sect. 6. Because the diurnal skin depth is very low with the typical values of density, specific heat, and thermal conductivity assumed for the comet surface, we studied only the first 4.5 cm below the surface. We recall that the diurnal skin depth is defined (Mellon 1997) as
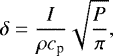 (16)
(16)
where I is the thermal inertia and P the rotational period. For the parameters assumed in our modeling, we obtain 0.8 cm for model M1, about 2 cm for model M2, and 0.3 cm for model M3. A schematic illustration of the vertical structures here adopted is given in Fig. 11B.
While the thermodynamic parameters (ρ, cp and K) of the dust were assumed to be independent of the temperature and the water-ice density, we assumed that the specific heat and the thermal conductivity of the water ice are functions of the temperature. In particular, the thermal conductivity of the water ice was corrected for by taking the high value of the porosity (Φ = 72−74%) into account(Pätzold et al. 2016) by applying the following equation as in Steiner & Kömle (1991):
![\begin{multline*}K_{\textrm{eff}}=\left(1-\sqrt{1-\Phi}\right)\Phi K_{\textrm{void}} \\ + \sqrt{1-\Phi}\left[\lambda K_{\textrm{ice}}+\left(1-\lambda\right)\left(\frac{B+1}{B}\right)\frac{K_{\textrm{ice}}\times K_{\textrm{void}}}{K_{\textrm{ice}}+K_{\textrm{void}}}\right], \end{multline*}](/articles/aa/full_html/2019/10/aa34907-18/aa34907-18-eq17.png) (17)
(17)
where Kice = 567K∕T (Klinger 1981), Kvoid = 4εσT3rp (Squyres et al. 1985), and the parameter B is defined as (Steiner & Kömle 1991)
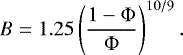 (18)
(18)
We assumed as mean pore radius rp = 10−3 m (Steiner & Kömle 1991), Φ = 0.75 (compatible with Pätzold et al. 2016) and λ = 10−5, which represents the so-called flattening coefficient (Steiner & Kömle 1991). All physical parameters adopted in this work are listed in Table 4.
Physical parameters.
7.3 Temperature profiles
Figure 12 shows the calculated temperature profiles for the three different configurations we investigated. In panels A, C, and E we show the temperature at several depths as a function of time, and in panels B, D, and F, we show the temperature as a function of depth at a given time. In models M1 and M2 (panel A and C), the surface temperatureis very high (up to 325 K) because the crust is covered by a dust blanket. In the case of low thermal conductivity (model M1), the layers at depths of 2.5 and 4.5 cm are not influenced by the external solar input. Conversely, in the case of model M2 (panel C), there is a general convergence of the profiles up to 0.50 cm because the thermal conductivity is higher. In this case, only the layer at 4.5 cm does not react to the solar input. In panel E the results of model M3 are shown: in this case, the exposure of the ice on the surface reduces the energy available to increase the temperature because part of it is required to sublimate the water ice. The decrease in temperatureis evident: the maximum on the surface is about 220 K, in contrast to 325 K for the previous two cases.
Panels B, D, and F show the temperature profiles versus depth for several parts of a day-night cycle. All of the models show an inversion in the profile during the cometary day, linked to the formation of a recondensation front (De Sanctis et al. 2015). Model M1 exhibits a very large temperature gradient inversion (>50 K) in the first 1 cm beneath the surface; in model M2, the gradient is smaller but involves a larger depth, up to 2 cm beneath the surface. The inversion in model M3 is confined to less than 0.5 cm, and the typical temperature gradient is <20 K.
That the temperature profiles in model M1 converge from about 1.5 cm below the surface means that the deeper layers do not experience external solar energy input. This is less evident in the case of model M2, where the profiles converge from about 3 cm because the thermal conductivity is higher and a deep penetration of the thermal wave is possible. In the last case, model M3, the convergence of the thermal profiles begins from about 1 cm. The depth at which the profiles converge gives us an indication of the thermal skin depth, which is evidently not more than a few centimeters.
 |
Fig. 12 Temperature profiles vs. time and depth for the three models. Panels A and B: M1. Panels C and D: M2. Panels E and F: M3. The times selected in panels B, D, and F refer to the last rotation. Only for the main case, M1, do we report an inset in panel B with the surface temperature profile vs. time. |
8 Conclusions
The Rosetta mission to comet 67P has given us the unprecedented opportunity of observing the regions of the coma within a few kilometers above the surface and to study dust activity on the night side (shadowed side) of the nucleus. We here analyzed a single VM hyperspectral cube. It was obtained on 2015 July 18, when the comet was close to perihelion at heliocentric distances near 1.28 au. At the time of the measurements, VM observed a dust plume that was identified as being generated on the far side of the nucleus relative to the spacecraft. Calculations of the illumination conditions at the time of the observation show that the identified spot was not directly exposed to the Sun, but that it was illuminated some hours before.
Shi et al. (2016) argued that the possible sources for these night-side dust activities are dusty terrains, and that their irregular distribution is possibly related to subsurface inhomogeneities. Our results show that this event can be sustained by a thermal lag of some hours in the shallow subsurface close to the depth of the water ice front, but it is uncertain whether it could be driven only by the sublimation of water ice.
Starting from the thermal lag, we found thermal inertia values between 25–36 J m−2 K−1 s−1∕2 for a 5 mm thick dust layer, which is compatible with the range obtained by Gulkis et al. (2015) and Spohn et al. (2015) and with the temperature measurements of the cometary surface performed by Groussin et al. (2007, 2013) and Tosi et al. (2019). In order to evaluate if these thermal inertia values are compatible with the estimation of the surface and subsurface temperatures found in the literature, we applied a 3D Finite-Element Method (FEM) thermophysical model to a portion of the likely emitting region.
We explored three different configurations: (1) a layer of water ice mixed with dust beneath a dust mantle that is 5 mm thick and has thermal inertia of 36 J m−2 K−1 s−0.5; (2) the same structure, but with thermal inertia of 100 J m−2 K−1 s−0.5; and (3) an ice-dust mixture that is directly exposed. Temperature variations of about 50 K in the first 0.5 cm are predicted for the case of low thermal conductivity and the presence of a dust mantle, while layers at a depth greater than 2 cm are not influenced by the solar input. Increasing the thermal conductivity by a factor 10 gives temperatures of the layers in the first 0.5 cm that are very similar, but now the deeper layers (down to 2.5 cm) are affected by the solar input. The surface temperatures are in agreement with the results of Kömle et al. (2017).
An inversion in the temperature profile is present, in agreement with the results obtained by De Sanctis et al. (2015). In the M1 model, the inversion is present in the first 1 cm with the consequent formation of an “accumulation water ice front”. In case of an exposed dust-ice mixture and no dust coverage (M3 model), temperatures are greatly reduced (by up to 100 K) as a result of the energy that is used to sublimate the directly exposed water ice. This result also agrees with Kömle et al. (2017).
Of the three models we studied, M1 could represent the most likely configuration, both due to the low thermal inertia and because of adust blanket that covers the ice-dust mixture. The model with high thermal inertia (M2), even if the surface temperatures are quite similar to those of M1 case, is probably less “realistic” than M1, in agreement with the results of Marshall et al. (2018). A configuration as in M3, where the ice-dust mixture is not covered by a dust mantle, could be possible, for example, if the mechanism of dust removal was more efficient than ice sublimation. This could be possible for short periods when the comet approaches perihelion. These numerical estimates could offer a more complete physical picture of the emitting source region.
The spectral properties of the dust in the dust plume show no detectable color gradient either in the plume itself or relative to the other parts of the coma that are visible in the observations analyzed here. The dust plume morphology can be classified as a narrow ejecta. The observed total ejected mass is estimated to be between 6 and 19 tons, assuming size distribution indices between −2.5 and −3. This would correspond to the formation of a fracture of a few meters wide and 150–478 m long, or to the formation of a circular pit on the surface with a radius of 150–270 m; pits like this have been observed elsewhere on the comet and might be due to sinkhole collapses associated with the formation of previous outbursts.
Acknowledgements
The authors wish to thank Norbert Kömle for his helpful suggestions and questions during the review process. We thank the following institutions and agencies for support of this work: Italian Space Agency (ASI, Italy) contract number I/024/12/1, Centre National d’Études Spatiales (CNES, France), DLR (Germany), NASA (USA) Rosetta Program, and Science and Technology Facilities Council (UK). VIRTIS was built by a consortium, which includes Italy, France, and Germany, under the scientific responsibility of the Istituto di Astrofisica e Planetologia Spaziali of INAF, Italy, which also guides the scientific operations. The VIRTIS instrument development, led by the prime contractor Leonardo-Finmeccanica (Florence, Italy), has been funded and managed by ASI, with contributions from Observatoire de Meudon financed by CNES, and from DLR. We thank the Rosetta Science Ground Segment and the Rosetta Mission Operations Centre for their support throughout all the phases of the mission. The VIRTIS calibrated data will be available through the ESA’s Planetary Science Archive Website (www.rssd.esa.int) and are available upon request until posted to the archive. This research has made use of the scientific software shapeViewer (www.comet-toolbox.com).
Appendix A Validation of the illumination calculations
On 2015 July 18 the Rosetta Navigation Camera (NavCam) performed two observations at 6:02 and at 6:47 UTC, before the outburst ejection, and one after, at 9:05 UTC (Table A.1).
NavCam observations.
In order to validate our illumination calculation tool, we have compared the three NavCam images with our numerical results. Figure A.1 shows that a good agreement is met.
 |
Fig. A.1 Left column: illumination of the cometary surface oriented as the NavCam observations shown on the right. The color scale indicates the cosine of the solar incidence. Right column: three observations acquired by the Rosetta NavCam on 2015 July 18 at 6:02, 6:47 and 9:05 UTC (Table A.1). |
References
- Acton, C. H. 1996, Planet. Space Sci., 44, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Agarwal, J., Della Corte, V., Feldman, P. D., et al. 2017, MNRAS, 469, s606 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2011, Science, 332, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Ammannito, E., Filacchione, G., Coradini, A., et al. 2006, Rev. Sci. Instrum., 77, 093109 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J. S., Feldman, P. D., A’Hearn, M. F., & Carcich, B. 2008, Icarus, 198, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J. S., Thomas, P., Carcich, B., et al. 2013, Icarus, 222, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Bockelée-Morvan, D., Rinaldi, G., Erard, S., et al. 2017, MNRAS, 469, S443 [CrossRef] [Google Scholar]
- Capaccioni, F., Coradini, A., Filacchione, G., et al. 2015, Science, 347, aaa0628 [Google Scholar]
- Capria, M. T., Tosi, F., De Sanctis, M. C., et al. 2014, Geophys. Res. Lett., 41, 1438 [NASA ADS] [CrossRef] [Google Scholar]
- Capria, M. T., Capaccioni, F., Filacchione, G., et al. 2017, MNRAS, 469, S685 [Google Scholar]
- Ciarniello, M., Capaccioni, F., Filacchione, G., et al. 2015, A&A, 583, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coradini, A., Capaccioni, F., Drossart, P., et al. 2007, Space Sci. Rev., 128, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J. R., Gutiérrez, P. J., Groussin, O., et al. 2013, Icarus, 224, 154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Sanctis, M. C., Capria, M. T., & Coradini, A. 2005, A&A, 444, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Sanctis, M., Lasue, J., Capria, M., et al. 2010, Icarus, 207, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Sanctis, M. C., Capaccioni, F., Ciarniello, M., et al. 2015, Nature, 525, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Delsemme, A., & Miller, D. 1971, Planet. Space Sci., 19, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Drossart, P., Semery, A., Bouye, M., et al. 2000, in Infrared Spaceborne Remote Sensing VIII, eds. M. Strojnik, & B. F. Andresen, Proc. SPIE, 4131, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Eddington, A. S. 1910, MNRAS, 70, 442 [NASA ADS] [Google Scholar]
- El-Maarry, M. R., Thomas, N., Gracia-Berná, A., et al. 2015, Geophys. Res. Lett., 42, 5170 [Google Scholar]
- El-Maarry, M. R., Thomas, N., Gracia-Berná, A., et al. 2016, A&A, 593, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellsworth, K., & Schubert, G. 1983, Icarus, 54, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Fanale, F. P., & Salvail, J. R. 1984, Icarus, 60, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Farnham, T. L., Wellnitz, D. D., Hampton, D. L., et al. 2007, Icarus, 187, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Feaga, L. M., A’Hearn, M. F., Sunshine, J. M., Groussin, O., & Farnham, T. L. 2007, Icarus, 190, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Filacchione, G., Ammannito, E., Coradini, A., et al. 2006, Rev. Sci. Instrum., 77, 103106 [NASA ADS] [CrossRef] [Google Scholar]
- Filacchione, G., de Sanctis, M. C., Capaccioni, F., et al. 2016, Nature, 529, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Formisano, M., De Sanctis, M. C., Magni, G., Federico, C., & Capria, M. T. 2016, MNRAS, 455, 1892 [NASA ADS] [CrossRef] [Google Scholar]
- Formisano, M., Federico, C., De Sanctis, M. C., et al. 2018, J. Geophys. Res. Planets, 123, 2445 [NASA ADS] [CrossRef] [Google Scholar]
- Formisano, M., Sanctis, M. D., Angelis, S. D., Carpenter, J., & Sefton-Nash, E. 2019a, Planet. Space Sci., 169, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Formisano, M., Federico, C., Magni, G., et al. 2019b, J. Geophys. Res. Planets, 124, 2 [NASA ADS] [Google Scholar]
- Fornasier, S., Hoang, V. H., Hasselmann, P. H., et al. 2019, A&A, 630, A7 (Rosetta 2 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulle, M., Della Corte, V., Rotundi, A., et al. 2016, MNRAS, 462, S132 [CrossRef] [Google Scholar]
- Gerig, S.-B., Marschall, R., Thomas, N., et al. 2018, Icarus, 311, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Groussin, O., A’Hearn, M. F., Li, J.-Y., et al. 2007, Icarus, 187, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Groussin, O., Sunshine, J. M., Feaga, L. M., et al. 2013, Icarus, 222, 580 [CrossRef] [Google Scholar]
- Gulkis, S., Frerking, M., Crovisier, J., et al. 2007, Space Sci. Rev., 128, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, aaa0709 [Google Scholar]
- Höfner, S., Vincent, J.-B., Blum, J., et al. 2017, A&A, 608, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hu, X., Shi, X., Sierks, H., et al. 2017, MNRAS, 469, S295 [CrossRef] [Google Scholar]
- Jewitt, D., & Meech, K. J. 1986, ApJ, 310, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Jorda, L., Gaskell, R., Capanna, C., et al. 2016, Icarus, 277, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Klinger, J. 1981, Icarus, 47, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Knollenberg, J., Lin, Z. Y., Hviid, S. F., et al. 2016, A&A, 596, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kömle, N. I., Macher, W., Tiefenbacher, P., et al. 2017, MNRAS, 469, S2 [Google Scholar]
- Kurucz, R. L. 1994, in Infrared Solar Physics, eds. D. M. Rabin, J. T. Jefferies, & C Lindsey, IAU Symp., 154, 523 [NASA ADS] [Google Scholar]
- Marshall, D., Groussin, O., Vincent, J.-B., et al. 2018, A&A, 616, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mellon, M. 1997, J. Geophys. Res. Planets, 102, 25617 [NASA ADS] [CrossRef] [Google Scholar]
- Miles, R., Faillace, G. A., Mottola, S., et al. 2016, Icarus, 272, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Pätzold, M., Andert, T., Hahn, M., et al. 2016, Nature, 530, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Preusker, F., Scholten, F., Matz, K.-D., et al. 2017, A&A, 607, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rinaldi, G., Bockelée-Morvan, D., Ciarniello, M., et al. 2018, MNRAS, 481, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Rotundi, A., Sierks, H., Della Corte, V., et al. 2015, Science, 347, aaa3905 [NASA ADS] [CrossRef] [Google Scholar]
- Schloerb, F. P., Keihm, S., von Allmen, P., et al. 2015, A&A, 583, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shi, X., Hu, X., Sierks, H., et al. 2016, A&A, 586, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sierks, H., Barbieri, C., Lamy, P. L., et al. 2015, Science, 347, aaa1044 [Google Scholar]
- Skorov, Y. V., Rezac, L., Hartogh, P., Bazilevsky, A. T., & Keller, H. U. 2016, A&A, 593, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spohn, T., Seiferlin, K., Hagermann, A., et al. 2007, Space Sci. Rev., 128, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Spohn, T., Knollenberg, J., Ball, A. J., et al. 2015, Science, 349, 6247 [CrossRef] [Google Scholar]
- Squyres, S. W., P., M. C., & T., R. R. 1985, J. Geophys. Res. Solid Earth, 90, 12381 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, G., & Kömle, N. I. 1991, Planet. Space Sci., 39, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, N., Sierks, H., Barbieri, C., et al. 2015, Science, 347, aaa0440 [CrossRef] [Google Scholar]
- Thomas, N., El Maarry, M., Theologou, P., et al. 2018, Planet. Space Sci., 164, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Tosi, F., Capaccioni, F., Capria, M., et al. 2019, Nat. Astron., in press [Google Scholar]
- Tubiana, C., Snodgrass, C., Bertini, I., et al. 2015, A&A, 573, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vincent, J.-B., A’Hearn, M. F., Lin, Z.-Y., et al. 2016, MNRAS, 462, S184 [CrossRef] [Google Scholar]
- Wang, J., Bras, R. L., Sivandran, G., & Knox, R. G. 2010, Geophys. Res. Lett., 37, L05404 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Configuration of the nucleus of the comet and jet with respect to the VIRTIS-M slit (horizontal red line) and its direction (red arrow). The VIRTIS-M data cubes are acquired with a temporal scan in which each line corresponds to a given time (white arrows). The orange thick line shows the Sun direction. The spacecraft is approximately in a terminator orbit with a phase angle of 90°, so that one side of the comet is illuminated by the Sun and the other side is in darkness. |
| In the text | |
 |
Fig. 2 Radiance at 0.55 μm on VIRTIS-M data cube V1_00395824539 acquired on 2015 July 18. Panel A: VM image at 0.55 μm. Panel B: same image, but the coma has been stretched to visualize the plume on the shadowed side (indicated by the oval). The cube details are listed in Table 1. The radiance has units of W m−2 sr−1 μm−1. |
| In the text | |
 |
Fig. 3 Top panel: radiance of the radial profile of the dust plume at 0.55 μm on July 18 along the distance from the nucleus center (ρ).Bottom panel: radial profile multiplied by ρ vs. ρ. |
| In the text | |
 |
Fig. 4 Panel A: dust continuum image of the July 18 plume at 0.55 μm. Panel B: spatial distribution of the color calculated in the yellow square of the dust image. The black contours are the radiance levels at 0.55 μm. The dust ejecta do not display an evident color gradient, as observed in other outbursts observed by VM (Rinaldi et al. 2018). |
| In the text | |
 |
Fig. 5 Solar illumination on the comet oriented as in Fig. 2, at 1.28 au on 2015 July 18 from 5:16 h to 8:16 h.The color scale indicates the cosine of the solar incidence above the surface. The time step between the frames is 20 min. |
| In the text | |
 |
Fig. 6 Solar illumination on the far side of the comet, i.e., the side that was not covered by the VM observation. The color scale indicates the cosine of the solar incidence above the surface. The time step between the frames is 20 min. |
| In the text | |
 |
Fig. 7 Definition of the normals (black lines) to the possible emitting regions by observing the illumination conditions of Fig. 6 at different local times. The color scale refers to the cosine of the solar incidence. Panel A: emitting region on the neck at 4:35 h (peak illumination), see panel A of Fig. 8. Panel B: another possible emitting region (in the head of the comet) at 6:16 h. Panel C: bottom region at 6:56 h. By observing the normal directions and comparing them with the emission of Fig. 2, the emitting region of panel A seems to be a more likely candidate. |
| In the text | |
 |
Fig. 8 Panel A: mean cosine of the solar incidence angle vs. rotation time of the likely emitting region (Fig. 7): the red interval ranges from about 4:35 h to 6:15 h, the time span in which the likely emitting region is illuminated.We selected 4:35 h because it corresponds to the peak of the cosine plot, while 6:15 h corresponds to the moment in which the region starts to move into shadow. The blue interval represents the observation time of the dust plume (7:42–7:48 h). We note that during the dust plume, the emitting region is completely in shadow. Panel B: source region of the night-side dust activity detected by VM. The red rectangle indicates the emitting region calculated with the method described in the first part of Sect. 5, with a latitude ranging from − 30° to +10° and a longitude from 265 to 280°. The green rectangle indicates the source region constrained by measuring the length of the plume shadow. The region is mainly in the Anuket and Hapi regions. |
| In the text | |
 |
Fig. 9 OSIRIS NAC image acquired on 2016 June 8 at 15:26:38 h and projected onto the shape model of 67P. A 500 m long fracture in the neck region of comet 67P can be seen at the bottom of this frame along the +280° meridian. |
| In the text | |
 |
Fig. 10 Simulation of the orientation, shadow length, and position of jets originating from the neck regions illuminated 1.75 h before the VIRTIS-M observations. Each point corresponds to the center of a facet in shape model version cg-dlr_ spg-shap7-v1.0, with 500 k facets. In the right panel, the score (see text) is plotted. Values of the score close to zero correspond to the best fit to the observations. |
| In the text | |
 |
Fig. 11 Panel A: computation domain characteristic of the neck region. The top area (surface) is 1 cm2 while the height is chosen larger than the diurnal skin depth, which is on the order of one centimeter. Self-heating between thefacets of the surface is taken into account. Panel B: illustration of the vertical structures assumed in this work. Left panel: dust mantle at the top (5 millimeters) and beneath a mixture of dust and water ice (blue spheres) with thermal inertia 36 TIU (model M1; derived from the method described in Sect. 6) and 100 TIU (model M2). Right panel: no dust mantle, with direct exposure of the dust-ice mixture layer (model M3). |
| In the text | |
 |
Fig. 12 Temperature profiles vs. time and depth for the three models. Panels A and B: M1. Panels C and D: M2. Panels E and F: M3. The times selected in panels B, D, and F refer to the last rotation. Only for the main case, M1, do we report an inset in panel B with the surface temperature profile vs. time. |
| In the text | |
 |
Fig. A.1 Left column: illumination of the cometary surface oriented as the NavCam observations shown on the right. The color scale indicates the cosine of the solar incidence. Right column: three observations acquired by the Rosetta NavCam on 2015 July 18 at 6:02, 6:47 and 9:05 UTC (Table A.1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


