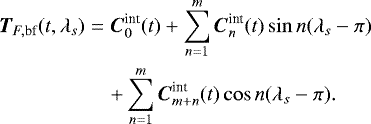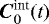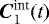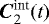© ESO 2019

1 Introduction

The Rosetta instruments have probed the gas and dust environment during almost the entire apparition of 67P/Churyumov-Gerasimenko (67P) from 2014 to 2016. The observed changes in rotation period and axis orientation provide an independent measure of the sublimation activity of the nucleus by the induced torque. The rotation period of 67P was shortened by 21 min. The same amount has been reported for the previous apparition by Mottola et al. (2014). Keller et al. (2015a) proposed a sublimation-driven model and explained the changing rotation period in terms of a homogeneous ice model of the entire surface (Keller et al. 2015b) without studying the axis orientation. For many comets, changes in rotation axis and of the orbital elements due to activity are observed and predicted (see Whipple 1950; Jewitt 1997; Samarasinha et al. 2004; Mueller & Samarasinha 2018). Before the shape of 67P was known in detail, Gutiérrez et al. (2003) explored several scenarios for rotation-axis changes of small, irregularly shaped comets. Typical changes in rotation axis caused by sublimation forces range from 0.1 to several tens of degrees. For 67P, the observed change is at the lower end of this range (0.5°).

For model A proposed by Keller et al. (2015a), our analysis predicts a change greater by five times of the direction of the rotation axis. This change is furthermore in a different direction compared to the observations. In addition, model A predicts a slower-than-observed increase in total gas production with decreasing heliocentric distance, while the analysis of the coma shows a faster increase in activity based on the pressure sensors (see Hansen et al. 2016; Kramer et al. 2017; Läuter et al. 2019). To overcome these discrepancies, we established a formalism to match models and observations in terms of a Fourier analysis of the gas-induced torque and derived a possible ice distribution on the surface that explains the rotation-period changes, the movement of the direction of the angular momentum, and the increase in activity with heliocentric distance (model P).

2 Forced rigid-body dynamics

We reviewed the response of the rotation state of the nucleus to sublimation and other processes that alter the rotation and motion, see Thomson (1986). The comet is viewed as a moving and rotating rigid body. The cometary nucleus is defined within the three-dimensional body frame by a prescribed body-frame density ρ_bf(x, t) for each x in the body frame at time t to accommodate slow changes within the internal mass distribution. The body frame is linked to the inertial frame by the coordinate transformation at time t 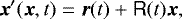$$x^{\prime }(x,t)=r(t)+ \text{R}(t)x,$$(1)

for each body-frame point x. Here, r(t) denotes the center of figure, R(t) the orthogonal rotation matrix with the property 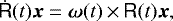$$\stackrel{.}{\text{R}}(t)x=\omega (t)\times \text{R}(t)x,$$(2)

and ω(t) the angular velocity. The mapping x′(x, t) reflects the movement of the center of figure with time t, but leaves the shape geometry (defined in the body frame) unchanged. The time-dependent density ρ_bf (x, t) allows incorporating slow changes in the density and porosity of the comet. The density in the inertial frame ρ(x′, t) = ρ_bf(x, t) is obtained from the body-frame density considering Eq. (1) and carries along the time dependence of the orbital and rotational movement. The comet mass M and the center of mass in the body frame 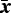$\overline{x}$ are in general time dependent: $$\begin{array}{lll}\hfill & \hfill & M(t)={\displaystyle \int \text{d}}{x}^{\prime }\rho (x^{\prime },t)={\displaystyle \int \text{d}}x{\rho }_{\text{bf}}(x,t),\hfill \\ \hfill & \hfill & \overline{x}(t)=\frac{1}{M}{\displaystyle \int \text{d}}xx{\rho }_{\text{bf}}(x,t).\hfill \end{array}$$

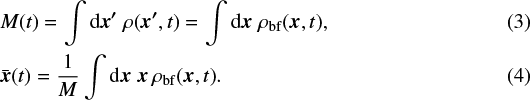
For the center of mass in the inertial frame, the relation holds that 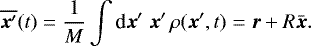$$\overline{x^{\prime }}(t)=\frac{1}{M}{\displaystyle \int \text{d}}{x}^{\prime }{x}^{\prime }\rho (x^{\prime },t)=r+R\overline{x}.$$(5)

The time derivative of Eq. (1) yields the inertial-frame velocity V of a fixed body-point 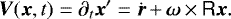$$V(x,t)={\partial }_t{x}^{\prime }=\stackrel{.}{r}+\omega \times \text{R}x.$$(6)

To obtain the linear momentum P and angular momentum L of the whole nucleus in the inertial system, we integrate $$\begin{array}{lll}P(t)\hfill & =\hfill & {\displaystyle \int \text{d}}{x}^{\prime }\rho (x^{\prime },t)V(x^{\prime },t)=M\stackrel{.}{r}+M\omega \times \text{R}\overline{x},\hfill \\ L(t)\hfill & =\hfill & {\displaystyle \int \text{d}}{x}^{\prime }\rho (x^{\prime },t)(x^{\prime }-r)\times V(x^{\prime },t)=\text{I}\omega -M\stackrel{.}{r}\times \text{R}\overline{x},\hfill \end{array}$$

with the tensor of inertia I(t) = RI_bf(t)R⁻¹ in the inertial frame with respect to the center of figure r and the tensor of inertia I_bf(t) with respect to the body-frame center 0. For the case of a time-dependent body density, I_bf(t) needs to be computed for the body-frame density at time t. The momentum changes are generated by the sum of non-gravitational and gravitational forces 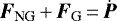$F_{\text{NG}}+F_{\text{G}}=\stackrel{.}{P}$ and torques 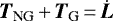$T_{\text{NG}}+T_{\text{G}}=\stackrel{.}{L}$. Gas sublimation at point x on the surface leads to a mass loss ṁ and generates the non-gravitational components $$\begin{array}{lll}{F}_{\text{NG}}(t)\hfill & =\hfill & {\displaystyle \int \text{d}}{\sigma }^{\prime }\dot{m}(x^{\prime },t)v_{\text{is}}(x^{\prime },t)\hfill \\ \hfill & =\hfill & \text{R}{\displaystyle \int \text{d}}\sigma \dot{m}(x,t)v_{\text{bf}}(x,t),\hfill \\ T_{NG}(t)\hfill & =\hfill & {\displaystyle \int \text{d}}{\sigma }^{\prime }\dot{m}(x^{\prime },t)(x^{\prime }-r)\times v_{\text{is}}(x^{\prime },t)\hfill \\ \hfill & =\hfill & \text{R}{\displaystyle \int \text{d}}\sigma \dot{m}(x,t)x\times v_{\text{bf}}(x,t).\hfill \end{array}$$

The gas velocity in the inertial frame 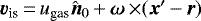$v_{\text{is}}=u_{\text{gas}}{\widehat{n}}_0+\omega \times (x^{\prime }-r)$ consists of two components, one into normal direction 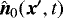${\widehat{n}}_0(x^{\prime },t)$ on the nucleus surface in the inertial frame, and another due to the body rotation, u_gas denotes the thermal gas velocity from Eq. (22). The gas velocity in the body frame is given by 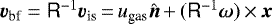$v_{\text{bf}}={\text{R}}^{-1}{v}_{\text{is}}=u_{\text{gas}}\widehat{n}+({\text{R}}^{-1}\omega )\times x$ with the outward surface normal 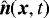$\widehat{n}(x,t)$ at surface location x within the body frame. According to Jorda & Gutiérrez (2002), Eq. (11), the mass production ṁ for a mixture of gas species reads 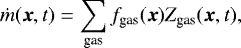$$\dot{m}(x,t)={\sum }_{\text{gas}}{f}_{\text{gas}}(x)Z_{\text{gas}}(x,t),$$(11)

with the surface active fraction f_gas and the sublimation rate Z_gas. The mass loss ṁ changes the shape, reduces the total mass, and affects the tensor of inertia of the nucleus. The integrated mass loss of comet 67P during the 2015 apparition is estimated to be about 1/1000 of the total mass (see Godard et al. 2015, 2017), and therefore we neglect botheffects and assume a time-independent mass and tensor of inertia. The gravitational components for force and torque yield $$\begin{array}{lll}{F}_{\text{G}}(t)\hfill & =\hfill & {\displaystyle \int \text{d}}{x}^{\prime }\rho (x^{\prime },t)a(x^{\prime },t)=Ma(\overline{x^{\prime }},t),\hfill \\ T_{\text{G}}(t)\hfill & =\hfill & {\displaystyle \int \text{d}}{x}^{\prime }\rho (x^{\prime },t)(x^{\prime }-r)\times a(x^{\prime },t)\hfill \\ \hfill & =\hfill & M(\text{R}\overline{x})\times a(\overline{x^{\prime }},t),\hfill \end{array}$$

with the gravitational acceleration a due to other solar system bodies. For both volume integrals in Eqs. (12) and (13), a(x′) is assumed to be constant over the cometary body, which implies that tidal forces, for instance, are neglected.

Equations (2), (7)–(10), (12), and (13) result in a system of coupled algebraic and differential equations, $$\begin{array}{lll}\hfill & \hfill & \stackrel{.}{P}=F_{\text{NG}}+Ma,\stackrel{.}{\text{R}}()=\omega \times \text{R}(),\stackrel{.}{L}=T_{\text{NG}}+M \text{R}\overline{x}\times a,\hfill \\ \hfill & \hfill & M\stackrel{.}{r}+M\omega \times \text{R}\overline{x}=P,\text{I}\omega -M\stackrel{.}{r}\times \text{R}\overline{x}=L,\hfill \end{array}$$

for the state variables r(t), P(t), R (t), and L(t). Equations (7) and (8) couple linear and rotational momenta through the center of mass in the body frame 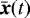$\overline{x}(t)$. If the density distribution ρ_bf satisfies 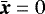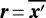$\overline{x}=0$, $r=\overline{x^{\prime }}$ becomes thecenter of mass in the inertial frame and Eq. (14) decouple into two blocks. The first block, 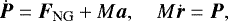$$\stackrel{.}{P}=F_{\text{NG}}+Ma,M\stackrel{.}{r}=P,$$(16)

describes the translational movement for the state variables r(t), P(t), and the second block, 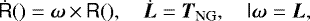$$\stackrel{.}{\text{R}}()=\omega \times \text{R}(),\stackrel{.}{L}=T_{\text{NG}},\text{I}\omega =L,$$(17)

describes the rotational dynamics for R(t) and L(t). The model for the changing rotation period by Keller et al. (2015a) is contained as a special case in Eq. (17). For this, we denote the eigenvector e of I_bf in the body frame with the largest moment of inertia I_z and assume that L is initially aligned with e′ = Re, that is, L(0) = L_ze′(0). Then ω(0) = L_z∕I_ze′(0) and consequently 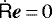$\stackrel{.}{\text{R}}e=0$. Thus, e′ = R e is constant in time, and the angular velocity changes with $\stackrel{.}{\omega }\cdot e^{\prime }=T_{\text{NG}}\cdot e^{\prime }/{\text{I}}_{\text{z}}$.

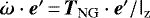For given initial conditions of all state variables, the system of Eqs. (14), (16), and (17) can be solved numerically. For accuracy, we used the LSODE package provided within Mathematica/FORTRAN (Radhakrishnan & Hindmarsh 1993). Following Shoemake (1985), the matrix–matrix operation R →ω × R was replaced by a quaternion multiplication for improved stability. There is a one-to-one mapping between R and a quaternion q such that the matrix–matrix operation is substituted by q →q ⋅ (0, ω)∕2.

3 Rotation state of 67P

After the arrival of Rosetta at 67P in 2014, observations of the rotation by Preusker et al. (2015) and Godard et al. (2017) showed 67P in an excited state of rotation, albeit with the rotation axis close to the axis e′ with the largest moment of inertia (rotation state with minimum energy). This points to an alignment of the two axes, which is also compatible with observations (Jorda et al. 2016). The total mass was estimated to be 10¹³ kg by Godard et al. (2015). The assumption of a strictly homogeneous density leads to a tensor of inertia 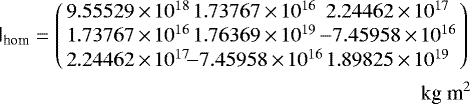$$\begin{array}{l}{\text{I}}_{\text{hom}}=\left(\begin{array}{ccc}9.55529\times {10}^{18}& \text{}\text{}\text{}1.73767\times {10}^{16}& \text{}\text{}\text{}2.24462\times {10}^{17}\\ 1.73767\times {10}^{16}& \text{}\text{}\text{}1.76369\times {10}^{19}& \text{}\text{}\text{}-7.45958\times {10}^{16}\\ 2.24462\times {10}^{17}& \text{}\text{}\text{}-7.45958\times {10}^{16}& \text{}\text{}\text{}1.89825\times {10}^{19}\end{array}\right)\\ \text{kg}{\text{\hspace{0.17em}m}}^{\text{2}}\end{array}$$(18)

with respect to the center of mass. This tensor is incompatible with the observations, since then the axis e′ would be tilted by 2.9° with respect to the rotation axis (Preusker et al. 2017), and in addition, an offset of the center of mass 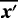$\overline{x^{\prime }}$ with respect to the center of figure r would exist (Jorda et al. 2016). Inhomogeneities in the density have also been reported by Brouet et al. (2016) and Knapmeyer et al. (2018) from the CONSERT and SESAME/MUPUS Rosetta data. In the following, we assume a time-independent, non-homogeneous density distribution that aligns the rotation axis with the e′ under the constraint that the total mass iskept fixed at M = 10¹³ kg and 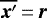$\overline{x^{\prime }}=r$. For clarity, we give a possible mass distribution with a resulting tensor of inertia 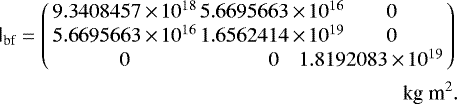$$\begin{array}{l}{\text{I}}_{\text{bf}}=\left(\begin{array}{ccc}9.3408457\times {10}^{18}& \text{}5.6695663\times {10}^{16}& \text{}\text{}\text{}0\\ 5.6695663\times {10}^{16}& \text{}1.6562414\times {10}^{19}& \text{}\text{}\text{}0\\ 0& 0& \text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}\text{}1.8192083\times {10}^{19}\end{array}\right)\\ \text{kg}{\text{\hspace{0.17em}m}}^{\text{2}}.\end{array}$$(19)

This solution equals placing (1∕11)M on a thin ring centered at {−159.8, 275.5, −220.5} m in the plane − 0.4065601x + 0.01699493y + 0.9134659z = −131.7705 m with radius 1 km, while distributing (10∕11)M homogeneously throughout the entire nucleus. The solution is not unique and leads to an increased density in the big lobe, in agreement with Jorda et al. (2016). The small off-diagonal entries in Eq. (19) align the shape file with the body frame by a rotation of 0.4°. The changes in rotation state of the comet is determined by the relative change in angular momentum with respect to the initial state. Changing the total mass does not affect the resulting dynamics if the average surface active fraction is changed in the same proportion.

3.1 Sublimation

Changes in rotation state are primarily due to the torque induced by sublimation of ice. The total production of water and CO₂ has been estimated by Hansen et al. (2016) and Läuter et al. (2019) from ROSINA COPS and DFMS data to be about 6.2 ± 2 × 10⁹ kg, corresponding to about 1∕1600 of the total mass of 67P (M = 10¹³ kg). The water production steeply increases with heliocentric distance 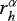$r_h^{\alpha }$ around southern solstice, with exponents α ranging from − 6.5 up to − 7. The total gas production from the radiation-driven sublimation model A by Keller et al. (2015a) yields smaller exponents α = − 2.8. Our model for the rotation state only considers water emission from the surface for driving the torque evolution. The CO₂ activity liberates decimeter-sized chunks (Keller et al. 2017) that contain additional water, which is seen as production but does not contribute to the torque and does not have the same diurnal signature as the surface. The CO₂ contribution(about 1/7 of the water mass estimated from ROSINA/DFMS by Läuter et al. 2019) is not considered separately since the CO₂ sources around perihelion coincide with the water regions (see Fougere et al. 2016a and Läuter et al. 2019)and drive the torque in a similar direction as water. In addition, the diurnal variation of CO₂ is less pronounced than for water (see Filacchione et al. 2016) and thus has less influence on the axis orientation, as discussed in Sect. 4. At heliocentric distances larger than 3 au, and in particular on the outbound orbit, CO₂ becomes thedominant species (Läuter et al. 2019) and does not follow the subsolar illumination. At these distances the rotation period of the comet has settled, and these times are beyond the scope of the present analysis. The rotation axis of 67P shows the largest movements around ± 100 days from perihelion, in agreement with the larger |α| exponents derived from the gas instruments. Keller et al. (2015a; model A) considered the gas production based on a shape model. On each surface element with a given Bond bolometric albedo A and solar irradiance 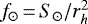$f_{\odot }=S_{\odot }/r_h^2$ at heliocentric distance r_h (au), solar constant S_⊙ = 1361 W m⁻², the energy balance 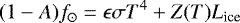$$(1-A)f_{\odot }=ϵ\sigma T^4+Z(T)L_{\text{ice}}$$(20)

is solved for the sublimation rate Z, given by the Hertz-Knudsen relation 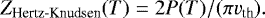$$Z_{\text{Hertz-Knudsen}}(T)=2P(T)/(\pi v_{\text{th}}).$$(21)

The parameters are taken from Keller et al. (2015a), with emissivity ϵ = 0.9, latent heat of sublimation for water ice L_ice = 2.6 × 10⁶ J kg⁻¹ (assumed to be constant), water vapor pressure P(T) = 3.56 × 10¹² e^{−6141.667∕T} (kg m⁻¹ s⁻²), and thermal velocity of water molecules with molar mass 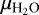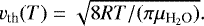${\mu }_{{\text{H}}_2\text{O}}$ $$v_{\text{th}}(T)=\sqrt{8RT/(\pi {\mu }_{{\text{H}}_2\text{O}})}.$$(22)

The gas constant is denoted by R and the Stefan-Boltzmann constant by σ. The solution to Eqs. (20) and (21) in terms of the sublimation rate 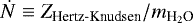$\dot{N}\equiv Z_{\text{Hertz-Knudsen}}/m_{{\text{H}}_2\text{O}}$ (s⁻¹ m⁻²) and mass of water molecule 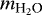$m_{{\text{H}}_2\text{O}}$ (kg), is shown in Fig. 1 for A = 0.01 (Keller et al. 2015a, model A). The changes observed by Hansen et al. (2016); Kramer et al. (2017); Läuter et al. (2019) point to a faster increase in total production with decreasing perihelion distance. To account for the observation requires assuming a sublimation rate that increases faster than linearly with illumination, as exemplified by the dashed red line in Fig. 1. A possible physical mechanism behind the increase in sublimation could be a decrease in dust layer when the comet approaches the Sun, leading to a steeper slope (transition of model C to model A, as described by Keller et al. 2015a). The required adjustment of the sublimation rate with heliocentric distance has also been suggested by Marsden et al. (1973) and is used in the DSMC coma models for 67P by Fougere et al. (2016b), Eq. (1).

3.2 Observed rotation axis changes

The (RA, Dec) orientation of the angular velocity ω of the comet nucleus was derived using the set of about 25 000 control points defined as the center of the maplets created in the stereophotoclinometry (SPC) method of Gaskell et al. (2008) applied to comet 67P by Jorda et al. (2016). The coordinates of the stereo control points measured on sequences of Rosetta/OSIRIS images (Keller et al. 2007) combined with star-tracker pointing measurements were used to determine the direction of the angular velocity vector in the equatorial J2000 (EME2000) reference frame during the Rosetta mission, see Fig. 2. The fluctuations in the resulting data set are caused by a possible nutation combined with the uncertainties in the determination of the direction of the ω vector. They led us to strongly smooth the data, as illustrated by the solid line in Fig. 2, which represents the time-averaged motion of the rotation axis by fitting the data to a Gaussian function for the RA and to a hyperbolic tangent function for the Dec, in addition to a third-order polynomial. A similar data set has been retrieved by Godard et al. (2017).

Fig. 1 Radiation-driven sublimation (a) rate and (b) velocity as function of received irradiation. Solid blue lines show model A (surface active fraction = 1) and dashed red lines the effective sublimation curve with enhanced radiation response near perihelion. The effective sublimation curve leads to agreement with observations (see Figs. 6 and 7).

4 Fourier theory of torque-induced motion

The shape model from Preusker et al. (2017) was remeshed using the approximated centroidal Voronoi diagrams (ACVD) tool by Valette et al. (2008) into N_faces = 3996 triangular elements with area A_i and surface normal 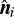${\widehat{n}}_i$, chosen to be approximately of equal area. The results are robust against variations in shape model as long as N_faces ≫ 100. The torque was evaluated according to Eqs. (10) and (11). The sublimation rate Z_gas on each facet was evaluated for a given subsolar latitude ϕ_s and heliocentric distance r_h during one rotation period, starting with subsolar longitude λ_s = 0. We computed the total torque arising from the water sublimation curves, either the Hertz-Knudsen rate from Eq. (21), or alternatively, the effective sublimation curve in Fig. 1: 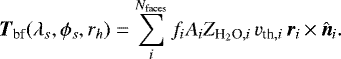$$T_{\text{bf}}({\lambda }_s,{\varphi }_s,r_h)={\sum }_i^{N_{\text{faces}}}{f}_i{A}_i{Z}_{{\text{H}}_2\text{O},i}{v}_{\text{th},i}{r}_i\times {\widehat{n}}_i.$$(23)

The contributions of shadowed (including self-shadowed) faces were set to zero and the entire surface active fraction was first set to the same value. In the next iteration, the surface active fraction was considered to be a spatial fit parameter (but fixed in time) to be determined from the observed axis changes. The heliocentric orbit (Cartesian coordinates r_h (t)) was taken from the NASA Horizon system (Earth mean equator and equinox of reference epoch J2000). The initial orientation of the rotation axis in the equatorial frame was set to be in the lowest energy state (rotation axis and angular momentum aligned, pointing to RA α = 69.427°, Dec δ = 64.000° at t = −350 days). For 67P, the observed axis changes are small, and we tabulated the subsolar latitude ϕ_s and heliocentric distance |r_h| in N_intervals = 81 10-day intervals and stored the body-frame torque as function of λ_s. A typical diurnal torque evolution at perihelion is shown in Fig. 3. To gain more physical insight into the dynamics underlying the axis changes, we expanded the torque components into a Fourier cosine/sine series. The periodic argument α = [−π : π[ of the Fourier series is not time, but the subsolar longitude λ_s = α + π to accommodate changes in the rotation period. In the ith time interval, we extracted the first N = 2m + 1 Fourier coefficients 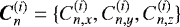$C_n^{(i)}=\{C_{n,x}^{(i)},C_{n,y}^{(i)},C_{n,z}^{(i)}\}$, which yield the Fourier series representation of the torque 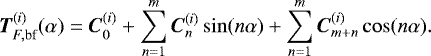$$T_{F,\text{bf}}^{(i)}(\alpha )=C_0^{(i)}+{\sum }_{n=1}^m{C}_n^{(i)}\sin (n\alpha )+{\sum }_{n=1}^m{C}_{m+n}^{(i)}\cos (n\alpha ).$$(24)

The final parameterization of the body torque as function of subsolar longitude along the entire orbit is given by the time evolution of the Fourier coefficients 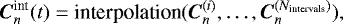$$C_n^{\text{int}}(t)=\text{interpolation}(C_n^{(i)},\dots ,C_n^{(N_{\text{intervals}})}),$$(25)

and rewriting $$\begin{array}{lll}{T}_{F,\text{bf}}(t,{\lambda }_s)\hfill & =\hfill & C_0^{\text{int}}(t)+{\sum }_{n=1}^m{C}_n^{\text{int}}(t)\sin n({\lambda }_s-\pi )\hfill \\ \hfill & \hfill & +{\sum }_{n=1}^m{C}_{m+n}^{\text{int}}(t)\cos n({\lambda }_s-\pi ).\hfill \end{array}$$(26)

The slowly changing subsolar latitude and heliocentric distance are implicitly contained through the time t argument. The time evolution of the coefficients is shown in Fig. 4 for N = 3. The first row in Fig. 4 displays the non-diurnal torque coefficients. Because the rotation axis is aligned with the z body-axis, the torque component 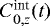$C_{0,z}^{\text{int}}(t)$ directly affects the rotation period. The orientation of the rotation axis changes by the action of the diurnal components 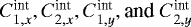$C_{1,x}^{\text{int}},C_{2,x}^{\text{int}},C_{1,y}^{\text{int}},\text{and }{C}_{2,y}^{\text{int}}$ (Fig. 3). The diurnal components are not linearly independent, as discussed in Sect. 4.1.

4.1 Computation of the torque in the inertial system

First, we neglected the changes in orbital elements that are due to non-gravitational momentum (Eq. (16)) and took the orbital evolution r_h (t) as fixed. For a given rotation matrix R(t) (body frame to equatorial inertial-system) and position of the comet r_h (t), the subsolar longitude is given by $$\begin{array}{lll}\hfill & \hfill & \{x(t),y(t),z(t)\}={\text{R}}^{-1}(t)(-r_h(t))\hfill \\ \hfill & \hfill & {\lambda }_s(t)=\arctan (y(t)/x(t)).\hfill \end{array}$$

At initial time t_S, the rotation matrix R(t_S), which transfers the body-frame z-axis to the rotation axis 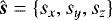$\widehat{s}=\{s_x,s_y,s_z\}$ in the equatorial inertial frame, is given by $$\text{R}(t_S)=\left(\begin{array}{ccc}\frac{s_z{s}_x^2+s_y^2}{s_x^2+s_y^2}& \frac{s_x{s}_y(s_z-1)}{s_x^2+s_y^2}& s_x\\ \frac{s_x{s}_y(s_z-1)}{s_x^2+s_y^2}& \frac{s_x^2+s_y^2{s}_z}{s_x^2+s_y^2}& s_y\\ -s_x& -s_y& s_z\end{array}\right).$$(29)

Equation (17) is then integrated with the initial angular velocity and momentum set to $$\begin{array}{lll}\hfill & \hfill & {\omega }_{\text{bf}}(t_S)=\{0,0,2\pi /T_{\text{rot}}\},T_{\text{rot}}=44650 \text{s},\hfill \\ \hfill & \hfill & L(t_S)= \text{R}(t_S){\text{I}}_{\text{bf}}{\omega }_{\text{bf}}(t_S).\hfill \end{array}$$

The Fourier decomposition provides additional insights into the axis changes. An important parameter is the angle 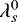${\lambda }_s^0$ around the z-axis to point the x–z-plane toward the Sun (zero sub-solar latitude). When the 0.5° tilt-change of the rotation axis is neglected, 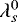${\lambda }_s^0$ is given by $$\begin{array}{lll}\hfill & \hfill & \{x_s^0(t),y_s^0(t),z_s^0(t)\}= \text{R}{(t_S)}^{-1}(-r_h(t))\hfill \\ \hfill & \hfill & {\lambda }_s^0(t)=\arctan (y_s^0/x_s^0).\hfill \end{array}$$

We obtain a good approximation of the angular momentum change 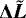$\Delta \tilde{L}$ during one rotation period T_rot = 2π∕ω by keeping 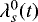${\lambda }_s^0(t)$ fixed during this rotation and integrating the torque in the body frame T_bf, parameterized by the subsolar longitude and the Fourier components from Eq. (26), $$\begin{array}{lll}\Delta \tilde{L}(t)\hfill & =\hfill & {\displaystyle {\int }_0^{T_{\text{rot}}}\text{d}}{t}^{\prime }\left(\begin{array}{rrr}\hfill \cos (\omega t^{\prime })& \hfill -\sin (\omega t^{\prime })& \hfill 0\\ \hfill \sin (\omega t^{\prime })& \hfill \cos (\omega t^{\prime })& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1\end{array}\right)T_{\text{bf}}(t^{\prime })\hfill \\ \hfill & =\hfill & \frac{T_{\text{rot}}}{2\pi }{\displaystyle {\int }_0^{2\pi }\text{}}\text{}\text{}\text{d}{\lambda }_s\left(\begin{array}{rrr}\hfill \cos ({\lambda }_s-{\lambda }_s^0)& \hfill \sin ({\lambda }_s-{\lambda }_s^0)& \hfill 0\\ \hfill -\sin ({\lambda }_s-{\lambda }_s^0)& \hfill \cos ({\lambda }_s-{\lambda }_s^0)& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1\end{array}\right)T_{\text{bf}}(t,{\lambda }_s)\hfill \\ \hfill & =\hfill & \frac{T_{\text{rot}}}{2}\left(\begin{array}{c}-(C_{x,1}-C_{y,2})\sin {\lambda }_s^0-(C_{x,2}+C_{y,1})\cos {\lambda }_s^0\\ +(C_{x,1}-C_{y,2})\cos {\lambda }_s^0-(C_{x,2}+C_{y,1})\sin {\lambda }_s^0\\ 2C_{z,0}\end{array}\right)\hfill \\ \hfill & =\hfill & \frac{T_{\text{rot}}}{2}\underset{\text{shape}}{\underbrace{\left(\begin{array}{c}-C_{x,1}+C_{y,2}\\ -C_{x,2}-C_{y,1}\\ 2C_{z,0}\end{array}\right)}}\underset{\text{orbit}}{\underbrace{\left(\begin{array}{rrr}\hfill \sin {\lambda }_s^0& \hfill -\cos {\lambda }_s^0& \hfill 0\\ \hfill \cos {\lambda }_s^0& \hfill \sin {\lambda }_s^0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 1\end{array}\right)}}.\hfill \end{array}$$(34)

The angular momentum change along the entire orbit is then approximated by adding all 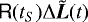$\text{R}(t_S)\Delta \tilde{L}(t)$ contributions to the initial angular momentum. The “orbit” matrix does not affect the magnitude of the “shape” vector. All shown results were obtained without this approximation and use the full numerical solution of Eq. (17). Equation (34) was used to determine the physically relevant Fourier components, 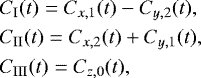$$\begin{array}{lll}\hfill & \hfill & C_{\text{I}}(t)=C_{x,1}(t)-C_{y,2}(t),\hfill \\ \hfill & \hfill & C_{\text{II}}(t)=C_{x,2}(t)+C_{y,1}(t),\hfill \\ \hfill & \hfill & C_{\text{III}}(t)=C_{z,0}(t),\hfill \end{array}$$(35)

for analyzing the observations.

Fig. 2 Orientation changes in rotation axis. Black dots denote the reconstructed right ascension multiplied with cos 64° and declination, and the solid line shows a smooth fit to the data.

Fig. 3 Calculated sublimation-induced torque at perihelion for one rotation period at perihelion as a function of subsolar longitude from model P using the effective sublimation curve from Fig. 1 with the best-fit solution from Fig. 10. The dashed lines show the Fourier representation (constant, cos, and sin terms) of the corresponding solid lines to parameterize the diurnal cycle.

4.2 Extract observed torque from the rotation-axis evolution

Next, we considered the inverse problem of finding a plausible torque function in the cometary body frame as function of subsolar coordinates and solar distance. We inferred the torque in the body frame from the observation as function of time t under the assumption of an initial alignment of rotation axis and angular momentum, and with the tensor of inertia given in Eq. (19).

To parameterize the observed torque as function of subsolar longitude, we computed λ_s (t) from Eq. (27) at each observation time. Every 10 days, we determined the closest instance t_i of λ_s (t_i) = 0 and computed the Fourier coefficients 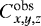$C_{x,y,z}^{\text{obs}}$ to represent T_bf(λ_s = 0…2π). Only the three Fourier combinations from the components of Eq. (35) should be retrieved from the fit (Fig. 5) because the axis motion is not sensitive to the other Fourier components (see Eq. (34)).

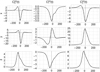Fig. 4 Torque evolution of a uniform active surface model with the effective sublimation curve from Fig. 1. The time evolution of the first three Fourier coefficients $C_0^{\text{int}}(t)$, $C_1^{\text{int}}(t)$, and $C_2^{\text{int}}(t)$ is shown for (−300 : 300) days from perihelion for each Cartesian component of the body-frame torque, Eq. (25). Units of 106 kg m2 s−2.

Fig. 5 Time evolution of the three physical relevant combinations of Fourier coefficients (Eq. (35)) for (−300 :300) days from perihelion, units of 106 kg m2 s−2. (a) Model A, global uniform active surface 1∕12. (b) Model P (patches with effective sublimation curve). (c) Observed Fourier coefficients inferred from the rotation-axis movement and the tensor of inertia.

5 Matching Fourier coefficients with the observed torque

The simplest sublimation model A results in a rotation axis movement shown in Fig. 6 with the green line. The evolution is rotated by 90° with respectto the observed torque movement (Fig. 6, red line) and leads to a largely increased axis tilt compared to observations. To explain the observations requires considering a spatially heterogeneous surface with varying water-ice coverage (model P). We could show that an alternative explanation is a large thermal lag of several hours of the maximum sublimation with respectto the maximum irradiation caused by a dust layer of some millimeters thickness. However, this scenario is unlikely because the response of sublimation rates to radiation is almost immediate, as seen by short (< 1 h) delays of jet outbreaks (see Lai et al. 2016; Shi et al. 2016) and the good agreement of inner dust structures with illumination-driven dust release (see Kramer & Noack 2016; Kramer et al. 2018). Measurements of VIRTIS and MIRO found that the thermal inertia is lower than 320 JK⁻¹m⁻²s^−0.5 when the error bars are included (see Marshall et al. 2018 for an overview). Thermal inertia this low is not able to provide the needed phase lag of several hours of the maximum sublimation with respect to the maximum irradiation, as shown by thermal simulations and measurements of the activity maxima compared to noon time, see Shi et al. (2016). We show that the often-invoked unrealistic thermal lag to explain the non-gravitational forces acting on the cometary orbit can be at least partly replaced by the effects of a complex nucleus shape and its slightly non-uniform activity (see Davidsson & Gutierrez 2005; Sosa & Fernández 2009).

For the non-uniform case, we divided the surface into 36 equally spaced patches and computed their separate contributions to the torque using the Fourier method described before. Each patch provides a specific contribution to the Fourier components C_I, C_II, and C_III in Eq. (35) of the complete comet. For a uniform activity, the resulting extrema of the Fourier components are shown in Fig. 8 for each patch. To match the observed rotation state, a linear combination of the patch contributions must yield the observed values of C_I, C_II, and C_III in Fig. 5, indicated by the dashed lines in Fig. 8. The relative ratio of the three components for a single patch is a prescribed property of the sublimation curve. The largest difference of a single-patch contribution to the observation is that for component C_I on patch 21. The activity of patch 21 has to be reduced, while patches 26–36 with opposite sign for C_I are candidates for an increased activity. Additional constraints on the activity arise from the simultaneous fitting of components C_II and C_III. To find the activity across all patches, we minimize the deviation of observed torque and observations every 20 days with respect to the L¹ norm. Solving a nonlinear optimization problem does not always provide a unique solution. By changing the norm and using different time slices, we verified that the resulting solution with the identified depleted and enhanced surface active regions remains unaffected by the data selection. The fit leads to a closer alignment of observation and model A/patches for the axis movement (Fig. 6), but does not fix the exponent of the total production rate, Fig. 7, which remains at Q_tot(r) ~ r^−2.8. In contrast, observations from COPS/DFMS point to a larger exponent α approximately −6 to − 7. The change in sublimation with heliocentric distance is directly reflected by a small southern excursion of the rotation axis (300–100 days) before perihelion. The observations show that the sublimation activity increases nonlinearly with insolation, as discussed in Sect. 3.1. The effective sublimation curve in Fig. 1a, dashed line, yields the total production displayed in Fig. 7, with larger exponent α < −5 as measuredby several Rosetta instruments (see, e.g., Hansen et al. 2016; Kramer et al. 2017; Läuter et al. 2019) and modeled by Hu et al. (2017). The rotation-axis motion of this modified sublimation model is shown in Fig. 6 and agrees better with observations than the other considered scenarios.

Fig. 6 Rotation-axis movement. The red line shows the observation from Fig. 2, and the other linesrepresent different sublimation models. Model A with a globally constant surface active fraction (1∕12), model A/patches with best-fit adjustment of patches, and model P with effective sublimation curve and best-fit adjustment of patches. The gray inset shows a magnification of the curves.

Fig. 7 Rotation period and total water production. The red line shows the observation, and the black lines the different sublimation models. Model A with globally constant surface active fraction (1∕12), model A/patches with best-fit adjustment of patches, and model P with effective sublimation curve and best-fit adjustment of patches. In all cases, the rotation period agrees reasonably well with observations. The total water production rate drops for model A and model A/patches scenarios with $r_h^{-2.8}$, while observations indicate $r_h^{-5}$.

Fig. 8 Influence of the different surface areas on the torque evolution for a uniform active surface. Shown are the extrema of the Fourier torque components for each surface patch (see Fig. 10 for the patch boundaries). Model P seeks linear combinations of patches that in sum match the extrema derived from the observation, indicated by the dashed lines.

6 Implication for the surface composition

The surface active fraction of the best-fit model is shown in Fig. 9 and as planar map in Fig. 10. The maps show the active fraction relative to the mean active fraction to highlight the differences to a uniformly active surface. The absolute value of the surface activity depends on the precise values of the cometary mass and the sublimation curve, while the relative distribution is not strongly affected. Patches with increased active water fraction are located in the southern hemisphere, which agrees with the increased southern relative activity shown in Fig. 6 by Fougere et al. (2016a) derived from Rosetta ROSINA/COPS/DFMS in situ gas densities. Toward the northern hemisphere, the zonal averaged active water fraction (side panel in Fig. 10) increases from the equatorial region, but stagnates on a lower value compared to the southern regions. Fougere et al. (2016a) retrieved a circular feature of increased relative activity around the north pole, which is not contained in our reconstruction. The direct use of measured gas densities from the ROSINA instruments to constrain the diurnal activity and the rotation state is limited because for operational reasons, Rosetta predominantly sampled gas in terminator illumination. Attree et al. (2019) discussed a fitting method for active fractions using three scalar properties: the Earth-comet distance, the total production rate, and the rotation period. They inferred a strong increase in active fraction on the southern hemisphere, limited to the time period of about 100 days around perihelion. In contrast, we worked with different observational data (all vector components of the rotation axis and the production rate) and derived an activity map that is constant in time.

Overall, the standard deviation from the homogeneous active surface (mean value 1.10) is 0.28, with the smallest activity on patch 21 (six times reduced active surface fraction). This confirms that the entire surface of 67P shows activity when it is insolated. A detailed correlation of our 36 patches with all geological regions cannot be expected because the resolution is just not good enough considering that the number of defined regions is now about twice as large; see Thomas et al. (2018). In Fig. 11 the surface active-fraction regions fromFig. 10 have been draped onto the shape model of 67P (shown as color overlay). Thirty OSIRIS NAC images were mapped onto the shape to provide the morphological context. The images were acquired during the SHAP4S and SHAP5 mission phases for the northern hemisphere (September to October 2014), and SHAP7 and SHAP8 for the southern hemisphere (April to June 2016). Some image boundaries are visible in the mosaic because of the varying illumination condition during the mission phases. In general, the surface active fraction shows a north-south trend, with the highest active fraction being in the roughconsolidated terrain of the south-oriented regions (in particular around the southern neck regions, Fig. 11 − Z). The northern dust-covered regions, such as the Seth and Hapi region in the northern neck (Fig. 11 + Z), show intermediate levels of active fraction. This is compatible with the northern neck region being the most active in dust production during the early parts of the Rosetta mission. Some other features are seen: the active-fraction map shows a dichotomy between the northern neck region of the big lobe (Seth) and the northern foot regions of the big lobe (see Fig. 12c). This dichotomy is not reflected in the surface morphology. Both sides of the big lobe show the same kind of smooth dust-covered terrain. It does, however, make sense from an insolation point of view. The northern neck is in polar night during the perihelion passage, while the foot of the big lobe is permanently illuminated throughout the comet year (Keller et al. 2015b). The volatiles in the northern neck are being replenished by seasonal mass transport on the comet (Keller et al. 2017). Mass transport on the foot of the comet will tend to accumulate in the Imhotep region, which is a gravitational low point on the comet. The Imhotep region (Fig. 11 − X) does indeed show comparable levels of active fraction to those of the northern neck. The Khonsu region (Fig. 12a) shows a southeast to northwest gradient in active fraction. The Khonsu region is a depression with a very rough terrain. Khonsu may be the result of an earlier fragmentation event that has caused parts of the surface to break off the nucleus. There is no significant morphological difference between one end of Khonsu and the other, and the integrated insolation is comparable. This may be a modeling artifact caused by the non-random choice of patch boundaries. The Wosret region (Fig. 12b) shows a surprisingly low level of active fraction. The Wosret region is the main part of the polar circle that receives permanent diurnal illumination during the perihelion passage of the comet. The region therefore has the highest potential level of activity of any region on the comet (highest integrated insolation). The morphology of the region is, however, quite different from the other south-oriented regions on the comet. Wosret has a highly smooth but consolidated terrain toward the top of the small lobe and a much rougher consolidated terrain toward the southern neck. The areas of the active-fraction map with lowest values are correlated with the smooth consolidated terrain. The rougher parts show a significantly higher active fraction. These active-fraction values are more compatible with the levels found in the southern neck, which has a comparable terrain morphology. A possible explanation is that the smooth consolidated terrain is simply depleted of volatiles and will therefore exhibit no activity, regardless of the insolation. The smooth consolidated Wosret region could represents the final state terrain of cometary evolution.

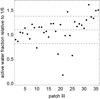Fig. 9 Surface active fraction fi (Eq. (23)) relative to 1∕6 determined from the torque fit using the effective sublimation curve from Fig. 1a, dashed line, with the 36 patches shown in Fig. 10. The dashed lines indicate the mean value and the standard deviation.

Fig. 10 Surface map showing the surface active fraction fi (Eq. (23)) relative to 1∕6 corresponding to Fig. 9. The numbers indicate the patch label. Side panel: zonal averaged active water fraction.

Fig. 11 Surface active fraction map projected onto the DLR SHAP7 shape model (Preusker et al. 2017). The shape has been textured using 30 OSIRIS NAC images acquired during the SHAP4S and SHAP5 mission phases for the norther hemisphere and the SHAP7 and SHAP8 mission phases for the southern hemisphere. The color overlay shows the active surface fraction from Fig. 10 with the view vector indicated by the basis vectors X, Y, Z in the body frame.

Fig. 12 Zoom into the shape shown in Fig. 11. Part A: Khonsu region on the big lobe of the comet nucleus. Part B: Wosret region of the small lobe of the comet nucleus. Part C: northern edge of the big lobe. The color intensity of the Wosret (panel B) view has been decreased as compared to Fig. 11 to allow better visibility of the background image data. The wedge-like feature from the left side is an image artifact caused by an image acquired with a high (~ 90°) Sun incidence angle.

7 Conclusions

We have presented a method to parameterize the observed rotation-axis movement in terms of a theory of Fourier coefficients. The sublimation-induced torques are encoded in three physically relevant combinations of the Fourier coefficients, which steer the rotation period changes and the rotation-axis movement. In particular, the rotation state of 67P is determined from the orbital evolution of the subsolar longitude and the specific shape. The increase in rotation period is caused by the diurnal average of the rotation-axis-aligned torque (Fourier coefficient C_III = C_0,z), while the orientation change is caused by the diurnal torque cycle of the perpendicular components (Fourier coefficients C_I and C_II). Only by taking all three Fourier components together does a consistent fit result that constrains the local surface active fraction. From our analysis we conclude the following:

• The sublimation model P contains a best fit for the surface active fraction to the observed rotation state, namely period and axis orientation.

• The model includes a sublimation curve that increases much faster than linearly with insolation and reproduces the water production of 67P in Hansen et al. (2016) and Läuter et al. (2019).

• A relatively small local variability (standard deviation 0.28) of the active surface fraction yields the required changes in rotation state.

• Some area around Wosret on the small lobe seems to be less active, while the southern latitudes <−60° show an increased surface active fraction.

A further argument for a mostly uniform gas release comes from the observation of the dust structures in the inner coma modeled by Kramer & Noack (2016) and Kramer et al. (2018). The developed Fourier theory could be applied to other solar system bodies for which accurate measurements of the rotation axis motion and the shape are available.

Acknowledgements

The authors acknowledge the North-German Supercomputing Alliance (HLRN) for providing computing time on the Cray XC40. This project has received funding from the European Unions Horizon 2020 research and innovation program under grant agreement No 686709 (MiARD).

References

All Figures

	Fig. 1 Radiation-driven sublimation (a) rate and (b) velocity as function of received irradiation. Solid blue lines show model A (surface active fraction = 1) and dashed red lines the effective sublimation curve with enhanced radiation response near perihelion. The effective sublimation curve leads to agreement with observations (see Figs. 6 and 7).
In the text

	Fig. 2 Orientation changes in rotation axis. Black dots denote the reconstructed right ascension multiplied with cos 64° and declination, and the solid line shows a smooth fit to the data.
In the text

	Fig. 3 Calculated sublimation-induced torque at perihelion for one rotation period at perihelion as a function of subsolar longitude from model P using the effective sublimation curve from Fig. 1 with the best-fit solution from Fig. 10. The dashed lines show the Fourier representation (constant, cos, and sin terms) of the corresponding solid lines to parameterize the diurnal cycle.
In the text

	Fig. 4 Torque evolution of a uniform active surface model with the effective sublimation curve from Fig. 1. The time evolution of the first three Fourier coefficients $C_0^{\text{int}}(t)$, $C_1^{\text{int}}(t)$, and $C_2^{\text{int}}(t)$ is shown for (−300 : 300) days from perihelion for each Cartesian component of the body-frame torque, Eq. (25). Units of 106 kg m2 s−2.
In the text

	Fig. 5 Time evolution of the three physical relevant combinations of Fourier coefficients (Eq. (35)) for (−300 :300) days from perihelion, units of 106 kg m2 s−2. (a) Model A, global uniform active surface 1∕12. (b) Model P (patches with effective sublimation curve). (c) Observed Fourier coefficients inferred from the rotation-axis movement and the tensor of inertia.
In the text

	Fig. 6 Rotation-axis movement. The red line shows the observation from Fig. 2, and the other linesrepresent different sublimation models. Model A with a globally constant surface active fraction (1∕12), model A/patches with best-fit adjustment of patches, and model P with effective sublimation curve and best-fit adjustment of patches. The gray inset shows a magnification of the curves.
In the text

Fig. 7 Rotation period and total water production. The red line shows the observation, and the black lines the different sublimation models. Model A with globally constant surface active fraction (1∕12), model A/patches with best-fit adjustment of patches, and model P with effective sublimation curve and best-fit adjustment of patches. In all cases, the rotation period agrees reasonably well with observations. The total water production rate drops for model A and model A/patches scenarios with $r_h^{-2.8}$, while observations indicate $r_h^{-5}$.

In the text

	Fig. 8 Influence of the different surface areas on the torque evolution for a uniform active surface. Shown are the extrema of the Fourier torque components for each surface patch (see Fig. 10 for the patch boundaries). Model P seeks linear combinations of patches that in sum match the extrema derived from the observation, indicated by the dashed lines.
In the text

	Fig. 9 Surface active fraction fi (Eq. (23)) relative to 1∕6 determined from the torque fit using the effective sublimation curve from Fig. 1a, dashed line, with the 36 patches shown in Fig. 10. The dashed lines indicate the mean value and the standard deviation.
In the text

	Fig. 10 Surface map showing the surface active fraction fi (Eq. (23)) relative to 1∕6 corresponding to Fig. 9. The numbers indicate the patch label. Side panel: zonal averaged active water fraction.
In the text

Fig. 11 Surface active fraction map projected onto the DLR SHAP7 shape model (Preusker et al. 2017). The shape has been textured using 30 OSIRIS NAC images acquired during the SHAP4S and SHAP5 mission phases for the norther hemisphere and the SHAP7 and SHAP8 mission phases for the southern hemisphere. The color overlay shows the active surface fraction from Fig. 10 with the view vector indicated by the basis vectors X, Y, Z in the body frame.

In the text

Fig. 12 Zoom into the shape shown in Fig. 11. Part A: Khonsu region on the big lobe of the comet nucleus. Part B: Wosret region of the small lobe of the comet nucleus. Part C: northern edge of the big lobe. The color intensity of the Wosret (panel B) view has been decreased as compared to Fig. 11 to allow better visibility of the background image data. The wedge-like feature from the left side is an image artifact caused by an image acquired with a high (~ 90°) Sun incidence angle.

In the text