| Issue |
A&A
Volume 629, September 2019
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201935899 | |
| Published online | 02 September 2019 | |
The millimeter-wave spectrum and astronomical search of succinonitrile and its vibrational excited states⋆
1
Instituto de Física Fundamental (IFF-CSIC), Group of Molecular Astrophysics, C/Serrano 121, 28006 Madrid, Spain
e-mail: carlos.cabezas@csic.es
2
Centro de Desarrollos Tecnológicos, Observatorio de Yebes (IGN), 19141 Yebes, Guadalajara, Spain
3
Observatorio Astronómico Nacional (OAN-IGN), C/Alfonso XII 3, 28014 Madrid, Spain
4
Instituto de Estructura de la Materia (IEM-CSIC), Molecular Physics Department, C/Serrano 123, 28006 Madrid, Spain
Received:
16
May
2019
Accepted:
10
July
2019
Context. Dinitriles with a saturated hydrocarbon skeleton and a −C≡N group at each end can have large electric dipole moments. Their formation can be related to highly reactive radicals such as CH2CN, C2N, or CN. Thus, these saturated dinitriles are potential candidates to be observed in the interstellar medium (ISM).
Aims. Our goal is the investigation of the rotational spectrum of one of the simplest dinitriles N≡C−CH2−CH2−C≡N, succinonitrile, whose actual rotational parameters are not precise enough to allow its detection in the ISM. In addition, the rotational spectra for its vibrational excited states will be analysed.
Methods. The rotational spectra of succinonitrile was measured in the frequency range 72−116.5 GHz using a new broadband millimeter-wave spectrometer based on radio astronomy receivers with Fast Fourier Transform backends. The identification of the vibrational excited states of succinonitrile was supported by high-level ab initio calculations on the harmonic and anharmonic force fields.
Results. A total of 459 rotational transitions with maximum values of J and Ka quantum numbers 70 and 14, respectively, were measured for the ground vibrational state of succinonitrile. The analysis allowed us to accurately determine the rotational, quartic, and sextic centrifugal distortion constants. Up to eleven vibrational excited states, resulting from the four lowest frequency vibrational modes ν13, ν12, ν24, and ν23 were identified. In addition to the four fundamental modes, we observed overtones together with some combination states. The rotational parameters for the ground state were employed to unsuccessfully search for succinonitrile in the cold and warm molecular clouds Orion KL, Sgr B2(N), B1-b, and TMC-1, using the spectral surveys captured by IRAM 30 m at 3 mm and the Yebes 40 m at 1.3 cm and 7 mm.
Key words: ISM: molecules / methods: laboratory: molecular / molecular data / line: identification
Tables with all the measured transitions are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/629/A35
© ESO 2019
1. Introduction
Among all the molecular species detected so far in the interstellar medium (ISM) or circumstellar shells1, around 200, the family of molecules containing a nitrile group represents a considerable fraction (approximately 15%). This group of molecules is constituted of simple molecular species like the CN radical or the CN− anion; of more complex structures like the alkyl nitriles CH3CN (Solomon et al. 1971), C2H5CN (Johnson et al. 1977), or C3H7CN (Belloche et al. 2009, 2014); of aromatic nitrile derivatives like c-C6H5CN (McGuire et al. 2018); or of metal-bearing species like AlNC (Ziurys et al. 2002) or FeCN (Zack et al. 2011). Despite the fact that dinitriles such as dicyanopolyynes like N≡C−(C≡C)n−C≡N are very stable species, only two dinitriles, the protonated cyanogen (NCCNH+; Agúndez et al. 2015) and isocyanogen (CNCN; Agúndez et al. 2018), a metastable isomer of NCCN, have been detected in the ISM. Dicyanopolyynes have been proposed to be abundant species in interstellar and circumstellar clouds (Kołos & Grabowski 2000; Petrie et al. 2003) but their detection is hampered by the fact that they do not have permanent electric dipole moment and therefore cannot be observed through their rotational spectra.
Dinitriles consisting of a saturated hydrocarbon skeleton ended by a −C≡N group at each edge, that is, N≡C−(CH2)n−C≡N, are potential candidates to be observed in the ISM since they can present large electric dipole moments and may be formed upon the reaction of abundant highly reactive radicals such as CH2CN, C2N, or CN. Apart from circumstellar and interstellar regions, these dinitriles are also important molecules in planetary bodies where the atmospheres are nitrogen-rich (Kunde et al. 1981; Jolly et al. 2015). A prime example is Titan, whose atmosphere is composed of about 95% of N2. The CH4 molecule is the next most abundant species in Titan’s atmosphere, and when combined with N2, their photochemistry leads to a rich variety of organic molecules including hydrocarbons, nitriles and dinitriles or tholins (Cernicharo et al., in prep.). The simplest molecule of this family of dinitriles, malononitrile (N≡C−CH2−C≡N) and its isomers isocyanoacetonitrile (N≡C−CH2−N≡C) and diisocyanomethane (C≡N−CH2−N≡C) have been already investigated in the laboratory (Motiyenko et al. 2019, 2012) but their detection in the ISM has not been achieved so far. The next member of this group of dinitriles is succinonitrile, N≡C−CH2−CH2−C≡N, a promising candidate to be detected in the space due to its high dipole moment. In addition, its formation may proceed through a different mechanism than that for malononitrile and its isomers, and it could be easier to observe despite the fact that the simpler analogs have not yet been detected.
Succinonitrile has been studied in the centimeter wave range, using a high-resolution Fourier transform microwave-pulsed supersonic jet spectrometer, and in the millimeter wave region up to 72 GHz, using a Stark modulation spectrometer (Jahn et al. 2014). The spectra of the 13C and 15N singly substituted isotopologues in natural abundance were also observed together with that of the chemically single-substituted deuterium isotopologues. The measurements for the parent isotopologue included 57 rotational transitions, nine of them with several nuclear quadruple coupling hyperfine components resolved with J ≤ 18 and Ka ≤ 6. In the final fit the rotational constants and all quartic distortion constants were well determined, but the astronomical search for succinonitrile at the observational frequency ranges of the radio telescopes becomes difficult only with these few rotational parameters.
The investigation of succinonitrile presented in this paper has two main aims. The first is to contribute to the astronomical search for succinonitrile by providing a more accurate spectral modelling of succinonitrile and thereby extending the measurements into the millimeter-wave region. The second one is to assign and analyse the rotational spectra in the low-lying vibrational states of succinonitrile, because a considerable proportion of the population resides in low-lying vibrationally excited states. The data necessary for dealing with spectral lines of these species can be obtained from detailed rotational measurements in the millimeter wave region performed in the laboratory. Consequently, in the present work new spectroscopic measurements of succinonitrile have been performed in the 72–116.5 GHz frequency range using a new broadband millimeter-wave spectrometer based on radio astronomy receivers with Fast Fourier Transform (FFT) backends (Cernicharo et al. 2019; Tanarro et al. 2018). The analysis of these data allowed the identification of the rotational transitions of eleven different vibrationally excited states belonging to fundamentals, overtones, and combination states of the low-frequency vibrational modes.
2. Quantum chemical calculations
Although quantum chemical calculations for the succinonitrile molecule are available in the literature (Umar & Morsy 2007; Ramasami 2007), we carried out our own ab initio calculations in order to estimate the molecular parameters necessary to the analysis of the rotational spectrum. As shown by Jahn et al. (2014) the coupled cluster with singles and doubles excitations with the Dunning’s correlation consistent polarized valence triple-ζ (CCSD/cc-pVTZ) level of theory is required to give an adequate description of the molecular geometry of succinonitrile. Hence, we optimized the succinonitrile molecular structure at the CCSD/cc-pVTZ level of theory using the Molpro 2018.1 ab initio program package (Werner et al. 2018). Two conformers, one antiperiplanar (trans) and another one synclinal (gauche) were found, with an energy difference of 321 cm−1. The antiperiplanar conformation was found as the global minimum but, as it presents a C2h symmetry, has no permanent dipole moment and no rotational spectrum. Therefore, we focused on the synclinal species, with a C2 symmetry and a very large μb dipole moment of 5.6 D. For this conformer, harmonic and anharmonic frequency calculations were done to estimate the energy and the rotational constants of the individual vibrationally excited states, facilitating the assignment of the experimental spectrum. These calculations were carried out at the CCSD/cc-pVTZ and MP2/cc-pVTZ (Møller–Plesset perturbation theory) levels of theory, using the Molpro 2018.1 and Gaussian16 (Frisch et al. 2016) program packages, respectively. An energy diagram for the vibrational levels below 500 cm−1 is shown in Fig. 1 and a complete list of the vibrational frequencies is given in Table A.1.
 |
Fig. 1. Diagram of harmonic vibrational energy levels for succinonitrile predicted below 500 cm−1. Calculations done at the CCSD/cc-pVTZ level of theory. |
3. Experimental
The emission rotational spectrum of succinonitrile was recorded from 72 to 116.5 GHz at room temperature using the GACELA (GAS CEll for Laboratory Astrophysics) spectrometer constructed at the Yebes Observatory (Spanish National Geographic Institute (IGN)). The detailed description can be found in Cernicharo et al. (2019). The broadband high-resolution rotational spectrometer is equipped with radio receivers similar to those used in radio astronomy to search for molecular emission in space. The receivers are equipped with 16 × 2.5 GHz FFT Spectrometers with a spectral resolution of 38.14 kHz allowing the observation of the rotational transitions in the Q (31.5–50 GHz) and W bands (72–116.5 GHz). The spectrometer’s cell consists of a stainless steel cylinder of 890 mm length and 490 mm diameter, and positioned horizontally with the long axis. The cylinder is closed by 30 mm thick plates that support the flanges for the microwave windows, which are tilted by 9°, one with respect to the vertical plane and the other with respect to the horizontal plane.
Succinonitrile (Sigma, purity > 99%) is solid at room temperature and it was placed into a PyrexTM vacuum Schlenk especially designed for these experiments, and degassed using the common freeze-pump-thaw cycling method. In order to avoid sample condensation during the experiment, the temperature of the sample container and the injection line were kept at 50°C using a dry heating tape and a PID (proportional integral derivative) temperature controller. Prior to the sample introduction, the pressure inside the vacuum chamber was 2.0 × 10−4 mbar and during the experiment, carried out in continuous flow mode, the pressure was kept at 7.0 × 10−3 mbar keeping in mind that higher pressures produce undesirable line broadenings. With the selected working pressure, the rotational lines of succinonitrile have a half width at half maximum (HWHM) of 0.3−0.45 MHz, which is well adapted to frequency measurements with high accuracy. In all these experiments frequency switching with a throw of 25 MHz was selected as the observing procedure. This has been previously confirmed as the most suitable mode since the lines are observed twice and the noise improves by a factor square root of two, allowing the derivation of accurate line profiles and intensities for lines of up to 2 MHz full width at half maximum (FWHM).
4. Rotational spectrum and analysis
Succinonitrile can adopt two different conformations in the gas phase, antiperiplanar or synclinal, but only the latter has a permanent dipole moment and thus shows rotational spectrum. This synclinal conformer is a near prolate molecule that has a C2 symmetry axis that coincides with its molecular b axis, and thus it has only one dipole moment component. Despite this, succinonitrile exhibits a very rich rotational spectrum, which arises from a large number of vibrational states. Figure 2 illustrates the line density in a selected frequency region of almost two GHz width. Even though the spectrum was congested, the ground state assignment was straightforward as the rotational transition frequencies with low Ka values were well predicted to within a few MHz by using the rotational and quartic centrifugal distortion constants reported by Jahn et al. (2014). First, we searched for b-type R-branch transitions with Ka ≤ 6 which were found relatively close to the predicted frequencies, and which were then fitted using the SPFIT program (Pickett 1991) with the A-reduction of Watson’s Hamiltonian in Ir representation (Watson 1977). The initial fit provided a set of refined experimental constants that were used for new spectral predictions that allowed in turn the identification of b-type Q-branch transitions with Ka values from 8 to 14. In the employed assignment method the measured transitions were used to improve the transition frequency predictions and search for new ones. Finally, a total of 459 rotational transitions with maximum values of J and Ka quantum numbers 70 and 14, respectively, were assigned for the ground vibrational state of succinonitrile. A list with all the measured transitions is available at CDS. The analysis rendered the experimental rotational constants listed in Table 1 together with the data from Jahn et al. (2014). Our rotational and quartic centrifugal distortion constants agree well with those reported by Jahn et al. (2014). The main difference is found in the δK and d2 values and is due to the use of different Watson’s rotor reductions. In the present work, we used a Watson’s asymmetric rotor reduction while Jahn et al. used the symmetric one. With the exception of δK and d2, the small discrepancies between the present rotational and quartic centrifugal distortion constants and those reported by Jahn et al. can be attributed to the fact that we have rendered five sextic centrifugal distortion constants, which slightly affects the value of the rest of the floated parameters.
 |
Fig. 2. Top: section of rotational spectrum of succinonitrile at room temperature showing the satellite pattern for 301, 30−290, 29 and 300, 30−291, 29 rotational transitions. Bottom: modelled spectrum based on anharmonic frequency MP2/cc-pVTZ calculations. Intensities are estimated using the Boltzmann population ratio at 300 K. |
Spectroscopic constants for the ground state of succinonitrile.
Succinonitrile has two equivalent 14N nuclei with a spin of I = 1, so that nuclear quadruple coupling hyperfine splittings should be expected (Gordy & Cook 1984). Using the diagonal elements of the 14N quadruple coupling tensor previously reported by Jahn et al. (2014) we predicted the 14N nuclear quadruple coupling hyperfine splittings but we could not observe them, not even for high Ka transitions, since these splittings are smaller than the experimental broadening of the lines. This is supported by the fact that Jahn et al. (2014) observed these splittings only for the rotational transitions measured below 18 GHz. We also searched for the rotational transitions for 13C and 15N species in natural abundance of succinonitrile, using the rotational constants reported by Jahn et al. (2014). The line intensities for these isotopic species are around 1/100 and 0.4/100, respectively, of the observed intensity for the main isotopologue of succinonitrile and thus the transitions could not be distinguished from the noise level.
As mentioned before, the observed conformer of succinonitrile has a C2 symmetry and thus the intensity of its rotational transitions are subjected to spin statistics. This is due to the geometry of the molecule, which allows an interchange of identical particles by the rotation about one of the principal axes. The C2b operation of the C2 symmetry point group, which corresponds to the rotation about the b axis by π radians, simultaneously exchanges the positions of two non-equivalent pairs of hydrogen (fermions with I = 1/2) and two nitrogen atoms (bosons with I = 1) in the molecule. The total wavefunction, expressed as ψtot = ψeleψvibψrotψns, must be symmetric, Fermi-Dirac statistics, with respect to the C2b operation, and considering the two pairs of fermions and the bosons. The corresponding wavefunctions ψele and ψvib for the ground electronic and vibrational states are symmetric. The parity of the rotational wavefunction ψrot depends on the Ka and Kc values, and is symmetric for the levels with Ka + Kc = even; while for the levels with Ka + Kc = odd it is antisymmetric. Hence, to satisfy Fermi-Dirac statistics symmetric and antisymmetric nuclear spin functions must be combined with symmetric and antisymmetric rotational wavefunctions, respectively. As shown in Bunker & Jensen (1998), the total nuclear statistics weights are (2IH + 1)2(2IH + 1)2(2IN + 1)2 = 144, and the nuclear statistical weight for the rotational levels with Ka + Kc = even and odd is 78 and 66, respectively. Figure 3 shows a series of R-branch rotational transitions illustrating the influence of nuclear spin statistics on the transition intensities.
 |
Fig. 3. Two series of R-branch rotational transitions of succinonitrile in its ground state. These illustrate the influence of nuclear spin statistics on the transition intensities, which are related as 13-to-11 depending on the Ka + Kc values. |
The relative intensities of all the rotational transitions for the ground state agree well with the predictions, done with the SPCAT program (Pickett 1991), considering the rotational partition function at maximum value of J = 90. The rotational, vibrational, and conformational partition functions at different temperatures are listed in Table 2. In addition, the abundance fraction of the gauche conformer (Xg) at different temperatures is listed in Table 2. Xg is defined as the ratio between the population of gauche and trans conformers, Xg = ngauche/ntrans. This value can be used to estimate the total column density of succinonitrile from the column density of the gauche conformer, as explained in Sect. 5.
Rotational, vibrational and conformational partition functions for succinonitrile together with the abundance fraction of the gauche conformer (Xg) at different temperatures.
The spectrum in Fig. 2 shows that each ground vibrational state line of succinonitrile was accompanied by many satellite lines attributable exclusively to pure rotational transitions in vibrationally excited states, since no other coupling interaction is expected for this closed shell molecule. In fact, a large number of vibrationally excited states are predicted below 500 cm−1, as can be seen in Fig. 1. In order to assist in the assignment of these satellite lines, the rotational spectra of the lower-energy excited states were modelled on the basis of calculated first-order vibration-rotation constants αi that define the vibrational dependence of rotational constants Bν = Be − ∑iαi (νi + 1/2), where Bν and Be substitute all three rotational constants in a given excited state and in equilibrium, respectively, and νi is the vibrational quantum number. The calculations were carried out with the Gaussian16 program package at the MP2/cc-pVTZ level of theory using the optimized geometry obtained at the CCSD/cc-pVTZ level. As can be seen in Fig. 2, the ab initio predicted pattern of transitions for the different vibrationally excited states reproduces the one observed in the experimental spectrum. Hence, the predictions shown in Fig. 2 were used as a guide for the vibrationally excited states assignments. Predictions using the vibration-rotation constants for structures optimized at levels of theory different from CCSD/cc-pVTZ, did not give reliable results. This is explained by a wrong estimation of the ∡CCCC dihedral angle, which strongly affects the relative position of the atoms involved in the motions of each normal mode and thus determines the αi vibration-rotation constants. As pointed out before by Jahn et al. (2014), the ∡CCCC dihedral angle is properly estimated only when CCSD/cc-pVTZ level of theory calculations are used in the optimization procedure.
Up to eleven different vibrationally excited states were identified following the same bootstrap method of assignment-prediction employed for the ground state. All the assigned states resulted from the four lowest frequency vibrational modes ν13(A), ν12(A), ν24(B), and ν23(B). Only ν13 is a torsion mode while the other three are CCN bending modes. Their harmonic frequencies together with the normal coordinate displacement vectors are shown in Fig. 4. In addition to these four fundamental modes, we found, between the eleven identified states, the second quanta of ν13 and ν12 (2ν13 and 2ν12), and the third and fourth quanta of ν13 (3ν13 and 4ν13), together with some combination states, namely ν13 + ν12, 2ν13 + ν12, and ν13 + ν24. The most intense rotational transitions were observed for ν13, for which a total of 351 rotational transitions were included in the fit. The derived centrifugal distortion constants, depicted in Table 3, are very similar to those found for the ground state with the difference that ΦJK could be determined with some accuracy, which was not the case for the ground state.
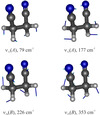 |
Fig. 4. Schematic visualization of four lowest frequency normal vibrational modes of succinonitrile ν13, ν12, ν24, and ν23 obtained from ab initio calculations. |
Spectroscopic constants for the ground state and vibrationally excited states of succinonitrile.
As can be seen in Fig. 1, some states may be involved in mutual interactions as a result of proximity of their vibrational energy levels. This is the case of the 2ν13 and ν12 states, whose ab initio estimated energy difference is smaller than 20 cm−1. These two states belong to the same symmetry (A) and therefore both Fermi and Coriolis interactions are allowed. However, only a few rotational transitions in limited J ranges (J > 45) showed anomalous deviations of their experimental frequencies, which were in most of the cases smaller than 2 MHz. In different fits considering a two-state perturbation analysis, we tried to determine Fermi and/or Coriolis interaction constants but these trials failed, probably because the number of perturbed transitions in our frequency range is not very large or because the interaction between both states is not strong enough to allow a combined analysis. In fact, each state could be analysed separately, excluding some of the perturbed transitions and obtaining reasonable fits with 251 and 293 rotational transitions for the ν12 and 2ν13 states, respectively. From the list of the derived constants in Table 3, it can be seen how the perturbations between these two states induce departures of the values of their centrifugal distortion constants, with respect to those for the unperturbed ground state.
The rotational transitions of the ν13 + ν12 and ν24 states appeared in the spectrum very close and as shown in Table 3 they have very similar rotational constants. In spite of this, the assignment of each state could be achieved. Since ν13 + ν12 and ν24 states belong to different symmetries, A and B respectively, the influence of the nuclear spin statistics on the intensities of their rotational transitions will be opposite one another, with respect to a Ka + Kc value. In this manner, the rotational transitions for ν13 + ν12 may be affected like those for the ground state, where a ratio of approximately 13-to-11 was found for Ka + Kc = even and Ka + Kc = odd. In contrast, for ν24 an inverse ratio of 11-to-13 should be observed for those values of Ka + Kc, since for ν24, ψvib is antisymmetric and therefore the nuclear statistical weights for the rotational levels are reversed. This effect is illustrated in Fig. 5. Taking this into account, the ν13 + ν12 and ν24 states were assigned and a total of 140 and 189 rotational transitions, including both Q- and R-branch transitions, were measured for each state, respectively. This assignment was supported by the fact that the experimental rotational constants for the ν13 + ν12 state agree very well, with uncertainties of less than 1 MHz, with those estimated by the independent experimental-theoretical correction factors for the ν13 and ν12 states. On the other hand, although our calculations predicted that the ν13 + ν12 and ν24 states lie close in energy, no perturbations were observed in the spectrum and both states could be analysed independently.
Following the same identification procedure reported above, we identified the third and fourth quanta of ν13 and the second quantum of ν12. The low intensity of the rotational transitions for these states resulted in fits containing a smaller number of lines, including only R-branch transitions with Ka ≤ 3. Hence, only the rotational constants and some of the quartic centrifugal distortion constants were determined from the analysis, where the sextic centrifugal distortion constants were kept fixed to the ground state values. The remaining observed states are ν23, ν13 + ν24, and 2ν13 + ν12. The identification of ν23 was trivial using its calculated first-order vibration-rotation constants. In contrast, ν13 + ν24 and 2ν13 + ν12 have similar rotational constants but they belong to different symmetries, so their identification was carried out using the same procedure followed to identify ν13 + ν12 and ν24 states. The rotational parameters derived for these states are summarized in Table 3.
 |
Fig. 5. Rotational transitions 230, 23−221, 22 and 231, 23−220, 22 for ν13 + ν12 and ν24 states showing effects of vibrational state symmetry and nuclear spin statistics on transition intensities. The intensities are related as 13-to-11 depending on the Ka + Kc values. |
5. Search for succinonitrile in space
In our search for succinonitrile, we used the rotational parameters for the ground state of the observed conformer, gauche, of succinonitrile obtained in this work and the MADEX code (Cernicharo 2012). Our frequency predictions are sufficiently reliable up to 200 GHz. We focused on two high-mass star-forming regions, Orion KL and Sagittarius (Sgr) B2, on a starless core in the Taurus Molecular Cloud (TMC-1), and in the cold dark cloud Barnard 1 (B1-b). The cold dense pre-stellar core TMC1-1 has been studied in detail through systematic observations at different wavelengths (Kaifu et al. 2004; Marcelino et al. 2007, 2009). Moreover, this source is particularly rich in carbon chains and −C≡N bearing species produced by gas phase ion-molecule reactions (see e.g. Kaifu et al. 2004). B1b is another well-studied prototypical cold core that contains two extremely young protostellar objects, B1b-N and B1b-S. The detection of complex molecules towards B1b-S suggests that a very young and compact object is already warming up its most immediate surroundings and, therefore, molecules from grain mantles are evaporating (Marcelino et al. 2018; Cernicharo 2012).
First, we searched for succinonitrile using the IRAM 30m data at 3 mm from TMC-1 and B1-b sources (see e.g. Marcelino et al. 2007; Cernicharo 2012). Since only a few transitions are expected at these frequencies, we focused on a couple of unresolved doublets with energies of the upper level below 20 K: 77, 1 − 76, 0 and 77, 0 − 76, 1 at 92 029 MHz, and 87, 2 − 76, 1 and 87, 1 − 76, 2 at 96 319 MHz. We did not detect succinonitrile above the 3σ detection limit of our data. The derived upper limits for the gauche conformer of succinonitrile column density in TMC-1 and B1-b, assuming local thermodynamic equilibrium (LTE) and previously assumed physical parameters are summarized in Table 4.
Physical parameters of cloud cores considered in the astronomical search of gauche-succinonitrile.
Considering that the transitions with energies above 10 K may be hardly detectable in TMC-1 and B1-b, especially in TMC-1, we also searched for succinonitrile in the Yebes 40 m data of those sources at 1.3 cm and 7 mm (Marcelino et al., in prep.). Nevertheless, none of the low energy lines (Tupp < 10 K) expected between 20−22 GHz and 30−50 GHz were detected.
These results are not totally unexpected since gauche conformer of succinonitrile is 321 cm−1 above the most stable conformer, the trans one, and thus its abundance fraction is very small at low temperatures (see Table 2). However, we searched for this species in the Taurus Molecular Cloud (TMC-1) and in the cold dark cloud Barnard 1 (B1-b) in order to provide upper limits to its column density. In addition, succinonitrile could be preferably formed in space by chemical reactions on dust grains. Thus, we also sought succinonitrile in two prototypical high-mass star-forming regions, Orion KL and Sgr B2 using the public IRAM 30 m data at 3 mm (Tercero et al. 2010; Belloche et al. 2013). As in the cold cores, we did not find succinonitrile above the detection limit in any of the surveys. To provide upper limits to the column density for the gauche conformer of succinonitrile in the ground state, we used the MADEX code to derive its synthetic spectrum in both sources. We assume LTE and the physical parameters derived by Belloche et al. (2013) and López et al. (2014) for CH3CN in Sgr B2 and CH2CHCN in Orion KL, respectively (see Table 4). Because the vibrational and conformational partition functions are significant above 100 K, we also estimate the total upper limit to succinonitrile column density, including both conformers, in these sources by NT = (Ngauche, g.s. × Qv × Qc)/(Xg). We find total succinonitrile column densities of ≤3 × 1015 cm−2 and ≤1 × 1018 cm−2 in Orion KL and Sgr B2, respectively.
These column densities are only a factor ≤10 below those derived for CH3CN in Orion KL (López et al. 2014) and Sgr B2 (Belloche et al. 2013). This suggests that the succinonitrile column density is most likely much smaller than the derived upper limit, mostly due to the high level of line confusion in the considered surveys. Moreover, as the most stable conformer is a non-polar species, we could not directly derive molecular column densities for the most abundant conformer of succinonitrile. This fact prevents us from expanding on the discussion by comparing our results with the abundances of other cyanides or column density ratios between the pairs CH3OH/(CH2OH)2 and CH3CN/(CH2CN)2, where (CH2CN)2 is succinonitrile.
Our results point out that the detection of the gauche conformer would imply huge abundances of trans-succinonitrile, as high as those of CH3CN in Orion KL and Sgr B2. Nevertheless, since −C≡N bearing species as complex as C3H7CN have been detected in these high-mass star-forming regions (Belloche et al. 2009, 2014; Pagani et al. 2017), succinonitrile could also be a moderately abundant product of surface reactions.
It is worth noting that whereas the formation of ethylene glycol (OHCH2CH2OH) has been discussed as a product of surface chemical reactions of the CH2OH radical (Garrod et al. 2008), the formation of succinonitrile has not been considered so far. Belloche et al. (2009) suggested that the formation of the larger cyanides begins with cosmic ray-induced photodissociation of a smaller grain-surface alkyl cyanide molecule. They also proposed another formation mechanism that starts with the accretion of a CH2CN radical (which may be formed in the gas phase following the evaporation of HCN). Nevertheless, the reaction of CH2CN + CH2CN on grains, which would strongly depend on the mobility of the CH2CN radical, is not considered in those models. In any case, it will not be straightforward to prove this production mechanism since the search of succinonitrile in space is limited to the gauche conformer.
6. Conclusions
The present work reports a comprehensive investigation of the rotational spectra for the ground state succinonitrile and its vibrationally excited states. The millimeter-wave spectrum between 72–116.5 GHz was measured using a new broadband millimeter-wave spectrometer based on radio astronomy receivers with FFT backends. From the analysis we obtained accurate rotational parameters for the ground state and eleven vibrationally excited states, comprising states with multiple excitation quanta and combination states. These new laboratory data were employed to unsuccessfully search for succinonitrile in the cold and warm molecular clouds Orion KL, Sgr B2(N), B1-b, and TMC-1 using the spectral surveys captured by IRAM 30 m at 3 mm and the Yebes 40 m at 1.3 cm and 7 mm.
CDMS 2018, The Cologne Database for Molecular Spectroscopy: Molecules in the Interstellar Medium or Circumstellar Shells (as of 11/2018), https://cdms.astro.uni-koeln.de/classic/molecules
Acknowledgments
We thank the European Research Council for funding support under Synergy Grant ERC-2013-SyG, G.A. 610256 (NANOCOSMOS). CB would like to thank the Ministerio de Ciencia, Innovación y Universidades for a Juan de la Cierva postdoctoral fellowship (FJCI-2016-27983). IT, VJH, and JLD acknowledge additional partial support from the Spanish State Research Agency (AEI) through grant FIS2016-77726-C3-1-P. We would also like to thank Rosa Lebrón, Jesús Quintanilla, and Cristina Soria for providing us with the sample of succinonitrile and Prof. Yasuki Endo for logistic support with the quantum chemical calculations. This work was also based on observations carried out with the IRAM 30-meter telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
References
- Agúndez, M., Cernicharo, J., de Vicente, P., et al. 2015, A&A, 579, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agúndez, M., Marcelino, N., & Cernicharo, J. 2018, ApJ, 861, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2009, A&A, 499, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Müller, H. S. P., Menten, K. M., Schilke, P., & Comito, C. 2013, A&A, 559, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., & Menten, K. M. 2014, Science, 345, 1584 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bunker, P. R., & Jensen, P. 1998, Molecular Symmetry and Spectroscopy, 2nd edn. (Ottawa: NRC Research Press) [Google Scholar]
- Cernicharo, J. 2012, in ECLA-2011: Proc. of the European Conf. on Laboratory Astrophysics, eds. C. Stehlé, C. Joblin, & L. d’Hendecourt (Cambridge: Cambridge Univ. Press), EAS Publ. Ser., 58, 251 [Google Scholar]
- Cernicharo, J., Gallego, J. D., López-Pérez, J. A., et al. 2019, A&A, 626, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16, revision A.03 [Google Scholar]
- Garrod, R. T., Widicus Weaver, S. L., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Gordy, W., & Cook, R. 1984, Microwave Molecular Spectra, Techniques of Chemistry (New York: Wiley) [Google Scholar]
- Jahn, M. K., Grabow, J.-U., Godfrey, P. D., & McNaughton, D. 2014, Phys. Chem. Chem. Phys., 16, 2100 [CrossRef] [Google Scholar]
- Johnson, D. R., Lovas, F. J., Gottlieb, C. A., et al. 1977, ApJ, 218, 370 [NASA ADS] [CrossRef] [Google Scholar]
- Jolly, A., Cottini, V., Fayt, A., et al. 2015, Icarus, 248, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Kaifu, N., Ohishi, M., Kawaguchi, K., et al. 2004, PASJ, 56, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kołos, R., & Grabowski, Z. R. 2000, Ap&SS, 271, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Kunde, V. G., Aikin, A. C., Hanel, R. A., et al. 1981, Nature, 292, 686 [NASA ADS] [CrossRef] [Google Scholar]
- López, A., Tercero, B., Kisiel, Z., et al. 2014, A&A, 572, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcelino, N., Cernicharo, J., Agúndez, M., et al. 2007, ApJ, 665, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Marcelino, N., Cernicharo, J., Tercero, B., et al. 2009, ApJ, 690, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Marcelino, N., Gerin, M., Cernicharo, J., et al. 2018, A&A, 620, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGuire, B. A., Burkhardt, A. M., Kalenskii, S., et al. 2018, Science, 359, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Motiyenko, R. A., Margulés, L., & Guillemin, J.-C. 2012, A&A, 544, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motiyenko, R. A., Armieieva, I. A., Margulés, L., et al. 2019, A&A, 623, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Favre, C., Goldsmith, P. F., et al. 2017, A&A, 604, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrie, S., Millar, T. J., & Markwick, A. J. 2003, MNRAS, 341, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M. 1991, J. Mol. Spectr., 148, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Ramasami, P. 2007, Sov. Acta Astron., 68, 752 [Google Scholar]
- Solomon, P. M., Jefferts, K. B., Penzias, A. A., & Wilson, R. W. 1971, ApJ, 168, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Tanarro, I., Alemán, B., de Vicente, P., et al. 2018, A&A., 609, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tercero, B., Cernicharo, J., Pardo, J. R., & Goicoechea, J. R. 2010, A&A, 517, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umar, Y., & Morsy, M. A. 2007, Sov. Acta. Astron., 66, 1133 [Google Scholar]
- Watson, J. K. G. 1977, in Vibration Spectra and Structure, ed. J. Durig (Amsterdam: Elsevier), Vol. 6, 1 [Google Scholar]
- Werner, H. J., Knowles, P. J., Knizia, G., et al. 2018, MOLPRO, version 2018.1 [Google Scholar]
- Zack, L. N., Halfen, D. T., & Ziurys, L. M. 2011, ApJ, 733, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Ziurys, L. M., Savage, C., Highberger, J. L., et al. 2002, ApJ, 564, L45 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Frequency calculations of succinonitrile
The CCSD/cc-pVTZ harmonic vibrational frequencies of succinonitrile.
All Tables
Rotational, vibrational and conformational partition functions for succinonitrile together with the abundance fraction of the gauche conformer (Xg) at different temperatures.
Spectroscopic constants for the ground state and vibrationally excited states of succinonitrile.
Physical parameters of cloud cores considered in the astronomical search of gauche-succinonitrile.
All Figures
 |
Fig. 1. Diagram of harmonic vibrational energy levels for succinonitrile predicted below 500 cm−1. Calculations done at the CCSD/cc-pVTZ level of theory. |
| In the text | |
 |
Fig. 2. Top: section of rotational spectrum of succinonitrile at room temperature showing the satellite pattern for 301, 30−290, 29 and 300, 30−291, 29 rotational transitions. Bottom: modelled spectrum based on anharmonic frequency MP2/cc-pVTZ calculations. Intensities are estimated using the Boltzmann population ratio at 300 K. |
| In the text | |
 |
Fig. 3. Two series of R-branch rotational transitions of succinonitrile in its ground state. These illustrate the influence of nuclear spin statistics on the transition intensities, which are related as 13-to-11 depending on the Ka + Kc values. |
| In the text | |
 |
Fig. 4. Schematic visualization of four lowest frequency normal vibrational modes of succinonitrile ν13, ν12, ν24, and ν23 obtained from ab initio calculations. |
| In the text | |
 |
Fig. 5. Rotational transitions 230, 23−221, 22 and 231, 23−220, 22 for ν13 + ν12 and ν24 states showing effects of vibrational state symmetry and nuclear spin statistics on transition intensities. The intensities are related as 13-to-11 depending on the Ka + Kc values. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


