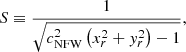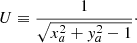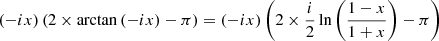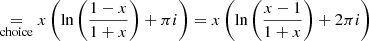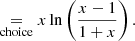| Issue |
A&A
Volume 628, August 2019
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201935261 | |
| Published online | 31 July 2019 | |
The slingshot effect as a probe of transverse motions of galaxies
1
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029, Blindern, 0315 Oslo, Norway
e-mail: robert.hagala@astro.uio.no
2
Institute of Cosmology and Gravitation, University of Portsmouth, Dennis Sciama Building, Portsmouth PO1 3FX, UK
Received:
12
February
2019
Accepted:
28
June
2019
Context. There are currently no reliable methods to measure the transverse velocities of galaxies. This is an important piece of information that is lacking in galaxy catalogues, and it could allow us to probe the physics of structure formation and to test the underlying theory of gravity. The slingshot effect (a special case of the integrated Sachs–Wolfe effect) is expected to create dipole signals in the temperature fluctuations of the cosmic microwave background (CMB) radiation. This effect creates a hot spot behind and a cold spot in front of moving massive objects. The dipole signal created by the slingshot effect can be used to measure transverse velocities, but because the signal is expected to be weak, the effect has not been measured yet.
Aims. Our aim is to show that the slingshot effect can be measured by stacking the signals of galaxies falling into a collapsing cluster. Furthermore, we evaluate whether the effect can probe modified gravity.
Methods. We used data from a simulated galaxy catalogue (MultiDark Planck 2) to mimic observations. We identified a 1015 M⊙ cluster, and made maps of the slingshot effect for photons passing near 8438 infalling galaxies. To emulate instrument noise, we added uncorrelated Gaussian noise to each map. We assumed that the average velocity is directed towards the centre of the cluster. The maps were rotated according to the expected direction of motion. This assures that the dipole signal adds up constructively when stacking the maps. We compared the stacked maps to a dipole stencil to determine the quality of the signal. We also evaluated the probability of fitting the stencil in the absence of the slingshot signal.
Results. Each galaxy gives a signal of around ΔT/T ≈ 10−9, while the current precision of CMB experiments is ΔT/T ≈ 4 × 10−6. By stacking around 10 000 galaxies and performing a stencil fit, the slingshot signal can be over the detectable threshold with today’s experiments. However, due to the difficulty of distinguishing an actual signal from false positives, future CMB experiments must be used to be certain of the strength of the observed signal.
Key words: dark energy / cosmology: theory / large-scale structure of Universe
© ESO 2019
1. Introduction
By precisely measuring the positions and velocities of galaxies, we can use them as tracers for mapping the underlying matter distribution of the large-scale structure of the Universe. Furthermore, in systems where the matter distribution is known from other methods, for instance from gravitational lensing, precise catalogues of the positions and velocities of galaxies can be used as a consistency check to test our models of gravity and structure formation. While the radial velocity with respect to the Earth is measurable through the Doppler effect, transverse velocities of galaxies are more challenging to measure. The only reliable method of estimating transverse velocities of an object directly is through detecting a change in position relative to the background between two observations, which is known as the proper motion of the object. The recent data release of Gaia (Gaia Collaboration 2018) presented the proper motions of over a billion stars in our galaxy, where the velocities were found using this method. However, this option becomes unfeasible at scales larger than our galaxy because many years must pass before distant galaxies will move far enough for the motion to be resolved.
When a galaxy is affected by an external force like gravity, the resulting acceleration first changes the velocity of the galaxy before the position of the galaxy changes significantly. Better knowledge of the peculiar velocities of observed galaxies will help us compare our models of gravity on large scales with the forces acting on those galaxies. This can be particularly useful when studying theories of modified gravity, but can also be used to measure the amount and distribution of dark matter in the context of Λ cold dark matter (CDM). Velocities can be used as a consistency check for our models of structure formation. The best models predict the matter distribution very well, but the velocity fields of the same models are not usually compared to observations (Stebbins 2006). Furthermore, measurements of tangential velocities can break the degeneracy between expansion velocity and peculiar velocity, which is a problem when using only the redshift to measure velocities.
The slingshot effect was first mentioned by Birkinshaw & Gull (1983), and is a promising probe for measuring transverse motions. It is a special case of the integrated Sachs–Wolfe (ISW) effect (Sachs & Wolfe 1967). The ISW contribution to the cosmic microwave background (CMB) is due to the evolution of a gravitational potential while photons are passing through it. The most relevant result of the late-time ISW is what is known as the Rees–Sciama effect (Rees & Sciama 1968). As structure collapses under gravity – or expands with the Hubble flow – while a photon passes through, the change in the gravitational potential of the structure will affect the photon energy. The Rees–Sciama effect results in an overall increase or decrease in the measured CMB temperature centred around clusters and voids. The Rees–Sciama effect can be estimated from galaxy surveys, and is expected to be important at the largest angular scales (Maturi et al. 2007a). In the literature, the slingshot effect is also called the Birkinshaw–Gull effect or the moving lens effect. Sometimes the name of the Rees–Sciama effect is used interchangeably with the slingshot effect, even though it describes a related but slightly different phenomenon.
The slingshot effect is related to the Rees–Sciama effect, but instead of a single hot spot centred on the halo, it creates a dipole pattern with a cold spot in front of a moving halo and a hot spot behind it. Stebbins (2006) states that transverse motions of galaxies can be measured on the small scales of the CMB by statistically analysing these dipole patterns. The intention of this paper is to propose a method for measuring this effect. Sufficiently precise measurements of the effect can be used as a self-consistency check of our models of structure formation, and as a more direct measure of the gravitational forces acting on large scales.
The mechanism behind the dipole pattern of the slingshot effect can be understood as follows. If a CMB photon enters in front of the moving halo, the gravitational potential becomes deeper while the photon is passing through the potential well, meaning that the photon has to spend more energy getting out and becomes redshifted. Likewise, if a CMB photon enters behind the moving halo, the gravitational potential along the photon trajectory becomes shallower while the photon passes, allowing the photon to gain some energy. The result is a dipole signal. An example of the signal is represented visually in Fig. 1. The increase or decrease in photon energy can be compared to the gravity assist manoeuvre: a spacecraft can gain velocity relative to the heliocentric reference frame by passing in the trail of a moving planet. An effect related to the slingshot effect was proposed by Molnar et al. (2013), where a difference in redshift between two lensed images from the same source can be used to infer the tangential velocity of the lens. Other attempts at indirectly inferring transverse velocities include analysing microlensing parallaxes in very specific set-ups, where a quasar can be found behind the galaxy whose velocity is to be found (see e.g. Gould 1994).
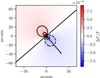 |
Fig. 1. Contour plot of the temperature dipole created by the slingshot effect. The arrow indicates the direction of motion of the galaxy. An increase in photon temperature is indicated in red; a decrease in temperature is illustrated in blue and with dashed contours. This example is a galaxy of virial mass 1.2 × 1012 M⊙, moving with a transverse velocity component of 880 km s−1, viewed at a distance of 100 Mpc. |
The slingshot signal grows stronger with more massive and faster moving structures. Birkinshaw & Gull (1983) predicted that a massive and rapidly moving galaxy cluster should produce a measurable signal, but to our knowledge the effect has not been measured yet. As indicated by Stebbins (2006), the difficulty in measuring the effect could be due to similar dipole patterns being produced by the kinematic Sunyaev–Zel’dovich effect and by the lensing of the CMB anisotropies. With the current CMB experiments it is therefore impossible to measure the slingshot effect of a single galaxy. Recently, Hotinli et al. (2018) investigated the detectability of the slingshot effect by estimating the corrections to the CMB power spectrum. Furthermore, Yasini et al. (2018) proposed an estimator for the pairwise peculiar velocities of clusters using the slingshot effect. Both of these recent studies found that the combined effects of transversely moving objects should be measurable with CMB surveys in the near future.
The process of image stacking has the ability to isolate the slingshot effect from that of the kinematic Sunyaev–Zel’dovich effect and the lensed CMB. These two confounding effects are not correlated with position and velocity in the same way as the slingshot effect, meaning that their contribution is expected to average to zero when stacking enough images. Maturi et al. (2007b) propose that the slingshot effect can be measured by stacking the CMB maps of 1000 cluster mergers. In the current work we present a method for detecting the average peculiar infall velocity of galaxies around a single cluster. By aligning and stacking the signal from galaxies in a mock catalogue, and then fitting the stacked image to a template, we show that the effect will be detectable with CMB experiments in the near future, such as CMB-S4 (Abazajian et al. 2016).
2. Methods
The ISW effect changes the temperature of the CMB photons during the time t they spend in an evolving gravitational potential Φ. Specifically,
where the dot indicates a time derivative. We adopt units such that c = 1.
The slingshot effect is the change in photon temperature due to the transverse motion of an unevolving gravitational well. Following a flow of photons travelling through a moving halo, this effect can be expressed as
We chose a coordinate system where light moves in the positive z-direction, along the line of sight. The projected motion v⊥ of the halo is taken to be constant and along the x-axis. In this frame, we define vx as the velocity component perpendicular to the line of sight. Since the photons move with the speed of light and we chose units where c = 1, the time integral can be changed into an integral along z:
The coordinates x, y, and z represent physical distances (measured in non-comoving megaparsecs). To estimate the magnitude of the slingshot effect, we assume a simple yet realistic model for the gravitational potential Φ derived from the halo model set-up.
2.1. Halo model set-up
For the purpose of calculating the signal from a single halo, we modelled the halo as a spherically symmetric matter distribution, centred at x = y = z = 0. We assumed that all of the dark matter halo mass is in a Navarro–Frenk–White (NFW) profile with concentration cNFW = 15 (Navarro et al. 1995). We populated the halo with baryons, consisting of an additional 10% of the dark matter mass. We used a Hernquist profile for the baryons (Hernquist 1990), applying a Hernquist scale length a that relates to the virial radius rvir of the dark matter halo according to
(see the Appendix for the detailed calculations of the slingshot effect from the NFW and the Hernquist component). The resulting expression we implemented to calculate the slingshot effect from a single halo is
where
and
Here, mDM is the virial mass of the dark matter halo. The constant g depends on the concentration cNFW according to Eq. (A.4). We use the following notation for dimensionless coordinates: xr ≡ x/rvir and xa ≡ x/a. Furthermore,
and
We note that the Q-expressions here are independent of halo parameters for the chosen model. This means that we only needed to calculate a template of the slingshot effect once, using units of the virial radius, we then re-scaled the template to galaxies of any size. The deciding factor for the amplitude of the slingshot effect is the combination mvx/rvir.
2.2. Realistic observational set-up
The slingshot effect, described by Eq. (5), increases with the mass of the halo, and with the transverse velocity vx relative to the CMB. We find that the slingshot signal from a single large galaxy with mass 1013 M⊙, moving at 1000 km s−1, is around ΔT/T ∼ 10−8, equivalent to 0.03 μK. Most galaxies would be less massive and move more slowly, giving an average signal of ΔT/T ≈ 3 × 10−9 (see Sect. 2.3). Figure 1 shows the raw slingshot signal from an example galaxy, with a cold spot in front of the moving galaxy and a hot spot behind. This example galaxy is slightly heavier and moves slightly faster than the average, resulting in a stronger signal than ΔT/T ≈ 3 × 10−9.
The Atacama Cosmology Telescope (ACT) has instrument noise down to 6 μK arcmin, or a per-pixel noise of σΔT/T ∼ 4 × 10−6 when assuming 0.5 arcmin pixels1 (see Hincks et al. 2010 for details on the expected sensitivity and beam profile point spread function of ACT). The given noise level indicates that measuring the signal from a single massive galaxy is impossible since the signal of ΔT/T ∼ 10−8 would be drowned out by noise. To get a signal-to-noise ratio (S/N) of the order of one, we would need to increase the signal, or reduce the noise, by a factor of 400. The signal increases with the square root of the number of stacked images, which means that we would have to stack the signal of over 160 000 fast and massive galaxies, or closer to 107 average galaxies. Furthermore, these galaxies must be close enough to us for the dipole to be resolved in the CMB map. The ACT has 1.3 arcmin full width at half maximum (FWHM) beam resolution. A typical galaxy with virial radius of 100 kpc must be within about 250 Mpc to be resolved with two or more pixels.
An important consideration when stacking these dipole images is that they need to be oriented correctly, such that the galaxy velocity directions point along approximately the same axis. Because there are no good ways to measure the transverse velocity of a single galaxy yet, it is necessary to stack observable galaxies only where the approximate direction of motion can be inferred from other means. While other papers suggest using the relative velocity of pairs of galaxy clusters (e.g. Yasini et al. 2018), in this work we study the infall velocity of galaxies in the large-scale structure of the cosmos. To estimate a direction of peculiar motion, we assumed that galaxies will fall towards not yet virialised cluster structures in their vicinity. This is not true for absolutely all galaxies, but when stacking images it is sufficient for the sample to have an average velocity in the radial direction. Another option not covered in this paper is stacking galaxies near the edges of voids. We expect void galaxies to have an average velocity directed out of the underdense region.
We suggest using the Coma Cluster to align the velocities of nearby galaxies in a realistic observational set-up. At a distance of about 100 Mpc (Liu & Graham 2002), the Coma Cluster is within the 250 Mpc needed to resolve a slingshot dipole. It is well studied, and not obscured by the Milky Way disc. The Coma Cluster is located approximately at a RA of 195° and Dec of +28°. Several current surveys cover this region, for instance the BOSS spectrographic survey of the SDSS (Sloan Digital Sky Survey). The Coma Cluster has a mass of about 1.9 × 1015 M⊙ (found through weak lensing by Kubo et al. 2007). Together with the Leo Cluster, it is part of the rich Coma Supercluster, which is large enough to have not yet completely virialised. The total number of galaxies falling towards the supercluster could be sufficient to achieve a S/N of the order of unity through stacking2. Reaching a S/N of one requires that all of the infalling galaxies should be catalogued with position and redshift, and that on average they are falling in as fast as expected from simulations. Furthermore, the presence of foreground sources in our own galaxy can interfere with the precise measurement of the CMB around some of these galaxies.
To identify the signal even when the total stacked S/N is less than one, we propose fitting the expected dipole signal to the stacked image. Furthermore, we propose to estimate the probability of having false positives by fitting a template of the expected signal to several stacks of uncorrelated noise maps. If it is sufficiently improbable to achieve the best fit dipole randomly with just noise, we can say that the dipole is detectable, even if it is not visible by eye in the stacked image.
2.3. Stacking images from a simulated halo catalogue
To emulate realistic halos, we used the halo catalogue from the MultiDark Planck 2 survey described by Prada et al. (2012). The data set contains dark matter halos identified with the Rockstar halo finder (Behroozi et al. 2013). In this (1Gpc/h)3-box simulation, we identified one of the largest halos. It has a virial mass of the order of Mvir, supercluster ≈ 1015 M⊙ and a virial radius rvir, supercluster ≈ 4 Mpc, which is similar to values for the Coma Cluster. We find that this is the centre of a massive supercluster that has not yet virialised, meaning that nearby smaller halos are falling towards the supercluster. The virial mass and virial radius estimated by the halo finder at redshift zero is significantly lower than the actual mass affected gravitationally.
When studying subhalos close to the identified supercluster, we find that they indeed have a velocity component directed towards the centre of the structure (see Fig. 2 for a scatter plot of the velocities of halos surrounding the supercluster). The net inward flow of matter is apparent from closer than 1 rvir, supercluster, up to distances of about 20 rvir, supercluster.
 |
Fig. 2. Scatter plot of the projected radial motion of halos close to the massive supercluster. The horizontal axis shows the projected distance from the centre of the structure (in units of the virial radius of the supercluster). The vertical axis shows the projected radial velocity of the halo in question; positive values indicate infalling motion. The red line shows the binned mean. The error of the mean is consistent with the width of the line. The colour of a point indicates the virial mass of that halo. |
We picked out nearby halos with virial mass above 1011 M⊙ within 10 rvir, supercluster (approximately 40 Mpc) of the central supercluster. The mass cut-off was chosen to exclude halos hosting dwarf galaxies because they are more difficult to observe and they add a weak signal to the stack. The distance cut-off was chosen by hand; repeating the analysis with a 15 rvir, supercluster distance cut-off instead did not significantly improve the results compared to 10 rvir, supercluster. We draw the conclusion that the halos that are further away add more noise than signal, for instance because their velocities are misaligned due to other nearby structure. The chosen cut of 10 rvir, supercluster and M > 1011 M⊙ leaves 8438 halos in our final sample. These halos mostly consist of galaxies, but also some galaxy groups and galaxy clusters. The selected halos have an average mass of 1.79 × 1012 M⊙. We chose the z-axis of the 3D simulation as the line of sight, and projected the velocity of each halo down to the plane perpendicular to this axis (the x–y plane).
To simulate the signal observed with ACT, we created a 2D map of ΔTslingshot/T for each galaxy halo. The map size was chosen to fit two times the virial radius of that galaxy, with 0.5 arcmin pixel size. We smoothed the map with Gaussian blur with 2.6 pixels FWHM to emulate the 1.3 arcmin beam of ACT (Hincks et al. 2010). We assumed that each pixel of each image has an independent noise, drawn from a normal distribution with standard deviation σΔT/T. We performed the full analysis with three different values for the noise standard deviation: 4 × 10−6, 1 × 10−6, and 1 × 10−7. We did not vary the other parameters, such as the angular resolution.
We neglected perturbations in the CMB background because we assumed the background can be modelled well enough, and subtracted on the relevant scales (corresponding to l > 500). We also neglected non-dipole contributions like foreground sources. All of these are either expected to average out when stacked (if they are not correlated with the galaxy position and direction of motion) or have a monopole signal that will not contribute to the dipole stencil fit. Furthermore, we also neglected galaxy lensing of large-scale CMB gradients, which will introduce dipoles on scales similar to the slingshot effect. The large-scale gradients of the CMB are not expected to be correlated with the velocity of low redshift galaxies falling into a massive cluster, so the amplitude of lensing of the CMB will be negligible with large enough data sets, as outlined by Stebbins (2006). To further help remove this confounding signal, a delensing algorithm can be applied to the map around each galaxy before stacking (see e.g. Manzotti 2018; a process of delensing for the purpose of isolating the slingshot signal is suggested in Maturi et al. 2007b). Similarly, we also neglected the signals from nearby galaxies or galaxies located behind the observed ones; if another galaxy is within 2rvir of the imaged galaxy, it will introduce an additional dipole which is not positioned at the centre of the map. The chance of such an overlap is not negligible, but since the relative positions are not considered correlated with the direction of infall velocity, the stacking and fitting process is not expected to be sensitive to this signal.
The combined maps of each nearby halo were, after applying the instrumental point spread function and adding noise, aligned according to the expected infall direction (i.e. radially towards the centre of the supercluster) to simulate real observations where we have no a priori knowledge of the individual peculiar velocities. Since we used realistic simulations, our mock data sets take into account the fact that the individual galaxy motion is not necessarily aligned with the radial direction. Before stacking, the maps were re-scaled with respect to the virial radius of each galaxy, using linear interpolation. This ensures that the stacked image will not be radially smeared due to size inconsistencies. In the main analysis we assumed that we have perfect knowledge of the virial radius, but we also did a smaller analysis consisting of fewer individual stacks than the main analysis, where we included the uncertainties on the virial mass and radius to show that our results are robust to this uncertainty.
The signal from each individual halo was summed up, and divided by the number of halos to achieve an average (or effective) signal. Example realisations of this average signal after stacking 8438 halos are shown in the top row of Fig. 3. The three columns are for three different noise levels: current ACT noise (σΔT/T = 4 × 10−6), a CMB-S4 noise level in the near future (σΔT/T = 1 × 10−6), and a futuristic survey (σΔT/T = 1 × 10−7). We do not vary the resolution between these experiments, because CMB-S4 is expected to have a similar spatial resolution to ACT (1 and a few arcminutes; see Abazajian et al. 2016). The ACT noise level is equivalent to 6 μK arcmin (Hincks et al. 2010), while the CMB-S4 noise level is equivalent to 1.5 μK arcmin, consistent with the ∼1 μK arcmin (Abazajian et al. 2016). The futuristic noise level in the rightmost column is shown to emphasise the expected visual signal if we had sufficiently good statistics, and is not considered realistic in the foreseeable future. The best fit stencil to the low noise stack suggests a signal amplitude of ΔT/T ≈ 3 × 10−9. We are stacking almost 10 000 halos, which is expected to increase the S/N by a factor of 100. The best fit and the residuals are of similar amplitude when the noise per pixel is 10−7, indicating a S/N ∼ 1 after stacking. The stacked signal is expected to be 100 times stronger than the average signal from a single halo, which confirms that an average halo has a signal of the order of ΔT/T ∼ 10−9. The realisation with the “near-future” noise level, shown in the middle column of Fig. 3, also recovers the expected signal with amplitude ΔT/T ≈ 3 × 10−9, but the ACT noise level of 4 × 10−6 results in a S/N that is too low for the fitting algorithm to find a statistically significant dipole pattern in the shown example.
 |
Fig. 3. Example realisations of the stacks (top row), and the residuals (bottom row) after stacking the slingshot signal of 8438 halos and subtracting the best fit. Left panels: noise per pixel of σΔT/T = 4 × 10−6, resembling current surveys. Central panels: “near-future” noise levels of σΔT/T = 1 × 10−6, and rightmost panels: very low noise per pixel (σΔT/T = 1 × 10−7) to visually see the emergence of an image. The individual images are scaled with respect to the virial radius of the halo before stacking. The x- and y-axes are in units of the virial radius of the halo. |
In the main analysis we used a uniform weighting when averaging the stacks. However, the S/N can possibly be improved by choosing a different weighting for the galaxy maps. Specifically the weighting can be chosen in such a way that bigger and faster galaxies contribute more to the stack than smaller and slower galaxies, which add mostly noise. As seen in Fig. 2, the average radial velocity is expected to be greatest around 1 virial radius from the central region of the supercluster, and then to reduce with distance. This suggests the possibility of weighting the galaxies according to distance. Another possibility is to weight them according to their estimated mass. In addition to the main analysis, we performed a small analysis with three weighting schemes. The first weights galaxies according to projected distance from the centre of the supercluster, r⊥ (normalised to the virial radius of the supercluster), with weight 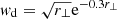 . The second weights galaxies according to the logarithm of the galaxy mass (including a random spread in the halo mass) as wm = log10(Mvir/1010 M⊙). The third weighting scheme combines the distance and mass weighting, wc = wd × wm.
. The second weights galaxies according to the logarithm of the galaxy mass (including a random spread in the halo mass) as wm = log10(Mvir/1010 M⊙). The third weighting scheme combines the distance and mass weighting, wc = wd × wm.
2.4. Observational challenges
The analysis assumes that we can identify 𝒪(104) galaxies near the Coma cluster. The area of the sky where these galaxies can be found is a 40 Mpc radius circle at a distance of 100 Mpc, corresponding to 1400–1500 deg2. There is a possibility that the least massive galaxies will not be visible in the galaxy surveys. The faintest galaxies we studied have a halo mass of 1011 M⊙. To estimate if the observed magnitude of these galaxies can be seen with optical surveys, we assume 1/10 mass in baryons and a mass-to-light ratio of 10 (in Faber & Gallagher 1979 all of the measured galaxies have a mass-to-light ratio lower than 12). This results in a luminosity of 109, and a bolometric magnitude of approximately 19 at the largest distances of up to 200 Mpc. This is within the scope of contemporary surveys like the SDSS. The slingshot signal contribution will be strongest from the most massive galaxies, so missing a few of the faintest galaxies is not expected to change the stack significantly.
To rescale the galaxy maps correctly, we suggest inferring the virial radius from the galaxy virial mass. In many cases when a lensing analysis has not been performed, the total halo mass is not known and must be estimated from the galaxy luminosity. A possibility is to go via the mass of neutral hydrogen (HI), which can be measured from the HI line or estimated from visible light. To distinguish galaxies in the vicinity of the cluster from distant background galaxies, it is important to know the redshift of each galaxy fairly well, within an error of approximately 50%. At a distance of 100 Mpc (corresponding to about z = 0.02), the uncertainty of a measurement of the photometric redshift is σz ≳ 0.03 (Bolzonella et al. 2000). This implies that we need spectroscopic data for all the galaxies used in the stacking process.
Several of the above problems can be partially solved if we consider data from the upcoming Square Kilometre Array (SKA) phase 2, expected to be online in 2030 (Bull 2016). SKA is a planned full-sky spectroscopic survey, and Norris et al. (2014) suggest that it is expected to identify the position and redshift of all galaxies of the relevant magnitudes up to z = 0.05. We expect SKA to find the HI mass of all viable slingshot galaxies with fair certainty.
Whether using data from SKA or the SDSS, the biggest source of error when estimating the virial radius is the conversion from HI mass to halo mass. Villaescusa-Navarro et al. (2018) and Padmanabhan & Kulkarni (2017) both indicate a spread of about one order of magnitude in the halo mass for a given HI mass. We did not include this error when rescaling the individual maps in the main analysis, but we performed a separate smaller analysis where we included the corresponding error in virial radius. We find that the error in rescaling of the virial radius does not induce a bias, and does not significantly increase the uncertainty of the results. We expand upon this in the results section (Sect. 4).
In this analysis, we assumed that the CMB behind the galaxies is known and can be subtracted. If there are no other significant contributions between the surface of last scattering and the observed galaxy, the CMB is a Gaussian random field with a standard deviation in ΔT/T of σΔT/T = 10−4. By masking out the signal surrounding the galaxy, the CMB signal from the external area can be interpolated it into the masked region (see e.g. Bucher & Louis 2012 for an example prescription to fill in masked regions of the CMB map). Subtracting the expected interpolated CMB from the actual observed signal will leave signal and noise, without the CMB perturbations. Likewise, the galaxy itself, lensing of gradients in the CMB, and foreground sources can outshine the dipole signal from the slingshot effect. None of these effects are expected to give a dipole correlated with the infall velocity, so the process of stacking in itself should suppress any apparent signals from other sources.
3. Statistical analysis
For realistic noise levels of 10−6 and above, it is impossible to see the dipole fit by eye. We compared the stacked image to the model in Eq. (5), using a least-squares method with two free parameters. The two free parameters used in the fit are the combination mvx/rvir, which gives the amplitude of the signal, and an image-smoothing radius rsmooth, which is related to the instrument beam. When stacking images that are re-scaled with respect to their radius, the stack will consist of images with different effective beam widths. The resulting merged image is not exactly equivalent to a dipole signal with a single-Gaussian smoothing like the one we apply in our least-squares procedure. We find that fitting the stencil with a single effective smoothing radius consistently overestimates the signal by 3–4%. This can be avoided by choosing a different stencil, for instance pre-generating a stencil from a stack of noiseless smoothed maps.
In the following sections we introduce measurements of the quality of the fit and amplitude of the signal. We also show that these two quantities can be combined into a single estimator that can be used to distinguish a true detection from a false positive.
3.1. Lower bound on the dipole amplitude
If the best fit of a stack corresponds to a very low amplitude mvx/rvir, it is indistinguishable from zero amplitude. A detection limit for this number should be estimated based on the error bars of the data, and on the expected masses and velocities of the stacked galaxies. This limit will therefore depend on the mass and structure of the central supercluster and on the precision of data in the galaxy catalogue in the real-world scenario. The least-squares method we applied has discrete values for the combination mvx/rvir. This means that below some threshold value, the amplitude will be rounded down to zero in our implementation. We chose this value conservatively in a way that does not significantly impact the results.
In our case, the average expected velocity is 𝒪(100) km s−1 (as seen in Fig. 2), and the average galaxy mass is 1.8 × 1012 M⊙. To be conservative, we set the threshold for a zero amplitude detection corresponding to a 1012 M⊙ galaxy, moving at less than 10 km s−1. This choice is arbitrary and different values can be chosen when handling actual observations. The chosen threshold is equivalent to a factor of about 0.05 of the expected value for mvx/rvir. This does not mean that we ignore individual images of galaxies that are smaller or slower than this threshold. We stacked all galaxies, and considered the stacked signal to have zero amplitude if the best fit indicates that the average value for mvx/rvir is less than ∼5% of the expected average.
3.2. Quality of fit
For each stack d we found the best fit template t with a least-squares method. The template t is a smoothed image of the pure slingshot signal (Eq. (5)). Both d and t are column vectors containing each pixel of the stacked image and the best fit template. To gauge the quality of the fit, we calculated the normal equations
where tT is a row vector equivalent to the transpose of t. This statistic is related to the χ2-statistic. If you imagine the t and d vectors of dimension n = nx × ny (with nx and ny being the amount of pixels in the x- and y-direction of the map, respectively), the q statistic is equivalent to the Euclidean dot product between the data and the template, normalised to the length of the expected template vector. The result is equal to 1 if the two vectors are of equal length and parallel to each other, and 0 if they are orthogonal. Calculating q is equivalent to summing up the pixel-by-pixel product of stack and template (vector dot product), and normalising to the squared norm of the template.
A true fit of a stack with a slingshot signal, like the ones shown in Fig. 3, gives q ≈ 1 if the noise is low. Fitting a template when no signal is present gives q ≈ 0. The probability distribution of the best fit q has a spread, which widens with higher noise levels. In practice it is possible to get q > 1 if the stack data d is parallel and has a bigger amplitude than the template t. It is also possible to get q < 0 if the dot product is negative (i.e. when the vectors are anti-parallel). Both of these options are worse quality fits than q = 1.
3.3. Combined statistic to identify false positives
In addition to the possibility of a low quality fit when the signal is present, there is also a chance for the algorithm to detect a signal in pure noise with no actual signal present. We call such a detection a false positive. We consider a signal to be a proper detection if two conditions are met simultaneously: the quality of fit q is close to 1, and the fitted amplitude of the combination mvx/rvir is close to the expected amplitude. We consider a signal to be a bad detection if the best fit amplitude is low or if the quality of fit q is small (or negative). To take into account both of these measures of the detection level, we define a combined statistic,
The B statistic combines both qualities we are interested in when looking for a good detection: a significant amplitude for the fitted dipole, and a decent quality of the fit. We made a probability distribution of the outcome for measurements of B given a specific noise level by creating several real stacks and several false stacks (with no dipole signal). We created several realisations of the real stack, by repeating the pipeline described in Sect. 2.3, but using a different random seed for the noise for each realisation. We also created several false stacks, where each of the stacks consists of images of the 8438 halos in our selection. The individual images pass through the same pipeline as the real stacks, but without the addition of the slingshot dipole. Each image consists purely of the per-pixel noise, and is later smoothed and re-scaled with respect to the expected virial radius of the halo.
For each realisation we calculated B, and combined the data from all samples to find a probability distribution for B. If there is significant overlap between the probability distributions from the stacks with a signal and without a signal, it is impossible to distinguish whether an observed stack contains a signal or not. If the distributions are sufficiently separated along B, the probability of a strong observed signal being a false positive is small, hence we can distinguish a true signal from a false positive.
4. Results
In this section, we first discuss the probability of a statistically significant detection, with current and future surveys. Then we present results from our smaller sets of test analyses, where we estimate the bias from having an uncertainty in the assumed virial radius of a galaxy, and evaluate the effectivity of our weighting schemes. Finally we consider how the results apply to modified gravity.
4.1. Detection probability
Histograms of B/Bexpected are shown in Fig. 4. The three panels correspond to the distributions found from stacks with 4 × 10−6, 1 × 10−6, and 1 × 10−7 noise, respectively. The histograms emerging from multiple realisations of the stack can be interpreted as an estimate of the probability distribution of measuring a certain value of B, given a known noise level. The orange histograms are for stacks of pure noise, while the blue histograms are for stacks of signal and noise. The values are binned in evenly spaced bins from B = 0 to B/Bexpected = 5. The expected value, Bexpected, is found by assuming q = 1 and taking the average mvx/rvir in the sample. The average mass of the halos in our sample is 1.79 × 1012 M⊙, the average radial infall velocity is 675 km s−1, and the average virial radius is 196 kpc. For the galaxies around the simulated supercluster we study, we find the value
 |
Fig. 4. Histogram of the B statistic from stacks of pure noise (orange) and of signal plus noise (blue). The three panels correspond to 4 × 10−6, 1 × 10−6, and 1 × 10−7 noise levels (from left to right). Values of B below 0 are not plotted. |
In the realisations with 4 × 10−6 noise, the histograms of the stacks with signal and with pure noise overlap significantly, and the probability of observing a value we can distinguish from noise is low. For near-future noise levels of 1 × 10−6, the situation is better. The mean value for B when no signal is present is about three standard deviations lower than the mean value for B with signal. This suggests a very good probability of measuring a value of B high enough to be reasonably sure it is not from noise. In the futuristic noise realisations, the histograms do not overlap at all, meaning that in this theoretical scenario we can always distinguish the existence of a signal from a case with no signal.
We present data for the different runs in Table 1. P(ND) is the probability of a non-detection. The chance of a non-detection is calculated as the probability for a given stack to be indistinguishable from B = 0 within one standard deviation. For noise levels of 4 × 10−6, we find a 45% probability for non-detections among the stacks that include a signal. This means that, even with current experiments, there is a better than 50–50 chance of achieving a fit that is distinguishable from zero. For the near-future noise levels, we get very few non-detections in the stacks that include an actual signal. However, because pure noise can also lead to a detection, we must also consider the chance of a false positive before labelling any detection above the threshold a true detection.
Details of the analysis of the simulated stacks.
The mean B shown in the table is normalised with respect to the expected value of B for the galaxies in the sample (i.e. the shown B is divided by Bexpected from Eq. (12)). Specifically, unbiased measurements of the normalised B have an expected mean of B = 1 when the dipole signal is present, and 0 when there is only noise. The amplitude mv/rvir of the signal is also normalised with respect to the expected amplitude, (mv/rvir)expected, which has the same value as Bexpected. The column labelled 95 OSCI contains the lower 95% one-sided confidence interval, or the 5th percentile of B/Bexpected; 95% of all stacks in this set of stacks has a B above this level. The probability of a false positive, P(FP), is shown in the last column of Table 1. This probability is found by computing what percentage of the stacks with pure noise, no signal, and that give a value of B that falls above the 5th percentile we would expect if there were a signal. Specifically, P(FP) = P(Bno−signal > B95 OSCI), where Bno−signal is B in a stack with pure noise, and B95 OSCI is the lower 95% OSCI for B in the stacks with signal.
A conservative estimate for the chances of measuring a false positive can be found in the rightmost column of Table 1. We focus on the results for the near future experiments with 1 × 10−6 noise. A true stack with this noise level has B/Bexpected > 0.661 with 95% confidence. If there is no signal in the stacks, the chance of getting B/Bexpected > 0.661 is just 2.89%. This means that with CMB-S4 we can distinguish the slingshot signal from pure noise with P < 0.05 certainty. Furthermore, if the signal is present in near-future observations, we should also be able to put error bars on the measurement of the combination mv/rvir because the expected value for this combination is approximately three standard deviations away from zero.
4.2. Testing assumptions and weighting schemes
We repeated four sets of a smaller analysis, where each set includes 5000 realisations of the stack instead of the 20 000 realisations used in the main analysis. One of the sets includes a random error in the assumed virial masses, which induces an error in the virial radius when assuming 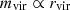 . The result of including this error is that the stack is slightly smeared, but the dipole stencil still clearly detects the signal. For the 10−6 noise level simulations, the chance of detecting a false positive increases from 2.89% to 4.06%, and the standard deviation of the recovered mv/rvir increases slightly. The detection is still greater than two sigma significance, indicating that the analysis is robust to the possible error in estimated virial radius.
. The result of including this error is that the stack is slightly smeared, but the dipole stencil still clearly detects the signal. For the 10−6 noise level simulations, the chance of detecting a false positive increases from 2.89% to 4.06%, and the standard deviation of the recovered mv/rvir increases slightly. The detection is still greater than two sigma significance, indicating that the analysis is robust to the possible error in estimated virial radius.
The other three sets of analyses include the three non-uniform weighting schemes described in Sect. 2.3. The distance-based weighting scheme, 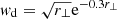 , has a maximum weight at 1.67 virial radius of the cluster. This weighting increases the signal by 5%, but also increases the averaged noise level similarly. The averaged noise increases when using a weighted average instead of uniform weights because the galaxies that are suppressed contribute less to the cancellation of noise. Other weighting schemes for distance are not considered, but the studied one does not improve the S/N according to our analysis. Even if the S/N does not improve, a benefit of this method is that we do not need to put in a sharp distance cut-off by hand, but rather we can tune the slope of the weighting function.
, has a maximum weight at 1.67 virial radius of the cluster. This weighting increases the signal by 5%, but also increases the averaged noise level similarly. The averaged noise increases when using a weighted average instead of uniform weights because the galaxies that are suppressed contribute less to the cancellation of noise. Other weighting schemes for distance are not considered, but the studied one does not improve the S/N according to our analysis. Even if the S/N does not improve, a benefit of this method is that we do not need to put in a sharp distance cut-off by hand, but rather we can tune the slope of the weighting function.
We also used a mass-based weighting scheme, with wm = log10(Mvir/1010 M⊙). This weighting increases the S/N significantly by weighting massive galaxies more than light galaxies. The expected detection of the slingshot signal with 10−6 noise level increases from 3σ to 5σ, and the chance of a false positive decreases from 2.89% to 0.02%. This suggests that a mass-based weighting scheme should be considered when using real observations. The final weighting scheme we tested is a combination of the distance- and mass-based weighting scheme, but it does not improve the results over the pure mass-based weighting scheme. A possible method for defining a more optimal weighting scheme in a future analysis is via matched filtering. For the noise levels of current surveys (4 × 10−6), the mass weighting does not increase the S/N sufficiently to avoid the confusion with false positives.
4.3. Applications to modified gravity
When using the method discussed in this paper, we estimate an average mvx/rvir of infalling galaxies around a cluster. This can be combined with other observables, like the velocity along the line of sight and the inferred halo mass from lensing. Compared with such additional data, the slingshot effect can be used as an independent probe of modified gravity. Many scalar–tensor theories will increase the clustering on scales of kiloparsecs to megaparsecs. For instance, the Chameleon model studied by Brax et al. (2013) shows increased clustering. If the modifications apply on galaxy scales, each galaxy can be more massive and more dense. If the modifications apply on megaparsec scales, galaxies will fall faster due to the fifth forces on large scales (Ivarsen et al. 2016). Both of these effects would increase the expected slingshot signal with respect to a similar scenario in ΛCDM, making it a possible probe for enhanced gravity over several different scales. Because the method described in this paper only measures the combination mvx/rvir, the separate effects of higher infall velocity and higher galaxy density are degenerate.
From the halo mass function of the pure Symmetron case in Hagala et al. (2016), we find that in a typical Symmetron scenario, the individual galaxies will have a 20% increase in mass. Assuming a 10% increase in infall velocity3, we estimate that the average mvx/rvir at redshift zero can increase by about 30% relative to GR. In the case of uniform weighting of the galaxy maps and 10−6 noise level, this increase is equivalent to the one standard deviation measurement error on the slingshot signal.
We find that the average mvx/rvir amongst the 4700 most massive clusters in the simulated catalogue has a standard deviation similar to the average of mvx/rvir. This means that, even in the context of ΛCDM, the amplitude of the slingshot signal around a single cluster is not decided by the mass of the cluster alone, but also by a combination of the surrounding large-scale structure and the merger history of the cluster. Unless we know such specifics about the studied cluster, we would need to observe ∼36 clusters to reduce the error of the mean for the “universal” mvx/rvir with a factor 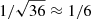 . If we can do this, the uncertainty of our measurements can be low enough for us to begin distinguishing gravitational models like the Symmetron from pure ΛCDM, with two sigma significance. Better knowledge of the mass distribution of the surroundings of the cluster and a better weighting scheme for the stacking of galaxy maps can both reduce the number of clusters needed to distinguish between different gravitational models.
. If we can do this, the uncertainty of our measurements can be low enough for us to begin distinguishing gravitational models like the Symmetron from pure ΛCDM, with two sigma significance. Better knowledge of the mass distribution of the surroundings of the cluster and a better weighting scheme for the stacking of galaxy maps can both reduce the number of clusters needed to distinguish between different gravitational models.
5. Conclusion
In this paper, we present a method for detecting transverse motions of galaxies by stacking the dipole signal of the slingshot effect. For this method to work we need to be able to identify a preferential direction to align the galaxies along their expected direction of motion. This can be done by taking into account galaxies that either fall into clusters or move away from the centre of the voids. We show a detection strategy for galaxies falling into a nearby cluster, like the Coma Cluster. A similar analysis can be performed for galaxies around voids.
The possibility of detecting the signal with certainty with CMB-S4 experiments is very high. There are some simplifications in this paper that should be considered more thoroughly when analysing real data. The most important considerations relate to the choice of cut-off in halo mass, and the cut-off in distance from the central cluster. We use a mass cut-off of M > 1011 M⊙ when considering a halo for stacking. A cut-off that is too low means adding mostly noise for each image, while a mass cut-off that is too high gives fewer halos to stack. Furthermore, we do not include an upper mass limit. This means that in practice we are stacking the dark matter halos of some smaller galaxy clusters as well as individual galaxies. Choosing the halo mass cut-offs in a more sophisticated way (e.g. using a weighting scheme) could improve the signal. Increasing the distance within which to consider infalling galaxies will allow us to include more galaxies and could result in better statistics. An inner radius cut-off can also be considered, since galaxies within approximately one virial radius of the cluster do not appear to have a preferred radial direction. When excluding these galaxies, a better signal can be expected. Another option is to use a distance-based weighting scheme instead of a hard cut-off. We tested a simple distance-based weighting scheme, which does not impact the S/N significantly. We also tested a mass-based weighting scheme, which we find to increase the S/N by weighting massive galaxies more than light galaxies. When used on real data, this weighting scheme can be more or less efficient depending on the confidence of the mass estimates in the galaxy catalogue.
In this paper, we stacked the CMB maps centred on 𝒪(104) simulated galaxies, and oriented them according to their expected infall direction towards a nearby massive cluster. By fitting a dipole template to the stacked signal, we show that the slingshot effect is statistically distinguishable from noise when using the next generation of CMB experiments. By measuring the slingshot signal around ∼36 clusters, we can constrain the signal sufficiently to test alternative theories for gravity.
For all Symmetron models except the one with the weakest coupling, Ivarsen et al. (2016) found a >10% increase in pairwise velocities.
Acknowledgments
We would like to thank several people at the Institute of Theoretical Astrophysics in Oslo for their ideas and comments, especially: Håkon Dahle, Hans Kristian Eriksen, Marta Bruno Silva, Håvard Tveit Ihle, Øyvind Christiansen, and Daniel Heinesen. A great thanks to Sigurd Kirkevold Næss for helping with technical details. Many thanks for detailed and helpful comments and questions from the referee, which helped strengthen the paper significantly. We thank the Research Council of Norway for their support. This paper is based upon work from the COST action CA15117 (CANTATA), supported by COST (European Cooperation in Science and Technology). The CosmoSim database used in this paper is a service by the Leibniz-Institute for Astrophysics Potsdam (AIP). The MultiDark database was developed in cooperation with the Spanish MultiDark Consolider Project CSD2009-00064.
References
- Abazajian, K. N., Adshead, P., Ahmed, Z., et al. 2016, CMB-S4 Science Book, 1st edn. [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Wu, H. Y. 2013, ApJ, 762, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Birkinshaw, M., & Gull, S. F. 1983, Nature, 302, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Miralles, J.-M., & Pello’, R. 2000, A&A, 363, 476 [NASA ADS] [Google Scholar]
- Brax, P., Davis, A. C., Li, B., Winther, H. A., & Zhao, G. B. 2013, JCAP, 4, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Bucher, M., & Louis, T. 2012, MNRAS, 424, 1601 [Google Scholar]
- Bull, P. 2016, ApJ, 817, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., & Gallagher, J. S. 1979, ARA&A, 17, 135 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gould, A. 1994, Transverse Velocities of Galaxies From Microlens Parallaxes [Google Scholar]
- Hagala, R., Llinares, C., & Mota, D. 2016, A&A, 585, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernquist, L. 1990, The Analytical Model for Spherical Galaxies and Bulges, Tech. rep. [Google Scholar]
- Hincks, A. D., Acquaviva, V. R., Ade, P. A., et al. 2010, The Atacama Cosmology Telescope (ACT): Beam Profiles and First SZ cluster Maps, Tech. rep. [Google Scholar]
- Hotinli, S. C., Meyers, J., Dalal, N., et al. 2018, Transverse Velocities with the Moving Lens Effect [Google Scholar]
- Ivarsen, M. F., Bull, P., Llinares, C., & Mota, D. F. 2016, A&A, 595, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kravtsov, A. V. 2013, ApJ, 764, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Kubo, J. M., Stebbins, A., Annis, J., et al. 2007, ApJ, 671, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, M. C., & Graham, J. R. 2002, ApJ, 557, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Łokas, E. L., & Mamon, G. A. 2001, MNRAS, 321, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Manzotti, A. 2018, Phys. Rev. D, 97, 043527 [NASA ADS] [CrossRef] [Google Scholar]
- Maturi, M., Dolag, K., Waelkens, A., Springel, V., & Ensslin, T. 2007a, A&A, 476, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maturi, M., Enßlin, T., Hernández-Monteagudo, C., & Rubiño-Martín, J. A. 2007b, A&A, 467, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molnar, S. M., Broadhurst, T., Umetsu, K., et al. 2013, ApJ, 774, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., White, S. D. M., & Fellow, B. J. B. 1995, The Structure of Cold Dark Matter Halos, Tech. rep. [Google Scholar]
- Norris, R. P., Basu, K., Brown, M., et al. 2014, Proceedings of Science, 9–13 June 2014 [Google Scholar]
- Padmanabhan, H., & Kulkarni, G. 2017, MNRAS, 470, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Prada, F., Klypin, A. A., Cuesta, A. J., Betancort-Rijo, J. E., & Primack, J. 2012, MNRAS, 423, 3018 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., & Sciama, D. W. 1968, Nature, 217, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Sachs, R. K., & Wolfe, A. M. 1967, Gen. Relativ. Grav., 39, 1929 [NASA ADS] [CrossRef] [Google Scholar]
- Stebbins, A. 2006, New Astron. Rev., 50, 918 [NASA ADS] [CrossRef] [Google Scholar]
- Villaescusa-Navarro, F., Genel, S., Castorina, E., et al. 2018, ApJ, 866, 1538 [Google Scholar]
- Yasini, S., Mirzatuny, N., & Pierpaoli, E. 2018, Pairwise Transverse Velocity Measurement with the Rees-Sciama Effect, Tech. rep. [Google Scholar]
Appendix A: Calculation of slingshot effect from a spherical halo model
We have that
Since gravitational potentials are additive, we will have a contribution from the NFW dark matter profile and from the Hernquist profile:
We now calculate these integrals separately. In principle the integral limits is from the surface of last scattering and until today, but as long as the kernel we are integrating peaks around z = 0, we can safely integrate from z = −∞ to z = ∞ instead.
NFW
From ᴌokas & Mamon (2001), the gravitational potential of the NFW halo is given by
where cNFW is the concentration (we assume cNFW = 15) and
Substituting 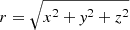 , we can do the derivative with respect to x,
, we can do the derivative with respect to x,
We can find the indefinite integral
We are interested in evaluating this integral with limits z = −∞ and z = ∞. We start by finding the limits of the arctangent expressions. We use that limx → ±∞ arctan (x) = ±π/2, and find that the first arctangent has the limit
and similarly
To evaluate the limits of the second arctangent, we note that
This leaves us with the following arguments for the second arctangent:
Regarding the logarithmic expressions, the limit at z → ∞ is
The limit of the logarithmic terms when z → −∞ is
where we use that 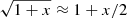 for small x.
for small x.
Combining all of these, we are left with
Here, we have defined
Hernquist
The gravitational potential of a Hernquist halo with mass m is simply given by
where a is a scale length, which is related to the half-mass radius as 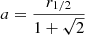 . We chose r1/2 = 0.015rvir based on Fig. 1 from Kravtsov (2013), where the data indicates r1/2 ≈ 0.015r200c.
. We chose r1/2 = 0.015rvir based on Fig. 1 from Kravtsov (2013), where the data indicates r1/2 ≈ 0.015r200c.
The derivative with respect to the x coordinate is
which results in the following indefinite integral along z:
We chose to define
which does not depend on z.
The limits of the first term when z → ±∞ are
and
The limits of the second term are
and
The last arctangent converges to ±π/2, giving
and
Finally, the slingshot integral for the Hernquist distribution can be written
Sum
Because we are assuming that the total mass mDM of the dark matter halo is in the NFW component, with an additional mDM/10 in baryons, we write the combined effect as
Here, we use the following notation for dimensionless coordinates: xr ≡ x/rvir and xa ≡ x/a. Furthermore,
and
The factor of 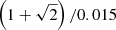 is to convert from the Hernquist scale a to rvir. We repeat the definitions
is to convert from the Hernquist scale a to rvir. We repeat the definitions
We note that S and U can become imaginary for light passing close to the centre of the halo. Specifically, both U and S are ∈[−i,−∞i). However, z(2×arctan(z)−π) always has one real value, even for imaginary z.
Proof: For a real x > 1, it follows that z = −ix is negative imaginary with the same domain as U and S. Using the logarithm definition of the complex arctangent, we have
In the last line, we used the fact that for complex logarithms, ln(z) = ln(−z) + πi. Furthermore, any addition of 2πi can be cancelled by the corresponding free choice of 2kπi in the multi-valued complex logarithm. With x > 1, this result proves that there is always a real branch of the expression z(2×arctan(z)−π). This expression is also continuous for values of r2 = x2 + y2 crossing through the singularity in U or S.
All Tables
All Figures
 |
Fig. 1. Contour plot of the temperature dipole created by the slingshot effect. The arrow indicates the direction of motion of the galaxy. An increase in photon temperature is indicated in red; a decrease in temperature is illustrated in blue and with dashed contours. This example is a galaxy of virial mass 1.2 × 1012 M⊙, moving with a transverse velocity component of 880 km s−1, viewed at a distance of 100 Mpc. |
| In the text | |
 |
Fig. 2. Scatter plot of the projected radial motion of halos close to the massive supercluster. The horizontal axis shows the projected distance from the centre of the structure (in units of the virial radius of the supercluster). The vertical axis shows the projected radial velocity of the halo in question; positive values indicate infalling motion. The red line shows the binned mean. The error of the mean is consistent with the width of the line. The colour of a point indicates the virial mass of that halo. |
| In the text | |
 |
Fig. 3. Example realisations of the stacks (top row), and the residuals (bottom row) after stacking the slingshot signal of 8438 halos and subtracting the best fit. Left panels: noise per pixel of σΔT/T = 4 × 10−6, resembling current surveys. Central panels: “near-future” noise levels of σΔT/T = 1 × 10−6, and rightmost panels: very low noise per pixel (σΔT/T = 1 × 10−7) to visually see the emergence of an image. The individual images are scaled with respect to the virial radius of the halo before stacking. The x- and y-axes are in units of the virial radius of the halo. |
| In the text | |
 |
Fig. 4. Histogram of the B statistic from stacks of pure noise (orange) and of signal plus noise (blue). The three panels correspond to 4 × 10−6, 1 × 10−6, and 1 × 10−7 noise levels (from left to right). Values of B below 0 are not plotted. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



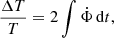
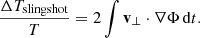
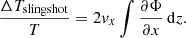
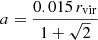
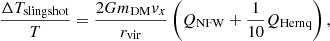
![$$ \begin{aligned} Q_{\mathrm{NFW} }\equiv \frac{{g}x_r}{x_r^{2}+{ y}_r^{2}} \left[ \ln \left(\frac{c_\mathrm{NFW} ^{2}\left(x_r^{2}+{ y}_r^{2}\right)}{4}\right) -S\left(2\arctan \left(S\right) - \pi \right) \right], \end{aligned} $$](/articles/aa/full_html/2019/08/aa35261-19/aa35261-19-eq6.gif)
![$$ \begin{aligned} Q_{\mathrm{Hernq} }\equiv \left( \frac{1 + \sqrt{2}}{0.015} \right) \frac{x_a}{x_a^2 + { y}_a^2 - 1} \left[ 2 +U\left( 2\arctan \left(U\right) -\pi \right) \right]. \end{aligned} $$](/articles/aa/full_html/2019/08/aa35261-19/aa35261-19-eq7.gif)
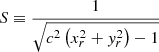
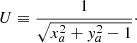
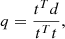
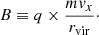
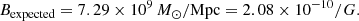
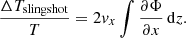
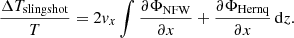
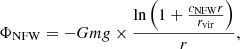
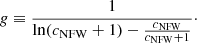
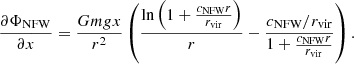

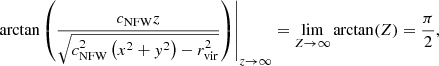
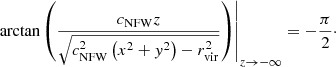
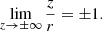
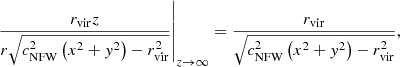
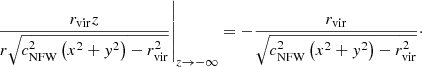
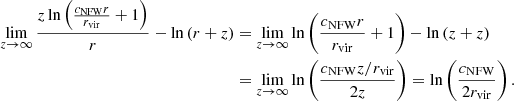
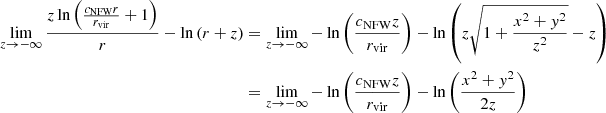
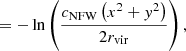
![$$ \begin{aligned} \int_{-\infty }^{\infty }\frac{\partial \Phi _{\mathrm{NFW} }}{\partial x}\mathrm{d} z&=\frac{Gm{g}x}{x^{2}+{ y}^{2}} \left[ S\left(\pi -2\arctan \left(S\right)\right)+\ln \left(\frac{c_\mathrm{NFW} ^{2}\left(x^{2}+{ y}^{2}\right)}{4r_\mathrm{vir} ^{2}}\right) \right] . \end{aligned} $$](/articles/aa/full_html/2019/08/aa35261-19/aa35261-19-eq33.gif)
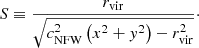
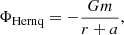
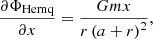
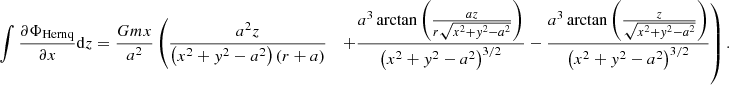
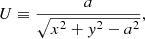
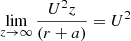
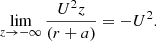
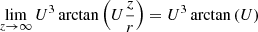
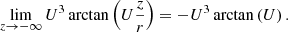
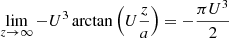

![$$ \begin{aligned} \int_{-\infty }^{\infty }\frac{\partial \Phi _{\mathrm{Hernq} }}{\partial x}\mathrm{d} z=Gmx \frac{U^2}{a^2} \left( 2 +U\left[ 2\arctan \left(U\right) -\pi \right] \right). \end{aligned} $$](/articles/aa/full_html/2019/08/aa35261-19/aa35261-19-eq46.gif)
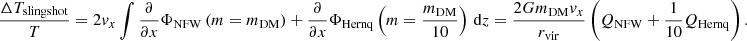
![$$ \begin{aligned} Q_{\mathrm{NFW} }\equiv \frac{gx_r}{x_r^{2}+{ y}_r^{2}} \left[ \ln \left(\frac{c_\mathrm{NFW} ^{2}\left(x_r^{2}+{ y}_r^{2}\right)}{4}\right) -S\left(2\arctan \left(S\right) - \pi \right) \right], \end{aligned} $$](/articles/aa/full_html/2019/08/aa35261-19/aa35261-19-eq48.gif)
![$$ \begin{aligned} Q_{\mathrm{Hernq} }\equiv \left( \frac{1 + \sqrt{2}}{0.015} \right) \frac{x_a}{x_a^2 + { y}_a^2 - 1} \left[ 2 +U\left( 2\arctan \left(U\right) -\pi \right) \right]. \end{aligned} $$](/articles/aa/full_html/2019/08/aa35261-19/aa35261-19-eq49.gif)