| Issue |
A&A
Volume 628, August 2019
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 15 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201834665 | |
| Published online | 02 August 2019 | |
2D chemical evolution model: The impact of Galactic disc asymmetries on azimuthal chemical abundance variations
1
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
e-mail: spitoni@phys.au.dk
2
I.N.A.F. Osservatorio Astronomico di Trieste, Via G.B. Tiepolo 11, 34131 Trieste, Italy
3
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
4
Dipartimento di Fisica, Sezione di Astronomia, Università di Trieste, Via G. B. Tiepolo 11, 34143 Trieste, Italy
5
Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
6
Dipartimento di Fisica, Università di Roma Tor Vergata, Via della Ricerca Scientifica 1, 00133 Rome, Italy
7
I.N.A.F. Osservatorio Astronomico di Roma, Via Frascati 33, 00078 Monte Porzio Catone, Italy
Received:
16
November
2018
Accepted:
24
June
2019
Context. Galactic disc chemical evolution models generally ignore azimuthal surface density variation that can introduce chemical abundance azimuthal gradients. Recent observations, however, have revealed chemical abundance changes with azimuth in the gas and stellar components of both the Milky Way and external galaxies.
Aims. Our aim is to quantify the effects of spiral arm density fluctuations on the azimuthal variations of the oxygen and iron abundances in disc galaxies.
Methods. We developed a new 2D Galactic disc chemical evolution model that is capable of following not just radial but also azimuthal inhomogeneities.
Results. The density fluctuations resulting from a Milky Way-like N-body disc formation simulation produce azimuthal variations in the oxygen abundance gradients of the order of 0.1 dex. Moreover, the azimuthal variations are more evident in the outer Galactic regions, which is in agreement with the most recent observations in external galaxies. Using a simple analytical model, we show that the largest fluctuations with azimuth result near the spiral structure co-rotation resonance where the relative speed between the spiral and gaseous disc is the slowest.
Conclusion. We provide a new 2D chemical evolution model capable of following azimuthal density variations. Density fluctuations extracted from a Milky Way-like dynamical model lead to a scatter in the azimuthal variations of the oxygen abundance gradient, which is in agreement with observations in external galaxies. We interpret the presence of azimuthal scatter at all radii by the presence of multiple spiral modes moving at different pattern speeds, as found in both observations and numerical simulations.
Key words: Galaxy: evolution / Galaxy: disk / stars: abundances / ISM: abundances
© ESO 2019
1. Introduction
In recent years, integral field spectrographs (IFSs) have largely substituted long-slit spectrographs in studies designed to characterise the abundance distribution of chemical elements in external galaxies. Also for the first time, IFSs have allowed abundances throughout the entire 2D extent of a galaxy to be measured (or a large part thereof), thus the detection of azimuthal and radial trends is possible (Vogt et al. 2017).
Several contemporary observational works have found evidence of significant azimuthal variations in the abundance gradients in external galaxies. Sánchez et al. (2015) and Sánchez-Menguiano et al. (2016) analysed the chemical inhomogeneities of the external galaxy NGC 6754 with the Multi Unit Spectroscopic Explorer (MUSE) in detail. They conclude that the azimuthal variations of the oxygen abundances are more evident in the external part of the considered galaxy.
Vogt et al. (2017) studied the galaxy HCG 91c with MUSE and arrive at the conclusion that the enrichment of the interstellar medium proceeds preferentially along spiral structures and less efficiently across them. Azimuthal variations have been detected in the oxygen abundance that is also in the external galaxy M 101 by Li et al. (2013). Ho et al. (2017) present the spatial distribution of oxygen in the nearby spiral galaxy NGC 1365. This galaxy is characterised by a negative abundance gradient for oxygen along the disc. However, systematic azimuthal variations of ∼0.2 dex occur over a wide radial range of galactic radii and peak at the two spiral arms in NGC 1365. In the same work, the authors present a simple chemical evolution model to reproduce the observations. Azimuthal variations can be explained by the following two physical processes: after a local self-enrichment phase in the inter-arm region, and a consequent mixing and dilution phase that is si dominant on a larger scale (kpc scale) when the spiral density waves pass through.
Probing azimuthal inhomogeneities of chemical abundances has also been attempted in the Milky Way system. Balser et al. (2011), while measuring HII region oxygen abundances, found that the slopes of the gradients differ by a factor of two in their three Galactic azimuth angle bins. Moreover, significant local iron abundance inhomogeneities have also been observed with Galactic Cepheids (Pedicelli et al. 2009; Genovali et al. 2014).
Balser et al. (2015) underline the importance of azimuthal metallicity structure in the Milky Way disc making, for the first time, radio recombination line and continuum measurements of 21 HII regions located between Galactic azimuth ϕ = 90°–130°. The radial gradient in [O/H] is −0.082 ± 0.014 dex kpc−1 for ϕ = 90°–130° and about a factor of two higher than the average value between ϕ = 0°–60°. It was suggested that this may be due to radial mixing from the Galactic Bar.
Analyzing the Scutum red-supergiant (RSG) clusters at the end of the Galactic Bar, Davies et al. (2009) conclude that a simple 1D parameterisation of the Galaxy abundance patterns is insufficient at low Galactocentric distances, as large azimuthal variations may be present. Combining these results with other data in the literature points towards large-scale (∼kpc) azimuthal variations in abundances at Galactocentric distances of 3−5 kpc. Therefore, it appears that the usual approximation of chemical evolution models, assuming instantaneous mixing of metallicity in the azimuthal direction, is unsubstantiated.
Azimuthal abundance gradients due to radial migration in the vicinity of spiral arms in a cosmological context have been studied in detail by Grand et al. (2012, 2014, 2016) and Sánchez-Menguiano et al. (2016). Alternatively, Khoperskov et al. (2018) investigated the formation of azimuthal metallicity variations in the discs of spiral galaxies in the absence of initial radial metallicity gradients. Using high-resolution N-body simulations, they modelled composite stellar discs, made of kinematically cold and hot stellar populations, and studied their response to spiral arm perturbations. They find that azimuthal variations in the mean metallicity of stars across a spiral galaxy are not necessarily a consequence of the reshaping of an initial radial metallicity gradient by radial migration. They also arise naturally in stellar discs that only have a negative vertical metallicity gradient at the beginning.
The aim of this paper is to develop a detailed 2D Galactic disc chemical evolution model that is able to follow the evolution of several chemical elements, as in previous 1D models, and also take azimuthal surface density variations into account. In this the paper, when we refer to the thin and thick discs, we mean the low- and high-[α/Fe] sequences in the [α/Fe]-[Fe/H] plane. Defining the thin and thick discs morphologically, rather than chemically, identifies a mixture of stars from both the low- and high-[α/Fe] sequences, and vise versa (Minchev et al. 2015; Martig et al. 2016). It is, therefore, very important to make this distinction in order to avoid confusion. We follow the chemical evolution of the thin disc component, that is the low-α population. We assume that the oldest stars of that low-α component are associated with ages of ∼11 Gyr, which is in agreement with asteroseismic age estimates (Silva Aguirre et al. 2018).
The classical 1D Matteucci & François (1989) approach assumes the Galactic disc is formed by an infall of primordial gas. For our purposes, we started by including 2D surface density fluctuation in the Milky Way disc chemo-dynamical model by Minchev et al. (2013, hereafter MCM13). We also used analytical spiral arm prescriptions.
Our paper is organised as follows: in Sect. 2, we describe the framework used for the new model. In Sect. 2.1, the adopted nucleosynthesis prescriptions are reported. In Sect. 2.2, the density fluctuation from the chemo-dynamical model by MCM13 are indicated. In Sect. 2.3, we present the analytical expressions for the density perturbations due to Galactic spiral arm. In Sect. 3, we present our results with the density fluctuation from chemo-dynamical models and with an analytical spiral arm prescription are reported. Finally, our conclusions are drawn in Sect. 4.
2. A 2D Galactic disc chemical evolution model
The basis for the 2D chemical evolution model we develop in this section is the classical 1D Matteucci & François (1989) approach, in which the Galactic disc is assumed to be formed by an infall of primordial gas. The infall rate for the thin disc (the low-α sequence) of a certain element i, at the time t, and Galactocentric distance R is defined as:
where XAi is the abundance by mass of the element i of the infall gas that is assumed to be primordial here, while the quantity τD(R) is the time-scale of gas accretion. The coefficient b(R) is constrained by imposing a fit to the observed current total surface mass density ΣD in the thin disc as a function of the Galactocentric distance given by:
where tG is the present time, ΣD, 0 is the central total surface mass density, and RD is the disc scale length. The fit of the ΣD(R) quantity using the infall rate law of Eq. (1) is given by:
The observed total disc surface mass density in the solar neighbourhood is ΣD (8 kpc, tG) = 54 M⊙ pc−2 (see Romano et al. 2000 for a discussion of the choice of this surface density). The infall rate of gas that follows an exponential law is a fundamental assumption adopted in most of the detailed numerical chemical evolution models in which the instantaneous recycling approximation (IRA) is relaxed.
An important ingredient to reproduce the observed radial abundance gradients along the Galactic disc is the inside-out formation on the disc (Spitoni & Matteucci 2011; Cescutti et al. 2007; Mott et al. 2013). The timescale τD(R) for the mass accretion is assumed to increase with the Galactic radius following a linear relation given by (see Chiappini et al. 2001):
for Galactocentric distances ≥4 kpc. For the star formation rate (SFR) we adopt a Kennicutt (1998) law proportional to the gas surface density:
where ν is the star formation efficiency (SFE) process and Σg(R, t) is the gas surface density at a given position and time. The exponent k is fixed to 1.5 (see Kennicutt 1998).
We divided the disc into concentric shells 1 kpc-wide in the radial direction. Each shell is itself divided into 36 segments of 10° width. Therefore, at a fixed Galactocentric distance, 36 zones were created.
With this new configuration we can take variations of the SFR along the annular region into account that are produced by density perturbations driven by spiral arms or bars. Therefore, an azimuthal dependence appears in Eq. (5), which can be written as follows:
In this paper we show the results related to the effects of density fluctuations of the chemo-dynamical model of MCM13. We also test the effects of an analytical formulation for the density perturbations created by spiral arm waves. The reference model, without any density azimuthal perturbation, is similar to the one by Cescutti et al. (2007), which has been shown to be quite successful in reproducing the most recent abundance gradients observed in Cepheids (Genovali et al. 2015).
2.1. Nucleosynthesis prescriptions
In this work we present the results for the azimuthal variations of abundance gradients for oxygen and iron. As done in a number of chemical evolution models in the past (e.g. Cescutti et al. 2006; Spitoni et al. 2015, 2019; Vincenzo et al. 2019), we adopt the nucleosynthesis prescriptions by François et al. (2004) who provide theoretical predictions of [element/Fe]-[Fe/H] trends in the solar neighbourhood for 12 chemical elements.
François et al. (2004) selected the best sets of yields required to best fit the data (details related to the observational data collection are in François et al. (2004). In particular, for Type II SNe yields, they found that the Woosley & Weaver (1995) ones provide the best fit to the data. This occurs because no modifications are required for iron yields, as computed for solar chemical composition, whereas the best results for oxygen are given by yields computed as functions of the metallicity. The theoretical yields by Iwamoto et al. (1999) are adopted for the Type SNeIa, and the prescription for single low-intermediate mass stars is by van den Hoek & Groenewegen (1997).
Although François et al. (2004) prescriptions still provide reliable yields for several elements, we must be cautious about oxygen. Recent results have shown that rotation can influence the oxygen nucleosynthesis in massive stars (Meynet & Maeder 2002) and, therefore, chemical evolution as well (Cescutti & Chiappini 2010), in particular at low metallicity. However, this does not affect our results since the data shown in this project are relatively metal rich. Moreover, we are mostly interested in differential effects, rather than absolute values.
2.2. 2D disc surface density fluctuations from the MCM13 model
We consider the gas density fluctuations present in the Milky Way, such as the simulation obtained by Martig et al. (2012) and chosen in MCM13 for their chemodynamical model. The simulated galaxy has a number of properties consistent with the Milky Way, including a central bar. MCM13 followed the disc evolution for a time period of about 11 Gyr, which is close to the age of the oldest low-α disc stars in the Milky Way. The classical 1D chemical evolution model is quite successful in reproducing abundance gradient along the Galactic disc (Cescutti et al. 2007).
The chemical evolution model used by MCM13 was very similar to the one adopted here; a comparison between its star formation history and that of the simulation is presented in Fig. A.1 by Minchev et al. (2014), showing good agreement. In order to extract the gas density variations, we binned the disc into 18, 1 kpc-wide radial bins and 10°-wide azimuthal bins at |z| < 1 kpc. The time resolution is 37.5 Myr for 11 Gyr of evolution. This is all used for our new model described below.
With the aim of preserving the general trend of the 1D chemical evolution model, we introduce a density contrast function f related to the perturbations originated by the MCM13 model. At a fixed Galactocentric distance R, time t, and azimuthal co-ordinate ϕ, the new surface mass density is:
We impose that the average value of the density contrast f is 1, that is:
This guarantees that, at a fixed Galactocentric distance R and a time t, the average surface mass density is the one predicted by the 1D chemical evolution model.
2.3. ISM density fluctuations from analytical spiral structure
Here we investigate the effect of an analytical spiral arm formulation on the azimuthal variations of the abundance gradients. In particular, we analyse steady wave spiral patterns. As suggested by Bertin et al. (1989) and Lin & Shu (1966), when the number of important spiral modes of oscillation is small, the spiral structure is expected to have a highly regular grand design and to evolve in time in a quasi- stationary manner.
In this work, we consider the model presented by Cox & Gómez (2002). The expression for the time evolution of the density perturbation, created by spiral arms, refers to an inertial reference frame not co-rotating with the Galactic disc in terms of the surface mass density, which is:
where χ(R, tG) is the present day amplitude of the spiral density:
while M(γ) is the modulation function for the “concentrated arms” given by Cox & Gómez (2002). The M(γ) function can be expressed as follows:
In Eq. (12), m is the number of spiral arms, α is the pitch angle, RS is the radial scale-length of the drop-off in density amplitude of the arms, Σ0 is the surface arm density at the fiducial radius R0, Ωs is the pattern angular velocity, the azimuthal co-ordinate ϕ increases counter-clockwise and has a clockwise rotation, and ϕp(R0) is the co-ordinate ϕ computed at t = 0 Gyr and R0. An important feature of this perturbation is that its average density at a fixed Galactocentric distance R and time t is zero,
In Fig. 1, we show the modulation function M(γ) of concentrated arms on the Galactic plane using the following model parameters suggested by Cox & Gómez (2002): R0 = 8 kpc, α = 15°, and RS = 7 kpc. The modulation function is computed at 5 Gyr assuming the angular velocity value of Ωs = 20 km s−1 kpc−1 and ϕp(R0) = 0. In this work we aim to investigate the effects of spiral arm density perturbations on the chemical enrichment by ejecta from stellar populations perfectly co-rotating with the Galactic disc. Our purpose here is to study the regular gas density perturbation linked to simple, but reliable, spiral arm descriptions.
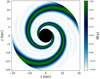 |
Fig. 1. Modulation function M(γ) of Eq. (11) for concentrated arms by Cox & Gómez (2002) with N = 2 spiral arms, fiducial radius R0 = 8 kpc, pitch angle α = 15°, and ϕp(R0) = 0. |
To properly describe the temporal evolution of local density perturbations, the relative spiral arm speed pattern compared to the Galactic disc motion must be computed (further details are provided throughout Sect. 3.2). Cox & Gómez (2002) provided a value for the spiral arm perturbation density at 8 kpc equal to 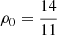 mH cm−3. Our implementation requires the surface density ΣS, 0, which can be recovered from the z direction amplitude provided by Cox & Gómez (2002, their Eq. (1)), with the following relation:
mH cm−3. Our implementation requires the surface density ΣS, 0, which can be recovered from the z direction amplitude provided by Cox & Gómez (2002, their Eq. (1)), with the following relation:
where H is the disc scale-height. Adopting H = 180 pc, which was chosen to match the scale-height of the thin stellar disc proposed by Dehnen & Binney (1998, Model2) and is in agreement with Spitoni et al. (2008), we obtain:
It is important to note that in our approach, the time dependence of the density perturbation by the spiral arms is only in the modulation function M(γ) through the term Ωst (see Eqs. (11) and (12)). Currently, there are no analytical prescriptions for the time evolution of both the amplitude of the spiral arm perturbation and its radial profile in the Galactic evolution context (spiral arm redshift evolution). Therefore, we make the reasonable assumption that during the Galactic evolution, the ratio between the amplitude of the spiral density perturbation χ(R, t) and the total surface density ΣD(R, t) computed at the same Galactic distance R remains constant in time, that is ![$ \frac{d}{\mathrm{d}t} \left[ \chi(R,t)/\Sigma_{\mathrm{D}}(R,t) \right] $](/articles/aa/full_html/2019/08/aa34665-18/aa34665-18-eq17.gif) = 0, assuming a co-eval evolution of these two structures in time. We define the dimensionless quantity δS(R, ϕ, t) as the following ratio:
= 0, assuming a co-eval evolution of these two structures in time. We define the dimensionless quantity δS(R, ϕ, t) as the following ratio:
With the assumption that the ratio χ(R, t)/ΣD(R, t) is constant in time, Eq. (16) becomes:
If we include the contribution of the perturbation originated by the spiral arm in the SFR driven by a linear Schmidt (1959) law (i.e. Ψ = νΣg(R, t), we then have:
We are aware that this is a simplification of the more complex behaviour seen in N-body simulations (Quillen et al. 2011; Minchev et al. 2012a; Sellwood & Carlberg 2014) and external galaxies (Elmegreen et al. 1992; Rix & Zaritsky 1995; Meidt et al. 2009) where multiple spiral patterns have been found. We address this description in Sect. 3.2.2 where we consider the simultaneous perturbation by a number of spiral patterns moving at different angular velocities.
As stated in the previous section, the average modulation function over the azimuth ϕ, at a fixed time t, and Galactocentric distance R is null (⟨M(γ)⟩ϕ = 0). Therefore, in the presence of a linear Schmidt (1959) law at a fixed Galactocentric distance, the average value of Ψ(R, t, ϕ)d + s over ϕ of the SFR defined in Eq. (18) is equal to the unperturbed SFR, this is illustrated by the following expression:
Here, we did not adopt a linear Schmidt (1959) law, and we used the SFR proposed by Kennicutt (1998) which exhibits the exponent k = 1.5. Hence, the SFR in the Galactic disc in the presence of spiral arm density perturbations becomes:
Roberts (1969) provided the exact shape of the steady gas distribution in spiral arms, finding an offset between the maximum of the stellar spiral arm and the maximum of the gas distribution driven by galactic shocks. In his Fig. 7, it is shown that the regions of newly born luminous stars and the HII regions lie on the inner side of the observable gaseous spiral arm of HI. The presence of a small but noticeable offset between the gas and stellar spiral arms has also been found in the study of interactions between disc galaxies and perturbing companions in 3D N-body and smoothed hydrodynamical numerical simulations by Pettitt et al. (2016).
Because of uncertainties related to the real magnitude of this offset (small offsets are predicted by Pettitt et al. 2016) in our work, we do not consider it. Additionally, the SFR is more enhanced in correspondence of the total density perturbation peak (see Eq. (17) and the modulation function in Fig. 1). We are aware that is true only near the co-rotation radius, however with our simpler approach we provide an upper limit estimate for the azimuthal abundance variations generated by steady spiral arm density perturbations. In the presence of an off-set, the density perturbation should be less “concentrated” and more smeared.
Our model in the presence of analytical spiral arms must be considered as a first attempt to include spiral structure in a classical chemical evolution model. As stated in Sect. 2.2, we also present results for the azimuthal abundance variations originated by chemodynamical Milky Way-like simulation in the presence of spiral arms and a bar in a self consistent way. Our analytical spiral arms model is meant to clarify the problem so we can then understand the reason for the causes of azimuthal variations. Assuming that modes add linearly, we can approximate a realistic galactic disc by adding several spiral sets with different pattern speeds, as seen in observations (e.g. Meidt et al. 2009) and simulations (e.g. Masset & Tagger 1997; Quillen et al. 2011; Minchev et al. 2012b).
3. Results
In this section we present our chemical evolution model results. We apply our 2D model by using surface density fluctuations from the MCM13 chemo-dynamical model and from an analytical prescription.
3.1. Density fluctuation from the MCM13 chemo-dynamical model
In this section we present our results based on the new 2D chemical evolution model including the density mass fluctuation extracted from the chemo-dynamical model by MCM13. Figure 2 shows the Galactic disc SFR computed at 0.1, 0.7, 6, and 11 Gyr after the start of disc formation for the chemical evolution model in which we tested the effects of the density fluctuation by MCM13 in units of M⊙ pc−2 Gyr−1. We notice that at early times (i.e the “1 Gyr” case reported in the upper left panel), the SFR is more concentrated in the inner Galactic regions. Also, the SFR in the innermost regions decreases and the outer parts have more star formation activity? because of the “inside-out” prescription coupled with the inclusion of the density fluctuation. At the Galactic epoch of 1 Gyr after the start of disc formation, regions with the same Galactocentric distances have approximately the same SFR. Already after 0.7 Gyr of Galactic evolution, azimuthal star formation inhomogeneities are not negligible. Concerning the panel with the model results at 6 Gyr, azimuthal inhomogeneities are evident. This is particularly the case at 8 kpc, the ratio between the maximum and the minimum values assumed by the SFR is SFRmax /SFRmin = 6.72.
 |
Fig. 2. Galactic disc SFR in units of M⊙ pc−2 Gyr−1 computed at 0.1, 0.7, 6, and 11 Gyr after start of disc formation for chemical evolution model in which we tested effects of density fluctuations resulting from MCM13 model. |
In Fig. 2, the bar and spiral arm features do not show up clearly, especially in early times. This is caused by the adopted inside out prescription (Eq. (4)) which leads to huge differences between the SFRs computed in inner and outer regions. In Fig. 3, the Galactic disc SFR(R, ϕ) is normalised to the maximum value SFRR, max of the annular region located at the Galactocentric distance R, that is SFR(R, ϕ)/SFRR, max computed at 0.1, 0.7, 6, and 11 Gyr after the start of disc formation, respectively. Here, different features related to density perturbations originated by spiral arms and bar can be noted.
 |
Fig. 3. Galactic disc SFR normalised to maximum value SFRR, max of annular region located at Galactocentric distance R, i.e SFR(R, ϕ)/SFRR, max, computed computed at 0.1, 0.7, 6, 11 Gyr after start of disc formation, for chemical evolution model in which we tested effects of density fluctuations by MCM13 model. |
In Fig. 4, the main results related to the present day oxygen abundance azimuthal variation are presented. The top panel shows the azimuthal distribution of the residual of the oxygen abundances computed with our chemical evolution model at 4, 8, 12, 16, and 18 kpc after subtracting the average radial gradient (i.e. the one obtained with the reference model without any density perturbation). Throughout this paper we adopt the photospheric values of Asplund et al. (2009) as our solar reference. We see that the behaviour is in excellent agreement with the observations by Sánchez et al. (2015). The data do indeed show that outer regions display larger azimuthal variations, and the amplitude of the risidual variations are of the order of 0.1 dex (see Fig. 7 by Sánchez et al. (2015). In our model the maximum variations are ∼0.12 dex for the chemical evolution models computed at 18 kpc. Our results appear to have a bit less scatter.
 |
Fig. 4. Results for the chemical evolution model in which we consider the density fluctuation by the chemo-dynamical model by MCM13. Upper panel: residuals of the ISM oxygen abundances as a function of Galactic azimuth computed with our chemical evolution model at 4, 8, 12, 16, and 18 kpc after subtracting the average radial gradient. Lower panel: our mock observation to mimic Sánchez et al. (2015) results in which we randomly plot residual ISM oxygen abundance predicted by our chemical evolution at 4, 8, 12, 16, and 18 kpc adding an uncertainty of 5° in the azimuthal component and taking into account [O/H] errors according to Sánchez et al. (2015); the colour-coding is identical to line colours of the upper panel: innermost disc regions are associated with the green points, and outermost ones with the purple points. |
In the lower panel of Fig. 4, we present our “mock” observations. We draw oxygen abundances of different ISM regions at different Galactocentric distance at random azimuthal co-ordinates ϕ. Hence, we add an error of σϕ = 5° to alleviate the fact that our model presents a resolution of 10° in the azimuthal component ϕ. Moreover, the average observational uncertainty associated with the oxygen abundances of σ[O/H] = 0.05 dex provided by Sánchez et al. (2015) has been considered. We define the “new” oxygen abundance including these uncertainties as follows:
where U is the random generator function. Similarly, we implement the uncertainty in the azimuthal component through the following relation:
Here, the similarities between the Sánchez et al. (2015) observations and our results are clearly visible. To summarise, the inclusions of density perturbations taken from a self-consistent dynamical model at different Galactic times leads to significant variations in chemical abundances in the outer Galactic regions.
In Fig. 5, we show results for the present day abundance gradient (after 11 Gyr of evolution) for iron that is computed for six azimuthal slices (as indicated) with 10° of width at different azimuthal co-ordinates. In the same plot, the shaded grey area indicates the maximum spread in the abundance ratio [Fe/H] obtained by the azimuthal co-ordinates we considered (0°, 60°, 120°, 180°, 240°, and 300°). Due to the results presented above, the shaded area is larger towards external regions. We also overplot the data from Genovali et al. (2014) in order to compare them to our model predictions. We notice that the predicted gradient is slightly steeper than the observed one in the external Galactic regions. However, we notice that the model lines pass within the standard deviation of the data, which was computed by dividing the data by Genovali et al. (2014) into six radial bins.
 |
Fig. 5. Results for the chemical evolution model in which we consider the density fluctuation by the chemo-dynamical model by MCM13. The present day Fe abundance gradient computed at different azimuthal co-ordinates. The shaded grey area limits are related to the maximum and minimum iron abundance values at the different Galactocentric distances. Observational data (light blue circles) are the Cepheids collected by Genovali et al. (2014). With the empty pentagons we report the average abundance values and relative errors of Genovali et al. (2014) when divided into six radial bins. In the zoomed region are presented the model lines computed between 16 and 18 kpc. |
In Fig. 6, we tested the effects of chemo-dynamical fluctuations on the time evolution of the oxygen abundance gradient at a fixed azimuth (ϕ = 0°). In agreement with Minchev et al. (2018), the abundance gradient flattens with time because of the chemical evolution model assumptions. As shown by Spitoni et al. (2015) and Grisoni et al. (2018), the inclusion of radial gas flows can indeed lead to even steeper gradients with time during the whole Galactic history.
 |
Fig. 6. Results for the chemical evolution model in which we consider the density fluctuation by the chemo-dynamical model by MCM13. Time evolution of the oxygen abundance gradient at ϕ = 0°. |
In Fig. 7, we compare the average iron abundance azimuthal variation in bins of ϕ = 15° presented by Genovali et al. (2014). This was computed at 6, 8, 10, and 12 kpc, respectively, with our 2D chemical evolution model, resulting from the MCM13 density variations. We see that the observed azimuthal variations are for limited Galactocentric distances (6−12 kpc) and with a narrow range of azimuthal co-ordinates. Although it is evident that the observed amplitude of azimuthal variations are larger than the ones predicted by our models, more precise Galactic Cepheid data are required to make firm conclusions.
 |
Fig. 7. Upper panel: average Fe abundances of Galactic Cepheids presented by Genovali et al. (2014) in bin of 15° for the azimuthal co-ordinate ϕ at different Galactocentric distances. Lower left panel: Fe abundances as functions of the azimuthal co-ordinates computed at 6, 8, 10, and 12 kpc predicted by the chemical evolution model in which we implemented the density fluctuation by the MCM13 model. Lower right panel: residual of the Fe abundances predicted by our model computed after subtracting the average radial gradient. |
Moreover, other dynamical processes that we have not considered in this work may play important roles in the evolution and development of the Galactic gradients in addition to their azimuthal variations. Additionally, radial migration processes can already introduce some variations in about a Gyr (Quillen et al. 2018).
3.2. Density fluctuations from an analytical spiral arm formulation
In this section, we discuss the results of chemical evolution models with only analytical prescriptions for spiral arm density perturbations without including any density fluctuations from chemo-dynamical models. The primary purpose here is to test the effect of regular perturbations (i.e. the evolution of spiral arms described by an analytical formulation) on the chemical evolution of a Milky Way-like galaxy. It is important to note that the results shown in the previous section reflect the complex behaviour of the Milky Way more closely. However, we are also interested in exploring the different spiral arm configurations that could characterise external galactic systems by varying the free parameters of the analytical expression of the spiral arms. In particular, we show the effects on the azimuthal variations of abundance gradients for oxygen by firstly varying the multiplicity m of spiral arms, then the spiral pattern speed Ωs, and lastly the pitch angle.
For all model results that will be presented, we assume the following Cox & Gómez (2002) prescriptions: the radial scale length of the drop-off in density amplitude of the arms is fixed at the value of RS = 7 kpc, the pitch angle is assumed constant at α = 15°, the surface arm density Σ0 is 20 M⊙ pc−2 at the fiducial radius R0 = 8 kpc, and finally we assume ϕp(R0)=0.
The disc rotational velocity Ωd(R) has been extracted from the simulation by Roca-Fàbrega et al. (2014, see their panel on the left-hand side of Fig. 1). The exponential fit of Ωd(R) variations as a function of the Galactocentric distance R (expressed in kpc) is:
We started by adopting the constant pattern angular velocity Ωs = 20 km s−1 kpc−1 that is consistent with the Roca-Fàbrega et al. (2014) model. A similar value was first estimated by moving groups in the U−V plane by Quillen & Minchev (2005, 18.1 ± 0.8 km s−1 kpc−1). Also, a summary of derived values for the Milky Way can be found in Bland-Hawthorn & Gerhard (2016). In Fig. 8, we show the Ωs and Ωd(R) quantities as well as the outer and inner Lindblad resonances as a function of the Galactocentric distance. It is interesting to note that the co-rotation radius is located at 8.31 kpc.
 |
Fig. 8. Spiral pattern speed Ωs and disc angular velocity Ωd computed by Roca-Fàbrega et al. (2014) are indicated with light blue and violet lines, respectively. With the long, vertical dashed red line, we show the position of the co-rotation radius located at the Galactocentric distance R = 8.31 kpc. Outer and inner Lindblad resonances extracted by the Roca-Fàbrega et al. (2014) simulation are also drawn with dotted magenta and dotted purple lines, respectively. |
3.2.1. Results with a single analytical spiral pattern
We begin our analysis discussing the results obtained with model S2A (see Table 1), which has a pattern speed of Ωs = 20 km s−1 kpc−1. This then places the co-rotation resonance at the solar radius.
Different spiral arm models tested with our 2D chemical evolution model for the disc, changing the number of spiral arms m (second column), then the pitch angle α (third column), and finally the spiral pattern speed Ωs (last column).
The upper panel of Fig. 9 shows the oxygen abundance residual azimuthal variations after 11 Gyr of disc evolution for different Galactocentric distances. The average radial gradient is subtracted. As expected, larger abundance azimuthal variations are found near the co-rotation radius. In this region, the chemical enrichment should be more efficient due to the lack of the relative gas-spiral motions. Higher SFR at the co-rotation radius, caused by locally higher gas overdensity, lasts for a longer time. Therefore, more massive stars can be created and more metals can be ejected into the local ISM under the spiral arm passage.
 |
Fig. 9. Results for the chemical evolution model in which we consider the density fluctuation associated with the analytical spiral arm formulation. Upper panel: azimuthal distribution of the residual of the oxygen abundances computed with our chemical evolution model at 4, 8, 12, 16, and 20 kpc (after subtracting the average radial gradient for a model with RS = 7, RD = 3.5, Σ0 = 20, ν = 1.1, Ωs = 20 km s−1 kpc−1, and m = 2 spiral arm; model S2A in Table 1). Lower panel: time evolution of the [O/H] abundance as a function of the azimuthal co-ordinate computed at 8 kpc. |
At 8 kpc, we have Δ[O/H] ≈ 0.05 dex. Variations are much smaller for other Galactocentric distances that are further away from the co-rotation. In the lower panel of Fig. 9, we present the temporal evolution of the oxygen abundance azimuthal variations for the model S2A as a function of the azimuthal co-ordinate ϕ computed at 8 kpc. As expected, larger inhomogeneities are present at early times that then decrease in time.
As discussed in Sect. 2.2, we assume that during the Galactic evolution the ratio between the amplitude of the spiral density perturbation and the total surface density computed at the same radius R, remain constant in time. However, it is not possible to put constraints on the temporal evolution of pattern speed with this analytical approach.
Galactic chemical evolution is an integral process in time. At early times, the stronger spiral structure induced azimuthal variations, which are, therefore, washed out by phase mixing.
Figure 10 depicts the SFR after 1 Gyr of evolution (upper panel) and at the present time (lower panel) on the Galactic plane computed with the model S2A. Here, it is evident the way in which the spiral arm density perturbation affects and modulates SFR, which is computed at the present time in the unit of M⊙ pc−2 Gyr−1. The shape of the two spiral arm over-densities is clearly visible in the SFR. This is in contrast with our results using the MCM13 density fluctuations (see Fig. 2) where multiple spiral density waves were present. Moreover, we can appreciate the inside-out disc formation: at later times the external regions become star formation active.
 |
Fig. 10. Upper panel: galactic disc SFR resulting from model S2A after 1 Gyr of evolution (see Table 1 and text for model details). The colour-coding indicates the SFR in units of M⊙ pc−2 Gyr−1. Lower panel: same as upper panel, but computed at 11 Gyr. |
3.2.2. The effect of different pattern speeds
In this section, we vary the spiral pattern speed, which has the effect of shifting the co-rotation resonance in radius. We argue that a combination of multiple spiral modes with different pattern speeds can be a realistic representation of a galactic disc. The horizontal and vertical lines in Fig. 11 show the different pattern speeds and corresponding co-rotation radii, respectively, that are used in this section. It is clear that smaller Ωs values lead to a more external co-rotation radius.
 |
Fig. 11. Disc angular velocity Ωd computed by Roca-Fàbrega et al. (2014) is indicated with light blue and violet lines. Different horizontal solid lines indicated the spiral pattern speed Ωs adopted in our models (see text and Table 1 for model details). The long, vertical dashed lines show the positions of the co-rotation radii assuming different Ωs values. |
In Fig. 12, we show the oxygen abundance gradients computed at different azimuths after 11 Gyr of disc evolution for models with spiral multiplicity m = 2 and different spiral pattern speed Ωs (see Table 1 for model details).
 |
Fig. 12. Present day oxygen abundance gradients for different azimuths, predicted by chemical models with spiral multiplicity m = 2 and different spiral pattern speed Ωs (see Table 1 for model details). In each panel the dashed vertical line indicates the location of the co-rotation radius. It is clear that allowing for multiple spiral patterns propagating through the disc at the same time affect the entire disc, similarly to the case of the MCM13 model. |
We notice that the more the co-rotation radius is shifted towards the external Galactic regions, the more the oxygen azimuthal abundance variations are amplified near the co-rotation radius. This result is reasonable in the light of our previous findings presented above with our model assuming chemo-dynamical fluctuations by MCM13. We recall that larger variations in the chemical abundance of outer galactic regions were found by observations in external galaxies (Sánchez et al. 2015).
In Fig. 13, we show the present day azimuthal residual of the oxygen abundances after subtracting the average radial gradient computed for the Galactic annular regions, which includes the relative co-rotation radius for the following models with m = 2 multiplicity: S2A, S2B, S2C, S2D, and S2F (see Table 1 for other parameter details). The model S2D computed at R = 13 kpc has Δ [O/H] ≈ 0.32 dex. The variations are important even in regions that are not so far from the solar neighbourhood. For example, the model S2C, whose co-rotation resides in the annular region centred at R = 11 kpc, presents an oxygen abundance variation of Δ [O/H] is ≈0.20 dex.
 |
Fig. 13. Present day residual azimuthal variations in oxygen abundance for the co-rotation regions (as indicated) of the different pattern speeds shown in Fig. 12. An increase in the effect is found as the co-rotation shifts to larger radius, i.e. for slower spiral patterns. Such a set of spirals with progressively slower patterns speeds as radius increases, can be a realistic representation of a galactic disc. |
As discussed in Sect. 2.3, it is well accepted that multiple patterns can be present in galactic discs (e.g. Meidt et al. 2009), including our own Milky Way (Minchev & Quillen 2006; Quillen et al. 2011) with slower patterns shifted to outer radii. This will have the effect of placing the co-rotation regions very similarly to how Fig. 13 presents them, having co-rotating arms at all radii as found by Grand et al. (2012) and Hunt et al. (2019). Therefore, the increasing scatter in abundance with Galactic radius can be explained as the effect of multiple patterns propagating at the same time. It is interesting to note that radial migration will introduce additional scatter that can, in principle, be accounted for.
3.2.3. Results with an m = 1 spiral pattern
We want to test whether the intensity of the amplitude of the azimuthal chemical abundance variations is dependant on the number m of spiral arms. In Table 1, we use the same labelling system for model S1A as for model S2A, but with an m = 1 spiral structure that only has only one spiral arm. Such a mode arises naturally from the coupling of m = 2 and m = 3 modes, as found by Quillen et al. (2011) and Minchev et al. (2012b) who used pure N-body and SPH simulations. This is also seen in external galaxies (Zaritsky & Rix 1997).
In the upper panel of Fig. 14, we notice that the abundance variations are larger than the ones obtained with the same model, but m = 2 (upper panel of Fig. 9): a fluctuation of about Δ [O/H] = 0.1 dex is seen at the co-rotation radius (∼8 kpc).
The same figure presents the time evolution of azimuthal abundance inhomogeneities for oxygen computed at 8 kpc with the model S1A at 2, 4, 6, 8, and 11 Gyr. In Fig. 15, the oxygen abundance gradients were computed at different azimuths after 11 Gyr of disc evolution for models with spiral multiplicity m = 1 and the same spiral pattern speeds Ωs as in Fig. 12 (see Table 1 for model details). We notice that around the co-rotation radii, the azimuthal abundance variations are generally more evident for models with one spiral arm as compared to ones with a spiral multiplicity of m = 2.
In Fig. 16, we show the present day azimuthal residual of the oxygen abundances after subtracting the average radial gradient computed in annular regions, which contain the co-rotation radii for the following models with m = 1 multiplicity: S1A, S1B, S1C, S1D, and S1F (see Table 1 for other parameter details). For the model S1D at the Galactic distance of 13 kpc, we have Δ [O/H] ≈ 0.40 dex, which is about ≈25% larger than the S2D case. As found for the model with m = 2, the oxygen abundance variations become important in regions that are not so far from the solar vicinity, that is the model S1C whose co-rotation resides at R = 11 kpc and Δ [O/H] ≈ 0.23 dex.
3.2.4. Results for different pitch angles
In this section, we consider different pitch angles α for the spiral arms in our Milky Way Galaxy. The recent work by Quillen et al. (2018) and Laporte et al. (2019) suggest that tightly wound spiral structure should be considered based on the modelling of phase-space structure found in the second Gaia data release Gaia Collaboration (2018).
A smaller pitch angle gives rise to more tightly wound spiral structure. The upper panel of Fig. 17 depicts the present time SFR that was computed with a pitch angle α = 7° (model S2G in Table 1), whereas the lower panel shows the case of α = 30° (model S2H in Table 1). For both panels, the other model parameters are the same as for model S2A. The spiral pattern is clearly visible in the SFR, and a tighter wound spiral structure is present for the model S2G.
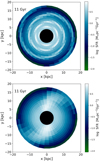 |
Fig. 17. Upper panel: Galactic disc SFR related to the model S2G computed after 11 Gyr of Galactic evolution (see Table 1 and text for model details) with a pitch angle α = 7°. The colour-coding indicates the SFR in units of M⊙ pc−2 Gyr−1. Lower panel: same as upper panel, but for the model S2H where the pitch angle α is 30°. |
In Fig. 18, we compare the azimuthal variations for models S2G and S2H. We see that the chemical variations are identical at the co-rotation radius and simply azimuthally shifted for other Galactocentric distances.
 |
Fig. 18. Effects of different pitch angles α on the azimuthal distribution of the residual of the oxygen abundances computed with our chemical evolution model at 4, 8, 12, 16, and 20 kpc. In the upper panel, the pitch able is set at the value of 7° (SE model in Table 1), while in the lower panelα = 30° (SF model in Table 1). |
4. Conclusions
In this paper, we present a new 2D chemical evolution model that is able to trace azimuthal variations in the Galactic disc density. We applied this model to (i) the density fluctuations arising in a disc formation simulation by Martig et al. (2012), used for the MCM13 Milky Way chemo-dynamical model, and (ii) the density perturbations originating from an analytical spiral arm formulation.
The main conclusions for density perturbation from the Milky Way chemo-dynamical model by MCM13 can be summarised as follows:
-
We found that the density fluctuations produce significant oxygen azimuthal variations in the abundance gradients of the order of 0.1 dex.
-
The azimuthal variations are more evident in the external Galactic regions, which is in agreement with the recent observations of the galaxy NGC 6754, using MUSE data (Sánchez et al. 2015).
In an effort to understand the above findings, we constructed simple analytical spiral arm models, for which we varied the pattern speed, multiplicity, and pitch angle with the following main findings:
-
The larger fluctuations in the azimuthal abundance gradients are found near the co-rotation radius where the relative velocity, with respect to the disc, is close to zero.
-
Larger azimuthal variations are found at co-rotation radii that are shifted to larger radii, that is the slower pattern speeds.
-
The variation is more enhanced for the model with only one spiral arm, which is expected to result from the combination of an m = 2 and m = 3 spiral structure.
-
We find that more significant azimuthal abundance variations seen at early times, in the presence of a regular periodic perturbation, tend to quench at later times. This is expected as Galactic chemical evolution is a cumulative process and as phase-mixing and radial migration tends to wipe structure with time.
We can obtain a realistic picture of azimuthal variations induced at stellar birth found in self-consistent models, such as the MCM13, when the effect of co-rotation radii is combined by assuming the simultaneous propagation of multiple spiral modes through galactic discs. Material spiral arms, propagating near the co-rotation at all galactic radii, have been described by a number of recent numerical work with different interpretations (see Grand et al. 2012; Comparetta & Quillen 2012; Hunt et al. 2019).
In our future work, we will improve upon the new 2D chemical evolution model introduced here by taking into account stellar radial migration of long-lived stars and the pollution to the ISM abundance, which is introduced by them at radii and azimuths that are different than their birth places. We will also use this model to update the Galactic habitable zone results presented by Spitoni et al. (2014, 2017) and study the effect of spiral structure and the Galactic bar.
Acknowledgments
We thank the anonymous referee for various suggestions that improved the paper. E. Spitoni and V. Silva Aguirre acknowledge support from the Independent Research Fund Denmark (Research grant 7027-00096B). V. Silva Aguirre acknowledges support from VILLUM FONDEN (Research Grant 10118). G. Cescutti acknowledges financial support from the European Union Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 664931. This work has been partially supported by the EU COST Action CA16117 (ChETEC). I. Minchev acknowledges support by the Deutsche Forschungsgemeinschaft under the grant MI 2009/1-1. F. Matteucci acknowledges research funds from the University of Trieste (FRA2016).
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Balser, D. S., Rood, R. T., Bania, T. M., & Anderson, L. D. 2011, ApJ, 738, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Balser, D. S., Wenger, T. V., Anderson, L. D., & Bania, T. M. 2015, ApJ, 806, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, G., Lin, C. C., Lowe, S. A., & Thurstans, R. P. 1989, ApJ, 338, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., & Chiappini, C. 2010, A&A, 515, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., François, P., Matteucci, F., Cayrel, R., & Spite, M. 2006, A&A, 448, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Matteucci, F., François, P., & Chiappini, C. 2007, A&A, 462, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Comparetta, J., & Quillen, A. C. 2012, ArXiv e-prints [arXiv:1207.5753] [Google Scholar]
- Cox, D. P., & Gómez, G. C. 2002, ApJS, 142, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., Origlia, L., Kudritzki, R.-P., et al. 2009, ApJ, 696, 2014 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W., & Binney, J. 1998, MNRAS, 294, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Piau, L., Mohanty, S., & Braine, J. 2011, MNRAS, 415, 3439 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Elmegreen, D. M., & Montenegro, L. 1992, ApJS, 79, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, C., Siebert, A., & Famaey, B. 2014, MNRAS, 440, 2564 [NASA ADS] [CrossRef] [Google Scholar]
- François, P., Matteucci, F., Cayrel, R., et al. 2004, A&A, 421, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Katz, D., et al.) 2018, A&A, 616, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genovali, K., Lemasle, B., Bono, G., et al. 2014, A&A, 566, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genovali, K., Lemasle, B., da Silva, R., et al. 2015, A&A, 580, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerhard, O. 2011, Mem. Soc. Astron. It. Suppl., 18, 185 [Google Scholar]
- Grand, R. J. J., Kawata, D., & Cropper, M. 2012, MNRAS, 426, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Grand, R. J. J., Kawata, D., & Cropper, M. 2014, MNRAS, 439, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Grand, R. J. J., Springel, V., Kawata, D., et al. 2016, MNRAS, 460, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Grisoni, V., Spitoni, E., & Matteucci, F. 2018, MNRAS, 481, 2570 [NASA ADS] [Google Scholar]
- Ho, I.-T., Seibert, M., Meidt, S. E., et al. 2017, ApJ, 846, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, J. A. S., Bub, M. W., Bovy, J., et al. 2019, MNRAS, submitted [arXiv:1904.10968] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Laporte, C. F. P., Minchev, I., Johnston, K. V., & Gómez, F. A. 2019, MNRAS, 485, 3134 [Google Scholar]
- Li, Y., Bresolin, F., & Kennicutt, Jr., R. C. 2013, ApJ, 766, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C. C., & Shu, F. H. 1966, Proc. Natl. Acad. Sci., 55, 229 [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Khoperskov, S., Di Matteo, P., Haywood, M., & Combes, F. 2018, A&A, 611, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martig, M., Bournaud, F., Croton, D. J., Dekel, A., & Teyssier, R. 2012, ApJ, 756, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., Minchev, I., Ness, M., Fouesneau, M., & Rix, H.-W. 2016, ApJ, 831, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F., & Tagger, M. 1997, A&A, 322, 442 [NASA ADS] [Google Scholar]
- Matteucci, F., & François, P. 1989, MNRAS, 239, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Rand, R. J., & Merrifield, M. R. 2009, ApJ, 702, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2002, A&A, 390, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., & Quillen, A. C. 2006, MNRAS, 368, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012a, A&A, 548, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012b, A&A, 548, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2014, A&A, 572, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Martig, M., Streich, D., et al. 2015, ApJ, 804, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Anders, F., Recio-Blanco, A., et al. 2018, MNRAS, 481, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Mott, A., Spitoni, E., & Matteucci, F. 2013, MNRAS, 435, 2918 [NASA ADS] [CrossRef] [Google Scholar]
- Pedicelli, S., Bono, G., Lemasle, B., et al. 2009, A&A, 504, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pettitt, A. R., Tasker, E. J., & Wadsley, J. W. 2016, MNRAS, 458, 3990 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C., & Minchev, I. 2005, AJ, 130, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C., Dougherty, J., Bagley, M. B., Minchev, I., & Comparetta, J. 2011, MNRAS, 417, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C., Carrillo, I., Anders, F., et al. 2018, MNRAS, 480, 3132 [NASA ADS] [CrossRef] [Google Scholar]
- Ragan, S. E., Moore, T. J. T., Eden, D. J., et al. 2018, MNRAS, 479, 2361 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Bournaud, F., Emsellem, E., et al. 2015, MNRAS, 454, 3299 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., & Zaritsky, D. 1995, ApJ, 447, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, W. W. 1969, ApJ, 158, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Roca-Fàbrega, S., Antoja, T., Figueras, F., et al. 2014, MNRAS, 440, 1950 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Matteucci, F., Salucci, P., & Chiappini, C. 2000, ApJ, 539, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Galbany, L., Pérez, E., et al. 2015, A&A, 573, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Menguiano, L., Sánchez, S. F., Kawata, D., et al. 2016, ApJ, 830, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Carlberg, R. G. 2014, ApJ, 785, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Siebert, A., Famaey, B., Binney, J., et al. 2012, MNRAS, 425, 2335 [NASA ADS] [CrossRef] [Google Scholar]
- Silva Aguirre, V., Bojsen-Hansen, M., Slumstrup, D., et al. 2018, MNRAS, 475, 5487 [NASA ADS] [Google Scholar]
- Spitoni, E., & Matteucci, F. 2011, A&A, 531, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Recchi, S., & Matteucci, F. 2008, A&A, 484, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Matteucci, F., & Sozzetti, A. 2014, MNRAS, 440, 2588 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., Romano, D., Matteucci, F., & Ciotti, L. 2015, ApJ, 802, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., Gioannini, L., & Matteucci, F. 2017, A&A, 605, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Matteucci, F., Jönsson, H., Ryde, N., & Romano, D. 2018, A&A, 612, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Silva Aguirre, V., Matteucci, F., Calura, F., & Grisoni, V. 2019, A&A, 623, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Hoek, L. B., & Groenewegen, M. A. T. 1997, A&AS, 123, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vincenzo, F., Spitoni, E., Calura, F., et al. 2019, MNRAS, 487, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, F. P. A., Pérez, E., Dopita, M. A., Verdes-Montenegro, L., & Borthakur, S. 2017, A&A, 601, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJ, 101, 181 [Google Scholar]
- Zaritsky, D., & Rix, H.-W. 1997, ApJ, 477, 118 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Different spiral arm models tested with our 2D chemical evolution model for the disc, changing the number of spiral arms m (second column), then the pitch angle α (third column), and finally the spiral pattern speed Ωs (last column).
All Figures
 |
Fig. 1. Modulation function M(γ) of Eq. (11) for concentrated arms by Cox & Gómez (2002) with N = 2 spiral arms, fiducial radius R0 = 8 kpc, pitch angle α = 15°, and ϕp(R0) = 0. |
| In the text | |
 |
Fig. 2. Galactic disc SFR in units of M⊙ pc−2 Gyr−1 computed at 0.1, 0.7, 6, and 11 Gyr after start of disc formation for chemical evolution model in which we tested effects of density fluctuations resulting from MCM13 model. |
| In the text | |
 |
Fig. 3. Galactic disc SFR normalised to maximum value SFRR, max of annular region located at Galactocentric distance R, i.e SFR(R, ϕ)/SFRR, max, computed computed at 0.1, 0.7, 6, 11 Gyr after start of disc formation, for chemical evolution model in which we tested effects of density fluctuations by MCM13 model. |
| In the text | |
 |
Fig. 4. Results for the chemical evolution model in which we consider the density fluctuation by the chemo-dynamical model by MCM13. Upper panel: residuals of the ISM oxygen abundances as a function of Galactic azimuth computed with our chemical evolution model at 4, 8, 12, 16, and 18 kpc after subtracting the average radial gradient. Lower panel: our mock observation to mimic Sánchez et al. (2015) results in which we randomly plot residual ISM oxygen abundance predicted by our chemical evolution at 4, 8, 12, 16, and 18 kpc adding an uncertainty of 5° in the azimuthal component and taking into account [O/H] errors according to Sánchez et al. (2015); the colour-coding is identical to line colours of the upper panel: innermost disc regions are associated with the green points, and outermost ones with the purple points. |
| In the text | |
 |
Fig. 5. Results for the chemical evolution model in which we consider the density fluctuation by the chemo-dynamical model by MCM13. The present day Fe abundance gradient computed at different azimuthal co-ordinates. The shaded grey area limits are related to the maximum and minimum iron abundance values at the different Galactocentric distances. Observational data (light blue circles) are the Cepheids collected by Genovali et al. (2014). With the empty pentagons we report the average abundance values and relative errors of Genovali et al. (2014) when divided into six radial bins. In the zoomed region are presented the model lines computed between 16 and 18 kpc. |
| In the text | |
 |
Fig. 6. Results for the chemical evolution model in which we consider the density fluctuation by the chemo-dynamical model by MCM13. Time evolution of the oxygen abundance gradient at ϕ = 0°. |
| In the text | |
 |
Fig. 7. Upper panel: average Fe abundances of Galactic Cepheids presented by Genovali et al. (2014) in bin of 15° for the azimuthal co-ordinate ϕ at different Galactocentric distances. Lower left panel: Fe abundances as functions of the azimuthal co-ordinates computed at 6, 8, 10, and 12 kpc predicted by the chemical evolution model in which we implemented the density fluctuation by the MCM13 model. Lower right panel: residual of the Fe abundances predicted by our model computed after subtracting the average radial gradient. |
| In the text | |
 |
Fig. 8. Spiral pattern speed Ωs and disc angular velocity Ωd computed by Roca-Fàbrega et al. (2014) are indicated with light blue and violet lines, respectively. With the long, vertical dashed red line, we show the position of the co-rotation radius located at the Galactocentric distance R = 8.31 kpc. Outer and inner Lindblad resonances extracted by the Roca-Fàbrega et al. (2014) simulation are also drawn with dotted magenta and dotted purple lines, respectively. |
| In the text | |
 |
Fig. 9. Results for the chemical evolution model in which we consider the density fluctuation associated with the analytical spiral arm formulation. Upper panel: azimuthal distribution of the residual of the oxygen abundances computed with our chemical evolution model at 4, 8, 12, 16, and 20 kpc (after subtracting the average radial gradient for a model with RS = 7, RD = 3.5, Σ0 = 20, ν = 1.1, Ωs = 20 km s−1 kpc−1, and m = 2 spiral arm; model S2A in Table 1). Lower panel: time evolution of the [O/H] abundance as a function of the azimuthal co-ordinate computed at 8 kpc. |
| In the text | |
 |
Fig. 10. Upper panel: galactic disc SFR resulting from model S2A after 1 Gyr of evolution (see Table 1 and text for model details). The colour-coding indicates the SFR in units of M⊙ pc−2 Gyr−1. Lower panel: same as upper panel, but computed at 11 Gyr. |
| In the text | |
 |
Fig. 11. Disc angular velocity Ωd computed by Roca-Fàbrega et al. (2014) is indicated with light blue and violet lines. Different horizontal solid lines indicated the spiral pattern speed Ωs adopted in our models (see text and Table 1 for model details). The long, vertical dashed lines show the positions of the co-rotation radii assuming different Ωs values. |
| In the text | |
 |
Fig. 12. Present day oxygen abundance gradients for different azimuths, predicted by chemical models with spiral multiplicity m = 2 and different spiral pattern speed Ωs (see Table 1 for model details). In each panel the dashed vertical line indicates the location of the co-rotation radius. It is clear that allowing for multiple spiral patterns propagating through the disc at the same time affect the entire disc, similarly to the case of the MCM13 model. |
| In the text | |
 |
Fig. 13. Present day residual azimuthal variations in oxygen abundance for the co-rotation regions (as indicated) of the different pattern speeds shown in Fig. 12. An increase in the effect is found as the co-rotation shifts to larger radius, i.e. for slower spiral patterns. Such a set of spirals with progressively slower patterns speeds as radius increases, can be a realistic representation of a galactic disc. |
| In the text | |
 |
Fig. 14. As in Fig. 9, but for model S1A, with with multiplicity m = 1 of spiral arms. |
| In the text | |
 |
Fig. 15. As Fig. 12, but for an m = 1 spiral. |
| In the text | |
 |
Fig. 16. As in Fig. 13, but for models with m = 1 multiplicity (see Table 1). |
| In the text | |
 |
Fig. 17. Upper panel: Galactic disc SFR related to the model S2G computed after 11 Gyr of Galactic evolution (see Table 1 and text for model details) with a pitch angle α = 7°. The colour-coding indicates the SFR in units of M⊙ pc−2 Gyr−1. Lower panel: same as upper panel, but for the model S2H where the pitch angle α is 30°. |
| In the text | |
 |
Fig. 18. Effects of different pitch angles α on the azimuthal distribution of the residual of the oxygen abundances computed with our chemical evolution model at 4, 8, 12, 16, and 20 kpc. In the upper panel, the pitch able is set at the value of 7° (SE model in Table 1), while in the lower panelα = 30° (SF model in Table 1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



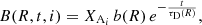
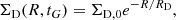
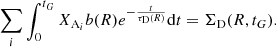
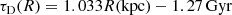
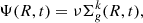
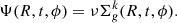
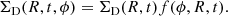
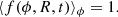
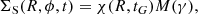
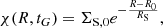
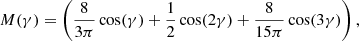
![$$ \begin{aligned} \gamma (R,\phi ,t)= m\left[\phi +\Omega _{\rm s} t -\phi _p(R_0) -\frac{\ln (R/R_0)}{\tan (\alpha )} \right]\cdot \end{aligned} $$](/articles/aa/full_html/2019/08/aa34665-18/aa34665-18-eq12.gif)
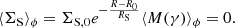
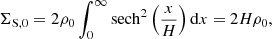
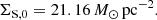
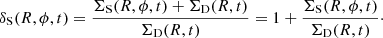
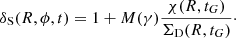
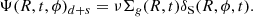
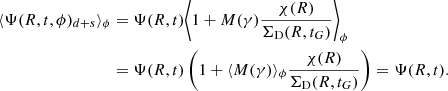
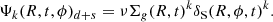
![$$ \begin{aligned}[\mathrm{O/H}]_{\rm new} = [\mathrm{O/H}]+ U([-\sigma _{\rm [O/H]}, \sigma _{\rm [O/H]}]), \end{aligned} $$](/articles/aa/full_html/2019/08/aa34665-18/aa34665-18-eq23.gif)
![$$ \begin{aligned} \phi _{\rm new} = \phi + U([-\sigma _{\phi }, \sigma _{\phi }]). \end{aligned} $$](/articles/aa/full_html/2019/08/aa34665-18/aa34665-18-eq24.gif)
![$$ \begin{aligned} \Omega _{\rm d}(R)=98.93 \, e^{-0.29 \, R}+ 11.11\,[\mathrm{km\,s^{-1}\,kpc^{-1}}]. \end{aligned} $$](/articles/aa/full_html/2019/08/aa34665-18/aa34665-18-eq25.gif)