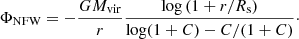| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 6 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935762 | |
| Published online | 09 July 2019 | |
Probing gaseous halos of galaxies with radio jets
1
Centre for Astrophysics Research, School of Physics, Astronomy and Mathematics, University of Hertfordshire, College Lane, Hatfield, Hertfordshire AL10 9AB, UK
e-mail: M.G.H.Krause@herts.ac.uk
2
School of Natural Sciences, Private Bag 37, University of Tasmania, Hobart, TAS 7001, Australia
Received:
24
April
2019
Accepted:
29
May
2019
Context. Gaseous halos play a key role in understanding inflow, feedback, and the overall baryon budget in galaxies. Literature models predict transitions of the state of the gaseous halo between cold and hot accretion, winds, fountains, and hydrostatic halos at certain galaxy masses. Since luminosities of radio AGN are sensitive to halo densities, any significant transition would be expected to show up in the radio luminosities of large samples of galaxies. The LOw Frequency ARray (LOFAR) Two-Metre Sky Survey (LoTSS) has identified a galaxy stellar mass scale, 1011 M⊙, above which the radio luminosities increase disproportionately.
Aims. We investigate if radio luminosities of galaxies, especially the marked rise at galaxy masses around 1011 M⊙, can be explained with standard assumptions regarding jet powers, scaling between black hole mass and galaxy mass, and gaseous halos.
Methods. Based on observational data and theoretical constraints, we developed models for the radio luminosity of radio AGN in halos under infall, galactic wind, and hydrostatic conditions. We compared these models to LoTSS data for a large sample of galaxies in the mass range between 108.5 M⊙ and 1012 M⊙.
Results. Under the assumption that the same characteristic upper limit to jet powers known from high galaxy masses holds at all masses, we find the maximum radio luminosities for the hydrostatic gas halos to lie close to the upper envelope of the distribution of the LOFAR data. The marked rise in radio luminosity at 1011 M⊙ is matched in our model and is related to a significant change in halo gas density around this galaxy mass, which is a consequence of lower cooling rates at a higher virial temperature. Wind and infall models overpredict the radio luminosities for small galaxy masses and have no particular steepening of the run of the radio luminosities predicted at any galaxy mass.
Conclusions. Radio AGN could have the same characteristic Eddington-scaled upper limit to jet powers in galaxies of all masses in the sample if the galaxies have hydrostatic gas halos in phases when radio AGN are active. We find no evidence of a change of the type of galaxy halo with the galaxy mass. Galactic winds and quasi-spherical cosmological inflow phases cannot frequently occur at the same time as powerful jet episodes unless the jet properties in these phases are significantly different from what we assumed in our model.
Key words: radio continuum: galaxies / galaxies: active / galaxies: halos / galaxies: jets / surveys
© ESO 2019
1. Introduction
Radio emission in galaxies is commonly attributed to supermassive black hole activity and the processes related to the formation of stars (for recent reviews see Hardcastle 2015; Tadhunter 2016; Norris 2017; Krause et al. 2018). The LOw Frequency ARray (LOFAR) radio telescope surveys the northern sky at low frequency with unprecedented resolution and sensitivity (Combes et al. 2019); giving us a much more comprehensive view of the radio emission of the local galaxy population. In the first data release of the LOFAR Two-Metre Sky Survey (LoTSS Shimwell et al. 2019), 70% of the 326 000 sources have optical counterparts (Williams et al. 2019), which include redshifts and absolute magnitudes (Duncan et al. 2019).
Sabater et al. (2019) cross-matched the LoTSS database with the Sloan Digital Sky Survey and classified the sources as galaxies with or without active galactic nuclei (AGN) based on diagnostic emission line and two-colour plots, the strength of the 4000 Å break, and the luminosity in Hα compared to the 150 MHz radio luminosity. This resulted in a local sample of 2121 galaxies with AGN and 8494 star-forming galaxies. They find that galaxy mass is the main driver of radio-AGN formation, all galaxies are switched on above a stellar mass of 1011 M⊙, and less than 10% of the galaxies show even the faintest sign of a radio AGN below 3 × 1010 M⊙. This is a significant improvement to previous results and a direct consequence of the more sensitive LoTSS observations compared to previous surveys.
Separating contributions from AGN activity and star formation to the total radio luminosity is, however, a difficult issue (e.g. Gürkan et al. 2018), even more so since even luminous radio AGN do frequently not show optical activity. The radio luminosity of an AGN depends on both jet power and environment (e.g. Kaiser et al. 1997; Manolakou & Kirk 2002; Hardcastle & Krause 2013, 2014; Maciel & Alexander 2014; Turner & Shabala 2015; English et al. 2016; Turner et al. 2018). The lack of radio AGN at lower galaxy masses may therefore indicate that such galaxies either have the capacity to produce radio jets to a much lesser extent or the gaseous halos of smaller galaxies differ significantly from those in bigger galaxies.
Empirical studies suggest that AGN may work differently in galaxies of different masses. For example, Best et al. (2005) found that the expression of optical activity is essentially independent of activity in the radio band; with lower mass galaxies showing more optical activity and higher mass galaxies showing more radio-loud AGN. Focussing solely on radio-loud AGN, Kauffmann et al. (2008) showed that the probability to express emission lines decreases with galaxy mass. However, this could be due to the fact that at low galaxy mass, it is harder to detect radio AGN with a low Eddington ratio, which tend to have little line emission (Best & Heckman 2012). On the other hand, the existence of scaling relations between black-hole mass and stellar velocity dispersion, bulge mass, and total galaxy mass (e.g. Magorrian et al. 1998; Häring & Rix 2004; Gültekin et al. 2009; Reines & Volonteri 2015; Bentz & Manne-Nicholas 2018) suggest most galaxies have supermassive black holes, which grow in a similar way during phases of nuclear activity (compare, e.g. Soltan 1982; Merloni & Heinz 2008; Tucci & Volonteri 2017). Radio AGN that also have strong emission lines tend to be associated with more strongly star-forming hosts (Hardcastle et al. 2013), higher Eddington ratios, and lower stellar mass (Best & Heckman 2012). Hence, the observational evidence suggests that lower mass galaxies have, on average, higher Eddington-scaled accretion rates on their central, supermassive black holes. In emission line AGN, the luminosity of optical emission lines is broadly correlated to the radio luminosity (McCarthy 1993; Kauffmann et al. 2008). Therefore, one should expect that the typical, Eddington-scaled jet power in low-mass galaxies is, if anything, higher than in high-mass galaxies.
However, galaxy halos may be expected to be qualitatively different in galaxies with different masses: a hot halo can form via an accretion shock in galaxies with a mass of their dark matter halo >1011 M⊙, whereas at lower masses, one expects that the accreting gas cools so fast that no shock forms (Birnboim & Dekel 2003). This difference has led to the concept that high mass galaxies accrete their gas mainly in the hot mode, that is by first shock-heating it to the virial temperature of the dark matter halo and subsequent gas cooling, whereas the lower mass galaxies accrete in the cold mode with cold gas being channeled into the galaxies along cosmic filaments (Dekel & Birnboim 2006). In a cosmological, hydrodynamic simulation, Kereš et al. (2005) find a critical dark matter mass, at a similar level of 3 × 1011 M⊙. We can use the halo occupation model of Moster et al. (2013) to derive a critical stellar mass of 1−3 × 109 M⊙ where the properties of the gas halos would be expected to change. However, this is different from the mass scale of 1011 M⊙ (stellar mass), now identified in the sensitive LOFAR measurements.
One might suspect that stellar feedback affects the properties of galaxy halos. Two types of interstellar medium-halo interactions are known: fountains, where the gas mainly circulates in the lower part of the halo (i.e. closer to the galactic disc), and galactic winds, where gas appears at above escape speed and the outflow likely proceeds beyond the virial radius of the galaxy (e.g. Chevalier & Clegg 1985; de Avillez & Breitschwerdt 2004, 2005; Veilleux et al. 2005; Dubois & Teyssier 2008; von Glasow et al. 2013; Gatto et al. 2015; Heckman & Thompson 2017; Kim & Ostriker 2018).
In the case of fountains, high entropy material accumulates at high altitudes and there is a smooth transition to a hydrostatic halo (e.g. de Avillez & Breitschwerdt 2004, 2005). This is confirmed by studies of the motion of HI clouds (e.g. Mirabel 1981; Kalberla & Dedes 2008; Marasco et al. 2012) and observations of the hot halo gas of the Milky Way in X-ray absorption and emission (Gupta et al. 2012, 2017; Bregman et al. 2018).
Simulations of galactic winds found that at the onset of the wind, any infalling or hydrostatic halo is swept up by a shock wave. The halo is left in a state of low density outflow with regions of turbulence and denser gas in filaments and the walls of the outflow cone (e.g. Strickland & Stevens 2000; Cooper et al. 2008; Dubois & Teyssier 2008; von Glasow et al. 2013; Ruszkowski et al. 2017). Multi-wavelength observations of the different gas phases are generally consistent with this structure (e.g. Veilleux et al. 2005; Strickland & Heckman 2007; Heckman & Thompson 2017).
The transition between wind and fountain solution occurs at different galaxy masses in different types of simulations; depending mainly on details of the feedback implementation. For example, Dubois & Teyssier (2008) use an effective equation of state for unresolved interstellar medium and energy input from clustered supernovae. They find a galactic wind for their galaxies with a circular velocity of 35 km s−1 (stellar mass ≈107 M⊙) and a fountain for 75 km s−1 galaxies (stellar mass ≈109 M⊙). Jacob et al. (2018), who also use an effective equation of state for unresolved interstellar medium and focus on cosmic rays as a driver of feedback, find galactic winds below 160 km s−1 (stellar mass ≈3 × 1010 M⊙) and a fountain solution at higher masses. Galactic winds consistently form in the simulations when a characteristic threshold of star formation rate per unit area is exceeded (e.g. von Glasow et al. 2013). Therefore, any given galaxy might switch repeatedly between wind and fountain, depending on the current availability of fuel for star formation.
Direct observations of hot gaseous halos of galaxies in X-rays are rare (for reviews see Putman et al. 2012; Tumlinson et al. 2017). For a few massive spirals and elliptical galaxies that have stellar mass ≳1011 M⊙, Bregman et al. (2018) report X-ray detections and also density profiles in some cases. The results are consistent with expectations for a gas halo at the virial temperature close to hydrostatic equilibrium. Strickland et al. (2004) show for a sample of disc galaxies with circular velocities between 100 and 244 km s−1 (stellar masses: ≈1010−1011 M⊙) that most of the extraplanar X-ray emission luminosity is likely related to superbubble blowout (see also Krause et al. 2014). However, the total vertical extent of the X-ray halos correlates with circular velocity and may therefore indicate a hydrostatic halo. Galaxies of all masses show multi-phase gas in their halos (e.g. Tumlinson et al. 2017; Bordoloi et al. 2018; Lan & Mo 2018). Winds at or above escape velocity have been reported up to circular velocities of 300 km s−1 (Heckman & Thompson 2017). Summarising, while trends of the state of gaseous halos (inflow, outflow or hydrostatic) with galaxy mass are expected, neither simulations nor observations currently provide a clear picture of these trends, or any particular galaxy masses where transitions would occur.
However, the new LOFAR LoTSS survey has clearly identified such a critical galaxy mass at ≈1011 M⊙. If this mass scale can be understood as a critical stellar mass at which the properties of gaseous halos of galaxies change significantly, we investigated with simple models for the maximum luminosity expected from the radio AGN of a galaxy of a given mass. We first constructed fiducial gaseous halo models for the different situations described above (Sect. 2). We describe our models for the radio emission of AGN-jets in the given halos (Sect. 3), compare to the LoTSS radio emitting galaxies in Sect. 4, and summarise our conclusions in Sect. 5.
2. Models for gaseous halos of galaxies
In this section we discuss three simple models for gaseous halos of galaxies. Hydrostatic halos are characterised by an overall equilibrium between gravity and pressure gradient. Both stellar and AGN feedback and gas cooling are unable to cause large perturbations to the overall equilibrium, but produce convection (a galactic fountain) in the lower part of the halo close to the stellar component, or buoyant bubbles. Wind halos occur where feedback in the galaxy is strong enough to lead to a global gaseous outflow from the galaxy beyond its virial radius. An inflow halo will occur where pressure forces in the halo and feedback from the galaxy are insufficient to balance the ram pressure of a global gas inflow into the galaxy. In reality, combinations of different halo types can occur in the same galaxy. For example, a disc galaxy could have a global inflow in its equatorial region when a starburst in its core drives an outflow in the polar directions at the same time. Since jets are a directed phenomenon, here we have only considered galaxies with one type of gaseous halo and imply that this is the type of halo relevant for the direction into which the jets are emitted.
2.1. Hydrostatic halos
We constructed a fiducial hydrostatic halo model from thermodynamic and cosmological constraints. Isothermal hydrostatic gas halos in Navarro et al. (1997) dark matter halos were derived in Makino et al. (1998). They indicated the resulting profile is similar to the conventional β-profile, which we adopt in the following: ρ(r) = ρ0(1 + (r/rc)2)−3β/2. Here ρ(r) is the gas density profile approximated as spherically symmetric and rc is the core radius. The Makino et al. (1998) gas profile is characterised by a core with a radius given by the scale radius Rs of the dark matter halo, which is related to the virial radius Rvir by the concentration C = Rvir/Rs. We used the fitting formula from Klypin et al. (2016) for redshift zero, C = 7.4(Mvir/(1012 M⊙/h))−0.12(1 + (Mvir/M0)0.4), with 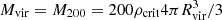 and M0 = 5.5 × 1017 M⊙/h. We used the Planck Collaboration XIII (2016) cosmology; for redshift zero, h = 0.68 and ρcrit = 8.62 × 10−30 g cm−3. Massive spiral as well as elliptical galaxies are well fit by the β-model with β ≈ 0.5 (Bregman et al. 2018) and we adopted this value. We note that this leads to a radio luminosity that declines with source size for radio sources larger than the core radius. Since we are primarily interested in the maximum luminosity a radio source can produce, the exact value of β is not important as long as β > 0.37, which is required for a radio luminosity that declines with source size (Hardcastle & Krause 2013; Yates et al. 2018). Since we are interested in the maximum radio luminosity of radio AGN for a given galaxy mass, we took the core density as the maximum density allowed, with the requirement that the radiative cooling time tc exceeds the dynamical time. For a given dark matter halo, we defined the dynamical time as tdyn = Rs/vvir with the virial velocity vvir = (G Mvir/Rvir)1/2. We linked virial masses to stellar masses M* by the halo occupation model of Moster et al. (2013), which we approximated as log10 M* = 2.2log10 Mvir − 15.4 for log10 Mvir < 11.8 and log10 M* = 0.4log10 Mvir + 5.8, otherwise. This yields dynamical times of the order of 100 Myr. Using the [Fe/H] = −0.5 and [Fe/H] = −1.0 (Bogdán et al. 2017; Bregman et al. 2018) collisional ionisation equilibrium cooling functions Λ(T) from Sutherland & Dopita (1993), the maximum particle density in a hydrostatic halo at the virial temperature is then given by nmax = kBTvir/(Λ(T) tc). We plot the maximum particle density in Fig. 1 and compared it to measurements for the Milky Way and a more massive spiral galaxy. The strong increase between M* = 1010 M⊙ and M* = 1011 M⊙ mirrors the behaviour of the cooling function for the relevant virial temperature. The scale radii become very large towards 1012 M⊙ and the model would lead to a strong overestimate of the total gas mass. Therefore, we restricted the valid range of the model to log10 M*/M⊙ ≤ 11.5. We adopted Fe/H = −0.5 as appropriate for the case of the Milky Way, most galaxies where it has been measured (Bregman et al. 2018), and the central galaxies of groups and clusters (Böhringer & Werner 2010). Assuming a metallicity of [Fe/H] = −1.0 would increase the gas density in the modelled halos by a factor of two or less. This would increase the predicted radio luminosities by less than 50% (compare, e.g. Maciel & Alexander 2014, their Fig. 10), which is not pertinent to the arguments presented here.
and M0 = 5.5 × 1017 M⊙/h. We used the Planck Collaboration XIII (2016) cosmology; for redshift zero, h = 0.68 and ρcrit = 8.62 × 10−30 g cm−3. Massive spiral as well as elliptical galaxies are well fit by the β-model with β ≈ 0.5 (Bregman et al. 2018) and we adopted this value. We note that this leads to a radio luminosity that declines with source size for radio sources larger than the core radius. Since we are primarily interested in the maximum luminosity a radio source can produce, the exact value of β is not important as long as β > 0.37, which is required for a radio luminosity that declines with source size (Hardcastle & Krause 2013; Yates et al. 2018). Since we are interested in the maximum radio luminosity of radio AGN for a given galaxy mass, we took the core density as the maximum density allowed, with the requirement that the radiative cooling time tc exceeds the dynamical time. For a given dark matter halo, we defined the dynamical time as tdyn = Rs/vvir with the virial velocity vvir = (G Mvir/Rvir)1/2. We linked virial masses to stellar masses M* by the halo occupation model of Moster et al. (2013), which we approximated as log10 M* = 2.2log10 Mvir − 15.4 for log10 Mvir < 11.8 and log10 M* = 0.4log10 Mvir + 5.8, otherwise. This yields dynamical times of the order of 100 Myr. Using the [Fe/H] = −0.5 and [Fe/H] = −1.0 (Bogdán et al. 2017; Bregman et al. 2018) collisional ionisation equilibrium cooling functions Λ(T) from Sutherland & Dopita (1993), the maximum particle density in a hydrostatic halo at the virial temperature is then given by nmax = kBTvir/(Λ(T) tc). We plot the maximum particle density in Fig. 1 and compared it to measurements for the Milky Way and a more massive spiral galaxy. The strong increase between M* = 1010 M⊙ and M* = 1011 M⊙ mirrors the behaviour of the cooling function for the relevant virial temperature. The scale radii become very large towards 1012 M⊙ and the model would lead to a strong overestimate of the total gas mass. Therefore, we restricted the valid range of the model to log10 M*/M⊙ ≤ 11.5. We adopted Fe/H = −0.5 as appropriate for the case of the Milky Way, most galaxies where it has been measured (Bregman et al. 2018), and the central galaxies of groups and clusters (Böhringer & Werner 2010). Assuming a metallicity of [Fe/H] = −1.0 would increase the gas density in the modelled halos by a factor of two or less. This would increase the predicted radio luminosities by less than 50% (compare, e.g. Maciel & Alexander 2014, their Fig. 10), which is not pertinent to the arguments presented here.
 |
Fig. 1. Maximum particle density of the hydrostatic halo as a function of stellar mass according to the model presented in Sect. 2.1 for two metallicities. For comparison, we show measurements for the Milky Way (Gupta et al. 2017, using the stellar mass estimate of 6 × 1010 M⊙ from Bovy & Rix 2013 and Taylor et al. 2016) and the massive spiral galaxy NGC 6753 (Bogdán et al. 2017). |
2.2. Galactic wind halos
Following the work of Chevalier & Clegg (1985), we assumed a core that has almost constant density and pressure, where the stellar mass and energy input take place and a free wind zone at constant outflow velocity with density declining as r − 2. The solution is fully determined by the energy and mass input rates Ṁ and Ė, which are both linear in the star formation rate. The core temperature is proportional to Ė/Ṁ and therefore constant for all systems. The initial temperature could be as high as ≈10 keV (Chevalier & Clegg 1985; Strickland & Heckman 2007). However, similar to the case of superbubbles (Krause et al. 2014; Rogers & Pittard 2014), mixing the material from swept-up shells and remnant cloud cores likely reduces the temperature of the hot phase quickly. We therefore adopted a temperature of 3 keV which is approximately the lower limit allowed by models for the nearby and probably best studied wind galaxy M 82 (Strickland & Heckman 2009). The density in the model increases with the star formation rate; nevertheless, realistic conditions should be dominated by mixing as well. Furthermore, following Strickland & Heckman (2009), we adopt a core density of 0.6 cm−3 M*/M82, where M82 is the stellar mass of M 82. The latter is between 109 M⊙ (Förster Schreiber et al. 2003) and 1010 M⊙ (dynamical mass estimate Greco et al. 2012). We adopted M82 = 1010 M⊙, because the lower value takes only the central parts of the galaxy into account. Using the lower value would increase the core densities by a factor of ten and the radio luminosities for this model would consequently be higher by a factor of a few (compare, e.g. Maciel & Alexander 2014, their Fig. 10). This would not change the conclusions of the present analysis (compare below, e.g. Fig. 3). We used a constant core radius of 500 pc, as for M82 (Greco et al. 2012), for all galaxies. We note that the thermal pressure quickly declines outside the core, and subsequently the isothermality assumed by our β-model ansatz is violated. We ignored this effect, because we expected the maximum radio luminosity to be on the scale of the core radius.
2.3. Infall halos
In the infalling halo picture, galaxies get their fuel for star formation from accretion of intergalactic gas. The accretion rate is therefore given by the star formation rate. For this, we used the average star formation rate of the main sequence enhanced by one standard deviation from Belfiore et al. (2018): −log Ṁ/M⊙ yr−1 =
log Ṁ∗/M⊙ yr−1 = 0.73 log(M∗/M⊙) − 6.94. While some of this gas might be clumpy, we get an upper limit on the gas density by assuming spherically symmetric accretion. To model this, we consider either a free fall or Bondi accretion into a Navarro et al. (1997) dark matter halo. The velocity close to the galaxy is in both cases given by 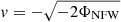 , where the Navarro-Frenk-White potential is given by (Hayashi et al. 2007):
, where the Navarro-Frenk-White potential is given by (Hayashi et al. 2007):
We then calculated the halo density from mass conservation, Ṁ = 4πr2ρv. Since the infalling medium is assumed to be cold, the relevant halo pressure is now the ram pressure of the infalling halo, ρv2. This leads to an almost constant velocity in the relevant inner part of the halo and thus a density and ram pressure distribution as r−2. This can be modelled by an isothermal beta profile with β = 2/3. We assumed the infall continues down to 0.5 kpc, where we assume normal star formation processes keep the density constant and the pressure balanced with the ram pressure of the infalling halo.
3. Radio luminosities of jets in different halos
The early evolution of radio AGN is addressed in Alexander (2006) and Maciel & Alexander (2014). As can be seen, for example from Fig. 5 in Maciel & Alexander (2014), the source luminosity increases throughout the early evolution into the self-similar phase. It reaches its peak approximately where the ambient density distribution starts to decline, that is near the core radius. In this phase, the radio lobes dominate the luminosity. For an estimate of the radio luminosity, it is therefore appropriate to use a standard model for the evolution of radio lobes, such as the one in Hardcastle (2018). The model requires that radio lobes have formed already, which first happens when the radio source has reached a certain size given, for example by Krause et al. (2012). We confirmed that the radio lobes form earlier than our scale of interest for all cases; therefore, we then used the standard radio lobe models of Hardcastle (2018). The model is based on 3D simulation results (Hardcastle & Krause 2013, 2014; English et al. 2016), distributes a constant fraction of the steadily supplied power Q0, respectively to radio lobes and shocked ambient gas, and advances the prolate spheroidal outer shock surface according to the Rankine-Hugoniot shock jump conditions. It assumes that the lobes consist of an electron-positron pair plasma (compare below) and that the ratio between the energy in the magnetic field and the one in particles is 0.1. We assumed an injection power law index for relativistic electrons of q = −2.2. Adiabatic, synchrotron, and inverse Compton losses at the cosmic microwave background (redshift z = 0) are taken into account. Sabater et al. (2019) probe the jet power distribution for massive galaxies, 1011 M⊙ < M* < 1012 M⊙, as a fraction of the Eddington luminosity LEd of the supermassive black hole. They find a strong decline towards higher jet powers. Only 0.3% of all galaxies have a radio AGN with Q0 > 10−2LEd. We therefore adopted this as the upper limit for radio sources in all galaxies. To estimate the black hole masses, we adopt a constant mass fraction, MSMBH = 0.0005 M* (Bentz & Manne-Nicholas 2018).
We show a plot of the resulting radio luminosities at 150 MHz over lobe length in Fig. 2 for an intermediate mass galaxy. Due to our assumption that wind and infall halos have a small core region of only 0.5 kpc, the radio luminosity also peaks on this scale. The relevant length scale for the hydrostatic halo is the scale radius of the dark matter halo. Consequently, the peak of the radio luminosity is reached at a scale of tens of kpc. The peak luminosities for the wind and infall models are much higher than for the hydrostatic halo case. This is because cooling severely restricts the density in a hydrostatic halo at the galaxy mass of the chosen example, M* = 3 × 1010 M⊙. If the core radius was assumed to be greater than 0.5 kpc, the luminosities in the wind and infall models would increase even further. The radio luminosity in our models scales directly with the kinetic jet power, which is linearly coupled to the black hole mass. Varying the black hole mass to galaxy mass ratio would therefore shift all models along the vertical axis in Figs. 2 and 3.
 |
Fig. 2. Example radio luminosity at 150 MHz versus lobe length plots for hydrostatic, galactic wind and infall halos for a galaxy of stellar mass M* = 3 × 1010 M⊙ and the maximum plausible jet power in our model of 2 × 1036 W. See Sect. 2 for details about the gaseous halo models and Sect. 3 for details about the radio source model. |
 |
Fig. 3. Maximum 150 MHz luminosity of radio AGN for a given galaxy mass for three different models of the gaseous halo of the galaxies (hydrostatic halo, infall halo, wind halo). Data points are from the LoTSS sample (Sabater et al. 2019), plotted separately for star forming galaxies (SFG), and radio AGN. The radio luminosity expected from star formation for galaxies on the main sequence of star formation at redshift zero is indicated as a solid thin green line (Sect. 2.3, Eq. (3) in Gürkan et al. 2018). The dotted black line denotes the completeness limit, i.e. the median limiting luminosity at the maximum redshift of the sample. For the hydrostatic halo model, radio AGN with the same Eddington-scaled jet power distribution could be hosted by galaxies of all masses. The lower densities in the halos of lower mass galaxies would, however, limit their radio luminosities. Radio AGN need to be intrinsically less powerful or otherwise different in low mass galaxies that are in galactic wind or any quasi-spherical infall phases in order not to exceed the LOFAR radio luminosity constraints. |
4. Comparison to the LoTSS sample
We compare the maximum of the predicted radio luminosities against galaxy mass for all halo models to the LoTSS measurements in Fig. 3. The radio sources in the hydrostatic halos approximate the upper envelope of the data points well. It is commonly known that the models reproduce radio luminosities of radio sources in large dark matter halos effectively (Hardcastle & Krause 2013; Hardcastle 2018). Another interesting feature of the present model is that the radio luminosities of smaller galaxies are not overpredicted by a large factor. A scenario where galaxies have hydrostatic gas halos and where radio AGN in low-mass galaxies have the same jet-power distribution as the ones in high-mass galaxies (in terms of the Eddington luminosity of the supermassive black hole) is therefore consistent with the data. The disproportionately lower radio luminosities at low galaxy masses are due to the lower halo gas densities, which are a direct consequence of the higher cooling rates at a lower halo temperature, which via the virial temperature is a function of the galaxy mass (compare Fig. 1). The radio luminosity in any given low-mass galaxy might still be due to star formation. The models only tell us that if the galaxy developed a radio AGN, its radio luminosity would not exceed a certain luminosity. The models therefore need to be compared to the upper envelope of the observed distribution.
Radio sources in wind galaxies or in halos dominated by spherical infall would have a luminosity far greater than observed. This could either indicate that galaxies do not have strong radio AGN in such phases or that such conditions are rare. This would coincide with findings in the literature that starburst and AGN phases are sequential rather than simultaneous (e.g. Krause 2005; Schawinski et al. 2007; Schartmann et al. 2010; Shabala et al. 2012). The predicted luminosities become very similar at high galaxy masses. At those masses, all halo models are consistent with the radio observations.
An interesting caveat here is the type of the radio source. It is possible that jets in more strongly star-forming systems suffer much more entrainment of proton-rich interstellar medium, and therefore develop more Fanaroff & Riley (1974) class I-like radio sources (Croston et al. 2018). In this case, the same jet power would also be distributed to additional protons, and thus the expected radio luminosity would be lower than in our model; possibly to a degree that could reconcile the prediction for wind and infall halos with the observations.
The spatial resolution of the LoTSS survey corresponds to 28 kpc at the redshift limit of z = 0.3 (6 arcsec resolution, Sabater et al. 2019). Radio AGN in infall and wind halos would therefore mostly be unresolved. The maximum radio luminosity in hydrostatic halos occurs around 20 (40, 100) kpc for 109(1010, 1011) M⊙ galaxies. Radio AGN would therefore also frequently be unresolved in less massive galaxies in our model, if they had a hydrostatic halo. This agrees with the findings of Shabala (2018) that the fraction of unresolved radio AGN decreases with increasing galaxy mass. This prediction could be tested with LOFAR observations that include international baselines (< 1 arcsec resolution, Ramírez-Olivencia et al. 2018). These are, however, not yet available for large samples of galaxies.
The maximum radio luminosity we predict in our models should not be regarded as a strict upper limit on the measured LOFAR 150 MHz luminosities. We estimate the measurement uncertainties for the luminosities due to uncertainties of the flux calibration scale to about 0.3 dex or more (compare Hardcastle et al. 2019). Also, jet powers are known to sometimes exceed our choice of 1% of the Eddington luminosity (Sabater et al. 2019). For example Turner et al. (2018) estimate jet powers around 1047 erg s−1 for several 3C radio sources in galaxies with 11.5 < log(M*/M⊙) < 12. The jet power in these sources likely exceeds 10% of the Eddington luminosity. Also, the black hole mass scaling relation has a scatter of about a factor of three. Taken together, individual sources could still be one or two dex more luminous than predicted by our model.
However, the high jet power phases might be rare and linked to galaxy merging (Ramos Almeida et al. 2012; Shabala et al. 2012; Tadhunter et al. 2014; Krause et al. 2019). The Sabater et al. (2019) sample is local (redshift z ≤ 0.3) and therefore contains relatively few recent mergers, especially for the lower galaxy masses (Hopkins et al. 2010). For the general population of galaxies, our assumptions cover the top end of the relevant distributions well. In Sabater et al. (2019), significantly less than 1% of the radio sources exceed our jet power limit and the halo properties that we assume take account of the scatter. For example, Fig. 1 demonstrates that observations fall comfortably below our limiting halo gas density.
5. Conclusions
We used an established model for the radio luminosity of radio AGN to estimate the maximum AGN-related LOFAR 150 MHz luminosities of galaxies. As input to our model, we assume a jet power of 1% of the Eddington luminosity with supermassive black hole masses following the observed scaling relation and models for the gaseous halos of galaxies based on theoretical constraints and observations. We considered hydrostatic, galactic wind, and infall halos. Our aim is to explain the marked rise of radio luminosities at stellar masses around 1011 M⊙. Our main findings are:
-
The shape of the cooling function translates into higher hydrostatic halo masses, and hence a marked increase in radio luminosity around 1011 M⊙.
-
Assuming hydrostatic gas halos in all galaxies and the jet power distribution seen in massive galaxies to hold for all galaxies (as fraction of the Eddington luminosity), we find an upper envelope for the radio luminosities that matches the data well.
-
Disproportionately lower radio luminosities in low-mass galaxies can therefore not be used as an argument that radio AGN are absent in such galaxies.
-
A model where low-mass galaxies are dominated either by winds or infall and higher mass galaxies by hydrostatic gas halos is not supported by the data. Models expect the presence of hydrostatic halos in galaxies with masses M* ≳ 109 M⊙ (Birnboim & Dekel 2003; Kereš et al. 2005). This corresponds to the mass range covered by the LOTSS sample. Our findings are hence consistent with these predictions.
-
We would predict higher radio luminosities than observed for low-mass galaxies, if their jets were frequently launched in phases of smooth, quasi-spherical inflow or galactic winds, unless jets in such environments suffer a lot of entrainment of proton-rich gas. This is consistent with the idea that galactic winds and AGN-jet outbursts do not happen at the same time.
-
Our results are also consistent with scenarios in which radio AGN occur much more rarely in lower mass galaxies, such that their radio luminosities are always completely dominated by star formation. We regard, however, the alternative, namely that AGN have similar jet power distributions at all galaxy masses, which is as well consistent with the data, as the simpler explanation.
Acknowledgments
We gratefully acknowledge the provision of the LOFAR radio data in electronic form by Jose Sabater Montes. MK thanks Jim Dale for comments on parts of the manuscript. We thank the anonymous referee for a very useful report.
References
- Alexander, P. 2006, MNRAS, 368, 1404 [NASA ADS] [CrossRef] [Google Scholar]
- Belfiore, F., Maiolino, R., Bundy, K., et al. 2018, MNRAS, 477, 3014 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., & Manne-Nicholas, E. 2018, ApJ, 864, 146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Best, P. N., & Heckman, T. M. 2012, MNRAS, 421, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., Kauffmann, G., Heckman, T. M., et al. 2005, MNRAS, 362, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Birnboim, Y., & Dekel, A. 2003, MNRAS, 345, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdán, Á., Bourdin, H., Forman, W. R., et al. 2017, ApJ, 850, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., & Werner, N. 2010, A&ARv, 18, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bordoloi, R., Prochaska, J. X., Tumlinson, J., et al. 2018, ApJ, 864, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., & Rix, H.-W. 2013, ApJ, 779, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Bregman, J. N., Anderson, M. E., Miller, M. J., et al. 2018, ApJ, 862, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Clegg, A. W. 1985, Nature, 317, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., Ferrara, A., Forveille, T., et al. 2019, A&A, 622, E1 [CrossRef] [EDP Sciences] [Google Scholar]
- Cooper, J. L., Bicknell, G. V., Sutherland, R. S., & Bland-Hawthorn, J. 2008, ApJ, 674, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Croston, J. H., Ineson, J., & Hardcastle, M. J. 2018, MNRAS, 476, 1614 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2004, A&A, 425, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2005, A&A, 436, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Dubois, Y., & Teyssier, R. 2008, A&A, 477, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, K. J., Sabater, J., Röttgering, H. J. A., et al. 2019, A&A, 622, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- English, W., Hardcastle, M. J., & Krause, M. G. H. 2016, MNRAS, 461, 2025 [NASA ADS] [CrossRef] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Lutz, D., & Sternberg, A. 2003, ApJ, 599, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Gatto, A., Walch, S., Low, M.-M. M., et al. 2015, MNRAS, 449, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Greco, J. P., Martini, P., & Thompson, T. A. 2012, ApJ, 757, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A., Mathur, S., Krongold, Y., Nicastro, F., & Galeazzi, M. 2012, ApJ, 756, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A., Mathur, S., & Krongold, Y. 2017, ApJ, 836, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Gürkan, G., Hardcastle, M. J., Smith, D. J. B., et al. 2018, MNRAS, 475, 3010 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. 2015, in The Formation and Disruption of Black Hole Jets, eds. I.Contopoulos, D.Gabuzda, & N.Kylafis, Astrophys. Space Sci. Lib., 414, 83 [NASA ADS] [Google Scholar]
- Hardcastle, M. J. 2018, MNRAS, 475, 2768 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., & Krause, M. G. H. 2013, MNRAS, 430, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., & Krause, M. G. H. 2014, MNRAS, 443, 1482 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Ching, J. H. Y., Virdee, J. S., et al. 2013, MNRAS, 429, 2407 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Williams, W. L., Best, P. N., et al. 2019, A&A, 622, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Häring, N., & Rix, H.-W. 2004, ApJ, 604, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, E., Navarro, J. F., & Springel, V. 2007, MNRAS, 377, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., & Thompson, T. A. 2017, ArXiv eprints [arXiv:1701.09062] [Google Scholar]
- Hopkins, P. F., Bundy, K., Croton, D., et al. 2010, ApJ, 715, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Jacob, S., Pakmor, R., Simpson, C. M., Springel, V., & Pfrommer, C. 2018, MNRAS, 475, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, C. R., Dennett-Thorpe, J., & Alexander, P. 1997, MNRAS, 292, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., & Dedes, L. 2008, A&A, 487, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, G., Heckman, T. M., & Best, P. N. 2008, MNRAS, 384, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Kereš, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, C.-G., & Ostriker, E. C. 2018, ApJ, 853, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Yepes, G., Gottlöber, S., Prada, F., & Heß, S. 2016, MNRAS, 457, 4340 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M. 2005, A&A, 436, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krause, M. 2018, in The Physical Universe, eds. S. J. Wagh, S. D. Maharaj, & G. Chon (Nagpur, India: Central India Research Institute), [astro-ph:1804.01741] [Google Scholar]
- Krause, M., Alexander, P., Riley, J., & Hopton, D. 2012, MNRAS, 427, 3196 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M., Diehl, R., Böhringer, H., Freyberg, M., & Lubos, D. 2014, A&A, 566, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krause, M. G. H., Shabala, S. S., Hardcastle, M. J., et al. 2019, MNRAS, 482, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Lan, T.-W., & Mo, H. 2018, ApJ, 866, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Maciel, T., & Alexander, P. 2014, MNRAS, 442, 3469 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Makino, N., Sasaki, S., & Suto, Y. 1998, ApJ, 497, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Manolakou, K., & Kirk, J. G. 2002, A&A, 391, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marasco, A., Fraternali, F., & Binney, J. J. 2012, MNRAS, 419, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, P. J. 1993, A&ARv, 31, 639 [Google Scholar]
- Merloni, A., & Heinz, S. 2008, MNRAS, 388, 1011 [NASA ADS] [Google Scholar]
- Mirabel, I. F. 1981, Mex. Astron. Astrofis., 6, 245 [NASA ADS] [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P. 2017, Nat. Astron., 1, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Putman, M. E., Peek, J. E. G., & Joung, M. R. 2012, ARA&A, 50, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez-Olivencia, N., Varenius, E., Pérez-Torres, M., et al. 2018, A&A, 610, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramos Almeida, C., Bessiere, P. S., Tadhunter, C. N., et al. 2012, MNRAS, 419, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Reines, A. E., & Volonteri, M. 2015, ApJ, 813, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, H., & Pittard, J. M. 2014, MNRAS, 441, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Ruszkowski, M., Yang, H.-Y. K., & Zweibel, E. 2017, ApJ, 834, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Sabater, J., Best, P. N., Hardcastle, M. J., et al. 2019, A&A, 622, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schartmann, M., Burkert, A., Krause, M., et al. 2010, MNRAS, 403, 1801 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Thomas, D., Sarzi, M., et al. 2007, MNRAS, 382, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Shabala, S. S. 2018, MNRAS, 478, 5074 [NASA ADS] [CrossRef] [Google Scholar]
- Shabala, S. S., Ting, Y.-S., Kaviraj, S., et al. 2012, MNRAS, 423, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Shimwell, T. W., Tasse, C., Hardcastle, M. J., et al. 2019, A&A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soltan, A. 1982, MNRAS, 200, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Strickland, D. K., & Heckman, T. M. 2007, ApJ, 658, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Strickland, D. K., & Heckman, T. M. 2009, ApJ, 697, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Strickland, D. K., & Stevens, I. R. 2000, MNRAS, 314, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Strickland, D. K., Heckman, T. M., Colbert, E. J. M., Hoopes, C. G., & Weaver, K. A. 2004, ApJ, 606, 829 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Tadhunter, C. 2016, A&ARv, 24, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Tadhunter, C., Dicken, D., Morganti, R., et al. 2014, MNRAS, 445, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, C., Boylan-Kolchin, M., Torrey, P., Vogelsberger, M., & Hernquist, L. 2016, MNRAS, 461, 3483 [NASA ADS] [CrossRef] [Google Scholar]
- Tucci, M., & Volonteri, M. 2017, A&A, 600, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tumlinson, J., Peeples, M. S., & Werk, J. K. 2017, ARA&A, 55, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, R. J., & Shabala, S. S. 2015, ApJ, 806, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, R. J., Shabala, S. S., & Krause, M. G. H. 2018, MNRAS, 474, 3361 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [Google Scholar]
- von Glasow, W., Krause, M. G. H., Sommer-Larsen, J., & Burkert, A. 2013, MNRAS, 434, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, W. L., Hardcastle, M. J., Best, P. N., et al. 2019, A&A, 622, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yates, P. M., Shabala, S. S., & Krause, M. G. H. 2018, MNRAS, 480, 5286 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Maximum particle density of the hydrostatic halo as a function of stellar mass according to the model presented in Sect. 2.1 for two metallicities. For comparison, we show measurements for the Milky Way (Gupta et al. 2017, using the stellar mass estimate of 6 × 1010 M⊙ from Bovy & Rix 2013 and Taylor et al. 2016) and the massive spiral galaxy NGC 6753 (Bogdán et al. 2017). |
| In the text | |
 |
Fig. 2. Example radio luminosity at 150 MHz versus lobe length plots for hydrostatic, galactic wind and infall halos for a galaxy of stellar mass M* = 3 × 1010 M⊙ and the maximum plausible jet power in our model of 2 × 1036 W. See Sect. 2 for details about the gaseous halo models and Sect. 3 for details about the radio source model. |
| In the text | |
 |
Fig. 3. Maximum 150 MHz luminosity of radio AGN for a given galaxy mass for three different models of the gaseous halo of the galaxies (hydrostatic halo, infall halo, wind halo). Data points are from the LoTSS sample (Sabater et al. 2019), plotted separately for star forming galaxies (SFG), and radio AGN. The radio luminosity expected from star formation for galaxies on the main sequence of star formation at redshift zero is indicated as a solid thin green line (Sect. 2.3, Eq. (3) in Gürkan et al. 2018). The dotted black line denotes the completeness limit, i.e. the median limiting luminosity at the maximum redshift of the sample. For the hydrostatic halo model, radio AGN with the same Eddington-scaled jet power distribution could be hosted by galaxies of all masses. The lower densities in the halos of lower mass galaxies would, however, limit their radio luminosities. Radio AGN need to be intrinsically less powerful or otherwise different in low mass galaxies that are in galactic wind or any quasi-spherical infall phases in order not to exceed the LOFAR radio luminosity constraints. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.