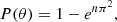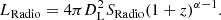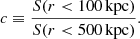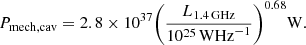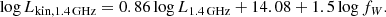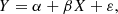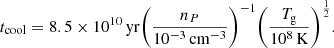EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A188 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A188
Number of page(s) 14
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202346912
Published online 25 September 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The hot gas in galaxy clusters, called the intracluster medium (ICM), is strongly affected by feedback of active galactic nuclei (AGN). AGN reside in the dominant cD galaxies of clusters, which host the most massive black holes of the Universe. Two different modes of AGN feedback are found in observations: the radiative or quasar mode, and the radio or jet mode (Cattaneo et al. 2009; Heckman & Best 2014). The radiative mode causes uniform heating of the environment around it, whereas in radio mode, AGN jets expel radio-heated gas from the accreting black hole matter into the ICM and push the existing X-ray heated cluster gas away (Shabala et al. 2020). Therefore, on the one hand, AGN activity prevents the cooling of gas and subsequent star formation, and on the other hand, AGN contribute to star formation by projecting jets toward the ICM and compressing the gas. An increment of radiative losses of the ICM in turn leads to an increment in heating of the gas by the AGN. The more gas cools, the higher the energy output that is able to quench the radiative losses. This is known as the AGN feedback loop (McNamara et al. 2016; Gaspari et al. 2020). AGN feedback has been observed in a wide range of systems, from isolated elliptical galaxies to massive clusters. The most powerful AGN operating in radio mode can be found in the brightest cluster galaxies (BCGs), which usually are massive elliptical galaxies residing at the bottom of the clusters potential (e.g., reviews by Fabian 2012; Gitti et al. 2012; McNamara & Nulsen 2012).

Ineson et al. (2013, 2015) performed a study of the interplay between AGN and their environment in a sample of radio-loud AGN galaxy clusters and galaxy groups. As a result, they found a correlation between the X-ray emission from the ICM and the power of the corresponding central radio source at 151 MHz. They argued that this correlation could arise from AGN in a phase of radiatively inefficient accretion, which are also called low-excitation radio galaxies (LERGs), while high-excitation radio galaxies (HERGs) stand out of the distribution and show higher radio powers. However, it is important to note that the origin of this relation is not obvious as X-ray emission in clusters and groups is mostly due to line emission and Bremsstrahlung that allows the ICM to cool. Therefore, the timescale of these radiative losses is strongly dependent on the distance of the diffuse gas from the cluster core, which varies from less than 1 Gyr in the center of the strongest cool-cores to a few billion years in the outskirts. Nipoti & Binney (2005), on the other hand, suggested that the AGN power output reoccurs and acts in cycles of ∼108 yr. As a consequence, the timescales of these two processes are usually significantly different. On the other hand, Hardcastle et al. (2019) suggested that the majority of sources are compact and therefore short-lived, and so the cycle is many short-lived (∼1 Myr) intermittent bursts (see also Shabala et al. 2008). Pasini et al. (2020, 2021, 2022) investigated the radio power of the central radio galaxy in galaxy clusters and in galaxy groups at different wavelengths. The authors also found positive correlations between the radio power of the central AGN at frequencies from 144 MHz to 1.4 GHz and the main properties of the diffuse X-ray intragroup and intracluster medium, again suggesting a link between AGN heating and cooling processes in the gaseous halo (Pope et al. 2012).

Deep X-ray observations with XMM-Newton and Chandra have revealed that most of the systems with radio-mode AGN have disturbed X-ray morphologies caused by AGN-ejected jets. These surface brightness features, including cavities in the X-ray images and sharp density discontinuities that are interpreted as shocks, indicate a strong correlation between the ICM and the central AGN. The thermodynamical properties of the intracluster gas is also affected by AGN feedback in teRMS of the gas entropy distribution and transport of high-metallicity gas from the center of the cluster to its outskirts. The X-ray cavities or bubbles that have been discovered in X-ray images of clusters are often filled with radio emission. This leads to the assumption that radio plasma produced by AGN outflows displaces the X-ray emitting gas of the ICM. One of the main results of these observations was the revelation of a scaling relation between the cavity power and the radio luminosity (Bîrzan et al. 2004, 2020; Rafferty et al. 2006; Timmerman et al. 2022).

The extended ROentgen Survey with an Imaging Telescope Array (eROSITA) on board the Spectrum-Roentgen-Gamma (SRG) mission was launched in July 2019 (Predehl et al. 2021). eROSITA will perform all-sky surveys (eRASS) with a significantly improved sensitivity compared to the ROSAT all-sky survey. In contrast to X-ray telescopes such as XMM-Newton or Chandra, which are used for long-exposure pointed observations of single targets, eROSITA allows unique survey science capabilities by scanning large areas of the X-ray sky fast and efficiently. The eRASS survey is detecting a large number of previously undetected galaxy clusters and will substantially extend existing galaxy cluster catalogs (Merloni et al. 2012; Liu et al. 2022).

In this work, we make use of the cluster catalog resulting from the first all-sky scan (eRASS:1), which was completed in 2020 (Bulbul et al., in prep.). We study the central radio galaxies in the cluster centers with 944 MHz radio data from the survey called Evolutionary Map of the Universe (EMU) that was performed by the Australian Square Kilometre Array Pathfinder (ASKAP; Norris et al. 2021).

The paper is structured as follows: in Sect. 2 we explain how our sample was created, and we display its main properties. In Sect. 3 we examine and discuss the correlation between the radio and the X-ray emission from our sample in comparison to other correlations. Finally, we conclude in Sect. 4. Throughout this paper, we assume the standard ΛCDM cosmology with H0 = 70 km s−1 Mpc−1, ΩΛ = 0.7, and ΩM = 0.3.

2. Data

2.1. eRASS:1 cluster catalog

eROSITA is an X-ray space telescope operating in the 0.2–10 keV energy range on board the SRG mission (Sunyaev et al. 2021; for more information on this mission, see, e.g., the instrument paper by Predehl et al. 2021). It has an effective area of 1365 cm2 and a spectral resolution of 80 eV FWHM (Full Width at Half Maximum) at 1 keV and an angular survey resolution of 26 arcsec. The first task of eROSITA is to scan the whole X-ray sky with a final depth of about 1.3 ks. The sensitivity will therefore be improved by at least a factor of 20 compared to the only previous X-ray all-sky survey performed by ROSAT 30 years ago. The main task of eROSITA is the study of evolution and nature of dark energy. eROSITA is expected to detect about 105 galaxy clusters and more than one million AGN (Merloni et al. 2012, 2020).

The first all-sky survey eRASS:1 imaged the whole X-ray sky over the course of 182 days from December 2019 to June 2020, with an average effective exposure of 150–200 s. About 104 clusters are detected as extended sources in eRASS:1 using the source detection algorithm in the eROSITA Standard Analysis Software System (eSASS; Brunner et al. 2022). Redshifts are determined using data from the Legacy Survey. Details about the eRASS:1 galaxy cluster catalog can be found in Bulbul et al. (in prep.). The X-ray luminosity that is used throughout this paper was calculated in the 0.2–2.3 keV band.

2.2. EMU pilot field

The Australian Square Kilometer Array Pathfinder (ASKAP) is a radio telescope in the Murchison region of Western Australia (Johnston et al. 2008; Hotan et al. 2021; Koribalski 2022). ASKAP is a radio interferometer consisting of 36 12-meter dish antennas, spread out in two dimensions with baselines up to 6 km. Each antenna is equipped with a wide-field phased array feed (PAF) that is used to form 36 beams, that is, each pointing reaches a field of view of ∼30 deg2.

The survey project called evolutionary map of the Universe (EMU) uses the ASKAP telescope. In July to August 2019, EMU observed a pilot field for 100 h to test the planned observing mode for the full EMU survey. The EMU pilot survey mapped 270 deg2 of sky with a RA from 305° to 335° and Dec from −62° to −48°, centered at 944 MHz down to an RMS of about 25–30 μJy beam−1 at an angular resolution of 10–18 arcsec (see Norris et al. 2011, 2021 for further details on the survey).

As images with large fields of view such as the EMU pilot field yield a large number of detected astronomical sources, an automated source detection technique that measures the properties of the sources is essential. The most common approach is to identify local peaks of emission above some threshold, and fitting two-dimensional Gaussians. As radio surveys have become deeper and wider in recent years, the number of sources in catalogs has grown enormously, such that manual source-finding and identification is no longer feasible. An ASKAP/EMU source-finding challenge by Hopkins et al. (2015) that was carried out before the start of EMU tested several approaches for an automatic source detection. Source-finding and cataloging is the last step in the ASKAP data-processing pipeline (ASKAPsoft; e.g., Guzman et al. 2019; Wieringa et al. 2020) for all surveys such as continuum, HI emission and absorption, and polarization, carried out using Selavy (Whiting et al. 2017). More powerful source finders will likely be applied by each team to their specific projects.

The image data were first processed by the ASKAPsoft pipeline, and the subsequent source extraction of the final calibrated image used the software tool Selavy. This tool identifies radio islands with emissions higher than five times the local RMS, and it fits Gaussians to peaks of emission within the islands. The peak as well as the integrated radio flux of each island is computed and stored in a FITS catalog containing a total number of ∼220 000 radio islands, ∼180 000 of which are single-component sources. In comparison with previous surveys, EMU explores a novel region of parameter space because of the ASKAP wide field of view combined with high angular resolution as well good sensitivity. For a summary of the EMU pilot survey specifications, see Table 1.

Table 1.

EMU pilot survey specifications.

2.3. Construction of the sample

The EMU pilot field is fully covered by eRASS:1. Therefore, we created a cluster sample with all eRASS:1 detected clusters within the EMU field, resulting in a total number of 75 confirmed eRASS:1 clusters. Each cluster was visually inspected in the EMU image as well as in WISE and in legacy optical data to identify the BCG of each cluster and the corresponding radio source to the BCG.

We identified the BCG and the corresponding central radio island for each cluster. For 64 of the 75 clusters, we found a central radio source within a distance of ∼θ to the BCG, where θ = 18 arcsec, which is the synthesized beam of the radio observation. For the remaining 11 clusters, we set an upper limit of 3σ, where σ is the RMS noise of the EMU image of RMS = 35 μJy. Magliocchetti & Brüggen (2007) examined radio emission of 550 X-ray selected clusters and reported that only 27% host a central radio source. However, the difference in these results can be attributed to the depth of the respective datasets because the depth of the survey they used reaches only 3 mJy, whereas the EMU has a depth of 35 μJy.

Visual inspection of each source is the most reliable way to minimize the number of false identifications because at all separations, some radio identifications selected by the position offset alone will be random coincidences (Condon et al. 2002; Sadler et al. 2002; Mauch & Sadler 2007). Nonetheless, we still expect a fraction of false associations, which we describe via the P-statistics. This quantifies the probability that a radio source has a chance coincidence within a distance θ from a certain point, here our BCG candidate. It is given by

(1)

with n denoting the number density of radio sources (Scott et al. 2008). When we assume a uniform distribution of radio sources of n = 815 deg−2, which is the average source density from an ASKAP observation, we obtain P(18 arcsec) = 6.6% contamination. For the 64 clusters with a radio match, we therefore expect about three false associations.

2.4. Properties of the sample

The upper panel of Fig. 1 shows a histogram of the redshift distribution of our cluster sample. The majority of the clusters lie within a redshift range of 0.1 < z < 0.7. Two outliers lie above z > 0.8. We used the best available redshift provided from the eRASS:1 cluster catalog, which can be spectroscopic or photometric redshifts. The lower panel of Fig. 1 shows the mass distribution. The mass was estimated via the LX − M500 correlation by Chiu et al. (2022). The masses of most of the clusters lie within 1–12 × 1014 M⊙.

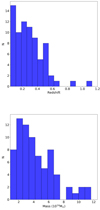thumbnail Fig. 1.

Redshift and mass distribution of all clusters. Upper panel: histogram showing the redshift distribution of the sample. Lower panel: mass distribution of M500 of the cluster sample. The mass was estimated via the LX − M500 correlation from Chiu et al. (2022).

The luminosity of all radio sources was calculated including the following k-correction:

(2)

DL is the luminosity distance at redshift z, and α is the spectral index, assumed to be 0.6. Figure 2 shows the radio luminosity distribution at 944 MHz versus the redshift of the sample. We also plot the theoretical flux cut in Fig. 2.

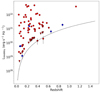thumbnail Fig. 2.

944 MHz radio luminosity vs. redshift. The dashed line represents the theoretical flux limit for point sources. The circles represent the clusters with a detected central radio source, and the triangles represent the upper limits. Resolved sources are plotted in red, and the blue points represent point sources.

Next, we calculated the largest linear size (LLS) for each radio source. The LLS is defined as the linear size of the major axis of a source, and it is displayed in Fig. 3. The LLS is calculated within a 3σ isophote. When the radio source was not resolved, which was the case for six clusters, we treated the source as an upper limit with an LLS corresponding to the beam size. The LLS varied from ∼50 to ∼250 kpc. We also show the offset from each BCG to the X-ray center of the corresponding cluster. The majority of BCGs are found within 200 kpc around the X-ray peak of the cluster.

thumbnail Fig. 3.

Characteristics of the central radio sources. Upper panel: histogram showing the LLS in kiloparsec of each extended radio source. Lower panel: histogram showing the BCG offsets from the X-ray emission peak of the cluster.

In Fig. 4 we show the radio and X-ray luminosity distribution functions of the cluster sample at 944 MHz and 0.5–2.0 keV. The overall radio luminosities lie within a range of ∼1029 and ∼1033 erg s−1 Hz−1. The X-ray luminosities exhibit values from ∼1043 to ∼1045 erg s−1.

thumbnail Fig. 4.

Radio and X-ray luminosities of the cluster sample. Left panel: 944 MHz radio luminosity distribution for the cluster sample. Right panel: X-ray luminosity distribution in the sample for the 0.5–2.0 keV band.

2.5. WISE colors

One approach to identify AGN is a mid-infrared color criterion that is deduced from the separation between the power-law AGN spectrum and the blackbody stellar spectrum of galaxies, which has its peak at a rest-frame of 1.6 μm (Assef et al. 2010). We applied this technique to our sample by using the Wide-field Infrared Survey Explorer (WISE) survey, which mapped the whole sky in four different bands: 3.4, 4.6, 12, and 22 μm, referred to as W1, W2, W3, and W4, respectively (Wright et al. 2010). The color criterion we used is the difference of the magnitudes of W1 − W2 (i.e., 3.4–4.6). For our sample, the W1 and W2 magnitudes and the W1 − W2 criterion are shown in Fig. 5. Our median value for the color criterion is μ ≈ 0.152, with a corresponding interquartile range of σ ≈ 0.155. This is in contrast to Stern et al. (2012), who reported a value of W1 − W2 ≥ 0.8 for their AGN selection, and Assef et al. (2018), who reported a value of W1 − W2 ≥ 0.77. However, LaMassa et al. (2019) and Mountrichas et al. (2019) studied AGN in stripe 82 and showed that two-thirds of the X-ray detected AGN are not identified via the mid-infrared criterion. Especially AGN with luminosities between 1042.5 < LX < 1044 erg s−1 are not detectable by the WISE criterion and show bluer W1 − W2 colors. In this population, the AGN does not seem to dominate the mid-infrared emission, and therefore, the color criterion is not applicable to our sample, where most of our objects meet this luminosity.

thumbnail Fig. 5.

WISE colors of the sample. Left panel: histogram showing the magnitude distribution of WISE colors W1 (blue) and W2 (red) in Vega magnitudes. Right panel: Distribution for W1 − W2.

3. Analysis and discussion

3.1. Linear size of the BCGs

Radio galaxies have a wide range of sizes and shapes, such as giant radio galaxies with largest linear sizes (LLS) of more than 0.7 Mpc, which were examined in Dabhade et al. (2020), for example, and small radio galaxies (e.g., Baldi et al. 2015). Hardcastle et al. (2019) examined the relation between radio power and the linear size of a sample of 23 344 radio-loud AGN, which is also referred to as the P − D diagram (e.g., Turner et al. 2017). This diagram and the location of each source in it is an indicator for its initial conditions and its evolutionary state. The tracks of a source are associated with different phases in the evolution of the source. Objects with specific properties follow tracks on the plane that are mainly defined by the physics of the object. Remnant sources with switched-off jets describe a different set of tracks (Hardcastle 2018). However, the environment can also have an impact on the P − D track. Sources in denser environments typically appear brighter than when they lie in more diluted environments (Turner & Shabala 2015; Yates-Jones et al. 2022).

We measured the angular sizes of the sources and then converted them into linear sizes using their redshift. The errors on the angular sizes were taken to be equal to the synthesized beam. The P − D diagram for our sample is shown in Fig. 6. Pasini et al. (2022; P22 hereafter) examined a sample of 542 galaxy clusters and groups that were detected in the early performance verification phase (eFEDS) of eROSITA and compared them to the emission of the central radio galaxies detected with LOFAR. In Fig. 6 we compare the projected sizes of P22 to our data. To this end, we rescaled the 944 MHz luminosity to a luminosity at the LOFAR HBA central frequency of 144 MHz using a spectral index α = 0.6. Our sample of eRASS:1 clusters extends the P − D diagram to lower LLS values, with the luminosities being comparable to the luminosities L144 MHz examined in P22, namely between ∼1023 and ∼1026 erg s−1 Hz−1.

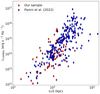thumbnail Fig. 6.

Projected LLS vs. the 144 MHz luminosity from P21 and our sample. We rescaled the luminosity from 944 MHz to 144 MHz using the spectral index α = 0.6.

The EMU sample reaches similar radio powers as the LOFAR data because EMU reaches a depth of 25–30 μJy beam−1 at 944 MHz, which responds to a depth of 110 μJy beam−1 at the LOFAR frequency of 144 MHz, while the LOFAR observation of the eFEDS field reaches ∼100 μJy beam−1. We also note that the resolution of ASKAP is ∼18 arcsec, in contrast to LOFAR, which reaches ∼6 arcsec (Shimwell et al. 2017, 2019).

The interpretation of the P − D diagram should be handled with care because several facts have to be taken into account. On the one hand, the environment and location within the cluster of the radio galaxy affects the position and track on the diagram. We also only observe the projected LLS, and we did not account for selection effects against large low-luminosity sources (Shabala et al. 2008; Turner & Shabala 2015). In addition, the redshift dependence might affect the P − D diagram and its slope. We did not take the individual redshifts into account, which may result in a bias that distorts the true correlation between LLS and radio power. Different redshifts correspond to different cosmic epochs, in which the properties and evolutionary stages of radio galaxies can vary. Without a correction for redshift, objects at different redshifts may not be directly comparable. However, the correlation between the LLS and the radio luminosity is clearly positive: larger radio galaxies usually have higher radio luminosities.

In Fig. 7 we show the projected LLS versus 944 MHz radio power of the EMU radio galaxies. As previously observed, the correlation between LLS and luminosity is positive: larger radio galaxies are more powerful (Owen et al. 2002; Kolokythas et al. 2018; Pasini et al. 2022). The mean value of the LLS is 130 kpc, with a standard deviation of 74 kpc. We calculated the relation between the radio power and the LLS to be log PR = (3.12 ± 0.1)×logLLS − (17.33 ± 0.22). Nonetheless, we note that we also expect a diagonal sensitivity limit because for a given luminosity of an extended source at a given redshift, larger sources are harder to detect because their surface brightness is lower (Shabala et al. 2008). For our sample, the theoretical cutoff limit does not play a role because it is four orders of magnitudes fainter that our measurements.

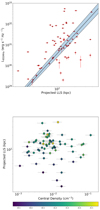thumbnail Fig. 7.

Projected LLS vs. radio power and central density. Upper panel: projected LLS vs. 944 MHz radio power of the EMU radio galaxies. The black line represents the best fit, and the blue region inside the dashed lines is the error band: log PR = (3.12 ± 0.10)×logLLS + (17.33 ± 0.22). Lower panel: projected LLS of the radio source vs. the central density of the cluster. The data points are color-coded with the logarithmic radio luminosity in erg s−1 Hz−1.

We also plot the projected LLS versus the central density of the ICM in Fig. 7. We conclude that these two observables are not correlated. However, color-coding the individual data points by the radio luminosity reveals that sources with a low central density and small LLS tend to exibit low radio luminosities. The lower central ICM density could imply a lower pressure in the radio lobes, leading to lower synchrotron emissivities, while smaller sources also favor lower luminosities.

3.2. BCG offset

In order to examine the BCG offset of each cluster, we calculated the physical distance between the X-ray center given in the eRASS:1 cluster catalog and the optically identified BCG. The result is shown in the lower panel of Fig. 3. The majority of BCGs are found within a radius of ∼100 kpc around the cluster center, which has been defined by the X-ray peak. This is consistent with the assumption of AGN feedback because the gas cooling out of the hot ICM can feed the central supermassive black hole (SMBH), while outer galaxies need to rely on more episodic triggers. Pasini et al. (2021) conducted a phase-space analysis by comparing the clustercentric velocity with the clustercentric offset of the hosted galaxies to investigate the assembly and accretion history of these objects. Their analysis suggests that powerful radio galaxies are always located close to the cluster center. The interpretation was that the cooling ICM can feed the AGN if the galaxy lies close to the cluster density peak, where the cooling is more efficient. Nonetheless, galaxies located in cluster outskirts can also host radio AGN, and triggers such as mergers or interactions might be important (Marshall et al. 2018). Small BCG offsets of less than 100 kpc are expected and found in most relaxed clusters because minor mergers can produce sloshing and displace the X-ray emission peak from the BCG (Hamer et al. 2016; Ubertosi et al. 2021). Larger offsets are usually an indication for major merger events, and therefore indicate strongly disturbed clusters (Hudson et al. 2010; Rossetti et al. 2016; De Propris et al. 2021; Ota et al. 2023; Seppi et al. 2023). In the next section, we compare the BCG offsets to the dynamical state of the clusters.

3.3. Morphological parameters

X-ray observations can be used to compute a quantitative measure of the dynamical status of a cluster. Different morphological parameters for quantifying the dynamical status of a cluster have been described in literature. We focus on the concentration parameter c. The concentration parameter is the ratio of the X-ray flux within a radius of 100 kpc around the cluster center to the X-ray flux within a radius of 500 kpc (Santos et al. 2008). It is defined as the ratio of the peak over the surface brightness S as

(3)

Clusters with a compact core that has not been disrupted by merger activity have higher concentration parameters. Hence, disturbed systems yield lower values for c. Cassano et al. (2010) and Bonafede et al. (2017) for example, have stated that considering the median value of c = 0.2, it is possible to distinguish between disturbed (c < 0.2) and more relaxed (c > 0.2) clusters. Figure 8 shows the plot of the concentration parameter against the BCG offset. Clusters that show a large offset from the BCG to the X-ray center clearly have concentration parameters of c < 0.2 and can thus be classified as disturbed systems. The link between the dynamical status of the clusters to their BCG offsets is clear, and larger offsets are found in more strongly disturbed systems.

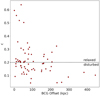thumbnail Fig. 8.

Concentration parameter plotted vs. the BCG offset. The median value of c = 0.2 subdivides the sample into relaxed and disturbed clusters.

Another commonly used morphological parameter is the power ratio P3/P0 (Buote & Tsai 1995). However, the number of photons in the eRASS:1 data is too low to yield a reliable estimate for the parameter P3/P0. We therefore will return to this in future work.

3.4. Correlation of the radio and X-ray luminosity

In this subsection, we investigate how the radio luminosity of the BCG relates to the global X-ray properties of the host cluster. Figure 9 shows the 944 MHz luminosity of the central radio galaxy versus the X-ray luminosity of the galaxy cluster in the 0.1–2.4 keV band. The colors display the redshift, and the size of the points the LLS. There is a trend for more luminous radio galaxies to be hosted in more X-ray luminous clusters, but the scatter is significant. Using the Python package hyperfit1, we calculated the correlation of the X-ray and radio luminosities (Robotham & Obreschkow 2015). This package provides a method for fitting a line to data allowing for both intrinsic scatter and (potentially correlated) errors on all the input variables, here x and y for our 2D fit. We ran this program on our data with a fully converged MCMC (Markov chain Monte Carlo) run. We obtained log LR = (0.89 ± 0.04)×log LX − (8.52 ± 1.44). The p-value of this fit equals 0.05. We therefore consider this relation to be statistically significant.

thumbnail Fig. 9.

944 MHz luminosity of the central radio galaxy vs. the X-ray luminosity of the galaxy cluster in the 0.1–2.4 keV band. Each point is colored by redshift and scaled by the LLS. The black line represents the best fit, and the blue region inside the dashed lines shows the error band: log LR = (0.89 ± 0.04)×log LX − (8.52 ± 1.44).

Clusters that host radio sources with high radio luminosities (> 5 × 1031 erg s−1 Hz−1) broaden the function and introduce large scatter into the correlation. A similar correlation was found by Hogan et al. (2015), even though they did not quantify their results. Our results are also consistent with the best-fit relation found by Pasini et al. (2022), who find log LR = (0.84 ± 0.09)×log LX − (6.46 ± 4.07) and Pasini et al. (2020, 2021). We refer to Table 2 for the corresponding relations. Although the results agree, our sample clearly has less scatter in the relation. One reason for this could be the large number of radio upper limits that were taken into account in former work. which adds larger uncertainties. Generally, we would expect more scatter at lower frequencies as lower frequencies are emitted by electrons that are older.

Table 2.

Overview of the X-ray/radio correlation found by other authors.

3.5. Mechanical powers of the jet

The radio lobes only radiate a small fraction of the total power away that is supplied to the lobes when the source is active. This small fraction of radiation is the radio luminosity, which is only a fraction of the energy produced by the AGN through accretion of matter toward the black hole itself. A larger fraction of the power is stored in the radio lobes and dissipated during the expansion of the jets into the ICM (Smolčić et al. 2017). A direct approach for calculating the mechanical power of a radio jet would be to derive it from the properties of the radio source in comparison with a radio source evolution model. In most cases, this is not possible because the radio environment of the sources is unknown. Moreover, the luminosity evolves with the age of the sources (Turner & Shabala 2015; Hardcastle 2018; Yates-Jones et al. 2022). A common approach to overcome this problem is to estimate the mechanical energy of the jet by estimating it directly from the radio luminosity (Sabater et al. 2019).

This conversion of the mechanical power of the jet into radio luminosity is usually estimated from the cavities that are inflated by radio sources in the surrounding ICM as observed in X-ray images. The total mechanical energy is then calculated to 4pV, with p the pressure of the surrounding medium, and V the volume of the cavity. The factor of 4 arises if the enthalpy of the relativistic plasma in the radio lobes, which is 3pV, is added to the work performed to inflate the cavities, which is pV. When an estimate of the source age (e.g., via the buoyancy timescale of the cavity) is also given, a lower limit of the mechanical power of the jet can be estimated. This is found to correlate with the observed radio luminosity (Rafferty et al. 2006; Bîrzan et al. 2008; Cavagnolo et al. 2010).

Another approach to relate the mechanical power of the jet to the radio luminosity is based on the synchrotron properties, and therefore, on the composition of the jet plasma (Willott et al. 1999). Heckman & Best (2014) found that both approaches provide consistent estimates of the mechanical powers of the jet and proposed a population-averaged conversion,

Furthermore, the kinetic luminosity at a rest-frame frequency of 1.4 GHz is described by

Lkin, 1.4 GHz describes the kinetic luminosity, and L1.4 GHz is the luminosity at 1.4 GHz. fW is an uncertainty parameter, which is estimated to be around 15 from observations (Smolčić et al. 2017). In order to determine the kinetic luminosity for our sample, we converted the radio power at 944 MHz to radio powers at a frequency of 1.4 GHz, assuming a spectral index of α = 0.6. We then compared our results to the X-ray luminosity of the host cluster. We again used the package hyperfit to estimate our relation in log-log scale in the form

where α and β represent the intercept and slope, and ε is the intrinsic scatter. We find α = −3.81 ± 1.01, β = 1.08 ± 0.03, and ε = 0.91 ± 0.61 (see Fig. 10). This approximately agrees with the values found by Pasini et al. (2022), who found α = −2.19 ± 4.05, β = 1.07 ± 0.11, and ε = 0.25 ± 0.05. However, we obtain a larger ε-factor for our sample, which represents a higher uncertainty in the observed values. As the conversion from the 944 MHz luminosity into kinetic luminosity at 1.4 GHz depends on a number of assumptions, we introduced large errors that result in a high scatter of the relation. Moreover, our sample is smaller than that of P22, which also results in a higher scatter. We also note that considering a sample over a wide redshift range can introduce a bias into this estimation (Godfrey & Shabala 2016). Previous results from P22 stating that in most clusters the heating from the central AGN balances the ICM radiative losses cannot be confirmed from our data (see also, e.g., McNamara & Nulsen 2012; McNamara et al. 2016 for a review). However, we note that P22 used additional COSMOS data of lower-luminosity galaxy groups than the initial eFEDS data (see their Fig. 10). When the COSMOS data are removed from their data, their correlation between the kinetic luminosity at 1.4 GHz and LX also becomes far lower. The scatter in the radio luminosity appears to increase strongly with LX, similar to the results of Main et al. (2017). At values LX > 1043 erg s−1, the correlation disappears. The kinetic luminosity acts as a proxy for the heating rate, and the X-ray luminosity acts as a proxy for the cooling rate. Hence, the central AGN appear to counterbalance radiative losses from the ICM in low-luminosity clusters and groups, but this relation breaks for high-luminosity clusters. Main et al. (2017) also investigated this relation and reported that the correlation between kinetic luminosity and X-ray observables only holds in clusters with short (< 1 Gyr) central cooling times. We derived the central cooling time tcool based on the X-ray temperature and color-code the individual points with respect to tcool in Fig. 10 to examine whether tcool affects the individual cluster position in the Lkin − LX diagram. We cannot confirm the results from Main et al. (2017) based on our data. In high-luminosity clusters, the variability among the AGN population seems to be higher, resulting in a higher scatter in the Lkin − LX correlation. However, the measurements are only a snapshot in the lifetime of an AGN at a certain point in their duty cycle. Averaged over a longer period, AGN heating could still balance cooling, but the implication is that at higher LX, the AGN are more variable.

thumbnail Fig. 10.

X-ray luminosity of the clusters sample vs. the corresponding radio luminosity of the central radio source and the 944 MHz radio luminosity of the central radio source vs. the central cooling time of each cluster. Left panel: 1.4 GHz kinetic luminosity extrapolated from 944 MHz vs. the X-ray luminosity of the corresponding cluster. The individual points are color-coded with respect to the logarithmic central cooling time. Right panel: 944 MHz radio luminosity of the central radio source vs. the central cooling time of each cluster. The vertical dashed blue line indicates tcool = 7.7 Gyr and separates CC and NCC clusters. The black line indicates the fit: log LR = ( − 0.31 ± 0.03)×log tcool + (34.17 ± 0.31).

3.6. Cooling time

Because AGN feedback heats the ICM and regulates its cooling rate, the correlation between central cooling time and radio luminosity can be used to investigate the relation between ICM cooling and AGN heating. Because the eRASS:1 cluster catalog provides the central density ne and the temperature TX for all clusters, the central cooling time can be approximated as (Sarazin 1986)

We assumed a hydrogen density nP = 0.83ne (McDonald et al. 2018). We plot the cooling time tcool versus the radio luminosity LR in the right panel of Fig. 10. We removed two outliers with derived central cooling times of > 1012 yr because these values are most likely the result of incorrect densities and temperatures in the catalog data. While the plot is messy, there seems to be a trend of an anticorrelation between the two quantities. To quantify this anticorrelation, we find log LR = ( − 0.31 ± 0.03)×log tcool + (34.17 ± 0.31). We also indicate tcool = 7.7 Gyr because this value is commonly used to distinguish between cool-core (CC) and non-cool-core clusters (NCC). Our sample contains 10 CC clusters, while the rest are NCC clusters. Mittal et al. (2009) examined a sample of 64 HIFLUGCS clusters and their central radio galaxies and found a similar trend for an anticorrelation between the cooling time of the cluster and the radio luminosity of its central AGN. For their sample, they reported a slope of −3.16 ± 0.38, which is in contrast to our relation, where we find a slope of −0.31 ± 0.03. We note that Mittal et al. (2009) used a central definition of 0.4% of r500, which is a radius that cannot be resolved by eROSITA. Hence, any comparison should be handled with care. In general, this apparent anticorrelation could be indicative of a need for more powerful AGN in clusters with short central cooling times. Cool-core clusters with very short cooling times seem to need much more powerful AGN, unlike NCC clusters, in which this trend is less obvious. Finally, the cluster mass also appears to play a role. Bharadwaj et al. (2014) investigated the same relation for galaxy groups and found no relation between the central cooling time and the radio luminosity of the central AGN. For a discussion of the difference of AGN feedback in clusters and groups, we refer to Pasini et al. (2021).

3.7. Density profiles

In order to investigate the connection between CC and NCC clusters and their corresponding radio luminosity, we plot the density profiles of all clusters of our sample and color-code them by their radio power. The resulting plot is shown in Fig. 11. We again removed the density profiles of two outliers with very low central densities of ne < 10−4 because we assume that these values are incorrect. Clusters with a higher central density (ne > 10−2 cm−3), subsequently CC clusters, tend to host more luminous radio sources with radio luminosities of LR > 1031 erg s−1 Hz−1. This confiRMS that CC clusters always host a powerful radio-mode AGN. Clusters with lower central densities (ne < 10−2 cm−3) show no connection, and we draw the conclusion that NCC clusters host low- as well as high-luminous radio sources. This agrees overall with the general findings that X-ray cavities and therefore powerful radio-mode AGN are usually found within CC clusters (e.g., O’Sullivan et al. 2011; Hlavacek-Larrondo et al. 2012; Bîrzan et al. 2020; Olivares et al. 2022). In contrast to this strong connection of AGN activity and CC clusters, NCC clusters and AGN activity do not appear to be correlated. Mittal et al. (2009) showed that NCC clusters may also host strong radio AGN, which can be explained by merging activities or other mechanisms, for instance.

thumbnail Fig. 11.

Electron density profiles of the cluster sample. Left panel: electron density profiles of all non-cool-core clusters vs. the radius scaled to R500. The colors of the profiles represent the radio luminosity of the central radio source of the corresponding cluster. Right panel: corresponding plot for the cool-core clusters.

3.8. Noteworthy clusters

Our cluster sample contains some interesting radio sources, four of which are presented in Fig. 12. The upper left panel shows galaxy cluster J201832.9-524656 (Abell S0861) at z = 0.05. The white circle is R500. This cluster contains two interesting radio sources with very elongated shapes. We also show the overlay with optical data from the legacy survey DR9, in which the upper radio source presumably consists of at least three galaxies exhibiting radio emission. The shape of the radio emission suggests a complex interplay between these galaxies. The southern radio source in J201832.9-524656 resembles the shape of a jellyfish galaxy. The optical overlay shows a bright galaxy in the upper part of the radio galaxy. This shape suggests that this galaxy is moving northwest.

thumbnail Fig. 12.

Special radio sources contained in the EMU field. Upper left panel: radio cutout from the EMU image of cluster J201832.9-524656 (Abell S0861) at z = 0.05 showing two elongated radio sources. The optical overlay reveals a complex interplay between at least three radio galaxies on the northern radio source and an infalling radio galaxy in the southern source. Upper right panel: the radio cutout of J205156.7-523752 (PLCKESZ G345.4-39) at z = 0.04 shows two connected elongated radio sources that seem to be hosted by at least three radio galaxies. Lower left panel: radio image of J202321.7-553524 (SPT-CL J2023-5535) at z = 0.22 revealing a large radio source. Lower right panel: cutout of the nearby cluster J215129.7-552019 (RXC J2151.3-5521) at z = 0.03 clearly showing the radio jets that originate from the central radio source. All optical overlays made use of legacy survey DS9 data, and the white circle represents R500.

The upper right panel of Fig. 12 shows cluster J205156.7-523752 (PLCKESZ G345.4-39) at z = 0.04. This cluster hosts two elongated radio sources in the southern part of the cluster that seem to be connected. The optical overlay with legacy survey DR9 data reveals that the upper radio source consists of two near galaxies, and the upper radio source is at least one radio galaxy. The shapes of these sources suggest that these galaxies have either undergone some merging activities in the past or will do so in the future. In the lower left panel, we display cluster J202321.7-553524 (SPT-CL J2023-5535) at z = 0.22. The radio image of this cluster reveals a radio source that covers large areas of the whole cluster, with a strong peak in the southeast. This radio source could be an indication for a radio halo and has also been studied by HyeongHan et al. (2020). In the lower right panel, we display the nearby cluster J215129.7-552019 (RXC J2151.3-5521) at z = 0.03. The radio jets clearly originate from the central radio source in the cluster.

4. Conclusions

We used the eROSITA eRASS:1 cluster catalog and the ASKAP pilot survey EMU to examine the central radio galaxies hosted in galaxy clusters covered in the EMU survey. We can draw the following conclusions:

  • Our sample consists of 75 galaxy clusters that are covered by the EMU pilot survey in the redshift range of 0.03 < z < 1.1. Ten clusters are cool-core clusters, while the rest are non-cool-core clusters. In 64 clusters we could identify a radio source that corresponds to the cluster BCG. The radio luminosities of the central radio galaxies at 944 MHz range between ∼1029 and ∼1033 erg s−1 Hz−1. The X-ray luminosities of the corresponding clusters range between ∼1043 and ∼1045 erg s−1.

  • We compared the offset of the BCG from the cluster center to its concentration parameter. We found a link between the dynamical state of the cluster to its BCG offset. Larger offsets were found in more strongly disturbed systems.

  • We find a statistically significant correlation between the radio and the X-ray luminosity, as in previous work (Mittal et al. 2009; Pasini et al. 2020, 2021, 2022).

  • We investigated the correlation between the LLS of the radio source and its radio power, finding that larger radio galaxies tend to be more powerful. We do not find a correlation between the central density and the LLS, which suggests that the radio power is more important than the ambient density for the size of the radio galaxy.

  • The 944 MHz luminosities were converted into 1.4 GHz kinetic luminosities using scaling relations. We found that in high-luminosity clusters with LX > 1043 erg s−1, the kinetic luminosity of the radio jets is not longer correlated with the X-ray luminosity. This indicates that the variability in the AGN population is higher in high luminous clusters.

  • We found an anticorrelation between the central cooling time tcool and the radio luminosity LR, indicating that more powerful AGN reside in clusters with short central cooling times.

  • The density profiles of the individual clusters show that cool-core clusters tend to host powerful radio sources, in contrast to non-cool-core clusters, which host both high- and low-luminosity radio sources.

  • A mid-infrared color criterion using WISE colors was applied to our sample. We conclude that the color criterion is not applicable for our sample, which is due to the luminosity range of our sample, for which the WISE criterion is not applicable.

The eRASS cluster catalog is a powerful tool that will prove useful for future studies. The combination with radio surveys by the forthcoming generation of radio telescopes will vastly extend samples such as ours.

Acknowledgments

The authors thank the anonymous referee for useful comments and suggestions. The Australian SKA Pathfinder is part of the Australia Telescope National Facility which is managed by CSIRO. Operation of ASKAP is funded by the Australian Government with support from the National Collaborative Research Infrastructure Strategy. ASKAP uses the resources of the Pawsey Supercomputing center. Establishment of ASKAP, the Murchison Radio-astronomy Observatory and the Pawsey Supercomputing center are initiatives of the Australian Government, with support from the Government of Western Australia and the Science and Industry Endowment Fund. We acknowledge the Wajarri Yamatji people as the traditional owners of the Observatory site. The Australia Telescope Compact Array (/Parkes radio telescope/Mopra radio telescope/Long Baseline Array) is part of the Australia Telescope National Facility which is funded by the Australian Government for operation as a National Facility managed by CSIRO. This paper includes archived data obtained through the Australia Telescope Online Archive (http://atoa.atnf.csiro.au). This work was supported by resources provided by the Pawsey Supercomputing center with funding from the Australian Government and the Government of Western Australia. We acknowledge and thank the builders of ASKAPsoft. This work is based on data from eROSITA, the soft X-ray instrument aboard SRG, a joint Russian-German science mission supported by the Russian Space Agency (Roskosmos), in the interests of the Russian Academy of Sciences represented by its Space Research Institute (IKI), and the Deutsches Zentrum für Luft- und Raumfahrt (DLR). The SRG spacecraft was built by Lavochkin Association (NPOL) and its subcontractors, and is operated by NPOL with support from the Max Planck Institute for Extraterrestrial Physics (MPE). The development and construction of the eROSITA X-ray instrument was led by MPE, with contributions from the Dr. Karl Remeis Observatory Bamberg and ECAP (FAU Erlangen-Nuernberg), the University of Hamburg Observatory, the Leibniz Institute for Astrophysics Potsdam (AIP), and the Institute for Astronomy and Astrophysics of the University of Tübingen, with the support of DLR and the Max Planck Society. The Argelander Institute for Astronomy of the University of Bonn and the Ludwig Maximilians Universität Munich also participated in the science preparation for eROSITA. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. KB and MB are funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy - EXC 2121 “Quantum Universe” – 390833306.

References

  1. Assef, R. J., Kochanek, C. S., Brodwin, M., et al. 2010, ApJ, 713, 970 [NASA ADS] [CrossRef] [Google Scholar]
  2. Assef, R. J., Stern, D., Noirot, G., et al. 2018, ApJS, 234, 23 [Google Scholar]
  3. Baldi, R. D., Capetti, A., & Giovannini, G. 2015, A&A, 576, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bharadwaj, V., Reiprich, T. H., Schellenberger, G., et al. 2014, A&A, 572, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bîrzan, L., Rafferty, D. A., McNamara, B. R., Wise, M. W., & Nulsen, P. E. J. 2004, ApJ, 607, 800 [Google Scholar]
  6. Bîrzan, L., McNamara, B. R., Nulsen, P. E. J., Carilli, C. L., & Wise, M. W. 2008, ApJ, 686, 859 [Google Scholar]
  7. Bîrzan, L., Rafferty, D. A., Brüggen, M., et al. 2020, MNRAS, 496, 2613 [CrossRef] [Google Scholar]
  8. Bonafede, A., Cassano, R., Brüggen, M., et al. 2017, MNRAS, 470, 3465 [Google Scholar]
  9. Brunner, H., Liu, T., Lamer, G., et al. 2022, A&A, 661, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Buote, D. A., & Tsai, J. C. 1995, ApJ, 452, 522 [Google Scholar]
  11. Cassano, R., Ettori, S., Giacintucci, S., et al. 2010, ApJ, 721, L82 [Google Scholar]
  12. Cattaneo, A., Faber, S. M., Binney, J., et al. 2009, Nature, 460, 213 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cavagnolo, K. W., McNamara, B. R., Nulsen, P. E. J., et al. 2010, ApJ, 720, 1066 [Google Scholar]
  14. Chiu, I. N., Ghirardini, V., Liu, A., et al. 2022, A&A, 661, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Condon, J. J., Cotton, W. D., & Broderick, J. J. 2002, AJ, 124, 675 [Google Scholar]
  16. Dabhade, P., Röttgering, H. J. A., Bagchi, J., et al. 2020, A&A, 635, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. De Propris, R., West, M. J., Andrade-Santos, F., et al. 2021, MNRAS, 500, 310 [Google Scholar]
  18. Fabian, A. 2012, ARA&A, 50, 455 [CrossRef] [Google Scholar]
  19. Gaspari, M., Tombesi, F., & Cappi, M. 2020, Nat. Astron., 4, 10 [Google Scholar]
  20. Gitti, M., Brighenti, F., & McNamara, B. R. 2012, Adv. Astron., 2012, 1 [CrossRef] [Google Scholar]
  21. Godfrey, L. E. H., & Shabala, S. S. 2016, MNRAS, 456, 1172 [NASA ADS] [CrossRef] [Google Scholar]
  22. Guzman, J., Whiting, M., Voronkov, M., et al. 2019, Astrophysics Source Code Library [record ascl:1912.003] [Google Scholar]
  23. Hamer, S. L., Edge, A. C., Swinbank, A. M., et al. 2016, MNRAS, 460, 1758 [Google Scholar]
  24. Hardcastle, M. J. 2018, MNRAS, 475, 2768 [Google Scholar]
  25. Hardcastle, M. J., Williams, W. L., Best, P. N., et al. 2019, A&A, 622, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Heckman, T. M., & Best, P. N. 2014, ARA&A, 52, 589 [Google Scholar]
  27. Hlavacek-Larrondo, J., Fabian, A. C., Edge, A. C., et al. 2012, MNRAS, 421, 1360 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hogan, M. T., Edge, A. C., Hlavacek-Larrondo, J., et al. 2015, MNRAS, 453, 1201 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hopkins, A. M., Whiting, M. T., Seymour, N., et al. 2015, PASA, 32, 23 [CrossRef] [Google Scholar]
  30. Hotan, A. W., Bunton, J. D., Chippendale, A. P., et al. 2021, PASA, 38, e009 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hudson, D. S., Mittal, R., Reiprich, T. H., et al. 2010, A&A, 513, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. HyeongHan, K., Jee, M. J., Rudnick, L., et al. 2020, ApJ, 900, 127 [NASA ADS] [CrossRef] [Google Scholar]
  33. Ineson, J., Croston, J. H., Hardcastle, M. J., et al. 2013, ApJ, 770, 136 [Google Scholar]
  34. Ineson, J., Croston, J. H., Hardcastle, M. J., et al. 2015, MNRAS, 453, 2682 [Google Scholar]
  35. Johnston, S., Taylor, R., Bailes, M., et al. 2008, Exp. Astron., 22, 151 [Google Scholar]
  36. Kolokythas, K., O’Sullivan, E., Raychaudhury, S., et al. 2018, MNRAS, 481, 1550 [NASA ADS] [Google Scholar]
  37. Koribalski, B. S. 2022, in 2022 3rd URSI Atlantic and Asia Pacific Radio Science Meeting (AT-AP-RASC), 1 [Google Scholar]
  38. LaMassa, S. M., Georgakakis, A., Vivek, M., et al. 2019, ApJ, 876, 50 [NASA ADS] [CrossRef] [Google Scholar]
  39. Liu, A., Bulbul, E., Ghirardini, V., et al. 2022, A&A, 661, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Magliocchetti, M., & Brüggen, M. 2007, MNRAS, 379, 260 [NASA ADS] [CrossRef] [Google Scholar]
  41. Main, R. A., McNamara, B. R., Nulsen, P. E. J., Russell, H. R., & Vantyghem, A. N. 2017, MNRAS, 464, 4360 [NASA ADS] [CrossRef] [Google Scholar]
  42. Marshall, M. A., Shabala, S. S., Krause, M. G. H., et al. 2018, MNRAS, 474, 3615 [NASA ADS] [CrossRef] [Google Scholar]
  43. Mauch, T., & Sadler, E. M. 2007, MNRAS, 375, 931 [Google Scholar]
  44. McDonald, M., Gaspari, M., McNamara, B. R., & Tremblay, G. R. 2018, ApJ, 858, 45 [Google Scholar]
  45. McNamara, B. R., & Nulsen, P. E. J. 2012, New J. Phys., 14, 055023 [NASA ADS] [CrossRef] [Google Scholar]
  46. McNamara, B. R., Russell, H. R., Nulsen, P. E. J., et al. 2016, ApJ, 830, 79 [Google Scholar]
  47. Merloni, A., Predehl, P., Becker, W., et al. 2012, ArXiv e-prints [arXiv:1209.3114] [Google Scholar]
  48. Merloni, A., Nandra, K., & Predehl, P. 2020, Nat. Astron., 4, 634 [Google Scholar]
  49. Mittal, R., Hudson, D. S., Reiprich, T. H., & Clarke, T. 2009, A&A, 501, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Mountrichas, G., Georgantopoulos, I., Ruiz, A., & Kampylis, G. 2019, MNRAS, 491, 1727 [Google Scholar]
  51. Nipoti, C., & Binney, J. 2005, MNRAS, 361, 428 [NASA ADS] [CrossRef] [Google Scholar]
  52. Norris, R. P., Hopkins, A. M., Afonso, J., et al. 2011, PASA, 28, 215 [Google Scholar]
  53. Norris, R. P., Marvil, J., Collier, J. D., et al. 2021, PASA, 38, e046 [NASA ADS] [CrossRef] [Google Scholar]
  54. Olivares, V., Su, Y., Nulsen, P., et al. 2022, MNRAS, 516, L101 [NASA ADS] [CrossRef] [Google Scholar]
  55. O’Sullivan, E., Giacintucci, S., David, L. P., et al. 2011, ApJ, 735, 11 [Google Scholar]
  56. Ota, N., Nguyen-Dang, N. T., Mitsuishi, I., et al. 2023, A&A, 669, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Owen, F., Ledlow, M., & Eilek, J. 2002, Highlights Astron., 12, 522 [NASA ADS] [CrossRef] [Google Scholar]
  58. Pasini, T., Brüggen, M., de Gasperin, F., et al. 2020, MNRAS, 497, 2163 [NASA ADS] [CrossRef] [Google Scholar]
  59. Pasini, T., Finoguenov, A., Brüggen, M., et al. 2021, MNRAS, 505, 2628 [NASA ADS] [CrossRef] [Google Scholar]
  60. Pasini, T., Brüggen, M., Hoang, D. N., et al. 2022, A&A, 661, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Pope, E. C. D., Mendel, J. T., & Shabala, S. S. 2012, MNRAS, 419, 50 [NASA ADS] [CrossRef] [Google Scholar]
  62. Predehl, P., Andritschke, R., Arefiev, V., et al. 2021, A&A, 647, A1 [EDP Sciences] [Google Scholar]
  63. Rafferty, D. A., McNamara, B. R., Nulsen, P. E. J., & Wise, M. W. 2006, ApJ, 652, 216 [NASA ADS] [CrossRef] [Google Scholar]
  64. Robotham, A. S. G., & Obreschkow, D. 2015, PASA, 32, e033 [Google Scholar]
  65. Rossetti, M., Gastaldello, F., Ferioli, G., et al. 2016, MNRAS, 457, 4515 [Google Scholar]
  66. Sabater, J., Best, P. N., Hardcastle, M. J., et al. 2019, A&A, 622, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Sadler, E. M., Jackson, C. A., Cannon, R. D., et al. 2002, MNRAS, 329, 227 [Google Scholar]
  68. Santos, J. S., Rosati, P., Tozzi, P., et al. 2008, A&A, 483, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Sarazin, C. L. 1986, Rev. Mod. Phys., 58, 1 [Google Scholar]
  70. Scott, K. S., Austermann, J. E., Perera, T. A., et al. 2008, MNRAS, 385, 2225 [NASA ADS] [CrossRef] [Google Scholar]
  71. Seppi, R., Comparat, J., Nandra, K., et al. 2023, A&A, 671, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Shabala, S. S., Ash, S., Alexander, P., & Riley, J. M. 2008, MNRAS, 388, 625 [NASA ADS] [CrossRef] [Google Scholar]
  73. Shabala, S. S., Jurlin, N., Morganti, R., et al. 2020, MNRAS, 496, 1706 [NASA ADS] [CrossRef] [Google Scholar]
  74. Shimwell, T. W., Röttgering, H. J. A., Best, P. N., et al. 2017, A&A, 598, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Shimwell, T. W., Tasse, C., Hardcastle, M. J., et al. 2019, A&A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Smolčić, V., Delvecchio, I., Zamorani, G., et al. 2017, A&A, 602, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Stern, D., Assef, R. J., Benford, D. J., et al. 2012, ApJ, 753, 30 [Google Scholar]
  78. Sunyaev, R., Arefiev, V., Babyshkin, V., et al. 2021, A&A, 656, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Timmerman, R., van Weeren, R. J., Botteon, A., et al. 2022, A&A, 668, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Turner, R. J., & Shabala, S. S. 2015, ApJ, 806, 59 [Google Scholar]
  81. Turner, R. J., Rogers, J. G., Shabala, S. S., & Krause, M. G. H. 2017, MNRAS, 473, 4179 [Google Scholar]
  82. Ubertosi, F., Gitti, M., Torresi, E., Brighenti, F., & Grandi, P. 2021, MNRAS, 503, 4627 [NASA ADS] [CrossRef] [Google Scholar]
  83. Whiting, M., Voronkov, M., Mitchell, D., & Askap Team 2017, ASP Conf. Ser., 512, 431 [NASA ADS] [Google Scholar]
  84. Wieringa, M., Raja, W., & Ord, S. 2020, ASP Conf. Ser., 527, 591 [NASA ADS] [Google Scholar]
  85. Willott, C. J., Rawlings, S., Blundell, K. M., & Lacy, M. 1999, MNRAS, 309, 1017 [Google Scholar]
  86. Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
  87. Yates-Jones, P. M., Turner, R. J., Shabala, S. S., & Krause, M. G. H. 2022, MNRAS, 511, 5225 [CrossRef] [Google Scholar]

Appendix A: eRASS:1 clusters in the EMU field

We show a table of all eRASS:1 detected clusters in the EMU field and their corresponding X-ray characteristics. The radio values of the corresponding central radio source are also listed.

Table A.1.

eRASS:1 clusters in the EMU field and their corresponding values.

All Tables

Table 1.

EMU pilot survey specifications.

In the text
Table 2.

Overview of the X-ray/radio correlation found by other authors.

In the text
Table A.1.

eRASS:1 clusters in the EMU field and their corresponding values.

In the text

All Figures

thumbnail Fig. 1.

Redshift and mass distribution of all clusters. Upper panel: histogram showing the redshift distribution of the sample. Lower panel: mass distribution of M500 of the cluster sample. The mass was estimated via the LX − M500 correlation from Chiu et al. (2022).
In the text
thumbnail Fig. 2.

944 MHz radio luminosity vs. redshift. The dashed line represents the theoretical flux limit for point sources. The circles represent the clusters with a detected central radio source, and the triangles represent the upper limits. Resolved sources are plotted in red, and the blue points represent point sources.
In the text
thumbnail Fig. 3.

Characteristics of the central radio sources. Upper panel: histogram showing the LLS in kiloparsec of each extended radio source. Lower panel: histogram showing the BCG offsets from the X-ray emission peak of the cluster.
In the text
thumbnail Fig. 4.

Radio and X-ray luminosities of the cluster sample. Left panel: 944 MHz radio luminosity distribution for the cluster sample. Right panel: X-ray luminosity distribution in the sample for the 0.5–2.0 keV band.
In the text
thumbnail Fig. 5.

WISE colors of the sample. Left panel: histogram showing the magnitude distribution of WISE colors W1 (blue) and W2 (red) in Vega magnitudes. Right panel: Distribution for W1 − W2.
In the text
thumbnail Fig. 6.

Projected LLS vs. the 144 MHz luminosity from P21 and our sample. We rescaled the luminosity from 944 MHz to 144 MHz using the spectral index α = 0.6.
In the text
thumbnail Fig. 7.

Projected LLS vs. radio power and central density. Upper panel: projected LLS vs. 944 MHz radio power of the EMU radio galaxies. The black line represents the best fit, and the blue region inside the dashed lines is the error band: log PR = (3.12 ± 0.10)×logLLS + (17.33 ± 0.22). Lower panel: projected LLS of the radio source vs. the central density of the cluster. The data points are color-coded with the logarithmic radio luminosity in erg s−1 Hz−1.
In the text
thumbnail Fig. 8.

Concentration parameter plotted vs. the BCG offset. The median value of c = 0.2 subdivides the sample into relaxed and disturbed clusters.
In the text
thumbnail Fig. 9.

944 MHz luminosity of the central radio galaxy vs. the X-ray luminosity of the galaxy cluster in the 0.1–2.4 keV band. Each point is colored by redshift and scaled by the LLS. The black line represents the best fit, and the blue region inside the dashed lines shows the error band: log LR = (0.89 ± 0.04)×log LX − (8.52 ± 1.44).
In the text
thumbnail Fig. 10.

X-ray luminosity of the clusters sample vs. the corresponding radio luminosity of the central radio source and the 944 MHz radio luminosity of the central radio source vs. the central cooling time of each cluster. Left panel: 1.4 GHz kinetic luminosity extrapolated from 944 MHz vs. the X-ray luminosity of the corresponding cluster. The individual points are color-coded with respect to the logarithmic central cooling time. Right panel: 944 MHz radio luminosity of the central radio source vs. the central cooling time of each cluster. The vertical dashed blue line indicates tcool = 7.7 Gyr and separates CC and NCC clusters. The black line indicates the fit: log LR = ( − 0.31 ± 0.03)×log tcool + (34.17 ± 0.31).
In the text
thumbnail Fig. 11.

Electron density profiles of the cluster sample. Left panel: electron density profiles of all non-cool-core clusters vs. the radius scaled to R500. The colors of the profiles represent the radio luminosity of the central radio source of the corresponding cluster. Right panel: corresponding plot for the cool-core clusters.
In the text
thumbnail Fig. 12.

Special radio sources contained in the EMU field. Upper left panel: radio cutout from the EMU image of cluster J201832.9-524656 (Abell S0861) at z = 0.05 showing two elongated radio sources. The optical overlay reveals a complex interplay between at least three radio galaxies on the northern radio source and an infalling radio galaxy in the southern source. Upper right panel: the radio cutout of J205156.7-523752 (PLCKESZ G345.4-39) at z = 0.04 shows two connected elongated radio sources that seem to be hosted by at least three radio galaxies. Lower left panel: radio image of J202321.7-553524 (SPT-CL J2023-5535) at z = 0.22 revealing a large radio source. Lower right panel: cutout of the nearby cluster J215129.7-552019 (RXC J2151.3-5521) at z = 0.03 clearly showing the radio jets that originate from the central radio source. All optical overlays made use of legacy survey DS9 data, and the white circle represents R500.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.