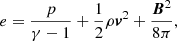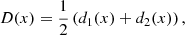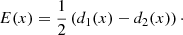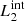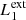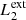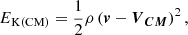| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201935539 | |
| Published online | 12 June 2019 | |
MHD simulations of the in situ generation of kink and sausage waves in the solar corona by collision of dense plasma clumps⋆
1
School of Mathematics and Statistics, University of St Andrews, North Haugh, St Andrews, Fife KY16 9SS, UK
e-mail: pp25@st-andrews.ac.uk
2
Rosseland Centre for Solar Physics, University of Oslo, PO Box 1029 Blindern 0315, Oslo, Norway
Received:
25
March
2019
Accepted:
29
April
2019
Context. Magnetohydrodynamic (MHD) waves are ubiquitous in the solar corona where the highly structured magnetic fields provide efficient wave guides for their propagation. While MHD waves have been observed originating from lower layers of the solar atmosphere, recent studies have shown that some can be generated in situ by the collision of dense counter-propagating flows.
Aims. In this theoretical study, we analyse the mechanism that triggers the propagation of kink and sausage modes in the solar corona following the collision of counter-propagating flows, and how the properties of the flows affect the properties of the generated waves.
Methods. To study in detail this mechanism we ran a series of ideal 2D and 3D MHD simulations where we varied the properties of the counter-propagating flows; by means of a simple technique to estimate the amplitudes of the kink and sausage modes, we investigated their role in the generation and propagation of the MHD waves.
Results. We find that the amplitude of the waves is largely dependent on the kinetic energy of the flows, and that the onset of kink or sausage modes depends on the asymmetries between the colliding blobs. Moreover, the initial wavelength of the MHD waves is associated with the magnetic configuration resulting from the collision of the flows. We also find that genuine 3D systems respond with smaller wave amplitudes.
Conclusions. In this study, we present a parameter space description of the mechanism that leads to the generation of MHD waves from the collision of flows in the corona. Future observations of these waves can be used to understand the properties of the plasma and magnetic field of the solar corona.
Key words: Sun: oscillations / Sun: corona / Sun: helioseismology / magnetohydrodynamics (MHD) / Sun: magnetic fields
The movies associated to Figs. 2 and 21 are available at https://www.aanda.org
© ESO 2019
1. Introduction
Magnetohydrodynamic (MHD) waves are an intrinsic feature of the solar corona, and for this reason have been studied in detail since the derivation of their existence (for a review, see e.g. De Moortel & Nakariakov 2012; Arregui 2015). The solar corona is a highly dynamic and structured environment where magnetic fields are often concentrated in coronal loops and active regions. The formation process of coronal loops is still under investigation, but these magnetised structures are efficient wave guides for MHD waves (Reale 2010).
This scenario has been observed a number of times and a photospheric or chromospheric origin has been suggested for most of the MHD waves propagating along these wave guides, as these modes are powered by the upward Poynting flux observed at the lower layers of the solar atmosphere (e.g. Matsumoto & Kitai 2010; Chitta et al. 2012; Krishna Prasad et al. 2015). At the same time, Morton et al. (2019) have shown that the power spectrum of the transverse oscillations in the corona is relatively stable and uniform throughout different regions and the solar cycle, suggesting that these oscillations must be fundamentally connected with the pulsation of the lower layers of the Sun’s atmosphere. However, various observational and theoretical studies have recently been suggested that not all the transverse waves observed in the solar corona are of chromospheric origin, but that some are generated in situ. For instance, a series of studies (Kohutova & Verwichte 2018, 2017; Verwichte et al. 2017; Verwichte & Kohutova 2017) have found that coronal rain can be an efficient source for these waves in coronal loops. When generated at photospheric level, Alfvénic waves suffer from strong reflection when travelling through the lower layers of the solar atmosphere. Therefore, a mechanism that allows in situ wave generation bypasses this problem, and constitutes an additional and potentially important source of energy for the corona.
Antolin et al. (2018, hereafter Paper I) have shown how MHD waves can be generated from the interaction of counter-propagating flows or clumps of plasma along coronal loops. It is not clear yet how frequently this mechanism is, but the scenario seems particularly plausible in loops with coronal rain (e.g. Antolin & Rouppe van der Voort 2012; Kleint et al. 2014), in prominences (e.g. Alexander et al. 2013), or when strong plasma evaporation is present (e.g. Brosius & Phillips 2004; Brosius 2013; Gupta et al. 2018).
In Paper I we focus on the observation and modelling of a specific event observed on 2014 April 3 during a coordinated observing campaign between the Interface Region Imaging Spectrograph (IRIS, De Pontieu et al. 2014) and Hinode (Kosugi et al. 2007), combined with support from the Solar Dynamics Observatory (SDO, Pesnell et al. 2012), pointing at a prominence and coronal rain complex on the west limb of the Sun. The observations clearly show two rain clumps moving along the same coronal structure in opposite directions. When the two clumps intersect in the plane of the sky (POS), a localised brightening is observed. At this point the two clumps merge into one and continue moving downwards along the same structure, and a transverse oscillation of the rain strand is observed in the POS. The analysis of the observations combined with the modelling have led us to interpret these observations as coupled kink and sausage modes triggered by the collision of the two clumps.
The model devised for this purpose consisted of an ideal 2D MHD simulation of two asymmetric clumps travelling towards each other in a uniform medium. The parameters of the MHD simulations were chosen to match the observations, and the magnetic field strength was picked to retrospectively match the observed kink amplitude. While the model was suitable to explain one specific observation, it has triggered new questions about this mechanism as a way to generate transverse MHD waves in the solar corona. In particular, the connection between the properties of the clumps and the properties of the induced transverse modes has not yet been clarified, nor has the evolution of the forces during the collision. A key open issue is the degree of asymmetry required to trigger kink modes, and whether sausage modes are also a common result. From a more general perspective, the primary question that needs to be answered in this and future studies is whether the excitation of MHD waves in the solar corona through flow collision is a common event or a rare phenomenon. This has important implications for the energy budget, and the fraction originating from the lower layers of the solar atmosphere. Additionally, this is a potentially very interesting tool for seismology studies.
The main focus of this work is to explain how the interaction of counter-propagating clumps in coronal loops can lead to the generation of transverse MHD waves. Also, we explore how the properties of the clumps can influence the properties of the excited kink and sausage modes. In order to do that, we start from the MHD simulations already presented in Paper I, and significantly expand that investigation by varying the key parameters of the clump collisions. We also extend the model to 3D, and investigate the changes relative to the 2D case.
The paper is structured as follows: in Sect. 2 we present the 2D MHD simulations used for our modelling; in Sect. 3 we analyse in detail how the collision of two counter-propagating clumps generates MHD waves; in Sect. 4 we expand the study by exploring the parameter space of the clump properties; in Sect. 5 we analyse how our results change in a 3D set-up; and in Sect. 6 we present our conclusions.
2. Model
To study the generation of transverse MHD waves in the solar corona from counter-propagating plasma flows, we devised a simple MHD model. This model is capable of reproducing some observed features, as demonstrated in Paper I. Two dense clumps are set to travel in opposite directions to reproduce the observed upward and downward travelling features, and the properties of the background plasma and magnetic field are chosen so that observed properties of the transverse waves following the interaction are reproduced.
We repeat here only the most important properties of our MHD model, and we refer the reader to Paper I for further details. We perform our numerical experiment in a Cartesian 2D domain and we solve the ideal MHD equations using the MPI-AMRVAC software (Porth et al. 2014):
where t is time, ρ density, v velocity, p the gas pressure, B the magnetic field, 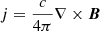 the current density, and c the speed of light. The total energy density e is given by
the current density, and c the speed of light. The total energy density e is given by
where γ = 5/3 denotes the ratio of specific heats.
The initial conditions are described in a Cartesian reference frame where the x-direction is aligned with the initial uniform magnetic field B = 6.5 G. The simulation domain extends from x = −6 Mm to x = 6 Mm and from y = −3 Mm to y = 3 Mm. The background plasma has a density of ρ = 10−15 g cm3, corresponding to a number density n = 1.2 × 109 cm−3 in a fully ionised plasma (or an electron density ne = 6 × 108 cm−3), and a uniform temperature of Te = 1 MK, leading to a plasma of β = 0.098. Although coronal rain is not a fully ionised plasma (Antolin & Rouppe van der Voort 2012), we do not expect this assumption to have a significant effect on the study carried out here. Oliver et al. (2016) found that even in the extreme case of 50% partially ionised plasma, the neutrals are still strongly coupled to the ions. The clumps are in pressure equilibrium with the background, but have a density ρC times higher and thus a temperature of T = Te/ρc K. The clumps are travelling at a speed VC in opposite directions. Each clump has a trapezoidal shape oriented so that the two opposite faces are parallel to one another with an angle θ of inclination between these faces and the direction perpendicular to the direction of travel (i.e. y-direction). The initial distance of the clumps is d = 3 Mm.
The numerical experiment runs for 300 s which is sufficiently long for the collision between the clumps to occur and for the system to approach a new equilibrium in the aftermath of the collision. The boundary conditions are treated with a system of ghost cells where we set zero gradient for all MHD variables at both x and y boundaries.
3. Simulation
As the main focus of this work is to describe the interaction of counter-propagating clumps in a coronal loop, in this section we illustrate in detail one of the characteristic simulations presented in Paper I. This section significantly expands the analysis described in Paper I, and it is essential to introduce the subsequent parameter space investigation. In particular, we illustrate in detail the mechanism through which MHD waves are generated in our numerical experiment. Figure 1 shows the initial condition of this numerical experiment where two dense clumps are aligned and travelling at the same speed in opposite directions.
 |
Fig. 1. Map of the number density n at t = 0 s. Green lines are magnetic field lines drawn from the left-hand boundary. Blue and red lines are the specific external (red) and internal (blue) pairs of magnetic field lines used in Sect. 3.2. |
In this representative simulation, two clumps of trapezoidal shapes are set to travel towards each other at a speed of vC = 70 km s−1. The two clumps have a density contrast ρC = 100, their width is w = 1 Mm, their length at the centre is L = 3 Mm, and the angle of the facing clump surfaces is θC = 50°. This set-up was found to produce the best match with the observed dynamics (Paper I).
3.1. Collision
The initial speed of the clumps relative to the background medium is lower than both the Alfvén speed (VA = 600 km s−1) and the sound speed (Cs = 165 km s−1), thus no shock initially develops and the two clumps travel at constant speed in opposite directions. In doing so, their motion leads to a compression of the plasma ahead of their propagation and a rarefaction behind.
At t = 7 s the two compressed regions touch and the collision phase begins. Figures 2a–c show ρ, T, and p of the system at t = 25 s, an intermediate stage during the collision. At this time the clumps have started to change shape at their fronts because of the interaction. In particular, the front of the clumps has expanded in the y-direction and the magnetic field lines have followed this deformation. It should be noted that the magnetic field is most deformed where the two clump surfaces are touching, thus at different x-coordinates for the upper and lower sides of the clumps because of their asymmetric shape. At this stage, the compression between the clumps has caused a significant increase in both pressure and temperature. The latter reaches about T = 3 MK, which is its maximum over the course of the simulation. This high temperature is maintained only for a few seconds before it drops again. At this time, the gas pressure distribution between the clumps follows the pattern of the two colliding fronts and strong gradients are generated along the collision region. Over the same region, the y-velocity of the plasma is directed outwards (vy ∼ ±10 km s−1) with respect to the collision and the magnetic field is displaced with the plasma.
 |
Fig. 2. Maps of number density, temperature T, and gas pressure p at different times of the MHD simulation. In the ρ maps, green lines are magnetic field lines drawn from the left-hand boundary. The rectangular box shows the region over which we average quantities for Fig. 3, and the white dashed line is the cut we use to plot the time-distance diagram in Fig. 4. A movie is available online. |
At this initial stage of the collision, the still unbalanced increase in the gas pressure between the clumps drives the dynamics. Figure 3a shows the evolution of the average forces as a function of time in the black rectangle shown in Fig. 2 that covers the y-positive part of the collision region. In this rectangle positive and negative forces are directed outwards and inwards, respectively, from the centre of the clumps along the direction perpendicular to their motion. The gas pressure gradient in this region remains always outward directed and in this phase (t < 40 s), it is about 30% stronger than the Lorentz force. At this stage the magnetic field deformation is still minimal and the magnetic tension force is a minor component of the total Lorentz force.
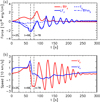 |
Fig. 3. Panel a: evolution of the y-axis components of the gas pressure gradient (−∇Py, red solid curve), Lorentz force (LFy, blue solid curve), magnetic tension (Ty, blue dashed curve), and magnetic pressure gradient (−∇Pmy, blue dash-dotted curve) averaged over the rectangular region shown in Fig. 2. Panel b: evolution of the x- and y-axis components of the velocity averaged over the rectangular region shown in Fig. 2. |
After the collision starts, the distortion of the magnetic field just outside of the clumps immediately generates forces directed inwards that resist any further expansion of the clumps in the y-direction and limits the distortion of the magnetic field. At the same time, as the clumps have a finite extent, the plasma coming into the collision region keeps the initial dynamic going and so the magnetic field distortion continues. However, in this system the restoring Lorentz force exerted by the magnetic field is proportional to the departure from the initial equilibrium condition and it overcomes the gas pressure gradient over time. This happens at t = 40 s for the average forces, as they become inward directed. However, the ongoing collision and the inertia of the plasma continue the distortion of the frozen in magnetic field, as can be seen in Fig. 3b where the average vx and vy components of the velocity are shown. We find that as the collision progresses, the average value of vy keeps growing until t = 60 s when it reaches a maximum, and only at this point do the restoring forces start decelerating the plasma. Then, vy remains positive for 6 s more, and at t = 66 s the forces finally invert the plasma motion and the Lorentz force starts decreasing, leading to the relaxation of the magnetic field.
Thus, at t = 66 s (Figs. 2d–f), the maximum magnetic field distortion is found and the restoring forces start driving the dynamics, leading to the excitation and propagation of MHD waves along the waveguide. In this system, the time elapsed between the beginning of the collision and the moment when the waves are released depends on (i) the duration of the clumps collision, which is proportional to their length, and (ii) the speed of the clumps as their inertia extends the collision phase. During the collision phase, the magnetic field starts showing a kink-like distortion due to the oblique angle of the colliding interfaces, i.e. two opposite peaks in the traced magnetic field lines, asymmetrically placed along x. The two peaks are symmetrically placed along x at first, but they travel apart over the collision time. When the collision finishes, it is this asymmetric magnetic configuration that determines the initial wavelength of the kink waves.
The average x-axis component of the velocity in the rectangular region shows a similar evolution over the course of the collision (t < 78 s in Fig. 3b). It is initially positive, decreases after t = 66 s, and becomes negative at t = 78 s. This evolution lags behind that of vy, demonstrating that the plasma is pushed back (negative vy) because the restoring magnetic forces push it inwards. The corresponding rectangle on the lower half of the domain gives instead an opposite average vy and vx evolution.
As soon as the collision terminates, the restoring magnetic forces act to bring the system back to equilibrium. However, this mechanism triggers oscillations and the density distribution changes because of the waves propagating in the system. Figures 2g–i show the system when the highest y-velocities are found after the collision, that is when restoring forces have induced a plasma motion opposite to the motion initially induced by the collision of the clumps. At this point, the plasma velocity in the y-direction is directed inwards (Fig. 3b) and a new regime sets in.
After t = 78 s, when the inertial force from the collision ends and the magnetic field is no longer driven by plasma motion, the system can fundamentally be regarded as a wave guide that contains an initial perturbation. After this time, the system starts oscillating around a configuration not far from equilibrium. This is visible in Fig. 3, where the average Lorentz force (the restoring force) and the average y-axis component of the velocity oscillate out of phase by π/2.
Throughout this evolution there are also clear signatures of fast MHD modes propagating away from the collision region when the collision ends and the total force exerted on the clumps becomes inward directed. This is shown in Fig. 4, where a time-distance map of the total pressure variations with respect to the initial pressure value are shown along the cut represented by the dashed line in Fig. 2. Distance is represented from the location closest to the centre of the domain. We find that after the collision time (t = 60 s) signals of total pressure increase (compression) travel away from the collision at the local Alfvén speed in what constitutes a train of fast MHD waves. Although this MHD simulation does not have the required output cadence to study in detail the propagation of these signals, it is worth mentioning them as they are a potential observational signature for the detection of clump collisions in the solar corona.
3.2. Analysis of kink and sausage modes
In this numerical experiment, the asymmetric fronts of the colliding clumps cause a distortion of the magnetic field that resembles a kink wave propagating along a waveguide. Similarly, we also find symmetric expansion and compression of the waveguide that resemble sausage modes. Figure 5 shows a state of the MHD simulation where it is possible to visually identify the presence of the kink mode distortion and the sausage mode expansion of the wave guide.
 |
Fig. 5. Map of the number density n at t = 105 s. Green lines are magnetic field lines drawn from the left-hand boundary. |
Based on this idea, we developed a simple technique for identifying the kind of wave modes induced and whether kink or sausage modes are predominantly present.
Figure 6 illustrates how this technique works. Let us consider any pair of initially straight magnetic field lines L1(x) and L2(x) that are placed symmetrically about the central axis of a magnetic wave guide. At a given time, after the wave guide is perturbed, we measure the displacement from their original position d1(x) and d2(x) for both magnetic field lines. We then combine these displacements to derive the functions:
 |
Fig. 6. Sketch showing that the distortion of a pair of magnetic field lines L1(x) and L2(x) can be interpreted in terms of the displacements d1(x) and d2(x) to derive the functions D(x) and E(x). |
Figure 6 shows the profile of D(x) and E(x) for a given pair of d1(x) and d2(x). The function D(x) follows the bulk displacement of the wave guide; it is proportional to the coherent displacement of L1 and L2, and it is zero when they move symmetrically in opposite directions. In contrast, E(x) is non-zero when the wave guide expands or contracts. Following this approach, we consider D(x) indicative of kink-like oscillations in the wave guide and E(x) of sausage-like oscillations. Applying this procedure to a given pair of magnetic field lines for all snapshots of our simulation and taking the maximum of D(x) and E(x) for each of them, we can see how the kink and sausage modes evolve during the simulation. It is important to note that the waveguide in our MHD simulation is highly variable in time and structured in space, and therefore the properties of the trapped kink and sausage modes are equally complex. Thus, we do not attempt to measure the total energy of these modes. Still, ours is an estimate of the amplitude of the waves and it can be helpful for comparisons with observed wave amplitudes that are equally complex measurements. Moreover, we are able to analyse whether some modes are likely to strengthen or weaken in time and whether their relative importance increases or decreases in connection with other parameters.
In our MHD simulation, we apply this procedure taking into consideration two different pairs of magnetic field lines. The first pair (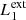 and
and 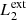 ) are magnetic field lines initially located at the y-edges of the clumps (red lines in Fig. 1). These magnetic field lines are useful to study the reaction of the background field to the clump collision. The second pair (
) are magnetic field lines initially located at the y-edges of the clumps (red lines in Fig. 1). These magnetic field lines are useful to study the reaction of the background field to the clump collision. The second pair (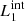 and
and 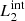 ) are magnetic field lines close to the y = 0 axis (blue lines in Fig. 1) and are therefore internal to the clumps. Figure 7 illustrates this analysis at t = 66 s, when we find the highest value for D(x) for
) are magnetic field lines close to the y = 0 axis (blue lines in Fig. 1) and are therefore internal to the clumps. Figure 7 illustrates this analysis at t = 66 s, when we find the highest value for D(x) for 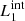 and
and 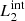 , and it also corresponds to the time when the internal magnetic field lines show the largest distortion.
, and it also corresponds to the time when the internal magnetic field lines show the largest distortion.
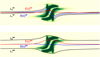 |
Fig. 7. Configuration of two pairs of magnetic field lines, |
We also define Ki(t) and Ke(t) as the difference between the maximum and minimum values of D(x) at each time t for the internal and external field lines, respectively, and Si(t) and Se(t) as the corresponding difference between the maximum and minimum values of E(x). Figure 8 shows the evolution of these functions in our MHD simulation. If we focus on the internal magnetic field, we find that Ki(t) rapidly increases in the first phase of the evolution when the magnetic field undergoes a significant distortion due to the collision of the clumps. It then quickly decreases after the end of the collision and it undergoes a couple of oscillations. The Si(t) trend shows a very similar pattern to that of Ki(t) after the collision, except that it always remains smaller than Ki(t). However, during the collision the ramp-up and decay phases are more gradual. The relative amplitude between Ki(t) and Si(t) is representative of the driving dynamics within the collision where the asymmetry of the colliding clumps leads to a magnetic field distortion, so that the wave guide is displaced and kinked, but it undergoes a marginal expansion. In contrast, for the external field lines, Se(t) is usually larger than Ke(t), and Se(t) follows a very similar pattern to that of Ki(t) initially. This happens because the external magnetic field lines react to the ongoing collision at this stage and they expand close to the middle of the domain where the pressure gradient becomes stronger. The longest lasting oscillatory behaviour is shown by the quantity Se(t), which in turn shows that after the collision terminates and the kink waves propagates out of the domain, the wave guide mostly shows sausage oscillations that set a standing wave. The last visible oscillations of Se(t) (around t = 200 s) show a period of about 20 s, which is consistent with the transverse Alfvén time in the wave guide. Similar conclusions were drawn by Nakariakov et al. (2004) and Li et al. (2018).
 |
Fig. 8. Evolution of the functions Ki(t), Ke(t), Si(t), and Se(t) used to estimate the amplitudes of the kink and sausage modes in our MHD simulation. |
In this scenario, we select the functions that show larger amplitudes to represent our kink and sausage modes, as they would be predominantly observed. So, we use K(t) = Ki(t) to represent the kink oscillation induced by the collision of the clumps that is generated within the collision region, and S(t) = Se(t) to represent the induced sausage mode oscillations that are mostly generated by the reaction of the background field against the expansion of the wave guide.
When we focus on the oscillations that follow the end of the collision, we find from Fig. 8 that two peaks of the kink oscillations are about 32 s apart (between t = 100 s and t = 132 s) which is half of the period of an oscillation. From the spatial profile of K(t = 105) and K(t = 132) (not shown here), we can estimate a travel distance of the peaks of about 4.7 Mm. These estimations give a velocity of about 73 km s−1 that corresponds to the Alfvén speed inside the wave guide after the collision, where we find |B|∼6 G and ρ = 5 × 10−14 g cm−3.
4. Parameter space investigations
In this section, we discuss how the collision mechanism is affected by some basic properties of the clumps. For this, we conducted a parameter space investigation taking as parameters the densities, velocities, lengths, and widths of the clumps, as well as the angle and offset between the colliding clumps.
4.1. Wave amplitude
We first investigate how the strength of the collision affects the wave amplitude. As mentioned in Paper I, the background plasma β is an important parameter that affects the amplitude of the induced kink in the wave guide as the magnetic field tension is stronger when the plasma β decreases. The sausage mode amplitude also increases when β increases; however, we find that kink mode amplitudes are roughly affected twice as much by the β variation relative to the sausage mode. Here, we keep the background properties unchanged and we vary the density contrast and the velocity of the two clumps. We ran 25 numerical experiments in a 5 × 5 grid of the two parameters we investigated. The reference simulation is presented in Sect. 3 (ρc = 100, vC = 70 km s−1) and we then ran numerical simulations with ![$ \mathit{v}_{\mathrm{C}}=\left[70/2,70/\sqrt{2},70\times\sqrt{2},70\times2\right] $](/articles/aa/full_html/2019/06/aa35539-19/aa35539-19-eq19.gif) km s−1 and
km s−1 and ![$ \rho_{\mathrm{C}}=\left[100/2,100/\sqrt{2},100\times\sqrt{2},100\times2\right] $](/articles/aa/full_html/2019/06/aa35539-19/aa35539-19-eq20.gif) .
.
Table 1 lists the maximum kink amplitude for each simulation in this investigation. It should be noted that the measurements of the kink amplitude used in Paper I followed a slightly different technique, resulting in a value of ∼1.10 Mm instead of 1.05 Mm for the central simulation in Table 1. We do not consider this difference critical for the results of this study. In the simulations where no kink amplitude is reported, the collision is significantly more disruptive than we have found so far, and the magnetic field distortion is too large to be analysed in terms of the excitation of kink or sausage modes. For instance, in these simulations the guide magnetic field becomes so distorted that Bx changes sign during the collision. The structure of this grid of experiments is such that two cornering experiments have the same initial momentum (∝ρCvC), and similarly, experiments with the same initial kinetic energy (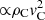 ) are always two cells in ρc and one cell in vC apart.
) are always two cells in ρc and one cell in vC apart.
Summary of the density contrast (vertically) and velocity (horizontally) of the clumps in a parameter space investigation.
Figure 9 shows how the kink amplitude evolves in time for some numerical experiments with constant momentum (Fig. 9a) and for some with constant kinetic energy (Fig. 9b). Figure 9a clearly shows that the same collision momentum does not lead to similar kink amplitudes, and that the velocity plays a dominant role. The difference in time of maximum kink amplitudes (in both panels in the figure) is just due to faster clumps leading to earlier collisions. However, the peak time does not linearly depend on the travelling time of the clumps. Faster travelling clumps lead to a delay in the times at which maxima are reached. This happens because these clumps need a longer deceleration time before the magnetic forces invert the plasma motion. In contrast, the simulations displayed in Fig. 9b show very similar maximum kink and sausage amplitudes. These experiments show that the amplitude of the waves generated by the collisions of counter-propagating clumps essentially depends on their kinetic energies. This implies that the efficiency of the mechanism that converts the initial kinetic energy into wave energy is a function of the kinetic energy. Indeed, as can be seen in Fig. 9b, the energy distribution between the kink and sausage modes does not seem to be affected by the contrast in density and velocity between the clumps either, as long as the kinetic energy of the collision is maintained.
 |
Fig. 9. Panel a: evolution of the function K(t) for simulations with constant initial clump momentum along the diagonal in Table 1. Panel b: evolution of the functions K(t) (blue lines) and S(t) (red lines) for simulations with constant initial kinetic energy in Table 1. |
It should be noted that the key parameter is the kinetic energy with respect to the centre of mass of the system EK(CM),
where VCM is the velocity of the centre of mass. We ran five different numerical experiments where we keep the relative speed between the clumps (140 km s−1) constant, and we varied the speed of each clump, and considered maximum speeds of 70 km s−1, 80 km s−1, 90 km s−1, 100 km s−1, and 110 km s−1. Figure 10a illustrates some of these simulations.
 |
Fig. 10. Panel a: sketch of some simulations of the parameter space investigation where the speeds between the clumps are varied. Panel b: evolution of the kinetic and magnetic energy for the simulations where the clump speeds are both 70 km s−1 and where they are 110 km s−1 and 30 km s−1. |
Figure 10b illustrates the evolution of the kinetic energy of two such numerical experiments: one in which both clumps have 70 km s−1 (blue, which corresponds to the numerical experiment presented in Sect. 3), and one where the clumps have different speeds and are travelling at 110 km s−1 and 30 km s−1. The evolution of the magnetic energy associated with the y-axis component of the magnetic field, and therefore with the distortion of the field, is fundamentally the same in both cases (within 3%). We thus find that the amplitude of the kink mode induced by the collision remains the same even though the speed changes between the two clumps. We find differences of about 0.04 Mm for the peak value and the evolution of the kink amplitudes largely overlap, as the kinetic energy with respect to the centre of mass is essentially the same in the two simulations.
4.2. Repartition of kink and sausage mode amplitudes
In this section we address the geometry of the colliding clumps in order to study how this affects the excitation of kink and sausage modes along the waveguide. We therefore vary the shape of the colliding clumps by changing the angle θ between the internal faces of the clumps and the direction perpendicular to the direction of travel. In particular, we consider values of θ = [0 ° ,20 ° ,40 ° ,45 ° ,50 ° ,60 ° ,80 ° ]. Figure 11 illustrates some of the configurations. The numerical experiment with θ = 50° is the one presented in Sect. 3. All the experiments in this section start with the same kinetic energy as the different clump shapes considered have the same area.
 |
Fig. 11. Sketch of the initial conditions of the simulations of the parameter space investigation where we vary the angle θ between the internal faces of the clumps and the direction perpendicular to the direction of travel. |
For all simulations, we analyse the amplitudes of the excited kink and sausage modes using the technique outlined in Sect. 3.2. Figure 12 shows the evolution of these amplitudes as a function of time for three specific simulations that illustrate three different regimes: when the clumps are symmetric (θ = 0°), when the clumps are not symmetric (θ = 50°), and when the clumps are significantly inclined (θ = 80°).
 |
Fig. 12. Evolution of the functions K(t) (blue lines) and S(t) (red lines) for some of the simulations where we vary the angle θ between the internal faces of the clumps and the direction perpendicular to the direction of travel. |
Figure 13 shows the profiles of the maximum kink and sausage amplitudes found in each numerical experiment as a function of the angle θ.
 |
Fig. 13. Maximum of K(t) (blue line) and Se(t) (red line) as a function of the angle θ. |
We find that when θ = 0°, only the sausage mode is excited and no kink is observed. This result is a consequence of the perfect symmetry of the system leading to no force imbalance in the y-direction, and thus only symmetric oscillations can be triggered. In the considered parameter space, the maximum of the sausage mode amplitude is about 0.5 Mm, which is obtained for all considered values of θ ≤ 60°. However, for θ ≠ 0 a kink oscillation is triggered as well. We also find that the oscillations after the collision follow a similar time evolution for all visible kink and sausage modes for θ ≤ 60 (Fig. 12). This means that the period of the oscillations does not crucially depend on the shape of the clumps, but on the local properties of the plasma, i.e. the local Alfvén speed.
As seen in Fig. 13, the amplitude of the sausage mode does strongly depend on the shape of the clumps, unless the collision angle is very large (θ > 60). When θ becomes too large, the geometric configuration leads to smaller gas pressure gradients and consequently smaller magnetic field distortion, and neither the sausage or kink modes are significantly excited. This result is in agreement with our previous finding that the kinetic energy with respect to the centre of mass is a key parameter. Since the asymmetry introduced by changing the collision angle does not really affect the centre of mass, it is expected that the sausage mode will not be affected (i.e. similar standing sausage modes are generated). In contrast, the kink mode is sensitive to the internal structure of the collision because it can lead to an imbalance of the forces along the y-direction. Its amplitude steadily increases from θ = 0° to θ = 50°, as in this range the asymmetry of the collision increases and the mechanism that triggers the kink mode becomes more efficient. After θ = 50°, the collision leads to smaller gas pressure gradients, as the clumps experience a weaker collision, and less energy is transferred to kink modes. As a result, an angle of θ ∼ 50° seems to be the optimal inclination to trigger kink modes through counter-streaming flow collisions. At this inclination, the ratio between the kink and sausage amplitude is at a maximum and it then remains roughly constant as increasing the clump inclination leads to weaker collisions, and kink and sausage modes both lose power.
Similarly, we investigate whether an initial offset in the travelling direction of the clumps has the same asymmetric properties that lead to the generation of both kink and sausage modes. Figure 14 illustrates this investigation, where we consider two clumps with a flat front (θ = 0°), but with nine different values of offset between the centres of the clumps, from 0% (the two clumps on the same y coordinate), to 100% (the two clumps displaced enough not to collide).
 |
Fig. 14. Sketch of the initial conditions of the simulations of the parameter space investigation where we vary the offset between the colliding clumps. |
Figure 15 shows the maximum kink and sausage amplitudes found in each simulation.
 |
Fig. 15. Maximum of K(t) (blue line) and S(t) (red line) as a function of the offset between the colliding clumps. |
By comparing it with Fig. 13, we find that this geometric configuration leads to generally smaller kink and sausage amplitudes. However, some of the pattern are the same when varying the offset between the clumps or the angle θ of the fronts In Fig. 15, we find that the sausage amplitude steadily decreases as the offset increases. Again, this can be explained by the variation of the centre of mass, which results in a reduction of the colliding surface between the two clumps. The behaviour of the kink mode is similar to that used earlier in that the offset produces a change in the forces along the y-direction. These forces reach a maximum for an offset of θ = 60° and decrease at higher offset values when the collision becomes weaker because of the limited interaction between the clumps. As for the previous case, the ratio between kink and sausage modes initially increases with the asymmetry in the system and then remains constant.
4.3. Lengths and widths of the clumps
In this section, we investigate the role of the lengths and widths of the clumps in generating kink and sausage modes. Figure 16 illustrates some of the experiments we run with a varying length of the clumps.
 |
Fig. 16. Sketch of the initial conditions of the simulations of the parameter space investigation where we vary the length of the clumps. |
We consider clumps with lengths L of 1.5 Mm, 2.4 Mm, 3 Mm, 3.6 Mm, 3.9 Mm, and 4.2 Mm and another simulation where the initial clumps are long enough to touch the x-boundaries of the simulation box. This arrangement makes this simulation equivalent to having infinitely long clumps because of the boundary conditions. This scenario may effectively correspond to very long clumps, as sometimes observed in coronal rain (Antolin et al. 2015).
Figure 17 shows the measured amplitudes for the kink and sausage modes as a function of time for these simulations. The basic evolution is common to both kink and sausage modes. The amplitude increases as long as the clumps are colliding, and the longer the clump length, the longer the period. Thus, the maximum is reached at different times. At the same time, the amplitude increases as the collision leads to an increased distortion of the magnetic field. We find that this distortion, i.e. the maximum kink amplitude, initially scales linearly with the kinetic energy, but we observe some saturation effects from L = 3.6 Mm. The saturation occurs because the magnetic tension force is proportional to the distortion of the magnetic field and at some point the resulting restoring force becomes strong enough to stop the magnetic field distortion. This is also seen in the simulation with infinite lengths. The kink amplitude keeps increasing and it then saturates shortly after t = 100 s. However, for this case we observe a permanent distortion of the field, and an additional stronger distortion at the end.
 |
Fig. 17. Evolution of the functions K(t) (blue lines) and S(t) (red lines) for some of the simulations where we vary the length of the clumps. |
Figure 18a compares the forces (gas pressure gradient and Lorentz force) that develop in the simulation where L = 3 Mm and L = ∞ averaged over the rectangular region defined in Fig. 2. The evolution of the forces for all the simulations with a finite clump length is similar and they only differ in the time when the magnetic restoring forces start driving the system. The evolution of the forces is qualitatively different when we consider infinite clumps as the gas pressure gradient does not undergo the stages we described in Sect. 3 and the restoring magnetic force grows until t = 150 s without showing an oscillatory behaviour afterwards. Similarly, Fig. 18b shows the average vx and vy over the same region. This evolution also confirms that when the clumps are infinite no oscillatory behaviour sets in on these spatial and temporal scales. Moreover, the average vx remains positive, effectively leading to counter-propagating streams, one positive flowing in the region y > 0 and one negative flowing in the region y < 0.
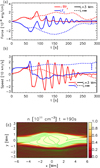 |
Fig. 18. Panel a: evolution of the y-axis components of the gas pressure gradient and Lorentz force averaged over the rectangular region shown in Fig. 2 for the simulations with clump length L = 3 Mm and infinite. Panel b: evolution of the x- and y-axis components of the velocity averaged over the rectangular region shown in Fig. 2 for the simulations with clump length L = 3 Mm and infinite. Panel c: map of the number density n at t = 190 s for the simulation with infinite clump length. Green lines are magnetic field lines drawn from the left-hand boundary. |
Figure 18c shows the system at t = 190 s for the simulation with infinite clumps, when the saturation is already well established. During the saturation phase, the distortion of the magnetic field remains constant in terms of the magnetic tension force, but it travels away from x = 0. When it reaches the boundaries the kink mode propagation is affected by the numerical boundary conditions and it alters the obtained stationary state. The explanation is that the constant addition of mass through the boundaries constitutes a constant addition of kinetic energy for the collision, which then forces the system to slowly reach a new state of equilibrium. At the same time, it should be noted that such a configuration when evolving in the presence of non-ideal MHD effects (such as magnetic field diffusion), could lead to the formation of an isolated plasmoid if the density structure gets fragmented where the magnetic field reconnects. Figure 18c shows a few locations where the magnetic field changes orientation and the magnetic reconnection could lead to the detachment of portions of dense clumps. This additional perturbation could lead to the generation of further MHD waves. Additionally, more energetic collision from shorter density clumps can lead to the same magnetic field distortion, as we found in the numerical experiments with highest kinetic energy in Table 1. Another numerical experiment that presents some similarities to our approach has been performed by Fang et al. (2016), in which the combination of collision and shear flow leads to the generation of Kelvin-Helmholtz instabilities and the onset of magnetic reconnection. Future studies will address the role of non-ideal MHD terms in this phenomenon.
Figure 19a shows the kink profile for two simulations with L = 1.5 Mm and L = 4.2 Mm at the respective times when the kink oscillations are at a maximum. We find that the amplitude of the kink is larger for L = 4.2 Mm and it also presents a larger distance between the two peaks of the oscillation. This happens because as soon as the collision starts, these peaks travel away from x = 0 at the local Alfvén speed. The distance between the two peaks can be thought of as half the wavelength of the kink mode. In Fig. 19 we plot this wavelength as a function of the clump’s length (excluding L = ∞). We find that the wavelength linearly depends on the clump’s length for the range we investigate in this study. This can be understood by the analysis of forces conducted in Sect. 3.
 |
Fig. 19. Panel a: profile of D(x) at the time of maximum K(t) for the simulations with L = 1.5 Mm and L = 4.2 Mm. Panel b: characteristic wavelength of D(x) at the time of maximum K(t) as a function of the length of the clumps. |
Finally, we study the effect of increasing the width of the clumps. Figure 20 shows different clump configurations when we vary the clump widths (keeping both widths equal). Since their lengths do not change we do not expect a significant change in the wavelength of the generated kink oscillations. We investigate three different cases with symmetric width values W of 1 Mm, 2 Mm, and 3 Mm.
 |
Fig. 20. Panel a: sketch of the initial conditions of the simulations of the parameter space investigation where we vary the width of the clumps. Panel b: evolution of the functions K(t) for the simulations where we vary the width of the clumps. |
Figure 20 shows the kink amplitude as a function of time for these three experiments. We find that the maximum amplitude is still linearly dependent on the initial kinetic energy, but as the width of the clumps increases, the post-collision oscillations show less damping, as the wave guide becomes larger as well. The damping, i.e. the ratio of the amplitudes of the first two peaks of the oscillation in Fig. 20 ranges between 0.34 for the simulation with W = 1 Mm and 0.87 for the simulation with W = 3 Mm. In contrast, for the sausage mode amplitude (not shown here), the damping does not significantly depend on the clump width.
5. 3D simulations
Finally, we consider the collision of two clumps and the subsequent excitation of MHD waves in a 3D configuration in order to understand how this mechanism occurs in a more realistic geometrical configuration.
The two clumps now have a cylindrical shape where the facing surfaces are still oblique. Panels a and d in Fig. 21 show the initial condition of this simulation from two perpendicular viewpoints. The numerical set-up is necessarily changed with respect to the 2D simulations as we take into consideration the z-direction extending from −3 Mm to 3 Mm. The normal to the colliding faces of the clumps is parallel to the xy−plane, and therefore does not have a z-axis component. Moreover the spatial resolution of the 3D simulation is a factor of 2 coarser than that in the 2D simulation.
 |
Fig. 21. Panels a and d: initial density contour projected on the xy-plane and on the xz-plane, respectively. Panels b and e: same contours at t = 84 s. Green lines are magnetic field lines drawn from the left-hand boundary. Evolution of the functions K(t) (blue lines) and S(t) (red lines) for the 3D MHD simulation on the z = 0 (panel c) and y = 0 planes (panel f). A movie is available online. |
The main difference when addressing the problem in a 3D geometry is that the diagnostic of its evolution crucially depends on the viewpoint. In the z = 0 plane the configuration is analogous to the 2D experiments we have already investigated, but when we consider the y = 0 plane, the clump collisions appear symmetric. Moreover, we expect that the thermal pressure gradient between the colliding clumps will exert a force in all directions perpendicular to B and this will result in a smaller deformation of the magnetic field in all directions. Panels d and e in Fig. 21 show the evolution of the system after 84 s, a time at which the clumps have merged after the collision. At this time, the plasma of the dense clumps has compressed the magnetic field after moving past the collision region. At a later stage, the plasma of the clumps fills fills the whole wave guide.
In order to analyse the kink and sausage modes induced in this case, we use the same technique introduced in Sect. 3.2. However, as this is an inherently 2D technique we apply it to the z = 0 plane and to the y = 0 plane separately. These two different cross sections cut the system perpendicularly along the directions where the asymmetry is most pronounced and where the system becomes symmetric. Figure 21 shows the kink and sausage mode evolutions for both planes.
The evolution along the z = 0 plane is more similar to the 2D scenario, showing the development of both kink and sausage modes. As expected, the amplitude of the kink modes is smaller than in the 2D configuration as the deformation occurs in a larger volume. The maximum kink amplitude found here is about 60% of that found in the corresponding 2D simulation. Additionally, the oscillatory behaviour of the kink mode amplitude is less evident in 3D. The maximum of the kink mode amplitude is reached at t = 82 s; afterwards it steadily decreases until t = 160 s when it reaches a minimum before growing again because of an apparent inclination of the waveguide, due to the magnetic field lines being tracked starting from one boundary. The kink modes are almost completely damped within the first oscillation, and this evolution is fundamentally different to that observed in 2D where we identify at lease three kink mode oscillations peaks in the kink mode amplitudes. The kink modes are not visible when we move to the y = 0 plane as the system becomes symmetric there. The amplitudes of the sausage modes are instead very similar for the z = 0 and y = 0 planes as the nature of this deformation does not depend on the asymmetry (as pointed out previously) and these are also about 60% of the amplitude found in the corresponding 2D simulation. In both planes, the sausage mode amplitude initially increases because of the collision as we have already shown, but it then shows a second peak at t ∼ 100 s. This second peak is due to the compression of the magnetic field lines when the clumps travel past the collision region.
6. Discussion and conclusions
In this paper, we have investigated the collision of counter-propagating clumps (density enhancements), a mechanism that can generate transverse MHD waves in situ in the solar corona. This mechanism has been observed in action in coordinated observations between SDO, IRIS, and Hinode of a prominence/coronal rain complex, as presented in Paper I.
The main focus of this study was to use MHD simulations to analyse in detail the generation of kink and sausage modes by means of such collisions. Hence, we analysed in detail a 2D ideal MHD simulation that could explain the observations and we then performed an extended parameter space investigation. In this paramater space investigation we varied both the clumps properties and the overall geometry, also running a 3D MHD ideal simulation of the same set-up.
In order to analyse our results, we developed a simple technique to identify the amplitude of kink and sausage modes in a wave guide. We associate the kink amplitude with the asymmetric distortion of magnetic field lines that are internal to the clumps and the sausage amplitude to the symmetric displacement of the magnetic field lines enveloping the collision region.
We find that the collision of two counter-propagating clumps is a viable way to generate kink and sausage modes. In particular, we identified two main phases in this process. The first is the collision of the clumps during which the dynamics are dominated by the motion and merging of the dense plasma. In this phase, trains of fast MHD waves travel outwards from the collision region. During this time, the magnetic field is distorted in a way that crucially depends on the clumps’ length and shape. Any asymmetry between the clumps will lead to the formation of kink modes, while the formation of sausage modes is largely unaffected by the symmetry of the system. This phase terminates when the clumps have lost their kinetic energy, after which the restoring magnetic forces (mostly magnetic tension) that are proportional to the displacement of the magnetic field lines from their equilibrium configuration trigger the oscillations that propagate along the wave guide.
By varying the physical properties of the colliding clumps, we established that the amplitude of the kink and sausage modes is mostly dependent on the kinetic energy of the system with respect to the centre of mass. At the same time, kink and sausage mode oscillations are more efficiently excited in different geometric configurations. By varying the angle of the colliding fronts or the overlap of the fronts, we found that the amplitude of the sausage modes does not depend on the symmetry of the system, but the interaction between clumps is significantly reduced in extreme cases leading to less energy in the resulting kink and sausage modes. In intermediate regimes the kink amplitude is always larger than the sausage mode amplitude. Moreover, the amplitude of the kink modes increases linearly with the clump’s length because of the associated kinetic energy. However, very long clumps can reach a saturation regime. This occurs when the restoring magnetic forces due to the deformation of the magnetic field become equal to the thermal pressure gradient driven by the collision. The initial wavelength of the kink modes increases with the length of the clumps. The generated kink modes propagate away from the collision, while the generated sausage modes become standing due to the symmetry in the longitudinal forces. Finally, we found that while the initial kink amplitude is proportional to the kinetic energy, less damping is obtained for larger clump widths in our model.
In order to better relate with a realistic scenario, we extended our analysis to a fully 3D configuration where the clumps are cylindrical. The key differences are first that the kink amplitude is nearly halved because the magnetic field line distortion occurs on the volume around the cylinders and that the observed mode amplitudes and the apparent asymmetry of the system crucially depend on the viewpoint. However, only through forward modelling can this effect be properly estimated.
In conclusion, this work has improved our understanding of the mechanism behind the generation of MHD waves in the solar corona due to the collision of counter-propagating plasma clumps. At the same time, more work is required in order to link this model with observations, and future efforts will focus on forward modelling more realistic numerical models for proper comparison with observations
Movies
Movie of Fig. 2 Access here
Movie of Fig. 21 Access here
Acknowledgments
This research has received funding from the UK Science and Technology Facilities Council (Consolidated Grant ST/K000950/1) and the European Union Horizon 2020 research and innovation programme (grant agreement No. 647214). P.A. acknowledges funding from the STFC Ernest Rutherford Fellowship (No. ST/R004285/1). This research was supported by the Research Council of Norway through its Centres of Excellence scheme, project number 262622. This work used the DiRAC@Durham facility managed by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). The equipment was funded by BEIS capital funding via STFC capital grants ST/P002293/1, ST/R002371/1, and ST/S002502/1, Durham University, and STFC operations grant ST/R000832/1. DiRAC is part of the National e-Infrastructure. We acknowledge the use of the open source (gitorious.org/amrvac) MPI-AMRVAC software, relying on coding efforts from C. Xia, O. Porth, and R. Keppens.
References
- Alexander, C. E., Walsh, R. W., Régnier, S., et al. 2013, ApJ, 775, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Antolin, P., & Rouppe van der Voort, L. 2012, ApJ, 745, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Antolin, P., Okamoto, T. J., De Pontieu, B., et al. 2015, ApJ, 809, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Antolin, P., Pagano, P., De Moortel, I., & Nakariakov, V. M. 2018, ApJ, 861, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Arregui, I. 2015, Trans. R. Soc. London Ser. A, 373, 20140261 [Google Scholar]
- Brosius, J. W. 2013, ApJ, 762, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Brosius, J. W., & Phillips, K. J. H. 2004, ApJ, 613, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Chitta, L. P., Jain, R., Kariyappa, R., & Jefferies, S. M. 2012, ApJ, 744, 98 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Nakariakov, V. M. 2012, Trans. R. Soc. London Ser. A, 370, 3193 [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014, Sol. Phys., 289, 2733 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, X., Yuan, D., Xia, C., Van Doorsselaere, T., & Keppens, R. 2016, ApJ, 833, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, G. R., Sarkar, A., & Tripathi, D. 2018, ApJ, 857, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Kleint, L., Antolin, P., Tian, H., et al. 2014, ApJ, 789, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Kohutova, P., & Verwichte, E. 2017, A&A, 606, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kohutova, P., & Verwichte, E. 2018, A&A, 613, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Krishna Prasad, S., Jess, D. B., & Khomenko, E. 2015, ApJ, 812, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Li, B., Guo, M.-Z., Yu, H., & Chen, S.-X. 2018, ApJ, 855, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, T., & Kitai, R. 2010, ApJ, 716, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, R. J., Weberg, M. J., & McLaughlin, J. A. 2019, Nat. Astron., 3, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Arber, T. D., Ault, C. E., et al. 2004, MNRAS, 349, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R., Soler, R., Terradas, J., & Zaqarashvili, T. V. 2016, ApJ, 818, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Porth, O., Xia, C., Hendrix, T., Moschou, S. P., & Keppens, R. 2014, ApJS, 214, 4 [Google Scholar]
- Reale, F. 2010, Sol. Phys., 7, 5 [Google Scholar]
- Verwichte, E., & Kohutova, P. 2017, A&A, 601, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verwichte, E., Antolin, P., Rowlands, G., Kohutova, P., & Neukirch, T. 2017, A&A, 598, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Summary of the density contrast (vertically) and velocity (horizontally) of the clumps in a parameter space investigation.
All Figures
 |
Fig. 1. Map of the number density n at t = 0 s. Green lines are magnetic field lines drawn from the left-hand boundary. Blue and red lines are the specific external (red) and internal (blue) pairs of magnetic field lines used in Sect. 3.2. |
| In the text | |
 |
Fig. 2. Maps of number density, temperature T, and gas pressure p at different times of the MHD simulation. In the ρ maps, green lines are magnetic field lines drawn from the left-hand boundary. The rectangular box shows the region over which we average quantities for Fig. 3, and the white dashed line is the cut we use to plot the time-distance diagram in Fig. 4. A movie is available online. |
| In the text | |
 |
Fig. 3. Panel a: evolution of the y-axis components of the gas pressure gradient (−∇Py, red solid curve), Lorentz force (LFy, blue solid curve), magnetic tension (Ty, blue dashed curve), and magnetic pressure gradient (−∇Pmy, blue dash-dotted curve) averaged over the rectangular region shown in Fig. 2. Panel b: evolution of the x- and y-axis components of the velocity averaged over the rectangular region shown in Fig. 2. |
| In the text | |
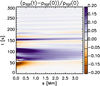 |
Fig. 4. Time-distance diagram of the total pressure along the cut shown in Fig. 2. |
| In the text | |
 |
Fig. 5. Map of the number density n at t = 105 s. Green lines are magnetic field lines drawn from the left-hand boundary. |
| In the text | |
 |
Fig. 6. Sketch showing that the distortion of a pair of magnetic field lines L1(x) and L2(x) can be interpreted in terms of the displacements d1(x) and d2(x) to derive the functions D(x) and E(x). |
| In the text | |
 |
Fig. 7. Configuration of two pairs of magnetic field lines, |
| In the text | |
 |
Fig. 8. Evolution of the functions Ki(t), Ke(t), Si(t), and Se(t) used to estimate the amplitudes of the kink and sausage modes in our MHD simulation. |
| In the text | |
 |
Fig. 9. Panel a: evolution of the function K(t) for simulations with constant initial clump momentum along the diagonal in Table 1. Panel b: evolution of the functions K(t) (blue lines) and S(t) (red lines) for simulations with constant initial kinetic energy in Table 1. |
| In the text | |
 |
Fig. 10. Panel a: sketch of some simulations of the parameter space investigation where the speeds between the clumps are varied. Panel b: evolution of the kinetic and magnetic energy for the simulations where the clump speeds are both 70 km s−1 and where they are 110 km s−1 and 30 km s−1. |
| In the text | |
 |
Fig. 11. Sketch of the initial conditions of the simulations of the parameter space investigation where we vary the angle θ between the internal faces of the clumps and the direction perpendicular to the direction of travel. |
| In the text | |
 |
Fig. 12. Evolution of the functions K(t) (blue lines) and S(t) (red lines) for some of the simulations where we vary the angle θ between the internal faces of the clumps and the direction perpendicular to the direction of travel. |
| In the text | |
 |
Fig. 13. Maximum of K(t) (blue line) and Se(t) (red line) as a function of the angle θ. |
| In the text | |
 |
Fig. 14. Sketch of the initial conditions of the simulations of the parameter space investigation where we vary the offset between the colliding clumps. |
| In the text | |
 |
Fig. 15. Maximum of K(t) (blue line) and S(t) (red line) as a function of the offset between the colliding clumps. |
| In the text | |
 |
Fig. 16. Sketch of the initial conditions of the simulations of the parameter space investigation where we vary the length of the clumps. |
| In the text | |
 |
Fig. 17. Evolution of the functions K(t) (blue lines) and S(t) (red lines) for some of the simulations where we vary the length of the clumps. |
| In the text | |
 |
Fig. 18. Panel a: evolution of the y-axis components of the gas pressure gradient and Lorentz force averaged over the rectangular region shown in Fig. 2 for the simulations with clump length L = 3 Mm and infinite. Panel b: evolution of the x- and y-axis components of the velocity averaged over the rectangular region shown in Fig. 2 for the simulations with clump length L = 3 Mm and infinite. Panel c: map of the number density n at t = 190 s for the simulation with infinite clump length. Green lines are magnetic field lines drawn from the left-hand boundary. |
| In the text | |
 |
Fig. 19. Panel a: profile of D(x) at the time of maximum K(t) for the simulations with L = 1.5 Mm and L = 4.2 Mm. Panel b: characteristic wavelength of D(x) at the time of maximum K(t) as a function of the length of the clumps. |
| In the text | |
 |
Fig. 20. Panel a: sketch of the initial conditions of the simulations of the parameter space investigation where we vary the width of the clumps. Panel b: evolution of the functions K(t) for the simulations where we vary the width of the clumps. |
| In the text | |
 |
Fig. 21. Panels a and d: initial density contour projected on the xy-plane and on the xz-plane, respectively. Panels b and e: same contours at t = 84 s. Green lines are magnetic field lines drawn from the left-hand boundary. Evolution of the functions K(t) (blue lines) and S(t) (red lines) for the 3D MHD simulation on the z = 0 (panel c) and y = 0 planes (panel f). A movie is available online. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



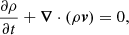
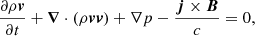
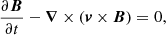
![$$ \begin{aligned} \displaystyle {\frac{\partial e}{\partial t}+{\boldsymbol{\nabla }}\cdot [(e+p){\boldsymbol{v}}]=0},\end{aligned} $$](/articles/aa/full_html/2019/06/aa35539-19/aa35539-19-eq4.gif)