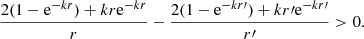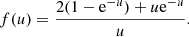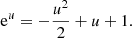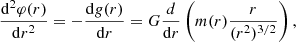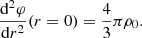| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A5 | |
| Number of page(s) | 7 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201935317 | |
| Published online | 30 May 2019 | |
Can a negative-mass cosmology explain dark matter and dark energy?⋆
1
Instituto de Astrofísica de Canarias, Avda Vía Láctea s/n, La Laguna 38205 Tenerife, Spain
2
Departamento de Astrofísica, Universidad de La Laguna, La Laguna 38205 Tenerife, Spain
e-mail: hsocas@iac.es
Received:
20
February
2019
Accepted:
17
April
2019
A recent study by Farnes (2018, A&A, 620, A92) proposed an alternative cosmological model in which both dark matter and dark energy are replaced with a single fluid of negative mass. This paper presents a critical review of that model. A number of problems and discrepancies with observations are identified. For instance, the predicted shape and density of galactic dark matter halos are incorrect. Also, halos would need to be less massive than the baryonic component, otherwise they would become gravitationally unstable. Perhaps the most challenging problem in this theory is the presence of a large-scale version of the “runaway effect”, which would result in all galaxies moving in random directions at nearly the speed of light. Other more general issues regarding negative mass in general relativity are discussed, such as the possibility of time-travel paradoxes.
Key words: cosmology: theory / dark matter / galaxies: kinematics and dynamics / large-scale structure of Universe
The simulation video is available at https://www.aanda.org
© ESO 2019
1. Introduction
In a recent paper, Farnes (2018; hereafter F18) put forward an audacious proposal to explain dark matter and dark energy in a unified scenario with a single fluid of negative-mass particles. This fluid would be continuously created everywhere to maintain its density at a constant level in spite of cosmological expansion. To support his hypothesis, F18 presented a number of simple numerical simulations showing the formation of halos around galaxies and indications of filament and void structures in a cosmological volume. In the spirit of healthy scientific debate, this paper presents the results of a critical look at the F18 model and some objections derived from the analysis of similar simulations.
The idea of matter with negative mass is not new in physics. In fact, some speculative work dates back to the nineteenth century (see e.g., the introduction of Bonnor 1989). After the development of general relativity, when physicists were struggling with the conflict between the crunching action of a universal gravity and the prevailing notion at the time of a static universe, negative mass was seen by some authors as a promising solution to one of the biggest problems in cosmology. A repulsive form of gravity emanating from negative masses could provide the necessary force to counterbalance the universal collapse (Einstein 1918). In reality, this statement is deceivingly simple and many important complications lurk behind it. To begin with, one has to define exactly what is meant by negative mass and this is not straightforward. In general relativity, the source of gravitation is the energy–stress tensor, a complex set of quantities that involves the density and flux of mass, energy, and stress. Remarkably, different observers in different reference frames might even measure opposite signs of some of these quantities.
It is tempting to draw a parallelism between a dual-sign gravitation (with positive and negative masses) and the dual-charge nature of electromagnetism. However, this would be a very naïve conception, as the two situations are completely different. The crucial difference is that, in the case of electromagnetism, two equal (opposite) charges repel (attract) each other, whereas in a dual-sign gravitation the opposite process would take place. The difference may appear subtle but it is of paramount importance. Gravity is able to attract many particles of the same sign together and make them coalesce into arbitrarily large structures.
In general relativity, the solution to the simple scenario where we have a point-like mass in an otherwise empty Minkowskian space-time is the Schwarzschild (1916) metric. This solution has a singularity at the mass position but the singularity is hidden from external observers by an event horizon that surrounds it. No information may propagate from the singularity to the outside world. The equivalent of the Schwarzschild solution for a negative mass does not represent a symmetric situation. It also has a singularity at the mass position but now there is no horizon. The singularity is naked, in violation of the weak cosmic censorship conjecture (Penrose 1969). While the cosmic censorship remains an unproven conjecture, it is widely recognized by the community as a sensible hypothesis and solutions with naked singularities are generally regarded as unsatisfactory. Of course, point-like masses do not exist in reality but it is often the case that one may mathematically construct a continuous mass distribution by integration of infinitesimal points. This raises yet another problem. If we consider a finite-size negative mass object, how are its pieces held together? In principle, each portion of it would be subject to a repulsive force from the rest of the object, with the force increasing to infinity for decreasing distances. Particles with electric charge are held together by quantum physics and the existence of an elementary charge. However, there is no such thing for gravity, at least in the context of general relativity. All of these are conceptual problems which, while not necessarily ruling out the existence of negative mass in the Universe, should at least serve as a warning sign that it is a complex issue and certainly not a symmetric counterpart of ordinary matter.
The concept of mass may have four different meanings in physics: the ability of matter to produce gravity (“active” gravitational mass), the response of matter to gravity (“passive” gravitational mass), the inertia of matter (its resistance to accelerate when subject to a force), or its energy equivalence. Classically, all of these definitions of mass refer to the same quantity and are positive by definition. General relativity requires by construction (by virtue of the equivalence principle) that passive gravitational and inertial mass must be the same. The theory does not explicitly require that they be positive, although some restrictions exist, as discussed in Sect. 4 below.
Various ideas were proposed and discussed in the decades following the development of general relativity regarding the interpretation and implications of negative sources of gravitation in that theory. Critically important was the work of Bondi (1957). First Luttinger (1951) and then Bondi (1957) (using Newtonian and relativistic frameworks, respectively), studied the concept of what is known as the “runaway motion”: two particles with opposite mass would start accelerating in one direction. In the Newtonian framework, this happens because the negative mass is attracted towards the positive one (the force is in the opposite direction but the negative inertial mass makes it accelerate towards the positive mass), whereas the positive mass is repelled and accelerates away from the negative. The same effect occurs in general relativity.
Following these developments, interest in the physics of negative masses declined, at least as a practical idea (exploratory theoretical works were still being pursued), for two main reasons. First, the runaway effect was considered so “preposterous” that it was viewed by many authors as unphysical. Second, the discovery of the Hubble–Lemaître law (Lemaître 1927; Hubble 1929) and the later confirmation of the Big Bang model with the detection of the cosmic microwave background (Penzias & Wilson 1965) removed what had been the original motivation for a repulsive gravitational force, that is, a means to sustain a steady-state universe (e.g., Bondi & Gold 1948).
However, the disinterest did not last long. A renewed interest in the issue of negative mass was sparked by the recent discovery of the accelerated cosmological expansion and its association with a mysterious dark energy and the cosmological constant (Riess et al. 1998; Peebles & Ratra 2003).
Modern negative-mass cosmologies typically attempt to explain dark energy as a repulsive form of gravity. Hossenfelder (2008) and Petit & d’Agostini (2014) explored an extension of general relativity with two different metrics, with positive and negative mass distributions, respectively (and a different speed of light). Benoit-Lévy & Chardin (2012) proposed the so-called Dirac-Milne universe, a cosmology combining positive-mass matter in a sea of negative-mass anti-matter (see also Manfredi et al. 2018). It is worth noting that, while anti-matter has positive mass in the standard model of particle physics, this prediction has not yet been tested experimentally due to the overwhelmingly larger effect of the electromagnetic force compared to gravity at the atomic scale. Experiments are currently underway that may soon resolve this question (see, e.g., Alemany et al. 2019), at least for the passive gravitational mass. In any case, the inertial mass of anti-matter must be positive, given that its acceleration has been measured in electro-magnetic fields.
The negative-mass cosmology proposed by F18 is fundamentally new in that it replaces both dark matter and dark energy with one single ingredient, namely the negative-mass fluid. His claim is sustained on numerical simulations of how this fluid would operate in different physical processes, such as galaxy evolution or cosmological collapse. The simulations presented in F18 are encouraging and show remarkable agreement with the observations (formation of halos, flat galactic rotation curves, cosmological structures, etc.). While we have rather robust constraints on the mass of dark matter concentrations by means of gravitational lensing observations, we are not able in most situations to determine the sign of the lensing mass (Takahashi & Asada 2013). If the F18 ideas were proven correct, the implications for all of physics would be formidable. A close scrutiny of this model is therefore clearly warranted.
This paper presents a critical analysis of the F18 results, identifying a number of problems and incompatibilities with existing observations. Section 2 has an analytical derivation of the expected properties of galactic halos in the F18 scenario. This will be helpful to understand and validate some of the results in Sect. 3, which presents simulations and the discrepancies with observations. Section 4 emphasizes other conceptual difficulties facing the model that are not directly testable against observations. Finally, the overall conclusions are summarized in Sect. 5.
2. Galactic halos
One of the remarkable results of F18 was the formation of negative mass halos around galaxies with a density structure strikingly similar to a Navarro–Frenk–White (NFW, Navarro et al. 1996) dark matter profile. This paper presents new simulations very similar in nature to those of F18 but the resulting halo densities exhibit what appears to be an exponential stratification instead. In order to develop a better understanding of the simulation results, or even to serve as a sanity check, it is usually helpful to conduct an analytical study of the system. In this section we seek the functional form of the density profile of a spherical negative mass halo surrounding a central core of positive masses.
Throughout this section we assume spherical symmetry, noninteracting particles (except for gravitation), and a steady-state equilibrium in which the system has reached a stable macroscopic configuration. The radial density profiles for the positive mass core and the negative mass halo are arbitrary and may overlap. For simplicity, let us consider a maximum radius RC and RH for the core and halo, respectively (RC < RH). We assume that the negative masses are initialized with a constant density 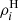 and no initial velocity. This last assumption is probably not very realistic but that is how the F18 simulations are initialized and those starting conditions are mimicked in the present work, as well.
and no initial velocity. This last assumption is probably not very realistic but that is how the F18 simulations are initialized and those starting conditions are mimicked in the present work, as well.
At any given time, the amount of halo particles contained in a spherical shell of radius r and thickness dr is given by the number of particles that have fallen from higher layers, balanced by those that have fallen from the opposite side, crossed the origin, and are moving upwards through r. Particles in layers below r will never reach this height. Consider another shell of radius r′ and thickness dr′. The probability that a particle that originated at shell r′ is inside shell r at any given time may be calculated as the time spent by such a particle within shell r divided by the total time it takes to fall all the way to the center:
with
and
In the expressions above, v(r′,r) is the velocity that particles originating at r′ have when they reach position r. Our initial conditions require v(r′,r′) = 0 ∀r′. We can then write the following equation for the halo density profile ρH(r):
Since both ρH and v are unknown, another relationship is needed to close the system, accounting for the action of gravity. The gravitational potential of an arbitrary mass distribution is given by Poisson’s equation:
Given the symmetry of our problem, we may take advantage of the Gaussian theorem1 (Gauss 1813), or even the shell theorem (Newton 1687), to express the gravitational field as:
where g(r) is the field, G is the universal gravitational constant, and m(r) is the total mass encircled by a sphere of radius r. This expression, along with the force derived from the field, remains valid in the Newtonian negative-mass formalism of F18, with m(r) accounting for masses of both signs.
For both positive and negative masses, the acceleration a is equal to the field g. Replacing dt with dr/v in the relation a = dv/dt and using a = g, we conclude that:
which may be integrated between two shells r and r′ to yield:
Since 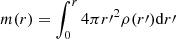 , and ρ is the addition of the core and halo mass densities, Eqs. (4) and (8) constitute a complete system whose solutions may be explored to investigate the properties of the density and velocity profiles.
, and ρ is the addition of the core and halo mass densities, Eqs. (4) and (8) constitute a complete system whose solutions may be explored to investigate the properties of the density and velocity profiles.
Motivated by the results presented in Sect. 3 below, we try an exponential profile ansatz for the halo density:
The total halo mass encircled below a certain radius r may be calculated after some tedious but straightforward series of integrations by parts:
At any point in the halo r > RC, the total (core and halo) mass encircled inside r is then m(r)=mH(r)+MC (with MC denoting the total core mass). Substituting in Eq. (8) and rearranging terms we obtain:
The first term in Eq. (11) accounts for the gravity produced by the core and has a simple form because it is always underneath. By virtue of the Gaussian or shell theorems, the field outside is equivalent to that of a point mass at the center. The second term is due to the gravitational field produced by the halo itself. If we take this equation and insert it into Eq. (4) we obtain the solution of the system.
We note that v(r′,r) appears in denominators in Eq. (4), which means that it must be nonzero for the system to have a physical solution. Moreover, Eq. (11) gives us an expression for the square of v(r′,r). Therefore, our system admits a real solution only if the right-hand side of Eq. (11) is strictly positive. If we can prove that this is the case, then our ansatz is correct and an exponential density profile is a solution to our equations.
The first term, proportional to MC, is trivially positive (recall that r′ is greater than r in the integration limits). The second term is more complex. With some rearrangement, our problem is equivalent to proving that ∀r < r′:
The above statement is equivalent to proving that the following function is monotonically decreasing:
Taking the derivative of f(u), we can deduce that f′(u) is zero only if u → ∞ or if:
We can prove that Eq. (14) has no solution for u > 0 because in this domain the left-hand side eu is always greater than 1, whereas the right-hand side is a convex parabola with a maximum value of 3/4. In other words, we have proven that the function f′(u) has no roots, which means that f(u) is monotonic (for u > 0). Now all that is left is to prove that f′(u) is negative somewhere, which is easy to see by evaluating the function. For large values of u, it is obvious that f′(u) is negative.
We have proven that f(u) is monotonically decreasing, which automatically means that the condition expressed in Eq. (12) is true for all r < r′ and that the right-hand side of Eq. (11) is positive. We have therefore proven that Eq. (4) has a real solution and that the ansatz is correct: An exponential profile of the form 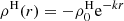 is a solution to our system.
is a solution to our system.
3. Numerical simulations
One of the most interesting novelties of F18 is that it presents the first negative-mass cosmological model to be implemented in actual numerical simulations. The author generously made his simulation code available to the community, a practice that will hopefully become increasingly widespread among researchers as it greatly facilitates verification and reproducibility of results. The importance of these two elements in the scientific method cannot be overstated. The results discussed in this section have been obtained with my own simulation code, which follows the philosophy of F18 as closely as possible but with some relevant differences, as explained in this section.
In the F18 code, the gravitational force between two masses situated at a distance d drops as the inverse of d, instead of the Newtonian form d2, resulting in a stronger force at large distances. Both forms produce qualitatively similar features, such as halo formation or cosmological collapse, obviously with quantiative differences. Assessing the influence of this peculiar gravity on the F18 results is beyond the scope of this paper. We adopt a realistic Newtonian gravity with a d2 dependence.
Although F18 claims to use a “leapfrog” integration scheme, his algorithm seems to operate as a first-order Euler integrator. I have implemented both schemes and verified that there are no significant qualitative or quantitative differences in the results obtained. The runs discussed in this paper have been computed with the leapfrog scheme.
The code employed here has been developed from scratch with the specific purpose of conducting these simulations. The source code, written in Fortran90 with MPI (message-passing interface, Forum 1994) parallelization, is publicly available2. The main difference with F18, apart from the d2 dependence of the gravitational force, resides in the boundary conditions. The boundary treatment was not explicitly discussed in F18 but it may be inferred by analyzing the source code. The simulations presented in F18 are initialized in a cubic box in which all particles are placed. The box has open boundaries and the particles are free to spread away from it throughout a much larger box. This second box has reflecting boundary conditions. Any particle that reaches one of its sides will bounce back by flipping the sign of the velocity vector component in the corresponding direction. In practice however, the second box is so much larger than the first one that very few particles ever reach its boundary within the time span of the simulations. Thus, for all practical purposes, we can consider the F18 simulations as defined in the initial box with open boundary conditions.
In cosmological simulations, it is customary to consider the opposite approach, with periodic boundary conditions. Periodic conditions are suitable in cosmology because they ensure that the Universe does not end abruptly outside the simulation domain. They produce simulations that are automatically compliant with the cosmological principle, in the sense that the box is a typical region and, in particular, there is no center of the Universe. In contrast, a simulation with open boundary conditions has a preferred direction and all matter tends to fall towards (or be repelled from, in the case of repulsive gravity) the center of the box. For instance, if we consider a homogeneous sea of negative-mass particles, open boundary conditions will make the initial box expand, as all particles repel each other into the empty space around it. With periodic boundary conditions, the fluid remains stable as every particle feels the same repulsive force from all directions, even those close to the edge of the domain. Another difference with modern large-scale simulations is the neglect of cosmological expansion, which is typically accounted for by adopting comoving coordinates and a modified potential. Cosmic expansion is neglected here in order to keep the simulations as close as possible to those of F18.
3.1. Halo mass
Let us begin by considering the galaxy halo formation, which according to F18 plays the role of dark matter in his unified model. I employed the same initial configuration and simulation parameters but using periodic boundary conditions and the correct form for the Newtonian gravitational force. Figure 1 shows the starting and final frames of the simulation, using the same isometric perspective as F18 to facilitate comparisons. The initial configuration has a spherical distribution of positive masses (the core) following the model of Hernquist (1990) embedded in a uniform sea of particles with negative mass.
 |
Fig. 1. Simulation of galactic halo formation. Blue (red) dots represent the positive (negative) mass particles. Upper image: Starting conditions, representing a Hernquist positive mass spherical galaxy embedded in a uniform distribution of negative masses. Lower image: Final state, exhibiting a nonspherical halo of enhanced negative-mass density around the galaxy. The galactic center of mass is initially at rest. In the final frame it is moving towards the left of the image. We note that the figure is represented in a 3D isometric perspective. Apparent particle densities may be misleading due to projection effects. |
This and other similar simulations produce halos of negative masses around the galaxies. However, they exhibit important differences with respect to the properties of real dark matter halos. To begin with, the halos in these simulations are too light. The ratio of halo to core mass in the simulations is between 0.3 and 0.8, whereas real galaxies have dark matter halos that are typically a factor of four to five more massive than their baryonic components. Furthermore, it is easy to intuitively understand why negative-mass halos must be light. Halo particles repel each other; they are held together by the attractive force from positive masses at the center. Invoking again the shell theorem (and assuming spherical symmetry), halo particles will only feel a central attractive potential if the total encircled mass is positive. If a halo had a ratio greater than one, the total mass encircled by the outer layers would be negative and such layers would be pushed away from the galaxy. This behavior is confirmed by simulations in which a galaxy is initialized with a massive halo. The halo is unstable and the outer layers are rapidly ejected from the galaxy.
3.2. Density profile and rotation curve
The radial density profile of the negative-mass halo is shown in Fig. 2. Outside the positive mass core, the simulation is in good agreement with the results of Sect. 2 of an exponential density profile (orange line). Dark matter halos on the other hand exhibit a more complex radial dependence (see, e.g., Navarro et al. 1996).
 |
Fig. 2. Radial density profile of the negative-mass halo in the galactic simulation. The axis of ordinates is logarithmic. The orange line shows an exponential density profile for reference. |
Another discrepancy with the F18 results (and with observations) is the galactic rotation curve. Without dark matter, the orbital velocity of stars should decrease as we move away from the galactic center. However, observations clearly show a flattening of this curve, in such a way that stars move with roughly the same linear velocity independently of their radial position. This observation is considered as one of the first pieces of historical evidence of dark matter (Rubin & Ford 1970). F18 claims that his simulation produces a flat rotation curve and argues that this is evidence in favor of the negative-mass model as an alternative to dark matter. However, this simulation exhibits different stellar dynamics. Figure 3 shows that the orbital velocity of stars drops with distance to the center, in disagreement with the observed flattened rotation curves.
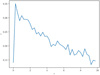 |
Fig. 3. Average orbital velocity as a function of radial distance to the galactic center. |
3.3. Accelerating galaxies
Perhaps the most important problem with the negative-mass simulations is that a galaxy, whose center of mass is initially at rest, immediately starts accelerating in a random direction and continues to gain speed during the entire run. This odd acceleration is present in all of the galactic simulations performed and, again, may be understood intuitively, in this case as a large-scale version of the runaway effect.
Let us imagine an isolated system consisting of a positive-mass particle standing at the center of a spherical negative-mass halo. The total force exerted over the positive mass is exactly zero because the forces from opposite directions balance each other out. However, this equilibrium is unstable in the sense that if the particle position is perturbed slightly, there would be more negative particles pushing from behind and fewer pushing from the front. Thus, there would be a net force pushing in the direction of the motion. Mathematically, the stability condition requires that the gravitational potential be concave at the origin, that is, a positive second derivative. Since by definition g(r)= − ∇φ(r), the second derivative of a spherically symmetric potential is:
where we now allow r to take positive or negative values to represent both sides of the origin. The density ρ must remain finite as r → 0 and therefore, for a sufficiently small r we may approximate it by its value at the origin ρ0 and then 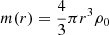 . It is then straightforward to show that
. It is then straightforward to show that
If ρ is positive, then the potential φ(r) is a concave function (it has a minimum at r = 0) and the central position is stable against perturbations. For negative ρ on the other hand, we have the opposite behavior. The potential φ(r) has a maximum at r = 0 and is a convex function of r. This latter situation is what we have in the simulation and explains the large-scale runaway effect.
Figure 4 shows the temporal evolution of both position and velocity of the galactic center of mass. Initially, the galaxy is at rest while the halo density builds up. After some time, at approximately t = 300 the halo is sufficiently dense to push the galaxy. The entire system starts accelerating and moves through the box with a sustained acceleration, as evidenced by the constant slope of the velocity curves in the lower panel.
 |
Fig. 4. Upper panel: evolution of the galactic core center-of-mass position as a function of time during the simulation run. The blue, orange, and green curves represent the position in x, y, and z, respectively. Lower panel: as above but in this case referring to the velocity vector components. After an initial period of time at rest while the halo is building up, the entire system starts accelerating (at approximately t = 300) and continues to gain speed with a constant acceleration. The sign of the x and y components has been reversed for better visualization in the figure. |
3.4. Halo shape
The shape of the halo produced in the negative-mass simulations is also problematic. Figure 1 (lower panel) already suggests that the distribution of red dots around the galaxy is not spherical. In particular, it is very elongated in the direction of the runaway motion. This is clearly seen in the simulation video available online3.
Figure 5 shows the distribution of halo mass enclosed in bins of azimuth around the galactic center at the end of the simulation. The vertical lines represent the instantaneous direction of motion, with green and orange representing the directions ahead and behind the galaxy. As seen in the figure, the halo is extremely elongated along the galactic motion, slightly narrower ahead and broader behind the galaxy.
 |
Fig. 5. Distribution of mass in the galactic halo integrated in bins of 10 degrees around the galactic center of mass in the xy-plane. The green (orange) line marks the direction ahead (behind) of the galactic runaway motion. |
3.5. Cosmological structure formation
The choice of boundary conditions is most critical in the simulation of structure formation inside a cosmological volume. Open boundary conditions result in a much more rapid gravitational collapse. The periodic boundary conditions imposed in the simulations presented here are more realistic, with each point feeling approximately the same gravitational pull from all directions (at least initially, with a homogeneous density initialization), except for the starting small random density fluctuations. Figure 6 shows the result of a structure formation simulation in a large cosmological volume. The box is one billion light-years (307 Mpc) in each direction and the time step is 10 Myr. A total of 50 000 particles are tracked in the simulation. They are initialized following a uniform distribution in the box with a total matter density of 2.6 × 10−27 kg m−3. This is approximately 0.3 times the cosmological critical density, which has a value of 8.6 × 10−27 kg m−3 (derived from cosmological parameters of Planck Collaboration XIII 2016). Two different runs are shown in the figure. In the first simulation, all particles have positive mass. In the second one, 84% of particles (the observed fraction of dark matter) have a negative mass. The positive mass simulation has the initial random inhomogeneities amplified by gravity to form concentrations and voids at an accelerated rate. The negative-mass simulation begins with the opposite behavior. The negative masses are dominant in number and mass. Their mutual repulsion in the initial overdensities creates an outward pressure which dilutes them and tends to smooth out inhomogeneities. In fact, this is a trick that is often employed to produce smooth initial conditions for regular cosmological simulations (White 1994). Later on, the positive masses begin to coalesce and form structures, dragging some negative halos around them. Structure formation occurs at a much slower rate in the negative-mass cosmological model.
 |
Fig. 6. Structure formation in a cosmological simulation. The plot represents the time evolution of relative overdensities, defined as the standard deviation of density variations among subdomains of 1 cubic Mlyr. Blue: run with positive masses. Orange: Run with 84% of negative masses. |
4. Other considerations
General relativity does not explicitly preclude the existence of negative mass but the dominant energy condition (Hawking & Ellis 1973) and the positive energy theorem (Schoen & Yau 1981) are difficult to reconcile with a negative mass (at least in the ADM sense, Arnowitt et al. 1960). Mbarek & Paranjape (2014) argued that loopholes may be found by relaxing the theorem assumptions and suggested that the best candidate is the requirement for an asymptotically Minkowskian space-time. These latter authors proved that for an asymptotically de Sitter space-time, negative-mass Schwarzschild solutions exist that everywhere satisfy the dominant energy condition. However, this result does not apply to the F18 cosmology, which is equivalent to an anti-de Sitter space-time (a negative cosmological constant). Therefore, while the existence of negative-mass particles is not ruled out, it remains to be proven that they may coexist with the energy condition in a background anti-de Sitter space-time.
The runaway effect is certainly problematic. While it has been argued that it does not violate momentum conservation, one needs to bear in mind that momentum conservation was formulated assuming that mass is a positive quantity. There are no physical, philosophical, or empirical arguments to assume that it also holds when a mass is negative. Extending the applicability of this principle to negative masses is a generalization that should stand on its own merits. It should not be considered as validated by an abuse of notation. A particularly troublesome thought experiment was considered by Gold in Bondi et al. (1957), in which one imagines attaching a pair of runaway particles to a wheel, essentially building a perpetual motion machine of the first kind.
If negative masses exist then it would be possible to build an Alcubierre drive (Alcubierre 1994). Such a device would enable faster-than-light travel and, in consequence, closed timelike loops, that is, the possibility to travel back in time (see, e.g. Everett & Roman 2012). A similar argument could be made about stabilizing traversable wormholes. Therefore, the existence of negative masses would facilitate the occurrence of physical paradoxes and causality violations.
The existence of a continuous negative-mass ocean of particles filling the intergalactic space would impact the propagation of gravitational waves from distant sources, which should lead to some effective screening of the waves (e.g., Mbarek & Paranjape 2014). However, no discrepancies have been found in the observation of several gravitational wave events by the LIGO and VIRGO collaborations between the wave signal amplitude and the theoretical expectation (The LIGO Scientific Collaboration & the Virgo Collaboration 2018). In particular, the GW170817 (kilonova) event, associated with an electromagnetic counterpart, yields the same distance when inferred from electromagnetic and gravitational waves (Abbott et al. 2017).
5. Conclusions
The model proposed by F18 is a testable alternative theory of gravity which if confirmed would have a profound impact on all areas of physics. This paper presents a detailed analysis of his model, which identifies a number of problems and discrepancies with observations. Perhaps the most obvious weakness is the constantly accelerating motion of galaxies. Instead of the orderly relation between distance and velocity given by the Hubble–Lemaître law, we would see all galaxies in the sky moving in random directions at nearly the speed of light. Other serious problems include predicting an incorrect shape, mass, and density profile for galactic halos, the keplerian rotation curves, low mass of galactic halos, and slow cosmological structure formation.
Other theoretical arguments are discussed that are not directly testable with observations. For instance, the relationship between negative mass and backwards time travel, opening the possibility of causality violations, is an important issue for any theory or model involving negative mass.
Overall, the conclusions of this study do not support the F18 model, at least in the original formulation. Since the simulations are of simplistic nature, as they were intended for exploratory purposes following the philosophy of F18, it is possible that some of these issues might be resolved with better, more realistic simulations. Likewise, some of the theoretical objections, such as a possible dampening of gravitational waves, would need actual calculations to be formalized before they can be considered conclusive evidence either for or against the theory.
Movie
Movie of Fig. 1 Access here
Acknowledgments
The author gratefully acknowledges financial support from the Spanish Ministry of Economy and Competitivity through project AYA2014-60476-P. This research has made use of NASA’s Astrophysics Data System Bibliographic Services. The Python Matplotlib Hunter (2007), Numpy Van Der Walt et al. (2011) and iPython Pérez & Granger (2007) modules have been employed to generate the figures and calculations in this paper. Thanks are also due to Isaac Alonso Asensio for his help identifying the F18 integration algorithm and implementing leapfrog in my code.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, ApJ, 848, L12 [Google Scholar]
- Alcubierre, M. 1994, Class. Quant. Grav., 11, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Alemany, R., Burrage, C., Bartosik, H., et al. 2019, ArXiv e-prints [arXiv:1902.00260] [Google Scholar]
- Arnowitt, R., Deser, S., & Misner, C. W. 1960, Ann. Phys. (NY), 11, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Benoit-Lévy, A., & Chardin, G. 2012, A&A, 537, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bondi, H. 1957, Rev. Mod. Phys., 29, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H., & Gold, T. 1948, MNRAS, 108, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H., Bergmann, P., Gold, T., & Pirani, F. 1957, in The Role of Gravitation in Physics, Report from the 1957 Chapel Hill Conference, eds. C. DeWitt, & D. Rickles [Google Scholar]
- Bonnor, W. B. 1989, Gen. Relativ. Grav., 21, 1143 [Google Scholar]
- Einstein, A. 1918, The Collected Papers of Albert Einstein. Vol. 7. The Berlin Years: Writings, 1918–1921 (Princeton, USA: Princeton University Press), 33 [Google Scholar]
- Everett, A., & Roman, T. 2012, Time Travel and Warp Drives: A Scientific Guide to Shortcuts Through Time and Space (Chicago: University of Chicago Press) [Google Scholar]
- Farnes, J. S. 2018, A&A, 620, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forum, M. P. I. 1994, MPI: A Message-Passing Interface Standard, Tech. Rep. (Knoxville, USA: University of Tennessee) [Google Scholar]
- Gauss, C. F. 1813, Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores (New York: Kraus Reprint), 1, 355 [Google Scholar]
- Hawking, S. W., & Ellis, G. F. R. 1973, The Large Scale Structure of Space-Time, Cambridge Monographs on Mathematical Physics (Cambridge: Cambridge University Press), 88 [Google Scholar]
- Hernquist, L. 1990, ApJ, 356, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Hossenfelder, S. 2008, Phys. Rev. D, 78, 044015 [NASA ADS] [CrossRef] [Google Scholar]
- Hubble, E. 1929, Proc. Natl. Acad. Sci., 15, 168 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Lemaître, G. 1927, Ann. Soc. Sci. Bruxelles, 47, 49 [Google Scholar]
- Luttinger, J. M. 1951, On “Negative” Mass in the Theory of Gravitation (Gravity Research Foundation. Awards for Essays on Gravitation) [Google Scholar]
- Manfredi, G., Rouet, J.-L., Miller, B., & Chardin, G. 2018, Phys. Rev. D, 98, 023514 [NASA ADS] [CrossRef] [Google Scholar]
- Mbarek, S., & Paranjape, M. B. 2014, Phys. Rev. D, 90, 101502 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Newton, I. 1687, Philosophiae Naturalis Principia Mathematica (London: J. Societatis Regiae ac Typis J. Streater) [CrossRef] [Google Scholar]
- Peebles, P. J., & Ratra, B. 2003, Rev. Mod. Phys., 75, 559 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Penrose, R. 1969, Nuovo Cimento Rivista Serie, 1, 252 [NASA ADS] [Google Scholar]
- Penzias, A. A., & Wilson, R. W. 1965, ApJ, 142, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Petit, J. P., & d’Agostini, G. 2014, Ap&SS, 354, 611 [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, V. C., & Ford, Jr., W. K. 1970, ApJ, 159, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Schoen, R., & Yau, S. T. 1981, Comm. Math. Phys., 79, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarzschild, K. 1916, Abh. Konigl. Preuss. Akad. Wissenschaften Jahre 1906, 92, Berlin, 1907 [Google Scholar]
- Takahashi, R., & Asada, H. 2013, ApJ, 768, L16 [NASA ADS] [CrossRef] [Google Scholar]
- The LIGO Scientific Collaboration & the Virgo Collaboration 2018, ArXiv e-prints [arXiv:1811.12907] [Google Scholar]
- Van Der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [CrossRef] [Google Scholar]
- White, S. D. M. 1994, ArXiv e-prints [arXiv:astro-ph/9410043] [Google Scholar]
All Figures
 |
Fig. 1. Simulation of galactic halo formation. Blue (red) dots represent the positive (negative) mass particles. Upper image: Starting conditions, representing a Hernquist positive mass spherical galaxy embedded in a uniform distribution of negative masses. Lower image: Final state, exhibiting a nonspherical halo of enhanced negative-mass density around the galaxy. The galactic center of mass is initially at rest. In the final frame it is moving towards the left of the image. We note that the figure is represented in a 3D isometric perspective. Apparent particle densities may be misleading due to projection effects. |
| In the text | |
 |
Fig. 2. Radial density profile of the negative-mass halo in the galactic simulation. The axis of ordinates is logarithmic. The orange line shows an exponential density profile for reference. |
| In the text | |
 |
Fig. 3. Average orbital velocity as a function of radial distance to the galactic center. |
| In the text | |
 |
Fig. 4. Upper panel: evolution of the galactic core center-of-mass position as a function of time during the simulation run. The blue, orange, and green curves represent the position in x, y, and z, respectively. Lower panel: as above but in this case referring to the velocity vector components. After an initial period of time at rest while the halo is building up, the entire system starts accelerating (at approximately t = 300) and continues to gain speed with a constant acceleration. The sign of the x and y components has been reversed for better visualization in the figure. |
| In the text | |
 |
Fig. 5. Distribution of mass in the galactic halo integrated in bins of 10 degrees around the galactic center of mass in the xy-plane. The green (orange) line marks the direction ahead (behind) of the galactic runaway motion. |
| In the text | |
 |
Fig. 6. Structure formation in a cosmological simulation. The plot represents the time evolution of relative overdensities, defined as the standard deviation of density variations among subdomains of 1 cubic Mlyr. Blue: run with positive masses. Orange: Run with 84% of negative masses. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



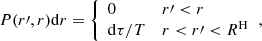
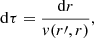
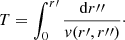
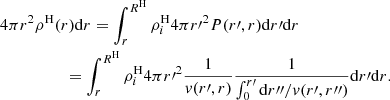
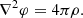
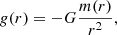
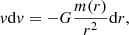
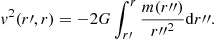
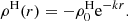
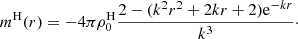
![$$ \begin{aligned}&{ v}^2(r{\prime },r)=-2G\left[ \int _{r{\prime }}^r {M^\mathrm{C} \over r{\prime }^2} \mathrm{d}r{\prime \prime }\right.\nonumber \\&\left.\qquad \qquad + {4\pi \rho _0^\mathrm{H} \over k^3}\left( {2(1-\mathrm{e}^{-kr^{\prime }})\over r{\prime }} - {2(1-\mathrm{e}^{-kr})\over r} + k(e{-kr}-\mathrm{e}^{-kr{\prime }}) \right) \right] . \end{aligned} $$](/articles/aa/full_html/2019/06/aa35317-19/aa35317-19-eq13.gif)