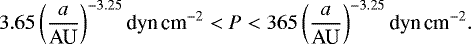| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834942 | |
| Published online | 05 June 2019 | |
Using deep neural networks to compute the mass of forming planets★
1
Physikalisches Institut & NCCR PlanetS, Universitaet Bern,
3012
Bern,
Switzerland
e-mail: alibert@space.unibe.ch
2
International Space Science Institute,
3012
Bern,
Switzerland
Received:
21
December
2018
Accepted:
28
February
2019
Context. Computing the mass of planetary envelopes and the critical mass beyond which planets accrete gas in a runaway fashion is important for studying planet formation, in particular, for planets up to the Neptune-mass range. This computation in principle requires solving a set of differential equations, the internal structure equations, for some boundary conditions (pressure, temperature in the protoplanetary disc where a planet forms, core mass, and the rate of accretion of solids by the planet). Solving these equations in turn proves to be time-consuming and sometimes numerically unstable.
Aims. The aim is to provide a way to approximate the result of integrating the internal structure equations for a variety of boundary conditions.
Methods. We computed a set of internal planetary structures for a very large number (millions) of boundary conditions, considering two opacities: that of the interstellar medium, and a reduced opacity. This database was then used to train deep neural networks (DNN) in order to predict the critical core mass and the mass of planetary envelopes as a function of the boundary conditions.
Results. We show that our neural networks provide a very good approximation (at the percent level) of the result obtained by solving interior structure equations, but the required computer time is much shorter. The difference with the real solution is much smaller than the difference that is obtained with some analytical formulas that are available in the literature, which only provide the correct order of magnitude at best. We compare the results of the DNN with other popular machine-learning methods (random forest, gradient boost, support vector regression) and show that the DNN outperforms these methods by a factor of at least two.
Conclusions. We show that some analytical formulas that can be found in various papers can severely overestimate the mass of planets and therefore predict the formation of planets in the Jupiter-mass regime instead of the Neptune-mass regime. The python tools that we provide allow computing the critical mass and the mass of planetary envelopes in a variety of cases, without the requirement of solving the internal structure equations. These tools can easily replace previous analytical formulas and provide far more accurate results.
Key words: methods: numerical / planets and satellites: formation
A copy of the Python code is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/626/A21
© ESO 2019
1 Introduction
Understanding the formation of planets (from terrestrial planets to gas giants) requires the development of theoretical models whose outcome can be compared with observations (e.g. Mordasini et al. 2009; Alibert 2019). One primary outcome of planet formation models is the mass and internal structure of planets (in particular, the mean density) because these two quantities can be obtained from radial velocity and transit observations of extrasolar planets.
In the core accretion model (e.g. Bodenheimer & Pollack 1986; Pollack et al. 1996; Hubickyj et al. 2005), the mass growth of planets is caused by two phenomena. The first is the accretion of solids (planetesimals or pebbles, e.g. Alibert et al. 2013; Ormel 2017), which depends on the properties of the accreted solids, the planetary mass, and the thermodynamical properties of the disk (Fortier et al. 2013; Ormel & Klahr 2010). The second phenomenon is the accretion of gas, which occurs in two regimes (see Helled et al. 2014, for a review). In the first regime, when the planet is small, the planetary gas envelope extends up to the protoplanetary disc at a radius that is generally between the Bondi and Hill radius (Lissauer et al. 2009). The planet is said to be attached to the disc, and the accretion rate of gas depends on the cooling efficiency of the planet. Planets must cool in order to accrete gas (Lee & Chiang 2015), and the mass of the gas envelope in this regime must be computed by solving the equations for the interior structure of the planet (Ikoma et al. 2000; Venturini et al. 2015). When the mass of the planetary core is higher than the so-called critical mass, the radiative loss at the surface of the planet cannot be compensated for by the accretion energy of solids (Mizuno 1980), and the planet starts to contract in a runaway fashion1 (Bodenheimer & Pollack 1986; Ikoma et al. 2000).
For sub-critical planets (when the core mass is lower than the critical mass), the computation of the planetary envelope requires solving a set of differential equations (see Sect. 2). Although standard procedure, solving these equations of the internal structure can require much computer time and may in some cases (e.g. close to the critical core) lead to some numerical instability. For this reason, some authors have developed a fitting formula that allows estimating the envelope mass as a function of different parameters (e.g. opacity and core mass), as well as some analytical approximation of the critical core mass. For example, Ikoma et al. (2000, hereafter I00) showed that the gas accretion rate is given by
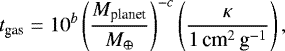 (1)
(1)
where b = 8 and c = 2.5. Mplanet is the planetary mass and κ is the envelope opacity. This formula was derived in the absence of solid accretion, but the authors showed that the accretion timescale for constant solid accretion follows a similar law, the pre-factor being multiplied by six. Certainly, the accretion energy of solids provides some thermal support that slows the accretion of gas down.
Using the same calculations, Ida & Lin (2004, hereafter IL04) showed that the critical core mass can be approximated as
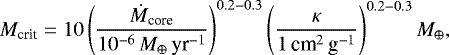 (2)
(2)
where Ṁcore is the accretion rate of solids.
More recently, based on the results from Piso & Youdin (2014), Bitsch et al. (2015, hereafter B15) used an accretion rate of gas given by
![\begin{eqnarray*} \dot{M}_{\textrm{gas}} & = & 0.00175 f^{-2} \left( {\kappa \over 1\, \textrm{cm}^2\,\textrm{g}^{-1}}\right)^{-1} \left( { \rho _c \over 5.5\,\textrm{g\,cm}^{-3}} \right)^{-1/6} \left( { M_{\textrm{core}} \over {{M}_{\oplus}} } \right)^{11/3} \nonumber \\[3pt] & & \left( {M_{\textrm{env}} \over 0.1\,{{M}_{\oplus}} } \right)^{-1} \left( {T \over 81 \textrm{K}} \right)^{-0.5} {{{M}_{\oplus}} \over {\textrm{Myr}}},\end{eqnarray*}](/articles/aa/full_html/2019/06/aa34942-18/aa34942-18-eq3.png) (3)
(3)
where κ is the opacity in the envelope, Mcore and Menv are the core and envelope mass, respectively, ρc is the core density, T is the temperature at the planet’s location in the disc, and f is a numerical factor of the order of 0.2. This formula is in principle valid in the absence of any solid accretion, but following the argument ofI00, this accretion rate can be used in the case of a constant solid accretion rate by reducing the pre-factor from 0.00175 to ~ 0.000292.
For super-critical planets, the accretion rate of gas can be approximated using the Kelvin-Helmoltz timescale tKH ~ tgas as
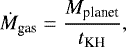 (4)
(4)
tKH itself depending on the planetary mass (see Eq. (1), I00, IL04).
The use of these simplified formulas, although convenient from the numerical point of view, is questionable when the formation oflow-mass planets in the range of super-Earths to the Neptune mass is to be computed. Because the envelope mass of these planets is low (lower than the core mass), an error of several Earth masses can notably change their radius and other properties such as their habitability (Alibert 2014). This has been demonstrated in the context of planet formation by pebble accretion by Brügger et al. (2018), for example, who compared the resulting mass function obtained using Eq. (3) on one hand, and the solutions to the equations of the internal structure on the other hand. These authors showed that the resulting planetary mass was very different in the two cases. When the approximate formula (Eq. (3)) was used, many planets were in the gas giant regime (Jupiter mass and beyond), whereas when the equations for the internal structure were solved properly, the planet mass was in the Neptune regime.
In this paper, we focus on these sub-critical planets, and we use deep-learning techniques to compute the critical core mass and the envelope mass as a function of the relevant parameters. Deep learning, specifically, deep neural networks (DNNs; see Goodfellow et al. 2016), is a sub-branch of machine learning that has recently been applied to different problems in planetary sciences, from exoplanet search by transit or direct-imaging methods (Pearson et al. 2018; Gomez Gonzalez et al. 2018) to dynamical analysis (Tamayo et al. 2016; Smirnov & Markov 2017; Lam & Kipping 2018) and spectrum analysis (Márquez-Neila et al. 2018). The advantage of using DNNs is twofold. First, the resulting critical core mass and envelope mass are close to the “real” mass (meaning computed by solving the differential equations of the internal structure). Second, the computer time required to compute these masses is far shorter.
The plan of the paper is as follows. We first present our models in Sect. 2, in particular, regarding the treatment of the micro-physics and boundary conditions. We then present the architecture of the DNNs we use, as well as the data we use to train them (Sect. 3). Finally, in Sect. 4 we compare the results of the DNN with the results obtained by solving the equations of the internal structure. All the tools we developed to use the DNNs are provided as Jupyter notebooks on github2 for an easy implementation in python codes.
2 Internal structure models
2.1 Planetary growth
In the core accretion model, a planet is formed first by the accumulation of heavy elements in a central core, followed by gas accretion, which builds an envelope that sheathes the core. The boundary between the protoplanet and the disc is in principle arbitrary and is usually taken as a weighted mean between the Bondi and the Hill radius (Lissauer et al. 2009). Between two time steps, the envelope mass grows by two mechanisms:
- (i)
the increase in core mass in hydrostatic equilibrium allows binding a higher mass envelope around the core;
- (ii)
the envelope radiates energy into the disc that cools the disc and therefore contracts it. This allows more gas to fill the radius of the protoplanet.
The standard procedure for computing the growth of a planet is to solve the equations of the internal structure (Sect. 2.2) from the top of the envelope to the core-envelope boundary. The energy radiated away in each time step is calculated based on energy conservation. This provides the updated luminosity L, which is required to solve the equations (see Venturini et al. 2016).
2.2 Equations
In order to generate the data we used to train and validate our DNNs, we first solved the equations of the internal structure (Kippenhahn et al. 2013)for a large set of boundary conditions. For this, the protoplanet was modelled as composed of an inert core of mean density ρcore = 5 g cm−3, surrounded by a gaseous envelope with a certain composition (see below). For the structure equations, we used v = r3∕Mr as the independent variable, where r is the radial coordinate of the planet, and Mr the mass enclosed inside a sphere of radius r. This variable is convenient to stop the integration of the equations at the exact core density and avoid interpolations. Thus, the equations are written as (Venturini et al. 2015)
![\begin{align*}& \frac{\textrm{d}P}{\textrm{d}v} = - G \rho \bigg(\frac{M_{\textrm{r}}}{v^2}\bigg)^{2/3} [3 - 4 \pi \rho v]^{-1}, \\[2pt] & \frac{\textrm{d}M_{\textrm{r}}}{\textrm{d}v} = \;4\pi \rho M_{\textrm{r}} [3 - 4 \pi \rho v]^{-1}, \nonumber \\[2pt] & \frac{\textrm{d}T}{\textrm{d}v} = \frac{T}{P}\frac{\textrm{d}P}{\textrm{d}v}\nabla , \nonumber \end{align*}](/articles/aa/full_html/2019/06/aa34942-18/aa34942-18-eq5.png) (5)
(5)
where P is the pressure, ρ the density, T the temperature, and G the gravitational constant. Following the Schwarzschild criterion, the gradient in Eq. (5) is ∇ = min(∇conv, ∇rad), where
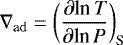 (6)
(6)
is the adiabatic gradient, and the radiative gradient is given by
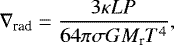 (7)
(7)
σ being the Stefan-Boltzmann constant, κ the opacity, and L the luminosity.
The luminosity was assumed to be uniform throughout the envelope and results from the energy that is released by the accretion of solids and from the contraction of the envelope (see detailed explanation in Venturini et al. 2016).
To close the system of structure equations, an equation of state (EOS) must be provided. The EOS gives ρ and ∇ad as a function of T, P, and composition.
2.3 Boundary conditions
The outer boundary conditions to solve Eq. (5) are set by the temperature (Tout) and pressure (Pout) at the planetary radius, defined as a combination of the Bondi and Hill radius (Lissauer et al. 2009):
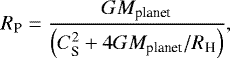 (8)
(8)
where  is the square of the sound velocity in the protoplanetary disc at the planet location a, and
is the square of the sound velocity in the protoplanetary disc at the planet location a, and 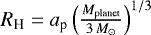 .
.
The inner boundary conditions are given by the planetary core mass and core radius. When these differential equations are solved in planet formation models (see e.g. Alibert et al. 2005), the total mass of the planet is iteratively adjusted until all the boundary conditions are fulfilled.
2.4 Microphysics
In this workwe assumed the envelope to be composed of a mixture of hydrogen and helium, with a helium mass fraction of Y = 0.28. We did not consider the effect of pollution by accreted solids (Venturini et al. 2015; Venturini & Helled 2017). This effect will be included in a future work. The density and adiabatic gradient of the internal structure equations are determined by T, P, and composition through the EOS. Because we assumed an H–He composition for the envelope, we adopted the EOS of Saumon et al. (1995). For temperatures and pressures below the limits of the Saumon et al. (1995) table, the EOS of ideal gas for the mixture of H2 and He was assumed, accounting for the corresponding degrees of freedom for the entropy and energy of the mixture.
The opacities are defined as
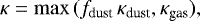 (9)
(9)
where the dust opacities were taken from Bell & Lin (1994; hereafter BL94), and the gas opacities from Freedman et al. (2014). The factor fdust accounts for the possibility that the dust opacities might have lower values than those of the interstellar medium (ISM). This may be caused by grain growth and settling (Movshovitz et al. 2010; Mordasini 2014). In this work we present calculations for fdust = 1 and fdust = 0.01. Because the dust opacity values peak at the top of the envelope and the gas values peak at the deeper, hotter regions, the definition in Eq. (9) is equivalent to considering κ = fdust κdust + κgas, as shown in Mordasini (2014).
The validity domain of the Freedman gas opacities in pressure and temperature is 1–300 bar and 75–4000 K. At the core-envelope boundary, higher values of temperature and pressure typically exist, but in that domain of high temperature and pressure, the envelopes are always convective. Therefore, even when we take a constant extrapolation in these regions, it does not affect the computation of the internal structure. An analytical fit to the Freedman gas opacities is given in Freedman et al. (2014). This is implemented to reduce computational time.
3 Deep neural network
3.1 Principle
In the past decades, machine learning has seen a tremendous development through the advancement of novel techniques and because very large amounts of data have become available. In particular, neural networks have been used more and more in the past decade to achieve very good performances in tasks such as image classification and text translation. This method has also been applied to regression, which is linked to the prediction of a continuous variable (see Goodfellow et al. 2016), and is the case of interest in this paper. In regression, the task of a neural network is to use some input variables (such as temperature and pressure at the outer radius of the planet) to predict one or more variables (the mass of the gas envelope in our case). In the machine-learning literature, the input variables are referred to as features and the predicted variable is the so-called target variable.
A neural network is made of different layers of units, each unit performing a simple task: linear combination of its inputs, followed by a non-linearity (see below). Each layer of a neural network typically takes as input the outputs of the previous layer to produce a series of outputs that are processed by the next layer. The first layer takes as input the features, and the last layer outputs a prediction of the target variable that is, hopefully, close to the actual target variable. A neural network is said to be deep (therefore DNN, deep neural network) when it has at least one hidden layer (i.e. a layer that is not the first or the last layer). A DNN is trained by providing a (large) number of data (features and target variable), and by adjusting the coefficients (also called weights) of all linear combinations of all units in an iterative way, in order to achieve the best match between the predicted target value and the actual value. The matching between the predicted and actual values is quantified using a cost function (see below), which is a function of all the parameters of the DNN. The gradient of the cost function is then computed (as a function of the parameters of the DNN) using a method called backpropagation (Goodfellow et al. 2016), which basically consists of applying the chain rule for derivation. Finally, the gradient descent is used to determine the optimum parameters. We note that the cost function is in general a non-convex function of the DNN parameters, and many local minima can exist. There is therefore no guarantee that the parameters found are those that lead to the absolute best performances of the DNN.
We have considered two DNNs. The first, DNN1, to predict the critical core mass (as a function of four parameters, see next section). The second, DNN2, to predict the gas envelope mass as a function of five parameters (the same four parameters plus the core mass). The architecture of the DNNs for the different values of fdust is the same, but the resulting weights are of course different.
DNN1 has three hidden layers with 128 units each. These numbers were found by a series of trial-and-error tests, for which we varied the number of layers and the number of units per layer in a grid search (see Sect. 5). We also compare the results obtained using other machine-learning methods in Sect. 5. The DNN is fully connected, meaning that each unit of a layer is connected to each unit of the previous and next layer. For each unit, we chose to use the ReLU function for the non-linearity, given by
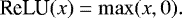 (10)
(10)
The cost function we minimise is the mean square error between the predicted and the actual critical mass:
 (11)
(11)
where N is the total number of data points we use, Mcritical,target,k is the critical core mass computed using the differential equations of the internal structure (see previous section), Mcritical,predicted,k is the value predicted by the DNN, and w are the weights.
DNN2 has five hidden layers with 128 units each, the non-linearity is also the ReLU function, and the cost function is similar, except that we compared the predicted and real envelope mass.
The twoDNN were trained using the ADAM optimiser (Geron 2017) for 10 000 training epochs. The learning rate was chosen to be equal to 0.0001 for the training. A higher learning rate could be chosen, but this would translate into a noisy decrease of the cost function. The other parameters of the ADAM optimiser were taken as the default values in TensorFlow3. We did not used mini-batch because we were able to fit the whole training dataset (of size 25 000 and 800 000 for DNN1 and DNN2, respectively) in the memory at once. The sizes of the test and validation sets were equal to 1000 for DNN1 and 300 000 for DNN2. Finally, the bias for all units was initialised at 0, whereas the weights were randomly initialised using a Gaussian distribution centred on 0, with a variance scaling with the square root of the number of input and output connections (Geron 2017).
3.2 Data
To generate the data, we selected in a first step ~10 000 points in a four-dimension space by drawing at random a semi-major axis a (uniform in log between 0.1 and 30 AU), a pressure Pout (uniform in log between 10−2 and 1500 dyn cm−2), a temperature Tout (uniform between 30 and 1500 K), and a luminosity L (uniform in log between 1022 and 1028 erg s−1). These luminosities encompass the energy per unit time that would be given by an accretion rate of solids of ṀZ = 10−10 M⊕ yr−1 onto a core of 1 M⊕ and ṀZ = 10−5 M⊕ yr−1 onto a core of 20 M⊕.
For each set of (a, L, Pout, Tout), we computed the core mass for a given planetary mass by solving the differential equations presented in Sect. 2. Pout and Tout were used as the outer boundary conditions (Sect. 2.3). For a planetary mass growing from Mplanet = 1 M⊕ onwards, the core mass first increases, reaches a local maximum, and then decreases. The critical core mass is the first local maximum core mass obtained in this way (Mizuno 1980; Papaloizou & Terquem 1999).
For each of these (a, L, Pout, Tout), we computed a full Mplanet–Mcore curve for a planetary mass ranging from 1 M⊕ to the corresponding critical mass. Each of these curves was sampled with a step of 0.01 M⊕ in Mplanet, and the resulting Menvelope as a function of the five parameters (a, L, Pout, Tout, Mcore) was finally computed. In addition to the relation between the envelope mass and the five input parameters (a, L, Pout, Tout, Mcore), these curves provide us with the critical core mass as a function of the four first parameters (a, L, Pout, Tout).
Importantly, because the critical core mass depends on the (a, L, Pout, Tout) parameters (it is e.g. lower for lower L), the number of points on an Mplanet–Mcore is not the same for each (a, L, Pout, Tout) choice. Because the cost function C(w) defined above for DNN2 gives the same importance to each data point, taking all the points of all the Mplanet–Mcore curves would resultin a more accurate performance for high critical core masses than for low critical core masses. Data points for which Mcritical(a, L, Pout, Tout) is high are more important in the cost function because they are more numerous. This approach might cause a DNN to accurately predict the envelope masses for large L (large critical cores), for instance, and to very inaccurately predict them for low L (small critical cores). To avoid this effect and achieve a similar prediction accuracy for all parts of the (a, L, Pout, Tout, Mcore) space, we used the same number of points for each of the Mplanet–Mcore curves (this technique is known as stratification). Finally, before we implemented them, all the data were pre-processed by removing the mean and separately scaling each to unit variance in each dimension.
We obtained ~27 000 data points that could be used with DNN1 (to predict the critical core) for each choice of the opacity parameter fdust, and ~ 10 million data points that could be used to train DNN2 (to predict the envelope mass), again for each choice of the opacity parameter fdust. Figure 1 shows the distribution of (a, L, Pout, Tout) for a subset of the data points.
These data points were split randomly into a training set, a validation set, and a test set. The training set was used to adjust the weights of the DNNs, the validation set was used to estimate the generalisation performances of the DNNs, and in particular, to avoid overfitting. After the optimum weights of the DNNs were computed (in praxis, when the cost function on the validation set was lowest), we used the test set to present the results shown in the rest of the paper (the data points used to generate the different plots shown below were therefore never used in any part of the optimisation process of the DNNs). It is important to verify that the parameter distribution is the same for the three sets (training, test, and validation). This should be the case because the sets were generated randomly, and this can be verified from the cumulative distribution of the input parameters for the three sets, as shown in Fig. 2.
The (a, L, Pout, Tout, Mcore) parameters were independently drawn at random in our data generation procedure. It is clear, on the other hand, that some of these parameters are strongly correlated: for example, the pressure and the temperature are a function of the semi-major axis in actual proto-planetary discs. This raises two questions: first, what kind of internal structure might unrealistic input parameters (e.g. high temperature and low pressure) lead to, and second, what is the effect of the these unrealistic data on the global optimisation process of the DNN. The cost function as presented above takes all considered data into account with equal importance. Taking unrealistic data into account might therefore degrade the performances of the whole DNN.
Regarding the first question, we verified that our internal structure code converges even for unrealistic cases. As an example, Fig. 3 shows the internal structure (envelope mass as a function of the radius) for two cases. The planetary core mass is equal to 2 M⊕, the semi-major axis is equal to 0.5 AU, and the luminosity is equal to 1025 erg s−1, which corresponds to an accretion rate of ~ 5.5 × 10−8 M⊕ yr−1. The temperature is equal to 400 K and the pressure is equal to 10 dyn cm−2 in the first (unrealistic) case, and equal to 350 dyn cm−2, in the second (more realistic) case. These values are typical for a protoplanetary disc (see Venturini & Helled 2017). The envelope mass in the unrealistic case is equalto 0.261 M⊕, to be compared to 0.437 M⊕ in the realistic case.
We address the second question (the potential effect of unrealistic data on the DNN performances) in Sect. 5 below.
 |
Fig. 1 Initial conditions for a subset of 1000 datapoints. Each panel shows the correlation between two quantities, the panels on the diagonal showing the histograms of the different quantities. |
4 Results
4.1 Critical mass
The DNNs were trained using the Tensorflow library4, the notebooks to use the DNN are available on github5.
As described above, the DNNs were trained using only a sub-sample of the generated data, the other part was split between a test set and a validation set. We used the test set to compute the difference between the predicted critical core mass and the mass derived using the equations of the internal structure. The correlation between the two masses is shown in Fig. 4; our results are plotted in blue and the critical mass from IL04 is shown in red (Eq. (2)). We emphasise that in the resolution of the equations of the internal structure, the envelope opacity is not constant but rather a function of the local temperature and pressure, and it varies between ~ 1 and ~ 10 cm2 g−1 in the radiative layers of the atmosphere (T ≲ 1000 K). We therefore used these two limiting values to compare our results with those of IL04, and plot the resulting critical mass as a vertical line in Fig. 4. The critical mass computed using Eq. (2) has a much greater variance than the results obtained using the DNN, and it is generally under-estimated. Using our DNN, the average difference between thepredicted critical core mass and the mass obtained by solving the equations of the internal structure is ~ 1.67%; the majority (99.3%) of the critical masses is predicted with an accuracy better than 5%, and the maximum error is ~ 14.2% for critical masses higher than 1.
We perform the same comparison in the right panel of Fig. 4, now assuming that the opacity is reduced by a factor 100 compared to the opacity of BL94. When the IL04 formula is used, the opacity ranges from 0.01 to 0.1 cm2 g−1. In this case, the critical core mass obtained using Eq. (2) is substantially biased towards lower values.
 |
Fig. 2 Cumulative distribution of the input parameters for DNN1, for the training, validation and test sets. |
4.2 Envelope mass
Similar to the prediction of the critical mass, we used the test set of envelope masses to compute the difference between the predicted envelope mass and the mass derived using the equations of the internal structure. The correlation between the two masses is shown in Fig. 5, where we also show the result estimated using Eqs. (1) (I00) and (3) (B15). In these two latter cases, we need to specify the timescale over which gas is accreted because these two formulas only provide a gas accretion rate. For the simple estimates provided in Fig. 5, we have assumed that gas is accreted on a timescale that is uniformly distributed between 0 and 5 Myr. This timescale should be equal to the disc lifetime. We emphasise that in a real situation, the core mass of the planet could increase during this timescale, which would modify the accretion rate of the gas. In the estimates provided in the figures, this effect is not included.
Comparing the three different cases, we see that the variance is much greater when the B15 and I00 formulas are used. Some of this variance of course results from assuming the distribution of the time during which gas is accreted. We remark that similar as for the case of the critical mass, it is not obvious which value of the envelope opacity should be used in order to obtain the most meaningful comparison between the DNN and the fitting formulas of I00 and B15. The masses are predicted with an accuracy better than 20% in more than 97% of the cases with our DNN.
 |
Fig. 3 Envelope mass as a function of the radius for two models. For both models, a planetary core of mass equal to 2 M⊕ is located at 0.5 AU, with a luminosity equal to 1025 erg s−1 and a temperature at the planet–disc interface equal to 400 K. The pressure at the disc–planet interface is equal to 10 dyn cm−2 (an unrealistic value) or 350 dyn cm−2. |
4.3 Planet formation tracks
In order to compare the result of the DNN and the result from resolving the equations of the internal structure in a more realistic way, we present in Fig. 6 planetary growth tracks for different cases. We consider different formation locations (5 and 10 AU), different accretion rates (Ṁcore = 10−6M⊕ yr−1 and Ṁcore = 5 × 10−7M⊕ yr−1), different temperatures (50 and 150 K), and two dust opacities. For each case, we also compare the evolution of the envelope mass with the mass that would be obtained with the approaches of I00 (Eq. (1)) and B15 (Eq. (3)). For these two latter cases, we consider in each case two possible values of the envelope opacity: 1 and 10 cm2 g−1 for the BL94opacity, and 0.01 and 0.1 cm2 g−1 when the BL94 opacity is reduced by a factor 100.
In all the cases, it is clear that the results of the DNNs are much closer to the results obtained by solving the equation of the internal structure than by implementing the I00 and B15 formulas. It is also notable that the envelope mass is over-estimated by far by Eq. (3). In all the cases presented here, the planet ends up as a Neptune-mass planet when the DNN is used (and therefore also when the equation for the internal structure is solved), whereas it ends up in the Jupiter-mass range when Eq. (3) is used. This result is compatible with the findings of Brügger et al. (2018). The results obtained by the formulas of I00 for the BL94 opacity are similar but still somewhat larger than the result obtained from the equations of the internal structure. In the case of the reduced opacity, the corresponding results (using Eq. (1)) are rather different from what is obtained by solving the equations of the internal structure. We finally note that the difference between the DNNs and the equations of the internal structure seems somewhat larger in the case of the low temperature. This could be solved by using DNNs with larger layers and/or more units per layer. The difference is much smaller than the difference obtained using either I00 or B15, however.
5 Discussion
5.1 Overfitting
The very high accuracy that we obtain may seem surprising, and it is important to verify that the network does not overfit the training data. To do this, we plot in Fig. 7 the training and validation accuracy as a function of the training epoch for the two DNNs that we considered. The validation accuracy decreases and starts to plateau after 8 000–10 000 epochs. In contrast, the training accuracy still decreases, indicating that the network starts to overfit the data at this point. For this reason, the results presented in this paper are those obtained after 10 000 epochs. This number is high but results from the choice of a low learning rate in the ADAM optimiser.
5.2 Effect of the dataset
As described above, our input parameters were generated randomly in an independent way. In reality, it is expected that the temperatureand pressure are strongly correlated with the semi-major axis, for example. As discussed previously, including such unrealistic data-points could degrade the performances of the DNN. In order to test this, we considered two cases where we trained DNN1 over 10 000 epochs, with the same initialisation of the weights. In the first case, we considered all the data we computed (including the unrealistic data), whereas in the second case, we only considered data points that fulfilled the two following conditions:
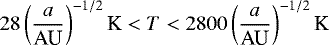 (12)
(12)
These two conditions were chosen by allowing for a variation of one order of magnitude of the pressure and temperature below and above the values used in Venturini & Helled (2017).
We then compared the output of the two trained DNN on the same set of validation data points (304 points). In order to have a fair comparison, all validation data points fulfilled the above conditions and were therefore “realistic”, and the two DNNs were trained using the same number of training data points (5738). We obtained an accuracy of 4.86% in the case of the full dataset and 4.38% in the case of the reduced dataset. When only “realistic” data points are used, the performances of the DNN is improved, as expected, although the change is not great. The accuracies reached in these two cases are not as good as in the previous section because both DNNs are trained using fewer points, which degrades their performances.
5.3 Comparison with other machine-learning methods
We compared our results with results that were obtained using other machine-learning methods, as linear regression random forest (with 10, 100, 1000, and 10 000 trees), gradient boosting (using the XGBoost library6), support vector regression and different architectures of the DNN. For each of these methods, we used the logarithm of the input quantities (except for the temperature), and the temperature, as features.
All these methods are described in the literature (e.g. Geron 2017). For each of these methods, several hyper-parameters can be tuned to improve the performances. For all the methods we considered, we kept the default parameters as defined in scikit-learn7, except when explicitly mentioned otherwise. An exhaustive evaluation of the influence of all these hyper-parameters is beyond the scope of this paper.
In the case of gradient boosting, we additionally performed a random grid search in order to infer whether some hyper-parameters might lead to better results. We ran 100 models in which we varied the boosting method (“gbtree”, “gblinear”, or “dart”)8, the maximum depth of the trees (from 1 to 8), the learning rate (0.05, 0.1, or 0.2), and the number of estimators (30, 100, or 300). For each of these 100 cases, we used a fivefold cross-validation. The best model was found to correspond to the dart boosting method, a learning rate of 0.05, a maximum depth of trees of 6, and 300 estimators. In this case, the error is of 6.82%. This is about three times worse than the best result we obtained with our baseline DNN.
In all the cases, we used the same data points for training and testing (including some “unrealistic” data points, see above), and we compared the resulting accuracy to the accuracy we obtained with our baseline DNN1 model (three hidden layers of 128 units each). The results are presented in Table 1. The table shows that the DNN outperforms all other methods we considered by at least a factor 2 in accuracy. Interestingly enough, the DNN with three and two hidden layers gives similar results, but the results with three hidden layers are slightly better.
However, the computer time required to train the DNN is much longer than for the other methods. For inference (computing the target value given a set of input values), the required computer power using DNN is also higher than for other methods. It is much faster than solving differential equations, however.
 |
Fig. 4 Predicted critical mass (in Earth masses, logarithmic scale) as a function of the critical mass obtained by solving the internal structure equations (blue), and using the IL04 formula (red; see Eq. (2), with exponents of the formulas equal to 0.25). Left: using the ISM opacity from BL94. The lower end of each line corresponds to the result obtained for an opacity of 1 cm2 g−1, the higher end to the result for an opacity of 10 cm2 g−1. Right: reducing the BL94 opacity by a factor 100. The lower end of each line corresponds to the result obtained for an opacity of 0.01 cm2 g−1, the higher end to the result for an opacity of 0.1 cm2 g−1. |
 |
Fig. 5 Predicted envelope mass (in Earth masses, logarithmic scale) as a function of the envelope mass obtained by solving the internal structure equations (blue). The green and red points show the estimate of the envelope mass using the I00 and B15 accretion rate, respectively. This accretion rate is integrated on the disc lifetime, itself assumed to be randomly uniformly distributed between 0 and 5 Myr. Only envelope masses for core masses higher than 1 M⊕ are represented. Left: using the ISM opacity from BL94. The envelope mass using I00 and B15 is computed assuming an opacity of 1 cm2 g−1. Right: reducing this opacity by a factor 100. The envelope mass using I00 and B15 is computed assuming an opacity of 0.01 cm2 g−1. |
 |
Fig. 6 Evolution of the envelope mass as computed with the solved equations of the internal structure (red lines) and with our DNN (blue lines). We also show the comparison with what would be obtained using the approach of I00 (grey areas), and B15 (green areas) for different choices of the envelope opacity (see text). The evolution of the core mass is shown by the red dashed line. Each figure has different scales for the time and the envelope mass. Upper left: with the BL94 opacity for a planet at 5 AU that accretes with Ṁcore = 10−6 M⊕ yr−1. Upper right: with the BL94 opacity for a planet at 5 AU that accretes with Ṁcore = 5 × 10−7 M⊕ yr−1. Lower left: with a reduced opacity for a planet at 10 AU that accretes with Ṁcore = 10−6 M⊕ yr−1. Lower right: with a reduced opacity for a planet at 5 AU that accrete with Ṁcore = 10−6 M⊕ yr−1, but assuming a disc temperature equal to 50 K (150 K in all other cases). The kink in the green areas is due to the rapid runaway accretion of gas when the planet reaches the cross-over mass (mass of accreted gas equal to the mass of accreted solids; see B15). |
 |
Fig. 7 Training and validation accuracy as a function of the epoch for DNN1 (computation of the critical mass). |
Validation set accuracy for different machine-learning methods to predict the critical mass.
6 Conclusion
We trained deep neural networks to compute the critical core mass and envelope masses of forming planets for a variety of conditions (formation location, temperature and pressure in the disc, core mass, and solid accretion rate). The resulting DNNs, which can be easily implemented with the tools we provide on github9, give very similar results to the results that are obtained by solving the equations of the internal structure, but they need far less computer time. We also showed that some fitting formulas found in the literature in general slightly over-estimate the resulting planetary envelope mass (e.g. I00 for high opacity) or over-estimate it strongly (e.g. with the approach of B15). With the formulas described above, the resulting mass of a forming planet may be severely over-estimated, which can be avoided using the deep neural networks we provide here.
Acknowledgements
This work was supported in part by the European Research Council under grant 239605. This work has been carriedout within the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation. The authors acknowledge the financial support of the SNSF. The plots shown in this paper made use of the seaborn software package https://seaborn.pydata.org.
References
- Alibert, Y. 2014, A&A, 561, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y. 2019, A&A, 624, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Mordasini, C., Benz, W., & Winisdoerffer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alibert, Y., Carron, F., Fortier, A., et al. 2013, A&A, 558, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodenheimer, P., & Pollack, J. B. 1986, Icarus, 67, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Brügger, N., Alibert, Y., Ataiee, S., & Benz, W. 2018, A&A, 619, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortier, A., Alibert, Y., Carron, F., Benz, W., & Dittkrist, K.-M. 2013, A&A, 549, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freedman, R. S., Lustig-Yaeger, J., Fortney, J. J., et al. 2014, ApJS, 214, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Geron, A. 2017, Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 1st edn. (Sebastopol, CA: O’Reilly Media, Inc.) [Google Scholar]
- Gomez Gonzalez, C. A., Absil, O., & Van Droogenbroeck M. 2018, A&A, 613, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodfellow, I., Bengio, Y., & Courville, A. 2016, Deep Learning (Cambridge: MIT Press) [Google Scholar]
- Helled, R., Bodenheimer, P., Podolak, M., et al. 2014, Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 643 [Google Scholar]
- Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2005, Icarus, 179, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2004, ApJ, 604, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ikoma, M., Nakazawa, K., & Emori, H. 2000, ApJ, 537, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2013, Stellar Structure and Evolution (Heidelberg: Springer) [Google Scholar]
- Lam, C., & Kipping, D. 2018, MNRAS, 476, 5692 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, E. J., & Chiang, E. 2015, ApJ, 811, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Hubickyj, O., D’Angelo, G., & Bodenheimer, P. 2009, Icarus, 199, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Márquez-Neila, P., Fisher, C., Sznitman, R., & Heng, K. 2018, Nat. Astron., 2, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, H. 1980, Prog. Theor. Phys., 64, 544 [Google Scholar]
- Mordasini, C. 2014, A&A, 572, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Movshovitz, N., Bodenheimer, P., Podolak, M., & Lissauer, J. J. 2010, Icarus, 209, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W. 2017, Proceedings of the Sant Cugat Forum on Astrophysics (Heidelberg: Springer) [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaloizou, J. C. B., & Terquem, C. 1999, ApJ, 521, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, K. A., Palafox, L., & Griffith, C. A. 2018, MNRAS, 474, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Piso, A.-M. A., & Youdin, A. N. 2014, ApJ, 786, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Smirnov, E. A., & Markov, A. B. 2017, MNRAS, 469, 2024 [NASA ADS] [CrossRef] [Google Scholar]
- Tamayo, D., Silburt, A., Valencia, D., et al. 2016, ApJ, 832, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Venturini, J., Alibert, Y., & Benz, W. 2016, A&A, 596, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturini, J., Alibert, Y., Benz, W., & Ikoma, M. 2015, A&A, 576, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturini, J., & Helled, R. 2017, ApJ, 848, 95 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Validation set accuracy for different machine-learning methods to predict the critical mass.
All Figures
 |
Fig. 1 Initial conditions for a subset of 1000 datapoints. Each panel shows the correlation between two quantities, the panels on the diagonal showing the histograms of the different quantities. |
| In the text | |
 |
Fig. 2 Cumulative distribution of the input parameters for DNN1, for the training, validation and test sets. |
| In the text | |
 |
Fig. 3 Envelope mass as a function of the radius for two models. For both models, a planetary core of mass equal to 2 M⊕ is located at 0.5 AU, with a luminosity equal to 1025 erg s−1 and a temperature at the planet–disc interface equal to 400 K. The pressure at the disc–planet interface is equal to 10 dyn cm−2 (an unrealistic value) or 350 dyn cm−2. |
| In the text | |
 |
Fig. 4 Predicted critical mass (in Earth masses, logarithmic scale) as a function of the critical mass obtained by solving the internal structure equations (blue), and using the IL04 formula (red; see Eq. (2), with exponents of the formulas equal to 0.25). Left: using the ISM opacity from BL94. The lower end of each line corresponds to the result obtained for an opacity of 1 cm2 g−1, the higher end to the result for an opacity of 10 cm2 g−1. Right: reducing the BL94 opacity by a factor 100. The lower end of each line corresponds to the result obtained for an opacity of 0.01 cm2 g−1, the higher end to the result for an opacity of 0.1 cm2 g−1. |
| In the text | |
 |
Fig. 5 Predicted envelope mass (in Earth masses, logarithmic scale) as a function of the envelope mass obtained by solving the internal structure equations (blue). The green and red points show the estimate of the envelope mass using the I00 and B15 accretion rate, respectively. This accretion rate is integrated on the disc lifetime, itself assumed to be randomly uniformly distributed between 0 and 5 Myr. Only envelope masses for core masses higher than 1 M⊕ are represented. Left: using the ISM opacity from BL94. The envelope mass using I00 and B15 is computed assuming an opacity of 1 cm2 g−1. Right: reducing this opacity by a factor 100. The envelope mass using I00 and B15 is computed assuming an opacity of 0.01 cm2 g−1. |
| In the text | |
 |
Fig. 6 Evolution of the envelope mass as computed with the solved equations of the internal structure (red lines) and with our DNN (blue lines). We also show the comparison with what would be obtained using the approach of I00 (grey areas), and B15 (green areas) for different choices of the envelope opacity (see text). The evolution of the core mass is shown by the red dashed line. Each figure has different scales for the time and the envelope mass. Upper left: with the BL94 opacity for a planet at 5 AU that accretes with Ṁcore = 10−6 M⊕ yr−1. Upper right: with the BL94 opacity for a planet at 5 AU that accretes with Ṁcore = 5 × 10−7 M⊕ yr−1. Lower left: with a reduced opacity for a planet at 10 AU that accretes with Ṁcore = 10−6 M⊕ yr−1. Lower right: with a reduced opacity for a planet at 5 AU that accrete with Ṁcore = 10−6 M⊕ yr−1, but assuming a disc temperature equal to 50 K (150 K in all other cases). The kink in the green areas is due to the rapid runaway accretion of gas when the planet reaches the cross-over mass (mass of accreted gas equal to the mass of accreted solids; see B15). |
| In the text | |
 |
Fig. 7 Training and validation accuracy as a function of the epoch for DNN1 (computation of the critical mass). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.