EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 625 (May 2019) A&A, 625 (2019) A140 Full HTML
Free Access
Issue
A&A
Volume 625, May 2019
Article Number A140
Number of page(s) 8
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201935367
Published online 28 May 2019

© ESO 2019

1 Introduction

Since the Pioneer and Voyager space probes investigated the Jovian system, the surface of Jupiter’s moon Europa has attracted special attention both because of its prominent water-ice surface and the supposed existence of a subsurface ocean. Jupiter hosts a giant magnetosphere and Europe is therefore exposed to a hard radiation environment (Johnson 1990; Johnson et al. 2004; Paranicas et al. 2009). Besides the ubiquitous H and He ions, heavy O and S ions are present (Radioti et al. 2005), with energies extending to beyond several tens of megaelectronvolts (Mauk et al. 1998). These heavy elements originate from volcanic eruptions on Jupiter’s innermost moon, Io, from which they were incorporated into the magnetosphere.

The exact composition of the ice surface of Europa is not well known. Previous space missions observed the icy moonsurfaces from a distance (Carlson et al. 2009). Carlson et al. (2009) propose a probable stoichiometry of the ice composition on Europa but emphasize that further data are needed. Indeed, ongoing space missions are on the way to exploring the Jovian system. The Juno mission is monitoring the planet Jupiter itself (Bolton 2010) and its magnetosphere (Bagenal et al. 2017). The JUICE mission is scheduled for 2022 for exploring the Galilean moons (Grasset et al. 2013).

To the best of our knowledge, sulfur is present in the water-rich ice surface of Europa (Carlson et al. 2009); it exists there in the form of frozen SO2 and of 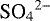SO 4 2− ${\textrm{SO}_4}^{2-}$ ions. The origin of these sulfur compounds may be in the deposition of the volcanic ejecta from Io; or in volcanic eruptions on Europa itself (more precisely, in the seafloor of its ocean); even biogenic origin of sulfur has been proposed, where waste products of bacteria were transported to the surface (Chela-Flores 2006). Interest in the sulfur content stems not only from such astrobiological implications, but has also another fundamental astrochemical origin: observed sulfur abundances in the dense interstellar medium are smaller than the cosmic abundance by two orders of magnitude (Jiménez-Escobar & Muñoz Caro 2011). To clarify this “problem of missing sulfur”, studies of the thermal and irradiation chemistry of solid-phase sulfur compounds need to be undertaken (Kanuchová et al. 2017).

Jupiter has the strongest magnetic field among the solar-system planets and so its magnetosphere is not only the most extended one but also allows for the storage of ions at high kinetic energies. In addition, due to the volcanic activity of Jupiter’s innermost Galilean moon, Io, sulfur is injected into the magnetosphere. Since sulfur has a relatively high mass of 32 amu, this ion has a particularly high stopping power, and hence the deposited energy density in the ion track will be particularly large. For these two reasons the processes occurring in the magnetosphere of Jupiter are rather peculiar, at least for solar-system planets and moons.

Other Jovian moons are also irradiated by sulfur ions within Jupiter’s magnetosphere. However, Europa is – after Io – the innermost of the Galilean moons, and hence the irradiation effects are particularly high on Europa. The effects on the other moons (Ganymede, Callisto) are less pronounced, as the radiative energy flux is one or two orders of magnitude smaller, respectively (Johnson et al. 2004), and Ganymede is additionally protected by its own magnetic field.

Evolution of ices in space is an important topic in astrobiology since organic or prebiotic molecules created by reactions can survive and evolve by further reactions in dense clouds of the interstellar medium (Mrad et al. 2015; Nuevo et al. 2007) as well as in the outer solar system (Johnson 1990; Gudipati & Castillo-Rogez 2013). Irradiation may lead to the formation of novel molecular species in the ice. The theoretical study of such processes is not straightforward since ab-initio modeling turns out to be computationally too expensive, although application to hot-atom chemistry does exist (Pietrucci & Saitta 2015; Kohanoff & Artacho 2017; Cassone et al. 2018; Fraile et al. 2019). Molecular dynamics simulations appear as a viable alternative, in particular since recent reactive (REAX) potentials allow for the inclusion of bond breakings and formations – and thus chemistry – in the simulation (van Duin et al. 2001; Senftle et al. 2016). Applications of REAX-based simulations now exist for various chemical applications (Chenoweth et al. 2008) including complex organic molecules and amino acids like glycine (Monti et al. 2012), and also for the sulfur-containing cysteine (Monti et al. 2016). In previous work, we used these potentials to study the irradiation-induced chemical transformations in a model ice mixture designed to describe cometary ice (Martins et al. 2013); irradiation by cosmic radiation, by the solar-wind and by magnetospheric ions was explored (Mainitz et al. 2016, 2017; Anders & Urbassek 2017, 2019).

As an alternative to space missions, laboratory experiments explore the effects of irradiation on well-characterized ice surfaces (Allodi et al. 2013; Rothard et al. 2017). While the composition of the ice surface of Europa seems to have been excluded from such laboratory experiments, dedicated studies for some of the major constituents do exist. Lv et al. (2014) perform sulfur ion impacts into CO and CO2 ices and Boduch et al. (2016) into O2 and CO2 ices, studying the formation of compounds with the implanted sulfur ion. Kanuchová et al. (2017) directly irradiate ice analogs rich in SO2 to investigate the induced chemistry.

In the present paper, we study the effects of magnetospheric sulfur ion irradiation on an ice mixture that is considered typical of the surface of Europa (Carlson et al. 2009); see Fig. 1. While sulfur ion energies up to 100 MeV have been measured, the maximum flux is at 100 keV or below (Radioti et al. 2005). Nevertheless, we model sulfur ion irradiation at an impact energy of 20 MeV – close to the maximum stopping power – since it is known from previous studies (Anders & Urbassek 2019; Mainitz et al. 2017) that the number of reactions scales approximately linearly with the deposited energy; hence the case studied here provides the maximum changes that can be expected for sulfur ion irradiation in the ice. We focus on the chemical transformations induced by the fast-ion track, and in particular on the chemistry occurring with the sulfur containing compounds. Our results will show both the formation of new sulfur compounds, in agreement with laboratory experiments, and the production of molecular gases that may contribute to the tenuous atmosphere surrounding Europa (Hall et al. 1995; Shematovich & Johnson 2001; Johnson et al. 2004; Carlson et al. 2009).

2 Method

The open-source parallel software package LAMMPS (Plimpton 1995) is used to perform the molecular dynamics simulations. In order to model the interactions between the molecules and atoms present in our system, we use the so-called REAX force field developed by van Duin (van Duin et al. 2001), which allows the molecular dissociations and reactions to be modeled. In the form published by Kim et al. (2013) the potential allows one to model the elements CHONS and also Na and Cl; in particular, stable SO2, SO4 and H2 S exist in this potential. Unfortunately, Mg cannot be reliably modeled in this potential and therefore we substitute Mg2+ ions by 2 Na+ ions; see below. We also note that we tried to use the more recent potential version published by Monti et al. (2016); however, we found that it allows no stable SO2 or SO4 in our test simulations, and therefore we had to dismiss it. We finally note that the REAX force fields calculate partial charges for each atom and ion self-consistently during each time step of the simulation meaning that no external charge assignment is necessary.

We splined a ZBL potential (Ziegler et al. 1985) to the pair potential part of the interatomic potentials to more reliably represent atom repulsion at higher interaction energies occurring early in our simulation; details of this procedure are described in Anders & Urbassek (2013).

An adaptive time step is employed which changes from less than 0.1 fs during the passage of the fast ion to 0.1 fs towards the end of the simulation, when the target temperature has sufficiently decreased.

A molecule detector was used to identify molecules during the simulation based on the atomic coordinates (Anders & Urbassek 2013). The detector is a modified version of the cluster detector by Stoddard (1978); all atoms closer than 1.7 Å are considered to belong to the same molecule. This radius is reduced to 1.28 Å for hydrogen (Anders & Urbassek 2013) and to 1.5 Å for sulfur.

Molecules are visualized by visual molecular dynamics (VMD; Humphrey et al. 1996).

thumbnail Fig. 1

Top: schematic simulation setup for studying the track of a sulfur ion at 20 MeV. Only a section of the track in the vicinity of the surface is simulated. The energy deposited by the swift ion is given to the atoms as local temperature increase (purple region). Insets show several of the most abundant ions and molecules originally present in the ice mixture – H2O, O2, Na, Cl, SO4, SO2 and H2 S – according to Table 1. Bottom: snapshot of the expanding track volume at a time of 0.5 ps after track formation. The width of the snapshot corresponds to 202 Å. The color represents the local temperature varying between cyan (101 K, corresponding to the surface temperature of Europa) and purple (>373 K).

2.1 Target preparation

Carlson et al. (2009) compile data on the estimated composition of the surface ice of Europa. We base the ice mixture used for our simulation on the abundances found in Sects. 2.4–2.9 of this latter study; for the species CN, NH3, and H2S, which are discussed therein, but have not yet been uniquely identified on Europa, small values of the order of 100–200 ppm were introduced into our mixture. In addition, instead of a contribution of 10% Mg2+ ions, we use 20% Na+ ions – in addition to the 0.8% Na+ reported – since the interatomic interaction potential used by us is not able to handle Mg appropriately; see above. The consequences of this change are that (i) the ice mass density, and hence the stopping power of the projectile ion in it, will be increased; (ii) since the metal ions do not take part in reactions, the number of potential reaction partners of H, C, O, N, S is slightly reduced. We expect the effects induced by the substitution of Mg by Na to be on the 10% level, since it is known that the number of chemical transformations changes in proportion to the energy deposited in the track (Anders & Urbassek 2017, 2019). Table 1 assembles our composition. In the majority of water ice, a strong contribution of SO 4 2− ${\textrm{SO}_4}^{2-}$ and Na+ ions – most of them substituting Mg2+ – are dissolved; besides some further C- and N-containing molecules in a concentration of less than one per thousand, only O2 molecules with 2.8% have a noticeable abundance. Figure 2 visualizes the composition by providing a “simulated mass spectrum” of this original composition.

The simulation system has a cuboid form with a length of 312 Å and lateral extensions of 202 Å. The total number of atoms in the simulation volume amounts to 1 033 508. We use Packmol (Martínez et al. 2009) to create an amorphous ice mixture with this composition. The molecules in this volume are not yet in their equilibrium positions; in addition this simulation target is essentially water ice into which a high concentration of ions are mixed; hence association and dissociation reactions are expected. We allow these processes to occur during a two-step relaxation process running for 19.1 ps under periodic boundary conditions. (i) First, for a time of around 5 ps, a molecular dynamics simulation is run by including a velocity-proportional damping force, which removes kinetic energy from the system. We found it advantageous to use a chain of damping simulations – with varying damping constants – to allow molecules to separate from unfavorable positions and change their orientations. At the end of this process, the system temperature has decreased to 2 K. (ii) The system is then heated up to the surface temperatureof Europa, that is 101 K, within 1 ps and kept at this temperature for 13 ps to allow for further equilibration.

After relaxation the target has an atomic number density of n = 83 nm−3 at a temperature of T = 101 K; its mass density amounts to 1.2 g cm−3.

Table 1

Molecular species in the surface of Europa assumed in our simulation and mainly based on Carlson et al. (2009).

thumbnail Fig. 2

Mass spectrum visualizing the original target composition before relaxation. The highest peaks belong to H2O, Na, SO4, and O2.

2.2 Chemical transformations during relaxation

Figure 3 shows how the number of major products changes with time. The most pronounced change occurs with water molecules, of which more than 1000 are dissociated during the relaxation process, amounting to around 0.4% of the water molecules. As dissociation products we find approximately 100 H+ and OH− as well as 400 H3O+; the remaining fragments underwent further reactions.

Since in atomistic simulations, the fate of each individual atom can be followed, we can analyze which reactions led to the emergence of new species. For example, methanol, CH3—OH, starts forming immediately at the beginning of the relaxation process. It originates from water reacting with unsaturated methylene, CH2. Shortly later, after 0.39 ps, the abundance of methanol decreases again, either because methanol loses an H or reacts on to methanediol, CH4O2.

Figure 4a displays the simulated mass spectrum after relaxation; the new peaks appearing – as compared to Fig. 2 – feature the new molecules produced. The changes in molecular abundances are visualized in Fig. 4b in the form of a difference mass spectrum showing the number of moleculesafter relaxation relative to those initially present in the simulation volume. A detailed list of the changes is provided in Appendix A. The most massive molecule formed during the relaxation, CH2S2O8, has a massof 206.2 u; its structural formula SO4—CH2—SO4 indicates that it is an association of two sulfates bridged by CH2.

We discuss the most pronounced changes. CH3O is producedin a similar manner to methanol by adding OH to CH2. Methanediol, CH4O2, has a more complex origin: in around 88% of cases, two water molecules are added to CH2, and in 12% CH4O2 is the product of the addition of water to formaldehyde, CH2O. Hydrogen sulphate, HSO4, results from protonation of SO4.

As a further important example of the reactions occurring, we discuss the formation of SO3. By analyzing the origin of the sulfur and oxygen atoms in these molecules we find that around 37% of SO3 is formed from SO2 by O addition and 63% by O loss from SO4. The O atoms have their origin in dissociations of or reactions with molecular oxygen O2.

We note that during this relaxation phase, due to the low temperatures present and the short interval of time available, no diffusion processes occur. Reactions occur between nearest neighbors only.

A main conclusion drawn from Fig. 3 is that after a relaxation time of 10–15 ps, the target composition has stabilized in the sense that no further spontaneous reactions occur. After this time we may use this target configuration to start the track simulation. As a second conclusion, we note that due to the high salt concentration in Europa’s ice, dissociation reactions are abundant and change the ice composition. In other words, the data in Table 1 are not in chemical equilibrium, not even at the low temperature of 101 K prevailing at Europa.

thumbnail Fig. 3

Temporal evolution of the change in the number of molecules, ΔN, during the relaxation process. Top: water and its dissociation products, as well as CH3OH and CH2O. Bottom: sulfur compounds.
thumbnail Fig. 4

Mass spectrum after relaxation (top) and difference mass spectrum (bottom) showing the number of molecules after relaxation relative to those initially present in the simulation volume. Positive values (blue) show species produced during the relaxation, negative values (red) show species destroyed during the relaxation.

2.3 Sulfur track simulation

After target preparation, we model the formation of an ion track and its consequences on the ice mixture. While the 20 MeV S ion penetrates into the target and performs some collisions with target atoms, it loses its energy dominantly by electronic stopping (Sigmund et al. 2005; Sigmund 2014). The electronic losses can be modeled as a velocity-proportional stopping force acting on the ion F = −γv, \begin{equation*}F\,{=}\,- \gamma v, \end{equation*}(1)

where the friction coefficient of sulfur is γ = 2.55 eVfsÅ−2 (Ziegler 2000; Anders & Urbassek 2019). At 20 MeV, this corresponds to a stopping power of 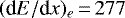(dE/dx) e  = 277 $(\textrm{d}E/\textrm{d}x)_e\,{=}\,277$ eV Å−1. We impart this energy lost by the projectile ion to all atoms in a cylindrical track around the S ion trajectory with a radius of R = 5 Å in the form of thermal energy; the size of this radius agrees with that taken in previous simulations (Mainitz et al. 2016, 2017; Anders & Urbassek 2019). The temperature increase corresponding to the electronic energy transfer is given by (Anders & Urbassek 2019) k B ΔT =  (dE/dx) e 3πn R 2 , \begin{equation*}k_{\textrm{B}} \Delta T\,{=}\,\frac{(\textrm{d}E/\textrm{d}x)_e}{3\pi n R^2}, \end{equation*}(2)

where kB is Boltzmann’s constant.

After the formation of the track, we calculate the subsequent effects in the ice mixture for a time of 38.5 ps by molecular dynamics simulation. This is done in an NVE simulation. Periodic boundary conditions are applied at all sides of the cuboid simulation box; in addition the lateral boundaries are thermostatted to a temperature of 101 K for a width of 5 Å.

3 Results

3.1 Chemical transformations in the ion track

In the following, we analyze the chemical changes brought about by the passage of the swift ion in the specimen. We note that a 20 MeV S ion moves at 11 000 km s−1 and hence passes through the simulation volume, 312 Å, in less than 3 fs; essentially all simulated processes therefore occur at a time when the ion has already left the simulation volume. Figure 5 shows the time evolution of several dominant species afterthe track formed. Indeed, this plot demonstrates that towards the end of the simulation time, 38 ps, an equilibrium has been established in the simulation volume in the sense that the molecular abundances have stabilized.

Most pronounced is the large amount of dissociations visible in water immediately after the track formed. However, half of these dissociations heal again in the course of the simulation. Concomitantly, the large numbers of H+, H3O+, and OH− formed are reduced again by follow-up reactions. We note in particular that H+ shows the quickest kinetics due to the high mobility of the proton.

We present the abundances of the molecular species produced by the ion track in graphical form as simulated mass spectra, Fig. 6. Quantitative data are assembled in Appendix B. Most notable are the changes in the sulfur compounds. Sulfate ions, 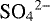SO 4 2− ${\textrm{SO}_4}^{2-}$, are initially destroyed in the track by dissociation events, but partly heal again. The numbers of SO2 initially increases – because it is a dissociation product of SO4– but then decreases again, as some molecules are oxidized to sulfite, 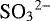SO 3 2− ${\textrm{SO}_3}^{2-}$. This production of sulfite, including the hydrogenated species, 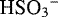HSO 3 − ${\textrm{HSO}_3}^-$, is interesting since it parallels experimental findings of S ion bombardment of oxygen-rich targets (O2 and CO2) (Boduch et al. 2016) and of ion-irradiation and thermal processing of H2O:SO2 mixtures (Kanuchová et al. 2017). In both experiments sulfite production was observed. We note that sulfite mostly originates from the dissociation of sulfate; this is in contrast to the relaxation stage of our simulation where sulfite was mostly produced by oxygen addition to SO2; see Sect. 2.2.

Formaldehyde, CH2O, is destroyed in the track. This gives rise to the formation of CO2 by oxidation reactions. In addition, an extensive production of methanediol, CH4O2, is observed; it forms by the reaction of water and formaldehyde (Kent et al. 2003).

An interesting feature is the production of acid molecules in the track. Sulfurous acid, H2SO3, and sulfuric acid, H2SO4, are formed by reactions of sulfite and sulfate with protons, respectively. In addition, we observe traces of carbonic acid, H2CO3; this is interesting since laboratory experiments on the impact of sulfur ions on CO and CO2 ices also demonstrated its production (Lv et al. 2014). Finally, we note that also alkaline molecules were formed in small traces, such as NaOH.

Furthermore, the formation of volatile gases, O2 and H2, is observed. Their constituents originate mostly from the dissociation of water molecules, but also from SO4. The formation of these gases is relevant, since it has been known for a long time that Europa has a rudimentary atmosphere, and its existencehas been ascribed to irradiation effects (Hall et al. 1995; Shematovich & Johnson 2001; Johnson et al. 2004; Carlson et al. 2009).

Because of the low nitrogen content of the ice mixture, where originally only CN and NH3 were present, only a few N compounds are produced in the track, such as CNO. The abundance of cyanic acid, CHNO, actually decreases after the sulfur impact. The only species containing both nitrogen and sulfur is CNSO4, a cyano groupattached to sulfate.

The changes induced by the ion track with respect to the relaxed sample are highlighted in Fig. 7, which provides a difference mass spectrum by showing the number of newly formed molecules minus those present after the relaxation of the target. The largest losses are observed for water, sulfate, formaldehyde, sulfur dioxide, hydrogen peroxide, CH3O and HS, while the largest gains are in OH, sulfite, molecular hydrogen, methanediol, H3O+ and molecular oxygen, protonated SO3, protons, CH3O2 (methanediol with a missing H), atomic oxygen, atomic S, protonated SO2, sulfurous acid, H2O+OH, hydroperoxyl (O2H), and CO2.

Figure 8 displays one of the most complex sulfur compounds created, an organosulfate, C2H5SO6, appearing late in the track at 157 u. Its structure is HO—CH2—SO4—CH2O with a sulfate bridging two carbon groups. This molecule is similar to dimethylsulfate, which is known for its methylation capabilities of amines and also DNA (Streitwieser et al. 1992), with one methyl group replaced by a methyl alcohol and the other one by formaldehyde. Since the latter carbon is overcoordinated this structure might not be in its final state and this molecule might react with other possibly prebiotic molecules.

thumbnail Fig. 5

Temporal evolution of the change in the number of molecules, ΔN, after track formation at time t = 0. Top: water and its dissociation products. Bottom: sulfur compounds.
thumbnail Fig. 6

Simulated mass spectrum of species found at the end of the simulation, 38.5 ps after track formation.
thumbnail Fig. 7

Difference mass spectrum showing the number of molecules at a time of 38.5 ps after track formation relative to those present in the relaxed simulation volume. Positive values (blue) show species produced in the track, negative values (red) show species destroyed in the track.
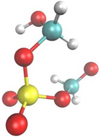thumbnail Fig. 8

One of the most complex molecules produced in the track, C2H5SO6: an organosulfate with sulfur bridging two carbon groups.

3.2 Total number of reactions

In total we find that the ion track induced Ndiss = 2265 dissociated molecules and Nprod = 2588 new products formed. In previous work (Anders & Urbassek 2017, 2019), we showed that these numbers are linearly related to the energy deposited by the projectile ion in the target, Edep, 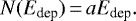N( E dep ) = a E dep . \begin{equation*}N({E_{\textrm{dep}}})\,{=}\,a {E_{\textrm{dep}}}. \end{equation*}(3)

The proportionality constant amounted to a = 25–40 keV−1 for dissociations and a = 60–76 keV−1 for product formation (Anders & Urbassek 2017, 2019).

In the present work, the energy deposited in the simulation volume is Edep = 86 keV, such that Eq. (3) would predict 2150–3440 dissociations, in good agreement with our simulation. However, the number of products would be predicted to be higher: 5160–6536 molecules.

A previous study analyzed the processes occurring after 20 MeV S ion impact into a H2O:CO2:NH3:CH3OH ice mixture (Anders & Urbassek 2019) and found Ndiss = 3672 and Nprod = 5284, that is, larger numbers than in the present study. A closer look however reveals that many of the molecules formed were simple fragments, such as 2037 CO molecules, 610 NH2, and 915 OH− ions. In the Europa surface ice mixture, we do not find such stable contributions of fragments as CO. A second major difference between the two studies is found in the behavior of water. In the previous study (Anders & Urbassek 2019), all fragmented water molecules healed again, and even new water molecules formed, mostly from O delivered from CO2 breakup and H from NH3 (and also CH3OH) breakup; in the present study 1283 water molecules are destroyed, since in particular no additional sources for H are available. We conclude that, while the order of magnitude of molecule dissociations and new-formations can be predicted by Eq. (3), the efficiency factor a depends strongly on the actual reaction partners available.

4 Summary and implications

The ice surface of Europa is special in that it contains a high concentration of sulfur compounds, in particular SO4, SO2, and H2S. Since it is within the magnetosphere of Jupiter, it is subject to high-energy irradiation by magnetospheric ions. We model the consequences of such irradiation by molecular dynamics simulation for the particular example of a 20 MeV sulfur ion impact. The use of a REAX potential allows us to follow the molecular dissociations and ensuing reactions in the vicinity of the projectile ion track. We find the following features.

  • 1.

    The irradiation dissociates sulfate, SO4, and produces sulfite, SO3. Sulfite is also produced by oxidation of SO2. The appearance of SO3 is in agreement with laboratory experiments (Boduch et al. 2016).

  • 2.

    Water is dissociated leaving a large amount of highly reactive H+, H3O+ and OH−.

  • 3.

    Protonation reactions produce acid molecules such as HCl, H2SO3, H2SO4; similarly, addition of OH− produces the alkaline NaOH.

  • 4.

    Free O is produced by dissociation of water and SO4 and serves as an oxygen source, leading to production of CO2 and in particular O2.

  • 5.

    The volatile molecular gases O2 and H2 are produced. These may diffuse – on longer time scales – to the surface and contribute to Europa’s tenuous atmosphere (Hall et al. 1995; Shematovich & Johnson 2001; Johnson et al. 2004; Carlson et al. 2009).

  • 6.

    In addition we found that the ice composition as compiled by Carlson et al. (2009) is probably not in chemical equilibrium since the high amount of ions present (Mg2+, Na+, Cl−, 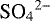SO 4 2− ${\textrm{SO}_4}^{2-}$) induces water dissociation and subsequent reactions.

Formation of volatile gases such as O2 and H2 found in our work is a general phenomenon encountered when irradiating ices (Johnson 1990; Johnson et al. 2009; Paranicas et al. 2009; Gudipati & Castillo-Rogez 2013). This is an important aspect, since upon outgassing these products will contribute to forming a neutral-gas atmosphere around the moons that may be detected directly in spacecraft missions.

The continuous irradiation of Europa’s surface by sulfur ions leads to the accumulation of sulfur and the formation of sulfur compounds in the ice surface. As we show here, these compounds are not formed stably but may decompose under the irradiation and form new products. This means that for the ice mixture studied exemplarily here, sulfate is partly transformed to sulfite under the irradiation. While the occurrence of such ion-induced changes under irradiation are in principle well known, this feature emphasizes the need for experimental and modeling studies of the influence of sulfur irradiation on ice surfaces in order to determine the composition of Europa’s ice surface with greater reliability.

From previous simulation studies we know that the number of reaction products emerging from the ion irradiation of ice surfaces scales approximately linearly with the stopping power of the projectile. Sulfur has its maximum stopping power in water ice at around 22.5 MeV (Ziegler et al. 2010); since ice targets consist of a majority of H2O, the maximum stopping power in the European ice mixture – as well as in other cosmic-ice mixtures – is also situated close to this energy. In the present study we therefore investigated the maximum effects that can be expected for the irradiation of ices by magnetospheric ions. Ions of smaller (and also of larger) impact energy will induce less reactions, proportional to their stopping power.

In this sense, our study illustrates the maximum changes that can be expected from a single impact. However, ice surfaces in space are subject to prolonged bombardment such that with increasing irradiation doses the effects sum up, and at higher doses similar cumulative effects can be expected as in our study. At smaller doses, the irradiation products will simply build up additively, as was shown by direct molecular dynamics simulation (Anders & Urbassek 2017). At higher doses however the production of novel species from the fragments of earlier products has to be expected. Such high doses have until now been outside the computational capabilities of molecular dynamics simulation.

Acknowledgements

We acknowledge financial support by the Deutsche Forschungsgemeinschaft within project Ur 32/27-2. Simulations were performed at the High Performance Cluster Elwetritsch (RHRK, TU Kaiserslautern, Germany).

Appendix A Molecular species created during target relaxation

A detailed list of the molecular species present in the simulation target after relaxation is provided in Table A.1; there, all molecular species that newly appear are marked. This list provides the data from which Fig. 4 – displaying the changes in molecular abundances – has been prepared.

Table A.1

Molecular species present in the simulation target after relaxation with numbers N ≥ 4.

Appendix B Molecular species created in the ion track

The species formed in the ion track and their abundances are assembled in Table B.1. This list provides thedata from which the simulated mass spectra of Figs. 6 and 7 have been prepared.

Table B.1

Molecular species present in the simulation target at a time of 38.5 ps after sulfur track formation.

References

  1. Allodi, M. A., Baragiola, R. A., Baratta, G. A., et al. 2013, Space Sci. Rev., 180, 101 [NASA ADS] [CrossRef] [Google Scholar]
  2. Anders, C., & Urbassek, H. M. 2013, Nucl. Instrum. Methods B, 303, 200 [NASA ADS] [CrossRef] [Google Scholar]
  3. Anders, C., & Urbassek, H. M. 2017, Icarus, 282, 351 [NASA ADS] [CrossRef] [Google Scholar]
  4. Anders, C., & Urbassek, H. M. 2019, MNRAS, 482, 2374 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bagenal, F., Adriani, A., Allegrini, F., et al. 2017, Space Sci. Rev., 213, 219 [NASA ADS] [CrossRef] [Google Scholar]
  6. Boduch, P., Brunetto, R., Ding, J. J., et al. 2016, Icarus, 277, 424 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bolton, S. J. 2010, Proc. IAU, 6, 92 [Google Scholar]
  8. Carlson, R. W., Calvin, W. M., Dalton, J. B., et al. 2009, in Europa, eds. R. T. Pappalardo, W. B. McKinnon, & K. K. Khurana (Tucson, AZ: Univ. Arizona Press), 283 [Google Scholar]
  9. Cassone, G., Sponer, J., Sponer, J. E., et al. 2018, Chem. Commun., 54, 3211 [CrossRef] [Google Scholar]
  10. Chela-Flores, J. 2006, Int. J. Astrobiol., 5, 17 [CrossRef] [Google Scholar]
  11. Chenoweth, K., van Duin, A. C. T., & Goddard III, W. A. 2008, J. Phys. Chem. A, 112, 1040 [CrossRef] [PubMed] [Google Scholar]
  12. Fraile, A., Smyth, M., Kohanoff, J., & Solov’yov, A. V. 2019, J. Chem. Phys., 150, 015101 [NASA ADS] [CrossRef] [Google Scholar]
  13. Grasset,O., Dougherty, M. K., Coustenis, A., et al. 2013, Planet. Space Sci., 78, 1 [NASA ADS] [CrossRef] [Google Scholar]
  14. Gudipati, M. S., & Castillo-Rogez, J. eds. 2013, The Science of Solar System Ices, Astrophys. Space Sci. Lib. (New York: Springer), 356 [Google Scholar]
  15. Hall, D. T., Strobel, D. F., Feldman, P. D., McGrath, M. A., & Weaver, H. A. 1995, Nature, 373, 677 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  16. Humphrey, W., Dalke, A., & Schulten, K. 1996, J. Mol. Graphics, 14, 33 [Google Scholar]
  17. Jiménez-Escobar, A., & Muñoz Caro, G. M. 2011, A&A, 536, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Johnson, R. E. 1990, Energetic Charged-Particle Interactions with Atmospheres and Surfaces (Berlin: Springer) [CrossRef] [Google Scholar]
  19. Johnson, R. E., Carlson, R. W., Cooper, J. F., et al. 2004, in Jupiter – The Planet, Satellites and Magnetosphere, eds. F. Bagenal, T. Dowling, & W. B. McKinnon (Cambridge: Cambridge University Press), 485 [Google Scholar]
  20. Johnson, R. E., Burger, M. H., Cassidy, T. A., et al. 2009, in Europa, eds. R. T. Pappalardo, W. B. McKinnon, & K. K. Khurana (Tucson: University of Arizona Press), 507 [Google Scholar]
  21. Kanuchová, Z., Boduch, P., Domaracka, A., et al. 2017, A&A, 604, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Kent, D. R., Widicus, S. L., Blake, G. A., & Goddard, W. A. 2003, J. Chem. Phys., 119, 5117 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kim, S.-Y., van Duin, A. C., & Kubicki, J. D. 2013, J. Mater. Res., 28, 513 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kohanoff, J., & Artacho, E. 2017, PLoS One, 12, e0171820 [CrossRef] [Google Scholar]
  25. Lv, X. Y., Boduch, P., Ding, J. J., et al. 2014, MNRAS, 438, 922 [NASA ADS] [CrossRef] [Google Scholar]
  26. Mainitz, M., Anders, C., & Urbassek, H. M. 2016, Astron. Astrophys., 592, A35 [CrossRef] [Google Scholar]
  27. Mainitz, M., Anders, C., & Urbassek, H. M. 2017, Nucl. Instrum. Meth. B, 393, 34 [NASA ADS] [CrossRef] [Google Scholar]
  28. Martínez, L., Andrade, R., Birgin, E. G., & Martínez, J. M. 2009, J. Comp. Chem., 30, 2157 [CrossRef] [PubMed] [Google Scholar]
  29. Martins, Z., Price, M. C., Goldman, N., Sephton, M. A., & Burchell, M. J. 2013, Nat. Geosci., 6, 1045 [NASA ADS] [CrossRef] [Google Scholar]
  30. Mauk, B. H., McEntire, R. W., Williams, D. J., et al. 1998, J. Geophys. Res., 103, 4715 [NASA ADS] [CrossRef] [Google Scholar]
  31. Monti, S., van Duin, A. C. T., Kim, S.-Y., & Barone, V. 2012, J. Phys. Chem. C, 116, 5141 [CrossRef] [Google Scholar]
  32. Monti, S., Carravetta, V., & Ågren, H. 2016, J. Phys. Chem. Lett., 7, 272 [CrossRef] [Google Scholar]
  33. Mrad, N. A., Vinogradoff, V., Duvernay, F., et al. 2015, Bull. Soc. Roy. Sci. Liége, 84, 21 [NASA ADS] [Google Scholar]
  34. Nuevo, M., Meierhenrich, U. J., d’Hendecourt, L., et al. 2007, Adv. Space Res., 39, 400 [NASA ADS] [CrossRef] [Google Scholar]
  35. Paranicas, C., Cooper, J. F., Garrett, H. B., Johnson, R. E., & Sturner, S. J. 2009, in Europa, eds. R. T. Pappalardo, W. B. McKinnon, & K. K. Khurana (Tucson: University of Arizona Press), 529 [Google Scholar]
  36. Pietrucci, F., & Saitta, A. M. 2015, Proc. Natl. Acad. Sci. USA, 112, 15030 [NASA ADS] [CrossRef] [Google Scholar]
  37. Plimpton, S. 1995, J. Comput. Phys., 117, 1 [Google Scholar]
  38. Radioti, A., Krupp, N., Woch, J., et al. 2005, J. Geophys. Res., 110, A07225 [NASA ADS] [CrossRef] [Google Scholar]
  39. Rothard, H., Domaracka, A., Boduch, P., et al. 2017, J. Phys. B: At. Mol. Opt. Phys., 50, 062001 [Google Scholar]
  40. Senftle, T. P., Hong, S., Islam, M. M., et al. 2016, npj Comput. Mat., 2, 15011 [CrossRef] [Google Scholar]
  41. Shematovich, V. I., & Johnson, R. E. 2001, Adv. Space Res., 27, 1881 [NASA ADS] [CrossRef] [Google Scholar]
  42. Sigmund, P. 2014, Penetration of Atomic and Molecular Ions. Particle Penetration and Radiation Effects, Volume II, Springer Series in Solid-State Sciences (Cham, Heidelberg, New York: Springer), 179 [Google Scholar]
  43. Sigmund, P., Bimbot, R., Geissel, H., Paul, H., & Schinner, A. 2005, J. ICRU, 5, 1, ICRU Report 73 [Google Scholar]
  44. Stoddard, S. D. 1978, J. Comput. Phys., 27, 291 [NASA ADS] [CrossRef] [Google Scholar]
  45. Streitwieser, A., Heathcock, C. H., Kosower, E. M., & Corfield, P. J. 1992, Introduction to Organic Chemistry (New York: Macmillan) [Google Scholar]
  46. van Duin, A. C. T., Dasgupta, S., Lorant, F., & Goddard III, W. A. 2001, J. Phys. Chem. A, 105, 9396 [CrossRef] [Google Scholar]
  47. Ziegler, J. F. 2000, SRIM: http://www.srim.org/ [Google Scholar]
  48. Ziegler, J. F., Biersack, J. P., & Littmark, U. 1985, The Stopping and Range of Ions in Solids (New York: Pergamon) [Google Scholar]
  49. Ziegler, J. F., Ziegler, M. D., & Biersack, J. P. 2010, Nucl. Instrum. Methods B, 268, 1818 [Google Scholar]

All Tables

Table 1

Molecular species in the surface of Europa assumed in our simulation and mainly based on Carlson et al. (2009).

In the text
Table A.1

Molecular species present in the simulation target after relaxation with numbers N ≥ 4.

In the text
Table B.1

Molecular species present in the simulation target at a time of 38.5 ps after sulfur track formation.

In the text

All Figures

thumbnail Fig. 1

Top: schematic simulation setup for studying the track of a sulfur ion at 20 MeV. Only a section of the track in the vicinity of the surface is simulated. The energy deposited by the swift ion is given to the atoms as local temperature increase (purple region). Insets show several of the most abundant ions and molecules originally present in the ice mixture – H2O, O2, Na, Cl, SO4, SO2 and H2 S – according to Table 1. Bottom: snapshot of the expanding track volume at a time of 0.5 ps after track formation. The width of the snapshot corresponds to 202 Å. The color represents the local temperature varying between cyan (101 K, corresponding to the surface temperature of Europa) and purple (>373 K).
In the text
thumbnail Fig. 2

Mass spectrum visualizing the original target composition before relaxation. The highest peaks belong to H2O, Na, SO4, and O2.
In the text
thumbnail Fig. 3

Temporal evolution of the change in the number of molecules, ΔN, during the relaxation process. Top: water and its dissociation products, as well as CH3OH and CH2O. Bottom: sulfur compounds.
In the text
thumbnail Fig. 4

Mass spectrum after relaxation (top) and difference mass spectrum (bottom) showing the number of molecules after relaxation relative to those initially present in the simulation volume. Positive values (blue) show species produced during the relaxation, negative values (red) show species destroyed during the relaxation.
In the text
thumbnail Fig. 5

Temporal evolution of the change in the number of molecules, ΔN, after track formation at time t = 0. Top: water and its dissociation products. Bottom: sulfur compounds.
In the text
thumbnail Fig. 6

Simulated mass spectrum of species found at the end of the simulation, 38.5 ps after track formation.
In the text
thumbnail Fig. 7

Difference mass spectrum showing the number of molecules at a time of 38.5 ps after track formation relative to those present in the relaxed simulation volume. Positive values (blue) show species produced in the track, negative values (red) show species destroyed in the track.
In the text
thumbnail Fig. 8

One of the most complex molecules produced in the track, C2H5SO6: an organosulfate with sulfur bridging two carbon groups.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.